第五章Chapter5-信赖域方法
Lingfeng NIU, FEDS
Chapter V
11/63
Outline of the Trust-Region Approach
Define the ratio ρk =
Lingfeng NIU, FEDS
Chapter V
7/63
Outline of the Trust-Region Approach
To obtain each step, we seek a solution of the subproblem 1 T minn mk (p) = fk + gk p + p T Bk p, p∈ 2 where ∆k > 0 is the trust-region radius. s.t. p ≤ ∆k , (3)
Lingfeng NIU, FEDS
Chapter V
9/63
Outline of the Trust-Region Approach
The size of the trust region is critical to the effectiveness of each step. If the region is too small, the algorithm misses an opportunity to take a substantial step that will move it much closer to the minimizer of the objective function. If too large, the minimizer of the model may be far from the minimizer of the objective function in the region, so we may have to reduce the size of the region and try again.
2
f (xk + tp)p,
(1)
where fk = f (xk ), gk = f (xk ) and t ∈ (0, 1).
Lingfeng NIU, FEDS
Chapter V
6/63
Outline of the Trust-Region Approach
In this chapter, we will assume that the model function mk that is used at each iteration xk is quadratic. Moreover mk is based on the Taylor-series expansion of f around xk , which is 1 T f (xk + p) = fk + gK p + p T 2
Lingfeng NIU, FEDS
Chapter V
10/63
Outline of the Trust-Region Approach
In practical algorithms, we choose the size of the region according to the performance of the algorithm during previous iterations. If the model is consistently reliable, producing good steps and accurately predicting the behavior of the objective function along these steps, the size of the trust region may be increased to allow longer, more ambitious, steps to be taken. A failed step is an indication that our model is an inadequate representation of the objective function over the current trust region. After such a step, we reduce the size of the region and try again.
6/63
Outline of the Trust-Region Approach
When Bk = 2 f (xk ), the approximation error in the model function mk is O( p 2 ), so this model is especially accurate when p is small. This choice Bk = 2 f (xk ) leads to the trust-region Newton method. In the other part, we emphasis the generality of the trust-region approach by assuming little about Bk except symmetry and uniform boundedness.
Lingfeng NIU, FEDS
Chapter V
1/63
Outline
Outline of the Trust-Region Approach Algorithms Based on the Cauchy Point Global Convergence Iterative Solution of the Subproblem Local Convergence of Trust-Region Newton Methods Other Enhancements Notes and References
Lingfeng NIU, FEDS
Chapter V
3/63
Outline of the Trustห้องสมุดไป่ตู้Region Approach
Line search methods and trust-region methods both generate steps with the help of a quadratic model of the objective function, but they use this model in different ways. Line search methods use it to generate a search direction, and then focus their efforts on fining a suitable step length α along this direction. Trust-region define a region around the current iterate within which they trust the model to be an adequate representation of the objective function, and then choose the step to be the approximate minimizer of the model in this region. In effect, they choose the direction and length of the step simultaneously. If a step is not acceptable, they reduce the size of the region and find a new minimizer. In general, the direction of the step changes whenever the size of the trust region is altered.
Lingfeng NIU, FEDS
Chapter V
8/63
Outline of the Trust-Region Approach
The classification of trust-region methods are decided by the choice of Bk and norm for trust region in the model (3). For example, If Bk = 0 in (3) and define the trust region using the Euclidean norm, the trust-region method identifies with the steepest descent line search approach; If Bk is chosen to be the exact Hessian 2 fk , the resulting approach is called the trust-region Newton method; If Bk is defined by means of a quasi-Newton approximation, we obtain a trust-region quasi-Newton method.
where Bk is some symmetric matrix. The difference between mk (p) and f (xk + p) is O( p 2 ), which is small when p is small.
Lingfeng NIU, FEDS
Chapter V
Chapter V: Trust-Region Methods
Lingfeng NIU
Research Center on Fictitious Economy & Data Science, Graduate University of Chinese Academy of Sciences niulf@
悬疑烧脑智力测试题(3篇)
第1篇【前言】在这场悬疑烧脑的智力测试中，你将踏入一个充满谜团的世界。
每个问题都隐藏着不为人知的秘密，需要你运用智慧、逻辑和洞察力来解开。
准备好了吗？让我们开始这场寻找真相的冒险之旅。
【第一幕：迷雾森林】1. 在一片迷雾森林中，有五个小屋，分别住着一位医生、一位律师、一位画家、一位作家和一位侦探。
你知道每个职业对应的小屋颜色吗？（提示：根据职业特点，推测颜色）2. 迷雾中，一位神秘人向你走来，他自称是迷雾森林的守护者。
他告诉你，每个小屋都有一把钥匙，能打开森林深处的宝箱。
你应该如何选择钥匙？（提示：考虑每个职业的特长）【第二幕：古堡之谜】3. 你来到了一座古老的城堡，城堡里住着一位富有且神秘的贵族。
他告诉你，城堡中有一幅画，藏着解开整个谜团的线索。
你该如何找到这幅画？（提示：观察城堡的布局和装饰）4. 在城堡的地下密室中，你发现了一本日记。
日记的主人是一位曾经被困在城堡中的女子。
她提到了五个神秘数字：3、7、11、13、17。
这些数字有什么含义？（提示：数字之间的关系）【第三幕：时间的陷阱】5. 你被卷入了一场关于时间的谜团。
一位科学家告诉你，他发明了一种可以倒流的时光机。
但你必须完成一个任务，才能使用它。
任务是什么？（提示：考虑时间的特性）6. 在时光机中，你回到了过去。
你发现自己身处一个古老的市集。
市集上有五个摊位，分别卖着不同的商品：珠宝、药材、书籍、武器和食物。
你应该如何选择？（提示：根据任务需求，判断商品的价值）【第四幕：记忆的碎片】7. 你发现了一个神秘的箱子，里面装满了记忆碎片。
每个碎片都记录了一个人的一生。
你需要通过这些碎片，找出一个共同点。
（提示：分析人物经历，寻找规律）8. 在分析过程中，你发现了一个关键信息：每个人的记忆碎片都缺失了一段，这段记忆被某种力量封印。
你该如何解开封印？（提示：考虑封印的特性）【第五幕：真相大白】9. 经过一系列的推理和探索，你终于找到了解开所有谜团的线索。
英雄传说 闪之轨迹攻略
英雄传说闪之轨迹攻略序章·前刚开始是以倒叙的形式，可控教官，想欣赏她S技的趁现在，因为下次加入要到第五章了。
同时可以先练习下本作的Link系统，简易上手。
A组的成员分别是男主角黎恩、劳拉、尤西斯、艾玛、盖乌斯。
参战队伍随机，可在战斗中L1键换人。
前进不久有一场练习战。
直接强制战斗三位一体攻击者R2*3，方阵兵J9*2。
不要忘记分析情报，之后走一小段路出了迷宫剧情，强制战斗玉簾*2。
战后在男主角狂喊中结束倒叙- -。
进入开章。
序章托尔茲军官学院3/31时间回到5个月前，男主角黎恩坐火车到达了托利斯塔小镇。
我们可以发现他和亚莉莎，艾略特，马奇亚斯馬奇亚斯，还有艾玛是坐同一班车来的。
在和亚莉莎展开狗血相遇剧情后，可以自由行动。
但是小镇上的店铺还未开放。
①可以在公园遇到睡觉的菲。
②在教堂遇到盖乌斯。
（注：这两人可遇可不遇）之后进入学院又看到女汉子和高富帅。
同班的同学相遇方式都全了。
结束开学典礼后，所有红色校服的学生被留下来，带到旧校舍。
莎拉开启了机关，众人倒地。
然后男亚莉莎又开始了的剧情剧情过后，全员分成了几路，分配给主角的是艾略特和盖乌斯。
第一张地图有两个宝箱，分別是：地水火风时空幻之耀晶石x50和岩石之刺（回路）所以多使用艾略特的恢复技能。
在第一张地图快结束的时候，马奇亚斯加入。
主线任务：配送导力器（AP4）报酬：无时限：4/18①到技术栋乔治领取任务，分别要去三个地点②到主校舍2楼的家庭料理室，在这里还能获得「料理手册」，之后可以开始做料理了，1楼戴眼镜的汤玛斯教官专门收集古怪料理，可以在以后做出后交给他。
而第一学生宿舍门口的女仆罗德是收集独门料理。
这时和她对话还能获得女仆罗德的人物信息「学习做菜」③到小镇的当铺《密休特》，以后可以在这里兑换不错的道具*2周目后可以在这里用U物质换塞姆利亚石的碎片④到小镇西南地图的广播台⑤完成后，回去乔治交任务。
BOSS：通缉魔兽：人面鸟属于飞行系的，亚莉莎攻击有特效。
第8讲信赖域方法
对于二次模型函数 ，定义其柯西点: 对于二次模型函数(2)，定义其柯西点 二次模型函数
s c = −τ k k ∆k gk , gk
其中, 其中
T 1, if g k Bk g k ≤ 0; gk 3 τk = min ∆ g T B g ,1 , or. k k k k
7
5．信赖域算法 ．信赖域算法 Step1. 给 出 初 始 点 x0 ， 信 赖 域 半 径 的 上 界 ∆ , ∆ 0 ∈ ( 0, ∆ ) , 0 ≤ ε ,
0 < η1 ≤ η 2 < 1, 0 < γ 1 ≤ 1 < γ 2 , k := 0 .
Step2. 如果 g k ≤ ε ,停止 停止. 停止 Step3. (近似 求解子问题 得到 sk . 近似)求解子问题 近似 求解子问题(2),得到 Step4. 计算 f ( xk + sk ) 和 rk .令 令
xk + sk , if rk ≥ η1 . xk +1 = or. xk ,
Step5.校正信赖域半径 令 校正信赖域半径.令 校正信赖域半径
∆ k +1 ∈ ∆ k , min {γ 2 ∆ k , ∆}
∆ k +1 ∈ ( 0, γ 1∆ k ] ∆ k +1 ∈ [γ 1∆ k , ∆ k ]
if rk < η1; if rk ∈ [η1 ,η2 ) ;
if rk ≥ η 2 .
8
5．信赖域算法 ．信赖域算法 Step6. 产生 Bk +1 ，校正 q( k ) ，令 k := k + 1, 转 Step 2. 很成功迭代: 很成功迭代 成功迭代: 成功迭代 不成功迭代: 不成功迭代 算法参数选择建议: 算法参数选择建议
（运筹学与控制论专业优秀论文）一类最优化问题的算法设计
知识水坝为您提供优质论文
承诺书
本人郑重声明：所呈交的学位论文，是本人在导师指导下，独立 进行研究工作所取得的成果。尽我所知，除文中已经注明引用的内容 外，本学位论文的研究成果不包含任何他人享有著作权的内容。对本 论文所涉及的研究工作做出贡献的其他个人和集体，均已在文中以明 确方式标明。
本人授权南京航空航天大学可以有权保留送交论文的复印件，允 许论文被查阅和借阅,可以将学位论文的全部或部分内容编入有关数 据库进行检索，可以采用影印、缩印或其他复制手段保存论文。
1.3 本文的主要内容
本文主要研究一类具有特殊形式的最优化问题，求解这一类最优化问题的全 局最优解，并应用到求解互补问题上。虽然目前已经有很多算法，但是我们考虑 到本最优化问题的约束条件是特殊的，因此可以利用约束条件的特殊性构造更为 简单有效的算法。
本文提出了一类新的函数，将它定义为半正定函数。利用这类函数将原问题； 分别转化为无约束最优化和含等式约束的最优化问，并分别设计了算法，进行了 数值实验，验证了算法的有效性。为了给出问题的全局最优解，我们又研究了算 法子问题的全局最优化算法，利用填充函数法来求解子问题。这样就保证了前面 设计的算法可以求得问题的全局最优解。最后，针对约束最优化问题（P），提出 了拟填充函数的概念，构造了一类拟填充函数并设计了算法。具体内容如下：
In this article we propose a new type of function, which is called a semi-positive function. We use this function to make another function, then we can turn the original problem into another one. We give algorithms and numerical results. Then we investigate the sub-problem. Also we propose the definition of quasi-filled function. We propose a quasi-filled function and design algorithm. It mainly contains the following six chapters:
信赖域方法
由于最优曲线的确定需要计算矩阵 的所有 特征值和特征向量，相当费时．
折线法在于用低维空间内满足一定要求的 折线，记为 代替最优曲线．通过求解：
信赖域半径的选择
根据模型函数 对目标函数 来调整信赖域半径
的拟合程度
对于问题(1)的解 定义比值：
它衡量模型函数 程度．
与目标函数 的一致性
注：(1) 越接近于１，表明模型函数与目标
函数的一致性程度越好，可以增大 以扩大 信赖域．
(2)
不接近于１，可以保持 不变．
(3) 接近于零或取负值，表明模型函数与目标
例1：设
在当前点
试用双折线法求
解：
由于
计算 有：
由于
使得 得 所以
故取双折线步长为：
解二次方程 因此
基本思想
牛顿法的基本思想是在迭代点 附近用二次
函数逼近
并以 的
的极小点 修正 得到：
以上方法只能保证算法的局部收敛性，为了建
立总体收敛性算法，我们采用了线搜索技术．虽然
这种策略是成功的，但它有一个缺点，即没有进一
步利用二次模型．
基本思想
牛顿法的基本思想是在迭代点 附近用二次
函数逼近
并以 的
的极小点 修正 得到：
信赖域子问题折线法基本思想如果令信赖域的半径在区间内连续变化则问题1的解在空间中形成一条光滑的连续曲线记为此时问题1等价于在信赖域内在最优曲线上确定一点使二次函数取极小即
信赖域方法
信赖域方法是求解最优化问题的另一类有效 方法．其最初的设计思想可追溯至Levenberg Marq和uart对Gauss－Newton法的修 正．线搜索方法是把一个复杂的最优化问题转化 成一系列简单的一维寻优问题．信赖域方法是把 最优化问题转化为一系列相对简单的局部寻优 问题．
最优化方法信赖域方法
最优化方法信赖域方法Trusted Domain Method of Optimization Methods一、概述信赖域（Trusted Domain）法是一种针对多目标最优化问题的优化方法，属于启发式优化技术，又被称为受信域法（Credible Domain）法或者受信域增强法（Credible Domain Enhancement）。
它由A.K.Chentsov在1980年提出，目前已经在工业优化、控制优化、混合模糊优化等领域有广泛的应用。
信赖域法使多目标最优化问题中的搜索变得更加有效和快捷，可以很好地处理多目标最优化问题中的非凸性和高维问题，使最优解更容易被获取。
二、原理信赖域方法优化的原理是：在解空间中划分子空间，在每个子空间中进行最优优化，同时进行领域大小的优化，以找到最优解。
（1）划分的子空间划分的子空间由一组不可分割的解空间，即称为“信赖域（Trusted Domain）”确定，有一种收敛性的在同一信赖域上的解空间集合，该信赖域中必须包含一个或多个最优解点。
（2）之分的子空间有效性在信赖域中，有一种收敛性的解空间，该解空间必须包含一个或多个最优解点，且此处解的收敛性可以满足要求。
由此可以看出，划分的子空间有效的充分利用解空间，能够使对最优解的搜索效率更高，更快地找到最优解。
（3）领域大小的优化在划分解空间时，信赖域方法重点考虑领域大小的优化，以缩小搜索空间大小，并引导搜索过程朝最优解的方向发展。
三、应用1.工业优化信赖域方法已经在工业优化领域得到应用，使多目标工业优化问题中的搜索更加有效和快捷，可以很好地处理多目标最优化问题中的非凸性和高维问题，使最优解更容易被获取。
2.控制优化由于信赖域方法能够有效地处理多目标非凸性和高维问题，因此已经在控制优化中得到应用，用于设计准确性好的控制系统。
3.混合模糊优化信赖域方法在混合模糊优化领域也有应用，可以用来解决特殊类型的模糊控制优化问题，来有效地提高优化中的效率和准确性。
《火焰纹章if》一周目困难难度规程攻略攻略_全通
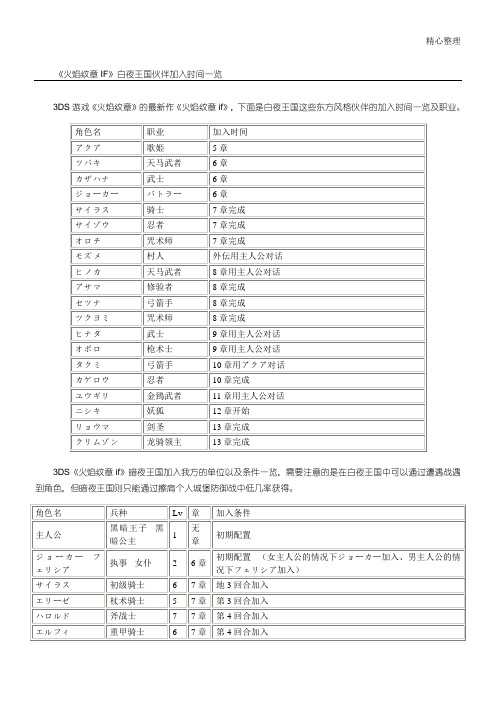
15
14章
主人公与フランネル对话
ギュンター
高级骑士
10
15章
初期配置
フェリシア
ジョーカー
女仆
执事
13
16章
出击准备时加入
（男主人公的情况下ジョーカー加入、女主人公的情况下フェリシア加入）
マークス
圣骑士
4
16章
初期配置
アシュラ
冒险者
2
16章
完成本章后选「いいえ」。
若选择「はい」则不会加入，取而代之获得移动+1的鞋子
在自宅中可以实现搞基和百合，增长人物的好感度开启支援对话。地图上按L键可以进入第一人称视角观看风景，但不能移动非常遗憾。斗技场战斗是
关于龙脉值的获取，这里暗夜的同学可能要悲剧了，因为白夜可以通过遭遇战获得龙脉，而且花钱可以开启遭遇战。当然也可以通信后通过拜访伙伴的城获得一点。前期基本建造一个房屋都是消耗一点龙脉，要升级建造可能就要花费三点以上。
サイラス
初级骑士
6
7章
地3回合加入
エリーゼ
杖术骑士
5
7章
第3回合加入
ハロルド
斧战士
7
7章
第4回合加入
エルフィ
重甲骑士
6
7章
第4回合加入
モズメ
村人
1
外伝
外传モズメ 主人公与モズメ对话
オーディン
暗黑法师
5
8章
第2回合加入
ゼロ
盗贼
8
8章
第2回合加入
アクア
歌姫
1
9章
初期配置
ニュクス
暗黑法师
9
9章
主人公与ニュクス对话
阿玛迪斯战记最详细攻略
阿玛迪斯战记最详细攻略文章列表:一、关于隐藏关的进入方法。
二、《阿玛迪斯战记》角色点评三、战棋版英雄无敌——《阿玛迪斯战记》流程攻略, 女主角全篇四、《阿玛迪斯战记》全道具功能一览五、魔兽转职表；完美结局；龙(Dragron)的礼物；碧绿原石、漆黑原石、纯白原石这三块石头取得法。
六、LOB中获得物品的简单功略七、无限复制道具大法八、补充关于“龙的礼物”九、阿玛迪斯战记基本资料十、各属性相关内容资料一关于隐藏关:1、网上盛传的隐藏关达成条件（但实践证明是不行的）一、触发黑暗圣书事件1.在第十八章雷雨中时以最快的速度消灭第一波，及第二波魔兽，此时留一些人在NPC 的附近，但不能站在桥上，等到一定回合，会出现八只鸟身女魔，这些留在桥上附近的人必需把那八只解决，等到消灭所有魔兽后，桥上的NPC会告诉主角们，城里有一个疯术士。
2。
进入城后和术士对话，术士会跟欧森巴哈相认,并传达「黑暗圣书」事件.二、解救皇帝事件1。
在接近皇帝前，将部队分成二队，一队走左边,一队走右边，走右边的人将皇帝打到低于2000时,基尔巴特便会出会，此时右边的队伍最好限制皇帝的行动.2。
走左边的人把基尔巴特消灭后，皇帝便会清醒,众人便将黑暗圣书的事件告知。
三、放走圣骑士事件1。
过关时选择放走圣骑士四、打倒法王事件1。
当基尔巴特攻击我方人员时,我方只能忍耐，此时可派欧兰朵以特技降低基尔巴特的魔攻，这样他施放魔法时,我方人员只会损伤600而已，但千万不能打死他，因为一打死他，法王便会开始行动.2.消灭地毯上的魔兽后，我方一人走上台阶,此时圣骑士会赶过救驾，此时派会使用限制行动的我方人员，把圣骑士冰冻。
3。
这时我们怎么打法王，他都不会反击,也不会行动,我方尽情砍杀法王，等打死后，圣骑士会冲过来抵挡最一击。
4.圣骑士说：「法王…。
我就知道您会清醒的……」,这时法王十分的悲恸,和主角谈起黑暗圣书的事，原来不是基尔巴特搞的鬼，而是枢机主教的阴谋，此时背景音乐开始紧张，原来黑暗圣书放在后山,大家要一鼓作气攻打后山。
关于楔形信赖域半径更新的两种方法
Ｃ ｍ ｕ ｒ ｎｉ ｅｉ ｄ ｐ ｌａｏｓ ｏｐ ｔ ｇ ｅｒ ｇ ｎ Ａ ｐｉ ｔ ｎ计算机 工程 与应凤霞， 周庆华， 张亚蕊， 耿 燕
Ｘ Ｆ ｎ ｘａ Ｚ Ｕ ｅ ｇ ｉ， ＨＯＵ Ｑｉｇ ｕ ， ＨＡ ａｕ ， Ｅ ａ ｎ ｈ ａＺ ＮＧ Ｙ ｒｉＧ ＮＧ Ｙ ｎ
ｓｄ ｓ ｔｅ ｒｄｕ ｐ ａｅ ｒ ｌｓ ｈ ｖ ｔｏ ｇ ｉｆ ｅ ｃ ｎ ｔｅ ｐ ｒｏｍａ ｃ ｆａ ｌｏ ｔｍ ． ｉ ａ ｅ ，ａ ｅ ｔ ｅ ｄｓｄ ａ － ｉｅ ， ａ ｉｓ ｕ ｄ ｔ ｕｅ ａ ｅ ａ ｓ ｎ ｎ ｕ ｎ ｅ ｏ ｅｆｒ ｎ ｅ ｏ ａｇ ｒ ｈ Ｉ ｔ ｓ ｐ ｐ ｒｆｃ ｄ ｗｉ ｔ ｉａ ｖ ｎ ｈ ｒ ｌ ｈ ｎ ｉ ｎ ｈ ｈ ｈ
ＸＵ Ｆ ｎ ｘａ Ｚ ｅ ｇ ｉ， ＨＯＵ Ｑｉｇ ｕ ， ＨＡＮＧ Ｙ ｒ ｉｅ １ ｗ ｔｏ ｓ Ｏ ｄ ｅ ｔｕ ｔｒｇｏ ａ ｉｓ ｕ ｄ ｔ． ｏ ｕｅ ｎ ｉ ｎｈ ａ Ｚ ａ ｕ， ｔａ． ｏ ｍｅｈ ｄ Ｎ ｗｅ ｇ ｒ ｓ ｅｉｎ ｒｄｕ ｐ ａｅＣ ｍｐ ｔｒ Ｅ ｇ－ Ｔ ｎ ｅｉｇ ａ ｄ Ａｐ ｌ ａ ｏ ｓ２ １ ，７ ３ ）３ －８ ｅｒｎ ｎ ｐｉ ｔ ｎ ，０ １ ４ （０ ：５３ ． ｃｉ
河北大学 数学与计算机学 院 ， 河北 保定 ０ １０ ７０２
解等式约束规划的信赖域SQP滤子方法
严格局 部解 时 ， 全牛 顿步 可能会 使 目标 函数值 和 约束 违 反度 上 升 ， 而不 被 滤子 接 受 ， 是破 坏 了算 法 的 完 从 于
收敛性 ． 文对 文献 ［ ３中的信 赖域 Ｓ 本 ３ ＱＰ滤子 方 法进 行 了修 改 ： 果 完全 步不 被接 受 ， 以通 过 一个 二 阶 校 如 可
能 是 一 个 超 线 性 收敛 步 ， 是 当 迭 代 点 充 分 靠 近 原 问题 的严 格 局 部 解 时 。 全 牛 顿 步可 能会 使 目标 函 数 值 和 约 束 但 完 违 反 度 上升 。 而 不 被 算 法 接 受 ， 是破 坏 了 算法 的 收 敛 性 ． 出 一 种 修 改 后 的 信 赖 域 Ｓ Ｐ滤 子 算 法 ， 完 全 步 从 于 给 Ｑ 当 不 被 接 受 时 ． 算 法 进 行 二 阶校 正 （ＯＣ ， 以 减 小 其 不 可 行 性 ． 改 后 的 算 法 可 以 避 免 Ｍａａｏ 效 应 。 算 法 达 对 Ｓ ）可 修 ｒｔｓ 使
到局部超线 性收敛． ‘
关 键 词 ： ＱＰ方 法 ； 赖 域 ；滤 子 ； 阶 校 正 ；Ｍａａ ｓ 应 ；局 部 收 敛 Ｓ 信 二 ｒｔ 效 ｏ
中 图 分 类 号 ： ） ２ ． （ ２ １２ 文 献标 识 码 ： Ａ 文 章 编 号 ：１ ０ － ７ ５ ２ Ｏ ） １ ｏ Ｏ 一 ５ ０ １ ８ ３ （ｏ ８ Ｏ 一 Ｏ １ Ｏ
基 金 项 目 ：国 家 自然 科 学 基 金 资助 项 目 （０ ７ １ ７ １５１３）
作 者 简介 ：王 华 （９ ９ ） 女 ， 东省 菏 泽 市 人 ， 济 大 学 博 士 研 究 生 ． １７ 一 ， 山 同 主要 从 事 非 线 性 规 划 研 究
维普资讯