MATLAB程序(线性拟合)
matlab各类拟合曲线代码

标题:探索MATLAB中各类拟合曲线的代码应用在MATLAB中,拟合曲线是数据分析和模型建立中常用的技术之一。
通过拟合曲线,我们可以了解数据之间的关联性并建立预测模型,为进一步分析和应用数据奠定基础。
本文将深入探讨MATLAB中各类拟合曲线的代码应用,帮助读者更深入地理解该主题。
一、线性拟合曲线1. 使用MATLAB进行线性拟合曲线的代码示例在MATLAB中,使用polyfit函数可以进行线性拟合。
对一组数据点(x, y)进行线性拟合,代码如下:```matlabx = [1, 2, 3, 4, 5];y = [2, 3.5, 5, 7, 8.5];p = polyfit(x, y, 1);```其中,x为自变量,y为因变量,1表示进行一次线性拟合。
通过polyfit函数,可以得到线性拟合的系数p。
2. 线性拟合曲线的应用和特点线性拟合曲线适用于线性关系较为明显的数据,例如物理实验数据中的直线关系。
通过线性拟合,可以获得各项系数,对数据进行预测和建模。
二、多项式拟合曲线1. 使用MATLAB进行多项式拟合曲线的代码示例在MATLAB中,使用polyfit函数同样可以进行多项式拟合。
对一组数据点(x, y)进行二次多项式拟合,代码如下:```matlabx = [1, 2, 3, 4, 5];y = [1, 4, 9, 16, 25];p = polyfit(x, y, 2);```其中,x为自变量,y为因变量,2表示进行二次多项式拟合。
通过polyfit函数,同样可以得到多项式拟合的系数p。
2. 多项式拟合曲线的应用和特点多项式拟合曲线适用于数据中存在曲线关系的情况,通过选择合适的最高次数,可以灵活地拟合各种曲线形状。
三、非线性拟合曲线1. 使用MATLAB进行非线性拟合曲线的代码示例在MATLAB中,使用fit函数可以进行非线性拟合。
对一组数据点(x, y)进行指数函数拟合,代码如下:```matlabx = [1, 2, 3, 4, 5];y = [2.1, 7.4, 16.1, 29.3, 48.2];f = fit(x', y', 'exp1');```其中,x为自变量,y为因变量,'exp1'表示进行指数函数拟合。
matlab回归拟合

在MATLAB中进行回归拟合的方法有很多种,包括线性回归、多项式回归和非线性回归。
1. 线性回归拟合:使用“polyfit”函数进行线性回归拟合。
例如,如果你有一组x和y数据,可以使用以下代码进行线性回归拟合:```matlabx = [1, 2, 3, 4, 5];y = [2, 4, 5, 4, 5];p = polyfit(x, y, 1);```这将返回一个多项式系数数组p,其中p(1)是斜率,p(0)是截距。
2. 多项式回归拟合:使用“polyfit”函数进行多项式回归拟合。
你需要指定多项式的阶数。
例如,如果你想进行二次多项式回归,可以使用以下代码:```matlabx = [1, 2, 3, 4, 5];y = [2, 4, 5, 4, 5];p = polyfit(x, y, 2);```这将返回一个二次多项式系数数组p。
3. 非线性回归拟合:非线性回归可以通过非线性函数来拟合数据,可以更好地适应复杂的数据模式。
在MATLAB中,可以使用“lsqcurvefit”函数来进行非线性回归拟合,需要指定拟合函数和初始参数。
例如,如果你有一个非线性函数形式,可以定义一个函数句柄,然后使用“lsqcurvefit”进行拟合:```matlab定义非线性函数句柄f = @(b,x) b(1)*exp(b(2)*x(:,1)) + b(3)*sin(b(4)*x(:,2));定义初始参数b0 = [1,1,1,1];进行非线性回归拟合xdata = [1:10];ydata = [2*exp(1)+sin(1:10)]; 生成一些模拟数据b = lsqcurvefit(f, b0, xdata', ydata');```这将返回拟合参数b,你可以使用这些参数来预测新的数据点。
MATLAB函数拟合指令MATLAB拟合函数使用说明

MATLAB函数拟合指令MATLAB拟合函数使用说明一维数据拟合:在MATLAB中,可以使用polyfit和fit函数进行一维数据的拟合。
1. polyfit函数:polyfit函数用于将数据集拟合到一个多项式模型。
语法如下:```[p, S] = polyfit(x, y, n)```其中,x和y表示数据集的x轴和y轴值,n是一个整数,表示拟合的多项式阶数。
p是一个包含多项式系数的向量,S是一个结构体,包含了拟合误差和其他信息。
2. fit函数:fit函数用于将数据集拟合到自定义的非线性函数模型。
语法如下:```f = fit(x, y, model)```其中,x和y表示数据集的x轴和y轴值,model表示自定义的非线性函数模型。
可以使用fittype函数创建一个函数模型对象,例如:```model = fittype('a * exp(b * x)');```然后,将这个函数模型传递给fit函数即可。
多维数据拟合:在MATLAB中,可以使用fit函数进行多维数据的拟合。
1. fit函数:fit函数也可以用于多维数据的拟合,只需将数据集转换为table格式。
语法如下:```f = fit(x, y, model)```其中,x和y表示多维数据集的自变量和因变量,model表示自定义的非线性函数模型。
自定义函数模型的建立:除了使用内置的多项式模型和其他简单模型,也可以自定义非线性函数模型。
需要定义一个函数句柄,例如:``````然后,将这个函数句柄传递给fittype函数,创建一个函数模型对象,例如:```model = fittype(func);```最后将这个函数模型对象传递给fit函数。
拟合结果的可视化:拟合结果可以通过绘制原始数据和拟合函数来进行可视化。
可以使用plot函数绘制原始数据点,使用plot函数、plotfit函数或者ezplot函数绘制拟合函数曲线。
总结:MATLAB提供了多种函数拟合方法,可以用于一维和多维数据拟合。
Matlab中的曲线拟合方法

Matlab中的曲线拟合方法引言在科学与工程领域,数据拟合是一个重要的技术,可用于分析实验数据、预测未知的对应关系,并量化观察到的现象。
其中,曲线拟合是一种常见的数据拟合方法,而Matlab作为一种功能强大的科学计算软件,提供了多种曲线拟合工具和函数,方便用户进行数据分析和模型建立。
本文将对Matlab中的曲线拟合方法进行详细介绍和讨论。
一、线性拟合线性拟合是最简单且常见的曲线拟合方法,其基本思想是通过一条直线拟合数据点,找到最佳拟合直线的参数。
在Matlab中,可以使用polyfit函数实现线性拟合。
该函数接受两个输入参数,第一个参数为数据点的x坐标,第二个参数为数据点的y坐标。
返回结果为一个一次多项式拟合模型的参数。
例如,我们有一组实验测量数据如下:x = [1, 2, 3, 4, 5];y = [3, 5, 7, 9, 11];通过polyfit函数进行线性拟合:coeff = polyfit(x, y, 1);其中,1表示要拟合的多项式的次数,这里我们选择了一次多项式(直线)。
coeff即为拟合得到的直线的参数,可以通过polyval函数将参数代入直线方程,得到对应x的y值。
y_fit = polyval(coeff, x);接下来,我们可以使用plot函数将原始数据点和拟合曲线都绘制在同一张图上:figure;plot(x, y, 'o', 'MarkerSize', 10); % 绘制原始数据点hold on;plot(x, y_fit); % 绘制拟合曲线xlabel('x');ylabel('y');legend('原始数据点', '拟合曲线');通过观察图像,我们可以初步判断拟合的效果如何。
如果数据点较为分散,直线拟合效果可能较差。
在此情况下,可以考虑使用更高次的多项式进行拟合。
二、多项式拟合多项式拟合是一种常见的曲线拟合方法,其基本思想是通过一个一定次数的多项式函数来拟合数据点。
matlab数值分析处理线性拟合
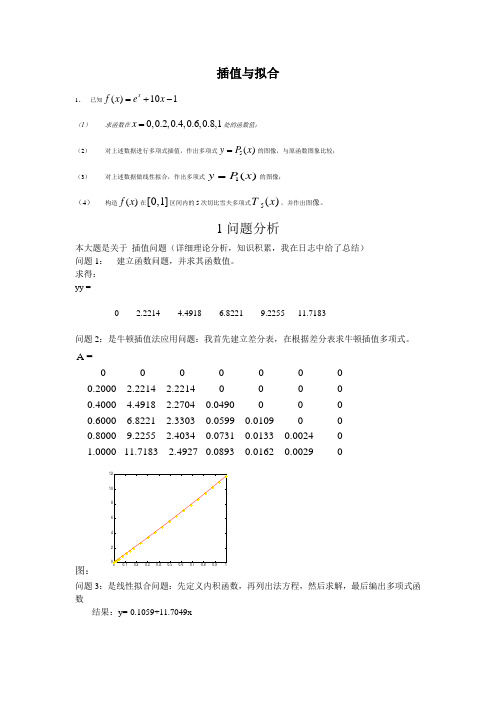
插值与拟合1、 已知()101x f x e x =+-(1) 求函数在0,0.2,0.4,0.6,0.8,1x =处的函数值;(2) 对上述数据进行多项式插值,作出多项式5()y P x =的图像,与原函数图象比较;(3) 对上述数据做线性拟合,作出多项式1()y P x =的图像;(4) 构造()f x 在[0,1]区间内的5次切比雪夫多项式5()T x ,并作出图像。
1问题分析本大题是关于 插值问题(详细理论分析,知识积累,我在日志中给了总结) 问题1: 建立函数问题,并求其函数值。
求得:yy =0 2.2214 4.4918 6.8221 9.2255 11.7183问题2:是牛顿插值法应用问题:我首先建立差分表,在根据差分表求牛顿插值多项式。
A =0 0 0 0 0 0 00.2000 2.2214 2.2214 0 0 0 00.4000 4.4918 2.2704 0.0490 0 0 0 0.6000 6.8221 2.3303 0.0599 0.0109 0 00.8000 9.2255 2.4034 0.0731 0.0133 0.0024 01.0000 11.71832.4927 0.0893 0.0162 0.0029 0图:问题3:是线性拟合问题:先定义内积函数,再列出法方程,然后求解,最后编出多项式函数结果:y=-0.1059+11.7049x问题4:是切比雪夫插值问题:先生成切比雪夫点,再列出差分表,再插值t =0.98,0.85,0.63,0.37,0.15,0.017差分表A =0.9800 11.4645 0 0 0 0 00.8500 9.8396 -1.6248 0 0 0 00.6300 7.1776 -2.6620 -1.0372 0 0 00.3700 4.1477 -3.0299 -0.3678 0.6694 0 00.1500 1.6618 -2.4859 0.5440 0.9118 0.2424 00.0170 0.1871 -1.4747 1.0112 0.4672 -0.4446 0图2问题解答:(1)建立函数:function y=funzhu(x)y=exp(x)+10*x-1;endxx=0:0.2:1;yy=zeros(1,6);for i=1:length(xx)yy(i)=funzhu(xx(i));结果:yy =0 2.2214 4.4918 6.8221 9.2255 11.7183(2) 对上述数据进行多项式插值,作出多项式5()y P x的图像,与原函数图象比较;1.阶数为7的均差的程序:global An=length(xx);n=6;A=zeros(n,n+1);A(:,1)=xx';A(:,2)=yy';for j=3:n+1for i=j-1:nA(i,j)=(A(i,j-1)-A(i-1,j-1))/(A(i,1)-A(i-(j-2),1));endendA差分表结果:A =A =0 0 0 0 0 0 00.2000 2.2214 2.2214 0 0 0 00.4000 4.4918 2.2704 0.0490 0 0 00.6000 6.8221 2.3303 0.0599 0.0109 0 00.8000 9.2255 2.4034 0.0731 0.0133 0.0024 01.0000 11.71832.4927 0.0893 0.0162 0.0029 02.建立多项式P5函数:function y=Pn(x)global A[m,n]=size(A);y=0;for i=1:madd=A(i,i+1);if i>1for j=1:i-1add=add*(x-A(j,1));endendy=y+add;画图:x=0:0.05:1;fplot(@funzhu,[0,1],'y*') hold onfplot(@Pn,[0,1],'r')(3)对上述数据做线性拟合,作出多项式1()y P x的图像;g0=0;g1=0;g2=0;G1=0;G2=0;for i=1:length(xx)g0=1+g0;g1=g1+xx(i);g2=g2+xx(i)^2;G1=G1+yy(i);G2=G2+yy(i)*xx(i);endA=[g0,g1;g1,g2];G=[G1;G2];d=A\G结果:d =-0.105911.7049所以:y=-0.1059+11.7049x画图:x=0:0.2:1;fplot(@funzhu,[0,1],'y*')hold onfplot(@Pn,[0,1],'r')hold ony=-0.1059+11.7049*x;plot(x,y,'b+')(4)构造()f x 在[0,1]区间内的5次切比雪夫多项式5()T x ,并作出图像。
如何在Matlab中进行数据拟合

如何在Matlab中进行数据拟合数据拟合是数据分析和建模中的一个重要环节,它可以帮助我们找到一个数学函数或模型来描述一组观测数据的变化规律。
在Matlab中,有多种方法和工具可以用来进行数据拟合,本文将介绍其中几种常用的方法和技巧。
一、线性回归线性回归是最简单和常见的数据拟合方法之一。
在Matlab中,我们可以使用polyfit函数来实现线性回归。
该函数基于最小二乘法,可以拟合一个给定度数的多项式曲线到一组数据点上。
假设我们有一组观测数据的x和y坐标,我们可以使用polyfit函数拟合一个一次多项式来获得最佳拟合曲线的系数。
代码示例如下:```x = [1, 2, 3, 4, 5];y = [1, 3, 5, 7, 9];p = polyfit(x, y, 1); % 一次多项式拟合```拟合得到的系数p是一个向量,其中p(1)表示一次项的系数,p(2)表示常数项的系数。
通过这些系数,我们可以得到一次多项式的表达式。
用polyval函数可以方便地计算在指定x值处的拟合曲线上的y值。
代码示例如下:```x = [1, 2, 3, 4, 5];y = [1, 3, 5, 7, 9];p = polyfit(x, y, 1);x_new = 6;y_new = polyval(p, x_new); % 在x_new处的预测值```二、非线性回归除了线性回归,我们还经常遇到需要拟合非线性数据的情况。
Matlab提供了curve fitting toolbox(曲线拟合工具箱),其中包含了很多用于非线性数据拟合的函数和工具。
在使用曲线拟合工具箱之前,我们需要先将需要拟合的非线性函数进行参数化。
常见的方法包括使用指数函数、对数函数、正弦函数等对原始函数进行转换,之后再进行拟合。
例如,我们有一组非线性数据,并怀疑其与指数函数有关。
我们可以通过以下代码进行拟合:```x = [1, 2, 3, 4, 5];y = [2.1, 3.9, 6.2, 8.1, 12];fun = @(p, x) p(1)*exp(p(2)*x) + p(3); % 指数函数p0 = [1, 0.5, 0]; % 初始值p = lsqcurvefit(fun, p0, x, y); % 非线性拟合```其中,fun是一个匿名函数,表示我们拟合的非线性函数形式,p是待求解的参数向量。
matlab拟合动力学参数

matlab拟合动力学参数
在Matlab 中,可以使用曲线拟合工具来拟合动力学参数。
以下是一些基本步骤:
1. 准备数据:将实验数据整理成数组形式,其中每一行代表一个时间点的数据,每一列代表一个参数的值。
2. 选择拟合函数:根据实验数据的特点,选择合适的拟合函数。
例如,如果数据呈现线性趋势,可以使用线性拟合函数;如果数据呈现指数增长或衰减趋势,可以使用指数拟合函数。
3. 调用拟合函数:在Matlab 中,可以使用`polyfit`函数进行线性拟合,使用`fit`函数进行非线性拟合。
调用拟合函数时,需要指定拟合函数的类型和参数。
4. 评估拟合结果:可以使用拟合函数的输出参数来评估拟合结果的质量。
例如,可以计算残差的平方和(SSE)或均方根误差(RMSE)等指标。
5. 可视化拟合结果:可以使用`plot`函数将实验数据和拟合曲线绘制在同一张图上,以便直观地比较拟合结果和实验数据的差异。
需要注意的是,拟合结果的准确性取决于实验数据的质量和拟合函数的选择。
在进行拟合之前,需要对实验数据进行预处理和筛选,以确保数据的可靠性和准确性。
同时,需要根据实际情况选择合适的拟合函数,并对拟合结果进行合理的解释和分析。
matlab的拟合函数

matlab的拟合函数拟合函数是MATLAB中非常常用的功能,它可以通过给定的一组数据点,找到最符合这些数据点的曲线或函数。
拟合函数在科学研究、工程应用和数据分析等领域都有广泛的应用。
在MATLAB中,拟合函数的使用非常简单。
首先,我们需要准备一组数据点,这些数据点可以是实验测量得到的,也可以是通过其他手段获得的数据。
然后,我们选择合适的拟合函数模型,并使用MATLAB提供的拟合函数进行拟合计算。
常用的拟合函数模型有多种,包括线性模型、多项式模型、指数模型、对数模型、幂函数模型等。
不同的模型适用于不同类型的数据。
在选择拟合函数模型时,我们需要根据数据的特点和需求进行选择。
以线性拟合为例,假设我们有一组数据点,表示了某种物理量在不同时间点的取值。
我们希望找到一个线性函数,最好地拟合这些数据点。
在MATLAB中,可以使用polyfit函数进行线性拟合。
我们需要将数据点存储在一个矩阵中,其中第一列是时间点,第二列是物理量的取值。
然后,使用polyfit函数进行线性拟合,拟合函数的形式为y = ax + b,其中a和b是待求的参数。
```matlabdata = [1, 2; 2, 3; 3, 4; 4, 5; 5, 6]; % 假设我们有一组数据点x = data(:, 1); % 提取时间点y = data(:, 2); % 提取物理量的取值p = polyfit(x, y, 1); % 进行线性拟合a = p(1); % 拟合得到的参数ab = p(2); % 拟合得到的参数b```通过以上代码,我们可以得到线性拟合函数的参数a和b的值。
然后,我们可以使用这些参数来计算拟合曲线在任意时间点的取值。
```matlabx_fit = 1:0.1:5; % 定义拟合曲线的时间点y_fit = a * x_fit + b; % 计算拟合曲线的取值```通过以上代码,我们可以得到拟合曲线在时间点x_fit处的取值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、一元线性拟合
求HNO 3的正常沸点温度T b 及摩尔汽化热。
程序如下:
>> t=[0 20 40 50 70 80 90 100]; >> t=t+273.15;
>> p=[1919.52 6385.07 17728.9 27726.4 62251.1 89311 124902.1 170890.6] p =
1.0e+005 *
0.0192 0.0639 0.1773 0.2773 0.6225 0.8931 1.2490 1.7089 >> subplot 121 >> plot(t,p,'o',t,p) >> t1=1./t;p2=log(p); >> pp=polyfit(t1,p2,1) pp =
1.0e+003 *
-4.5691 0.0243 >> subplot 122
>> plot(t1,p2,'o',t1,p2)
>> gtext('p/pa'),gtext('T/K'),GTEXT('lnP/Pa'),gtext('T^-^1/K')
由克拉贝龙-克劳修斯方程式,~
ln v
H P C RT
∆=-+ 作1
ln ~P T
-得一直线:3
1
ln 4.5691024.30P T -=-⨯+
斜率为:~
3
4.56910v
H R
∆-⨯=-
所以摩尔汽化热为:~
314.569108.31437.99()v H kJ mol -∆=⨯⨯=⋅ 并根据拟合方程,求得一大气压时 1
32.8010T
--=⨯
则正常沸点为:357b T K =
2、多元线性拟合:
某气体混合物由四种气体组成,在常压或低压下其粘度η与各组分摩尔分数x 1,x 2,x 3,x 4之间有如下线性关系:011223344b b x b x b x b x η=++++
试根据下表所列实验数据用最小二乘法确定上式中的各个系数,并计算其复相关系数。
Matlab 程序如下:
>> a=[1.0 0.402 0.153 0.058 0.387;1.0 0.503 0.301 0.183 0.013; 1.0 0.306 0.109 0.224 0.361; 1.0 0.296 0.365 0.009 0.330; 1.0 0.309 0.405 0.109 0.177; 1.0 0.055 0.153 0.506 0.289] a =
1.0000 0.4020 0.1530 0.0580 0.3870 1.0000 0.5030 0.3010 0.1830 0.0130 1.0000 0.3060 0.1090 0.2240 0.3610 1.0000 0.2960 0.3650 0.0090 0.3300 1.0000 0.3090 0.4050 0.1090 0.1770 1.0000 0.0550 0.1530 0.5060 0.2890
>> y=[0.00625 0.00826 0.01182 0.01944 0.02372 0.03243]' y =
0.0063 0.0083 0.0118 0.0194 0.0237 0.0324
>> b=a.'*a
b =
6.0000 1.8710 1.4860 1.0890 1.5570
1.8710 0.6944 0.4879 0.2481 0.4408
1.4860 0.4879 0.4466 0.2132 0.3388
1.0890 0.2481 0.2132 0.3550 0.2742
1.5570 0.4408 0.3388 0.2742 0.5040 >> c=a.'*y
c =
0.1019
0.0252
0.0264
0.0237
0.0268
>> coeff=b\c
coeff =
0.2267
-0.2627
-0.1620
-0.1889
-0.2058
>> regress(c,b,0.05)
ans =
0.2267
-0.2627
-0.1620
-0.1889
-0.2058。
