2014通信原理第10章解析
通信原理第10章 同步原理

第10章 同 步 原 理
10.1 同步的概念及分类 10.2 载波同步 10.3 码元同步 10.4 群同步 10.5* 网同步
返回主目录
10.1 同步的概念及分类
主要内容
★ 同步的概念 ★ 同步的分类 ★ 同步的意义
第10章 同 步 原 理
一、同步的概念
所谓同步是指收发双方在时间上步调一致,故又称定时。 同步是数字通信系统以及某些采用相干解调的模拟通信系 统中一个重要的实际问题。由于收、发双方不在一地,要使它 们能步调一致地协调工作,必须要有同步系统来保证。
t4
第二帧
(a )
图中接,收t信2~号t3就带是通插入导频的时间,它一般插解入调 在群同步脉冲
之后。这种插入的结果线只性 门是在每帧的一小段时间内才出现载波
标准,在接收门端控应信 号用控制信号将载波标准取出。
锁相环
鉴相器
环路 滤波器
压控 振荡器
第10章 同 步 原 理
从理论上讲可以用窄带滤波器直接取出这个载波,但实际
输 入 已 调平 方 律 信 号 部 件
鉴相器
环路 滤波器
压控 振荡器
二分频载 波 输 出
锁 相 环
图10.2-7 平方环法提取载波
我 们 以 2PSK 信 号 为 例 , 来 分 析 采 用 平 方 环 的 情 况 。 2PSK
e(t) [ a ng(t nS)T 2]c2 o w cts (10.2 - 4)
(10.2 - 2)
经过低通滤除高频部分后,就可恢复调制信号m(t)。
如果发端加入的导频不是正交载波,而是调制载波,则收端 v(t)中还有一个不需要的直流成分,这个直流成分通过低通滤波 器对数字信号产生影响, 这就是发端正交插入导频的原因。
通信原理(陈启兴版)第10章课后习题答案

第10章 正交编码与伪随机序列10.1 学习指导 10.1.1 要点正交编码与伪随机序列的要点主要包括正交编码的概念、常见的正交编码和伪随机序列。
1. 正交编码的概念对于二进制信号,用一个数字序列表示一个码组。
这里,我们只讨论二进制且码长相同的编码。
两个码组的正交性可用它们的互相关系数来表述。
设码长为n 的编码中码元只取值+1和-1。
如果x 和y 是其中的两个码组:x = (x 1, x 2, …, x n ),y = (y 1, y 2, …, y n ),其中,x i , y i ∈ {+1, -1},i = 1, 2, …, n ,则码组x 和y 的互相关系数被定义为2. i i 11(, ) (10-1)==∑ni x y x y n ρ如果码组x 和y 正交,则ρ(x , y ) = 0。
两两正交的编码称为正交编码。
类似地,我们还可以定义一个码组的自相关系数。
一个长为n 的码组x 的自相关系数被定义为x i i + j 11(),0, 1, , 1 (10-2)===-∑ni j x x j n n ρ其中,x 的下标按模n 运算,即x n +k ≡ x k 。
在二进制编码理论中,常采用二进制数字“0”和“1”表示码元的可能取值。
若规定用二进制数字“0”代替上述码组中的“-1”,用二进制数字“1”代替“+1”,则码组x 和y 的互相关系数被定义为(, ) (10-3)a bx y a bρ-=+ 其中,a 表示码组 x 和y 中对应码元相同的个数,b 表示码组x 和y 中对应码元不同的个数。
例如,对于4个码组:x 1 = (1,1, 1, 1),x 2 = (1, 1, 0,0),x 3 = (1, 0, 0, 1),x 4 = (1, 0, 1, 0),它们任意两者之间的相关系数都为0。
对于采用二进制数字“0”和“1”表示的码元,若用x 的j 次循环移位代替y ,就得到x 的自相关系数ρx (j )。
通信原理樊昌信版9,10章课后答案

通信原理樊昌信版9,10章课后答案9.9 采⽤13折线A律编码,设最⼩量化间隔为1个单位,已知抽样脉冲值为+635单位:(1)试求此时编码器输出码组,并计算量化误差;(2)写出对应于该7位码(不包括极性码)的均匀量化11位码。
(采⽤⾃然⼆进制码) 解(1)已知抽样脉冲值它位于第7段序号为3的量化级,因此输出码组为量化误差为635-(512+3*32)=27(2) 对应的11位均匀量化码为010********9-10采⽤13折线A律编码电路,设接收端收到的码组为“01010011”最⼩量化间隔为1个量化单位,并已知段内码改⽤折叠⼆进码:(l) 试问译码器输出为多少量化单位;(2) 试写出对应于该.7位码(不包括极性码)的均匀量化11位码。
解(1)接收端收到的码组由C1=0知,信号为负值;由段落码知,信号样值位于第6段,起点电平为256,量化间隔为16;由段内码码器输出为C5C6C7C8 =0011 采⽤折叠码) C5C6C7C8 =0011 采⽤折叠码,对应⾃然⼆进制码为0100可知,信号样值位于第6段的第5级(序号为4),故译码器输出为256416162328 (/)I=-+?+=-(2)均匀量化11位码为001010010009.11采⽤13折线A律编码,设最⼩的量化间隔为1个量化单位,已知抽样脉冲值为-95量化单位:(1)试求此时编码器输出码组,并计算量化误差;(2)试写出对应于该7位码(不包括极性码)的均匀量化11位码。
解(1)因为样值为负值.所以极性码⼜因64 < 95 < 128,所以码组位于第四段,段落码为量化间隔为4。
由于95=64 +7 *4 +3,所以段内码为故编码器输出为量化误差为3个单位。
(2)对应的均匀量化11位码为(92=64 +7 *4)9.13 对10路带宽均为300Hz-3400Hz的模拟信号进⾏PCM时分复⽤传输。
设抽样速率为8000Hz,抽样后进⾏8级量化,并编为⾃然⼆进制码,码元波形是宽度为的矩形脉冲,且占空⽐为1。
通信原理樊昌信版9,10章课后答案

9.9 采用13折线A律编码,设最小量化间隔为1个单位,已知抽样脉冲值为+635单位:(1)试求此时编码器输出码组,并计算量化误差;(2)写出对应于该7位码(不包括极性码)的均匀量化11位码。
(采用自然二进制码) 解(1)已知抽样脉冲值它位于第7段序号为3的量化级,因此输出码组为量化误差为635-(512+3*32)=27(2) 对应的11位均匀量化码为010********9-10采用13折线A律编码电路,设接收端收到的码组为“01010011”最小量化间隔为1个量化单位,并已知段内码改用折叠二进码:(l) 试问译码器输出为多少量化单位;(2) 试写出对应于该.7位码(不包括极性码)的均匀量化11位码。
解(1)接收端收到的码组由C1=0知,信号为负值;由段落码知,信号样值位于第6段,起点电平为256,量化间隔为16;由段内码码器输出为C5C6C7C8 =0011 采用折叠码) C5C6C7C8 =0011 采用折叠码,对应自然二进制码为0100可知,信号样值位于第6段的第5级(序号为4),故译码器输出为256416162328 (/)I=-+⨯+=-(2)均匀量化11位码为001010010009.11采用13折线A律编码,设最小的量化间隔为1个量化单位,已知抽样脉冲值为-95量化单位:(1)试求此时编码器输出码组,并计算量化误差;(2)试写出对应于该7位码(不包括极性码)的均匀量化11位码。
解(1)因为样值为负值.所以极性码又因64 < 95 < 128,所以码组位于第四段,段落码为量化间隔为4。
由于95=64 +7 *4 +3,所以段内码为故编码器输出为量化误差为3个单位。
(2)对应的均匀量化11位码为(92=64 +7 *4)9.13 对10路带宽均为300Hz-3400Hz的模拟信号进行PCM时分复用传输。
设抽样速率为8000Hz,抽样后进行8级量化,并编为自然二进制码,码元波形是宽度为 的矩形脉冲,且占空比为1。
《通信系统原理教程》课件第10章

第 10 章 差错控制编码
10.1.2 差错控制方式 常用的差错控制方式有三种:检错重发、前向纠错和
混合纠错。它们的系统构成如图10-1所示, 图中有斜线的 方框图表示在该端检出错误。
第 10 章 差错控制编码
第 10 章 差错控制编码
10.1 概述 10.2 检错与纠错原理 10.3 简单差错控制码 10.4 线性分组码 10.5 循环码 10.6 卷积码
第 10 章 差错控制编码
10.1 概 述
10.1.1 信源编码与信道编码
在数字通信中,根据不同的目的,编码可分为信源编码和 信道编码。信源编码是为了提高数字信号的有效性以及为了使 模拟信号数字化而采取的编码。信道编码是为了降低误码率, 提高数字通信的可靠性而采取的编码。
第 10 章 差错控制编码
另外,按照噪声或干扰的变化规律,可把信道分为三 类:随机信道、突发信道和混合信道。恒参高斯白噪声信 道是典型的随机信道,其中差错的出现是随机的,而且错 误之间是统计独立的。具有脉冲干扰的信道是典型的突发 信道, 错误是成串成群出现的,即在短时间内出现大量错 误。短波信道和对流层散射信道是混合信道的典型例子, 随机错误和成串错误都占有相当比例。对于不同类型的信 道,应采用不同的差错控制方式。
设码字A=[an-1,an-2,…,a1,a0],对偶监督码有
an1 an2 a1 a0 0
(10-2)
奇监督码情况相似, 只是码组中“1”的数目为奇数, 即 满足条件
an1 an2 a0 1
精品课件-通信系统原理-第10章

第10章 信道编辑原理
混合纠错(HEC,Hybrid Error Correction):是FEC与ARQ 的混合,发端发出便于检错和纠错的码,通过正向信道送到收 端,收端对错误能纠正的就自动纠正,纠正不了时自动发出判 决信号并送回发端,发端把收端认为有错并且无法纠正的消息 重发到收端,以达到正确传输。这种方式具有 FEC与ARQ的特点, 能充分发挥码的纠错和检错性能,在较差的信道中仍然可以收 到好的效果,缺点是需要反馈信道以及复杂的译码设备。
第10章 信道编辑原理
信息反馈(IF,Information Feedback):又称反馈检验,收 端把收到的消息原封不动地通过反馈信道送回发端,发端把反馈 回来的信息与原发送信息进行比较,从而发现错误,并把二者不 一致的部分重发到收端。其特点是没有纠(检)错编码,电路较简 单,但是需要反馈信道并且传输速率较低。
第10章 信道编辑原理
(5) 根据纠(检)错码的类型区分,纠错码可分为纠(检) 随机错码、纠(检)突发错码及既能纠(检)随机错又能纠(检)突 发错的码。
(6) 根据码元取值的进制,纠错码可分为二进制码和多 进制码。本章主要介绍二进制纠错码。
第10章 信道编辑原理
10.1.3 差错控制的工作方式 差错控制的基本工作方式有4种,如图10.1所示。图中有
第10章 信道编辑原理
数字通信要求传输过程中所造成的码元差错足够低。引起 传输差错的根本原因是信道内存在噪声以及信道传输特性不理 想所造成的码间串扰。通常,由于信道线性畸变所造成的码间 串扰可以通过均衡的办法来消除, 因此,常常只把信道中的噪 声作为造成传输差错的根本原因。为了提高数字通信系统的抗 噪声性能,可以采取增大发射功率、降低接收设备本身的噪声、 选择好的调制制度和解调方式、加强天线的方向性等措施。但 是, 这些措施只能将差错减小到一定程度, 要进一步提高通信 的可靠性,就需要采用信道编码技术,对可能或者已经出现的 差错进行控制。
《数字通信原理》第10章 扩频通信

f (x) 1 x x3
n级的移位寄存器的线性反馈电路产生的序列周期不会超过2n – 1, 若序列周期的最大值为2n – 1,那么该序列就是m序列
产生m序列的充要条件是:特征多项式是本原多项式,即满足: 1)f(x)是既约型的,即f(x)是不能分解因子的多项式; 2)f(x)可整除xm + 1,m = 2n – 1 3)f(x)不可整除xq + 1,q < 2n – 1
地面战术移动通信系统、 民用移动通信系统、 全球定位系统(GPS)、 无线局域网(WLAN)、 测距与测速系统等
引言(续) 扩频的三个特点:
1.信号占用的带宽远远大于发送信息所需的最小带宽,而且几乎 与信息比特速率无关; 2.在发送端需要利用扩频码进行扩频,所采用的扩频码通常是伪 随机序列,与所发送信息本身无关; 3.在接收端需要利用与发送端同步的扩频码进行解扩,以恢复原 始信号。
第 10 章 扩展频谱通信技术
本章的基本内容: 基本概念; 伪随机序列; 直接序列扩频技术; 调频技术; 扩频系统的同步; 扩频技术的应用
10.1 基本概念
引言 扩展频谱技术是数字通信的一个重要发展方向之一 最初应用于军事通信中,具有抗干扰能力强和低检测概率等优
点,以实现战场抗干扰和保密通信 随着技术的发展,已广泛应用于军事通信和民用通信中
10.3 直接序列扩频技术
直接序列扩频技术 发送端:直接利用扩频序列进行扩频处理; 接收端:则需要利用与发送端同步的扩频序列进行解扩处理 BPSK 直接序列扩频是直扩中最简单的形式 假设待发送的数字信号d(t) 为二进制双极性脉冲信号,载波功率 为P,角频率为 0 ,初始相位为零,则载波信号s(t)可以表示为
数字通信原理与技术(第四版)第10章伪随机序列及应用

扩频技术
通过将信号扩展到更宽的频带,降 低信号的功率谱密度,从而减小信 号被截获或干扰的风险。
编码技术
采用差分编码、卷积编码等编码技 术,提高信号的纠错能力和抗干扰 能力。
保密性能优化
加密技术
利用伪随机序列对明文进行加密,使非法用户无 法获取通信内容,保证通信的安全性。
跳频技术
通过快速跳变频率,使得敌方难以跟踪和截获信 号,提高通信的保密性。
扩频通信
在扩频通信中,伪随机序列用于扩频和解扩频过程,实现 信号的频谱扩展和还原,从而提高信号的抗干扰能力和隐 蔽性。
02 伪随机序列的生成方法
线性反馈移位寄存器
线性反馈移位寄存器是一种常用的伪随机序列 生成器,其基本原理是利用线性反馈函数对寄 存器的状态进行运算,产生新的状态序列。
线性反馈移位寄存器有多种类型,如扭结型、 斐波那契型等,它们生成的伪随机序列具有不 同的特性和应用场景。
相关性
相关性定义
伪随机序列的相关性是指序列中不同位置的元素之间的相互关系。
自相关和互相关
自相关表示序列与其自身相关的情况,互相关表示两个不同序列 之间的相关情况。
相关函数
相关函数用于描述伪随机序列的相关性,其值越接近于0表示相 关性越弱,越接近于1表示相关性越强。
均匀分布性
均匀分布性定义
伪随机序列的每个元素出 现的机会应该是相等的, 即具有均匀分布性。
特性
伪随机序列具有良好的随机性、 周期性、可重复性和可预测性, 通常用于模拟噪声环境、加密通 信、扩频通信等领域。
伪随机序列的应用领域
模拟噪声环境
在无线通信、雷达和声呐等系统中,伪随机序列常被用作 噪声源,模拟自然界的噪声环境,以提高系统的抗干扰性 能。
通信原理(第二版)第10章信道编码

信道编码的基本原理
信息比特与冗余比特的映射
信道编码通过将信息比特映射到包含冗余比特的码字,使 得在传输过程中出现错误时,能够被检测并纠正。
错误检测与纠正
信道编码利用各种算法和规则,对接收到的码字进行解码 和校验,检测并纠正其中的错误。
码字的选择与设计
信道编码中码字的选择与设计是关键,不同的码字具有不 同的纠错能力和性能。根据实际需求选择合适的码字,能 够提高通信系统的性能和可靠性。
信道编码
目录
• 信道编码概述 • 常见信道编码方式 • 信道编码性能分析 • 信道编码的应用 • 信道编码的未来发展
01
信道编码概述
信道编码的定义
01
信道编码是一种通过在原始信息 中添加冗余以增加数据传输可靠 性的技术。
02
它通过对信息比特进行一系列的 数学变换,使得在传输过程中出 现错误时,能够被检测并纠正。
编码增益是指采用信道编码技术后相 对于未编码情况下的信噪比改善程度。
编码增益越大,说明信道编码技术的 性能越好,能够更好地提高通信系统 的可靠性。
编码增益计算
编码增益可以通过比较相同误码率下, 采用信道编码技术的系统所需的信噪 比与未采用信道编码的系统所需的信 噪比来计算。
编码效率
编码效率定义
编码效率是指信道编码过程中, 每传输一个比特所需的总的比特
循环码
定义 原理 优点 应用
循环码是一类特殊的线性分组码,其码字具有循环特性。
循环码的编码过程是将信息比特经过有限域运算映射到码字中 ,其中冗余比特由信息比特循环移位和模运算得到。
循环码具有高效的编码算法和良好的错误纠正能力,且易于实 现。
循环码广泛应用于数字通信和数据存储领域,如移动通信、卫 星通信和磁存储器等。
现代通信原理(罗新民)第十章+差错控制编码习题答案

第十章 差错控制编码图见附图:10 ①、19、2010-1 请说明随机信道、突发信道、混合信道各自的特点。
答:随机信道的特点是错码的出现是随机的。
且错码之间是统计独立的。
突发信道的特点是错码集中成串出现。
混合信道的特点是既存在随机错码又存在突发错码。
10-2 请说明差错控制方式的目的是什么?常用的差错控制方式有哪些?答:差错控制方式的目的是在数字通信过程中发现(检测)错误,并采取措施纠正,把差错限制在所允许的尽可能小的范围内。
常用的差错控制方式包括:ARQ 、反馈校验、FEC 、HEC 。
10-3请说明ARQ 方式有哪几种?答:停止等待ARQ 、连续ARQ 、选择重发ARQ 。
10-4 已知线性分组码的八个码字为:000000,001110,010101, 011011,100011,101101,110110,111000,求该码组的最小码距。
解:线性分组码的最小码距等于码的最小码重,故30=d。
10-5 上题给出的码组若用于检错,能检出几位错码?若用于纠错, 能纠几位错?若同时用于纠错,检错如何? 答:1230+≥=d ,故可检出2个错。
11230+⨯≥=d ,故可纠正1个错。
11130++≥=d ,(1≥1)故纠检结合时可检1个错同时纠正1个错。
10-6 若两个重复码字0000,1111,纠检错能力如何?解:d=4,故可检出3个错,纠正1个错,可同时检出2个错、纠正1个错。
10-7 写出k=1,n=5时重复码的一致检验矩阵[H]及生成矩阵[G],并 讨论它的纠、检错能力。
解:①n=5,k=1,r=4。
设码字为01234|c c c c c ,只取11111或00000,0123c c c c为监督码元。
则有⎪⎪⎩⎪⎪⎨⎧====4414243c c c c c c c c⇒⎪⎪⎩⎪⎪⎨⎧=⊕=⊕=⊕=⊕000040414243cc c c c c c c⇒⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡00001|10000|10010|10100|110001234c c c c c故⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⨯1000110010101001100054H,[]111141==⨯TPQ。
通信原理教程(第2版)课后答案12-10
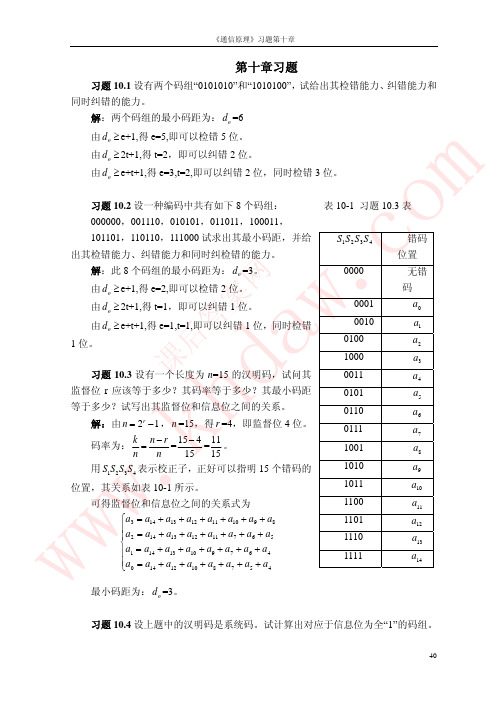
h 试问由它可以构成多少种码长为 15 的循环码?并列出它们的生成多项式。
解:因为 2r 1 n ,而 n =15,所以 4 r 13 。因为
生成多项式 g(x) x3 x 1 ,从而生成矩阵为
42
《通信原理》习题第十章
x3 g ( x)
1 0 0 1 0 0
G(
x
)=
x
2
g
(
x)
xg ( x)
g(x)
,或
G=
0 0 0
1 0 0
0 1 0
1 0 1
0 1 1
0 ,
x7 g(x)
0 0 0 1 1 0 0 1 0 0 0 0 0 0 0
x6 g(x)
0 0 0 0 1 1 0 0 1 0 0 0 0 0 0
G(x)
=
x5
g(x)
,或
G=
0
0
0
0
0
1
1
0
01
0
0
0
0
0
x4 g(x)
0 0 0 0 0 0 1 1 0 0 1 0 0 0 0
d 习题 10.11 已知一个(15,11)汉明码的生成多项式为 hg(x) x4 x3 1
试求出其生成矩阵和监督矩阵。
www.k 解:由g(x) x4 x3 1得
43
《通信原理》习题第十章
x10 g(x)
现代通信原理教程10章部分习题解答

10.1 已知码集合中有8个码组为(000000)、(001110)、(010101)、(011011)、(100011)、(101101)、(110110)、(111000),求该码集合的最小码距。
解 因为该码集合中包含全零码组(000000),所以对于线性分组码,最小码距等于除全零码外的码组的最小重量,即3min =d 。
10.2 上题给出的码集合若用于检错,能检出几位错码?若用于纠错,能纠正几位错码?若同时用于检错与纠错,问纠错、检错的能力如何?解 只用于检错时,由条件:最小码距1min +≥e d ,求出2=e ,即能检出2位错码。
只用于纠错时,由12min +≥t d ,可得1=t ,既能纠正1位错码。
同时用于检错与纠错,且3min =d 时,无法满足下列条件⎩⎨⎧>++≥te e t d 1m i n故该码不能同时用于检错与纠错。
10.4 已知(7,3)码的生成矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=001110101001111001110G列出所有许用码组,并求监督矩阵。
解 分别将信息段(000)、(001)、(010)、(011)、(100)、(101)、(110)和(111)代入式A =m G ,得到许用码组如下 0000000 0011101 0100111 0111010 1001110 1010011 1101001 1110100生成矩阵G 为典型阵,有⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=110101111110Q 所以⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡==011110111101TQ P监督矩阵[]⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡==0110001110001011101001011000r I P H 10.5 已知一个(7,4)系统汉明码监督矩阵如下:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=110100101110101110100H 试求:(1) 生成矩阵G ;(2) 当输入信息序列()101101011010=m 时,求输出码序列A=? (3) 若译码器输入()1001001B =,请计算校正子S ,并指出可能的错误图样。
通信原理各章习题集的答案解析

第一章 通信系统概论一 填空选择题1.数字通信系统的主要优点是 __抗干扰能力强噪声不积累 、差错可控、容易加密_、可实现综合化(便于集成)等_。
2.通信系统的主要质量指标通常用_有效性_和可靠性_衡量, FSK 系统指标具体用_传输速率(传码率、传信率)和_差错率(误码率、误信率)_衡量,FM/PM 系统具体指标用_有效传输频带 和_信噪比_衡量。
3.已知二进制数字信号在2分钟内共传送72000个码元,0、1码等概率出现,则码元速率为600B ,信息速率为600b/s ;传送1小时后,接收到的错码为216个,其误码率为10-4;若保持码元速率不变,变换为8进制传输,每个码元所含信息量为3 ,信息速率为1800b/s 。
4.通信是指消息由一地向另一地进行______,主要质量指标是_____和_____,它们在数字通信系统中具体为_____和_____。
5.在码元速率相同的条件下,16进制数字调制系统的信息速率是二进制的4 倍。
6.按传输媒介,通信系统可分为有线通信系统、无线通信系统。
7.数字通信系统的有效性指标包括 ( D )A.信息传输速率B.符号传输速率C.频带利用率D.以上都包括8.在码元速率相同条件下,m 进制数字调制系统的信息速率是二进制的 log 2m 倍。
9.通信系统按其传输信号形式分可分为模拟通信系统和数字通信系统 。
10.通信系统按信道中传输的信号不同分为模拟通信系统 和 数字通信系统11.衡量通信系统主要指标是有效性和可靠性,前者主要是消息传输速率问题,而后者是指消息传输的 质量问题。
12.设有四个信息A 、B 、C 、D 分别以概率1/4、1/8、1/8、1/2传送,每个消息出现是相互独立的,其平均信息量H=__1.75b/符号__。
13.设有4个消息符号,其出现概率是21、41、81、81各消息符号出现是相对独立的,该符号集的平均信息量为 1.75b/符号 。
14.某四元制信源,各符号对应的概率分别为21、41、81、1,则该信源符号的平均信息量为 1.75b/符号 。
通信原理(樊昌信)第10章-信源编码可编辑全文

(3)段内码: C5 C6 C7 C8 = 0011
IW6
IW7 1270
IW5
IW4
PCM码组 C1~ C8 =1 111 0011
例
解
由上例可知,编码电平 :
0
段内码
M5M6M7M8
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
0
0
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
表
10-6
10-5
表
段落码
M2M3M4
段
内
码
(幅值)
起始电平和量化间隔
——之三,确定样值所在的段落和量化级
各折线段落
1
2
3
4
5
6
7
8
各段落长度(∆)
段内码
极性码:表示样值的极性。正编“1”,负编“0”
段落码:表示样值的幅度所处的段落
段内码:16种可能状态对应代表各段内的16个量化级
段落序号
段
落
码
8
1 1 1
7
1 1 0
6
1 0 1
通信原理第10章 通信抗干扰技术

10.1.1基本原理及关键技术 10.1.1基本原理及关键技术
1、干扰方式与样式 按作用时间的不同可分为连续干扰 连续干扰和 连续干扰 脉冲干扰。干扰在时间上无须完全覆盖信 脉冲干扰 号,只要干扰在时域分布上达到一定密度 ,脉冲干扰也能完全压制通信。 干扰样式:是对干扰的时域、频域的统计 干扰样式 特性的总概括。不同方式样式不同,同种 方式也可采用不同样式。干扰样式按干扰 是否具有随机性分为确定干扰和随机干扰 ;按幅度分布特性可分为平滑干扰、脉冲 干扰。常见样式有:白噪声、单频连续波 、噪声调制(AM/DSB/SSB/FM)波、 随机键控(ASK/FSK/PSK)干扰等
第十章 通信抗干扰技术
2007年12月
1
引
言
定义: 一般可理解为,通信装备及 系统为对抗干扰方利用电磁能和定 向能控制、攻击通信电磁频谱,以 提高其在通信对抗中的生存能力所 采取的通信反对抗技术体系、方法 和措施。
2007年12月 2
抗干扰的基本体系、方法、 抗干扰的基本体系、方法、措施
1、信号处理。如直接序列扩频技术(DS-SS) ,其关键参量是作为时间函数的相位;跳 频技术(FH-SS)其关键参量是作为时间函数 的载频;等等。 2、空间处理。如采用自适应天线调零技术, 当接收端受到干扰时,使其天线方向图零 点自动指向干扰方向,以提高通信接收机 的信干比。 3、时间处理。如猝发传输技术,由于通信信 号在传输过程中暴露的时间很短暂,从而 大大降低了被干扰方侦察、截获的概率。
10.1.1基本原理及关键技术 10.1.1基本原理及关键技术
1、干扰方式与样式 宽带拦阻式干扰:辐射宽带干扰,可以干 宽带拦阻式干扰 扰多个窄带信号,其频谱均匀分布或梳形 分布。按产生方法不同分为扫频式、脉冲 式和多干扰源线性叠加式阻拦干扰。 特点:与瞄准式相反,无需严格的侦察和 特点 频率瞄准,设备简单、方便实施,但干扰 利用率低,需要的干扰功率很大。
通信原理 第10章 码间干扰

《通信原理课件》
《通信原理课件》
由该图可以获得以下信息:
(1)最佳抽样时刻应是“眼睛”张开最大的时刻; (2)眼图斜边的斜率决定了系统对抽样定时误差的灵 敏程度;斜率越大,对定时误差越灵敏; (3)眼图的阴影区的垂直高度表示信号的畸变范围; (4)眼图中央的横轴位置对应于判决门限电平; (5)过零点失真为压在横轴上的阴影长度,有些接收 机的定时标准是由经过判决门限点的平均位置决定的,所 以过零点失真越大,对定时标准的提取越不利。 (6)抽样时刻上、下两阴影区的间隔距离之半为噪声 容限,噪声瞬时值超过它就可能发生错误判决;
间串扰的条件。
方法2:
将实际传输速率RB代入奈奎斯特第一准则(无ISI的频域条件),
若仍能使H(ω) 等效成一个理想低通滤波器,则可实现ISI传输。
《通信原理课件》
值得注意的是,奈奎斯特第一准则,即
H ( 2i ) C
i
Ts
所对应的无ISI的最高传码率
输速率为
RB m ax
2 Ts
Ts
RB m ax
《通信原理课件》
即眼图分析法
观察眼图的方法:
①用示波器跨接在接受滤波器的输出端 ②调整扫描周期,使示波器水平扫描周期与接收码元周期同步 ③此时在示波器上可看到很想人的眼睛的图像,及眼图
无
噪
声 条
无码间串扰
件
下
《通信原理课件》
有码间串扰
图5-21(a)是接收滤波器输出的无码间串扰的二进 制双极性基带波形,用示波器观察它,并将示波器扫描周 期调整到码元周期,由于示波器的余辉作用,扫描所得的 每一个码元波形将重叠在一起,示波器屏幕上显示的是一 只睁开的迹线细而清晰的大“眼睛”,
通信原理第10章数据通信接口和设备

HTTP协议支持多种请求方法, 如GET、POST、PUT、 DELETE等,用于获取、创建、 更新或删除资源。
FTP协议
FTP协议是用于文件传输的互联网标 准协议。
FTP协议支持匿名访问和用户认证两 种模式,提供文件传输的可靠性和安 全性。
FTP协议基于客户端/服务器模型,客 户端通过FTP客户端软件连接到FTP服 务器,进行文件的上传和下载。
TCP负责数据的可靠传输,通过建立连接、发送数据、确认接收、流量控制和错误 校验等功能,确保数据在网络中的可靠传输。
IP协议负责数据的路由,通过IP地址将数据从一个网络节点传送到另一个网络节点。
HTTP协议
HTTP协议是用于访问和传输网 页内容的互联网标准协议。
HTTP协议基于请求/响应模型, 客户端向服务器发送请求,服 务器返回响应。
Thunderbolt接口
高速数据传输接口
VS
Thunderbolt接口是一种基于PCIe 和DisplayPort技术的串行总线接口, 被广泛应用于高速数据传输和视频信 号传输。它使用双通道传输数据,支 持多种设备连接,最高传输速率可达 40Gbps。
03
数据通信设备
调制解调器
总结词
将数字信号转换为模拟信号或模拟信号转换为数字信号的设备
02
数据通信接口
RS-232接口
传统的串行通信接口
RS-232是一种标准的串行通信接口,被广泛应用于计算机和其他设备之间的通 信。它使用单根线来传输数据,支持全双工通信,最高传输速率可达20kbps。
USB接口
通用串行总线接口
USB接口是一种常用的串行通信接口,支持热插拔和即插即用。它可以连接多种设备,如鼠标、键盘、打印机等,最高传输 速率可达480Mbps。
通信原理(陈启兴版) 第10章作业和思考题参考答案
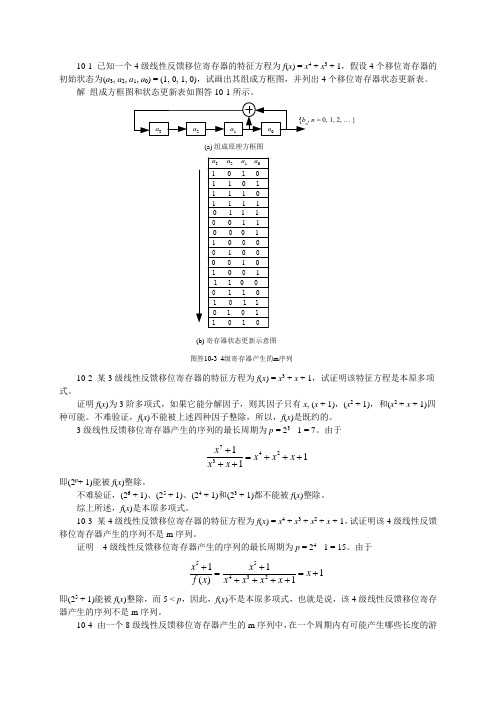
10-1 已知一个4级线性反馈移位寄存器的特征方程为f (x ) = x 4 + x 3 + 1,假设4个移位寄存器的初始状态为(a 3, a 2, a 1, a 0) = (1, 0, 1, 0),试画出其组成方框图,并列出4个移位寄存器状态更新表。
解 组成方框图和状态更新表如图答10-1所示。
图答10-3 4级寄存器产生的m 序列, n = 0, 1, 2, … }(a) 组成原理方框图(b) 寄存器状态更新示意图1 0 1 0a 3 a 2 a 1 a 01 1 0 11 1 1 01 1 1 10 1 1 10 0 1 10 0 0 11 0 0 00 1 0 00 0 1 01 0 0 11 1 0 00 1 1 01 0 1 10 1 0 11 0 1 010-2 某3级线性反馈移位寄存器的特征方程为f (x ) = x 3+ x + 1,试证明该特征方程是本原多项式。
证明f (x )为3阶多项式,如果它能分解因子,则其因子只有x , (x + 1),(x 2 + 1),和(x 2 + x + 1)四种可能。
不难验证,f (x )不能被上述四种因子整除,所以,f (x )是既约的。
3级线性反馈移位寄存器产生的序列的最长周期为p = 23 - 1 = 7。
由于 7423111x x x x x x +=+++++ 即(2p + 1)能被f (x )整除。
不难验证,(26 + 1)、(25 + 1)、(24 + 1)和(23 + 1)都不能被f (x )整除。
综上所述,f (x )是本原多项式。
10-3 某4级线性反馈移位寄存器的特征方程为f (x ) = x 4 + x 3 + x 2 + x + 1,试证明该4级线性反馈移位寄存器产生的序列不是m 序列。
证明 4级线性反馈移位寄存器产生的序列的最长周期为p = 24 - 1 = 15。
由于55432111()1x x x f x x x x x ++==+++++即(25 + 1)能被f (x )整除,而5 < p ,因此,f (x )不是本原多项式,也就是说,该4级线性反馈移位寄存器产生的序列不是m 序列。
北京邮电大学通信原理课件 第10章 正交码与伪随机码

第十章 正交码与伪随机码10.1 利用m 序列的移位相加特性证明双极性m 序列的周期性自相关函数为二值函数,且主副峰之比等于码长(周期)。
证:m 序列的移位相加特性特性是说,单极性m 序列和它的移位相加后仍然是m 序列。
相加的结果在一个周期内1比0多一个。
双极性m 序列是把0、表示的m 序列映射为表示,其中0映射为+1,1映射为-1。
对于双极性m 序列,一个周期内-1比+1多一个。
在这种映射下,模2加运算变成了乘法运算,如下表所示:1±⊕1 0 1 0 1 0 1 0×-1 1 -1 1 -1 1 -1 1因此m 序列的移位相加特性特性对于双极性m 序列表现为:m 序列和它的移位相乘后仍然是m 序列。
周期为p 的双极性m 序列的周期性自相关函数定义为()11pk k jk R j b p +==∑b ,其中的下标按模p 运算,即。
b k pk b b += 当j 为p 的整倍数时,k j j b b +=,1=+j k k b b ,因此()()01R j R ==,这是自相关函数的主峰值;对于0j p <<,令,则m 序列的移位相加特性表明序列kk k c b b +=j {}k c 也是m 序列,表示一个周期内求和,由于-1比+1多一个,所以,从而得1ppk k j kk k b b c +==∑∑1=11pkk c==−∑()1mod 1j p R j elsep 0=⎧⎪=⎨−⎪⎩这就证明了周期为p 的m 序列的周期性自相关函数为二值函数,且主副峰之比等于码长。
10.2 已知线性反馈移存器序列的特征多项式为,求此序列的状态转移图,并说明它是否是m 序列。
1)(3++=x x x f 解:该序列的发生器逻辑框图为:定义状态为向量()123,,s s s =s ,假设起始状态是100,则状态转移图如下:由于其周期为,所以此序列是m 序列。
7123=−10.3 已知m 序列的特征多项式为,写出此序列一个周期中的所有游程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Pe P(1) P( A0 / 1) P(0) P( A1 / 0)
P (1)
r0'
f1 (r )dr P (0) ' f 0 ( r )dr
r0
表示Pe是r0的函数。最佳分界点r0的条件:
Pe ' ' P ( 1 ) f ( r ) P ( 0 ) f ( r 1 0 0 0) 0 ' r0 P(1) f 0 (r0 ) P(0) f1 (r0 )
k
2 n n0 f H
f k (n)
2 n
k
Ts 1 2 exp 2 f H n (t )dt 0 2n0 f H
1 2 n
k
1 exp n0
Ts
0
n (t )dt
2
n (n1 , n2 ,nk )
k维空间一个点
“最佳”准则:错误概率最小
错误原因:噪声。
判决规则:设在二进制通信系统中发“1”的概率为P(1), 发“0”的概率为P(0),总误码率
Pe P(1) Pe1 P(0) Pe0
接收矢量决定的两个联合概率密度函数f0(r)和f1(r)的曲线
A0 f0(r) P(A0/1) r0 A1 P(A1/0) f1(r)
Ts、n0、k定,f(n)仅取决于码元内噪声能量,与t无关
4
1 f k (n) exp k 10.1数字信号的统计特性 n0 2 n
1
Ts
0
n (t )dt
2
接收信号:r = s+ n,k 维矢量,一个码元内接收电压的抽样值。 发送码元确定后,接收信号仍服从高斯分布,其方差仍为n2, 均值变为s(t)。 发码元波形为s0(t)、 s1(t)时,接收电压r(t)的k维联合概率密度 函数为:
f (ni ) ni2 exp 2 2 2 n n 1
按抽样定理对带限白噪声进行抽样,各抽样值是互不相 关的随机变量,Page 58,高斯彼此独立
2
10.1数字信号的统计特性
k个噪声抽样值的k维联合概率密度函数为
f k (n1 , n2 , , nk ) f (n1 ) f (n2 ) f (nk )
k很大时,噪声平均功率可表示为: 1 Ts 2 n (t )dt Ts 0
1 k 2 ni k i 1 1 2 f H Ts
k 2 i Ts 0
1
2 n
k
1 exp 2 2 n
n i 1
k 2 i
k 2 f H Ts
2 n i i 1
第10章
数字信号的最佳接收
1
10.1数字信号的统计特性
数字通信系统可靠性以误码率衡量,判决是统计判决, 基础是统计判决理论。 数字信号的统计描述: 由于噪声的影响,接收的信号是随机的。 接收电压统计特性描述: 假设条件 信道噪声: 0均值、谱密度为n0,带限高斯白噪声; 信号: 二进制码元,P(0) + P(1) = 1 基带截止频率小于fH,抽样率fs≥2fH。Ts内得到k = 2fHTs个抽样值。 噪声抽样值一维概率密度为
推广到多进制
f i( r ) > f j( r ) 判发Si(t)
9
10.3 确知信号的最佳接收机
确知信号:取值在任何时间是确定、可预知的 理想恒参信道收到的数字信号 假设:二进制两码元功率相同,持续时间Ts; 2 带限高斯白噪声,单边功率谱密度n0,功率 n 接收电压r(t)的k维概率密度:
f1 (r )
1 2 n
k
1 exp n0
Ts
0
r (t ) s1 (t ) dt
2
f 0 (r )
1 2 n
k
1 exp n0
Ts
0
r (t ) s0 (t ) dt
2
10
10.3 确知信号的最佳接收机
代入判决准则,判决发送s0(t)的条件为:
r
6
10.2 数字信号的最佳接收
A0 f0(r) P(A1/0) P(A0/1) r0 r
A1
r 当作1维矢量
f1(r)
两区域A0和A1,边界r0,判决规则: 若接收矢量落在区域A0内,则判发送码元是“0”; 若接收矢量落在区域A1内,则判发送码元是“1”。
7
10.2 数字信号的最佳接收
总误码率为
k
2 n 2 f n (t )dt H i 1
3
10.1数字信号的统计特性
f k (n1 , n2 , , nk )
1
1 2 n
k
1 k 2 exp 2 ni 2 n i 1
2 n 2 f n (t )dt H i 1 2 i Ts 0
2 1 Ts 1 P(1) exp r (t ) s1 (t ) dt P(0) exp n0 0 n0 取对数,×(-n0),判s0(t)条件为:
Ts
0
r (t ) s0 (t ) dt
2
Ts Ts 1 1 2 2 n0 ln r (t ) s1 (t ) dt n0 ln r (t ) s0 (t ) dt 0 P(1) P(0) 0
f 0 (r )
1 2 n
k
1 exp n0源自Ts0 r (t ) s0 (t ) dt
2
f1 (r )
1 2 n
k
1 exp n0
Ts
0
r (t ) s1 (t ) dt r
2
5
10.2 数字信号的最佳接收
当P(1) = P(0) ,f0(r0) = f1(r0) 交点
8
10.2 数字信号的最佳接收
判决边界确定后,判决准则为:
f 0 (r ) P (1) , 判 "1" P ( 0 ) f1 ( r )
P(1) f 0 (r ) , 判 "0" P(0) f1 (r )
在 “0”、“1”先验概率相等时,上式简化为: 若f0(r) > f1(r),则判为“0” 若f0(r) < f1(r),则判为“1” 最大似然准则。按此准则判决可得理论最小误码率。
