Matlab 上机题及答案
matlab上机习题详细讲解-试题答案解析

学习指导参考P 第一次实验答案1. 设要求以0.01秒为间隔,求出y 的151个点,并求出其导数的值和曲线。
clc clearx=0:0.01:1.5;y=sqrt(3)/2*exp(-4*x).*sin(4*sqrt(3)*x+pi/3) y1=diff(y) subplot(2,1,1) plot(x,y)subplot(2,1,2) plot(x(1:150),y1)2绘制极坐标系下曲线(a,b,n 自定数据)clc clear a=10; b=pi/2; n=5;theta=0:pi/100:2*pi; rho=a*cos(b+n*theta); polar(theta,rho)3. 列出求下列空间曲面交线的程序clc clearx=[-5:0.5:5];[X,Y]=meshgrid(x); z1=X.^2-2*Y.^2;z2=X.*2-Y.*3; xlabel('x') ylabel('y') zlabel('z') surf(X,Y,z1) hold onsurf(X,Y,z2)k=find(abs(z1-z2)<0.5); x1=X(k) y1=Y(k)z3=x1.^2-2*y1.^2 hold onplot3(x1,y1,z3,'*')4、设 ⎥⎦⎤⎢⎣⎡++=)1(sin 35.0cos 2x x x y 把x=0~2π间分为101点,画出以x 为横坐标,y 为纵坐标的曲线,要求有图形标注。
clc clearx=-2*pi:0.1: 2*pi;y=cos(x).*(0.5+sin(x)*3./(1+x.^2)); plot(x,y,'b*-'); title('绘图'); xlabel('x 坐标'); ylabel('y 坐标'); legend('原函数')gtext('y=cos(x)(0.5+3*sin(x)/(1+x^2))')5、求下列联立方程的解 81025695832475412743-=+-+-=-+-=++-=--+w z y x w z x w z y x w z y xclc cleara=[3,4,-7,-12;5,-7,4,2;1,0,8,-5;-6,5,-2,10]; b=[4,-3,9,-8]; c=b/a; x=c(1,1) y=c(1,2) z=c(1,3) w=c(1,4)6. 假设一曲线数据点为x = 0:2:4*pi;y = sin(x).*exp(-x/5);试将x 的间距调成 0.1,采用不同插值方法进行插值,并通过子图的形式将不同插值结果和原始数据点绘制在同一图形窗口。
MATLAB 上机 习题及答案

15、今有多项式P1(x)=x4-2x+1,P2(x)=x2+4x-0.5,要求先求得P(x)=P1(x)+P2(x),然后计算xi=0.2*i各点上的P(xi)(i=0,1,2,…,5)值。
p1=[1.0 0.0 0.0 -2.0 1.0];>> p2=[0.0 0.0 1.0 4.0 -0.5];>> p1x=poly2sym(p1);p2x=poly2sym(p2);>> p=p1x+p2xp =x^4+2*x+1/2+x^2>> x=0:5;>> x.^4+2*x+1/2+x.^2ans =0.5000 4.5000 24.5000 96.5000 280.5000 660.50001、试个MATLAB的工作空间中建立以下2个矩阵:A=[1 2]1234B⎡⎤=⎢⎥⎣⎦,求出矩阵A和B的乘积,并将结果赋给变量C。
>> A=[1 2]A =1 2>> B=[1 23 4]B =1 23 4>> C=A*BC =7 102、利用MATLAB提供的帮助信息,了解inv命令的调用格式,并作简要说明。
help invINV Matrix inverse.INV(X) is the inverse of the square matrix X.A warning message is printed if X is badly scaled ornearly singular.See also SLASH, PINV, COND, CONDEST, LSQNONNEG, LSCOV. Overloaded methodshelp gf/inv.mhelp zpk/inv.mhelp tf/inv.mhelp ss/inv.mhelp lti/inv.mhelp frd/inv.mhelp sym/inv.mhelp idmodel/inv.m3、使用help命令查询函数plot的功能以及调用方法,然后利用plot命令绘制函数y=sin(x)的图形,其中0xπ≤≤。
Matlab上机练习题及答案

Matlab 上机练习题及答案---------------------------------------------------------------------1、矩阵Y=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡3472123100451150425,给出元素1的全下标和单下标,并用函数练习全下标和单下标的转换,求出元素100的存储位置。
取出子矩阵⎥⎦⎤⎢⎣⎡21301,并求该矩阵的维数。
解:命令为:Y=[5,2,4;0,15,1;45,100,23;21,47,3]Y(2,3)Y(10)sub2ind([43],2,3)[i,j]=ind2sub([43],10)find(Y==100)sub2ind([43],3,2)B=Y(2:2:4,3:-2:1)或B=Y([24],[31])[m n]=size(Y)---------------------------------------------------------------------2、已知矩阵A=[10-1;241;-205],B=[0-10;213;112]求2A+B 、A 2-3B 、A*B 、B*A 、A.*B ,A/B 、A\B 解:命令为:A=[10-1;241;-205]B=[0-10;213;112]E=2*A+B F=A^2-3*B G=A*B H=B*A I=A.*B J=A/B K=A\B---------------------------------------------------------------------3、利用函数产生3*4阶单位矩阵和全部元素都为8的4*4阶矩阵,并计算两者的乘积。
解:命令为:A=eye(3,4)B=8*ones(4)C=A*B---------------------------------------------------------------------4、创建矩阵a=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------7023021.5003.120498601,取出其前两列构成的矩阵b ,取出前两行构成矩阵c ,转置矩阵b构成矩阵d ,计算a*b 、c<d ,c&d,c|d ,~c|~d 解:命令为:a=[-1,0,-6,8;-9,4,0,12.3;0,0,5.1,-2;0,-23,0,-7]b=a(:,[12])c=a([12],:)d=b’e=a*b f=c<d g=c&d h=c|d i=~c|~d---------------------------------------------------------------------5、求!201∑=n n 解:命令文件为sum=0;s=1;for n=1:20s=n*s;sum=sum+s;end sum---------------------------------------------------------------------6、求a aa aaa aa a S n ++++=得值,其中a 是一个数字,由键盘输入,表达式中位数最多项a 的个数,也由键盘输入。
matlab上机练习(附答案)-推荐下载

对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电通,力1根保过据护管生高线产中0不工资仅艺料可高试以中卷解资配决料置吊试技顶卷术层要是配求指置,机不对组规电在范气进高设行中备继资进电料行保试空护卷载高问与中题带资2负料2,荷试而下卷且高总可中体保资配障料置2试时32卷,3各调需类控要管试在路验最习;大题对限到设度位备内。进来在行确管调保路整机敷使组设其高过在中程正资1常料中工试,况卷要下安加与全强过,看度并25工且52作尽22下可护都能1关可地于以缩管正小路常故高工障中作高资;中料对资试于料卷继试连电卷接保破管护坏口进范处行围理整,高核或中对者资定对料值某试,些卷审异弯核常扁与高度校中固对资定图料盒纸试位,卷置编工.写况保复进护杂行层设自防备动腐与处跨装理接置,地高尤线中其弯资要曲料避半试免径卷错标调误高试高等方中,案资要,料求编试技写5卷术、重保交电要护底气设装。设备置管备高4动线调、中作敷试电资,设高气料并技中课试3且术资件、卷拒中料管试绝包试调路验动含卷试敷方作线技设案,槽术技以来、术及避管系免架统不等启必多动要项方高方案中式;资,对料为整试解套卷决启突高动然中过停语程机文中。电高因气中此课资,件料电中试力管卷高壁电中薄气资、设料接备试口进卷不行保严调护等试装问工置题作调,并试合且技理进术利行,用过要管关求线运电敷行力设高保技中护术资装。料置线试做缆卷到敷技准设术确原指灵则导活:。。在对对分于于线调差盒试动处过保,程护当中装不高置同中高电资中压料资回试料路卷试交技卷叉术调时问试,题技应,术采作是用为指金调发属试电隔人机板员一进,变行需压隔要器开在组处事在理前发;掌生同握内一图部线纸故槽资障内料时,、,强设需电备要回制进路造行须厂外同家部时出电切具源断高高习中中题资资电料料源试试,卷卷线试切缆验除敷报从设告而完与采毕相用,关高要技中进术资行资料检料试查,卷和并主检且要测了保处解护理现装。场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
Matlab上机练习参考答案

Matlab 上机练习二班级 学号 姓名按要求完成题目,并写下指令和运行结果。
(不需要画图)1、 求⎥⎦⎤⎢⎣⎡+-+-+-+-++=i 44i 93i 49i 67i 23i 57i 41i 72i 53i 84x 的共轭转置。
>> x=[4+8i 3+5i 2-7i 1+4i 7-5i;3+2i 7-6i 9+4i 3-9i 4+4i];>> x’ans =- -- ++ -- ++ -2、计算⎥⎦⎤⎢⎣⎡=572396a 与⎥⎦⎤⎢⎣⎡=864142b 的数组乘积。
>> a=[6 9 3;2 7 5];>> b=[2 4 1;4 6 8];>> a.*bans =12 36 38 42 403、 对于B AX =,如果⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=753467294A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=282637B ,求解X 。
>> A=[4 9 2;7 6 4;3 5 7];>> B=[37 26 28]’;>> X=A\BX =4、 ⎥⎦⎤⎢⎣⎡-=463521a ,⎥⎦⎤⎢⎣⎡-=263478b ,观察a 与b 之间的六种关系运算的结果。
>> a=[1 2 3;4 5 6];>> b=[8 –7 4;3 6 2];>> a>bans =0 1 01 0 1 >> a>=bans =0 1 01 0 1 >> a<bans =1 0 1 0 1 0 >> a<=bans =1 0 1 0 1 0 >> a==bans =0 0 0 0 0 0>> a~=bans =1 1 11 1 15、[]7.0=-a,在进行逻辑运算时,a相当于什么样的逻辑量。
82.05-相当于a=[1 1 0 1 1]。
Matlab上机作业部分参考答案

1
1
( x s inx )x2d x
的命
(2 ,4 .9 ) 4. 假设已知一组数据,试用插值方法绘制出 x
区间内的光滑函数曲线,比较各种值算法的优劣。
x
-2
i
-1.7
-1.4
-1.1
-0.8
-0.5
-0.2
0.1
0.4
0.7
1
1.3
y
x
i
.102 .117 .131 .144 .156 .166 .173 .177 .178 .176 .171 .163 89 41 58 83 56 22 32 5 53 35 09 02
11. 用单选框做一个如图所示的界面,通过选择不同的单选 框来决定使用不同的色彩图。
1 0.8 0.6 0.4 0.2 0 -0.2 -0.4 -0.6 -0.8
0
2
4
6
8
10
12
14
假设 求
f (x ,y ) e d t
t2 0
x y
x 2 f 2 f 2 f 2 ,试 2 y x x y y2
.17853 .17635 .17109 .16302
y
x
i
1.6
i
1.9
2.2
2.5
2.8
3.1
3.4
3.7
4
4.3
4.6
4.9
.15255 .1402
.12655 .11219 .09768 .08353 .07015 .05786 .04687 .03729 .02914 .02236
y
i
【求解】用下面的语句可以立即得出给定样本点数据的三次插值与样条 插值,得出的结果如,可见,用两种插值方法对此例得出的结果几乎一 致,效果均很理想。 >> x=[-2,-1.7,-1.4,-1.1,-0.8,-0.5,-0.2,0.1,0.4,0.7,1,1.3,... 1.6,1.9,2.2,2.5,2.8,3.1,3.4,3.7,4,4.3,4.6,4.9]; y=[0.10289,0.11741,0.13158,0.14483,0.15656,0.16622,0.17332,... 0.1775,0.17853,0.17635,0.17109,0.16302,0.15255,0.1402,... 0.12655,0.11219,0.09768,0.08353,0.07019,0.05786,0.04687,... 0.03729,0.02914,0.02236]; x0=-2:0.02:4.9; y1=interp1(x,y,x0,'cubic'); y2=interp1(x,y,x0,'spline'); plot(x0,y1,':',x0,y2,x,y,'o')
MATLAB期末上机试题带答案
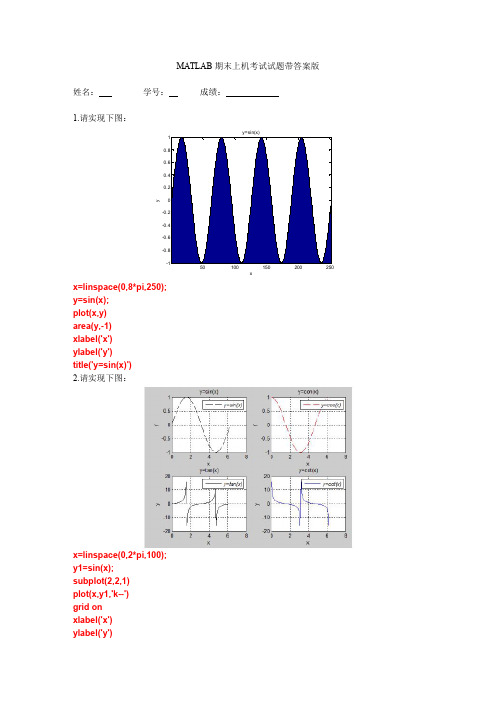
MATLAB 期末上机考试试题带答案版姓名:学号:成绩:1.请实现下图:50100150200250x y x=linspace(0,8*pi,250);y=sin(x);plot(x,y)area(y,-1)xlabel('x')ylabel('y')title('y=sin(x)')2.请实现下图:x=linspace(0,2*pi,100);y1=sin(x);subplot(2,2,1)plot(x,y1,'k--')grid onxlabel('x')ylabel('y')title('sin(x)')legend('y=sin(x)')y2=cos(x);subplot(2,2,2)plot(x,y2,'r--')grid onxlabel('x')ylabel('y')title('cos(x)')legend('y=cos(x)')y3=tan(x);subplot(2,2,3)plot(x,y3,'k-')grid onxlabel('x')ylabel('y')title('tan(x)')legend('y=tan(x)')y4=cot(x);subplot(2,2,4)plot(x,y4)grid onxlabel('x')ylabel('y')title('cot(x)')legend('y=cot(x)')3.解方程组:a=[321;1-13;24-4];b=[7;6;-2];x=a\b4.请实现下图:x y x=linspace(0,4*pi,1000);y1=sin(x);y2=sin(2*x);plot(x,y1,'--',x,y2,'b*')grid onxlabel('x');ylabel('y');title('耿蒙蒙')legend('sin(x)','sin(2*x)')5.请在x ,y 在(-2,2)内的z=xexp (-x 2-y 2)绘制网格图[x,y]=meshgrid(-2:0.1:2);z=x.*exp (-x.^2-y.^2);mesh(x,y,z)6.请实现peaks 函数:-33x Peaksy [x,y]=meshgrid(-3:1/8:3);z=peaks(x,y);mesh(x,y,z)surf(x,y,z)shading flataxis([-33-33-88])xlabel('x');ylabel('y');title('Peaks')7.请在x=[0,2],y=[-0.5*pi,7.5*pi],绘制光栅的振幅为0.4的三维正弦光栅。
matlab上机练习及答案

第二、三次上机练习:目的:运行课本第四章及课堂上讲过的例子,掌握Matlab 的流程控制语句、函数及脚本文件的编程、调试方法。
作业:1、 完成下列操作:1) 求[100,999]之间能被21整除的个数。
2) 建立一个字符串向量(要求字符串向量中必须包含自己的姓名首字母,大小写均可),删除其中的大写字母2. 编写脚本文件,实现用magic(6)产生一矩阵,用for 循环指令求解其所有元素的和。
3. 定义一个函数文件,求∑=ni m i 1,要求在函数文件中包含能够通过help 查询到的说明;然后调用该函数文件求∑∑∑===++101501210011k k k k k k 的值。
4. 已知)7.1cos(12ln )7.1sin(++++=x xx y π,当x 取-3.0,-2.9,-2.8,…,2.8,2.9,3.0时, 1) 求各点的函数值;2) 求这些数据的平均值;5、求分段函数的值。
222603565231x x x x y x x x x x x x ⎧+-<≠-⎪=-+≤<≠≠⎨⎪--⎩, 且, 0且及, 其它用if 语句实现,分别输出x=-5.0,-3.0,1.0,2.0,2.5时的值。
6、输入一个百分制成绩,要求输出成绩等级A 、B 、C 、D 、E 。
其中90分~100分为A ,80分~89分为B ,70分~79分为C ,60分~69分为D ,60分以下为E 。
要求:分别用if 语句和switch 语句实现。
7、根据222221111...,6123n ππ=++++求的近似值。
当n 分别取100、1000、10000时,结果是多少?(要求:分别用循环结构和向量运算来实现)8、已知n=1时,f 1=1;n=2时,f 2=0;n=3时,f 3=1;n>3时,f n =f n-1 -2f n-2+ f n —3; 求f 1~ f 100中,最大值、最小值以及各数之和。
Matlab上机实验题及参考解答

Matlab上机实验题及参考解答目录实验一Matlab初步实验 (2)一matlab基本功能介绍 (2)二Matlab扩展功能 (2)三练习 (2)四练习题参考解答 (3)实验二概率模型实验 (5)一复习 (5)二事件的响应 (5)三Matlab中随机数字的生成与处理 (5)四练习 (5)五练习题参考解答 (5)实验三插值与拟合 (7)实验四线性规划与非线性规划 (8)4.1 实验目的 (8)4.2 实验内容 (9)4.3 综合练习 (10)4.4 课外作业 (11)实验五数值计算 (12)5.1 实验目的 (12)5.2 实验内容 (12)4.3 综合练习 (15)4.4 课外作业 (15)实验六计算机图像处理 (16)6.1 实验目的 (16)6.2 实验内容 (16)6.3 综合练习 (17)6.4 课外作业 (19)实验七综合练习 (19)7.1 实验目的 (19)7.2 实验内容 (19)7.3 综合练习 (20)7.4 课外作业 (21)实验一 Matlab 初步实验 一 matlab 基本功能介绍1 编程环境2语法规范:for … end; if …else if …end; 3 矩阵运算 4 图形绘制二 Matlab 扩展功能1 编程练习:(1) 绘出序列kk x x r r 0(1),0.2083=+=;(2) 绘出曲线rtx t x e t 0(),0=>2 扩展功能(1) 矩阵中全部数据、部分数据的截取、更改; (2) 矩阵的初始化与赋值如:A=zeros(5,5); A(2:2:)=[1,2 3 4 5] 3 微积分基础(见实验4) 符号计算三 练习(课上编程完成下列练习,课后上机验证) 1 求和S=1+2+3+…+100; 2 求和e 1111!2!10!1...=++++3求和S 1112310!1...=++++4设A 234576138⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦, 求A 的逆、特征值和特征向量;验证Ax=λx 5 画函数图()011mrtm x x t x e x -=⎛⎫+- ⎪⎝⎭6 展开 (x-1)(x-2)…(x-100)7 因式分解 x 8—y 8; 因数分解200520068 求极限312lim +∞→⎪⎭⎫⎝⎛++n n n n9 )](sin[cos 22x x y += 求dxdy10 求积分x xdx 10ln ⎰11 求积分3⎰并且画出所求的平面区域12 设x+2y=1, 2x+3y=6, y=2x 2, 画出各个方程图形,求出曲线交点.四 练习题参考解答%MatlabTrain1.m clear all % 2nd e=1; temp=1; for I=1:1:10temp=temp*I; e=e+1/temp; end e%%%%%%%%%%% clear all % 3nd S=0; temp=1;for I=1:1:100temp=temp*I; endfor J=1:1:temp S=S+1/J; end S%%%%%%%%%%%%%% clear all % 11ndx=linspace(0,4); y=1./sqrt(x.^5+1); plot(x,y) for t=1:0.1:3yt=1./sqrt(t.^5+1);hold online([t,t],[0,yt]);end%fill(t,yt,'b') %%%%%%%%%%%%% clear all% 12ndx=linspace(-2,2);y=[0.5-0.5*x; 2-2/3.*x; 2*x.^2]; plot(x,y)grid实验二概率模型实验一复习1 小结上次编程练习中存在的问题,讲述部分习题答案2 画图命令介绍:line二事件的响应(1) 获取鼠标的位置%MatlabTrain2.mclear all% 鼠标响应p=ginput(3)plot(p(:,1),p(:,2),'r*')(2) 键盘输入相应t=input('How many apples? t=');m=t+3三Matlab中随机数字的生成与处理1 随机数的生成2 产生随机数字3 产生某区间的整数4 生日模拟问题的Montecaro法设计技术、思路学生尝试编程四练习(1) 编程验证人数在不同年龄段的生日的概率计算(2) 编程实现游戏”聪明伶俐100分”(3) 编程实现两家电影院的座位数问题(4) 编程实现某图形面积的计算五练习题参考解答(1) 生日问题程序示例:%birthPro.mn=0;nStudents=30;for I=1:1000 %how many times testy=0;x=1+floor(365*rand(1,nStudents));%get nStudents random numbersfor J=1:nStudents-1for K=J+1:nStudentsif x(J)==x(K)y=1;break;endendendn=n+y;%count, n times of that there are two people's dirthday in the same dayendfreq=n/I % caculating the frequently(2) 编程实现游戏”聪明伶俐100分”参考答案%MatlabTrain2.mclear all% 鼠标响应x=floor(10*rand(1,4))t=input('填入四个数字[n1 n2 n3 n4]=');flag=0;A=0;B=0;for I=1:1:8flag=flag+1;A=0;B=0;if t==xswitch flagcase 1disp('聪明绝顶!');case 2disp('聪明!');case 3disp('有点聪明!');case 4disp('还可以!');case 5disp('聪明伶俐100分!');case 6disp('聪明伶俐90分!');case 7disp('聪明伶俐85分!');case 8disp('聪明伶俐80分!');otherwisedisp('赫赫!');endbreak;endfor J=1:1:4for K=1:1:4if x(J)==t(K) & J==KA=A+1;else if x(J)==t(K) & J~=KB=B+1;endendendends='AABB';s(1)=INT2STR(A);s(3)=INT2STR(B);disp(s);t=input('不重复填入四个数字[n1 n2 n3 n4]=');endif flag>0disp('太烂了! 正确答案是:');xend实验三插值与拟合一复习讲述聪明伶俐100分的编程中的问题二插值三拟合课堂练习2 某之股票价格from 2003 09 01 to 2004 01 02,试进行插值、拟合%TimerS.m%from 2003 09 01 to 2003 01 02clear all;dataST=[15.09 14.7514.95 14.722.88 21.8619.82 19.09];plot(dataST)四课外练习112)进行多项式拟合,求出拟合多项式,并求出多项式在t=4, 5处的值.实验四线性规划与非线性规划4.1 实验目的1 用Matlab求解线性规划2 用Matlab求解非线性规划4.2 实验内容4.2.1 线性规划求解实用格式:x=lp(c, A, b, xLB,xUB,x0,nEq)可以求解下列线性规划模型:min f=c’xs.t. Ax=<=b(其中前nEq个约束为等式约束,即等式约束的个数,其余是不等式约束<=) xLB<=x<=xUB函数中x0参数是算法迭代的初始点,任意取值例1 求解下列线性规划1)123123123123min2..360210200,1,2,3jz x x xs t x x xx x xx x xx j=--+⎧⎪++≤⎪⎪-+≤⎨⎪+-≤⎪≥=⎪⎩,2)1235635623416367min..3621060,1,,7jz x x x x xs t x x xx x xx xx x xx j=-++-⎧⎪++=⎪⎪+-=⎪⎨-+=⎪⎪++=⎪≥=⎪⎩例1求解示例c=[-2 -1 1]';%book page 72 Number 16-1A=[3 1 1;1 -1 2;1 1 -1];b=[60 10 20]';xlb=[0 0 0]';xub=[inf inf inf]';x0=[0 0 0]'; x=lp(c,A,b,xlb,xub,x0,0)% x=(15 5 0)'例2 求解示例c2=[1 -1 1 0 1 -1 0]';%book page 72 Number 16-3A2=[0 0 3 0 1 1 0;...0 1 2 -1 0 0 0;...-1 0 0 0 0 1 0;...0 0 1 0 0 1 1];b2=[6 10 0 6]';xlb2=[0 0 0 0 0 0 0]';xub2=[inf inf inf inf inf inf inf]';x02=[0 0 0 0 0 0 0]';x2=lp(c2,A2,b2,xlb2,xub2,x02,4)% unbounded4.2.2 非线性规划1)命令格式1:[X, OPTIONS]=constr(‘FUN’, X, OPTIONS,VLB,VUB)2)命令格式2:X=FMINCON(FUN,X0,A,B,Aeq,Beq)% minimizes FUN subject to the linear equalities% Aeq*X = Beq as well as A*X <= B. (Set A=[] and B=[] if no inequalities exist.)例2 求解非线性规划y x x x x s t x3211221min22 ..1=++-≤-求解示例%unconop.mfunction y=unconop(x)y=x(1).^3+2*x(1).*x(2)+2*x(2).^2;%book page 148 ex.7-1 后建立调用函数xx=fmincon('unconop',[0 0]',[-1 0],-1,[],[])%book page 148 ex.7-1 4.3 综合练习学生独立编写程序,求解一个含有2个变量的线性规划问题,要求:1)编写程序,把可行域画上阴影;2)求出最优解,在可行域上标出最优解;3)求出基本解,并在上图中表示出来;4)求出基本可行解,观察单纯形方法迭代时,顶点的变化.可行域画图与表出阴影示例:syms x y[u(1),v(1)]=solve('y=x+2','y=2*x');%求出交点坐标[u(2),v(2)]=solve('y=-x+2','y=2*x');[u(3),v(3)]=solve('y=x+2','y=-x+2');x=linspace(0,3,5); %直线作图y=[2*x;-x+2;x+2];line(x,y); gridpatch(double(u),double(v),'b'); 运行结果:4.4 课外作业1 求解线性规划131223min ..250.530,1,2,3i x x s t x x x x x i +⎧⎪+≤⎪⎨+=⎪⎪≥=⎩ (1) 求解线性规划;x *=()(2) 目标函数中c 1由1变为(-1.25)时求最优解;(3) 目标函数中c 1由1变为(-1.25),c 3由1变为2时求最优解;(4) 约束条件中53b ⎛⎫= ⎪⎝⎭变为21b -⎛⎫'= ⎪⎝⎭时,求解;(5) 约束条件中53b ⎛⎫= ⎪⎝⎭变为23b ⎛⎫'= ⎪⎝⎭时,求解[刁在筠,运筹学(第二版),高等教育出版社,2004,01 p74第20题]2 求解非线性规划y x x x x x x x 3221122233min 2223=++++ 注:无约束非线性规划问题, 命令:fminunc子函数% unconop.mfunction y=unconop(x)y=x(1).^2+2*x(1).*x(2)+2*x(2).^2+2*x(2).*x(3)+3*x(3).^2;%book page 148 ex.7-1 主函数:xx=fminunc('unconop',[0.1 0.1 1]')思考:绘出两个变量的线性规划问题的可行域、标出可行的整数解和求出可行解;演示单纯形方法的迭代过程,如j z x x s t x x x x x j 121212min 2..360200,1,2=--⎧⎪+≤⎪⎪+≤⎨⎪⎪≥=⎪⎩实验五 数值计算5.1 实验目的1 掌握代数数值计算2 掌握常微分方程数值计算5.2 实验内容5.2.1 关于多项式设多项式1110()n n n n p x a x a x a x a --=++++表示为110[,,,,]n n p a a a a -=1)求多项式的根 roots(p) %求出p(x)=0的解。
matlab上机练习答案

实验一MA TLAB的基本命令与基本函数1已知矩阵a =11 12 13 1421 22 23 2431 32 33 3441 42 43 44求(1) A(:,1) (2) A(2,:)(3) A(:,2:3) (4) A(2:3,2:3)(5) A(:,1:2:3) (6) A(2:3)(7) A(:) (8) A(:,:)(9) ones(2,2) (10) eye(2)(11) [A,[ones(2,2);eye(2)]](12) diag(A) (13) diag(A,1)(14) diag(A,-1) (15) diag(A,2)2(1)输入如下矩阵A0π/3A=π/6 π/2(2) 求矩阵B1,B1中每一元素为对应矩阵A中每一元素的正弦函数(3) 求矩阵B2, B2中每一元素为对应矩阵A中每一元素的余弦函数(4) 求B12+B22(5) 求矩阵A的特征值与特征矢量:称特征矢量为M,而特征值矩阵为L(6) 求Msin(L)M-13已知水的黏度随温度的变化公式为μ=μ0/(1+at+bt2)其中μ0=1.785×10-3,a=0.03368,b=0.000221,求水在0,20,40,80℃时的黏度。
程序如下:miu0=1.785e-3;a=0.03368;b=0.000221;t=0:20:80miu=miu0./ (1+a*t+b*t.^2)(2)一个长管,其内表面半径为a,温度为Ta ;外表面半径为Tb;则其径向和切向应力可分别表示为:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛+----=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛----=r b a b r b a b a a b v T T E r b a b r b a b a a b v T T E b a t b a r ln ln 11)/ln()1(2)(ln ln 1)/ln()1(2)(2222222222ασασ式中r 为管子的径向坐标,E 为管子材料的弹性模量,ɑ为热膨胀系数。
Matlab上机题库及详细答案_Tonyxie

ax 2 + bx + c 0.5 ≤ x < 1.5 = y a sin c b + x 1.5 ≤ x < 3.5 c ln b + 3.5 ≤ x < 5.5 x
clc;clear; a=input('Please input a= '); b=input('Please input b= '); c=input('Please input c= '); x=input('Please input x= '); disp('#if#'); if x>=0.5&x<1.5 y=a*x^2+b*x+c elseif x<3.5&x>=1.5 y=a*sin(b)^c+x elseif x>=3.5&x<5.5 y=log(abs(b+(c./x))) else y='ERROR!' end disp('#switch#') switch(x*10/5) case {1 2} y=a*x^2+b*x+c case {3 4 5 6} y=a*sin(b)^c+x case {7 8 9 10} y=log(abs(b+(c./x))) otherwise y='ERROR!' end
பைடு நூலகம்
8、数值与符号计算
ex (1)求极限 lim x →+∞ a + be x
(3)已知线性方程组 Ax=b,其中
(2)求不定积分
∫ xe
ax
Matlab上机题及答案

1 一个三位整数各位数字的立方和等于该数本身则称该数为水仙花数。
输出全部水仙花数。
for m=100:999m1=fix(m/100); %求m的百位数字m2=rem(fix(m/10),10); %求m的十位数字m3=rem(m,10); %求m的个位数字if m==m1*m1*m1+m2*m2*m2+m3*m3*m3disp(m)endend2.从键盘输入若干个数,当输入0时结束输入,求这些数的平均值和它们之和。
sum=0;n=0;val=input('Enter a number (end in 0):');while (val~=0)sum=sum+val;n=n+1;val=input('Enter a number (end in 0):');endif (n > 0)summean=sum/nend3. 若一个数等于它的各个真因子之和,则称该数为完数,如6=1+2+3,所以6是完数。
求[1,500]之间的全部完数。
for m=1:500s=0;for k=1:m/2if rem(m,k)==0s=s+k;endendif m==sdisp(m);endend4. 从键盘上输入数字星期,在屏幕上显示对应英文星期的单词。
function weekn=input('input the number:');if isempty(n)errror('please input !!')endif n>7|n<1error('n between 1 and 7')endswitch ncase 1disp('Monday')case 2disp('Tuesday')case 3disp('Wednesday')case 4disp('Thursday')case 5disp('Friday')case 6disp('Saturday')case 7disp('Sunday')end5. 某公司销售电脑打印机的价格方案如下:()如果顾客只买一台打印机,则一台的基本价格为$150。
Matlab上机实验答案

0.2000 0.1667 0.1429 0.1250 0.1111
1 1 1 1 1
1 2 3 4 5
1 3 6 10 15
1 4 10 20 35
1 5 15 35 70
>> Hh=det(H) Hh =
3.7493e-12 >> Hp=det(P) Hp =
1
>> Th=cond(H) Th =
0 0 1.0000 0 0
0.8147 0.9058 0.1270 1.0000 0
0.9134 0.6324 0.0975 0 2.0000
>> A^2
ans =
1.0000 0 0 0 0 >> [E,R+R*S;O,S^2]
0 1.0000 0 0 0
0 0 1.0000 0 0
1.6294 1.8116 0.2540 1.0000 0
阵和对角阵,试通过数值计算验证 A >> E=eye(3); >> R=rand(3,2); >> O=zeros(2,3); >> S=diag(1:2); >> A=[E,R;O,S]
E O
R RS 。 S2
A=
1.0000 0 0 0 0
0 1.0000 0 0 0
3. 建立一个 5×5 矩阵,求它的行列式值、迹、秩和范数。 >> A=rand(5) A= 0.2785 0.5469 0.9575 0.9649 0.1576 >> det(A) ans = -0.1322 >> trace(A) ans = 3.4127 >> rank(A) ans = 0.9706 0.9572 0.4854 0.8003 0.1419 0.4218 0.9157 0.7922 0.9595 0.6557 0.0357 0.8491 0.9340 0.6787 0.7577 0.7431 0.3922 0.6555 0.1712 0.7060
Matlab上机题库及详细答案

解:c=input('请输入一个字符','s');
if c>='A' & c<='Z'
disp(setstr(abs(c)+abs('a')-abs('A')));
elseif c>='a'& c<='z'
disp(setstr(abs(c)- abs('a')+abs('A')));
(2)均值为0.6方差为0.1的5阶正态分布随机矩阵
解:>>x=20+(50-20)*rand(5);
>>y=0.6+sqrt(0.1)*randn(5)
例13:将101~125等25个数填入一个5行5列的表格中,使其每行每列及对角线的和均为565。
解:M=100+magic(5)
M =117 124 101 108 115
-0.4606
0.3848
例2、用简短命令计算并绘制在0x6范围内的sin(2x)、sinx2、sin2x。
解:x=linspace(0,6)
y1=sin(2*x),y2=sin(x.^2),y3=(sin(x)).^2;
plot(x,y1,x, y2,x, y3)
例3:画出指数衰减曲线y1=exp(-t/3)*sin(3*t)和它的包络y2=exp(-t/3),t的取值范围是(0,4pi)。
matlab上机考试题及答案

matlab上机考试题及答案1. 题目:编写一个MATLAB函数,计算并返回一个向量中所有元素的平方和。
答案:函数定义如下:```matlabfunction sumOfSquares = calculateSumOfSquares(vector)sumOfSquares = sum(vector.^2);end```2. 题目:使用MATLAB的内置函数,找出一个矩阵中的最大元素及其位置。
答案:可以使用`max`函数来找出矩阵中的最大元素,同时使用`find`函数来获取其位置。
示例代码如下:```matlabA = [1, 2, 3; 4, 5, 6; 7, 8, 9];[maxValue, linearIndex] = max(A(:));[row, col] = ind2sub(size(A), linearIndex);```3. 题目:给定一个向量,使用MATLAB编写代码,实现向量元素的逆序排列。
答案:可以使用`flip`函数来实现向量的逆序排列。
示例代码如下:```matlabvector = [1, 2, 3, 4, 5];reversedVector = flip(vector);```4. 题目:编写一个MATLAB脚本,计算并绘制一个正弦波的图像。
答案:可以使用`sin`函数生成正弦波数据,并使用`plot`函数绘制图像。
示例代码如下:```matlabx = linspace(0, 2*pi, 100);y = sin(x);plot(x, y);xlabel('x');ylabel('sin(x)');title('Sine Wave');```5. 题目:给定一个3x3的矩阵,使用MATLAB编写代码,计算其行列式。
答案:可以使用`det`函数来计算矩阵的行列式。
示例代码如下:```matlabmatrix = [1, 2, 3; 4, 5, 6; 7, 8, 9];determinant = det(matrix);```结束语:以上是MATLAB上机考试的题目及答案,希望能够帮助大家更好地掌握MATLAB的编程技巧和函数使用。
Matlab上机题库及详细答案

case num2cell(25:49) %价格大于等于2500但小于5000
Байду номын сангаасrate=10/100;
otherwise %价格大于等于5000
rate=14/100;
end
price=price*(1-rate) %输出商品实际销售价格
例19已知,当n=100时,求的值。
解:程序如下:
y=0;n=100;for i=1:n;y=y+1/(2*i-1);End
例20:一个三位整数各位数字的立方和等于该数本身则称该数为水仙花数。输出全部水仙花数
解:for m=100:999
m1=fix(m/100);m2=rem(fix(m/10),10);m3=rem(m,10);
if m==m1*m1*m1+m2*m2*m2+m3*m3*m3;disp(m);end
D=diag(1:5);D*A %用D左乘A,对A的每行乘以一个指定常数
例15:输入x,y的值,并将它们的值互换后输出。
程序如下:
x=input('Input x please.');y=input('Input y please.');z=x;x=y;y=z;
disp(x);disp(y);
例16::求一元二次方程ax2 +bx+c=0的根。
switch fix(price/100)
case {0,1} %价格小于200
rate=0;
case {2,3,4} %价格大于等于200但小于500
rate=3/100;
case num2cell(5:9) %价格大于等于500但小于1000
完整版本matlab上机练习试题含答案

1.计算 a6 9 3 2 4 1 的数组乘积1 71618 82 7 与 b6 8 5 计算多项式除法 (3x 3+13 x 2+6x+8)/( x+4)54>> a=[6 9 3;2 7 5]; >> d=deconv([3 13 6 8],[1 4])>> b=[2 4 1;4 6 8]; d =>> a.*b 31 2ans =6 求欠定方程组2 4 7 4x 8 的最小范数解12 3639 35 6 584240>> a=[2 4 7 4;9 3 5 6];4 9 2 37>> b=[8 5]';>> x=pinv(a)*b2.对于 AXB ,假如 A7 6 4 ,B 26,求解 X 。
3 5 728x =-0.2151>> A=[4 9 2;7 6 4;3 5 7]; 0.4459 >> B=[37 26 28] ’;0.7949 >> X=A\B 0.2707X =7 用符号函数法求解方程 at 2+b* t+c=0-0.5118 >> r=solve('a*t^2+b*t+c=0','t') 4.0427 r =1.3318[ 1/2/a*(-b+(b^2-4*a*c)^(1/2))] 1 2 5 , b8 7 4 [ 1/2/a*(-b-(b^2-4*a*c)^(1/2))]3. a64 362 ,察看 a 与 b 之间的3a 11 a 12六种关系运算的结果8求矩阵 A的队列式值、逆和特点根a 21 a 22 >> a=[1 2 3;4 5 6];>> b=[8 –7 4;3 6 2]; >> syms a11 a12 a21 a22; >> a>b >> A=[a11,a12;a21,a22]ans =>> AD=det(A) % 队列式 0 1 0 >> AI=inv(A) % 逆 11>> AE=eig(A) % 特点值>> a>=b A =ans =[ a11, a12] 0 1 0 [ a21, a22] 11AD =>> a<b a11*a22-a12*a21 ans =AI =1 0 1 [ -a22/(-a11*a22+a12*a21), a12/(-a11*a22+a12*a21)]1[ a21/(-a11*a22+a12*a21), -a11/(-a11*a22+a12*a21)] >> a<=b AE =ans =1 0 1 [ 1/2*a11+1/2*a22+1/2*(a11^2-2*a11*a22+a22^2+4*a12*a21)^(1/2)]1>> a==b [ 1/2*a11+1/2*a22-1/2*(a11^2-2*a11*a22+a22^2+4*a12*a21)^(1/2)]ans =9 因式分解: x 45x 3 5 x 2 5x 60 0 0 >> syms x;>> f=x^4-5*x^3+5*x^2+5*x-6; >> a~=b >> factor(f) ans =ans =1 1 1 (x-1)*(x-2)*(x-3)*(x+1) 111ax 214 计算多项式乘法 (x 2+2x+2)(x 2+5x+4),用符号微分求 df/dx 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 一个三位整数各位数字的立方和等于该数本身则称该数为水仙花数。
输出全部水仙花数。
for m=100:999
m1=fix(m/100); %求m的百位数字
m2=rem(fix(m/10),10); %求m的十位数字
m3=rem(m,10); %求m的个位数字
if m==m1*m1*m1+m2*m2*m2+m3*m3*m3
disp(m)
end
end
2.从键盘输入若干个数,当输入0时结束输入,求这些数的平均值和它们之和。
sum=0;
n=0;
val=input('Enter a number (end in 0):');
while (val~=0)
sum=sum+val;
n=n+1;
val=input('Enter a number (end in 0):');
end
if (n > 0)
sum
mean=sum/n
end
3. 若一个数等于它的各个真因子之和,则称该数为完数,如6=1+2+3,所以6是完数。
求[1,500]之间的全部完数。
for m=1:500
s=0;
for k=1:m/2
if rem(m,k)==0
s=s+k;
end
end
if m==s
disp(m);
end
end
4. 从键盘上输入数字星期,在屏幕上显示对应英文星期的单词。
function week
n=input('input the number:');
if isempty(n)
errror('please input !!')
end
if n>7|n<1
error('n between 1 and 7')
end
switch n
case 1
disp('Monday')
case 2
disp('Tuesday')
case 3
disp('Wednesday')
case 4
disp('Thursday')
case 5
disp('Friday')
case 6
disp('Saturday')
case 7
disp('Sunday')
end
5. 某公司销售电脑打印机的价格方案如下:
()如果顾客只买一台打印机,则一台的基本价格为$150。
()如果顾客购买两台以上打印机,则第二台价格为$120。
()第三台以后,每台$110。
写一段程序分别计算出购买1--10台打印机所需的钱数。
打印机台数可以在程序开始处指定,或通过input命令读入。
运行程序,计算出购买10台打印机的总价格。
写出程序,生成分别购买1--10台打印机所需价格的图表(使用fprintf命令输出图表,不允许手算)。
x=input('请输入购买的打印机台数:');
for m=1:x
if m<=1
y(m)=150*m;
elseif m<=2
y(m)=150+120*(m-1);
else y(m)=150+120+110*(m-2);
y(1,m)=y(m);
end
end
y(x)
plot(1:m,y,'r*--')
6. 有一组学生的考试成绩(见表),根据规定,成绩在100分时为满分,成绩在90~99之间时为优秀,成绩在80~89分之间时为良好,成绩在60~79分之间为及格,成绩在60分以下时为不及格,编制一个根据成绩划分等级的程序。
作业4 绘图练习
1、有一组测量数据满足-at e=y,t的变化范围为0~10,用不同的线型和标记点画出a=0.1、a=0.2和a=0.5三种情况下的曲线。
图中添加标题-at e=y(title)和图例框(图注legend)。
2.20 在5.1题结果图中添加标题-at e=y,并用箭头线标识出各曲线a的取值。
2.21 在5.1题结果图中添加标题-at e y和图例框。
2、绘制三维曲线:x=sin(t); y=cos(t); z=cos(2*t);并设计标题和图注。
>>t=(0:0.02:2)*pi;
>>x=sin(t);y=cos(t);z=cos(2*t);
>>plot3(x,y,z,'b-',x,y,z,'bd')
>>view([-82,58]),box on
>>xlabel('x'),ylabel('y'),zlabel('z')
>>legend('链','宝石','Location','best')
3、在同一窗口中画出一个正六变形、半径为1的圆以及球。
并标明各自的标题
4、2
2y x xe z --=,当x 和y 的取值范围均为-2到2时,用建立子窗口的方法在同一个图形窗口中绘制出三维线图(plot3)、网线图(mesh)、表面图(surf)和带渲染效果(shading interp)的表面图,标明图形的标题,使图像完美。
>> [x,y]=meshgrid([-2:.2:2]);
>> z=x.*exp(-x.^2-y.^2);
>> mesh(x,y,z)
>> subplot(2,2,1),plot3(x,y,z)
>> title('plot3(x,y,z)')
>> subplot(2,2,2),mesh(x,y,z)
>> title('mesh(x,y,z)')
>> subplot(2,2,3),surf(x,y,z)
>> title('surf(x,y,z)')
>> subplot(2,2,4),surf(x,y,z),shading interp >> title('surf(x,y,z),shading interp')。
