三角形培优训练100题集锦(学生用)
初一下学期三角形培优专题训练

初一下学期三角形培优专题训练专题一:8字形图型1. 如图所示•求 / A+Z B+Z C+Z D+Z E的大小。
3 .如图:Z A+Z B+Z C+Z D+Z E+Z F 等于()A、180° B 、360 ° C 、270 ° D 、540°A+Z B+Z C+Z D+Z E+Z F 的大小.4.已知,如图, A B C D E F的度数为B C D E F G n度DE是Z CDB的平分线,ZA1 + Z2 +Z3 +Z 4+Z 5+Z 6+Z 7=6. 如图,7. 如图Z&如图AE是Z CAB的平分线,90 ,则n=C=40°,Z E=35° .求Z B的度数.ECEB2•如图是一个六角星,其中AOE60 , A5.如图所示.求Z专题二:燕尾形图型1. (2010?帛州)如图,/ BDC=98,A. 61°B. 60°2. 如图所示,已知/ 1=20°,/ 2=25°A. 60°B. 70 °3. 如图,已知DABC边BC延长线上一点,DF丄AB于F交AC于E, / A=35° ,? / D=42°求/ ACD的度数.4. 如图,直线DE交厶ABC的边AB、AC于D E,/ACB= 74°,/ AED= 48°,则/ BDF的度数是—5.知:如图,点E在AC上,点F在AB上, BE CF交于点O且/ C—/B= 20°,/ EO F/ A= 70°,求/ C的度数.6.下图,BE是/ ABD的角平分线,CF是/ ACD的角平分线,BE与CF交于点G,点/BDC=140 , / BGC=110,则/ A的度数为()A. 70°B. 75C.80°D.85°:C=38,/ /B=23°,/ A的度数是()C.37°D. 39°,/ A=35,则/ BDC的度数为()C.80°D. 85°专题三:双垂直型1 如图所示,在△ ABC 中,/ ACB=90,/ ABC=25 , CDLAB 于 D,则/ AC ________________ 度2.图,在△ ABC 中,/ ACB=90 , CDLAB,垂足为 D.下列说法不正确的是( )A.与/ 1互余的角只有/ 2 B .Z A 与/ B 互余C.Z 仁/ B D.若/ A=2/ 1,则/ B=30°3 .如图,AC 丄BD, DE I AB,下列叙述正确的是()4 如图,△ ABC 中,Z BAC=90 , AD 丄BC 于 D, E 是 AD 上一点, 求证:Z BED>Z C5. 如图,在 VABC C 中, ACB 90 , CD 1 2A.Z A=Z BB.Z B=Z DC.Z A=ZDD.AB , AF 是角平分线,交 CD 于点E ,求证专题四:三角形三条角平分线型1如图①,BD CD 是/ ABC 和/ACB 的角平分线且相交于点 D,请猜想/ A 与/ BDC 之间的 数量关系,并说明理由。
三角形培优精选题大全
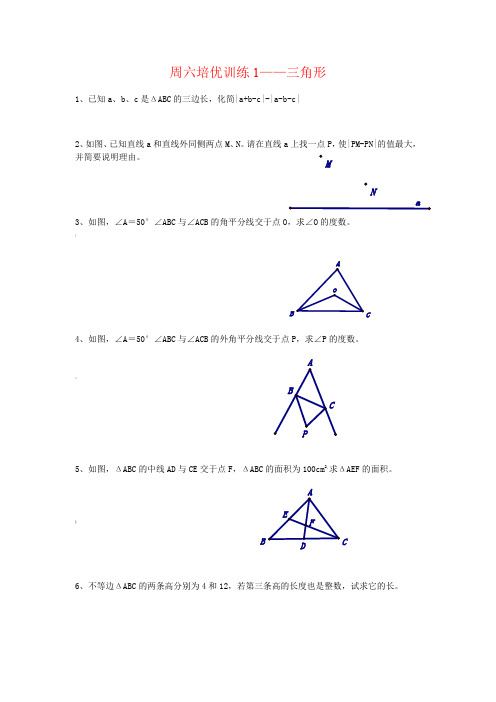
周六培优训练1——三角形1、已知a、b、c是ΔABC的三边长,化简|a+b-c|-|a-b-c|2、如图、已知直线a和直线外同侧两点M、N。
请在直线a上找一点P,使|PM-PN|的值最大,并简要说明理由。
3、如图,∠A=50°∠ABC与∠ACB的角平分线交于点O,求∠O的度数。
\4、如图,∠A=50°∠ABC与∠ACB的外角平分线交于点P,求∠P的度数。
^5、如图,ΔABC的中线AD与CE交于点F,ΔABC的面积为100cm2,求ΔAEF的面积。
)6、不等边ΔABC的两条高分别为4和12,若第三条高的长度也是整数,试求它的长。
aMNBB C~10、“转化”是数学中的一种重要思想,即把陌生的问题转化成熟悉的问题,把复杂的问题转化为简单的问题,把抽象的问题转化为具体的问题。
(1) 根据已经学过的知识求知道星形(图1)中∠A+∠B+∠C+∠D+∠E= ,若对图1中星形截去一个角,如图2,请你求出∠A+∠B+∠C+∠D+∠E+∠F 的度数。
(需要写出解题过程)(2)若再对图2中的角进一步截去,你能由题1中所得的方法或规律,猜想出图3中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N 的度数吗(只要写出结论,不需要写出解题过程。
)|1、①求下图各角度数之和。
②如图,已知∠BOF=120°,则∠A+∠B+∠C+∠D+∠E+∠F=__________.]3、如图△ABC 中, ∠BAD=∠CBE=∠ACF, ∠ABC=50°,∠ACB=62°,求∠DFE 的大小。
EDCBA FMK N7、三角形的最大角与最小角之比是4:1,则最小内角的取值范围是多少)9.如图,在△ABC 中,∠ABC = ∠ACB ,∠A = 40°,P 是△ABC 内一点,且∠1 = ∠2.则∠BPC =________。
第七章 三角形7.已知a,b,c 是△ABC 的三边 (1)化简|a+b-c |+|b-a-c |-|c+b-a | (2)|a-b+c |+|b-c+a |-|a-b-c |8.如图,P 是△ABC 内一点,试证明PA+PB+PC>1/2(AB+BC=AC)9.在△ABC 中,∠A=50°,点D,E 分别在AB,AC 上,EF 平分∠CED,DF 平分∠BDE,则∠F='11.在△ABC 中,AB=AC,AC 边上的中线BD 把△ABC 的周长分为12CM 和15CM 两部求三角形的各边长12.五种基本图形(必会):写出∠BOC 与∠A 之间的数量关系。
三角形认识培优

1、下列条件:①∠A+∠B=∠C ,②∠A :∠B :∠C=2:3:4,③∠A=90°-∠B ,④∠A=∠B= 12∠C ;其中能判断△ABC 是直角三角形的有( )个 A 、1 B 、2 C 、3 D 、42、如图,在△ABC 中,CD ⊥BC 于点C ,点D 在AB 的延长线上,则CD 是△ABC 的( )A 、BC 边上的高B 、AB 边上的高C 、AC 边上的高D 、以上都不对3、已知不等腰三角形的两边长分别是2cm 和9cm ,如果第三边长是整数,那么第三边长为( )cmA 、8B 、10C 、8或10D 、8或9或104、下列说法中正确的是( )①三角形三条中线都在三角形内部,②三角形三条角平分线都在三角形内部,③三角形三条高都在三角形内部;A 、①②③B 、①②C 、②③D 、①③5、如图所示,在△ABC 中,已知点D ,E ,F 分别为BC ,AD ,CE 的中点,且S △BEF =4cm 2,则△AEC 的面积是( )cm 2A 、4.5B 、2.25C 、4D 、56、以下列长度的线段为边,能构成三角形的是( )A 、3,6,9B 、3,5,9,C 、2,6,4D 、4,6,97、在△ABC 中,∠A :∠B :∠C=12:7:5,则△ABC 是( )A 、钝角三角形B 、锐角三角形C 、直角三角形D 、等腰三角形8、如图,将纸片△ABC 沿着DE 折叠压平,则( )A 、∠A =∠1+∠2;B 、∠A =12 (∠1+∠2);C 、∠A =13 (∠1+∠2);D 、∠A =14(∠1+∠2)9、如图,△ABC 中,∠A ,∠B ,∠C 的外角分别记为α,β和γ,若α:β:γ=3:4:5,则∠A :∠B :∠C=( )A 、3:2:1;B 、1:2:3;C 、3:4:5;D 、5:4:310、如图,BP 是△ABC 中∠ABC 的平分线,CP 是∠ACB 领补角的平分线,若∠ABP=20°,∠ACP=50°,则∠A+∠P=( )A 、 70°B 、80°C 、90°D 、100°11、如图,若直线l 1∥l 2,∠A=125°,∠B=85°,则∠1+∠2=( )A 、30°B 、35°C 、36°D 、40°12、如图,△ABC 中,∠ABC=50°,∠ACB=60°,点E 在BC 延长线上,∠ABC 的平分线BD 与∠ACE 的平分线相较于点D ,连接AD ,则下列结论不正确的是( )A 、∠ACE=70°B 、∠ACE= 90°C 、∠ACE=35°D 、∠ACE=55°13、如图,已知△ABC 中,∠A =∠ACB ,CP 平分∠ACB ,BD 、CD 分别为△ABC 的外角平分线,给出以下结论:①CP ⊥CD ;②∠D=90°- 12∠A ;③PD ∥AC ,其中正确结论的个数是( )个A 、0B 、1C 、2D 、314、如图,∠ABC=31°,又∠BAC 的平分线AE 与∠FCB 的平分线CE相交于E 点,则∠AEC 的度数为( )A、14.5°B、15.5°C、16.5°D、20°15、如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC,给出下列结论:①∠BAD=∠C;②∠AEF=∠AFE;③∠EBC=∠C;④AG⊥EF,其中正确结论的序号是()A、②③④;B、①③④;C、①②④;D、①②③16、三角形三边长分别为8,19,a,则最长边a的取值范围是______________17、如图,∠A=65°,∠B=75°,将纸片一角折叠,使得点C落在△ABC内,若∠2=33°,则∠1=_____________18、用9根相同的火柴棒拼成一个三角形,火柴棒不允许剩余、折叠、折断,则能摆出_____________个不同的三角形19、如图,在6×6正方形网格中,每个小正方形的边长为1,格点上已有两个点A、B,再找一个格点C,使得△ABC的面积为2,这样的C点有_____________个20、在长方形网格中,每个小长方形长为2,宽为1,A、B两点是格点,再找一个格点C,使得△ABC的面积为2,满足条件的C点有_____________个21、如图,a∥b,∠1+∠2=75°,则∠3+∠4=_____________22、如图1是长方形纸带,∠DEF=20°,将纸带沿EF折叠成图2,再沿BF折叠成图3,则图3中∠CFE=____________23、如图,D、E分别是△ABC的边AB、BC上的点,AD=2BD,BE=CE,设△ADC面积为S1,△ACE面积为S2,若S△ABC=6,则S1 -S2=____________24、小亮家离校1km,小明家离校3km,如果小亮家和小明家距离xkm,则x的取值范围是_____________25、如图,BM是△ABC中AC边上的中线,AB=5cm,BC=3cm,那么△ABM和△BCM的周长之差是_____________26、已知AD为△ABC的中线,E为AD的中点,若△ABC的面积为20,BD=4,求点E到BC的距离27、如图,BE是∠ABD的平分线,CF是∠ACD的平分线,BE与CF交于G,若∠BDC=140°,∠BGC=110°,求∠A的度数28、如图,已知∠AOB=90°,点C、D分别在射线OA、OB上,CE是∠ACD的平分线,CE的反向延长线与∠CDO的平分线交于F点,(1)当∠OCD=50°时(如图1),试求∠F(2)当点C、D在射线OA,OB上任意移动时(不与点O重合)(如图2),∠F的度数是否发生变化,若变化,说明理由;若不变,求出∠F的度数。
全等三角形培优(含答案)
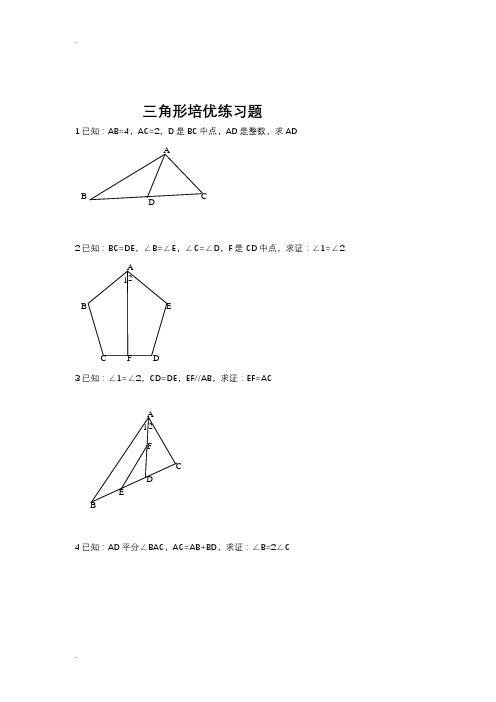
三角形培优练习题1已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD2已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠23已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC4已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C AD BCB ACD F2 1 E5已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE6 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
求证:BC=AB+DC 。
7已知:AB=CD ,∠A=∠D ,求证:∠B=∠C8.P 是∠BAC 平分线AD 上一点,AC>AB ,求证:PC-PB<AC-AB C D B A B C D A9已知,E 是AB 中点,AF=BD ,BD=5,AC=7,求DC10.如图,已知AD ∥BC ,∠PAB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD +BC =AB .11如图,△ABC 中,AD 是∠CAB 的平分线,且AB =AC +CD ,求证:∠C =2∠B12如图:AE 、BC 交于点M ,F 点在AM 上,BE ∥CF ,BE=CF 。
P D A C B FA E D CB P E DC BA D CB A求证:AM 是△ABC 的中线。
13已知:如图,AB =AC ,BD ⊥AC ,CE ⊥AB ,垂足分别为D 、E ,BD 、CE 相交于点F 。
求证:BE =CD .14在△ABC 中,︒=∠90ACB ,BC AC =,直线MN 经过点C ,且MN AD ⊥于D ,MN BE ⊥于E .(1)当直线MN 绕点C 旋转到图1的位置时,求证: ①ADC ∆≌CEB ∆;②BE AD DE +=;(2)当直线MN 绕点C 旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.15如图所示,已知AE ⊥AB ,AF ⊥AC ,AE=AB ,AF=AC 。
初中数学专项练习《三角形》100道选择题包含答案(易考题)

初中数学专项练习《三角形》100道选择题包含答案一、选择题(共100题)1、如图,小明把一块三角形玻璃打碎成三块,现在要到玻璃店去配一块完全一样的玻璃,则最省事的方法是带第③块去,理由是根据全等的判定定理()A.SASB.AASC.SSSD.ASA2、如果等腰三角形两边长为和,那么它的周长是().A. B. C. 或 D.3、如图,在等腰Rt△ABC中,∠BAC=90°,BC=2,点P是△ABC内部的一个动点,且满足∠PBC=∠PCA,则线段AP长的最小值为()A.0.5B. ﹣1C.2﹣D.4、已知△ABC的三边分别为a.b、c,则下列条件中不能判定△ABC是直角三角形的是()A.b 2=a 2﹣c 2B.C.∠C=∠A﹣∠BD.∠A:∠B:∠C=3:4:55、下列各组线段中的三个长度:①9,12,15;②7,24,25;③32, 42,52;④3a,4a,5a(a>0);⑤m2-n2, 2mn,m2+n2(m,n为正整数,且m>n)其中可以构成直角三角形的有()组。
A.2B.3C.4D.56、如图,在矩形ABCD中,O为AC中点,EF过O点且EF⊥AC分别交DC于F,交AB于E,点G是AE中点且∠AOG=30°,①DC=3OG;②OG=BC;③△OGE是等边三角形;④S=S矩形ABCD,则下列结论正确的△AOE个数为()A.1个B.2个C.3个D.4个7、如图,已知∠1=∠2,欲得到△ABD≌△ACD,则从下列条件中补选一个,不正确的选法是()A.∠ADB=∠ADCB.DB=DCC.∠B=∠CD.AB=AC8、设三角形三边之长分别为3,8,1﹣2a,则a的取值范围为()A.﹣6<a<﹣3B.﹣5<a<﹣2C.﹣2<a<5D.a<﹣5或a>29、一把直尺与一块三角板如图放置,若∠1=45°,则∠2的度数为()A.125°B.135°C.145°D.155°10、在Rt△ABC,∠BAC=90°,AB=8,AC=6,DE是AB边的垂直平分线,垂足为D,交边BC于点E,连结AE,则△ACE的周长是()A.8B.10C.14D.1611、如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD,BE,CE,若∠CBD=32°,则∠BEC的度数为()A.128°B.126°C.122°D.120°12、如图,已知AB=AD,∠1=∠2=50°,∠D=100°,那么∠ACB的度数为()A.30B.40C.50D.6013、一个等腰三角形的周长为14,其一边长为4那么它的底边长为()A.5B.4C.6D.4或614、如图,在△ABC中,∠ACB=α,将△ABC绕点C顺时针方向旋转到△A′B′C的位置,使AA′∥BC,设旋转角为β,则α,β满足关系()A.α+β=90°B.α+2β=180°C.2α+β=180°D.α+β=180°15、在下列图形中,既是轴对称图形,又是中心对称图形的是()A. B. C. D.16、如图,在中,已知∠B=50°,∠C=30°.分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点E,F,作直线EF,交BC于点D,连接AD,则∠BAD的度数为()A.70°B.60°C.55°D.45°17、如图,在锐角三角形ABC中,CD和BE分别是AB和AC边上的高,且CD和BE交于点P,若∠A=50° ,则∠BPC的度数是()A.100°B.120°C.130°D.150°18、若等腰三角形的一边长是2,另一边长是4,则它的周长为()A.8B.10C.8或10D.不能确定19、如图,在Rt△ABC中,∠BCA=90° ,△PAB中AB边上的高等于AB的长度,△QBC中BC边上的高等于BC的长度,△HAC中AC边上的高等于AC的长度,且△PAB,△QBC的面积分别是10和8,则△ACH的面积是( )A.2B.4C.6D.920、下列选项中,线段BD是△ABC的高的是()A. B. C. D.21、如图,△ABC的角平分线BE,CF相交于点O,且∠FOE=121°,则∠A的度数是()A.52°B.62°C.64°D.72°22、如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是()A.∠A=∠CB.AD=CBC.BE=DFD.AD∥B C23、如果一个多边形的每一个外角都是36°,那么这个多边形的边数是()A.7B.8C.9D.1024、如图,正方形的对角线,相交于点,,为上一点,,连接,过点作于点,与交于点,则的长为().A. B. C. D.25、直线l1∥l2∥l3,且l1与l2的距离为1,l2与l3的距离为3,把一块含有45°角的直角三角形如图放置,顶点A,B,C恰好分别落在三条直线上,AC与直线l2交于点D,则线段BD的长度为()A. B. C. D.26、如图,点、、在圆上,若,,则图中阴影部分的面积是( )A. B. C. D.27、如图,,为的角平分线,、分别是和的角平分线,且,则以下与的关系正确的是()A. B. C. D.28、已知Rt△ABC,∠ACB=90°,AC=3,BC=4,AD平分∠BAC,则点B 到射线AD的距离是()A.2B.C.D.329、如图,中,,点从点出发,以的速度沿向点运动,同时点从点出发,以的速度沿向点运动,知道它们都到达点为止.若的面积为,点的运动时间为,则与的函数图象是()A. B. C. D.30、如图,一束光线与水平面成60°的角度照射地面,现在地面AB上支放一个平面镜CD,使这束光线经过平面镜反射后成水平光线,则平面镜CD与地面AB所成角∠DCB的度数等于()A.30°B.45°C.50°D.60°31、下列各组长度的线段能构成三角形的是()A.1,2,4B.4,5,9C.4,6,8D.5,5,1132、如果一个三角形的三边长分别为1,k,3,则化简的结果是()A.﹣5B.1C.13D.19﹣4k33、如图所示,△ABD≌△CDB,下面四个结论中,不正确的是()A.△ABD和△CDB的面积相等B.△ABD和△CDB的周长相等 C.∠A+∠ABD=∠C+∠CBD D.AD∥BC,且AD=BC34、能把一个三角形分成面积相等的两部分的是该三角形的()A.角平分线B.中线C.高D.一边的垂直平分线35、在如图所示的四个图形中,属于全等形的是( )A.①和③B.①和④C.②和③D.②和④36、下列长度的三条线段能组成三角形的是()A.2,2,4B.3,4,1C.5,6,12D.5,5,837、已知四边形ABCD中,∠A与∠B互补,∠D=70°,则∠C的度数为()A.70°B.90°C.110°D.140°38、在正方形ABCD的边AB、BC、CD、DA上分别任意取点E、F、G、H ,这样得到的四边形EFGH中,是正方形的有().A.1个B.2个C.4个D.无穷多个39、一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为()A.7B.7或9C.8或9D.7或8或940、已知三角形的三边长分别是3,8,x,若x的值是偶数,则x值的个数为( )A.3B.4C.5D.641、如图,点A在反比例函数图象上,过点A作AC⊥x轴于点B,则△AOB的面积是().A.3B.2.5C.2D.1.542、如图,若△ABC≌△DEF,四个点B、E、C、F在同一直线上,BC=7,EC=5,则CF的长是()A.2B.3C.5D.743、在ΔABC中,BD 为 AC边上的高,∠ABD=30°, ∠BAC的度数为().A.60°B.65°C.125°D.60°或120°44、下列图形中具有稳定性的是()A. B. C. D.45、如图,若,,,则的大小是()A. B. C. D.46、如图,在4×4方格中作以AB为一边的Rt△ABC,要求点C也在格点上,这样的Rt△ABC能作出()A.2个B.3个C.4个D.6个47、下列命题中:①等腰三角形底边的中点到两腰的距离相等;②等腰三角形的高、中线、角平分线互相重合;③若与成轴对称,则一定与全等;④有一个角是度的三角形是等边三角形;⑤等腰三角形的对称轴是顶角的平分线.正确命题的个数是()A. B. C. D.48、如图,下面是利用尺规作∠AOB的角平分线OC的作法,在用尺规作角平分线过程中,用到的三角形全等的判定方法是()A.ASAB.SASC.SSSD.AAS49、如图所示,b∥c,a⊥b,∠1=130°,则∠2=().A.30°B.40°C.50°D.60°50、如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,连结CE 交AD于点F,连结BD交CE于点G,连结BE.下列结论中,正确的结论有()①CE=BD;②△ADC是等腰直角三角形;③∠ADB=∠AEB;④S=四边形BCDE BD•CE;⑤BC2+DE2=BE2+CD2.A.1个B.2个C.3个D.4个51、下列各组数中,不可能成为一个三角形三边长的是().A. ,,B. ,,C. ,,D. ,,52、下列命题是假命题的是()A.三角形的三条高交于一点B.直角三角形有三条高C.三角形的一条中线把三角形的面积分成相等的两部分D.三角形的三条中线交于一点53、如图,则的度数是()A.30°B.40°C.50°D.60°54、若直线y=4x﹣4与x轴交于点A,与y轴交于点B,则的面积是()A.2B.4C.11D.555、若等腰三角形的周长为16cm,其中一边长为4cm,则该等腰三角形的底边为()A.4cmB.6cmC.4cm或8cmD.8cm56、已知等腰三角形的周长为14,其腰长为4,则它的底边长为()A.4B.5C.6D.4或657、如图,一块三角形玻璃碎成了4块,现在要到玻璃店去配一块与原来的三角形玻璃完全一样的玻璃,那么最省事的办法是带()去.A.①B.②C.③D.④58、如果三角形的两边分别为3和5,那么这个三角形的周长可能是()A.8B.16C.14D.1059、如图所示,△ABC是边长为20的等边三角形,点D是BC边上任意一点,DE⊥AB于点E,DF⊥AC于点F,则BE+CF=()A.5B.10C.15D.2060、方程x2﹣12x+27=0的两个根是等腰三角形的底和腰,则这个三角形的周长为()A.21B.21或15C.15D.不能确定61、下列图形既是轴对称图形,又是中心对称图象的是()A. B. C. D.62、如图,三条公路把A,B,C三个村庄连成一个三角形区域,政府决定在这个三角形区域内修建一个集贸市场,使集贸市场到三条公路的距离相等,则该集贸市场应建在()A.AC,BC两边高线的交点处B.AC,BC两边中线的交点处C.AC,BC两边垂直平分线的交点处D. ,两内角平分线的交点处63、如图,AB=AC,AE=EC,∠ACE=28°,则∠B的度数是()A.60°B.70°C.76°D.45°64、如图,四边形ABCD为正方形,AB=1,把△ABC绕点A逆时针旋转60°得到△AEF,连接DF,则DF的长为()A. B. C. D.65、由下列条件不能判定为直角三角形的是()A. B.C. D. ,,66、如图,等腰三角形ABC中,AB=AC,BD平分∠ABC,∠A=36°,则∠1的度数为()A.36°B.60°C.72°D.108°67、下列图形中,既是中心对称图形又是轴对称图形的是()A. B. C. D.68、一个多边形的内角和等于1080°,这个多边形的边数为()A.6B.7C.8D.969、如图,下列角中是△ACD 的外角的是()A.∠ EADB.∠ BACC.∠ ACBD.∠ CAE70、有下列命题:①等腰三角形的角平分线、中线和高重合;②等腰三角形两腰上的高相等;③有个外角等于120°的等腰三角形是等边三角形;④等边三角形的高线、中线、角平分线都相等;其中正确的有( )A.1个B.2个C.3个D.4个71、已知等腰三角形的腰和底的长分别是一元二次方程x2﹣4x+3=0的根,则该三角形的周长可以是()A.5B.7C.5或7D.1072、下列图形中,既是中心对称图形又是轴对称图形的是()A. B. C. D.73、如图,等边三角形的边长为4,点是△ 的中心,.绕点旋转,分别交线段于两点,连接,给出下列四个结论:① ;② ;③四边形的面积始终等于;④△ 周长的最小值为6,上述结论中正确的个数是( )A.1B.2C.3D.474、如图,在中,为中线,E为中点,连结的面积为,则三角形的面积为()A. B. C. D.75、已知Rt△ABC中,∠ABC=90°,点D是BC中点,分别过B、C为圆心,大于线段BC长为半径作弧,两弧交于点P,作直线PD交AC于点E,连接BE,则下列结论中不正确的是()A.ED⊥BCB.BE平分∠AEDC.E为△ABC的外接圆圆心D.ED= AB76、如图,在△ABC中,AC=BC,点D和E分别在AB和AC上,且AD=AE.连结DE,过点A的直线GH与DE平行,若∠C=40°,则∠GAD的度数为 ( )A.40°B.45°C.55°D.70°77、在Rt△ABC中,∠C=90°,c为斜边,a、b为直角边,则化简的结果为()A.3a+b﹣cB.﹣a﹣3b+3cC.a+3b﹣3cD.2a78、已知,如图:AD与BC相交于点O,AB∥CD,如果∠B=20°,∠D=40°,那么∠BOD为()度.A.40°B.50°C.60°D.70°79、如图,一客轮以16海里/时的速度从港口A出发向东北方向航行,另一客轮同时以12海里/时的速度从港口A出发向东南方向航行,离开港口2小时后,则两船相距()A.25海里B.30海里C.35海里D.40海里80、如图,已知AB⊥CD,△ABD,△BCE 都是等腰直角三角形,如果CD=8,BE=3,则AC 等于()A.8B.5C.3D.81、小颖有两根长度为 6cm和 9cm 的木条,桌上有下列长度的几根木条,从中选出一根使三根木条首尾顺次相连,钉成三角形木框,她应该选择长度为( )的木条A.2cmB.3cmC.12cmD.15cm82、等边三角形的边长为2,则该三角形的面积为()A. B. C. D.383、在△ABC中,∠ABC=30°,AB边长为10,AC边的长度可以在3、5、7、11中取值,满足这些条件的互不全等的三角形的个数是()A.3B.4C.5D.684、如图,为了估计池塘两岸A、B间的距离,小明在池塘的一侧选到了一点,测得PA=16m,PB=12m,那么AB间的距离不可能是()A.5 mB.15 mC.20 mD.28 m85、若,且,,,则的长为()A.6B.8C.9D.1086、下列叙述中,正确的有()①三角形的一个外角等于两个内角的和;②一个五边形最多有3个内角是直角;③任意一个三角形的三条高所在的直线相交于一点,且这点一定在三角形的内部;④△ABC中,若∠A=2∠B=3∠C,则这个三角形ABC为直角三角形.A.0个B.1个C.2个D.3个87、在ΔABC中,BD 为 AC边上的高,∠ABD=30°, ∠BAC的度数为().A.60°B.65°C.125°D.60°或120°88、如图,等腰的周长为17,底边,的垂直平分线交于点,交于点,则的周长为()A.11B.12C.13D.1689、如图,锐角△ABC 中,D 、E 分别是 AB 、AC 边上的点,△ADC≌△ADC',△AEB≌△AEB' ,且C'D∥EB'∥BC , BE 、CD 交于点F ,若∠BAC = α,∠BFC = β,则( )A.2α+β= 180°B.2β-α= 145°C.α+β= 135°D.β-α= 60°90、如图,在中,,,则的度数是()A. B. C. D.91、如图,在中,为的中点,有下列四个结论:①;② ;③ ;④ .其中正确的结论有()A.1个B.2个C.3个D.4个92、如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB= AC,现添加以下的哪个条件仍无法判定△ABE △ACD的是( )A.AD= AEB.∠B=∠CC.CD=BED.∠ADC=∠AEB93、如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1, l2, l3上,且l1, l2之间的距离为1,l2, l3之间的距离为2,则AC的长是()A. B. C. D.594、如图所示,木工师傅在板材边角处作直角时,往往使用“三弧法”,其作法是:⑴作线段,分别以为圆心,以长为半径作弧,两弧的交点为;⑵以为圆心,仍以长为半径作弧交的延长线于点;(3)连接.下列说法错误的是()A. B. C.点是的外心 D.95、用下列图形不能进行平面镶嵌的是()A.正三角形和正四边形B.正三角形和正六边形C.正四边形和正八边形D.正四边形和正十二边形96、如图:.按下列步骤作图:①在射线上取一点C,以点O为圆心,长为半径作圆弧,交射线于点F.连结;②以点F为圆心,长为半径作圆弧,交弧于点G;③连结、.作射线.根据以上作图过程及所作图形,下列结论中错误的是()A. B. 垂直平分 C. D.97、如图,在△ABC中,AB=AC,且D为BC上一点,CD=AD,AB=BD,则∠B 的度数为()A.30°B.36°C.40°D.45°98、若一个三角形三个内角度数的比为11︰7︰3,那么这个三角形是()A.直角三角形B.锐角三角形C.等边三角形D.钝角三角形99、如图,为等边的内部一点,,,,则等于()A. B. C. D.100、等腰三角形的一个角是70°,则它的一个底角的度数是()A.70° B.70°或55° C.80° D.55°参考答案一、选择题(共100题)1、D2、B3、C4、D5、C6、C7、B8、B9、B11、C12、A13、D14、C15、D16、A17、C18、B19、A20、D21、B22、B23、D24、A25、A26、A27、B28、C29、C30、A31、C32、B33、C35、D36、D37、C38、D39、D40、A41、D42、A43、D44、C45、D46、D47、A48、C49、B50、C51、C52、A53、A54、A55、A56、C57、D59、B60、A61、D62、D63、C64、A65、B66、C67、D68、C69、C70、C71、B72、D73、C74、B75、B76、C77、B78、C79、D80、D81、C83、B84、D85、A86、B87、D88、A89、A90、B91、D92、C93、C94、D95、D96、D97、B98、D99、C 100、B。
三角形培优训练100题集锦(一)2024

三角形培优训练100题集锦(一)【引言概述】三角形是数学中的一个重要几何概念,对于学生的数学培优训练具有重要意义。
本文整理了一份包含一百道三角形相关题目的训练集锦,旨在帮助学生系统地掌握三角形的性质、定理和计算方法,提高解题能力。
以下将从五个大点来阐述这份题集的内容。
【大点1:三角形基础知识】1. 三角形的定义及分类2. 三角形内角和的性质3. 三角形边长关系:三角不等式定理4. 三角形的周长和面积计算公式5. 三角形的特殊点:重心、垂心、外心、内心、费马点等【大点2:三角形的相似与全等】1. 相似三角形的性质2. 判定三角形相似的方法3. 三角形的全等的条件4. 利用相似三角形或全等三角形解题的方法5. 实际问题中的应用:测量、定位、相似比例等【大点3:三角形的角与线段关系】1. 角的平分线与垂直平分线的特点2. 三角形的角平分线定理3. 三垂线定理与垂心定理4. 外角与内角的关系5. 角与弧的关系及其应用:圆周角、弦切角、弧度制等【大点4:三角形的特殊性质与定理】1. 等腰三角形的性质与判定2. 直角三角形的性质与判定3. 正三角形的性质及计算4. 等边三角形的性质及计算5. 锐角三角形和钝角三角形的性质及判定【大点5:三角形的应用问题】1. 三角形的角度测量与边长测量2. 三角形在建筑工程中的应用:测量高度、角度与距离3. 三角形在地理学中的应用:测量地底深度、地图测量等4. 三角形在航空航天领域的应用:导航、角度计算等5. 三角形在日常生活中的应用:地理问题、旅行导航、地震角度计算等【总结】通过对本文中所整理的三角形培优训练100题集锦的学习,同学们将能够掌握三角形的基础知识,灵活运用三角形的相似与全等等性质和定理,熟练解决三角形的角与线段关系问题,理解各种特殊三角形的性质,并能够应用三角形的知识解决实际问题。
这将为学生的数学学习和思维能力的提高提供坚实的基础。
解三角形题型培优(学生版)
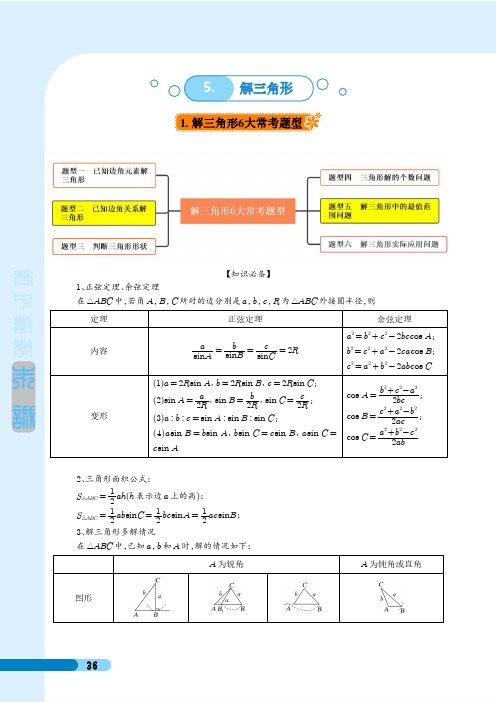
5.解三角形1.解三角形6大常考题型【知识必备】1、正弦定理、余弦定理在△ABC中,若角A,B,C所对的边分别是a,b,c,R为△ABC外接圆半径,则定理正弦定理余弦定理内容asin A=bsin B=csin C=2Ra2=b2+c2-2bc cos A;b2=c2+a2-2ca cos B;c2=a2+b2-2ab cos C变形(1)a=2R sin A,b=2R sin B,c=2R sin C;(2)sin A=a2R,sin B=b2R,sin C=c2R;(3)a∶b∶c=sin A∶sin B∶sin C;(4)a sin B=b sin A,b sin C=c sin B,a sin C=c sin Acos A=b2+c2-a22bc;cos B=c2+a2-b22ac;cos C=a2+b2-c22ab2、三角形面积公式:S△ABC=12ah(h表示边a上的高);S△ABC=12ab sin C=12bc sin A=12ac sin B;3、解三角形多解情况在△ABC中,已知a,b和A时,解的情况如下:A为锐角A为钝角或直角图形a =b sin A b sin A <a <b a ≥关系式b a >b a ≤b解的个数一解两解一解一解无解4、实际应用(1)仰角和俯角在视线和水平线所成的角中,视线在水平线上方的角叫仰角,在水平线下方的角叫俯角(如图①).(2)方位角从指北方向顺时针转到目标方向线的水平角,如B 点的方位角为α(如图②).(3)方向角:相对于某一正方向的水平角.(1)北偏东α,即由指北方向顺时针旋转α到达目标方向(如图③).(2)北偏西α,即由指北方向逆时针旋转α到达目标方向.(3)南偏西等其他方向角类似.(4)坡角与坡度(1)坡角:坡面与水平面所成的二面角的度数(如图④,角θ为坡角).(2)坡度:坡面的铅直高度与水平长度之比(如图④,5、相关应用(1)正弦定理的应用①边化角,角化边⇔a :b :c =sin A :sin B :sin C②大边对大角大角对大边a >b ⇔A >B ⇔sin A >sin B ⇔cos A <cos i 为坡度).坡度又称为坡比.Ba +b +c③合分比:sin A +sin B +sin Ca +b =sin A +sin B b +c =sin B +sin C a +c =sin A +sin C a =sin A b =sin B c =sin C=2R (2)△ABC 内角和定理:A +B +C =π①sin C =sin (A +B )=sin A cos B +cos A sin B ⇔c =a cos B +b cos A 同理有:a =b cos C +c cos B ,b =c cos A +a cos C .②-cos C =cos (A +B )=cos A cos B -sin A sin B ;A +tan ③斜三角形中,-tan C =tan (A +B )=1Btan -tan ⋅A tan B⇔tan A +tan B +tan C =tan A ⋅tan B ⋅tan C④sin A +2B =cos C 2;cos A +2B=sin C 2⑤在ΔABC 中,内角A ,B ,C 成等差数列⇔B =π3,A +C =2π3.Z 【题型精讲】题型一:【已知边角元素解三角形】必备技巧已知边角元素解三角形技巧正弦定理、余弦定理的作用是在已知三角形部分元素的情况下求解其余元素,基本思想是方程思想,即根据正弦定理、余弦定理列出关于未知元素的方程,通过解方程求得未知元素.1.1(多选)(山东济南一模)在ΔABC中,角A,B,C所对的边分别为a,b,c,下列结论正确的是()A.a2=b2+c2-2bc cos AB.a sin B=b sin AC.a=b cos C+c cos BD.a cos B+b cos A=sin C1.2(多选)(重庆市高三二模)已知在△ABC中,角A,B,C所对的边分别为a,b,c,且A=60°,b=2,c=3+1,则下列说法正确的是A.C=75°或C=105°B.B=45°C.a=6D.该三角形的面积为3+1 21.3在△ABC中,角A,B,C所对的边分别为a,b,c若sin A=35,A=2B,角C为钝角,b=5.(1)求sin(A-B)的值;(2)求边c的长.Z【跟踪精练】1.3.1在△ABC中,角A,B,C所对的边分别为a,b,c,若(a+b)2-c2=ab,则C=()A.π6 B.π3或2π3 C.2π3 D.π6或5π61.3.2在△ABC中,内角A,B,C所对的边分别是a,b,c.若A=π3,a=23,b=22,则B=()A.π4 B.π3 C.π4或3π4 D.π3或2π31.3.3△ABC的内角A、B、C的对边分别为a、b、c,若a=4,b=3,c=2,则中线AD的长为()A.5B.10C.52 D.102题型二:【已知边角关系解三角形】必备技巧已知边角关系解三角形正弦定理、余弦定理的另一个作用是实现三角形边角关系的互化,解题时可以把已知条件化为角的三角函数关系,也可以把已知条件化为三角形边的关系.1.1在△ABC中,内角A,B,C的对边分别为a,b,c,已知2cos C a cos B+b cos A=c.(1)若cos A=64,求sin2A+C的值;(2)若c=7,△ABC的面积为332,求边a,b的值.21a △ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知△ABC 1.2的面积为2-b 2sin C .(1)证明:sin A =2sin B ;(2)若a cos C =32b ,求cos A .Z 【跟踪精练】ΔABC 的内角A ,B ,C 的对边分别为a ,b ,c .设(sin B -sin C )2=sin 2A 1.2.1-sin B sin C .(1)求A ;(2)若2a +b =2c ,求sin C .在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,b tan A +b tan B 1.2.2=3ccos A.(1)求角B ;(2)D 是AC 边上的点,若CD =1,AD =BD =3,求sin A 的值.题型三:【判断三角形形状】必备技巧判断三角形形状的方法(1)化边:通过因式分解、配方等得出边的相应关系.(2)化角:通过三角恒等变换,得出内角的关系,此时要注意应用A +B +C =π这个结论.在△ABC 中,已知a 2+b 2-c 2=ab ,且2cos A sin B =sin C 1.1,则该三角形的形状是()A.直角三角形B.等腰三角形C.等边三角形D.钝角三角形在△ABC 中,已知(b +c -a )(b +c +a )=3bc ,且2cos B sin C =sin A ,则△ABC 1.2的形状为()A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形Z 【跟踪精练】对于△ABC ,有如下四个命题1.2.1:①若sin2A =sin2B ,则△ABC 为等腰三角形,②若sin B =cos A ,则△ABC 是直角三角形③若sin 2A +sin 2B <sin 2C ,则△ABC 是钝角三角形④若acos 2A =b cos 2B =cC cos 2,则△ABC 是等边三角形.其中正确的命题序号是1.2.2a在△ABC 中,已知a +b =tan Ab +tan B ,则△ABC 的形状一定是()A.等腰三角形B.直角三角形C.等边三角形D.等腰或直角三角形题型四:【三角形解的个数问题】1.1已知在△ABC 中,a 、b 、c 分别为角A 、B 、C 的对边,则根据条件解三角形时恰有一解的一组条件是()A.a =3,b =4,A =π6 B.a =4,b =3,A =π3C.a =1,b =2,A =π4D.a =2,b =3,A =2π31.2△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,A =30°,a =3,若这个三角形有两解,则b 的取值范围是()A.3<b ≤6B.3<b <6C.b <6D.b ≤6Z 【跟踪精练】1.2.1在△ABC 中,根据下列条件解三角形,则其中有两个解的是()A.b =10,A =45°,C =70°B.a =60,c =48,B =60°C.a =5,b =7,c =8D.a =14,b =16,A =45°1.2.2在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,若,满足条件a =3,A =60°的三角形有两个,则b 的取值范围是()A.2,3B.3,33C.3,23D.22,23题型五:【解三角形中的最值范围问题】方法技巧解三角形中最值范围问题基本处理方法1、用余弦定理结合基本不等式求解,2、要求的量转化为某角的三角函数,求函数的最值或值域。
人教版八年级数学上册第11章三角形培优专题训练(含答案)

人教版八年级数学上册第11章三角形培优专题训练一、选择题1.下列长度的三条线段能组成三角形的是()A.5cm,2cm,4cm B.5cm,2cm,2cmC.5cm,2cm,3cm D.5cm,12cm,6cm2.如图,在△ABC中,CD是AB边上的高,CM是∠ACB的角平分线,若∠CAB=45°,∠CBA=75°,则∠MCD的度数为()A.15°B.20°C.25°D.30°3.下面四个图形中,线段BE是△ABC的高的图是()A.B.C.D.4.下列说法中正确的是()A.三角形的三条高都在三角形内B.直角三角形只有一条高C.锐角三角形的三条高都在三角形内D.三角形每一边上的高都小于其他两边5.已知AD为△ABC的中线,且AB=10cm,AC=8cm,则△ABD与△ACD的周长之差为()A.2cm B.4cm C.6cm D.18cm6.盖房子时,木工师傅常常先在窗框上斜钉一根木条,利用的几何原理是()A.三角形的稳定性B.两点之间线段最短C.两点确定一条直线D.垂线段最短7.如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,则下列结论不一定成立的是()A.∠1+∠2=90°B.∠3=60°C.∠2=∠3 D.∠1=∠48.如图所示,∠1=∠2=145°,则∠3=()A.80°B.70°C.60°D.50°9.如图,CF是△ABC的外角∠ACM的平分线,且CF∥AB,∠ACF=50°,则∠B的度数为()A.80°B.40°C.60°D.50°10.一个多边形截去一个角后,形成的另一个多边形的内角和是1620°,则原来多边形的边数是()A.10或11 B.11或12或13 C.11或12 D.10或11或12 11.若一个多边形的内角和与外角和之差是720°,则此多边形是()边形.A.6 B.7 C.8 D.912.如图,五边形ABCDE是正五边形,则x为()A.30°B.35°C.36°D.45°13.如图∠1,∠2,∠3是五边形ABCDE的三个外角,若∠A+∠B=215°,则∠1+∠2+∠3=()A.140°B.180°C.215°D.220°二、填空题14.如图,在△ABC中,BD平分∠ABC.CD是△ABC外角的角平分线,若∠A=50°,则∠D=.15.如图,在△ABC中,已知DE∥BC,∠1=∠2,∠BEC=96°,则∠FGE=°.16.小华用三根木棒搭一个三角形,其中两根木棒的长度分别为10cm和2cm,第三根木棒的长度为偶数,则第三根的长度是cm.17.如图,将正六边形与正五边形按此方式摆放,正六边形与正五边形的公共顶点为O,且正六边形的边AB与正五边形的边DE共线,则∠BOE的度数是.三、解答题18.如图,已知△ABC,AD平分∠BAC交BC于点D,AE⊥BC于点E,∠B<∠C.(1)若∠B=44°,∠C=72°,求∠DAE的度数;(2)若∠B=27°,当∠DAE=度时,∠ADC=∠C.19.如图,在△ABC中,BD平分∠ABC,DE∥BC交AB于点E,∠C=50°,∠BDC=95°,求∠BED的度数.20.如图,已知CD是△ABC的角平分线,∠CDE=∠DCE.(1)求证:DE∥BC;(2)若CD⊥AB,∠A=30°,求∠CED的度数.21.如图,已知四边形ABCD中,∠B=90°,点E在AB上,连接CE、DE.(1)若∠1=35°,∠2=25°,则∠CED=°;(2)若∠1=∠2,求证:∠3+∠4=90°.参考答案1.解:A、2+4>5,能构成三角形,符合题意;B、2+2<5,不能构成三角形,不符合题意;C、2+3=5,不能构成三角形,不符合题意;D、5+6<12,不能构成三角形,不符合题意.故选:A.2.解:∵∠CAB=45°,∠CBA=75°,∴∠ACB=180°﹣∠CAB﹣∠CBA=60°.∵CM是∠ACB的角平分线,∴∠ACM=∠ACB=30°.∴∠CMB=∠CAB+∠ACM=75°.∵CD是AB边上的高,∴∠CDA=∠CDB=90°.∵∠CDB=∠MCD+∠CMB.∴∠MCD=∠CDB﹣∠CMB=90°﹣75°=15°.故选:A.3.解:A选项中,BE与AC不垂直;B选项中,BE与AC不垂直;C选项中,BE与AC不垂直;∴线段BE是△ABC的高的图是D选项.故选:D.4.解:A、三角形的三条高不一定都在三角形内,如钝角三角形的高在三角形外部,说法错误,不符合题意;B、直角三角形有三条高,说法错误,不符合题意;C、锐角三角形的三条高都在三角形内,说法正确,符合题意;D、三角形每一边上的高不一定小于其他两边,说法错误,不符合题意;故选:C.5.解:∵AD为中线,∴BD=CD,∴△ABD与△ACD的周长之差=(AB+AD+BD)﹣(AC+AD+CD)=AB﹣AC,∵AB=10,AC=8,∴△ABD与△ACD的周长之差=10﹣8=2(cm).故选:A.6.解:盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,这样就构成了三角形,故这样做的数学道理是三角形的稳定性.故选:A.7.解:Rt△ABC中,∵∠ACB=90°,∴∠1+∠2=90°,故A正确;∵CD⊥AB,∴∠ADC=90°,∴∠1+∠3=90°,∴∠2=∠3,故C正确;∵∠3+∠4=90°,∴∠1=∠4,故D正确;故选:B.8.解:∵∠1、∠2、∠3是△ABC的三个外角,∴∠1+∠2+∠3=360°,∵∠1=∠2=145°,∴∠3=360°﹣145°×2=70°,故选:B.9.解:∵CF∥AB,∴∠B=∠FCM,∵CF平分∠ACM,∠ACF=50°,∴∠FCM=∠ACF=50°,∴∠B=50°,故选:D.10.解:设多边形截去一个角的边数为n,则(n﹣2)•180°=1620°,解得n=11,∵截去一个角后边上可以增加1,不变,减少1,∴原来多边形的边数是10或11或12.故选:D.11.解:∵一个多边形的内角和与外角和之差为720°,多边形的外角和是360°,∴这个多边形的内角和为720°+360°=1080°,设多边形的边数为n,则(n﹣2)×180°=1080°,解得:n=8,即多边形是八边形,故选:C.12.解:因为五边形ABCDE是正五边形,所以∠E=∠CDE==108°,AE=DE,所以,所以x=∠CDE﹣∠1﹣∠3=36°.故选:C.13.解:五边形ABCDE的内角和为(5﹣2)×180°=540°,∵∠A+∠B=215°,∴∠AED+∠EDC+∠BCD=540°﹣215°=325°,又∵∠AED+∠EDC+∠BCD+∠1+∠2+∠3=180°×3=540°,∴∠1+∠2+∠3=540°﹣325°=215°.故选:C.14.解:∵∠ACE是△ABC的一个外角,∴∠A=∠ACE﹣∠ABC,同理:∠D=∠DCE﹣∠DBC,∵BD平分∠ABC,CD平分∠ACE,∴∠DBE=∠ABC,∠DCE=∠ACE,∴∠D=(∠ACE﹣∠ABC)=∠A=×50°=25°,故答案为:25°.15.解:∵DE∥BC,∴∠2=∠EBC,∵∠1=∠2,∴∠EBC=∠1,∴GF∥BE,∴∠BEC+∠FGE=180°,∵∠BEC=96°,∴∠FGE=180°﹣∠BEC=180°﹣96°=84°.故答案为:84.16.解:根据三角形的三边关系,得10﹣2<第三根木棒<10+2,即8<第三根木棒<12.又∵第三根木棒的长选取偶数,∴第三根木棒的长度只能为10cm.故答案为:10.17.解:由题意:∠OED=108°,∠OBA=120°,∴∠OEB=72°,∠OBE=60°,∴∠BOE=180°﹣72°﹣60°=48°,故答案为:48°.18.解:∵AD平分∠BAC交BC于点D,AE⊥BC于点E,∴∠BAD=∠CAD=∠BAC,∠AED=90°.(1)∵∠B=44°,∠C=72°,∴∠BAC=180°﹣∠B﹣∠C=180°﹣44°﹣72°=64°.∴∠BAD=×64°=32°.∵∠ADC=∠B+∠BAD=44°+32°=76°,∴∠DAE=90°﹣∠ADC=90°﹣76°=24°.(2))∵∠B=27°,∠C=∠ADC,∴∠BAC=180°﹣∠B﹣∠C=180°﹣27°﹣∠C=153°﹣∠C.∴∠BAD=×(153°﹣∠C)=76.5°﹣.∴∠ADC=∠B+∠BAD=27°+76.5°﹣∠C=103.5°﹣∠C.∵∠ADC=∠C,∴103.5°﹣∠C=∠C.∴∠ADC=∠C=69°.∴∠DAE=∠AED﹣∠ADC=90°﹣69°=21°.故答案为:21.19.解:∵∠C=50°,∠BDC=95°,∴∠DBC=180°﹣∠C﹣∠BDC=180°﹣50°﹣95°=35°.∵BD平分∠ABC,∴∠EBC=2∠DBC=70°,∵DE∥BC,∴∠BED+∠EBC=180°,∴∠BED=180°﹣70°=110°.20.(1)证明:∵CD是△ABC的角平分线,∴∠BCD=∠ECD,∵∠CDE=∠DCE,∴∠EDC=∠BCD,∴DE∥BC;(2)解:∵CD⊥AB,∴∠ADC=90°,∵∠A=30°,∴∠ACD=60°,∴∠EDC=∠ACD=60°,∴∠CED=180°﹣∠EDC﹣∠ECD=60°.21.解:(1)∵∠1=35°,∠2=25°,∠B=90°,∴∠BEC=180°﹣∠B﹣∠2=180°﹣90°﹣25°=65°,∠CED=180°﹣∠1﹣∠CEB=180°﹣35°﹣65°=80;故答案为:80.(2)∵∠1=∠2,∵∠B=90°,∴∠2+∠BEC=90°,∴∠1+∠BEC=90°,∴CDE=180°﹣90°=90°,∴∠3+∠4=180°﹣∠CDE=180°﹣90°=90°。
三角形培优训练题集锦资料

ED F CB A三角形培优训练专题【三角形辅助线做法】图中有角平分线,可向两边作垂线。
也可将图对折看,对称以后关系现。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看。
线段垂直平分线,常向两端把线连。
要证线段倍与半,延长缩短可试验。
三角形中两中点,连接则成中位线。
三角形中有中线,延长中线等中线。
【常见辅助线的作法有以下几种】1、遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思维模式是全等变换中的“对折”。
2、遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全等变换中的“旋转”。
3、遇到角平分线,可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中的“对折”,所考知识点常常是角平分线的性质定理或逆定理。
4、过图形上某一点作特定的平分线,构造全等三角形,利用的思维模式是全等变换中的“平移”或“翻转折叠”。
5、截长法与补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,是之与特定线段相等,再利用三角形全等的有关性质加以说明。
这种作法,适合于证明线段的和、差、倍、分等类的题目。
6、已知某线段的垂直平分线,那么可以在垂直平分线上的某点向该线段的两个端点作连线,出一对全等三角形。
7、特殊方法:在求有关三角形的定值一类的问题时,常把某点到原三角形各顶点的线段连接起来,利用三角形面积的知识解答。
1、已知,如图△ABC中,AB=5,AC=3,求中线AD的取值范围.2、如图,△ABC中,E、F分别在AB、AC上,DE⊥DF,D是中点,试比较BE+CF与EF的大小.3、如图,△ABC中,BD=DC=AC,E是DC的中点,求证:AD平分∠BAE.ED CBA4、以ABC∆的两边AB、AC为腰分别向外作等腰Rt ABD∆和等腰Rt ACE∆,90,BAD CAE∠=∠=︒连接DE,M、N分别是BC、DE的中点.探究:AM与DE的位置关系及数量关系.(1)如图①当ABC∆为直角三角形时,探究:AM与DE的位置关系和数量关系;(2)将图①中的等腰Rt ABD∆绕点A沿逆时针方向旋转︒θ(0<θ<90)后,如图②所示,(1)问中得到的两个结论是否发生改变?并说明理由.5、如图,ABC∆中,AB=2AC,AD平分BAC∠,且AD=BD,求证:CD⊥AC.CBACBACBA6、如图,AD ∥BC ,EA,EB 分别平分∠DAB,∠CBA ,CD 过点E ,求证;AB =AD+BC 。
三角形全等培优证明题100题(有答案)
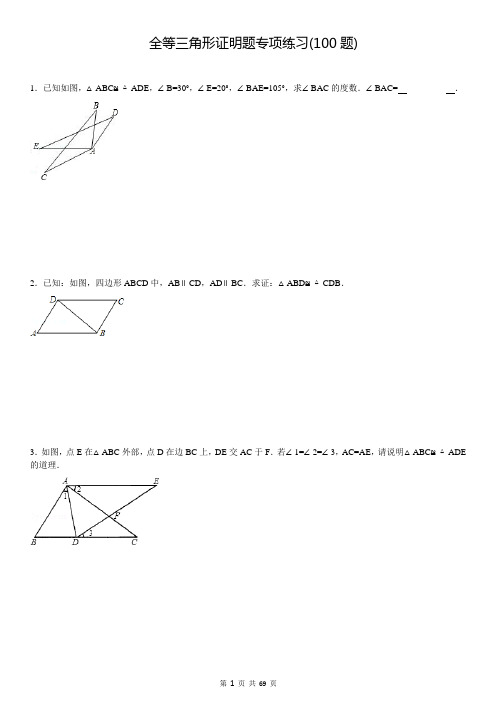
全等三角形证明题专项练习(100题)1.已知如图,△ABC≌△ADE,∠B=30°,∠E=20°,∠BAE=105°,求∠BAC的度数.∠BAC=_________.2.已知:如图,四边形ABCD中,AB∥CD,AD∥BC.求证:△ABD≌△CDB.3.如图,点E在△ABC外部,点D在边BC上,DE交AC于F.若∠1=∠2=∠3,AC=AE,请说明△ABC≌△ADE 的道理.4.如图,△ABC的两条高AD,BE相交于H,且AD=BD.试说明下列结论成立的理由.(1)∠DBH=∠DAC;(2)△BDH≌△ADC.5.如图,在△ABC中,D是BC边的中点,DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF,则AB=AC,并说明理由.6.如图,AE是∠BAC的平分线,AB=AC,D是AE反向延长线的一点,则△ABD与△ACD全等吗?为什么?7.如图所示,A、D、F、B在同一直线上,AF=BD,AE=BC,且AE∥BC.求证:△AEF≌△BCD.8.如图,已知AB=AC,AD=AE,BE与CD相交于O,△ABE与△ACD全等吗?说明你的理由.9.如图,在△ABC中,AB=AC,D是BC的中点,点E在AD上,找出图中全等的三角形,并说明它们为什么是全等的.10.如图所示,CD=CA,∠1=∠2,EC=BC,求证:△ABC≌△DEC.11.已知AC=FE,BC=DE,点A、D、B、F在一条直线上,要使△ABC≌△FDE,应增加什么条件?并根据你所增加的条件证明:△ABC≌△FDE.12.如图,已知AB=AC,BD=CE,请说明△ABE≌△ACD.13.如图,△ABC中,∠ACB=90°,AC=BC,将△ABC绕点C逆时针旋转角α(0°<α<90°)得到△A1B1C,连接BB1.设CB1交AB于D,A1B1分别交AB,AC于E,F,在图中不再添加其他任何线段的情况下,请你找出一对全等的三角形,并加以证明.(△ABC与△A1B1C1全等除外)14.如图,AB∥DE,AC∥DF,BE=CF.求证:△ABC≌△DEF.15.如图,AB=AC,AD=AE,AB,DC相交于点M,AC,BE相交于点N,∠DAB=∠EAC.求证:△ADM≌△AEN.16.将两个大小不同的含45°角的直角三角板如图1所示放置在同一平面内.从图1中抽象出一个几何图形(如图2),B、C、E三点在同一条直线上,连接DC.求证:△ABE≌△ACD.17.如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF.请在图中找出所有全等的三角形,用符号“≌”表示,并选择一对加以证明.18.如图,已知∠1=∠2,∠3=∠4,EC=AD.(1)求证:△ABD≌△EBC.(2)你可以从中得出哪些结论?请写出两个.19.等边△ABC边长为8,D为AB边上一动点,过点D作DE⊥BC于点E,过点E作EF⊥AC于点F.(1)若AD=2,求AF的长;(2)求当AD取何值时,DE=EF.20.巳知:如图,AB=AC,D、E分别是AB、AC上的点,AD=AE,BE与CD相交于G.(Ⅰ)问图中有多少对全等三角形?并将它们写出来.(Ⅱ)请你选出一对三角形,说明它们全等的理由(根椐所选三角形说理难易不同给分,即难的说对给分高,易的说对给分低)21.已知:如图,AB=DC,AC=BD,AC、BD相交于点E,过E点作EF∥BC,交CD于F,(1)根据给出的条件,可以直接证明哪两个三角形全等?并加以证明.(2)EF平分∠DEC吗?为什么?22.如图,己知∠1=∠2,∠ABC=∠DCB,那么△ABC与△DCB全等吗?为什么?23.如图,B,F,E,D在一条直线上,AB=CD,∠B=∠D,BF=DE.试证明:(1)△DFC≌△BEA;(2)△AFE≌△CEF.24.如图,AC=AE,∠BAF=∠BGD=∠EAC,图中是否存在与△ABE全等的三角形?并证明.25.如图,D是△ABC的边BC的中点,CE∥AB,E在AD的延长线上.试证明:△ABD≌△ECD.26.如图,已知AB=CD,∠B=∠C,AC和BD相交于点O,E是AD的中点,连接OE.(1)求证:△AOB≌△DOC;(2)求∠AEO的度数.27.如图,已知AB∥DE,AB=DE,AF=DC.(1)求证:△ABF≌△DEC;(2)请你找出图中还有的其他几对全等三角形.(只要直接写出结果,不要证明)28.如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.(1)求证:△ABD≌△GCA;(2)请你确定△ADG的形状,并证明你的结论.29.如图,点D、F、E分别在△ABC的三边上,∠1=∠2=∠3,DE=DF,请你说明△ADE≌△CFD的理由.30.如图,在△ABC中,∠ABC=90°,BE⊥AC于点E,点F在线段BE上,∠1=∠2,点D在线段EC上,给出两个条件:①DF∥BC;②BF=DF.请你从中选择一个作为条件,证明:△AFD≌△AFB.31.如图,在△ABC中,点D在AB上,点E在BC上,AB=BC,BD=BE,EA=DC,求证:△BEA≌△BDC.32.阅读并填空:如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.请说明△ADC≌△CEB的理由.解:∵BE⊥CE于点E(已知),∴∠E=90°_________,同理∠ADC=90°,∴∠E=∠ADC(等量代换).在△ADC中,∵∠1+∠2+∠ADC=180°_________,∴∠1+∠2=90°_________.∵∠ACB=90°(已知),∴∠3+∠2=90°,∴_________.在△ADC和△CEB中,.∴△ADC≌△CEB (A.A.S)33.已知:如图所示,AB∥DE,AB=DE,AF=DC.(1)写出图中你认为全等的三角形(不再添加辅助线);(2)选择你在(1)中写出的全等三角形中的任意一对进行证明.34.如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2=∠3,AC=AE.试说明下列结论正确的理由:(1)∠C=∠E;(2)△ABC≌△ADE.35.如图,在Rt△ABC中,∠ACB=90°,AC=BC,D是斜边AB上的一点,AE⊥CD于E,BF⊥CD交CD的延长线于F.求证:△ACE≌△CBF.36.如图,在△ABC中,D是BC的中点,DE∥CA交AB于E,点P是线段AC上的一动点,连接PE.探究:当动点P运动到AC边上什么位置时,△APE≌△EDB?请你画出图形并证明△APE≌△EDB.37.已知:如图,AD∥BC,AD=BC,E为BC上一点,且AE=AB.求证:(1)∠DAE=∠B;(2)△ABC≌△EAD.38.如图,D为AB边上一点,△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,CA=CB,CD=CE,图中有全等三角形吗?指出来并说明理由.39.如图,AB=AC,AD=AE,∠BAC=∠DAE.求证:△ABD≌△ACE.40.如图,已知D是△ABC的边BC的中点,过D作两条互相垂直的射线,分别交AB于E,交AC于F,求证:BE+CF>EF.41.如图所示,在△MNP中,H是高MQ与NE的交点,且QN=QM,猜想PM与HN有什么关系?试说明理由.42.如图,在△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥GF,交AB于点E,连接EG.(1)求证:BG=CF;(2)请你判断BE+CF与EF的大小关系,并证明你的结论.43.如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,AD=2.5cm,DE=1.7cm,求BE的长.44.如图,小明在完成数学作业时,遇到了这样一个问题,AB=CD,BC=AD,请说明:∠A=∠C的道理,小明动手测量了一下,发现∠A确实与∠C相等,但他不能说明其中的道理,你能帮助他说明这个道理吗?试试看.45.如图,AD是△ABC的中线,CE⊥AD于E,BF⊥AD,交AD的延长线于F.求证:CE=BF.46.如图,已知AB∥CD,AD∥BC,F在DC的延长线上,AM=CF,FM交DA的延长线上于E.交BC于N,试说明:AE=CN.47.已知:如图,△ABC中,∠C=90°,CM⊥AB于M,AT平分∠BAC交CM于D,交BC于T,过D作DE∥AB 交BC于E,求证:CT=BE.48.如图,已知AB=AD,AC=AE,∠BAE=∠DAC.∠B与∠D相等吗?请你说明理由.49.D是AB上一点,DF交AC于点E,DE=EF,AE=CE,求证:AB∥CF.50.如图,M是△ABC的边BC上一点,BE∥CF,且BE=CF,求证:AM是△ABC的中线.51.四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E、F.(1)求证:△ADE≌△CBF;(2)若AC与BD相交于点O,求证:AO=CO.52.如图,已知点B,E,C,F在一条直线上,AB=DF,AC=DE,∠A=∠D.(1)求证:AC∥DE;(2)若BF=13,EC=5,求BC的长.53.如图,BD⊥AC于点D,CE⊥AB于点E,AD=AE.求证:BE=CD.54.如图,点O是线段AB和线段CD的中点.(1)求证:△AOD≌△BOC;(2)求证:AD∥BC.55.如图:点C是AE的中点,∠A=∠ECD,AB=CD,求证:∠B=∠D.56.如图,已知△ABC和△DAE,D是AC上一点,AD=AB,DE∥AB,DE=AC.求证:AE=BC.57.如图,AB∥CD,E是CD上一点,BE交AD于点F,EF=BF.求证:AF=DF.58.如图,点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF,求证:AB∥DE.59.如图,点D是AB上一点,DF交AC于点E,DE=FE,FC∥AB求证:AE=CE.60.如图,点A、C、D、B四点共线,且AC=BD,∠A=∠B,∠ADE=∠BCF,求证:DE=CF.61.如图,点A,B,C,D在同一条直线上,CE∥DF,EC=BD,AC=FD.求证:AE=FB.62.已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.(1)求证:BD=CE;(2)求证:∠M=∠N.63.如图,BE⊥AC,CD⊥AB,垂足分别为E,D,BE=CD.求证:AB=AC.64.如图,在△ABC和△CED中,AB∥CD,AB=CE,AC=CD.求证:∠B=∠E.65.如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.(1)求证:AB=AC;(2)若AD=2,∠DAC=30°,求AC的长.66.如图,Rt△ABC≌Rt△DBF,∠ACB=∠DFB=90°,∠D=28°,求∠GBF的度数.67.如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.求证:△ABC≌△BAD.68.已知:如图,点B、F、C、E在一条直线上,BF=CE,AC=DF,且AC∥DF.求证:△ABC≌△DEF.69.已知:点A、C、B、D在同一条直线,∠M=∠N,AM=CN.请你添加一个条件,使△ABM≌△CDN,并给出证明.(1)你添加的条件是:;(2)证明:.70.如图,AB=AC,AD=AE.求证:∠B=∠C.71.如图,在△ABC中,AD是△ABC的中线,分别过点B、C作AD及其延长线的垂线BE、CF,垂足分别为点E、F.求证:BE=CF.72.一个平分角的仪器如图所示,其中AB=AD,BC=DC.求证:∠BAC=∠DAC.73.在数学课上,林老师在黑板上画出如图所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.题设:;结论:.(均填写序号)证明:74.如图,在△ABC和△DEF中,AB=DE,BE=CF,∠B=∠1.求证:AC=DF.(要求:写出证明过程中的重要依据)75.如图,已知AB=DC,AC=DB.求证:∠1=∠2.76.如图,D、E分别为△ABC的边AB、AC上的点,BE与CD相交于O点.现有四个条件:①AB=AC;②OB=OC;③∠ABE=∠ACD;④BE=CD.(1)请你选出两个条件作为题设,余下的两个作为结论,写出一个正确的命题:命题的条件是和,命题的结论是和(均填序号);(2)证明你写出的命题.77.如图,已知AB∥DE,AB=DE,AF=DC,请问图中有哪几对全等三角形并任选其中一对给予证明.78.如图所示,在梯形ABCD中,AD∥BC,∠B=∠C,点E是BC边上的中点.求证:AE=DE.79.如图,给出下列论断:①DE=CE,②∠1=∠2,③∠3=∠4.请你将其中的两个作为条件,另一个作为结论,构成一个真命题,并加以证明.80.已知:如图,∠ACB=90°,AC=BC,CD是经过点C的一条直线,过点A、B分别作AE⊥CD、BF⊥CD,垂足为E、F,求证:CE=BF.81.如图,在△ABC中,AC⊥BC,AC=BC,D为AB上一点,AF⊥CD交于CD的延长线于点F,BE⊥CD于点E,求证:EF=CF﹣AF.82.如图,在△ABC中,∠BAC=90°,AB=AC,若MN是经过点A的直线,BD⊥MN于D,EC⊥MN于E.(1)求证:BD=AE;(2)若将MN绕点A旋转,使MN与BC相交于点O,其他条件都不变,BD与AE边相等吗?为什么?(3)BD、CE与DE有何关系?83.已知:如图,△ABC中,AB=AC,BD和CE为△ABC的高,BD和CE相交于点O.求证:OB=OC.84.在△ABC中,∠ACB=90°,D是AB边的中点,点F在AC边上,DE与CF平行且相等.试说明AE=DF的理由.85.如图,在△ABC中,D是边BC上一点,AD平分∠BAC,在AB上截取AE=AC,连接DE,已知DE=2cm,BD=3cm,求线段BC的长.86.如图:已知∠B=∠C,AD=AE,则AB=AC,请说明理由.87.如图△ABC中,点D在AC上,E在AB上,且AB=AC,BC=CD,AD=DE=BE.(1)求证△BCE≌△DCE;(2)求∠EDC的度数.88.已知:∠A=90°,AB=AC,BD平分∠ABC,CE⊥BD,垂足为E.求证:BD=2CE.89.如图,已知:AB=CD,AD=BC,过BD上一点O的直线分别交DA、BC的延长线于E、F.(1)求证:∠E=∠F;(2)OE与OF相等吗?若相等请证明,若不相等,需添加什么条件就能证得它们相等?请写出并证明你的想法.90.如下图,AD是∠BAC的平分线,DE垂直AB于点E,DF垂直AC于点F,且BD=DC.求证:BE=CF.91.如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B 落在点F处,连接FC,(1)求CF的长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精心整理精心整理三角形培优训练专题【三角形辅助线做法】图中有角平分线,可向两边作垂线。
也可将图对折看,对称以后关系现。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看。
线段垂直平分线,常向两端把线连。
要证线段倍与半,延长缩短可试验。
三角形中两中点,连接则成中位线。
三角形中有中线,延长中线等中线。
【常见辅助线的作法有以下几种】123456、71解:∴∆∵即2∴41 AD2、如图,ABC ∆中,E 、F 分别在AB 、AC 上,DF DE ⊥,D 是中点,试比较CF BE +与EF 的大小。
证明:延长FD 到点G ,使DF DG =,连接BG 、EG ∵CD BD =,DG FD =,CDF BDG ∠=∠ ∴CDF BDG ∆≅∆∴CF BG =EFECABD图1C图2∵DF DE ⊥∴EG EF =在BEG ∆中,EG BG BE + ∵CF BG =,EG EF = ∴EF CF BE +3、如图,ABC ∆中,AC DC BD ==,E 是DC 的中点,求证:AD 平分BAE ∠. 证明方法一:利用相似论证。
证明:∵AC DC BD == ∴∵E ∴∴∴∵∴∴∴即∴∴∴∴∴即AD 平分BAE ∠4、以ABC ∆的两边AB 、AC 为腰分别向外作等腰Rt ABD ∆和等腰Rt ACE ∆,︒=∠=∠90CAE BAD ,连接DE ,M 、N 分别是BC 、DE 的中点。
探究:AM 与DE 的位置关系及数量关系。
(1)如图1当ABC ∆为直角三角形时,AM 与DE 的位置关系是,线段AM 与DE 的数量关系是; (2)将图1中的等腰Rt ABD ∆绕点A 沿逆时针方向旋转︒θ(︒︒︒900 θ)后,如图2所示,(1)问中得到的两个结论是否发生改变?并说明理由。
精心整理∵AD 平分BAC ∠ ∴CAD BAD ∠=∠ 在ADC ∆和ADM ∆中AM AC =,CAD BAD ∠=∠,AD AD = ∴ADC ADM ∆≅∆∴︒=∠=∠90ADM ACD 即:AC CD ⊥6、如图,BD AC //,EA ,EB 分别平分CAB ∠,DBA ∠,CD 过点E ,求证:BD AC AB +=精心整理证明:在AB 上截取AC AF =,连接EF在CAE ∆和FAE ∆中⎪⎩⎪⎨⎧=∠=∠=AE AE FAE CAE AF AC ∴∴∴即在∴∴∴7,BQ 分别是∠∵∴∴又∴在AP ∴∴即∴8、如图,在四边形ABCD 中,BA BC ,CD AD =,BD 平分ABC ∠. 求证:︒=∠+∠180C A解:过点D 作BC DE ⊥于E ,过点D 作AB DF ⊥交BA 的延长线于F ∵BD 平分ABC ∠∴DF DE =,︒=∠=∠90DEB F在CDE Rt ∆和ADF Rt ∆中 ∴≅∆CDE Rt ADF Rt ∆(HL ) ∴C FAD ∠=∠∴︒=∠+∠=∠+∠180FAD BAD C BAD EFDC A B精心整理9、如图,在ABC ∆中,AC AB ,CAD BAD ∠=∠,P 为AD 上任意一点。
求证:PC PB AC AB --判断AE AD +与BC 的关系并证明你的结论。
周长记为B P .求证:A B P P .证明:延长BA 到F ,使AC AF =,连接EF ∵AD 为ABC ∆的角平分线 ∴CAD BAD ∠=∠ ∵AD MN ⊥∴CAE CAD BAD FAE ∠=∠-︒=∠-︒=∠9090 ∵AC AF =,AE AE = ∴ACE AFE ∆≅∆ ∴EC EF = FNMD EACB精心整理∵BF EF BE +∴AC AB AF AB EC BE +=++∴BC+BE+CE>AB+AC+BC BC AC AB BC EC BE ++++ ∴ABC ∆的周长小于EBC ∆的周长,即A B P P12、已知:△ABC 和△ADE 是两个不全等的等腰直角三角形,其中BA =BC ,DA =DE ,联结EC ,取EC 的中点M ,联结BM 和DM .(1)如图1,如果点D 、E 分别在边AC 、AB 上,那么BM 、DM 的数量关系与位置关系是; (2)将图1中的△ADE 绕点A 旋转到图2的位置时,判断(1)中的结论是否仍然成立,并说明解:(1(2易证△∴ED =∵AB =∴∠2=∴∠∵∠∴∠=360°∴∠8=又AD =∴∠∵MF =13、如图,已知在ABC ∆中,︒=∠60B ,ABC ∆的角平分线AD ,CE 相交于点O . 求证:OD OE =证明:在AC 上取点F ,使AE AF =,连接OF ∵AD 是A ∠的平分线 ∴FAO EAO ∠=∠ ∵AO AO = ∴AFO AEO ∆≅∆∴FO EO =,AOF AOE ∠=∠ ∵CE 是C ∠的平分线 FODEAB E9精心整理O P AMNEBCD FACEFB D图①图②图③ ∴FCO DCO ∠=∠∵︒=∠60B∴︒=∠+∠120ACB BAC∴=∠+∠=∠OCA CAO COD ()︒=∠+∠6021ACB BAC ∴︒=︒-︒-︒=∠-∠-︒=∠606060180180AOF COD COF ∴COD COF ∠=∠ ∵OC OC =∴OCF OCD ∆≅∆ ∴OF OD =∴14F .(1)说明BE (1∵∴∵∴∴∴(2∴∴∴∴∴a 15(1)如图②,在ABC ∆中,ACB ∠是直角,︒=∠60B ,AD 、CE 分别是BAC ∠、BCA ∠的平分线,AD 、CE 相交于点F 。
请你判断并写出FE 与FD 之间的数量关系;(2)如图③,在ABC ∆中,如果ACB ∠不是直角,而(1)中的其它条件不变,请问,你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由。
解:(1)FE 与FD 之间的数量关系为FD FE =(2)答:(1)中的结论FD FE =仍然成立。
精心整理证法一:如图1,在AC 上截取AE AG =,连结FG ∵21∠=∠,AF 为公共边, ∴AGF AEF ∆≅∆∴AFG AFE ∠=∠,FG FE =∵∴∴∴∵∴∴∴∵∴∴∴16的度数。
∴∴∴∴17、。
(1)当MDN ∠绕点D 转动时,求证:DF DE =; (2)若2=AB ,求四边形DECF 的面积。
分析:(1)连CD ,根据等腰直角三角形的性质得到CD 平分ACB ∠,AB CD ⊥,︒=∠45A ,DA CD =,则︒=∠45BCD ,︒=∠90CDA ,由DN DM ⊥得︒=∠90EDF ,根据等角的余角相等得到ADF CDE ∠=∠,根据全等三角形的判定易得ADF DCE ∆≅∆,即可得到结论;(2)由ADF DCE ∆≅∆,则ADF DCE S S ∆∆=,于是四边形DECF 的面积ACD S ∆=,由而2=AB 可得1==DA CD ,根据三角形的面积公式易求得ACD S ∆,从而得到四边形DECF 的面积。
解:(1)连CD ,如图,∵D 为等腰ABC Rt ∆斜边AB 的中点精心整理图1A B CDE FM N AB CDE FM N图2FE ANDCB 图3∴CD 平分ACB ∠,AB CD ⊥,︒=∠45A ,DA CD =∴︒=∠45BCD ,︒=∠90CDA ∵DN DM ⊥ ∴︒=∠90EDF ∴ADF CDE ∠=∠ 在∴∴(2∴S 而∴性质。
18D 为顶∴∵∴∴在∴∴∴6=+=++=++AC AB AN BM NC MN AN AM ∴AMN ∆的周长为619、已知四边形ABCD 中,AD AB ⊥,CD BC ⊥,BC AB =,︒=∠120ABC ,︒=∠60MBN ,MBN ∠绕B 点旋转,它的两边分别交AD 、DC (或它们的延长线)于E 、F .(1)当MBN ∠绕B 点旋转到CF AE =时(如图1),易证EF CF AE =+.(2)当MBN ∠绕B 点旋转到CF AE ≠时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,线段AE 、CF 、EF 又有怎样的数量关系?请写出你的猜想,不需证明。
解:(1)∵AD AB ⊥,精心整理CD BC ⊥,BC AB =,CF AE =∴CBF ABE ∆≅∆(SAS ); ∴CBF ABE ∠=∠,BF BE = ∵︒=∠120ABC ,︒=∠60MBN∴︒=∠=∠30CBF ABE ,BEF ∆为等边三角形 ∴BF EF BE ==,BE AE CF 21==∴EF BE CF AE ==+(2)图2成立,图3不成立。
证明图2,延长DC 至点K ,使AE CK =,连接BK 则∴∵∴∴∴∴∴∴图20的两侧。
(1(2AB ,可得PAD ≅∆于G ,在Rt ∆P D F 中,(2)将P A D ∆绕点A 顺时针旋转︒90,得到AB P '∆,PD 的最大值即为B P '的最大值,故当P '、P 、B 三点共线时,B P '取得最大值,根据PB P P B P +'='可求B P '的最大值,此时︒='∠-︒=∠135180P AP APB .解:(1)①如图,作PB AE ⊥于点E∵PAE Rt ∆中,︒=∠45APB ,2=PA ∴()1222===PE AE∵4=PB ∴3=-=PE PB BE EPADCB图1N M AD CB 图2N M AD CB图3NMA CB在ABE Rt ∆中,︒=∠90AEB∴1022=+=BE AE AB②解法一:如图,因为四边形ABCD 为正方形,可将将PAD ∆绕点A 顺时针旋转︒90得到AB P '∆,,可得AB P PAD '∆≅∆,B P PD '=,A P PA '=∴︒='∠90P PA ,︒='∠45P AP ,︒='∠90PB P ∴2='P P ,2=PA∴52422222=+=+'='=PB P P B P PD ;于G . 在在在(2 ∵此='P P B P 6此时=∠APB 21、︒=60,=∠BDC 关系及(1)如图1,当点M 、N 边AB 、AC 上,且DN DM =时,BM 、NC 、MN 之间的数量关系是;__________=LQ; 此时(2)如图2,点M 、N 边AB 、AC 上,且当DN DM ≠时,猜想(1)问的两个结论还成立吗?写出你的猜想并加以证明;P ′PA CBDEC(3)如图3,当M 、N 分别在边AB 、CA 的延长线上时,若x AN =,则_____=Q (用x 、L 表示).分析:(1)如果DN DM =,DNM DMN ∠=∠,因为DC BD =,那么︒=∠=∠30DCB DBC ,也就有︒=︒+︒=∠=∠903060NCD MBD ,直角三角形MBD 、NCD 中,因为DC BD =,DN DM =,根据HL 定理,两三角形全等。
