人教版初二数学竞赛试题及答案
八年级(上)数学竞赛试题及答案(新人教版)
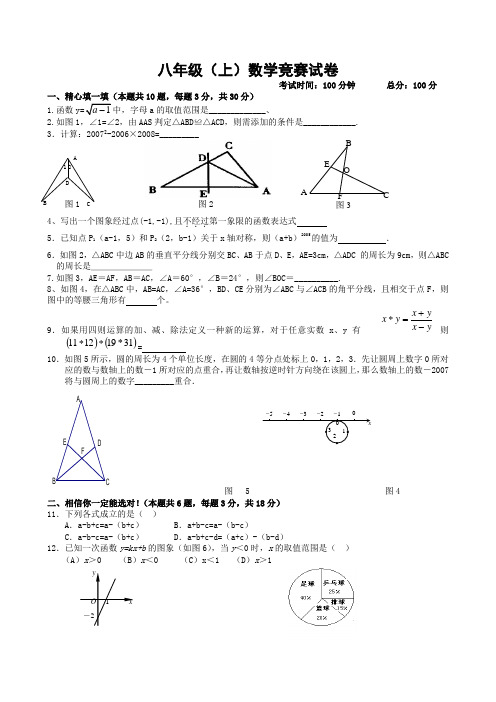
八年级（上）数学竞赛试卷考试时间：100分钟 总分：100分一、精心填一填（本题共10题，每题3分，共30分）1.函数a 的取值范围是_____________、2.如图1，∠1=∠2，由AAS 判定△ABD ≌△ACD ，则需添加的条件是____________. 3．计算：20072-2006×2008=_________图1 图24、写出一个图象经过点(-1,-1),且不经过．．．第一象限的函数表达式 5．已知点P 1（a-1，5）和P 2（2，b-1）关于x 轴对称，则（a+b ）2005的值为 ．6．如图2，△ABC 中边AB 的垂直平分线分别交BC 、AB于点D 、E ，AE=3cm ，△ADC•的周长为9cm ，则△ABC 的周长是＿＿＿＿＿＿＿7.如图3，AE ＝AF ，AB ＝AC ，∠A ＝60°，∠B ＝24°，则∠BOC ＝__________.8、如图4，在△ABC 中，AB=AC ，∠A=36°，BD 、CE 分别为∠ABC 与∠ACB 的角平分线，且相交于点F ，则图中的等腰三角形有 个。
9．如果用四则运算的加、减、除法定义一种新的运算，对于任意实数x 、y 有y x y x y x -+=* 则()()31*191211**=10．如图5所示，圆的周长为4个单位长度，在圆的4等分点处标上0，1，2，3．先让圆周上数字0所对应的数与数轴上的数－1所对应的点重合，再让数轴按逆时针方向绕在该圆上，那么数轴上的数－2007将与圆周上的数字_________重合．FEDACB图 5图4 二、相信你一定能选对！（本题共6题，每题3分，共18分） 11．下列各式成立的是（ ）A ．a-b+c=a-（b+c ）B ．a+b-c=a-（b-c ）C ．a-b-c=a-（b+c ）D ．a-b+c-d=（a+c ）-（b-d ） 12．已知一次函数y=kx+b 的图象（如图6），当y ＜0时，x 的取值范围是（ ）（A ）x ＞0 （B ）x ＜0 （C ）x ＜1 （D ）x ＞1A B C D12 AEBO F C图3图6 图713.在△ABC 中，∠B ＝∠C ，与△ABC 全等的三角形有一个角是100°，那么在△ABC 中与这100°角对应相等的角是 （ ）A.∠AB.∠BC.∠CD.∠B 或∠C 14．某校八（2）班的全体同学喜欢的球类运动用图7所示的扇形统计图来表示，下面说法正确的是（ ） A 、从图中可以直接看出喜欢各种球类的具体人数； B 、从图中可以直接看出全班的总人数；C 、从图中可以直接看出全班同学初中三年来喜欢各种球类的变化情况；D 、从图中可以直接看出全班同学现在喜欢各种球类的人数的大小关系 15．已知一次函数y=mx+│m+1│的图像与y 轴交于点（0，3），且y 随x 的增大而减小，则m 的值为（ ）． A ．2 B ．-4 C ．-2或-4 D ．2或-416．设y=ax 15+bx 13+cx 11-5(a 、b 、c 为常数)，已知当x=7时，y=7，则x= -7时，y 的值等于( )A 、-7B 、-17C 、17D 、不确定 三、认真解答，一定要细心哟！（各6分，共18分） 17. 先化简再求值：[]y y x y x y x 4)4()2)(2(2÷+--+，其中x =5，ｙ=2。
人教版数学八年级上册竞赛训练试卷八附参考答案
八年级数学比赛试卷（8）1．已知x 13 ，那么多项式 x 3 x 2 7x 5 的值是（）xA．11 B．9 C． 7 D．52．设 P 是质数，如有整数对（ a，b）知足a b (a)2P，则这样的整数对b，（）（a b）共有A．3 对B．4 对C．5 对D．6 对3．骰子相对两面上的数字和为 7，现同时掷出7 颗骰子后，向上7 个面上数字的≠10）的概率相等，那么 a 等于和是 10 的概率与向下 7 个面的数的和是 a（a（）A．7B．9C．19D．394．如图在四边形ABCD中，∠ DAB=∠BCD=90°，AB=AD，若这个四边形的面积是 10，则 BC+CD等于A．4 5B．2 10CD（）C．4 6 D．8 2A B1 5．线段y a （≤ x ≤，），当a的值由- 1增添到2时，该线段运动所经2 x1 3过的平面地区的面积为（）A．6 B．8 C．9 D．106．5 个足球队进行循环赛，规定胜一场得 3 分，输一场得 0 分，平手各得 1 分．比赛结果， 4 个球队分别获取 1 分、 4 分、 7 分、 8 分，那么第 5 个球队起码获取分．7．如图△ ABC中，∠A=96°，延伸BC到 D，∠ ABC的均分线与∠ACD的均分线交于点 A1，∠ 1 的均分线与∠ 1 的均分线交于点2，以此类推，∠ 4 的A BC A CD A A BC均分线与∠A4 的均分线交于点5，则∠ 5 的大小是．CD A A8．如图，一个正三角形被切割成9 个小正三角形，把91 到 99 这九个数分别填入此中，并使与原三角形每边相邻的 5 个小三角形内的数之和均相等，这个和的最大值是．C B1A AA2 E B C D D AF 第 7 题第 8 题第 9 题9．如图，正方形ABCD的边长为 a， E 是 AB 的中点， CF均分∠DCE，交 AD 于 F，则 AF的长为．10．某种运动鞋进价是不超出200 元的整元数，按150%订价，节日优惠销售打9折，交易金额满 1000 元返还 60 元．那么，每笔交易起码双，店家每双能赢利45 元．11．一只猴子在一架共有n 级的梯子爬上爬下，每次或许上涨 18 级，或许降落 10 级．假如它能从地面爬到最上边的一级，而后再回到地面． n 的最小值是多少？12．如图，△ABC中，AB=AC，∠ABC=36°，边的地点，作∠ACE=12°，交 BD 于点 E，连接请说明原因．B AC 绕点 A 逆时针旋转 60°，至 AD AE．试判断△ AEC是什么三角形？DAEC13．如图 1，在一个 7×7的正方形 ABCD网格中，实线将它切割成 5 块，再把这 5 块拼成如图 2，中间会出现一个小孔，假如正方形 ABCD的边长为 a，试计算图2 中小孔的面积．A DB C图1图214．某市对电话费作了调整，原市话费为每3 分钟0.2 元（不足3 分钟按3 分钟计算）．调整后，前 3 分钟为 0.2 元，此后每分钟加收 0.1 元（不足 1 分钟按 1 分钟计算）．设通话时间 x 分钟时，调整前的话费为 y1元，调整后的话费为 y2元．（1）当 x=4，4.3，5.8 时，计算对应的话费值y1、 y2各为多少，并指出x 在什么范围取值时， y1≤ y2；（2）当 x=m（ m＞5，m 为常数）时，设计一种通话方案，使所需话费最小．八年级数学比赛试卷（8）答案一．选择题（每题 6 分，共 30 分）1． C 2． D 3． D 4．B 5． A二．填空题(每题 6 分，共 30 分)6．5 7．3 度8．478 9．35 a 10．8三．解答题（每題15 分，共 60 分）211．解： n=26 6 分猴子每次爬行后所处的地点（在梯子中的第几级）18,8,26,16,6,24,14,4,22,12,2,20,10,0 15 分12．△ AEC 是等腰三角形1 分连 CD ， ∵ AC 绕点 A 逆时针旋转 60°至 AD 的地点，∴ AD=AC ，∠ CAD=60°则△ ACD 是等边三角形， 5 分 ∴∠ ECD=72°， 7 分∵ AB=AC ，∠ BAC=36°，∴∠ BAC=108°， 9 分∴∠ DAB=168°，∴∠ ABD=∠ADB=6° 11 分∴∠ EDC=54°而∠ CED=180°-∠ EDC-∠ DCE=54° 13 分 ∴ CE=CD=AC 15 分即△ AEC 是等腰三角形13．解：1 a2 1 分49如图，连接 AE ，则S AEF1 2a 4a2 7 7S AED S ADF S AEF ∴GE=6a49∴EM=GM-GE=36a49∴小孔面积S=a(27 a491a 24a 2493a 2498 分36 a) a 2 15 分4914．解：（ 1）当 x=4 时， y 1=0.4， y 2=0.31 分 当 x=4.3 时， y 1=0.4， y 2=0.42 分 当 x=5.8 时， y 1=0.4， y 2=0.53 分 当 0＜ x ≤3 或 x ＞4 时， y 1≤ y 26 分（ 2）参照方案：设 n ≥ 2 且 n 是正整数，通话 m 分钟所需话费为 y 元，①当 3n-1 ＜ m ≤ 3n 时，使所需话费最小的通话方案是：分 n 次拨打，此中（ n-1 ）次每次通话 3 分钟，一次通话（ m-3n+3）分钟， 9 分最小话费是 y=0.2n②当 3n ＜ m ≤ 3n+1 时，使所需话费最小的通话方案是：分 n 次拨打，此中（ n-1 ）次每次通话 3 分钟，一次通话（ m-3n+3）分钟， 12 分最小话费是 y=0.2(n-1)+0.3=0.2n+0.1 ③当 3n+1＜ m ≤ 3n+2 时，使所需话费最小的通话方案是：分 n 次拨打，此中（ n-2 ）次每次通话 3 分钟，一次通话 4 分钟，一次通话（ m-3n+2）分钟，15 分最小话费是y=0.2(n-2)+0.6=0.2n+0.2 （注：其余切合要求的方案相应给分）。
八年级数学竞赛试题及参考答案
八年级数学竞赛试题及参考答案八年级数学竞赛试题(一)一、选择题（每小题5分，共30分） 1．已知2220082008,2ca b a b c k k +=-==++=，且那么的值为（ ）． A ．4 B ．14 C ．－4 D ．14- 2．若方程组312433x y k x y k x y x y +=+⎧<<-⎨+=⎩的解为，，且，则的取值范围是（ ）． A ．102x y <-<B ．01x y <-<C ．31x y -<-<-D ．11x y -<-< 3．计算：2399100155555++++++=（ ）．A ．10151- B ．10051- C ．101514- D ．100514-4．如图，已知四边形ABCD 的四边都相等，等边△AEF 的顶点E 、F 分别在BC 、CD 上，且AE=AB ，则∠C=（ ）． A ．100° B ．105° C ．110° D ．120°5．已知5544332222335566a b c d a b c d ====，，，，则、、、的大小关系是（ ）． A ．a b c d >>> B ．a b d c >>> C ．b a c d >>> D ．a d b c >>> 6．如果把分数97的分子、分母分别加上正整数913a b 、，结果等于，那么a b +的最小 值是（ ）．A ．26B ．28C ．30D ．32 二、填空题：（每小题5分，共30分）（第4题图）DCB（第15题图）EDCBA7．方程组200820092007200720062008x y x y -=⎧⎨-=⎩的解是 ．8．如图，已知AB 、CD 、EF 相交于点O ，EF ⊥AB ，OG 为∠COF 的平分线，OH 为∠DOG 的平分线，若∠AOC ：∠COG=4：7，则∠GOH= ．9．小张和小李分别从A 、B 两地同时出发，相向而行，第一次在距A 地5千米处相遇，继续往前走到各地（B 、A ）后又立即返回，第二次在距B 地4千米处两人再次相遇，则A 、B 两地的距离是 千米．10．在△ABC 中，∠A 是最小角，∠B 是最大角，且2∠B=5∠A ，若∠B 的最大值为m °，最小值为n °，则m °+n °= ．11．已知21()()()04b c b c a b c a a a+-=--≠=，且，则 ． 12．设p q ，均为正整数，且7111015p q <<，当q 最小时，pq 的值为 ． 以下三、四、五题要求写出解题过程． 三、（本题满分20分）13．在一次抗击雪灾而募捐的演出中，晨光中学有A 、B 、C 、D 四个班的同学参加演出，已知A 、B 两个班共16名演员，B 、C 两个班共20名演员，C 、D 两个班共34名演员，且各班演员的人数正好按A 、B 、C 、D 次序从小到大排列，求各班演员的人数． 四、（本题满分20分）14．已知2211x x y y x y =+=+≠，，且． ⑴ 求证：1x y +=． ⑵ 求55x y +的值．五、（本题满分20分）15．如图，在△ABC 中AC ＞BC ，E 、D 分别是AC 、BC 上的点，且∠BAD=∠ABE ，AE=BD ．求证：∠BAD=12∠C ．G（第8题图）HOFED CBA参考答案一、选择题1．A 2．B 3．C 4．A 5．A 6．B 二、填空题： 7、21x y =⎧⎨=⎩ 8、72.5° 9、11 10、175° 11、2 12、68213、解：依题意得：A+B=16，B+C=20，C+D=34∵A ＜B ＜C ＜D ，∴A ＜8，B ＞8，B ＜10，C ＞10，C ＜17，D ＞17 由8＜B ＜10且B 只能取整数得，B=9 ∴C=11，D=23，A=7答：A 、B 、C 、D 各班演员人数分别是7人、9人、11人、23人。
初二 数学竞赛试卷机答案 (人教新课标初二下)(12套)初二 数学竞赛 (8)doc初中数学 (1)
初二 数学竞赛试卷机答案 （人教新课标初二下）（12套）初二 数学竞赛 (8)doc 初中数学 (1)第2试一、选择题〔每题6分，共30分〕1．如图，三个图形的周长相等，那么〔 〕〔A 〕b a c 〔B 〕c b a 〔C 〕b c a 〔D 〕a b c2a2aaabbbc cccc c cc2．b a ，那么)()(3b x a x ++--的值等于〔 〕 〔A 〕))(()(b x a x a x +++- 〔B 〕))(()(b x a x a x +++〔C 〕)()()(b x a x a x ++-+- 〔D 〕))(()(b x a x a x ++-+ 3．假设关于x 的方程ax =--12有三个整数解，那么a 的值是〔 〕〔A 〕0 〔B 〕1 〔C 〕2 〔D 〕3 4．AD 与BE 是ABC ∆的角平分线，E D ,分不在AC BC ,上，假设BC BE AB AD ==,，那么=∠C 〔 〕（A ） 690〔B 〕0)9623( 〔C 〕0)13900( 〔D 〕不能确定5．正数b a ,满足87222233-=+-+ab ab b a ab b a ，=-22b a 〔 〕〔A 〕1 〔B 〕3 〔C 〕5 〔D 〕不能确定二、填空题〔每题6分，共30分〕6．如图，三角形数表第82行的第3个数是______________________.ABCDE……12345678910111213141516（第6题）953351016第7题7.如图,16×9的矩形分成四块后可拼成一个正方形,该正方形的周长为_________. 8.n a a a ,,,21 是正整数,且n a a a 21,,1021=+++n a a a,2422221=+++n a a a 那么=),,,(21n a a a ______________________________.9.今天是星期日,假设改日是第一天,那么第333333122000200120022003+-+-+- 天是星期__________________.10.在2×2的正方形表中填入4个不同的非零平方数,使每一行、每一列的和差不多上平方数。
数学初二竞赛试题及答案
数学初二竞赛试题及答案一、选择题（每题3分，共30分）1. 下列哪个数是最小的正整数？A. 0B. 1C. -1D. 22. 如果一个数的立方等于它本身，那么这个数可以是：A. 0B. 1C. -1D. 以上都是3. 一个等腰三角形的两边长分别为3cm和4cm，那么它的周长可能是：A. 10cmB. 11cmC. 12cmD. 13cm4. 下列哪个选项是完全平方数？A. 12B. 13C. 14D. 155. 一个数的相反数是它本身，这个数是：A. 0C. -1D. 26. 一个数的绝对值是它本身，这个数是：A. 正数B. 负数C. 0D. 非负数7. 如果一个角是直角的一半，那么这个角的度数是：A. 45°B. 60°C. 90°D. 120°8. 一个数列的前三项是1, 1, 2，从第四项开始，每一项都是前三项的和，那么第五项是：A. 4B. 5C. 6D. 79. 一个圆的直径是10cm，那么它的面积是：A. 25π cm²B. 50π cm²C. 100π cm²D. 200π c m²10. 一个等差数列的前三项是2, 5, 8，那么它的公差是：A. 1C. 3D. 4二、填空题（每题4分，共20分）1. 一个数的平方根是3，那么这个数是________。
2. 如果一个三角形的三个内角分别是30°，60°，90°，那么这个三角形是________三角形。
3. 一个数的立方根是2，那么这个数是________。
4. 一个数的倒数是1/2，那么这个数是________。
5. 一个圆的半径是5cm，那么它的直径是________cm。
三、解答题（每题10分，共50分）1. 已知等差数列的前三项是3, 6, 9，求这个数列的第10项。
2. 一个直角三角形的两个直角边长分别是6cm和8cm，求这个三角形的斜边长。
人教版初二数学竞赛试卷
一、选择题（每题5分，共25分）1. 下列各数中，不是有理数的是（）A. -2.5B. 3/4C. √16D. √22. 下列各式中，正确的是（）A. a + b = b + aB. a - b = b - aC. a × b = b × aD. a ÷ b = b ÷ a3. 若x² - 3x + 2 = 0，则x的值为（）A. 1B. 2C. 1或2D. 1和34. 已知等腰三角形底边长为6，腰长为8，则该三角形的面积为（）A. 24B. 32C. 36D. 405. 若a、b、c、d为等差数列，且a + b + c + d = 24，则d的值为（）A. 6C. 8D. 9二、填空题（每题5分，共25分）6. 已知一元二次方程x² - 5x + 6 = 0，则其因式分解为______。
7. 若等边三角形的一边长为a，则其面积为______。
8. 若x + 1/x = 5，则x² + 1的值为______。
9. 若等差数列的第一项为a₁，公差为d，则第n项为______。
10. 若a、b、c、d为等比数列，且a + b + c + d = 16，则d的值为______。
三、解答题（每题15分，共45分）11. （10分）已知一元二次方程x² - 4x + 3 = 0，求：（1）方程的解；（2）方程的判别式。
12. （15分）已知等腰三角形底边长为8，腰长为10，求：（1）该三角形的周长；（2）该三角形的面积。
13. （15分）已知等差数列的第一项为3，公差为2，求：（1）该数列的前10项和；（2）该数列的第n项。
答案：一、选择题1. D2. A4. B5. D二、填空题6. (x - 3)(x - 1)7. (√3/4)a²8. 269. a₁ + (n - 1)d10. 2三、解答题11. （1）x₁ = 1，x₂ = 3；（2）判别式为Δ = 16 - 4×3×1 = 4。
初二数学竞赛试题及答案
初二数学竞赛试题及答案一、选择题（每题4分，共40分）1. 下列哪个数是无理数？A. 0.5B. √2C. 0.33333…D. 3答案：B2. 一个等腰三角形的底边长为6，腰长为5，那么这个三角形的面积是多少？A. 12B. 15C. 18D. 20答案：B3. 如果一个数的平方等于它本身，那么这个数可能是：A. 0B. 1C. -1D. 以上都是答案：D4. 一个两位数，十位上的数字比个位上的数字大3，这个两位数可能是：A. 23B. 47C. 52D. 69答案：B5. 下列哪个分数是最简分数？A. 3/6B. 4/8C. 5/10D. 7/14答案：A6. 一个圆的直径是10厘米，那么这个圆的面积是多少平方厘米？A. 25πB. 50πC. 100πD. 200π答案：C7. 一个数的相反数是-5，那么这个数是：A. 5C. 0D. 10答案：A8. 一个数的绝对值是5，那么这个数可能是：A. 5B. -5C. 0D. 以上都是答案：D9. 一个等差数列的前三项分别是2，5，8，那么这个数列的第五项是多少？A. 11B. 12C. 13答案：A10. 下列哪个图形是轴对称图形？A. 平行四边形B. 梯形C. 等腰三角形D. 不规则多边形答案：C二、填空题（每题4分，共20分）11. 一个等腰直角三角形的斜边长为10厘米，那么这个三角形的面积是______平方厘米。
答案：2512. 如果一个数的立方等于8，那么这个数是______。
答案：213. 一个数的平方根是3，那么这个数是______。
答案：914. 一个数的倒数是1/4，那么这个数是______。
答案：415. 一个圆的周长是31.4厘米，那么这个圆的半径是______厘米。
答案：5三、解答题（每题10分，共40分）16. 已知一个等腰三角形的底边长为8，腰长为10，求这个三角形的高。
解：根据勾股定理，设高为h，则有：h^2 + (8/2)^2 = 10^2h^2 + 16 = 100h^2 = 84h = √84 = 2√21答：这个三角形的高是2√21。
八年级(上)数学竞赛试题及答案(新人教版)
一、精心填一填（本题共 10题，每题3分，共30分） 1. 函数y= JT 万中，字母a 的取值范围是 ______________ 2. 如图1, 3. 计算:4、写出一个图象经过点（-1,-1）,且不经过第一象限的函数表达式5. 已知点P 1 （a-1 , 5）和P 2 （2, b-1 ）关于x 轴对称，则（a+b ） 2005的值为6. 如图2,A ABC 中边AB 的垂直平分线分别交 BC AB 于点D 、E , AE=3cm △ ADC?勺周长为9cm 则厶ABC 的周长是 ________________7. 如图 3, AE = AF , AB = AC, / A = 60°,/ B = 24°，则/ BOC= ___________ . 8.如图4,在厶ABC 中，AB=AC / A=36°, BD CE 分别为/ ABC 与/ ACB 的角平分线，且相交于点 F ,贝U 图中的等腰三角形有 个。
9 •如果用四则运算的加、减、除法定义一种新的运算，对于任意实数11 12 19*31 =10•如图5所示，圆的周长为 4个单位长度，在圆的4等分点处标上0, 1, 2, 应的数与数轴上的数一1所对应的点重合， 将与圆周上的数字 __________ 重合./戴尊7 *J)八年级（上）数学竞赛试卷考试时间：100分钟总分：100分/仁/ 2,由AAS 判定△ ABD^A ACD 则需添加的条件 20072-2006 X 2008=3 •先让圆周上数字0所对 那么数轴上的数一2007 再让数轴按逆时针方向绕在该圆上, 、相信你一定能选对！ 下列各式成立的是（ a-b+c=a- a-b-c=a- 已知一次函数 （A ） x > 0 11.A C 12. (b+c ) (b+c ) （本题共 ） B 6题，每题 图 53分，共18分）.a+b-c=a- (b-c ) .a-b+c-d= (a+c ) - (b-d ) y=kx+b 的图象(如图6),当y v 0时，x 的取值范围是()(B ) x v 0(C ) x v 1( D ) x > 1图3图6图713.在厶ABC 中，/ B =Z 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
八 年 级 数 学 竞 赛 试 题
一、精心选一选，相信你选得准！（每小题5分，共30分）
1．三角形的三边长分别为6，1－3a ，10，则a 的取值范围是（ ）
A ．－6＜a ＜－3
B ．5＜a ＜1
C ．－5＜a ＜－1
D ．a ＞－1或a ＜－5
2．使分式x
x y z x 5201020092010201020092008--+有意义的x 的取值范围是（ ）
A ．x ≠0
B ．x ≠0且x ≠±402
C ．x ≠0且x ≠402
D ．x ≠0且x ≠－402 3．如图，将纸片△ABC 沿着D
E 折叠压平，且∠1＋∠2＝72°，则∠A ＝（ ）
A ．72°
B ．24°
C ．36°
D ．18° 4．已知一个梯形的四条边长分别为2、3、4、5，则此梯形的面积为（ ）
A ．5
B ．8
C ．
3
3
10 D ．
3
5
14 5．如图，E 、F 分别是矩形ABCD 的边AB 、BC 的中点，连CE 、AF ，设CE 、AF
相交于G ，则S BEGF 四边形∶S ABCD 四边形等于（ ）
A ．41
B ．92
C ．6
1 D ．103
6．已知x 为实数，且13-x ＋14-x ＋15-x ＋…＋1
17-x 的值是一个确定的常数，则这个常数是（ ） A ．5 B ．10 C ．15 D ．75
二、细心填一填，相信你填得对！（每小题5分，共30分）
7．已知实数x 、y 满足x 2
—3x ＋4y ＝7，则3x ＋4y 的最大值为__________． 8．如果a 、b 是整数，且x 2＋x —1是a x 3＋b x ＋1的因式，则b 的值为__________． 9．如图，E 、F 分别是矩形ABCD 的BC 边和CD 边上的点，且S △ABE ＝3，S △ECF ＝8，
S △ADF ＝5，则矩形ABCD 的面积为__________． 10．如图△ABC 中，AD 平分∠BAC ，且AB ＋BD ＝AC ，若
∠B ＝62°，则∠C ＝__________． 11．已知k ＝
a
c
b a b
c b a c c b a ++-=
+-=-+，且n 2＋16＋ B
D
E
C
A 1
2
（第3
题图） C
（第9题图） （第10题图）
A
B
C
D
C F
B
（第5题图）
6 m ＝8n ，则关于x 的一次函数y ＝－kx ＋n －m 的图象一定经过第
__________象限．
12．若a ＋x 2＝2008，b ＋x 2＝2009，c ＋x 2＝2010，且abc ＝24，则
bc a ＋ac b ＋ab
c －a
1－b
1－c
1的值为__________．
三、用心做一做，试试你能行！（共40分） 13．（8分）蕲春红人电器行“家电下乡”指定型号的冰箱彩电的进价和售价如右表所示： ⑴按国家政策，农民购买“家电下乡”产品
可享受售价13%的政府补贴；农民蕲大伯到
该电器行购买了冰箱一台，彩电两台，可以享受多少元的政府补贴？（2分）
⑵为满足农民需求，红人电器行决定用不超过85000元采购冰箱和彩电共40
台，且冰箱的数量不少于彩电数量的6
5．
①请你帮助该电器行设计相应的进货方案；（3分）
②哪种进货方案电器行获得的利润最大？(利润＝售价－进价)最大利润是多少？(3分)
14．（8分）如图，已知 ：正△OAB 的面积为34，双曲线y ＝x
k
经过点B ，点
P (m ，n )(m ＞0)在双曲线y ＝x
k 上，PC ⊥x 轴于点C ，PD ⊥y 轴于点D ，设矩形OCPD 与正△OAB 不重叠部分的面积为S ． ⑴求点B 的坐标及k 的值； ⑵求m ＝1和m ＝3时，S 的值．
15．（8分）已知a 、b 、c 均为正数，且满足如下两个条件：
⎪⎩⎪
⎨⎧=-++-++-+=++4132
ab c b a ac b a c bc
a c
b
c b a
证明：以a 、b 、c 为三边长可构成一个直角三角形．
16．（加油啊！加油！加油！！）（8分）2010年4月14日青海省玉树发生了7.1级大
地震，驻军某部（位于距玉树县城结古镇91公里处的上拉秀镇）接到上级命令，须火速前往结古镇救援．已知该部有120名官兵，且步行的速度为每小时10公里，现仅有一辆时速为80公里的卡车，可乘坐40人，请你设计一个乘车兼步行方案，使该部120人能在最短时间内赶往重灾区结古镇救
x
援．其中中途换车（上、下车）的时间均忽略不计，最快多少时间可以赶到？（可用分数表示）
17．（6分）计算：2sin 45°＋sin 2α＋cos 2α＋3
30cos 23
60tan ︒
-︒
18．（8分）如图，△ABC 的边AB ＝3，AC ＝2，Ⅰ、Ⅱ、Ⅲ 分别表示以AB 、AC 、
BC 为边的正方形，求图中三个阴影部分的面积之和的最大值是多少？
H
（第18题图）。