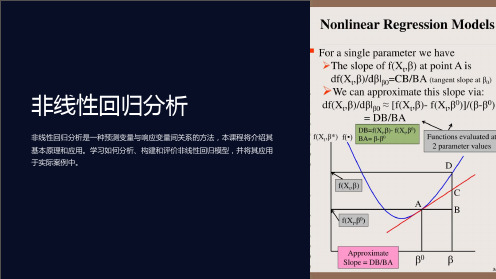
非线性回归

合集下载

《非线性回归分析》课件

• 常用的过滤方法包括皮尔逊相关系数、方差分析和卡方检验等。
封装式
• 基于模型的错误率和复杂性进行特征选择。
• 常用的封装方法包括递归特征消除法和遗传算法等。
嵌入式
• 特征选择和模型训练同时进行。
• 与算法结合在一起的特征选择方法，例如正则化（Lasso、Ridge）。
数据处理方法：缺失值填充、异常值处理等
1
网格搜索
通过预定义的参数空间中的方格进行搜
随机搜索
2
索。
在预定义的参数空间中进行随机搜索。
3
贝叶斯调参
使用贝叶斯优化方法对超参数进行优化。
集成学习在非线性回归中的应用
集成学习是一种将若干个基学习器集成在一起以获得更好分类效果的方法，也可以用于非线性回归建模中。
1 堆叠
使用多层模型来组成一个超级学习器，每个模型继承前一模型的输出做为自己的输入。
不可避免地存在数据缺失、异常值等问题，需要使用相应的方法对其进行处理。这是非线性回归分析中至关重要的一环。
1 缺失值填充
常见的方法包括插值法、代入法和主成分分析等。
2 异常值处理
常见的方法包括删除、截尾、平滑等。
3 特征缩放和标准化
为了提高模型的计算速度和准确性，需要对特征进行缩放和标准化。
偏差-方差平衡与模型复杂度
一种广泛用于图像识别和计算机视觉领域的神经网络。
循环神经网络
一种用于处理序列数据的神经网络，如自然语言处理。
sklearn库在非线性回归中的应用
scikit-learn是Python中最受欢迎的机器学习库之一，可以用于非线性回归的建模、评估和调参。
1 模型建立
scikit-learn提供各种非线性回归算法的实现，如 KNN回归、决策树回归和支持向量机回归等。

非线性回归分析的入门知识

非线性回归分析的入门知识在统计学和机器学习领域，回归分析是一种重要的数据分析方法，用于研究自变量和因变量之间的关系。

在实际问题中，很多情况下自变量和因变量之间的关系并不是简单的线性关系，而是呈现出一种复杂的非线性关系。

因此，非线性回归分析就应运而生，用于描述和预测这种非线性关系。

本文将介绍非线性回归分析的入门知识，包括非线性回归模型的基本概念、常见的非线性回归模型以及参数估计方法等内容。

一、非线性回归模型的基本概念在回归分析中，线性回归模型是最简单和最常用的模型之一，其数学表达式为：$$Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + ... + \beta_pX_p +\varepsilon$$其中，$Y$表示因变量，$X_1, X_2, ..., X_p$表示自变量，$\beta_0, \beta_1, \beta_2, ..., \beta_p$表示模型的参数，$\varepsilon$表示误差项。

线性回归模型的关键特点是因变量$Y$与自变量$X$之间呈线性关系。

而非线性回归模型则允许因变量$Y$与自变量$X$之间呈现非线性关系，其数学表达式可以是各种形式的非线性函数，例如指数函数、对数函数、多项式函数等。

一般来说，非线性回归模型可以表示为：$$Y = f(X, \beta) + \varepsilon$$其中，$f(X, \beta)$表示非线性函数，$\beta$表示模型的参数。

非线性回归模型的关键在于确定合适的非线性函数形式$f(X,\beta)$以及估计参数$\beta$。

二、常见的非线性回归模型1. 多项式回归模型多项式回归模型是一种简单且常见的非线性回归模型，其形式为： $$Y = \beta_0 + \beta_1X + \beta_2X^2 + ... + \beta_nX^n +\varepsilon$$其中，$X^2, X^3, ..., X^n$表示自变量$X$的高次项，$\beta_0, \beta_1, \beta_2, ..., \beta_n$表示模型的参数。

非线性回归方法

非线性回归方法非线性回归是机器学习中的一种重要方法，用于建立输入和输出之间的非线性关系模型。

线性回归假设输入和输出之间存在线性关系，而非线性回归则允许更复杂的模型形式，可以更好地适应现实世界中的复杂数据。

下面将介绍几种常见的非线性回归方法，并说明它们的原理、应用场景和优缺点。

1. 多项式回归多项式回归通过引入高次多项式来拟合数据。

例如，在一元情况下，一阶多项式即为线性回归，二阶多项式即为二次曲线拟合，三阶多项式即为三次曲线拟合，依此类推。

多项式回归在数据不规则变化的情况下能够提供相对灵活的拟合能力，但随着多项式次数的增加，模型的复杂度也会增加，容易出现过拟合问题。

2. 非参数回归非参数回归方法直接从数据中学习模型的形式，并不对模型的形式做出先验假设。

常见的非参数回归方法包括局部加权回归（LWLR）、核回归（Kernel Regression）等。

局部加权回归通过给予离目标点较近的样本更大的权重来进行回归，从而更注重对于特定区域的拟合能力。

核回归使用核函数对每个样本进行加权，相当于在每个样本周围放置一个核函数，并将它们叠加起来作为最终的拟合函数。

非参数回归方法的优点是具有较强的灵活性，可以适应各种不同形状的数据分布，但计算复杂度较高。

3. 支持向量回归（SVR）支持向量回归是一种基于支持向量机的非线性回归方法。

它通过寻找一个超平面，使得样本点离该超平面的距离最小，并且在一定的松弛度下允许一些样本点离超平面的距离在一定范围内。

SVR通过引入核函数，能够有效地处理高维特征空间和非线性关系。

SVR的优点是对异常点的鲁棒性较好，并且可以很好地处理小样本问题，但在处理大规模数据集时计算开销较大。

4. 决策树回归决策树回归使用决策树来进行回归问题的建模。

决策树将输入空间划分为多个子空间，并在每个子空间上拟合一个线性模型。

决策树能够处理离散特征和连续特征，并且对异常点相对较鲁棒。

决策树回归的缺点是容易过拟合，因此需要采取剪枝等策略进行降低模型复杂度。

计量经济学_詹姆斯斯托克_第8章_非线性的回归模型

Ln(TestScore) = 6.336 + 0.0554 ln(Incomei) (0.006) (0.0021)
假设 Income 从$10,000 增加到$11,000（或者 10%）。
则 TestScore 增加大约 0.0554 10% = 0.554%。
如果 TestScore = 650, 意味着测试成绩预计会增加
非线性的回归模型
非线性的回归函数
“非线性”的含义：
（1）非线性的函数自变量与解释变量之间的非线性
函数形式。
（2）非线性的回归参数与随机项的非线性形式。
非线性的回归函数
一、多项式回归二、对数回归三、自变量的交互作用四、其他非线性形式的回归五*、非线性回归（参数非线性）
一、多项式回归
1、指数函数曲线
指数函数方程有两种形式：
yˆ aebx yˆ abx
y a＞0，b＞0
a＞0，b＜0
x
图11.1方yˆ 程 aebx 的图象
二、对数函数曲线
对数函数方程的一般表达式为：
yˆ a b ln x
y
b＞0
b＜0
x
图11.2 方程yˆ =a+blnx 的图象
（2）根据拟合程度的好坏来确定（如，利用spss 的相关功能）在社会科学领域里，阶数不会太高！
一、多项式回归
形式： Y 0 1X 2 X 2 ...r X r u
（2）多项式的本质泰勒展开
一、多项式回归
形式： Y 0 1X 2 X 2 ...r X r u
Y——收入； D1——性别（1——男；0——女） D2——学历（1——大学学历；0——没有）

非线性回归方程公式详解

非线性回归方程公式详解一、非线性回归的定义和方程1、非线性回归非线性回归是回归函数关于未知回归系数具有非线性结构的回归。

常用的处理方法有回归函数的线性迭代法、分段回归法、迭代等。

非线性回归分析的主要内容与线性回归分析相似。

2、回归分析对具有相关关系的两个变量进行统计分析的方法叫回归分析。

其基本步骤是：（1）画散点图；（2）求回归直线方程；（3）用回归直线方程作预报。

3、回归直线如果具有相关关系的两个变量的一组数据(x1,y1)(x1,y1)，(x2,y2)(x2,y2)，⋯⋯，(xn,yn)(xn,yn)大致分布在一条直线附近，那么我们称这样的变量之间的关系为线性相关关系，这条直线就是回归直线，记为yˆ=bˆx+aˆy^=b^x+a^。

4、回归直线方程的求法——最小二乘法设具有线性相关关系的两个变量xx，yy的一组观察值为(xi,yi)(xi,yi)(i=1,2,⋯,n)(i=1,2,⋯,n)，则回归直线方程yˆ=bˆx+aˆy^=b^x+a^的系数为bˆ=b^=∑ni=1(xi−x¯¯¯)(yi−y¯¯¯)∑ni=1(xi−x¯¯¯)2=∑ni=1(xi−x¯)(yi−y¯)∑ni=1(xi−x¯)2=∑ni=1xiyi−nx¯¯¯y¯¯¯∑ni=1x2i−nx¯¯¯2∑ni=1xiyi−nx¯ y¯∑ni=1xi2−nx¯2，aˆ=y¯¯¯−bˆx¯¯¯a^=y¯−b^x¯，其中(xi,yi)(xi,yi)为样本数据，x¯¯¯=x¯=1n∑ni=1xi1n∑ni=1xi，y¯¯¯=y¯=1n∑ni=1yi1n∑ni=1yi为样本平均数。

数据建模—非线性回归

数据建模—非线性回归
什么是非线性回归
一般线性回归假设因变量与自变量呈线性关系，但现实中有很
多问题并非是线性相关的。

而非线性回归可以用来拟合非线性关系。

非线性模型示例
下面以一些示例来介绍非线性回归：
1. 多项式回归
多项式回归就是一种非线性回归，它将线性模型中的自变量的
各次幂作为回归系数，即将 $y=a_0+a_1x+a_2x^2+...+a_nx^n$ 作为
模型进行回归。

这种方法适用于自变量$x$与因变量$y$之间的关系
大致呈多项式分布。

2. 对数函数回归
对数函数回归是一类将对数函数作为函数形式的非线性回归方法，它们适用于特定类型的数据。

如指数增长、充分增长、衰减等类型的数据。

3. Sigmoid函数回归
Sigmoid函数（S型函数）经常用于二分类问题，由于其形状为S型，经过合适的处理可以用来拟合非线性关系。

Sigmoid函数的形式为： $y=\frac{1}{1+e^{-ax+b}}$
非线性回归方法
与线性回归不同，非线性模型中的回归系数无法直接求解，需要使用非线性优化算法对其进行拟合。

非线性优化算法有很多种，常见的有：梯度下降法、拟牛顿法、Levenberg-Marquardt算法等。

总结
非线性回归适用于许多实际问题，可以通过多项式回归、对数函数回归、Sigmoid函数回归等方法进行建模。

然后，我们可以使用非线性优化算法对模型进行优化拟合以得到最优参数。

非线性回归分析

非线性回归分析随着数据科学和机器学习的发展，回归分析成为了数据分析领域中一种常用的统计分析方法。

线性回归和非线性回归是回归分析的两种主要方法，本文将重点探讨非线性回归分析的原理、应用以及实现方法。

一、非线性回归分析原理非线性回归是指因变量和自变量之间的关系不能用线性方程来描述的情况。

在非线性回归分析中，自变量可以是任意类型的变量，包括数值型变量和分类变量。

而因变量的关系通常通过非线性函数来建模，例如指数函数、对数函数、幂函数等。

非线性回归模型的一般形式如下：Y = f(X, β) + ε其中，Y表示因变量，X表示自变量，β表示回归系数，f表示非线性函数，ε表示误差。

二、非线性回归分析的应用非线性回归分析在实际应用中非常广泛，以下是几个常见的应用领域：1. 生物科学领域：非线性回归可用于研究生物学中的生长过程、药物剂量与效应之间的关系等。

2. 经济学领域：非线性回归可用于经济学中的生产函数、消费函数等的建模与分析。

3. 医学领域：非线性回归可用于医学中的病理学研究、药物研发等方面。

4. 金融领域：非线性回归可用于金融学中的股票价格预测、风险控制等问题。

三、非线性回归分析的实现方法非线性回归分析的实现通常涉及到模型选择、参数估计和模型诊断等步骤。

1. 模型选择：在进行非线性回归分析前，首先需选择适合的非线性模型来拟合数据。

可以根据领域知识或者采用试错法进行模型选择。

2. 参数估计：参数估计是非线性回归分析的核心步骤。

常用的参数估计方法有最小二乘法、最大似然估计法等。

3. 模型诊断：模型诊断主要用于评估拟合模型的质量。

通过分析残差、偏差、方差等指标来评估模型的拟合程度，进而判断模型是否适合。

四、总结非线性回归分析是一种常用的统计分析方法，可应用于各个领域的数据分析任务中。

通过选择适合的非线性模型，进行参数估计和模型诊断，可以有效地拟合和分析非线性关系。

在实际应用中，需要根据具体领域和问题的特点来选择合适的非线性回归方法，以提高分析结果的准确性和可解释性。

第四章非线性回归与非线性约束

具体检验时，用来对原假设进行检验的似然比统用来对原假设进行检验的似然比统具体检验计量定义为：计量定义为： L( β R ) LR = −2(ln L( β R ) − ln L( βUR )) = −2 ln L( βUR )
LR ~ χ , m为限制条件的个数。
2 m 2 若LR大于给定显著性水平下的χ m临界值，
2
exp[−
1 2σ
2
(Yi − f ( X 1i , X 2i , L X ki , β1 , β 2 ,L β p )) 2 ]
则N个观测值的对数似然函数为 LnL = ∑ p (Yi , X i β ) = − ( N / 2) ln(2π ) − ( N / 2) ln(σ )
2
− (σ / 2)∑ (Yi − f ( X 1i , X 2i , L X ki , β1 , β 2 , L β p ))
L( β R ) 则似然比定义为λ = . L( βUR )
L( β R ) 则似然比定义为λ = . L( βUR )
L越大表明对数据的拟合程度越好，分母来自无条越大表明对数据的拟合程度越好，越大表明对数据的拟合程度越好件模型，变量个数越多，拟合越好，件模型，变量个数越多，拟合越好，因此分子小于分似然比在0到间母，似然比在到1间。分子是在原假设成立下参数的极大似然函数值，是零假设的最佳表示。极大似然函数值，是零假设的最佳表示。而分母则表示在在任意情况下参数的极大似然函数值。示在在任意情况下参数的极大似然函数值。比值的最大极限值为1，其值靠近1，大极限值为，其值靠近，说明局部的最大和全局最大近似，零假设成立可能性就越大。大近似，零假设成立可能性就越大。
设L( βUR )代表没有限制条件时似然函数的极大值, L( β R )代表有限制条件时似然函数的极大值,

非线性回归模型

• 由于逻辑表达式只能是1或0，于是当X<=0时，结果为1*0+0*X+0*1=0 当X>0&X<1时,结果为0*0+1*X+0*1=X 当X>1时, 结果为0*0+0*X+1*1=1 • 字符串变量也可以用于逻辑表达式,如:
(city=‘New York’)*costliv+(city=Washington)*0.59*costliv
缺点：a.计算复杂；b.初始值不适当时，估计不准确.
采用SPSS进行曲线拟合
曲线直线化
Analyze Regression Curve Estimation … 可选Power 、Logarithmic、Exponential、 Quadratic、Cubic 等
非线性回归
Analyze Regression Nonlinear … 设置模型： Model Expression 参数赋初值：Parameters…
Parameter Estimates 95% Confidence Interval Lower Bound Upper Bound .088 .234 .075 .097
Parameter A B
Estimate .161 .086
Std. Error .035 .005
Correlations of Parameter Estimates A B A 1.000 -.990 B -.990 1.000
ANOVAa Source Reg ression Residual Uncorrected Total Corrected Total Sum of Squares 201.543 3.510 205.053 108.796 df 2 19 21 20 Mean Squares 100.771 .185

非线性回归分析

非线性回归分析随着经济和社会的发展，数据分析和统计方法越来越受到重视。

在统计学中，回归分析是一种广泛应用的方法，它可以帮助我们研究两个或多个变量之间的关系，并用数学模型描述它们之间的关系。

线性回归是最基本的回归分析方法，但在实际应用中，很多现象并不是线性的，这时候就需要用到非线性回归分析。

什么是非线性回归分析？非线性回归分析是一种研究两个或多个变量之间关系的方法，但假设它们之间的关系不是线性的。

因此，在非线性回归模型中，自变量和因变量之间的关系可以被描述为一个非线性函数，例如指数函数、对数函数、幂函数等。

非线性回归模型的公式可以表示为：y = f(x, β) + ε其中，y是因变量，x是自变量，β是待估计参数，f是非线性函数，ε是随机误差项。

非线性回归模型的目的就是估计参数β，找出最佳的拟合函数f，使预测值与实际值的误差最小。

常见的非线性回归模型包括：1. 指数模型：y = αeβx + ε2. 对数模型：y = α + βln(x) + ε3. 幂函数模型：y = αxβ + ε4. S型曲线模型：y = α / (1 + e^(βx)) + ε为何要使用非线性回归分析？非线性回归模型可以更好地描述真实世界中的现象。

例如，在生态学中，物种数量和资源的关系往往是非线性的，这时候就需要用到非线性回归分析来研究它们之间的关系。

再如，在经济学中，通货膨胀率和经济增长率之间的关系也是非线性的。

此外，非线性回归还可以应用于医学、生物学、工程学、地球科学等领域，用于研究复杂的现象和关系。

如何进行非线性回归分析？1. 数据准备首先需要收集相关数据，并进行数据清洗和处理。

确保数据的准确性和完整性。

2. 模型选择根据数据的特征和研究目的，选择适合的非线性回归模型。

如果不确定，可以尝试多种模型进行比较。

3. 参数估计使用统计方法估计模型中的参数值。

常用的方法包括最小二乘法、极大似然法等。

4. 模型诊断诊断模型的拟合程度和假设是否成立。

非线性回归分析简介

非线性回归分析简介在统计学和机器学习领域，回归分析是一种重要的数据分析方法，用于研究自变量和因变量之间的关系。

在实际问题中，很多情况下自变量和因变量之间的关系并不是简单的线性关系，而是呈现出一种复杂的非线性关系。

因此，非线性回归分析应运而生，用于描述和预测这种非线性关系。

本文将介绍非线性回归分析的基本概念、方法和应用。

一、非线性回归分析概述1.1 非线性回归模型在回归分析中，最简单的模型是线性回归模型，即因变量和自变量之间的关系可以用一个线性方程来描述。

但是在实际问题中，很多情况下因变量和自变量之间的关系并不是线性的，而是呈现出曲线、指数、对数等非线性形式。

这时就需要使用非线性回归模型来拟合数据，通常非线性回归模型可以表示为：$$y = f(x, \beta) + \varepsilon$$其中，$y$为因变量，$x$为自变量，$f(x, \beta)$为非线性函数，$\beta$为参数向量，$\varepsilon$为误差项。

1.2 非线性回归分析的优势与线性回归相比，非线性回归分析具有更强的灵活性和适用性。

通过使用适当的非线性函数，可以更好地拟合实际数据，提高模型的预测能力。

非线性回归分析还可以揭示数据中潜在的复杂关系，帮助研究人员更好地理解数据背后的规律。

1.3 非线性回归分析的挑战然而，非线性回归分析也面临一些挑战。

首先，选择合适的非线性函数是一个关键问题，需要根据实际问题和数据特点进行合理选择。

其次，非线性回归模型的参数估计通常比线性回归模型更复杂，需要使用更为复杂的优化算法进行求解。

因此，在进行非线性回归分析时，需要谨慎选择模型和方法，以确保结果的准确性和可靠性。

二、非线性回归分析方法2.1 常见的非线性回归模型在实际应用中，有许多常见的非线性回归模型，常用的包括多项式回归模型、指数回归模型、对数回归模型、幂函数回归模型等。

这些模型可以根据实际问题的特点进行选择，用于描述和预测自变量和因变量之间的非线性关系。

非线性回归

第11章非线性回归本章内容311.1 非线性回归概述11.2 曲线回归的线性化11.3 多项式回归11.4 曲线配合的拟合度非线性回归线性回归11.1 非线性回归概述•变量之间的关系经常是非线性的–例：奶牛的日泌乳量与泌乳日龄4•非线性回归分析–已知曲线类型•判断：根据专业知识（理论和经验），或样本数据的散点分布趋势–未知曲线类型拟合几种常用曲线方程，从中选择最优方程。

5分析方法：1.曲线方程线性化2.直接配合曲线方程11.1非线性回归概述bxae y=ˆ221xb x b ay ++=33221xb x b x b a y +++=例题11.112解：将样本数据在平面坐标上做散点图，结果如图11-6，可以看出它的分布趋势与幂函数曲线（b<0）很接近，故可选用幂函数曲线来配合回归方程，即求回归方程ˆbaXY=13nX X nY X Y X b X Y 22)())((∑′−∑′∑′∑′−∑′′=′′89.11597.101415.91536.2497.106983.152−=−×−=62.11524.36 73.01597.10====Y X 01.373.0)90.1(62.1=×−−=′−′=′X b Y a 用转换后的数据做线性回归分析Y X r ′′=1511.3 未知曲线类型的回归分析—多项式回归当变量间曲线关系很难确定时，可以使用多项式去逼近。

二次多项式：三次多项式：221xb x b a y++=33221xb x b x b a y +++=16例题11.1 配合二项式回归方程221.484.8545.409ˆXX Y +−=221,XX X X ==令转变为建立二元直线回归方程建立的二元直线回归方程。

非线性回归分析简介

非线性回归分析简介非线性回归分析是一种用于建立非线性关系模型的统计方法。

与线性回归不同，非线性回归可以更好地拟合非线性数据，提供更准确的预测结果。

在许多实际问题中，数据往往呈现出非线性的趋势，因此非线性回归分析在实际应用中具有广泛的应用价值。

一、非线性回归模型的基本形式非线性回归模型的基本形式可以表示为：y = f(x, β) + ε其中，y是因变量，x是自变量，β是模型参数，f(x, β)是非线性函数，ε是误差项。

非线性函数可以是任意形式的函数，如指数函数、对数函数、幂函数等。

二、非线性回归模型的参数估计与线性回归不同，非线性回归模型的参数估计不能直接使用最小二乘法。

常见的非线性回归参数估计方法有以下几种：1. 非线性最小二乘法（NLS）非线性最小二乘法是一种常用的参数估计方法，它通过最小化残差平方和来估计模型参数。

具体而言，通过迭代的方式不断调整参数，使得残差平方和最小化。

2. 非线性广义最小二乘法（GNLS）非线性广义最小二乘法是对非线性最小二乘法的改进，它在最小化残差平方和的同时，还考虑了误差项的方差结构。

通过引入权重矩阵，可以更好地处理异方差性的数据。

3. 非线性加权最小二乘法（WNLS）非线性加权最小二乘法是对非线性广义最小二乘法的进一步改进，它通过引入加权矩阵，对不同数据点赋予不同的权重。

可以根据数据的特点，调整权重矩阵，提高模型的拟合效果。

三、非线性回归模型的评估指标在进行非线性回归分析时，需要对模型进行评估，以确定模型的拟合效果。

常见的评估指标有以下几种：1. 残差分析残差分析是一种常用的评估方法，通过分析残差的分布情况，判断模型是否符合数据的分布特征。

如果残差呈现随机分布，说明模型拟合效果较好；如果残差呈现一定的规律性，说明模型存在一定的问题。

2. 决定系数（R-squared）决定系数是衡量模型拟合优度的指标，其取值范围为0到1。

决定系数越接近1，说明模型对数据的解释能力越强；决定系数越接近0，说明模型对数据的解释能力越弱。

非线性回归

点analaze—regressin--nonlinear
对参数1 ,2 ,3赋予初始值20,1,0, 则运行结果如下：
它是模型参数拟合具体的迭代过程。本例迭代22次停止迭代。
• 此表是模型中参数的估计值。具体给出了各参数的估计值，标准误和95%置信区间。根据参数估计值可得模型的拟合结果为
对参数不做任何限制
用户自定义参数限制条件
点Save,出现下列窗口,用来定义需要保存的中间统计量。
从上到下，依次为保存预测值、残差、各参数的导数和损失函数值。
点Options,出现下列窗口,用来设置参数迭代拟合过程中的一些选项
定义参数的估计方法。选择是否利用Bootstrap法估计参数的标准误。序列二次规划法，对于有无限制的模型都适用。此法只适用于无限制的模型定义最大迭代次数，超出此次数则停止迭代定义迭代停止的条件，如果模型的损失函数的改变值小于此值时则停止迭代。进一步定义序列二次规划法的迭代过程定义最大迭代次数，超出此次数则停止迭代定义迭代过程中步长允许的最大变化值。若超出此值，则停止迭代定义模型中损失函数的精度定义拟合的非线性回归模型的精度定义迭代停止的条件，如果模型中所有参数的改变量小于此值时停止迭代
用最小二乘法估计模型的参数，损失函数为Q [Y f ( )][Y f ( )] 求损失函数的最小值，得到模型参数的估计值，由于这组解很难解出来，只能通过迭代法求出其近似解。通过[Nonlinear]过程实现，也可以自己定义各类损失函数。
2、Nonlinear过程的操作界面点analyze—regression---nonlinear
Yi 19.027e
3.486 0.042 X i

非线性回归

非线性回归一、可化为线性回归的曲线回归在实际问题当中，有许多回归模型的被解释变量y 与解释变量x 之间的关系都不是线性的，其中一些回归模型通过对自变量或因变量的函数变换可以转化为线性关系，利用线性回归求解未知参数，并作回归诊断。

如下列模型。

εββ++=x e y 10-------（1） εββββ+++++=p p x x x y 2210--------（2） εe ae y bx =--------------------（3） ε+=bx ae y -------------（4）对于（1）式，只需令x e x ='即可化为y 对x '是线性的形式εββ+'+=x y 10，需要指出的是，新引进的自变量只能依赖于原始变量，而不能与未知参数有关。

对于（2）式，可以令1x =x ,2x =2x ,…, p x =p x ,于是得到y 关于1x ,2x ,…, p x 的线性表达式εββββ+++++=p p x x x y 22110对与（3）式，对等式两边同时去自然数对数，得ε++=bx a y ln ln ,令 y y ln =',a ln 0=β,b =1β，于是得到y '关于x 的一元线性回归模型： εββ++='x y 10。

对于（4）式，当b 未知时，不能通过对等式两边同时取自然数对数的方法将回归模型线性化，只能用非线性最小二乘方法求解。

回归模型（3）可以线性化，而（4）不可以线性化，两个回归模型有相同的回归函数bx ae ，只是误差项ε的形式不同。

（3）式的误差项称为乘性误差项，（4）式的误差项称为加性误差项。

因而一个非线性回归模型是否可以线性化，不仅与回归函数的形式有关，而且与误差项的形式有关，误差项的形式还可以有其他多种形式。

乘性误差项模型和加性误差项模型所得的结果有一定差异，其中乘性误差项模型认为t y 本身是异方差的，而t y ln 是等方差的。

非线性回归

∂�� ∂θ
= −2
�� − �� = 0
(3)
设法求出θ 的解，用��（hat 西塔）表示，整理（3）式有：
�� = (�� )��2��
�� = �� + ��
(1)
此模型与线性模型类似，我们采用最小二乘法极小化：
�� 2 �� = (�� − �� )
(2)
估计θ ，S 代替 S（θ ），S 对θ 求微分后导数等于零得到 S 的最小值，
�� , = ��0 + ��1 �� = ��0 + ��1 �� , �� , = ��0 + ��1 �� ,
, �� , = ��0 + ��1 ��
但此种方式存在明显的局限性，为了说明它，我们先来回顾一下线性回归模型中核心的最小二乘法（OLS）。 1.1 最小二乘法回顾在线性回归中,我们学会了普通最小二乘法(OLS),但它在使用时有相应的前提假设: （1）正确的期望函数。第一个条件意味着计量模型的适用性，它不仅指出期望函数部分包括所有重要的自变量，同时随机变量部分包括不重要的可以忽略的自变量；此外，还意味着我们需要确定一个较为合理的模型形式（不论是线性还是非线性模型），这一点可以通过观察散点图进行判定。（2）自变量(Y)等于期望函数与随机变量之和，这一条假设使得 Y 的概率密度函数可以通过随机变量的概率密度函数加以计算： �� = �� ，�� 2 = ��随机变量 y − Xβ �� 2

非线性回归数学知识点总结

非线性回归数学知识点总结非线性回归分析通常基于统计原理和方法，通过对观测数据的分析来估计模型参数，从而找到自变量和因变量之间的关系。

对于不同类型的非线性关系，可以采用不同的非线性回归模型来进行分析。

本篇文章将从以下几个方面来总结非线性回归的相关数学知识点：非线性回归模型的基本概念、非线性回归模型的参数估计、非线性回归模型的假设检验、非线性回归模型的模型选择和验证等。

1. 非线性回归模型的基本概念非线性回归模型是一种描述自变量和因变量之间非线性关系的数学模型。

非线性回归模型通常可以表示为如下形式：Y = f(X,θ) + ε其中，Y是因变量，X是自变量，f()是非线性函数，θ是模型参数，ε是误差项。

在实际问题中，我们可以根据问题的特点选择合适的非线性函数f()来描述自变量和因变量之间的关系。

比如，如果我们观测到因变量Y与自变量X之间存在指数关系，那么我们可以选择指数函数来描述这种关系。

如果我们观测到因变量Y与自变量X之间存在对数关系，我们可以选择对数函数来描述这种关系。

2. 非线性回归模型的参数估计在实际问题中，我们通常需要通过观测数据来估计非线性回归模型的参数。

参数估计的目标是求解模型参数θ的值，使得模型与观测数据的拟合程度最好。

参数估计的方法通常包括最小二乘法、最大似然估计、贝叶斯方法等。

其中，最小二乘法是应用最广泛的一种参数估计方法。

最小二乘法的基本思想是求解参数θ，使得模型预测值与观测数据的残差平方和最小。

3. 非线性回归模型的假设检验在参数估计之后，我们通常需要对非线性回归模型的拟合效果进行假设检验。

假设检验的目的是判断模型的拟合程度是否显著。

在假设检验中，通常会进行F检验、t检验、残差分析等。

F检验是用来判断整个模型的符合程度，t检验是用来判断模型参数的显著性。

残差分析是用来检验模型对观测数据的拟合程度。

4. 非线性回归模型的模型选择和验证在实际问题中，我们通常会遇到多个可能的非线性回归模型。

非线性回归

非线性回归一、介绍线性回归是一种基本的统计方法，在许多领域中都有广泛的应用。

然而，在现实世界中，很多问题并不满足线性关系。

这时，非线性回归就成为了一种更加适用的方法。

二、非线性回归模型非线性回归模型是通过拟合非线性函数来描述自变量和因变量之间的关系。

一般来说，非线性回归模型可以分为参数模型和非参数模型。

1. 参数模型参数模型是指非线性函数中包含一些参数，通过最小化残差的平方和来估计这些参数的值。

常见的参数模型包括指数模型、幂函数模型、对数模型等。

2. 非参数模型非参数模型是指非线性函数中没有参数，通过直接拟合数据来建立模型。

常见的非参数模型包括样条函数模型、神经网络模型等。

三、非线性回归的应用非线性回归在许多领域中都有广泛的应用，特别是在生物学、经济学、工程学等领域中。

下面介绍几个非线性回归的应用实例：1. 生物学研究非线性回归在生物学研究中有很多应用，其中一个典型的例子是用来描述酶动力学的反应速率方程。

酶动力学研究中，根据酶底物浓度和反应速率的关系来建立非线性回归模型，从而研究酶的活性和底物浓度之间的关系。

2. 经济学分析非线性回归在经济学中也有许多应用，其中一个典型的例子是用来描述经济增长模型。

经济增长模型中，根据投资、人口增长率等因素来建立非线性回归模型，从而预测国家的经济增长趋势。

3. 工程学设计非线性回归在工程学设计中有很多应用，其中一个典型的例子是用来描述材料的应力-应变关系。

材料的应力-应变关系通常是非线性的，通过非线性回归模型可以更准确地描述材料的力学性能。

四、非线性回归的优缺点非线性回归相对于线性回归具有一些优点和缺点。

下面分别介绍：1. 优点非线性回归可以更准确地描述自变量和因变量之间的关系，适用于不满足线性关系的问题。

非线性回归的模型形式更灵活，可以通过选择适当的函数形式来更好地拟合数据。

2. 缺点非线性回归相比线性回归更复杂，需要更多的计算资源和时间。

非线性回归的参数估计也更加困难，需要依赖一些优化算法来找到最优解。

非线性回归模型概述

非线性回归模型概述非线性回归模型是一种用于建立非线性关系的统计模型，它可以用来描述自变量和因变量之间的复杂关系。

与线性回归模型相比，非线性回归模型可以更准确地拟合非线性数据，并提供更准确的预测结果。

在本文中，我们将对非线性回归模型进行概述，包括其基本原理、常见的非线性回归模型以及应用案例。

一、非线性回归模型的基本原理非线性回归模型的基本原理是通过拟合非线性函数来描述自变量和因变量之间的关系。

与线性回归模型不同，非线性回归模型的函数形式可以是任意的非线性函数，例如指数函数、对数函数、幂函数等。

通过最小化残差平方和来确定模型的参数，使得模型的预测值与观测值之间的差异最小化。

二、常见的非线性回归模型1. 多项式回归模型多项式回归模型是一种常见的非线性回归模型，它通过多项式函数来拟合数据。

多项式回归模型的函数形式为：y = β0 + β1x + β2x^2 + ... + βnx^n其中，y是因变量，x是自变量，β0、β1、β2...βn是模型的参数，n是多项式的阶数。

通过最小二乘法来估计模型的参数，可以得到最佳的拟合曲线。

2. 对数回归模型对数回归模型是一种常用的非线性回归模型，它通过对数函数来拟合数据。

对数回归模型的函数形式为：y = β0 + β1ln(x)其中，y是因变量，x是自变量，β0、β1是模型的参数。

对数回归模型适用于自变量和因变量之间呈现指数增长或指数衰减的情况。

3. 指数回归模型指数回归模型是一种常见的非线性回归模型，它通过指数函数来拟合数据。

指数回归模型的函数形式为：y = β0e^(β1x)其中，y是因变量，x是自变量，β0、β1是模型的参数。

指数回归模型适用于自变量和因变量之间呈现指数增长或指数衰减的情况。

三、非线性回归模型的应用案例非线性回归模型在实际应用中具有广泛的应用领域，以下是一些常见的应用案例：1. 生物学研究非线性回归模型在生物学研究中被广泛应用，例如用于描述生物体的生长曲线、药物的剂量-反应关系等。

非线性回归

《非线性回归分析》课件

非线性回归分析的入门知识

非线性回归 方法

计量经济学_詹姆斯斯托克_第8章_非线性的回归模型

非线性回归方程公式详解

数据建模—非线性回归

非线性回归分析

第四章 非线性回归与非线性约束

非线性回归模型

非线性回归分析

非线性回归分析简介

非线性回归

非线性回归分析简介

非线性回归

非线性回归

非线性回归

非线性回归数学知识点总结

非线性回归

非线性回归模型概述

非线性回归方法

第四章非线性回归与非线性约束