美国数学建模竞赛优秀论文阅读报告
美国大学生数学建模竞赛数据及评阅分析_吴孟达
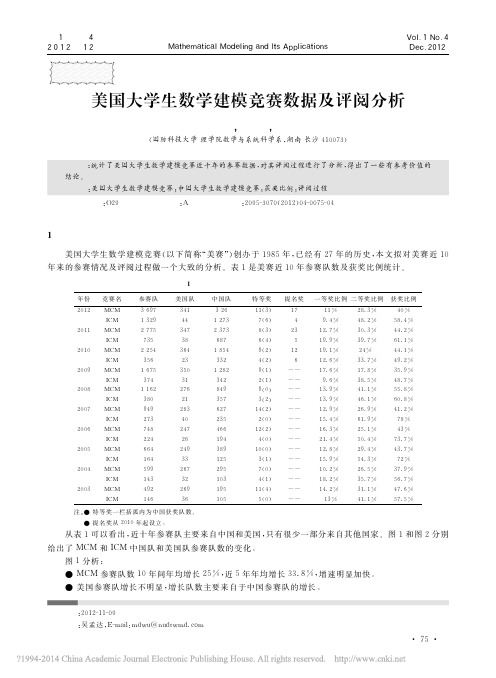
给出了 MCM 和ICM 中国队和美国队参赛队数的变化。
图1分析:
● MCM 参赛队数10年间年均增长25%,近5年年均增长33.8%,增速明显加快。
● 美国参赛队增长不明显,增长队数主要来自于中国参赛队的增长。
收 稿 日 期 :2012-11-09 通 讯 作 者 :吴 孟 达 ,E-mail:mdwu@nudtwmd.com
摘 要:统计了美国大学生数学建模竞赛近十年的参赛数据,对其评阅过程进行 了 分 析,得 出 了 一 些 有 参 考 价 值 的 结论。 关 键 词 :美 国 大 学 生 数 学 建 模 竞 赛 ;中 国 大 学 生 数 学 建 模 竞 赛 ;获 奖 比 例 ;评 阅 过 程
中 图 分 类 号 :O29 文 献 标 志 码 :A 文 章 编 号 :2095-3070(2012)04-0075-04
3 26 1 273 2 373 687 1 854 332 1 282 342 849 357 627 235 466 194 389 125 295 103 195 105
11(3) 7(6) 8(3) 6(4) 9(2) 4(2) 9(1) 2(1) 9(0) 3(2)
图2 ICM 参赛队数变化图 图3 MCM 获奖比例 图4 ICM 获奖比例
2 评 阅 过 程 分 析
据 美 赛 “评 委 评 论 ”介 绍 ,美 赛 评 阅 过 程 大 致 分 为 三 轮 。 第一轮可以称为“淘汰轮(the Triage Round)”。此轮评阅主要以摘要信息以及论文整体结构为 评 判 依 据 ,时 间 大 约 是 5~10 分 钟 。 每 个 评 委 以 “通 过 ”、“不 通 过 ”计 分 ,事 先 应 当 设 置 有 大 致 的 “通 过 ”比 例 (此 轮 与 国内研赛的网评阶段相类似)。当两位 评 委 意 见 不 一 致 时 可 以 协 商 达 成 一 致 意 见,如 果 仍 不 能 达 成 一 致 意 见 ,则 请 第 三 位 评 委 评 阅 。 有 “评 论 ”介 绍 说 ,这 一 轮 的 淘 汰 率 大 约 为 45% ,通 过 这 一 轮 评 审 的 参 赛 队 大 约 有 80% 的 获 奖 概 率 。 关 于 如 何 通 过 这 一 轮 评 审 ,评 委 给 出 的 建 议 是 : 1)摘 要 至 关 重 要 ,必 须 清 晰 且 信 息 量 充 分 。 评 委 关 心 的 是 你 对 问 题 的 理 解 是 否 准 确 ,你 建 立 的 模 型 及 使 用的方法是否恰当,以及根据你所建模型得到的主要结果和主要结论是否合理 。 过 于 冗 长 的 技 术 性 描 述 将 · 76 ·
美国大学生数学建模竞赛优秀论文

For office use onlyT1________________ T2________________ T3________________ T4________________Team Control Number7018Problem ChosencFor office use onlyF1________________F2________________F3________________F4________________ SummaryThe article is aimed to research the potential impact of the marine garbage debris on marine ecosystem and human beings,and how we can deal with the substantial problems caused by the aggregation of marine wastes.In task one,we give a definition of the potential long-term and short-term impact of marine plastic garbage. Regard the toxin concentration effect caused by marine garbage as long-term impact and to track and monitor it. We etablish the composite indicator model on density of plastic toxin,and the content of toxin absorbed by plastic fragment in the ocean to express the impact of marine garbage on ecosystem. Take Japan sea as example to examine our model.In ask two, we designe an algorithm, using the density value of marine plastic of each year in discrete measure point given by reference,and we plot plastic density of the whole area in varies locations. Based on the changes in marine plastic density in different years, we determine generally that the center of the plastic vortex is East—West140°W—150°W, South—North30°N—40°N. According to our algorithm, we can monitor a sea area reasonably only by regular observation of part of the specified measuring pointIn task three,we classify the plastic into three types,which is surface layer plastic,deep layer plastic and interlayer between the two. Then we analysis the the degradation mechanism of plastic in each layer. Finally,we get the reason why those plastic fragments come to a similar size.In task four, we classify the source of the marine plastic into three types,the land accounting for 80%,fishing gears accounting for 10%,boating accounting for 10%,and estimate the optimization model according to the duel-target principle of emissions reduction and management. Finally, we arrive at a more reasonable optimization strategy.In task five,we first analyze the mechanism of the formation of the Pacific ocean trash vortex, and thus conclude that the marine garbage swirl will also emerge in south Pacific,south Atlantic and the India ocean. According to the Concentration of diffusion theory, we establish the differential prediction model of the future marine garbage density,and predict the density of the garbage in south Atlantic ocean. Then we get the stable density in eight measuring point .In task six, we get the results by the data of the annual national consumption ofpolypropylene plastic packaging and the data fitting method, and predict the environmental benefit generated by the prohibition of polypropylene take-away food packaging in the next decade. By means of this model and our prediction,each nation will reduce releasing 1.31 million tons of plastic garbage in next decade.Finally, we submit a report to expediction leader,summarize our work and make some feasible suggestions to the policy- makers.Task 1:Definition:●Potential short-term effects of the plastic: the hazardeffects will be shown in the short term.●Potential long-term effects of the plastic: thepotential effects, of which hazards are great, willappear after a long time.The short- and long-term effects of the plastic on the ocean environment:In our definition, the short-term and long-term effects of the plastic on the ocean environment are as follows.Short-term effects:1)The plastic is eaten by marine animals or birds.2) Animals are wrapped by plastics, such as fishing nets, which hurt or even kill them.3)Deaden the way of the passing vessels.Long-term effects:1)Enrichment of toxins through the food chain: the waste plastic in the ocean has no natural degradation in theshort-term, which will first be broken down into tinyfragments through the role of light, waves,micro-organisms, while the molecular structure has notchanged. These "plastic sands", easy to be eaten byplankton, fish and other, are Seemingly very similar tomarine life’s food,causing the enrichment and delivery of toxins.2)Accelerate the greenhouse effect: after a long-term accumulation and pollution of plastics, the waterbecame turbid, which will seriously affect the marineplants (such as phytoplankton and algae) inphotosynthesis. A large number of plankton’s deathswould also lower the ability of the ocean to absorbcarbon dioxide, intensifying the greenhouse effect tosome extent.To monitor the impact of plastic rubbish on the marine ecosystem:According to the relevant literature, we know that plastic resin pellets accumulate toxic chemicals , such as PCBs、DDE , and nonylphenols , and may serve as a transport medium and soure of toxins to marine organisms that ingest them[]2. As it is difficult for the plastic garbage in the ocean to complete degradation in the short term, the plastic resin pellets in the water will increase over time and thus absorb more toxins, resulting in the enrichment of toxins and causing serious impact on the marine ecosystem.Therefore, we track the monitoring of the concentration of PCBs, DDE, and nonylphenols containing in the plastic resin pellets in the sea water, as an indicator to compare the extent of pollution in different regions of the sea, thus reflecting the impact of plastic rubbish on ecosystem.To establish pollution index evaluation model: For purposes of comparison, we unify the concentration indexes of PCBs, DDE, and nonylphenols in a comprehensive index.Preparations:1)Data Standardization2)Determination of the index weightBecause Japan has done researches on the contents of PCBs,DDE, and nonylphenols in the plastic resin pellets, we illustrate the survey conducted in Japanese waters by the University of Tokyo between 1997 and 1998.To standardize the concentration indexes of PCBs, DDE,and nonylphenols. We assume Kasai Sesside Park, KeihinCanal, Kugenuma Beach, Shioda Beach in the survey arethe first, second, third, fourth region; PCBs, DDE, andnonylphenols are the first, second, third indicators.Then to establish the standardized model:j j jij ij V V V V V min max min --= (1,2,3,4;1,2,3i j ==)wherej V max is the maximum of the measurement of j indicator in the four regions.j V min is the minimum of the measurement of j indicatorstandardized value of j indicator in i region.According to the literature [2], Japanese observationaldata is shown in Table 1.Table 1. PCBs, DDE, and, nonylphenols Contents in Marine PolypropyleneTable 1 Using the established standardized model to standardize, we have Table 2.In Table 2,the three indicators of Shioda Beach area are all 0, because the contents of PCBs, DDE, and nonylphenols in Polypropylene Plastic Resin Pellets in this area are the least, while 0 only relatively represents the smallest. Similarly, 1 indicates that in some area the value of a indicator is the largest.To determine the index weight of PCBs, DDE, and nonylphenolsWe use Analytic Hierarchy Process (AHP) to determine the weight of the three indicators in the general pollution indicator. AHP is an effective method which transforms semi-qualitative and semi-quantitative problems into quantitative calculation. It uses ideas of analysis and synthesis in decision-making, ideally suited for multi-index comprehensive evaluation.Hierarchy are shown in figure 1.Fig.1 Hierarchy of index factorsThen we determine the weight of each concentrationindicator in the generall pollution indicator, and the process are described as follows:To analyze the role of each concentration indicator, we haveestablished a matrix P to study the relative proportion.⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=111323123211312P P P P P P P Where mn P represents the relative importance of theconcentration indicators m B and n B . Usually we use 1,2,…,9 and their reciprocals to represent different importance. The greater the number is, the more important it is. Similarly, the relative importance of m B and n B is mn P /1(3,2,1,=n m ).Suppose the maximum eigenvalue of P is m ax λ, then theconsistency index is1max --=n nCI λThe average consistency index is RI , then the consistencyratio isRICI CR = For the matrix P of 3≥n , if 1.0<CR the consistency isthougt to be better, of which eigenvector can be used as the weight vector.We get the comparison matrix accoding to the harmful levelsof PCBs, DDE, and nonylphenols and the requirments ofEPA on the maximum concentration of the three toxins inseawater as follows:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=165416131431P We get the maximum eigenvalue of P by MATLAB calculation0012.3max =λand the corresponding eigenvector of it is()2393.02975.09243.0,,=W1.0042.012.1047.0<===RI CI CR Therefore,we determine the degree of inconsistency formatrix P within the permissible range. With the eigenvectors of p as weights vector, we get thefinal weight vector by normalization ()1638.02036.06326.0',,=W . Defining the overall target of pollution for the No i oceanis i Q , among other things the standardized value of threeindicators for the No i ocean is ()321,,i i i i V V V V = and the weightvector is 'W ,Then we form the model for the overall target of marine pollution assessment, (3,2,1=i )By the model above, we obtained the Value of the totalpollution index for four regions in Japanese ocean in Table 3T B W Q '=In Table3, the value of the total pollution index is the hightest that means the concentration of toxins in Polypropylene Plastic Resin Pellets is the hightest, whereas the value of the total pollution index in Shioda Beach is the lowest(we point up 0 is only a relative value that’s not in the name of free of plastics pollution)Getting through the assessment method above, we can monitor the concentration of PCBs, DDE and nonylphenols in the plastic debris for the sake of reflecting the influence to ocean ecosystem.The highter the the concentration of toxins,the bigger influence of the marine organism which lead to the inrichment of food chain is more and more dramatic.Above all, the variation of toxins’ concentration simultaneously reflects the distribution and time-varying of marine litter. We can predict the future development of marine litter by regularly monitoring the content of these substances, to provide data for the sea expedition of the detection of marine litter and reference for government departments to make the policies for ocean governance.Task 2:In the North Pacific, the clockwise flow formed a never-ending maelstrom which rotates the plastic garbage. Over the years, the subtropical eddy current in North Pacific gathered together the garbage from the coast or the fleet, entrapped them in the whirlpool, and brought them to the center under the action of the centripetal force, forming an area of 3.43 million square kilometers (more than one-third of Europe) .As time goes by, the garbage in the whirlpool has the trend of increasing year by year in terms of breadth, density, and distribution. In order to clearly describe the variability of the increases over time and space, according to “Count Densities of Plastic Debris from Ocean Surface Samples North Pacific Gyre 1999—2008”, we analyze the data, exclude them with a great dispersion, and retain them with concentrated distribution, while the longitude values of the garbage locations in sampled regions of years serve as the x-coordinate value of a three-dimensional coordinates, latitude values as the y-coordinate value, the Plastic Count per cubic Meter of water of the position as the z-coordinate value. Further, we establish an irregular grid in the yx plane according to obtained data, and draw a grid line through all the data points. Using the inverse distance squared method with a factor, which can not only estimate the Plastic Count per cubic Meter of water of any position, but also calculate the trends of the Plastic Counts per cubic Meter of water between two original data points, we can obtain the unknown grid points approximately. When the data of all the irregular grid points are known (or approximately known, or obtained from the original data), we can draw the three-dimensional image with the Matlab software, which can fully reflect the variability of the increases in the garbage density over time and space.Preparations:First, to determine the coordinates of each year’s sampled garbage.The distribution range of garbage is about the East - West 120W-170W, South - North 18N-41N shown in the “Count Densities of Plastic Debris from Ocean Surface Samples North Pacific Gyre 1999--2008”, we divide a square in the picture into 100 grids in Figure (1) as follows:According to the position of the grid where the measuring point’s center is, we can identify the latitude and longitude for each point, which respectively serve as the x- and y- coordinate value of the three-dimensional coordinates.To determine the Plastic Count per cubic Meter of water. As the “Plastic Count per cubic Meter of water” provided by “Count Densities of P lastic Debris from Ocean Surface Samples North Pacific Gyre 1999--2008”are 5 density interval, to identify the exact values of the garbage density of one year’s different measuring points, we assume that the density is a random variable which obeys uniform distribution in each interval.Uniform distribution can be described as below:()⎪⎩⎪⎨⎧-=01a b x f ()others b a x ,∈We use the uniform function in Matlab to generatecontinuous uniformly distributed random numbers in each interval, which approximately serve as the exact values of the garbage density andz-coordinate values of the three-dimensional coordinates of the year’s measuring points.Assumptions(1)The data we get is accurate and reasonable.(2)Plastic Count per cubic Meter of waterIn the oceanarea isa continuous change.(3)Density of the plastic in the gyre is a variable by region.Density of the plastic in the gyre and its surrounding area is interdependent , However, this dependence decreases with increasing distance . For our discussion issue, Each data point influences the point of each unknown around and the point of each unknown around is influenced by a given data point. The nearer a given data point from the unknown point, the larger the role.Establishing the modelFor the method described by the previous,we serve the distributions of garbage density in the “Count Pensities of Plastic Debris from Ocean Surface Samples North Pacific Gyre 1999--2008”as coordinates ()z y,, As Table 1:x,Through analysis and comparison, We excluded a number of data which has very large dispersion and retained the data that is under the more concentrated the distribution which, can be seen on Table 2.In this way, this is conducive for us to get more accurate density distribution map.Then we have a segmentation that is according to the arrangement of the composition of X direction and Y direction from small to large by using x co-ordinate value and y co-ordinate value of known data points n, in order to form a non-equidistant Segmentation which has n nodes. For the Segmentation we get above,we only know the density of the plastic known n nodes, therefore, we must find other density of the plastic garbage of n nodes.We only do the sampling survey of garbage density of the north pacificvortex,so only understand logically each known data point has a certain extent effect on the unknown node and the close-known points of density of the plastic garbage has high-impact than distant known point.In this respect,we use the weighted average format, that means using the adverse which with distance squared to express more important effects in close known points. There're two known points Q1 and Q2 in a line ,that is to say we have already known the plastic litter density in Q1 and Q2, then speculate the plastic litter density's affects between Q1、Q2 and the point G which in the connection of Q1 and Q2. It can be shown by a weighted average algorithm22212221111121GQ GQ GQ Z GQ Z Z Q Q G +*+*=in this formula GQ expresses the distance between the pointG and Q.We know that only use a weighted average close to the unknown point can not reflect the trend of the known points, we assume that any two given point of plastic garbage between the changes in the density of plastic impact the plastic garbage density of the unknown point and reflecting the density of plastic garbage changes in linear trend. So in the weighted average formula what is in order to presume an unknown point of plastic garbage density, we introduce the trend items. And because the greater impact at close range point, and thus the density of plastic wastes trends close points stronger. For the one-dimensional case, the calculation formula G Z in the previous example modify in the following format:2212122212212122211111112121Q Q GQ GQ GQ Q Q GQ Z GQ Z GQ Z Z Q Q Q Q G ++++*+*+*=Among them, 21Q Q known as the separation distance of the known point, 21Q Q Z is the density of plastic garbage which is the plastic waste density of 1Q and 2Q for the linear trend of point G . For the two-dimensional area, point G is not on the line 21Q Q , so we make a vertical from the point G and cross the line connect the point 1Q and 2Q , and get point P , the impact of point P to 1Q and 2Q just like one-dimensional, and the one-dimensional closer of G to P , the distant of G to P become farther, the smaller of the impact, so the weighting factor should also reflect the GP in inversely proportional to a certain way, then we adopt following format:221212222122121222211111112121Q Q GQ GP GQ GQ Q Q GQ GP Z GQ Z GQ Z Z P Q Q Q Q G ++++++*+*+*=Taken together, we speculated following roles:(1) Each known point data are influence the density of plastic garbage of each unknown point in the inversely proportional to the square of the distance;(2) the change of density of plastic garbage between any two known points data, for each unknown point are affected, and the influence to each particular point of their plastic garbage diffuse the straight line along the two known particular point; (3) the change of the density of plastic garbage between any two known data points impact a specific unknown points of the density of plastic litter depends on the three distances: a. the vertical distance to a straight line which is a specific point link to a known point;b. the distance between the latest known point to a specific unknown point;c. the separation distance between two known data points.If we mark 1Q ,2Q ,…,N Q as the location of known data points,G as an unknown node, ijG P is the intersection of the connection of i Q ,j Q and the vertical line from G to i Q ,j Q()G Q Q Z j i ,,is the density trend of i Q ,j Q in the of plasticgarbage points and prescribe ()G Q Q Z j i ,,is the testing point i Q ’ s density of plastic garbage ,so there are calculation formula:()()∑∑∑∑==-==++++*=Ni N ij ji i ijGji i ijG N i Nj j i G Q Q GQ GPQ Q GQ GP G Q Q Z Z 11222222111,,Here we plug each year’s observational data in schedule 1 into our model, and draw the three-dimensional images of the spatial distribution of the marine garbage ’s density with Matlab in Figure (2) as follows:199920002002200520062007-2008(1)It’s observed and analyzed that, from 1999 to 2008, the density of plastic garbage is increasing year by year and significantly in the region of East – West 140W-150W, south - north 30N-40N. Therefore, we can make sure that this region is probably the center of the marine litter whirlpool. Gathering process should be such that the dispersed garbage floating in the ocean move with the ocean currents and gradually close to the whirlpool region. At the beginning, the area close to the vortex will have obviously increasable about plastic litter density, because of this centripetal they keeping move to the center of the vortex ,then with the time accumulates ,the garbage density in the center of the vortex become much bigger and bigger , at last it becomes the Pacific rubbish island we have seen today.It can be seen that through our algorithm, as long as the reference to be able to detect the density in an area which has a number of discrete measuring points,Through tracking these density changes ,we Will be able to value out all the waters of the density measurement through our models to determine,This will reduce the workload of the marine expedition team monitoring marine pollution significantly, and also saving costs .Task 3:The degradation mechanism of marine plasticsWe know that light, mechanical force, heat, oxygen, water, microbes, chemicals, etc. can result in the degradation of plastics . In mechanism ,Factors result in the degradation can be summarized as optical ,biological,and chemical。
数学建模优秀论文的阅读心得

数学建模优秀论文的阅读心得在阅读数学建模优秀论文时,我深刻领悟到数学建模的重要性和应用价值。
优秀论文不仅在理论和方法上具有突出的创新性,而且能够将数学模型与实际问题相结合,为解决实际问题提供有力支持。
经过研究,我发现优秀论文在问题选择、模型建立、求解方法和结果分析等方面有着共同的特点和亮点,这些亮点能够帮助我们更好地理解和应用数学建模。
首先,优秀论文在问题选择上能够紧密联系实际,关注社会热点问题。
数学建模是针对实际问题的数学方法研究,因此问题选择的合理性至关重要。
优秀论文选取的问题通常具有实际意义和社会影响,能够帮助决策者做出有针对性的决策。
同时,问题选择也需要具备一定的挑战性,有利于推动数学建模方法和理论的发展。
其次,优秀论文在模型建立上能够精确把握实际问题的特点,并利用数学知识将问题抽象成可计算的模型。
数学建模是基于数学理论和方法解决实际问题的过程,模型的建立是数学建模的核心环节。
优秀论文在模型建立上通常能够准确地描述问题的本质特征,通过合适的数学工具和方法将问题抽象成数学模型。
同时,优秀论文在模型建立时也会考虑问题的复杂度和可计算性,尽可能简化模型,提高计算效率。
第三,优秀论文在求解方法上能够利用现有的数学理论和方法,灵活运用求解技巧。
数学建模的目的是要找到问题的最优解或近似解,因此求解方法的选择和运用是关键。
优秀论文通常会综合运用现有的数学理论和方法,选择合适的求解技巧来解决问题。
同时,在求解过程中也会灵活运用数学思维和技巧,解决问题中的难点和瓶颈。
优秀论文的求解方法往往具有一定的创新和独特性,能够为问题的解决提供有效的方案。
最后,优秀论文在结果分析上能够对模型的有效性和适用性进行评估,并提出相应的改进和优化建议。
数学建模的结果分析是对模型建立和求解过程的检验和评价,也是为问题解决提供合理性和可行性证明的环节。
优秀论文通常会对模型的有效性和适用性进行全面的评估,包括对模型的准确性、稳定性和敏感性等方面进行分析。
2014年美国大学生数学建模竞赛A题论文综述

数学建模综述2014年美国大学生数学建模竞赛A题论文综述我们小组精读两篇14年美赛A题论文,选择了其中一篇来进行学习,总结。
1、问题分析The Keep-Right-Except-To-Pass Rule除非超车否则靠右行驶的交通规则问题:建立数学模型来分析这条规则在低负荷和高负荷状态下的交通路况的表现。
这条规则在提升车流量的方面是否有效?如果不是,提出能够提升车流量、安全系数或其他因素的替代品(包括完全没有这种规律)并加以分析。
在一些国家,汽车靠左形式是常态,探讨你的解决方案是否稍作修改即可适用,或者需要一些额外的需要。
最后,以上规则依赖于人的判断,如果相同规则的交通运输完全在智能系统的控制下,无论是部分网络还是嵌入使用的车辆的设计,在何种程度上会修改你前面的结果论文:基于元胞自动机和蒙特卡罗方法,我们建立一个模型来讨论“靠右行”规则的影响。
首先,我们打破汽车的运动过程和建立相应的子模型car-generation的流入模型,对于匀速行驶车辆,我们建立一个跟随模型,和超车模型。
然后我们设计规则来模拟车辆的运动模型。
我们进一步讨论我们的模型规则适应靠右的情况和,不受限制的情况, 和交通情况由智能控制系统的情况。
我们也设计一个道路的危险指数评价公式。
我们模拟双车道高速公路上交通(每个方向两个车道,一共四条车道),高速公路双向三车道(总共6车道)。
通过计算机和分析数据。
我们记录的平均速度,超车取代率、道路密度和危险指数和通过与不受规则限制的比较评估靠右行的性能。
我们利用不同的速度限制分析模型的敏感性和看到不同的限速的影响。
左手交通也进行了讨论。
根据我们的分析,我们提出一个新规则结合两个现有的规则(靠右的规则和无限制的规则)的智能系统来实现更好的的性能。
该论文在一开始并没有作过多分析,而是一针见血的提出了自己对于这个问题的做法。
由于题目给出的背景只有一条交通规则,而且是题目很明确的提出让我们建立模型分析。
参加美国建模大赛的心得体会

参加美国建模大赛的心得体会第一篇:参加美国建模大赛的心得体会参加美国建模大赛的心得体会这次美国建模大赛我们学校取得了非常好的成绩。
从去年美赛到今年美赛,我们整体实力的提高是非常明显的。
这是学校和系里领导的重视,建模辅导老师们在平时的指导,系里开设的建模课程和暑期的建模培训,以及同学们自身努力的共同结果。
我们小组从赛前的校内筛选到最终参加比赛获得Meritorious Winner,这个过程中经历了很多,也收获了很多。
在这里,我们和大家分享一下自己比赛中的经验和教训,希望能为以后准备参赛的同学扫清障碍。
先说一下赛前的筛选过程吧。
每个队伍要翻译一篇自己曾经写过的建模论文交给老师供老师筛选。
由于我们之前缺乏写英文论文的经验,所以在翻译过程中遇到了很多问题。
这里面涉及专业词汇的表达,英文的一些表达习惯,以及意思是否能够表达的精准等很多问题。
有些时候,一个人理解了中文意思后翻译出来的英文拿给另外一个队友并不能看懂,或者与原来的本意产生了偏差。
而这些都是要参加美赛必须注意的地方。
因为,也许很多时候并不是同学们的模型建的不好,而是没有表达清楚,评委们看不懂,所以才被淘汰的。
在时间的压力下,我们三个人分工协作,之后又一起讨论商榷,最终才把一份自己比较满意的翻译稿交给了老师。
虽然我们通过了选拔,老师还是把我们论文中出现的语法错误,格式错误,尤其是摘要部分出现的问题都用红笔圈了出来,并对如何书写英文论文提出了建议。
大家一定要重视这个过程,因为翻译一篇论文和翻译一篇普通的文章差距是很大的,因为论文有更高的简洁性,精确性和逻辑性的要求。
大家可以在平时就锻炼自己这方面的能力,多读英文论文,或更针对性的读历届的美模获奖论文,去仔细斟酌它们的语言。
关于组队,一个公认的不错的组合是:一个数学系的同学,一个计算机系的同学和一个擅长写论文的同学。
这样的组合诚然不错,但我建议大家首先还是要找熟悉的人组队,这样比赛时候会配合的更加默契。
美国大学生数学建模竞赛对我国高校数学教学的启示

研 究 问题 、 解决 方 案 的 原创 性 、 团队合作、 交 流 以 及
结 果 的合理 性 。MC M 的 宗 旨 是 鼓 励 大 学 师 生 对 范
V o 1 . 1 l N o . 3
Fe b .2 0 1 3
I ) Ol : 1 0 . 3 9 6 9 / j . i s s n . 2 0 9 5 — 3 3 3 X. 2 0 1 3 . 0 3 . 0 2 7
美 国 大 学 生 数 学 建 模 竞 赛 对 我 国 高 校 数 学 教 学 的 启 示
吕小光 , 姜 乐 , 成 青松
( L淮海工学院 理学 院 , 江苏 连云港 2 2 2 0 0 5 ;2 . 电子科技大学 数学科学学 院, 四川 成都 6 3 1 7 l 1 )
摘 要 : 作为数 学建模 领域 内的 国际性权 威 赛事 , 美 国 大 学 生数 学 建 模 竞 赛 受 到 了全 世 界 各 大 高校
当今 社 会 发 展 越 来 越 快 , 各 种 竞 争 压 力 越 来 越 大 , 对人 才 的要求 也 越来越 高 。人 才 的竞争 , 实 际 上 就 是 教 育 的竞 争 、 能 力 发 展 的 竞 争 。 在 传 统 的 教 育
人 ( 本 科 生) 一 组在 四天 时 间 内 , 就 指 定 的 问 题 完 成 从 建 立模 型 、 求解 、 验 证 到 论 文 撰 写 的 全 部 工 作 。 竞
大 洲 的 数 千 名 大 学 生 参 加 。 M CM / I CM 着 重 强 调
建 模 竞 赛 对 高 校 教 师 队 伍 的 能 力 是 一 个 很 大 的 挑 战, 需 要他 们 进一步 提高 能力 和素 质 , 同 时 也 需 要 各
2014年美国大学生数学建模竞赛心得

2014美赛心得在2014年美国大学生数学建模比赛中,我们小组奋战了几天,最终获得了H奖的成绩。
这个成绩虽然不是最理想的,但是总体来讲还是十分令人满意的。
而且这也是我们第一次参加美国数学建模比赛,经历这几天的比赛,我们收获的不仅仅是一张奖状,更多的是对数学建模的兴趣和相互合作的进一步认识。
首先,参加这个比赛,使我们对数学建模的认识更进了一步。
我们小组的三个同学都曾修过数学建模课程,对数学建模还是有一定的认识的。
而以前,我们对于数学建模的认识,可能只是停留在课程与考试的阶段。
但是,通过参加本次美国大学生数学建模比赛,我们有了更深刻的认识:数学建模不是去做一个题目,而是真正地分析问题、解决问题、优化问题,在茫茫的数学海洋之中寻觅最合适的模型,甚至是自己创造一个新的模型。
而这也是十分关键的,如果只是生搬硬套公式而不去创新,便很难从众多论文中脱颖而出,也很难真正地解决问题。
例如我们本次参赛所选择的B题,从最基本的意义上来说,这道题目很难有所创新。
初看起来这只是一个评价问题,利用一般的评价模型便可以解决。
但是,几乎所有的参赛组都能够利用评价模型来解决此类问题,没有创新也就不会从成千上万的论文中显现出自己的独特之处,也就不会在比赛中有所斩获。
因此,我们把两种方法加以综合,提出一种新的方法来对大学体育教练进行评价。
而且通过与已有的教练评价对比,我们发现这样的评价方法更具有代表性。
其次,我们对于小组成员之间的合作与分工有了更深的认识。
美国大学生数学建模竞赛要求一个参赛组有很好的资料和数据搜集能力、建模能力、编程能力、论文编写能力等等。
我们小组的三位同学分别在某些方面有着不错的能力。
首先,要恰当地评价大学体育教练,需要大量的数据,包括这些教练的胜场、胜率以及所获荣誉等等,这就要求我们搜集大量的资料。
正是xx同学编写的程序,使得我们能够从网站上搜集到大量的有关这些教练的资料。
在这之后,由于我们都对各类数学模型和算法比较了解,于是我们三人同心,其利断金,顺利地将模型初步建立起来。
当我谈数学建模时我谈些什么——美赛一等奖经验总结

前言:2012年3月28号晚,我知道了美赛成绩,一等奖(Meritorious Winner),没有太多的喜悦,只是感觉释怀,一年以来的努力总算有了回报。
从国赛遗憾丢掉国奖,到美赛一等,这一路走来太多的不易,感谢我的家人、队友以及朋友的支持,没有你们,我无以为继。
个人背景:我2010年入学,所在的学校是广东省一所普通大学,今年大二,学工商管理专业,没学过编程。
学校组织参加过几届美赛,之前唯一的一个一等奖是三年前拿到的,那一队的主力师兄凭借这一奖项去了北卡罗来纳大学教堂山分校,学运筹学。
今年再次拿到一等奖,我创了两个校记录:一是第一个在大二拿到数模美赛一等奖,二是第一个在文科专业拿数模美赛一等奖。
我的数模历程如下:2011.4 校内赛三等奖2011.8 通过选拔参加暑期国赛培训(学校之前不允许大一学生参加)2011.9 国赛广东省二等奖2011.11 电工杯三等奖2012.2 美赛一等奖(Meritorious Winner)动机:我参加数学建模的动机比较单纯,完全是出于兴趣。
我的专业是工商管理,没有学过编程,觉得没必要学。
我所感兴趣的是模型本身,它的思想,它的内涵,它的发展过程、它的适用问题等等。
我希望通过学习模型,能够更好的去理解一些现象,了解其中蕴含的数学机理。
数学模型中包含着一种简洁的哲学,深刻而迷人。
当然获得荣誉方面的动机可定也有,谁不想拿奖呢?模型:数学模型的功能大致有三种:评价、优化、预测。
几乎所有模型都是围绕这三种功能来做的。
比如,今年美赛A题树叶分类属于评价模型,B题漂流露营安排则属于优化模型。
对于不同功能的模型有不同的方法,例如评价模型方法有层次分析、模糊综合评价、熵值法等;优化模型方法有启发式算法(模拟退火、遗传算法等)、仿真方法(蒙特卡洛、元胞自动机等);预测模型方法有灰色预测、神经网络、马尔科夫链等。
在数学中国网站上有许多关于这些方法的相关介绍与文献。
关于模型软件与书籍,这方面的文章很多,这里只做简单介绍。
数学建模美赛一等奖优秀专业论文

For office use onlyT1________________ T2________________ T3________________ T4________________ Team Control Number52888Problem ChosenAFor office use onlyF1________________F2________________F3________________F4________________Mathematical Contest in Modeling (MCM/ICM) Summary SheetSummaryIt’s pleasant t o go home to take a bath with the evenly maintained temperature of hot water throughout the bathtub. This beautiful idea, however, can not be always realized by the constantly falling water temperature. Therefore, people should continually add hot water to keep the temperature even and as close as possible to the initial temperature without wasting too much water. This paper proposes a partial differential equation of the heat conduction of the bath water temperature, and an object programming model. Based on the Analytic Hierarchy Process (AHP) and Technique for Order Preference by Similarity to Ideal Solution (TOPSIS), this paper illustrates the best strategy the person in the bathtub can adopt to satisfy his desires. First, a spatiotemporal partial differential equation model of the heat conduction of the temperature of the bath water is built. According to the priority, an object programming model is established, which takes the deviation of temperature throughout the bathtub, the deviation of temperature with the initial condition, water consumption, and the times of switching faucet as the four objectives. To ensure the top priority objective—homogenization of temperature, the discretization method of the Partial Differential Equation model (PDE) and the analytical analysis are conducted. The simulation and analytical results all imply that the top priority strategy is: The proper motions of the person making the temperature well-distributed throughout the bathtub. Therefore, the Partial Differential Equation model (PDE) can be simplified to the ordinary differential equation model.Second, the weights for the remaining three objectives are determined based on the tolerance of temperature and the hobby of the person by applying Analytic Hierarchy Process (AHP) and Technique for Order Preference by Similarity to Ideal Solution (TOPSIS). Therefore, the evaluation model of the synthesis score of the strategy is proposed to determine the best one the person in the bathtub can adopt. For example, keeping the temperature as close as the initial condition results in the fewer number of switching faucet while attention to water consumption gives rise to the more number. Third, the paper conducts the analysis of the diverse parameters in the model to determine the best strategy, respectively, by controlling the other parameters constantly, and adjusting the parameters of the volume, shape of the bathtub and the shape, volume, temperature and the motions and other parameters of the person in turns. All results indicate that the differential model and the evaluation model developed in this paper depends upon the parameters therein. When considering the usage of a bubble bath additive, it is equal to be the obstruction between water and air. Our results show that this strategy can reduce the dropping rate of the temperatureeffectively, and require fewer number of switching.The surface area and heat transfer coefficient can be increased because of the motions of the person in the bathtub. Therefore, the deterministic model can be improved as a stochastic one. With the above evaluation model, this paper present the stochastic optimization model to determine the best strategy. Taking the disparity from the initial temperature as the suboptimum objectives, the result of the model reveals that it is very difficult to keep the temperature constant even wasting plentiful hot water in reality.Finally, the paper performs sensitivity analysis of parameters. The result shows that the shape and the volume of the tub, different hobbies of people will influence the strategies significantly. Meanwhile, combine with the conclusion of the paper, we provide a one-page non-technical explanation for users of the bathtub.Fall in love with your bathtubAbstractIt’s pleasant t o go home to take a bath with the evenly maintained temperature of hot water throughout the bathtub. This beautiful idea, however, can not be always realized by the constantly falling water temperature. Therefore, people should continually add hot water to keep the temperature even and as close as possible to the initial temperature without wasting too much water. This paper proposes a partial differential equation of the heat conduction of the bath water temperature, and an object programming model. Based on the Analytic Hierarchy Process (AHP) and Technique for Order Preference by Similarity to Ideal Solution (TOPSIS), this paper illustrates the best strategy the person in the bathtub can adopt to satisfy his desires. First, a spatiotemporal partial differential equation model of the heat conduction of the temperature of the bath water is built. According to the priority, an object programming model is established, which takes the deviation of temperature throughout the bathtub, the deviation of temperature with the initial condition, water consumption, and the times of switching faucet as the four objectives. To ensure the top priority objective—homogenization of temperature, the discretization method of the Partial Differential Equation model (PDE) and the analytical analysis are conducted. The simulation and analytical results all imply that the top priority strategy is: The proper motions of the person making the temperature well-distributed throughout the bathtub. Therefore, the Partial Differential Equation model (PDE) can be simplified to the ordinary differential equation model.Second, the weights for the remaining three objectives are determined based on the tolerance of temperature and the hobby of the person by applying Analytic Hierarchy Process (AHP) and Technique for Order Preference by Similarity to Ideal Solution (TOPSIS). Therefore, the evaluation model of the synthesis score of the strategy is proposed to determine the best one the person in the bathtub can adopt. For example, keeping the temperature as close as the initial condition results in the fewer number of switching faucet while attention to water consumption gives rise to the more number. Third, the paper conducts the analysis of the diverse parameters in the model to determine the best strategy, respectively, by controlling the other parameters constantly, and adjusting the parameters of the volume, shape of the bathtub and the shape, volume, temperature and the motions and other parameters of the person in turns. All results indicate that the differential model and the evaluation model developed in this paper depends upon the parameters therein. When considering the usage of a bubble bath additive, it is equal to be the obstruction between water and air. Our results show that this strategy can reduce the dropping rate of the temperature effectively, and require fewer number of switching.The surface area and heat transfer coefficient can be increased because of the motions of the person in the bathtub. Therefore, the deterministic model can be improved as a stochastic one. With the above evaluation model, this paper present the stochastic optimization model to determine the best strategy. Taking the disparity from the initial temperature as the suboptimum objectives, the result of the model reveals that it is very difficult to keep the temperature constant even wasting plentiful hotwater in reality.Finally, the paper performs sensitivity analysis of parameters. The result shows that the shape and the volume of the tub, different hobbies of people will influence the strategies significantly. Meanwhile, combine with the conclusion of the paper, we provide a one-page non-technical explanation for users of the bathtub.Keywords:Heat conduction equation; Partial Differential Equation model (PDE Model); Objective programming; Strategy; Analytical Hierarchy Process (AHP) Problem StatementA person fills a bathtub with hot water and settles into the bathtub to clean and relax. However, the bathtub is not a spa-style tub with a secondary hearing system, as time goes by, the temperature of water will drop. In that conditions,we need to solve several problems:(1) Develop a spatiotemporal model of the temperature of the bathtub water to determine the best strategy to keep the temperature even throughout the bathtub and as close as possible to the initial temperature without wasting too much water;(2) Determine the extent to which your strategy depends on the shape and volume of the tub, the shape/volume/temperature of the person in the bathtub, and the motions made by the person in the bathtub.(3)The influence of using b ubble to model’s results.(4)Give a one-page non-technical explanation for users that describes your strategyGeneral Assumptions1.Considering the safety factors as far as possible to save water, the upper temperature limit is set to 45 ℃;2.Considering the pleasant of taking a bath, the lower temperature limit is set to 33℃;3.The initial temperature of the bathtub is 40℃.Table 1Model Inputs and SymbolsSymbols Definition UnitT Initial temperature of the Bath water ℃℃T∞Outer circumstance temperatureT Water temperature of the bathtub at the every moment ℃t Time hx X coordinates of an arbitrary point my Y coordinates of an arbitrary point mz Z coordinates of an arbitrary point mαTotal heat transfer coefficient of the system 2()⋅/W m K1SThe surrounding-surface area of the bathtub 2m 2S The above-surface area of water2m 1H Bathtub’s thermal conductivity/W m K ⋅() D The thickness of the bathtub wallm 2H Convection coefficient of water2/W m K ⋅() a Length of the bathtubm b Width of the bathtubm h Height of the bathtubm V The volume of the bathtub water3m c Specific heat capacity of water/()J kg ⋅℃ ρ Density of water3/kg m ()v t Flooding rate of hot water3/m s r TThe temperature of hot water ℃Temperature ModelBasic ModelA spatio-temporal temperature model of the bathtub water is proposed in this paper. It is a four dimensional partial differential equation with the generation and loss of heat. Therefore the model can be described as the Thermal Equation.The three-dimension coordinate system is established on a corner of the bottom of the bathtub as the original point. The length of the tub is set as the positive direction along the x axis, the width is set as the positive direction along the y axis, while the height is set as the positive direction along the z axis, as shown in figure 1.Figure 1. The three-dimension coordinate systemTemperature variation of each point in space includes three aspects: one is the natural heat dissipation of each point in space; the second is the addition of exogenous thermal energy; and the third is the loss of thermal energy . In this way , we build the Partial Differential Equation model as follows:22212222(,,,)(,,,)()f x y z t f x y z t T T T T t x y z c Vαρ-∂∂∂∂=+++∂∂∂∂ (1) Where● t refers to time;● T is the temperature of any point in the space;● 1f is the addition of exogenous thermal energy;● 2f is the loss of thermal energy.According to the requirements of the subject, as well as the preferences of people, the article proposes these following optimization objective functions. A precedence level exists among these objectives, while keeping the temperature even throughout the bathtub must be ensured.Objective 1(.1O ): keep the temperature even throughout the bathtub;22100min (,,,)(,,,)t t V V F t T x y z t dxdydz dt t T x y z t dxdydz dt ⎡⎤⎡⎤⎛⎫=-⎢⎥ ⎪⎢⎥⎢⎥⎣⎦⎝⎭⎣⎦⎰⎰⎰⎰⎰⎰⎰⎰ (2) Objective 2(.2O ): keep the temperature as close as possible to the initial temperature;[]2200min (,,,)tV F T x y z t T dxdydz dt ⎛⎫=- ⎪⎝⎭⎰⎰⎰⎰ (3) Objective 3(.3O ): do not waste too much water;()30min tF v t dt =⋅⎰ (4) Objective 4(.4O ): fewer times of switching.4min F n = (5)Since the .1O is the most crucial, we should give priority to this objective. Therefore, the highest priority strategy is given here, which is homogenization of temperature.Strategy 0 – Homogenization of T emperatureThe following three reasons are provided to prove the importance of this strategy. Reason 1-SimulationIn this case, we use grid algorithm to make discretization of the formula (1), and simulate the distribution of water temperature.(1) Without manual intervention, the distribution of water temperature as shown infigure 2. And the variance of the temperature is 0.4962. 00.20.40.60.8100.51 1.5200.5Length WidthH e i g h t 4242.54343.54444.54545.5Distribution of temperature at the length=1Distribution of temperatureat the width=1Hot water Cool waterFigure 2. Temperature profiles in three-dimension space without manual intervention(2) Adding manual intervention, the distribution of water temperature as shown infigure 3. And the variance of the temperature is 0.005. 00.5100.51 1.5200.5 Length WidthH e i g h t 44.744.7544.844.8544.944.9545Distribution of temperatureat the length=1Distribution of temperature at the width=1Hot water Cool waterFigure 3. Temperature profiles in three-dimension space with manual interventionComparing figure 2 with figure 3, it is significant that the temperature of water will be homogeneous if we add some manual intervention. Therefore, we can assumed that222222()0T T T x y zα∂∂∂++≠∂∂∂ in formula (1). Reason 2-EstimationIf the temperature of any point in the space is different, then222222()0T T T x y zα∂∂∂++≠∂∂∂ Thus, we find two points 1111(,,,)x y z t and 2222(,,,)x y z t with:11112222(,,,)(,,,)T x y z t T x y z t ≠Therefore, the objective function 1F could be estimated as follows:[]2200200001111(,,,)(,,,)(,,,)(,,,)0t t V V t T x y z t dxdydz dt t T x y z t dxdydz dt T x y z t T x y z t ⎡⎤⎡⎤⎛⎫-⎢⎥ ⎪⎢⎥⎢⎥⎣⎦⎝⎭⎣⎦≥->⎰⎰⎰⎰⎰⎰⎰⎰ (6) The formula (6) implies that some motion should be taken to make sure that the temperature can be homogeneous quickly in general and 10F =. So we can assumed that: 222222()0T T T x y zα∂∂∂++≠∂∂∂. Reason 3-Analytical analysisIt is supposed that the temperature varies only on x axis but not on the y-z plane. Then a simplified model is proposed as follows:()()()()()()()2sin 000,0,,00,000t xx x T a T A x l t l T t T l t t T x x l π⎧=+≤≤≤⎪⎪⎪==≤⎨⎪⎪=≤≤⎪⎩ (7)Then we use two ways, Fourier transformation and Laplace transformation, in solving one-dimensional heat equation [Qiming Jin 2012]. Accordingly, we get the solution:()()2222/22,1sin a t l Al x T x t e a l πππ-=- (8) Where ()0,2x ∈, 0t >, ()01|x T f t ==(assumed as a constant), 00|t T T ==.Without general assumptions, we choose three specific value of t , and gain a picture containing distribution change of temperature in one-dimension space at different time.00.20.40.60.811.2 1.4 1.6 1.8200.511.522.533.54Length T e m p e r a t u r e time=3time=5time=8Figure 4. Distribution change of temperature in one-dimension space at different timeT able 2.V ariance of temperature at different timet3 5 8 variance0.4640 0.8821 1.3541It is noticeable in Figure 4 that temperature varies sharply in one-dimensional space. Furthermore, it seems that temperature will vary more sharply in three-dimension space. Thus it is so difficult to keep temperature throughout the bathtub that we have to take some strategies.Based on the above discussion, we simplify the four dimensional partial differential equation to an ordinary differential equation. Thus, we take the first strategy that make some motion to meet the requirement of homogenization of temperature, that is 10F =.ResultsTherefore, in order to meet the objective function, water temperature at any point in the bathtub needs to be same as far as possible. We can resort to some strategies to make the temperature of bathtub water homogenized, which is (,,)x y z ∀∈∀. That is,()(),,,T x y z t T t =Given these conditions, we improve the basic model as temperature does not change with space.112213312()()()()/()p r H S dT H S T T H S T T c v T T c V V dt D μρρ∞⎡⎤=++-+-+--⎢⎥⎣⎦(9) Where● 1μis the intensity of people’s movement ;● 3H is convection between water and people;● 3S is contact area between water and people;● p T is body surface temperature;● 1V is the volume of the bathtub;● 2V is the volume of people.Where the μ refers to the intensity of people ’s movement. It is a constant. However , it is a random variable in reality, which will be taken into consideration in the following.Model T estingWe use the oval-shaped bathtub to test our model. According to the actual situation, we give initial values as follows:0.19λ=,0.03D =,20.54H =,25T ∞=,040T =00.20.40.60.8125303540Time T e m p e r a t u r eFigure 5. Basic modelThe Figure 5 shows that the temperature decreases monotonously with time. And some signs of a slowing down in the rate of decrease are evident in the picture. Reaching about two hours, the water temperature does not change basically and be closely to the room temperature. Obviously , it is in line with the actual situation, indicating the rationality of this model.ConclusionOur model is robust under reasonable conditions, as can be seen from the testing above. In order to keep the temperature even throughout the bathtub, we should take some strategies like stirring constantly while adding hot water to the tub. Most important of all, this is the necessary premise of the following question.Strategy 1 – Fully adapted to the hot water in the tubInfluence of body surface temperatureWe select a set of parameters to simulate two kinds of situation separately.The first situation is that do not involve the factor of human1122()()/H S dT H S T T cV dt D ρ∞⎡⎤=+-⎢⎥⎣⎦(10) The second situation is that involves the factor of human112213312()()()/()p H S dT H S T T H S T T c V V dt D μρ∞⎡⎤=++-+--⎢⎥⎣⎦(11) According to the actual situation, we give specific values as follows, and draw agraph of temperature of two functions.33p T =,040T =204060801001201401601803838.53939.540TimeT e m p e r a t u r eWith body Without bodyFigure 6a. Influence of body surface temperature50010001500200025003000350025303540TimeT e m p e r a t u r eWith body Without bodyCoincident pointFigure 6b. Influence of body surface temperatureThe figure 6 shows the difference between two kinds of situation in the early time (before the coincident point ), while the figure 7 implies that the influence of body surface temperature reduces as time goes by . Combing with the degree of comfort ofbath and the factor of health, we propose the second optimization strategy: Fully adapted to the hot water after getting into the bathtub.Strategy 2 –Adding water intermittentlyInfluence of adding methods of waterThere are two kinds of adding methods of water. One is the continuous; the other is the intermittent. We can use both different methods to add hot water.1122112()()()/()r H S dT H S T T c v T T c V V dt D μρρ∞⎡⎤=++-+--⎢⎥⎣⎦(12) Where r T is the temperature of the hot water.To meet .3O , we calculated the minimum water consumption by changing the flow rate of hot water. And we compared the minimum water consumptions of the continuous with the intermittent to determine which method is better.A . Adding water continuouslyAccording to the actual situation, we give specific values as follows and draw a picture of the change of temperature.040T =, 37d T =, 45r T =5001000150020002500300035003737.53838.53939.54040.5TimeT e m p e r a t u r eadd hot waterFigure 7. Adding water continuouslyIn most cases, people are used to have a bath in an hour. Thus we consumed that deadline of the bath: 3600final t =. Then we can find the best strategy in Figure 5 which is listed in Table 2.T able 3Strategy of adding water continuouslystart t final tt ∆ vr T varianceWater flow 4 min 1 hour56 min537.410m s -⨯45℃31.8410⨯0.2455 3mB . Adding water intermittentlyMaintain the values of 0T ,d T ,r T ,v , we change the form of adding water, and get another graph.5001000150020002500300035003737.53838.53939.540TimeT e m p e r a t u r et1=283(turn on)t3=2107(turn on)t2=1828(turn off)Figure 8. Adding water intermittentlyT able 4.Strategy of adding water intermittently()1t on ()2t off 3()t on vr T varianceWater flow 5 min 30 min35min537.410m s -⨯45℃33.610⨯0.2248 3mConclusionDifferent methods of adding water can influence the variance, water flow and the times of switching. Therefore, we give heights to evaluate comprehensively the methods of adding hot water on the basis of different hobbies of people. Then we build the following model:()()()2213600210213i i n t t i F T t T dtF v t dtF n -=⎧=-⎪⎪⎪=⎨⎪⎪=⎪⎩⎰∑⎰ (13) ()112233min F w F w F w F =++ (14)12123min ..510mini i t s t t t +>⎧⎨≤-≤⎩Evaluation on StrategiesFor example: Given a set of parameters, we choose different values of v and d T , and gain the results as follows.Method 1- AHPStep 1:Establish hierarchy modelFigure 9. Establish hierarchy modelStep 2: Structure judgment matrix153113511133A ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦Step 3: Assign weight1w 2w3w 0.650.220.13Method 2-TopsisStep1 :Create an evaluation matrix consisting of m alternatives and n criteria, with the intersection of each alternative and criteria given as ij x we therefore have a matrixStep2:The matrix ij m n x ⨯()is then normalised to form the matrix ij m n R r ⨯=(), using thenormalisation method21r ,1,2,,;1,2,ijij mij i x i n j m x====∑…………,Step3:Calculate the weighted normalised decision matrix()(),1,2,,ij j ij m n m nT t w r i m ⨯⨯===⋅⋅⋅where 1,1,2,,nj j jj w W Wj n ===⋅⋅⋅∑so that11njj w==∑, and j w is the original weight given to the indicator,1,2,,j v j n =⋅⋅⋅.Step 4: Determine the worst alternative ()w A and the best alternative ()b A()(){}{}()(){}{}max 1,2,,,min 1,2,,1,2,,n ,min 1,2,,,max 1,2,,1,2,,n ,w ij ij wjbijij bjA t i m j J t i m j J t j A t i m j J t i m j J tj -+-+==∈=∈====∈=∈==where, {}1,2,,J j n j +==⋅⋅⋅ associated with the criteria having a positive impact, and {}1,2,,J j n j -==⋅⋅⋅associated with the criteria having a negative impact. Step 5: Calculate the L2-distance between the target alternative i and the worst condition w A()21,1,2,,m niw ij wj j d tt i ==-=⋅⋅⋅∑and the distance between the alternative i and the best condition b A()21,1,2,,m nib ij bj j d t t i ==-=⋅⋅⋅∑where iw d and ib d are L2-norm distances from the target alternative i to the worst and best conditions, respectively .Step 6 :Calculate the similarity to the worst condition Step 7 : Rank the alternatives according to ()1,2,,iw s i m =⋅⋅⋅ Step 8 : Assign weight1w2w 3w 0.55 0.170.23ConclusionAHP gives height subjectively while TOPSIS gives height objectively. And the heights are decided by the hobbies of people. However, different people has different hobbies, we choose AHP to solve the following situations.Impact of parametersDifferent customers have their own hobbies. Some customers prefer enjoying in the bath, so the .2O is more important . While other customers prefer saving water, the .3O is more important. Therefore, we can solve the problem on basis of APH . 1. Customers who prefer enjoying: 20.83w =,30.17w =According to the actual situation, we give initial values as follows:13S =,11V =,2 1.4631S =,20.05V =,33p T =,110μ=Ensure other parameters unchanged, then change the values of these parameters including 1S ,1V ,2S ,2V ,d T ,1μ. So we can obtain the optimal strategies under different conditions in Table 4.T able 5.Optimal strategies under different conditions2.Customers who prefer saving: 20.17w =,30.83w =Just as the former, we give the initial values of these parameters including1S ,1V ,2S ,2V ,d T ,1μ, then change these values in turn with other parameters unchanged. So we can obtain the optimal strategies as well in these conditions.T able 6.Optimal strategies under different conditionsInfluence of bubbleUsing the bubble bath additives is equivalent to forming a barrier between the bath water and air, thereby slowing the falling velocity of water temperature. According to the reality, we give the values of some parameters and gain the results as follows:5001000150020002500300035003334353637383940TimeT e m p e r a t u r eWithour bubbleWith bubbleFigure 10. Influence of bubbleT able 7.Strategies (influence of bubble)Situation Dropping rate of temperature (the larger the number, the slower)Disparity to theinitial temperatureWater flow Times of switchingWithout bubble 802 1.4419 0.1477 4 With bubble 34499.85530.01122The Figure 10 and the Table 7 indicates that adding bubble can slow down the dropping rate of temperature effectively . It can decrease the disparity to the initial temperature and times of switching, as well as the water flow.Improved ModelIn reality , human ’s motivation in the bathtub is flexible, which means that the parameter 1μis a changeable measure. Therefore, the parameter can be regarded as a random variable, written as ()[]110,50t random μ=. Meanwhile, the surface of water will come into being ripples when people moves in the tub, which will influence the parameters like 1S and 2S . So, combining with reality , we give the range of values as follows:()[]()[]111222,1.1,1.1S t random S S S t random S S ⎧=⎪⎨=⎪⎩Combined with the above model, the improved model is given here:()[]()[]()[]11221121111222()()()/()10,50,1.1,1.1a H S dT H S T T c v T T c V V dt D t random S t random S S S t random S S μρρμ∞⎧⎡⎤=++-+--⎪⎢⎥⎣⎦⎨⎪===⎩(15)Given the values, we can get simulation diagram:050010001500200025003000350039.954040.0540.140.15TimeT e m p e r a t u r eFigure 11. Improved modelThe figure shows that the variance is small while the water flow is large, especially the variance do not equals to zero. This indicates that keeping the temperature of water is difficult though we regard .2O as the secondary objective.Sensitivity AnalysisSome parameters have a fixed value throughout our work. By varying their values, we can see their impacts.Impact of the shape of the tub0.70.80.91 1.1 1.2 1.3 1.433.23.43.63.84Superficial areaT h e t i m e sFigure 12a. Times of switching0.70.80.91 1.11.21.31.43890390039103920393039403950Superficial areaV a r i a n c eFigure 12b. V ariance of temperature0.70.80.91 1.1 1.2 1.3 1.40.190.1950.20.2050.21Superficial areaW a t e r f l o wFigure 12c. Water flowBy varying the value of some parameters, we can get the relationships between the shape of tub and the times of switching, variance of temperature, and water flow et. It is significant that the three indexes will change as the shape of the tub changes. Therefore the shape of the tub makes an obvious effect on the strategies. It is a sensitive parameter.Impact of the volume of the tub0.70.80.91 1.1 1.2 1.3 1.4 1.533.544.55VolumeT h e t i m e sFigure 13a. Times of switching。
美赛感想[五篇模版]
![美赛感想[五篇模版]](https://img.taocdn.com/s3/m/5226bb79302b3169a45177232f60ddccdb38e646.png)
美赛感想[五篇模版]第一篇:美赛感想ICM参赛感想建模是解决问题的重要环节,一个美妙地解决实际问题的好方案通常由一个贴近现实而又提炼本质的模型以及若干巧妙严谨的求解工具所构成。
由于平时所接触的内容过多地囿于自己学习与研究领域中,因此为了接触新的领域并同时训练自身学习建模能力,我们聚集了来自电子系、经管学院、交叉信息研究院的三名队员参加了2014年2月举行的美国大学生数学建模及交叉学科建模大赛。
美赛要求在4天(96个小时)内针对选定的题目完成一篇完整的科技论文,因此高效合理地利用时间至关重要。
我们在比赛前进行了一定的准备,例如熟悉比赛的基本形式,准备好科技论文的LaTeX模板,并且借助清华大学数学系赛前分发的往届赛事材料对题目风格进行初步了解,并思考优秀作品所共有的特点。
通过这些准备,我们认准了比赛时的一些注意事项,包括:无论题目如何提问,整篇论文都需要有一条明确的主线;论文逻辑必须清晰,排版合理,符号与语法的使用需要符合科技论文规范;一定要完成题目里所有要求完成的部分;等等。
最重要的一点是,我们意识到若想获得好成绩,或者要有明显的创新亮点,或者要循规蹈矩地在每一点上都做得无懈可击,这也正是我们所设想的不同方向。
同时我们也确定了基本分工,即让编程能力强的交叉信息研究院队员邝仲弘负责主编程工作,让批判性思维比较好、数据收集能力强的经管学院队员孙映宁负责头脑风暴与数据收集,而让以前有科技论文撰写经验、同时在各学科上都有一定基础的电子系队员韩衍隽作为队长负责整体流程的安排与文书工作。
今年比赛于中国时间上午九点开始。
根据以往的建议,我们第一天完全仅用于确定选题。
对题目进行翻译和初步讨论后,我们首先放弃对中国学生没有优势的B题,然后分工对A题和C题进行初始建模。
由于队员邝仲弘学过有关网络科学的课程,因此我们最终选定思路更清晰也更有把握的C题,同时学习邝仲弘所共享的网络科学教材。
第二天的主要任务则是主体建模,确定整体框架,明确大部分问题的基本解答思路,完成数据搜集、编程等工作。
92年美国数学建模竞赛优秀论文介绍

由华盛顿大学三名学生(简称华队)完成的92年美国大学党建是竞赛B题的一篇优秀论文1.题目与背景题目:研究室紧急电力修复系统的修复计划背景:沿海地区由于经常受风暴袭击,电力公司必须有相应的修复系统。
过去电力公司(HECO)由于缺少优先排序受到媒体批评,故欲聘请顾问提出合理修复计划。
风暴修复申请报告如表所列。
(略)表上提供了报告时间(即申请提出时间)、申请单位类型、估计修复所需时间以及单位位置。
2.基本假设与条件公司对于修复工作,给出下述假设与条件:(1)有两个修复中心,其位置为(0,0)、(40,40)、修复区域为6565,5050-<<-<<;x y(2)道路系统良好,修理工只需在交接班时返回修理中心;(3)除了交通枢纽及医院需立即修理外,其余的修理工作必须在风暴过后(6:00以后)开始进行;(4)每个中心有三名熟练工人全天轮流值班,每人工作8小时,紧急修理时每个点有6名工人可启用,每个工人在一个工作日里可加班8小时,加班报酬为正常报酬的1.5倍。
此外命题者允许参赛者作必要的简化或假设。
除上述假设外华队又增加了一些假设,可概括为:(1)街道为东西---南北向,两点间路程公式为||||ab a b a b d x x y y =-++道路状况良好,均匀,路途时间只取决于距离。
车辆路途运行费用与工资相比可忽略不计。
(2) 每个正常班工资为$10/小时,加班费为$15/小时。
工人在未完成一项任务时不得移动地点,每个工人可以加班8小时,但已超过时不得开始新工作。
各工人联系充公,保证工作指派不合冲突。
(3) 同一作业不因指派多于1 人而加速。
所有工作人员均有相同的能力与效率。
(4) 车辆行驶速度规定为60哩/小时。
(5) 在未发生风暴前每点有1 人值班,风暴后每点有6人安排在3班上(午夜12点,早8点,下午4点)。
3. 对问题的分析华队认为问题的关键是将修复单位合理排序并合理指派工人。
美国中学生数学建模竞赛获奖论文

Abstract
In this paper, we undertake the search and find problem. In two parts of searching, we use different way to design the model, but we use the same algorithm to calculate the main solution. In Part 1, we assume that the possibilities of finding the ring in different paths are different. We give weight to each path according to the possibility of finding the ring in the path. Then we simplify the question as pass as more weight as possible in limited distance. To simplify the calculating, we use Greedy algorithm and approximate optimal solution, and we define the values of the paths(according to the weights of paths) in Greedy algorithm. We calculate the possibility according to the weight of the route and to total weights of paths in the map. In Part 2, firstly, we limit the moving area of the jogger according to the information in the map. Then we use Dijkstra arithmatic to analysis the specific area of the jogger may be in. At last, we use greedy algorithm and approximate optimal solution to get the solution.
建模美赛获奖范文

建模美赛获奖范文标题:《探索与创新:建模美赛获奖作品范文解析》建模美赛(MCM/ICM)是全球大学生数学建模竞赛的盛事,每年都吸引了众多优秀的学生参与。
在这个舞台上,获奖作品往往展现了卓越的数学建模能力、创新思维和问题解决技巧。
本文将解析一份获奖范文,带您领略建模美赛获奖作品的风采。
一、背景与问题阐述(此处详细描述范文所针对的问题背景、研究目的和意义,以及问题的具体阐述。
)二、模型建立与假设1.模型分类与选择:根据问题特点,范文选择了适当的模型进行研究和分析。
2.假设条件:明确列出建模过程中所做的主要假设,并解释其合理性。
三、模型求解与结果分析1.数据收集与处理:介绍范文中所用数据来源、处理方法及有效性验证。
2.模型求解:详细阐述模型的求解过程,包括算法选择、计算步骤等。
3.结果分析:对求解结果进行详细分析,包括图表展示、敏感性分析等。
四、模型优化与拓展1.模型优化:针对原模型存在的问题,范文提出了相应的优化方案。
2.拓展研究:对模型进行拓展,探讨其在其他领域的应用和推广价值。
五、结论与建议1.结论总结:概括范文的研究成果,强调其创新点和贡献。
2.实践意义:分析建模结果在实际问题中的应用价值和意义。
3.建议:针对问题解决,提出具体的建议和措施。
六、获奖亮点与启示1.创新思维:范文在模型选择、求解方法等方面展现出创新性。
2.严谨论证:文章结构清晰,逻辑严密,数据充分,论证有力。
3.团队合作:建模美赛强调团队协作,范文体现了成员间的紧密配合和分工合作。
总结:通过分析这份建模美赛获奖范文,我们可以学到如何从问题背景出发,建立合理的模型,进行严谨的求解和分析,以及如何优化和拓展模型。
同时,也要注重创新思维和团队合作,才能在建模美赛中脱颖而出。
美赛总结报告

美赛总结报告2022年美国数学建模竞赛总结报告亲爱的评委们:首先,我代表我们的团队,向您致以最诚挚的问候和感谢。
2022年的美国数学建模竞赛对我们来说是一次难得的经历和机会,我们珍惜并充分发挥我们的最佳水平。
通过这次竞赛,我们不仅收获了许多宝贵的经验和知识,也锻炼了我们的团队合作能力和解决问题的能力。
这次竞赛的题目是关于城市扩张与环保问题的,我们团队选择了其中一道题目进行研究和建模。
在初步了解问题后,我们进行了大量的文献查阅和数据分析,以便更好地了解城市扩张对环境的影响,并找到有效的解决方案。
在研究过程中,我们运用了许多数学模型的技巧和方法,如回归分析、优化模型和概率模型等。
同时,我们也结合实际情况,考虑到了城市发展的多个方面,如人口增长、经济发展和环境保护等因素。
通过建立数学模型,我们成功地分析了城市扩张对环境的潜在影响,并给出了一些合理的建议和解决方案。
在团队合作方面,我们深刻体验到了团队合作的重要性。
每个队员都充分发挥自己的优势,积极参与讨论和建模过程,在紧张的竞赛中,我们相互支持、相互鼓励,共同解决了许多难题。
通过团队合作,我们有效地利用每个队员的才能和潜力,最大程度地提高了团队的整体水平。
此外,这次竞赛对我们的时间管理和应变能力也提出了很高的要求。
我们充分利用有限的时间,提前做好了计划和准备,确保了我们在规定的时间内能够完成建模和分析任务。
同时,在面对一些突发情况时,我们能够迅速应对和调整,保持了团队的稳定和良好的工作状态。
最后,我想再次感谢评委们对我们的认可和支持。
这次竞赛是我们在数学建模方面的一个重要的里程碑,它不仅给我们带来了宝贵的经验和机会,也激发了我们对数学建模的热情和兴趣。
我们将继续努力学习和提升自己,在未来的学习和工作中,更好地应用数学模型解决实际问题。
谢谢评委们的聆听!祝愿您们工作顺利!我们团队敬上。
XXX团队。
对美国大学生数学建模竞赛的一些认识及感受(2012426)

有固定的模式,要求赛前准备的知识非常多 ,诸如微分方程及数值解,运筹学,图论, 高级算法等。 题目中往往不提供数据或提供很多数据。
6
2012 MCM A:The Leaves of a Tree
"How much do the leaves on a tree weigh?" How might one estimate the actual weight of the leaves (or for that matter any other parts of the tree)? How might one classify leaves? Build a mathematical model to describe and classify leaves. Consider and answer the following:
1999年起,美国数学及其应用联合会又同时推出 交叉学科竞赛(Interdisciplinary Contest in Modeling ),简称 ICM(涉及数学、环境科学、 生物学、化学、资源管理等交叉学科)。
美国大学生数学建模竞赛的宗旨
MCM的宗旨:鼓励大学师生对范围并不固定 的各种实际问题予以阐明、分析并提出解法, 通过这样一种结构,鼓励师生积极参与并强调 实现完整的模型构造的过程。
美国大学生数学建模竞赛题2009--2011
09A Designing a Traffic Circle(交通环岛) 09B Energy and the Cell Phone(能源与手
机) 10A The Sweet Spot((犯罪学) 11A Snowboard Course(单板滑雪场地) 11B Repeater Coordination(中继站的协调)
美国大学生数学建模竞赛二等奖论文

美国⼤学⽣数学建模竞赛⼆等奖论⽂The P roblem of R epeater C oordination SummaryThis paper mainly focuses on exploring an optimization scheme to serve all the users in a certain area with the least repeaters.The model is optimized better through changing the power of a repeater and distributing PL tones,frequency pairs /doc/d7df31738e9951e79b8927b4.html ing symmetry principle of Graph Theory and maximum coverage principle,we get the most reasonable scheme.This scheme can help us solve the problem that where we should put the repeaters in general cases.It can be suitable for the problem of irrigation,the location of lights in a square and so on.We construct two mathematical models(a basic model and an improve model)to get the scheme based on the relationship between variables.In the basic model,we set a function model to solve the problem under a condition that assumed.There are two variables:‘p’(standing for the power of the signals that a repeater transmits)and‘µ’(standing for the density of users of the area)in the function model.Assume‘p’fixed in the basic one.And in this situation,we change the function model to a geometric one to solve this problem.Based on the basic model,considering the two variables in the improve model is more reasonable to most situations.Then the conclusion can be drawn through calculation and MATLAB programming.We analysis and discuss what we can do if we build repeaters in mountainous areas further.Finally,we discuss strengths and weaknesses of our models and make necessary recommendations.Key words:repeater maximum coverage density PL tones MATLABContents1.Introduction (3)2.The Description of the Problem (3)2.1What problems we are confronting (3)2.2What we do to solve these problems (3)3.Models (4)3.1Basic model (4)3.1.1Terms,Definitions,and Symbols (4)3.1.2Assumptions (4)3.1.3The Foundation of Model (4)3.1.4Solution and Result (5)3.1.5Analysis of the Result (8)3.1.6Strength and Weakness (8)3.1.7Some Improvement (9)3.2Improve Model (9)3.2.1Extra Symbols (10)Assumptions (10)3.2.2AdditionalAdditionalAssumptions3.2.3The Foundation of Model (10)3.2.4Solution and Result (10)3.2.5Analysis of the Result (13)3.2.6Strength and Weakness (14)4.Conclusions (14)4.1Conclusions of the problem (14)4.2Methods used in our models (14)4.3Application of our models (14)5.Future Work (14)6.References (17)7.Appendix (17)Ⅰ.IntroductionIn order to indicate the origin of the repeater coordination problem,the following background is worth mentioning.With the development of technology and society,communications technology has become much more important,more and more people are involved in this.In order to ensure the quality of the signals of communication,we need to build repeaters which pick up weak signals,amplify them,and retransmit them on a different frequency.But the price of a repeater is very high.And the unnecessary repeaters will cause not only the waste of money and resources,but also the difficulty of maintenance.So there comes a problem that how to reduce the number of unnecessary repeaters in a region.We try to explore an optimized model in this paper.Ⅱ.The Description of the Problem2.1What problems we are confrontingThe signals transmit in the way of line-of-sight as a result of reducing the loss of the energy. As a result of the obstacles they meet and the natural attenuation itself,the signals will become unavailable.So a repeater which just picks up weak signals,amplifies them,and retransmits them on a different frequency is needed.However,repeaters can interfere with one another unless they are far enough apart or transmit on sufficiently separated frequencies.In addition to geographical separation,the“continuous tone-coded squelch system”(CTCSS),sometimes nicknamed“private line”(PL),technology can be used to mitigate interference.This system associates to each repeater a separate PL tone that is transmitted by all users who wish to communicate through that repeater. The PL tone is like a kind of password.Then determine a user according to the so called password and the specific frequency,in other words a user corresponds a PL tone(password)and a specific frequency.Defects in line-of-sight propagation caused by mountainous areas can also influence the radius.2.2What we do to solve these problemsConsidering the problem we are confronting,the spectrum available is145to148MHz,the transmitter frequency in a repeater is either600kHz above or600kHz below the receiver frequency.That is only5users can communicate with others without interferences when there’s noPL.The situation will be much better once we have PL.However the number of users that a repeater can serve is limited.In addition,in a flat area ,the obstacles such as mountains ,buildings don’t need to be taken into account.Taking the natural attenuation itself is reasonable.Now the most important is the radius that the signals transmit.Reducing the radius is a good way once there are more users.With MATLAB and the method of the coverage in Graph Theory,we solve this problem as follows in this paper.Ⅲ.Models3.1Basic model3.1.1Terms,Definitions,and Symbols3.1.2Assumptions●A user corresponds a PLz tone (password)and a specific frequency.●The users in the area are fixed and they are uniform distribution.●The area that a repeater covers is a regular hexagon.The repeater is in the center of the regular hexagon.●In a flat area ,the obstacles such as mountains ,buildings don’t need to be taken into account.We just take the natural attenuation itself into account.●The power of a repeater is fixed.3.1.3The Foundation of ModelAs the number of PLz tones (password)and frequencies is fixed,and a user corresponds a PLz tone (password)and a specific frequency,we can draw the conclusion that a repeater can serve the limited number of users.Thus it is clear that the number of repeaters we need relates to the density symboldescriptionLfsdfminrpµloss of transmission the distance of transmission operating frequency the number of repeaters that we need the power of the signals that a repeater transmits the density of users of the areaof users of the area.The radius of the area that a repeater covers is also related to the ratio of d and the radius of the circular area.And d is related to the power of a repeater.So we get the model of function()min ,r f p µ=If we ignore the density of users,we can get a Geometric model as follows:In a plane which is extended by regular hexagons whose side length are determined,we move a circle until it covers the least regular hexagons.3.1.4Solution and ResultCalculating the relationship between the radius of the circle and the side length of the regular hexagon.[]()()32.4420lg ()20lg Lfs dB d km f MHz =++In the above formula the unit of ’’is .Lfs dB The unit of ’’is .d Km The unit of ‘‘is .f MHz We can conclude that the loss of transmission of radio is decided by operating frequency and the distance of transmission.When or is as times as its former data,will increase f d 2[]Lfs .6dB Then we will solve the problem by using the formula mentioned above.We have already known the operating frequency is to .According to the 145MHz 148MHz actual situation and some authority material ,we assume a system whose transmit power is and receiver sensitivity is .Thus we can conclude that ()1010dBm mW +106.85dBm ?=.Substituting and to the above formula,we can get the Lfs 106.85dBm ?145MHz 148MHz average distance of transmission .()6.4d km =4mile We can learn the radius of the circle is 40mile .So we can conclude the relationship between the circle and the side length of regular hexagon isR=10d.1)The solution of the modelIn order to cover a certain plane with the least regular hexagons,we connect each regular hexagon as the honeycomb.We use A(standing for a figure)covers B(standing for another figure), only when As don’t overlap each other,the number of As we use is the smallest.Figure1According to the Principle of maximum flow of Graph Theory,the better of the symmetry ofthe honeycomb,the bigger area that it covers(Fig1).When the geometric centers of the circle andthe honeycomb which can extend are at one point,extend the honeycomb.Then we can get Fig2,Fig4:Figure2Fig3demos the evenly distribution of users.Figure4Now prove the circle covers the least regular hexagons.Look at Fig5.If we move the circle slightly as the picture,you can see three more regular hexagons are needed.Figure 52)ResultsThe average distance of transmission of the signals that a repeater transmit is 4miles.1000users can be satisfied with 37repeaters founded.3.1.5Analysis of the Result1)The largest number of users that a repeater can serveA user corresponds a PL and a specific frequency.There are 5wave bands and 54different PL tones available.If we call a code include a PL and a specific frequency,there are 54*5=270codes.However each code in two adjacent regular hexagons shouldn’t be the same in case of interfering with each other.In order to have more code available ,we can distribute every3adjacent regular hexagons 90codes each.And that’s the most optimized,because once any of the three regular hexagons have more codes,it will interfere another one in other regular hexagon.2)Identify the rationality of the basic modelNow we considering the influence of the density of users,according to 1),90*37=3330>1000,so here the number of users have no influence on our model.Our model is rationality.3.1.6Strength and Weakness●Strength:In this paper,we use the model of honeycomb-hexagon structure can maximize the use of resources,avoiding some unnecessary interference effectively.It is much more intuitive once we change the function model to the geometric model.●Weakness:Since each hexagon get too close to another one.Once there are somebuildingsor terrain fluctuations between two repeaters,it can lead to the phenomenon that certain areas will have no signals.In addition,users are distributed evenly is not reasonable.The users are moving,for example some people may get a party.3.1.7Some ImprovementAs we all know,the absolute evenly distribution is not exist.So it is necessary to say something about the normal distribution model.The maximum accommodate number of a repeater is 5*54=270.As for the first model,it is impossible that 270users are communicating in a same repeater.Look at Fig 6.If there are N people in the area 1,the maximum number of the area 2to area 7is 3*(270-N).As 37*90=3330is much larger than 1000,our solution is still reasonable to this model.Figure 63.2Improve Model3.2.1Extra SymbolsSigns and definitions indicated above are still valid.Here are some extra signs and definitions.symboldescription Ra the radius of the circular flat area the side length of a regular hexagon3.2.2Additional AdditionalAssumptionsAssumptions ●The radius that of a repeater covers is adjustable here.●In some limited situations,curved shape is equal to straight line.●Assumptions concerning the anterior process are the same as the Basic Model3.2.3The Foundation of ModelThe same as the Basic Model except that:We only consider one variable(p)in the function model of the basic model ;In this model,we consider two varibles(p and µ)of the function model.3.2.4Solution and Result1)SolutionIf there are 10,000users,the number of regular hexagons that we need is at least ,thus according to the the Principle of maximum flow of Graph Theory,the 10000111.1190=result that we draw needed to be extended further.When the side length of the figure is equal to 7Figure 7regular hexagons,there are 127regular hexagons (Fig 7).Assuming the side length of a regular hexagon is ,then the area of a regular hexagon is a .The area of regular hexagons is equal to a circlewhose radiusis 22a =1000090R.Then according to the formula below:.221000090a R π=We can get.9.5858R a =Mapping with MATLAB as below (Fig 8):Figure 82)Improve the model appropriatelyEnlarge two part of the figure above,we can get two figures below (Fig 9and Fig 10):Figure 9AREAFigure 10Look at the figure above,approximatingAREA a rectangle,then obtaining its area to getthe number of users..The length of the rectangle is approximately equal to the side length of the regular hexagon ,athe width of the rectangle is ,thus the area of AREA is ,then R ?*R awe can get the number of users in AREA is(),2**10000 2.06R a R π=????????9.5858R a =As 2.06<<10,000,2.06can be ignored ,so there is no need to set up a repeater in.There are 6suchareas(92,98,104,110,116,122)that can be ignored.At last,the number of repeaters we should set up is,1276121?=2)Get the side length of the regular hexagon of the improved modelThus we can getmile=km 40 4.1729.5858a == 1.6* 6.675a =3)Calculate the power of a repeaterAccording to the formula[]()()32.4420lg ()20lg Lfs dB d km f MHz =++We get32.4420lg 6.67520lg14592.156Los =++=32.4420lg 6.67520lg14892.334Los =++=So we get106.85-92.156=14.694106.85-92.334=14.516As the result in the basic model,we can get the conclusion the power of a repeater is from 14.694mW to 14.516mW.3.2.5Analysis of the ResultAs 10,000users are much more than 1000users,the distribution of the users is more close toevenly distribution.Thus the model is more reasonable than the basic one.More repeaters are built,the utilization of the outside regular hexagon are higher than the former one.3.2.6Strength and Weakness●Strength:The model is more reasonable than the basic one.●Weakness:Repeaters don’t cover all the area,some places may not receive signals.And thefoundation of this model is based on the evenly distribution of the users in the area,if the situation couldn’t be satisfied,the interference of signals will come out.Ⅳ.Conclusions4.1Conclusions of the problem●Generally speaking,the radius of the area that a repeater covers is4miles in our basic model.●Using the model of honeycomb-hexagon structure can maximize the use of resources,avoiding some unnecessary interference effectively.●The minimum number of repeaters necessary to accommodate1,000simultaneous users is37.The minimum number of repeaters necessary to accommodate10,000simultaneoususers is121.●A repeater's coverage radius relates to external environment such as the density of users andobstacles,and it is also determined by the power of the repeater.4.2Methods used in our models●Analysis the problem with MATLAB●the method of the coverage in Graph Theory4.3Application of our models●Choose the ideal address where we set repeater of the mobile phones.●How to irrigate reasonably in agriculture.●How to distribute the lights and the speakers in squares more reasonably.Ⅴ.Future WorkHow we will do if the area is mountainous?5.1The best position of a repeater is the top of the mountain.As the signals are line-of-sight transmission and reception.We must find a place where the signals can transmit from the repeater to users directly.So the top of the mountain is a good place.5.2In mountainous areas,we must increase the number of repeaters.There are three reasons for this problem.One reason is that there will be more obstacles in the mountainous areas. The signals will be attenuated much more quickly than they transmit in flat area.Another reason is that the signals are line-of-sight transmission and reception,we need more repeaters to satisfy this condition.Then look at Fig11and Fig12,and you will know the third reason.It can be clearly seen that hypotenuse is larger than right-angleFig11edge(R>r).Thus the radius will become smaller.In this case more repeaters are needed.Fig125.3In mountainous areas,people may mainly settle in the flat area,so the distribution of users isn’t uniform.5.4There are different altitudes in the mountainous areas.So in order to increase the rate of resources utilization,we can set up the repeaters in different altitudes.5.5However,if there are more repeaters,and some of them are on mountains,more money will be/doc/d7df31738e9951e79b8927b4.html munication companies will need a lot of money to build them,repair them when they don’t work well and so on.As a result,the communication costs will be high.What’s worse,there are places where there are many mountains but few persons. Communication companies reluctant to build repeaters there.But unexpected things often happen in these places.When people are in trouble,they couldn’t communicate well with the outside.So in my opinion,the government should take some measures to solve this problem.5.6Another new method is described as follows(Fig13):since the repeater on high mountains can beFig13Seen easily by people,so the tower which used to transmit and receive signals can be shorter.That is to say,the tower on flat areas can be a little taller..Ⅵ.References[1]YU Fei,YANG Lv-xi,"Effective cooperative scheme based on relay selection",SoutheastUniversity,Nanjing,210096,China[2]YANG Ming,ZHAO Xiao-bo,DI Wei-guo,NAN Bing-xin,"Call Admission Control Policy based on Microcellular",College of Electical and Electronic Engineering,Shijiazhuang Railway Institute,Shijiazhuang Heibei050043,China[3]TIAN Zhisheng,"Analysis of Mechanism of CTCSS Modulation",Shenzhen HYT Co,Shenzhen,518057,China[4]SHANGGUAN Shi-qing,XIN Hao-ran,"Mathematical Modeling in Bass Station Site Selectionwith Lingo Software",China University of Mining And Technology SRES,Xuzhou;Shandong Finance Institute,Jinan Shandon,250014[5]Leif J.Harcke,Kenneth S.Dueker,and David B.Leeson,"Frequency Coordination in the AmateurRadio Emergency ServiceⅦ.AppendixWe use MATLAB to get these pictures,the code is as follows:1-clc;clear all;2-r=1;3-rc=0.7;4-figure;5-axis square6-hold on;7-A=pi/3*[0:6];8-aa=linspace(0,pi*2,80);9-plot(r*exp(i*A),'k','linewidth',2);10-g1=fill(real(r*exp(i*A)),imag(r*exp(i*A)),'k');11-set(g1,'FaceColor',[1,0.5,0])12-g2=fill(real(rc*exp(i*aa)),imag(rc*exp(i*aa)),'k');13-set(g2,'FaceColor',[1,0.5,0],'edgecolor',[1,0.5,0],'EraseMode','x0r')14-text(0,0,'1','fontsize',10);15-Z=0;16-At=pi/6;17-RA=-pi/2;18-N=1;At=-pi/2-pi/3*[0:6];19-for k=1:2;20-Z=Z+sqrt(3)*r*exp(i*pi/6);21-for pp=1:6;22-for p=1:k;23-N=N+1;24-zp=Z+r*exp(i*A);25-zr=Z+rc*exp(i*aa);26-g1=fill(real(zp),imag(zp),'k');27-set(g1,'FaceColor',[1,0.5,0],'edgecolor',[1,0,0]);28-g2=fill(real(zr),imag(zr),'k');29-set(g2,'FaceColor',[1,0.5,0],'edgecolor',[1,0.5,0],'EraseMode',xor';30-text(real(Z),imag(Z),num2str(N),'fontsize',10);31-Z=Z+sqrt(3)*r*exp(i*At(pp));32-end33-end34-end35-ezplot('x^2+y^2=25',[-5,5]);%This is the circular flat area of radius40miles radius 36-xlim([-6,6]*r) 37-ylim([-6.1,6.1]*r)38-axis off;Then change number19”for k=1:2;”to“for k=1:3;”,then we get another picture:Change the original programme number19“for k=1:2;”to“for k=1:4;”,then we get another picture:。
正确写作美国大学生数学建模竞赛论文

1)、鉴别阶段: (10分钟)
所有论文在此阶段按其质量分别归入一下三类:第一类 是可以进入下一评审阶段的论文(略少于二分之一);第二类 是满足竞赛要求,但不足以进入下一评审阶段的论文(这一类 就被定为合格论文);第三类是不符合竞赛要求的论文(不合 格论文)。 由于在第一阶段中,评委只有10分钟左右的时间评审一 篇论文,因此评委常常只能通过阅读摘要来判断论文水平的高 低。
例如,2010年MCM竞赛中有一道赛题,要求参赛小 组根据以往的作案地点预测连环犯罪的位置。
3.1)、假设条件和解释 解答这道赛题的重点是犯罪活动方式。在一篇题为 “Centroids, Clusters, and Crime: Anchoring the Geographic Profiles of Serial Criminals”的论文中,有一条假设是“罪犯 的活动不受限制”,但罪犯是在市区的活动,实际上会受 到街道的布局及街道两旁建筑物的限制。由于街道布局通 常类似于网格,所以参赛小组对这个假设做了如下解释: Criminal’s movement is unconstrained. Because of the difficulty of finding real-world distance data, we invoke the „Manhattan assumption‟: There are enough streets and sidewalks in a sufficiently grid-like pattern that movements along real-world movement routes is the same as „straight-line‟ movement in a space discretized into city blocks…
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.优秀论文一具体要求:1月28日上午汇报1)论文主要内容、具体模型和求解算法(针对摘要和全文进行概括);In the part1, we will design a schedule with fixed trip dates and types and also routes. In the part2, we design a schedule with fixed trip dates and types but unrestrained routes.In the part3, we design a schedule with fixed trip dates but unrestrained types and routes.In part 1, passengers have to travel along the rigid route set by river agency, so the problem should be to come up with the schedule to arrange for the maximum number of trips without occurrence of two different trips occupying the same campsite on the same day.In part 2, passengers have the freedom to choose which campsites to stop at, therefore the mathematical description of their actions inevitably involve randomness and probability, and we actually use a probability model. The next campsite passengers choose at a current given campsite is subject to a certain distribution, and we describe events of two trips occupying the same campsite y probability. Note in probability model it is no longer appropriate to say that two trips do not meet at a campsite with certainty; instead, we regard events as impossible if their probabilities are below an adequately small number. Then we try to find the optimal schedule.In part 3, passengers have the freedom to choose both the type and route of the trip; therefore a probability model is also necessary. We continue to adopt the probability description as in part 2 and then try to find the optimal schedule.In part 1, we find the schedule of trips with fixed dates, types (propulsion and duration) and routes (which campsites the trip stops at), and to achieve this we use a rather novel method. The key idea is to divide campsites into different “orbits”that only allows some certain trip types to travel in, therefore the problem turns into several separate small problem to allocate fewer trip types, and the discussion of orbits allowing one, two, three trip types lead to general result which can deal with any value of Y. Particularly, we let Y=150, a rather realistic number of campsites, to demonstrate a concrete schedule and the carrying capacity of the river is 2340 trips.In part 2, we find the schedule of trips with fixed dates, types but unrestrained routes. To better describe the behavior of tourists, we need to use a stochastic model(随机模型). We assume a classical probability model and also use the upper limit value of small probability to define an event as not happening. Then we use Greedy algorithm to choose the trips added and recursive algorithm together with Jordan Formula to calculate the probability of two trips simultaneously occupying the same campsites. The carrying capacity of the river by this method is 500 trips. This method can easily find theoptimal schedule with X given trips, no matter these X trips are with fixed routes or not. In part 3, we find the optimal schedule of trips with fixed dates and unrestrained types and routes. This is based on the probability model developed in part 2 and we assign the choice of trip types of the tourists with a uniform distribution to describe their freedom to choose and obtain the results similar to part 2. The carrying capacity of the river by this method is 493 trips. Also this method can easily find the optimal schedule with X given trips, no matter these X trips are with fixed routes or not.2)论文结构概述(列出提纲,分析优缺点,自己安排的结构);1 Introduction2 Definitions3 Specific formulation of problem4 Assumptions5 Part 1 Best schedule of trips with fixed dates, types and also routes.5.1 Method5.1.1 Motivation and justification5.1.2 Key ideas5.2 Development of the model5.2.1Every campsite set for every single trip type5.2.2 Every campsite set for every multiple trip types5.2.3One campsite set for all trip types6 Part 2 Best schedule of trips with fixed dates and types, but unrestrained routes.6.1 Method6.1.1 Motivation and justification6.1.2 Key ideas6.2 Development of the model6.2.1 Calculation of p(T,x,t)6.2.2 Best schedule using Greedy algorithm6.2.3 Application to situation where X trips are given7 Part 3 Best schedule of trips with fixed dates, but unrestrained types and routes.7.1 Method7.1.1 Motivation and justification7.1.2 Key ideas7.2 Development of the model8 Testing of the model----Sensitivity analysis8.1Stability with varying trip types chosen in 68.2The sensitivity analysis of the assumption 4④8.3 The sensitivity analysis of the assumption 4⑥9 Evaluation of the model9.1 Strengths and weaknesses9.1.1 Strengths9.1.2 Weakness9.2 Further discussion10 Conclusions11 References12 Letter to the river managers3)论文中出现的好词好句(做好记录);用于问题的转化We regard the carrying capacity of the river as the maximum total number of trips available each year, hence turning the task of the river managers into looking for the best schedule itself.表明我们在文中所做的工作We have examined many policies for different river…..问题的分解We mainly divide the problem into three parts and come up with three different….对我们工作的要求:Given the above considerations, we want to find the optimal。
