定积分在经济问题中的应用[1]

合集下载

定积分的几个简单应用

定积分的几个简单应用一、定积分在经济生活中的应用在经济管理中，由边际函数求总函数，一般采用不定积分来解决，或者求一个变上限的定积分；如果求总函数在某个范围的改变量，则采用定积分来解决．例1 某商场某品牌衬衫的需求函数是q p 15.065-=，如果价格定在每件50元，试计算消费者剩余．解由p 50=，q p 15.065-=，得10000=q ，于是dq q )5015.065(100000--⎰10000023)1.015(q q -=50000=，所求消费者剩余为50000元．例2 已知某产品总产量的变化率为t t Q 1240)(+='（件／天），求从第5天到第10天产品的总产量．解所求的总产量为⎰⎰+='=105105)1240()(dt t dt t Q Q 1052)640(t t +=650=（件）．二、用定积分求极限例1 求极限 ∑=∞→n k n n k 123lim ．解 nn n n n n n n k n k 12111123+++=∑= )21(1nn n n n +++= ．上式是函数[]1,0)(在x x f =的特殊积分和．它是把[]1,0分成n 等分，i ξ取⎥⎦⎤⎢⎣⎡-n i n i ,1的右端点构成的积分和．因为函数[]1,0)(在x x f =可积，由定积分定义，有∑=∞→n k n n k 123lim ⎥⎦⎤⎢⎣⎡+++=∞→)21(1lim n n n n n n 3210==⎰dx x ．例2 求极限 2213lim k n n k n k n -∑=∞→．解 212213)(11n k nk n k n n k n k n k -⋅=-∑∑==．上式是函数[]1,01)(2在x x x f -=的特殊积分和．它是把区间[]1,0分成n 等分，i ξ取⎥⎦⎤⎢⎣⎡-n i n i ,1的右端点构成的积分和．因为函数21)(x x x f -=在[]1,0可积，由定积分定义，有2213lim k n n k n k n -∑=∞→31)1(31110232102=⎥⎦⎤⎢⎣⎡--=-=⎰x dx x x ．三、用定积分证明不等式定积分在不等式的证明中有着重要的应用．在不等式的证明中，可根据函数的特点，利用定积分的性质来证明．例1 设)(x f 是闭区间[]b a ,上的连续函数，且单调增加，求证：⎰⎰+≥b ab a dx x f b a dx x xf )(2)(．证明作辅助函数 dt t f x a dt t tf x xa x a ⎰⎰+-=)(2)()(ϕ，显然0)(=a ϕ，且)(2)(21)()(x f x a dt t f x xf x x a ⎰+--='ϕ )(2))((21)(2x f a a x f x f x ---=ξ [])()(2ξf x f a x --=，其中[]x a ,∈ξ．因为)(x f 在[]b a ,上单调增加，所以0)(≥'x ϕ，从而)(x ϕ在闭区间[]b a ,上单调增加，所以0)()(=≥a x ϕϕ，取b x =得⎰⎰+≥b a ba dx x fb a dx x xf )(2)(．定积分在许多领域中有着重要应用，它是解决一些几何学问题、物理学问题和经济学问题的重要工具．这一章主要介绍了定积分在不同学科中的应用问题．。

定积分在经济问题中的应用

而是在两者之问，即劳伦兹曲线是图中的凹曲线ＯＬＤ。
＝
・
一
丢。＝一ｌ一吉＝
＝３３３
易见劳伦兹曲线与完全平等线的偏离程度的大小（即图
中阴影面积），决定了该国国民收入分配不平等的程度。
为计算方便，取横轴ＯＨ为轴，纵轴ＯＭ为轴，再假定该国某一时期国民收入分配的劳伦兹曲线可近似表示为
根据不同的价格水平所提供的商品数量，一般假定价格上涨时。供应量将会增加。因此，把供给量看成价格的函数
Ｐ＝ｌＱ，Ｓ）供给曲线是单调递增的．－（需求曲线则反映了顾客的购买行为，通常假定价格上涨，购买的数量下降，即需
．称为生产者剩余（）由，图可以看出
库０．
．
于是
（ｏ・５一０２５一０２Ｑ）Ｏ４ｘ０
ＣＤ（ｄＳ＝Ｑ）Ｑ—Ｐ— Ｏ
收稿日期：２ｌｒｏ — ２Ｏ０－９３－
作者简介：王伟珠，女，黑龙江哈尔滨人，辽宁对外经贸学院讲师，研究方向为经济数学。
差为消费者省下来的钱，即消费者剩余。同理，对生产者来说，有时也有一些生产者愿意以比市场价格尸’ 低的价格出售他们的商品，由此他们所得到的好处
、
消费者剩余和生产者剩余
在市场经济中，生产并销售某曲线来描述。供给曲线描述的是生产者
得Ｏ‘ ，＝１．是＝３Ｐ’ 于５
＝
ｆ４１３２一９４孚（２－ｘ（号５，，５＝４９＝

定积分在医学和经济学中的应用

定积分在医学和经济学中的应用
定积分在医学和经济学中的应用
一、定积分在医学的应用
1、采用定积分法求出体积密度的温度指数
定积分法是一种用来衡量体积密度的温度指数的有效方法，它通过推算出物体某一温度下的体积密度，再用这个温度值求出体积密度的温度指数。

2、定积分法求解医学中人体的各种比热容和抵抗力
定积分法可以帮助医学研究人员求解出人体各种比热容和抵抗力，这些数据可以用于研究人体对环境变化的反应。

3、定积分用于细胞学研究
定积分法可以用于细胞学研究，其中，可以推算出细胞的朗道数量。

朗道数量是衡量细胞活动能力的重要标志，对于病理的预测和研究有重要意义。

二、定积分在经济学中的应用
1、获得投资回报率和投资风险的指标
定积分法可以用来衡量一项投资的回报率，以及投资风险的大小。

如果某个项目的回报率较高，可以判定这个投资项目较为稳健，而投资风险较低。

2、分析市场消费者群体行为模式
定积分法可以用来分析市场消费者群体的行为模式，可以推算出消费者群体的消费习惯，再根据消费习惯进行市场细分。

3、定积分法求解企业的长期成长趋势
定积分法可以用来求解企业的长期成长趋势，可以精确进行企业财务成绩的预测，从而为企业管理决策提供依据。

(完整版)定积分在经济中的应用

定积分在经济中的应用一、由经济函数的边际，求经济函数在区间上的增量根据边际成本，边际收入，边际利润以及产量x 的变动区间[,]a b 上的改变量（增量）就等于它们各自边际在区间[,]a b 上的定积分：()()()ba Rb R a R x dx '-=⎰ （1）()()()baC b C a C x dx '-=⎰ （2）()()()baL b L a L x dx '-=⎰ （3）例 1 已知某商品边际收入为0.0825x -+（万元/t ），边际成本为5（万元/t ），求产量x 从250t 增加到300t 时销售收入()R x ，总成本C ()x ，利润()I x 的改变量（增量）。

解首先求边际利润()()()0.082550.0820L x R x C x x x '''=-=-+-=-+所以根据式（1）、式（2）、式（3），依次求出：300250(300)(250)()R R R x dx '-=⎰300250(0.0825)x dx =-+⎰=150万元300300250250(300)(250)()C C C x dx dx '-==⎰⎰=250万元300300250250(300)(250)()(0.0820)L L L x dx x dx '-==-+⎰⎰=-100万元二、由经济函数的变化率，求经济函数在区间上的平均变化率设某经济函数的变化率为()f t ，则称2121()t t f t dtt t -⎰为该经济函数在时间间隔21[,]t t 内的平均变化率。

例2 某银行的利息连续计算，利息率是时间t （单位：年）的函数：()0.08r t =+求它在开始2年，即时间间隔[0，2]内的平均利息率。

解由于22()(0.08r t dt dt =+⎰⎰20.160.010.16=+=+所以开始2年的平均利息率为2()0.0820r t dtr ==+-⎰0.094≈例3 某公司运行t （年）所获利润为()L t （元）利润的年变化率为()310L t '=⨯/年）求利润从第4年初到第8年末，即时间间隔[3，8]内年平均变化率解由于3885852333()310210(1)3810L t dt t '=⨯=⨯⋅+=⨯⎰⎰所以从第4年初到第8年末，利润的年平均变化率为853()7.61083L t dt '=⨯-⎰（元/年）即在这5年内公司平均每年平均获利57.610⨯元。

(完整版)定积分在经济中的应用

定积分在经济中的应用一、由经济函数的边际，求经济函数在区间上的增量根据边际成本，边际收入，边际利润以及产量x 的变动区间[,]a b 上的改变量（增量）就等于它们各自边际在区间[,]a b 上的定积分：()()()ba Rb R a R x dx '-=⎰ （1） ()()()ba Cb C a C x dx '-=⎰ （2） ()()()ba Lb L a L x dx '-=⎰ （3）例1 已知某商品边际收入为0.0825x -+（万元/t ），边际成本为5（万元/t ），求产量x 从250t 增加到300t 时销售收入()R x ，总成本C ()x ，利润()I x 的改变量（增量）。

解首先求边际利润()()()0.082550.0820L x R x C x x x '''=-=-+-=-+所以根据式（1）、式（2）、式（3），依次求出：300250(300)(250)()R R R x dx '-=⎰300250(0.0825)x dx =-+⎰=150万元 300300250250(300)(250)()C C C x dx dx '-==⎰⎰=250万元 300300250250(300)(250)()(0.0820)L L L x dx x dx '-==-+⎰⎰=-100万元二、由经济函数的变化率，求经济函数在区间上的平均变化率设某经济函数的变化率为()f t ，则称2121()t t f t dt t t -⎰ 为该经济函数在时间间隔21[,]t t 内的平均变化率。

例2 某银行的利息连续计算，利息率是时间t （单位：年）的函数：()0.08r t =+求它在开始2年，即时间间隔[0，2]内的平均利息率。

解由于2200()(0.08r t dt dt =+⎰⎰20.160.010.16=+=+所以开始2年的平均利息率为20()0.0820r t dtr ==+-⎰0.094≈例3 某公司运行t （年）所获利润为()L t （元）利润的年变化率为()310L t '=⨯/年）求利润从第4年初到第8年末，即时间间隔[3，8]内年平均变化率解由于3885852333()310210(1)3810L t dt t '=⨯=⨯⋅+=⨯⎰⎰所以从第4年初到第8年末，利润的年平均变化率为853()7.61083L t dt'=⨯-⎰（元/年）即在这5年内公司平均每年平均获利57.610⨯元。

关于定积分在经济学中积累问题的应用

关于定积分在经济学中积累问题的应用作者：陈昆刘亚婷来源：《科教导刊》2013年第31期摘要定积分在经济学中有着广泛的应用，本文通过几个例子说明定积分在经济学的简单应用。

关键词定积分经济学积累问题中图分类号：F224 文献标识码：AAbout the Application of Definite IntegralAccumulated Problems in the EconomicsCHEN Kun， LIU Yating（Department of Mathematics， Xingyi Normal University for Nationalities， Xingyi，Guizhou 562400）Abstract Definite integral has been widely applied in economics， the paper through a few examples to talk about definite integrals' simple applications in economics.Key words definite integral； economics； long-standing and deep-seated prolems定积分是微积分学的重要组成部分，同时在经济学中有很多直接的应用，本文将运用定积分知识分析和解决某些经济学中的积累问题。

1 利用定积分求消费者剩余和生产者剩余经济学中定义消费者剩余是指消费者消费某种商品所获得的净收益，消费者在购买商品是有愿意付出的货币总额，还有一实际付出的货币总额，在一般情况下，消费者愿意付出的货币总额大于实际付出的货币总额，其间形成一个差额，这就是消费者剩余，用定积分的形式表示就是（）其中（）表示消费者为每一个单元商品所愿支付的最高边际价格，当价格为时，消费者共购买了单元的商品。

同样在经济学中定义企业从生产经营中得到的净收益为生产剩余，用定积分的形式表示就是：（）其中（）表示厂家的边际成本函数，当价格为时，消费者共购买了单元的商品。

试论定积分在物理及其他领域的应用

试论定积分在物理及其他领域的应用1. 引言1.1 定积分的基本概念定积分是微积分的一个重要概念，它在数学中有着广泛的应用。

定积分的基本概念可以简单地理解为一个函数在一定区间内的累积效果。

在几何学中，定积分可以用来计算曲线下面积，图形的面积和体积等问题。

在数学上，定积分可以看作是不定积分的反运算，通过定积分我们可以求解函数的定积分值。

在实际应用中，定积分被广泛运用于物理、工程、经济等领域。

它的应用使得复杂问题的计算变得简单清晰。

通过定积分，我们可以计算出物体的质量、力的大小、功的大小等物理量。

在力学中，定积分可以用来描述物体的运动规律，计算出物体的位置、速度和加速度等。

在电磁学中，定积分常常用来计算电场强度、磁场强度等问题。

在热力学中，定积分可以用来计算热量、熵等热力学量。

在工程学中，定积分可以帮助工程师计算出工程设计中的各种参数。

在经济学中，定积分在求解供求关系、成本、收益等问题上起着重要作用。

定积分在各个领域中都有着重要的应用价值。

它的基本概念对于理解定积分的应用具有重要意义。

通过深入研究定积分的基本概念，可以更好地理解其在不同领域中的具体应用。

1.2 定积分在物理领域的重要性定积分在物理领域的重要性体现在多个方面，首先在力学中，定积分可以用来描述物体的质量、速度、加速度、力和能量等物理量随时间的变化，从而帮助解决力学中的各种问题。

在电磁学中，定积分可以用来描述电流、电荷、电场、磁场等物理量在空间中的分布和变化规律，从而帮助解决电磁学中的各种问题。

在热力学中，定积分可以用来描述热量、温度、熵等热力学量在空间中的分布和变化规律，从而帮助解决热力学中的各种问题。

在工程学和经济学中，定积分也有着重要的应用，可以用来描述工程和经济系统中的各种物理量的变化规律，从而帮助解决工程和经济学中的各种问题。

定积分在物理领域中的重要性不可忽视，它为我们理解和应用物理定律提供了重要的数学工具和方法。

2. 正文2.1 定积分在力学中的应用在力学中，定积分是一个非常重要的数学工具，它可以用来描述物体在运动过程中的各种性质和运动规律。

定积分的应用

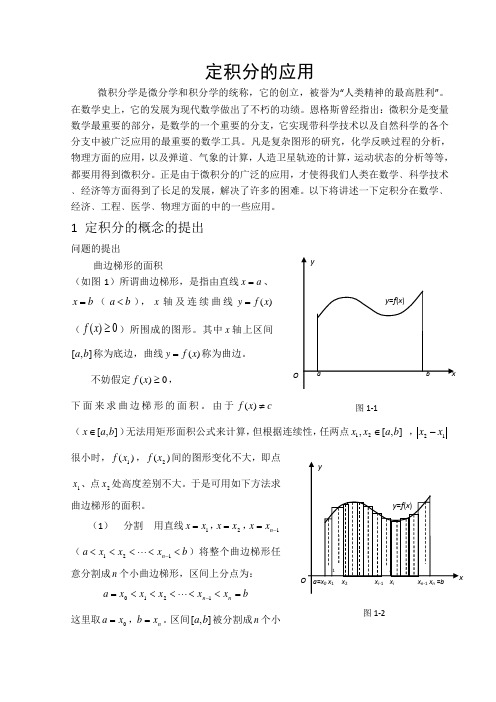
图1-1图1-2a =x x x x x x x i1定积分的应用微积分学是微分学和积分学的统称，它的创立，被誉为“人类精神的最高胜利”。

在数学史上，它的发展为现代数学做出了不朽的功绩。

恩格斯曾经指出：微积分是变量数学最重要的部分，是数学的一个重要的分支，它实现带科学技术以及自然科学的各个分支中被广泛应用的最重要的数学工具。

凡是复杂图形的研究，化学反映过程的分析，物理方面的应用，以及弹道﹑气象的计算，人造卫星轨迹的计算，运动状态的分析等等，都要用得到微积分。

正是由于微积分的广泛的应用，才使得我们人类在数学﹑科学技术﹑经济等方面得到了长足的发展，解决了许多的困难。

以下将讲述一下定积分在数学﹑经济﹑工程﹑医学﹑物理方面的中的一些应用。

1 定积分的概念的提出问题的提出曲边梯形的面积（如图1）所谓曲边梯形，是指由直线a x =、b x =（b a <），x 轴及连续曲线)(x f y =（0)(≥x f ）所围成的图形。

其中x 轴上区间],[b a 称为底边，曲线)(x f y =称为曲边。

不妨假定0)(≥x f ，下面来求曲边梯形的面积。

由于cx f ≠)(（],[b a x ∈）无法用矩形面积公式来计算，但根据连续性，任两点],[,21b a x x ∈ ，12x x -很小时，)(1x f ，)(2x f 间的图形变化不大，即点1x 、点2x 处高度差别不大。

于是可用如下方法求曲边梯形的面积。

（1）分割用直线1x x =，2x x =，1-=n x x （b x x x a n <<<<<-121 ）将整个曲边梯形任意分割成n 个小曲边梯形，区间上分点为：b x x x x x a n n =<<<<<=-1210这里取0x a =，n x b =。

区间],[b a 被分割成n 个小区间],[1i i x x -，用i x ∆表示小区间],[1i i x x -的长度，i S ∆表示第i 块曲边梯形的面积，),,2,1(n i =，整个曲边梯形的面积S 等于n 个小曲边梯形的面积之和，即∑=∆=ni i S S 1（2）近似代替: 对每个小曲边梯形，它的高仍是变化的，但区间长度i x ∆很小时，每个小曲边梯形各点处的高度变化不大，所以用小矩形面积近似代替小曲边梯形的面积，就是，在第i 个小区间],[1i i x x -上任取一点i ξ，用以],[1i i x x -为底，)(i f ξ为高的小矩形面积i i x f ∆)(ξ，近似代替这个小曲边梯形的面积（图1-1），即i i i x f S ∆≈∆)(ξ.（3）求和整个曲边梯形面积的近似值为 n 个小矩形面积之和，即n S S S S ∆++∆+∆= 21=∆++∆+∆≈n n x f x f x f )()()(2211ξξξ ini ix f ∆∑=)(1ξ上式由于分割不同，i ξ选取不同是不一样的，即近似值与分割及i ξ选取有关（图1－2）。

定积分

定积分在经济学中的应用The Application of Definite Integral in Economics摘要随着社会主义市场经济的迅速发展，经济学与数学这两个学科的联系已越来越紧密，数学知识广泛地应用于经济学中。

而数学中的定积分又是微积分中重要的组成部分，在经济学中有着广泛的应用，而且内容十分丰富。

因此，研究运用定积分来解决经济方面的问题就显得十分重要。

这篇文章借鉴其它学者研究成果的方法。

首先回顾了一些关于定积分的性质、定理。

然后列举出定积分在经济学中的应用的一些具体事例。

最后归纳整理，从两个大方面进行研究：定积分在生产上的应用；定积分在投资、决策上的应用。

并获得相应结果。

这篇文章从不同角度研究了定积分在经济学的应用，对其他作者有一定的借鉴意义。

关键词：定积分；经济学；边际函数；投资；决策AbstractWith the rapid development of the socialist market economy, economics and mathematics has become more and more closely linked together. Mathematics knowledge is widely used in economics. And the definite integral in mathematics is an important part of calculus, which is widely used in economics and is very rich in content. Therefore, it is important to study the economical problems by using definite integrals.This article draws on the methods of other scholars' research. Firstly, we review some properties and theorems of definite integral. Secondly, some examples are presented about the application of definite integral in economics. Finally, the paper summarizes the two major aspects: the application of definite integral in production and the application of definite integral in investment and decision making. And these get the results. This paper studies the application of definite integral in economics from different angles, and it has some significance for other authors.Key Words: Definite integral; Economics; Marginal functions; Investment; Decision making目录1.引言 (1)2.预备知识 (2)3.定积分在经济学中的应用 (2)3.1定积分在生产方面的应用 (2)3.1.1定积分在生产中求总成本、总收益方面的应用 (2)3.1.2定积分在最优化生产方面的应用 (4)3.1.3定积分在生产消费方面的应用 (4)3.1.4定积分在生产中预测所耗费劳动时数方面的应用 (6)3.2定积分在投资、决策方面的应用 (7)3.2.1定积分在投资方面的应用 (7)3.2.2定积分在广告策划方面的应用 (9)3.2.3定积分在企业决策方面的应用 (9)结语 (10)参考文献 (12)致谢 (13)1.引言随着社会主义市场经济的迅速发展，经济学与数学这两个学科的联系已越来越紧密，数学知识广泛地应用于经济学中。

简述不定积分和定积分在经济生活中的应用

简述不定积分和定积分在经济生活中的应用经济学中不定积分和定积分是一种重要的计算工具，具有广泛的实际应用。

不定积分和定积分在经济生活中有着重要的意义，它可以帮助经济学家和经济管理者更好地了解和研究经济问题，有助于更好地推进经济发展和管理经济。

本文将简要介绍不定积分和定积分在经济生活中的应用。

不定积分在经济生活中的应用不定积分的应用在经济学中很广泛，可以用来解决许多经济中的问题。

首先，它可以用来计算价格。

不定积分可以用来计算出给定价格下消费者需求量和生产商供给量之间的关系，进而了解消费者和生产商在某一价格水平下多大程度上能够受到价格影响。

其次，不定积分可以用来计算投资成本。

不定积分可以用来计算投资成本，以判断投资成本究竟有多大，是否值得投入。

投资者也可以运用不定积分法来分析所考虑的投资项目的投资回报率，以更快地、更高效地学习投资过程的风险和收益。

定积分在经济生活中的应用定积分也在经济生活中有着重要的应用。

首先，它可以用来计算消费函数。

函数可以用来展示消费者在不同收入水平下的消费水平，这有助于经济学家和政策制定者更好地理解消费者的消费行为，推动经济发展。

其次，定积分也可以用来计算税收函数。

税收函数可以用来计算税收对投资的影响，以判断出税收的调节幅度，有助于政府制定出合理的税收政策，推动经济发展。

此外，定积分还可以用来计算产出函数。

产出函数可以用来计算不同生产要素投入水平下生产总量的大小，有助于计算出不同生产要素对总产出的贡献度，以及它们投入和产出间的关系。

结论从上述内容可以看出，不定积分和定积分在经济生活中有着重要的应用。

不定积分可以用来计算价格和投资成本，而定积分则可以用来计算消费函数、税收函数和产出函数。

因此，不定积分和定积分都是经济学上重要的工具，它们对经济管理者来说是不可或缺的。

它们的正确运用可以帮助经济学家和经济管理者更深入地理解和研究经济状况，有助于推动经济发展。

6.6 定积分在经济上的应用

B = ∫ f (t )er (T −t ) dt
0
T
若收入流(或支出流) f (t ) = a(常数) ，则称此为均匀收入流(或支出流)．
例题四
求收入流为 1000(元 / 年) 在 20 年时间内的现值与将来值，这里以 10%的年利率连续复利方式赢取利息．
解
据公式有现值
P = ∫ 1000 ⋅ e
dF (t ) = f (t )) ，则从 a 时期到 b dt
时期净投资与资本存量之间的关系可用定积分表示为
F (b) − F (a) = ∫ f (t )dt
a
b
假设某个体老板在时期 t = 0 时拥有资本存量
例题六
解
500 000 元，除了资本折旧之外，计划在未来 10 年以
f (t ) = 600t 2 的速度进行新资本投资，计算从现
0 20 −0.1t
1000 −0.1t 20 dt = − e 0 0.1
= 10000(1 − e−2 ) ≈ 8646.65(元)
将来值
P = ∫ 1000 ⋅ e
0
20
0.1(20 −t )
1000 0.1(20−t ) 20 dt = − e 0 0.1
= 10000(e 2 − 1) ≈ 63890.56(元)
固定成本是 2000，试确定总成本函数．
总成本函数
C (Q) = ∫ (3Q 2 − 118Q + 1315)dQ + C0
0
Q
= Q 3 − 59Q 2 + 1315Q + 2000
例题二
解
．
已知某产品的边际成本 C '(Q) = 1 (万元/百台)，边际收益 R '(Q) = 5 − Q (万元/百台)，其中 Q 为产量，固定成本 1 万元，问（1）求收益函数和成本函数；（2）产量等于多少时利润最大?

定积分及其应用

六、参考概率书籍，说明分布函数怎么计算参考概率书籍，（p231，13），）
分布函数取值充满整个实数轴的随机变量，就不可能用分轴的随机变量，布列来表述它取值的概率规律，布列来表述它取值的概率规律，一般可统一用分布函数来表述。一般可统一用分布函数来表述。分布函数是定义在实数轴上而取值为大于等于0且小于等于且小于等于1 取值为大于等于且小于等于的实数，对于实轴上任何一点x，的实数，对于实轴上任何一点，随机变量X的分布函数的分布函数F（）随机变量的分布函数（x）点的值为随机变量X小于在x点的值为随机变量小于点的值为随机变量小于x 这个事件发生的概率。这个事件发生的概率。分布函数是单调非降的右连续函数，数是单调非降的右连续函数，在负无穷大时为0，在负无穷大时为，在正无穷大时为1。时为。
三、不定积分与定积分有什么联系和区别
不定积分原函数的集合；集合；用换元法计算时在的计算回；回；原函数的
在区间[a,b]上连续 ⑴若f(x)在区间在区间上连续则∫ (a,x)f(t)dt=G(x)是f(x)在是在区间上的一个原函数，区间上的一个原函数，即 G’(X)=f(x) ，即φ’(x)= ∫ (a,x)f(t)dt= f(x)【第一基本【定是连续函数，若f(x)是连续函数，F(x) 是连续函数的一个原函数，是f(x)的一个原函数，则∫ 的一个原函数 (a,b)f(x)dx=F(b) F(a) 【第基本定
需求函数：在某一特定时期内， ①需求函数：在某一特定时期内，市场上某种商品的各种可能的购买量与决需求量Q是价格是价格p的函定这些购买量的因素的关系 Q(p)= ∫(0,p)Q(t)dt+Q0 需求量是价格的函价格为0时需求量最大时需求量最大。数，价格为时需求量最大。 ②总成本函数：产品成本是以货币形式实现的企业生产销售产品全部费用支总成本函数：固定成本+变动成本变动成本=总成本出，固定成本变动成本总成本 C(x)= ∫(0,x)C′(t)dt+C0 C0=C 价格× ③总收入函数：总收入=价格×销售量总收入函数：总收入价格 R(x)= ∫(0,x)R′(t)dt （∫(0,x)L′(t)dt产量产量利润=收入 ④利润函数:利润收入－成本 L(x)= ∫(0,x)L′(t)dt－C0 利润函数利润收入－－时的毛利，为x时的毛利，毛利减去固定成本为纯利）时的毛利毛利减去固定成本为纯利）

定积分在经济问题中的应用

（）＝０一３
（万元／。台）
（）固定成本为Ｃ（）＝１１若００万元，总成本函求数、收入函数和总利润函数；总导数就是边际函数（如边际成本、际收益、际利润边边（）２当产量从４０台增加到８Ｏ台时，其总成本求等）当已知初始条件时，，即可用定积分求出总量函与总收人的增量。数 … 。在经济活动中经常遇到的求总量问题，以下有
品无积压时（：＝，：）则 ①所获总利润函数Ｌ）＝Ｒ（（）一Ｃ）（
＝
．
（）＝Ｒ（）一Ｃ（）＝（０一）一［０＋３ｘ～１１
ｆ［）一Ｃ（］ｘ—ｃｏ；ｏＲ（）ｄ（）
＝
１０（５１＋√ｌ）ｎ＋＋］
（）２当产量从４Ｏ台增加到８０台时，总成本的增量为
边际收入为
ｃ（：（，）
＋１：［５１（）１０＋
作者简介：许雁琴（９３）女，１６一，河南新乡人，副教授，主要从事应用数学研究。
２９
收稿日期：０００－９２１－Ｏ６
河南机电高等专科学校学报
２１００年５期
＾ｌ）］１３９（／＋＋４．６万元）／
现在起存人银行，则年末的本利之和为Ａ元）那ｅ（，
年当产量从４０台增加到８０台时，收入的增量为幺弥为Ａ元资金在ｔ末的将来值。总如果ｔ年末希望得到Ａ元资金，按年利率ｒ且作．Ｒ（）＝∞３一ｄ（／） ∞ 连续复利计算，么现在需要投入资金Ａ —ｒ元，ｆｄ．（｛）３一８加ｘ／ｆ００７８Ｏｘ０７Ｉ８０那ｅｔ称

不定积分和定积分在经济生活中的应用

不定积分和定积分在经济生活中的应用
不定积分和定积分是微积分中的重要概念，它们在经济生活中有广泛的应用。

计算收益和成本：不定积分可以用于计算企业的收益和成本。

对于一个企业来说，经营过程中会有许多收入和支出，这些数据可以通过建立合适的数学模型进行计算。

不定积分可以帮助企业对收入和支出进行积分计算，以便更好地掌握经营状况。

评估投资价值：定积分可以用于评估不同投资方案的价值。

在投资决策中，需要综合考虑各种因素，如收益率、风险等。

通过建立合适的数学模型，可以用定积分计算不同投资方案的总收益或总成本，从而比较它们的优劣，作出合理的决策。

估算市场需求：定积分可以用于估算市场的需求量。

对于某种商品或服务，需求量通常随着价格的变化而变化。

通过建立合适的数学模型，可以用定积分计算不同价格下的市场需求量，以便制定合适的价格策略。

风险分析和管理：定积分可以用于分析和管理风险。

在金融领域中，不同的金融工具会涉及不同的风险，如市场风险、信用风险等。

通过建立合适的数学模型，可以用定积分计算不同风险下的概率和损失，从而更好地进行风险管理和控制。

综上所述，不定积分和定积分在经济生活中有广泛的应用，可以帮助企业和个人更好地理解和应对经济变化，制定合理的决策和策略，实现自身和社会的利益最大化。

简述不定积分和定积分在经济生活中的应用

简述不定积分和定积分在经济生活中的应用不定积分和定积分是数学中的重要概念，也是经济生活中经常用到的概念。

它们都具有重要的经济价值，在实际应用中发挥着重要作用，有助于社会经济发展。

本文以“简述不定积分和定积分在经济生活中的应用”为标题，结合相关知识结构和实例，就它们在社会经济中的应用进行分析和论述。

首先，介绍一下不定积分。

不定积分是数学中比较复杂的概念，也是一种无穷小的运算，它会产生连续的解决方案。

根据微分积分理论，不定积分可以替换某些一些固定积分，它可以解决一些在固定积分中解决不了的问题。

不定积分可以在社会经济领域中用来分析一些金融机构或市场以及其他经济行为，例如分析股票投资的回报报酬率、股息收入比例等问题。

例如，一家公司的股东希望了解股票投资的回报率，这时就可以使用不定积分技术进行分析，从而使该公司的股东更好地了解投资回报率的情况。

其次，介绍一下定积分。

定积分是数学中关于求定积分的一种方法，是一种端到端的数学计算，可以用来计算一个函数的积分值。

定积分可以在经济学和社会经济学中用于各种应用，例如经济分析、投资评价、价格分析等。

例如，当一家投资公司考虑一项投资时，可以使用定积分技术来计算这项投资所带来的预期回报，以及投资过程中可能存在的风险，从而辅助公司决策。

它还可用于金融市场的定价分析，例如期权、期货等金融工具的定价，以及股票投资的定价分析。

最后，结合具体的实例来总结不定积分和定积分在经济生活中的应用。

比如，在社会经济方面，可以使用不定积分和定积分分析投资回报率、股票投资价格或股息收入比例等问题，也可以使用定积分方法计算投资所带来的预期回报和投资过程中的风险等问题。

此外，不定积分和定积分的技术也可以用于市场分析、价格分析等，可以增强市场参与者对市场开发有效的投资策略和操作策略，促进市场的发展。

综上所述，不定积分和定积分有重要的应用价值，在经济生活中发挥着重要作用，有助于社会经济发展。

经济参与者应当仔细研究不定积分和定积分的原理，以有效应用这些技术，促进社会经济的发展。

高数三：函数平均值和定积分的经济学应用

三、平均值在实际问题中，常常用一组数据的算术平均值来描述这组数据的概貌。

例如：对某一零件的长度进行n 次测量，每次测得的值为。

通常用算术平均值作为这个零件长度的近似值。

然而，有时还需要计算一个连续函数在区间上的一切值的平均值。

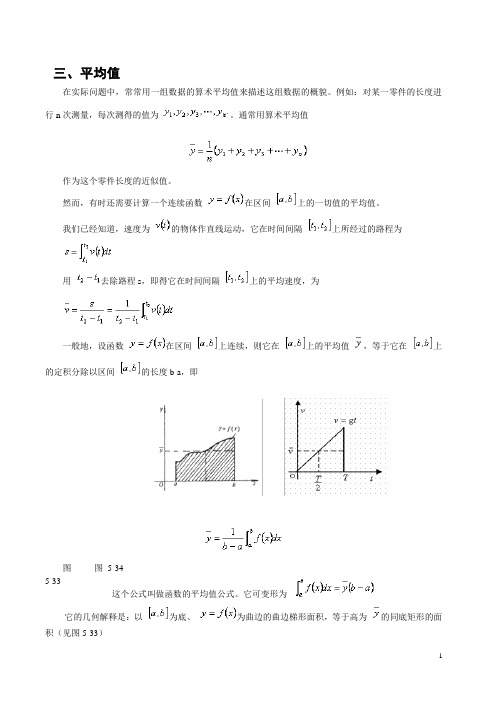
我们已经知道，速度为的物体作直线运动，它在时间间隔上所经过的路程为用去除路程s ，即得它在时间间隔上的平均速度，为一般地，设函数在区间上连续，则它在上的平均值，等于它在上的定积分除以区间的长度b-a ，即图 5-34这个公式叫做函数的平均值公式。

它可变形为它的几何解释是：以为底、为曲边的曲边梯形面积，等于高为的同底矩形的面积（见图5-33）图 5-33例6 求从O到T这段时间内自由落体的平均速度。

解：自由速度为。

所以要计算的平均速度（见图5-34）为例7 计算纯电阻电路中正弦交流电在一个周期内功率的平均值。

解设电阻为R，那么电路中R两端的电压为而功率因为交流电的周期为，所以在一个周期上，P的平均值为就是说，纯电阻电路中正弦交流电的平均功率等于电流和电压的峰值乘积的一半。

通常交流电器上标明的功率是平均功率。

四、定积分在经济上的应用举例定积分在经济活动中应用很广泛。

如，已知某经济函数的边际函数的条件下，求原经济函数的改变量时，就需用定积分来解决。

例8 设某工厂生产某产品，边际产量为时间t的函数，已知求从t=1到t=3这两个小时的总产量。

解：因为总产量是它的边际产量的原函数。

所以，从t=1到t=3这两小时的总产量是（千件）例9 已知生产某产品x件的边际收入是( 元/件)求生产此产品1000件时的总收入，平均收入，及生产1000件到2000件时所增加的收入和平均收入。

解：设总收入函数为，总产量为1000件时的总收入R（1000），为平均收入产量从1000件到2000件所增加的收入为，其平均收入为例10 设某产品的总成本C（单位：万元）的边际成本是产量x（单位：百台）的函数，;总收入（单位：万元）的边际收入是产量x的函数，求：1）产量由1百台增加到5百台总成本，总收入各增加多少？2）已知固定成本C（0）为1万元，分别求出总成本、总收入，总利润与产量的关系式。

计算机编程求解定积分及其在经济中的应用

关键词：计算机程序；定积分；经济问题中图分类号：Ｔ３１Ｐ１文献标志码：Ａ
０引言
随着市场经济的不断发展，利用计算机和数学知识解决经济问题显得越来越重要，而定积分的应用范围很广，也是解决很多问题的有力工具，如几何、物理、经济等领域都有
对于任意函数，均可用莱布尼兹公式求其定积分。由于
计算机对实数的表示精度有限，无法表示无穷大和无穷小，所以对于所求图形不能分成无限个小梯形来精确的计算面
点。在此点供需达到均衡。如果消费者以比均衡价格购得某
ｆ
ｅ一ｌ
，找其原函数却十分困可近似把该面积分成若难。
的
ｐ因消者余彳（Ｑ如生者＊，此费剩为厂）— 果产ｏ－ＰＱＱｄ
以均衡价格Ｐ出售某商品，而没有他们本来计划的以较低
干个小梯形。如果把占到０区间分成长度为ｈ：０的
总额，故生产者剩余为尸Ｑ・・
一
彳ｌ。ｇＱ＿）（
一
个梯形的上底和下底分别为
和 ±
ｅ一１ｅ
，故其面
一１
例１设产的求数Ｐ３— ．Ｑ。果：某品需函是＝００４如２
价格固定在每件１０元，试计算消费者剩余。首先求出对应
ＭｉｏｏｕｅＡｐｌａｉｎｏ．８Ｎ．，０２ｃｃｍｐｔｒｐｉｔｓ１２，ｏ１２１ｒｃｏＶ

经济数学基础——定积分在经济学中的应用

河北省高等教育自学考试定积分在经济学中的应用——定积分在经济学中的应用地市：沧州市专业：投资管理姓名：郭梦帆准考证号：1 身份证号：联系电话：内容摘要经济数学基础本着基础教学为专业服务及注重应用、培养能力的原则，根据微积分、线性代数、概率统计的基本知识逻辑，以知识介绍为重点，详略得当；叙述上力求简明、通俗，又不失科学性。

关键词：定积分微分经济学边际函数投资经济数学基础知识点1.一元函数极值设函数f（x）在X0的一个邻域内有定义，若对于该邻域内异于X0的X恒有:f(x)<f(x0)，则称f(X0)为函数的极大值，称X0为函数的极大值点.f(X)>f(X0)，则f(X0)称为函数的极小值，称X0为极小值点．函数的极大值、极小值统称为函数的极值．极大值点、极小值点统称为函数的极值点。

极值反映函数的局部性态，是一个局部概念．极大值不一定大于极小值，极大（小）值不一定是区间上的最大（小）值，但就极值点附近的范围来说极大（小）值就是最大（小）值；区间上的极值点可能有若干个。

2.二元函数极值设函数Z=f(x, y)在点(x0,y0)的邻域内有定义，对于该邻域内异于(x0,y0)的点，如果都有f(x, y)<f(x0,y0)，则称f(x0,y0)为函数Z=f（x, y）的极大值；如果都有f(x, y)>f(x0,y0)，则称f(x, y)为函数Z=f(x, y)的极小值；极大值和极小值统称为二元函数Z=(x, y)的极值；使二元函数Z=（x, y）取得极大值的点或者极小值的点f(x0,y0)，称为极大值点或者极小值点；极大值点和极小值点统称为极值点．求多元函数的极值，一般可以利用偏导数来解决．及一元函数类似，可以利用函数的极大值、极小值求解函数的最大值、最小值，但是由于自变量个数的增加，应特别注意概念中的一些变化和计算．对于二元以上的函数极值问题可类似的加以解决，如可以将二元函数极值问题的理论推广到多元函数的情形，以及利用泰勒公式推导出判断多元函数极值存在的充分条件、极值不存在的必要条件等。

定积分的求解方法及其应用

定积分的求解方法及其应用摘要：在数学分析这门课程里,定积分是最普遍而又重要的内容之一,同时也是数学研究中的重要工具,随着数学在生活中的广泛应用,定积分的相关解法和应用所蕴藏的巨大潜力越来越引起人们的关注.本论文从定积分的基本理论出发,系统阐述了牛顿莱布尼茨公式、换元法、分部积分法、凑微分法等几种常见的求解方法,并列举了相关的例子,更直观的了解求解定积分的方法的精髓.另外本文又介绍了定积分在数学、物理学和经济学当中的应用,实现了定积分在实际生活中的应用.通过这一系列的总结,可以进一步提升对定积分的认识,为以后的学习奠定了基础.关键词：定积分；求解方法；应用一、定积分的求解方法1.1 定积分概念定义1 不妨设在闭区间[m ,n ]中，不包含两个端点，共有1-k 个点,按照大小分别为m =0x <1x <2x <…<1-k x <k x =n ,这些点将闭区间[m ,n ]分割为大小不一的子区间，共有k 个，用i ∆表示这些子区间，即i ∆=[1-i x ,i x ],i =1,2, …,k 。

可以将k x x x ......,10点或[]n i xi x i i ......12,,1==∆-子区间视为分割了闭区间[m ,n ]，令集合=A {0x ,1x ,…,k x }或{1∆,2∆,…,k ∆}.定义2 假设函数g 的定义域为 [m ,n ]。

将区间[m ,n ]分割为k 个，得分割区间的集合=A {1∆,2∆,…,k ∆}，在区间i ∆上随意取点i ψ，即i ψ∈i ∆,i =1,2, …,k ，将该点函数值与自变量之差做乘积，累次相加得()iki ix g ∆∑=1ψ，该式是函数g 在定义域[m ,n ]上的积分和.定义3 假设函数g 的定义域为 [m ,n ]，S 是给定的实数。

假如总能找到某个的正数θ，以及任何正数σ，在定义域 [m ,n ]进行任意大小的分割A ，并且在分割出来的区间中随意选择一个点组成集合{i φ}，当A <θ时，存在σφ<-∆∑=S xg ni ii1)(，则函数g在定义域[m ,n ]上可积，即⎰=nmdx x g S )(。

定积分经济学应用

定积分经济学应用
定积分是微积分的一个重要分支，它在经济学中有广泛的应用。

下面将从不同的角度来阐述定积分在经济学中的应用。

一、利润和成本的计算
在商业经济学中，利润和成本是企业最为关注的指标。

通过定积分，可以精确地计算企业的利润和成本。

例如，利润可以用销售额减去成本来计算，而成本中的各项费用可以通过定积分来计算。

这样，企业就可以更加准确地了解自己的利润和成本情况，从而做出更好的经营决策。

二、消费者剩余的测算
在市场经济中，商品的价格由供需关系决定。

为了衡量市场价格的合理性，经济学家引入了消费者剩余这一概念。

消费者剩余是指消费者愿意为某种商品支付的最高价格与实际支付的价格之差。

通过定积分的计算，可以精确地测算消费者剩余的大小，进而了解市场经济的运行情况，为政策制定和市场规划提供参考。

三、市场需求的计算
市场需求是指所有购买该商品的消费者的数量总和。

定积分常常用于计算市场需求，这能够帮助企业预测未来市场的走势以及生产规模。

除此之外，市场需求的计算还可以帮助政府了解市场需求量的大小，从而决定政策的制定方向。

四、投资决策的分析
在投资决策中，经济学家需要对不同投资方案的收益率进行计算。

通过定积分，可以计算出不同时期内各种投资方案的收益率，并选择其中最优的投资方案。

这样，企业就可以获得更大的收益。

总而言之，定积分在经济学中有着广泛的应用。

其中，利润和成本的计算、消费者剩余的测算、市场需求的计算以及投资决策的分析都是常见的应用。

这些应用帮助企业和政府更好地了解市场经济的运行情况，从而做出更加合理的决策。