东北大学软件学院数值分析程序实践报告

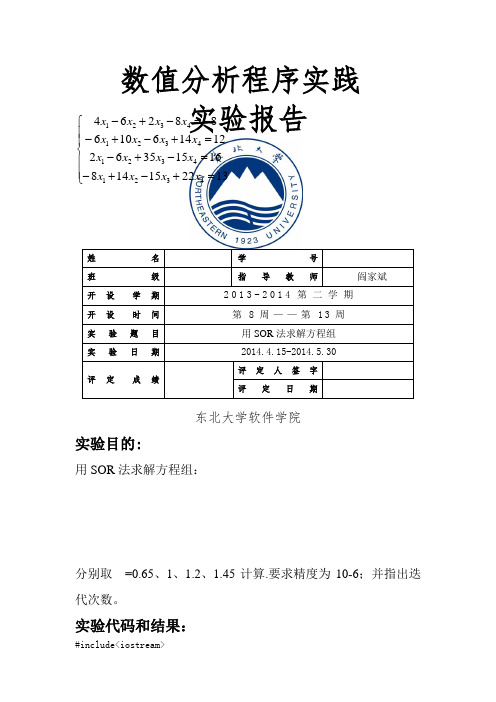
数值分析程序实践 实验报告
东北大学软件学院
实验目的:
用SOR 法求解方程组：
=0.65、1、1.2、1.45计算.要求精度为10-6；并指出迭代次数。

实验代码和结果：
#include<iostream>
⎪⎪⎩⎪⎪⎨⎧=+-+-=-+-=+-+--=-+-1322151481615356212146106882644321432143214321x x x x x x x x x x x x x x x x
#include<iomanip>
#include<cmath> // fabs();
using namespace std;
void SolveEquation(const int &dim)
{
double *Arr = new double[dim*dim]; //方程矩阵
double *B = new double[dim]; //方程右端系数
double *X = new double[dim]; //初始解
double *dX = new double[dim];
double e; //解的精度
double w; //w==1时，为GS迭代
double S, S1;
const int N = 5000; //最大迭代次数,防止死机
int n=0;
bool hasSolved = false;
cout << endl << "初始化方程组左端系数矩阵!" << endl;
for (int i=0; i<dim; i++)
{
for (int j=0; j<dim; j++){
cout << "Arr[" << i << "][" << j << "]: ";
cin >> Arr[i*dim+j];
}
}
cout << "初始化方程组右端系数矩阵!" << endl;
for (i=0; i<dim; i++)
{
cout << "B[" << i << "]: ";
cin >> B[i];
}
system("cls");
cout << "方程组如下: " << endl << endl;
for (i=0; i<dim; i++)
{
for (int j=0; j<dim; j++)
{
cout << setw(8) << Arr[i*dim+j] << " X" << j+1;
if (j < dim-1) cout << " + ";
else if (j == dim-1) cout << " = ";
}
cout << setw(8) << B[i] << endl;
}
cout << endl << "设置解的精度要求:(比如1e-6)" << endl; cin >> e;
cout << endl;
cout << "输入初始向量!" << endl;
for (i=0; i<dim; i++){
cout << "X[" << i+1 << "]: ";
cin >> X[i];
}
cout << endl << "设置参数ω ( 0<ω<2 )!" << endl;
cin >> w;
for (int k=0; k<N; k++) //3-8
{
S = 0.0;
for (i=0; i<dim; i++) //5-7
{
double sum = 0.0;
for (int j=0; j<dim; j++)
{
sum += Arr[i*dim+j]*X[j];
}
if (fabs(Arr[i*dim+i]) < 1e-10)
{
cout << "被零除!" << endl << Arr[i*dim+i] << endl; exit(0);
}
dX[i] = w * (B[i] - sum) / Arr[i*dim+i];
S1 = dX[i];
if (fabs(S1) > fabs(S))
{//fabs()取绝对值函数
S = S1;
}
X[i] = X[i] + S1;
}
n++;
if (fabs(S) <= e)
{
cout<<"迭代次数为："<<endl;
cout<<n<<endl;
hasSolved = true;
//system("cls");
cout << "线性方程组的解为：" << endl;
for (int t=0; t<dim; t++)
{
cout << "X" << t+1 << "=" << X[t] << "\t";
}
cout << endl;
break;
}
}
if (!hasSolved)
{
cout << "初始向量或ω不合理, 请重新设置!" << endl; }
delete[] Arr;
delete[] B;
delete[] X;
delete[] dX;
}
void main()
{
int dim;
cout << "输入线性方程组未知数个数: ";
cin >> dim;
SolveEquation(dim);
}
w=0.65
W=1
W=1.2
W=1.45。