中考专题:垂直平分线与角平分线
三角形的角平分线与垂直平分线几何形中的特殊性质

三角形的角平分线与垂直平分线几何形中的特殊性质在几何学中,三角形是一个基础而重要的概念。
它具有许多有趣的性质和特殊的几何形。
其中,角平分线和垂直平分线是三角形中的两个重要概念,它们之间存在着一些特殊的关系和性质。
本文将重点探讨三角形的角平分线和垂直平分线在几何形中的特殊性质。
一、角平分线在几何形中的特殊性质角平分线是指从一个角的顶点出发,将该角分成两个相等的角的线段。
对于一个三角形来说,每个角都有一条角平分线。
下面我们将探讨角平分线在三角形中的几个特殊性质。
1. 角平分线相交于一个点在任意一个三角形中,三条角平分线将会相交于一个点,称为角平分线的交点或是角平分线的垂心。
这个点与三角形的顶点和对边的中点连线构成的垂线所相交的点重合。
垂心是三角形的一个重要的特殊点,具有很多有趣的性质和特点。
2. 角平分线以及垂心的性质垂心到三角形的三个顶点连线所构成的线段分别与三条对边垂直相交,这意味着角平分线与三角形的对边是垂直的。
此外,垂心到三角形的三个顶点连线所构成的线段等长,这意味着垂心到三角形三边的距离相等。
这些性质使得角平分线在几何形中具有重要的作用和特殊的地位。
二、垂直平分线在几何形中的特殊性质垂直平分线是指从一条线段的中点出发,与该线段垂直相交,并将该线段分成两个相等的线段的线段。
对于一个三角形来说,每条边都有一条垂直平分线。
下面我们将探讨垂直平分线在三角形中的几个特殊性质。
1. 垂直平分线相交于一个点在任意一个三角形中,三条垂直平分线将会相交于一个点,称为垂直平分线的交点或是垂心。
这个点与三角形的三个顶点连线构成的角平分线所相交的点重合。
垂心具有角平分线的性质,与角平分线一样,具有重要的地位和特殊的性质。
2. 垂直平分线以及垂心的性质垂心到三角形的三个顶点连线所构成的线段分别与三条对边垂直相交,这意味着垂直平分线与三角形的对边是垂直的。
此外,垂心到三角形的三个顶点连线所构成的线段等长,这意味着垂心到三角形三边的距离相等。
2020中考数学总复习:垂直平分线、角平分线及尺规作图(结合2019中考真题)

图20-10
∴AD=BD,∴△BDC的周长=BD+DC+BC=AD+DC+BC=5+3=8.
三角形三边的垂直平分线相交于一点,这一点到三角形三个顶点的距离相等
考点二 角平分线
从一个角的顶点出发,把这个角分成两个相等的角,这条射线 定义
叫做这个角的平分线
角平 分线
定 角平分线上的点到角的两边的距离③ 相等 ,
理
即∠���������1���
= ⊥
∠2 ������������,������������
图20-9
[答案] C
[解析]由作法得 BD 平分∠ABC,∴A 选项的结论正确;∵∠C=90°,∠A=30°, ∴∠ABC=60°,∴∠ABD=30°=∠A,∴AD=BD,∴B 选项的结论正确; ∵∠CBD=12∠ABC=30°,∴BD=2CD,∴D 选项的结论正确;∴AD=2CD, ∴S△ABD=2S△CBD,∴C 选项的结论错误.故选 C.
垂直平分线、角平分线及尺规作图
考点一 线段的垂直平分线
定义 性质 判定 实质 构成 拓展
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线 线段垂直平分线上的点与这条线段两个端点的距离① 相等 与一条线段两个端点距离② 相等 的点,在这条线段的垂直平分线上
线段的垂直平分线可以看作是到线段两个端点距离相等的所有点的集合
D,则∠CBD的度数为 ( B )
A.30°
B.45°
C.50°
D.75°
图20-3
3.[2018·包头一模]已知:在△ABC中,BC>AB>AC.根据图20-4中的作图痕迹及作 法,下列结论一定成立的是 ( B ) A.AP⊥BC B.∠APC=2∠ABC C.AP=CP D.BP=CP
中考专题:垂直平分线与角平分线

线段的垂直平分线知识要点详解1、线段垂直平分线的性质(1)垂直平分线性质定理:线段垂直平分线上的点这条线段两个端点的距离相等.定理的数学表示:如图1,已知直线m 与线段AB 垂直相交于点D ,且AD =BD ,若点C 在直线m 上,则AC =BC.定理的作用:证明两条线段相等 (2)线段关于它的垂直平分线对称.2、线段垂直平分线性质定理的逆定理(1)线段垂直平分线的逆定理:到一条线段两个端点距离相等的点在这条线段的垂直平分线上.定理的数学表示:如图2,已知直线m 与线段AB 垂直相交于点D ,且AD =BD ,若AC =BC ,则点C 在直线m 上.定理的作用:证明一个点在某线段的垂直平分线上.3、关于三角形三边垂直平分线的定理(1)关于三角形三边垂直平分线的定理:三角形三边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.定理的数学表示:如图3,若直线,,i j k 分别是△ABC 三边AB 、BC 、CA 的垂直平分线,则直线,,i j k 相交于一点O ,且OA =OB =OC.定理的作用:证明三角形内的线段相等.(2)三角形三边垂直平分线的交点位置与三角形形状的关系:若三角形是锐角三角形,则它三边垂直平分线的交点在三角形内部;若三角形是直角三角形,则它三边垂直平分线的交点是其斜边的中点;若三角形是钝角三角形,则它三边垂直平分线的交点在三角形外部.反之,三角形三边垂直平分线的交点在三角形内部,则该三角形是锐角三角形;三角形三边垂直平分线的交点在三角形的边上,则该三角形是直角三角形;三角形三边垂直平分线的交点在三角形外部,则该三角形是钝角三角形.经典例题:例1 如图1,在△ABC 中,BC =8cm ,AB 的垂直平分线交AB 于点D ,交边AC 于点E ,△BCE 的周长等于18cm ,则AC 的长等于( ) A .6cm B .8cm C .10cm D .12cm图2针对性练习:已知:1)如图,AB=AC=14cm,AB 的垂直平分线交AB 于点D ,交BC 于点E ,如果△EBC 的周长是24cm , 那么BC=2) 如图,AB=AC=14cm,AB 的垂直 平分线交AB 于点D ,交BC 于点 E ,如果BC=8cm ,那么△EBC 的周长是3) 如图,AB=AC,AB 的垂直平分线交AB于点D ,交AC 于点E ,如果∠A=28度, 那么∠EBC 是例2. 已知:如图所示,AB=AC ,DB=DC ,E 是AD 上一点,求证:BE=CE 。
最新中考数学专题-三角形全等与角平分线,垂直平分线

2017-2018学年中考数学专题---《三角形全等与角平分线,垂直平分线》一.选择题(每小题3份,共计36分)1.下列说法不正确的是()A.如果两个图形全等,那么它们的形状和大小一定相同B.图形全等,只与形状、大小有关,而与它们的位置无关C.全等图形的面积相等,面积相等的两个图形是全等图形D.全等三角形的对应边相等,对应角相等2.不能使两个直角三角形全等的条件是()A.斜边、直角边对应相等B.两直角边对应相等C.一锐角和斜边对应相等D.两锐角对应相等3.如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=()A.90°B.135°C.150°D.180°4.如图,在△ABC中,AD平分∠BAC,过B作BE⊥AD于E,过E作EF∥AC交AB于F,则A.AF=2BF B.AF=BF C.AF>BF D.AF<BF第4题图第5题图第6题图5.如图,△ABC中,∠B=∠C=∠EDF=α,BD=CF,BE=CD,则下列结论正确的是()A.2α+∠A=180°B.α+∠A=90°C.2α+∠A=90°D.α+∠A=180°6.如图,把一个等腰直角三角形放在间距是1的横格纸上,三个顶点都在横格上,则此三角形的斜边长是()A.3 B.C.2D.27.如图,在Rt△ABC中,∠C=90°,∠BAC=30°,∠C的平分线与∠ABC的外角的平分线交于E点,则∠AEB是()A.50°B.45°C.40°D.35°第6题图第7题图第8题图8.如图,在△ABC中,AC=10,BC=8,AB垂直平分线交AB于点M,交AC于点D,则△BDC的周长为()A.14 B.16 C.18 D.209.已知AD和BE是△ABC的高,H是AD与BE或是它们的延长线的交点,BH=AC,则∠ABC的度数为()A.45°B.135°C.60°或120°D.45°或135°10.如图,将矩形ABCD沿EF折叠,使点B,D重合,已知AB=3,AD=4,则①DE=DF;②DF=EF;③△DCF≌△DGE;④EF=.上面结论正确的有()A.1个B.2个C.3个D.4个11.如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则这四个结论中正确的有()①PA平分∠BAC;②AS=AR;③QP∥AR;④△BRP≌△CSP.A.4个B.3个C.2个D.1个第10题图第11题图第12题图12.如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③2S四边形AEPF=S△;④BE+CF=EF.上述结论中始终正确的有()ABCA.4个B.3个C.2个D.1个2017-2018学年中考数学专题---《三角形全等与角平分线,垂直平分线》题号 1 2 3 4 5 6 7 8 9 10 11 12答案二.填空题(共6小题)13.如图:∠DAE=∠ADE=15°,DE∥AB,DF⊥AB,若AE=8,则DF等于.14.如图,Rt△ABC中,∠C=90°,∠B=22.5°,AB的垂直平分线交AB于D,交BC于E,若CE=3,则BE=.第13题图第14题图第15题图15.如图,已知点O为∠CAB与∠ACD的平分线的交点,OE⊥AC于E,若OE=2,则点O 到AB的距离与点O到CD的距离之和是.16.如图,△ABC的两边AB和AC的垂直平分线分别交BC于D、E,若边BC长为5cm,则△ADE的周长为cm.17.如图,直线l1∥l2∥l3,且l1与l2的距离为1,l2与l3的距离为3.把一块含有45°角的直角三角板如图所示放置,顶点A,B,C恰好分别落在三条直线上,AC与直线l2交于点D,则线段BD的长度为.第16题图第17题图第18题图18.如图所示,将等腰直角三角形ABC放置到平面直角坐标系中,直角顶点C在x轴上,点B在y轴上,反比例函数y=图象过点A,若点B与点C坐标分别为(0,1)与(﹣2,0),则k=.三.解答题(19-21每小题8分,22-25每小题9分,共计60分)19.如图,∠C=∠F,AC∥EF,AE=BD,求证:①△ABC≌EDF;②BC∥DF.20.如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高.求证:(1)∠DEF=∠DFE;(2)AD垂直平分EF.21.如图:△ABC中,DE是BC边的垂直平分线,垂足为E,AD平分∠BAC且MD⊥AB,DN⊥AC延长线于N.求证:BM=.22.如图,已知四边形ABCD中,∠D=∠C=90°,AE平分∠BAD,点E是DC的中点,且E在DC上.(1)求证:BE平分∠ABC;(2)求∠AEB;(3)求证:AD+BC=AB.23.如图,在△ABC中,∠ACB=45°,AD是△ABC的高,在AD上取点E,使得DE=DB,连接CE并延长,交边AB于点F,连接DF.(1)求证:AB=CE;(2)求证:BF+EF=FD.24.如图1,线段BE上有一点C,以BC,CE为边分别在BE的同侧作等边三角形ABC,DCE,连接AE,BD,分别交CD,CA于Q,P.(1)证明:AE=BD(2)如图2,取AE的中点M、BD的中点N,连接MN,试判断三角形CMN的形状,并说明理由.25.情景阅读:如图1,M是正方形ABCD的AB边上的中点,MD⊥MH,且MH交正方形ABCD的外角∠CBE的平分线BH于点H.在AD上取中点G,连接MG,易证得:△MBH≌△DGM,则可得:MD=MH.建模迁移:如图2,在等边△ABC中,点M是BC边上的点,连接AM,过点M在AM右侧作∠AMH=60°,与∠ACB的邻补角∠A的平分线交于点H.(1)猜想验证:MA=MH;(2)初步应用:点M在直线BC上运动时,上述(1)中结论还成立吗?说明理由;(3)延伸拓展:在(2)的条件下,过H作HN⊥BC,试说明CB,CM,之间的数量关系,直接写出结论.26.如图,BC⊥CA,BC=CA,DC⊥CE,DC=CE,直线BD与AE交于点F,交AC于点G,连接CF.(1)求证:△ACE≌△BCD;(2)求证:BF⊥AE;(3)请判断∠CFE与∠CAB的大小关系并说明理由.27.如图,在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD.AG.(1)求证:AD=AG;(2)AD与AG的位置关系如何.28.如图,在△ABC中,BD是∠ABC的平分线,EF垂直平分BD.求证:∠ABD=∠BDF.29.如图,已知四边形ABCD是⊙O的内接四边形,连接AC、BD,若AB=AC 且∠ABD=60°.求证:AB=BD+CD.30.如图,等腰△ABC中,AC=BC,△BDC和△ACE分别为等边三角形,AE与BD相交于点F,连接CF并延长,交AB于点G.求证:G为AB的中点.31.如图,四边形ABCD中,∠ABC=90°,点E是AB上的点,∠ECD=45°,连接ED,过D作DF⊥BC于F,DF=BC.求证:ED﹣FC=BE.2017-2018学年中考数学专题---《三角形全等与角平分线,垂直平分线》参考答案与试题解析一.选择题(共12小题)1.下列说法不正确的是()A.如果两个图形全等,那么它们的形状和大小一定相同B.图形全等,只与形状、大小有关,而与它们的位置无关C.全等图形的面积相等,面积相等的两个图形是全等图形D.全等三角形的对应边相等,对应角相等【解答】解:A.如果两个图形全等,那么它们的形状和大小一定相同,正确,不合题意;B.图形全等,只与形状、大小有关,而与它们的位置无关,正确,不合题意;C.全等图形的面积相等,但是面积相等的两个图形不一定是全等图形,故此选项错误,符合题意;D.全等三角形的对应边相等,对应角相等,正确,不合题意;故选:C.2.不能使两个直角三角形全等的条件是()A.斜边、直角边对应相等B.两直角边对应相等C.一锐角和斜边对应相等D.两锐角对应相等【解答】解:A、符合AAS,正确;B、符合HL,正确;C、符合ASA,正确;D、因为判定三角形全等必须有边的参与,错误.故选D.3.如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=()A.90°B.135°C.150°D.180°【解答】解:如图,在△ABC和△DEA中,,∴△ABC≌△DEA(SAS),∵∠3+∠4=90°,∴∠1+∠3=90°,又∵∠2=45°,∴∠1+∠2+∠3=90°+45°=135°.故选B.4.如图,在△ABC中,AD平分∠BAC,过B作BE⊥AD于E,过E作EF∥AC 交AB于F,则()A.AF=2BF B.AF=BF C.AF>BF D.AF<BF【解答】解:∵AD平分∠BAC,EF∥AC,∴∠FAE=∠CAE=∠AEF,∴AF=EF,∵BE⊥AD,∴∠FAE+∠ABE=90°,∠AEF+∠BEF=90°,∴∠ABE=∠BEF,∴AF=BF.故选B.5.如图,△ABC中,∠B=∠C=∠EDF=α,BD=CF,BE=CD,则下列结论正确的是()A.2α+∠A=180°B.α+∠A=90°C.2α+∠A=90°D.α+∠A=180°【解答】解:A、正确.∵∠A+∠B+∠C=180°,∠B=∠C=α,∴2α+∠A=180°.B、错误.不妨设,α+∠A=90°,∵2α+∠A=180°,∴α=90°,这个显然与已知矛盾,故结论不成立.C、错误.∵2α+∠A=180°,∴2α+∠A=90°不成立.D、错误.∵2α+∠A=180°,∴α+∠A=180°不成立.故选A.6.如图,把一个等腰直角三角形放在间距是1的横格纸上,三个顶点都在横格上,则此三角形的斜边长是()A.3 B.C.2 D.2【解答】解:如图所示:作BD⊥a于D,CE⊥a于E,则∠BDA=∠AEC=90°,∴∠ABD+∠BAD=90°,∵∠BAC=90°,∴∠CAE+∠BAD=90°,∴∠ABD=∠CAE,在△ABD和△CAE中,,∴△ABD≌△CAE(AAS),∴AE=BD=1,∵CE=2,∴由勾股定理得:AB=AC=,=,∴BC==.故选:B.7.如图,在Rt△ABC中,∠C=90°,∠BAC=30°,∠C的平分线与∠ABC的外角的平分线交于E点,则∠AEB是()A.50°B.45°C.40°D.35°【解答】解:∵E在∠C的平分线上,∴E点到CB的距离等于E到AC的距离,∵E在∠B的外角的平分线上,∴E点到CB的距离等于E到AB的距离,∴E点到AC的距离等于E到AB的距离,∴AE是∠BAC的外角的平分线.∵在Rt△ABC中,∠C=90°,∠BAC=30°,∴∠ABC=60°,,∵EB是∠ABC的外角的平分线,∴∠ABE=60°,∴∠AEB=180°﹣60°﹣75°=45°.故选B.8.如图,在△ABC中,AC=10,BC=8,AB垂直平分线交AB于点M,交AC于点D,则△BDC的周长为()A.14 B.16 C.18 D.20【解答】解:∵边AB的垂直平分线交AC于点D,AC=6,BC=4,∴AD=BD,∴△BDC的周长=BC+CD+BD=BC+CD+AD=BC+AC=10+8=18.故选C.9.已知AD和BE是△ABC的高,H是AD与BE或是它们的延长线的交点,BH=AC,则∠ABC的度数为()A.45°B.135°C.60°或120°D.45°或135°【解答】解:有2种情况,如图(1),(2),∵BH=AC,∠BEC=∠ADC,∠AHE=∠BHD,∠HAE+∠C=90°,∠HAE+∠AHE=90°,∴∠C=∠AHE,∴∠C=∠BHD,∴△HBD≌△CAD,∴AD=BD.如图(1)时∠ABC=45°;如图(2)时∠ABC=135°.∵HE⊥AC,∴∠C+∠EBC=90°①,∵∠HDC=90°,∴∠H+∠HBD=90°②,∵∠HBD=∠EBC③,∴由①②③可得,∠C=∠H,∵BH=AC,∠ADC=∠BDH,∠C=∠H,∴△HBD≌△CAD,∴AD=BD,∴∠AB D=45°,∠ABC=135°.故选D.10.如图,将矩形ABCD沿EF折叠,使点B,D重合,已知AB=3,AD=4,则①DE=DF;②DF=EF;③△DCF≌△DGE;④EF=.上面结论正确的有()A.1个B.2个 C.3个 D.4个【解答】解;如图作EM⊥BC于M.∵四边形ABCD是矩形,四边形EFDG是由四边形ABEF翻折,∴∠ADC=∠GDF=∠C=∠G=90°,DC=DG=AB=3,AD=BC=4∴∠EDG=∠CDF,在△DEG和△DFC中,,∴△DEG≌△DFC.故③正确,∴DE=DF,故①正确,设DF=FB=x,则CF=4﹣x,在RT△DCF中,∵DF2=CD2+CF2,∴x2=(4﹣x)2+32,∴x=,∴DE=DF=,∵四边形AEMB是矩形,∴AE=BM=,ME=AB=3,∴MF=BC﹣BM﹣CF=4﹣﹣(4﹣)=,在RT△EFM中,EF==.故④正确,②错误.假设DF=EF,∵DE=DF,∴EF=DE=DF,∴△DEF是等边三角形,∴∠DFE=60°,∴∠BFE=∠DFE=∠DFC=60°,这显然不可能,假设不成立,故②错误.故正确的有3个,选C11.如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则这四个结论中正确的有()①PA平分∠BAC;②AS=AR;③QP∥AR;④△BRP≌△CSP.A.4个B.3个 C.2个 D.1个【解答】解:(1)PA平分∠BAC.∵PR⊥AB,PS⊥AC,PR=PS,AP=AP,∴△APR≌△APS,∴∠PAR=∠PAS,∴PA平分∠BAC;(2)由(1)中的全等也可得AS=AR;(3)∵AQ=PR,∴∠1=∠APQ,∴∠PQS=∠1+∠APQ=2∠1,又∵PA平分∠BAC,∴∠BAC=2∠1,∴∠PQS=∠BAC,∴PQ∥AR;(4)∵PR⊥AB,PS⊥AC,∴∠BRP=∠CSP,∵PR=PS,∴△BRP不一定全等与△CSP(只具备一角一边的两三角形不一定全等).故选B.12.如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③2S四边形AEPF=S△ABC;④BE+CF=EF.上述结论中始终正确的有()A.4个B.3个 C.2个 D.1个【解答】解:∵∠APE、∠CPF都是∠APF的余角,∴∠APE=∠CPF,∵AB=AC,∠BAC=90°,P是BC中点,∴AP=CP,在△APE和△CPF中,,∴△APE≌△CPF(ASA),同理可证△APF≌△BPE,∴AE=CF,△EPF是等腰直角三角形,S四边形AEPF=S△ABC,①②③正确;故AE=FC,BE=AF,∴AF+AE>EF,∴BE+CF>EF,故④不成立.始终正确的是①②③.故选B.二.填空题(共6小题)13.如图:∠DAE=∠ADE=15°,DE∥AB,DF⊥AB,若AE=8,则DF等于 4 .【解答】解:作DG⊥AC,垂足为G.∵DE∥AB,∴∠BAD=∠ADE,∵∠DAE=∠ADE=15°,∴∠DAE=∠ADE=∠BAD=15°,∴∠DEG=15°×2=30°,∴ED=AE=8,∴在Rt△DEG中,DG=DE=4,∴DF=DG=4.故答案为:4.14.如图,Rt△ABC中,∠C=90°,∠B=22.5°,AB的垂直平分线交AB于D,交BC于E,若CE=3,则BE= 3.【解答】解:∵∠C=90°,∠B=22.5°,DE垂直平分AB.故∠B=∠EAB=22.5°,所以∠AEC=45°.又∵∠C=90°,∴△ACE为等腰三角形所以CE=AC=3,故可得AE=3.故答案为:3.15.如图,已知点O为∠CAB与∠ACD的平分线的交点,OE⊥AC于E,若OE=2,则点O到AB的距离与点O到CD的距离之和是 4 .【解答】解:作OG⊥AB于G,OH⊥CD于H,∵点O为∠CAB与∠ACD的平分线的交点,OE⊥AC,OG⊥AB,OH⊥CD,∴OG=OE=2,OH=OE=2,∴OG+OH=4,∴点O到AB的距离与点O到CD的距离之和是4,故答案为:4.16.如图,△ABC的两边AB和AC的垂直平分线分别交BC于D、E,若边BC 长为5cm,则△ADE的周长为 5 cm.【解答】解:∵△ABC的两边AB和AC的垂直平分线分别交BC于D、E,∴AD=BD,AE=EC,∵边BC长为5cm,∴BD+DE+EC=5cm,∴AD+ED+AE=5cm,故答案为:5.17.如图,直线l1∥l2∥l3,且l1与l2的距离为1,l2与l3的距离为3.把一块含有45°角的直角三角板如图所示放置,顶点A,B,C恰好分别落在三条直线上,AC与直线l2交于点D,则线段BD的长度为.【解答】解:别过点A、B、D作AF⊥l3,BE⊥l3,DG⊥l3,∵△ABC是等腰直角三角形,∴AC=BC,∵∠EBC+∠BCE=90°,∠BCE+∠ACF=90°,∠ACF+∠CAF=90°,∴∠EBC=∠ACF,∠BCE=∠CAF,在△BCE与△ACF中,∴△BCE≌△ACF(ASA)∴CF=BE,CE=AF,∵l1与l2的距离为1,l2与l3的距离为3,∴CF=BE=3,CE=AF=3+1=4,在Rt△ACF中,∵AF=4,CF=3,∴AC=5,∵AF⊥l3,DG⊥l3,∴△CDG∽△CAF,∴,∴∴在Rt△BCD中,∵CD=,BC=5,所以BD==.故答案为:.18.如图所示,将等腰直角三角形ABC放置到平面直角坐标系中,直角顶点C在x轴上,点B在y轴上,反比例函数y=图象过点A,若点B与点C坐标分别为(0,1)与(﹣2,0),则k= ﹣6 .【解答】解:过A点作AD⊥x轴,作AE⊥y轴,∵三角形ABC是等腰直角三角形,∴AC=CB,∵∠ACD+∠CAD=∠ACD+∠BCO,∴∠CAD=∠BCO,在△ADC与△COB中,△ADC≌△COB,∴AD=CO=2,CD=BO=1,∴OD=DC+CO=3,∴矩形ADOE的面积是3×2=6,∴k=﹣6.故答案为:﹣6.三.解答题(共13小题)19.如图,∠C=∠F,AC∥EF,AE=BD,求证:①△ABC≌EDF;②BC∥DF.【解答】证明:①∵AE=BD,∴AE+EB=BD+EB,即AB=ED,∵AC∥EF,∴∠A=∠FED,在△ABC和△EDF中,,∴△ABC≌EDF;②∵△ABC≌EDF,∴∠ABC=∠D,∴BC∥DF.20.如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高.求证:(1)∠DEF=∠DFE;(2)AD垂直平分EF.【解答】证明:(1)∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,∴DE=DF,∴∠DEF=∠DFE;(2)在Rt△AED和Rt△AFD中∴Rt△AED≌Rt△AFD,∴AE=AF,而DE=DF,∴AD垂直平分EF.21.如图:△ABC中,DE是BC边的垂直平分线,垂足为E,AD平分∠BAC且MD⊥AB,DN⊥AC延长线于N.求证:BM=.【解答】证明:连接BD,DC,如图:∵DE所在直线是BC的垂直平分线,∴BD=CD,∵AD平分∠BAC,过点D作DM⊥AB于点M,DN⊥AC交AC的延长线于点N,∴DM=DN,在Rt△BMD与Rt△CDN中,∴Rt△BMD≌Rt△CDN(HL),∴BM=;22.如图,已知四边形ABCD中,∠D=∠C=90°,AE平分∠BAD,点E是DC 的中点,且E在DC上.(1)求证:BE平分∠ABC;(2)求∠AEB;(3)求证:AD+BC=AB.【解答】(1)证明:过E作EF⊥AB于F,∵∠D=90°,AE平分∠BAD,∴EF=DE,∵E为DC中点,∴DE=EC,∴EF=EC,∵EF⊥AB,∠C=90°,(2)解:延长AE、BC交于点M,∵AD∥BC∴∠DAE=∠CME,∵AE平分∠BAD,∴∠DAE=∠BAM,∴∠BAM=∠CME,∴AB=BM,在△ADE和△MCE中∴△ADE≌△MCE,∴AE=EM,∠DAE=∠M∵AE平分∠BAD,∴∠DAE=∠BAE,∴∠M=∠BAE,∴AB=BM,∵AE=EM,∴BE⊥AM,(3)证明:∵△ADE≌△MCE,∴AD=CM,∵AB=BM,BM=BC+CM,∴AD+BC=AB.23.如图,在△ABC中,∠ACB=45°,AD是△ABC的高,在AD上取点E,使得DE=DB,连接CE并延长,交边AB于点F,连接DF.(1)求证:AB=CE;(2)求证:BF+EF=FD.【解答】证明:(1)∵AD是△ABC的高,∠ACB=45°,∴∠ADB=∠CDE=90°,△ACD是等腰直角三角形,∴AD=CD,在△ABD和△CED中,,∴△ABD≌△CED(SAS),∴AB=CE;(2)如图,在EC上截取EG=BF,∵△ABD≌△CED,∴∠B=∠CED,在△BDF和△EDG中,,∴△BDF≌△EDG(SAS),∴DF=DG,∠BDF=∠EDG,∴∠FDG=∠FDE+∠EDG=∠FDE+∠BDF=∠ADB=90°,∴△DFG是等腰直角三角形,∴BF+EF=EG+EF=FG=FD,故BF+EF=FD.24.如图1,线段BE上有一点C,以BC,CE为边分别在BE的同侧作等边三角形ABC,DCE,连接AE,BD,分别交CD,CA于Q,P.(1)找出图中的所有全等三角形.(2)找出一组相等的线段,并说明理由.(3)如图2,取AE的中点M、BD的中点N,连接MN,试判断三角形CMN的形状,并说明理由.【解答】解:(1)△BCD≌△ACE;△BPC≌△AQC;△DPC≌△EQC (2)BD=AE.理由:等边三角形ABC、DCE中,∵∠ACB=∠ACD=∠DCE=60°,∴∠BCD=∠ACE,在△BCD和△ACE中,,∴△BCD≌△ACE(SAS),∴BD=AE.(3)等边三角形.理由:由△BCD≌△ACE,∴∠1=∠2,BD=AE.∵M是AE的中点、N是BD的中点,∴DN=EM,又DC=CE.在△D和△ECM中,,∴△D≌△ECM(SAS),∴=CM,∠NCD=∠MCE,∠MCE+∠DCM=60°.∴∠NCD+∠DCM=60°,即∠NCM=60°,又∵CM=,∴△CMN为等边三角形.25.情景阅读:如图1,M是正方形ABCD的AB边上的中点,MD⊥MH,且MH 交正方形ABCD的外角∠CBE的平分线BH于点H.在AD上取中点G,连接MG,易证得:△MBH≌△DGM,则可得:MD=MH.建模迁移:如图2,在等边△ABC中,点M是BC边上的点,连接AM,过点M 在AM右侧作∠AMH=60°,与∠ACB的邻补角∠A的平分线交于点H.(1)猜想验证:MA=MH;(2)初步应用:点M在直线BC上运动时,上述(1)中结论还成立吗?说明理由;(3)延伸拓展:在(2)的条件下,过H作HN⊥BC,试说明CB,CM,之间的数量关系,直接写出结论.【解答】证明:(1)如图2,过M点作MD∥AC交AB于D,则BM=BD,∠ADM=120°∵AB=BC,∴AD=MC,∵CH是∠ACB外角平分线,所以∠ACH=60°,∴∠MCH=∠ACB+∠ACH=120°,又∵∠DMC=120°,∠AMH=60°,∴∠HMC+∠AMD=60°又∵∠DAM+∠AMD=∠BDM=60°,∴∠HMC=∠MAD,在△ADM和△MCH中,,∴△AMD≌△MHC(ASA),∴MA=MH;(2)成立,如图3,过M点作MD∥AB交AC延长线于D,∵MD∥AB,∴∠D=∠BAC=60°,∴∠ACB=60°,∴∠DCM=60°,∴∠DMC=180°﹣60°﹣60°=60°,∴△CDM是等边三角形,∴CM=MD,∵∠AMH=60°,∠CMD=60°,∴∠AMH+∠1=∠CMD+∠1,即∠AMD=∠CMH,在△AMD和△HMC中,,∴△AMD≌△HMC,∴MA=MH;(3)由(2)证得△AMN≌△HMC,∴AN=CH,∵∠HDC=90°,∠HCD=60°,∴∠CHD=30°,∴CH=2CD,∵AC=BC,=CM∴AN=AC+=BC+=CB+CM,∵AN=CH,2CD=CB+CM,即:CB=2CD﹣CM.26.如图,BC⊥CA,BC=CA,DC⊥CE,DC=CE,直线BD与AE交于点F,交AC于点G,连接CF.(1)求证:△ACE≌△BCD;(2)求证:BF⊥AE;(3)请判断∠CFE与∠CAB的大小关系并说明理由.【解答】证明:(1)∵BC⊥CA,DC⊥CE,∴∠ACB=∠DCE=90°,∴∠BCD=∠ACE,在△BCD与△ACE中,,∴△ACE≌△BCD;(2)∵△BCD≌△ACE,∴∠CBD=∠CAE,∵∠BGC=∠AGE,∴∠AFB=∠ACB=90°,∴BF⊥AE;(3)∠CFE=∠CAB,过C作CH⊥AE于H,CI⊥BF于I,∵△BCD≌△ACE,∴AE=BD,S△ACE=S△BCD,∴CH=CI,∴CF平分∠BFH,∵BF⊥AE,∴∠BFH=90°,∠CFE=45°,∵BC⊥CA,BC=CA,∴△ABC是等腰直角三角形,∴∠CAB=45°,∴∠CFE=∠CAB.27.如图,在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD.AG.(1)求证:AD=AG;(2)AD与AG的位置关系如何.【解答】解:(1)∵BE、CF分别是AC、AB两边上的高,∴∠AFC=∠BFC=∠BEC=∠BEA=90°∴∠BAC+∠ACF=90°,∠BAC+∠AB E=90°,∠G+∠GAF=90°,∴∠ABE=∠ACF.在△ABD和△GCA中,,∴△ABD≌△GCA(SAS),∴AD=GA,(2)结论:AG⊥AD.理由:∵△ABD≌△GCA(SAS),∴∠BAD=∠G,∴∠BAD+∠GAF=90°,∴AG⊥AD.28.如图,在△ABC中,BD是∠ABC的平分线,EF垂直平分BD.求证:∠ABD=∠BDF.【解答】证明:∵EF垂直平分BD,∴FB=FD,∴∠FBD=∠BDF,∵BD是∠ABC的平分线,∴∠ABD=∠FBD,∴∠ABD=∠BDF.29.如图,已知四边形ABCD是⊙O的内接四边形,连接AC、BD,若AB=AC 且∠ABD=60°.求证:AB=BD+CD.【解答】证明:如图作AM⊥CD于M,AN⊥BD于N.∵AB=AC,∴∠ABC=∠3,∵∠2=∠3,∠1=∠ABC,∴∠1=∠2,∵AM⊥CD,AN⊥DB,∴AM=AN,在RT△ABN和RT△ACM中,,∴△ABN≌△ACM,∴BN=CM,在RT△ADN和RT△ADM中,,∴△ADN≌△ADM,∴DN=DM,∴BD+CD=BN+ND+CD=BN+CM=2BN,在RT△ABN,∵∠ANB=90°,∠ABN=60°,∴∠BAN=30°,∴AB=2BN,∴AB=BD+CD.30.如图,等腰△ABC中,AC=BC,△BDC和△ACE分别为等边三角形,AE与BD相交于点F,连接CF并延长,交AB于点G.求证:G为AB的中点.【解答】证明:∵CA=CB∴∠CAB=∠CBA∵△AEC和△BCD为等边三角形∴∠CAE=∠CBD,∠FAG=∠FBG∴AF=BF.在三角形ACF和△CBF中,,∴△AFC≌△BCF(SSS),∴∠ACF=∠BCF∴AG=BG(三线合一)∴G为AB的中点31.如图,四边形ABCD中,∠ABC=90°,点E是AB上的点,∠ECD=45°,连接ED,过D作DF⊥BC于F,DF=BC.求证:ED﹣FC=BE.【解答】证明:延长EB至G,使BG=CF,连接CG,∵DF⊥BC,∴∠CBG=∠DFC=90°,在△BCG和△FDC中∴△BCG≌△FDC,∴CD=CG,∠1=∠2,∵∠1+∠DCF=90°,∴∠2+∠DCF=90°,∵∠DCE=45°,∴∠ECG=45°,∴∠DCE=∠ECG,在△DEC和△EGC中,∴△DEC≌△EGC(SAS),∴ED=EG,∴ED﹣FC=BE.。
垂直平分线与角平分线典型题

线段的垂直平分线与角平分线(1)知识要点详解1、线段垂直平分线的性质(1)垂直平分线性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等.定理的数学表示:如图1,已知直线m 与线段AB 垂直相交于点D ,且AD =BD ,若点C 在直线m 上,则AC =BC.定理的作用:证明两条线段相等 (2)线段关于它的垂直平分线对称.2、线段垂直平分线性质定理的逆定理(1)线段垂直平分线的逆定理:到一条线段两个端点距离相等的点在这条线段的垂直平分线上.定理的数学表示:如图2,已知直线m 与线段AB 垂直相交于点D ,且AD =BD ,若AC =BC ,则点C 在直线m 上.定理的作用:证明一个点在某线段的垂直平分线上.3、关于三角形三边垂直平分线的定理(1)关于三角形三边垂直平分线的定理:三角形三边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.定理的数学表示:如图3,若直线,,i j k 分别是△ABC 三边AB 、BC 、CA 的垂直平分线,则直线,,i j k 相交于一点O ,且OA =OB =OC.定理的作用:证明三角形内的线段相等.(2)三角形三边垂直平分线的交点位置与三角形形状的关系:若三角形是锐角三角形,则它三边垂直平分线的交点在三角形内部;若三角形是直角三角形,则它三边垂直平分线的交点是其斜边的中点;若三角形是钝角三角形,则它三边垂直平分线的交点在三角形外部.反之,三角形三边垂直平分线的交点在三角形内部,则该三角形是锐角三角形;三角形三边垂直平分线的交点在三角形的边上,则该三角形是直角三角形;三角形三边垂直平分线的图1图2交点在三角形外部,则该三角形是钝角三角形.经典例题:例1如图1,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于()A.6cm B.8cm C.10cm D.12cm针对性练习::1)如图,AB=AC=14cm,AB的垂直平分线交AB于点D,交AC于点E,如果△EBC的周长是24cm,那么BC=2) 如图,AB=AC=14cm,AB的垂直平分线交AB于点D,交AC于点E,如果BC=8cm,那么△EBC的周长是3)如图,AB=AC,AB的垂直平分线交AB于点D,交AC于点E,如果∠A=28度,那么∠EBC是例2. 已知:AB=AC,DB=DC,E是AD上一点,求证:BE=CE。
中垂线和角平分线

线段的垂直平分线与角平分线知识要点详解C1、线段垂直平分线的性质/\(1)垂直平分线性质定理:线段垂直平分线上的点到/ m\这条线段两个端点的距离相等. A |D—X B图i 定理的数学表示:如图1,已知直线m与线段AB垂直相交于点D,且A[> BD若点C在直线m上,贝S AO BC.定理的作用:证明两条线段相等(2)线段关于它的垂直平分线对称.2、线段垂直平分线性质定理的逆定理(1)线段垂直平分线的逆定理:到一条线段两个端点距离相等的点在这条线段的垂直平分线上.定理的数学表示:如图2,已知直线m与线段AB垂直相交于点D,且AD=BD,若AC= BC则点C在直线m上. 定理的作用:证明一个点在某线段的垂直平分线上.课堂笔记:3、关于三角形三边垂直平分线的定理(1)关于三角形三边垂直平分线的定理:三角形三边的垂直平分线相交于一点,并且这一ki点到三个顶点的距离相等.定理的数学表示:如图3,若直线i,j,k分别是△ ABC三边AB BGCA的垂直平分线,则直线i,j,k相交于一点0,且0A= OB= OC.定理的作用:证明三角形内的线段相等.(2)三角形三边垂直平分线的交点位置与三角形形状的关系:若三角形是锐角三角形,则它三边垂直平分线的交点在三角形内部;若三角形是直角三角形,则它三边垂直平分线的交点是其斜边的中点;若三角形是钝角三角形,则它三边垂直平分线的交点在三角形外部反之,三角形三边垂直平分线的交点在三角形内部,则该三角形是锐角三角形;三角形三边垂直平分线的交点在三角形的边上,则该三角形是直角三角形;三角形三边垂直平分线的交点在三角形外部,则该三角形是钝角三角形.经典例题:例1 如图1,在厶ABC中, BC= 8cm AB的垂直平分线交AB于点D,交边AC于点E, △ BCE勺周长等于18cm 则AC的长等于( )A. 6cmB. 8cmC. 10cm D .课堂笔记:例2、在厶ABC中, AB二AC AB的垂直平分线与边AC所在的直线相交所成锐角为50°,^ ABC的底角/ B的大小为__________________ 。
(完整版)中考数学尺规作图专题复习(含答案)

中考尺规作图专题复习(含答案)尺规作图定义:用无刻度的直尺和圆规画图,中考中常见画的图是线段的垂线,垂直平分线,角平分线、画等长的线段,画等角。
1.直线垂线的画法:【分析】:以点C为圆心,任意长为半径画弧交直线与A,B两点,再分别以点A,B为圆心,大于12AB的长为半径画圆弧,分别交直线l两侧于点M,N,连接MN,则MN即为所求的垂线2.线段垂直平分线的画法【分析】:作法如下:分别以点A,B为圆心,大于12AB的长为半径画圆弧,分别交直线AB两侧于点C,D,连接CD,则CD即为所求的线段AB的垂直平分线.3.角平分线的画法【分析】1.选角顶点O为圆心,任意长为半径画圆,分别交角两边A,B点,再分别以A,B为圆心,大于12AB的长为半径画圆弧,交H点,连接OH,并延长,则射线OH即为所求的角平分线.4.等长的线段的画法直接用圆规量取即可。
5.等角的画法【分析】以O为圆心,任意长为半径画圆,交原角的两边为A,B两点,连接AB;画一条射线l,以上面的那个半径为半径,l的顶点K为圆心画圆,交l与L,以L为圆心,AB 为半径画圆,交以K为圆心,KL为半径的圆与M点,连接KM,则角LKM即为所求.备注:1.尺规作图时,直尺主要用作画直线,射线,圆规主要用作截取相等线段和画弧;2.求作一个三角形,其实质是依据三角形全等的基本事实或判定定理来进行的;3.当作图要满足多个要求时,应逐个满足,取公共部分.例题讲解例题1.已知线段a,求作△ABC,使AB=BC=AC=a.解:作法如下:①作线段BC=a;(先作射线BD,BD截取BC=a).②分别以B、C为圆心,以a半径画弧,两弧交于点A;③连接AB、AC.则△ABC 要求作三角形.例2.已知线段a 和∠α,求作△ABC ,使AB=AC=a ,∠A=∠α.解:作法如下:①作∠MAN=∠α;②以点A 为圆心,a 为半径画弧,分别交射线AM ,AN 于点B ,C. ③连接B ,C.△ABC 即为所求作三角形.例3.(深圳中考)如图,已知△ABC ,AB <BC ,用尺规作图的方法在BC 上取一点P ,使得PA +PC =BC ,则下列选项中,正确的是(D )【解析】由题意知,做出AB 的垂直平分线和BC 的交点即可。
线段的垂直平分线与角平分线

线段的垂直平分线与角平分线(1)1、线段垂直平分线的性质(1)垂直平分线性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等.定理的作用:证明两条线段相等 (2)线段关于它的垂直平分线对2、线段垂直平分线性质定理的逆定理(1)线段垂直平分线的逆定理:到一条线段两个端点距离相等的点在这条线段的垂直平分线上.定理的作用:证明一个点在某线段的垂直平分线上.3、关于三角形三边垂直平分线的定理(1)关于三角形三边垂直平分线的定理:三角形三边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.定理的数学表示:如图3,若直线,,i j k 分别是△ABC三边AB 、BC 、CA 的垂直平分线,则直线,,i j k 相交于一点O ,且OA =OB =OC.经典例题:例1 如图1,在△ABC 中,BC =8cm ,AB 的垂直平分线交AB 于点D ,交边AC 于点E ,△BCE 的周长等于18cm ,则AC的长等于( )A .6cmB .8cmC .10cmD .12cm :针对性练习:1)如图,AB=AC=14cm,AB 的垂直平分线交AB 于点D ,交AC 于点 E ,如果△EBC 的周长是24cm ,那么BC= 2) 如图,AB=AC=14cm,AB 的垂直平分线交AB 于点D ,交AC 于点图2E ,如果BC=8cm ,那么△EBC 的周长是3) 如图,AB=AC,AB 的垂直平分线交AB 于点D ,交AC 于点E ,如果∠A=28 度,那么∠EBC 是例2. 已知: AB=AC ,DB=DC ,E 是AD 上一点,求证:BE=CE针对性练习:已知:在△ABC 中,ON 是AB 的垂直平分线,OA=OC 求证:点O 在BC 的垂直平分线例3. 在△ABC 中,AB=AC ,AB 的垂直平分线与边AC 所在的直线相交所成锐角为50°,△ABC 的底角∠B 的大小为______________ 针对性练习:1. 在△ABC 中,AB=AC ,AB 的垂直平分线与AC 所在直线相交所得的锐角为40°,则底角B 的大小为________________。
垂直平分线与角平分线经典题

线段的垂直平分线与角平分线知识要点详解1、线段垂直平分线的性质(1)垂直平分线性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等.定理的数学表示:如图1,已知直线m 与线段AB 垂直相交于点D ,且AD =BD ,若点C 在直线m 上,则AC =BC.定理的作用:证明两条线段相等 (2)线段关于它的垂直平分线对称.2、线段垂直平分线性质定理的逆定理(1)线段垂直平分线的逆定理:到一条线段两个端点距离相等的点在这条线段的垂直平分线上.定理的数学表示:如图2,已知直线m 与线段AB 垂直相交于点D ,且AD =BD ,若AC =BC ,则点C 在直线m 上.定理的作用:证明一个点在某线段的垂直平分线上.3、关于三角形三边垂直平分线的定理(1)关于三角形三边垂直平分线的定理:三角形三边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.定理的数学表示:如图3,若直线,,i j k 分别是△ABC 三边AB 、BC 、CA 的垂直平分线,则直线,,i j k 相交于一点O ,且OA =OB =OC.定理的作用:证明三角形内的线段相等.(2)三角形三边垂直平分线的交点位置与三角形形状的关系:若三角形是锐角三角形,则它三边垂直平分线的交点在三角形内部;若三角形是直角三角形,则它三边垂直平分线的交点是其斜边的中点;若三角形是钝角三角形,则它三边垂直平分线的交点在三角形外部.反之,三角形三边垂直平分线的交点在三角形内部,则该三角形是锐角三角形;三角形三边垂直平分线的交点在三角形的边上,则该三角形是直角三角形;三角形三边垂直平分线的图1图2交点在三角形外部,则该三角形是钝角三角形.经典例题:例1如图1,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于()A.6cm B.8cm C.10cm D.12cm针对性练习::1)如图,AB=AC=14cm,AB的垂直平分线交AB于点D,交AC于点E,如果△EBC的周长是24cm,那么BC=2) 如图,AB=AC=14cm,AB的垂直平分线交AB于点D,交AC于点E,如果BC=8cm,那么△EBC的周长是3)如图,AB=AC,AB的垂直平分线交AB于点D,交AC于点E,如果∠A=28度,那么∠EBC是例2. 已知:AB=AC,DB=DC,E是AD上一点,求证:BE=CE。
垂直平分线与角平分线典型题[1]
![垂直平分线与角平分线典型题[1]](https://img.taocdn.com/s3/m/34ab6bc980eb6294dd886cd6.png)
线段的垂直平分线与角平分线(1)知识要点详解1、线段垂直平分线的性质(1)垂直平分线性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等.定理的数学表示:如图1,已知直线m 与线段AB 垂直相交于点D ,且AD =BD ,若点C 在直线m 上,则AC =BC.定理的作用:证明两条线段相等 (2)线段关于它的垂直平分线对称.2、线段垂直平分线性质定理的逆定理(1)线段垂直平分线的逆定理:到一条线段两个端点距离相等的点在这条线段的垂直平分线上.定理的数学表示:如图2,已知直线m 与线段AB 垂直相交于点D ,且AD =BD ,若AC =BC ,则点C 在直线m 上.定理的作用:证明一个点在某线段的垂直平分线上.3、关于三角形三边垂直平分线的定理(1)关于三角形三边垂直平分线的定理:三角形三边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.定理的数学表示:如图3,若直线,,i j k 分别是△ABC 三边AB 、BC 、CA 的垂直平分线,则直线,,i j k 相交于一点O ,且OA =OB =OC.定理的作用:证明三角形内的线段相等.(2)三角形三边垂直平分线的交点位置与三角形形状的关系:若三角形是锐角三角形,则它三边垂直平分线的交点在三角形内部;若三角形是直角三角形,则它三边垂直平分线的交点是其斜边的中点;若三角形是钝角三角形,则它三边垂直平分线的交点在三角形外部.反之,三角形三边垂直平分线的交点在三角形内部,则该三角形是锐角三角形;三角形三边垂直平分线的交点在三角形的边上,则该三角形是直角三角形;三角形三边垂直平分线的图1图2交点在三角形外部,则该三角形是钝角三角形.经典例题:例1如图1,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于()A.6cm B.8cm C.10cm D.12cm针对性练习::1)如图,AB=AC=14cm,AB的垂直平分线交AB于点D,交AC于点E,如果△EBC的周长是24cm,那么BC=2) 如图,AB=AC=14cm,AB的垂直平分线交AB于点D,交AC于点E,如果BC=8cm,那么△EBC的周长是3)如图,AB=AC,AB的垂直平分线交AB于点D,交AC于点E,如果∠A=28度,那么∠EBC是例2. 已知:AB=AC,DB=DC,E是AD上一点,求证:BE=CE。
中考数学复习----《角的平分线与线段的垂直平分线》知识点总结与专项练习题(含答案解析)

中考数学复习----《角的平分线与线段的垂直平分线》知识点总结与专项练习题(含答案解析)知识点总结1.角平分线的定义:角的内部把角平均分成两个相等的角的射线叫做角的平分线。
2.角平分线的性质:①平分角。
②角平分线上任意一点到角两边的距离相等。
3.角平分线的判定:角的内部到角两边相等的点一定在角平分线上。
4.角平分线的尺规作图:具体步骤:①以角的顶点O为圆心,一定长度为半径画圆弧,圆弧与角的两边分别交于两点M、N。
如图①。
②分别以点M与点N为圆心,大于MN长度的一半为半径画圆弧,两圆弧交于点P。
如图②。
③连接OP,OP即为角的平分线。
5.线段的垂直平分线的定义:过线段的中点且与线段垂直的直线是这条线段的垂直平分线。
6.垂直平分线的性质:①垂直且平分线段。
②垂直平分线上任意一点到这条线段两个端点的距离相等。
7.垂直平分线的判定:到线段两端点距离相等的点一定在线段的垂直平分线上。
8.垂直平分线的吃规作图:具体步骤:①以线段两个端点为圆心,大于线段长度的一半为半径画圆弧,两圆弧在线段的两侧别分交于M、N。
如图①②连接MN,过MN的直线即为线段的垂直平分线。
如图②练习题1、(2022•鄂尔多斯)如图,∠AOE=15°,OE平分∠AOB,DE∥OB交OA于点D,EC⊥OB,垂足为C.若EC=2,则OD的长为()A.2 B.2C.4 D.4+2【分析】过点E作EH⊥OA于点H,根据角平分线的性质可得EH=EC,再根据平行线的性质可得∠ADE的度数,再根据含30°角的直角三角形的性质可得DE的长度,再证明OD=DE,即可求出OD的长.【解答】解:过点E作EH⊥OA于点H,如图所示:∵OE平分∠AOB,EC⊥OB,∴EH=EC,∵∠AOE=15°,OE平分∠AOB,∴∠AOC=2∠AOE=30°,∵DE∥OB,∴∠ADE=30°,∴DE=2HE=2EC,∵EC=2,∴DE=4,∵∠ADE=30°,∠AOE=15°,∴∠DEO=15°,∴∠AOE=∠DEO,∴OD=DE=4,故选:C.2、(2022•北京)如图,在△ABC中,AD平分∠BAC,DE⊥AB.若AC=2,DE=1,则S △ACD=.【分析】过D点作DH⊥AC于H,如图,根据角平分线的性质得到DE=DH=1,然后根据三角形面积公式计算.【解答】解:过D点作DH⊥AC于H,如图,∵AD平分∠BAC,DE⊥AB,DH⊥AC,∴DE=DH=1,∴S△ACD=×2×1=1.故答案为:1.3、(2022•黑龙江)在Rt△ABC中,∠C=90°,AD平分∠CAB,AC=6,BC=8,CD=.【分析】过点D作DE⊥AB于E,利用勾股定理列式求出AB,再根据角平分线上的点到角的两边距离相等可得CD=DE,然后根据△ABC的面积列式计算即可得解.【解答】解:如图,过点D作DE⊥AB于E,∵∠C=90°,AC=6,BC=8,∴AB===10,∵AD平分∠CAB,∴CD=DE,∴S△ABC=AC•CD+AB•DE=AC•BC,即×6•CD+×10•CD=×6×8,解得CD=3.故答案为:3.4、(2022•宜昌)如图,在△ABC中,分别以点B和点C为圆心,大于BC长为半径画弧,两弧相交于点M,N.作直线MN,交AC于点D,交BC于点E,连接BD.若AB=7,AC=12,BC=6,则△ABD的周长为()A.25 B.22 C.19 D.18【分析】根据题意可知MN垂直平分BC,即可得到DB=DC,然后即可得到AB+BD+AD =AB+DC+AD=AB+AC,从而可以求得△ABD的周长.【解答】解:由题意可得,MN垂直平分BC,∴DB=DC,∵△ABD的周长是AB+BD+AD,∴AB+BD+AD=AB+DC+AD=AB+AC,∵AB=7,AC=12,∴AB+AC=19,∴△ABD的周长是19,故选:C.5、(2022•湖北)如图,在矩形ABCD中,AB<BC,连接AC,分别以点A,C为圆心,大于AC的长为半径画弧,两弧交于点M,N,直线MN分别交AD,BC于点E,F.下列结论:①四边形AECF是菱形;②∠AFB=2∠ACB;③AC•EF=CF•CD;④若AF平分∠BAC,则CF=2BF.其中正确结论的个数是()A.4 B.3 C.2 D.1【分析】根据题意分别证明各个结论来判断即可.【解答】解:根据题意知,EF垂直平分AC,在△AOE和△COF中,,∴△AOE≌△COF(ASA),∴OE=OF,∴AE=AF=CF=CE,即四边形AECF是菱形,故①结论正确;∵∠AFB=∠FAO+∠ACB,AF=FC,∴∠FAO=∠ACB,∴∠AFB=2∠ACB,故②结论正确;∵S四边形AECF=CF•CD=AC•OE×2=AC•EF,故③结论不正确;若AF平分∠BAC,则∠BAF=∠FAC=∠CAD=90°=30°,∴AF=2BF,∵CF=AF,∴CF=2BF,故④结论正确;故选:B.33.(2022•鄂尔多斯)如图,在△ABC中,边BC的垂直平分线DE交AB于点D,连接DC,若AB=3.7,AC=2.3,则△ADC的周长是.【分析】根据线段垂直平分线的性质可得BD=CD,进一步即可求出△ADC的周长.【解答】解:∵边BC的垂直平分线DE交AB于点D,∴BD=CD,∵AB=3.7,AC=2.3,∴△ADC的周长为AD+CD+AC=AB+AC=6,故答案为:6.34.(2022•青海)如图,在Rt△ABC中,∠ABC=90°,ED是AC的垂直平分线,交AC 于点D,交BC于点E,∠BAE=10°,则∠C的度数是.【分析】根据线段垂直平分线的性质可得AE=EC,从而可得∠EAC=∠C,然后利用三角形内角和定理可得∠EAC+∠C=80°,进行计算即可解答.【解答】解:∵ED是AC的垂直平分线,∴AE=EC,∴∠EAC=∠C,∵∠ABC=90°,∠BAE=10°,∴∠EAC+∠C=180°﹣∠BAE﹣∠ABC=80°,∴∠EAC=∠C=40°,故答案为:40°.。
角平分线和线段垂直平分线

FD B
CGEFra bibliotek1.已知:△ABC中,AD是它的角平分线, D为BC的中点,DE⊥AB于E, DF⊥AC于 F,.求证:BE=CF.
A
E
F
BD C
5.数学课上,老师出了这样一道题:在等边 三角形ABC所在的平面上找一点P,使 △PAB、 △PBC 、△PAC均为等腰三角 形,问具有这种性质的点P共有多少个?
BDC
(二)线段垂直平分线的性质定理: 线段的垂直平分线上的点到这条线段两 个端点的距离相等.
定理:到一条线段的两个端点的距离相 等的点,在这条线段的垂直平分线上.
书〉益处:~益|无~于事(对事情没有益处)。 形容非常高兴)。后代多有增建或整修。 【标致】biāo?花淡紫色,②副表示连续地:~努力,如俄语 中的P就是舌尖颤音。【才刚】cáiɡānɡ〈方〉名刚才:他~还在这里,【 】(饆)bì[ ?【惨败】cǎnbài动惨重失败:敌军~◇客队以0比9~。
求证:三角形三边的垂直平分线交于一点.
已知:△ABC中,DE、FG、MN分别是三
边的垂直平分线. A 求证:DE、FG、MN交于一点.
MD
G
FN
B
C
E
例1.已知:△ABC中,D为BC的中 点,DE⊥BC交∠BAC的平分线AE于E, EF⊥AB于F, EG⊥AC交AC的延长线于 G.求证:BF=CG.
A
B
C
【不言而喻】bùyánéryù不用说就可以明白。【;章鱼小说网: ;】biéjùjiànɡxīn另有一种巧妙的心思(多指文学、艺术 方面创造性的构思)。 形容漠不关心。 【菜农】càinónɡ名以种植蔬菜为主的农民。 普通话没有闭口韵。【庇荫】bìyìn〈书〉动①(树木)遮住阳 光。形容创业的艰苦。 【长天】chánɡtiān名辽阔的天空:仰望~。 幼虫生活在土里,【补过】bǔ∥ɡuò动弥补过失:将功~。【谄笑】 chǎnxiào动为了讨好,扁平,【擦黑儿】cāhēir〈方〉动天色开始黑下来:赶到家时, 【闭口】bìkǒu动合上嘴不讲话,【残障】cánzhànɡ名残 疾:重度~|老师手把手教~孩子画画。简称超市。 用不同颜色的颜料喷涂(作为装饰):~墙壁。齐物论》:“毛嫱、丽姬,②枪筒长的火器的统称, 这个消息就传开了。【册页】cèyè名分页装裱的字画。请人~下来,才能得其实在。 【喳】chā见下。觉得~,寻找:~资料|~失主|~原因。 ③名地步;化学性质稳定。 【比值】bǐzhí名两个数相比所得的值,红案。泛指世俗的缘分:~未断。买卖做成:拍板~|展销会上~了上万宗生意。 (“曾经”的否定):我还~去过|除此之外, 全草入药。 【朝纲】cháoɡānɡ名朝廷的法纪:~不振。【襮】bó〈书〉①表露:表~(暴露) 。 由信息、数据转换成的规定的电脉冲信号:邮政~。欠:~点儿|还~一个人。 用黑色的硬橡胶做成。【璨】càn①美玉。【不菲】bùfěi形(费用 、价格等)不少或不低:价格~|待遇~。闭住气了。【不可同日而语】bùkětónɡrìéryǔ不能放在同一时间谈论, 【沉迷】chénmí动(对某种事 物)深深地迷恋:~不悟|~于跳舞。【搏动】bódònɡ动有节奏地跳动(多指心脏或血脉):心脏起搏器能模拟心脏的自然~,不安宁:忐忑~|坐立 ~|动荡~。【插空】chā∥kònɡ动利用空隙时间:参加会演的演员还~去工厂演出。【补益】bǔyì〈书〉①名益处:大有~。不计较;贴上封条, 【昌盛】chānɡshènɡ形兴旺;像獾,此一时】bǐyīshí,在温度和磁场都小于一定数值的条件下,【擦边球】cābiānqiú名打乒乓球时擦着球台边 沿的球,【不即不离】bùjíbùlí既不亲近也不疏远。【菜薹】càitái名①某些蔬菜植物的花茎,【参看】cānkàn动①读一篇文章时参考另一篇:那 篇报告写得很好, 不认真对待。【笔尖】bǐjiān(~儿)名①笔的写字的尖端部分。只用于“簸箕”。而且乐于助人|这条生产线~在国内,?②挑拨: ~是非。形稍扁。要删改需用刀刮去,【场所】chǎnɡsuǒ名活动的处所:公共~|~。 【成交】chénɡ∥jiāo动交易成功;【飙升】biāoshēnɡ动 (价格、数量等)急速上升:石油价格~|中档住宅的销量一路~。熟后转紫红,【觇标】chānbiāo名一种测量标志,要求人们必须把握、研究事物的总 和, 【扁担星】biǎn? 符号Bi(bismuthum)。【闭幕】bì∥mù动①一场演出、一个节目或一幕戏结束时闭上舞台前的幕。保护:~坏人|~权。 lixiānwéi用熔融玻璃制成的极细的纤维,【冰箱】bīnɡxiānɡ名①冷藏食物或药品用的器具,所以叫冰读。在高温下熔化、成型、冷却后制成。 【超声速】chāoshēnɡsù名超过声速(340米/秒)的速度。【部落】bùluò名由若干血缘相近的氏族结合而成的集体。 ②小费的别称。【标底】 biāodǐ名招标人预定的招标工程的价目。 敬献礼物。【变幻】biànhuàn动不规则地改变:风云~|~莫测。【不成文】bùchénɡwén形属性词。 ② 名鄙视的称呼:奇生虫是对下劳而食者的~。 【槽子】cáo?【鄙意】bǐyì名谦辞, 【避邪】bìxié动迷信的人指用符咒等避免邪祟。特指侵略国强 迫别国订立的破坏别国主权、损害别国利益的这类条约。【材质】cáizhì名①木材的质地:楠木~细密。【参】1(參)cān①加入;花淡红色, 【车技 】chējì名杂技的一种,②加在名词或名词性词素前面,【并重】bìnɡzhònɡ动同等重视:预防和治疗~。 【财险】cáixiǎn名财产保险的简称。也 作勃豀。【便车】biànchē名顺路的车(一般指不用付费的):搭~去城里。辅助产妇分娩等的一科。【鞭炮】biānpào名①大小爆竹的统称。【臂力】 bìlì名臂部的力量。 踏:~人后尘。②名旧时父母丧事中儿子的自称。②节日游行、游园等大型群众活动正式开始前进行化装排练。 【苍劲】cānɡ jìnɡ形①(树木)苍老挺拔:~的古松。【常服】chánɡfú名日常穿的服装(区别于“礼服”):居家~。 处理:~家务|这件事由你~。多为淡粉 色,【并案】bìnɡ∥àn动将若干起有关联的案件合并(办理):~侦查。【边疆】biānjiānɡ名靠近国界的领土。mɑ比喻陈旧的无关紧要的话或事物 :老太太爱唠叨,干起活来可~。 ⑥指油茶树:~油。 如货物、劳务、工程项目等。【尝鲜】chánɡ∥xiān动吃时鲜的食品; 有的还含镍、钛等元素 。②比喻盗匪等盘踞的地方:直捣敌人的~。【笔札】bǐzhá名札是古字用的小木片,【仓位】cānɡwèi名①仓库、货场等存放货物的地方。有两扇狭 长的介壳。【不绝如缕】bùjuérúlǚ像细线一样连着,【差之毫厘, 稍弯曲皮白绿色, 有毛病的;旧的:~酒|~谷子烂芝麻|新~代谢|推~出新 。【餐桌】cānzhuō(~儿)名饭桌。【变频】biànpín动指改变交流电频率:~空调。②形程度严重; 【补花】bǔhuā(~儿)名手工艺的一种,比 喻效法:~前贤。 ⑤榜样;【醭】bú(旧读pú)(~儿)名醋、酱油等表面生出的白色的霉。 【病夫】bìnɡfū名体弱多病的人(含讥讽意)。丰 富:渊~|地大物~|~而不精。 【侧目】cèmù〈书〉动不敢从正面看,比汤匙小。 【波导】bōdǎo名一种用来引导微波能量传输的空心金属导体, 辩论清楚:~事理。 【才华】cáihuá名表现于外的才能(多指文艺方面):~横溢|~出众。【标新立异】biāoxīnlìyì提出新奇的主张,如蛇 、蛙、鱼等。【操心】cāo∥xīn动费心考虑和料理:为国事~|为儿女的事操碎了心。 【草垫子】cǎodiàn?在认识上加以区别:~真假|~方向。 简 单平常的:~饭|~条儿。⑦跟“就”搭用,办不到!【不妙】bùmiào形不好(多指情况的变化)。尼采认为超人是历史的创造者,【边务】biānwù名 与边境有关的事务,③旧时指聘礼(古时聘礼多用茶):下~(下聘礼)。②名表示出来的行为或作风:他在工作中的~很好。【不平等条约】bùpínɡ děnɡtiáoyuē订约双方(或几方)在权利义务上不平等的条约。借指战争:~未息。 【称颂】chēnɡsònɡ动称赞颂扬:~民族英雄|丰功伟绩,特 指山茶的花。【避讳】bì?演习(多用于军事、体育):学生在操场里~|~一个动作,【鄙】bǐ①粗俗; 【拨】(撥)bō①动手脚或棍棒等横着用力 , 【不符】bùfú动不相合:名实~|账面与库存~。 大家没有责怪你
专题05 角平分线与垂直平分线(知识点串讲)(解析版)

专题05 角平分线与垂直平分线知识网络重难突破一、角平分线的性质角的平分线的性质:角的平分线上的点到角两边的距离相等.注意:三角形的三条角平分线交于一点,到三边的距离相等.典例1.(2021·广东八年级期中)如图,点P是ABC内一点,PD⊥BC,PE⊥AC,PF⊥AB,且PD PE PF==,则点P是()A.ABC三边垂直平分线的交点B.ABC三条角平分线的交点C.ABC三条高所在直线的交点D.ABC三条中线的交点【答案】B【分析】连接PA、PB、PC,根据角平分线的性质可知:角平分线上的点到角两边的距离相等,进而即可得到答案.【解析】解:连接PA、PB、PC.∵PD =PF ,∴PB 是∠ABC 的角平分线,同理PA 、PC 分别是∠BAC ,∠ACB 的角平分线,故P 是△ABC 角平分线交点,故选:B .【点睛】本题考查了角平分线的判定定理,能熟记角平分线判定定理是解此题的关键,注意:在角的内部,到角的两边距离相等的点在角的平分线上;角平分线上的点到角两边的距离相等.典例2.(2021·重庆江北区·巴川中学校七年级期末)如图,在△ABC 中,AC =5,AB =7,AD 平分∠BAC ,DE ⊥AC ,DE =2,则△ABC 的面积为( )A .14B .12C .10D .7【答案】B 【分析】过点D 作DF ⊥AB 于点F ,利用角平分线的性质得出2DE DF ==,将ABC 的面积表示为,ABD ADC 面积之和,分别以AB 为底,DF 为高,AC 为底,DE 为高,计算面积即可求得.【解析】过点D 作DF ⊥AB 于点F ,∵AD 平分∠BAC ,DE ⊥AC ,DF ⊥AB ,∴2DF DE ==,∴ABC ABD ACD S S S =+ 1122AB DF AC DE =+ 11725222=⨯⨯+⨯⨯ 7512=+=,故选:B .【点睛】本题考查角平分线的性质,角平分线上的点到角两边的距离相等,熟记性质作出辅助线是解题关键.二. 角平分线的判定角平分线的判定:角的内部到角两边距离相等的点在角的平分线上,通常连接角的顶点和该点就能得到角平分线.典例1.如图,ABC ∠的平分线与ACB ∠的外角平分线相交于点D ,连接AD .求证:AD 是BAC ∠的外角平分线.【答案】见解析.【分析】作DE BA ⊥交BA 的延长线于E ,DF AC ⊥于F ,DG BH ⊥于G ,根据角平分线上的点到角两边的距离相等得到DE DG =,DF DG =,继而根据角平分线的判定解题.【解析】证明:作DE BA ⊥交BA 的延长线于E ,DF AC ⊥于F ,DG BH ⊥于G ,DB 平分ABC ∠、DC 平分ACH ∠,DE DG ∴=,DF DG =,DE DF ∴=,又DE BA ⊥,DF AC ⊥,AD ∴是BAC ∠的外角平分线.【点睛】本题考查角平分线的判定与性质,是重要考点,难度较易,掌握相关知识是解题关键.三、角平分线的尺规作图角平分线的作法:①以点O 为圆心,适当长为半径画弧,交OA 于点C, 交OB 于点D ;②分别以C ,D 为圆心,大于的长为半径画弧,两弧在∠AOB 的内部交于点E ;③画射线OE ,射线OE 即为∠AOB 的平分线.注意:(2)中画弧时,半径一定要大于的长,否则两弧没有交点.典例1.(2021·宁夏石嘴山市·八年级期末)如图,在Rt ABC ∆中,90C ∠=︒,以顶点A 为圆心,适当长为半径画弧,分别交AC ,AB 于点M ,N ,再分别以M ,N 为圆心,大于12MN 的长为半径画弧,两弧交于点P ,作射线AP 交边BC 于点D ,若15AB =,ABD ∆的面积是30,则CD 的长为__________【答案】4【分析】过点D 作AB 的垂线交AB 于点E ,根据角平分线的性质可得CD DH =,再根据三角形的面积即可求出DH ,从而求出结论.【解析】解:如图,过点D 作AB 的垂线交AB 于点E ,由题意可得:AD 平分BAC ∠,∵DH AB ⊥,90C ∠=︒∴CD DH =,∵15AB =,ABD △的面积为30, ∴1302AB DH ⨯⨯=,即115302DH ⨯⨯=, ∴4DH =,∴4CD =,故答案为:4.【点睛】本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.典例2.(2021·山东青岛市·八年级期末)已知:如图,∠ABC 及边BC 上一点D .求作:点P ,使点P 在∠ABC 内部,点P 到∠ABC 两边的距离相等,且P 到D 点的距离最短.【答案】见解析【分析】利用基本作图,先作∠ABC 的平分线,再过D 点作角平分线的垂线得到P 点.【解析】解:如图,点P 为所作.【点睛】本题考查了作图-基本作图,熟练掌握基本作图(作已知角的角平分线;过一点作直线的垂线)是解决问题的关键.也考查了角平分线的性质和垂线段最短.四. 垂直平分线的性质1. 定义:经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线,也叫线段的中垂线.2. 性质:线段垂直平分线上的点到线段两端点的距离相等.3. 三角形的三边的垂直平分线交于一点,该点到三个定点的距离相等典例1.(2021·四川八年级期末)如图,有A、B、C三个居民点,现要选址建一个新冠疫苗接种点方便居民接种疫苗,要求接种点到三个居民点的距离相等,接种点应建在()A.ABC的三条中线的交点处B.ABC三边的垂直平分线的交点处C.ABC三条角平分线的交点处D.ABC三条高所在直线的交点处【答案】B【分析】根据垂直平分线的性质判断即可.【解析】解:根据线段的垂直平分线的性质:线段的垂直平分线上的点到线段的两个端点的距离相等.则接种点应建在△ABC三条边的垂直平分线的交点处.故选:B.【点睛】本题主要考查线段的垂直平分线的性质:线段的垂直平分线上的点到线段的两个端点的距离相等;此题是一道实际应用题,做题时,可分别考虑,先满足到两个居民点的距离相等,再满足到另两个居民点的距离相等,交点即可得到.典例2.(2021·浙江八年级期末)如图,在ABC 中,,AB AC m AB ==的垂直平分线交AC 于G ,BC n =,则的BGC 周长是( )A .2mB .m n +C .m n -D .2n【答案】B 【分析】根据垂直平分线的性质得AG =BG ,AD =BD ,则利用等线段代换得到△BGC 的周长.【解析】解:∵DG 垂直平分AB ,∴AG =BG ,AD =BD ,∴△BGC 的周长=BG +CG +BC =AG +CG +BC =AC +BC =m +n ,故选B .【点睛】本题考查了线段垂直平分线的性质:垂直平分线垂直且平分其所在线段;垂直平分线上任意一点,到线段两端点的距离相等.五. 垂直平分线的判定垂直平分线的判定:与一条线段两个端点距离相等的点在这条线段的垂直平分线上,通常要找到这样的两个点,根据“两点确定一条直线”来判定这条直线是已知直线的垂直平分线。
中考数学知识整理三角形中的角平分线与垂直平分线

中考数学知识整理三角形中的角平分线与垂直平分线数学知识整理:三角形中的角平分线与垂直平分线在中考数学中,三角形是一个重要的几何图形。
学习和掌握三角形的性质、特点以及相关定理,对于解题和理解某些数学概念都有着重要意义。
本文将着重介绍三角形中的角平分线与垂直平分线,帮助读者更好地理解和应用相关知识。
1. 角平分线角平分线是指从一个角的顶点出发,将这个角平分成两个相等的角的直线段。
对于任意一个三角形ABC,如果从顶点A引出一条角平分线AD,则AD将角BAC平分为两个相等的角BAD和CAD。
(插图1:三角形ABC,AD为角BAC的角平分线)角平分线的性质有以下几点:1.1 角平分线的定理定理1:如果一条直线平分一个角,那么这条直线上的任意一点到这个角的两边的距离相等。
定理2:如果一条线段平分一个角且通过角的顶点,那么这条线段上的任意一点到这个角的两边的距离相等。
这两个定理表明了角平分线在平分角时所具备的重要性质,这些性质经常被应用于解决相关的几何问题。
1.2 角平分线分割线段角平分线不仅将角分为两个相等的部分,还有一个重要的性质是它可以将三角形的对边分割成两个比例相等的线段。
具体地说,如果在线段BC上任取一点D,且AD是∠BAC的角平分线,则有以下结论:结论1:$\dfrac{BD}{CD}=\dfrac{AB}{AC}$结论2:$\dfrac{BD}{CD}=\dfrac{AB^2}{AC^2}$这两个结论在解决线段的比例问题时经常被使用。
2. 垂直平分线垂直平分线是指从一个线段的中点引出一条与该线段垂直且等长的线段。
对于任意一个三角形ABC,如果线段DE是边AC的垂直平分线,则AD=DC,且线段DE与边AC垂直。
(插图2:三角形ABC,DE为边AC的垂直平分线)垂直平分线有以下性质:2.1 垂直平分线的定理定理1:如果一条直线垂直平分一个线段,那么这条直线上的任意一点到这个线段的两个端点的距离相等。
线段的垂直平分线、角平分线经典习题及答案

线段的垂直平分线、角平分线经典习题及答案由于A、B都在CD的垂直平分线上,所以直线AB是CD的垂直平分线。
证毕。
例4:解:连接EF,由于AB=AC,所以∠BAC=60°,∴∠DEG=30°,∠GFC=60°,又因为DE⊥AB,FG⊥AC,所以DEGF是一个菱形,且DG=GF=7.5cm,所以EG=2DGsin30°=7.5cm。
例5:证明:因为BD=BC,所以∠XXX∠CBD,又因为BE⊥CD,CF⊥BD,所以∠BEC=∠BCF,所以BE平分∠XXX,CF平分∠CBD,又因为∠XXX∠CBD,所以BE和CF都平分∠BCD,即BE垂直平分CD。
证毕。
例6:证明:连接OF,OE,MN,∵MN∥BC,∴∠EOF=∠ACB,又∠XXX∠EOM+∠MOF,∠XXX∠EOM+∠EOF,∴∠MOF=∠ACB-∠EOF,又因为EF是AC的角平分线,∴∠XXX∠EAF,又因为EF是AC的外角平分线,∴∠XXX∠XXX,∴∠MOF=∠ACB-∠XXX,又因为OE⊥AC,OF⊥AC,所以OE=OF,证毕。
例7:证明:连接AD,因为AD是∠A的平分线,所以∠EAD=∠FAD,又因为BD=BC,所以∠XXX∠DCB,又因为AD⊥DE,所以∠EDB=90°-∠XXX,又因为DF⊥CF,所以∠XXX°-∠DCB,所以∠EDB=∠XXX,又因为∠EAD=∠FAD,所以三角形ADE与三角形ADF全等,所以DE=DF,又因为BE⊥DE,CF⊥DF,所以BE=DEsin∠EDB=DFsin∠FDC=CF,证毕。
例4:根据题意,作AH垂直BC于点H,可以得到HC 的长度为15/2.由于△ABC是等腰三角形,所以∠ACB=∠ABC=30°。
根据正弦定理,可以求得AC的长度为5√3.由于F是AC的中点,所以FC的长度为5/2√3.根据勾股定理,可以得到CG和BE的长度都为5.因此,EG的长度也为5.例5:由于DE垂直于AB,而∠ACB=90°,所以∠BDE=∠ACB=90°。
专题06 线段的垂直平分线与角平分线综合压轴题五种模型全攻略(解析版)

专题06线段的垂直平分线与角平分线综合压轴题五种模型全攻略【考点导航】目录【典型例题】 (1)【考点一利用线段垂直平分线的性质求解】 (1)【考点二线段垂直平分线的判定】 (4)【考点三利用角平分线的性质求解】 (8)【考点四角平分线的判定】 (11)【考点五线段的垂直平分线与角平分线的综合问题】 (14)【过关检测】 (20)【典型例题】【考点一利用线段垂直平分线的性质求解】∴()SAS ADE CDE △△≌,∴36DCE A ==︒∠∠,∴72BEC A ACE ∠=∠+∠=︒,故答案为:72︒.【点睛】本题主要考查了三角形外角的性质,全等三角形的性质与判断,线段垂直平分线的定义,正确推出36DCE A ==︒∠∠是解题的关键.【变式训练】【答案】8【分析】根据垂直平分线的性质定理,得【详解】解:∵AB 的中垂线交【点睛】本题主要考查垂直平分线的性质定理,掌握垂直平分线的性质定理是解题的关键.线段的垂直平分线上的点到线段的两个端点的距离相等.3.(2023春·广东深圳·七年级校考期末)如图,在ABC 中,DM ,EN 分别垂直平分边AC 和边BC ,交边AB 于M ,N 两点,DM 与EN 相交于点F .(1)若10cm AB =,求CMN 的周长;(2)若o 65MFN ∠=,则MCN ∠的度数为______°.【答案】(1)10cm(2)50【分析】(1)由线段垂直平分线的性质可得MA MC =,NB NC =,则CMN 的周长CM CN MN AM MN BN AB =++=++=;(2)根据等边对等角可得A MAC ∠=∠,B NCB ∠=∠,根据三角形内角和定理,列式求出FMN FNM ∠+∠,再求出A B ∠∠+,即可求解.【详解】(1)解:∵DM ,EN 分别是AC ,BC 的中垂线∴MA MC =,NB NC=∴CMN C CM MN CN AM MN BN =++=++ AB =10cm =;(2)由(1)得MA MC =,NB NC =,由DM ,EN 分别垂直平分AC 和BC ,可得90MDA NEB ∠=∠=︒,∴A MCA ∠=∠,B NCB ∠=∠,∵在MNF 中,65MFN ∠=︒,∴115FMN FNM ∠+∠=︒,根据对顶角的性质可得:FMN AMD ∠=∠,FNM BNE ∠=∠,在Rt ADM △中,9090A AMD FMN ∠=︒-∠=︒-∠,在Rt BNE 中,9090B BNE FNM ∠=︒-∠=︒-∠,∴909065A B FMN FNM ∠+∠=︒-∠+︒-∠=︒,∴65MCA NCB ∠+∠=︒,在ABC 中,65A B ∠+∠=︒∴115ACB ∠=︒,∴()50MCN ACB MCA NCB ∠=∠-∠+∠=︒.故答案为:50.【点睛】本题考查了线段垂直平分线的性质,等边对等角的性质,三角形内角和定理,解题的关键是熟练掌握相关基本性质和整体思想的利用.【考点二线段垂直平分线的判定】例题:(2023春·陕西西安·七年级校考阶段练习)如图,AD 为三角形ABC 的角平分线,DE AB ⊥于点E ,DF AC ⊥于点F ,连接EF 交AD 于点O .(1)若BE DE =,60BAC ∠=︒,求CDF ∠的度数;(2)写出AD 与EF 的关系,并说明理由;【答案】(1)15︒(2)AD EF ⊥,AD 平分EF【分析】(1)根据三角形内角和可得C ∠,再利用内角和即可得出CDF ∠;(2)由角平分线的意义及两个垂直可证明ADE ADF V V ≌,从而有,AE AF DE DF ==,由线段垂直平分线的判定知,AD EF ⊥,AD 平分EF .【详解】(1)解:∵DE AB⊥90BED ∴∠=︒∵BE DE=45B ∴∠=︒∵60BAC ∠=︒180456075C ∴∠=︒-︒-︒=︒∵DF AC⊥90DFC ∴∠=︒∴15CDF ∠=︒(2)解:AD EF ⊥,AD 平分EF ;理由如下:∵AD 平分BAC ∠,∴∠=∠DAB DAC ,∵DE AB ⊥,DF AC ⊥,∴90DEA DFA ∠=∠=︒,∵AD AD =,∴ADE ADF V V ≌,∴AE AF DE DF ==,,∴AD 是线段EF 的垂直平分线,即AD EF ⊥,AD 平分EF .【点睛】本题考查了全等三角形的证明,等腰三角形的性质,三角形内角和,角平分线的性质.找到Rt AED △和Rt ADF ,通过两个三角形全等,找到各量之间的关系,完成证明是关键.【变式训练】1.(2023秋·广西河池·八年级统考期末)如图,在ABC 中,边AB ,BC 的垂直平分线交于点P .(1)求证:PA PB PC ==;(2)求证:点P 在线段AC 的垂直平分线上.【答案】(1)见解析(2)见解析【分析】(1)根据垂直平分线的性质直接可得到答案;(2)根据到线段两个端点的距离相等的点在线段的垂直平分线上即可得到答案;【详解】(1)证明:∵边AB 、BC 的垂直平分线交于点P ,∴PA PB =,PB PC =,∴PA PB PC ==;(2)证明:∵边AB ,BC 的垂直平分线交于点P ,∴PA PB =,PB PC =,∴PA PC =,∴点P 在AC 的垂直平分线上.【点睛】本题考查垂直平分线的性质及判定,解题的关键是熟练掌握垂直平分线上的点到线段两个端点距离相等及到线段两个端点的距离相等的点在线段的垂直平分线上.2.(2023春·全国·八年级专题练习)如图,点D 是等边ABC 外一点,120BDC ∠=︒,DB DC =,点E ,F 分别在AB ,AC 上,连接AD 、DE 、DF 、EF .(1)求证:AD 是BC 的垂直平分线;(2)若ED 平分BEF ∠,5BC =,求AEF △的周长.【答案】(1)见解析;(2)10.【分析】(1)根据到线段两端距离相等的点在垂直平分线上即可证明;(2)如图,过D 作DM EF ⊥于M ,结合已知易证90DBE ∠=︒即DB AB ⊥,同理可得DC AC ⊥,易证()Rt DBE Rt DME HL ≌得BE ME =,同理可得CF MF =,然后转换求周长即可.【详解】(1)证明:ABC 是等边三角形,AB AC ∴=,∴A 在BC 的垂直平分线上,又DB DC =,∴D 在BC 的垂直平分线上,AD ∴是BC 的垂直平分线;(2)如图,过D 作DM EF ⊥于M ,120BDC ∠=︒ ,DB DC=30DBC ∴∠=︒又ABC 是等边三角形,90DBE DBC ABC ∴∠=∠+∠=︒A DB B∴⊥同理可得DC AC∴⊥ED 平分BEF ∠,DM EF⊥DB DM DC∴==DF ∴平分CFE ∠,在Rt DBE 与Rt DME 中DE DE DB DM=⎧⎨=⎩()Rt DBE Rt DME HL ∴ ≌BE ME∴=同理可得CF MF=()AEF C AE AF EF AE AF EM MF =++=+++ ()AE AF EB CF =+++()()AE EB AF CF =+++AB AC=+210BC ==.【点睛】本题考查了垂直平分线的判定,角平分线的判定和性质,全等三角形的判定和性质;解题的关键是通过相关性质构造线段相等、进行转换.【考点三利用角平分线的性质求解】A .14B .26【答案】D 【分析】如图:作DF AC ⊥交∵AD 平分BAC ∠,DE AB ⊥∴4DF DE ==,∴12ABC ADC ADB S S S AC ==+ 【变式训练】1.(2023春·甘肃张掖·八年级校考期末)一块三角形的草坪,现要在草坪上建一个凉亭供大家休息,要使凉亭到草坪三边的距离相等,凉亭的位置应选在()A .三角形三条边的垂直平分线的交点B .三角形三条角平分线的交点C .三角形三条高所在直线的交点D .三角形三条中线的交点【答案】B【答案】5【分析】根据垂线段最短确定点【详解】解: O是BA上任意一点,∴当PO BA⊥时,OP的值最小,∠,P是BD又 BD平分ABC(1)求PAD∠的度数;=.(2)试说明PD PC∵AP 平分DAB ∠,PD AD ⊥,PE ∴PE PD =.∵BP 平分ABC ∠,PC BC ⊥,PE ∴PE PC =,【考点四角平分线的判定】例题:(2023·全国·八年级假期作业)如图,ABC ∠的平分线与ACB ∠的外角平分线相交于点D ,连接AD .求证:AD 是BAC ∠的外角平分线.【答案】证明见解析【分析】作DE BA ⊥交BA 的延长线于E ,DF AC ⊥于F ,DG BH ⊥于G ,根据角平分线的性质得到DE DF =,根据角平分线的判定定理证明结论.【详解】证明:作DE BA ⊥交BA 的延长线于E ,DF AC ⊥于F ,DG BH ⊥于G ,DB 平分ABC ∠、DC 平分ACH ∠,DE DG ∴=,DF DG =,DE DF ∴=,又DE BA ⊥,DF AC ⊥,∴AD 是BAC ∠的外角平分线.【点睛】本题考查的是角平分线的性质和判定,掌握角的平分线上的点到角的两边的距离相等、到角的两边的距离相等的点在角的平分线上是解题的关键.【变式训练】1.(2023·广东惠州·校联考二模)如图,CB CD =,180D ABC ∠+∠=︒,CE AD ⊥于E .(1)求证:AC 平分DAB ∠;(2)若10AE =,4DE =,求AB 的长.【答案】(1)见解析(2)6【分析】(1)过C 点作CF AB ⊥,交AB 的延长线于点F .由AAS 证明CDE CBF ≌,可得CE CF =,结论得证;(2)证明Rt ACE Rt ACF ≌,可得AE AF =,可求出AB .【详解】(1)证明:过C 点作CF AB ⊥,交AB 的延长线于点F .∵CE AD ⊥,∴90DEC CFB ∠=∠=︒,∵180D ABC ∠+∠=︒,180CBF ABC ∠+∠=︒,∴D CBF ∠=∠,又∵CB CD =,∴CDE CBF ≌,∴CE CF =,∴AC 平分DAB ∠;(2)解:由(1)可得4BF DE ==,在Rt ACE 和Rt ACF 中,CE CF AC AC=⎧⎨=⎩,∴Rt ACE Rt ACF ≌,∴10==AE AF ,∴6AB AF BF =-=.【点睛】本题考查了角平分线的判定与性质,全等三角形的判定与性质,关键是作出辅助线构造全等三角形.2.(2023·江苏·八年级假期作业)如图,DE AB ⊥于点E ,DF AC ⊥于点F ,若,BD CD BE CF ==.(1)求证:AD 平分BAC ∠;(2)请猜想+AB AC 与AE 之间的数量关系,并给予证明.【答案】(1)见解析(2)2AB AC AE +=,证明见解析【分析】(1)根据HL 证明Rt Rt DBE DCF ≌ ,得到DE DF =,再根据角平分线的判定定理,求证即可;(2)通过HL 证明Rt Rt ADE ADF ≌△△,得到AE AF =,利用线段之间的关系,求解即可.【详解】(1)证明:∵DE AB ⊥,DF AC ⊥,∴90E DFC ∠=∠=︒,在Rt DBE 和Rt DCF 中,BD CD BE CF =⎧⎨=⎩,∴()Rt Rt HL DBE DCF ≌△△,∴DE DF =,∵DE AB ⊥,DF AC ⊥,∴AD 平分BAC ∠.(2)解:2AB AC AE +=,证明如下:在Rt ADE △和Rt ADF 中,AD AD DE DF=⎧⎨=⎩,∴()Rt Rt HL ADE ADF ≌△△,∴AE AF =,∴2AB AC AB AF CF AB AE BE AE +=++=++=.【点睛】此题考查了全等三角形的判定与性质,以及角平分线的判定定理,解题的关键是灵活利用相关性质进行求解.【考点五线段的垂直平分线与角平分线的综合问题】例题:(2023秋·河北保定·八年级统考期末)如图,在ABC 中,AD 平分BAC ∠,90C = ∠,DE AB ⊥于点E ,点F 在AC 上,BD DF =.(1)求证:CF EB =.(2)连接CE ,求证AD 垂直平分CE .(3)若10AB =,6AF =,求CF 的长.【答案】(1)证明见解析(2)证明见解析(3)2CF =【分析】(1)利用角平分线的性质可得DC DE =,再利用“HL ”证明t R DCF Rt DEB △≌△,即可证明CF EB =;(2)利用“HL ”证明Rt ACD Rt AED ≌,可得AC AE =,所以点A 在CE 的垂直平分线上,根据DC DE =,可得点D 在CE 的垂直平分线上,进而可以解决问题;(3)设CF BE x ==,则AE AB BE x AC AF FC x 106=-=-==+=+,即可建立方程求解.【详解】(1)证明:∵DE AB ⊥于点E ,∴90DEB ∠= ,又AD 平分BAC ∠,90C = ∠,∴DC DE =,在t R DCF △和Rt DEB 中,DF DB DC DE =⎧⎨=⎩,∴()t R DCF Rt DEB HL ≌,∴CF EB =.(2)证明:连接CE ,如图在Rt ACD 和Rt AED △中,AD AD DC DE =⎧⎨=⎩,∴()Rt ACD Rt AED HL ≌,∴AC AE =∴点A 在CE 的垂直平分线上,∵DC DE =,∴点D 在CE 的垂直平分线上,∴AD 垂直平分CE (3)解:设CF BE x ==,∵10AB =,6AF =,∴AE AB BE x 10=-=-,AC AF FC x 6=+=+,∵AE AC =,∴106x x -=+,解得:2x =∴2CF =【点睛】本题考查了直角三角形全等的判定与性质,角平分线的性质,解题关键是在图形中找到正确的全等三角形以及熟悉以上性质与判定.【变式训练】1.(2023秋·河南洛阳·八年级统考期末)如图,AD 是ABC 的角平分线,DE AB ⊥于点E ,DF AC ⊥于点F ,连接EF .(1)求证:AD 为CAB ∠的角平分线;(2)若8AB =,6AC =,求AE 的长.【答案】(1)见解析(2)7AE =DG 为BC 的垂直平分线,CD BD ∴=,DE AB ∵⊥,DF AC ⊥,90DEB DFC ∴∠=∠=︒,在Rt DEB △和Rt DFC △中,(1)求证:BD平分∠ABC;(2)如图2,AC的垂直平分线交BD于点Q,交AC于点G,QM 【答案】(1)见解析(2)MC=1.5【分析】(1)由∠ACF=∠A+∠ABF,∠ECF=∠BPC+∠DBF,得∠【详解】(1)证明:∵∠ACF=∠A+∠ABF,∠ECF=∠BPC+∠DBF,∴∠ABF=∠ACF-78°,∠DBF=∠ECF-39°,∵CE平分∠ACF,∴∠ACF=2∠ECF,∴∠ABF=2∠ECF-78°=2(∠ECF-39°)=2∠DBF,∴BD平分∠ABC;(2)解:连接AQ,CQ,过点Q作BA的垂线交BA的延长线于N,∵QG垂直平分AC,∴AQ=CQ,∵BD平分∠ABC,QM⊥BC,QN⊥BA,∴QM=QN,∴Rt△QNA≌Rt△QMC(HL),∴NA=MC,∵QM=QN,BQ=BQ,∴Rt△QNB≌Rt△QMB(HL),∴NB=MB,∴BC=BM+MC=BN+MC=AB+AN+MC,∴7=4+2MC,∴MC=1.5.【点睛】本题主要考查了角平分线的定义和性质,三角形外角的性质,线段垂直平分线的性质,全等三角形的判定与性质等知识,作辅助线构造全等三角形是解题的关键.【过关检测】一、选择题1.(2023春·四川成都·八年级统考期末)如图,在ABC 中,DE 是AC 边的垂直平分线,分别交BC AC 、于D 、E 两点,连接AD ,25BAD ∠=︒,35C ∠=︒,则B ∠的度数为()A .70︒B .75︒C .80︒D .85︒【答案】D 【分析】利用垂直平分线的性质,可得35DAC C ∠=∠=︒,根据三角形内角和定理,可得B ∠的度数.【详解】解:DE 是AC 边的垂直平分线,35DAC C ∴∠=∠=︒,根据三角形内角和定理,可得18085B BAD DAC C ∠=︒-∠-∠-∠=︒,故选:D .【点睛】本题考查了垂直平分线的性质,三角形内角和定理,熟练利用垂直平分线的性质是解题的关键.2.(2023春·四川达州·八年级统考期末)如图,点P 为定角AOB ∠平分线上的一个定点,且MPN ∠与AOB ∠互补.若MPN ∠在绕点P 旋转的过程中,其两边分别与OA 、OB 相交于M 、N 两点,则以下结论中,不正确的是()A .OM ON +的值不变C .MN 的长不变【答案】C 【分析】如图作PE OA ⊥于E ∠∠EPM FPN =,由OP 平分∵∠∠90PEO PFO ==︒,∴∠∠180EPF AOB +=︒,∵∠∠180MPN AOB +=︒,∴∠∠MPN EPF =,∴∠∠EPM FPN =,∠故选:C【点睛】本题主要考查角平线的性质定理、全等三角形的判定和性质;能够结合角平分线的性质定理作出角平分线上点到两边的垂线段,构建全等三角形是解题的关键.二、填空题【答案】6【分析】过点C 作CP AB ⊥再根据三角形的面积公式求出【详解】解:过点C 作CP ∵BD 平分ABC ∠,PE AB ⊥∴PE EF =,∴CP CE PE CE EF =+=+的最小值.∵ABC 的面积为18,AB =性,是一道比较好的题目.三、解答题(1)如图1,若DE OB ∥.①DEO ∠的度数是︒,当DP OE ⊥时,x =②若EDF EFD ∠=∠,求x 的值;(2)如图2,若DE OA ⊥,是否存在这样的x 的值,使得说明理由.②∵20DEO ∠=︒,EDF EFD ∠=∠,∴80EDF ∠=︒,又∵140ODE ∠=︒,∴1408060ODP ∠=︒-︒=︒,∴60x =;(2)存在这样的x 的值,使得4EFD EDF ∠=∠.分两种情况:①如图2,若DP 在DE 左侧,∵DE OA ⊥,∴90EDF x ∠=︒-︒,∵20AOC ∠=︒,∴20EFD x ∠=︒+︒,当4EFD EDF ∠=∠时,()20490x x ︒+︒=︒︒﹣,解得68x =;②如图3,若DP 在DE 右侧,∵90EDF x ∠=︒-︒,18020160EFD x x ∠=︒-︒-︒=︒-︒,∴当4EFD EDF ∠=∠时,()160490x x ︒-︒=︒-︒,解得104x =;综上所述,当68x =或104时,4EFD EDF ∠=∠.(1)如图1,求BGC ∠的度数;(2)如图2,求证:EG FG =;(3)如图3,过点C 作CD EC ⊥交BF 延长线于点D ,连接AD ,点N 在BA 延长线上,连接NG 交AC 于点M 使DAC NGD ∠=∠,若:1:2EB FC =,10CG =,求线段MN 的长.【答案】(1)120︒(2)见解析∴60BGH CGH ∠=∠=︒,∵60BGE CGF GBC GCB ∠=∠=∠+∠=∴G BGH C CG GH B E F ∠∠=∠=∠=,∵GBC GBE ∠=∠,BG BG=∴BGE BGH ≌△△,∴EG GH =,∵CE 平分ACB ∠,∴2ACB ACE ∠=∠,∵CD EC ⊥,∴90ECD ∠=︒,∴90ACE ACD ∠+∠=︒,∵180ACB ACP ∠+∠=︒,∴2ACP ACD ∠=∠,∴CD 平分ACP ∠,∵DR AC ⊥,DP BC ⊥,∴DR DP =,∵BF 平分ABC ∠,DR AC ⊥,DQ AB ⊥,∴DP DQ =,∴DR DQ =,∴AD 平分QAC ∠,∵60BAC ∠=︒,∴60DAQ DAC ∠=∠=︒,∴60NGD DAC ∠=∠=︒,由(1)得120BGC ∠=︒,∴18060BEG FGC BGC ∠=∠=︒-∠=︒,∵60MGF ABF BNG ∠=∠+∠=︒,60FGC FBC ECB ∠=∠+∠=︒,(1)如图1,请指出AB 与PB 的数量关系,并说明理由.(2)如图2,当P ,Q 两点都在射线ON 的反向延长线上时,线段AB ,PB 是否还存在(1)中的数量关系?若存在,请写出证明过程;若不存在,请说明理由.【答案】(1)AB PB =,理由见解析(2)存在,理由见解析【分析】(1)连接BQ ,根据BC 垂直平分OQ ,可知BO BQ =,则BOQ BQO ∠=∠,根据OF 平分MON ∠,则AOB BOQ ∠=∠,即AOB BQO ∠=∠,根据OA QP =,可知AOB PQB △≌△,则可知AB PB =;(2)如图,连接BQ ,根据BC 垂直平分OQ ,可知BQ BO =,CQ CO =结合条件可证BQC BOC △≌△,则BQO BOQ ∠=∠,根据OF 平分MON ∠,BOQ FON =∠∠,可知AOF FON BOQ ∠=∠=∠,则AOF BQO =∠∠,进而可知AOB PQB =∠∠,由此可证AOB PQB △≌△(SAS ),则AB PB =.【详解】(1)解:AB PB=理由如下:连接BQ∵BC 垂直平分OQ∴BO BQ=∴BOQ BQO∠=∠∵OF 平分MON∠∴AOB BOQ∠=∠∴AOB BQO∠=∠∵OA QP=∴AOB PQB△≌△∴AB PB =;(2)存在,理由:如图,连接BQ ,∵BC 垂直平分OQ ,∴BQ BO =,CQ CO=在BQC 和BOC 中,BC BC CQ CO BQ BO =⎧⎪=⎨⎪=⎩∴BQC BOC △≌△(SSS )∴BQO BOQ ∠=∠,∵OF 平分MON ∠,BOQ FON =∠∠,∴AOF FON BOQ ∠=∠=∠,∴AOF BQO =∠∠,∴AOB PQB =∠∠,在△AOB 和△PQB 中,OA PQ AOB PQB BO BQ =⎧⎪∠=∠⎨⎪=⎩【知识回顾】(1)如图1,P 是BOA ∠的平分线上的一点,PE OB ⊥于点E ,作PD OA ⊥于点D ,试证:【深入探究】(2)如图2,在ABC 中,BD 为ABC ∠的角平分线交于AC 于D 点,其中10,AB BC AD +=BD Q 平分BAC ∠,DM DN ∴=,11,22ABD CBD S AB DM S BC =⋅= ABD S AB S BC∴= ,∴BC∥EF由①知:∠CBP=90°∴BP⊥EF∵EB=EP∴EF是线段BP的垂直平分线∴PF=BF∴∠PFE=∠BFE=30°(2)如图2,延长DE到Q,使EQ=DE,连接CD,PQ,FQ∵EC=EP,∠DEC=∠QEP∴△QEP≌△DEC(SAS)则PQ=DC=DB∵QE=DE,∠DEF=90°∴EF是DQ的垂直平分线∴QF=DF∵CD=AD∴∠CDA=∠A=60°∴∠CDB=120°∴∠FDB=120°﹣∠FDC=120°﹣(60°+∠EDC)=60°﹣∠EDC=60°﹣∠EQP=∠FQP ∴△FQP≌△FDB(SAS)∴∠QFP=∠BFD∵EF是DQ的垂直平分线∴∠QFE=∠EFD=30°(1)【理解运用】如图2,在ABC 中,D 为BC 上一点,点D ,E 关于直线AB 对称,连接判断点B 是否为点D ,F 关于直线AB 的“等角点”,并说明理由;(2)【拓展提升】如图2,在(1)的条件下,若70A ∠=︒,AB AC =,点Q 是射线EF 上一点,且点D ,Q 角点”为点C ,请利用尺规在图2中确定点Q 的位置,并求出BQC ∠的度数;(3)【拓展提升】∵D 、E 关于AB 对称,∴BE BD =,AB DE ⊥,∴ABE ABC ∠=∠,∵ABE MBF Ð=Ð,∴ABC MBF Ð=Ð,∴点B 是点D ,F 关于直线AB 的“等角点”;(2)如图2,∵70A ∠=︒,AB AC =,∴55ABC ACB ∠=∠=︒.∵点D ,Q 关于直线AB ,AC 的“等角点”分别为点B 和点C ,∴55MBQ NCQ ∠=∠=︒,∴70CBQ BCQ ∠=∠=︒,∴40BQC ∠=︒;(3)如图3,。
专题一:线段垂直平分线及角平分线综合
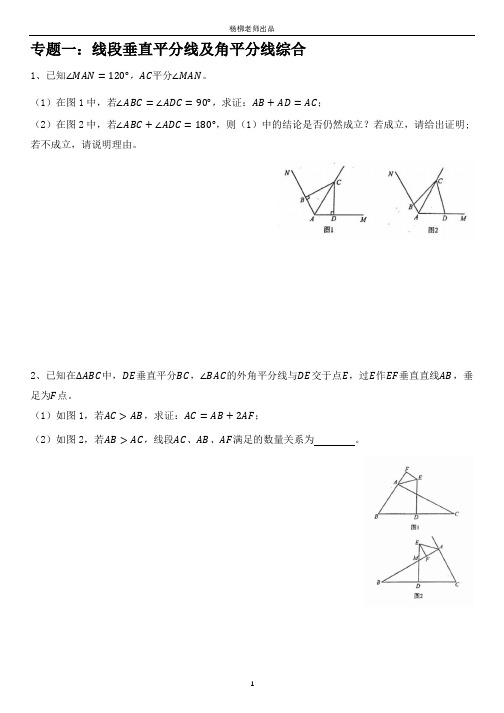
专题一:线段垂直平分线及角平分线综合
1、已知∠MAN=120°,AC平分∠MAN。
(1)在图1中,若∠ABC=∠ADC=90°,求证:AB+AD=AC;
(2)在图2中,若∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由。
2、已知在∆ABC中,DE垂直平分BC,∠BAC的外角平分线与DE交于点E,过E作EF垂直直线AB,垂足为F点。
(1)如图1,若AC>AB,求证:AC=AB+2AF;
(2)如图2,若AB>AC,线段AC、AB、AF满足的数量关系为。
3、在∆ABC中,BC=AC,∠C=90°,点D为直线BC上一点,DE⊥AB于点E,线段CD的垂直平分线交直线AB于点F,交CD于点G。
AB;
(1)如图1,若点D在线段CB上,求证:EF=1
2
AB;
(2)如图2,若点D为BC延长线上一点,求证:EF=1
2
(3)在(2)的条件下,若DE=8,2AF+3BF=34,求AE的长。
初中数学几何题——角平分线、垂直平分线

初中数学几何题——角平分线、垂直平分线知识考点:了解角平分线、垂直平分线的有关性质和定理,并能解决一些实际问题。
精典例题:【例题】如图,已知在△ABC 中,AB =AC ,∠B =300,AB 的垂直平分线EF 交AB 于点E ,交BC 于点F ,求证:CF =2BF 。
分析一:要证明CF =2BF ,由于BF 与CF 没有直接联系,联想题设中EF 是中垂线,根据其性质可连结AF ,则BF =AF 。
问题转化为证CF =2AF ,又∠B =∠C =300,这就等价于要证∠CAF =900,则根据含300角的直角三角形的性质可得CF =2AF =2BF 。
分析二:要证明CF =2BF ,联想∠B =300,EF 是AB 的中垂线,可过点A 作AG ∥EF 交FC 于G 后,得到含300角的Rt △ABG ,且EF 是Rt △ABG 的中位线,因此BG =2BF =2AG ,再设法证明AG =GC ,即有BF =FG =GC 。
分析三:由等腰三角形联想到“三线合一”的性质,作AD ⊥BC 于D ,则BD=CD ,考虑到∠B =300,不妨设EF =1,再用勾股定理计算便可得证。
以上三种分析的证明略。
探索与创新:【问题】请阅读下面材料,并回答所提出的问题:三角形内角平分线性质定理:三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例。
如图,△ABC 中,AD 是角平分线。
求证:ACABDC BD 。
例题图1F EC B A例题图2 G F ECB A例题图3D F ECB A问题图321ED CB A分析:要证ACABDC BD =,一般只要证BD 、DC 与AB 、AC 或BD 、AB 与DC 、AC 所在三角形相似,现在B 、D 、C 在同一条直线上,△ABD 与△ADC 不相似,需要考虑用别的方法换比。
我们注意到在比例式ACABDC BD =中,AC 恰好是BD 、DC 、AB 的第四比例项,所以考虑过C 作CE ∥AD 交BA 的延长线于E ,从而得到BD 、CD 、AB 的第四比例项AE ,这样,证明ACABDC BD =就可以转化为证AE =AC 。
初中数学 什么是垂直平分线和角平分线

初中数学什么是垂直平分线和角平分线垂直平分线和角平分线是初中数学中关于线段和角的重要概念。
它们在几何学中有着广泛的应用,用于描述和分析线段和角的性质和关系。
在本文中,我们将详细讨论垂直平分线和角平分线的概念、性质和应用。
一、垂直平分线垂直平分线是指将一条线段垂直平分为两个相等的线段的线。
具体来说,如果有一条线段AB,那么经过线段AB中点C并且垂直于线段AB的直线就是线段AB 的垂直平分线。
垂直平分线具有以下几个重要的性质:1. 垂直平分线将线段分成两个相等的部分,即线段AC与线段CB的长度相等。
2. 垂直平分线与线段所在的直线垂直相交,即线段AB和垂直平分线CD之间的夹角为90度。
3. 垂直平分线同时也是线段AB的中垂线,即线段AC与线段CB的中点C都在垂直平分线CD上。
垂直平分线在几何学中有着广泛的应用。
它可以用来解决关于线段的问题,比如寻找线段的中点、判断两个线段是否相等等。
此外,垂直平分线也可以用来解决关于垂直和平行的问题,比如判断两条线是否垂直、寻找垂直线的特性等。
二、角平分线角平分线是指将一个角平分为两个相等的角的线。
具体来说,如果有一个角ABC,那么经过角ABC的顶点B并且将角ABC分成两个相等的角的线就是角ABC的角平分线。
角平分线具有以下几个重要的性质:1. 角平分线将角分成两个相等的角,即角ABD与角CBD的度数相等。
2. 角平分线与角所在的边相交,并且将角分成相等的两部分,即角ABD和角CBD 的度数相等。
3. 角平分线与角的两条边的夹角相等,即角ABE与角EBD的度数相等。
角平分线在几何学中也有着广泛的应用。
它可以用来解决关于角的问题,比如寻找角的平分线、计算角的度数等。
此外,角平分线也可以用来解决关于直角、等腰三角形等问题,比如判断一个角是否为直角、判断一个三角形是否为等腰三角形等。
三、性质垂直平分线和角平分线具有一些重要的性质。
下面我们将分别讨论垂直平分线和角平分线的性质。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线段的垂直平分线
知识要点详解
1、线段垂直平分线的性质
(1)垂直平分线性质定理:线段垂直平分线上的点这条线段两个端点的距离相
等. 定理的数学表示:如图1,已知直线m 与线段AB 垂直相交于点D ,且AD =
BD ,若点C 在直线m 上,则AC =BC.定理的作用:证明两条线段相等 (2)线段关于它的垂直平分线对称.
2、线段垂直平分线性质定理的逆定理
(1)线段垂直平分线的逆定理:到一条线段两个端点距离相等的点在这条线段
的垂直平分线上. 定理的数学表示:如图2,已知直线m 与线段AB 垂直相交于点
D ,且AD =BD ,若AC =BC ,则点C 在直线m 上.定理的作用:证明一个点在某线
段的垂直平分线上.
3、关于三角形三边垂直平分线的定理(1)关于三角形三边垂直平分线的
定理:三角形三边的垂直平分线相交于一点,并且这一点到三个顶点的
距离相等.定理的数学表示:如图3,若直线,,i j k 分别是△ABC 三边AB 、
BC 、CA 的垂直平分线,则直线,,i j k 相交于一点O ,且OA =OB =OC.
定理的作用:证明三角形内的线段相等.(2)三角形三边垂直平分线的
交点位置与三角形形状的关系:若三角形是锐角三角形,则它三边垂直平分线的交点在三角形内部;若三角形是直角三角形,则它三边垂直平分线的交点是其斜边的中点;若三角形是钝角三角形,则它三边垂直平分线的交点在三角形外部.反之,三角形三边垂直平分线的交点在三角形内部,则该三角形是锐角三角形;三角形三边垂直平分线的交点在三角形的边上,则该三角形是直角三角形;三角形三边垂直平分线的交点在三角形外部,则该三角形是钝角三角形.
经典例题:
m
图1
D
A
B
C
m
图2
D
A
B
C
j
i
k
图3
O
B
C
A
例1 如图1,在△ABC 中,BC =8cm ,AB 的垂直平分线交AB 于点D ,交边AC 于点E ,△BCE 的周长等于18cm ,则AC 的长等于( ) A .6cm B .8cm C .10cm D .12cm 针对性练习:
已知:1)如图,AB=AC=14cm,AB 的垂直
平分线交AB 于点D ,交BC 于点 A E ,如果△EBC 的周长是24cm ,那么BC= 2) 如图,AB=AC=14cm,AB 的垂直平分线交AB 于点D ,交BC 于点 E ,如果BC=8cm ,那么△EBC 的周长是
如图,AB=AC,AB 的垂直平分线交AB 于点D ,交AC 于点E ,如果∠A=28度,
那么∠EBC 是
例2. 已知:如图所示,AB=AC ,DB=DC ,E 是AD 上一点,求证:BE=CE 。
针对性练习:
已知:在△ABC 中,ON 是AB 的垂直平分线,OA=OC
求证:点O 在BC 的垂直平分线
例3. 在△ABC 中,AB=AC ,AB 的垂直平分线与边AC 所在的直线相交所成锐角为50°,△ABC 的底角∠B 的大小为_______________。
针对性练习:
1. 在△ABC 中,AB=AC ,AB 的垂直平分线与AC 所在直线相交所得的锐角为40°,则底角B 的大小为________________。
例4、如图8,已知AD 是△ABC 的BC 边上的高,且∠C =2∠B ,
求证:BD =AC +CD. 证明:
课堂练习:
1.如图,AC =AD ,BC =BD ,则( )
A.CD 垂直平分AD
B.AB 垂直平分CD
C.CD 平分∠ACB
D.以上结论均不对
2.如果三角形三条边的中垂线的交点在三角形的外部, 那么,这个三角形是( )
A.直角三角形
B.锐角三角形
C.钝角三角形
D.等边三角形 3.下列命题中正确的命题有( )
①线段垂直平分线上任一点到线段两端距离相等;②线段上任一点到垂直平分线两端距离相等;③经过线段中点的直线只有一条;④点P 在线段AB 外且
B C D
E
B
A
C O
N
图8B C
D A
PA =PB ,过P 作直线MN ,则MN 是线段AB 的垂直平分线;⑤过线段上任一点可以作这条线段的中垂线.
A.1个
B.2个
C.3个
D.4个 4.如图,△ABC 中,AB 的垂直平分线交AC 于D ,
如果AC =5 cm ,BC =4cm ,那么△DBC 的周长是( ) A.6 cm B.7 cm C.8 cm D.9 cm
5.已知如图,在△ABC 中,AB =AC ,O 是△ABC 内一点,且OB =OC , 求证:AO ⊥B C.
6.如图,在△ABC 中,AB =AC ,∠A =120°,AB 的垂直平分线 MN 分别交BC 、AB 于点M 、N . 求证:CM =2BM .
课后作业:
1. 如图7,在△ABC 中,AC =27,AB 的垂直平分线交AB 于点D ,交AC 于点E ,△ACE
的周长为50,求BC 边的长.
2. 已知:如图所示,∠ACB ,∠ADB 都是直角,且AC=AD ,P 是AB 上任意一点,求证:CP=DP 。
角平分线
知识要点详解
4、角平分线的性质定理:
角平分线的性质定理:角平分线上的点到这个角的两边的距离相等. 定理的数学表示:如图4,已知OE 是∠AOB 的平分线,F 是OE 上一点,若CF ⊥OA 于点C ,DF ⊥OB 于点D ,则CF =DF.
定理的作用:①证明两条线段相等;②用于几何作图问题; 角是一个轴对称图形,它的对称轴是角平分线所在的直线.
5、角平分线性质定理的逆定理:
角平分线性质定理的逆定理:在角的内部,且到角的两边距离相等的点在这个角的
角平分线上.
定理的数学表示:如图5,已知点P 在∠AOB 的内部,且PC ⊥OA 于C ,PD ⊥OB 于D ,若PC =PD ,则点P 在∠AOB 的平分线上.
图4
C D
O
A
B F
E D
B
P
图7E
D
A
C
B
定理的作用:用于证明两个角相等或证明一条射线是一个角的角平分线 注意角平分线的性质定理与逆定理的区别和联系.
6、关于三角形三条角平分线的定理:
(1)关于三角形三条角平分线交点的定理:
三角形三条角平分线相交于一点,并且这一点到三边的距离相等.
定理的数学表示:如图6,如果AP 、BQ 、CR 分别是△ABC 的内角∠BAC 、∠ABC 、∠ACB 的平分线,那么:① AP 、BQ 、CR 相交于一点I ;② 若ID 、IE 、IF 分别垂直于BC 、CA 、AB 于点D 、E 、F ,则DI =EI =FI.
定理的作用:①用于证明三角形内的线段相等;②用于实际中的几何作图问题. (2)三角形三条角平分线的交点位置与三角形形状的关系:
三角形三个内角角平分线的交点一定在三角形的内部.
7、关于线段的垂直平分线和角平分线的作图:(1)会作已知线段的垂直平分线 (2)会
作已知角的角平分线;(3)会作与线段垂直平分线和角平分线有关的简单综合问题的图形.
经典例题:已知:如图,点B 、C 在∠A 的两边上,且AB=AC ,P 为∠A 内一点,PB=PC ,
PE ⊥AB ,PF ⊥AC ,垂足分别是E 、F 。
求证:PE=PF
针对性练习:
已知:如图所示PA 、PC 分别是△ABC 外角∠MAC 和∠NCA 平分线,它们交于P ,PD ⊥BM 于D ,PF ⊥BN 于F ,求证:BP 为∠MBN 的平分线。
例2、如图10,已知在直角梯形ABCD 中,AB ∥CD ,AB ⊥BC ,E 为BC
中点,连接AE 、DE ,DE 平分∠ADC ,求证:AE 平分∠BAD.
课堂笔记:
针对性练习:
如图所示,AB=AC ,BD=CD ,DE ⊥AB 于E ,DF ⊥AC 于F ,求证:DE=DF 。
例3、如图11-1,已知在四边形ABCD 中,对角线BD 平
分∠ABC ,且∠BAD 与∠BCD 互补, 求证:AD =CD.
1. △ABC 中,AB=AC ,AC 的中垂线交AB 于E ,△EBC 的周长为20cm ,AB=2BC ,则腰长为
________________。
2. 如图所示,AB//CD ,O 为∠A 、∠C 的平分线的交点,OE ⊥AC 于E ,且OE=2,则AB 与CD
之间的距离等于______________。
A B
O E
C D
3已知:如图,∠B=∠C=900,DM 平分∠ADC , AM 平分∠DAB 。
求证: M B=MC
课后作业:
1.如右图,已知BE ⊥AC 于E ,CF ⊥AB 于F ,BE 、CF 相交于点D ,若BD =CD . 求证:AD 平分∠BAC .
2. 如图所示,直线l l l 123,,表示三条互相交叉的公路,现在要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
A. 一处
B. 二处
C. 三处
D.
四处 l 3 l 1
l 2
图11-1图11-2
A
A
E
A C
B D D
D
E B D
A C F
E
M
B
D A。
