最新05 字典排列法与树形图法.ppt
合集下载
三年级数学思维训练[1]1
![三年级数学思维训练[1]1](https://img.taocdn.com/s3/m/3be3bb9eba4cf7ec4afe04a1b0717fd5370cb27a.png)
50-三年级期末复习与检测4
整数计算综合
还原问题
数阵图初步
竖式问题
几何图形简拼
路程、时间、速度
01-整数计算综合（1）
02-整数计算综合（2）
03-还原问题（1）
04-还原问题（2）
05-数阵图初步（1）
06-数阵图初步（2）
07-竖式问题（1）
08-竖式问题（2）
09-竖式问题（3）
10-竖式问题（4）
37-长度计算1
38-长度计算2
39-长度计算3
40-角度的计算1
41-角度的计算2
42-角度的计算3
43-找位置1
44-找位置2
火柴棍算式与生活趣题
三年级期末复习与检测
45-火柴棍算式与生活趣题1
46-火柴棍算式与生活趣题2
47-三年级期末复习与检测1
48-三年级期末复习与检测2
49-三年级期末复习与检测3
11-几何图形简拼（1）
12-几何图形简拼（2）
13-几何图形简拼（3）
14-几何图形简拼（4）
15-路程、时间、速度（1）
16-路程、时间、速度（2）
17-路程、时间、速度（3）
18-路程、时间、速度（4）
行程中的线段图
简单抽屉原理
基本直线形面积公式
底、高的选取与组合
变倍问题
和差倍中的分组比较
19-行程中的线段图（1）
复杂数阵图
有特殊要求的挑选
捆绑法与插空法
最值问题一
40-多次往返相遇与追与1
41-多次往返相遇与追与2
42-多次往返相遇与追与3
43-多次往返相遇与追与4
44-从洛书到幻方1
45-从洛书到幻方2
整数计算综合
还原问题
数阵图初步
竖式问题
几何图形简拼
路程、时间、速度
01-整数计算综合（1）
02-整数计算综合（2）
03-还原问题（1）
04-还原问题（2）
05-数阵图初步（1）
06-数阵图初步（2）
07-竖式问题（1）
08-竖式问题（2）
09-竖式问题（3）
10-竖式问题（4）
37-长度计算1
38-长度计算2
39-长度计算3
40-角度的计算1
41-角度的计算2
42-角度的计算3
43-找位置1
44-找位置2
火柴棍算式与生活趣题
三年级期末复习与检测
45-火柴棍算式与生活趣题1
46-火柴棍算式与生活趣题2
47-三年级期末复习与检测1
48-三年级期末复习与检测2
49-三年级期末复习与检测3
11-几何图形简拼（1）
12-几何图形简拼（2）
13-几何图形简拼（3）
14-几何图形简拼（4）
15-路程、时间、速度（1）
16-路程、时间、速度（2）
17-路程、时间、速度（3）
18-路程、时间、速度（4）
行程中的线段图
简单抽屉原理
基本直线形面积公式
底、高的选取与组合
变倍问题
和差倍中的分组比较
19-行程中的线段图（1）
复杂数阵图
有特殊要求的挑选
捆绑法与插空法
最值问题一
40-多次往返相遇与追与1
41-多次往返相遇与追与2
42-多次往返相遇与追与3
43-多次往返相遇与追与4
44-从洛书到幻方1
45-从洛书到幻方2
字典排列法高等代数
字典排列法高等代数
字典排列法是指根据字典序进行排列的方法。
在高等代数中，字典排列法常用于解决排列组合问题，特别是涉及排列的问题。
字典排列法的基本步骤如下：
1. 将待排列的元素按照字典序进行排序，通常是按照字母顺序或数字大小进行排序。
2. 根据元素的个数，确定排列的总数。
设有n个元素，则总共有n!个排列，其中n!表示n的阶乘。
3. 根据排列的总数，确定排列的序号。
每个排列均有一个唯一的序号，从1到n!依次排列。
4. 根据序号，确定排列的具体顺序。
可以使用迭代法或递归法来确定每个元素在排列中的位置。
字典排列法在高等代数中有广泛的应用，特别是在组合数学、概率论和计算机科学等领域。
它可以用来解决排列组合问题，计算组合数和概率，以及生成排列的全集。
树状图、列表法共26页文档
树状图、列表法
1、 舟 遥 遥 以 轻飏， 风飘飘 而吹衣 。 2、 秋 菊 有 佳 色，裛 露掇其 英。 3、 日 月 掷 人 去，有 志不获 骋。 4、 未 言 心 相 醉，不 再接杯 酒。 5、 黄 发 垂 髫 ，并怡 然自乐 。
▪
26、要使整个人生都过得舒适、愉快，这是不可能的，因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情，化为上进的力量，才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者，好之者不如乐之者。——孔子
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
▪
30、意志是一个强壮的盲人，倚靠在明眼的跛子肩上。——叔本华
谢谢！
26
1、 舟 遥 遥 以 轻飏， 风飘飘 而吹衣 。 2、 秋 菊 有 佳 色，裛 露掇其 英。 3、 日 月 掷 人 去，有 志不获 骋。 4、 未 言 心 相 醉，不 再接杯 酒。 5、 黄 发 垂 髫 ，并怡 然自乐 。
▪
26、要使整个人生都过得舒适、愉快，这是不可能的，因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情，化为上进的力量，才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者，好之者不如乐之者。——孔子
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
▪
30、意志是一个强壮的盲人，倚靠在明眼的跛子肩上。——叔本华
谢谢！
26
3学通数学奥数计数专题-01 字典排列法和树形图法
中小学数学精品视频课程
字典排列法
像字典里的单词顺序一样排列出所有答案
中小学数学精品视频课程
字典排列法
【例题】盼豆、红豆和蓝豆三个人去游乐园玩，三人在藏宝屋中一共
发现了5件宝物，三人找到的宝物数量共有多少种不同的可能？（可以 有人没有发现宝物）
中小学数学精品视频课程
字典排列法
【例题】商店里有12种不同的签字笔，价格分别是1、2、3、4、5、 ···、
11、12元.盼豆准备买3支不同价钱的签字笔，并且希望恰好花掉15元.请 问：盼豆一共有多少种不同的买法？
中小学数学精品视频课程
• 树形图法
中小学数学精品视频课程
树形图法
简单枚举
【例题】老师给了盼豆14个相同的练习本，如果盼豆把这些本子全部分
给了红豆和蓝豆，并且每人都要分到练习本，共有几种不同的分法？
有序枚举
中小学数学精品视频课程
简单枚举
【例题】盼豆买回了两袋糖豆，每袋10个，要把这两袋糖豆分成3堆，每
堆至少要有5个，那么至少有多少种不同的分法？
无序枚举
中小学数学精品视频课程
简单枚举
【例题】班主任要从甲、乙、丙、丁、戊这五个小朋友里面选出四个人
参加乒乓球赛，有多少种不同的选法？如果已经选出了甲、乙、丙、丁， 现在要把他们分成两组，进行双打比赛，有多少种不同的分法？
中小学数学精品视频课程
• 字典排列法
个座位换到另一个座位，结果她换了5次之后，还在座位������上。请问： 视频课程
字典排列法和树形图法
主讲：土豆 助教：五豆
中小学数学精品视频课程
• 简单枚举 • 字典排列法 • 树形图法
中小学数学精品视频课程
• 简单枚举
排列组合生成算法之字典序法和换位法动画ppt
2
例题：请写出1234的全排列
Step1：以1234开始排序，在每个数字上标一向 左箭头。 箭头所指一侧相邻的数若比它小，则称该数处于活 动状态 Step2：找最大的处于活动状态的数m Step3：将m与其箭头所指的邻数互换位置 Step4：将所得排列中比m大的数p的方向调整， 即改为相反方向 Step5：重复Step2~Step4直至无活动状态的数
2
例题：请写出1234的全排列 1 2 3 4
1234
2
例题：请写出1234的全排列 1 2 4 3
1234 1243
2
例题：请写出1234的全排列 1 4 2 3
1234 1243 1423
2
例题：请写出1234的全排列 4 1 2 3
1234 1243 1423 4123
2
例题：请写出1234的全排列 4 1 3 2
i-1者)
(4) 反排pj后面的数得到(q):
p1…pi-2 pj pnpj+1pi-1pj-1 ….pi+1 pi
1
例题：设有排列(p) =2763541, 按照字典式排 序, 它的下一个排列是谁?
Step1:求 i=maxj pj-1pj (找最后一个正序)
2
7
6
3
5
4
1
1
例题：设有排列(p) =2763541, 按照字典式排序, 它的下一个 排列是谁?
2
例题：请写出1234的全排列
Step1：以1234开始排序，在每个数字上标一向 左箭头。 箭头所指一侧相邻的数若比它小，则称该数处于活 动状态 Step2：找最大的处于活动状态的数m Step3：将m与其箭头所指的邻数互换位置 Step4：将所得排列中比m大的数p的方向调整， 即改为相反方向 Step5：重复Step2~Step4直至无活动状态的数
部编版数学三年级上册第13讲.字典排列法和树形图 教师版
那么比赛的进程有多少种可能？ [分析] 令常昊为 a，古力为 b，则进行分类枚举有：
如果第一场常昊胜，共有 6 种：
a
【对应学案】【学案 1】
例２
（明心教育 2005 年秋季三年级）婷婷到游乐园游玩，游乐园有一张价目表：
类型
价格 时间
骑木马 1 元 10 分钟
蹦床
2 元 10 分钟
电动车 5 元 10 分钟
碰碰车 8 元 10 分钟 爸爸只让婷婷玩 20 分钟，那么，婷婷共有多少种不同的搭配方式可以玩？请你一一列举出来。 【分析】共有 10 种不同的搭配方.骑木马+骑木马；蹦床+蹦床；电动车+电动车；碰碰车+碰碰 车；
[分析]（1）2 种；两间房依次住着艾迪、薇儿或者薇儿、艾迪。 （2）6 种；三间房依次住着①艾迪、薇儿、哈哈，②艾迪、哈哈、薇儿，③薇儿、艾迪、哈 哈，④薇儿、哈哈、艾迪，⑤哈哈、艾迪、薇儿，⑥哈哈、薇儿、艾迪。
【巩固】（第七届“小机灵杯”小学生数学竞赛（决赛）试题）自然数 12、135、1349 这些数有一个共 同的特点，相邻两个数字，左边的数字小于右边的数字，我们取名为“上升数”。用 5、6、7、8 这四个数字，可以组成（ ）个“上升数”.
而中文字典的排列是什么样的呢？现在绝大多数的中文字典的排列和英文词典是差不多的，每 个汉字是按照它的汉语拼音的字母顺序去排列的 ，同样的拼音再按声调的顺序排列 。而在拼音发明 之前 ，中文字典都是按照部首来排列的 。
按照这样的顺序排出的字典、词典方便易查，比如想在一本英文词典中找到“apple”。我们只要 先找到第一个字母是 a 的单词的位置，再找第二个字母是 p 的字母的位置，以此类推，由于每个字 母的排列都是从 a 到 z 的，我们可以很快找到 apple 的位置。 同学们可以想一想，如果这本词典是 胡乱排列每个单词的，那么我们想找到“apple”就只能靠“撞大运”了，假如真有这样的词典，我们也 不会去买的。
如果第一场常昊胜，共有 6 种：
a
【对应学案】【学案 1】
例２
（明心教育 2005 年秋季三年级）婷婷到游乐园游玩，游乐园有一张价目表：
类型
价格 时间
骑木马 1 元 10 分钟
蹦床
2 元 10 分钟
电动车 5 元 10 分钟
碰碰车 8 元 10 分钟 爸爸只让婷婷玩 20 分钟，那么，婷婷共有多少种不同的搭配方式可以玩？请你一一列举出来。 【分析】共有 10 种不同的搭配方.骑木马+骑木马；蹦床+蹦床；电动车+电动车；碰碰车+碰碰 车；
[分析]（1）2 种；两间房依次住着艾迪、薇儿或者薇儿、艾迪。 （2）6 种；三间房依次住着①艾迪、薇儿、哈哈，②艾迪、哈哈、薇儿，③薇儿、艾迪、哈 哈，④薇儿、哈哈、艾迪，⑤哈哈、艾迪、薇儿，⑥哈哈、薇儿、艾迪。
【巩固】（第七届“小机灵杯”小学生数学竞赛（决赛）试题）自然数 12、135、1349 这些数有一个共 同的特点，相邻两个数字，左边的数字小于右边的数字，我们取名为“上升数”。用 5、6、7、8 这四个数字，可以组成（ ）个“上升数”.
而中文字典的排列是什么样的呢？现在绝大多数的中文字典的排列和英文词典是差不多的，每 个汉字是按照它的汉语拼音的字母顺序去排列的 ，同样的拼音再按声调的顺序排列 。而在拼音发明 之前 ，中文字典都是按照部首来排列的 。
按照这样的顺序排出的字典、词典方便易查，比如想在一本英文词典中找到“apple”。我们只要 先找到第一个字母是 a 的单词的位置，再找第二个字母是 p 的字母的位置，以此类推，由于每个字 母的排列都是从 a 到 z 的，我们可以很快找到 apple 的位置。 同学们可以想一想，如果这本词典是 胡乱排列每个单词的，那么我们想找到“apple”就只能靠“撞大运”了，假如真有这样的词典，我们也 不会去买的。
树状图、列表法 ppt课件
2、如图,袋中装有两个完全相同的球,分别 标有数字“1”和“2”.小明设计了一个游 戏:游戏者每次从袋中随机摸出一个球,并自 由转动图中的转盘(转盘被分成相等的三个 扇形).
1 2
3
游戏规则是: 如果所摸球上的数字与转盘转出的数字 之和为2,那么游戏者获胜.求游戏者获胜 的概率.
ppt课件 15
由上图可知，两次摸球可能出现的结果共有 9种，而出现（白，白）的结果只有4种， 因此小亮两次都摸到白球的概率为4/9
变式：若上例中小亮第一次摸出一球后 不放回，则两次都摸到白球的概率为多 少？
解析：画出树状图
第一次 第二次 红 白1 白2
红 白1 红 白 2 白1 白2 ppt课件 由上图可知，两次都摸到白球的概率为 1/3
ppt课件
1
“剪刀，石头，布”这个 游戏公平吗
ppt课件
2
．
概率的计算公式：
关注结果的个数
所有等可能结果的个数
P(关注的结果)=
(1)要清楚所有等可能(机会均等)的结果； (2)要清楚我们所关注发生哪个或哪些结 果.
ppt课件
3
预习指导: 1、我们可以用列表法 和 画树状图 的方法来 计算 随机事件 发生的概率； 2、将一枚硬币连掷3次，出现“两正，一 反”的概率是多少？ 3、小晶和小红玩掷骰子游戏，每人将一个 各面分别标有1,2,3,4,5,6的正方体骰子掷一 次，把两人掷得的点数相加，并约定：点数 之和等于6，小晶赢；点数之和等于7，小 红赢；点数之和是其他数，两人不分胜负。 问他们谁获胜的概率大?请你用“画树状图” 或“列表”的方法加以分析说明。
1一个袋子中放有1个红球2个白球它们除颜色外其他都一样小亮从袋中摸出一个球后个白球它们除颜色外其他都一样小亮从袋中摸出一个球后放回摇匀再摸出一个球请你利用画树状图分析并求出小亮两次都能摸到白球的概率摇匀再摸出一个球请你利用画树状图分析并求出小亮两次都能摸到白球的概率第一次红白第一次红白1白2红红红白1白1白1白2白2白2第二次解
第五讲 枚举法二-树形图与分类枚举
百位为 2：258、259、269； 3 个
百位为 3：369
1个
共 6+3+1=10 个
巨人秋季培优班 第五讲枚举法（二） 朱海涛
步骤少，每个步骤选择少适用 ②分类枚举：找到题目中的分类方法，按类进行有序枚举 二、做题步骤：①按一定顺序对题目进行分类；
②按类对题目进行枚举； ③多回头做到不重不漏，
本讲例题
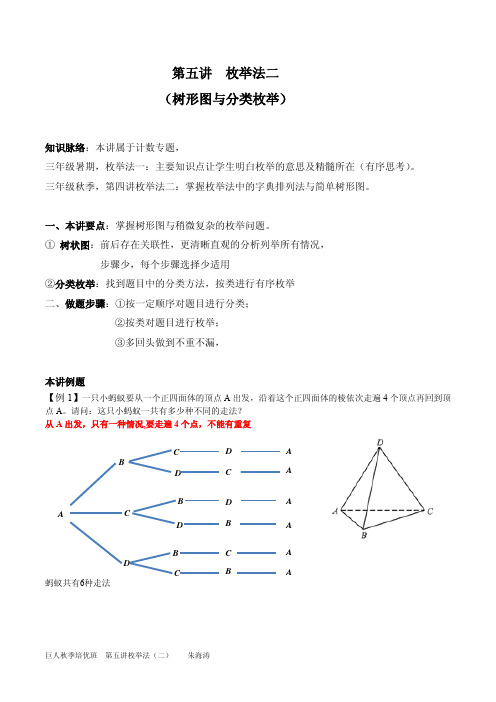
【例 1】一只小蚂蚁要从一个正四面体的顶点 A 出发，沿着这个正四面体的棱依次走遍 4 个顶点再回到顶
点 A。请问：这只小蚂蚁一共有多少种不同的走法？ 从 A 出发，只有一种情况,要走遍 4 个点，不能有重复
此类题目需要把题看清楚，比如
【培优大闯关 3】满足下面性质的数称为“美数“：它的个位比十位大，十位比百位大，并且相邻
两位数字的差不小于 3. 这样的“美数”共有多少个，
按照百位、十位、、个位依次增大来进行枚举，需注意差不小于 3，不小于可以等于 3
百位为 1：147、148、149、158、159；169 6 个
共有 1+4+3=8 种吃法，枚举时要注意每天至少 2 个和总个数。
【例 4】有一些数，它们小于 1000，各个数位上数字为 1 或 2。并且 1 的个数比 2 的个数多，那么这样的
数一共有多少个？
首先：想想以什么来分类进行枚举，按位数、1 的个数、2 的个数都可以分类
1.位数：最多为 3 位数（先从全一样的数字开始枚举）
首先：想想以什么来分类进行枚举，都是 4 位数，千位最小，可以从千位进行分类枚举
按照千位、百位、十位、个位、依次增大来进行枚举，需注意差不超过 2，不超过 2 可以等于 2
千位为 1：1234、1235、1245、1246、1345、1346、1356、1357 共 8 个
2024版《数据结构图》ppt课件
重要性
良好的数据结构可以带来更高的运 行或存储效率，是算法设计的基础， 对程序设计的成败起到关键作用。
常见数据结构类型介绍
线性数据结构
如数组、链表、栈、队 列等，数据元素之间存
在一对一的关系。
树形数据结构
如二叉树、多叉树、森 林等，数据元素之间存
在一对多的关系。
图形数据结构
由顶点和边组成，数据 元素之间存在多对多的
队列定义、特点及应用场景
队列的特点 只能在队尾进行插入操作，队头进行删除操作。
队列是一种双端开口的线性结构。
队列定义、特点及应用场景
应用场景 操作系统的任务调度。 缓冲区的实现，如打印机缓冲区。
队列定义、特点及应用场景
广度优先搜索（BFS）。
消息队列和事件驱动模型。
串定义、基本操作及实现方法
最短路径问题 求解图中两个顶点之间的最短路径，即路径上边 的权值之和最小。
3
算法介绍 Prim算法、Kruskal算法、Dijkstra算法、Floyd 算法等。
拓扑排序和关键路径问题探讨
拓扑排序
对有向无环图（DAG）进行排序， 使得对每一条有向边(u,v)，均有
u在v之前。
关键路径问题
求解有向无环图中从源点到汇点 的最长路径，即关键路径，它决
遍历二叉树和线索二叉树
遍历二叉树
先序遍历、中序遍历和后序遍历。遍历算 法可以采用递归或非递归方式实现。
VS
线索二叉树
利用二叉链表中的空指针来存放其前驱结 点和后继结点的信息，使得在遍历二叉树 时可以利用这些线索得到前驱和后继结点， 从而方便地遍历二叉树。
树、森林与二叉树转换技巧
树转换为二叉树
加线、去线、层次调整。将树中的每个结点的所有孩子结点用线连接起来，再去掉与原结点相连的线，最后 将整棵树的层次进行调整，使得每个结点的左子树为其第一个孩子，右子树为其兄弟结点。
良好的数据结构可以带来更高的运 行或存储效率，是算法设计的基础， 对程序设计的成败起到关键作用。
常见数据结构类型介绍
线性数据结构
如数组、链表、栈、队 列等，数据元素之间存
在一对一的关系。
树形数据结构
如二叉树、多叉树、森 林等，数据元素之间存
在一对多的关系。
图形数据结构
由顶点和边组成，数据 元素之间存在多对多的
队列定义、特点及应用场景
队列的特点 只能在队尾进行插入操作，队头进行删除操作。
队列是一种双端开口的线性结构。
队列定义、特点及应用场景
应用场景 操作系统的任务调度。 缓冲区的实现，如打印机缓冲区。
队列定义、特点及应用场景
广度优先搜索（BFS）。
消息队列和事件驱动模型。
串定义、基本操作及实现方法
最短路径问题 求解图中两个顶点之间的最短路径，即路径上边 的权值之和最小。
3
算法介绍 Prim算法、Kruskal算法、Dijkstra算法、Floyd 算法等。
拓扑排序和关键路径问题探讨
拓扑排序
对有向无环图（DAG）进行排序， 使得对每一条有向边(u,v)，均有
u在v之前。
关键路径问题
求解有向无环图中从源点到汇点 的最长路径，即关键路径，它决
遍历二叉树和线索二叉树
遍历二叉树
先序遍历、中序遍历和后序遍历。遍历算 法可以采用递归或非递归方式实现。
VS
线索二叉树
利用二叉链表中的空指针来存放其前驱结 点和后继结点的信息，使得在遍历二叉树 时可以利用这些线索得到前驱和后继结点， 从而方便地遍历二叉树。
树、森林与二叉树转换技巧
树转换为二叉树
加线、去线、层次调整。将树中的每个结点的所有孩子结点用线连接起来，再去掉与原结点相连的线，最后 将整棵树的层次进行调整，使得每个结点的左子树为其第一个孩子，右子树为其兄弟结点。
多元多项式字典排列法
多元多项式字典排列法
哎呀呀，一听到“多元多项式字典排列法”这个名字，是不是感觉脑袋都大啦？哈哈，一开始我也是这样呢！
先来说说啥是多项式吧。
就像我们平时吃的水果，有苹果、香蕉、橙子，每个水果都不一样。
多项式呢，就是由好多“数字和字母的组合”这些“小伙伴”凑在一起形成的。
那多元又是啥呢？想象一下，我们的班级里不只有男生，还有女生，这就是多元呀！在多项式里，就是不止一个未知数，比如说有x ，还有y 。
那字典排列法又是啥玩意儿呢？咱们都知道查字典吧，是按照字母的顺序来的。
这个字典排列法也差不多，就是按照一定的顺序来排列这些多元多项式。
比如说，有两个多项式，一个是2x + 3y ，另一个是3x + 2y 。
那按照字典排列法，就先看x 前面的系数，2 比3 小，所以2x + 3y 就排在前面。
再复杂一点的，像5x²y + 2xy² - 3x + 4y 这样的多项式。
先看最高次项，就是x 的次数和y 的次数加起来最大的那一项，这里就是5x²y 。
然后再依次比较其他项。
我一开始学这个的时候，那叫一个头疼！我就跟同桌说：“这也太难了吧，咋能记住啊？”同桌瞪大眼睛说：“别着急，咱们多练练肯定能行！” 老师也鼓励我们：“同学们，这就像搭积木，一块一块来，总能搭出漂亮的城堡！”
经过好多好多的练习，我慢慢发现，其实也没那么可怕啦！每次做出一道题，我都兴奋得不行，感觉自己像个小英雄！
你说，这多元多项式字典排列法是不是像个调皮的小精灵，一开始让我们摸不着头脑，等我们熟悉了，它就乖乖听话啦？
反正我觉得，虽然过程有点难，但是只要我们不放弃，就一定能把它拿下！。
相关主题