基数和序数练习 (2)
最新基数与序数专项练习
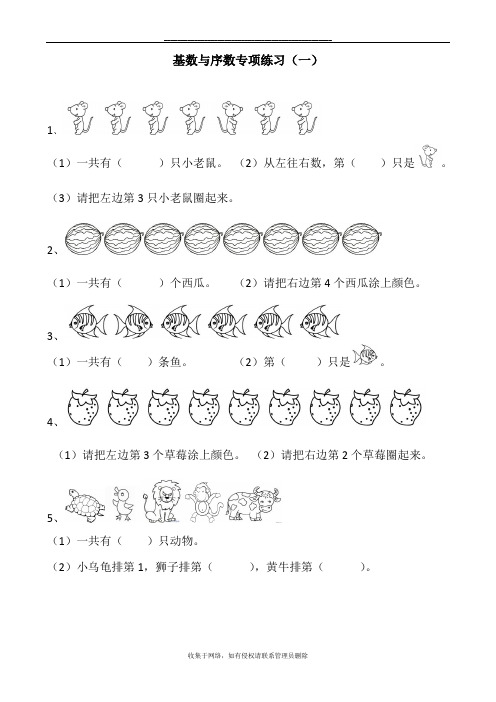
基数与序数专项练习(一)
1、
(1)一共有()只小老鼠。
(2)从左往右数,第()只是。
(3)请把左边第3只小老鼠圈起来。
2、
(1)一共有()个西瓜。
(2)请把右边第4个西瓜涂上颜色。
3、
(1)一共有()条鱼。
(2)第()只是。
4、
(1)请把左边第3个草莓涂上颜色。
(2)请把右边第2个草莓圈起来。
5、
(1)一共有()只动物。
(2)小乌龟排第1,狮子排第(),黄牛排第()。
基数与序数专项练习(二)
1、
(1)一共有()个灯笼,是第()个。
(2)请把右边第一个圈起来。
2、
(1)一共有()个萝卜。
(2)请把最中间的萝卜涂上颜色,它的左右两边分别有()个萝卜。
(3)请把最左边的2个萝卜圈起来。
3、
(1)从左边起,第1个是,第()个是。
(2)从右边起,),排第(),排第()。
(3)请把左边2个图案涂上颜色,把右边2个图案圈起来。
4、
(1的左边是(),右边是()。
(2)请把左边第6个图案圈起来,右边第二个图案涂上颜色。
(3)一共有()个图案。
排第1,排第(),排第()排第()。
7.3.4.2 故障代码
故障的代码、产生原因及修正方法见下表。
灰影部分是A故障。
对于表中以黑底白字标明的故障,可在应用中编
辑对此类故障的响应方式。
见变频器保护参数组。
幼儿园中班教案《基数与序数》

幼儿园中班教案《基数与序数》一、教学内容本节课选自幼儿园中班数学教材第四章《数的认识》第三节“基数与序数”。
详细内容包括:理解基数与序数的概念,学会用基数词和序数词描述物品的数量和顺序,并能运用到实际生活中。
二、教学目标1. 知识与技能:掌握基数与序数的概念,能正确使用基数词和序数词描述物品的数量和顺序。
2. 过程与方法:通过观察、操作、交流等实践活动,培养幼儿的观察能力、动手能力和语言表达能力。
3. 情感态度与价值观:激发幼儿对数学的兴趣,培养其合作意识和团队精神。
三、教学难点与重点难点:基数与序数的概念区分,正确使用基数词和序数词。
重点:理解基数与序数的意义,学会用基数词和序数词描述物品的数量和顺序。
四、教具与学具准备教具:卡片、图片、磁性教具、白板、白板笔。
学具:幼儿用书、练习册、画笔、剪刀、胶水。
五、教学过程1. 实践情景引入(5分钟)(1)组织幼儿排队洗手,引导幼儿观察并描述队伍中的顺序。
(2)提问:我们排队的时候,每个人都在什么位置?这个位置是怎么表示的?2. 教学基数与序数概念(15分钟)(1)教师通过卡片、图片等教具,展示不同数量的物品,引导幼儿用基数词描述数量。
(2)教师用磁性教具演示序数的概念,让幼儿用序数词描述顺序。
(3)讲解基数与序数的区别,让幼儿举例说明。
3. 例题讲解(15分钟)(1)教师出示例题,讲解解题思路。
(2)教师引导幼儿独立完成练习题,并给予评价。
4. 随堂练习(10分钟)(1)教师发放练习册,组织幼儿进行随堂练习。
(2)教师对练习情况进行检查,及时解答幼儿的疑问。
5. 小组活动(10分钟)(1)将幼儿分成若干小组,每组完成一个与基数和序数相关的任务。
(2)教师巡回指导,观察幼儿在活动中的表现。
(2)教师针对幼儿的表现进行点评,提出改进意见。
六、板书设计1. 基数与序数的概念2. 基数词和序数词的用法3. 例题及解题思路4. 小组活动任务七、作业设计1. 作业题目:(2)请举例说明基数与序数的区别。
基数词与序数词的区别和用法(细整理)

基数词与序数词的区别和用法在日常生活中,我们经常需要使用数字来表示数量。
然而,数字不仅可以用来表示数量,还可以用来表示顺序。
这就涉及到了两种数字:基数词和序数词。
虽然它们看起来很相似,但它们各有其特定用法和区别。
在本文中,将通过细整理来详细解释它们之间的区别和用法。
什么是基数词?基数词,又称基数数字,是用来表示数量或数目的数字,如1、2、3、4等。
基数词通常用于描述数量的大小或数量的增加和减少。
在英文中,基数词是形容词,通常放在名词前面。
下面是一些例子:•I have two dogs.(我有两只狗。
)•We need five pencils.(我们需要五支铅笔。
)什么是序数词?序数词,又称序数数字,是用来表示顺序或顺序位置的数字,如第一、第二、第三、第四等。
序数词通常用来表示比较、排名、次序或事件顺序。
下面是一些例子:•I’m the third person in line.(我是排队的第三个人。
)•He finished in second place.(他获得了第二名。
)需要注意的是,在英文中,序数词通常需要加上“th”后缀。
而在汉语中,不需要使用后缀或修饰词。
基数词和序数词的区别:基数词和序数词的区别可以归纳为以下方面:1.用途不同:基数词用来表示数量,而序数词用来表示顺序或顺序位置。
2.表达方式不同:基数词是常规数字,而序数词是在基数词前加上“第”字,表示顺序位置。
例如,基数词“5”的序数词是“第五”。
3.语法作用不同:基数词在句子中通常用来作主语、宾语、形容词等。
而序数词则通常用来在句子中修饰名词、描述某一物品在某个顺序中的位置。
基数词和序数词的用法:基数词和序数词的用法有很多,下面将重点介绍一些最常见的用法:基数词的用法:1.描述数量或数目:例如:There are five apples on the table.(桌子上有五个苹果。
)2.表示年龄:例如:She is ten years old.(她十岁了。
基数词变序数词规律

基数词变序数词规律一.口诀:一、二、三,特殊记;th从四起;八加h,九去e;ve 要用f替;整十基数变序数,先把ty变成tie;要是遇到几十几,前半基数后半序。
基数词序数词基数词序数词1 one 第一 first2 two 第二second3 three 第三 third4 four第四fourth5 five 第五fifth6 six第六 sixth7 seven 第七seventh 8 eight第八eighth9 nine 第九ninth 10 ten第十 tenth11 eleven 第十一eleventh 12 twelve 第十二twelfth13thirteen 第十三thirteenth14fourteen 第十四 fourteenth15 fifteen 第十五fifteenth16 sixteen 第十六sixteenth7seventeen 第十七 seventeenth18 eighteen 第十八eighteenth19 nineteen 第十九nineteenth20 twenty 第二十twentieth21 twenty-one 第二十一 twenty-first22 twenty-two 第二十二twenty-second23 twenty-three 第二十三 twenty-third基数词序数词34 thirty-four 第三十四 thirty-fourth 45 forty-five 第四十五forty-fif th56 fifty-six 第五十六 fifty-sixt h99 ninety-nine 第九十九 ninety-nint h100 hundred 第一百 hundredt h二、巩固练习:(一)写出下列词的序数词形式。
1. one2.two3.six 4.five5.nine6.twelve7.eight8.twenty-one(二)写出下列单词的基数词形式。
6到9的认识教案及反思

6到9的认识教案及反思
教学目标:
让学生掌握6到9的顺序,明白基数和序数的意义,会用9以内数的加减法。
培养学生学习数学的兴趣和良好的学习习惯。
教学内容:
复习1到5的顺序。
学习6到9的顺序。
练习:做一做,练习二。
教学重点:
掌握6到9的顺序。
教学难点:
理解基数和序数的意义。
教具准备:
数字卡片、算盘。
教学过程:
一、复习导入
复习1到5的顺序。
做练习二第1题,集体订正。
导入新课:我们已经学习了1到5的顺序,现在我们来学习6到9的顺序。
二、学习新课
学习6到9的顺序。
(1)出示数字卡片6,让学生读出并说出6的意义。
(2)用同样的方法学习7、8、9。
2. 做练习二第2题,集体订正。
做练习二第3题,先让学生独立完成,再集体订正。
做练习二第4题,先让学生读题,再让学生独立完成,最后集体订正。
做练习二第5题,先让学生读题,再让学生独立完成,最后集体订正。
做练习二第6题,先让学生读题,再让学生独立完成,最后集体订正。
做练习二第7题,先让学生读题,再让学生独立完成,最后集体订正。
做练习二第8题,先让学生读题,再让学生独立完成,最后集体订正。
做练习二第9题,先让学生读题,再让学生独立完成,最后集体订正。
做练习二第10题,先让学生读题,再让学生独立完成,最后集体订正。
高斯奥数一年级上册含答案第13讲 基数与序数

第十三讲基数与序数前续知识点:一年级第一讲;XX模块第X讲后续知识点:X年级第X讲;XX模块第X讲把画风换一下.我们通常说的基数就是表示前面或后面有几个的意思,而序数则是表示按一定顺序排第几个.【提示】以你的左边为左边,数一数。
请你把从左往右数的第3个笑脸涂上红色,将右边4个笑脸圈起来.在解答这类问题时,我们需要弄清计数方向,是从左往右还是从前往后计数。
例题1将左边3个月亮圈起来,把从右往左数的第5个月亮涂上自己喜欢的颜色.练习1【提示】给每个小动物编号!下面共有几张数字卡片?数字卡片7从左数起排第几?它的左边有几张数字卡片?它的右边有几张数字卡片?3 4 7 9 8 5 21例题2一天,小动物们相约去春游.你们看,它们举着旗子,由小乌龟领队,一个个多开心呀!请小朋友们数一数: (1)共有几只小动物?(2)从前往后数,狮子排在第几位?狮子的前面有几只小动物,后面还有几只小动物呢?(3)从后往前数,大公鸡排在第几位?大公鸡的后面有几只小动物?前面还有几只小动物呢?春游练习2【提示】排第4,它的左边应该画几个三角形?公交车是从后面数起的第4辆,大树挡住了几辆车?公交车的前面有几辆车?一共有几辆车?【提示】大树挡住了几只小动物?(1)大树左边有几只小动物?大树右边呢?(2)从左往右数,小狗排在第6位,一共有几只小动物?(3)从右往左数,小虎排在第几位?例题4从左往右数,排第4,左边还有几个三角形?把它们画出来.从右往左数,排第6,右边还有几个三角形?把它们画出来.这排一共有几个三角形?例题3练习3下图中,从左往右数,排在第8个,一共有几个圆圈?从右往左数,排在第几个?【提示】林林的前面有3个人,数到林林了吗?【提示】花花被数了几次?例题6小狗花花参加“汪汪”合唱队表演.回家后,妈妈问花花:“你们合唱队一共有多少只小动物啊?”花花想了想说:“从左数起,我是第6个,从右数起,我也是第6个.”同学们,你们知道花花的合唱队一共有多少只小动物吗?…… ……花花例题5一队小朋友上山植树,林林的前面有3个人,从后面数林林是第8个,这一队一共有多少个小朋友?练习4课外阅读关于三、四、五世界三大饮料:茶叶、咖啡、可可.江南三大名楼:武汉的黄鹤楼、湖南的岳阳楼、江西南昌的滕王阁.我国的三大石窟:莫高窟、云冈石窟、龙门石窟.花木四君子:松、竹、梅、兰.书生四艺:琴、棋、书、画.文房四宝:笔、墨、纸、砚.(湖笔、徽墨、宣纸、端砚)囊括中国全部古籍的精华的四库全书:经、史、子、集.佛教四大名山:五台山、普陀山、峨眉山、九华山.五香:茴香、花椒、大料、桂皮、丁香.五彩:金、银、铜、铁、锡.五行:金、木、水、火、土.五方:东、南、西、北、中.五岳:东岳泰山、南岳衡山、西岳华山、北岳恒山、中岳嵩山.五色:青、赤、黄、白、黑.五音:宫、商、角(jué)、徵(zhí)、羽.五脏:心、肝、脾、肺、胃.作业1.把左边的4个“☆”圈起来,把从右边数第2个“☆”涂上自己喜欢的颜色.2. (1)图中共有几个水果?(2)从左往右数,第________个和第________个是,第________个和第________个是,第________个和第________个是.(3)从右往左数,第________个和第________个是,第________个和第________个是,第________个和第________个是.3. 从右往左数,■排第5,一共有几个正方形?4. 下图中,从右往左数,排在第9个,从左往右数,排在第几个?5. 小动物们排成一排去春游,猴子的前面有4只小动物,猴子的后面有8只小动物,参加春游的小动物共有几只?第十三讲基数与序数1.例题1答案:详解:分清“有几”和“第几”,认识基数与序数:基数是“有几”,序数是“第几”.2.例题2答案:(1)一共有7只小动物;(2)从前往后数,狮子排在第3位,狮子的前面有2只小动物,后面还有4只小动物;(3)从后往前数,大公鸡排在第4位,大公鸡的后面有3只小动物,前面还有3只小动物详解:分清“有几”和“第几”,数一数即可.3.例题3答案:如图所示,这排一共有13个三角形详解:从左往右数排第4,说明左边有3个三角形,从右往左数排第6,说明右边有5个三角形,一共有35513++=个三角形.4.例题4答案:(1)大树左边有3只小动物,大树右边有4只小动物;(2)一共有9只小动物;(3)小虎排在第7位详解:小狗排在第6位说明小狗前面有5只小动物,一共有5139++=(只)小动物.说明大树挡住了2只小动物,从右往左数则小虎排在第7位.5.例题5答案:一共有11个小朋友详解:如图所示,用○代表小朋友,则一共有3811+=(个)小朋友.6.例题6答案:一共有11只小动物详解:从左数起,花花排在第6个,花花被数了一次;从右边数起,花花排在第6个,花花又被数了一次.花花一共被数了2次,所以应该是66111+-=(只)小动物.7.练习1答案:简答:分清“有几”和“第几”,认识基数与序数.8.练习2答案:一共有8张数字卡片;数字卡片7从左数起排第3;它的左边有2张数字卡片;它的右边有5张数字卡片简答:仔细观察数一数即可.9.练习3答案:大树挡住了3辆车;公交车的前面有3辆车;一共有7辆车简答:公交车是从后面数起的第4辆,说明公交车后面还有3辆车,一共有3137++=(辆)车.10.练习4答案:如图所示,一共有12个圆圈,排在第10个简答:从左往右数,8个,7个圆圈,则一共有34512++=个圆圈,从右往左数,10个.11.作业1答案:简答:4个是基数,第2个是序数,注意区分,另外要分清左右方向.12.作业2答案:(1)共有8个水果;(2)从左往右数,第3个和第8个是,第1个和第7个是,第4个和第5个是;(3)从右往左数,第3个和第7个是,第4个和第5个是,第1个和第6个是简答:如图所示,从左边起和从右边起分别标数.13.作业3答案:如图所示,一共有7个正方形简答:第5是序数,它右边正方形的个数514=-=(个),共有2147++=(个)正方形.14.作业4答案:从左往右数,排在第10个简答:从右往左数,排在第9个,则的右边还有8个笑脸,框外有4个笑脸,则框内有844-=(个)笑脸,一共有4812+=(个)或44412++=(个)笑脸;左边有4419++=(个)笑脸,所以从左往右数,排在第9110+=(个);如下图所示:左 1 2 3 4 5 6 7 88 7 6 5 4 3 2 1 右15.作业5答案:参加春游的小动物共有13只简答:这是最简单的排队问题,这只队伍里的前4只和后8只小动物都不包含小猴子,所以总数要加上小猴子本身,即共有48113++=(只)小动物.。
一年级数学上2.2 基数和序数最新版

认识几和第几学习任务单

一年级数学认识几和第几学习任务单课题基数和序数(几和第几)
学习目标1、使学生明白序数表示的意义,理解第几的含义;
2、能正确区分几个和第几;
3、初步培养学生的数感;
学习重难点1、序数表示的意义,理解第几的含义;
2、能正确区分几个和第几。
一、观看微视频自学
1、按顺序写数:1、
2、()、4、()6,7,(),(),10。
2、涂一涂,圈一圈
涂4个
涂第4个
3、把左边第2个水果圈出来。
4、圈出3个水果。
二、课中互动释疑
你还有哪些疑惑?(通过自主学习,找出自己的疑惑或者新的发现)
三、合作探究
第 1, 第 2, 第 , 第, 第是 ,第是。
的前面有()个运动员, 的后面有()个运动员。
场上共有()个运动员。
四、巩固练习
1、上图一共有()只动物。
2. 从右边起,是在第()个。
3. 从左边起,把排在第3的动物圈起来。
五、反思总结
(课堂小结)
六、课后延伸
狐狸、小狗、猴子比赛跑步,狐狸没有得第一,小狗看到狐狸在自己的前面。
谁得了第一呢?()得了第一。
一年级数学上册练习题序数

一年级数学上册练习题序数数学是一门重要的学科,它在我们生活中无处不在。
从我们的日常生活到学业发展,数学扮演着重要的角色。
而在一年级数学上册中,练习题序数是一个需要我们掌握的知识点。
本文将通过分析练习题序数的概念、性质和应用,帮助一年级学生们更好地理解和掌握这个知识点。
一、练习题序数的概念在学习练习题序数之前,我们首先要了解什么是序数。
序数是表示事物顺序的数字,它与基数(表示数量的数字)有所不同。
例如,基数“1”表示一个,而相应的序数为“第一”。
序数的使用在我们的日常生活中非常常见,比如我们常说的日期、年级、排名等等。
二、练习题序数的性质练习题序数也有一些独特的性质,我们可以通过以下几点来了解:1. 序数的构成:大部分序数由基数加上后缀“-th”构成,例如“first”表示第一,“second”表示第二。
但是在英语中,一到十几之间的序数有一些特殊的形式,比如“first”、“second”、“third”、“fourth”等。
2. 序数的变化规律:当序数大于20时,只需将基数部分变为相应的序数形式,然后加上“-th”后缀即可。
例如“21”为“twenty-first”(第二十一),“39”为“thirty-ninth”(第三十九)。
3. 序数的读法:在读序数时,我们通常要注意一些特殊读法。
例如11和12的序数读作“eleventh”(第十一)和“twelfth”(第十二),而不是“oneth”和“twonth”。
三、练习题序数的应用掌握练习题序数的概念和性质后,我们可以将其应用到实际的练习题中,提升我们的数学能力。
以下是一些例题:1. ABCD四个点按顺序排列,点C在点A和点D之间。
请问C的序数是多少?解析:根据题意,我们可以得知C是ABCD四个点中“第二”个点,因此C的序数为“second”。
2. 有三个小男孩,他们的生日分别是1月5日、3月10日和5月15日,问谁的生日在最后?解析:根据月份的大小关系,我们可以得知5月是最后一个月,因此生日在5月15日的男孩生日最后,他的序数为“third”。
大班活动《认识序数和基数》

认识序数和基数
本节知识概况:
1、认识20以内的序数,学习序数词“第几”。
2、幼儿认识基数和序数的区别。
基础部分
一、数一数、填一填
1、
(1)上面一共有()种水果。
(2)从左数,苹果是第()个,从右数它是第()个。
(3)把右边第3种水果圈起来。
(4)菠萝的左边有()种水果,柠檬的右边有()种水果。
2、
(1)一共有( )只动物。
(2)从左数,排第( )。
排第( )。
3、
(1)一共有()只小动物,
(2)从右数起()排第4 ,排第(),(3)前面有()只小动物,后面有()只小动物。
4、
(1)上面一共有( )个图形。
(2)把右边3个圈起来。
把从左数第7个涂上红色。
5、
(1)一共有()个小朋友。
(2)从左边数小红排在第( )个,小兰前面有()个小朋友;(3)从左边数排在第5个的是();
(4)从右边数排在第1个的是(),()排在第2个。
2、按照从小到大的顺序排列。
(写出“>”或“<”)
6 2 1 5 9
()()()()()
3、按照从大到小的顺序排列起来。
(写出“>”或“<”)
7 5 0 4
()()()()。
【详解】一年级第13讲 基数与序数

第十三讲基数与序数1.例题1答案:详解:分清“有几”和“第几”,认识基数与序数:基数是“有几”,序数是“第几”.2.例题2答案:(1)一共有7只小动物;(2)从前往后数,狮子排在第3位,狮子的前面有2只小动物,后面还有4只小动物;(3)从后往前数,大公鸡排在第4位,大公鸡的后面有3只小动物,前面还有3只小动物详解:分清“有几”和“第几”,数一数即可.3.例题313个三角形详解:从左往右数排第4,说明左边有3个三角形,从右往左数排第6,说明右边有5个三角形,一共有35513++=个三角形.4.例题4答案:(1)大树左边有3只小动物,大树右边有4只小动物;(2)一共有9只小动物;(3)小虎排在第7位详解:小狗排在第6位说明小狗前面有5只小动物,一共有5139++=(只)小动物.说明大树挡住了2只小动物,从右往左数则小虎排在第7位.5.例题5答案:一共有11个小朋友详解:如图所示,用○代表小朋友,则一共有3811+=(个)小朋友.6.例题6答案:一共有11只小动物详解:从左数起,花花排在第6个,花花被数了一次;从右边数起,花花排在第6个,花花又被数了一次.花花一共被数了2次,所以应该是66111+-=(只)小动物.7.练习1答案:简答:分清“有几”和“第几”,认识基数与序数.8.练习2答案:一共有8张数字卡片;数字卡片7从左数起排第3;它的左边有2张数字卡片;它的右边有5张数字卡片简答:仔细观察数一数即可.9.练习3答案:大树挡住了3辆车;公交车的前面有3辆车;一共有7辆车简答:公交车是从后面数起的第4辆,说明公交车后面还有3辆车,一共有3137++=(辆)车.10.练习4答案:如图所示,一共有12个圆圈,排在第10个简答:从左往右数,排在第8个,的左边有7个圆圈,则一共有34512++=个圆圈,从右往左数,排在第个.11.作业1答案:简答:4个是基数,第2个是序数,注意区分,另外要分清左右方向.12.作业2答案:(1)共有8个水果;(2)从左往右数,第3个和第8个是,第1个和第7个是,第4个和第5个是;(3)从右往左数,第3个和第7个是,第4个和第5个是,第1个和第6个是简答:如图所示,从左边起和从右边起分别标数.13.作业3答案:如图所示,一共有7个正方形简答:第5是序数,它右边正方形的个数514=-=(个),共有2147++=(个)正方形.14.作业4答案:从左往右数,排在第10个简答:从右往左数,排在第9个,则的右边还有8个笑脸,框外有4个笑脸,844-=(个)笑脸,一共有4812+=44412++=(个)笑脸;左边有4419++=(个)笑脸,所以从左往右数,排在第9110+=(个);如下图所示:左 1 2 3 4 5 6 7 88 7 6 5 4 3 2 1 右15.作业5答案:参加春游的小动物共有13只简答:这是最简单的排队问题,这只队伍里的前4只和后8只小动物都不包含小猴子,所以总数要加上小猴子本身,即共有48113++=(只)小动物.。
基数效用论和序数效用论

基数效用论和序数效用论在经济学和社会学领域,效用是一个重要的概念,指的是个体对某种物品或行为的满足程度。
效用理论是经济学的重要分支之一,旨在解释个体的决策行为和市场的运作规律。
在效用理论中,有两种不同的效用概念,即基数效用和序数效用。
本文将探讨这两种效用概念的含义、区别和应用。
一、基数效用基数效用指的是个体对某种物品或行为的满足程度的绝对大小,也就是说,基数效用可以用数字来表示。
基数效用理论最早由德国经济学家赫尔曼·海因里希·戈斯特提出,他认为人们对于物品的需求是有限的,而且每个人对物品的需求是不同的,因此每个人对物品的基数效用也是不同的。
基数效用的大小可以通过个体在不同情境下的偏好排序来测量。
例如,如果一个人认为拥有一台电视比拥有一辆车更重要,那么他对于电视的基数效用就更高。
基数效用的应用主要体现在消费者行为和福利经济学中。
在消费者行为中,基数效用可以帮助我们理解为什么人们会选择某些物品而不是其他物品,以及为什么人们会愿意支付更高的价格来获得某些物品。
在福利经济学中,基数效用可以帮助我们评估不同政策对个体福利的影响,从而为政策制定提供参考。
二、序数效用序数效用指的是个体对不同物品或行为的偏好排序,也就是说,序数效用只能用等级来表示,而不能用数字来表示。
序数效用理论最早由英国经济学家弗朗西斯·约翰·埃德沃德·耶茨提出,他认为人们对物品的需求是有序的,而且每个人对物品的需求排序也是不同的,因此每个人对物品的序数效用也是不同的。
序数效用的大小可以通过个体在不同情境下的选择行为来测量。
例如,如果一个人更愿意选择拥有一台电视而不是拥有一辆车,那么他对于电视的序数效用就更高。
序数效用的应用主要体现在决策理论和行为经济学中。
在决策理论中,序数效用可以帮助我们理解人们在面临不同选择时如何进行决策,以及决策过程中的心理机制。
在行为经济学中,序数效用可以帮助我们理解人们在面临不完全信息或风险时如何进行决策,以及为什么人们会出现某些行为偏差。
数词的基数和序数的用法

数词的基数和序数的用法数词在日常生活中使用频繁,基数和序数是其中最常见的两种形式。
基数表示数量或顺序中的具体数字,而序数则表示次序或顺序。
正确使用基数和序数形式非常重要,下面将对其用法进行详细讨论。
一、基数的用法1. 表示具体数量:基数词可用来表示具体的数量,如:one(1),two(2),three(3),以此类推。
例如:“There are five apples on the table.”(桌子上有五个苹果。
)2. 表示年龄:基数词也可以用来表示人或事物的年龄。
例如:“Heis thirty years old.”(他三十岁。
)3. 表示顺序:当基数词表示顺序时,通常在前面加上序数词。
例如:“He came in the second place.”(他获得了第二名。
)4. 表示小数:基数词可以表示小数,通常用分数形式或小数点后加数字的方式表示。
例如:“She scored 3.5 in the exam.”(她在考试中得了3.5分。
)二、序数的用法1. 表示顺序:序数词表示事物或人在顺序中的排位。
通常在基数词后加上-th,-st,-nd,-rd等后缀构成序数词。
例如:“W e won the first prize in the competition.”(我们在比赛中获得了第一名。
)2. 表示日期:序数词也可用于表示日期,例如表示月份的序数词如:first(1st),second(2nd),third(3rd),以及表示年份的序数词如:twenty-fourth(24th),fifty-sixth(56th)等。
3. 表示小数位:有时序数词也可以用来表示小数位,通常用于科学或技术文献中。
例如:“The experiment achieved an accuracy of0.03%.”(该实验达到了0.03%的准确率。
)总结:基数词用于表示具体数量或顺序,而序数词用于表示顺序或排位。
正确使用基数和序数形式是十分重要的,可以避免语言交流中的误解和混淆。
幼儿园中班优质教案《基数与序数》

幼儿园中班优质教案《基数与序数》一、教学内容本节课选自幼儿园中班数学教材第3章《数的认识》,详细内容为基数与序数的概念及其应用。
主要围绕让幼儿理解并掌握10以内的基数和序数,学会用数来描述生活中的事物。
二、教学目标1. 让幼儿理解基数和序数的概念,能够正确区分两者。
2. 培养幼儿运用基数和序数描述生活中事物的能力。
3. 激发幼儿对数学的兴趣,培养其数学思维。
三、教学难点与重点教学难点:基数与序数的概念区分,以及在实际生活中的应用。
教学重点:让幼儿掌握10以内的基数与序数,并能够运用到实际情景中。
四、教具与学具准备1. 教具:数字卡片、图片、PPT、磁性黑板。
2. 学具:画纸、画笔、剪刀、胶棒。
五、教学过程1. 实践情景引入(5分钟)利用磁性黑板展示一幅有10个小朋友排队买冰淇淋的图片,引导幼儿观察并提问:“谁能告诉我,排在第1个的小朋友是谁?排在第5个的小朋友有几个?”2. 新课导入(10分钟)通过讲解基数与序数的概念,让幼儿理解并区分两者。
基数表示数量,如10个小朋友;序数表示顺序,如第1个小朋友。
3. 例题讲解(10分钟)利用PPT展示例题,引导幼儿解答并解释答案。
例如:“小兔子家里有5个苹果,小猴子要吃第3个苹果,那么小猴子吃的是哪个苹果?”4. 随堂练习(10分钟)分组进行练习,让幼儿用数字卡片完成练习题。
教师巡回指导,及时纠正错误。
六、板书设计1. 板书《基数与序数》2. 内容:基数:表示数量,如5个苹果序数:表示顺序,如第3个苹果七、作业设计1. 作业题目:(1)数一数,你家里有多少个玩具?用基数表示。
(2)你排在教室的第几位?用序数表示。
2. 答案:(1)例如:我家有8个玩具。
(2)例如:我排在教室的第6位。
八、课后反思及拓展延伸1. 课后反思:观察幼儿在课堂上的表现,针对掌握程度进行课后辅导,巩固知识点。
2. 拓展延伸:让幼儿在家长的帮助下,观察家里的物品,用基数和序数进行描述,并记录下来,下节课分享。
基数与序数专项练习

基数与序数专项练习(一)
1、
(1)一共有()只小老鼠。
(2)从左往右数,第()不过。
(3)请把左侧第 3 只小老鼠圈起来。
2、
(1)一共有()个西瓜。
(2)请把右侧第 4 个西瓜涂上颜色。
3、
(1)一共有()条鱼。
(2)第()不过。
4、
(1)请把左侧第 3 个草莓涂上颜色。
(2)请把右侧第2个草莓圈起来。
5、
(1)一共有()只动物。
(2)小乌龟排第 1,狮子排第(),黄牛排第()。
基数与序数专项练习(二)
1、
(1)一共有()个灯笼,是第()个。
(2)请把右侧第一个圈起来。
2、
(1)一共有()个萝卜。
(2)请把最中间的萝卜涂上颜色,它的左右两边分别有()个萝卜。
(3)请把最左侧的 2 个萝卜圈起来。
3、
(1)从左侧起,第 1 个是,第()个是。
(2)从右侧起,排第(),排第(),排第()。
(3)请把左侧 2 个图案涂上颜色,把右侧 2 个图案圈起来。
4、
(1)的左侧是(),右侧是()。
(2)请把左侧第 6 个图案圈起来,右侧第二个图案涂上颜色。
(3)一共有()个图案。
排第1,排第(),排第(),排第()。
基数词变序数词规律

基数词变序数词规律时间:2021.03. 04创作:欧阳地一.口诀:一.二.三,特殊记;th从四起;八加h,九去e; ve 要用f替;整十基数变序数,先把ty变成tie;要是遇到几十几,前半基数后半序。
基数词词序数基数词序数词1 one 第- first 2 two 第-二second3 three 第—三third 4 four 第四fourth5 five 第五fifth 6 six 第六si xth7 seve n 第七seve nth 8 eight 第八eighth9 nine 第九ninth 10 ten 第十t en th11 e1 even 第十e1eve nth 12 twe I ve 第十—tweIfth 13 th i rteen 第十三th i rteen th14fourteen 第十四fourteenth15 fifteen 第十五fifteenth16 s i xteen 第十六six teen th7seven teen 第十七seven teen th18 e i ghteen 第十八e i ghteenth19 nineteen 第十九n i neteenth20 twenty 第二十t went i eth21 t wenty-one 第二十—一t wenty-f i rst22 twen ty-two 第二十二twenty -second23twenty-three 第二十三twenty-th i rd基数词序数词34 thi rty-four 第三十四th i rty-fourth45 fifth forty-five第四十五forty-56 fi fty-six 第五十六fifty-sixth99 nin ety-n ine 第九十九nin ety-n inth100 hun dred 第一百hun dredth 、巩固练习:(一)写出下列词的序数词形式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.★★★☆★★★★
从左数,☆排在第();从右数,☆排在第()。
2.☆☆☆☆☆☆☆☆
把左边的5个☆圈起来,给从左数第5个☆涂上颜色
3.
(1)把左边的4只小鸟圈起来。
(2)从左边数,给第4只小鸟涂上颜色。
(3)从右边数的第1只小鸟飞走了,还剩()只小鸟。
4.
把右边的5个圈起来,在从左数第6个的上面画个○。
5.
6.
一共有()缸鱼,从左边数第7缸有()条,有7条鱼的是第()缸。
7.
5136 4 2
(1)小动物身上最大的数是( ), 最小的数是( )。
(2)从右边数,第3只与第5只小动物身上的数的和是( )。
(3)把左边的5只小动物身上的数,从大到小排列。
( )>( )>( )>( )>( )
8.
1.把左边的7朵花圈在一起。
2.在右数第7朵花的上面画一个○。
