工程流体力学(孔珑版)第四章_题解
工程流体水力学第四章习题答案
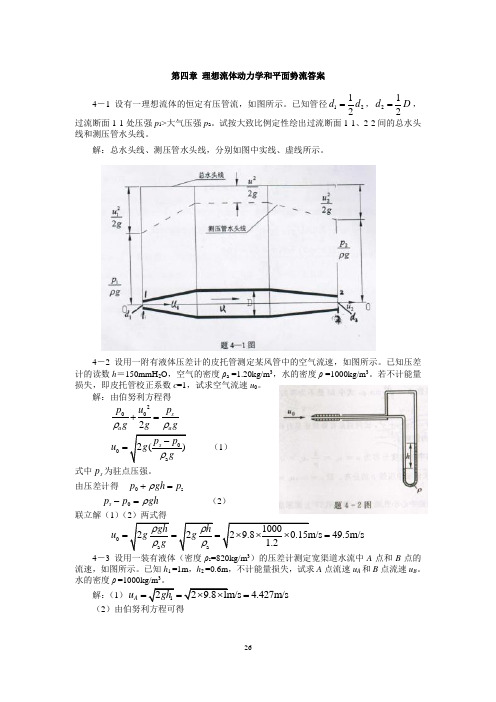
第四章 理想流体动力学和平面势流答案4－1 设有一理想流体的恒定有压管流，如图所示。
已知管径1212d d =，212d D =，过流断面1-1处压强p 1>大气压强p a 。
试按大致比例定性绘出过流断面1-1、2-2间的总水头线和测压管水头线。
解：总水头线、测压管水头线，分别如图中实线、虚线所示。
4－2 设用一附有液体压差计的皮托管测定某风管中的空气流速，如图所示。
已知压差计的读数h ＝150mmH 2O ，空气的密度ρa =1.20kg/m 3，水的密度ρ =1000kg/m 3。
若不计能量损失，即皮托管校正系数c =1，试求空气流速u 0。
解：由伯努利方程得2002s a a p u p g g gρρ+= 00a 2()s p p u g gρ-=（1） 式中s p 为驻点压强。
由压差计得 0s p gh p ρ+=0s p p gh ρ-= （2）联立解（1）（2）两式得0a a 10002229.80.15m/s 49.5m/s 1.2gh h u gg g ρρρρ===⨯⨯⨯= 4－3 设用一装有液体（密度ρs =820kg/m 3）的压差计测定宽渠道水流中A 点和B 点的流速，如图所示。
已知h 1 =1m ，h 2 =0.6m ，不计能量损失，试求A 点流速u A 和B 点流速u B 。
水的密度ρ =1000kg/m 3。
解：（1）1229.81m/s 4.427m/s A u gh ==⨯⨯= （2）由伯努利方程可得22A AA u p h g gρ+= （1）22B BB u p h g gρ+= （2）式中A h 、A p 和B h 、B p 分别为A 点和B 点处的水深和驻点压强。
由（1）、（2）式可得2222A B A BA B p p u u h h g g gρ-=+-- （3） 由压差计得，22ρρρρ--++=A A s B B p gh gh gh gh p ，所以220.82A BA B p p h h h h gρ-=+-- (4) 由（3）式、（4）式得2222 4.427(10.82)0.6(10.82)0.8922229.8B A u u h g g =--=--=⨯ 29.80.892m/s 4.18m/s B u =⨯⨯=。
工程流体力学的_第四版_孔珑_作业答案及解析_详解
第二章2-1.已知某种物质的密度ρ=2.94g/cm3，试求它的相对密度d。
解：d=ρ/ρw=2.94（g/cm3）/1（g/cm3）=2.942-2.已知某厂1号炉水平烟道中烟气组分的百分数为α（co2）=13.5%，a(SO2)=0.3%，a(O2)=5.2%，a(N2)=76%，a(H2O)=5%。
试求烟气的密度。
2-3.上题中烟气的实测温度t=170℃，实测静计压强Pe=1432Pa，当地大气压强Pa=10058Pa。
试求工作状态下烟气的密度和运动粘度。
2-4.当压强增量为50000Pa时，某种液体的密度增长0.02%，试求该液体的体积模量。
2-5.绝对压强为3.923×10^5Pa的空气的等温体积模量和等熵体积模量各等于多少？2-6. 充满石油的油槽内的压强为4.9033×10^5Pa,今由槽中排出石油40kg，使槽内压强降到9.8067×10^4Pa，设石油的体积模量K＝1.32×10^9 Pa。
试求油槽的体积。
2-7. 流量为50m3/h，温度为70℃的水流入热水锅炉，经加热后水温升到90℃，而水的体胀系数αV=0.000641/℃，问从锅炉中每小时流出多少立方米的水？2-8. 压缩机压缩空气，绝对压强从9.8067×104Pa升高到5.8840×105Pa，温度从20℃升高到78℃，问空气体积减少了多少？2-9. 动力粘度为2.9×10^-4Pa·S，密度为678kg/m3的油，其运动粘度等于多少？解：V=u/ρ=2.9×10^-4/678=4.28×10^-7m²/s2-10. 设空气在0℃时的运动粘度ν0=13.2×10-6m2/s,密度ρ0=1.29kg/m3。
试求在150℃时空气的动力粘度。
2-11. 借恩氏粘度计测得石油的粘度为8.5oE,如石油的密度为ρ=850kg/m3,试求石油的动力粘度。
流体力学课后习题答案自己整理孔珑4版
《工程流体力学》课后习题答案孔珑第四版第2章流体及其物理性质 (4)2-1 (4)2-3 (4)2-4 (6)2-5 (6)2-6 (6)2-7 (7)2-8 (7)2-9 (8)2-11 (8)2-12 (9)2-13 (9)2-14 (10)2-15 (10)2-16 (11)第3章流体静力学 (12)3-1 (12)3-2 (12)3-3 (13)3-5 (13)3-6 (14)3-9 (14)3-10 (15)3-21 (18)3-22 (19)3-23 (20)3-25 (20)3-27 (20)第4章流体运动学及动力学基础 (22)4-2 (22)4-5 (22)4-6 (23)4-8 (23)4-11 (24)4-12 (24)4-14 (25)4-22 (25)4-24 (26)4-26 (27)第6章作业 (28)6-1 (28)6-3 (28)6-7 (29)6-10 (29)6-11 (29)6-12 (30)6-17 (31)第2章流体及其物理性质2-1已知某种物质的密度ρ=2.94g/cm3，试求它的相对密度d。
【2.94】解：ρ=2.94g/cm3=2940kg/m3，相对密度d=2940/1000=2.942-2已知某厂1号炉水平烟道中烟气组分的百分数为，α(CO2)=13.5%α(SO2)=0.3%，α(O2)=5.2%，α(N2)=76%，α(H2O)=5%。
试求烟气的密度。
解：查课表7页表2-1，可知ρ(CO2)=1.976kg/m3，ρ(SO2)=2.927kg/m3，ρ(O2)=1.429kg/m3，ρ(N2)=1.251kg/m3，ρ(H2O)=1.976kg/m3，ρ(CO2)=1.976kg/m3，3ρ=∑i iαρ=341.1kg/m2-3上题中烟气的实测温度t=170℃，实测静计示压强Pe=1432Pa，当地大气压Pa=100858Pa。
试求工作状态下烟气的密度和运动粘度。
工程流体力学第四版孔珑作业答案详解
第二章2-1.已知某种物质的密度P =2. 94g/cm3.试求它的相对密度d。
解：d二P/P w=2. 94 (g/cm3) /I (g/cm3) =2. 94 2-2. B知某厂1号炉水平烟道中烟气组分的百分数为a (co2) =13. 5%, a(S02)=0. 3%, a(02) =5. 2%, a(N2)=76%,a(H20)=5%o 试求烟气的密度。
毎;一山■乍彳董2 J另怎堰卜Pg二I-壮曲.兰267划7,严二/饵切沖//I = Z巾1 \ 0U二上血｝勺.…； '伶/二傩&^ _才弊^气佝一少 5 4 一广么2 二-1月7& 乂加3Sq/2、靈7 乂仇“仝jt 14:2】£ g轧.+丿'旳.人&7「才0：如• Y2-3. ±题中烟气的实测温度t=170°C,实测静计压强Pe=1432Pa,当地大气压强Pa=10058Pa。
试求工作状态下烟气的密度和运动粘度。
、/匕工心20竺- 21^ 十(7。
二£4引＜士丄一____ 一一( •一” 一亠―- •*—址」2小P昱二I "亍pQ三传$几-二...2- 4.当压强增量为50000Pa 时，某种液体的密度增长0. 02%,试求该液体的体积模量。
毎、j£ 琵托々 龙_ _______________________ ____________________________卅 =(》iL冋件二亦寸.干处險铀直■£.X *上•:__也卒丄祐 _________ 二、‘、徐朕按逐k - d - J 厉滋 X Io8琢2- 5.绝对压强为3. 923X10"5Pa 的空气的等温体积模量和等埔体积模量各等于多少?2- 6.充满石油的油槽内的压强为4. 9033X10"5Pa,今由槽中排出石油40血，使槽内压强降到9・8067Xl(r4Pa,设石油的体积模量K=l. 32X10^9 Pa 。
工程流体力学第四版孔珑作业答案详细讲解
第二章2-1、已知某种物质的密度ρ=2、94g/cm3,试求它的相对密度d。
解:d=ρ/ρw=2、94(g/cm3)/1(g/cm3)=2、942-2、已知某厂1号炉水平烟道中烟气组分的百分数为α(co2)=13、5%,a(SO2)=0、3%,a(O2)=5、2%,a(N2)=76%,a(H2O)=5%。
试求烟气的密度。
2-3、上题中烟气的实测温度t=170℃,实测静计压强Pe=1432Pa,当地大气压强Pa=10058Pa。
试求工作状态下烟气的密度与运动粘度。
2-4、当压强增量为50000Pa时,某种液体的密度增长0、02%,试求该液体的体积模量。
2-5、绝对压强为3、923×10^5Pa的空气的等温体积模量与等熵体积模量各等于多少？2-6、充满石油的油槽内的压强为4、9033×10^5Pa,今由槽中排出石油40kg,使槽内压强降到9、8067×10^4Pa,设石油的体积模量K＝1、32×10^9 Pa。
试求油槽的体积。
2-7、流量为50m3/h,温度为70℃的水流入热水锅炉,经加热后水温升到90℃,而水的体胀系数αV=0、000641/℃,问从锅炉中每小时流出多少立方米的水？2-8、压缩机压缩空气,绝对压强从9、8067×104Pa升高到5、8840×105Pa,温度从20℃升高到78℃,问空气体积减少了多少？2-9、动力粘度为2、9×10^-4Pa·S,密度为678kg/m3的油,其运动粘度等于多少？解:V=u/ρ=2、9×10^-4/678=4、28×10^-7m²/s2-10、设空气在0℃时的运动粘度ν0=13、2×10-6m2/s,密度ρ0=1、29kg/m3。
试求在150℃时空气的动力粘度。
2-11、借恩氏粘度计测得石油的粘度为8、5oE,如石油的密度为ρ=850kg/m3,试求石油的动力粘度。
工程流体力学第四版孔珑作业答案详细讲解
第二章2-1.已知某种物质的密度ρ=cm3，试求它的相对密度d。
解：d=ρ/ρw=（g/cm3）/1（g/cm3）=2-2.已知某厂1号炉水平烟道中烟气组分的百分数为α（co2）=%，a(SO2)=%，a(O2)=%，a(N2)=76%，a(H2O)=5%。
试求烟气的密度。
2-3.上题中烟气的实测温度t=170℃，实测静计压强Pe=1432Pa，当地大气压强Pa=10058Pa。
试求工作状态下烟气的密度和运动粘度。
2-4.当压强增量为50000Pa时，某种液体的密度增长%，试求该液体的体积模量。
2-5.绝对压强为×10^5Pa的空气的等温体积模量和等熵体积模量各等于多少？2-6. 充满石油的油槽内的压强为×10^5Pa,今由槽中排出石油40kg，使槽内压强降到×10^4Pa，设石油的体积模量K＝×10^9 Pa。
试求油槽的体积。
2-7. 流量为50m3/h，温度为70℃的水流入热水锅炉，经加热后水温升到90℃，而水的体胀系数αV=℃，问从锅炉中每小时流出多少立方米的水？2-8. 压缩机压缩空气，绝对压强从×104Pa升高到×105Pa，温度从20℃升高到78℃，问空气体积减少了多少？2-9. 动力粘度为×10^-4Pa·S，密度为678kg/m3的油，其运动粘度等于多少？解：V=u/ρ=×10^-4/678=×10^-7m²/s2-10. 设空气在0℃时的运动粘度ν0=×10-6m2/s,密度ρ0=m3。
试求在150℃时空气的动力粘度。
2-11. 借恩氏粘度计测得石油的粘度为,如石油的密度为ρ=850kg/m3,试求石油的动力粘度。
2-12. 一平板距离另一固定平板,两板间充满液体，上板在每平方米上有2N的力作用下以s的速度移动，试求该液体的粘度。
2-13. 已知动力滑动轴承的轴直径d=，转速 n=2830r/min，轴承内径 D=，宽度 l=，润滑油的动力粘度=·s，试求克服摩擦阻力所消耗的功率。
工程流体力学第四版孔珑作业答案详解
第二章ρ=2.94g/cm3，试求它的相对密度d。
解：d=ρ/ρ2-2.已知某厂1号炉水平烟道中烟气组分的百分数为α（co2）=13.5%，a(SO2)=0.3%，a(O2)=5.2%，a(N2)=76%，a(H2O)=5%。
试求烟气的密度。
2-3.上题中烟气的实测温度t=170℃，实测静计压强Pe=1432Pa，当地大气压强Pa=10058Pa。
试求工作状态下烟气的密度和运动粘度。
2-4.当压强增量为50000Pa时，某种液体的密度增长0.02%，试求该液体的体积模量。
×10^5Pa的空气的等温体积模量和等熵体积模量各等于多少？×××10^9 Pa。
试求油槽的体积。
2-7. 流量为50m3/h，温度为70℃的水流入热水锅炉，经加热后水温升到90℃，而水的体胀系数α℃，问从锅炉中每小时流出多少立方米的水？2-8.××105Pa，温度从20℃升高到78℃，问空气体积减少了多少？2-9. ×10^-4Pa·S，密度为678kg/m3的油，其运动粘度等于多少？解：V=u/ρ××10^-7m²/s2-10. 设空气在0℃时的运动粘度ν×10-6m2/s,密度ρ0=1.29kg/m3。
试求在150℃时空气的动力粘度。
2-11. 借恩氏粘度计测得石油的粘度为8.5oE,如石油的密度为ρ=850kg/m3,试求石油的动力粘度。
2-12. 一平板距离另一固定平板0.5mm,两板间充满液体，上板在每平方米上有2N的力作用下以0.25m/s的速度移动，试求该液体的粘度。
2-13. 已知动力滑动轴承的轴直径，转速 n=2830r/min，轴承内径，宽度，润滑油的动力粘度=0.245Pa·s，试求克服摩擦阻力所消耗的功率。
2-14. 一重500N的飞轮的回转半径为30cm，由于轴套间流体粘度的影响，当飞轮600r/min旋转时，它的角减速度为0.02rad/s2。
流体力学课后习题答案(孔珑编)
2-5 解：如图示，设 A 点
距 1-2 等压面的距离为 h1 ，B 点距 3-4 等压面的
距离为 h2 ，1-2 等压面距基准面的距离为 h3 ，
在等压面 1-2 处列平衡方程， P1 P2 PA H2O gh1 在等压面 3-4 处列平衡方程， P3 P4 PB -H2O gh2 因为 P2 P3 Hg gh ，所以 PA H2O gh1 PB -H2O gh2 Hg gh ， 故 Hg gh=PA -PB H2O g (h1+h2 ) ， 又因为， h1 548102 - h3 ， h2 h h3 - 304 102 ，所以
2
在容器顶部距中心 r 处取微圆环 dr ，则微圆环所受到的压力为
dF pdA 2 rpdr 2 r( gh 2 (r2 r02 ) )dr 2
所以整个容器顶盖受到的总压力为
F
d
2 dF
d 2
2
r(
gh
2 (r 2
r02
)
)dr
2 [
因为 P1 P2 ，所以， Pa PF oi gh1 H2O gh2 =Pa Hg gH ， 所以
H
=
PF
oi gh1 H2O gh2 Hg g
=
46059.4+800 9.81 3010-2 103 13.6103 9.81
9.81 50 10-2
pA oi g (h1 hB ) p3 Hg gh1
在 3-3 等 压 面 处 列 等 压 面 方 程 得 P3 pB +oi g(hB - h2 )+Hg gh2 ， 所 以
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
得
则
【习题4-31】如图4-37所示，平板向着射流以等速v运动，导出使平板运动所需功率的表达式。
图4-37习题4-31示意图
【解】由上一题的结论，在平板不运动的情况下，流体对板面的作用力为
(1)
设射流的的截面积为A0，则
(2)
代入式(1)
(3)
平板向着射流以等速v运动，将坐标系建立在平板上，则射流的速度为
得
(1)
（2） 沿y方向的外力有：由p2e引起的压力p2eA1；由管道给流体作用力R的分力Ry。所以
系统流体的动量沿y方向的变化为：
由y方向动量方程
得
(2)
（3） 根据连续方程
(3)
其中， ， ，则
(4)
（4）列入口、出口断面的能量方程：
不计损失，hw=0，取α1=α2=1，z1=z2，则
(5)
得
(6)
图4-29 习题4-16示意图
【解】设皮托管入口前方未受扰动处为点1，皮托管入口处为点2，水与测量液体左侧界面处为点3，水与测量液体右侧界面处压强为点4，水与测量液体左侧界面与静压管入口处距离为x。
由于在同一流线上，
(1)
根据静压强分布
(2)
(3)
(4)
在方程(1)中v1=v，z1=z2，v2=0，则
沿板面方向，流体没有受力；沿板面法线方向，设流体受到的作用力为F。沿板面方向列写动量方程
(2)
沿板面法线方向列写动量方程
(3)
又有
(4)
解方程组(2)(4)，得
(5)
(6)
由式(3)，得
(7)
根据牛顿第三运动定律，流体对板面的作用力与流体受到的作用力大小相等，方向相反，即
(8)
【习题4-30】如图4-36所示的流动，如果沿一侧的流动的流体流量为总流量的45％，问平板倾斜角θ多大?
(4)
用v’代替式(3)中的v0，得
(5)
此例在水平方向上的分力为
(6)
平板在水平方向上等速运动，根据牛顿第一运动定律，使平板运动施加的力应为
(7)
因此，使平板运动所需功率为
(8)
由式(2)得
(9)
无论平板是否运动，A0保持不变，将式(9)代入式(8)，得
(10)
（5）支撑弯管在其位置所需的水平力：
(7)
由(1)(2)(3)(4)(6)(7)，得
代入数值，得
R=1427.8 (N)
【习题4-29】如图4-36所示，一股射流以速度v0水平射到倾斜光滑平板上，体积流量为qV0。求沿板面向两侧的分流流量qV1与qV2的表达式，以及流体对板面的作用力。忽略流体撞击的损失和重力影响，射流的压强分布在分流前后都没有变化。
第四章 流体运动学和流体动力学基础
【4-2】已知平面流动的速度分布规律为
式中Γ为常数。求流线方程并画出若干条流线。
【解】由题设， ，
代入流线的微分方程
得
【4-4】已知流场的速度分布为
（1）问属于几维流动？（2）求（x,y,z）=（1,2,3）点的加速度。
【解】（1）由于速度分布可以写为
(1)
流动参量是两个坐标的函数，因此属于二维流动。
【解】根据牛顿运动定律，支撑弯管在其位置所需的水平力等于管道给流体的作用力。令xoy平面为水平面，入口段沿x轴负半轴，出口段沿y轴正半轴，弯头在原点，建立坐标系。
（1） 沿x方向的外力有：由入口压强p1e引起的压力p1eA2；由管道给流体的作用力R的分力Rx。所以
系统流体的动量沿x方向的变化为：
由x方向动量方程
图4-36 习题4-29、4-30示意图
【解】当射流接触平板后，将沿平板表面分成两股射流。取A0截面为射流进入冲击区的断面，A1与A2截面为射流冲击平板后离开冲击区的断面。由于是平面流动并忽略撞击损失，射流压力在分流前后又无变化，所以
(1)
进入断面A0的速度v0，可分解为沿板面方向的v0cosθ和沿板面法线方向的v0sinθ
(2)
(3)
设液体ρm左侧界面的坐标为z3，由流体静力学基本方程，得
(4)
(5)
(6)
(7)
由式(3)(7)，得
(8)
由于连续方程
(9)
(10)
(11)
(12)
由式(8)，得
(13)
将式(12)代入式(13)，得
(14)
(15)
(16)
流量为
(17)
即
(18)
【4-16】 按图4-29所示的条件求当H=30cm时的流速v。 [1．085m／s]
(5)
方程(3)减去方程(2)，得
(6)
将方程(4)(5)带入(6)，得
(7)
则
(8)
(9)
【习题4-24】连续管系中的90º渐缩弯管放在水平面上，管径d1=15cm，d2=7.5cm，入口处水的平均流速v1=2.5m/s，静压p1e=6.86×104Pa（计示压强）。如不计能量损失，试求支撑弯管在其位置所需的水平力。
（2）由题设，
(2)
(3)
(4)
(5)
(6)
(7)
将x=1，y=2，z=3代入式(5)(6)(7)，得
【4-15】图8所示为一文丘里管和压强计，试推导体积流量和压强计读数之间的关系式。
图4-28 习题4-15示意图
【解】列1-1、2-2断面的能量方程：
(1)
不计损失，hw=0，取α1=α2=1，则