高一数学必修一必修二难题

合集下载

高中数学必修一第二章一元二次函数方程和不等式典型例题(带答案)

高中数学必修一第二章一元二次函数方程和不等式典型例题单选题1、已知x >0，则下列说法正确的是（） A ．x +1x −2有最大值0B ．x +1x −2有最小值为0 C ．x +1x−2有最大值为－4D ．x +1x−2有最小值为－4答案：B分析：由均值不等式可得x +1x ≥2√x ×1x =2，分析即得解由题意，x >0，由均值不等式x +1x≥2√x ×1x=2，当且仅当x =1x，即x =1时等号成立故x +1x −2≥0，有最小值0 故选：B2、不等式x (2x +7)≥−3的解集为（） A ．(−∞,−3]∪[−12,+∞)B ．[−3,−12] C ．(−∞,−2]∪[−13,+∞)D ．[−2,−13] 答案：A分析：解一元二次不等式即可.x (2x +7)≥−3可变形为2x 2+7x +3≥0，令2x 2+7x +3=0，得x 1=−3，x 2=−12，所以x ≤−3或x ≥−12，即不等式的解集为(−∞,−3]∪[−12,+∞).故选：A.3、已知命题“∀x ∈R ，4x 2+(a −2)x +14>0”是假命题，则实数a 的取值范围为（） A ．(−∞,0]∪[4,+∞)B ．[0,4] C ．[4,+∞)D ．(0,4)答案：A分析：先求出命题为真时实数a的取值范围，即可求出命题为假时实数a的取值范围.若“∀x∈R，4x2+(a−2)x+14>0”是真命题，即判别式Δ=(a−2)2−4×4×14<0，解得：0<a<4，所以命题“∀x∈R，4x2+(a−2)x+14>0”是假命题，则实数a的取值范围为：(−∞,0]∪[4,+∞).故选：A.4、设a>b>c>0，则2a2+1ab +1a(a−b)−10ac+25c2取得最小值时，a的值为（）A．√2B．2C．4D．2√5答案：A解析：转化条件为原式=1ab +ab+1a(a−b)+a(a−b)+(a−5c)2，结合基本不等式即可得解.2a2+1ab+1a(a−b)−10ac+25c2=1ab+ab+1a(a−b)+a(a−b)−ab−a(a−b)+2a2−10ac+25c2 =1ab+ab+1a(a−b)+a(a−b)+a2−10ac+25c2=1ab+ab+1a(a−b)+a(a−b)+(a−5c)2≥2√1ab ⋅ab+2√1a(a−b)⋅a(a−b)+0=4，当且仅当{ab=1a(a−b)=1a=5c，即a=√2，b=√22，c=√25时，等号成立.故选：A.小提示：易错点睛：利用基本不等式求最值时，要注意其必须满足的三个条件：（1）“一正”就是各项必须为正数；（2）“二定”就是要求和的最小值，必须把构成和的二项之积转化成定值；要求积的最大值，则必须把构成积的因式的和转化成定值；（3）“三相等”是利用基本不等式求最值时，必须验证等号成立的条件，若不能取等号则这个定值就不是所求的最值，这也是最容易发生错误的地方.5、若“﹣2<x <3”是“x 2+mx ﹣2m 2<0（m >0）”的充分不必要条件，则实数m 的取值范围是（） A ．m ≥1B ．m ≥2C ．m ≥3D ．m ≥4 答案：C分析：x 2+mx ﹣2m 2<0（m >0），解得﹣2m <x <m .根据“﹣2<x <3”是“x 2+mx ﹣2m 2<0（m >0）”的充分不必要条件，可得﹣2m ≤﹣2，3≤m ，m >0.解出即可得出. 解：x 2+mx ﹣2m 2<0（m >0），解得﹣2m <x <m .∵“﹣2<x <3”是“x 2+mx ﹣2m 2<0（m >0）”的充分不必要条件，∴﹣2m ≤﹣2，3≤m ，(两个等号不同时取)m >0. 解得m ≥3.则实数m 的取值范围是[3，+∞）. 故选：C.6、关于x 的不等式ax 2−(a 2+1)x +a <0的解集为{x|x 1<x <x 2}，且x 2−x 1=1，则a 2+a −2=（） A ．3B ．32C ．2D ．23答案：A分析：根据一元二次不等式与解集之间的关系可得x 1+x 2=a +1a 、x 1x 2=1，结合 (x 2−x 1)2=(x 1+x 2)2−4x 1x 2计算即可.由不等式ax 2−(a 2+1)x +a <0的解集为{x |x 1<x <x 2}，得a >0，不等式对应的一元二次方程为ax 2−(a 2+1)x +a =0，方程的解为x 1、x 2，由韦达定理，得x 1+x 2=a 2+1a=a +1a ，x 1x 2=1，因为x 2−x 1=1，所以(x 2−x 1)2=(x 1+x 2)2−4x 1x 2=1，即(a +1a )2−4=1，整理，得a 2+a −2=3. 故选：A7、已知关于x 的不等式ax 2+bx +c <0的解集为{x|x <−1或x >4}，则下列说法正确的是（）A．a>0B．不等式ax2+cx+b>0的解集为{x|2−√7<x<2+√7}C．a+b+c<0D．不等式ax+b>0的解集为{x|x>3}答案：B分析：根据解集形式确定选项A错误；化不等式为x2−4x−3<0,即可判断选项B正确；设f(x)=ax2+ bx+c，则f(1)>0，判断选项C错误；解不等式可判断选项D错误.解：因为关于x的不等式ax2+bx+c<0的解集为{x|x<−1或x>4}，所以a<0，所以选项A错误；由题得{a<0−1+4=−ba−1×4=ca,∴b=−3a,c=−4a，所以ax2+cx+b>0为x2−4x−3<0,∴2−√7<x<2+√7.所以选项B正确；设f(x)=ax2+bx+c，则f(1)=a+b+c>0，所以选项C错误；不等式ax+b>0为ax−3a>0,∴x<3，所以选项D错误.故选：B8、不等式1+x1−x≥0的解集为（）A．{x|x≥1或x≤−1}B．{x∣−1≤x≤1} C．{x|x≥1或x<−1}D．{x|−1≤x<1}答案：D分析：不等式等价于x+1x−1≤0，即(x+1)(x−1)≤0，且x−1≠0，由此求得不等式的解集．不等式等价于x+1x−1≤0，即(x+1)(x−1)≤0，且x−1≠0，解得−1≤x<1，故不等式的解集为{x|−1≤x<1}，故选：D．多选题9、已知关于x的不等式ax2+bx+c>0解集为{x|−2<x<3}，则（）A．a>0B．不等式ax+c>0的解集为{x|x<6}C．a+b+c>0D．不等式cx2−bx+a<0的解集为{x|−13<x<12}答案：BCD解析：根据已知条件得−2和3是方程ax2+bx+c=0的两个实根，且a<0，根据韦达定理可得b=−a,c=−6a，根据b=−a,c=−6a且a<0,对四个选项逐个求解或判断可得解.因为关于x的不等式ax2+bx+c>0解集为{x|−2<x<3}，所以−2和3是方程ax2+bx+c=0的两个实根，且a<0，故A错误；所以−2+3=−ba ，−2×3=ca，所以b=−a,c=−6a，所以不等式ax+c>0可化为ax−6a>0，因为a<0，所以x<6，故B正确；因为a+b+c=a−a−6a=−6a，又a<0，所以a+b+c>0，故C正确；不等式cx2−bx+a<0可化为−6ax2+ax+a<0，又a<0，所以−6x2+x+1>0，即6x2−x−1<0，即(3x+1)(2x−1)<0，解得−13<x<12,故D正确.故选：BCD.小提示：利用一元二次不等式的解集求出参数a,b,c的关系是解题关键.本题根据韦达定理可得所要求的关系，属于中档题.10、设0<b<a<1，则下列不等式不成立的是（）A．ab<b2<1B．√a<√b<1C．1<1a <1bD．a2<ab<1答案：ABD分析：对于ABD举例判断即可，对于C，利用不等式的性质判断对于A，取a=12,b=13，则ab=16>b2=19，所以A错误，对于B，取a=14,b=19，则√a=12>√b=13，所以B错误，对于C，因为0<b<a<1，所以1ab >0，所以b⋅1ab<a⋅1ab，即1a<1b，因为0<a<1，所以0<a⋅1a <1×1a，即1<1a，综上1<1a<1b，所以C正确，对于D，取a=12,b=13，则ab=16<a2=14，所以D错误，故选：ABD11、下面所给关于x的不等式，其中一定为一元二次不等式的是（）A．3x+4<0B．x2+mx-1>0C．ax2+4x-7>0D．x2<0答案：BD分析：利用一元二次不等式的定义和特征对选项逐一判断即可.选项A是一元一次不等式，故错误；选项B，D，不等式的最高次是二次，二次项系数不为0，故正确；当a=0时，选项C是一元一次不等式，故不一定是一元二次不等式，即错误.故选：BD.填空题12、若x>0,y>0,xy=10，则2x +5y的最小值为_____．答案：2分析：化简2x +5y=2x+102y=2x+xy2y=2x+x2，结合基本不等式，即可求解.由x>0,y>0,xy=10，则2x +5y=2x+102y=2x+xy2y=2x+x2≥2√2x×x2=2，当且仅当x=2时取“=”，即2x +5y的最小值为2．所以答案是：2.13、已知x，y为正数，且12+x +4y=1，则x+y的最小值为________.答案：7解析：由题设等式有x+y+2=5+y2+x +4(x+2)y，利用基本不等式可求x+y+2的最小值，从而可得x+y的最小值.x+y+2=[(x+2)+y]×(1x+2+4y)=5+y2+x+4(x+2)y，由基本不等式有y2+x +4(x+2)y≥4，当且仅当x=1,y=6时等号成立，故x+y+2的最小值为9即x+y的最小值为7.所以答案是：7.小提示：应用基本不等式求最值时，需遵循“一正二定三相等”，如果原代数式中没有积为定值或和为定值，则需要对给定的代数变形以产生和为定值或积为定值的局部结构.求最值时要关注取等条件的验证.14、已知函数f(x)=√mx2+mx+1的定义域是R，则m的取值范围为______．答案：[0,4]分析：根据函数的定义域为R可得mx2+mx+1≥0对x∈R恒成立，对参数m的取值范围分类讨论，分别求出对应m 的范围，进而得出结果.因为函数f(x)=√mx2+mx+1的定义域为R，所以mx2+mx+1≥0对x∈R恒成立，当m=0时，mx2+mx+1=1>0，符合题意；当m>0时，由Δ=m2-4m≤0，解得0<m≤4；当m<0时，显然mx2+mx+1不恒大于或等于0．综上所述，m的取值范围是[0,4].所以答案是：[0,4].解答题15、设a，b，c∈R，a+b+c=0，abc=1．（1）证明：ab+bc+ca<0；（2）用max{a，b，c}表示a，b，c中的最大值，证明：max{a，b，c}≥√43．答案：（1）证明见解析（2）证明见解析.分析：（1）方法一：由(a+b+c)2=a2+b2+c2+2ab+2ac+2bc=0结合不等式的性质，即可得出证明；（2）方法一：不妨设max{a,b,c}=a，因为a+b+c=0,abc=1，所以a>0,b<0,c<0,a=(−b)+(−c)≥2√bc=2√1a ，则a3≥4,a≥√43．故原不等式成立．（1）［方法一］【最优解】：通性通法∵(a+b+c)2=a2+b2+c2+2ab+2ac+2bc=0，∴ab+bc+ca=−12(a2+b2+c2).∵abc=1,∴a,b,c均不为0，则a2+b2+c2>0，∴ab+bc+ca=−12(a2+b2+c2)<0．［方法二］：消元法由a+b+c=0得b=−(a+c)，则ab+bc+ca=b(a+c)+ca=−(a+c)2+ac=−(a2+ac+c2)=−(a +c 2)2−34c 2≤0，当且仅当a =b =c =0时取等号，又abc =1，所以ab +bc +ca <0．［方法三］：放缩法方式1：由题意知a ≠0, a +b +c =0, a =−(c +b ), a 2=(c +b )2=c 2+b 2+2cb ≥4bc ，又ab +bc +ca =a (b +c )+bc =−a 2+bc ≤−a 2+a 24=−3a 24<0，故结论得证．方式2：因为a +b +c =0，所以0=(a +b +c )2=a 2+b 2+c 2+2ab +2bc +2ca=12[(a 2+b 2)+(b 2+c 2)+(c 2+a 2)]+2ab +2bc +2ca ≥12(2ab +2bc +2ca )+2ab +2bc +2ca =3(ab +bc +ca )．即ab +bc +ca ≤0，当且仅当a =b =c =0时取等号，又abc =1，所以ab +bc +ca <0．［方法四］：因为a +b +c =0,abc =1，所以a ，b ，c 必有两个负数和一个正数，不妨设a ≤b <0<c,则a =−(b +c ), ∴ab +bc +ca =bc +a (c +b )=bc −a 2<0. ［方法五］：利用函数的性质方式1：6b =−(a +c )，令f (c )=ab +bc +ca =−c 2−ac −a 2，二次函数对应的图像开口向下，又abc =1，所以a ≠0，判别式Δ=a 2−4a 2=−3a 2<0，无根，所以f (c )<0，即ab +bc +ca <0．方式2：设f (x )=(x −a )(x −b )(x −c )=x 3+(ab +bc +ca )x −1，则f (x )有a ，b ，c 三个零点，若ab +bc +ca ≥0，则f (x )为R 上的增函数，不可能有三个零点，所以ab +bc +ca <0．（2）［方法一］【最优解】：通性通法不妨设max {a,b,c }=a ，因为a +b +c =0,abc =1，所以a >0, b <0, c <0, a =(−b )+(−c )≥2√bc =2√1a，则a 3≥4,a ≥√43．故原不等式成立．［方法二］：不妨设max {a,b,c }=a ，因为a +b +c =0,abc =1，所以a >0，且{b +c =−a,bc =1a , 则关于x 的方程x 2+ax +1a =0有两根，其判别式Δ=a 2−4a ≥0，即a ≥√43．故原不等式成立．［方法三］：不妨设max {a,b,c }=a ，则a >0, b =−(a +c ), abc =1, −(a +c )ac =1, ac 2+a 2c +1=0，关于c 的方程有解，判别式Δ=(a 2)2−4a ≥0，则a 3≥4,a ≥√43．故原不等式成立．［方法四］：反证法假设max {a,b,c }<√43，不妨令a ≤b <0<√43，则ab =1c >√43,−a −b =c <√43，又√43>−a −b ≥2√ab >√√43=21−13=√43，矛盾，故假设不成立．即max {a,b,c }≥√43，命题得证．【整体点评】（1）方法一：利用三项平方和的展开公式结合非零平方为正数即可证出，证法常规，为本题的通性通法，也是最优解法；方法二：利用消元法结合一元二次函数的性质即可证出；方法三：利用放缩法证出；方法四：利用符号法则结合不等式性质即可证出；方法五：利用函数的性质证出．（2）方法一：利用基本不等式直接证出，是本题的通性通法，也是最优解；方法二：利用一元二次方程根与系数的关系以及方程有解的条件即可证出；方法三：利用消元法以及一元二次方程有解的条件即可证出；方法四：利用反证法以及基本不等式即可证出．。

(word完整版)高一数学必修一必修二难题

21、已知二次函数宫（工）对任意实数x不等式-厂恒成立，且或-1） = 0，令孑（庄）二呂拄）+唧In工+ ] （肌E&）（I ）求二「的表达式;（II ）若三时二’：使- ■'成立，求实数m的取值范围;证明：对站岛运[1屈，恒有屮佃）-豆也）|=1（ill）设1怎朋冬叭月（对=/5）一（冷+ 1）兀，2、某三棱锥的三视图如图所示，该三棱锥的体积是C.3、一个棱锥的三视图如右图所示，则它的体积为+心+1，*应的以下性质中，错误的是（5、设上为非零实数，则关于函数 '''A •函数'- 一定是个偶函数B . 一定没有最大值C •区间［叽+00) —定是/(尿)的单调递增区间D •函数1 -不可能有三个零点「，当x ― .时，均有'''1 ,则实数-；的取值范围是(7、如图，四棱锥 P-^BCD 中，底面 ABC ［为平行四边形，P 从底面 ABCD M 是棱PD 的中点，且 PA = AB = AC =2 , 眈=2葩. (I )求证：CDL 平面PAC(H)求二面角-----的大小；西 AN_(皿)如果 N 是棱AB 上一点，且直线 CN 与平面MA 断成角的正弦值为，求丄主‘的值. 8、已知幕函数-?1< ：1； ' '' 1?"- " 「为偶函数，且在区间' '：'上是单调递增函数。

(I)求函数-的解析式；6、已知-；：> 0,且』孑., =.V A.「IBD(H)设；，若二」能取遍W'内的所有实数，求实数二的取值范围./空、=——1 ----------------9、已知定义域为丘的函数. 是奇函数.(1)求实数匚」的值； (2)判断并证明.’「在：上的单调性；(3 )若1 -对任意•【一-恒成立，求匕的取值范围.参考答案一、计算题1、解(])设 ” ｛一 I ..•••屮-恒成立.•.丄「一 ■.二.；一和L,^....恒成立f(x)=呂学)+叨Ln x+— 肿已氏，工n 0) (II 厂一 11 3 ,=—2T +W21n X 2 a -b^-c =a +<7f （疋）二A + —工当；，「时，「八的值域为R/（JC）= 1^ >0StVx>0, f（x）>o当；一「时，恒成立当朋吒o时，令y（x）—o x—J-也，（町心==-等+朋In上云这时若三「「使成立则只须-「「丄「厂"一,综上所述，实数m的取值范围= -'-1■ ■ ' 丁^^1所」「"单减屮佃）Fg）护⑴一二冷一胡n珂一|于是- -1 . 1 1| //(丙)一/f (叼j |<1<= —觀him——cl <=>，啊—In 也- h (?K)=—m—In m+ -— (1 <.懑壬劭记’' ：' ，则. 1 1 331 1，1 n' '2 強2莎Tm y3—<0 Im所以函数'’- 〔是单增函数M I沐、誉1 3 〔根一刃& + 1）nc 血隹）二一一1一——= -------------------------------------- < 0所以'故命题成立.、选择题2、D3、A4、B5、C6、C三、简答题7、证明：（I）连结AC因为为在中，血"—2 BC=2^2所以所以■-因为AB/ CD所以又因为匸上一地面ABCD所以一空因为’所以「匸—平面PAC（II）如图建立空间直角坐标系，则丄.丄:一因为M是棱PD的中点，所以为平面MAB的法向量, 所以莎=（-1丄1）,耳（2皿令丁=1,则2所以平面MAB的法向量一■ ■-因为F上一平面ABCD所以心：人、二是平面ABC的一个法向量. 所以设直线CN 与平面MAB 所成角为，因为平面MAB 勺法向量，AN d-- =1 解得・：一 1,即 0 - 1, ^ --,所以賈 .8、（I ）T J 八为幕函数 •••2m - n = \又丿」■'在区间-'上是单调递增函数 •込'J - ■] .：■ . 2分贝0 7 二丨「；-•）- 吃三三 .•.：◎=〕或[或 2 3分因为二面角 ”一」匸'一 -J 为锐二面角,71所以二面角3/ L -U'」的大小为4 .(ill)因为 N 是棱AB 上一点，所以设 , 」虛；：' ；所以2-J2 x J”十匚当玄二〔时，-'「’ - ''为奇函数，不合题意，舍去当卫二1时为偶函数，符合题意当■ ■-：时，」_ '为奇函数，不合题意，舍去f （对二工①当二:时，」-，则- -.单调递增，其值域为 R ，满足题意②当•小时，由得•；— 1：..，则」一在单调递减，在； ■.•.或叽加二呂㈠卫）二冷"加-2,则其值域为[皿+少-2他）•••二「-能取遍丁内的所有实数 .只需则N 「在-■--单调递增又宀 -.•.In 2^2 - 2 < 0 » 卩(总) < 卩(1) O 0 < 1 四、综合题r/（o ）=o 29、解：（1） M-帖一了⑴ “-市门，经检验成立。

2019高一数学函数难题汇编(含解析)

高一数学必修一（难）一．选择题（共12小题）1．已知定义在R上的偶函数f（x）满足f（x+1）=﹣f（x），且当x∈[﹣1，0]时，，函数，则关于x的不等式f（x）＜g（x）的解集为（）A．（﹣2，﹣1）∪（﹣1，0）B．C．D．2．已知定义在R上的奇函数f（x）满足：当x≥0时，f（x）=x3，若不等式f（﹣4t）＞f（2m+mt2）对任意实数t恒成立，则实数m的取值范围是（）A．（﹣∞，﹣） B．（﹣，0）C．（﹣∞，0）∪（，+∞）D．（﹣∞，﹣）∪（，+∞）3．定义域为R的函数f（x）满足：f（x+2）=2f（x），当x∈[0，2）时，，若x∈[﹣4，﹣2）时，恒成立，则实数t的取值范围是（）A．B．C．（0，1]D．（0，2]4．对于函数f（x），若∀a，b，c∈R，f（a），f（b），f（c）为某一三角形的三边长，则称f（x）为”可构造三角形函数“，已知函数f（x）=（0＜x＜）是“可构造三角形函数”，则实数t的取值范围是（）A．[1，4]B．[1，2]C．[，2] D．[0，+∞）5．已知函数f（x）是定义在R上的奇函数，当x≤0时，f（x）=x（1﹣x），若数列{a n}满足a1=，且a n+1=，则f（a2015）+f（a2016）=（）A．﹣8 B．8 C．﹣4 D．46．函数f（x）=，若x＞0时，不等式f（x）≤恒成立，则实数m的取值范围为（）A．[4，+∞）B．[3，+∞）C．[2，+∞）D．[，+∞）7．已知x＞0，y＞0，若不等式a（x+y）≥x+恒成立，则a的最小值为（）A．B． C．+2 D．+8．已知函数f（x）=若函数g（x）=f[f（x）]﹣2的零点个数为（）A．3 B．4 C．5 D．69．已知定义在R上的偶函数g（x）满足g（x）+g（2﹣x）=0，函数f（x）=的图象是g（x）的图象的一部分．若关于x的方程g2（x）=a（x+1）2有3个不同的实数根，则实数a的取值范围为（）A．（，+∞）B．（，）C．（，+∞）D．（2，3）10．已知函数f（x）定义域为[0，+∞），当x∈[0，1]时，f（x）=sinπx，当x∈[n，n+1]时，f（x）=，其中n∈N，若函数f（x）的图象与直线y=b有且仅有2016个交点，则b的取值范围是（）A．（0，1） B．（，）C．（，）D．（，）11．已知函数：，，设函数F（x）=f（x+3）•g（x﹣5），且函数F（x）的零点均在区间[a，b]（a＜b，a，b∈Z）内，则b﹣a的最小值为（）A．8 B．9 C．10 D．1112．已知函数，其中m＞0，且函数f（x）=f（x+4），若方程3f（x）﹣x=0恰有5个根，则实数m的取值范围是（）A．B． C．D．二．填空题（共7小题）13．设函数f（x）=2ax2+2bx，若存在实数x0∈（0，t），使得对任意不为零的实数a，b均有f（x0）=a+b成立，则t的取值范围是．14．若正数x，y满足=1，则的最小值为．15．已知集合{φ|f（x）=sin[（x﹣2φ）π]+cos[（x﹣2φ）π]为奇函数，且|log aφ|＜1}的子集个数为4，则a的取值范围为．16．已知函数y=f（x）是定义在R上的奇函数，对∀x∈R都有f（x﹣3）=f（x ﹣1）成立，当，x∈（0，1]且x1≠x2时，有＜0，给出下列命题：（1）f（x）在[﹣2，2]上有5个零点（2）点（2016，0）是函数y=f（x）的一个对称中心（3）直线x=2016是函数y=f（x）图象的一条对称轴（4）f（9.2）＜f（π）则正确的是．17．已知函数f（x）=e x，对于实数m、n、p有f（m+n）=f（m）+f（n），f（m+n+p）=f（m）+f（n）+f（p），则p的最大值等于．18．定义在R上的单调函数f（x）满足：f（x+y）=f（x）+f（y），若F（x）=f（asinx）+f（sinx+cos2x﹣3）在（0，π）上有零点，则a的取值范围是．19．已知函数f（x）=，g（x）=（k＞0），对任意p∈（1，+∞），总存在实数m，n满足m＜0＜n＜p，使得f（p）=f（m）=g（n），则整数k的最大值为．三．解答题（共11小题）20．已知f（x）=log a是奇函数（其中a＞1）（1）求m的值；（2）判断f（x）在（2，+∞）上的单调性并证明；（3）当x∈（r，a﹣2）时，f（x）的取值范围恰为（1，+∞），求a与r的值．21．已知向量=（cos，sin），=（cos，﹣sin），函数f（x）=•﹣m|+|+1，x∈[﹣，]，m∈R．（1）当m=0时，求f（）的值；（2）若f（x）的最小值为﹣1，求实数m的值；（3）是否存在实数m，使函数g（x）=f（x）+m2，x∈[﹣，]有四个不同的零点？若存在，求出m的取值范围；若不存在，说明理由．22．已知二次函数f（x）=ax2+bx+c．（1）若a=c＞0，f（1）=1，对任意x∈|[﹣2，2]，f（x）的最大值与最小值之和为g（a），求g（a）的表达式；（2）若a，b，c为正整数，函数f（x）在（﹣，）上有两个不同零点，求a+b+c的最小值．23．已知函数f（x）=．（1）求f（f（））；（2）若x0满足f（f（x0））=x0，且f（x0）≠x0，则称x0为f（x）的二阶不动点，求函数f（x）的二阶不动点的个数．24．已知a∈R，函数．（1）当a=0时，解不等式f（x）＞1；（2）当a＞0时，求函数y=2f（x）﹣f（2x）的零点个数；（3）设a＜0，若对于t∈R，函数在区间[t，t+1]上的最大值与最小值之差都不超过1，求实数a的取值范围．25．已知a∈R，函数f（x）=．（1）若f（2）=﹣3，求实数a的值；（2）若关于x的方程f（x）﹣log2[（a﹣4）x+2a﹣5]=0的解集中恰好有一个元素，求a的取值范围．（3）设a＞0，若对任意t∈[，1]，函数f（x）在区间[t，t+1]上的最大值与最小值的差不超过1，求a的取值范围．26．设a∈R，函数f（x）=x|x﹣a|+2x．（1）若a=3，求函数f（x）在区间[0，4]上的最大值；（2）若存在a∈（2，4]，使得关于x的方程f（x）=t•f（a）有三个不相等的实数解，求实数t的取值范围．27．如图，在半径为，圆心角为60°的扇形的弧上任取一点P，作扇形的内接矩形PNMQ，使点Q在OA上，点N，M在OB上，设矩形PNMQ的面积为y，∠P OB=θ．（Ⅰ）将y表示成θ的函数关系式，并写出定义域；（Ⅱ）求矩形PNMQ的面积取得最大值时•的值；（Ⅲ）求矩形PNMQ的面积y≥的概率．28．已知函数f（x）=x|x﹣a|，a∈R，g（x）=x2﹣1．（1）当a=1时，解不等式f（x）≥g（x）；（2）记函数f（x）在区间[0，2]上的最大值为F（a），求F（a）的表达式．29．已知函数g（x）=，且函数f（x）=log a g（x）（a＞0，a≠1）奇函数而非偶函数．（1）写出f（x）在（a，+∞）上的单调性（不必证明）；（2）当x∈（r，a﹣3）时，f（x）的取值范围恰为（1，+∞），求a与r的值；（3）设h（x）=﹣m（x+2）﹣2是否得在实数m使得函数y=h（x）有零点？若存在，求出实数m的取值范围，若不存在，请说明理由．30．已知函数f（x）=1+log2x，g（x）=2x．（1）若F（x）=f（g（x））•g（f（x）），求函数F（x）在x∈[1，4]的值域；（2）令G（x）=f（8x2）f（）﹣kf（x），已知函数G（x）在区间[1，4]有零点，求实数k的取值范围；（3）若H（x）=，求H（）+H（）+H（）+…+H（）的值．2018高一数学必修一（难）参考答案与试题解析一．选择题（共12小题）1．（2016秋•渝中区校级期末）已知定义在R上的偶函数f（x）满足f（x+1）=﹣f（x），且当x∈[﹣1，0]时，，函数，则关于x的不等式f（x）＜g（x）的解集为（）A．（﹣2，﹣1）∪（﹣1，0）B．C．D．【解答】解：由题意知，f（x+1）=﹣f（x），∴f（x+2）=﹣f（x+1）=f（x），即函数f（x）是周期为2的周期函数．若x∈[0，1]时，﹣x∈[﹣1，0]，∵当x∈[﹣1，0]时，，∴当x∈[0，1]时，，∵f（x）是偶函数，∴f（x）=，即f（x）=．∵函数，∴g（x）=，作出函数f（x）和g（x）的图象如图：当﹣1＜x＜0时，由=，则，由选项验证解得x=，即此时不等式式f（x）＜g（|x+1|）的解为﹣1＜x＜，∵函数g（x）关于x=﹣1对称，∴不等式式f（x）＜g（x）的解为﹣1＜x＜或＜x＜﹣1，即不等式的解集为（，﹣1）∪（﹣1，），故选：D．2．（2016秋•通渭县期末）已知定义在R上的奇函数f（x）满足：当x≥0时，f （x）=x3，若不等式f（﹣4t）＞f（2m+mt2）对任意实数t恒成立，则实数m的取值范围是（）A．（﹣∞，﹣） B．（﹣，0）C．（﹣∞，0）∪（，+∞）D．（﹣∞，﹣）∪（，+∞）【解答】解：∵当x≥0时，f（x）=x3，①∴当x＜0时，﹣x＞0，f（﹣x）=（﹣x）3=﹣x3，又f（x）为定义在R上的奇函数，∴﹣f（x）=﹣x3，∴f（x）=x3（x＜0），②综合①②知，f（x）=x3，x∈R．又f′（x）=3x2≥0，∴f（x）=x3为R上的增函数，∴不等式f（﹣4t）＞f（2m+mt2）对任意实数t恒成立⇔﹣4t＞2m+mt2对任意实数t恒成立，即mt2+4t+2m＜0对任意实数t恒成立，∴，解得：m＜﹣．故选：A．3．（2016秋•宜春期末）定义域为R的函数f（x）满足：f（x+2）=2f（x），当x ∈[0，2）时，，若x∈[﹣4，﹣2）时，恒成立，则实数t的取值范围是（）A．B．C．（0，1]D．（0，2]【解答】解：当x∈[0，2）时，∈[﹣，0]∪[﹣1，﹣]，∴当x∈[0，2）时，f（x）的最小值为f（）=﹣1，又∵函数f（x）满足f（x+2）=2f（x），∴f（x）=f（x+2），当x∈[﹣2，0）时，f（x）的最小值为f（﹣）=f（）=﹣，当x∈[﹣4，﹣2）时，f（x）的最小值为f（﹣）=f（﹣）=﹣若x∈[﹣4，﹣2]时，恒成立，∴﹣≥恒成立．即≤0，则0＜t≤1，故选：C．4．（2016春•琅琊区校级期末）对于函数f（x），若∀a，b，c∈R，f（a），f（b），f（c）为某一三角形的三边长，则称f（x）为”可构造三角形函数“，已知函数f （x）=（0＜x＜）是“可构造三角形函数”，则实数t的取值范围是（）A．[1，4]B．[1，2]C．[，2] D．[0，+∞）【解答】解：f（x）===2+，①若t=2，则f（x）=2，此时f（x）构成边长为2的等边三角形，满足条件，设m=tanx，则m=tanx＞0，则函数f（x）等价为g（m）=2+，②若t﹣2＞0即t＞2，此时函数g（m）在（0，+∞）上是减函数，则2＜f（a）＜2+t﹣2=t，同理2＜f（b）＜t，2＜f（c）＜t，则4＜f（a）+f（b）＜2t，2＜f（c）＜t，由f（a）+f（b）＞f（c），可得4≥t，解得2＜t≤4．③当t﹣2＜0，f（x）在R上是增函数，t＜f（a）＜2，同理t＜f（b）＜2，t＜f（c）＜2，则2t＜f（a）+f（b）＜4，t＜f（c）＜2，由f（a）+f（b）＞f（c），可得2t≥2，解得1≤t＜2．综上可得，1≤t≤4，故实数t的取值范围是[1，4]；故选：A5．（2015秋•菏泽期末）已知函数f（x）是定义在R上的奇函数，当x≤0时，f （x）=x（1﹣x），若数列{a n}满足a1=，且a n+1=，则f（a2015）+f（a2016）=（）A．﹣8 B．8 C．﹣4 D．4【解答】解：设x＞0，则﹣x＜0；∵f（x）是定义在R上的奇函数；∴f（x）=﹣f（﹣x）=﹣[﹣x（1+x）]=x（1+x）；由，且得：，，，…；∴数列{a n}是以3为周期的周期数列；∴a2015=a671×3+2=a2=2，a2016=a671×3+3=a3=﹣1；∴f（a2015）+f（a2016）=f（2）+f（﹣1）=2（1+2）+（﹣1）（1+1）=4．故选：D．6．（2015秋•吉安期末）函数f（x）=，若x＞0时，不等式f（x）≤恒成立，则实数m的取值范围为（）A．[4，+∞）B．[3，+∞）C．[2，+∞）D．[，+∞）【解答】解：当0≤x≤4时，函数f（x）在[0，2]上为增函数，则[2，4]上为减函数，则当x=2时，函数f（x）取得最大值f（2）=，当4≤x≤8时，0≤x﹣4≤4，即f（x）=f（x﹣4）=，此时的最大值为f（6）=，当8≤x≤12时，4≤x﹣4≤8，即f（x）=f（x﹣4）=，此时的最大值为f（10）=，作出函数f（x）的图象如图，要使当x＞0时，不等式f（x）≤恒成立，则m＞0，设g（x）=，则满足，即，即，即m≥3，故选：B．7．（2015秋•杭州校级期末）已知x＞0，y＞0，若不等式a（x+y）≥x+恒成立，则a的最小值为（）A．B． C．+2 D．+【解答】解：∵x＞0，y＞0，∴不等式a（x+y）≥x+等价为a≥=，令，∴a≥，令u=，∴u′=令u′=0，∴t=﹣（负值舍去）∴函数在（0，）上单调增，在（，+∞）上单调减∴t=时，函数u=取得最大值为∴a≥∴实数a的最小值为故选：A8．（2016秋•沙市区校级期末）已知函数f（x）=若函数g（x）=f[f（x）]﹣2的零点个数为（）A．3 B．4 C．5 D．6【解答】解：∵函数f（x）=，∴f（x）=．∴x∈（﹣∞，log23）时，f（f（x））=∈[0，3]，令f（f（x））=2，解得x=log2（1+log23）．同理可得：x∈[log23，2）时，=2，解得x=．x∈时，=2，解得x=．时，=2，解得x=1+．综上可得：函数g（x）=f[f（x）]﹣2的x零点个数为4．故选：B．9．（2016春•重庆校级期末）已知定义在R上的偶函数g（x）满足g（x）+g（2﹣x）=0，函数f（x）=的图象是g（x）的图象的一部分．若关于x的方程g2（x）=a（x+1）2有3个不同的实数根，则实数a的取值范围为（）A．（，+∞）B．（，）C．（，+∞）D．（2，3）【解答】解：∵定义在R上的偶函数g（x）满足g（x）+g（2﹣x）=0，∴g（x）=﹣g（2﹣x）=﹣g（x﹣2），则g（x+2）=﹣g（x），即g（x+4）=﹣g（x+2）=﹣（﹣g（x））=g（x），则函数g（x）是周期为4的周期函数，函数f（x）=的定义域为[﹣1，1]，若1≤x≤2，则﹣2≤﹣x≤﹣1，则0≤2﹣x≤1，此时g（x）=﹣g（2﹣x）=﹣，当﹣2≤x≤﹣1，则1≤﹣x≤2，则g（x）=g（﹣x）=﹣则由g2（x）=a（x+1）2得，当﹣2≤x≤﹣1时，1﹣（x+2）2=a（x+1）2，作出函数g（x）的图象如图：若方程g2（x）=a（x+1）2有3个不同的实数根，则当a≤0时，不满足条件．则当a＞0时，方程等价为g（x）=±=|x+1|，则当x=﹣1时，方程g（x）=|x+1|恒成立，此时恒有一解，当直线y=﹣（x+1）与g（x）在（﹣4，﹣3）相切时，此时方程g（x）=|x+1|有6个交点，不满足条件．当y=﹣（x+1）与g（x）在（﹣4，﹣3）不相切时，满足方程g（x）=|x+1|有三个交点，此时直线方程为x+y+=0，满足圆心（﹣4，0）到直线x+y+=0，的距离d=＞1，即＞1，即3＞，平方得9a＞a+1，得8a＞1，则a＞，故选：A10．（2016秋•荆门期末）已知函数f（x）定义域为[0，+∞），当x∈[0，1]时，f（x）=sinπx，当x∈[n，n+1]时，f（x）=，其中n∈N，若函数f（x）的图象与直线y=b有且仅有2016个交点，则b的取值范围是（）A．（0，1） B．（，）C．（，）D．（，）【解答】解：根据题意，x∈[0，1]时，f（x）=sinπx，x∈[n，n+1]时，f（x）=，其中n∈N，∴f（n）=sinnπ=0，f（）=sin=1，f（）===，f（）===，…；画出图形如图所示；当b∈（，1）时，函数f（x）的图象与直线y=b有2个交点；当b∈（，）时，函数f（x）的图象与直线y=b有4个交点；当b∈（，）时，函数f（x）的图象与直线y=b有6个交点；…；当b∈（，）时，函数f（x）的图象与直线y=b有2016个交点．故选：D．11．（2015秋•汕头校级期末）已知函数：，，设函数F（x）=f（x+3）•g（x﹣5），且函数F（x）的零点均在区间[a，b]（a＜b，a，b∈Z）内，则b﹣a的最小值为（）A．8 B．9 C．10 D．11【解答】解：∵f（0）=1＞0，f（﹣1）=1﹣1﹣+﹣…+＜0，∴函数f（x）在区间（﹣1，0）内有零点；当x∈（﹣1，0）时，f′（x）=＞0，∴函数f（x）在区间（﹣1，0）上单调递增，故函数f（x）有唯一零点x∈（﹣1，0）；∵g（1）=1﹣1+﹣+…﹣＞0，g（2）=1﹣2+﹣+…+﹣＜0．当x∈（1，2）时，g′（x）=﹣1+x﹣x2+x3﹣…+x2013﹣x2014=＞0，∴函数g（x）在区间（1，2）上单调递增，故函数g（x）有唯一零点x∈（1，2）；∵F（x）=f（x+3）•g（x﹣4），且函数F（x）的零点均在区间[a，b]（a＜b，a，b∈Z）内，∴f（x+3）的零点在（﹣4，﹣3）内，g（x﹣4）的零点在（5，6）内，因此F（x）=f（x+3）•g（x﹣3）的零点均在区间[﹣4，6]内，∴b﹣a的最小值为10．故选：C．12．（2015秋•衡水校级期末）已知函数，其中m ＞0，且函数f（x）=f（x+4），若方程3f（x）﹣x=0恰有5个根，则实数m的取值范围是（）A．B． C．D．【解答】解：∵当x∈（﹣1，1]时，将函数化为方程x2+=1（y≥0），∴实质上为一个半椭圆，其图象如图所示，∵函数f（x）=f（x+4），∴函数的周期是4，同时在坐标系中作出当x∈（1，3]得图象，再根据周期性作出函数其它部分的图象，若方程3f（x）﹣x=0恰有5个根，则等价为f（x）=恰有5个根，由图易知直线y=与第二个椭圆（x﹣4）2+=1（y≥0）相交，而与第三个半椭圆（x﹣8）2+=1 （y≥0）无公共点时，方程恰有5个实数解，将y=代入（x﹣4）2+=1 （y≥0）得，（9m2+1）x2﹣72m2x+135m2=0，令t=9m2（t＞0），则（t+1）x2﹣8tx+15t=0，由△=（8t）2﹣4×15t （t+1）＞0，得t＞15，由9m2＞15，且m＞0得m，同样由y=与第三个椭圆（x﹣8）2+=1 （y≥0）由△＜0可计算得m＜，综上可知m∈（，），故选：A．二．填空题（共7小题）13．（2017春•杭州期末）设函数f（x）=2ax2+2bx，若存在实数x0∈（0，t），使得对任意不为零的实数a，b均有f（x0）=a+b成立，则t的取值范围是（1，+∞）．【解答】解：f（x）=a+b成立等价于（2x﹣1）b=（1﹣2x2）a，当x=时，左边=0，右边≠0，不成立，当x≠时，（2x﹣1）b=（1﹣2x2）a等价于=，设k=2x﹣1，则x=，则===（﹣k﹣2），∵x∈（0，t），（t＜），或x∈（0，）∪（，t），（t＞），∴k∈（﹣1，2t﹣1），（t＜），或k∈（﹣1，0）∪（0，2t﹣1），（t＞），（*）∵∀a，b∈R，∴=（﹣k﹣2），在（*）上有解，∴（﹣k﹣2），在（*）上的值域为R，设g（k）=（﹣k）﹣1，则g（k）在（﹣∞，0），（0，+∞）上单调递减，∴，解得t＞1，故答案为：（1，+∞）14．（2016春•沙坪坝区校级期末）若正数x，y满足=1，则的最小值为2．【解答】解：∵正数x，y满足+=1，∴=1﹣=，∴（y＞1），∴x﹣1=（x＞1）．则+=（y﹣1）+≥2=2，当且仅当y﹣1=，即y ﹣1=时取等号．∴的最小值为2．故答案为：215．（2016秋•武昌区校级期末）已知集合{φ|f（x）=sin[（x﹣2φ）π]+cos[（x ﹣2φ）π]为奇函数，且|log aφ|＜1}的子集个数为4，则a的取值范围为（）∪（）．【解答】解：∵集合{φ|f（x）=sin[（x﹣2φ）π]+cos[（x﹣2φ）π]为奇函数，∴f（0）=sin（﹣2φπ）+cos（﹣2φπ）=cos2φπ﹣sin2φπ=0，∴cos2φπ=sin2φπ，即tan2φπ=1，∴2φπ=kπ+，则φ=+，k∈Z．验证φ=+，k∈Z时，f（x）=sin[（x﹣2φ）π]+cos[（x﹣2φ）π]=sin[（x﹣k﹣）π]+cos[（x﹣k﹣）π]=sin（πx﹣）+cos（）=为奇函数．∴φ=+，k∈Z．∵集合{φ|f（x）=sin[（x﹣2φ）π]+cos[（x﹣2φ）π]为奇函数，且|log aφ|＜1}的子集个数为4，∴满足|log aφ|＜1的φ有2个，即满足﹣1＜log aφ＜1的φ有2个．分别取k=0，1，2，3，得到φ=，，，，若0＜a＜1，可得a∈（）时，满足﹣1＜log aφ＜1的φ有2个；若a＞1，可得a∈（）时，满足﹣1＜log aφ＜1的φ有2个．则a的取值范围为（）∪（）．故答案为：（）∪（）．16．（2016秋•清城区期末）已知函数y=f（x）是定义在R上的奇函数，对∀x∈R都有f（x﹣3）=f（x﹣1）成立，当，x∈（0，1]且x1≠x2时，有＜0，给出下列命题：（1）f（x）在[﹣2，2]上有5个零点（2）点（2016，0）是函数y=f（x）的一个对称中心（3）直线x=2016是函数y=f（x）图象的一条对称轴（4）f（9.2）＜f（π）则正确的是（1）（2）（4）．【解答】解：对于（1），∵函数y=f（x）是定义在R上的奇函数，∴f（0）=0，又f（x﹣3）=f（x﹣1），∴函数y=f（x）是以2为周期的函数，且f（1﹣3）=f（1﹣1），即f（﹣2）=f（0）=0，又f（2）=﹣f（﹣2），∴f（2）=0；同理可得，f（1）=f（﹣1）=0，又当x∈（0，1]且x1≠x2时，有＜0，即奇函数y=f（x）在区间（0，1]上单调递减，故函数y=f（x）在区间[﹣1，0）上也单调递减，由函数y=f（x）是以2为周期的函数可知函数y=f（x）在区间（﹣2，﹣1]、[1，2）上单调递减，∴f（x）在区间[﹣2，2]上有±1、0、±2共5个零点，故（1）正确；对于（2），∵函数y=f（x）是定义在R上的奇函数，∴（0，0）为其对称中心，又函数y=f（x）的是以2为周期的函数，∴点（2016，0）是函数y=f（x）的一个对称中心，故（2）正确；对于（3），作出函数y=f（x）的图象如下：（3）直线x=2016不是函数y=f（x）图象的一条对称轴，故（3）错误；对于（4），∵函数y=f（x）的是以2为周期的函数且在区间[1，2）上为减函数，∴f（9.2）=f（1.2）＜f（π﹣2）=f（π），故（4）正确．综上所述，正确的是：（1）（2）（4），故答案为：（1）（2）（4）．17．（2016春•扬州期末）已知函数f（x）=e x，对于实数m、n、p有f（m+n）=f（m）+f（n），f（m+n+p）=f（m）+f（n）+f（p），则p的最大值等于2ln2﹣ln3．【解答】解：由f（x）=e x得：f（m+n）=f（m）f（n），∵f（m+n）=f（m）+f（n），∴f（m）f（n）=f（m）+f（n），设f（m）f（n）=f（m）+f（n）=t，则f（m）、f（n）是x2﹣tx+t=0的解，∵△=t2﹣4t≥0，∴t≥4或t≤0（舍去）．又f（m+n+p）=f（m）f（n）f（p）=f（m）+f（n）+f（p），∴tf（p）=t+f（p），∴f（p）==1+（t≥4），显然t越大，f（p）越小，∴当t=4时，f（p）取最大值，又f（p）=e p，∴f（p）取到最大值时，p也取到最大值，即p max=ln=2ln2﹣ln3．故答案为：2ln2﹣ln3．18．（2016秋•江岸区校级期末）定义在R上的单调函数f（x）满足：f（x+y）=f （x）+f（y），若F（x）=f（asinx）+f（sinx+cos2x﹣3）在（0，π）上有零点，则a的取值范围是[2，+∞）．【解答】解：①令x=y=0，则f（0）=2f（0），则f（0）=0；再令y=﹣x，则f（x﹣x）=f（x）+f（﹣x）=0，且f（x）定义域为R，关于原点对称．∴f（x）是奇函数．②F（x）=f（asinx）+f（sinx+cos2x﹣3）在（0，π）上有零点．∴f（asinx）+f（sinx+cos2x﹣3）=0在（0，π）上有解；∴f（asinx）=﹣f（sinx+cos2x﹣3）=f（﹣sinx﹣cos2x+3）在（0，π）上有解；又∵函数f（x）是R上的单调函数，∴asinx=﹣sinx﹣cos2x+3在（0，π）上有解．∵x∈（0，π），∴sinx≠0；∴a==sinx+﹣1；令t=sinx，t∈（0，1]；则a=t+﹣1；∵y=t+，＜0，因此函数y在（0，1]上单调递减，∴a≥2．故答案为：[2，+∞）．19．（2016春•盐城期末）已知函数f（x）=，g（x）=（k＞0），对任意p∈（1，+∞），总存在实数m，n满足m＜0＜n＜p，使得f（p）=f（m）=g（n），则整数k的最大值为7．【解答】解：显然g（x）=（k＞0），在区间（1，+∞）上为减函数，于是g（n）＞g（p），若f（p）=g（n），则对任意p＞1，有f（p）＞g（p）．当x＞1时，＞，∴k＜，设t=x﹣1（t＞0），则==2（t++2）≥8，∴k＜8∴k≤7．下面证明：当k=7时，对0＜x＜1，有f（x）＜g（x）．当0＜x＜1时，f（x）＜g（x）⇔﹣ln（1﹣x）＞0．令ψ（x）=﹣ln（1﹣x）（0＜x＜1），则ψ′（x）=﹣+＜0，故ψ（x）在（0，1）上为减函数，于是ψ（x）＞0．同时，当x∈（0，+∞）时，g（x）=∈（0，+∞）．当x∈（0，1）时，f（x）∈R；当x∈（1，+∞）时，f（x）∈（0，+∞）．结合函数的图象可知，对任意的正数p，存在实数m、n满足0＜m＜n＜p，使得f（p）=f（m）=g（n）．综上所述，正整数k的最大值为7．故答案为：7．三．解答题（共11小题）20．（2016秋•惠来县校级期末）已知f（x）=log a是奇函数（其中a＞1）（1）求m的值；（2）判断f（x）在（2，+∞）上的单调性并证明；（3）当x∈（r，a﹣2）时，f（x）的取值范围恰为（1，+∞），求a与r的值．【解答】解：（1）由题意：f（x）是奇函数，则f（﹣x）+f（x）=0，即log a+=0∴，解得：m=±1，当m=﹣1时，f（x）无意义，所以，故得m的值为1．（2）由（1）得，设2＜x1＜x2，则f（x2）﹣f（x1）=﹣=∴2＜x1＜x2，∴0＜2x1x2+2（x1﹣x2）﹣4＜x1x2﹣（x1﹣x2）﹣4，∵a＞1，∴f（x2）＜f（x1）所以：函数f（x）在（2，+∞）上的单调减函数．（3）由（1）得，∴得，函数f（x）的定义域为（﹣∞，﹣2）∪（2，+∞）又∵，得f（x）∈（﹣∞，0）∪（0，+∞）令f（x）=1，则=，解得：．所以：f（）=1当a＞1时，＞2，此时f（x）在在（2，+∞）上的单调减函数．所以：当x∈（2，）时，得f（x）∈1，+∞）；由题意：r=2，那么a﹣2=，解得：a=5．所以：当x∈（r，a﹣2），f（x）的取值范围恰为（1，+∞）时，a和r的值分别为5和2．21．（2016秋•无锡期末）已知向量=（cos，sin），=（cos，﹣sin），函数f（x）=•﹣m|+|+1，x∈[﹣，]，m∈R．（1）当m=0时，求f（）的值；（2）若f（x）的最小值为﹣1，求实数m的值；（3）是否存在实数m，使函数g（x）=f（x）+m2，x∈[﹣，]有四个不同的零点？若存在，求出m的取值范围；若不存在，说明理由．【解答】解：（1）•=（cos，sin）•（cos，﹣sin）=cos cos﹣sin sin=cos（+）=cos2x，当m=0时，f（x）=•+1=cos2x+1，则f（）=cos（2×）+1=cos+1=；（2）∵x∈[﹣，]，∴|+|===2cosx，则f（x）=•﹣m|+|+1=cos2x﹣2mcosx+1=2cos2x﹣2mcosx，令t=cosx，则≤t≤1，则y=2t2﹣2mt，对称轴t=，①当＜，即m＜1时，当t=时，函数取得最小值此时最小值y=﹣m=﹣1，得m=（舍），②当≤≤1，即m＜1时，当t=时，函数取得最小值此时最小值y=﹣=﹣1，得m=，③当＞1，即m＞2时，当t=1时，函数取得最小值此时最小值y=2﹣2m=﹣1，得m=（舍），综上若f（x）的最小值为﹣1，则实数m=．（3）令g（x）=2cos2x﹣2mcosx+m2=0，得cosx=或，∴方程cosx=或在x∈[﹣，]上有四个不同的实根，则，得，则≤m＜，即实数m的取值范围是≤m＜．22．（2016秋•义乌市期末）已知二次函数f（x）=ax2+bx+c．（1）若a=c＞0，f（1）=1，对任意x∈|[﹣2，2]，f（x）的最大值与最小值之和为g（a），求g（a）的表达式；（2）若a，b，c为正整数，函数f（x）在（﹣，）上有两个不同零点，求a+b+c的最小值．【解答】解：（1）a=c＞0，f（1）=1，则a+b+a=1，b=1﹣2a，∴f（x））=ax2+（1﹣2a）x+a=a+，当1﹣≤﹣2，即0＜a≤时，g（a）=f（﹣2）+f（2）=10a；当﹣2＜1﹣≤0，即＜a≤时，g（a）=f（1﹣）+f（2）=a﹣+3，当a＞时，g（a）=f（1﹣）+f（﹣2）=9a﹣﹣1，综上所述，g（a）=；（2）函数f（x）在（﹣，）上有两个不同零点x1，x2，则x1+x2=﹣＜0，＞x1x2=＞0∴a＞16c，由根的分布可知f（﹣）=a﹣b+c＞0，即a+16c＞4b，∵a，b，c为正整数，∴a+16c≥4b+1f（0）=c＞0，△＞0，b，∴a+16c＞8+1，可得（）2＞1，∵a＞16c，∴＞1，∴，∴a＞25，∴a≥26，∴b≥，∴b≥11，c≥1．f（x）=26x2+11x+1，经检验符合题意，故a+b+c的最小值为38．23．（2016秋•佛山期末）已知函数f（x）=．（1）求f（f（））；（2）若x0满足f（f（x0））=x0，且f（x0）≠x0，则称x0为f（x）的二阶不动点，求函数f（x）的二阶不动点的个数．【解答】解：（1）∵f（x）=．∴f（））=ln=，∴f（f（））=f（）=2﹣2×=1；（2）函数f（x）=．x∈[0，），f（x）=2﹣2x∈（1，2]，x∈[，1），f（x）=2﹣2x∈（0，1]，x∈[1，e]，f（x）=lnx∈（0，1），∴f（f（x））=，若x0满足f（f（x0））=x0，且f（x0）≠x0，则称x0为f（x）的二阶不动点，所以：x0∈[0，），ln（2﹣2x0）=x0，由y=ln（2﹣x0），y=x0，图象可知：存在满足题意的不动点．x0∈[，1），﹣2+4x0=x0，解得x0=，满足题意．x0∈[1，e]，2﹣2lnx0=x0，即2﹣x0=2lnx0，由y=2﹣x0，y=2lnx0，图象可知：存在满足题意的不动点．函数f（x）的二阶不动点的个数为：3个．24．（2016秋•海安县校级期末）已知a∈R，函数．（1）当a=0时，解不等式f（x）＞1；（2）当a＞0时，求函数y=2f（x）﹣f（2x）的零点个数；（3）设a＜0，若对于t∈R，函数在区间[t，t+1]上的最大值与最小值之差都不超过1，求实数a的取值范围．【解答】解：（1）a=0时，f（x）=，∵f（x）＞1，即＞1，∴0＜2x＜1，解得x＜0．（2）y=2f（x）﹣f（2x）=，∴函数y=2f（x）﹣f（2x）的定义域为{x|x≠log2a，且x≠log2a}．令y=0得22x+1﹣2x﹣a=0，令t=2x（t＞0，且t≠a，t），方程为2t2﹣t﹣a=0，△=1+8a＞0，若a=1，t=1或﹣，方程无解，即函数y=2f（x）﹣f（2x）的零点个数为0若0＜a＜1或a＞1，方程有两个不相等的解，即函数y=2f（x）﹣f（2x）的零点个数为2；（3）函数f（x）在区间[t，t+1]上单调递减，由题意得f（t）﹣f（t+1）≤1，即﹣≤1，∴22t+1﹣（3a+1）•2t+a2≥0，设x=2t（x＞0），则2x2﹣（3a+1）x+a2≥0，∴△≤0或，∴a≤﹣．25．（2016秋•西陵区校级期末）已知a∈R，函数f（x）=．（1）若f（2）=﹣3，求实数a的值；（2）若关于x的方程f（x）﹣log2[（a﹣4）x+2a﹣5]=0的解集中恰好有一个元素，求a的取值范围．（3）设a＞0，若对任意t∈[，1]，函数f（x）在区间[t，t+1]上的最大值与最小值的差不超过1，求a的取值范围．【解答】解：（1）f（2）=﹣3，∴log2（+a）=﹣3=log2，∴+a=，解得a=﹣（2）由f（x）﹣log2[（a﹣4）x+2a﹣5]=0得log2（+a）﹣log2[（a﹣4）x+2a ﹣5]=0．即log2（+a）=log2[（a﹣4）x+2a﹣5]，即+a=（a﹣4）x+2a﹣5＞0，①则（a﹣4）x2+（a﹣5）x﹣1=0，即（x+1）[（a﹣4）x﹣1]=0，②，当a=4时，方程②的解为x=﹣1，代入①，成立当a=3时，方程②的解为x=﹣1，代入①，成立当a≠4且a≠3时，方程②的解为x=﹣1或x=，若x=﹣1是方程①的解，则+a=a﹣1＞0，即a＞1，若x=是方程①的解，则+a=2a﹣4＞0，即a＞2，则要使方程①有且仅有一个解，则1＜a≤2．综上，若方程f（x）﹣log2[（a﹣4）x+2a﹣5]=0的解集中恰好有一个元素，则a 的取值范围是1＜a≤2，或a=3或a=4．（3）函数f（x）在区间[t，t+1]上单调递减，由题意得f（t）﹣f（t+1）≤1，即log2（+a）﹣log2（+a）≤1，即+a≤2（+a），即a≥﹣=设1﹣t=r，则0≤r≤，==，当r=0时，=0，当0＜r≤时，=，∵y=r+在（0，）上递减，∴r+≥+4=，∴=≤=，∴实数a的取值范围是a≥26．（2016秋•徐汇区期末）设a∈R，函数f（x）=x|x﹣a|+2x．（1）若a=3，求函数f（x）在区间[0，4]上的最大值；（2）若存在a∈（2，4]，使得关于x的方程f（x）=t•f（a）有三个不相等的实数解，求实数t的取值范围．【解答】解：（1）当a=3，x∈[0，4]时，f（x）=x|x﹣3|+2x=，可知函数f（x）在区间[0，]递增，在（，3]上是减函数，在[3，4]递增，则f（）=，f（4）=12，所以f（x）在区间[0，4]上的最大值为f（4）=12．（2）f（x）=，①当x≥a时，因为a＞2，所以＜a．所以f（x）在[a，+∞）上单调递增．②当x＜a时，因为a＞2，所以＜a．所以f（x）在（﹣∞，）上单调递增，在[，a]上单调递减．当2＜a≤4时，知f（x）在（﹣∞，]和[a，+∞）上分别是增函数，在[，a]上是减函数，当且仅当2a＜t•f（a）＜时，方程f（x）=t•f（a）有三个不相等的实数解．即1＜t＜=（a++4）．令g（a）=a+，g（a）在a∈（2，4]时是增函数，故g（a）max=5．∴实数t的取值范围是（1，）．27．（2016春•信阳期末）如图，在半径为，圆心角为60°的扇形的弧上任取一点P，作扇形的内接矩形PNMQ，使点Q在OA上，点N，M在OB上，设矩形PNMQ的面积为y，∠POB=θ．（Ⅰ）将y表示成θ的函数关系式，并写出定义域；（Ⅱ）求矩形PNMQ的面积取得最大值时•的值；（Ⅲ）求矩形PNMQ的面积y≥的概率．【解答】解：（Ⅰ）在Rt△PON中，∠PNO=90°，∠POB=θ，，所以，，在Rt△QMO中，∠QMO=90°，∠QON=60°，QM=PN=所以OM=所以：MN=ON﹣OM=所以y=即：y=3sinθcosθ﹣sin2θ，（）（Ⅱ）由（Ⅰ）得y=3sinθcosθ﹣sin2θ=﹣=）﹣=∵θ∈（0，）∴∴sin（）∈∴，即时，y的最大值为．此时ON=cos==，则•=||•||cos=×=．（Ⅲ）若矩形PNMQ的面积y≥，则≥，即sin（）≥，则sin（）≥，∵∴≤≤，即≤θ≤，则对应的概率P==28．（2016春•苏州期末）已知函数f（x）=x|x﹣a|，a∈R，g（x）=x2﹣1．（1）当a=1时，解不等式f（x）≥g（x）；（2）记函数f（x）在区间[0，2]上的最大值为F（a），求F（a）的表达式．【解答】解：f（x）≥g（x），a=1时，即解不等式x|x﹣1|≥x2﹣1，…（1分）当x≥1时，不等式为x2﹣x≥x2﹣1，解得x≤1，所以x=1；…（3分）当x＜1时，不等式为x﹣x2≥x2﹣1，解得，所以；…（5分）综上，x∈．…（6分）（2）因为x∈[0，2]，当a≤0时，f（x）=x2﹣ax，则f（x）在区间[0，2]上是增函数，所以F（a）=f（2）=4﹣2a；…（7分）当0＜a＜2时，，则f（x）在区间上是增函数，在区间上是减函数，在区间[a，2]上是增函数，所以F（a）=max{f（），f（2）}，…（9分）而，f（2）=4﹣2a，令即，解得，所以当时，F（a）=4﹣2a；…（11分）令即，解得或，所以当时，；…（12分）当a≥2时，f（x）=﹣x2+ax，当即2≤a＜4时，f（x）在间上是增函数，在上是减函数，则；…（13分）当，即a≥4时，f（x）在间[0，2]上是增函数，则F（a）=f（2）=2a﹣4；…（14分）所以，，…（16分）29．（2015秋•黄浦区校级期末）已知函数g（x）=，且函数f（x）=log a g（x）（a＞0，a≠1）奇函数而非偶函数．（1）写出f（x）在（a，+∞）上的单调性（不必证明）；（2）当x∈（r，a﹣3）时，f（x）的取值范围恰为（1，+∞），求a与r的值；（3）设h（x）=﹣m（x+2）﹣2是否得在实数m使得函数y=h（x）有零点？若存在，求出实数m的取值范围，若不存在，请说明理由．【解答】解：（1）函数g（x）=，且函数f（x）=log a g（x）（a＞0，a≠1）奇函数而非偶函数，可得f（﹣x）=﹣f（x），即log a=﹣log a，可得•=1，即p2﹣x2=4﹣x2，即p2=4，解得p=2（﹣2舍去），即有f（x）=log a，当a＞1时，f（x）在（2，+∞），（﹣∞，﹣2）递减；当0＜a＜1时，f（x）在（2，+∞），（﹣∞，﹣2）递增．（2）由（1）得f（x）=log a，函数f（x）的定义域为（﹣∞，﹣2）∪（2，+∞）又≠1，得f（x）∈（﹣∞，0）∪（0，+∞），令f（x）=1，则log a=1，解得x=．所以：f（）=1，当a＞1时，＞2，此时f（x）在（2，+∞）上的单调减函数．所以：当x∈（2，）时，得f（x）∈1，+∞）；由题意：r=2，那么a﹣3=，解得：a=3+2．所以：当x∈（r，a﹣3），f（x）的取值范围恰为（1，+∞）时，a和r的值分别为3+2和2；（3）假设h（x）=﹣m（x+2）﹣2即h（x）=﹣m（x+2）﹣2，存在实数m使得函数y=h（x）有零点．由题意可知，方程=m（x+2）+2在{x|x≥﹣2且x≠2}中有实数解，令=t，则t≥0且t≠2，问题转化为关于t的方程mt2﹣t+2=0①，有非负且不等于2的实数根．若t=0，则①为2=0，显然不成立，故t≠0，方程①可变形为m=﹣2（）2+，问题进一步转化为求关于t的函数（t≥0且t≠2）的值域，因为t≥0且t≠2，所以＞0且≠，所以m=﹣2（）2+∈（﹣∞，0）∪（0，]，所以实数m的取值范围是（﹣∞，0）∪（0，]．30．（2015秋•无锡校级期末）已知函数f（x）=1+log2x，g（x）=2x．（1）若F（x）=f（g（x））•g（f（x）），求函数F（x）在x∈[1，4]的值域；（2）令G（x）=f（8x2）f（）﹣kf（x），已知函数G（x）在区间[1，4]有零点，求实数k的取值范围；（3）若H（x）=，求H（）+H（）+H（）+…+H（）的值．【解答】解：（1）若F（x）=f（g（x））•g（f（x））=（1+log22x）•=（1+x）•2×=2x（1+x）=2x2+2x=2（x+）2﹣当x∈[1，4]上函数F（x）为增函数，则函数的最大值为F（4）=40，函数的最小值为F（1）=4，则函数的值域为[4，40]．（2）令G（x）=f（8x2）f（）﹣kf（x）=（1+log28x2）（1+log2）﹣k（1+log2x）=（1+og28+log2x2））（1+log2x）﹣k（1+log2x）=（4+2log2x））（1+log2x）﹣k（1+log2x）=（log2x）2+4log2x+4﹣k﹣klog2x=（log2x）2+（4﹣k）log2x+4﹣k，设t=log2x，当x∈[1，4]，则t∈[0，2]，则函数等价为y=h（t）=t2+（4﹣k）t+4﹣k若函数G（x）在区间[1，4]有零点，则等价为y=h（t）=t2+（4﹣k）t+4﹣k在t∈[0，2]上有零点，即h（t）=t2+（4﹣k）t+4﹣k=0在t∈[0，2]上有解，即t2+4t+4﹣k（1+t）=0在t∈[0，2]上有解，即k===t+1++2，设m=t+1，则m∈[1，3]，则k=m++2，则k=m++2在m∈[1，3]上递增，则当m=1时，k=1+1+2=4，当m=3时，k=3++2=，∴4≤m++2≤，即4≤k≤，即实数k的取值范围是4≤k≤；（3）若H（x）=，则H（x）==，则H（x）+H（1﹣x）=+=+=+=1，设H（）+H（）+H（）+…+H（）=S，H（）+H（）+…H（）+H（）=S，两式相加得2015[H（）+H（）]=2S，即2S=2015，则S=．。

高一数学知识点难题及解答

高一数学知识点难题及解答随着高中学习的深入，数学作为一门理科学科，对于学生来说常常是最令人头疼的。

特别是在高一这个阶段，新的数学知识点和难题不断涌现。

本文将围绕高一数学知识点中的几个难题展开讲述，并提供相应的解答。

一、平方根的处理问题高一数学中，平方根的处理经常会对学生造成困扰。

在计算平方根时，首先需要明确一个原则：不能直接对负数开平方。

因此，当题目中出现像√(-16)这样的表达时，我们首先要做的是将其转化成复数的形式。

通过定义我们知道，√(a × b) = √a × √b。

因此，我们可以将√(-16)转化为√(-1) × √16。

根据定义√(-1) = i，其中i是虚数单位。

所以√(-16) = i × 4 = 4i。

二、函数的复合问题在高一数学中，函数的复合也是一个常见的难点。

当两个函数进行复合运算时，很多学生容易弄混运算的顺序。

以f(x) = 2x + 1和g(x) = x^2为例，我们可以先求f(g(x))。

首先将g(x)代入f(x)的表达式中，得到f(g(x)) = 2(g(x)) + 1 = 2(x^2) + 1。

类似地，我们也可以求g(f(x))。

将f(x)代入g(x)的表达式中，得到g(f(x)) = (f(x))^2 = (2x + 1)^2 = 4x^2 + 4x + 1。

通过这个例子，我们可以看到函数的复合运算顺序的影响。

因此，在解题过程中，要注意先执行内层函数的运算，再执行外层函数的运算。

三、不等式的求解问题在高一数学中，不等式的求解是一个需要注意的难点。

首先，我们要掌握不等式的性质：等号两边同时加（减）一个数时，不等号不变；等号两边同时乘（除）一个正数时，不等号不变；等号两边同时乘（除）一个负数时，不等号反向。

以2x - 5 > 3为例，我们首先将不等式转化成等价的形式：2x -5 - 3 > 0，即2x - 8 > 0。

高中数学必修一第二章一元二次函数方程和不等式经典大题例题(带答案)

高中数学必修一第二章一元二次函数方程和不等式经典大题例题单选题1、实数a,b满足a>b，则下列不等式成立的是（）A．a+b<ab B．a2>b2C．a3>b3D．√a2+b2<a+b答案：C分析：利用不等式的性质逐一判断即可.A，若a=1,b=0，则a+b>ab，故A错误；B，若a=1,b=−2，则a2<b2，故B错误；C，若a>b，则a3−b3=(a−b)(a2+ab+b2)=(a−b)[(a+b2)2+3b24]>0，所以a3>b3，故C正确；D，若a=1,b=−2，则√a2+b2>a+b，故D错误.故选：C2、将进货价为每个80元的商品按90元一个出售时，能卖出400个，每涨价1元，销售量就减少20个，为了使商家利润有所增加，则售价a（元/个）的取值范围应是（）A．90<a<100B．90<a<110C．100<a<110D．80<a<100答案：A分析：首先设每个涨价x元，涨价后的利润与原利润之差为y元，结合条件列式，根据y>0，求x的取值范围，即可得到a的取值范围.设每个涨价x元，涨价后的利润与原利润之差为y元，则a=x+90,y=(10+x)⋅(400−20x)−10×400=−20x2+200x.要使商家利润有所增加，则必须使y>0，即x2−10x<0，得0<x<10,∴90<x+90<100，所以a的取值为90<a<100.故选：A3、已知y=(x−m)(x−n)+2022(n>m)，且α,β(α<β)是方程y=0的两实数根，则α，β，m，n的大小关系是（）A．α<m<n<βB．m<α<n<βC．m<α<β<n D．α<m<β<n答案：C分析：根据二次函数图像特点，结合图像平移变换即可得到答案.∵α，β为方程y=0的两实数根，∴α，β为函数y=(x−m)(x−n)+2022的图像与x轴交点的横坐标，令y1=(x−m)(x−n)，∴m，n为函数y1=(x−m)(x−n)的图像与x轴交点的横坐标，易知函数y= (x−m)(x−n)+2022的图像可由y1=(x−m)(x−n)的图像向上平移2022个单位长度得到，所以m<α<β<n.故选:C.4、关于x的不等式ax2−|x|+2a≥0的解集是(−∞,+∞)，则实数a的取值范围为（）A．[√24,+∞)B．(−∞,√24]C．[−√24,√24]D．(−∞,−√24]∪[√24,+∞)答案：A分析：不等式ax2−|x|+2a≥0的解集是(−∞,+∞)，即对于∀x∈R，ax2−|x|+2a≥0恒成立，即a≥|x|x2+2，分x=0和a≠0两种情况讨论，结合基本不等式即可得出答案.解：不等式ax2−|x|+2a≥0的解集是(−∞,+∞)，即对于∀x∈R，ax2−|x|+2a≥0恒成立，即a≥|x|x2+2，当x=0时，a≥0，当a≠0时，a≥|x|x2+2=1|x|+2|x|，因为1|x|+2|x|≤2√|x|⋅2|x|=√24，所以a≥√24，综上所述a∈[√24,+∞). 故选：A.5、不等式1+5x −6x 2>0的解集为（）A ．{x|x >1或x <−16}B ．{x |−16<x <1 }C ．{x|x >1或x <−3}D ．{x |−3<x <2 } 答案：B分析：解一元二次不等式，首先确保二次项系数为正，两边同时乘−1，再利用十字相乘法，可得答案，法一：原不等式即为6x 2−5x −1<0，即(6x +1)(x −1)<0，解得−16<x <1，故原不等式的解集为{x |−16<x <1 }．法二：当x =2时，不等式不成立，排除A ，C ；当x =1时，不等式不成立，排除D ．故选：B ．6、已知正实数a ，b 满足a +1b=2，则2ab +1a的最小值是（）A ．52B ．3C ．92D ．2√2+1 答案：A分析：由已知得， a =2−1b 代入得2ab +1a =2(2b −1)+b2b−1，令2b −1=t ，根据基本不等式可求得答案. 解：因为a +1b=2，所以a =2−1b>0，所以0<b <2 ，所以2ab +1a =2(2−1b )b +b 2b−1=2(2b −1)+b2b−1，令2b −1=t ，则b =t +12，且−1<t <3 ，所以2ab +1a =2t +t +12t=2t +12t +12≥2√2t ⋅12t +12=52，当且仅当2t =12t ，即t =12，b =34,a =23时，取等号，所以2ab +1a 的最小值是52. 故选：A.7、已知−1≤x +y ≤1,1≤x −y ≤5，则3x −2y 的取值范围是（） A ．[2,13]B ．[3,13]C ．[2,10]D ．[5,10] 答案：A分析：设3x −2y =m (x +y )−n (x −y )=(m −n )x +(m +n )y ，求出m,n 的值，根据x +y,x −y 的范围，即可求出答案.设3x −2y =m (x +y )−n (x −y )=(m −n )x +(m +n )y ，所以{m −n =3m +n =−2，解得：{m =12n =−52,3x −2y =12(x +y )+52(x −y ), ，因为−1≤x +y ≤1,1≤x −y ≤5，所以3x −2y =12(x +y )+52(x −y )∈[2,13]，故选：A.8、已知a >b >0，下列不等式中正确的是（） A ．ca >cb B ．ab <b 2C ．a −b +1a−b ≥2D ．1a−1<1b−1 答案：C分析：由a >b >0，结合不等式的性质及基本不等式即可判断出结论. 解：对于选项A ，因为a >b >0,0<1a<1b，而c 的正负不确定，故A 错误；对于选项B ，因为a >b >0，所以ab >b 2，故B 错误；对于选项C ，依题意a >b >0，所以a −b >0,1a−b >0，所以a −b +1a−b ≥2√(a −b )×1a−b =2，故C 正确；对于选项D ，因为a >b >0,a −1>b −1>−1,1a−1与1b−1正负不确定，故大小不确定，故D 错误；故选：C. 多选题9、已知函数y =ax 2+bx -3，则下列结论正确的是（） A ．关于x 的不等式ax 2+bx -3<0的解集可以是{x |x >3 } B ．关于x 的不等式ax 2+bx -3>0的解集可以是∅C ．函数y =ax 2+bx -3的图象与x 轴正半轴可以有两个交点D ．“关于x 的方程ax 2+bx -3=0有一个正根和一个负根”的充要条件是“a >0” 答案：BCD分析：根据不等式的解集求出a 、b ，再解不等式ax 2+bx -3<0可判断A ；取a =-1，b =0，解不等式-x 2-3>0可判断B ；取a =-1，b =4可判断C ；根据根的分布、充要条件的定义可判断D ．若不等式ax 2+bx -3<0的解集是{x |x >3}，则a =0且3b -3=0，得b =1，而当a =0，b =1时，不等式ax 2+bx -3<0，即x -3<0，得x <3，与x >3矛盾，故A 错误；取a =-1，b =0，此时不等式-x 2-3>0的解集为∅，故B 正确；函数y =ax 2+bx -3的图象与x 轴正半轴可以有两个交点,即ax 2+bx -3=0可以有2个正根，取a =-1，b =4，则由y =-x 2+4x -3=0，得x =1或3，故C 正确；若关于x 的方程ax 2+bx -3=0有一个正根和一个负根，则{a ≠0,−3a<0,得a >0，若a >0，则Δ=b 2+12a >0，故关于x 的方程ax 2+bx -3=0有两个不等的实根x 1,x 2，且x 1x 2=-3a <0，即关于x 的方程ax 2+bx -3=0有一个正根和一个负根．因此“关于x 的方程ax 2+bx -3=0有一个正根和一个负根”的充要条件是“a >0”，故D 正确．故选：BCD ．10、已知x ，y 是正实数，则下列选项正确的是（） A ．若x +y =2，则1x+1y 有最小值2B ．若x +y =3，则x(y +1)有最大值5C ．若4x +y =1，则2√x +√y 有最大值√2D ．x4+y 2x+1y有最小值94答案：AC分析：将已知转化，再利用基本不等式可判断ABC 选项；利用特值法判断选项D 。

高一数学最难试题及答案

高一数学最难试题及答案一、选择题：（每题5分，共20分）1. 已知函数f(x)=x^2-4x+3，若f(a)=0，则a的值为（）。

A. 1B. 3C. -1D. 02. 集合A={1,2,3}，集合B={2,3,4}，则A∩B等于（）。

A. {1}B. {2,3}C. {3,4}D. {1,2,3}3. 若直线y=2x+3与直线y=-x+4相交，则交点的坐标为（）。

A. (1,5)B. (-1,5)C. (1,-1)D. (-1,-1)4. 函数f(x)=x^3-3x^2+4x-2的导数f'(x)为（）。

A. 3x^2-6x+4B. x^2-6x+4C. 3x^2-6x+2D. x^2-3x+4二、填空题：（每题5分，共20分）5. 已知等差数列{an}的前三项分别为2，5，8，则该数列的通项公式为an=______。

6. 函数y=x^2-6x+8的顶点坐标为（______，______）。

7. 圆x^2+y^2-6x+8y-24=0的圆心坐标为（______，______）。

8. 已知函数f(x)=x^3-3x^2+2x+1，若f'(x)=0，则x的值为______。

三、解答题：（每题15分，共30分）9. 已知函数f(x)=x^3-6x^2+11x-6，求证：该函数在区间[1,2]上单调递增。

10. 已知三角形ABC的顶点坐标分别为A(1,2)，B(4,6)，C(7,2)，求三角形ABC的面积。

四、综合题：（每题30分，共30分）11. 已知函数f(x)=x^4-4x^3+6x^2-2x+1，求函数的极值点，并讨论函数在这些极值点处的性质。

答案：一、选择题：1. B2. B3. A4. A二、填空题：5. an=3n-16. (3,-1)7. (3,-4)8. 1或2三、解答题：9. 证明：首先求导f'(x)=3x^2-12x+11，令f'(x)=0，解得x=1或x=3。

高一数学必修一必修二难题

精心整理1、已知二次函数对任意实数x不等式恒成立，且，令.（I）求的表达式；（II）若使成立，求实数m的取值范围；（III）设，恒有2A．??????????3A．．?4、函数，在同一直角坐标系第一象限中的图像可能是）5、设为非零实数，则关于函数，A．函数一定是个偶函数B．C．区间一定是的单调递增区间???????D．函数不可能有三个零点6、已知＞0,且,=,当x∈时,均有,则实数的取值范围是(???)A ．?????????B ．??C ．?D ．7、如图，四棱锥中，底面ABCD 为平行四边形，PA ⊥底面ABCD ，M 是棱PD 的中点，且PA =AB =AC =2，．（I ）求证：CD ⊥平面PAC ；所成角的正弦值为，求的值．8为偶函数，且在区间上是单调递增函数。

（Ⅱ）设，若能取遍内的所有实数，求实数9的函数是奇函数．（1）求实数的值；（3）若对任意恒成立，求参考答案一、计算题1、解（I ）设由题意令得??∴∴得∵恒成立∴和恒成立得∴（II）当当时，恒成立当时，令这时若使成立则只须，综上所述，实数m的取值范围（III）∵，所以单减于是记，则所以函数所以2、D3、A4、B5、C?6、C7因为为在中，，，所以，所以．因为AB//CD，所以．又因为地面ABCD，所以因为所以?(II)则．因为M所以所以，．设为平面MAB的法向量，所以，即，令，则，所以平面MAB的法向量．因为所以所以的大小为．．，所以．解得，即，，所以．8、（Ⅰ）∵为幂函数?∴??????????????????????????????????????????1分???????又在区间上是单调递增函数?∴?????????????????2分???????则?∵?∴或或???????????????3分???????当时，为奇函数，不合题意，舍去???????当时，为偶函数，符合题意???????为奇函数，不合题意，舍去???????????????????????????????????????????????????????????????????5??①当单调递增，其值域为，满足题意?????时，由得，则在单调递减，在，则其值域为???????∵能取遍内的所有实数?????????????9 ???????令?单调递增???????又?∴????????????????11分??????综合①②知，实数的取值范围为??????????????????????????????????12分四、综合题9、解：（1），经检验成立。

高中数学必修一难题个人整理的,里面有详细答案的,供大家看看推荐一下吧!

三、解答题1. 判断一次函数,b kx y +=反比例函数xk y =，二次函数c bx ax y ++=2的单调性.2. 已知函数()f x 的定义域为()1,1-，且同时满足下列条件：（1）()f x 是奇函数；（2）()f x 在定义域上单调递减；（3）2(1)(1)0,f a f a -+-<求a 的取值范围.3. 利用函数的单调性求函数x x y 21++=的值域；4. 已知函数[]2()22,5,5f x x ax x =++∈-.① 当1a =-时，求函数的最大值和最小值；② 求实数a 的取值范围，使()y f x =在区间[]5,5-上是单调函数.1. 解：当0k >，y kx b =+在R 是增函数，当0k <，y kx b =+在R 是减函数；当0k >，ky x =在(,0),(0,)-∞+∞是减函数，当0k <，ky x=在(,0),(0,)-∞+∞是增函数；当0a >，2y ax bx c =++在(,]2b a -∞-是减函数，在[,)2b a -+∞是增函数，当0a <，2y ax bx c =++在(,]2b a -∞-是增函数，在[,)2b a -+∞是减函数.2. 解：22(1)(1)(1)f a f a f a -<--=-，则2211111111a a a a -<-<⎧⎪-<-<⎨⎪->-⎩,∴01a <<3. 解：1210,2x x +≥≥-，显然y 是x 的增函数，12x =-，min 1,2y =- 1[,)2y ∴∈-+∞ 4. 解：2(1)1,()22,a f x x x =-=-+对称轴min max 1,()(1)1,()(5)37x f x f f x f =====∴max m ()37,()1in f x f x ==（2）对称轴,x a =-当5a -≤-或5a -≥时，()f x 在[]5,5-上单调 ∴5a ≥或5a ≤-.17. 已知函数f(x)=x 2+2ax+2, x []5,5-∈.(1)当a=-1时，求函数的最大值和最小值；(2) 若y=f(x)在区间[]5,5- 上是单调函数，求实数 a 的取值范围。

高一数学必修1,2,3,4,5试题及答案

高二数学必修部分测试题一、选择题（本大题共12小题，每小题５分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．0sin 390=()A ．21B ．21-C ．23 D ．23- 2．已知2tan()5αβ+=,1tan()44πβ-=,则tan()4πα+的值为() A 1223133A 4.，b 满足：|3a =，|2b =，||a b +=||a b -=()A 3D ．105.下面结论正确的是（）C.6A C 789、函数⎪⎩⎪⎨⎧+∞∈--∞∈-=--),2(,22]2,(,2211x x y x x 的值域为______________。

A 、),23(+∞- B 、]0,(-∞ C 、23,(--∞ D 、]0,2(- 10.当x>1时，不等式x+11-x ≥a 恒成立，则实数a 的取值范围是 A ．(－∞,2] B ．[2,+∞) C ．[3,+∞) D ．(－∞,3]11．已知a,b,c 成等比数列，且x,y 分别为a 与b 、b 与c 的等差中项，则y c x a +的值为（）（A ）21（B ）-2（C ）2（D ）不确定 12．已知数列{a n }的通项公式为a n =n n ++11且S n =1101-,则n 的值为（）（A ）98（B ）99（C ）100（D ）101二、填空题（本大题共4小题，每题4分，共16分，把答案填在题中横线上）13141516。

17得到y 1819（本小题满分12分）已知向量a ,b 的夹角为60,且||2a =,||1b =,(1)求a b ;(2)求||a b +.20.已知数列{a n }，前n 项和S n =2n-n 2,a n =log 5bn ，其中bn>0，求数列{bn}的前n 项和。

21（本小题满分14分）已知(3sin ,cos )a x m x =+，(cos ,cos )b x m x =-+,且()f x a b =(1)求函数()f x 的解析式;(2)当,63x ππ⎡⎤∈-⎢⎥⎣⎦时,()f x 的最小值是－4,求此时函数()f x 的最大值,并求出相应的x 的值. 22如图如图，在底面是直角梯形的四棱锥S-ABCD ，∠ABC=90°，SA ⊥面ABCD ，SA=AB=BC=1，AD=1/2.ACAD 13.3π171)2-+x ，∴18.19.解：(1)1||||cos602112a b a b ==⨯⨯= (2)22||()a b a b +=+所以||3a b +=20.当n=1时，a 1=S 1=1当n ≥2时，a 1=S n -S n-1=3-2n ∴a n =3-2nb n =53-2n∵25155123)1(23==+-+-n n bn bn b 1=5∴{b n }是以5为首项，251为公比的等比数列。

高一数学必修一经典高难度测试题含答案

高中数学必修1复习测试题（难题版）1.设5log 31=a ，513=b ，3.051⎪⎭⎫⎝⎛=c ，则有（）A ．a b c <<B ．c b a <<C ．c a b <<D ．b c a <<2.已知定义域为R 的函数)(x f 在),4(∞+上为减函数，且函数()y f x =的对称轴为4x =，则（）A ．)3()2(f f >B ．)5()2(f f >C ．)5()3(f f >D ．)6()3(f f >3.函数lg y x = 的图象是（）4.下列等式能够成立的是（）A ．ππ-=-3)3(66B =C =34()x y =+5.若偶函数)(x f 在(]1,-∞-上是增函数，则下列关系式中成立的是（）A ．)2()1()23(f f f <-<-B ．)1()23()2(-<-<f f fC ．)23()1()2(-<-<f f fD ．)2()23()1(f f f <-<-6.已知函数()f x 是定义在R 上的奇函数，且当0x ≥时，2()2f x x x =-,则()y f x =在R 上的解析式为 A ． ()(2)f x x x =-+ B ．()||(2)f x x x =- C ．()(||2)f x x x =- D. ()||(||2)f x x x =-7.已知函数log (2)a y ax =-在区间[0,1]上是x 的减函数，则a 的取值范围是（） A ．(0,1) B ．(1,2) C ．(0,2) D ．(2,)+∞解：先求函数定义域: 由2-ax ＞0,得ax ＜2, 又a 是对数的底数,∴a ＞0且a≠1.∴x ＜.由递减区间［0,1］应在定义域内,可得＞1,∴a ＜2.又2-ax 在x ∈［0,1］上是减函数,∴在区间［0,1］上也是减函数.由复合函数单调性可知a ＞1, ∴1＜a ＜2.8.已知(31)4,1()log ,1aa x a x f x x x -+<=>⎧⎨⎩是(,)-∞+∞上的减函数，那么a 的取值范围是（）A (0,1)B 1(0,)3C 11[,)73D 1[,1)79.定义在R 上的偶函数()f x 满足(1)()f x f x +=-，且当x ∈[1,0]-时()1xf x ⎛⎫= ⎪，则2(log 8)f 等于（）A ． 3B ． 18C ． 2-D ． 210.函数2()1log f x x =+与1()2x g x -+=在同一直角坐标系下的图象大致是（）11.已知f(x)= ⎩⎨⎧>≤+)0(2)0(12x x x x 若()10f x =,则x = ．12.1x≤，则x 的取值范围是____________13. 设函数()x f 在)2,0(上是增函数，函数()2+x f 是偶函数，则()1f 、⎪⎭⎫ ⎝⎛25f 、⎪⎭⎫⎝⎛27f 的大小关系是.___________14.若f(x)＝(a－2)x2＋(a－1)x＋3是偶函数，则函数f(x)的增区间是．∵函数f（x）=（a-2）x2+（a-1）x+3是偶函数，∴a-1=0∴f（x）=-x2+3，其图象是开口方向朝下，以y轴为对称轴的抛物线故f（x）的增区间（-∞，0]故答案为：（-∞，0]15.已知函数f(x)＝2|x＋1|＋ax(x∈R)．(1)证明：当a＞2时，f(x)在R上是增函数．(2)若函数f(x)存在两个零点，求a的取值范围．15.(1)证明：化简f (x )＝⎩⎨⎧1221 ≥22＜－，－)－(－，＋)＋(x x a x x a 因为a ＞2，所以，y 1＝(a ＋2)x ＋2 (x ≥－1)是增函数，且y 1≥f (－1)＝－a ；另外，y 2＝(a －2)x －2 (x ＜－1)也是增函数，且y 2＜f (－1)＝－a ．所以，当a ＞2时，函数f (x )在R 上是增函数．(2)若函数f (x )存在两个零点，则函数f (x )在R 上不单调，且点(－1，－a )在x 轴下方，所以a 的取值应满足⎩⎨⎧0022＜－)＜－)(＋(a a a 解得a 的取值范围是(0，2)．16.试用定义讨论并证明函数11()()22ax f x a x +=≠+在(),2-∞-上的单调性17.已知定义域为R 的函数12()2x x b f x a+-+=+是奇函数。

高一数学必修一第二章基本初等函数练习题难题带答案

高一数学必修一基本初等函数一．选择题（共30小题）1．设a＝log43，b＝log54，c＝2﹣0.01，则a，b，c的大小关系为（）A．b＜a＜c B．a＜b＜c C．a＜c＜b D．b＜c＜a2．已知a＝3ln2π，b＝2ln3π，c＝3lnπ2，则下列选项正确的是（）A．a＞b＞c B．c＞a＞b C．c＞b＞a D．b＞c＞a3．函数f（x）＝（|x|﹣7）e|x|则（）A．B．f（0.76）＜f（60.5）＜f（log0.76）C．D．4．已知P（x，y）为函数f（x）＝图象上一动点，则的最大值为（）A．B．C．2D．5．设a＝3，b＝3log3π，c＝πlogπ3，则a，b，c的大小关系为（）A．a＜b＜c B．a＜c＜b C．c＜a＜b D．c＜b＜a6．若a＝0.220.33，b＝0.330.22，c＝log0.330.22，则（）A．a＞b＞c B．b＞a＞c C．c＞a＞b D．c＞b＞a7．已知a，b，c∈R，满足＝＝﹣＜0，则a，b，c的大小关系为（）A．c＞a＞b B．a＞c＞b C．c＞b＞a D．b＞a＞c8．已知2a＝log2|a|，，c＝sin c+1，则实数a，b，c的大小关系是（）A．b＜a＜c B．a＜b＜c C．c＜b＜a D．a＜c＜b9．已知实数a，b，c分别满足2a＝﹣a，log0.5b＝b，log2c＝，那么（）A．a＜b＜c B．a＜c＜b C．b＜c＜a D．c＜b＜a10．已知a＝log1213，b＝（），c＝log1314，则a，b，c的大小关系为（）A．a＞b＞c B．c＞a＞b C．b＞c＞a D．a＞c＞b11．已知a＞b＞0，ab＝1，设，则log x2x，log y2y，log z2z的大小关系为（）A．log x2x＞log y2y＞log z2z B．log y2y＞log z2z＞log x2xC．log x2x＞log z2z＞log y2y D．log y2y＞log x2x＞log z2z12．已知，，c＝log23，则a，b，c的大小关系为（）A．b＞a＞c B．a＞c＞b C．a＞b＞c D．b＞c＞a13．下列命题为真命题的个数是（）①②③A．0B．1C．2D．314．设，实数c满足e﹣c＝lnc，（其中e为自然常数），则（）A．a＞b＞c B．b＞c＞a C．b＞a＞c D．c＞b＞a15．若实数x，y，z满足，则x，y，z的大小关系是（）A．x＜y＜z B．x＜z＜y C．z＜x＜y D．z＜y＜x16．已知x1＝ln，x2＝e，x3满足e＝lnx3，则下列各选项正确的是（）A．x1＜x3＜x2B．x1＜x2＜x3C．x2＜x1＜x3D．x3＜x1＜x217．已知t＞1，x＝log2t，y＝log3t，z＝log5t，则（）A．2x＜3y＜5z B．5z＜2x＜3y C．3y＜5z＜2x D．3y＜2x＜5z18．已知定义在R上的函数y＝f（x）对任意的x都满足f（x+2）＝f（x），当﹣1≤x＜1时，f（x）＝x3．若函数g（x）＝f（x）﹣log a|x|恰有6个不同零点，则a的取值范围是（）A．（，]∪（5，7] B．（，]∪（5，7]C．（，]∪（3，5] D．（，]∪（3，5]19．已知函数f（x）＝，g（x）＝x2﹣2x，设a为实数，若存在实数m，使f（m）﹣2g（a）＝0，则实数a的取值范围为（）A．[﹣1，+∞）B．（﹣∞，﹣1]∪[3，+∞）C．[﹣1，3] D．（﹣∞，3]20．已知函数y＝f（x）（x∈R）满足f（x+2）＝2f（x），且x∈[﹣1，1]时，f（x）＝﹣|x|+1，则当x∈[﹣10，10]时，y＝f（x）与g（x）＝log4|x|的图象的交点个数为（）A．13B．12C．11D．1021．设a＝log46，，，则（）A．a＞b＞c B．b＞c＞a C．a＞c＞b D．c＞b＞a22．已知实数a＞0，b＞0，a≠1，且满足lnb＝，则下列判断正确的是（）A．a＞b B．a＜b C．log a b＞1D．log a b＜123．设a＝π﹣e，b＝lnπ﹣1，c＝eπ﹣e e，则（）A．a＜b＜c B．b＜c＜a C．c＜b＜a D．b＜a＜c24．若函数f（x）＝在区间[2019，2020]上的最大值是M，最小值是m，则M﹣m（）A．与a无关，但与b有关B．与a无关，且与b无关C．与a有关，但与b无关D．与a有关，且与b有关25．正数a，b满足1+log2a＝2+log3b＝3+log6（a+b），则的值是（）A．B．C．D．26．已知实数a，b，c，d满足，则（a﹣c）2+（b﹣d）2的最小值为（）A．8B．4C．2D．27．函数y＝log a（x+3）﹣1（a＞0，且a≠1）的图象恒过定点A，若点A在直线mx+ny+2＝0上（其中m，n＞0），则的最小值等于（）A．10B．8C．6D．428．若m，n，p∈（0，1），且log3m＝log5n＝lgp，则（）A．B．C．D．29．已知a＝log2e，b＝ln3，c＝log，则a，b，c的大小关系为（）A．a＞b＞c B．b＞a＞c C．c＞b＞a D．b＞c＞a30．若函数f（x）＝ln（ax2﹣2x+3）的值域为R，则实数a的取值范围是（）A．[0，]B．（，+∞）C．（﹣∞，]D．（0，]二．填空题（共6小题）31．已知函数f（x）在R上连续，对任意x∈R都有f（﹣3﹣x）＝f（1+x）；在（﹣∞，﹣1）中任意取两个不相等的实数x1，x2，都有（x1﹣x2）[f（x1）﹣f（x2）]＜0恒成立；若f（2a﹣1）＜f（3a﹣2），则实数a的取值范围是．32．若存在正数x，y，使得（y﹣2ex）（lny﹣lnx）z+x＝0（其中e为自然对数的底数），则实数z的取值范围是33．已知函数f（x）＝log2（x+2）与g（x）＝（x﹣a）2+1，若对任意的x1∈[2，6），都存在x2∈[0，2]，使得f（x1）＝g（x2），则实数a的取值范围是．34．已知函数f（x）的图象与函数g（x）＝2x关于直线y＝x对称，令h（x）＝f（1﹣|x|），则关于函数h（x）有以下命题：（1）h（x）的图象关于原点（0，0）对称；（2）h（x）的图象关于y轴对称；（3）h（x）的最小值为0；（4）h（x）在区间（﹣1，0）上单调递增．中正确的是．35．设a，b为非零实数，x∈R，若，则＝．36．函数f（x）＝log2x在区间[a，2a]（a＞0）上的最大值与最小值之差为．三．解答题（共4小题）37．已知函数f（x）＝的图象关于原点对称，其中a为常数．（1）求a的值；（2）当x∈（1，+∞）时，f（x）+（x﹣1）＜m恒成立，求实数m的取值范围；（3）若关于x的方程f（x）＝（x+k）在[2，3]上有解，求k的取值范围．38．已知函数f（x）＝log a（2﹣x）﹣log a（2+x）（a＞0且a≠1），且1是函数y＝f（x）+x的零点．（1）求实数a的值；（2）求使f（x）＞0的实数x的取值范围．39．已知函数f（x）＝（a2﹣3a+3）a x是指数函数．（1）求f（x）的解析式；（2）判断函数F（x）＝f（x）﹣f（﹣x）的奇偶性，并证明；（3）解不等式log a（1﹣x）＞log a（x+2）．40．已知f（x）是定义在R上的偶函数，且x≤0时，f（x）＝（﹣x+1）（1）求f（3）+f（﹣1）；（2）求函数f（x）的解析式；（3）若f（a﹣1）＜﹣1，求实数a的取值范围．参考答案与试题解析一．选择题（共30小题）1．【解答】解：因为0＝log41＜a＝log43＜log44＝1，0＜b＝log54＜log55＝1，c＝2﹣0.01＞2≈0.92，log54＝≈0.86，＝＝log43×log45＜（）2＝（）2＜1，∴a，b，c的大小关系为a＜b＜c．故选：B．2．【解答】解：，，＝，∵6π＞0，∴a，b，c的大小比较可以转化为的大小比较．设f（x）＝，则f′（x）＝，当x＝e时，f′（x）＝0，当x＞e时，f′（x）＜0，当0＜x＜e时，f′（x）＞0∴f（x）在（e，+∞）上，f（x）单调递减，∵e＜3＜π＜4∴，∴b＞c＞a，故选：D．3．【解答】解，60.5＞1＞0.76＞0＞log0.76，函数f（x）为偶函数，则，当x＞0时，f（x）＝（x﹣7）e x，则f′（x）＝（x﹣6）e x，易知函数f（x）在（0，6）上单调递减，又，故，即﹣log0.76＜6，又，故，即﹣log0.76＞3，则0＜0.76＜1＜60.5＜﹣log0.76＜6，所以f（0.76）＞f（60.5）＞f（﹣log0.76）＝f（log0.76），故选：D．4．【解答】解：设Q（，1），原点O，则＝（，1），＝（x，y），∴即．∴当OP与f（x）在y轴右侧相切时取最大值，设直线y＝kx（k＞0）与函数f（x）相切于点P0（x0，y0），y′＝k，f′（x）＝2x，则，解得．即切点P0（，），∴，即的最大值为．故选：D．5．【解答】解：构造函数f（x）＝（x＞1），则f′（x）＝，当x∈（1，e2）时，f′（x）＞0，则f（x）在（1，e2）上为增函数，∴f（π）＞f（3），即＞，∴＞，即3log3π＞πlogπ3，则b＞c；设g（x）＝，则g′（x）＝，当x＞3时，g′（x）＞30ln3﹣1＞0，∴g（x）在（3，+∞）上为增函数，则g（π）＞g（3）＝0，即＞π，则3π＞π3．又πlogπ3＝＞．∴a＜c＜b．故选：B．6．【解答】解：由1＞a＝0.220.33＞0，1＞b＝0.330.22＞0，c＝log0.330.22＞log0.330.33＝1，所以c＞a，且c＞b；又ln0.220.33＝0.33ln0.22，ln0.330.22＝0.22ln0.33；不妨设0.33ln0.22＜0.22ln0.33，则有＜；构造函数f（x）＝，x＞0，所以f′（x）＝，令f′（x）＝0，解得x＝e；所以x∈（0，e）时，f′（x）＞0，f（x）是单调增函数；所以f（0.22）＜f（0.33），即＜，所以b＞a；综上知，c＞b＞a．故选：D．7．【解答】解：已知a，b，c∈R，令＝＝﹣＝﹣1，则：，所以c＞1．由于3b＞0，且，故lnb＜0，解得0＜b＜1，同理2a＞0，且，故lna＜0，解得0＜a＜1．由于0＜a＜1，0＜b＜1，＝＝﹣＜0，所以2a＜3b，故lnb＜lna，整理得b＜a，所以c＞1＞a＞b＞0．故选：A．8．【解答】解：作出函数y＝2x和y＝log2|x|的图象，由图1可知，交点A的横坐标a＜0；作出函数y＝和y＝的图象，由图2可知，交点B的横坐标0＜b＜1；作出函数y＝x和y＝sin x+1的图象，由图3可知，交点C的横坐标c＞1所以，a＜b＜c．故选：B．9．【解答】解：∵log0.5b＝﹣log2b＝b，∴log2b＝﹣b，在同一坐标系内画出函数y＝2x，y＝﹣x，y＝log2x，y＝的图象．可知a＜0＜b＜1＜c．故选：A．10．【解答】解：＝，∵＝＜1，∴log1314＜log1213，且log1314＞1，，∴a＞c＞b．故选：D．11．【解答】解：，＝，，∵a＞b＞0，ab＝1，∴a＞1＞b＞0，∴，log2（a+b）＜2，∴，∴，∴，又0＜，∴，∴log y2y＞log z2z＞log x2x．故选：B．12．【解答】解：根据指数运算与对数运算的性质，＞3，1＜＜2，1＜c＝log23＜2，设b＝，c＝log23，由于函数m＝log2t为增函数，由于的值接近于4，所以a＞b＞c．故选：C．13．【解答】解：构造函数f（x）＝，x∈（0，+∞），∴，令f'（x）＝0得：x＝e，∵当x∈（0，e）时，f'（x）＞0，f（x）单调递增；当x∈（e，+∞）时，f'（x）＜0，f（x）单调递减，∴f（e）＞f（3）＞f（π），即，故①正确，②错误，构造函数g（x）＝，x∈（0，+∞），∵，令g'（x）＝0得：x＝e，∵当x∈（0，e）时，g'（x）＜0，g（x）单调递减；当x∈（e，+∞）时，g'（x）＞0，g（x）单调递增，∴g（e）＜g（3），即0＜，∴ln3＜，∴，故③正确，∴真命题的个数是2个，故选：C．14．【解答】解：∵e﹣c＞0，∴lnc＞0，∴c＞1，∴，∴，∴1＜c＜2，又，∴b＞c＞a．故选：B．15．【解答】解：设＝p，∴p＞0，设y1＝log2x，y2＝log3y，y3＝2z，作出3个函数的图象，如图所示：由图可知：z＜x＜y，故选：C．16．【解答】解：依题意，因为y＝lnx为（0，+∞）上的增函数，所以x1＝ln＜ln1＝0；因为y＝e x为R上的增函数，且e x＞0，所以0＜x2＝e＜e0＝1；x3满足e＝lnx3，所以x3＞0，所以＞0，所以lnx3＞0＝ln1，又因为y＝lnx为（0，+∞）的增函数，所以x3＞1，综上：x1＜x2＜x3．故选：B．17．【解答】解：∵t＞1，∴lgt＞0．又0＜lg2＜lg3＜lg5，∴2x＝2＞0，3y＝3＞0，5z＝＞0，∴＝＞1，可得5z＞2x．＝＞1．可得2x＞3y．综上可得：3y＜2x＜5z．故选：D．18．【解答】解：首先将函数g（x）＝f（x）﹣log a|x|恰有6个零点，这个问题转化成f（x）＝log a|x|的交点来解决．数形结合：如图，f（x+2）＝f（x），知道周期为2，当﹣1＜x≤1时，f（x）＝x3图象可以画出来，同理左右平移各2个单位，得到在（﹣7，7）上面的图象，以下分两种情况：（1）当a＞1时，log a|x|如图所示，左侧有4个交点，右侧2个，此时应满足log a5≤1＜log a7，即log a5≤log a a＜log a7，所以5≤a＜7．（2）当0＜a＜1时，log a|x|与f（x）交点，左侧有2个交点，右侧4个，此时应满足log a5＞﹣1，log a7≤﹣1，即log a5＜﹣log a a≤log a7，所以5＜a﹣1≤7．故≤a＜综上所述，a的取值范围是：5≤a＜7或≤a＜，故选：A．19．【解答】解：∵g（x）＝x2﹣2x，设a为实数，∴2g（a）＝2a2﹣4a，a∈R，∵y＝2a2﹣4a，a∈R，∴当a＝1时，y最小值＝﹣2，∵函数f（x）＝，f（﹣7）＝6，f（e﹣2）＝﹣2，∴值域为[﹣2，6]∵存在实数m，使f（m）﹣2g（a）＝0，∴﹣2≤2a2﹣4a≤6，即﹣1≤a≤3，故选：C．20．【解答】解：由题意，函数f（x）满足：定义域为R，且f（x+2）＝2f（x），当x∈[﹣1，1]时，f（x）＝﹣|x|+1；在同一坐标系中画出满足条件的函数f（x）与函数y＝log4|x|的图象，如图：由图象知，两个函数的图象在区间[﹣10，10]内共有11个交点；故选：C．21．【解答】解：，，，∵0＜log34＜log35＜log36，∴，∴a＞b＞c．故选：A．22．【解答】解：∵lnb＝，∴lnb﹣lna＝，构造函数∴f（x）＝；∴＝＝；∴≥0；∴f（x）在（0，+∞）单调递增．且f（1）＝0；当x∈（0，1）时，f（x）＜0，当x∈（1．+∞）时f（x）＞0；∵a≠1∴当0＜a＜1时，f（a）＜0⇒0即lnb﹣lna＜0⇒b＜a，∴lnb＜lna＜0⇒⇒log a b＞1，当a＞1时，f（a）＞0⇒即lnb﹣lna＞0⇒b＞a，∴lnb＞lna＞0⇒⇒log a b＞1，故选：C．23．【解答】解：∵a＝π﹣e＞0，b＝lnπ﹣1＝lnπ﹣lne＞0，c＝eπ﹣e e＞0；设y＝lnx，则＝，表示了连接两点（π，lnπ），（e，lne）的割线的斜率，而y'＝，当x＞1时，曲线切线的斜率0＜k＜1；故0＜＝＜1，故b＜a；设y＝e x，则＝，表示了连接两点（π，eπ），（e，e e）的割线的斜率，而y'＝e x，当x＞1时，曲线切线的斜率k＞1；故＝＞1，故c＞a；故b＜a＜c；故选：D．24．【解答】解：，令，则y＝2019t2+bt+a的最大值是M，最小值是m，而a是影响图象的上下平移，此时最大和最小值同步变大或变小，故M﹣m与a无关，而b是影响图象的左右平移，故M﹣m与b有关，故选：A．25．【解答】解，依题意，设1+log2a＝2+log3b＝3+log6（a+b）＝k，则a＝2k﹣1，b＝3k﹣2，a+b＝6k﹣3，所以＝＝＝＝＝，故选：A．26．【解答】解：∵实数a，b，c，d满足，∴b＝lna，d＝c+1．考查函数y＝lnx，与y＝x+1．∴（a﹣c）2+（b﹣d）2就是曲线y＝lnx与直线y＝x+1之间的距离的平方值，对曲线y＝lnx求导：y′＝，与直线y＝x+1平行的切线斜率k＝1＝，解得：x＝1，将x＝1代入y＝lnx得：y＝0，即切点坐标为（1，0），∴切点（1，0）到直线y＝x+1的距离d＝＝，即d2＝2，则（a﹣c）2+（b﹣d）2的最小值为2．故选：C．27．【解答】解：令x+3＝1，求得x＝﹣2，可得函数y＝log a（x+3）﹣1（a＞0，且a≠1）的图象恒过定点A（﹣2，﹣1），若点A在直线mx+ny+2＝0上（其中m，n＞0），则﹣2m﹣n+2＝0，即2m+n＝2．由基本不等式可得2≥2，即mn≤，即≥2，当且仅当2m＝n＝1时，取等号．则＝＝≥4，故选：D．28．【解答】解：∵m，n，p∈（0，1），且log3m＝log5n＝lgp＝k，∴lgm，lgn，lgp＜0，m＝3k，n＝5k，p＝10k，∴＝＝，＝＝，＝＝，因为，＝53＝125，所以，同理＝5×5＝25，＝10，所以，所以＞0，又因为y＝x k（k＜0）在（0，+∞）上单调递减，∴即＜＜．故选：A．29．【解答】解：根据题意，c＝log＝ln2＜lne＝1，则c＜1，ln3＞ln2，∴c＜b，a＝log2e＞log22＝1，即a＞c，ln3﹣log2e＝ln3﹣＝，∵2＝lne2＞ln6＝ln2+ln3＞2，∴＜1，即ln2ln3＜1，则ln3﹣log2e＝ln3﹣＝＜0，即ln3＜log2e，即a＞b，综上a＞b＞c，故选：A．30．【解答】解：若函数f（x）＝ln（ax2﹣2x+3）的值域为R，即有t＝ax2﹣2x+3取得一切的正数，当a＝0时，t＝3﹣2x取得一切的正数，成立；当a＜0不成立；当a＞0，△≥0即4﹣12a≥0，解得0＜a≤，综上可得0≤a≤．故选：A．二．填空题（共6小题）31．【解答】解：由f（﹣3﹣x）＝f（1+x）可知函数f（x）关于直线x＝﹣1对称；在（﹣∞，﹣1）中任意取两个不相等的实数x1，x2，都有（x1﹣x2）[f（x1）﹣f（x2）]＜0恒成立；可知函数f（x）在区间（﹣∞，﹣1）上单调递减，由对称性可知函数f（x）在区间（﹣1，+∞）上单调递增，不妨设f（x）＝（x+1）2，则由f（2a﹣1）＜f（3a﹣2）可得4a2＜（3a﹣1）2，整理得5a2﹣6a+1＞0，即（a﹣1）（5a﹣1）＞0，解得或a＞1，所以实数a的取值范围是．故答案为：．32．【解答】解：则（y﹣2ex）（lny﹣lnx）z+x＝0可化为：，令t＝，得（t﹣2e）lnt＝﹣．令f（t）＝（t﹣2e）lnt，（t＞0），则f′（t）＝g（t）＝lnt+1﹣，则g′（t）＝，故g（t）为（0，+∞）上的增函数，又因为f′（e）＝g（e）＝1+1﹣2＝0，故当t∈（0，e）时，f′（t）＜0，当t＞e时，f′（t）＞0，所以f（t）在（0，e）上单调递减，在（e，+∞）上单调递增，所以f（t）在（0，+∞）存在最小值f（e）＝﹣e，即f（t）的值域为（﹣e，+∞），∴﹣∈（﹣e，+∞），所以z∈（﹣∞，0）∪[，+∞），故填：（﹣∞，0）∪[，+∞），33．【解答】解：∵x1∈[2，6），∴f（2）≤f（x1）＜f（6），即2≤f（x1）＜3，∴f（x1）的值域为[2，3）．g（x）的图象开口向上，对称轴为x＝a，（1）若a≤0，则g（x）在[0，2]上是增函数，∴g（0）≤g（x2）≤g（2），即g（x2）的值域为[a2+1，a2﹣4a+5]，∴，解得﹣1≤a≤0．（2）若a≥2，则g（x）在[0，2]上是减函数，∴g（2）≤g（x2）≤g（1），即g（x2）的值域为[a2﹣4a+5，a2+1]，∴，解得2≤a≤3．（3）若0＜a≤1，则g min（x）＝g（a）＝1，g max（x）＝g（2）＝a2﹣4a+5，∴g（x）的值域为[1，a2﹣4a+5]，∴，解得0．（4）若1＜a＜2，则g min（x）＝g（a）＝1，g max（x）＝g（0）＝a2+1，∴g（x）的值域为[1，a2+1]，∴，解得a＜2．综上，a的取值范围是[﹣1，0]∪[2，3]∪（0，2﹣）∪（，2）＝[﹣1，2﹣]∪[，3]．故答案为[﹣1，2﹣]∪[，3]．34．【解答】解：由于函数f（x）的图象与函数g（x）＝2x关于直线y＝x对称，故函数f（x）与函数g（x）＝2x互为反函数．故函数f（x）＝log2x．∴h（x）＝f（1﹣|x|）＝log2（1﹣|x|），故函数h（x）是偶函数，图象关于y对称，故（2）正确而（1）不正确．函数h（x）的定义域为（﹣1，1），在（﹣1，0）上是增函数，在（0，1）上是减函数，故（4）正确．故当x＝0时，函数h（x）取得最大值为0，故（3）不正确．故答案为②④．35．【解答】解：由成立，得＝（sin2x+cos2x）2，化简得：，即，∴，又sin2x+cos2x＝1，得，．∴．则＝＝•（sin2x+cos2x）＝．故答案为：．36．【解答】解：∵f（x）＝log2x在区间[a，2a]上是增函数，∴f（x）max﹣f（x）min＝f（2a）﹣f（a）＝log22a﹣log2a＝1．故答案为：1．三．解答题（共4小题）37．【解答】解：（1）函数f（x）＝的图象关于原点对称，∴f（x）+f（﹣x）＝0，即+＝0，∴（）＝0，∴＝1恒成立，即1﹣a2x2＝1﹣x2，即（a2﹣1）x2＝0恒成立，所以a2﹣1＝0，解得a＝±1，又a＝1时，f（x）＝无意义，故a＝﹣1；（2）x∈（1，+∞）时，f（x）+（x﹣1）＜m恒成立，即+（x﹣1）＜m，∴（x+1）＜m在（1，+∞）恒成立，由于y＝（x+1）是减函数，故当x＝1，函数取到最大值﹣1，∴m≥﹣1，即实数m的取值范围是m≥﹣1；（3）f（x）＝在[2，3]上是增函数，g（x）＝（x+k）在[2，3]上是减函数，∴只需要即可保证关于x的方程f（x）＝（x+k）在[2，3]上有解，下解此不等式组．代入函数解析式得，解得﹣1≤k≤1，即当﹣1≤k≤1时关于x的方程f（x）＝（x+k）在[2，3]上有解．38．【解答】解：（1）∵1是函数y＝f（x）+x的零点，∴f（1）＝﹣1，即log a（2﹣1）﹣log a（2+1）+1＝0，即log a3＝1，解得a＝3．（2）由（1）可知函数f（x）是递增函数，f（x）＞0得log3（2﹣x）＞log3（2+x），所以：有解得﹣2＜x＜0，所使f（x）＞0的实数x的取值集合为{x|﹣2＜x＜0}．39．【解答】解：（1）a2﹣3a+3＝1，可得a＝2或a＝1（舍去），∴f（x）＝2x；（2）F（x）＝2x﹣2﹣x，∴F（﹣x）＝﹣F（x），∴F（x）是奇函数；（3）不等式：log2（1﹣x）＞log2（x+2），即1﹣x＞x+2＞0，∴﹣2＜x＜﹣，解集为{x|﹣2＜x＜﹣}．40．【解答】解：（I）∵f（x）是定义在R上的偶函数，x≤0时，f（x）＝（﹣x+1），∴f（3）+f（﹣1）＝f（﹣3）+f（﹣1）＝4+2＝﹣2﹣1＝﹣3；（II）令x＞0，则﹣x＜0，f（﹣x）＝（x+1）＝f（x）∴x＞0时，f（x）＝（x+1），则f（x）＝．（Ⅲ）∵f（x）＝（﹣x+1）在（﹣∞，0]上为增函数，∴f（x）在（0，+∞）上为减函数∵f（a﹣1）＜﹣1＝f（1）∴|a﹣1|＞1，∴a＞2或a＜0。

高一数学必修部分难题总结及答案

1．在△ABC 中，角A 、B 、C 的对边分别是a 、b 、c ，面积S ＝14(b 2＋c 2－a 2)，若a ＝10，则bc 的最大值是( )A ．100＋50 2B ．50＋1002C ．50 2D ．10022.在不等边三角形ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，a 为最大边，如果sin 2(B ＋C )<sin 2B ＋sin 2C ，则角A 的取值范围为 ( )3.已知O 是坐标原点，点A (－1,1)，若点M (x ，y )为平面区域⎩⎪⎨⎪⎧ x ＋y ≥2，x ≤1，y ≤2上的一个动点，则OA →·OM →的取值范围是( ) 4.已知实数x 、y 满足205040x y x y y -≤⎧⎪+-≥⎨⎪-≤⎩，若不等式222()()a x y x y +≥+恒成立，则实数a 的最小值是( )7.在锐角ΔABC 中，A 、B 、C 的对边分别为a 、b 、c ，6cos b a C a b+=，则tan tan tan tan C C A B+= ． 14.设x ，y 为实数，若4x 2＋y 2＋xy ＝1，则2x ＋y 的最大值是________．16.在△ABC 中，A ，B 为锐角，角A ，B ，C 所对应的边分别为a ，b ，c ，且cos 2A ＝35，sin B ＝1010. (1)求A ＋B 的值；(2)若a －b ＝2－1，求a ，b ，c 的值．17.在△ABC 中，a ，b ，c 分别是∠A ，∠B ，∠C 的对边长，已知2sin A ＝3cos A .(1)若a 2－c 2＝b 2－mbc ，求实数m 的值；(2)若a ＝3，求△ABC 面积的最大值.18．已知函数2()13sin22cos f x x x =-+．（1）求)(x f 的最大值及取得最大值时的x 集合；（2）设ABC ∆的角C B A ,,的对边分别为c b a ,,，且1,()0a f A ==．求c b +的取值范围．19．在等差数列{}n a 中，31=a ，其前n 项和为n S ，等比数列{}n b 的各项均为正数，11=b ，公比为q ，且1222=+S b ， 22b S q =．（Ⅰ）求n a 与n b ；（Ⅱ）证明：31≤3211121<+++n S S S ． 20．已知数列{}n a ，{}n b 满足：31=a ，当2≥n 时，n a a n n 41=+-；对于任意的正整数n ，11222n n n b b b na -+++=L ．设{}n b 的前n 项和为n S . （Ⅰ）计算32,a a ，并求数列{}n a 的通项公式；（Ⅱ）求满足1413<<n S 的n 的集合.21．已知数列{}n a 满足：21=a 且()na a n a n n n ++=+121（*∈N n ）（1）求证：数列⎭⎬⎫⎩⎨⎧-1n a n 为等比数列，并求数列{}n a 的通项公式；（2）证明：2...321321+<++++n na a a a n （*∈N n ）。

高一数学必修2习题(答案详解)

一、选择题【共10道小题】1、给出的下列命题中,正确命题的个数是( )①梯形的四个顶点在同一平面内②三条平行直线必共面③有三个公共点的两个平面必重合④每两条都相交且交点各不相同的四条直线一定共面A.1B.2C.3D.4参考答案与解析:思路解析:逐个对各选项分析:梯形是一个平面图形,所以其四个顶点在同一个平面内,①对;两条平行直线是可以确定一个平面的,三条平行直线有可能确定三个平面,②错;三个公共点可以同在两个相交平面的公共直线上,③错;设这四条直线分别为l1、l2、l3、l4,取其中两条相交直线l1和l2,则它们可确定一个平面α,取l3,设其与l1、l2的交点分别为A、B,则由题意知这两点不同,且A∈l1,B∈l2,所以有A、B∈α,从而l3∈α;同理可证明l4∈α.所以每两条都相交且交点各不相同的四条直线一定共面,④对.答案:B主要考察知识点:空间直线和平面2、如图2-1-17,空间四边形SABC中,各边及对角线长都相等,若E、F分别为SC、AB的中点,那么异面直线EF与SA所成的角等于( )A.90°B.60°C.45°D.30°图2-1-17参考答案与解析:思路解析:求EF与SA所成的角,可把SA平移,使其角的顶点在EF上,为此取SB的中点G,连结GE、GF、BE、AE.由三角形中位线定理得GE=BC,GF=SA,且GF∥SA,所以∠GFE就是EF与SA所成的角.若设此空间四边形边长为a,那么GF=GE=a,EA=a,EF=a,因此△EFG为等腰直角三角形,∠EFG=45°,所以EF与SA所成的角为45°.答案:C主要考察知识点:空间直线和平面3、如果直线a∥平面α,那么直线a与平面α内的( )A.一条直线不相交B.两条直线不相交C.无数条直线不相交D.任意一条直线不相交参考答案与解析:思路解析:利用线面平行的定义.直线a∥平面α,则a与α无公共点,与α内的直线当然均无公共点.答案:D主要考察知识点:空间直线和平面4、若点M在直线α上，α在平面α内，则M、a、α间的上述关系可记为( )A.M∈a,a∈αB.M∈a,aαC.M a,aαD.M a,aα参考答案与解析:B主要考察知识点:空间直线和平面5、在空间四边形ABCD的边AB、BC、CD、DA上分别取E、F、G、H四点,如果EF与HG交于点M，则( )A.M一定在直线AC上B.M一定在直线BD上C.M可能在AC上，也可能在BD上D.M不在AC上，也不在BD上参考答案与解析:A主要考察知识点:空间直线和平面6、下列说法正确的是()A.三点确定一个平面B.四边形一定是平面图形C.梯形一定是平面图形D.平面α和平面β有不同在一条直线上的三个交点参考答案与解析:解析：A错,不共点的三点;B错,如空间四边形;D错,两平面的三个交点在同一直线上.答案：C主要考察知识点:空间直线和平面7、若点M在直线a上,a在平面α内，则M，a,α间的上述关系可记为（）A.M∈a,a∈αB.M∈a,C.,D.,参考答案与解析:解析：要明确数学符号语言的表示.答案：B主要考察知识点:空间直线和平面8、异面直线是指()A.空间中两条不相交的直线B.分别位于两个不同平面内的两条直线C.平面内的一条直线与平面外的一条直线D.不同在任何一个平面内的两条直线参考答案与解析:解析：A错,有可能平行；B错,有可能平行或相交；C错,有可能平行或相交；D正确.答案：D主要考察知识点:空间直线和平面9、若a∥α,b∥α,则直线a、b的位置关系是()A.平行B.相交C.异面 D.A、B、C均有可能参考答案与解析:解析：平行、相交、异面都有可能,此题的难点在于可能选平行,易和平行公理混淆.答案：D主要考察知识点:空间直线和平面10、下列命题:①若直线l平行于平面α内的无数条直线,则l∥α;②若直线a在平面α外,则a∥α;③若直线a∥b,直线,则a∥α;④若直线a∥b,bα,那么直线a就平行于平面α内的无数条直线.其中真命题的个数为( )A.1B.2C.3D.4参考答案与解析:解析：对于①,∵直线l虽与平面α内无数条直线平行,但l有可能在平面α内,∴l不一定平行于α.∴①是假命题.对于②,∵直线a在平面α外包括两种情况:a∥α和a与α相交,∴a和α不一定平行.∴②是假命题.对于③,∵直线a∥b, ,则只能说明a和b无公共点,但a可能在平面α内,∴a不一定平行于α.∴③是假命题.对于④,∵a∥b, ,那么aα或a∥α,∴a可以与平面α内的无数条直线平行.∴④是真命题.综上所述,真命题的个数为1.答案：A主要考察知识点:空间直线和平面二、填空题【共4道小题】1、空间三条直线两两相交，点P不在这三条直线上，那么由点P和这三条直线最多可以确定的平面的个数为__________.参考答案与解析:解析：(1)当题中三条直线共点但不共面相交时，可确定3个平面；而P点与每条直线又可确定3个平面，故共确定6个.主要考察知识点:空间直线和平面2、和两条平行直线中的一条是异面直线的直线与另一条直线的位置关系是_______.参考答案与解析:思路解析:由公理4可知不可能平行,只有相交或异面.答案:相交或异面主要考察知识点:空间直线和平面3、看图填空.(1)AC∩BD=_______;(2)平面AB1∩平面A1C1=________；(3)平面A1C1CA∩平面AC=________；(4)平面A1C1CA∩平面D1B1BD=_________;(5)平面A1C1∩平面AB1∩平面B1C=_________；(6)A1B1∩B1B∩B1C1=_________.参考答案与解析:解析：两个面的两个公共点连线即为交线.答案：（1）O（2）A1B1（3）AC（4）OO1（5）B1（6）B1主要考察知识点:空间直线和平面4、已知平面α、β相交,在α、β内各取两点,这四点都不在交线上,这四点能确定平面_______个.参考答案与解析:解析：分类,如果这四点在同一平面内,那么确定一个平面,如果这四点不共面,则任意三点可确定一个平面,可确定四个.答案：1或4主要考察知识点:空间直线和平面三、解答题【共3道小题】1、如图，已知△ABC在平面α外，它的三边所在直线分别交平面α于点P、Q、R，求证：P、Q、R三点共线.参考答案与解析:解析：本题是一个证明三点共线的问题，利用公理3，两平面相交时，有且只有一条公共直线.因此只需证明P、Q、R三点是某两个平面的公共点，即可得这三个点都在两平面的交线上，因此是共线的.证明：设△ABC确定平面ABC，直线AB交平面α于点Q,直线CB交平面α于点P,直线AC 交平面α于点R,则P、Q、R三点都在平面α内，又因为P、Q、R三点都在平面ABC内，所以P、Q、R三点都在平面α和平面ABC的交线上，而两平面的交线只有一条，所以P、Q、R三点共线.主要考察知识点:空间直线和平面2、如图，已知正方体ABCD—A′B′C′D′.①哪些棱所在直线与直线BA′是异面直线？②直线BA′和CC′的夹角是多少？③哪些棱所在的直线与直线AA′垂直？参考答案与解析:解析：①由异面直线的定义可知，棱AD，DC，CC′，DD′，D′C′,B′D′所在直线分别与直线BA′是异面直线.②由BB′∥CC′可知，∠B′BA′为异面直线BA′与CC′的夹角，∠B′BA′=45°，所以BA′与CC′的夹角为45°.③直线AB，BC，CD，DA，A′B′,B′C′,C′D′,D′A′分别与直线AA′垂直.主要考察知识点:空间直线和平面3、已知直线b∥c,且直线a与b、c都相交,求证:直线a,b,c共面.参考答案与解析:证明:∵b∥c,∴不妨设b,c共面于平面α.设a∩b=A,a∩c=B,∴A∈a,B∈a,A∈α,B∈α,即.∴三线共面.主要考察知识点:空间直线和平面一、选择题【共10道小题】1、若两个平面互相平行，则分别在这两个平行平面内的直线( )A.平行B.异面C.相交 D.平行或异面参考答案与解析:解析：两平行平面内的直线可能平行，也可能异面，就是不可能相交.答案：D主要考察知识点:空间直线和平面2、下列结论中，正确的有( )①若aα,则a∥α②a∥平面α,bα则a∥b③平面α∥平面β,aα,bβ,则a∥b④平面α∥β,点P∈α,a∥β,且P∈a，则aαA.1个B.2个C.3个 D.4个参考答案与解析:解析：若aα，则a∥α或a与α相交，由此知①不正确若a∥平面α,bα,则a与b异面或a∥b，∴②不正确若平面α∥β，aα，bβ，则a∥b或a与b异面，∴③不正确由平面α∥β，点P∈α知Pβ过点P而平行平β的直线a必在平面α内，是正确的.证明如下：假设aα，过直线a作一面γ，使γ与平面α相交，则γ与平面β必相交.设γ∩α=b,γ∩β=c,则点P∈b.由面面平行性质知b∥c；由线面平行性质知a∥c,则a∥b,这与a∩b=P矛盾，∴aα.故④正确.答案：A主要考察知识点:空间直线和平面3、在空间四边形ABCD中，E、F分别是AB和BC上的点，若AE∶EB=CF∶FB=1∶3，则对角线AC和平面DEF的位置关系是( )A.平行B.相交C.在内 D.不能确定参考答案与解析:解析：在平面ABC内.∵AE：EB=CF：FB=1：3，∴AC∥EF.可以证明AC平面DEF.若AC平面DEF，则AD平面DEF，BC平面DEF.由此可知ABCD为平面图形，这与ABCD是空间四边形矛盾，故AC平面DEF.∵AC∥EF，EF平面DEF.∴AC∥平面DEF.答案：A主要考察知识点:空间直线和平面4、a，b是两条异面直线，A是不在a，b上的点，则下列结论成立的是( )A.过A有且只有一个平面平行于a,bB.过A至少有一个平面平行于a,bC.过A有无数个平面平行于a,bD.过A且平行a,b的平面可能不存在参考答案与解析:解析：如当A与a确定的平面与b平行时，过A作与a,b都平行的平面不存在.答案：D主要考察知识点:空间直线和平面5、已知直线a与直线b垂直,a平行于平面α,则b与α的位置关系是( )A.b∥αB.bαC.b与α相交D.以上都有可能参考答案与解析:思路解析:a与b垂直,a与b的关系可以平行、相交、异面,a与α平行,所以b与α的位置可以平行、相交、或在α内,这三种位置关系都有可能.答案:D主要考察知识点:空间直线和平面6、下列命题中正确的命题的个数为( )①直线l平行于平面α内的无数条直线，则l∥α;②若直线a在平面α外，则a∥α;③若直线a∥b,直线bα,则a∥α;④若直线a∥b,b平面α，那么直线a就平行于平面α内的无数条直线.A.1B.2C.3D.4参考答案与解析:解析：对于①,∵直线l虽与平面α内无数条直线平行，但l有可能在平面α内(若改为l与α内任何直线都平行，则必有l∥α),∴①是假命题.对于②，∵直线a在平面α外，包括两种情况a∥α和a与α相交，∴a与α不一定平行，∴②为假命题.对于③,∵a∥b,bα,只能说明a与b无公共点，但a可能在平面α内，∴a不一定平行于平面α.∴③也是假命题.对于④,∵a∥b,bα.那么aα,或a∥α.∴a可以与平面α内的无数条直线平行.∴④是真命题.综上，真命题的个数为1.答案：A主要考察知识点:空间直线和平面7、下列命题正确的个数是( )(1)若直线l上有无数个点不在α内，则l∥α(2)若直线l与平面α平行，l与平面α内的任意一直线平行(3)两条平行线中的一条直线与平面平行，那么另一条也与这个平面平行(4)若一直线a和平面α内一直线b平行，则a∥αA.0个B.1个C.2个 D.3个参考答案与解析:解析：由直线和平面平行的判定定理知，没有正确命题.答案：A主要考察知识点:空间直线和平面8、已知m、n是两条不重合的直线，α、β、γ是三个两两不重合的平面，给出下列四个命题：①若m⊥α,m⊥β,则α∥β;②若α⊥γ,β⊥γ,则α∥β;③若mα,nβ,m∥n,则α∥β;④若m、n是异面直线，mα,m∥β,nβ,n∥α,则α∥β.其中真命题是( )A.①和②B.①和③C.③和④ D.①和④参考答案与解析:解析：利用平面平行判定定理知①④正确.②α与β相交且均与γ垂直的情况也成立，③中α与β相交时，也能满足前提条件答案：D主要考察知识点:空间直线和平面9、长方体ABCD-A1B1C1D1中,E为AA1中点,F为BB1中点,与EF平行的长方体的面有()A.1个B.2个C.3个 D.4个参考答案与解析:解析：面A1C1,面DC1,面AC共3个.答案：C主要考察知识点:空间直线和平面10、对于不重合的两个平面α与β，给定下列条件：①存在平面γ，使得α、β都垂直于γ；②存在平面γ，使α、β都平行于γ；③α内有不共线的三点到β的距离相等；④存在异面直线l，M，使得l∥α,l∥β,M∥α,M∥β.其中可以判断两个平面α与β平行的条件有（）A.1个B.2个C.3个 D.4个参考答案与解析:解析：取正方体相邻三个面为α、β、γ，易知α⊥γ，β⊥γ，但是α与β相交，不平行，故排除①，若α与β相交，如图所示，可在α内找到A、B、C三个点到平面β的距离相等，所以排除③.容易证明②④都是正确的.答案：B主要考察知识点:空间直线和平面1、在棱长为a的正方体ABCD—A1B1C1D1中，M、N分别是棱A1B1、B1C1的中点，P是棱AD上一点，AP=,过P、M、N的平面与棱CD交于Q，则PQ=_________.参考答案与解析:解析：由线面平行的性质定理知MN∥PQ(∵MN∥平面AC，PQ=平面PMN∩平面AC，∴MN∥PQ).易知DP=DQ=.故.答案：主要考察知识点:空间直线和平面2、如果空间中若干点在同一平面内的射影在一条直线上，那么这些点在空间的位置是__________.参考答案与解析:共线或在与已知平面垂直的平面内主要考察知识点:空间直线和平面3、若直线a和b都与平面α平行，则a和b的位置关系是__________.参考答案与解析:相交或平行或异面主要考察知识点:空间直线和平面4、正方体ABCD-A1B1C1D1中，E为DD1中点，则BD1与过点A，C，E的平面的位置关系是_________.参考答案与解析:解析：如图所示，连结BD，设BD∩AC=O，连结BD1，在△BDD1中，E 为DD1的中点，O为BD的中点，∴OE为△BDD1的中位线.∴OE∥BD1.又平面ACE，OE平面ACE，∴BD1∥平面ACE.答案：平行主要考察知识点:空间直线和平面1、如图，直线AC，DF被三个平行平面α、β、γ所截.①是否一定有AD∥BE∥CF；②求证：.参考答案与解析:解析：①平面α∥平面β，平面α与β没有公共点，但不一定总有AD∥BE. 同理不总有BE∥CF.②过A点作DF的平行线，交β，γ于G，H两点，AH∥DF.过两条平行线AH，DF的平面，交平面α,β,γ于AD，GE，HF.根据两平面平行的性质定理，有AD∥GE∥HF.AGED为平行四边形.∴AG=DE.同理GH=EF.又过AC，AH两相交直线之平面与平面β,γ的交线为BG，CH.根据两平面平行的性质定理，有BG∥CH.在△ACH中，.而AG=DE，GH=EF，∴.主要考察知识点:空间直线和平面2、如图，ABCD是平行四边形，S是平面ABCD外一点，M为SC的中点.求证：SA∥平面MDB.参考答案与解析:解析：要说明SA∥平面MDB，就要在平面MDB内找一条直线与SA平行，注意到M是SC的中点，于是可找AC的中点，构造与SA平行的中位线，再说明此中位线在平面MDB内，即可得证.证明：连结AC交BD于N，因为ABCD是平行四边形，所以N是AC的中点.又因为M是SC的中点，所以MN∥SA.因为MN平面MDB，所以SA∥平面MDB.主要考察知识点:空间直线和平面3、如图,已知点M、N是正方体ABCD-A1B1C1D1的两棱A1A与A1B1的中点，P是正方形ABCD 的中心，求证：MN∥平面PB1C.参考答案与解析:证明：如图，连结AC，则P为AC的中点，连结AB1，∵M、N分别是A1A与A1B1的中点，∴MN∥AB1.又∵平面PB1C，平面PB1C，故MN∥面PB1C.一、选择题【共10道小题】1、二面角指的是( )A.两个平面相交所组成的角B.经过同一条直线的两个平面所组成的图形C.一条直线出发的两个半平面组成的图形D.两个平面所夹的不大于90°的角参考答案与解析:解析：根据二面角的定义讨论，故选C.答案：C主要考察知识点:空间直线和平面2、α、β、γ、ω是四个不同平面，若α⊥γ，β⊥γ，α⊥ω，β⊥ω，则( )A.α∥β且γ∥ωB.α∥β或γ∥ωC.这四个平面中可能任意两个都不平行D.这四个平面中至多有一对平面平行参考答案与解析:解析：若α∩β=a.∵α⊥γ,β⊥γ，∴α⊥γ.同理a⊥ω.∴γ∥ω;若α∥β,则γ与ω相交或平行，∴α∥β或γ∥ω.答案：B主要考察知识点:空间直线和平面3、已知直线m、n与平面α、β，给出下列三个命题：①若m∥α,n∥α,则m∥n;②若m∥α,n⊥α，则n⊥m;③若m⊥α,m∥β,则α⊥β.其中真命题的个数是( )A.0B.1C.2D.3参考答案与解析:解析：①m∥α,n∥α不一定有m∥α.②③正确.答案：C主要考察知识点:空间直线和平面4、如图2-3-15,设P是正方形ABCD外一点,且PA⊥平面ABCD,则平面PAB与平面PBC、平面PAD的位置关系是( )图2-3-15A.平面PAB与平面PBC、平面PAD都垂直B.它们两两都垂直C.平面PAB与平面PBC垂直、与平面PAD不垂直D.平面PAB与平面PBC、平面PAD都不垂直参考答案与解析:思路解析:∵PA⊥平面ABCD,∴PA⊥BC.又∵BC⊥AB,PA∩AB=A,∴PC⊥平面PAB,从而平面PBC⊥平面PAB.由AD⊥PA,AD⊥AB,PA∩AB=A得AD⊥平面PAB.∵AD平面PAD,∴平面PAD⊥平面PAB.答案:A主要考察知识点:空间直线和平面5、如图2-3-16,等边三角形ABC的边长为1,BC边上的高为AD,若沿AD折成直二面角,则A 到BC的距离是……()图2-3-16A.1B.C.D.参考答案与解析:思路解析:折叠后BD=DC=,且∠BDC为二面角的平面角,∠BDC=90°,∴BC=.取BC中点E,连结DE,则DE⊥BC,进一步易证AE⊥BC,AE的长为所求距离.∵AD=,DE=BC=,∴AE=.答案:C主要考察知识点:空间直线和平面6、下列命题正确的是( )A.垂直于同一条直线的两直线平行B.垂直于同一条直线的两直线垂直C.垂直于同一个平面的两直线平行D.垂直于同一条直线的一条直线和平面平行参考答案与解析:思路解析:在空间中垂直于同一直线的两条直线,可能平行相交,也可能异面,所以A,B错,垂直于同一直线的直线和平面的位置关系可以是直线在平面内,直线和平面平行,所以D错.答案:C主要考察知识点:空间直线和平面7、空间四边形ABCD的四边相等，则它的两对角线AC、BD的关系是( )A.垂直且相交B.相交但不一定垂直C.垂直但不相交D.不垂直也不相交参考答案与解析:解析：取BD中点E，连结AE、CE.∵AB=AD=BC=CD,∴AE⊥BD,CE⊥BD.∴BD⊥平面AEC.又AC面AEC，∴BD⊥AC.答案：C主要考察知识点:空间直线和平面8、线段AB的长等于它在平面α内射影长的2倍，则AB所在直线与平面α所成的角为（）A.30°B.45°C.60°D.120°参考答案与解析:解析：由直角三角形的边角关系，可知直线与平面α所成的角为60°.答案：C主要考察知识点:空间直线和平面9、设α,β为两个不重合的平面,l,M,n为两两不重合的直线,给出下列四个命题:①若α∥β,,则l∥β;②若, ,M∥β,n∥β，则α∥β；③若l∥α,l⊥β,则α⊥β;④若,,且l⊥M,l⊥n,则l⊥α.其中正确命题的序号是( )A.①③④B.①②③C.①③D.②④参考答案与解析:解析：由面面平行的判定定理,知②错误;由线面垂直的判定定理知④错误.答案：C主要考察知识点:空间直线和平面10、下列说法中正确的是()①过平面外一点有且只有一条直线和已知平面垂直②过直线外一点有且只有一个平面和已知直线垂直③过平面外一点可作无数条直线与已知平面平行④过直线外一点只可作一条直线与已知直线垂直A.①②③B.①②③④C.②③D.②③④参考答案与解析:解析：由线面垂直的性质及线面平行的性质,知①②③正确;④错,过直线外一点作平面与直线垂直,则平面内的所有直线都与该直线垂直.答案：A主要考察知识点:空间直线和平面二、填空题【共4道小题】1、α、β是两个不同的平面，m、n是平面α、β外的两条不同直线，给出四个结论：①m⊥n;②α⊥β;③n⊥β;④m⊥α.以其中三个论断作为条件，余下一个论断作为结论，写出你认为正确的一个命题______.参考答案与解析:解析：假设①③④为条件，即m⊥n,n⊥β,m⊥α成立，如图.过m上一点P 作PB∥N，则PB⊥m，PB⊥β，设垂足为B.又设m⊥α，垂足为A，过PA、PB的平面与α、β的交线l交于点C.∵l⊥PA,l⊥PB,∴l⊥平面PAB.∴l⊥AC，l⊥BC.∴∠ACB是二面角α-l-β的平面角.由m⊥n,显然PA⊥PB，∴∠ACB=90°,∴α⊥β.由①③④②成立.反过来，如果②③④成立，与上面证法类似可得①成立.答案：②③④①或①③④②.主要考察知识点:空间直线和平面2、α、β是两个不同的平面，m、n是平面α、β外的两条不同直线，给出四个结论：①m⊥n;②α⊥β;③n⊥β;④m⊥α.以其中三个论断作为条件，余下一个论断作为结论，写出你认为正确的一个命题______.参考答案与解析:解析：假设①③④为条件，即m⊥n,n⊥β,m⊥α成立，如图.过m上一点P 作PB∥N，则PB⊥m，PB⊥β，设垂足为B.又设m⊥α，垂足为A，过PA、PB的平面与α、β的交线l交于点C.∵l⊥PA,l⊥PB,∴l⊥平面PAB.∴l⊥AC，l⊥BC.∴∠ACB是二面角α-l-β的平面角.由m⊥n,显然PA⊥PB，∴∠ACB=90°,∴α⊥β.由①③④②成立.反过来，如果②③④成立，与上面证法类似可得①成立.答案：②③④①或①③④②.主要考察知识点:空间直线和平面3、设三棱锥P ABC的顶点P在平面ABC上的射影是H，给出下列命题：①若PA⊥BC，PB⊥AC，则H是△ABC的垂心；②若PA、PB、PC两两互相垂直，则H是△ABC的垂心；③若∠ABC=90°，H是AC的中点，则PA=PB=PC；④若PA=PB=PC，则H是△ABC的外心.请把正确命题的序号填在横线上:______________.参考答案与解析:解析：①若P A⊥BC，PB⊥AC，则H为垂心.②∵PA⊥PB，PA⊥PC,∴PA⊥面PBC.∴PA⊥BC.又PH⊥面ABC，∴PH⊥BC.∴BC⊥面PAH.∴AH⊥BC.同理BH⊥AC，∴H为垂心.③∵H为AC中点，∠ABC=90°,∴AH=BH=CH.又PH⊥面ABC，由勾股定理知PA=PB=PC.④∵PA=PB=PC，又PH⊥面ABC，同③可知AH=BH=CH，∴H为外心.答案：①②③④主要考察知识点:空间直线和平面4、如图，P是二面角α-AB-β的棱AB上一点，分别在α、β上引射线PM、PN,截PM=PN，如果∠BPM=∠BPN=45°，∠MPN=60°，则二面角α-AB-β的大小是___________.参考答案与解析:解析：过M在α内作MO⊥AB于点O，连结NO，设PM=PN=a,又∠BPM=∠B PN=45°,∴△OPM≌△OPN.∴ON⊥AB.∴∠MON为所求二面角的平面角.连结MN，∵∠MPN=60°,∴MN=a.又,∴MO2+NO2=MN2.∴∠MON=90°.答案：90°主要考察知识点:空间直线和平面三、解答题【共3道小题】1、如图，在正方体ABCD—A1B1C1D1中，EF⊥A1D，EF⊥AC，求证：EF∥BD1.参考答案与解析:解析：要证明EF∥BD1，可构造与它们都垂直的一个平面.由于A1D，AC 均为各面的对角线，通过对角线的平行性可构造垂直关系.证明：连结A1C1，由于AC∥A1C1，EF⊥AC，∴EF⊥A1C1.又EF⊥A1D，A1D∩A1C1＝A1,∴EF⊥平面A1C1D. ①∵BB1⊥平面A1B1C1D1，A1C1平面A1B1C1D1,∴BB1⊥A1C1.又A1B1C1D1为正方体,∴A1C1⊥B1D1.∵BB1∩B1D1＝B1,∴A1C1⊥平面BB1D1D.而BD1平面BB1D1D,∴BD1⊥A1C1.同理，DC1⊥BD1，DC1∩A1C1＝C1,∴BD1⊥平面A1C1D. ②由①②可知EF∥BD1.主要考察知识点:空间直线和平面2、在长江汽车渡口,马力不足或装货较重的汽车上岸时,采用沿着坡面斜着成S形的方法向上开,这是为什么？你能从数学的角度进行解释吗？参考答案与解析:答案:在汽车马力恒定的情况下,行驶单位路程内,垂直上升高度愈大,汽车愈费“力”,当“力”所不及时,就会发生危险.日常经验告诉我们,走S形可减少这种危险,从数学的角度看,可作如下解释.图2-3-22如图,AB表示笔直向上行走的路线(AB⊥CA),α表示它与水平面所成的交角,CB表示斜着向上行走的路线,β表示它与水平面所成的夹角,它们所达到的高度都是BD.现在的问题就是要研究α和β这两个角哪个大,越大越费力.在Rt△BAD中,sinα=.①在Rt△BCD中,sinβ=.②比较①与②,因为AB、CB分别是直角三角形ABC的直角边和斜边,也就是说AB＜CB,所以＞.又因为α、β都是锐角,所以α＞β.因此汽车沿着CB方向斜着向上开要省力.山区修筑的公路,采取盘山而上的方法,也是这个道理.主要考察知识点:空间直线和平面3、如图，在四面体ABCD中，△ABD、△ACD、△BCD、△ABC都全等，且，BC=2，求以BC为棱、以面BCD和面BCA为面的二面角的大小.参考答案与解析:解:取BC的中点E，连结AE、DE，∵AB=AC，∴AE⊥BC.又∵△ABD≌△ACD，AB=AC，∴DB=DC.∴DE⊥BC.∴∠AE D为二面角A-BC-D的平面角.又∵△ABC≌△DBC,且△ABC为以BC为底的等腰三角形，故△DBC也是以BC为底的等腰三角形，∴.又△ABD≌△BDC，∴AD=BC=2.在Rt△DEB中，，BE=1，∴,同理.在△AE D中，∵AE=DE=,AD=2,∴AD2=AE2+DE2.∴∠AE D=90°.∴以面BCD和面BCA为面的二面角的大小为90°.主要考察知识点:空间直线和平面一、选择题【共12道小题】1、下列说法中正确的是( )A.棱柱的侧面可以是三角形B.正方体和长方体都是特殊的四棱柱C.所有的几何体的表面都能展成平面图形D.棱柱的各条棱都相等参考答案与解析:B主要考察知识点:简单几何体和球2、将一个等腰梯形绕着它的较长的底边所在的直线旋转一周，所得的几何体包括( )A.一个圆台、两个圆锥B.两个圆台、一个圆柱C.两个圆台、一个圆柱D.一个圆柱、两个圆锥参考答案与解析:D主要考察知识点:简单几何体和球3、过球的一条半径的中点，作垂直于该半径的平面，则所得截面的面积与球的表面积的比为( )A. B. C.D.参考答案与解析:解析：设球半径为R，截面半径为r.+r2=R2,∴r2=.∴.答案：A主要考察知识点:简单几何体和球4、如图所示的直观图是将正方体模型放置在你的水平视线的左上角而绘制的，其中正确的是( )参考答案与解析:解析：由几何体的直观图画法及主体图形中虚线的使用，知A正确.答案：A主要考察知识点:简单几何体和球5、长方体的高等于h，底面积等于S，过相对侧棱的截面面积为S′，则长方体的侧面积等于( )A. B.C. D.参考答案与解析:解析：设长方体的底面边长分别为a、b，过相对侧棱的截面面积S′=①,S=ab②,由①②得：(a+b)2=+2S,∴a+b=,S侧=2(a+b)h=2h.答案：C主要考察知识点:简单几何体和球6、设长方体的对角线长度是4，过每一顶点有两条棱与对角线的夹角都是60°,则此长方体的体积是( )A. B. C.D.参考答案与解析:解析：设长方体的过一顶点的三条棱长为a、b、c，并且长为a、b的两条棱与对角线的夹角都是60°，则a=4cos60°=2,b=4cos60°=2.根据长方体的对角线性质，有a2+b2+c2=42,即22+22+c2=42.∴c=.因此长方体的体积V=abc=2×2×=.答案：B主要考察知识点:简单几何体和球7、棱锥被平行于底面的平面所截，当截面分别平分棱锥的侧棱、侧面积、体积时，相应的截面面积分别为S1、S2、S3，则( )A.S1＜S2＜S3B.S3＜S2＜S1C.S2＜S1＜S3 D.S1＜S3＜S2参考答案与解析:解析：由截面性质可知，设底面积为S.;;可知：S1＜S2＜S3故选A.用平行于底面的平面截棱锥所得截面性质都是一些比例关系：截得面积之比就是对应高之比的平方，截得体积之比，就是对应高之比的立方，所谓“高”，是指大棱锥、小棱锥的高，而不是两部分几何体的高.答案：A主要考察知识点:简单几何体和球8、正四面体的内切球球心到一个面的距离等于这个正四面体高的( )A. B. C.D.参考答案与解析:解析：球心到正四面体一个面的距离即球的半径r，连结球心与正四面体的四个顶点.把正四面体分成四个高为r的三棱锥，所以4×S·r=·S·h,r= h (其中S为正四面体一个面的面积，h为正四面体的高)答案：C主要考察知识点:简单几何体和球9、若圆台两底面周长的比是1∶4，过高的中点作平行于底面的平面，则圆台被分成两部分的体积比是( )A.1∶16B.3∶27C.13∶129D.39∶129参考答案与解析:解析：由题意设上、下底面半径分别为r，4r，截面半径为x，圆台的高为2h，则有,∴x=.∴.答案：D主要考察知识点:简单几何体和球10、在棱长为1的正方体上，分别用过共顶点的三条棱中点的平面截该正方体，则截去8个三棱锥后，剩下的凸多面体的体积是( )A. B. C.D.。

高一数学必修二知识难点总结2021

高一数学必修二知识难点总结2021高一数学必修二知识点梳理1空间两条直线只有三种位置关系：平行、相交、异面1、按是否共面可分为两类：(1)共面：平行、相交(2)异面：异面直线的定义：不同在任何一个平面内的两条直线或既不平行也不相交。

异面直线判定定理：用平面内一点与平面外一点的直线，与平面内不经过该点的直线是异面直线。

两异面直线所成的角：范围为(0°，90°)esp.空间向量法两异面直线间距离:公垂线段(有且只有一条)esp.空间向量法2、若从有无公共点的角度看可分为两类：(1)有且仅有一个公共点——相交直线;(2)没有公共点——平行或异面直线和平面的位置关系：直线和平面只有三种位置关系：在平面内、与平面相交、与平面平行①直线在平面内——有无数个公共点②直线和平面相交——有且只有一个公共点直线与平面所成的角：平面的一条斜线和它在这个平面内的射影所成的锐角。

高一数学必修二知识点梳理21.函数的奇偶性。

(1)若f(x)是偶函数，那么f(x)=f(__)。

(2)若f(x)是奇函数，0在其定义域内，则f(0)=0(可用于求参数)。

(3)判断函数奇偶性可用定义的等价形式：f(x)±f(__)=0或(f(x)≠0)。

(4)若所给函数的解析式较为复杂，应先化简，再判断其奇偶性。

(5)奇函数在对称的单调区间内有相同的单调性;偶函数在对称的单调区间内有相反的单调性。

2.复合函数的有关问题。

(1)复合函数定义域求法：若已知的定义域为[a，b]，其复合函数f[g(x)]的定义域由不等式a≤g(x)≤b解出即可;若已知f[g(x)]的定义域为[a，b]，求f(x)的定义域，相当于x∈[a，b]时，求g(x)的值域(即f(x)的定义域);研究函数的问题一定要注意定义域优先的原则。

(2)复合函数的单调性由“同增异减”判定。

3.函数图像(或方程曲线的对称性)。

(1)证明函数图像的对称性，即证明图像上任意点关于对称中心(对称轴)的对称点仍在图像上。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

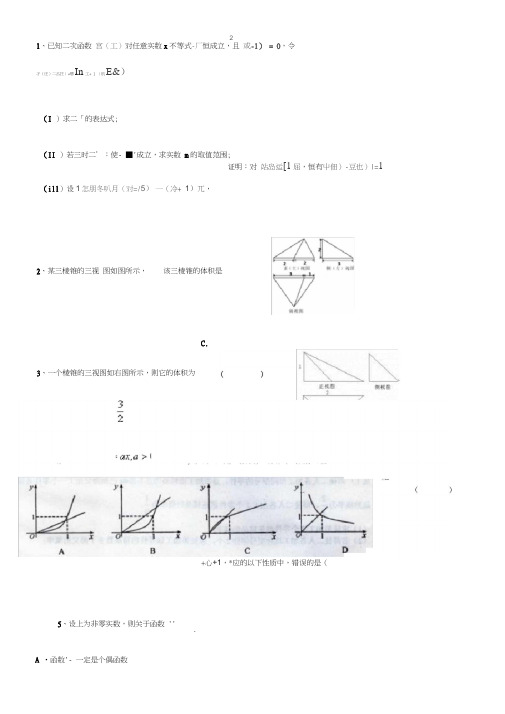
1、已知二次函数对任意实数x不等式恒成立，且，令
.
（I）求的表达式；
（II）若使成立，求实数m的取值范围；
（III）设，，证明：对，恒有
2、某三棱锥的三视图如图所示，该三棱锥的体积是
A． B．C．2D．4
3、一个棱锥的三视图如右图所示，则它的体积为( )
A． B． C．1 D．
4、函数，在同一直角坐标系第一象限中的图像可能
是
（）
5、设为非零实数，则关于函数，的以下性质中，错误的是（）
A．函数一定是个偶函数
B．一定没有最大值
C．区间一定是的单调递增区间
D．函数不可能有三个零点
6、已知＞0,且, =,当x∈时,均有, 则实数的取值范围是( ) A． B． C． D．
7、如图，四棱锥中，底面ABCD为平行四边形，PA⊥底面ABCD，M是棱PD的中点，且PA =AB =AC =2，
．
（I）求证：CD⊥平面PAC；
（Ⅱ）求二面角的大小；
（Ⅲ）如果N是棱AB上一点，且直线CN与平面MAB所成角的正弦值为，求的值．
8、已知幂函数为偶函数，且在区间上是单调递增函数。

（Ⅰ）求函数的解析式；
（Ⅱ）设，若能取遍内的所有实数，求实数的取值范围．
9、已知定义域为的函数是奇函数．
（1）求实数的值；（2）判断并证明在上的单调性；
（3）若对任意恒成立，求的取值范围．
参考答案
一、计算题
1、解（I）设
由题意令得∴
∴得
∵恒成立
∴和恒成立
得
∴
（II）
当时，的值域为R
当时，恒成立
当时，令
－0 +
↘极小↗
这时
若使成立则只须，
综上所述，实数m的取值范围
（III）∵，所以单减于是
记，则
所以函数是单增函数
所以
故命题成立.
二、选择题
2、D
3、A
4、B
5、C
6、C
三、简答题
7、证明：(I)连结AC．
因为为在中，
，，
所以，
所以．
因为AB//CD，
所以．
又因为地面ABCD，
所以．
因为，
所以平面PAC．
(II)如图建立空间直角坐标系，
则．
因为M是棱PD的中点，
所以．
所以，．
设为平面MAB的法向量，所以，
即，
令，则，
所以平面MAB的法向量．
因为平面ABCD，
所以是平面ABC的一个法向量．
所以．
因为二面角为锐二面角，
所以二面角的大小为．
(III)因为N是棱AB上一点，所以设，．
设直线CN与平面MAB所成角为，
因为平面MAB的法向量，
所以．
解得，即，，所以．
8、（Ⅰ）∵为幂函数∴
1分又在区间上是单调递增函数∴
2分
则∵∴或或
3分
当时，为奇函数，不合题意，舍去
当时，为偶函数，符合题意
当时，为奇函数，不合题意，舍去
故
5分
（Ⅱ）由（Ⅰ）知，
①当时，，则单调递增，其值域为，满足题意 7分
②当时，由得，则在单调递减，在单调递增，∴，则其值域为
∵能取遍内的所有实数∴只需
9分
令则在单调递增
又∴
11分
综合①②知，实数的取值范围为
12分
四、综合题
9、解：（1），经检验成立。

—————————4分
（2）证明：设任意
，，
在上是减函数—————————————————————— 8分
（3）
对任意恒成立
设在上增时，——12。

高一数学必修一必修二难题

高中数学必修一第二章一元二次函数方程和不等式典型例题(带答案)

(word完整版)高一数学必修一必修二难题

2019高一数学函数难题汇编(含解析)

高一数学知识点难题及解答

高中数学必修一第二章一元二次函数方程和不等式经典大题例题(带答案)

高一数学最难试题及答案

高一数学必修一必修二难题

高中数学必修一难题个人整理的,里面有详细答案的,供大家看看推荐一下吧!

高一数学必修1,2,3,4,5试题及答案

高一数学必修一经典高难度测试题含答案

高一数学必修一第二章基本初等函数练习题难题带答案

高一数学必修部分难题总结及答案

高一数学必修2习题(答案详解)

最新高一数学必修一必修二基础题目练习(含答案)

高一数学必修二知识难点总结2021