(新规范)偏心受压构件例题
偏心受压构件承载力计算例题

13
6.验算垂直于弯矩作用平面的承载力
l0/b=2500/300=8.33>8
1
1 0.002 (l0 / b 8)2
1
1 0.002(8.33 8)2
=0.999 Nu =0.9[(As+As′)fy′+Afc]
=0.9×0.999[(1375+1375) ×300+300×500×11.9]
40)
198
为大偏心受压。
4
(4)求As=Asˊ
e
ei
h 2
as
(1.024 59
400 2
40)mm
771mm
x
=90.3mm
>2a
' s
=80mm,
则有
Asˊ=As=
Ne
1
f cbx h0
x 2
f
y
h0
as
260 103
460
0.55
(0.8 0.55)(460 40)
=0.652
12
x h0
=0.652×460=299.9mm
5.求纵筋截面面积As、As′
As=As′=
Ne 1 fcbx(h x / 2)
f
' y
(h0
as'
)
1600 103 342.5 1.0 11.9 300 299.9(500 299.9 / 2) 300 (460 40)
=2346651N>N=1600kN
偏心受压构件承载力

第5章偏心受压构件承载力一、选择题1.配有普通箍筋的轴心受压构件的稳定系数φ的含义是()的比值。
A.细长构件的长度与同截面的短粗构件的长度B.细长构件的截面面积同短粗构件的截面面积C.细长构件的重量同短粗构件的重量D.细长构件的承载力与同截面短粗构件的承载力2.钢筋混凝土轴心受压构件随着构件长细比的增大,构件的承载力将()。
A.逐步增大B.逐步降低C.不变D.与长细比无关3.钢筋混凝土轴心受压构件的应力重分布,就是随着轴力的增大截面中()。
A.混凝土承担荷载的百分比降低,钢筋承担荷载的百分比提高。
B.混凝土承担荷载的百分比提高,钢筋承担荷载的百分比降低。
C.混凝土承担荷载的百分比和钢筋承担荷载的百分比都提高。
D.混凝土承担荷载的百分比和钢筋承担荷载的百分比都降低。
4.配置螺旋箍筋的轴心受压构件其核芯混凝土的受力状态是()。
A.双向受压B.双向受拉C.三向受压D.三向受拉5.大、小偏心受压破坏的根本区别在于:截面破坏时,()。
A.受压钢筋是否能达到钢筋抗压屈服强度B.受拉钢筋是否能达到钢筋抗拉屈服强度C.受压混凝土是否被压碎D.受拉混凝土是否破坏6.截面上同时作用有轴心压力N、弯矩M和剪力V的构件称为()。
A.偏心受压构件B.受弯构件C.轴心受拉构件D.轴心受压构件7.大偏心受压构件在偏心压力的作用下,截面上的应力分布情况是()。
A.截面在离偏心力较近一侧受拉,而离偏心力较远一侧受压B.截面在离偏心力较近一侧受压,而离偏心力较远一侧受拉C.全截面受压D.全截面受拉8.小偏心受压构件在偏心压力的作用下,当偏心距较大时,截面上的应力分布情况是()。
A.截面在离偏心力较近一侧受压,而离偏心力较远一侧受拉B.截面在离偏心力较近一侧受拉,而离偏心力较远一侧受压C.全截面受压D.全截面受拉9.由偏心受压构件的M与N相关曲线可知:在大偏心受压范围内()。
A.截面所能承担的弯矩随着轴向压力的增加而增大B.截面所能承担的弯矩随着轴向压力的增加而减小C.截面所能承担的弯矩与轴向压力的大小无关10.由偏心受压构件的M与N相关曲线可知:在小偏心受压范围内()。
钢筋混凝土偏心受压构件(2)

As 太 多
ssAs
f'yA's
ssAs
f'yA's
◆构件的破坏是由于受压区混凝土到达
其抗压强度,距轴力较远一侧的钢筋, 无论受拉或受压,一般均未到达屈服, 其承载力主要取决于受压区混凝土及 受压钢筋,故为受压破坏 。
“受拉破坏”和“受压
破坏”都属于材料发
生了破坏,相同之处
是截面的最终破坏是
2
0 .5 f c A c N
c 1, c 1
M Cmns M 2
M1 Cm 0.7 0.3 M2
三个条件同时满足时,
ns
M ei ea N
直接取 1
5.3 非对称配筋 偏心受压构件正截面承载力计算
◆ 偏心受压正截面受力分析方法与受弯情况是相同的, 即仍采用以平截面假定为基础的计算理论。 ◆ 等效矩形应力图的强度为α1 fc,等效矩形应力图的 高度与中和轴高度的比值为β。
M M0 ◆ 虽然最终在M和N的共同作用下达到截面承载力极限状态,但 轴向承载力明显低于同样截面和初始偏心距情况下的短柱。
◆ 对于中长柱,在设计中应考虑附加挠度 f 对弯矩增大的影响。
N
◆长细比l0/h >30的细长柱 ◆侧向挠度 f 的影响已很大
N0 Nusei Numei Num fm Nul fl
N ( ei+ f )
x ei
N
偏心距增大系数
ei y
y f × sin
N
px
le
f
l0le
ei f f 1 ei ei
x ei
N
对于小偏心受压构件,离纵向力较远一侧钢筋可能 受拉不屈服或受压,且受压区边缘的混凝土的应变小 一般小于0.0033,截面破坏时的曲率小于界限破坏时 的曲率。规范用偏心受压构件截面曲率修正系数ζ1
偏心受压构件承载力计算例题

【解】fc=11.9N/mm2,fy=
1 =1.0, 1 =0.8
1.求初始偏心距ei
f
= 300N/mm2,
y
b=0.55,
M e0= N
180103 112.5 1600
ea=(20,
h 30
)= max (20, 500
30
)=20mm
ei=e0+ea=112.5+20=132.5mm
3 0 0 (4 6 0 4 0 ) =1375mm2
6.验算垂直于弯矩作用平面的承载力
l0/b=2500/300=8.33>8
1
10.00(l20/b8)2源自10.002(18.338)2
=0.999 Nu =0.9[(As+As′)fy′+Afc]
=0.9×0.999[(1375+1375) ×300+300×500×11.9]
=1235mm2
(5)验算配筋率
As=Asˊ=1235mm2> 0.2%bh=02% ×300×400=240mm2, 故配筋满足要求。
(6)验算垂直弯矩作用平面的承载力
lo/ b=3000/300=10>8
1
10.00(l20/b8)2
10.0021(108)2
=0.992
Nu =0.9φ[fc A + fyˊ(As +Asˊ)] =0.9×0.992[9.6×300×400+300(1235+1235)]
eo=M/N=150×106/260×103=577mm ea=max(20,h/30)= max(20,400/30)=20mm ei=eo+ea = 577+20=597mm
(新规范)偏心受压构件例题

[ 例7-1 ] 某矩形截面钢筋混凝土柱,构件环境类别为一类。
600mm mm 400==h b ,,柱的计算长度.m 2.70=l 。
承受轴向压力设计值.kN 1000=N ,柱两端弯矩设计值分别为m kN 450.m kN 40021⋅=⋅=M M ,。
该柱采用HRB400级钢筋(2N/mm 360='=y y f f )混凝土强度等级为C25(2t 2c N/mm 27.1N/mm 9.11==f f ,)。
若采用非对称配筋,试求纵向钢筋截面面积并绘截面配筋图。
[解] 1.材料强度和几何参数C25混凝土,2c N/mm 9.11=fHRB400级钢筋2N/mm 360='=yy f f HRB400级钢筋,C25混凝土,8.00.1518.011b ===βαξ,,由构件的环境类别为一类,柱类构件及设计使用年限按50年考虑,构件最外层钢筋的保护层厚度为20mm ,对混凝土强度等级不超过C25的构件要多加5mm ,初步确定受压柱箍筋直径采用8mm ,柱受力纵筋为20~25mm ,则取mm 45128520s =+++='=s a a 。
600mm mm 400==h b ,,2.求弯矩设计值(考虑二阶效应后)由于889.0450/400/21==M M ,mm 2.173600121121====h A I i mm 33.23M M 12-34mm 57.412.173/7200/210=>==i l 。
应考虑附加弯矩的影响。
根据式(7-6 )~式( 7-9 )有:0.1428.11010006004009.115.05.03c >=⨯⨯⨯⨯==N A f c ζ,取0.1c =ζ 9667.04504003.07.03.07.021m =+=+=M M C mm 203060030a ===h e 13.10.1)6007200(555/)20101000/10450(130011/)/(1300112362002ns =⨯+⨯⨯+=⎪⎭⎫ ⎝⎛++=c a h l h e N M ζη考虑纵向挠曲影响后的弯矩设计值为:m kN 57.49145013.19667.02⋅=⨯⨯==M C M ns m η3.求i e ,判别大小偏心受压mm 57.4911010001057.491360=⨯⨯==N M e mm 57.5112057.4910=+=+=a i e e e mm 5.1665553.03.00=⨯=>h e i 可先按大偏心受压计算。
桥梁新规范偏心受压构件计算

圆形截面沿周边均匀配筋偏心受压构件承载力计算
圆形截面沿周边均匀配筋偏心受压构件承载力计算
说明:1、本表根据规范JTG D62-2004 5.3.9及附录C编写。
2、规范对相对受压区高度精度要求为0.02。
3、当偏心很大或很小时可改精度(Q23处)。
4、计算时,填入R列相应数据,点击“开始计算”按钮。
5、计算可以选择查表计算和按公式计算,由于查表计算未考虑g对C,D的影响,
两者将有所差别,但经测试对结果影响很小。
6、公式计算的ε增量为0.001,查表计算ε增量为0.01,故公式计算更容易找到满足要求的ε值。
偏心受压构件(小偏心)

h e ei as 320 300 35 565 mm 2
取=b,则可得
Ne 1 f c bh02 b (1 0.5 b ) As f y (h0 as' ) 600 565103 114.3 0.550 300 5652 (1 0.5 0.550) 300 (565 35) 0 0.002bh 360m m2
故按大偏心受压构件进行计算。 3、计算A’s
h e ei as 220 250 35 435 mm 2
取=b,则可得
Ne 1 f cbh02 b (1 0.5 b ) As f y (h0 as' ) 860 435103 111.9 0.550 300 4652 (1 0.5 0.550) 300 (465 35) 514m m2 0.002bh 300m m2
4、计算As
1 f cbbh0 f y As N As fy
111.9 0.550 300 465 300 514 860103 300 690.8m m2 0.002bh 300m m2
5、选择钢筋
受拉钢筋选用选配2 22,As=760mm2, 受压钢筋选用2 18,A’s=509mm2。
故按大偏心受压构件进行计算。
3、计算A’s
h e ei as 560 .6 300 35 825 .6mm 2
取=b,则可得
Ne 1 f c bh02 b (1 0.5 b ) As f y (h0 as' ) 940 825.6 103 114.3 0.520 400 5652 (1 0.5 0.520) 360 (565 35) 385m m2 0.002bh 480m m2
7 偏心受压构件承载力计算09土木XIN

(c)双向偏心受压
受压构件( 受压构件(柱)往往在结构中具有重要作用,一旦产生破坏,往往导致整 往往在结构中具有重要作用,一旦产生破坏, 个结构的损坏,甚至倒塌。 个结构的损坏,甚至倒塌。
7.2 偏心受压构件受力性能分析 心受压构件受力性能分析
N M=N e0 As
′ As
e0
N
=
As
′ As
压弯构件
《混凝土结构设计规范》 混凝土结构设计规范》 (GB50010-2010): ):
是否考虑附加弯矩的判别条件
l 0 / i ≤ 34 − 12( M 1 / M 2 )
偏心受压长柱设计弯矩计算方法
设计弯矩的计算方法 混凝土规范(GB50010-2010)规定,将柱端的附加弯矩计算用偏心距调节系 混凝土规范(GB50010-2010)规定,将柱端的附加弯矩计算用偏心距调节系 数和弯矩增大系数来表示,即偏心受压柱的设计弯矩( 数和弯矩增大系数来表示,即偏心受压柱的设计弯矩(考虑了附加弯矩影响 表示
方法二:界限偏心距判别大、 方法二:界限偏心距判别大、小偏心
求出ξ后做第 二步判断
2 两类偏心受压破坏的界限
根本区别: 是否屈服。 根本区别:破坏时受拉纵筋 As 是否屈服。 界限状态: 屈服, 界限状态:受拉纵筋 As 屈服,同时受压区边缘混凝土达到极限压应变ε cu 界限破坏特征与适筋梁、与超筋梁的界限破坏特征完全相同,因此, 界限破坏特征与适筋梁、与超筋梁的界限破坏特征完全相同,因此, 的表达式与受弯构件的完全一样。 ξ b 的表达式与受弯构件的完全一样。 大、小偏心受压构件判别条件: 小偏心受压构件判别条件: 判别条件 偏心受压; 当 ξ ≤ ξ b 时,为 大 偏心受压; 偏心受压。 当 ξ > ξ b 时,为 小 偏心受压。
(整理)大偏压与小偏压解决方案比较.

大偏压与小偏压解决方案比较偏心受压构件正截面承载力计算一、偏心受压构件正截面的破坏特征(一)破坏类型1、受拉破坏:当偏心距较大,且受拉钢筋配置得不太多时,发生的破坏属大偏压破坏。
这种破坏特点是受拉区、受压区的钢筋都能达到屈服,受压区的混凝土也能达到极限压应变,如图7—2a 所示。
2、受压破坏:当偏心距较小或很小时,或者虽然相对偏心距较大,但此时配置了很多的受拉钢筋时,发生的破坏属小偏压破坏。
这种破坏特点是,靠近纵向力那一端的钢筋能达到屈服,混凝土被压碎,而远离纵向力那一端的钢筋不管是受拉还是受压,一般情况下达不到屈服。
(二)界限破坏及大小偏心受压的分界1、界限破坏在大偏心受压破坏和小偏心受压破坏之间,从理论上考虑存在一种“界限破坏”状态;当受拉区的受拉钢筋达到屈服时,受压区边缘混凝土的压应变刚好达到极限压应变值。
这种特殊状态可作为区分大小偏压的界限。
二者本质区别在于受拉区的钢筋是否屈服。
2、大小偏心受压的分界由于大偏心受压与受弯构件的适筋梁破坏特征类同,因此,也可用相对受压区高度比值大小来判别。
当时,截面属于大偏压;当时,截面属于小偏压;当时,截面处于界限状态。
二、偏心受压构件正截面承载力计算(一)矩形截面非对称配筋构件正截面承载力1、基本计算公式及适用条件:(1)大偏压():,(7-3),(7-4)(7-5)注意式中各符号的含义。
公式的适用条件:(7-6)(7-7)界限情况下的:(7-8)当截面尺寸、配筋面积和材料强度为已知时,为定值,按式(7-8)确定。
(2)小偏压():(7-9)(7-10)式中根据实测结果可近似按下式计算:(7-11)注意:﹡基本公式中条件满足时,才能保证受压钢筋达到屈服。
当时,受压钢筋达不到屈服,其正截面的承载力按下式计算。
(7-12)为轴向压力作用点到受压纵向钢筋合力点的距离,计算中应计入偏心距增大系数。
﹡﹡矩形截面非对称配筋的小偏心受压构件,当N >f c bh时,尚应按下列公式验算:(7-13)(7-14)式中,——轴向压力作用点到受压区纵向钢筋合力点的距离;——纵向受压钢筋合力点到截面远边的距离;2、垂直于弯矩作用平面的受压承载力验算当轴向压力设计值N较大且弯矩作用平面内的偏心距较小时,若垂直于弯矩作用平面的长细比较大或边长较小时,则有可能由垂直于弯矩作用平面的轴心受压承载力起控制作用。
06-2偏心受压构件
第28页,共36页。
适用条件:
➢对矩形截面受压构件,其截面应符合:
V
Vu
1.75
1.0
f t bh0
0.07N )
➢对矩形截面受压构件,截面剪力如果符合:
V 0.25c fcbh0
则可不进行承载力计算,直接按构造要求配箍。
第29页,共36页。
偏心受压构件的构造要求
轴心受压柱的纵向受力钢筋、箍筋以及混凝土保护层的各项构造措施 均适用于偏心受压柱,此外,在值心受压拄中还应满足下列构造要求: (一)截面形式及尺寸 ➢偏心受压柱多采用矩形截面,且将长边布置在弯矩作用方向。长短 边的比值一般在1.0~2.0范围内变化,当偏心距较大时,可适当加大, 但最大不宜超过3.0。
第25页,共36页。
矩形截面偏心受压构件的斜截面承载力
➢受弯构件的斜截面抗剪: ✓一般荷载作用梁的斜截面抗剪
✓以集中荷载为主的独立矩形梁的斜截面抗剪
➢偏心受压柱的斜截面抗剪: ✓以集中荷载为主的矩形截面,同时作用有轴力。
第26页,共36页。
实验曲线:
➢在偏心受压构件中除作用有弯矩和轴向压力外尚有剪力,还应进 行斜截面受剪承载力计算,
➢B:计算x(用规范提供的方法),并判断适用条件: x>xb ;
x
N b1 fcbhh
N e 0.431 fcbh02 (1 b )(h0 as' )
1 fcbh0
b
h0
➢C:计算As=As’
As
As '
N
e
N
(h0
x) 2
f y ' (h0 as ' )
第18页,共36页。
弯曲变形(挠度),以f表示。
受压构件承载力计算例题

受压构件承载力计算1、某现浇框架柱,截面尺寸为 300X 300,轴向压力设计值 N = 1400 kN ,计算 长度3.57 m ,采用C30混凝土、U 级(HRB335)钢筋。
求所需纵筋面积。
解:I 。
., b =3570 300 二“.9,查得书=0.9515, A' 1159 3:'亠= =0.01288 > fin =0.006A 300 汇3002、已知某正方形截面轴心受压柱,计算长度 7.5 m ,承受轴向压力设计值 N = 1800 kN ,混凝土强度等级为 C20,采用U (HRB335)级钢筋。
试确定构件截面 尺寸及纵向钢筋截面面积。
3、 已知一偏心受压柱,b X h = 450 X 450,a = a' = 4,0C30, HRB335 钢筋, E b = 0.55,承受纵向力 N = 350 kN ,计算弯距 M = 220 kN • m 。
柱计算长度 为10= 3.0m ,受压区钢筋 A's = 402 (2#16),求受拉区钢筋面积。
解:(1) 设计参数:1=1.0, a =a ' = 40 h 0=410 ,f c =14.3 N/mm 2 , f y =300N/mm 2e 0= 630,取 c a =20,e i = e 0 + e a = e 0+20=648&.5fcA _0.514.3江450 汉450 _4.[取匸 1=11N3500002 =1.15-0.01b=1.15-0.01 3000=1.08,取 Z 2=1 h 450=1 -- 1(_3000)2 1 1=1.026484501400 - 450 (2) 受压区高度 n e i = 661> 0.3 h 0 按大偏压计算e =661+(450/2- 40)= 846,X ' ' 'Ne 二:1 f c bx(h °) f y A s (h ° -a ) 2*1400咒103l0.9 汉 0.962 -14.3 300 3002=1159.5m解:A'sdb = 7500 400 =18.75,查得书=0.7875 2— 9.6 汇 400 汉 400 = 3345.6mm ,=0.021>;-min-0.006匚=1 --1400eh °1300 1800X03^0.^ 0.7875A'sA 3345.6 400 400350000 846 =1 14.3 450x(410 -x2)300 402(410 -40)x 二110mm::: X b 二b h0二0.55 410 二225.5mm2a = 80mm(3) 求钢筋面积N = :r f c bx f y A s - f y A sA s =1594mm2,取 4 # 22, A s = 1520mm2(4) 验算配筋率A s _ bh1520450 450= 0.75%」min0.2%垂直于弯矩作用方向的承载力验算l0/b=6.6 , 可得,=1.0N =°.9 [f c bh f y(A s A s)] =3125kN>350kN 满足要求。
混凝土结构设计原理习题之四、五(含答案)钢筋混凝土受压受拉构件承载力计算试题

混凝土结构设计原理习题集之四6钢筋混凝土受压构件承载力计算一、填空题:1 .偏心受压构件的受拉破坏特征是_ _,通常称之为_______________ _ ;偏心受压构件的受压破坏特征是通常称之为 _______________ 。
2 •矩形截面受压构件截面,当l o/h —时,属于短柱范畴,可不考虑纵向弯曲的影响,即取_ _ ;当l o/h _ _时为细长柱,纵向弯曲问题应专门研究。
3 •矩形截面大偏心受压构件,若计算所得的E0,可保证构件破坏时_ 一 ;x= $h o场a s可保证构件破坏时 ________________ 。
4 •对于偏心受压构件的某一特定截面(材料、截面尺寸及配筋率已定),当两种荷载组合同为大偏心受压时,若内力组合中弯矩M值相同,则轴向 N越 ______________ 就越危险;当两种荷载组合同为小偏心受压时,若内力组合中轴向力N值相同,则弯矩 M越___________ _ 就越危险。
5 •由于轴向压力的作用,延缓了_____________ 得出现和开展,使混凝土的____________ 高度增加,斜截面受剪承载力有所 ____________ ,当压力超过一定数值后,反而会使斜截面受剪承载力__________ 。
6 •偏心受压构件可能由于柱子长细比较大,在与弯矩作用平面相垂直的平面内发生_______ 而破坏。
在这个平面内没有弯矩作用,因此应按__________________ 受压构件进行承载力复核,计算时须考虑_ _的影响。
7.矩形截面柱的截面尺寸不宜小于mm ,为了避免柱的长细比过大,承载力降低过多,常取l o/b < , l o/d w (b为矩形截面的短边,d为圆形截面直径,I o为柱的计算长度)。
8 •《规范》规定,受压构件的全部纵向钢筋的配筋率不得小于 ____,且不应超过。
9 •钢筋混凝土偏心受压构件在纵向弯曲的影响下,其破坏特征有两种类型: _________ 和_____________ ;对于短柱和长柱属于;细长柱属于_。
第七章偏心受力构件联系题

第七章偏心受力构件一、选择题1.偏心受压构件计算中,通过哪个因素来考虑二阶偏心矩的影响( )。
A.e ; B.ae ; C.ie ; D.η;2.判别大偏心受压破坏的本质条件是:( )。
A .03.0h e i >η; B .03.0h e i <η;C .B ξξ<; D .B ξξ>;3.由uu M N -相关曲线可以看出,下面观点不正确的是:( )。
A .小偏心受压情况下,随着N 的增加,正截面受弯承载力随之减小;B .大偏心受压情况下,随着N 的增加,正截面受弯承载力随之减小;C .界限破坏时,正截面受弯承载力达到最大值;D .对称配筋时,如果截面尺寸和形状相同,混凝土强度等级和钢筋级别也相同,但配筋数量不同,则在界限破坏时,它们的uN 是相同的;4.钢筋混凝土大偏压构件的破坏特征是:( )。
A.远侧钢筋受拉屈服,随后近侧钢筋受压屈服,混凝土也压碎;B.近侧钢筋受拉屈服,随后远侧钢筋受压屈服,混凝土也压碎;C.近侧钢筋和混凝土应力不定,远侧钢筋受拉屈服;D.远侧钢筋和混凝土应力不定,近侧钢筋受拉屈服;5.一对称配筋的大偏心受压构件,承受的四组内力中,最不利的一组内力为:( )。
A .m kN M ⋅=500 kN N 200=;B .m kN M ⋅=491 kN N 304=;C .m kN M⋅=503 kN N 398=; D .m kN M ⋅-=512 kN N 506=;6.一对称配筋的小偏心受压构件,承受的四组内力中,最不利的一组内力为:( )。
A .m kN M ⋅=525 kN N 2050=;B .m kN M ⋅=520 kN N 3060=;C .m kN M⋅=524 kN N 3040=; D .m kN M ⋅=525 kN N 3090=;7.偏压构件的抗弯承载力( )。
A.随着轴向力的增加而增加;B.随着轴向力的减少而增加;C.小偏压时随着轴向力的增加而增加;D.大偏压时随着轴向力的增加而增加;8.钢筋混凝土偏心受拉构件,判别大、小偏心受拉的根据是( )。
第5章受压构件思考的题目和习的题目问题解释

钢筋混凝土受压构件计算题1、某轴心受压柱,截面尺寸b ×h =400×500mm ,计算长度l 0=4.8m ,采用混凝土强度等级为C25,HPB235级钢筋,承受轴向力设计值N =1670kN ,计算纵筋数量。
【解】由已知条件知:ƒc =11.9N/mm 2, f y '=210N/mm 2⑴计算稳定系数φ l 0/b =4800/400=12,查表得:φ=0.95⑵计算纵筋截面面积A s ',并校验ρ'由于11.940050023801670c f A KN KN =⨯⨯=>,即混凝土的抗压能力已经满足轴向力的要求,所以纵筋按照构造要求配置即可。
2min 0.6%4005001200sA A mm ρ''=⨯=⨯⨯= ⑶配筋采用4Φ20,2212561200sA mm mm '=>,可以。
截面每一侧配筋率0.512560.003140.2%400500ρ⨯'==>⨯,可以。
所以,选用4根直径20mm 的HPB235级钢筋,21256sA mm '=。
2、某钢筋混凝土偏心受压柱,承受轴向压力设计值N =250kN ,弯矩设计值M =158kN ·m ,截面尺寸为b ×h =300×400mm ,a s =a s '=40mm ,柱的计算长度l 0=4.0m ,采用C25混凝土和HRB335钢筋,进行截面对称配筋设计。
【解】由已知条件知:ƒc =11.9N/mm 2, f y '=f y =300N/mm 2⑴计算初始偏心距e i e 0=N M =631581025010⨯⨯=632mm e a ={30h ,20mm }max ={13mm ,20mm }max =20mmi 0a ⑵计算偏心距增大系数ηh 0=400-40=360mml 0/h =4000/400=10>5,应考虑附加弯矩的影响。
第八章 偏心受力构件

ea=h/30≥20mm 则 ei= ea+ e0 e0=M/N ei----为偏心受压柱的初始偏心距 由于附加偏心距的存在,柱的弯矩增加量为 取 ∆M = Nea
第
钢筋混凝土结构设计原理
章
八
8.3.6. 偏心距增大系数 纵向弯曲 • 钢筋混凝土受压构件在承受偏心荷载后,将产 生纵向弯曲变形即会产生侧向挠度,对长细比 小的短柱,计算时一般忽略不计;对于长细比 较大的长柱,由于侧向挠度的影响,各个截面 的弯矩都有所增加,而弯矩的增加势必造成侧 向挠度的增加 ——“细长效应”或“压弯效用” Ne——为初始弯矩或一阶弯矩 增加弯矩——附加弯矩或二阶弯矩
2、什么情况下使用复合式箍筋?复合式箍筋 有什么具体要求?
第
钢筋混凝土结构设计原理
章
八
§8.3 偏心受压构件的受力性能 8.3.1 试验研究分析 偏心受压构件是介于轴压构件和受弯构件之间 的受力状态。 e0 → 0 e0 → ∝ 轴压构件 受弯构件
大量试验表明:构件截面中的符合 平截面假定 ,偏压 构件的最终破坏是由于混凝土压碎而造成的。其影响因 素主要与 偏心距 的大小和所配 钢筋数量 有关。
8.2.2 截面形式 截面形式应考虑到受力合理和模板制作方便。 矩形 b ≥250mm
( ) 工字型(截面尺寸较大时) h′f ≥ 100mm d ≥ 80mm 且 为避免长细比过大降低构件承载力 l0/h≤25, l0/d≤25。
第
l0/b ≤ 30
八 章
钢筋混凝土结构设计原理
8.2.3 配筋形式 • 纵筋布置于弯矩作用方向两侧面 d≥12mm 纵筋间距>50mm 中距≤ 350mm
(a)
N
(b)
(c)
偏心受压构件斜截面受剪承载力计算示例

截面截面尺寸满足条件
(2)验算是否可按构造配箍
Hn 4800 5.223 >3 2h0 2 460
取
3
Page 9
0.3 f c A 0.3 14.3 400 500 858kN>N 850kN
由规范公式6.3.13可得
1.75 ftbh0 0.07N λ 1 1.75 1.43 400 460 0.07 850 103 3 1 174.6kN >150kN
【解】查表得:
fc=14.3N/mm2,ft =1.43N/mm2,
fyv =270N/mm2,β 1.0
c
Page 8
(1)验算截面限制条件
h 0 h 40 500 40 460 0.25 β c fc bh0 0.25 1.0 14.3 400 460 657.8kN >150kN
Page 5
如符合规范公式(6.3.13)的要求时,可不进行斜截面承
载力的计算,而直接按构造要求配置箍筋。
1.75 V f t bh0 0.07 N 1
(规范6.3.13)
Page 6
偏心受压柱对称配筋承载力计算示例

0.90.99[214.3300400360(994994)]N 2171003N.92N60kN 故垂直于弯矩的 作承 用载 平力 面满足要求。
纵向钢筋选配
(As=As’=1017mm2), 箍筋选用
φ8@250 ,如图所示。
请思考如下问题:
(1)偏心受压柱的配筋方式有哪几种? (2)对称配筋偏心受压柱承载力计算的步骤是什么?
【解】cf14.3N/mm2,α1 1.0,fy fy' 360N/mm2,ξb 0.518。 1.验算是否需要考附 虑加弯矩
M1/M2 145/148 0.98(混凝土规范 6.2.3) 因此需要考虑附加弯的矩影响。
2.计算考虑二阶效的 应弯矩设计值
ζc
0.5fcA N0.514.330040Fra bibliotek 260103
60.6mm
<ξ bh0 0.518 360 186.5mm
故为大偏心受压
4.求A s A s ' x 60.6mm 2a s ' 80mm
eeih 2as6004 .20 40 40 440.4mm
A s A s
fy
Ne
h 0 a s
260 10 3 440.4
360 360 40
1
1
130(0M2 N
ea)/h0
(lh0 )2ζc
(混凝土规范公2式 .4-63.)
113 0(1 204 6 1 1 8 1 06 3 0 020)/ (34 300 6) 02 0 001.01.026
MC m η nM s 20. 9 19 . 4 0 12 4 16 8 60 150.9kN.m
994mm 2
5.验算配筋率 AsAs 9942m0m.2 %0b.h 23%00 4002m2m402 mm 故配筋满足要求。
第5章 受压构件思考题和习题答案

钢筋混凝土受压构件计算题1、某轴心受压柱,截面尺寸b ×h =400×500mm ,计算长度l 0=4.8m ,采用混凝土强度等级为C25,HPB235级钢筋,承受轴向力设计值N =1670kN ,计算纵筋数量。
【解】由已知条件知:ƒc =11.9N/mm 2, f y '=210N/mm 2⑴计算稳定系数φl 0/b =4800/400=12,查表得:φ=0.95⑵计算纵筋截面面积A s ',并校验ρ'由于11.940050023801670c f A KN KN =⨯⨯=>,即混凝土的抗压能力已经满足轴向力的要求,所以纵筋按照构造要求配置即可。
2min0.6%4005001200s A A mm ρ''=⨯=⨯⨯= ⑶配筋采用4Φ20,2212561200sA mm mm '=>,可以。
截面每一侧配筋率0.512560.003140.2%400500ρ⨯'==>⨯,可以。
所以,选用4根直径20mm 的HPB235级钢筋,21256sA mm '=。
2、某钢筋混凝土偏心受压柱,承受轴向压力设计值N =250kN ,弯矩设计值M =158kN·m ,截面尺寸为b ×h =300×400mm ,a s =a s '=40mm ,柱的计算长度l 0=4.0m ,采用C25混凝土和HRB335钢筋,进行截面对称配筋设计。
【解】由已知条件知:ƒc =11.9N/mm 2, f y '=f y =300N/mm 2⑴计算初始偏心距e ie 0=N M =631581025010⨯⨯=632mm e a ={30h ,20mm }max ={13mm ,20mm }max =20mmi 0a ⑵计算偏心距增大系数ηh 0=400-40=360mml 0/h =4000/400=10>5,应考虑附加弯矩的影响。
双向偏心受压构件
将截面划分为有限多个混凝土单元、纵向钢筋单 元,并近似取单元内的应变和应力为均匀分布,其 合力点在单元重心处。不考虑受拉区混凝土的作用, 把受压区混凝土划分为m个单元,用Acj、σcj和εcj (j =1~ m)分别表示第j单元的面积、应力和应变。把每 根钢筋作为一个单元,共有n个单元,其应变和应力 分别用εsi和σsi (i =1~n)表示。 取εsi=0.0033,根据平截面假定和应变的几何关 系可以得到各根钢筋和各混凝土单元的应变
m
cj
cj Asi si
i 1 cj
n
M uy M ux
A A
j 1
cj xcj Asi si xsi
i 1 n i 1
n
cj
cj ycj Asi si y si
► 双向偏心受压构件利用上式进行计算颇为繁琐,
须借助计算机进行求解。对于常用的截面尺寸、 不同配筋布置情况,可利用计算机计算并编制成 图表手册,供设计时使用。Байду номын сангаас
双向偏心受压构件正截面承载力计算
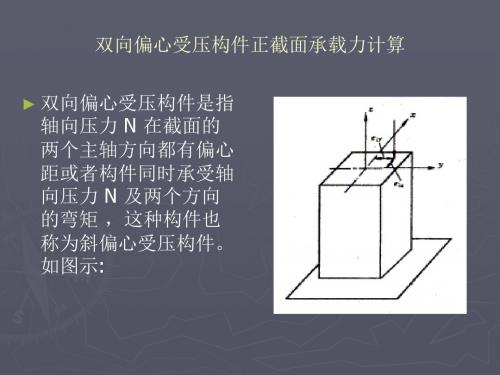
► 双向偏心受压构件是指
轴向压力 N 在截面的 两个主轴方向都有偏心 距或者构件同时承受轴 向压力 N 及两个方向 的弯矩 ,这种构件也 称为斜偏心受压构件。 如图示:
实验结果表明,双向偏心受压构件 正截面的破坏形态相似,也可以为 大偏心受压和小偏心受压。因此, 单向偏心受压构件正截面承载力计 算时所采用的基本假设也可应用于 双向偏心受压构件正截面承载力的 计算。
y si 0.0033 (1 si ) R ycj cj 0.0033 (1 ) R
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[ 例7-1 ] 某矩形截面钢筋混凝土柱,构件环境类别为一类。
600mm mm 400==h b ,,柱的计算长度.m 2.70=l 。
承受轴向压力设计值.kN 1000=N ,柱两端弯矩设计值分别为
m kN 450.m kN 40021⋅=⋅=M M ,。
该柱采用HRB400级钢筋(2N/mm 360='=y y f f )混凝土强度等级为C25(2t 2c N/mm 27.1N/mm 9.11==f f ,)。
若采用非对称配筋,试求纵向钢筋截面面积并绘截面配筋图。
[解] 1.材料强度和几何参数
C25混凝土,2c N/mm 9.11=f
HRB400级钢筋2N/mm 360='=y
y f f HRB400级钢筋,C25混凝土,8.00.1518.011b ===βαξ,,
由构件的环境类别为一类,柱类构件及设计使用年限按50年考虑,构件最外层钢筋的保护层厚度为20mm ,对混凝土强度等级不超过C25的构件要多加5mm ,初步确定受压柱箍筋直径采用8mm ,柱受力纵筋为20~25mm ,则取mm 45128520s =+++='=s a a 。
600mm mm 400==h b ,,
2.求弯矩设计值(考虑二阶效应后)
由于889.0450/400/21==M M ,
mm 2.17360012
1121====h A I i mm 33.23M M 12
-34mm 57.412.173/7200/210=>==i l 。
应考虑附加弯矩的影响。
根据式(7-6 )~式( 7-9 )有:
0.1428.110
10006004009.115.05.03c >=⨯⨯⨯⨯==N A f c ζ,取0.1c =ζ 9667.04504003.07.03
.07.021m =+=+=M M C mm 2030
60030a ===h e 13.10.1)6007200(555/)20101000/10450(130011/)/(1300112362002ns =⨯+⨯⨯+=⎪⎭
⎫ ⎝⎛++=c a h l h e N M ζη
考虑纵向挠曲影响后的弯矩设计值为:
m kN 57.49145013.19667.02⋅=⨯⨯==M C M ns m η
3.求i e ,判别大小偏心受压
mm 57.4911010001057.4913
6
0=⨯⨯==N M e mm 57.5112057.4910=+=+=a i e e e mm 5.1665553.03.00=⨯=>h e i 可先按大偏心受压计算。
4.求s A 及s
A ' 因s A 及s
A '均为未知,取518.0==b ξξ,且0.11=α mm 57.7664530057.5112=-+=-+
=s i a h e e 由式( ):
2
2230201mm 480002.0mm 65.1108)
45555(360)518.05.01(518.05554009.110.157.766101000)
()5.01(=>=-⨯-⨯⨯⨯⨯-⨯⨯=-'--='bh a h f bh f Ne A s y b b c s ξξα 再按式( )求s A
2
3
01mm 12.2132360
10100065.1108360518.05554009.110.1=⨯-⨯+⨯⨯⨯⨯=-''+=y
s
y b c s f N A f bh f A ξα 5.选择钢筋及截面配筋图
选择受压钢筋为3φ22(2mm 1140='s A );受拉钢筋为3φ25+2φ222mm 2233=s A 。
则2mm 337322331140=+=+'s s A A ,全部纵向钢筋的配筋率:
%55.0%4.16004003373>=⨯=
ρ 满足要求。
箍筋按构造要求选用,配筋图如图 所示。
[ 例7-9 ] 条件同[例7-1],但采用对称配筋。
[解]: 1.已知条件 由例7-1:mm
45='=s s a a ,mm 5554000⨯=⨯h b 0
.1,518.0,N/mm 360kN,100012==='==αξb y y f f N ,
mm 57.766,mm 57.511,mm /9.112===e e N f i c
2.判别偏心受压类型
由式(7-18) N
bh f N b
c b >=⨯⨯⨯⨯==.kN 4.1368518.05554009.110.101ξα
为大偏心受压。
3.计算ξ和配筋
162.0555
4522378.05554009.110.11010000301=⨯='>=⨯⨯⨯⨯==h a bh f N s c αξ 2
2230201mm 480002.0mm 1.1727)
45555(360)378.05.01(378.05554009.110.157.766101000)
()5.01(=>=-⨯-⨯⨯⨯⨯-⨯⨯=-'--='=bh a h f bh f Ne A A s y c s s ξξα 每边选用纵筋3φ22+2φ20对称配置(2mm 1769='=s s A A )
,按构造要求箍筋选用φ8@250。
与例7-1比较可知,采用对称配筋时,钢筋总量2
mm 2.345421.1727
=⨯要比非对称配筋2mm 77.324012.213265.1108=+为多,并且偏心距越大,对称配筋的总用钢量越多。
一、小偏心受压的计算与大偏心受压相同,只要确定了设计弯矩M 后其余的计算与规范没有差别。
二、排架柱的截面设计是一偏心受压构件,其计算与偏心受压构件相同。
但排架柱的特点有二点:
1. 排架柱的计算长度按本学期教材《混凝土结构设计》P293
页附表11.2取用,附表下的第3条件不要考虑了。
2. 排架柱的设计弯矩M 计算如下。
考虑二阶效应排架结构的计算方法基本上维持2002版
规范不变,但考虑了工业厂房排架的荷载特点。
说简单一点应是把子排架分析时的各截面设计弯矩 放大一个系数
——截面曲率修正系数; ——初始偏心距。
——一阶弹性分析柱端弯矩设计值。
——轴向压力对截面重心的偏心距
——附加偏心距。
——排架柱的计算长度。
0M M s η=0l a e 0e 0M i e c ζN M e /00=0101..c =>ζζ取时当,c 0M。
