高等电力网络分析
高等电力系统分析-第二章-电力系统网络矩阵

第二章电力系统网络矩阵作业:2-1, 2-6, 2-722.1 节点导纳矩阵Y●N 个节点(不含地),b 条支路●A 0-(N+1)×b 阶, y b -b ×b 阶●则(N+1)×(N+1)阶节点不定导纳矩阵为:T 00b 0Y A y A2.1.1 Y 的性质、特点及物理意义(1)节点不定导纳矩阵0Y301bT k k kk y ===∑Y M M k kkky y yy --想象:透明胶片的叠加4节点方程1,11,21,1,1112,12,22,2,122,1,2,,1`1,11,21,1,111N N N N N N N N N N N N N N N NN N N N Y Y Y Y V I Y Y Y Y V I Y Y Y Y V I Y Y Y Y V I ++++++++++⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦参考节点6节点不定导纳矩阵Y 0的性质性质1:无移相器时,Y 0对称:=T 00b 0Y A Y A中的每个非零元都是实数,而Y b 是对角线矩阵。
0A 由于=T 00Y Y8性质3:Y 0是奇异矩阵,并有0Y 1=0证明:=T 00b 0Y A Y A01bT k k kk y =∴==∑Y M M k k kky y y y --011()()b bT T k k kk k kk k y y ==∴==∑∑Y 1M M 1M M 10T k=M 1而9◆齐次方程存在非零解,所以Y 0奇异(数学上的理解);◆所有节点电位相同时,支路无电流(物理意义上的理解);0Y 1=0怎样理解?10T ∴1I = 0∴T1Y =0 V 0Y 1=00T1Y =0对任意节点电压都成立13241I 2I 3I 4I 1,11,21,31,4112,12,22,32,4223,13,23,33,4334,14,24,34,444Y Y Y Y V I Y Y Y Y V I Y Y Y Y V I Y Y Y Y V I ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦12340I I I I +++= N=3, N+1=411如果电力网络无接地支路,这时是一个浮空网:13241I 2I 3I 4I 40I = 1230I I I ++= N 个节点的网络Y 0奇异此时不独立3I 例12(2)节点定导纳矩阵Y选地为参考节点,排在N+1位置,参考电压是零T Iy = V 0o T oo o y I ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦Y y I y V 是地节点电流平衡方程是网络方程,不含地节点Y =IV 不独立1313241I 2I 3I 4I 1,11,21,31,4112,12,22,32,4223,13,23,33,4334,14,24,34,440Y Y Y Y I V Y Y Y Y I V Y Y Y Y I V Y Y Y Y I ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦1,11,21,3112,12,22,3223,13,23,333Y Y Y V I Y Y Y V I Y Y Y V I ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦节点不定导纳矩阵节点定导纳矩阵例Y =IV14433Y V 411Y V 14,14,24,3243V Y Y Y V I V ⎡⎤⎢⎥⎡⎤=⎣⎦⎢⎥⎢⎥⎣⎦4411422433I Y V Y V Y V =++ 13241I 2I 3I 4I 422Y V 411y V 4141Y y =-地节点电流平衡方程4123I I I I =--- 各节点接地支路电流•天网上节点注入电流之和=接地支路电流之和的负值=流出地节点电流TI y = V15节点定导纳矩阵的性质性质1:无移相器支路时,Y 是N ×N 阶对称矩阵Tb Y =Ay A性质2:Y 是稀疏矩阵对Y 的贡献k k kky y y y --iky j16[]T lm l l k T mk ky y yy ⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦M M M M T T T Tl l ll m kk m lk k ky y y y =+++M M M M M M M M1l m lm m k mk z z y y z z y y -⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦ilz jpkz qmz 两条支路有互感时,它们对应的支路导纳子矩阵是:对节点导纳矩阵的贡献是17l m l m m k m k l m l m mkmki p j q y y y y i y y y y p y y y y j y y y y q ⎡⎤⎢⎥--⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎣⎦对节点导纳矩阵的贡献是ijpq新增耦合等值支路ilz jpkz qmz ijpqm y -my -my my l y ky18性质3:有接地支路时,Y非奇异,Y每行元素之和等于该节点接地导纳13241I 2I 3I 4I 1,11,21,32,12,22,33,13,23,3Y Y Y Y Y Y Y Y Y ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦节点4不包括在内如果节点接地支路的导纳较小时,Y接近奇异例19121310121321122320233132132330y y y y y y y y y y y y y y y ++--⎡⎤⎢⎥=-++-⎢⎥⎢⎥--++⎣⎦Y N =3,b =6,N +1=41321I 2I 3I 0I 节点定导纳矩阵的形态例21(3)Y 的物理意义表示短路参数:在节点i 接单位电压源,其余节点短路接地,流入节点i 的电流数值为自导纳Y ii ,流入节点j 的电流数值为互导纳Y ji32Y 12312Y 22Y +_1[]1222321Y Y Y ⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦Y2213222112I Y y ==- 111121310I Y y y y ==++ 12y 33113I Y y ==- 13y 10y 1+_ 示例例(自导纳)(互导纳)(互导纳)242.1.3 Y 的修改◆支路追加和移去T l l ly '=±Y Y M M◆节点合并(母联开关合上)注意移去连支、树支、桥支路的情况行相加(电流之和等于总电流)1,11,21,3112,12,22,3223,13,23,333Y Y Y V I Y Y Y V I Y Y Y V I ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦2V 3V 23V V = 23I I I +=列相加(节点电压相等)251,11,21,3112,12,22,3223,13,23,323Y Y Y V I Y Y Y V I Y Y Y V I ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦1,11,21,3112,12,22,3223,13,23,33Y Y Y I V Y Y Y I V Y Y Y I ⎡⎤⎡⎤+⎡⎤⎢⎥⎢⎥+=⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥+⎣⎦⎣⎦1,11,21,3112,13,12,22,33,23,3232Y Y Y I V Y Y Y Y Y Y I I V +⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥+++++⎣⎦⎣⎦⎣⎦23V V = 23I I I +=26节点p消去n p T p pp Y ⎡⎤⎢⎥⎣⎦Y Y Y p T ppp Y ⎡⎤⎢⎥⎣⎦Y Y 1T n n p pp pY -=-Y Y Y Y 1T p pp pY --Y Ypp擦除增加27◆某节点s 电压给定,V s 是已知量,求其余节点的电压n s n n T sss s s Y V I ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦Y Y ΙY V n n n s sV =-Y ΙY V 把节点s的电压源变成电流源减少一个待求量,方程减少一阶和s 相连的节点,注入电流有一个增量28◆变压器变比变化时的修正变比由变成tt '[]111/1/l y tt ⎡⎤⎢⎥⎢⎥=-⎢⎥-⎢⎥⎣⎦Y []111/1/l y t t ⎡⎤⎢⎥⎢⎥''=-'⎢⎥-⎢⎥⎣⎦Y '∆=-Y Y Y可在原网络上贴◆支路参数变化时的修正l y l y '参数由变成在原网络上贴y y y'∆=-变压器支路对导纳矩阵的贡献29(1)以地为参考节点的Z ,N ⨯N 阶(有接地支路)2.2 节点阻抗矩阵Z1-=Z Y2.2.1 Z 的性质、特点及其物理意义.Z I = V(2)Z 元素的物理意义开路参数(3)Z 矩阵的性质Z矩阵对称(互易定理)Z是非奇异的满阵(为什么非奇异?为什么满阵?)对纯感性支路组成的无源网,节点自阻抗更大,即| Z ii|≥| Z ij|对纯感性支路组成的无源网,节点对的自阻抗更大,| Z ij,ij|≥| Z ij,kl|节点对的自阻抗| Z ij,ij|≠0,除非ij端口存在短路。
高等电力系统分析_课后习题

《高等电力系统分析》课后习题第一部分:电力网络方程●对于一个简单的电力网络,计算机实现节点导纳矩阵节点导纳矩阵的修改方法。
●编制LDU分解以及因子表求解线性方程组消元,回代。
●试对网络进行等值计算。
多级电网参数的标么值归算,主要元件的等值电路。
第二部分:潮流计算简单闭式网络潮流的手算方法步骤第三部分:短路计算对称分量法简单不对称故障边界条件计算,复合序网的形成。
第四部分:同步机方程派克变换同步电机三相短路的物理过程分析第五部分:电力系统稳定概述●什么是电力系统的稳定问题?什么是功角稳定和电压稳定?广义的电力系统稳定性实际上指的就是电力系统的供电可靠性,如果系统能够满足对负荷的不间断的、高质量的供电要求,系统就是稳定的,否则系统就是不稳定的。
通常所说的电力系统稳定性实际上专指系统的功角稳定。
电力系统的功角稳定指的是系统中各发电机之间的相对功角失去稳定性的现象。
电力系统的电压稳定性是电力系统维持负荷电压于某一规定的运行极限(如不低于额定电压的70%)之内的能力,它与系统的电源配置,网络结构,运行方式及负荷特性等因素有关,带自动负荷调节分接头的变压器也对系统的电压稳定性有十分显著的影响。
●电力系统送端和受端稳定的特点是什么?送端指电源,其稳定性主要是系统的各台发电机维持同步运行的能力,即功角稳定。
受端稳定一般指负荷节点的电压稳定性和频率稳定性。
电动机负荷则是一个以微分方程描述的动态元件,其无功功率与电压的平方成正比,电压下降时,其吸收的无功功率会显著下降。
当电压低于系统的临界电压时可能出现电压崩溃。
●常用的电力系统稳定计算的程序都有哪些?各有什么特点?常用仿真程序:1.PSASP中国电科院(PSCAD属于系统级仿真软件)2.BPA美国3.PowerWorld Simulator美国4.UROSTAG法国和比利时OMAC德国西门子公司6.PSCAD/EMTDC (PSCAD属于装置级仿真软件)7.PSS/E美国8.MATLAB9.RTDS实时仿真器●大停电的影响是什么?● 什么是电力系统的三道防线?1. 第一道防线:继电保护速断2. 第二道防线:切机、快关、电气制动、快速励磁调节等3. 第三道防线:低频减载甩负荷、解列● 简述提高电力系统静态稳定和暂态稳定的主要措施有哪些?静态稳定:1. 采用自动励磁调节装置;2. 采用分裂导线;3. 提高线路的额定电压等级;4. 改善系统结构、减小电气距离;5. 采用串联补偿设备;6. 采用并联补偿设备。
国网考试总结-高等电力系统分析

电力系统静态安全分析的基本概念电力系统静态安全分析是电力系统规划和调度的常用手段,用以判断在发生预想事故(输变电设备强迫退出运行)后系统是否会过负荷或电压越限的功能。
电力系统动态安全分析用于判断在发生预想事故后系统是否会失稳的功能。
静态安全分析的基本方法:补偿法,直流潮流法,灵敏度分析法。
直流输电的基本原理及稳态数学模型1、直流输电线路输送的电流和功率由线路两端的直流电压所决定,与两端的交流系统的频率和电压相位无关。
直流电压的调节是通过调节换流器的触发角和交流系统的电压来实现的,换流器输出直流电压的改变,将决定直流电流的大小。
(直流潮流的控制)2、由于交流变压器等值电感的存在,相电流不能突变,因而换流器的供电电源从一相换到另一相时不能瞬时完成,需要经过一个换相期,换相期所对应的电角度称为换相角。
(换相角定义,范围)3、由于换相角的存在,直流电压的平均值将随直流电流的增大而减小;换流器正常工作的触发角的变化范围减小。
(换相角对直流系统的影响)4、换相电流中包含两个分量,分别为常数分量和正弦分量。
其中,常数分量随着触发角的增大而减小,正弦分量滞后于换相电压90°。
常数分量是短路电流中的自有分量,其产生机理是电感回路中的电流不能发生突变;正弦分量是短路电流中的强迫分量,由于短路回路是纯电感回路,所以正弦分量的相位滞后于电源电压90度。
因此,换流器的稳态工况是在换相期使交流系统两相短路,在非换相期使交流系统单相断线。
(换相电流的理解)5、直流潮流的基本方程:整流器、逆变器、交流基波电流和直流电流、直流电压和交流电压的关系。
6、直流稳态运行方程中引入了等值换相电阻,等值换相电阻并不具有真实电阻的全部意义,它不吸收有功功率,其大小体现了直流电压平均值随直流电流增大而减小的斜率。
等值换相电阻是一个网络参数,不随系统运行状态的改变而改变。
由于等值电阻的引入,换相角不显含在直流潮流公式中,换相效应完全由换相电阻与直流电流的乘积表征。
(完整word版)高等电力系统分析

1. 对极坐标牛顿拉夫逊法简化,可以得到快速解耦潮流。
给出简化步骤,说明后者的优、缺点。
答:(1)简化步骤:快速解耦法是基于两个基本假设: R<<X 以及线路两端相角差比较小(小于10度-20度)。
反映在电力系统中的特性是:有功功率的变化主要决定于电压相位角的变化;无功功率的变化则主要决定于电压模值的变化。
反映在牛顿法修正方程式雅克比矩阵的元素上,是N 和M 两个子块元素的数值相对于H 、L 两个子块的元素要小得多。
⎥⎦⎤⎢⎣⎡∆∆⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡∆∆U U L M N H Q P /θ是一个2n-m-2阶方程组。
略去N 和M ,得到:⎩⎨⎧∆-=∆∆-=∆)/(U U L Q H P θ将原来2n-m-2阶方程组化为一个n-1及一个n-m-1阶方程组。
假设:线路两端的相角差不大(小于10度-20度),而且ij ij B G <<;与节点无功功率相对应的导纳2/i i U Q 通常远小于节点的自导纳ii B ,即ii i ij B U Q 2<<。
⎩⎨⎧==ij j i ijij j i ij B U U L B U U H 即⎩⎨⎧==U UB L U UB H '''得,⎩⎨⎧∆-=∆∆-=∆U B U Q U B U P ''/)('/θ 系数矩阵'B 及''B 由节点导纳矩阵的虚部所组成,从而是一个常数矩阵。
对'B 及''B 的构成进行进一步修改得:⎩⎨⎧∆=∆∆=∆UB U Q B U P ''/'/θ 其中,ij ij X B 1'-=,∑∑=-=jwi jwi ijij ii X B B 1'',ij ij ij ij ij B X R X B -=+-=22'',ii jwi ij ij iji ii B X R X B B -=++-=∑220''。
高等电力网络分析考题
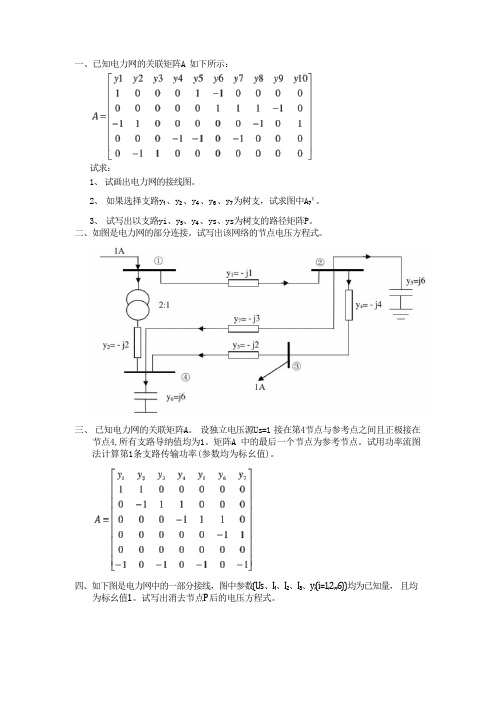
一、已知电力网的关联矩阵A 如下所示:
试求:
1、试画出电力网的接线图。
2、如果选择支路y₁、y₂、y₄、y₆、y₇为树支,试求图中A₇¹。
3、试写出以支路yi、y₃、y₄、ys、ys为树支的路径矩阵P。
二、如图是电力网的部分连接。
试写出该网络的节点电压方程式。
三、已知电力网的关联矩阵A。
设独立电压源Us=1 接在第4节点与参考点之间且正极接在
节点4,所有支路导纳值均为1。
矩阵A 中的最后一个节点为参考节点。
试用功率流图法计算第1条支路传输功率(参数均为标幺值)。
四、如下图是电力网中的一部分接线,图中参数(Us、I₁、I ₂、I ₃、y;(i=1,2, .,6))均为已知量,且均
为标幺值1。
试写出消去节点P 后的电压方程式。
五、已知电力网的关联矩阵A 如下所示。
若在节点1和节点4分别注入1安的电流源,网
络中各支路的导纳y;(i=1,2,.,7)的值均为1S。
若在节点③处将电力网络分解为两个部分,求节点3和节点4之间线路的功率损耗。
六、如图所示电压源U,=5V, 内阻yo=0Ω;线路长度: Li₂=10m、Li₃=5m, 单位线路阻抗
zo=0.2Ω/m。
负载Z₂和Z₃大小见图中标示。
试求:
1. 用系统法画出电力网的流图。
2. 用功率流图计算图中Z₃吸收的功率及线路Li₂的功率损耗。
高等电力网络分析考点

11
消去子块N(=∂ΔP/∂ΔVT ,是P和V之间的耦合项)
−
⎡H ⎢ ⎣
-
NL-1M M
0⎤ L⎥⎦
⎡ Δθ ⎢⎣ΔV
⎤ ⎥ ⎦
=
⎡ΔP ⎢ ⎣
− NL−1ΔQ⎤
ΔQ
⎥ ⎦
⎧−HΔθ = ΔP ⎨⎩−MΔθ − LΔV = ΔQ
H = H - NL-1M ΔP = ΔP − NL−1ΔQ … …①
两种情况下的联络线功率控制问题? z 电压控制问题中,当调整一台发电机时,其他发电机无功也
会变化,如何考虑其他发电机无功出力达界和不达界问题?
23
参考文献:
¾ H.B.Sun, B.M.Zhang, A Systematic Analytical Method for Quasi-Steady-State Sensitivity, Electric Power System Research, Vol. 63, No.2, Sept, 2002, pp.141-147.
假定Vi=Vj=1;θij ≈ 0, cosθij =1, sinθij =θij ; rij << xij , 忽略 rij
支路电流
Pij
=
θi −θ j
xij
节点电压 支路电阻
(是线性方程)
2
对节点i 运用KCL
Pij
j
Pi sp
k
i
∑ ∑ Pisp
=
Pij
j∈i
=
θi −θ j
x j∈i
ij
¾ 邓佑满,张伯明,相年德等,“联络线族的有功安 全校正控制”,电力系统自动化,Vol. 18,No. 6, 1994年,pp. 47-51
高等电力系统分析--ppt课件

重写规范形式如下 :
Y11V1 Y12V2 Y13V3 Y14V4 Y15V5 I1
Y21V1 Y22V2 Y23V3 Y24V4 Y25V5 I2
Y31V1
Y32V2
Y33V3
Y34V4
Y35V5
I3
Y41V1
Y42V2
Y43V3
Y44V4
Y45V5
I4
边界条件
I Sn AYU S AI S
节点电压方程简化为
YU I
nn
Sn
矩阵A反映了网络的拓扑约束, Y反映了网络的支路特性约束,
所以节点导纳矩阵集中了网络 两种约束的全部信息。
2024/7/16
高等电力网络分析
19
若网络参数用阻抗形式表示,则节点网络方程有如下形 式:
Z I U
n sn
n
Zn
.
I 1 Y11V1 Y12V2
.
I 2 Y21V1 Y22V2
.
I i Yi1V1 Yi2V2
.
I n Yn1V1 Yn2V2
Y1iVi
Y1nVn
Y2iVi Y2nVn
YiiVi
YinVn
YniVi YnnVn
节点自导纳Yii =节点i加单位电压,其它节点接地 时,节点i向电网注入的电流。
V4
y1
y3
2
3
4
i1
i3
用节点电压方程描述电力 网络的一个例子
y4
y5
i4
i5
1 V1
i6
y6
y2
V5
i2
5
V4
4
以基尔霍夫电流定律列出节点方程:
华北电力大学研究生课程-电力网络分析

华北电力大学 电力市场研究所 王雁凌 Yanling.wang@
内容: 内容:
第一节 非含源多口网络的常见矩阵表示法 第二节 含源多口网络表示方法 第三节 多口网络的等效电路 Matrix) 第六节 不定导纳矩阵(Indefinite Admittance Matrix) 不定导纳矩阵(
∑y
j =1
n
y1 + y 2 + L L + y n
j
(2)目的:消去网络中的无可达结点 (3)应用 p116 例3-3-1(自己看)
不定导纳矩阵( 第六节 不定导纳矩阵(Indefinite Admittance Matrix) )
一.不定导纳矩阵及其性质 1. 用途 用于不同网络的联接和同一网络的变换。 Yi U n = J Yi(n×n) 2. 定义
'
U1 U2 I = T− I 1 2 U1 I1 I = HU 2 2
U2 ' U 1 − I = T I 2 1
U I1 ' 1 U = H I 2 2
二.非含源多口网络常见矩阵表示法
1、双口网络和多口网络的Y Z阵区别仅在于端口数目的不同 p98式3-1-1 p100式3-1-2 2、双口网络中参数的下标:1——输入端口;2——输出端口 n端口网络中: 1——一类端口;2——二类端口 一类端口:电流作为激励的端口 二类端口:电压作为激励的端口 混合参数1阵:p103 (Hybrid1 Matrix) 混合参数2阵:p103 (Hybrid2 Matrix)
4. 开路抑制(端子的删减)( 开路抑制(端子的删减)( )(Suppression) ) (1)可及结点、半可及结点及不可及结点 p137 (2)开路抑制 p137
高等电力网络分析.总结

高等电力网络分析.电力网络是一个复杂的系统,在实际应用中需要进行大量的分析和优化。
高等电力网络分析作为电力系统工程领域的一个重要研究方向,涉及诸多理论和技术。
在这篇文档中,我们将简要介绍电力网络的基本概念和特点,以及高等电力网络分析的基本方法和技术。
电力网络的基本概念和特点电力网络由多个发电厂、变电站、输电线路和配电网络连接而成,形成一个互相交互作用的复杂系统。
电力网络的特点包括:1.大规模性。
电力网络通常包含数百个或数千个节点,系统规模巨大,需要高效的算法和技术进行分析和优化。
2.多元化。
电力系统结构复杂,包括不同类型和功率的发电机、变电站和负载,需要针对不同特点进行分析和建模。
3.高度互连性。
电力网络中不同节点之间互相依存,相互作用紧密,一个节点的变化可能会导致整个系统的变化。
4.动态性。
电力系统的运行状态随时变化,需要进行实时监测和控制。
高等电力网络分析的基本方法和技术高等电力网络分析是对电力网络进行复杂分析和优化的一种技术。
下面我们将介绍一些常用的高等电力网络分析方法和技术:1.潮流计算。
潮流计算是电力系统分析中最基本、最重要的问题之一。
通过求解电网中各个节点的电压、电流、有功、无功等参数,判断各个设备的负荷能否正常运行。
潮流计算的方法主要有潮流方程法、牛拉法和戴孟法等。
2.稳态稳定分析。
稳态稳定分析是电力系统分析中的一项重要工作。
主要研究电力系统的稳定性问题,如安全裕度和暂态稳定等。
常用的稳态稳定分析方法包括等值模型法、直接分析法和瞬时定子反应机模型法等。
3.电力系统优化。
电力系统优化以如何在满足各种约束条件下,使得电力系统达到最优的目标为研究对象,包括计划运行优化、潮流优化和安全限制优化等。
常用的优化方法包括极端点法、基于线性规划的算法和遗传算法等。
4.智能电网技术。
智能电网是电力系统的一种新型形态,利用现代通信等技术实现智能化、高效化、安全化的智能化电网系统。
智能电网技术包括电力通信、数据管理和分布式智能等技术,可以提高电力系统的效率和可靠性。
电力系统网络拓扑结构分析_(3)

华中科技大学博士学位论文1 绪论1.1 问题的提出根据系统学原理,结构和功能是任何一个系统都存在的两种属性,系统的结构和功能相互联系、相互影响。
结构决定功能,规定、制约着功能的性质和水平,限制着功能的范围和大小;功能是结构的外在表现,结构的改变往往伴随着功能的改变[1]。
例如在力学中,用同样三根木条,当用钉子把它们分别钉为字母“N”、“H”和“A”的形状时,其稳定性有很大差别。
同样地,电网的拓扑结构将对电力系统的稳定性产生直接影响[2-4],合理的电网结构能为其本身的可靠性提供物质基础,减少电网发生重大事故的可能性,或者能快速灵活地从事故状态恢复到正常状态。
因此,分析和研究电力系统网络拓扑结构,对于理解、掌握电力系统静态和动态行为[5]、保障电力系统安全稳定运行具有重要的意义。
电力系统是由发电机、变电站、输电线及负荷等电力元件按一定形式联结成的总体,其电气运行性能受到两个约束,即元件特性的约束和联结关系的约束(拓扑约束)。
当不考虑网络中元件的特性,即各支路的物理参数,网络可以抽象成一些支路及由它们联结成的节点组成的几何图形。
综合考虑电力系统的元件特性约束和联结关系约束,电网实际上包含了两类拓扑结构:几何拓扑和物理拓扑。
几何拓扑反映了电网设备的几何连接状态,物理拓扑则体现了电网元件物理上的电气耦合关系。
电力系统网络拓扑结构分析一般分为以下两个方面的内容:①电力系统几何网络拓扑结构的建立。
根据开关状态把各种设备连接的电网表示成能用于电力系统分析计算的节点—支路几何连接关系模型,并且识别相互连通孤立的子系统,是电力系统物理分析、计算和研究的基础。
②研究和利用电网拓扑结构,挖掘拓扑结构和物理功能之间的内在联系,从而方便和简化电力系统分析和控制。
网络拓扑结构是电力系统分析和控制的宝贵资源,电力系统中的很多问题与网络拓扑结构有着紧密的联系,如链式狭长电网结构与暂态稳定问题密切相关[6];网络拓扑的结构特点可以为许多问题的处理和实际应用提供便利,如无功电压的分层分区控制[7-8];利用网络拓扑结构特点也可以有效提高电力系统华中科技大学博士学位论文问题分析的效率,如电力系统分析计算中的拓扑分解及网络分割[9-13]。
高等电力网络分析PPT课件

ji
Qi Vi
Vj(Gijsinij Bijcosij) i1,2,
(1-6)
,N
ji
式(1-6)是用极坐标表示的潮流方程。
牛顿-拉夫逊法的一般描述
牛顿-拉夫逊法的求解步骤如下。在给定的初值 x ( 0 )
处作一阶泰勒展开:
f(x(0)) f x0 xT
x(0)
(1-7)
定处义的值J ,则xfT 为有潮:流方程的雅可比矩阵,J 0 为J在 x ( 0 )
牛顿-拉夫逊法的极坐标形式
P
J
f xT
T
Q
T
P
V T
n
Q n-r
V T
P
J
f xT
T
Q
T
P V T
V
Q V T
V
n
(1-12)
n-r
上式右侧的对n 电压n-r幅值的偏导数项n 中的n电-r 压幅值的阶
次减少了1,为使雅可比矩阵的各部分子矩阵具有一致
的形式,在实际计算中,常将该项乘以电压幅值,并
(1-10)
牛顿-拉夫逊法的一般描述
上式也可以写成下面的简单迭代法的计算格式
x ( k 1 ) x k J ( x k ) 1 fx k x k
因为
( x ) x ( T x ) I J x T 1 fx J 1 fx T x J x T 1 fx
上式就是潮流方程的复数形式,是N维的非线性复 数代数方程组。将其展开,有:
P ijQ i V ˆ YijVj j1,2, ,N (1-3) j i
式中,j i 表示所有的和i相连的节点j,包括j=i。
如 代果入节 到点 式电 (压1-用3)直中角有坐:标表示,即令Vi ei jfi ,
高等电力网络分析-基本概念

2)电感
i
L u
di uL dt
u,i取关联参考 方向
j L I U
jLI jx I U L xL L ——感抗
du iC dt
u,i取关联参考 方向
3)电容
i C
u
1 j C I
U
jCU I 1 xC C
bt
bl ( n 1)b
qij 1
qij 0
C1 [Q f ] E QL Cn 1
例
C1
按T-L编号的割集矩阵矩阵
y1 y2 C2 y4 y3 y5
C3
1 0 0 1 0 Q 0 1 0 0 1 0 0 1 1 1
树支数目=独立节点数目=n
如上图T1、T2中:
T1:
y6
T2
y6
①
y4
y1
②
y3y2③①来自y4y1②
y3
y2
③
y5
y5
④
④
( y4 , y5, y6 ) 为连支。
( y3 , y5, y6 ) 为连支
1.4 电力网络的的4个基本矩阵
1、关联矩阵A
①
y1
A表示节点与支路的关联关系。A 的元素 aij 1,1,0
,
z 1,2,1;2,3,2;2,0,3;1,0,4;3,0,5;1,3,6;
k1 0, Ak 2 , i 1
k 2 0, Ak1 , i 1
Ak1 , i 1, Ak 2 , i 1
§1.6 网络运行拓扑约束的电压、电流表示法
1 2 b 1 [ B] l
IEEE14节点电力网络分析

《高等电力网络分析》—— IEEE14节点电力网络分析专业班级:电力工程1403班姓名:学号:Z14050394同组成员:导师:刘润华二〇一四年十二月第1章IEEE14简介 (1)第2章汇报内容总结 (3)用支路追加法建立节点阻抗矩阵 (3)补偿法求网络方程的修正解(前补偿、中补偿、后补偿) (9)统一的网络分块解法 (14)第3章调节变比使中枢点电压控制在给定值 (21)第4章连续潮流法在静态电压稳定性分析和计算中的应用 (23)连续潮流算法 (23)连续潮流计算方法在静态电压稳定性的分析和计算中的应用 (24)正确认识连续潮流及其对静态稳定分析的作用 (26)第5章课程总结 (27)第1章IEEE14简介本文选用14节点系统作为分析对象,绘制IEEE14节点标准试验系统图如图1.1所示:图1.1 IEEE14系统图母线系统数据如下表格:表1.1 母线数据表表1.2 支路数据表第2章 汇报内容总结2.1 用支路追加法建立节点阻抗矩阵1、部分网络部分网络是指所要分析的电网的一个连通子网络。
支路追加法形成节点阻抗矩阵是在部分网络上进行的。
支路追加法的主要思想是以部分网络的节点阻抗矩阵()0Z 为基础,每次追加一条新的支路,每次都对()0Z 进行更新,形成追加之路后的节点阻抗矩阵。
如此重复,当全部支路追加完毕,部分网络最终变成全网络,就得到了全网络的节点阻抗矩阵。
2、追加连枝支路如果支路α作为连枝追加到部分网络中,部分 网络增加了新支路,但未增加节点,如图所示。
可以用关联矩阵描述部分网络和追加支路之间的连接关系。
图2.1 部分网络追 追加支路后,所得网络节点导纳矩阵如式(2-1) 加一条连枝 )0(21αα1)0()0(1Z C z C Z Z Y Z-Λ--== (2-1)式中⎪⎪⎩⎪⎪⎨⎧-=+==---Λ-α0100ααα1αα1)0(21αααα1)0()0(z z z z y C Z C y z Y Z (2-2)式(2-1)和式(2-2)就是采用支路追加法追加连枝时形成节点阻抗矩阵的一般公式。
高等电力网络分析 第一章

物理模型是对被研究对象的抽象和简化:要根据研究的目的和内 容以及研究、计算的手段和工具选择物理模型
·
数学模型:寻找合适的数学形式,表达物理模型中物理量之间的 关系,吧一个物理问题抽象成一个数学问题
· ·
网络的数学模型:网络方程(将网络的约束用数学表达) “物理量的选取、物理模型和数学模型的建立都不是唯一的”
第二节 电力网络的拓扑约束
割集:图G的一个支路的最小集合,若把图G分割成两个 互不连通的子图,则该最小值路集合称为割集 基本割集:仅包含一条树支的割集(单树支割集) 割集可以看做广义节点 “基本割集数=树支数” *对于图G:N+1个节点,b条支路,连支数L 独立节点数N=树支数=基本割集数=秩=N 基本回路数=连支数=bN=L 二、关联矩阵和关联矢量 计算机分析电路用矩阵,二维,点和边 网络的拓扑结构用关联矩阵来描述。由于角度不同有不同的关联矩阵 A(N+1)*b 表示N+1行,b列矩阵 1、关联矩阵A (节点支路关联矩阵Aa)NodeBranch Incident Martrix 反应结构问题 节点和支路的关系
节点‐支路关联矩阵Aa(或全‐关联矩阵Aa、增广关联矩阵Aa) Aa=
① é 1 1 ②ê ê ③ ê 0 ê ④ ë 0 0 0 0 1 1 ù 1 0 1 0 0 ú ú 1 1 0 1 0 ú ú 0 1 1 0 1 û
Aa:行对应节点,行数等于节点数;列对应支路,列术等于支路数
ì1:表示出发 ï :表示终止 Aa列矢量对应支路,与两个节点相连 í 1 ï0 :与该节点无关
第二节 电力网络的拓扑约束
Aa 行矢量:非零元素表示与节点相关联,非零元素个数对应节点的度
【高等电力网络分析】2网络拓扑、可观测性分析

网络拓扑分析(TOPO)
• ◆目的 — 利用元件的拓扑联结关系和遥信 值确定网络的拓扑岛
• ◆厂站拓扑分析
•
(开关–节点) + (开关状态) => (节点–母线)
网络拓扑分析(TOPO) (续)
网络拓扑分析(TOPO) (续)
网络拓扑分析(TOPO) (续)
• ◆系统的拓扑分析
• • • (支路–节点) + (节点–母线) => (支路–母线) • 分析整个系统的节点由支路(线路、绕组)联结成多少的子系
25
内网等值概念
S1
岛1 n1
S3
n3 岛2 n2 Sij
S2
• 性质: • (1)系统中的量测可以分为两类:量测岛内量测和边界注入量测 • (2)支路可以分为岛内支路和岛际互联支路 • (3)岛际互联支路上不存在支路量测
内网等值概念
.
S 1m
内部网
1
.
S 2m
2
(a)
. U2 f (U1)
.
2
1
岛II
可计算岛I
3
3
4
p34,q34
p4,q4
无可观测区域
10
1 2
9
8
7
3
4
6
5
10
1 2
9
8
7
3
4
6
5
10
1 2
9
8
7
3
4
6
5
10
1 2
9
8
7
3
4
6
5
2021/6/8 Tuesday
39
12
13
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《高等电力网络分析》—— IEEE30节点电力网络分析专业:电力电子与电力传动同组成员:杨珊宋晓英孙长如导师:王艳松马文忠二〇一二年四月第一、二章第一部分:本组选用IEEE30节点作为分析对象,首先,根据标准数据,画出电力网络图,如图1所示。
然后根据网路图,本单元计算了网络的关联矩阵、节点导纳和节点阻抗矩阵以及添加和移去一条支路的处理。
图1 IEEE30节点电力网络图一、计算关联矩阵:为了计算关联矩阵,首先对网络进行节点和支路进行编号和标注方向,尤其是道-支关联矩阵,要求支路必须有方向。
选取树枝和连枝,重新编号,如图2所示。
图2 有向图利用Matlab 编程,可直接求出节-支关联矩阵A:然后根据关联矩阵之间的关系,可分别求出回-支关联矩阵、割-支关联矩阵和道-支关联矩阵。
1. 回-支关联矩阵B:和A 的关系:2.割-支关联矩阵Q :和A 的关系:3.道-支关联矩阵T :和A 的关系:具体程序如下:function IEEE30[x,y]=xlsread('C:\Documents and Settings\Administrator\work\30节点数据.xls','sheet3','A2:C51');A=zeros(30,50);A1=zeros(31,50);for s=1:50start=x(s,2);tail=x(s,3);zong=x(s,1);A1(start,zong)=1;A1(tail,zong)=-1;end%去掉参考节点的最后一行,降阶for s=1:30for j=1:50A(s,j)=A1(s,j);endendfprintf(‘节-支关联矩阵A=%8.5f\n')Afor s=1:30[ ]T L A A A =[ ]T B B I =0, 0T T N L L N AB BA ⨯⨯==1()T T T L T B A A -=-[ ]L Q I Q =11(())T T T L T T L Q A A A A --==[ ]T L T T T =TI AT =for j=1:30AT(s,j)=A(s,j); %树支endendfor s=1:30for j=31:50AL(s,j-30)=A(s,j); %连支endendBL=eye(20);QT=eye(30); BT=-1*(AL')*inv(AT');B=[BT,BL];fprintf('回-支关联矩阵B=%8.5f\n')BQL=-BT';Q=[QT,QL];fprintf('割-支关联矩阵=%8.5f\n')QTT=(inv(AT))';TL=zeros(30,20);T=[TT,TL];fprintf('道-支关联矩阵T=%8.5f\n')T运行结果如下:A=B=Q=T=二、计算节点导纳(阻抗)矩阵在本节中,本组采用了两种方法对网络进行求解节点导纳矩阵Y,法一,先求解网络的不定导纳矩阵,然后去掉参考节点或者地,形成定导纳矩阵;法二,根据导纳矩阵的定义,利用网络直接求出Y。
通常阻抗导纳矩阵有三种求解方法,即部分网络法、追加树枝支路法和追加连枝支路法,但是由于Y满秩,所以可以通过直接求逆得出阻抗导纳矩阵,简单快捷。
下面是两种方法的程序:方法1:function IEEE30b[B,y1]=xlsread('C:\Documents and Settings\Administrator\work\30节点数据.xls', 'sheet1','A2:I44');n1=30;%节点数n2=41;%支路数Y=zeros(n1,n1);%创建节点导纳矩阵for j=1:n1for m=1:n2if B(m,2)==j&B(m,3)~=0 %支路首段与节点j相连,并且不是补偿电容支路if B(m,4)==0 %支路无变压器,是线路支路Y(j,j)=Y(j,j)+1/(B(m,7)+i*B(m,8))+i*B(m,9)/2;p=B(m,3);Y(j,p)=-1/(B(m,7)+i*B(m,8));else%支路有变压器,是变压器支路B(m,4)==1k=B(m,6)/B(m,5);zt=B(m,7)+i*B(m,8);y=1/(k*zt);y1=(k-1)/(k*zt);y2=(1-k)/(k*k*zt);Y(j,j)=Y(j,j)+y+y1;p=B(m,3);Y(j,p)=-y;endelseif B(m,2)==j&B(m,3)==0Y(j,j)=Y(j,j)+i*B(m,9);elseif B(m,3)==j %支路末端与节点j相连,并且不是补偿支路if B(m,4)==0 %支路是线路支路Y(j,j)=Y(j,j)+1/(B(m,7)+i*B(m,8))+i*B(m,9)/2;p=B(m,2);Y(j,p)=-1/(B(m,7)+i*B(m,8));else%支路有变压器,是变压器支路B(m,4)==1k=B(m,6)/B(m,5);zt=B(m,7)+i*B(m,8);y=1/(k*zt);y1=(k-1)/(k*zt);y2=(1-k)/(k*k*zt);Y(j,j)=Y(j,j)+y+y2;p=B(m,2);Y(j,p)=-y;endendendendfprintf('节点导纳矩阵Y=%8.5f\n')YZ=inv(Y);fprintf('节点阻抗矩阵Z=%8.5f\n')Z方法2:function IEEE30a%节点导纳矩阵yb(1,1)=5.2246-j*15.6467;yb(2,2)=1.2437-j*5.096;yb(3,3)=1.7055-j*5.1974;yb(4,4)=8.1954-j*23.5309;yb(5,5)=1.1360-j*4.7 725;yb(6,6)=1.6861-j*5.1165;yb(7,7)=6.4131-j*22.3112;yb(8,8)=2.954-j*7.4493;yb(9,9)=3.5902-j*11.0261;yb(10,10)=6.2893-j*22 .0126;yb(11,11)=-j*4.8077;yb(12,12)=-j*1.7986;yb(13,13)=-j*9.0909;yb( 14,14)=-j*4.8077;yb(15,15)=-j*3.9063;yb(16,16)=-j*7.1429;yb(17,17)=1. 5266-j*3.1734;yb(18,18)=3.0954-j*6.0973;yb(19,19)=1.9520-j*4.1044;yb( 20,20)=2.4910-j*2.2509;yb(21,21)=1.8678-j*4.3794;yb(22,22)=1.8077-j*3.6914;yb(23,23)=3.0757-j*6.2188;yb(24,24)=5.8824-j*11.7647;yb(25,25)=1.7848-j*3.9854;yb(26,2 6)=3.9560-j*10.3174;yb(27,27)=5.1019-j*10.9807;yb(28,28)=2.6193-j*5.4 008;yb(29,29)=16.7746-j*34.1277;yb(30,30)=1.9683-j*3.9761;yb(31,31)=2 .5405-j*3.9544;yb(32,32)=1.4614-j*2.9892;yb(33,33)=1.3099-j*2.2876; yb(34,34)=1.2183-j*1.8127;yb(35,35)=1.9693-j*3.7602;yb(36,36)=-j*2.52 53;yb(37,37)=0.9955-j*1.8810;yb(38,38)=0.6875-j*1.2940;yb(39,39)=0.91 21-j*1.7234;yb(40,40)=1.4440-j*4.5408;yb(41,41)=4.3628-j*15.4636; %普通支路数据yb(42,42)=j*0.0468;yb(43,43)=j*0.0844;yb(44,44)=j*0.0246;yb(45,45)=j* 0.0271;yb(46,46)=j*0.0311;yb(47,47)=j*0.0427;yb(48,48)=j*0.0187;yb(49 ,49)=j*0.0259;yb(50,50)=j*0.0279;%由支路阻抗数据,求节-支关联矩阵AA(1,1)=1;A(1,2)=1;A(2,3)=1;A(3,4)=1;A(2,5)=1;A(2,6)=1;A(4,7)=1;A(5,8) =1;A(6,9)=1;A(6,10)=1;A(9,11)=1;A(6,12)=1;A(9,13)=1;A(9,14)=1;A(12,15 )=1;A(12,16)=1;A(12,17)=1;A(12,18)=1;A(12,19)=1;A(14,20)=1;A(16,21)=1 ;A(15,22)=1;A(18,23)=1;A(19,24)=1;A(10,25)=1;A(10,26)=1;A(10,27)=1;A(1 0,28)=1;A(21,29)=1;A(15,30)=1;A(22,31)=1;A(23,32)=1;A(24,33)=1;A(25,3 4)=1;A(25,35)=1;A(28,36)=1;A(27,37)=1;A(27,38)=1;A(29,39)=1;A(8,40)=1;%输出节点对应的A元素值A(6,41)=1;A(1,42)=1;A(2,43)=1;A(3,44)=1;A(4,45)=1;A(5,46)=1;A(6,47)=1;A(7,48)=1;A(8,49)=1;A(28,50)=1;%对地电容支路A(2,1)=-1;A(3,2)=-1;A(4,3)=-1;A(4,4)=-1;A(5,5)=-1;A(6,6)=-1;A(6,7)=-1;A(7,8)=-1;A(7,9)=-1;A(8,10)=-1;A(6,11)=-1;A(10,12)=-1;A(11,13)=-1;A(10,14)=-1;A(4,15)=-1;A(13,16)=-1;A(14,17)=-1;A(15,18)=-1;A(16,19)=-1;A(15,20)=-1;A(17,21)=-1;A(18,22)=-1;A(19,23)=-1;A(20,24)=-1;A(20,25)=-1;A(17,26)=-1;A(21,27)=-1;A(22,28)=-1;A(22,29)=-1;A(23,30)=-1;A(24,31)=-1;A(24,32)=-1;A(25,33)=-1;A(26,34)=-1;A(27,35)=-1;A(27,36)=-1;A(29,37)=-1;A(30,38)=-1;A(30,39)=-1;A(28,40)=-1;A(28,41)=-1;Y=A*yb*A';% 6条变压器支路按变比发生变化处理,设原变比为1,变化后变比为t:1,即变压器在原边侧T1=[9 6 1.0155]; %变压器支路1的首节点、末节点及变比T2=[6 10 0.9629]; %变压器支路2的首节点、末节点及变比T3=[12 4 1.0129]; %变压器支路3的首节点、末节点及变比T4=[28 27 0.9581];% 变压器支路4的首节点、末节点及变比Y(T1(1,1),T1(1,2))=Y(T1(1,1),T1(1,2))+(1-1/T1(1,3))*yb(11,11);Y(T1(1,2),T1(1,1))=Y(T1(1,1),T1(1,2)); % Yji'=Yij'=Yij+detaYijY(T1(1,1),T1(1,1))=Y(T1(1,1),T1(1,1))+(1/(T1(1,3)^2)-1)*yb(11,11);% Yii'=Yii+detaYiiY(T2(1,1),T2(1,2))=Y(T2(1,1),T2(1,2))+(1-1/T2(1,3))*yb(12,12);Y(T2(1,2),T2(1,1))=Y(T2(1,1),T2(1,2));Y(T2(1,1),T2(1,1))=Y(T2(1,1),T2(1,1))+(1/(T2(1,3)^2)-1)*yb(12,12); Y(T3(1,1),T3(1,2))=Y(T3(1,1),T3(1,2))+(1-1/T3(1,3))*yb(15,15);Y(T3(1,2),T3(1,1))=Y(T3(1,1),T3(1,2));Y(T3(1,1),T3(1,1))=Y(T3(1,1),T3(1,1))+(1/(T3(1,3)^2)-1)*yb(15,15); Y(T4(1,1),T4(1,2))=Y(T4(1,1),T4(1,2))+(1-1/T4(1,3))*yb(36,36);Y(T4(1,2),T4(1,1))=Y(T4(1,1),T4(1,2));Y(T4(1,1),T4(1,1))=Y(T4(1,1),T4(1,1))+(1/(T4(1,3)^2)-1)*yb(36,36); %2条并联电容支路,按支路的添加来修改Y矩阵l1=[10 0 j*0.19]; %要添加支路1的首末节点及对应的支路导纳l2=[24 0 j*0.04]; %要添加支路2的首末节点及对应的支路导纳[m,n]=size(Y);M1=zeros(m,1); M2=zeros(m,1);if l1(1,1)~=0M1(l1(1,1),1)=1;endif l1(1,2)~=0M1(l1(1,2),1)=-1;endif l2(1,1)~=0M2(l2(1,1),1)=1;endif l2(1,2)~=0M2(l2(1,2),1)=-1;endY=Y+M1*l1(1,3)*M1';Y=Y+M2*l2(1,3)*M2'; %Y'=Y-Ml*yl*Ml' %最后的节点导纳矩阵:display('节点导纳矩阵如下所示')YZ=inv(Y);display('节点阻抗矩阵如下所示')Z计算结果:三、添加和移去一条支路(一)添加一条支路:相当于在原网络的支路l 上并联一个y i 的支路 本组选择在原网络上添加支路9-11(二)移去一条支路:相当于在原网络的支路l 上并联一个yi 的支路本组选择在原网络上添加支路6-10 程序如下:%//////////////////////移去支路6-10//////////////////////////////// [m,n]=size(Y);l3=[6 10 -5.2246 +i*15.64678];%要移去的支路的首末节点及对应支路导纳 M3=zeros(m,1); if l3(1,1)~=0'y T l l l Y Y M M =+'y T l l l Y Y M M =--y lM3(l3(1,1),1)=1;endif l3(1,2)~=0M3(l3(1,2),1)=-1;endY=Y-M3*l3(1,3)*M3';display('移去支路后新的节点导纳矩阵如下所示:') Y计算结果:%//////////////////////添加支路9-11////////////////////////////// l4=[9 11 i*9.0909];%要添加支路首末节点及对于支路导纳M4=zeros(m,1);if l4(1,1)~=0M4(l4(1,1),1)=1;endif l4(1,2)~=0M4(l4(1,2),1)=-1;endY=Y+M4*l4(1,3)*M4';display('添加支路后新的节点导纳矩阵如下所示:')Y计算结果:第三章本节主要做的内容有:节点优化编号;三角检索存储;Y因子分解的两种方法;求解稀疏线性方程组;Y因子分解图论描述。
