§5.5 布里渊区

合集下载

布里渊区图示

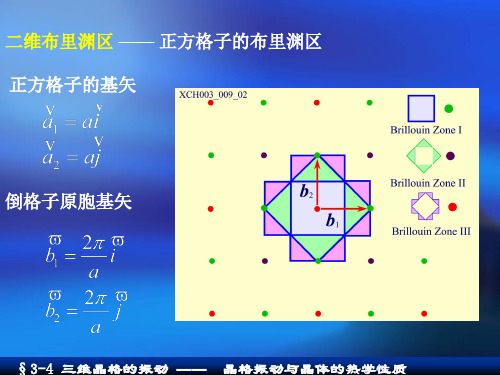
a 3 正格子原胞基矢 a1 ai, a2 i aj 2 2 取单位矢量k垂直于i, j 则，a1，a2和k构成的体积 3 2 a 2
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
倒格子原胞的基矢为 2 (a2 k ) 2 2 b1 i j a 3a 2 (k a1 ) 4 b2 j 3a
的垂直平分线和第一布里渊区边界所围成 —— 第二布里渊区大小
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
第三布里渊区
由4个倒格点
的垂直平分线和第二布里渊区边界边界所围成第三布里渊区大小
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
第一、第二和第三布里渊区
§3-4 三维晶格的振动 ——
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
选一个倒格点为原点，原点的最近邻倒格矢有6个，分别是
b1 , b2 , (b1 b2 )
§3-4 三维晶格的振动 —— 晶格振动与晶体的热学性质
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
晶格振动与晶体的热学性质

正方格子其它布里渊区的形成
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质

正方格子其它布里渊和第一布里渊区重合
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
二维斜格子的第一布里渊区
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质

二维斜格子其它布里渊区的形成
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
二维斜格子其它布里渊区的形状

布里渊区通俗理解

布里渊区通俗理解-概述说明以及解释1.引言1.1 概述布里渊区是一个在物理和数学领域中具有重要意义的概念，它主要用来描述在给定条件下某一物体或物体集合的邻域。

布里渊区的概念源于法国物理学家亚历山大·布里渊的研究成果，他发现了一种描述物体在空间中的局部特性的方法。

布里渊区的概念不仅在物理学领域中被广泛应用，同时也在计算机图形学、材料科学、生物学等领域中具有重要作用。

在本文中，我们将深入探讨布里渊区的概念、应用以及重要性，希望能够对读者有所启发和帮助。

通过了解布里渊区的相关知识，我们可以更好地理解物体在空间中的局部结构和特性，为我们探索和应用这些知识提供了理论基础。

在日常生活中，布里渊区的概念也有着重要的意义，可以帮助我们更好地理解世界的复杂性，促进科学技术的发展和创新。

展望未来，布里渊区的研究和应用将会不断深化和拓展，为人类社会的进步和发展做出更大的贡献。

1.2 文章结构本文将分为三个主要部分来讨论布里渊区的通俗理解。

在引言部分，我们将简要介绍布里渊区的概念、文章结构和撰写本文的目的。

在正文部分，我们将详细探讨布里渊区的概念，其在实际应用中的情况以及在各领域中的重要性。

最后，在结论部分，我们将总结布里渊区的作用，讨论其在日常生活中的意义，并展望未来布里渊区的发展方向。

通过这样的结构安排，读者可以系统地了解布里渊区的相关知识，并深入理解其在现实生活中的应用和意义。

1.3 目的2.正文2.1 布里渊区的概念布里渊区（英文名为Boulevard区）是一种在计算机科学领域中常用的概念，用于描述一种数据结构的布局方式。

布里渊区是指内存中的一段连续地址空间，通常用来存储程序代码、全局变量和静态变量。

在操作系统中，布里渊区还可以用于存放动态链接库和共享库的代码段和数据段。

布里渊区的特点是具有一定的大小和位置，可以在运行时被操作系统动态地分配和回收。

布里渊区的概念主要用于优化内存管理和提高程序的执行效率。

布里渊区图示

a 3 正格子原胞基矢 a1 = ai, a2 = i + aj 2 2 取单位矢量k垂直于i, j 则，a1，a2和k构成的体积 3 2 Ω= a 2
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
倒格子原胞的基矢为 2π (a2 × k ) 2π 2π b1 = i− j = Ω a 3a 2π (k × a1 ) 4π b2 = = j Ω 3a
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
正方格子其它布里渊区的形成
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
正方格子其它布里渊区的形状
—— 每个布里渊区经过适当的平移之后和第一布里渊区重合
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
二维斜格子的第一布里渊区
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
二维斜格子其它布里渊区的形成
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
二维斜格子其它布里渊区的形状
—— 每个布里渊区经过适当的平移之后和第一布里渊区重合
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
平面正三角形，相邻原子间距为求正格矢和倒格矢求正格矢和倒格矢，平面正三角形，相邻原子间距为a,求正格矢和倒格矢，画出第一和第二布里渊区
的垂直平分线和第一布里渊区边界所围成 —— 第二布里渊区大小
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
第三布里渊区由4个倒格点个倒格点
的垂直平分线和第二布里渊区边界边界所围成第三布里渊区大小
§3-4 三维晶格的振动 ——

倒格子和布里渊区

于是：
Gh1h2 h3 CA a1 a3 (h1b1 h2b2 h3b3 ) ( ) h1 h3 2 2 0
同理 Gh1h2 h3 CB 0 而且 CA, CB 都在（ABC)面上，所以 Gh1h2h3 与晶面系 (h1h2h3 ) 正交。
三维例子：
正点阵为简单点阵，倒易点阵也是简单点阵。
正格子空间中长的基矢a3对应于倒格子空间短的基矢b3，反之亦然。推广，正格子空间长的线条对应于倒格子空间短的线条。
正点阵为有心点阵时，倒易点阵也是有心点阵，但有心类型可能不同，例如：体心立方点阵的倒格子为面心立方点阵。
而面心立方点阵的倒格子为体心立方点阵。
倒易点阵仍是简立方点阵：
2 2 2 b1 i, b2 j , b3 k, a a a
所以倒格子也是布拉菲格子。六角点阵：六角点阵的倒易点阵：见Ashcroft p88 c 轴方向不变，a 轴在垂直于c 轴的平面上旋转30度。
正格子空间六方结构，在倒格子空间亦为六方结构。不过其基矢尺寸关系发生变化，基矢方向也转了一个角度。
显然： b1 a 2 a 3 , b 2 a 3 a1 , b 3 a1 a 2 ,
b1 2 2 3 a1 a 2 a3 a3 a1 b2 2 a1 a 2 a3 a1 a 2 b3 2 a1 a 2 a3

G G ( k ) 0 2
k

k
G 2
G

G 2
正方点阵布里渊区
第二到第九Brillouin区约化到第一布里渊区

布里渊区

固体物理固体物理
布里渊区
主讲人：主讲人：许本超答疑人：答疑人：李海龙封福明
固体物理固体物理
内容
• • • • • • • • • 1.倒易空间 2. 布里渊区基本概念 3. 典型格子的第一布里渊区 4.布里渊区的几何性质 5. 衍射条件在布里渊区诠释 6.布里渊区中的K点 7.布里渊区和能带的关系 8.布里渊区和费米面 9.MS计算能带实例图
14
固体物理固体物理
7.2布里渊区和能带的关系
能带论的基本出发点: 能带论的基本出发点固体中的电子可以在整个固体中运动电子在运动过程中要受晶格原子势场的作用由于周期场的微扰，由于周期场的微扰，
E
E6
E(k)函数在布里渊区函数在布里渊区
允许带
E5
边界k=± 边界 ±nπ/a处出现处出现
3.2体心立方晶格的F.B.Z 体心立方晶格的F.B.Z 体心立方晶格的体心立方晶格的倒格子为面心立方晶格
可以看出，可以看出，面心立方倒格子（即体心立方晶格）格子（即体心立方晶格）的F.B.Z为正菱形十二为正菱形十二面体（非正十二面体）面体（非正十二面体）
8
固体物理固体物理
3.3面心立方晶格的F.B.Z 面心立方晶格的面心立方晶格的F.B.Z 面心立方晶格的倒格子为体心立方晶格
如右图所示，如右图所示，黑框为体心立方倒格子，取其体心（黄点）倒格子，取其体心（黄点）作为原点，红点（8个为原点，红点（8个）为此原点最相邻的倒格点，蓝点（6 点最相邻的倒格点，蓝点（个）为此原点次相邻倒格点可以看出，可以看出，体心立方倒格子（即面心立方晶格）格子（即面心立方晶格）的F.B.Z为截角的八面体为截角的八面体十四面体）（十四面体）

布里渊区gamma点的物理意义

布里渊区gamma点的物理意义
【原创版】
目录
1.布里渊区的定义与物理意义
2.布里渊区与倒格子的关系
3.γ点的定义及其在布里渊区中的作用
4.γ点在晶体电子态中的应用
5.总结
正文
布里渊区是固体物理学中的一个重要概念，它描述了晶体中电子状态的分布情况。

布里渊区可以用波矢 k 来描述，其中 kx、ky、kz 构成一个 k 空间（属于倒格子）。

晶体电子的所有状态对应的全部 k，都将均匀分布在倒格子的一个 W-S 原胞中，这个原胞就称为布里渊区。

布里渊区与倒格子有密切的关系。

倒格子是实际空间中晶格点的倒数空间，而布里渊区是描述电子状态的虚拟空间。

在波矢空间中，倒格子的体积就是第一布里渊区所围成的空间的体积。

也就是说，它们实际上是同一个空间，只是基矢不同而已。

在布里渊区中，γ点是一个重要的概念。

γ点是倒格子中的一个特殊点，它与晶体中的电子态有直接的关系。

γ点在布里渊区中的作用是描述电子态的能量和动量。

通过γ点，我们可以了解电子在晶体中的行为和性质。

γ点在晶体电子态中的应用非常广泛。

在晶体的能带理论中，各种电子态按照它们的波矢分类。

通过γ点，我们可以研究电子态的能量分布、电子态的相互作用以及电子态的激发等物理现象。

此外，γ点还可以用于分析晶体的光学性质、电学性质以及磁学性质等。

总之，布里渊区和γ点是固体物理学中非常重要的概念。

布里渊区的积分

4
(9)
(10)
I (E ) =
V
f (k )δ (E − ε(k ))dk =
i=1
pi Ii (E )
(11)
其中 Ii (E ) =
V
µi (x, y, z )δ (E − εl (x, y, z ))dxdydz
(12)
对于i=1,2,3,4，有µi (x,y,z)=1,x,y,z。这样，I(E)变为四个独立的积分。接下来换元，令
计算体积分的一种办法是对面积分I(e)进行数值积分： J (E ) =
E −∞
I (e)de =
E Emin
I (e)de
(22)
但是我们更希望得到解析解。首先对J(E)作变换： J (E ) =
tetra
f (k )θ (E − ε(k )) d3 k = Vtetra (E ) f occ
x = f (e, u, v )
y = g (e, u, v ) z = h(e, u, v )
(13)
3
4
ε1<e<ε2
ε2<e<ε3
4
ε3<e<ε4
4
e
e 1 3
1
e 3
1
3
2
2
2
Figure 2: 图2 得到εl (x,y,z)= εl (e,u,v)=e。于是 Ii (E ) =
对于三维体系由于二次曲面形式复杂除了态密度dos即ie中的被积函数恒等于1的计算能做到解析求解23以外目前最多只能做到半解析求解10即在某些维度上是解析的其它维度上是数值的因此积分的计算量稍大
布里渊区的积分
January 20, 2007

§5.5 布里渊区

§5.5 布里渊区本节我们举例说明二维和三维晶格的布里渊区。

一、二维正方格子正格子原胞基矢 a a a a == 2,1；倒格子原胞基矢 ab a b π=π=22,21 。

如图5.10所示，倒格子空间离原点最近的倒格点有四个，相应的倒格矢为b b b b 2,2,1,1--，它们的垂直平分线的坐标是 ak x π±= 及 a k y π±= 这些垂直平分线围成的区域就是简约布里渊区。

它也是一个正方形，其中一些特殊点和线有惯用的符号表示，中心：Γ；边界线中心：X ；角顶点：M; ΓX 线：∆; ΓM 线：∑。

离Γ点次近邻的四个倒格点相应的倒格矢是b b b b b b b b 21,21),2(1,21+--+-+它们的垂直平分线，同第一布里渊区边界围成的区域合起来成为第二布里渊区，这个区的各部分别平移一个倒格矢，可以同第一个区重合。

同理可得第三，第四，……，一系列布里渊区。

二、体心立方格子正基矢 )(21k j i a a ++-=， )(22a a +-= ， )(23a a -+= 。

可证倒基矢 )(21k j ab +π= ， )(22k i ab +π= ， )(23i j ab +π= 。

（习题：证明bcc 的倒格子是fcc 。

）倒格矢：图5.10])21()31()32[(2332211k n n j n n i n n ab n b n b n G n +++++π=++= 离原点最近的有12个倒格点，其坐标可一般地写为)21,31,32(2n n n n n n a +++π. 具体写出是)0,1,1(2a π， )0,1,1(2aπ )0,1,1(2a π， )0,1,1(2aπ )1,0,1(2a π， )1,0,1(2aπ )1,0,1(2a π， )1,0,1(2aπ )1,1,0(2a π， )1,1,0(2aπ )1,1,0(2a π， )1,1,0(2aπ 相应的倒格矢长度为 π=22),,(321an n n G 这12个倒格矢的中垂线围成菱形正面体，称为简约布里渊区，如图5.11所示，其体积正好是倒格子原胞的大小。

布里渊区PPT课件

(1)一维情况下傅立叶级数
具有一维晶格周期 a 的函数 f (x)满足 f (x) f (x a)
可以展开为傅立叶级数
2
2
f (x) f0
p1
Cp cos( a
px)
p1
Sp sin( a
px)
（2.4.6）
其中 p 是整数， f0,Cp, Sp 是傅立叶系数。
这个展开式可以写成更简洁的形式
F dVn(r )eik r solid
散射波的强度与振幅的平方 F 2 成正比，因此，
振幅 F 决定散射波的强度和衍射峰值的宽度。
（2.4.1）
（2.4.2）
第27页/共52页
2、电荷密度的傅立叶展开（Fourier series of charge density）
在理想晶体中，电荷密度和晶格一样具有平移周期性，也就是说，平移任意格矢的长度，电荷密度不变，即
它有八个正六边形和六个正方形，即十四面体。而截去的体积恰好是
1 ( 2 )3 2a
可见，这个截角以后的八面体是第一布里渊区，如图2.8所示。
第20页/共52页
图2.8 面心立方正格子的第一布里渊区
第一布里渊区种典型对称点的坐标为：
: 2 (0, 0, 0)
a
X : 2 (1, 0, 0)
a
K : 2 ( 3 , 3 , 0)
1433简单立方格子的布里渊区简单立方格子的布里渊区简单立方格子的倒格子仍然是简立方离原点最近简单立方格子的倒格子仍然是简立方离原点最近的有六个倒格点第一布里渊区就是原点和这六个近邻的有六个倒格点第一布里渊区就是原点和这六个近邻的格点连线的垂直平分面围成的立方体
一、劳厄衍射条件和布拉格定律等价

固体物理学：布里渊区(brillouin zone )

2π i j k a
2π i j k a
已知体心立方正格基矢:
a1
a
a 2 a
2
i
i
j
jk k
a3
2 a
2
i
jk
可见，面心立方的倒格子是体心立方。
同上例，先写出倒格矢，再写出离原点最近的倒格点坐标，最后做中垂面。
可以得到面心立方的布里渊区。如图所示，为截角8面体或叫14面体。
a
3
2 a
2
i
j
可见，体心立方的倒格子是面心立方。离原点最近邻的有12个倒格点，它们分别位于：
2 (1,1,0); 2 (1,1,0); 2 (1，1,0); 2 (1,1,0);
a
a
a
a
2 (1，0,1); 2 (1,0，1); 2 (1,0，1); 2 (1,0，1);
a
a
a
a
2 (0，1,1); 2 (0,1,1); 2 (0,1,1); 2 (0,1,1)
高序号布里渊区的各个分散的碎片平移一个或几个倒格矢进入简约布里渊区，形成布里渊区的简约区图。
二维正方晶格的十个布里渊区
第一区第二区第三区第四区第五区第六区第七区第八区第九区第十区
例1：简单立方格子
解:
正格子基矢：
倒格子基矢：
简单立方格子的第一布里渊区：原点和6个近邻格点的垂直平分面围成的立方体。
布里渊区（brillouin zone ）（1）布里渊区的定义
在k空间（倒格子空间）中，以任意一个倒格点为原点，做原点和其它所有倒格点连线（倒格矢）的中垂面(或中垂线)，这些中垂面(或中垂线)将倒格子空间分割成许多区域，每个区域内 E ~ k 是连续变化的, 而在这些区域的边界上能量E(k)发生突变, 这些区域称为布里渊区。

布里渊区文档

布里渊区什么是布里渊区？布里渊区（BZ）是固体物理学中一个重要的概念，其最早由法国物理学家列昂·布里渊（León Brillouin）在20世纪20年代提出。

布里渊区是借助倒晶格空间来描述晶体中电子和光子的行为的一种方法。

在晶体中，原子排列周期性地重复组成晶格结构。

而倒晶格则是指晶体中的电子和光子在晶格结构的倒数上的重复。

布里渊区即为倒晶格的第一布里渊区，或称为第一布里渊区（First Brillouin Zone，简写为BZ）。

布里渊区的特性布里渊区具有一些重要的特性：1.紧密堆积：布里渊区是以最紧密堆积的原则生成的。

最紧密堆积是指在给定的晶体结构中，原子之间的距离最接近，空隙最小。

2.对称性：布里渊区具有一定的对称性。

这是因为晶体结构在倒晶格上也应当具有一定的周期性。

3.边界：布里渊区是由一系列平面所围成的多面体。

这些边界平面的位置和形状决定了布里渊区的形状。

4.特征矢量：布里渊区内存在一系列称为特征矢量（eigenwave vectors）的矢量。

特征矢量描述了晶格中的固有振动和电子的运动行为。

布里渊区与能带结构布里渊区在研究晶体的能带结构时扮演着重要的角色。

能带结构是指在固体中，能量与波矢之间的关系。

布里渊区的形状和大小直接影响着能带结构和材料的物理特性。

晶体中的电子在能带间跃迁时，受到能量和动量守恒定律的限制。

这意味着电子只能在布里渊区内跃迁。

因此，布里渊区可以看作是晶体中允许电子跃迁的特定动量范围。

通过绘制能带图，我们可以清楚地看到布里渊区内的能带结构。

能带图可以帮助我们理解晶体的电子行为和导电性质。

应用领域布里渊区的概念在固体物理学和材料科学的研究中有着广泛的应用。

一些典型的应用领域包括：1.半导体器件设计：在半导体器件的设计和优化中，布里渊区的概念可以帮助工程师理解晶体中电子的行为，从而指导材料的选择和器件性能的调整。

2.光学材料：布里渊区的理论框架为研究光学材料的光学性质提供了基础。

布里渊区的几何定义

布里渊区的几何定义稿子一嘿，亲爱的小伙伴们！今天咱们来聊聊那个有点神秘但其实也挺有趣的“布里渊区”的几何定义。

你知道吗？布里渊区就像是晶体结构里的一个独特小天地。

想象一下，晶体中的原子们排排站，它们形成的晶格就像一个大迷宫。

而布里渊区呢，就是这个迷宫里划分出来的特别区域。

比如说，它可以看作是在倒格子空间里的一些区域。

倒格子听起来是不是有点晕？别担心，其实就是一种数学上的表示啦。

简单来讲，布里渊区就像是给晶格中的各种波动，比如电子的运动，划分了不同的“领地”。

在每个领地内，这些波动都有自己独特的性质。

比如说，在这个区域里，电子的能量可能会有特定的范围和变化规律。

这就好像每个布里渊区都是电子的一个“专属俱乐部”，只有符合条件的才能进去玩耍。

而且哦，布里渊区的形状和大小，是由晶体的结构决定的。

不同的晶体结构，就有不同形状和大小的布里渊区。

怎么样，是不是觉得布里渊区也没那么难理解啦？稿子二嗨呀，朋友们！今天咱们来探索一下布里渊区的几何定义，准备好了吗？咱们先想象一下，晶体是一个超级大的城市，原子们就是城市里的居民。

而布里渊区呢，就像是城市里划分出来的不同街区。

那它到底是怎么划分出来的呢？这就得提到倒格子啦。

倒格子就像是给这个城市画了一幅特别的地图。

在这张地图上，布里渊区就是那些有特殊意义的区域。

比如说，它们能告诉我们晶体中电子的运动情况。

每个布里渊区都有自己的边界，就像街区有自己的围墙一样。

这些边界可不是随便定的，是根据晶体的对称性和周期性来的。

而且哦，布里渊区的大小和形状能反映出晶体的很多特性。

如果布里渊区比较大，可能说明晶体中电子的活动范围比较广；要是形状比较特别，那也暗示着晶体有独特的性质。

再想想，当我们研究晶体的各种物理性质时，布里渊区就像是一把神奇的钥匙，能帮我们打开很多秘密的大门。

是不是觉得布里渊区挺有意思的？其实只要多想想，这些看似复杂的概念也能变得很简单有趣哟！。

布里渊区

的Wigner-Seitz原胞给出。

金刚石结构的Si、Ge和闪锌矿结构的Ⅲ-Ⅴ族半导体等, 都具有面心立方Bravais格子, 因此都具有体心立方的倒格子, 从而也都具有相同形状的第一Brilouin区, 为截角八面体(即是由6个正方形和8个正六边形构成的14面体)。

3布里渊区的特殊k点采样问题研究介绍在各种周期性边界条件的第一原理计算方法中，需要涉及到在布里渊区的积分问题，例如总能、电荷密度分布，以及金属体系中费米面的确定等等。

如果采用普通的在布里渊区内均匀选取k点的方法，那么为了得到精确的结果点的密度必须很大，从而导致非常大的计算量。

这使得计算的效率非常低下。

因此，需要寻找一种高效的积分方法，可以通过较少的点运算取得较高的精度。

而这些k点被称之为“平均值点”（Baldereschi）或者“特殊点”（Chadi, Cohen）。

[1]基本思想Chadi和Cohen最早提出了这种特殊点的数学基础[1]。

考虑一个光滑函数，我们可以将其展为傅立叶级数：假设另有一个拥有体系全部对称性（对称性用对称群表示）的函数，满足条件，则我们可以将用展开如下：其中是对称群的阶数。

设，将上式的求和顺序重新组合可以得到其中是距离原点第近邻的球半径，按升序排列，且。

需要注意的是限制条件具有球对称性，也即高于的对称性，所以满足限制条件的格点集合并不一定都是等价的——或说可以通过中的操作联系起来的——格点。

方程(3)中的函数满足下列条件：上式中是倒格矢，是满足条件的格点数。

五个方程分别表明函数在第一布里渊区内成奇函数、具有正交性、周期性、体系对称性和完备性。

对于特殊点法而言，前两条更为重要。

注意到上面公式中的求和从1开始，因此需要对的情况进行单独定义。

我们定义，则函数的平均值为：那么该如何得到呢？注意方程(3)，如果存在这样的特殊点，使其满足：>那么立刻可以得到，这样的点被称为“平均值点”。

但是普遍的讲，满足上述条件的点并不存在。

简约布里渊区定义

简约布里渊区定义
在固体物理学中，简约布里渊区是指倒易格子中第一布里渊区对应的波矢空间区域。

这个区域内的波矢对应于固体中可能的电子态。

简约布里渊区通常用于描述周期性结构中电子的运动行为，以及电子在固体中的能带结构。

简约布里渊区的定义是，在倒易格子中，将第一布里渊区对应的波矢空间区域进行简化，得到的一个抽象概念。

这个区域的波矢表示了固体中电子可能的运动状态，而简约布里渊区正是由这些波矢构成的。

它常被用于研究周期性结构中电子的量子行为，以及电子在固体中的能带结构。

简约布里渊区的定义是指倒易格子中第一布里渊区对应的波矢空间区域。

这个区域内的波矢对应于固体中可能的电子态。

在物理学中，布里渊区是一个重要的概念，它描述了电子在固体晶格中的运动行为和能量状态。

通过研究简约布里渊区，科学家们可以更好地理解固体晶格中的电子结构和物理性质，为材料科学、电子工程等领域的发展提供理论支持。

简约布里渊区是固体物理学中的一个重要概念，它描述了电子在固体晶格中的运动行为和能量状态。

通过研究简约布里渊区，科学家们可以更好地理解固体晶格中的电子结构和物理性质，为材料科学、电子工程等领域的发展提供理论支持。

简约布里渊区的定义是，在倒易格子中，将第一布里渊区对应的波矢空间区域进行简化，得到的一个抽象概念。

这个区域的波矢表示了固体中电子可能的运动状态，而简约布里渊区正是由这些波矢构成的。

它常被用于研究周期性结构中电子的量子行为，以及电子在固体中的能带结构。

1。

I布里渊区简正模和格波

但他们的研究当时被忽视了，因为同年发表的更为简单的Debye热容
理论（弹性波近似）已经可以很好的说明当时的实验结果了，但后来
更为精确的测量却表明了Debye模型不足，所以1935年Blakman才重新
利用Born和Von-Karman近似讨论晶格振动，发展成现在的晶格动力学
理论。后来黄昆先生在晶格振动研究上成就突出，特别是 1954 年和
了“黄方程”，提出了声子极化激元的概念，并与李爱扶（A.Rhys，妻子）建立了多声子跃迁理论。
1947-1952年，与玻恩教授合著《晶格动力学》一书（英国牛津出版社， 1954年）。（2006年中文版）
黄昆对晶格动力学和声子物理学的发展做出了卓越的贡献。他的名字与多声子跃迁理论、X光漫散射理论、晶格振动长波唯象方程、二维体系光学声子模联系在一起。他是“极化激元”概念的最早阐述者。
b1
2
a
i和b2

2
a
j
作原点0至其它倒格点连线的中垂线，它们将二维倒格子平面分割成许多区域
二维正方格子的第一、二、三布里渊区
③ ①②
O
简单立方（sc）
第一布里渊区边界是下面六个倒格矢的中点，并与之正交的平面：
±12��=±
��
��റ��;
Born共同写作的《晶格动力学》一书已成为该领域公认的权威著作。
我国科学家黄昆院士在晶格振动理论上做出了重要贡献。
黄昆院士简介: （摘录） 1945-1947年，在英国布列斯托（Bristol）大学物理系学习，获哲学博士
学位；发表《稀固溶体的X光漫散射》论文，理论上预言“黄散射”。 1948-1951年，任英国利物浦大学理论物理系博士后研究员，这期间建立

布里渊区

第二到第九Brillou形状，不管被分成多少部分，对原点都是对称的
六方点阵布里渊区图
见黄昆书图4－24 （p194)
Kittel
（p28)
黄昆书图4－12（p179)
见黄昆书图4－12 （p179)
体心立方的Wigner-Seitz原胞及第一布里渊区
面心立方的Wigner-Seitz原胞及第一布里渊区
Kittel （p29）,黄昆书图4－13（p179)
见黄昆书图4－13 （p179)
倒易点阵和14种晶体点阵是一一对应的，因此也只有14种类型的倒易点阵和14种不同形状的第一布里渊区。第一布里渊区的形状只与晶体的布拉维点阵的几何性质有关，与晶体的化学成分、晶胞中的原子数目无关。布里渊区是一个对称性原胞，它保留了相应的布拉菲点阵的点群对称性。因此第一布里渊区里依然可以划分为几个完全等同的区域。对一种晶体来说，它的所有布里渊区都有同样大小的体积，利用平移对称性可以找出第一布里渊区和所有较高的布里渊区之间的全等性。
五. 布里渊区：第一布里渊区的确定：取法和正点阵中Wigner-Seitz 原胞取法相同。它是倒易点阵的原胞。
Léon Brilliouin
（1889-1969）
布里渊区定义：在倒易点阵中，以某一格点为坐标原点，做所有倒格矢的垂直平分面，倒易空间被这些平面分成许多包围原点的多面体区域，这些区域称作布里渊区，其中最靠近原点的平面所围成的区域称作第一布里渊区，第一布里渊区界面
与次远垂直平分面所围成的区域称作第二布里渊区，依次类
推得到二维正方格子的布里渊区图见下页。由于布里渊区界面是某倒格矢 G 的垂直平分面，如果用 k 表示从原点出发、端点落在布里渊区界面上的倒易空间矢量，它必然满足方程：

布里渊区求和及模式密度

S ∑M exp iq l
l
k1

M，因此
N M
∑M f
k1
qk
可以作为∑ f
BZ
q
NA0的
一个较好的近似。
如何选取有这种良好性质的q k？以一维晶体为例，如果M 2m 1是奇数，则
qk
2∗k Ma
，k

−m, … , m这M个qk使得对所有的非M整数倍的
Sna

∑m expi
BZ
难点：除非知道f q 的解析表达式，否则不可能严格算出A0
解决方法：找M适当的个q k，使得对尽可能多的不太大的 l ≠ 0都有
∑M exp iq k l 0，于是
k1
∑M
f qk
k1
∑ A l ∑M exp iq l
l
k1
∑ MA0
AlSl
l 较大
0，
由于随着 l 的增大傅立叶系数A l 会比较快地趋于零，
布里渊区求和、模式密度在固体物理中经常遇到需要对所有的晶体运动模式的某个物理量求和，由于晶体的微观平移对称性，晶体的基本运动模式都可以用布里渊区BZ内均匀分布的波矢量
q标记，相应的物理量都可以写成f q 形式，且f q G f q 。
如何求这些物理量∑ f q f q q d3 q ？
ቤተ መጻሕፍቲ ባይዱ
≈
N
Mi M
N是晶体原胞数。优点：无需知道频谱全体 q 即可较精确地计算近似的模式密度g
缺点：需要计算大量的数值点才能得到好的结果。
方法二：定义模式密度的主要目的是为了计算∑ f q ，应该回归本源，直接从
BZ
求和式本身着手。由于f q 是q的周期函数，因此可以把它写成傅立叶级数

布里渊区与倒格子原胞

第16 卷第1 期1 9 9 7 年 1 月大学物理COL L E G E PH YS I C SV o l.16 N o. 1J an. 1997 布里渊区与倒格子原胞进1)李光惠2)李(1) 东京大学机械工学系, 东京, 113, 日本; 2) 荆州师范专科学校物理系, 湖北荆沙434104) α摘要用简单数学方法就体心立方晶格和面心立方晶格证明了三维情况下布里渊区体积等于倒格子原胞体积. 同时提出证明高阶布里渊区与简约布里渊区体积相等的一种简捷方法.关键词布里渊区; 倒格子原胞; 维格纳- 赛兹原胞分类号O 481. 1a3×a1(2)b2 =1 引言 a r ()2 a3×a1在正空间中, 正格子原胞体积等于维格纳—赛兹原胞体积; 在倒空间中, 倒格子原胞体积等于简约布里渊区体积, 这已被公认. N. W .A sh c r o f t仅就二维布拉菲格子中的一种特例用割补平移法做了证明1 . 但对于三维倒格子, 由于布里渊区形状比较复杂, 迄今未见定量证明. 本文就体心立方和面心立方格子两种特例用简单数学方法证明了布里渊区体积等于倒格子原胞体积, 这种方法对于任意布拉菲格子都适用. 本文还指出了证明高阶布里渊区与简约布里渊区体积相等的一种方法.a1×a2b3 =a3r (a1×a2)则以b1、b2、b3 为边矢量的平行六面体是倒格子中最小的周期性重复单元, 称之为倒格子原胞,其体积为8 = b1 r (b2 ×b3 )(3)不难证明, 正格子原胞体积和倒格子原胞体积2互为倒数,8 = 1ƒV0(4)虽然, 正格其矢a1、a2、a3 的选取不是唯一的, 但是对于确定的晶格, 其倒格子是唯一确定的. 若a1、a 2、a 3 选定, 则相应的b1、b2、b3 也是确定的. 然而, 对于上述的原胞, 只描述了最小周期性一个侧面, 为了使选取的单元既有最小周期性, 又参反映出对称性, 则有时在正格子中选某一格点为原点, 作最近邻或最近邻和次近邻2 正格子原胞与倒格子原胞固体物理中, 若正格基矢为a 1、a 2、a 3 , 则以a1、a2、a3 , 为边矢量的平行六面体是晶格中最小的周期性重复单元, 称之为原胞, 其体积为V 0 = a1r (a2×a3)(1)正格矢的垂直平分面围成的区域作为原胞,这定义倒格基矢b1、b2、b3 , 它们与a1、a 2、a 3 的关系为- 赛兹原胞1 .就是所谓的维格纳相应地,在倒格子中也可以作出所有倒格a2×a3b1 = 矢的中垂面围成一些区域, 这就是由方程3a r (a1 2 ×a )3K h r (k + 1K h ) = 0(5) 2收稿日期: 1996- 05- 28 α所描述的各个面所围成的区域, 即布里渊区. 式中, k 是波矢, K h 是倒格矢.下面我们将分别以体心方立晶格和面心立方晶格为倒, 证明布里渊区体积等于倒格子原胞体积.C =1(100)aD =1(111) (8)2a由式 (8) 可得3 体心立方晶格(9)A C =2 ƒaB D = 1ƒa所以菱形 A B CD 的面积不难证明, 对于体心立方晶格, 正格子原胞体积为a 3ƒ2 V 0 = a 1 r (a 2 × a3 ) = 其倒格子原胞体积为(6) 1S =A C ×B D = (10)2不难求出, 以菱形 A B CD 为底、顶点为 # 角锥之高的四 2ƒa 38 = b 1 r (b 2 × b 3 ) = (7) 式中, a 是体心立方晶格正格子中典型立方单元的边长.众所周知, 体心立方晶格的倒格子是面心立方晶格, 由最近邻倒格矢中垂面围成的区域是菱形十二面体, 即第一布里渊区, 如图 1 所示.1 2 2 h =2 r= (11)42aa四角锥 #A B CD 的体积8 1 = S h ƒ3 = 1ƒ6a 3所以菱形十二面体的体积为8 ’ = 128 1 = 2ƒa 3(12) (13)比较式 (13) 和 ( 7) , 可以得出, 对于体心立方晶格第一布里渊区体积与倒格子原胞体积相等.4 面心立方晶格对于面心立方格子其倒格子是体心立方格子. 正格子原胞体积为V 0 = a 1 r (a 2 × a 3 ) = a 3ƒ4则倒格子原胞体积为8 = b 1 r (b 2 × b 3 ) = 4ƒa 3式中, a 是正格子中典型立方单元边长. (14) 图 1 体心立方晶格第一布里渊区(15)由式下面将证明此菱形十二面体的体积与上述的以 b 1、b 2、b 3 为边矢量的平行六面体即倒格子原胞的体积相等.因为正格子中典型立方单元边长为 a , 则倒格子中典型立方单元边长 E F = 2ƒa . 不难看出, 此菱形十二面体是由面积相等的十二个菱形面为底、顶点均在 # 点的十二个四角锥组成的. 我们先求底面为菱形 A B CD 的四角锥的体积. 显然, ( 5) 所决定的第一布里渊区是由近邻和次近邻倒格矢中垂面围成的区域, 即图 2 所示的截角A 、B 、C 、D 四个点的坐标分别为A =1(001)a- B =1(1 1 1) 2a图 2 面心立方晶格第一布里渊区八面体. 由于正格子中典型立方单元边长为a,不难求出其倒格子中典型立方单元边长M N = 2ƒa( 图2). 欲求此截角八面体体积, 可以把它看成是由正方形A B CD 为底, 顶点在# 的六个因此, 图2 所示的截角八面体体积为8 ’ = 68 1 + 88 2 = 4ƒa3(21)比较式(15) 和(21) , 可以看出, 对于面心立方格子第一布里渊区体积与倒格子原胞体积也相等.体积相等的四角锥与以正六边形A B E F G H为底、顶点也在# 点的八个体积相等的六角锥构成的. 由图2 可以看出, A 、B 两点的坐标分别为5 结语用类似的方法也可证明其他类型的布拉菲格子中第一布里渊区体积与倒格子原胞体积相等. 对于高阶布里渊区, 也可以用此方法先求出第n 布里渊区所属的外边界面所围的总的体A = 1a (012)2(16)B = 1a (102) 2所以正方形A B CD 的边长A B =积, 然后再扣除第n- 1 区所属的外边界面所围2 ƒ2a,面积(17)的体积, 这样可以得出第n 布里渊区的体积. 同样可以证明, 对于确定的布拉菲格子各个布里渊区的体积相等, 它们均等于其倒格子原胞体积. 由此可以看出, 尽管用简单数学方法仅就体心立方和面心立方两种晶格特例作了证明, 但这种处理方法对任意类型的布拉菲格子都是适用的.(A B ) 2 = 1ƒ2a2S 1 =显然, 以正方形A B CD 为底、#锥之体积为为顶点的四角8 1 = 1 S 1 h1 = 1 1 1 1××=3 2a2 a 6a33(18)而正六边形A B E F G H的面积S 2 = 6 ×1 (A B ) 2 sin 60. =3 3 6参考文献(19)4a221 A sh c r o f t N e i l W , M e r m in N D av i d. So lid S t a t e P h y s ic s.H o lt R ineh a r t and W in sto n, 1976. 72, 75刘友之, 聂向富, 蒋生蕊. 固体物理学习题指导. 北京: 高等教育出版社, 1988. 56～57黄昆原著, 韩汝琦改编. 固体物理学. 北京: 高等教育出版社, 1988. 175所以, 以正六边形A B E F G H 为底、# 为顶点的六角锥体积为28 2 = 1 S 2 h2= 1 ×3 3 3 3×=4a28a3(20)3 3 2a 3BR I LLO U IN Z O NE A N D REC IPROCAL L A T T I CE PR I M IT IVE CELLL i J in1)L i Gu a n g h u i2)(1) M ech a n ica l E n g inee r i ng C lu ste r, U n ive r s ity o f T o k y o , J ap a n, 113;2) D ep a r t m en t o f P h y s ic s, J ingzho u T each e r’s Co llege, J ing sh a, H ube i, 434104, C h ina)A b stra c t It is p ro v ed th a t th e vo lum e o fB r i llo u in zo n e an d th a t o f th e rec i p ro c a l la t t i ce p r i m it i ve ce l l a re equ a l fo r b c c la t t i ce an d fcc la t t i ce in th ree d i m en si o n s b y a si m p le m a th e m a t i ca l m e t ho d. A co n c i se m e t ho d is g iven to p ro v e th a t th e vo lum e o f th e h igh -o rde r B r i llo u in zo n e an d th a t o f th e redu c ed B r i llo u in zo n e a re equ a l.Key word s B r i llo u in zo n e; rec i p ro c a l la t t i ce p r i m it i ve ce l l; W ign e r- Se i tz p r i m it i ve ce l l。

布里渊区固体的能带理论中2

晶胞：构成晶格的最基本的几何单元称为晶胞（Unit Cell），其形状、大小与空间格子的平行六面体单位相同，保留了整个晶格的所有特征。

晶胞是能完整反映晶体内部原子或离子在三维空间分布之化学-结构特征的平行六面体最小单元。

其中既能够保持晶体结构的对称性而体积又最基本特称“单位晶胞”，但亦常简称晶胞。

原胞：在晶格取一个格点为顶点，以三个不共面的方向上的周期为边长形成的平行六面体作为重复单元，这个平行六面体沿三个不同的方向进行周期性平移，就可以充满整个晶格形成晶体，这个平行六面体即为原胞。

晶面：在晶体学中，通过晶体中原子中心的平面叫作晶面（Faces)。

晶系：倒格失：晶体对称性：布里渊区固体的能带理论中，各种电子态按照它们的波矢分类。

在波矢空间中取某一倒易阵点为原点，作所有倒易点阵矢量的垂直平分面，这些面波矢空间划分为一系列的区域：其中最靠近原点的一组面所围的闭合区称为第一布里渊区；在第一布里渊区之外，由于一组平面所包围的波矢区叫第二布里渊区；依次类推可得第三、四、…等布里渊区。

各布里渊区体积相等，都等于倒易点阵的元胞体积。

周期结构中的一切波在布里渊区界面上产生布拉格反射,对于电子德布罗意波,这一反射可能使电子能量在布里渊区界面上（即倒易点阵矢量的中垂面）产生不连续变化。

根据这一特点,1930年L.-N.布里渊首先提出用倒易点阵矢量的中垂面来划分波矢空间的区域，从此被称为布里渊区。

绝热近似它基于这样一个事实：电子与核的质量相差极大，当核的分布发生微小变化时，电子能够迅速调整其运动状态以适应新的核势场，而核对电子在其轨道上的迅速变化却不敏感。

这种近似是量子化学和凝聚态物理学中的一种常用方法，用于对原子核和电子的运动进行退耦合。

布洛赫定理共价键理论：分子轨道理论杂化轨道理论布洛赫定理：相变理论：密度泛函理论：密度泛函理论是一种研究多电子体系电子结构的量子力学方法。

密度泛函理论在物理和化学上都有广泛的应用，特别是用来研究分子和凝聚态的性质，是凝聚态物理和计算化学领域最常用的方法之一。