定量资料统计描述PPT
合集下载
第二章--定量资料的统计描述

定量资料的统计描述
分类变量(名义变量 分类变量 名义变量) 名义变量 定性变量 有序变量(等级变量 有序变量 等级变量) 等级变量
变量
离散型变量 定量变量 连续型变量 统计描述: 统计描述:用统计图表或计算统计指标的方法表达一个特定群 这个群体可以是总体也可以是样本)的某种现象或特征, 体(这个群体可以是总体也可以是样本)的某种现象或特征, 称为统计描述。 称为统计描述。 统计描述可以使人们对资料有一个大致的了解, 统计描述可以使人们对资料有一个大致的了解,为进一步的统 计分析打下基础。 计分析打下基础。
图2-1 某地96名妇女产前检查次数频率分布 某地96名妇女产前检查次数频率分布 96
30 25 20
频率(%)
15 10 5 0 0 1 2 3 4 产前检查次数 5 >5
横坐标为产前检查 横坐标为产前检查 频率, 次数,纵坐标为频率 次数,纵坐标为频率, 即产前检查k次的妇 即产前检查 次的妇 女在被统计妇女中所 占的比例(%) 占的比例( ) 从表2-1和图 和图2-1可 从表 和图 可 以看出, 以看出,产前检查次 数为4次或 次或5次的孕妇 数为 次或 次的孕妇 数目最多, 数目最多,不检查或 检查次数很多的孕妇 不多, 不多,产前检查很多 次的孕妇也不多。 次的孕妇也不多。
与表2-2相比, 与表 相比,直方图可以更直观 相比 地表达出血清铁数据在各组段的分 布情况。 布情况。
三、频率分布表(图)的用途 频率分布表( (一)揭示资料的分布类型 1、对称分布 集中位置位于中央,左右两侧频数对称。 集中位置位于中央,左右两侧频数对称。
12 10 频 率 密度 (%) 8 6 4 2 0 7 9 11 13 15 17 19 血清铁 21 23 25 27 29
分类变量(名义变量 分类变量 名义变量) 名义变量 定性变量 有序变量(等级变量 有序变量 等级变量) 等级变量
变量
离散型变量 定量变量 连续型变量 统计描述: 统计描述:用统计图表或计算统计指标的方法表达一个特定群 这个群体可以是总体也可以是样本)的某种现象或特征, 体(这个群体可以是总体也可以是样本)的某种现象或特征, 称为统计描述。 称为统计描述。 统计描述可以使人们对资料有一个大致的了解, 统计描述可以使人们对资料有一个大致的了解,为进一步的统 计分析打下基础。 计分析打下基础。
图2-1 某地96名妇女产前检查次数频率分布 某地96名妇女产前检查次数频率分布 96
30 25 20
频率(%)
15 10 5 0 0 1 2 3 4 产前检查次数 5 >5
横坐标为产前检查 横坐标为产前检查 频率, 次数,纵坐标为频率 次数,纵坐标为频率, 即产前检查k次的妇 即产前检查 次的妇 女在被统计妇女中所 占的比例(%) 占的比例( ) 从表2-1和图 和图2-1可 从表 和图 可 以看出, 以看出,产前检查次 数为4次或 次或5次的孕妇 数为 次或 次的孕妇 数目最多, 数目最多,不检查或 检查次数很多的孕妇 不多, 不多,产前检查很多 次的孕妇也不多。 次的孕妇也不多。
与表2-2相比, 与表 相比,直方图可以更直观 相比 地表达出血清铁数据在各组段的分 布情况。 布情况。
三、频率分布表(图)的用途 频率分布表( (一)揭示资料的分布类型 1、对称分布 集中位置位于中央,左右两侧频数对称。 集中位置位于中央,左右两侧频数对称。
12 10 频 率 密度 (%) 8 6 4 2 0 7 9 11 13 15 17 19 血清铁 21 23 25 27 29
医学统计学课件第二章 定量资料的统计描述

第四节
正态分布
一、正态分布的概念和特征
正态分布(normal distribution ):也 称高斯分布,是医学和生物学最常见的连续性 分布。如身高、体重、红细胞数、血红蛋白等。
图2-1 120名12岁健康男孩身高的频数分布
图2-2 频数分布逐渐接近正态分布示意
㈠ 正态分布的函数和图形
第二章 定量资料的统计描述
目 录
第一节 频数分布表
第二节 集中趋势的描述 第三节 离散趋势的描述
第四节 正态分布
学习要求
1.掌握频数分布表的编制步骤和方法 2.熟悉频数分布表的用途 3.掌握集中趋势、离散趋势的概念,适用条件和计
算方法 4.掌握正态分布的概念,意义和特点;正态曲线下 面积的分布规律
159.99 33.46 / 7 S . 0.089 7 1
2
加权法-标准差计算实例:
例
对表2-4资料用加x=17168,∑fx2 =2460040, 代入公式
2460040 17168 / 120 S 5.70(cm) 120 1
算术均数 (arithmetic mean): 简称均数。
适用条件:对称分布或近似对称分布的资料。
以希腊字母μ---总体均数(population mean)
以英文字母 ---样本均数(sample mean)
计算方法
1. 直接法:用于观察值个数不多时
X X n
2.加权法(weighting method):用于变量 值个数较多时
适用条件:对于变量值呈倍数关系或呈对 数正态分布(正偏态分布),如抗体效价及抗体 滴度,某些传染病的潜伏期,细菌计数等。 计算公式:有直接法和加权法。
定量的统计描述分析课件

正态QQ图:图中的点代表数据,直线代表理想的正态数据,如果各个点都 落在了直线的周围并且在平均值的部分点的分布比较均匀,这就说明是符 合正态分布的,显然这组年龄数据不符合正态分布
总结
频数分析(Frequencies ):频数分布表、条图和直方图以及 集中趋势和离散趋势的各种统计量。 描述统计(Descriptives ):描述近似正态分布定量变量的集 中趋势和离散趋势的各种统计量,对变量做标准化转换(Z 转换)。 探索分析(Explore ):未知分布类型数据的统计描述,对 数据的分布形态进行检验,功能强大。
End Thanks
中位数
各种分布类型的资料,特别是偏峰分布资料; 分布一端或两端无确切数值的资料; 分布类型不明
百分位数 各种分布类型的资料
离散趋势
指标
应用条件
极差
对资料类型没有要求
四分位数 间距
方差与标 准差
变异系数
各种分布类型的资料,特别是偏峰分布资料
对称分布,特别是正态或近似正态分布 观察指标单位不同时变异程度的比较; 均数相差较大时变异程度的比较
重点掌握 1.频数分布图和频数分布表的制作 2.定量资料统计指标的计算
离散Байду номын сангаас定量资料
下面我们打开SPSS软件自带的数据demo.sav,找到reside, 这是一组同居人数的资料,我们将结合这组数据学习离散型 定量资料频数分布表和频数分布图的绘制。
变量视图
输出结果
输出结果
连续型定量资料
输出结果
探索分析(Explore )
探索分析(Explore )主要可以分为两个部分 1.未知分布类型数据的统计描述 2.对数据的分布形态进行检验
探索分析(Explore )
总结
频数分析(Frequencies ):频数分布表、条图和直方图以及 集中趋势和离散趋势的各种统计量。 描述统计(Descriptives ):描述近似正态分布定量变量的集 中趋势和离散趋势的各种统计量,对变量做标准化转换(Z 转换)。 探索分析(Explore ):未知分布类型数据的统计描述,对 数据的分布形态进行检验,功能强大。
End Thanks
中位数
各种分布类型的资料,特别是偏峰分布资料; 分布一端或两端无确切数值的资料; 分布类型不明
百分位数 各种分布类型的资料
离散趋势
指标
应用条件
极差
对资料类型没有要求
四分位数 间距
方差与标 准差
变异系数
各种分布类型的资料,特别是偏峰分布资料
对称分布,特别是正态或近似正态分布 观察指标单位不同时变异程度的比较; 均数相差较大时变异程度的比较
重点掌握 1.频数分布图和频数分布表的制作 2.定量资料统计指标的计算
离散Байду номын сангаас定量资料
下面我们打开SPSS软件自带的数据demo.sav,找到reside, 这是一组同居人数的资料,我们将结合这组数据学习离散型 定量资料频数分布表和频数分布图的绘制。
变量视图
输出结果
输出结果
连续型定量资料
输出结果
探索分析(Explore )
探索分析(Explore )主要可以分为两个部分 1.未知分布类型数据的统计描述 2.对数据的分布形态进行检验
探索分析(Explore )
定性资料的统计描述幻灯片PPT

Standardization rate
1.标准化直接法的计算方法
P ' N 1 P 1N 2P 2N kP k N iP i
N
N
式中P’为标准化率,N1 , N2 ,…Nk为某一影响因素 (如病型、年龄等)标准构成的每层例数,P1 , P2 ,…Pk为原始数据中各层的率,N为标准构成的总
例数。上式也可写成:
Odds ratio
四、标准化率
标准化率( standardization rate ):比较两个不同 人群的患病率、发病率、死亡率等资料时,为消 除其内部构成(如年龄、性别、工龄、病程长短 、病情轻重等)对率的影响,可以使用标准化率 。
Standardization rate
例4-5 试对下表资料计算甲乙两个医院的标准化
定性资料的统计描述幻灯片PPT
本PPT课件仅供大家学习使用 请学习完及时删除处理 谢谢!
第四章 定性资料的统计描述
计量资料(定量资料) 统计资料类型:
计数资料(定性资料)
计数资料:先将研究对象按其性质或特征分类,再 分别计数每一类的例数。
描述定性资料的数据特征,通常需要计算相对数。 根据不同的研究目的,常用率、构成比、相对比等 指标来进行统计描述。
需要注意的是,分母中所规定的平均人口是指可 能会发生该病的人群。
Prevalence rate
2.患病率: 也称现患率,表示某一时点某人群人口 中患某病的频率,通常用来表示病程较长的慢性 病的发生或流行情况,其计算公式为
某 病 患 病 率 某 该 地 地 某 同 时 期 点 内 某 平 病 均 患 人 病 口 例 数 数 比 例 基 数
三、相对比
相对比( relative ratio ):相对比是A、B两个有关 联指标值之比,用以描述两者的对比水平,说明 A是B的若干倍或百分之几,通常用倍数或分数表 示。这两个指标可以是性质相同,如不同时期的 患病人数;也可以是性质不同,如体重与身高的 平方之比(体重指数,BMI)。其计算公式为
定量资料的统计描述

定量资料的统计描述
LOREM IPSUM DOLOR
主要内容
频数分布 集中趋势 离散趋势
被平均
中国人公共假期每年已有115天; 中国全国家庭平均住房面积116.4㎡; 北京平均月薪9227元; 中国男性平均身高174.2厘米; 中国人平均生育1.18个孩子; 中国家庭资产平均为121.69万元,城市家庭平均为
( kg )原始 数据如下, 试编制频数
表。
25.2 34.9 34.3 38.1 41.3 27.8 33.8 37.7 28.4 33.5 47.3 34.8 30.5 36.2 51.0 38.0 43.8 40.9 37.5 36.6 33.4 47.4 36.4 41.4 36.5 42.5 33.7 29.3 39.6 37.5 39.6 33.2 32.1 29.9 43.7 33.8 35.1 37.8 32.4 38.5 28.2 36.5 23.4 35.8 34.1 27.6 42.6 23.1 37.1 44.0 35.6 44.5 46.5 35.0 31.8 36.4 36.2 47.9 38.7 20.5 37.1 29.2 38.2 41.1 36.2 43.5 32.8 36.3 31.8 30.6 38.5 39.6 28.7 33.7 35.1 42.9 20.1 35.4 26.5 42.0 39.6 38.7 35.4 51.2 31.4 34.1 25.3 29.6 38.2 43.7 33.8 24.5 29.2 45.9 32.5 23.5 36.8 27.2 34.0 34.7 44.4 41.2 35.3 42.6 34.1 30.0 31.4 40.8 27.3 48.6 35.8 29.7 45.6 41.8 33.0 28.3 33.3 35.1 40.6 38.2 37.6 25.5 37.3 37.5 41.5 38.4 44.2 43.2 31.5 40.2 34.5 37.4
LOREM IPSUM DOLOR
主要内容
频数分布 集中趋势 离散趋势
被平均
中国人公共假期每年已有115天; 中国全国家庭平均住房面积116.4㎡; 北京平均月薪9227元; 中国男性平均身高174.2厘米; 中国人平均生育1.18个孩子; 中国家庭资产平均为121.69万元,城市家庭平均为
( kg )原始 数据如下, 试编制频数
表。
25.2 34.9 34.3 38.1 41.3 27.8 33.8 37.7 28.4 33.5 47.3 34.8 30.5 36.2 51.0 38.0 43.8 40.9 37.5 36.6 33.4 47.4 36.4 41.4 36.5 42.5 33.7 29.3 39.6 37.5 39.6 33.2 32.1 29.9 43.7 33.8 35.1 37.8 32.4 38.5 28.2 36.5 23.4 35.8 34.1 27.6 42.6 23.1 37.1 44.0 35.6 44.5 46.5 35.0 31.8 36.4 36.2 47.9 38.7 20.5 37.1 29.2 38.2 41.1 36.2 43.5 32.8 36.3 31.8 30.6 38.5 39.6 28.7 33.7 35.1 42.9 20.1 35.4 26.5 42.0 39.6 38.7 35.4 51.2 31.4 34.1 25.3 29.6 38.2 43.7 33.8 24.5 29.2 45.9 32.5 23.5 36.8 27.2 34.0 34.7 44.4 41.2 35.3 42.6 34.1 30.0 31.4 40.8 27.3 48.6 35.8 29.7 45.6 41.8 33.0 28.3 33.3 35.1 40.6 38.2 37.6 25.5 37.3 37.5 41.5 38.4 44.2 43.2 31.5 40.2 34.5 37.4
医学统计学课件:02_统计描述(定量定性)

中位数(median,M)
将一组观察值从小到大按顺序排列,居于中心位置 的数值。在全部观察值中有半数的值比M大,另有半数 的值比M小。 适用于当大部分观测值比较集中,少数观测值偏向 一侧时;或资料分布情况不清楚时;或数据的最大值
(最小值)无准确测量数据时。如传染病的潜伏期。任
何分布的定量数据均可用中位数描述其分布的集中趋势, 使用范围广。
2003年4月22日全国SARS发病人数频数表
发病地区 北京 山西 广东 河北 内蒙 天津 广西 其他省市 频数 105 16 14 6 3 2 1 0 频率/% 71.4 10.9 9.5 4.1 2.0 1.4 0.7 0.0 累积频数 105 121 135 141 144 146 14移,向右侧拖尾
负偏态(左偏态)
峰向右偏移,向左侧拖尾
集中趋势的特征值
—— 平均水平的度量
算术均数(arithmetic mean,M)
适用于正态分布和近似正态分布的资
料。
总体均数用µ表示;样本均数用 x 表示。
直接计算法
将所有观察值直接相加再除以观察值的个数。
f i lg X i f1 lg X 1 f 2 lg X 2 f n lg X n 1 lg G lg f f i i
1
频数表资料的几何均数
抗体滴度 ⑴
人数,f ⑵
滴度倒数,X ⑶
lgX ⑷
f· lgX ⑸
累积频率/%
71.4 82.3 91.8 95.9 98.0 99.3 100.0 100.0
合计
147
100.0
某药物疗效的频数表
治疗效果 治愈 频数 65 频率/% 43.3 累积频数 65
定量资料统计描述和正态分布ppt课件

单侧
只有 只有 下限 上限 P5 P95
双侧 范围
P2.5-P97.5
99
P1 P99
P0.5-P99.5
四、变异系数 变异系数(coefficient of variation,简 记 为 CV), 又 称 为 离 散 系 数 (coefficient of dispersion)
计算方法: CV S 100%
X
应用:
a.比较度量衡单位不同的多组资料 的变异程度。
b. 比较均数相差悬殊的多组 资料 的 变异程度(如舒张压和收缩压 ; 儿 童身高与成人身高) 。
二、几何均数(geometric mean) 计算方法 1.直接法:适用于样本量较小的计
量资料。
或
2.加权法:适用于样本量较大的计量 资料,如频数表资料。
几何均数的应用注意事项
1)常用于等比资料或对数正态分 布资料,如血清抗体滴度、细菌计 数等。
2)观察值中若有0或负值,则不宜 直接使用几何均数。
位数
一、算术均数
算术均数简称均数(mean),描述一组 同质资料的平均水平。
总体均数:
样本均数:
计算方法 1. 直接计算法:适用于样本量较小
的计量资料。
2.频数表法:适用于样本量较大的计量 资料。
均数的应用: 均数适用于描述单峰对称分布,特
别是正态或近似正态分布资料的集中 趋势。
极端值(outlier)
中位数应用:
1.中位数可用于各种分布的资料。
2.中位数不受极端值的影响,因此, 实际工作中主要用于:
(1)偏态分布或不明确分布资 料
(2)端点无确切值的资料
(3)有特大或特小值的资料
第三节 离散趋势的描述
卫生统计学课件 第二章 计量资料的统计描述(共33张PPT)

11111,11111,11111 中位数是50%位的数值,其为百分位数的特殊形式。
●计算公式: 13cm之间的占该地7岁男童的百分 比。
∑f · X=1638
双侧界值:P 2.5 ~ P 97..5 定义:又称参考值范围,是指特定健康人群的解剖、生理、生化等各种数据的波动范围。
特征: ∑(X- X)=0 估计误差之和为0。
估计的方法: 1、正态分布法
2、百分位数法
28
1.正态分布法
应用条件:正态分布或近似正态分布资料 ●计算 (双侧) 95% 正常值(医学参考值)范围公式:
(x1.96 · S,x1.96 · S )
即(x±1.96 · S ) 例:
1.96 × 3.79 )
即(156.41 cm , 171.27 cm )
1998年100名18岁健康女大学生身高的频数分布
数。 (3) 估计该地7岁男童身高在107.
确定组段:第一组段包括最小值,如本例为154 89 cm 取整数 2 cm 应用:单位不同的多组数据比较
13cm之间比的。占该地7岁男频童的数百分表(频数分布):表示各组及它们对
注意:合理分组,才能求均数,否则没有意义。
96 ·S,x 1. Q = Qu 一 Ql
单侧 上界: P 95
单侧 下界: P 5
31
习题:
1.各观察值加同一数后: A.均数不变,标准差改变 B.均数改变,标准差不
变
2.用均数和标准差可全面描述:
3.正态分布曲线下,从均数u 到u 的面积为; A.95% B.45% C. 97.5% D.47.5%
19
相关概念:离均差、离均差平方和、方差(2 S2 ) 标准差的符号: S
●计算公式: 13cm之间的占该地7岁男童的百分 比。
∑f · X=1638
双侧界值:P 2.5 ~ P 97..5 定义:又称参考值范围,是指特定健康人群的解剖、生理、生化等各种数据的波动范围。
特征: ∑(X- X)=0 估计误差之和为0。
估计的方法: 1、正态分布法
2、百分位数法
28
1.正态分布法
应用条件:正态分布或近似正态分布资料 ●计算 (双侧) 95% 正常值(医学参考值)范围公式:
(x1.96 · S,x1.96 · S )
即(x±1.96 · S ) 例:
1.96 × 3.79 )
即(156.41 cm , 171.27 cm )
1998年100名18岁健康女大学生身高的频数分布
数。 (3) 估计该地7岁男童身高在107.
确定组段:第一组段包括最小值,如本例为154 89 cm 取整数 2 cm 应用:单位不同的多组数据比较
13cm之间比的。占该地7岁男频童的数百分表(频数分布):表示各组及它们对
注意:合理分组,才能求均数,否则没有意义。
96 ·S,x 1. Q = Qu 一 Ql
单侧 上界: P 95
单侧 下界: P 5
31
习题:
1.各观察值加同一数后: A.均数不变,标准差改变 B.均数改变,标准差不
变
2.用均数和标准差可全面描述:
3.正态分布曲线下,从均数u 到u 的面积为; A.95% B.45% C. 97.5% D.47.5%
19
相关概念:离均差、离均差平方和、方差(2 S2 ) 标准差的符号: S
医学统计学5定性数据的统计描述PPT课件

中 西 医 结 合 疗 法 组 病例数 治愈数 治愈率(%)
普通型 重 型 暴发型 合 计
60 20 20 100
36 8 4 48
60 40 20 48
20 60 20 100
13 27 5 45
65 45 25 45
标准化直接法
P’=( N1P1 + N2P2 +…+ NKPK )/ N =(ΣNi Pi)/ N
1.选取标准构成。标准构成选取方法有三种:
( 1 )选取一个包含比较各组(如各地区)的有代表性的、 较稳定的、数量较大的构成为标准。如世界的、全国的、全
省的数据为标准构成。
(2)取比较各组的各层例数的合计为标准构成。 ( 3 )从比较的各组(如各地区)中任选其一的构成作为标 准构成。
2.在标准构成下,以原分层率计算各组的预 期发生数。
3.计算标准化率。
实例计算
将上表资料中的两组同病型的人数之和作为标准
构成 ,计算如下:
病 型 标准 构成 人数 西 医 疗 法 组 中西 医 结 合 疗 法组 原治愈率(%) 预期治愈数
原治愈率(%) 预期治愈数
普通型 重 型 暴发型 合 计
80 80 40 200
60 40 20
48 32 8 88
构成比
• 概念:又称构成指标,表示事物内部各个组成部分 所占整体的比重,通常以100%为比例基数,以百分 比表示 • 计算公式:
构成比 其中一组例数 100% 各组例数之和
• 注意:各组成部分的构成比之和为100%,某一部分 比重增大,则其它部分相应减少。
例
某医院某月各科室住院病人数及死亡人数
• 式中P’为标准化率,N1,N2,…,NK为某一影响因素标
第2章 定量资料的统计描述

20~
18 15.00
95
79.17
22~
12 10.00 107
89.17
24~
8 6.67 115
95.83
26~
4 3.33 119
99.17
28~30 1 0.83
120
100.00
合计 120 100
P25
14
2 12
25 120 100
15
16(,ol
/
L)
P75
20
2 12
75 120 100
f
77 50
百分位数(percentileP)X
20
总体中, 数值小于它的个体恰有X %,大于它的个 体恰有1-X %
样本估计:按照升序排列的数列里, 其左侧(即 小于它)的个体数在整个样本中所占百分比为 X%。
21
频率 f L
n X %
fL f
区间 L ? PX L ? L i
? in X% fL f
组段 频数 频率 累计频数 累计频率
26
(1)
(2) (3)
(4)
(5)
6~
1 0.83
1
0.83
8~
3 2.50
4
3.33
10~
6 5.00
10
8.33
12~
8 6.67
18
15.00
14~
12 10.00
30
25.00
16~18 20 16.67
50
41.67
18~20 27 22.50
77
64.17
R = 最大值-最小值 = 29.64-7.42 = 22.22 (3)确定组段数与组距
医学统计学-定量资料统计描述集中离散PPT课件
通常人们用图与表的形式展现频数分布,通 过频数分布可以了解数据的分布规律
对于定量变量,据其数值取值特征又可分为 连续型与离散型
.2章
6
离散型资料频数分布(图、表)
GCS(分) (1)
3 4 5 6 7 8 9 10 11 12 13 14 15
合计
频数(f) (2)
10 5 6 2 12 15 18 14 15 21 13 17 16
例如:教务处得到13 与14两个年级的医学 统计学成绩,如何判 断优劣?
分数段
13级
例数
%
<60
4
3.7
60~
19
17.6
70~
38
35.2
80~
35
32.4
90~100 12
11.1
14级 例数 %
7
6.9
22
21.8
26
25.7
30
29.7
16
15.9
.2章
19
第二节 集中趋势的描 述
算数均数 几何均数 中位数和百分位数
级数据 适用于服从对称分布定量资料(正态或
近似正态)的集中趋势描述
.2章
28
新问题:平均发展速度
假设某投资者拥有资金1000元,第一年他取得10%的收益,第 二年为20%,第三年为40%,求平均收益?
第一年末所拥有的资金为其原始的1.1倍 第二年末所拥有的资金为其原始的1.1×1.2倍 第三年末所拥有的资金为其原始的1.1×1.2×1.4倍
3.列表划计
11
连续型定量变量的频数分布
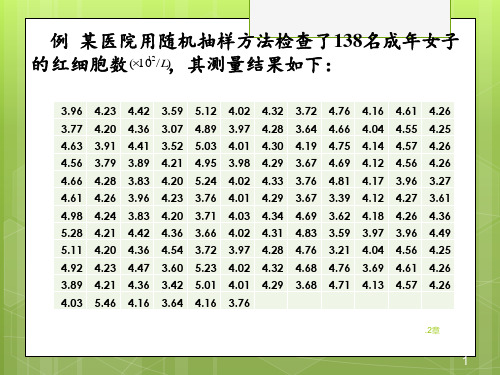
红细胞数(1012/L) 3.07~ 3.27~ 3.47~ 3.67~ 3.87~ 4.07~
对于定量变量,据其数值取值特征又可分为 连续型与离散型
.2章
6
离散型资料频数分布(图、表)
GCS(分) (1)
3 4 5 6 7 8 9 10 11 12 13 14 15
合计
频数(f) (2)
10 5 6 2 12 15 18 14 15 21 13 17 16
例如:教务处得到13 与14两个年级的医学 统计学成绩,如何判 断优劣?
分数段
13级
例数
%
<60
4
3.7
60~
19
17.6
70~
38
35.2
80~
35
32.4
90~100 12
11.1
14级 例数 %
7
6.9
22
21.8
26
25.7
30
29.7
16
15.9
.2章
19
第二节 集中趋势的描 述
算数均数 几何均数 中位数和百分位数
级数据 适用于服从对称分布定量资料(正态或
近似正态)的集中趋势描述
.2章
28
新问题:平均发展速度
假设某投资者拥有资金1000元,第一年他取得10%的收益,第 二年为20%,第三年为40%,求平均收益?
第一年末所拥有的资金为其原始的1.1倍 第二年末所拥有的资金为其原始的1.1×1.2倍 第三年末所拥有的资金为其原始的1.1×1.2×1.4倍
3.列表划计
11
连续型定量变量的频数分布
红细胞数(1012/L) 3.07~ 3.27~ 3.47~ 3.67~ 3.87~ 4.07~
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
17
ቤተ መጻሕፍቲ ባይዱ
§2 集中趋势的描述
18
定量资料集中趋势的描述,常用平均数(average) —表达一组同质定量数据的平均水平或集中位置。
算术均数 几何均数 中位数 众数 调和均数
19
算术均数(arithmetic mean) 又称均数(mean),是用一组观察值 相加除以观察值的个数所得。样本均
0.8 2.5 3.3 6.7 10.0 14.2 17.5 16.7 11.7 8.3 5.0 2.5 0.8
100.0
累计频数 (4)
1 4 8 16 28 45 66 86 100 110 116 119 120
—
累计频率(%) (5)
0.8 3.3 6.7 13.3 23.3 37.5 55.0 71.7 83.3 91.7 96.7 99.2 100.0
数用 x ,总体均数用 。
20
1. 计算方法 直接法:样本含量较少
x xx1x2 xn
n
表4-1 2006年某市120名10岁男孩身高(cm)的频数表
身高 (1)
130~ 132~ 134~ 136~ 138~ 140~ 142~ 144~ 146~ 148~ 150~ 152~ 154~156
合计
频数 (2)
1 3 4 8 12 17 21 20 14 10 6 3 1
120
频率(%) (3)
—
11
(三)、频数表的用途
1. 揭示资料的频数分布特征和频数分布类型 ✓ 频数分布的特征:
集中趋势(central tendency) 离散趋势(dispersion) ✓ 频数分布的类型: 对称分布 偏态分布
12
2.便于进一步计算指标和统计处理 利用频数表计算百分位数、中位数、标准差等
3. 便于发现某些特大或特小的可疑值。 对于频数表,如果连续某几个组段的频数为0, 接下来的组段出现频数不为0的数值,此数值 即为可疑值。
13
二、频数图(graph of frequency)
(一)、频数图的概念
频数图(graph of frequency)是以变 量值为横坐标、频数(频率)为纵坐标 (不等距分组时以频率/组距=频率密度为 纵坐标),以每个等宽的矩形面积表示每 组的频数(或频率)。
14
连续型定量资料:频数图中各矩形是相 连的,又称直方图(histogram);
【思考如下问题】
根据前面所学判断数据为何种类型资料? 如何描述10岁男孩身高的数量特征?
3
本章主要内容
频数表和频数图 集中趋势的描述 离散趋势的描述 正态分布及其应用
4
§1 频数表和频数图
5
一、频数表(Frenquency table)
(一)、频数表的概念 表达变量取值及其不同取值频数分
布情况的统计表称为频数分布表,简 称频数表(frequency table)。
离散型定量资料:频数图中各矩形是间 隔的,又称直条图(bar graph)。
15
图4-1 2006年某市120名10岁男孩身高的频数图
30
20
10
0 0.0
250.0
500.0
750.0
抗体滴度
1000.0
1250.0
人数
12
10
8
6
4
2
Std. Dev = 10
Mean = 27.1
0
N = 91.00
0.0 5.0 10.0 15.0 20.0 25.0 30.0 35.0 40.0 45.0
2.5 7.5 12.5 17.5 22.5 27.5 32.5 37.5 42.5 47.5
肌红蛋白
图 69例RA患者血清EBV-VCA-IgG 抗体滴度的频数分布
图 101名正常人血清肌红蛋白的频数分布
Chapter 4
定量资料的统计描述
2006年某市120名10岁男孩的身高(cm)资料如:
135.4 139.8 144.0 147.3 146.3 142.5 138.1 143.6 141.6 152.6 132.1 144.7 143.6 146.8 144.2 141.3 137.5 142.8 140.6 150.4 145.9 140.2 144.5 148.2 146.4 142.4 138.5 148.9 146.2 155.4 134.2 139.2 143.5 141.6 143.5 142.3 148.9 143.6 141.5 151.1 132.5 138.7 149.6 146.9 148.7 141.5 137.8 142.7 144.6 151.8 136.4 140.0 144.3 147.5 145.6 142.5 138.5 143.7 149.5 153.6 130.2 138.9 143.7 146.5 138.8 141.7 136.9 142.0 140.5 150.3 135.7 145.7 144.2 147.8 145.8 142.6 138.6 143.8 141.3 153.9 133.4 139.6 143.7 147.5 144.8 148.0 137.4 142.1 140.8 141.8 134.5 139.4 142.9 147.5 144.7 141.8 136.9 143.5 140.7 151.4 145.6 147.3 143.9 141.9 151.6 145.6 148.9 144.3 139.1 145.8 145.6 145.3 147.6 148.6 145.5 137.3 146.5 140.3 148.4 136.5
8
3. 确定组段 即确定每一组的起点(下限)和终 点(上限) 。
✓起点称为下限(lower limit) ✓终点称为上限(upper limit)
上限=下限+组距
9
4. 归组计数,整理成表 确定组段界限后,采用计算机或用划 记法将各原始数据归入各组汇总,得 出各组段的观察例数,也就是频数 。
10
6
(二)、频数表的编制
1. 求极差(range) 2. 找出一组观察值中的最大值与最
小值,其差值即为极差(或全距), 用R表示。 3. 如例4-1中:R=155.4-130.2=25.2
7
2. 确定组数和组距(i) 根据样本含量的大小及研究目的确定 组数;一般设8~15个组。 例4-1:i=25.2/10=2.52,取整数2做组距。
ቤተ መጻሕፍቲ ባይዱ
§2 集中趋势的描述
18
定量资料集中趋势的描述,常用平均数(average) —表达一组同质定量数据的平均水平或集中位置。
算术均数 几何均数 中位数 众数 调和均数
19
算术均数(arithmetic mean) 又称均数(mean),是用一组观察值 相加除以观察值的个数所得。样本均
0.8 2.5 3.3 6.7 10.0 14.2 17.5 16.7 11.7 8.3 5.0 2.5 0.8
100.0
累计频数 (4)
1 4 8 16 28 45 66 86 100 110 116 119 120
—
累计频率(%) (5)
0.8 3.3 6.7 13.3 23.3 37.5 55.0 71.7 83.3 91.7 96.7 99.2 100.0
数用 x ,总体均数用 。
20
1. 计算方法 直接法:样本含量较少
x xx1x2 xn
n
表4-1 2006年某市120名10岁男孩身高(cm)的频数表
身高 (1)
130~ 132~ 134~ 136~ 138~ 140~ 142~ 144~ 146~ 148~ 150~ 152~ 154~156
合计
频数 (2)
1 3 4 8 12 17 21 20 14 10 6 3 1
120
频率(%) (3)
—
11
(三)、频数表的用途
1. 揭示资料的频数分布特征和频数分布类型 ✓ 频数分布的特征:
集中趋势(central tendency) 离散趋势(dispersion) ✓ 频数分布的类型: 对称分布 偏态分布
12
2.便于进一步计算指标和统计处理 利用频数表计算百分位数、中位数、标准差等
3. 便于发现某些特大或特小的可疑值。 对于频数表,如果连续某几个组段的频数为0, 接下来的组段出现频数不为0的数值,此数值 即为可疑值。
13
二、频数图(graph of frequency)
(一)、频数图的概念
频数图(graph of frequency)是以变 量值为横坐标、频数(频率)为纵坐标 (不等距分组时以频率/组距=频率密度为 纵坐标),以每个等宽的矩形面积表示每 组的频数(或频率)。
14
连续型定量资料:频数图中各矩形是相 连的,又称直方图(histogram);
【思考如下问题】
根据前面所学判断数据为何种类型资料? 如何描述10岁男孩身高的数量特征?
3
本章主要内容
频数表和频数图 集中趋势的描述 离散趋势的描述 正态分布及其应用
4
§1 频数表和频数图
5
一、频数表(Frenquency table)
(一)、频数表的概念 表达变量取值及其不同取值频数分
布情况的统计表称为频数分布表,简 称频数表(frequency table)。
离散型定量资料:频数图中各矩形是间 隔的,又称直条图(bar graph)。
15
图4-1 2006年某市120名10岁男孩身高的频数图
30
20
10
0 0.0
250.0
500.0
750.0
抗体滴度
1000.0
1250.0
人数
12
10
8
6
4
2
Std. Dev = 10
Mean = 27.1
0
N = 91.00
0.0 5.0 10.0 15.0 20.0 25.0 30.0 35.0 40.0 45.0
2.5 7.5 12.5 17.5 22.5 27.5 32.5 37.5 42.5 47.5
肌红蛋白
图 69例RA患者血清EBV-VCA-IgG 抗体滴度的频数分布
图 101名正常人血清肌红蛋白的频数分布
Chapter 4
定量资料的统计描述
2006年某市120名10岁男孩的身高(cm)资料如:
135.4 139.8 144.0 147.3 146.3 142.5 138.1 143.6 141.6 152.6 132.1 144.7 143.6 146.8 144.2 141.3 137.5 142.8 140.6 150.4 145.9 140.2 144.5 148.2 146.4 142.4 138.5 148.9 146.2 155.4 134.2 139.2 143.5 141.6 143.5 142.3 148.9 143.6 141.5 151.1 132.5 138.7 149.6 146.9 148.7 141.5 137.8 142.7 144.6 151.8 136.4 140.0 144.3 147.5 145.6 142.5 138.5 143.7 149.5 153.6 130.2 138.9 143.7 146.5 138.8 141.7 136.9 142.0 140.5 150.3 135.7 145.7 144.2 147.8 145.8 142.6 138.6 143.8 141.3 153.9 133.4 139.6 143.7 147.5 144.8 148.0 137.4 142.1 140.8 141.8 134.5 139.4 142.9 147.5 144.7 141.8 136.9 143.5 140.7 151.4 145.6 147.3 143.9 141.9 151.6 145.6 148.9 144.3 139.1 145.8 145.6 145.3 147.6 148.6 145.5 137.3 146.5 140.3 148.4 136.5
8
3. 确定组段 即确定每一组的起点(下限)和终 点(上限) 。
✓起点称为下限(lower limit) ✓终点称为上限(upper limit)
上限=下限+组距
9
4. 归组计数,整理成表 确定组段界限后,采用计算机或用划 记法将各原始数据归入各组汇总,得 出各组段的观察例数,也就是频数 。
10
6
(二)、频数表的编制
1. 求极差(range) 2. 找出一组观察值中的最大值与最
小值,其差值即为极差(或全距), 用R表示。 3. 如例4-1中:R=155.4-130.2=25.2
7
2. 确定组数和组距(i) 根据样本含量的大小及研究目的确定 组数;一般设8~15个组。 例4-1:i=25.2/10=2.52,取整数2做组距。
