基于排队论的麦当劳服务系统优化研究
排队管理系统研究报告

排队管理系统研究报告排队管理系统是指通过应用科学的手段,对排队的人员进行合理的管理和调度,提高排队效率、缩短等候时间的一种管理系统。
本报告将从系统概述、目的和意义、功能特点、应用实例等方面进行研究与讨论。
一、系统概述排队管理系统是一种基于先进科技的智能化管理系统,主要通过电子终端设备、网络技术等手段,对排队的人员进行智能化的管理和调度,实现高效、快捷的排队服务。
该系统采用先进的算法和模型,能够根据实时的人流量和系统的运行状态,进行智能的调度和分配。
二、目的与意义排队管理系统的目的是为了提高排队效率、减少等候时间,增加服务效率和用户满意度。
通过该系统的应用,可以实现排队的有序、高效进行,避免因排队时间过长而引发的不满和纷争,提高办公、服务等各个场所的管理水平和效率。
三、功能特点1. 排队预约功能:用户可以通过手机APP或网络平台进行排队预约,避免到场排队等候的时间消耗;2. 实时数据监控:系统可以实时监控各个排队节点的人数和等候时间,准确地反映排队情况,从而进行科学的调度;3. 智能排队调度:系统通过算法模型,对排队情况进行智能化调度,按照先来先服务的原则,合理地调配资源,提高排队效率;4. 多渠道服务:系统支持多种渠道进行排队取号,如手机APP、网络平台、自助终端等,方便用户选择;5. 数据分析与报表展示:系统能够对排队数据进行分析和统计,生成各类报表展示,为管理者提供科学依据。
四、应用实例1. 医院排队管理系统:患者可以提前通过手机APP预约挂号,在到达医院时直接取号排队,避免了长时间的等候;2. 餐厅排队管理系统:用户可通过手机APP进行外卖预订或到店取号,实现排队取号的准确和高效;3. 机场安检排队管理系统:旅客可以通过自助取号终端进行取号,准确掌握等候时间,提高旅行体验;4. 银行排队管理系统:用户可以通过手机APP预约柜员服务,提前规划行程,减少等候时间。
综上所述,排队管理系统具有重要的意义和价值,可以提高排队效率、减少等候时间,提高服务水平和用户满意度,广泛应用于各个领域,实现智能化、科学化的排队管理。
麦当劳餐厅排队系统

麦当劳餐厅排队系统一、系统说明1、系统目标:通过模拟仿真麦当劳餐厅晚间时段运行情况,判断麦当劳餐厅在此时段是否应该像银行排队系统一样发放号码进行排队。
2、系统模型描述:麦当劳餐厅,晚上8:30—9:30一个小时内,服务情况。
该餐厅,在这个时段内,一般是开设两个服务台进行点餐服务。
本仿真模拟该餐厅两个服务台的点餐情况,顾客进入餐厅,如果发现两个服务台都忙碌的话,则假设进入最短队列进行排队;若服务台有一个是闲置的,顾客则选择闲置的服务台接受点餐服务进行点餐,若两个服务台都闲置,则就近选择1号服务台接受服务、进行点餐。
顾客接受完服务以后,离开服务台。
下图为该模型描述的流程图:3、系统实体功能:顾客:排队,接受服务,顾客离开。
图2 顾客功能图麦当劳服务台:空闲,忙碌。
图3 麦当劳服务台功能图二、数据采集与整理1、数据采集:系统可以分为离散系统和连续系统两类。
因为麦当劳餐厅点餐系统的状态变量——如来吃饭的餐厅里的顾客总数、顾客在某一时间段到达人数——尽在有顾客到达或有顾客结束服务离开时发生变化。
而离散系统就是一类状态变量随时间在一组离散值上跳转的系统。
所以麦当劳点餐系统是一个离散系统。
进行建模的先决条件是必须有一定的现实数据为依据,我们的目的是为了对点餐服务台的服务人员是否有空闲,是否达到最大利用率,服务更加贴近客户要求,增强麦当劳餐厅的竞争能力。
数据的搜集与整理是进行统计研究的基础,统计研究所需的基础资料,就是通过数据的搜集和对这些数据进行分类整理后建立的。
有了这些基础资料,我们才能对总体数量特征和数量关系做进一步描述和推断。
统计数据的搜集是统计整理和分析,以及统计推断和预测的基础。
统计数据的搜集就是根据统计研究的目的和要求,有组织、有计划地向调查对象搜集原始资料和次级资料的过程。
我们这次的数据搜集采取了直接观察法,通过对仿真对象某麦当劳餐厅的营运进行观察,搜集了连续一周的晚上8:30至9:30时间段内顾客的数量和到达时间。
排队论在服务系统中的应用

排队论在服务系统中的应用随着现代社会服务行业的不断发展,长时间的排队等待已经成为了服务系统中的一大难题。
而解决这个难题的重要方法之一就是排队论。
所谓排队论,是指对服务系统进行定量的分析和设计,通过数学模型来预测系统的性能,以优化服务体验。
本文将介绍排队论在服务系统中的应用,以及如何通过排队论来提升服务效率和用户满意度。
一、排队论的基本概念排队论的核心理论是排队模型,由五个元素构成:顾客到达(Arrivals)、服务设施(Service)、队列(Queue)、系统容量(Capacity)和服务策略(Discipline)。
其中,顾客到达是指有多少顾客到达系统,服务设施是指系统中有多少服务台,队列是指排队等待的顾客数目,系统容量是指服务台的总容纳量,服务策略则是指服务员如何安排服务顺序。
排队论的主要目的是优化顾客的等待时间和服务设施的利用率,从而提升顾客满意度。
通过排队模型,可以对服务系统进行分析和设计,找出并解决痛点,提升服务效率和质量。
二、排队论在服务系统中的应用排队论在服务系统中的应用非常广泛,几乎涉及到我们生活中的各个领域。
比如餐饮服务、医疗服务、公共交通等等,都可以使用排队论来优化服务流程。
(一)餐饮服务在餐厅中,大多数顾客都是在饭点时同时到达,如果服务不及时,则顾客就会出现长时间的等待排队。
为了减少等待时间,餐厅可以通过排队论来进行预测和控制,如何增加就餐的流水线,启用预定等服务。
(二)医疗服务医院就诊的排队也是服务行业中比较重要的一个环节。
通过排队论,医院可以对病人就诊流程进行合理规划设计,如通过加速检查和缩短检查时间来减少等待时间,或者设置呼叫系统来提高就医效率。
对于需要等待手术,就诊时间较长的病人,更可以加入就医者评价、服务员质量管理等个性服务的安排,优化就医体验。
(三)公共交通在公共交通领域中,排队论的应用也很广泛。
如公交车站、地铁站等等。
这些服务系统中许多时候会存在因等待时间过长而带来的等待焦虑、排队安全问题等相关问题。
基于排队论的校园服务系统的分析及优化

基于排队论的校园服务系统的分析及优化摘要:服务窗口的排队问题在生活中随处可见,为提高系统效率,本文以我校食堂超市等服务窗口问题为例,基于泊松分布和排队论分析来确定所需要的服务窗口和服务人员数目,理论计算结果和实际情况相比较,为解决目前大学生在校就餐购物排队等时间问题,构建了基于排队论的校园窗口设置优化模型。
关键词:排队论;数学建模;系统优化Analysis and optimization of campus service system based on queuing theory. Abstract: Service window of queuing problem can be seen everywhere in our daily life, to improve the efficiency of system, this article in our school canteen service window problem such as supermarkets, for example, based on the poisson distribution and queuing theory analysis to determine the required number of service Windows, compared with the theoretical calculation results and actual situation, to solve the problem of the current college students in the school dining shopping queuing time, build the campus window set optimization model based on queuing theory.Key words: queuing theory; Mathematical modeling; System optimization一、引言排队是在日常生活中经常遇到的问题,比如顾客到商店购物去火车站买票等都需要排队。
基于计算机仿真的排队系统优化问题研究

基于计算机仿真的排队系统优化问题研究一、本文概述随着信息技术的快速发展和广泛应用,排队系统在各种实际场景中的应用越来越普遍,如银行、医院、商场、交通等各个领域。
然而,传统的排队系统往往存在效率不高等待时间长、服务质量不稳定等问题,这些问题不仅影响了服务效率,也降低了客户满意度。
因此,如何优化排队系统,提高服务效率和质量,成为了当前研究的热点之一。
基于计算机仿真的排队系统优化问题研究,旨在通过计算机仿真技术,对排队系统的运行过程进行模拟和分析,发现系统存在的问题和瓶颈,进而提出有效的优化策略。
本文首先介绍了排队系统的基本概念和分类,分析了传统排队系统存在的问题和挑战。
然后,详细介绍了计算机仿真技术在排队系统优化中的应用,包括仿真模型的建立、仿真实验的设计和实施、仿真结果的分析和评估等方面。
接着,本文重点探讨了基于计算机仿真的排队系统优化策略,包括服务流程优化、资源配置优化、排队规则优化等方面,并通过案例分析和实验验证,证明了这些优化策略的有效性和可行性。
本文的研究不仅有助于解决传统排队系统存在的问题,提高服务效率和质量,也有助于推动计算机仿真技术在排队系统优化中的广泛应用和发展。
本文的研究方法和成果也可以为其他领域的系统优化问题提供借鉴和参考。
二、排队系统理论基础排队系统,也称为随机服务系统,是一种广泛存在于现实生活中的数学模型。
这种模型通常描述顾客到达服务机构,等待并接受服务的过程。
排队系统理论的核心在于分析并优化这种服务过程的效率。
在计算机仿真领域,通过模拟排队系统的运行过程,可以深入理解其内部机制,为优化系统性能提供理论支持。
排队系统主要由三个基本部分构成:输入过程、排队规则和服务机构。
输入过程描述了顾客到达服务系统的规律,常见的输入过程包括定长输入、泊松输入等。
排队规则决定了顾客在系统中的等待和服务顺序,常见的有先到先服务(FCFS)、最短作业优先(SJF)等。
服务机构则负责为顾客提供服务,其服务能力通常受到多种因素的影响,如服务速度、服务人员数量等。
排队论在超市收银系统中的应用研究

排队论在超市收银系统中的应用研究排队论是一种描述和分析人们在等待队伍中的行为及其影响的学科,它研究了排队过程中各种因素和决策的影响。
本文将介绍如何将排队论运用于超市收银系统,并对其可能的效益进行分析。
首先,超市的收银系统是实现收银的关键。
超市的收银系统是一种处理连续出现的客户等待和收银的系统,在大量消费者出现时,由于收银机等资源有限,收银系统可能运行缓慢,导致排队拥堵,影响消费者的体验。
因此,通过排队论的应用,可以改进收银系统的工作效率,以满足消费者的期望。
其次,将排队论应用于超市收银系统可以更好地处理客户的等待时间问题。
排队论可以帮助我们分析客户的排队行为,从而决定如何更有效地管理排队流程,降低排队时间。
此外,还可以通过收集客户信息,分析客户在排队中的行为,以期建立一套完善的超市收银系统。
再次,排队论还可以将资源利用起来,提高收银中心的效率。
排队论可以帮助我们确定收银机的使用效率,并合理分配收银机的使用时间。
此外,还可以采取措施提高收银机的排队速度,减少客户的等待时间,从而提升超市收银系统的效率。
此外,排队论还可以用来评估超市收银系统的服务质量和客户满意度。
排队论可以帮助我们了解客户在收银中的等待情况,从而改进收银系统,提升收银中心的服务质量,以满足客户的期望,提高客户满意度。
最后,排队论可以帮助收银中心制定有效的资源分配策略,提高收银效率。
根据排队论的原理,可以建立一个模型来评估客户的排队时间,根据模型的结果提出有效的资源分配策略,以优化收银效率。
综上所述,排队论可以有效地改善超市收银系统的工作效率,减少排队时间,优化服务质量,提高收银效率,提高客户满意度,实现更高效的超市收银。
因此,排队论是超市收银系统优化的重要手段,应该得到全面考虑和应用。
排队论在改进银行服务系统中应用探究

排队论在改进银行服务系统中应用探究一、论文报告题目:1.排队论在改进银行服务系统中的应用2.排队论在提高客户满意度中的作用3.基于排队论的银行服务质量改进策略4.排队论在银行服务设施改善中的利用5.基于排队论的银行服务优化方案二、排队论在改进银行服务系统中的应用银行是现代社会的重要服务行业之一,不仅是现代经济的重要组成部分,也是人们财富管理的重要场所。
然而,人们前往银行办理业务,常常会面对长时间的排队等待,这不仅浪费了时间,也影响了客户的满意度与银行形象。
为了提高银行服务水平,解决排队等待的问题,排队论成为关键的研究领域之一。
排队论,也称为等待队列论,研究排队系统的性质、行为及其应用。
银行作为典型的排队系统,排队论可以帮助银行改进服务,提高工作效率和客户满意度。
下面从排队模型、排队参数和排队优化三个角度,探究排队论在改进银行服务系统中的应用。
1. 排队模型排队模型是排队论最基本的研究对象,根据不同的规则和分布方式,分为单线程、多线程、单服务点和多服务点等形式。
在银行服务系统中,单线程模型和多线程模型是应用最广泛的两种模型。
单线程模型指的是只有一个服务窗口的排队系统,顾客依次排队等待服务。
多线程模型指的是有多个服务窗口的排队系统,顾客可以选择不同窗口进行服务,具有较高的效率。
2. 排队参数排队参数是排队论中的基本概念,指代排队流程中的各种参数。
排队参数主要由到达率、服务率和队列容量三个维度构成。
到达率指的是单位时间内到达该服务系统的顾客数,服务率是指每个服务窗口在单位时间内能够完成服务的顾客数,队列容量是指排队区域内的最大容纳人数,当到达率过高或服务效率过低时,顾客数目将会超出队列容量,从而影响顾客的等待时间和满意度。
3. 排队优化排队优化是通过调整排队参数来提高服务效率和顾客满意度的方法。
在银行服务系统中,排队优化主要包括以下内容:(1)人员调配。
对于单线程模型,可以通过提高服务人员的数量来减少客户排队的时间和等待的长度。
基于排队论的超市收银员的优化

基于排队论的超市收银员的优化随着超市业务的不断发展,节约时间和提高效率变得越来越重要。
超市收银员是超市业务的核心环节之一,因此优化超市收银员的排队系统可以提高整体的效率。
本文将基于排队论的理论和方法,探讨如何优化超市收银员的排队系统。
首先,我们需要了解排队论的基本概念。
排队论是研究排队系统的数学理论,它可以帮助我们分析和优化排队系统的运营效率。
在超市收银员的排队系统中,顾客到达超市的时间间隔和找零的时间是两个重要的因素。
顾客到达超市的时间间隔可以用到达率来表示,找零的时间可以用服务率来表示。
到达率和服务率决定了排队系统的稳定性和效率。
为了优化超市收银员的排队系统,我们可以进行以下几个方面的优化:1.提高服务效率。
收银员的服务效率直接影响到顾客等待时间的长短。
因此,提高收银员的服务效率是优化排队系统的一个重要途径。
可以通过培训收银员技术,采用更高效的收银设备等方式来提高服务效率。
2.降低等待时间。
等待时间是顾客在排队系统中最关心的因素之一、为了降低等待时间,可以考虑增加收银员的数量,或者根据需求合理调整收银员的工作时间。
此外,还可以采用多个排队线程,避免出现单一排队线程导致的拥堵。
3.预测和调整到达率。
了解到达率的变化规律,可以帮助我们更好地调整收银员的数量和工作时间。
例如,在早晚高峰期,到达率通常较高,此时可以增加收银员的数量,以满足市场需求。
4.利用技术手段优化排队系统。
随着技术的发展,可以借助科技手段来优化排队系统。
例如,可以引入自助结账机,让顾客可以自行操作结账,提高服务效率。
同时,可以利用数据分析和预测技术,根据历史数据和趋势来合理安排收银员数量和工作时间。
总之,基于排队论的超市收银员的优化需要综合考虑到达率、服务率和系统容量等因素。
通过提高服务效率、降低等待时间、合理调整人员数量和工作时间以及利用技术手段等措施,可以有效地优化超市收银员的排队系统,提高超市的运营效率,为顾客提供更好的购物体验。
麦当劳的服务系统

麦当劳的服务系统随着经济水平的提高,外出用餐的人越来越多,强大的品牌力量, 正确的市场定位, 优秀的运作水准, 有效的促销手段-—造就了麦当劳这一世界快餐业的巨人.麦当劳的黄金准则是顾客至上,顾客永远第一。
麦当劳具有明确的经营理念与规范化管理,麦当劳的运营系统一麦当劳的运作战略为QSCV优质(Quality)品质:麦当劳重视品质的精神,体现在所有环节都遵循“麦当劳食品标准”。
–麦当劳建立起完整的产品供应网络,确立了严格的质量控制标准。
首先是与优秀的生产商建立密切关系,确保新餐厅得到最高质量的产品供应;而后,食品必须经过一连串严格的质量检验,仅牛肉饼就有40多项质量控制的检查,最后才会送到顾客面前。
严格的标准使顾客在任何时间、任何地点所品尝的麦当劳食品都是同一品质的。
–无论是原料食品采购、生产操作、烹调时间与条件等,麦当劳餐厅对每一个步骤都遵从严谨的标准。
Service服务:快捷、友善、可靠的服务,已经成了麦当劳的标志。
每一名职工都会被灌输“永远以顾客为先”的基本原则。
Cleanliness清洁:为顾客提供了一个干净、舒适、愉快的用餐环境,是麦当劳营业场所追求的目标。
–麦当劳对员工的行为规范中明文规定:男士必须每天刮胡子,女士要带发网,每天修指甲,随时保持口腔清洁,经常洗澡,不留长发。
–所有员工必须遵守这样一条规定:“与其背墙休息,不如起身打扫”,使店内始终保持“窗明、地洁、桌面净”。
–餐馆内不许出售香烟和报纸,器具全部都是不锈钢的。
–麦当劳的每一个餐厅都是一样的清洁舒适,无论是餐厅大堂,还是在一般饮食店不看重的厨房。
甚至连餐厅前面人行道也务求清洁,不让其影响顾客进食的气氛。
餐厅的每一个用具、位臵和角落都体现出麦当劳对卫生清洁的注重。
–顾客一进入这样的就餐环境,也都习惯于自觉清除垃圾,同服务人员一起保持一个幽雅清洁的环境。
Value物有所值:–麦当劳在给顾客提供了高品质的、营养均衡的美味食品的同时,还为顾客带来了更多的选择和更多的欢笑,顾客在麦当劳大家庭充分体验到“物有所值”的承诺。
DXC22基于排队论的服务系统优化研究以XX超市收银台为例
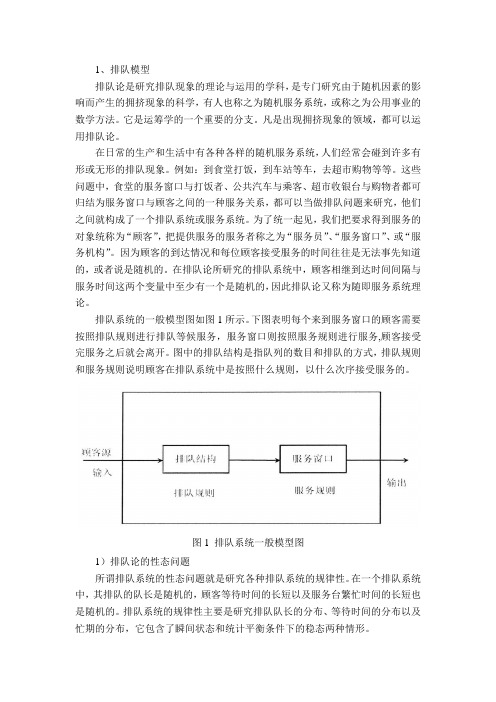
1、排队模型排队论是研究排队现象的理论与运用的学科,是专门研究由于随机因素的影响而产生的拥挤现象的科学,有人也称之为随机服务系统,或称之为公用事业的数学方法。
它是运筹学的一个重要的分支。
凡是出现拥挤现象的领域,都可以运用排队论。
在日常的生产和生活中有各种各样的随机服务系统,人们经常会碰到许多有形或无形的排队现象。
例如:到食堂打饭,到车站等车,去超市购物等等。
这些问题中,食堂的服务窗口与打饭者、公共汽车与乘客、超市收银台与购物者都可归结为服务窗口与顾客之间的一种服务关系,都可以当做排队问题来研究,他们之间就构成了一个排队系统或服务系统。
为了统一起见,我们把要求得到服务的对象统称为“顾客”,把提供服务的服务者称之为“服务员”、“服务窗口”、或“服务机构”。
因为顾客的到达情况和每位顾客接受服务的时间往往是无法事先知道的,或者说是随机的。
在排队论所研究的排队系统中,顾客相继到达时间间隔与服务时间这两个变量中至少有一个是随机的,因此排队论又称为随即服务系统理论。
排队系统的一般模型图如图1所示。
下图表明每个来到服务窗口的顾客需要按照排队规则进行排队等候服务,服务窗口则按照服务规则进行服务,顾客接受完服务之后就会离开。
图中的排队结构是指队列的数目和排队的方式,排队规则和服务规则说明顾客在排队系统中是按照什么规则,以什么次序接受服务的。
图1 排队系统一般模型图1)排队论的性态问题所谓排队系统的性态问题就是研究各种排队系统的规律性。
在一个排队系统中,其排队的队长是随机的,顾客等待时间的长短以及服务台繁忙时间的长短也是随机的。
排队系统的规律性主要是研究排队队长的分布、等待时间的分布以及忙期的分布,它包含了瞬间状态和统计平衡条件下的稳态两种情形。
2)排队系统的最优化问题排队系统的最优化问题主要有两类:包括系统的最优化设计和系统的最优化运行控制。
前者又称为静态最优化,后者又称为动态最优化。
前者是在服务系统设置之前就对未来的运行情况进行估计,从而使设计人员有所依据。
麦当劳前台操作系统分析

麦当劳前台操作系统分析通过对武汉市某麦当劳快餐店进行实地考察,收集了消费者到该店接受服务的几组重要相关数据,首先根据排队理论对排队现象进行分析,其次指出实际观察中发现的问题,同时根据以上分析提出一定的改进措施,以较大的可行性实现麦当劳服务系统的优化。
标签:麦当劳;前台操作;排队论1 前言随着我国经济的发展,快餐业迅速崛起,尤其以国外快餐品牌,如肯德基、麦当劳等,成为中国国民消费的重要选择。
曾几何时,麦当劳对于中国国民是奢侈的消费,因为秉持优良服务带来的高昂费用让普通民众望而却步,那时的国人还没有“客户满意度”的概念,更多的是追求“物美价廉”。
今非昔比,国内各快餐品牌云集,为占领市场形成激烈的竞争之势。
节约成本,最大化资源利用率,提升顾客满意度成为快餐品牌脱颖而出的一把利器。
快餐消费中“服务”和“效率”直接地影响着人们对一个品牌的认同,在这一过程中,顾客在与快餐店直接接触环节中体验到“服务”与“效率”,这决定着顾客对该快餐店的满意度。
排队现象是我们生活中常遇见的现象,当队伍中某个时刻要求服务的数量超过服务机构的容量时,就会出现排队现象。
不同于工厂生产中的排队,作为服务场所的快餐店,排队系统就显得特别的重要。
排队系统服务质量的好坏将会直接影响到顾客的满意度,从而影响快餐店的整体效益。
所以,快餐店必须在可接受的经营成本下,尽可能的减少顾客的等待时间和等待队长,来获得顾客的满意度。
排队现象作为前台操作最重要的一环,我们要实现优化。
但是人员配置利用及新兴服务方式的探寻也是前台操作得以优化的关键。
2 排队系统2.1 模型介绍排队论是研究排队现象理论与运用的学科,是专门研究由于随机因素的影响产生的拥挤现象的科学方法,它是运筹学的一个重要分支。
排队过程模型如图1。
图 1 排队过程模型输入过程一般是用顾客到达间隔时间来描述的。
根据到达间隔时间所服从的分布,输入过程可分为定长输入(负)指数分布(POISSON 输入)几何分布与一般分布等到达规则是指在这些输入的每一种中又可分为单个到达、批到达等。
基于排队论的某食品零售店收银系统优化研究

基于排队论的某食品零售店收银系统优化研究
周素霞;杨璐
【期刊名称】《价值工程》
【年(卷),期】2024(43)11
【摘要】对于某食品零售店高峰期排队结账时间较长的问题,提出两种针对性的解决方案。
通过选取节假日客流高峰时间段的数据进行现场采集,基于运筹学中的排队理论对该食品零售门店高峰期两小时的实际客流进行统计,运用python建立
M/G/2模型,利用真实数据进行模拟仿真,根据仿真结果提出两种可行的优化方案,并对优化方案进行仿真计算。
计算结果表明,不论是收银系统的改变还是排队模式的改变,都能够更加充分地利用环境资源、硬件资源和人力资源,能帮助该类门店缓解高峰时期客流拥堵的现象,由此见得,优化后的系统相较于优化前更加高效合理。
这样门店就能够将更好的服务提供给消费者,从而提高消费者的满意程度,为企业带来更大的效益,门店可以根据实际情况安排合适的优化方式。
【总页数】5页(P9-13)
【作者】周素霞;杨璐
【作者单位】北京建筑大学城市轨道交通车辆服役性能保障北京市重点实验室;北京建筑大学机电与车辆工程学院
【正文语种】中文
【中图分类】O226
【相关文献】
1.基于排队论的超市收银系统优化研究
2.超市收银排队服务系统优化分析
3.基于排队论模型的淮南市泉山华润苏果超市收银服务系统优化
4.基于排队理论的超市收银系统的分析与改善
5.基于排队论的北京某超市收银系统优化研究
因版权原因,仅展示原文概要,查看原文内容请购买。
排队论在服务系统优化中的运筹学方法研究

排队论在服务系统优化中的运筹学方法研究服务系统是现代社会中不可或缺的组成部分,如银行、医院、机场等各类场所的服务流程都需要进行优化,以提高效率和用户体验。
排队论作为运筹学的一个重要分支,研究如何合理组织和管理服务系统中的排队现象,对于服务系统优化具有重要意义。
本文将探讨排队论在服务系统优化中的运筹学方法。
一、排队论基本模型排队论是研究排队现象的一门学科,其基本模型由顾客到达过程、顾客排队等待过程和顾客接受服务过程组成。
下面我们将介绍三个基本模型。
1. M/M/1模型M/M/1模型是最简单的排队论模型,代表顾客到达过程和服务过程都符合随机过程。
其中的M表示到达过程和服务过程都满足泊松过程,/表示到达过程和服务过程是独立的,1表示只有一个服务台。
该模型可以通过计算平均等待时间、平均队长等指标,来评估系统的运行效果。
2. M/M/c模型M/M/c模型是多通道排队系统的模型,代表顾客到达过程和服务过程都符合随机过程,但服务台的数量有多个。
该模型可以用于评估多个服务台的效率分配问题,提高服务系统的整体服务水平。
3. M/G/1模型M/G/1模型是顾客到达过程满足泊松分布,而服务过程满足一般分布的排队系统模型。
该模型相比于前两个模型更加复杂,但也更加接近现实服务系统的情况。
通过研究和优化M/G/1模型,可以为实际服务系统提供更准确的优化方案。
二、排队论方法在服务系统中的应用排队论方法在服务系统中的应用十分广泛,涉及到客户流量预测、服务水平评估、服务台数量决策等多个方面。
1. 客户流量预测客户流量预测是排队论方法在服务系统优化中的重要应用之一。
通过对历史数据的分析和建模,可以预测未来客户到达的概率分布,进而确定合理的服务台数量和服务水平指标。
例如,某银行可以通过排队论方法预测未来客户到达和离开的概率,从而优化柜员人数和窗口开放时间,提高客户满意度。
2. 服务水平评估排队论方法可以用于评估服务系统的服务水平,比如平均等待时间、平均队长等指标。
基于排队论的超市收银系统优化毕业论文

文论 文业 论毕 业题 目:基于排队论的超市收银系统优化评阅者:日5 日6 月2015年 6月 5毕业论文中文摘要基于排队论的超市收银系统优化摘要: 二十一世纪以来,大型超市取代了传统的生活用品销售模式走进了我们的生活,给我们带来了极大的便利。
但是由于我国超市行业发展还不够成熟,种种原因造成了超市排队拥挤现象,常常会出现顾客队列过长或收银台空闲等很多问题,因此对大型超市收银服务系统进行排队优化,合理设置收银台具有重大的实际意义。
意义。
本文针对JX超市御景蓝湾店的收银排队服务系统进行改进优化。
首先对排队论等相关理论知识进行了介绍,对多服务台等待的M/M/n/∞/∞排队论模型进行了描述。
其次调研了JX超市顾客到达时间和顾客服务时间的数据,并对原始数据带入排队论模型进行分析,计算出了所需的目标参数,确定了工作日和节假日各时段JX超市开放收银台的最佳数量。
然后运用仿真模拟软件Flexsim对收银排队服务系统进行了仿真模拟论证了优化出的收银台开放数量的可行性。
并且在此基础上对收银的基本流程进行了优化,并且改进了收银台周边物品摆放不合理的问题,最后对JX超市提出了发展意见。
不合理的问题,最后对JX超市提出了发展意见。
关键词:关键词: 超市收银 排队论排队论 仿真 优化仿真 优化毕业论文外文摘要Title Supermarket cashier system optimization based onqueuing theoryAbstractThe 21st century, large supermarket replaced the traditional life suppliessales model walked into our life, brings us great convenience. But becauseof China's supermarket industry development is not mature enough, a varietyof reasons caused the supermarket line crowded phenomenon, often there willbe a customer queue is too long or spare time a lot of problems. Aiming at JX royal blue bay scene store supermarket cashier line up improve the service system optimization. First, the queuing theory and related theory knowledge, the more the front desk waiting for M/M/n/up/upqueuing theory model are described. Secondly research for JX supermarket customer arrival time and customer service time of data, and analyze th raw data into the queuing theory model, calculate the required target parameter, in each period to determine the working days and holidays th optimal number of JX supermarket open the cash register. Then using th simulation software Flexsim cashier line service system for the simulation demonstrate the feasibility of optimization of open the register number. And on this basis, the basic process of cashier is optimized, the l of JX supermarket development Suggestions are put forward.theory Simulation Sptimization Keywords:S upermarket cashier Queuing目 录1 1 绪论绪论.................................................................................................................................... ................................................................................................................................... 1 1 1.1 研究背景研究背景.................................................................................................................................... .................................................................................................................................... 11 1.2 研究目的和意义研究目的和意义........................................................................................................................ ........................................................................................................................ 11 1.2.1 1.2.1 研究目的研究目的........................................................................................................................ ........................................................................................................................ 11 1.2.2 1.2.2 研究意义研究意义........................................................................................................................ ........................................................................................................................ 22 1.3国内外研究现状国内外研究现状......................................................................................................................... ......................................................................................................................... 22 1.3.1 1.3.1 国外研究现状国外研究现状 ................................................................................................................ . (2)2 1.3.2 1.3.2 国内研究现状国内研究现状 ................................................................................................................ . (2)2 1.4论文结构论文结构..................................................................................................................................... ..................................................................................................................................... 33 2 2 文献综述文献综述............................................................................................................................ ........................................................................................................................... 4 4 2.1 排队排队............................................................................................................................................ ............................................................................................................................................ 44 2.1.1 2.1.1 排队论排队论............................................................................................................................ ............................................................................................................................ 44 2.1.2 2.1.2 排队系统排队系统........................................................................................................................ ........................................................................................................................ 44 2.1.3 2.1.3 排队系统的基本概念及符号表示排队系统的基本概念及符号表示 .. (6)2.1.4排队系统的常用分布 ..................................................................................................... .. (7)7 2.1.5多服务台排队模型 ......................................................................................................... (8)8 2.2 排队问题的仿真排队问题的仿真........................................................................................................................ ........................................................................................................................ 88 2.2.1 2.2.1 离散事件系统仿真离散事件系统仿真 ........................................................................................................ .. (8)8 2.2.2 Flexsim 2.2.2 Flexsim 软件介绍软件介绍 ........................................................................................................ .. (9)9 2.2.3 Flexsim 软件可以解决的问题 (9)2.3 5W1H 和ECES 技术 ................................................................................... 错误!未定义书签。
基于排队等候时间计算模型的服务管理整合创新

B
55
C
11 4
4
C
2
D
排队有条不紊,客户 可以观察到前一个类 似业务顾客办理流程,
可观摩学习。
合理安排台席数量,某个台席办理某一类别业务
A类为全球通专席普通类专席根据平均受理时长不 同分BCD三类
台席数量可结合统计数据计算设置
B类业务在普通台席里优先级最高,B类C类次之
低级别的台席若无人办理即向高级别柜台相应客 户开放。
营业厅排队等候时间计算模型
Y
w Q / Bn xn n1
w: 客户办理业务平均等待人数 Q:顾客排队等候时间平均值 B: 某类业务占比 x: 营业员处理某类业务的平均时长 n:业务种类数 Y:营业厅办理业务台席数
等候时长难度等级划分-挑战10分钟
营业厅排队现状 w≥5人;x≥2.0分钟
彩信班前会:
市场部发布的重点热点业务,运用第二天的晨会及闲时等其他时间进行抽测,巩固效果。
飞信或QQ学习群:
通过飞信或QQ等方式建立学习群,针对疑难业务或热点业务进行讨论。
业务PK赛、业务宝典点击赛等:
通过组织各类PK赛,激励营业员不断地去熟悉并掌握业务知识,提升业务处理的准确程度和熟练程
度。
预填单示例
店的具体方位; 摆放:营业厅咨询区或入口处。
分流名片示例
第13页
片区营业网点分布图名片
形式:名片; 内容:正面营业网点(包括营业厅或代办点)名称、地址、联系电话、
负责人;背面附上附近片区营业网点分布图; 摆放:营业厅咨询台、 休息区、业务受理台。
排队问题改善策略2–传统排队系统模型
单线/单一服务台席/单一阶段 单线/单一台席/顺序阶段
DXC22-基于排队论的服务系统优化研究——以XX超市收银台为例

1、排队模型排队论是研究排队现象的理论与运用的学科,是专门研究由于随机因素的影响而产生的拥挤现象的科学,有人也称之为随机服务系统,或称之为公用事业的数学方法。
它是运筹学的一个重要的分支。
凡是出现拥挤现象的领域,都可以运用排队论。
在日常的生产和生活中有各种各样的随机服务系统,人们经常会碰到许多有形或无形的排队现象。
例如:到食堂打饭,到车站等车,去超市购物等等。
这些问题中,食堂的服务窗口与打饭者、公共汽车与乘客、超市收银台与购物者都可归结为服务窗口与顾客之间的一种服务关系,都可以当做排队问题来研究,他们之间就构成了一个排队系统或服务系统。
为了统一起见,我们把要求得到服务的对象统称为“顾客”,把提供服务的服务者称之为“服务员”、“服务窗口”、或“服务机构”。
因为顾客的到达情况和每位顾客接受服务的时间往往是无法事先知道的,或者说是随机的。
在排队论所研究的排队系统中,顾客相继到达时间间隔与服务时间这两个变量中至少有一个是随机的,因此排队论又称为随即服务系统理论。
排队系统的一般模型图如图1所示。
下图表明每个来到服务窗口的顾客需要按照排队规则进行排队等候服务,服务窗口则按照服务规则进行服务,顾客接受完服务之后就会离开。
图中的排队结构是指队列的数目和排队的方式,排队规则和服务规则说明顾客在排队系统中是按照什么规则,以什么次序接受服务的。
图1 排队系统一般模型图1)排队论的性态问题所谓排队系统的性态问题就是研究各种排队系统的规律性。
在一个排队系统中,其排队的队长是随机的,顾客等待时间的长短以及服务台繁忙时间的长短也是随机的。
排队系统的规律性主要是研究排队队长的分布、等待时间的分布以及忙期的分布,它包含了瞬间状态和统计平衡条件下的稳态两种情形。
2)排队系统的最优化问题排队系统的最优化问题主要有两类:包括系统的最优化设计和系统的最优化运行控制。
前者又称为静态最优化,后者又称为动态最优化。
前者是在服务系统设置之前就对未来的运行情况进行估计,从而使设计人员有所依据。
免排队服务系统设计与优化研究

免排队服务系统设计与优化研究摘要:随着社会的不断发展,人们对服务效率的要求越来越高,排队成为了大多数服务场所常见的问题。
本文旨在通过设计与优化免排队服务系统,提高服务效率,优化用户体验。
一、引言排队问题在各行各业都普遍存在,如银行、医院、机场等公共场所,以及餐厅、超市等商业场所。
长时间排队不仅影响用户的体验,还会导致资源浪费,因此免排队服务系统的设计与优化是解决这一问题的关键。
二、免排队服务系统设计1. 系统流程设计针对不同场所的需求,免排队服务系统可以采用不同的流程设计。
一般包括用户预约、在线取号、叫号服务等环节。
在设计流程时,应考虑用户操作的便捷性和系统的智能化程度,以提高用户的满意度。
2. 预约与取号功能用户可以通过手机应用或网站进行预约,选择适合自己的时间段。
预约成功后,系统会生成一个唯一的取号码。
用户到达服务场所后,只需通过扫码或输入取号码即可领取号码牌,无需排队等候。
3. 叫号与排队管理服务场所通过叫号系统呼叫用户,用户根据叫号屏上显示的信息前往对应窗口办理业务。
系统应具备智能排队管理功能,能实时更新等待时间,并根据不同业务类型的优先级进行排序,以减少用户的等待时间。
4. 数据统计与分析免排队服务系统应具备数据统计与分析的功能,对用户的预约情况、等待时间、服务效率等数据进行实时监控和分析。
这些数据将帮助管理者优化服务流程,提高服务质量和效率。
三、优化研究1. 人员调度与资源优化基于数据分析结果,管理者可以合理调整窗口人员的分配和工作时间,以应对不同时间段的客流量变化。
同时,可以通过优化布局和增加设备来提高办公效率,避免资源浪费。
2. 智能化技术应用引入人工智能、大数据分析等智能化技术,可以让免排队服务系统更加智能化。
例如,通过用户历史数据分析,系统可以根据用户的喜好推荐最合适的服务窗口,提高服务的个性化程度。
3. 用户反馈与满意度评估免排队服务系统设计应充分考虑用户的需求和意见。
通过用户反馈机制,管理者可以及时了解用户对服务流程的体验和不满意之处,并作出相应的改进,以提升用户的满意度。
基于排队论的麦当劳服务系统优化研究

基于排队论的麦当劳服务系统优化研究摘要:本论文通过实际测量数据的拟合,验证麦当劳的顾客到达分布为泊松分布,服务时间服从指数分布。
运用排队理论建立服务窗口与顾客流量需求相匹配的模型,根据顾客量的变化情况给出服务窗口的合理数量,并提出了几点建议、措施。
关键词:麦当劳;服务窗口;排队论;建议0 引言随着人们生活节奏的加快,越来越多的人选择快餐来节约时间。
麦当劳作为快餐服务行业的代表,逐渐受到大多数年轻群体的喜爱。
通常,人们步入麦当劳就餐会不可避免的遇到排队现象,主要原因在于顾客到达的时间和接受服务的时间都是不确定的。
增加人员和服务设备势必会缓解排队现象,但是会导致投资的增加,也在一定程度上导致了人员和设备空闲的浪费。
如果服务设备过少又会导致排队现象的加重,丧失潜在顾客,收益的减少等风险。
如何找到一个适当的平衡点是管理人员的重要工作之一。
排队理论及其相关模型适合解决排队问题,为解决实际中遇到的难题提供了有效手段。
1 麦当劳就餐排队分析在麦当劳就餐服务系统是一个典型的随机服务系统,其主要包括顾客到达过程、排队规则、服务机构3个基本组成部分。
1)顾客到达过程。
顾客的到达时间只和时间区间的长度有关,不相交的时间区间内到达麦当劳的顾客是独立的,而且顾客到达是一个随机的过程。
2)排队规则。
到达顾客以先到先服务的原则接受服务,且是等待制。
顾客到达麦当劳时,可以根据实际排队的情况选择相对较短的队列接受服务。
有空闲的窗口时,顾客可以直接接受服务,服务结束后离开服务台;若到达时,没有服务窗口空闲,就需要排队等候服务。
3)就餐服务窗口。
它是一个时间确定型的,概率分布为指数分布。
2 相关数据分析与检验(1)顾客到达率的达分布检验一般顾客到达属离散型分布,经验上常用泊松分布拟合。
对于顾客的到达是否遵循泊松分布,相关文献中缺少顾客实际到达观测数据的实际验证研究。
本文中,通过采集顾客的实际到达数据,采用非参数检验方法检验顾客到达的统计分布特性。
《2024年基于排队论的枢纽内出租车上客区服务台优化》范文

《基于排队论的枢纽内出租车上客区服务台优化》篇一一、引言在现代化交通枢纽中,出租车上客区是连接乘客与出租车服务的重要环节。
为了提升服务质量,减少乘客等待时间,本文将基于排队论对枢纽内出租车上客区服务台进行优化研究。
本文首先阐述研究背景及意义,然后介绍排队论的基本原理及其在出租车服务台优化中的应用,最后提出本文的研究目的和研究方法。
二、排队论基本原理及应用排队论,又称为随机服务系统理论,主要研究排队等候和排队系统的设计和分析。
在出租车上客区服务台中,排队现象主要指乘客等待出租车服务的场景。
排队论通过对系统的到达率、服务时间、队列长度等参数进行分析,为服务台优化提供理论依据。
在枢纽内出租车上客区服务台中,排队论的应用主要体现在以下几个方面:1. 到达率分析:通过对乘客到达规律的分析,确定乘客到达的频率和分布情况,为服务台的配置提供依据。
2. 服务时间分析:分析出租车服务台的服务时间分布,找出服务瓶颈,提高服务效率。
3. 队列长度分析:通过对队列长度的分析,确定服务台的合理数量和布局,以减少乘客等待时间。
三、枢纽内出租车上客区现状分析本文以某大型交通枢纽为例,对其出租车上客区进行现状分析。
通过实地调查和数据分析,发现存在以下问题:1. 服务台数量不足:导致乘客等待时间过长,影响乘客体验。
2. 服务效率低下:部分服务台存在服务瓶颈,导致服务时间过长。
3. 布局不合理:服务台布局混乱,不利于乘客快速找到空余服务台。
四、基于排队论的枢纽内出租车上客区服务台优化策略针对上述问题,本文提出以下基于排队论的优化策略:1. 增加服务台数量:根据乘客到达率和排队规律,合理增加服务台数量,以缩短乘客等待时间。
2. 提高服务效率:通过优化服务流程、提高服务质量等措施,降低单个服务台的服务时间。
同时,对存在瓶颈的服务台进行改造升级。
3. 优化布局:根据乘客流量和流动方向,合理规划服务台布局,使乘客能够快速找到空余服务台。
同时,设置指示牌和导引标识,方便乘客快速找到目的地。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于排队论的麦当劳服务系统优化研究摘要:本论文通过实际测量数据的拟合,验证麦当劳的顾客到达分布为泊松分布,服务时间服从指数分布。
运用排队理论建立服务窗口与顾客流量需求相匹配的模型,根据顾客量的变化情况给出服务窗口的合理数量,并提出了几点建议、措施。
关键词:麦当劳;服务窗口;排队论;建议0 引言随着人们生活节奏的加快,越来越多的人选择快餐来节约时间。
麦当劳作为快餐服务行业的代表,逐渐受到大多数年轻群体的喜爱。
通常,人们步入麦当劳就餐会不可避免的遇到排队现象,主要原因在于顾客到达的时间和接受服务的时间都是不确定的。
增加人员和服务设备势必会缓解排队现象,但是会导致投资的增加,也在一定程度上导致了人员和设备空闲的浪费。
如果服务设备过少又会导致排队现象的加重,丧失潜在顾客,收益的减少等风险。
如何找到一个适当的平衡点是管理人员的重要工作之一。
排队理论及其相关模型适合解决排队问题,为解决实际中遇到的难题提供了有效手段。
1 麦当劳就餐排队分析在麦当劳就餐服务系统是一个典型的随机服务系统,其主要包括顾客到达过程、排队规则、服务机构3个基本组成部分。
1)顾客到达过程。
顾客的到达时间只和时间区间的长度有关,不相交的时间区间内到达麦当劳的顾客是独立的,而且顾客到达是一个随机的过程。
2)排队规则。
到达顾客以先到先服务的原则接受服务,且是等待制。
顾客到达麦当劳时,可以根据实际排队的情况选择相对较短的队列接受服务。
有空闲的窗口时,顾客可以直接接受服务,服务结束后离开服务台;若到达时,没有服务窗口空闲,就需要排队等候服务。
3)就餐服务窗口。
它是一个时间确定型的,概率分布为指数分布。
2 相关数据分析与检验(1)顾客到达率的达分布检验一般顾客到达属离散型分布,经验上常用泊松分布拟合。
对于顾客的到达是否遵循泊松分布,相关文献中缺少顾客实际到达观测数据的实际验证研究。
本文中,通过采集顾客的实际到达数据,采用非参数检验方法检验顾客到达的统计分布特性。
以2013年3月在武汉市未来城麦当劳餐饮服务店为研究对象,现场测试并记录了顾客单位时间到达麦当劳的数量,集体数据如下表Table 1 所示。
Table 1 麦当劳顾客单位到达时间统计时间组距到达人数时间组距到达人数11:29-11:31511:59-12:01611:31-11:33712:01-12:03211:33-11:35412:03-12:05111:35-11:37012:05-12:07211:37-11:39112:07-12:09411:39-11:41612:09-12:11511:41-11:43212:11-12:13511:43-11:45512:13-12:15711:45-11:47212:15-12:17511:47-11:49712:17-12:19311:49-11:51212:19-12:21611:51-11:53712:21-12:231211:53-11:55612:23-12:25511:55-11:57212:25-12:27511:57-11:59712:27-12:292基于Table1的数据,运用,运用柯尔莫哥洛夫斯米洛夫检验方法(Kolmogorov Smirnov,1-K S检验),利用SPSS软件分析,对麦当劳的顾客到达是否服从泊松分布进行检验,计算得出样本数据的均值为4.43,最大正差值为0.152,最大负差值为0.111,泊松检验参数双尾渐近概率值为0.491,大于0.05(即P>0.05 ),通过显著性检验,可以认为顾客到达服从泊松分布。
Table 2 顾客到达时间 Kolmogorov -Smirnov 检验(2)λ值的确定由于Poisson 分布中的参数λ是未知的,需采用极大似然估计法来估计这个参数。
设总体X 服从参数为λ的Poisson 分布,即P (X =k )= !ke k λλ-,k =0,1,2….12,,...n X X X 为来自总体X 的样本,12,,...n x x x 是相应样本12,,...n X X X 的一个样本值,则样本的极大似然函数是11()()!innii i i L P X x e i λλ-=====∏∏对上式两边取对数得11ln ()ln ln(!)n ni i i i L x n x λλλ===--∑∑,令1ln ()nii xd L n d λλλ==-=∑则λ的最大似然估计值为11ˆn i i x x n λ===∑由于样本的均值为4.43,统计的时间间隔为2分钟,则ˆλ=2.22人/min 。
(3)顾客服务时间的检验根据原始数据,我们可以计算出平均服务时间为150.31s. 服务时间统计结果见表Table 3Table 3 麦当劳顾客的服务时间统计运用SPSS 软件对数据进行处理,对麦当劳的顾客服务时间是否服从指数分布进行检验,计算得出样本数据的均值为7.25,最大正差值为0.469,最大负差值为0.089,泊松检验参数双尾渐近概率值为0.342,大于0.05,通过显著性检验,可以认为顾客到达服从指数分布。
结果如下:Table 4 顾客服务时间 Kolmogorov -Smirnov 检验 参数描述服务时间统计N5a 指数参数。
b, c 均值 7.25 最极端差别绝对值 .469 正差值 .469 负差值-.089 Kolmogorov -Smirnov Z .939 渐近显著性(双侧) .3422) μ值的确定负指数分布中包含参数μ,我们还是采用极大似然来估计该参数值。
设总体T 服从负指数分布,即,0()0,t<0t e t f t μμ-⎧≥=⎨⎩12,,...n T T T 为来自总体T 的样本,12,,...n t t t 是相应于12,,...n T T T 的一个样本值,则样本的似然函数是:11()(,)in nt i i i L P t e μμθμ-====∏∏对上式两边取对数得:1ln ()ln ()ni i L n t λμμ==-∑,令1ln ()0ni i d L nt d μλμ==-=∑则μ的最大似然估计值为11ˆ/ni i n t tμ===∑ 由t =150.31s 知ˆ 2.505μ=3 麦当劳服务窗口排队模型的建立由于顾客到达率服从泊松分布,顾客的服务时间服从负指数分布,其分布函数为:(),0t f t e t ββ-=≥,其中1/βλ=,λ表示一定时间内到达顾客的数目。
可以将其设定为M/M/s 排队系统,M/M/s 分布表示到达时间为泊松分布。
服务时间为指数分布,服务设备的数量。
对于每个顾客可以用3个变量来描述,即:与前一个顾客到达时间的间隔,排队时间及接受服务的时间。
顾客到达的时间间隔t 、接受服务时间μ、服务窗口s 和单位时间内顾客到达数量λ为输入值,模型的计算值为顾客排队等待时间(包括等待时间q W 、逗留时间s W )和队列长度(包括队长s L 队列长q L )变化,令 /s ρλμ=模型的特征指标如下: 1)服务窗口的空闲概率0P011/)/)()!!n s s n P s n s s λμλμμμλ-==+-∑(( 式中:n 为s 的过程变量,n =0,1,…s 2)队列中平均等待的顾客数量q L2(/)(1)!(s 1)s q L P s λμλμμ=--3)服务区的平均旅客数量s L/s q L L λμ=+4)顾客排队的平均等待时间q W q W =/q L λ5)顾客排队的平均逗留时间s Wq W =+1/q W μ4相关计算与结果分析(1)由前知:λ=x =2.22人/min ;μ=1t =2.505人/min ;s P 0 ρ L q /人 L s /人 W q /min W s /min 1 0.1138 0.8862 6.9032 7.7895 3.1096 3.5088 2 0.3859 0.4431 0.2165 1.103 0.0975 0.4967 3 0.4092 0.2954 0.0282 0.9145 0.0127 0.4119 4 0.41190.22160.00390.89010.00170.4009(2)s 的最优解的确定、分析模型中的s 的最优解,可以通过建立s 的目标函数来求解,由于ρ<1,系统处于稳定的状态,此时单位时间的全部费用的期望值:Z()s s ws s C L C ⨯+⨯=式子中:s 表示服务台的数量,s C 是服务台服务员的单位时间服务成本,s L 为顾客的平均数量,w C 是顾客停留在服务系统中的等待的单位时间成本。
由于s 只可以去整数值,所以最优的服务窗口数目*s 不能用()f s 对s 的微分法求得,只能用边际分析法求得。
根据Z(s)最小的特点,有:****()(1)()(1)z s z s z s z s ⎧≤-⎨≤+⎩; 将Z (s )带入式中有:********()(1)(1)()(1)(1)s s w s s ws s w s s wL C L C L C L C ⎧⋅+⋅≤-⋅+-⋅⎨⋅+⋅≤+⋅++⋅⎩s C s s C s s C s s C s , 化简后得:****()(1)/(1)()s s s w s s L L C L L -+≤≤--s s C s s依次求s=2,3,4时的L 值,并作两相邻的L 值之差,因为/s w C C 是已知数,根据这个数落在那个不等式的区间就可以确定*s 的最优解,这个区间就是最优区间。
1)s C 和w C 值的确定①在武汉地区,麦当劳餐饮服务中, 从事服务业工作的员工的平均月工资为2200元。
每天正常工作7小时,休息1小时,采用三班制轮流值班。
因此,可以确定每个服务台的单位时间成本,s C =2200/(30*8*60)=0.1528元/min ;②w C 是顾客在系统中等待造成的损失。
一旦顾客在系统中停留的时间超过其能够忍耐的时间,顾客就会离去,造成一定程度的损失。
通过调查问卷或者查询系统中顾客每笔消费,我们可以大体知道平均的消费水平,以消费金额除以顾客的消费时间即w C 的值。
本文中w C 的统计计算值为5.25元/min. 2)由上可知/s w C C =0.1528/5.25=0.0291。
3)最优解的求解:4)计算结果分析/s w C C 落在区间(0.0244~0.1885)中,满足边际分析要求。
此时,*s =3时,总费用达到最小,*z=5.259 (元)。
目前,服务系统的服务台数s=2,所以需要再增加一个服务窗口。
5 结束语本文通过实际调查和测量数据,用SPSS软件检验通过了麦当劳顾客的到达率分布为Poisson分布,顾客的服务时间服从指数分布;通过M/M/s模型的建立与费用优化配置,使该服务系统达到最优状态。
