材料力学(金忠谋)第六版答案第16章
材料力学(金忠谋)第六版课后习题及答案

解
(1) ∆l1
=
1 3
Ρxl1
Ε 1Α1
∆l1 = ∆l2 x = 0.6m
∆l 2
=
1 3
Ρ (3 − x)l2
Ε 2Α2
(2) Ρ ≤ 3Ε1Α1 = 3× 200 × 2 ×10−1 = 200ΚΝ
xl1
0.6× 2
2-11 铰接的正方形结构如图所示,各杆材料皆为铸铁,许用拉应力[σ +]=400kg/cm2, 许用压应力[σ − ]=600kg/cm2,各杆的截面积均等于25cm2。试求结构的许用载荷P。
习题
2-1 一木柱受力如图示,柱的横截面为边长20cm的正方形,材料服从虎克定律,其
弹性模量 E = 0.10 ×105 MPa.如不计柱自重,试求:
(1) (2) (3) (4)
作轴力图; 各段柱横截面上的应力; 各段柱的纵向线应变; 柱的总变形.
解:
(1) 轴力图
(2) AC 段应力
σ
=
−100 ×103 0.2 2
= −2.5×106 Ρa = −2.5ΜΡa
CB 段应力
σ
=
− 260 ×103 0.2 2
= −6.5×106 Ρa = −6.5ΜΡa
(3) AC 段线应变
ε = σ = −2.5 = −2.5×10−4 Ε 0.1×105 CB 段线应变
ε
=σ Ε
=
−6.5 0.1×10 5
解:
AC、CB、BD、DA 杆受拉力,大小为 Τ1 =
Ρ 2
DC 杆受压力,大小为 Τ2 = Ρ
[σ
+
]≥
Τ1 Α
得 Ρ1 ≤ 2 × 400 × 25 = 14142kg
材料力学(金忠谋)第六版答案第15章

习 题14-1 195-2c 型柴油机连杆大头螺栓如图示,工作时所受最大拉力P max =9.58 kN ,P min=8.71 kN ,螺栓最小直径d =8.5mm 。
试求其应力幅a σ,平均应力m σ和循环特征r ,并作出t -σ曲线。
解:()()MPaA P P A P a a67.7105.814.3412/1071.858.92//623min max =⨯⨯⨯⨯⨯-=-==-σ ()()MPaA P P A P m m161105.814.3412/1071.858.92//623min max =⨯⨯⨯⨯⨯+=+==-σ91.0maxmin ==σσr14-2 某阀门弹簧如图所示,当阀门关闭时,最小工作载荷P min =200N , 当阀门顶开时最大工作载荷P max =500N 。
设簧丝的直径d =5mm ,弹簧外径mm D 361=,试求平均应力m τ,应力振幅a τ,循环特性r ,并作出t -τ曲线。
解:4.14/==d D C∴()()09.134/24=-+=C C K∴MPadD P Km m 28010514.31023625002001609.12/169333=⨯⨯⨯⨯+⨯⨯==--πτMPadD P Ka a 12010514.31023622005001609.12/169333=⨯⨯⨯⨯-⨯⨯==--πτ4.0/max min ==P P r14-3 阶梯轴如图所示。
材料为铬镍合金钢,MPa b 920=σ,MPa 4201=-σ,MPa 2501=-τ。
轴的尺寸d =40mm ,D =50mm ,r =5mm 。
试计算弯曲和 扭转时的有效应力集中系数和尺寸系数。
解: 由已知条件25.1=d D ,125.0=dr查图表14-12(c )可得57.1=σK 由图表14-16,当d=40mm 时对MPa b 500=σ的钢材,84.0=σε 对MPa b 1200=σ的钢材,73.0=σε 对MPa b 920=σ的钢材, ()774.073.084.05001200920120073.0=-⨯--+=σε14-4 图示为一货车车轴,轴上的载荷P =110kN ,轴的材料为碳钢,MPa b 550=σ,MPa 2401=-σ,mm a 118=,mm l 1435=,mm d 133=,mm D 146=,mm r 20=,轴表面经磨削加工,规定安全系数8.1=n 。
材料力学(金忠谋编)第六版答案第13章

第十二章超静定系统12-1 试问下列结构(梁或刚架)中那些是静定的?哪些是超静定的?若是超静定的,试说明它的次数。
答:a , 静定b , f , 一次超静定d ,e , 二次超静定g , h , 三次超静定c , 几何可变12-2 试求下列各超静定梁的支反力,设各梁均为等截面梁,其抗弯刚度为EI。
a)解:图a 可分解如下图0=+BR BP f f ---------(1) EIL R f EIPL L L EIPlf B BR BP 3485)23(2432=-=--=代入(1)式得 163;)(1611;)(165PL MR P R AA B =↑=↑=( )b)解:设支承B 反力为B R由P 和B R 共同作用下B 点的总挠度要求为零,即有 ()()↓=↑==+-⨯-=+P R P EI L R L L EIPLf f C B BR BP 43;47R 03)5.13(60B 32PL MC41=(⌫)c)解:设支承B 反力为B R ,则必定有0=+BR BP f f ---------(1)EIlR EIl R f EIb l Pb f B B BR BP 648)2(48]4)2(3[3322==--=代入(1)式 得 3222)3(lb l Pb R B -=d)解:0M MA-= ( ))(23)(2323;23,3)(,2002032↓=↑+==-=--=-==+lM R P l M R lM P R EIl M l EIP R l EIP R f EI Mlf f f A B B B B BRP BM BRP BMe)解:e 图可由下图e ’和e ”叠加而成因为BB RB qp RB qp R EIlEIl R f qlEIl l EIl ql l EIqlEI qlf f f 383)2(4895)236(6))((68)1(033422334==-=--⋅--=-----=+代入(1)式得 )(12895↑=q l R B ; )(256`161↑=q l R A ;26433q l MA-= ( )f)解:A , B 端转角为零,则有:0,0=+BAMAMAq θθ ----------(1) 0,0=+BAMBMBq θθ ----------(2)式中,EIlq Aq 3608300-=θ ; EIlq Bq 3607300=θEI lMEI lMBAMAMBA63,⋅+⋅=θEIlMEIlMABMBMBA63,⋅-⋅-=θ将以上θ表达式代入(1),(2)联立求解得:20201l q MA=; 20301l q MB=; l q R A 0207= ; l q R B 0203=12-3 梁AB 的一端固定,另端由拉杆拉住,梁与杆系用同一材料两成,其弹性模量为E ,梁截面惯矩为I ,拉杆的截面积为A ,梁上承受均布载荷q ,试求拉杆BC 的内力。
材料力学(金忠谋)第六版答案-附录

材料力学(金忠谋)第六版答案-附录附录I 截面图形的几何性质I-1 求下列截面图形对z 轴的静矩与形心的位置。
解:(a ))2)2((2)2(2h t h b t h ht t h bt s z ++=⋅++=hb h t h b h b t h t h b t A s y zc +++=+++==2)2()()2)2((22(b )322332219211)}2)4()43()41()43(32(])4()43[(2{4442DD D D D D D D D D s z =--⨯-+⨯⨯-=ππDD D D D DAs y z c 1367.0])2()43[(2)44(219211223=-⨯+⨯==π(c )]22)[(22)(2h t t b t h ht t t t b s z +⋅-=⨯+⨯⨯-=tb)(2)(2t b h h t t b A s y z c -++-==I-2 试求(1)图示工字形截面对形心轴 y 及 z 的惯性矩zI 与I y 。
(2)图示 T 字形截面对形心轴的惯矩zI 与I y 。
解(a)12)2)((12)2)((123333t h t b bh t h t b bh J z ---=---=12))2(2(12))(2(1222333t t h b t t t h tb J y -+=-+=(b) cmy c 643.9)520515(2)515(552522=⨯+⨯-⨯+⨯=(b433423231615121551252010186520)643.91025(12205515)5.2643.9(12515cm J cm J y z =⨯+⨯==⨯⨯--+⨯+⨯⋅-+⨯=I-3 求图示椭圆截面对长轴的惯矩、惯性半径与对形心的极惯矩。
解:θθcos ,sin ⋅=⋅=a z b yθθd b dy cos = ⎰⎰--⋅==∴b bbbz zdyy dA y J 222322223224cos sin 2cos cos sin 2ab d abd b a b J bb z πθθθθθθθππ==⋅=⎰⎰--)(4)(42422333b a ab b a ab J J J b ab ab AJ i y z p zz +=+=+====ππππI-4 试求图示的41的圆面积(半径a )对于z ,yyy 轴的惯性积zyI 。
材料力学(金忠谋)第六版完整版问题详解

第一章 绪论1-1 求图示杆在各截面(I )、(II )、(III )上的力,并说明它的性质.解:(a )I-I 截面: N = 20KN (拉)II-II 截面: N = -10KN (压)III-III 截面: N = -50KN (压)(b )I-I 截面: N = 40KN (拉)II-II 截面: N = 10KN (拉)III-III 截面: N = 20KN (拉)1-2 已知P 、M 0、l 、a ,分别求山下列图示各杆指定截面(I )、(II)上的力解:(a ):(I )截面:力为零。
(II )截面:M = Pa (弯矩)Q = -P (剪力)(b ):(I )截面:θsin 31P Q =θsin 61PL M = (II )截面:θsin 32P Q = θsin 92PL M =(c ):(I )截面:L M Q 0-= 021M M = (II )截面:L M Q 0-= 031M M =1-3 图示AB 梁之左端固定在墙,试求(1)支座反力,(2)1-1、2-2、3-3各横截面上的力(1-1,2-2是无限接近集中力偶作用点.)解:10110=⨯=A Y (KN )1055.110-=+⨯-=A M (KN-M )(1-1) 截面:10110=⨯=Q (KN )521110-=⨯⨯-=M (KN-M ) (2-2)截面:10=Q (KN )055=-=M (KN-M )(2-3)截面:10=Q (KN )551110-=+⨯⨯-=M (KN-M )1-4 求图示挂钩AB 在截面 1-1、2-2上的力.解:(1-1)截面:P N 32=a P M ⋅=43 (2-2)截面:P Q 32=a P M ⋅=321-5 水平横梁AB 在A 端为固定铰支座,B 端用拉杆约束住,求拉杆的力和在梁1-1截面上的力.解:(1)拉杆力T :1230sin 0⨯=⨯⋅=∑P T M A ο 10030sin 2100=⨯=οT (KN )(拉) (2)(1-1)截面力:Q 、N 、M :5030sin -=-=οT Q (KN )6.8630cos -=-=οT N (KN )(压)()2550.030sin =⨯=οT M (KN-M )1-6 一重物 P =10 kN 由均质杆 AB 及绳索 CD 支持如图示,杆的自重不计。
材料力学(金忠谋)第六版答案第14章

材料力学(金忠谋)第六版答案第14章第十三章 动载荷13-1 铸铁杆AB 长m l 8.1=,以等角速度绕垂直轴O -O 旋转如图示。
已知铸铁的比重3/74m kN =γ,许用拉应力[]MPa 40=σ,材料的弹性模量E =160 Gpa 。
试求此杆的极限转速,并计算此杆在转速m r n /100=时的绝对伸长。
解: (1) 极限转速m rn s s l g l g A A Ndl gA dr r qd r Nd x r gAdr ma r qd x r a jx dl n n 1092260137.114175.130799.010*******.92)2(][2][)2(21][)2(21)()()()()(235222222222====⨯⨯⨯⨯⨯=≤≤≤======⎰πωωγσωσωγσσωγωγω(2) 当n =1000m rcm m Eg l r EA r Nd l s n l 0252.01052.28.91016039.072.104107423)2(2)(2172.1046010002602492233220=⨯=⨯⨯⨯⨯⨯⨯⨯===∆=⨯==-⎰ωππω(2)吊索: MPa A P d d 55.2105276.14max=⨯==-σ13-3 轴上装一钢质圆盘,盘上有一圆孔。
若轴与盘以s140=ω的匀角速度旋转,论求轴内由这一圆孔引起的最大正应力。
解:23max max 22225.1212.021*********.01060041411060064003.03.047800640404.0mMN W M mN L P N Na gA ma P s m r a z d d d d n n d n =⨯⨯==⋅=⨯⋅===⨯⨯⨯⨯=⋅⋅⋅===⨯==πσπδγω13-4 飞轮轮缘的平均直径D =1.2m ,材料比重3/72m kN =γ,弹性模量GPa E 200=,轮缘与轮幅装配时的过盈量mmD2.0=∆,若不计轮相的影响,求飞轮允许的最大转速。
材料力学(金忠谋)第六版完整编辑版规范标准答案

解:(a):(I)截面:内力为零。
(II)截面:M = Pa(弯矩)
Q = -P(剪力)
(b):(I)截面:
(II)截面:
(c):(I)截面:
(II)截面:
1-3图示AB梁之左端固定在墙内,试求(1)支座反力,(2)1-1、2-2、3-3各横截面上的内力(1-1,2-2是无限接近集中力偶作用点.)
解:
(1)
(2)
即
解得
各杆的长度为
2-37图示三杆结构中,杆(1)是铸铁的,E1=120Gpa, =80MPa;杆(2)是铜的,EA=100GPa, =60Gpa;杆(3)是钢的,EA=200GPa, =120Mpa。载荷P=160kN,设A1:A2:A3=2:2:1,试确定各杆的截面积。
解:
各杆的应力关系为
解
(1)
(2)
2-11铰接的正方形结构如图所示,各杆材料皆为铸铁,许用拉应力[ +]=400kg/cm2,许用压应力[ ]=600kg/cm2,各杆的截面积均等于25cm2。试求结构的许用载荷P。
解:
AC、CB、BD、DA杆受拉力,大小为
DC杆受压力,大小为
得
得
故
2-12图示拉杆沿斜截面m-n由两部分胶合而成,设在胶合面上许用拉应力[ ]=100MPa,许用剪应力 =50MPa,胶合面的强度控制杆件的拉力,试求:为使杆件承受最大拉力P, 角的值应为多少?若横截面面积为4cm2,并规定 ,试确定许可载荷P。
解:
只计P时,有
只计2P时,有
且有
联立,解得
(方向水平向左) (方向水平向右)
(b)
材料力学课后标准答案

解:取轴向长为 的管分析:微元 上,作用力为
向分量 ,积分得
则: ,而
则:
题6-12图题6-13图
6-13长输水管受内压 ,管的内径为 , , ,用第四强度理论计算壁厚。(提示:可设管的轴向应变为零。)
解: ,数据代入,得:
,
所以
现已知
,
得
题6-5图
题6-6图题6-7图
6-6图示简支梁为 工字梁, , 。 点所在截面在集中力 的左侧,且无限接近 力作用的截面。试求: 点在指定斜截面上的应力; 点的主应力及主平面位置(用单元体表示)。
解: 所处截面上弯矩、剪力:
,
查型钢表后, 点以下表面对中性轴静矩:
,
同理,积分得
所以, 处转角为 ,为顺时针方向; 处挠度为 ,为竖直向下。
8-6试求图示各刚架 点的竖直位移,已知刚架各杆的 相等。
解: 段: ; 段上
由卡氏定理, 处的竖直位移
分段带入后面积分:
为正值,则与 同向,竖直向下
分析可知, 处已经作用有竖直方向的力,为了能利用卡氏定理解题, 处和竖杆中间处的 分别为
(压), (拉)
进而求得 (拉),由
求得:
8-3计算图示各杆件结构的变形能。
题8-3图
解: 首先求解 处的约束反力为
弯矩方程为:
则
分段积分:
解: 以逆时针方向为正,
,积分得
8-4试求图示各梁的 点的挠度的转角。
题8-4图
解: 以 点为 轴起点,结构的弯矩方程为:
则:
得
撤去 和 ,在 处作用逆时针向
(完整版)材料力学课后习题答案
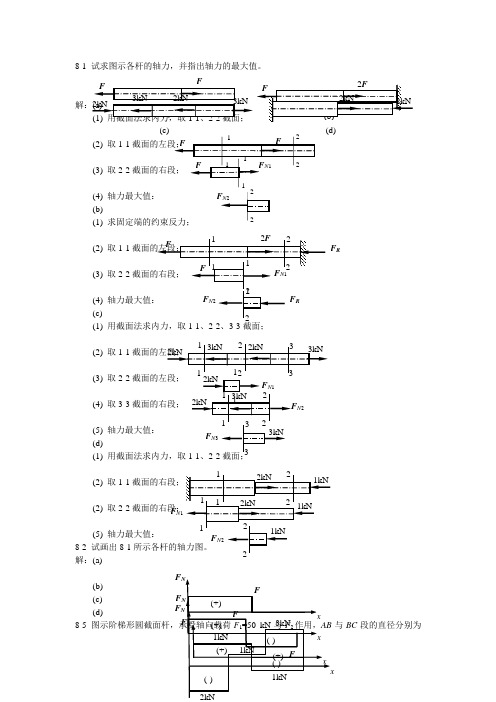
8-1 试求图示各杆的轴力,并指出轴力的最大值。
(2) 取1-1(3) 取2-2(4) 轴力最大值: (b)(1) 求固定端的约束反力; (2) 取1-1(3) 取2-2(4) (c)(1) 用截面法求内力,取1-1、2-2、3-3截面;(2) 取1-1(3) 取2-2 (4) 取3-3截面的右段;(5) 轴力最大值: (d)(1) 用截面法求内力,取1-1、(2) 取1-1(2) 取2-2(5) 轴力最大值: 8-2 试画出8-1解:(a) (b) (c) (d) 8-5与BC 段的直径分别为(c) (d)F RN 2F N 3 F N 1F F Fd 1=20 mm 和d 2=30 mm ,如欲使AB 与BC 段横截面上的正应力相同,试求载荷F 2之值。
解:(1) 用截面法求出(2) 求1-1、2-28-6 题8-5段的直径d 1=40 mm ,如欲使AB 与BC 段横截面上的正应力相同,试求BC 段的直径。
解:(1)用截面法求出1-1、2-2截面的轴力;(2) 求1-1、2-2截面的正应力,利用正应力相同;8-7 图示木杆,承受轴向载荷F =10 kN 作用,杆的横截面面积A =1000 mm 2,粘接面的方位角θ= 450,试计算该截面上的正应力与切应力,并画出应力的方向。
解:(1) (2) 8-14 2=20 mm ,两杆F =80 kN 作用,试校核桁架的强度。
解:(1) 对节点A(2) 列平衡方程 解得: (2) 8-15 图示桁架,杆1A 处承受铅直方向的载荷F 作用,F =50 kN ,钢的许用应力[σS ] =160 MPa ,木的许用应力[σW ] =10 MPa 。
解:(1) 对节点A (2) 84 mm 。
8-16 题8-14解:(1) 由8-14得到的关系;(2) 取[F ]=97.1 kN 。
8-18 图示阶梯形杆A 2=100 mm 2,E =200GPa ,试计算杆AC 的轴向变形 解:(1) (2) AC 8-22 图示桁架,杆1与杆2的横截面面积与材料均相同,在节点A 处承受载荷F 作用。
材料力学(金忠谋)第六版答案第12章
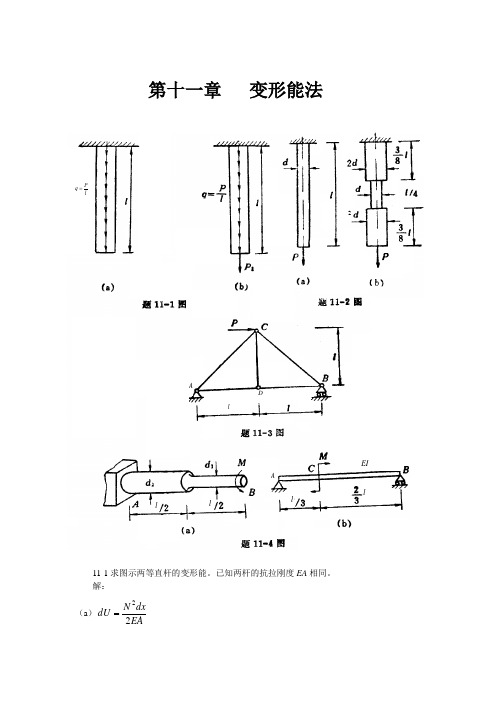
(3)求 和 ,由
得
11-15桁架结构尺寸受载如图示,各杆的抗拉压刚度均相同,试求:(a)A点的铅直位移,(b)节点A和E之间的相对位移。
解:
各杆编号如图示,分别计算出外载内力 、A点作用铅直向下单位力时内力 及在节点A.E处分别加一单位力时各杆内力 ,列表计算如下:
解:
AE、AF、BE、BF各杆轴力为零,画 图;在A、B各点加一等值共线反向力“1”,各杆轴力均为“1”,作 图,如图示。
根据位移互等定理,若在A、B处加一对等值反向的力P,则
11-18试证明在图示两相同的悬臂梁上,图(a)截面A的挠度和图(b)截面B的挠度相等。
证明:在(a)图A点加单位力,在(b)图B点加单位力。
在图(a)中,
在图(b)中
证毕。
11-19图示刚架的各组成部分的抗弯刚度EI相同,抗扭刚度GIp也相同。在P力作用下,试求截面A和C的水平位移。
解:
AD段,
CD段,
DB段,
在A点作用一个水平单位力,如图,各段 均为零。
在C点作用一水平单位力,各段弯矩和扭矩分别为
AD段,
的EI、GIp相等,A处有一缺口,受一对垂直于刚架平面的铅直力P作用,试求缺口两侧的相对位移δ。
解:
11-13图示结构在截面C处受垂直集中力P的作用,试用能量法计算截面C的垂直位移。设BC杆的抗弯刚度为EI,AD杆的拉压刚度为EA,BD=DC=a。
解:
外力作用下得
在单位力(C点)作用下得
11-14图示桁架的各杆拉压刚度EA均相同,在P力作用下,求节点A的位移和AB杆
的转角。
材料力学习题及答案

资料力学-学习指导及习题谜底之迟辟智美创作第一章绪论1-1 图示圆截面杆,两端接受一对方向相反、力偶矩矢量沿轴线且年夜小均为M的力偶作用.试问在杆件的任一横截面m-m上存在何种内力分量,并确定其年夜小.解:从横截面m-m将杆切开,横截面上存在沿轴线的内力偶矩分量M x,即扭矩,其年夜小即是M.1-2 如图所示,在杆件的斜截面m-m上,任一点A处的应力p=120 MPa,其方位角θ=20°,试求该点处的正应力σ与切应力τ.解:应力p与斜截面m-m的法线的夹角α=10°,故σ=p cosα=120×cos10°=118.2MPaτ=p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆,横截面上的正应力沿截面高度线性分布,截面顶边各点处的正应力均为σmax=100 MPa,底边各点处的正应力均为零.试问杆件横截面上存在何种内力分量,并确定其年夜小.图中之C点为截面形心.解:将横截面上的正应力向截面形心C简化,得一合力和一合力偶,其力即为轴力F N=100×106×××103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示.试求棱边AB与AD的平均正应变及A 点处直角BAD的切应变.解:第二章轴向拉压应力2-1试计算图示各杆的轴力,并指出其最年夜值.解:(a) F N AB=F,F N BC=0,F N,max=F=F(b) F N AB=F,F N BC=-F,F N,max(c) F N AB=-2 kN, F N2BC=1 kN,F N CD=3 kN,F N=3 kN,max(d) F N AB=1 kN,F N BC=-1 kN,F N=1 kN,max2-2 图示阶梯形截面杆AC,接受轴向载荷F1=200 kN与F2=100 kN,AB段的直径d1=40 mm.如欲使BC与AB段的正应力相同,试求BC段的直径.解:因BC与AB段的正应力相同,故2-3 图示轴向受拉等截面杆,横截面面积A=500 mm2,载荷F=50 kN.试求图示斜截面m-m上的正应力与切应力,以及杆内的最年夜正应力与最年夜切应力.解:2-4(2-11)图示桁架,由圆截面杆1与杆2组成,并在节点A接受载荷F=80kN作用.杆1、杆2的直径分别为d1=30mm和d2=20mm,两杆的资料相同,屈服极限σ=320MPa,平安因数n s.试校核桁架的强度.s解:由A点的平衡方程可求得1、2两杆的轴力分别为由此可见,桁架满足强度条件.2-5(2-14)图示桁架,接受载荷F作用.试计算该载荷的许用值[F].设各杆的横截面面积均为A,许用应力均为[σ].解:由C点的平衡条件由B点的平衡条件1杆轴力为最年夜,由其强度条件2-6(2-17)图示圆截面杆件,接受轴向拉力F作用.设拉杆的直径为d,端部墩头的直径为D,高度为h,试从强度方面考虑,建立三者间的合理比值.已知许用应力[σ]=120MPa,许用切应力[τ]=90MPa,许用挤压应力[σbs]=240MPa.解:由正应力强度条件由切应力强度条件由挤压强度条件式(1):式(3)得式(1):式(2)得故D:h:d::12-7(2-18)图示摇臂,接受载荷F1与F2作用.试确定轴销B的直径d.已知载荷F1=50kN,F2,许用切应力[τ]=100MPa,许用挤压应力[σ]=240MPa.bs解:摇臂ABC受F1、F2及B点支座反力F B三力作用,根据三力平衡汇交定理知F B的方向如图(b)所示.由平衡条件由切应力强度条件由挤压强度条件故轴销B的直径第三章轴向拉压变形3-1 图示硬铝试样,厚度δ=2mm,试验段板宽b=20mm,标距l=70mm.在轴向拉F=6kN的作用下,测得试验段伸长Δl,板宽缩短Δb.试计算硬铝的弹性模量E与泊松比μ.解:由胡克定律3-2(3-5) 图示桁架,在节点A处接受载荷F作用.从试验中测得杆1与杆2的纵向正应变分别为ε1×10-4与ε2×10-4.试确定载荷F及其方位角θ之值.已知杆1与杆2的横截面面积A1=A2=200mm2,弹性模量E1=E2=200GPa.解:杆1与杆2的轴力(拉力)分别为由A点的平衡条件(1)2+(2)2并开根,便得式(1):式(2)得3-3(3-6) 图示变宽度平板,接受轴向载荷F作用.试计算板的轴向变形.已知板的厚度为δ,长为l,左、右真个宽度分别为b1与b2,弹性模量为E.解:3-4(3-11) 图示刚性横梁AB,由钢丝绳并经无摩擦滑轮所支持.设钢丝绳的轴向刚度(即发生单位轴向变形所需之力)为k,试求当载荷F作用时端点B的铅垂位移.解:设钢丝绳的拉力为T,则由横梁AB的平衡条件钢丝绳伸长量由图(b)可以看出,C点铅垂位移为Δl/3,D点铅垂位移为2Δl/3,则B点铅垂位移为Δl,即 3-5(3-12) 试计算图示桁架节点A的水平与铅垂位移.设各杆各截面的拉压刚度均为EA.解:(a) 各杆轴力及伸长(缩短量)分别为因为3杆不变形,故A点水平位移为零,铅垂位移即是B点铅垂位移加2杆的伸长量,即(b)点的水平与铅垂位移分别为(注意AC杆轴力虽然为零,但对A位移有约束)3-6(3-14) 图a所示桁架,资料的应力-应变关系可用方程σn=Bε暗示(图b),其中n和B为由实验测定的已知常数.试求节点C的铅垂位移.设各杆的横截面面积均为A.(a) (b)解:2根杆的轴力都为2根杆的伸长量都为则节点C的铅垂位移3-7(3-16) 图示结构,梁BD为刚体,杆1、杆2与杆3的横截面面积与资料均相同.在梁的中点C接受集中载荷F作用.试计算该点的水平与铅垂位移.已知载荷F=20kN,各杆的横截面面积均为A=100mm2,弹性模量E=200GPa,梁长l=1000mm.解:各杆轴力及变形分别为梁BD作刚体平动,其上B、C、D三点位移相等3-8(3-17) 图示桁架,在节点B和C作用一对年夜小相等、方向相反的载荷F.设各杆各截面的拉压刚度均为EA,试计算节点B和C间的相对位移ΔB/C.解:根据能量守恒定律,有3-9(3-21) 由铝镁合金杆与钢质套管组成一复合杆,杆、管各载面的刚度分别为E1A1与E2A2.复合杆接受轴向载荷F作用,试计算铝镁合金杆与钢管横载面上的正应力以及杆的轴向变形.解:设杆、管接受的压力分别为F N1、F N2,则F N1+F N2=F (1)变形协调条件为杆、管伸长量相同,即联立求解方程(1)、(2),得杆、管横截面上的正应力分别为杆的轴向变形3-10(3-23) 图示结构,杆1与杆2的弹性模量均为E,横截面面积均为A,梁BC为刚体,载荷F=20kN,许用拉应力[σt]=160MPa,许用压应力[σc]=110MPa.试确定各杆的横截面面积.解:设杆1所受压力为F N1,杆2所受拉力为F N2,则由梁BC的平衡条件得变形协调条件为杆1缩短量即是杆2伸长量,即联立求解方程(1)、(2)得因为杆1、杆2的轴力相等,而许用压应力小于许用拉应力,故由杆1的压应力强度条件得3-11(3-25) 图示桁架,杆1、杆2与杆3分别用铸铁、铜和钢制成,许用应力分别为[σ1]=40MPa,[σ2]=60MPa,[σ3]=120MPa,弹性模量分别为E1=160GPa,E2=100GPa,E3=200GPa.若载荷F=160kN,A1=A2=2A3,试确定各杆的横截面面积.解:设杆1、杆2、杆3的轴力分别为F N1(压)、F N2(拉)、F N3(拉),则由C点的平衡条件杆1、杆2的变形图如图(b)所示,变形协调条件为C点的垂直位移即是杆3的伸长,即联立求解式(1)、(2)、(3)得由三杆的强度条件注意到条件 A1=A2=2A3,取A1=A2=2A3=2448mm2.3-12(3-30) 图示组合杆,由直径为30mm的钢杆套以外径为50mm、内径为30mm的铜管组成,二者由两个直径为10mm的铆钉连接在一起.铆接后,温度升高40°,试计算铆钉剪切面上的切应力.钢与铜的弹性模量分别为E s=200GPa与E c=100GPa,线膨胀系数分别为αl s×10-6℃-1与αl c=16×10-6℃-1.解:钢杆受拉、铜管受压,其轴力相等,设为F N,变形协调条件为钢杆和铜管的伸长量相等,即铆钉剪切面上的切应力3-13(3-32) 图示桁架,三杆的横截面面积、弹性模量与许用应力均相同,并分别为A、E与[σ],试确定该桁架的许用载荷[F].为了提高许用载荷之值,现将杆3的设计长度l酿成l+Δ.试问当Δ为何值时许用载荷最年夜,其值[F max]为何.解:静力平衡条件为变形协调条件为联立求解式(1)、(2)、(3)得杆3的轴力比杆1、杆2年夜,由杆3的强度条件若将杆3的设计长度l酿成l+Δ,要使许用载荷最年夜,只有三杆的应力都到达[σ],此时变形协调条件为第四章扭转4-1(4-3) 图示空心圆截面轴,外径D=40mm,内径d=20mm,扭矩T=1kN•m.试计算横截面上的最年夜、最小扭转切应力,以及A点处(ρA=15mm)的扭转切应力.解:因为τ与ρ成正比,所以4-2(4-10) 实心圆轴与空心圆轴通过牙嵌离合器连接.已知轴的转速n=100 r/min,传递功率P=10 kW,许用切应力[τ]=80MPa,d1/d2.试确定实心轴的直径d,空心轴的内、外径d1和d2.解:扭矩由实心轴的切应力强度条件由空心轴的切应力强度条件4-3(4-12) 某传动轴,转速n=300 r/min,轮1为主动轮,输入功率P1=50kW,轮2、轮3与轮4为从动轮,输出功率分别为P2=10kW,P3=P4=20kW.(1) 试求轴内的最年夜扭矩;(2) 若将轮1与轮3的位置对换,试分析对轴的受力是否有利.解:(1) 轮1、2、3、4作用在轴上扭力矩分别为轴内的最年夜扭矩若将轮1与轮3的位置对换,则最年夜扭矩酿成最年夜扭矩变小,固然对轴的受力有利.4-4(4-21) 图示两端固定的圆截面轴,接受扭力矩作用.试求支反力偶矩.设扭转刚度为已知常数.解:(a) 由对称性可看出,M A=M B,再由平衡可看出M A=M B=M(b)显然M A=M B,变形协调条件为解得(c)(d)由静力平衡方程得变形协调条件为联立求解式(1)、(2)得4-5(4-25) 图示组合轴,由套管与芯轴并借两端刚性平板牢固地连接在一起.设作用在刚性平板上的扭力矩为M=2kN·m,套管与芯轴的切变模量分别为G1=40GPa与G2=80GPa.试求套管与芯轴的扭矩及最年夜扭转切应力.解:设套管与芯轴的扭矩分别为T1、T2,则T1+T2 =M=2kN·m (1)变形协调条件为套管与芯轴的扭转角相等,即联立求解式(1)、(2),得套管与芯轴的最年夜扭转切应力分别为4-6(4-28) 将截面尺寸分别为φ100mm×90mm 与φ90mm×80mm的两钢管相套合,并在内管两端施加扭力矩M0=2kN·m后,将其两端与外管相焊接.试问在去失落扭力矩M0后,内、外管横截面上的最年夜扭转切应力.解:去失落扭力矩M0后,两钢管相互扭,其扭矩相等,设为T,设施加M0后内管扭转角为φ0.去失落M0后,内管带动外管回退扭转角φ1(此即外管扭转角),剩下的扭转角(φ0-φ1)即为内管扭转角,变形协调条件为内、外管横截面上的最年夜扭转切应力分别为4-7(4-29) 图示二轴,用突缘与螺栓相连接,各螺栓的资料、直径相同,并均匀地排列在直径为D=100mm的圆周上,突缘的厚度为δ=10mm,轴所接受的扭力矩为M=5.0 kN·m,螺栓的许用切应力[τ]=100MPa,许用挤压应力 [σbs]=300MPa.试确定螺栓的直径d.解:设每个螺栓接受的剪力为F S,则由切应力强度条件由挤压强度条件故螺栓的直径第五章弯曲应力1(5-1)、平衡微分方程中的正负号由哪些因素所确定?简支梁受力及Ox坐标取向如图所示.试分析下列平衡微分方程中哪一个是正确的.解:B正确.平衡微分方程中的正负号由该梁Ox坐标取向及分布载荷q(x)的方向决定.截面弯矩和剪力的方向是不随坐标变动的,我们在处置这类问题时都按正方向画出.可是剪力和弯矩的增量面和坐标轴的取向有关,这样在对梁的微段列平衡方程式时就有所分歧,参考下图.当Ox坐标取向相反,向右时,相应(b),A是正确的.但无论A、B弯矩的二阶导数在q向上时,均为正,反之,为负.2(5-2)、对接受均布载荷q的简支梁,其弯矩图凸凹性与哪些因素相关?试判断下列四种谜底中哪一种是毛病的.解:A是毛病的.梁截面上的弯矩的正负号,与梁的坐标系无关,该梁上的弯矩为正,因此A是毛病的.弯矩曲线和一般曲线的凸凹相同,和y轴的方向有关,弯矩二阶导数为正时,曲线开口向着y轴的正向.q(x)向下时,无论x轴的方向如何,弯矩二阶导数均为负,曲线开口向着y轴的负向,因此B、C、D都是正确的.3(5-3)、应用平衡微分方程画出下列各梁的剪力图和弯矩图,并确定|F Q|max和|M|max.(本题和下题内力图中,内力年夜小只标注相应的系数.)解:4(5-4)、试作下列刚架的弯矩图,并确定|M|max.解:5(5-5)、静定梁接受平面载荷,但无集中力偶作用,其剪力图如图所示.若已知A端弯矩M(0)=0,试确定梁上的载荷(包括支座反力)及梁的弯矩图.解:6(5-6)、已知静定梁的剪力图和弯矩图,试确定梁上的载荷(包括支座反力).解:7(5-7)、静定梁接受平面载荷,但无集中力偶作用,其剪力图如图所示.若已知E端弯矩为零.请:(1)在Ox坐标中写出弯矩的表达式;(2)试确定梁上的载荷及梁的弯矩图.解:8(5-10) 在图示梁上,作用有集度为m=m(x)的分布力偶.试建立力偶矩集度、剪力及弯矩间的微分关系.解:用坐标分别为x与x+d x的横截面,从梁中切取一微段,如图(b).平衡方程为9(5-11) 对图示杆件,试建立载荷集度(轴向载荷集度q或扭力矩集度m)与相应内力(轴力或扭矩)间的微分关系.解:(a) 用坐标分别为x与x+d x的横截面,从杆中切取一微段,如图(c).平衡方程为(b) 用坐标分别为x与x+d x的横截面,从杆中切取一微段,如图(d).平衡方程为10(5-18) 直径为d的金属丝,环绕在直径为D的轮缘上.试求金属丝内的最年夜正应变与最年夜正应力.已知资料的弹性模量为E.解:11(5-23) 图示直径为d的圆木,现需从中切取一矩形截面梁.试问:(1) 如欲使所切矩形梁的弯曲强度最高,h和b应分别为何值;(2) 如欲使所切矩形梁的弯曲刚度最高,h和b应分别为何值;解:(1) 欲使梁的弯曲强度最高,只要抗弯截面系数取极年夜值,为此令(2) 欲使梁的弯曲刚度最高,只要惯性矩取极年夜值,为此令12(5-24) 图示简支梁,由№18工字钢制成,在外载荷作用下,测得横截面A底边的纵向正应变ε×10-4,试计算梁内的最年夜弯曲正应力.已知钢的弹性模量E=200GPa,a=1m.解:梁的剪力图及弯矩图如图所示,从弯矩图可见:13(5-32) 图示槽形截面铸铁梁,F=10kN,M e=70kN·m,许用拉应力[σt]=35MPa,许用压应力[σc]=120MPa.试校核梁的强度. 解:先求形心坐标,将图示截面看成一年夜矩形减去一小矩形惯性矩弯矩图如图所示,C 截面的左、右截面为危险截面. 在 C 左截面,其最年夜拉、压应力分别为夜拉、压应力分别为在 C 右截面,其最年 故14(5-35) 图示简支梁,由四块尺寸相同的木板胶接而成,试校核其强度. 已 知 载 荷 F=4kN , 梁 跨 度 l=400mm , 截 面 宽 度 b=50mm , 高 度 h=80mm,木板的许用应力[σ]=7MPa,胶缝的许用切应力[τ]=5MPa.解:从内力图可见木板的最年夜正应力由剪应力互等定理知:胶缝的最年夜切应力即是横截面上的最年夜切 应力 可见,该梁满足强度条件.15(5-41) 图示简支梁,接受偏斜的集中载荷 F 作用,试计算梁内的最年 夜弯曲正应力.已知 F=10kN,l=1m,b=90mm,h=180mm.解: 16(5-42) 图示悬臂梁,接受载荷 F1 与 F2 作用,已知 F1=800N,F2,l=1m,许用应力[σ]=160MPa.试分别按下列要求确定截面尺寸: (1) 截面为矩形,h=2b; (2) 截面为圆形.解:(1) 危险截面位于固定端(2)17(5-45) 一铸铁梁,其截面如图所示,已知许用压应力为许用拉应力 的 4 倍,即[σc]=4 [σt].试从强度方面考虑,宽度 b 为何值最佳. 解: 又因 y1+y2=400 mm,故 y1=80 mm,y2=320 mm.将截面对形心轴 z 取静 矩,得18(5-54) 图示直径为 d 的圆截面铸铁杆,接受偏心距为 e 的载荷 F 作用. 试证明:当 e≤d/8 时,横截面上不存在拉应力,即截面核心为 R=d/8 的圆形区域. 解: 19(5-55) 图示杆件,同时接受横向力与偏心压力作用,试确定 F 的许用 值.已知许用拉应力[σt]=30MPa,许用压应力[σc]=90MPa. 解:故 F 的许用值为.第 七 章 应力、应变状态分析7-1(7-1b) 已知应力状态如图所示(应力单位为 ),试用解析法计算 图中指定截面的正应力与切应力.解: 与 截面的应力分别为:;;;MPa7-2(7-2b)已知应力状态如图所示(应力单位为 ),试用解析法计算 图中指定截面的正应力与切应力.解: 与 截面的应力分别为:;;;7-3(7-2d)已知应力状态如图所示(应力单位为 ),试用图解法计算 图中指定截面的正应力与切应力.解:如图,得: 指定截面的正应力 切应力7-4(7-7) 已知某点 A 处截面 AB 与 AC 的应力如图所示(应力单位为 ),试用图解法求主应力的年夜小及所在截面的方位.解:由图,根据比例尺,可以获得:,,最年夜切应力.7-5(7态如图 向应力 力、最10c)已知应力状 所示,试画三 圆,并求主应 年夜正应力与解:对图示应力状态, 是主应力状态,其它两个主应力由 、 、 确定.在 平面内,由坐标( , )与( , )分别确定 和 点,以 为直径画 圆与 轴相交于 和 .再以 及 为直径作圆,即得三向应力圆.由上面的作图可知,主应力为,,,7-6(7-12)已知应力状态如图所示(应力单位为 ),试求主应力的年 夜小.解: 与 截面的应力分别为:;;;在 截面上没有切应力,所以是主应力之一.;;;7-7(7-13)已知构件概况某点处的正应变,,切应变,试求该概况处 方位的正应变 与最年夜应变 及其所在方位.解:得:7-8(7-20)图示矩形截面杆,接受轴向载荷 F 作用,试计算线段 AB 的正 应变.设截面尺寸 b 和 h 与资料的弹性常数 E 和μ均为已知.解:,,,AB 的正应酿成7-9(7-21)在构件概况某点 O 处,沿 , 与 方位,粘贴三个应变片,测得该三方位的正应变分别为,与,该概况处于平面应力状态,试求该点处的应力 , 与 .已知资料的弹性模量,泊松比解:显然,,并令,于是得切应变:7-10(7-6)图示受力板件,试证明 A 点处各截面的正应力与切应力均为零.证明:若在尖点 A 处沿自由鸿沟取三角形单位体如图所示,设单位体 、 面上的应力分量为 、 和 、 ,自由鸿沟上的应力分量为 ,则有由于、,因此,必有 、 、.这时,代表 A 点应力状态的应力圆缩为 坐标的原点,所以 A 点为零应力状态.7-11(7-15)构件概况某点 处,沿 , , 与 方位粘贴四个应变片,并测得相应正应变依次为,,与,试判断上述测试结果是否可靠.解:很明显,,得:又得:根据实验数据计算获得的两个 结果纷歧致,所以,上述丈量结果不 成靠.第 八 章应力状态与强度理论 1、 (8-4)试比力图示正方形棱柱体在下列两中情况下的相当应力 , 弹性常数 E 和μ均为已知. (a) 棱柱体轴向受压; (b) 棱柱体在刚性方模中轴向受压.解:对图(a)中的情况,应力状态如图(c) 对图(b)中的情况,应力状态如图(d)所以,,2、 (8-6)图示钢质拐轴,接受集中载荷 F 作用.试根据第三强度理论确 定轴 AB 的直径.已知载荷 F=1kN,许用应力[σ]=160Mpa. 解:扭矩弯矩 由 得:所以,3、 (8-10)图示齿轮传动轴,用钢制成.在齿轮Ⅰ上,作用有径向力、切向力;在齿轮Ⅱ上,作用有切向力、径向力.若许用应力[σ]=100Mpa,试根据第四强度理论确定轴径.解:计算简图如图所示,作 、 、 图.从图中可以看出,危险截面为 B 截面.其内力分量为: 由第四强度理论 得:4、8-4 圆截面轴的危险面上受有弯矩My、扭矩Mx 和轴力FNx 作 用,关于危险点的应力状态有下列四种.试判断哪一种是正确的. 请选择正确谜底. (图中微元上平行于纸平面的面对应着轴的横截面) 答:B5、 (8-13)图示圆截面钢杆,接受载荷 , 与扭力矩 作用.试根据第三强度理论校核杆的强度.已知载荷N,,扭力矩,许用应力[σ]=160Mpa.解:弯矩满足强度条件.6、 (8-25)图示铸铁构件,中段为一内径 D=200mm、壁厚δ=10mm 的圆筒,圆筒内的压力p=1Mpa,两真个轴向压力F=300kN,资料的泊松比μ,许用拉应力[σt]=30Mpa.试校核圆筒部份的强度.解:,,由第二强度理论:满足强度条件.7、(8-27)图薄壁圆筒,同时接受内压p与扭力矩M作用,由实验测得筒壁沿轴向及与轴线成方位的正应变分别为和.试求内压p与扭力矩M之值.筒的内径为D、壁厚δ、资料的弹性模量E与泊松比μ均为已知.解:,,,很显然,8、(8-22)图示油管,内径D=11mm,壁厚δ,内压p,许用应力[σ]=100Mpa.试校核油管的强度.解:,,由第三强度理论,满足强度条件.9、(8-11)图示圆截面杆,直径为d,接受轴向力F与扭矩M作用,杆用塑性资料制成,许用应力为[σ].试画出危险点处微体的应力状态图,并根据第四强度理论建立杆的强度条件.解:危险点的应力状态如图所示.,由第四强度理论,,可以获得杆的强度条件:10、(8-17)图示圆截面圆环,缺口处接受一对相距极近的载荷作用.已知圆环轴线的半径为,截面的直径为,资料的许用应力为,试根据第三强度理论确定的许用值.解:危险截面在A或B截面A:,,截面B:,由第三强度理论可见,危险截面为A截面.,得:即的许用值为:11、(8-16)图示等截面刚架,接受载荷与作用,且.试根据第三强度理论确定的许用值.已知许用应力为,截面为正方形,边长为,且.解:危险截面在A截面或C、D截面,C截面与D截面的应力状态一样. C截面:由第三强度理论,得:A截面:由第三强度理论,得:比力两个结果,可得:的许用值:12、(8-25)球形薄壁容器,其内径为,壁厚为,接受压强为p之内压.试证明壁内任一点处的主应力为,.证明:取球坐标,对球闭各点,以球心为原点.,,由于结构和受力均对称于球心,故球壁各点的应力状态相同.且由于球壁很薄.,对球壁上的任一点,取通过该点的直径平面(如图),由平衡条件对球壁内的任一点,因此,球壁内的任一点的应力状态为:,证毕.。
材料力学课后习题答案详细

N1 N 2 0.5F 0.5 20 10(kN )
10
(2)求 C 点的水平位移与铅垂位移。 变形协调图
A
点的铅垂位移:l1
N1l EA1
10000N 1000mm 210000N / mm2 100mm2
0.476mm
B 点的铅垂位移: l2
材料可认为符合胡克定律,其弹性模量 E 10GPa 。如不计柱的自重,试求:
(1)作轴力图;
(2)各段柱横截面上的应力;
(3)各段柱的纵向线应变;
(4)柱的总变形。
解:(1)作轴力图
N AC 100kN NCB 100 160 260(kN )
轴力图如图所示。
(2)计算各段上的应力
第二章 轴向拉(压)变形
[习题 2-1] 试求图示各杆 1-1 和 2-2 横截面上的轴力,并作轴力图。 (a) 解:(1)求指定截面上的轴力
N11 F N 22 2F F F
(2)作轴力图 轴力图如图所示。
(b) 解:(1)求指定截面上的轴力
N11 2F N 22 2F 2F 0
如以 表示斜截面与横截面的夹角,试求当 0o ,30o ,45o ,60o ,90o 时各斜截面
上的正应力和切应力,并用图表示其方
向。
解:斜截面上的正应力与切应力的公式
为:
5
0 cos 2
0 2
sin 2
式中, 0
N A
10000 N 100mm 2
100MPa ,把
示。
由平平衡条件可得:
X 0
N EG N EA cos 0
材料力学刘德华版课后习题答案word版
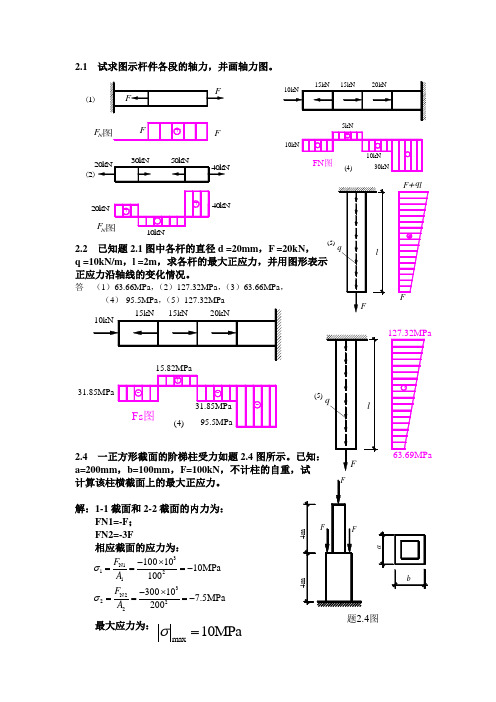
2.1 试求图示杆件各段的轴力,并画轴力图。
2.2 已知题2.1图中各杆的直径d =20mm ,F =20kN ,q =10kN/m ,l =2m ,求各杆的最大正应力,并用图形表示 正应力沿轴线的变化情况。
答 (1)63.66MPa ,(2)127.32MPa ,(3)63.66MPa ,(4)-95.5MPa ,(5)127.32MPa2.4 一正方形截面的阶梯柱受力如题2.4a=200mm ,b=100mm ,F=100kN ,不计柱的自重,试 计算该柱横截面上的最大正应力。
解:1-1截面和2-2截面的内力为: FN1=-F ;FN2=-3F相应截面的应力为:最大应力为:10kNF40kN10kN 20kN (2(1)F N N F (5)q (5)31.85MPa 题2.4图3N11213N22221001010MPa 100300107.5MPa200F A F A σσ-⨯===--⨯===-max 10MPaσ=2.6 钢杆受轴向外力如图所示,横截面面积为500mm2ab 斜截面上的应力。
解: FN=20kN2.8 图示钢杆的横截面积 A=1000mm2,材料的弹性模量E=200GPa ,试求:(1)各段的轴向变形;(2)各段的轴向线应变;(3)杆的总伸长。
解:轴力图如图所示2.10 图示结构中,五根杆的抗拉刚度均为EA ,杆AB 长为l ,ABCD 是正方形。
在小变形条件下,试求两种加载情况下,AB 杆的伸长。
解 (a )受力分析如图,由C 点平衡可知:p αo N N 0cos30F F p A A ααo 2oN 03cos30cos 302010330MPa 5004F p A σ==⨯=⨯=ααo o o N020sin30cos30sin305004F p A ⨯===αατ12320N 0N 20N N N N F k F k F k ===-11196243339620120010100010020221020010100010N N F l L EA L m F l L m EA ---⨯∆==⨯⨯⨯∆=⨯∆===-⨯⨯⨯⨯4411122244333101010210102L m l mL l L ml mεεε----∆===∆==∆-⨯===-41243100210L m L m L m--∆=∆=∆=-⨯I II III 0.1mm 00.2mm 0.1mm l l l l ∆=∆+∆+∆=+-=-F ’AC=F ’CB=0;由D 点平衡可知: F ’AD=F ’BD=0再由A 点的平衡:因此(b )受力分析如图,由C 点平衡可知:再由A 点的平衡:因此2.12 图示结构中,水平刚杆AB 不变形,杆①为钢杆,直径d1=20mm ,弹性模量E1=200GPa ;杆②为铜杆,直径d2=25mm ,弹性模量E2=100GPa 。
材料力学金忠谋第六版答案第章
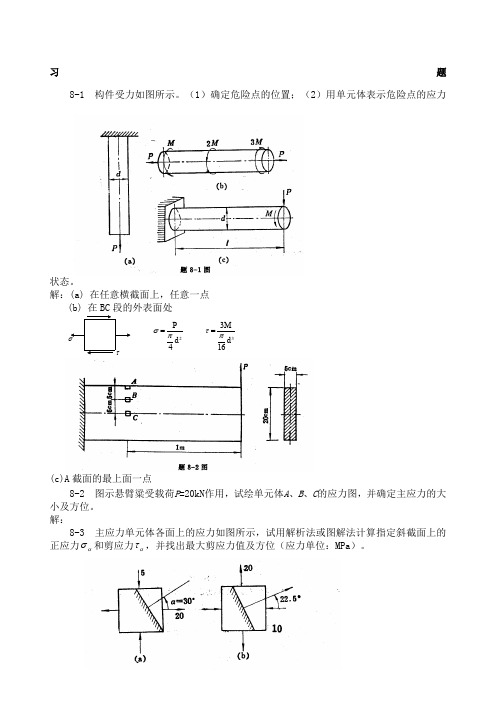
习 题8-1 构件受力如图所示。
(1)确定危险点的位置;(2)用单元体表示危险点的应力状态。
解:(a) 在任意横截面上,任意一点(b) 在BC 段的外表面处 24P d σπ=3316M dτπ=(c)A 截面的最上面一点8-2 图示悬臂粱受载荷P =20kN 作用,试绘单元体A 、B 、C 的应力图,并确定主应力的大小及方位。
解:8-3 主应力单元体各面上的应力如图所示,试用解析法或图解法计算指定斜截面上的正应力ασ和剪应力ατ,并找出最大剪应力值及方位(应力单位:MPa )。
解:(a) ()()1212205205cos 2cos 6013.752222MPa ασσσσσα+---+-=+=+= 45α= (与120σ=方向夹角) (b)()()()121220102010cos 2cos 135 5.6062222MPa ασσσσσα+---+-=+=+-=-()()122010sin 2sin 13510.60622MPa ασστα---==-=- 45α= (与1σ方向夹角)或135(与水平方向交角) (c)45α= (与140σ=方向夹角)(d)8-4 单元体各面的应力如图示(应力单位为MPa ),试用解析法和图解法计算主应力的大小及所在截面的方位,并在单元体内注明。
解:(a)(b)(c)(d)8-5 作出图示单元体的三向应力图,并求出主应力和最大剪应力,画出主单元体。
解:(a) (b)(c ) (d)(e)8-6 已知矩形截面梁某截面上的弯矩和剪力分别为M =10kN ·m ,F S =120kN ,试绘出截面上1、2、3、4各点单元体的应力状态,并求其主应力。
解:8-7 在棱柱形单元体的AB 面上以及与ABC 面平行的前后面上(与纸平面平行的面),均无应力作用。
在AC 面和BC 面上的正应力均为-15MPa ,试求AC 和BC 面上的剪应力与此单元体主应力的大小和方向。
材力习题册(第六版)参考答案(1-3章)

D
)
2.轴向拉伸细长杆件如图 2 所示,其中 1-1 面靠近集中力作用的左端面,则正确的说法 A.1-1、2-2 面上应力皆均匀分布 B.1-1、2-2 面上应力皆非均匀分布 C.1-1 面上应力非均匀分布, 2-2 面上应力均匀分布 D.1-1 面上应力均匀分布, 2-2 面上应力非均匀分布
(图 B 端 D 任意点 A ) B 都是横截面 D 都是 45 斜截面
0 0
14. 轴向拉伸杆,正应力最大的截面和剪应力最大的截面 (
15. 设轴向拉伸杆横截面上的正应力为 σ ,则 45 斜截面上的正应力和剪应力 ( D )。 B 均为 σ D 均为 σ /2 C δ 和ψ D σ s、 δ 和 ψ
17. 由拉压变形公式 l A C A C
F l FN l 即 E N 可知,弹性模量 ( A )。 A l EA
B 与载荷成正比 D 与横截面面积成正比
与载荷、杆长、横截面面积无关 与杆长成正比 A )是正确的。 内力随外力增大而增大 内力随外力增大而减小 C B D
18. 在下列说法,(
B 内力与外力无关 D 内力沿杆轴不变 ) 。 σ >300MPa σ <200MPa B ) 。 B. 剪切面面积为 bh,挤压面面积为 bc; D. 剪切面面积为 bh,挤压面面积为 ch。 C ) ,计算挤压面积
19. 一拉伸钢杆,弹性模量 E=200GPa,比例极限为 200MPa,今测得其轴向应变 ε = 0.0015,则横截面上的正应力 ( A C σ =Eε =300MPa 200MPa<σ <300Mpa
= -2(arctan
)=2.5×
rad
2.试求图示结构 m m 和 n n 两截面的内
-2-
材料力学(金忠谋)第六版答案第07章
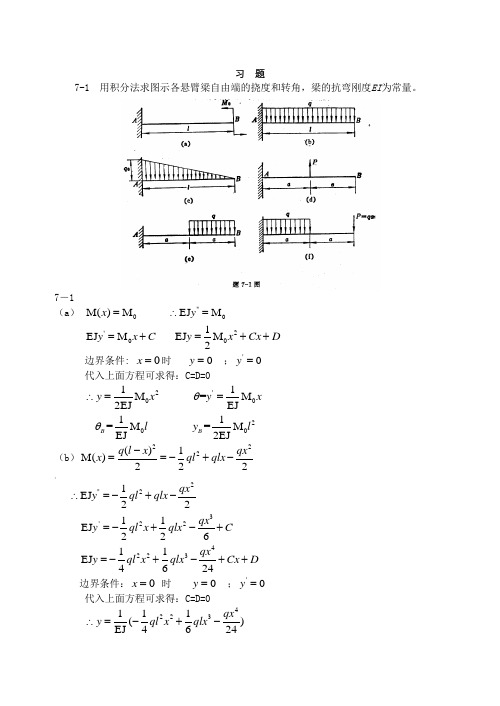
习 题7-1 用积分法求图示各悬臂梁自由端的挠度和转角,梁的抗弯刚度EI 为常量。
7-1(a ) 0M()M x = ''0EJ M y ∴='0EJ M y x C =+ 201EJ M 2y x Cx D =++ 边界条件: 0x =时 0y = ;'0y = 代入上面方程可求得:C=D=0201M 2EJ y x ∴='01=M EJ y x θ= 01=M EJ B l θ 201=M 2EJ B y l(b )222()1M()222q l x qx x ql qlx -==-+- 。
2''21EJ 22qx y ql qlx ∴=-+-3'2211EJ 226qx y ql x qlx C =-+-+422311EJ 4624qx y ql x qlx Cx D =-+-++边界条件:0x = 时 0y = ;'0y =代入上面方程可求得:C=D=04223111()EJ 4624qx y ql x qlx ∴=-+-'2231111=(-)EJ 226y ql x qlx qx θ=+- 3-1=6EJ B ql θ 4-1=8EJ B y ql(c )()()()()()0303''04'050()1()()286EJ 6EJ 24EJ 120l xq x q lq l x M x q x l x l x l q y l x l q y l x Cl q y l x Cx Dl-=-⎛⎫=--=-- ⎪⎝⎭∴=-=--+=-++】边界条件:0x = 时0y = ;'0y =代入上面方程可求得:4024q l C l -= 50120q l D l=()455000232230120EJ 24EJ 120EJ(10105)120EJq q l q l y l x x l l l q x l l lx x l ∴=---+-=-+- 3024EJ B q l θ=- 4030EJB q l y =-(d)'''223()EJ 1EJ 211EJ 26M x Pa Pxy Pa Pxy Pax Px C y Pax Px Cx D=-=-=-+=-++ 边界条件:0x = 时 0y = ;'0y =代入上面方程可求得:C=D=023'232321112611253262B C C B y Pax Px EJy Pax Px EJ Pa Pa Pay y a a EJ EJ EJPa EJθθθ⎛⎫∴=- ⎪⎝⎭⎛⎫==-⎪⎝⎭=+=+==(e)"()()()21222''1'211231113()02()2223EJ 231EJ ()2231EJ ()46a M x q qax x a q M x a x a x a a y q qaxa y qa x x C a y qa x x C x D =-+≤≤=--≤≤=-+=-++=--+++ 边界条件:0x = 时 0y = ;'0y =代入上面方程可求得:C=D=0()()()22118492024EJ 12EJ qax qax y a x a x x a ∴=--=--≤≤''2223'222242232221EJ ((2)4)21EJ (42)2312EJ (2)2312y q a ax x x y q a x ax C x y q a x ax C x D =--+=--++=---+++边界条件:x a = 时 12y y = ;12θθ=代入上面方程可求得:2296a C = 4224qa D =-()()43223421612838464162384q y x ax a x a a a x a EJ-=-+-+≤≤43412476B B qa y EJqa EJθ=-=-(f)!()()221222''212'231122341115()20225()2225251EJ 22251EJ 26511EJ 4324qa qx M x qax x a qa qa a M x qax x a x a a y q ax x a y q x ax x C a y q x ax x C x D =-+-≤≤⎛⎫=-+--≤≤ ⎪⎝⎭⎛⎫=--+ ⎪⎝⎭⎛⎫=--++ ⎪⎝⎭⎛⎫=--+++ ⎪⎝⎭边界条件:0x = 时 0y = ;'0y =代入上面方程可求得:C 1=D 1=0''22'2222223222EJ (2)1EJ (2)21EJ ()6y q a ax y q a x ax C y q a x ax C x D =--=--+=---++ 边界条件:x a = 时 12y y = ; ''''12y y =3296a C =- 4224a D =-437124136B B qa y EJqa EJθ=-=-7-2 用积分法求图示各梁的挠曲线方程,端截面转角θA 和θB ,跨度中点的挠度和最大挠度,梁的抗弯刚度EI 为常量。
习题第16章答案.docx
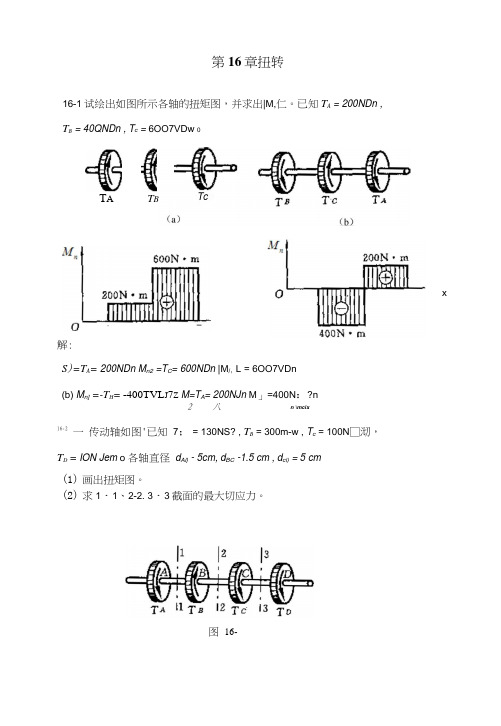
第16章扭转16-1试绘出如图所示各轴的扭矩图,并求出|M,仁。
已知T A = 200NDn , T B = 40QNDn , T c = 6OO7VDw 0解:S )=T A = 200NDn M n2 =T C = 600NDn |M /;L = 6OO7VDn (b) M n] =-T H = -400TVL J 7Z M=T A = 200NJn M 」=400N :?n2 八 n \mcix16-2 一 传动轴如图'已知 7; = 130NS? , T B = 300m-w , T c = 100N □沏, T D = ION Jem o 各轴直径 d Al} - 5cm, d BC -1.5 cm , d cl) = 5 cm(1) 画出扭矩图。
(2) 求1・1、2-2. 3・3截面的最大切应力。
T A TcT B x图 16-2解:(1)画出扭矩图。
(2)求1・1、2-2. 3・3截面的最大切应力。
仏=心〃皿wP16-3已知如图,变截面钢轴上的外力偶矩7;=18OO7VLkn, T c=nQ0N[^试求最大切应力和最大相对扭转角。
已知G = SOGPa o16%w”兀如B%- 16M〃2兀吒16%兀心)16x170x10—2^max\%ix2^x(7.5xl0-2)3 20'52kPa""Ox】。
:血^x(5x!0'2)3170N • cm-3000N • m图16-3横截面上的扭矩T 二10007VI 曲解:(1)最大切应力5沁=5皿=48.89 MPa(2)最大和对扭转角十警=吟.亦叶。
―宀厂螢+站3000x0.75 ( 1200x0.5 \21.27xlO"3raJ k 80xl09x6.136xl0-7 +80xl09x3.106x10^; 如图所示空心轴,外径D = SOmm ,内径d = 62.5加加,承受T = 1000NM。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
材料力学(金忠谋)第六版答案第16章15-1 两端为球铰的压杆,当它的横截面为图示各种不同形状时,试问杆件会在哪个平面内失去稳定(即在失稳时,杆的截面绕哪一根轴转动)?解:(a),(b),(e)任意方向转动,(c),(d),(f)绕图示Z 轴转动。
15-2 图示各圆截面压杆,横截面积及材料都相同,直径d =1.6cm ,杆材A 3钢的弹性模量E =200MPa ,各杆长度及支承形式如图示,试求其中最大的与最小的临界力之值。
解:(a) 柔度: 2301500.4λ⨯==相当长度:20.30.6l m μ=⨯=(b) 柔度: 1501250.4λ⨯== 相当长度:10.50.l m μ=⨯= (c) 柔度: 0.770122.50.4λ⨯== 相当长度:0.70.70.l m μ=⨯= (d) 柔度: 0.590112.50.4λ⨯== 相当长度:0.50.90.l m μ=⨯= (e) 柔度: 145112.50.4λ⨯== 相当长度:10.450.l m μ=⨯= 由E=200Gpa 及各柔度值看出:各压杆的临界力可用欧拉公式计算。
即:()22crEJ P l πμ=各压杆的EJ 均相同,故相当长度最大的压杆(a)临界力最小,压杆(d)与(e)的临界力最大,分别为:()2948222320010 1.610640.617.6410cr EJP l N πππμ-⨯⨯⨯⨯⨯===⨯ ()2948222320010 1.610640.4531.3010cr EJP l Nπππμ-⨯⨯⨯⨯⨯===⨯15-3 某种钢材Pσ=230MPa ,sσ=274MPa ,E =200GPa ,直线公式λσ22.1338-=cr,试计算该材料压杆的P λ及Sλ值,并绘制1500≤≤λ范围内的临界应力总图。
解:92.633827452.51.22p s s a b λπσλ===--===15-4 6120型柴油机挺杆为45钢制成的空心圆截面杆,其外径和内径分别为,12mm 和10mm ,杆长为383mm ,两端为铰支座,材料的E =210GPa ,Pσ=288MPa ,试求此挺杆的临界力crP 。
若实际作用于挺杆的最大压缩力P =2.33kN ,规定稳定安全系数Wn =2~5。
试校核此挺杆的稳定性。
解:(1)()()()444422222284.336411641210 3.90544413839884.833.905p p J D d D d J i D d mm AD d liλππππμλλ====--===+=+=-⨯===>=该压杆属大柔度杆()()2229222223210100.0120.019847.4610cr EJ E P A l Nππππλμ⨯⨯===⨯+=⨯ (2)7.463.22.33cr w P n n ===>工作P该杆的稳定性足够。
15-5 设图示千斤顶的最大承载压力为P =150kN ,螺杆内径d=52mm ,l =50cm .材料为A 3钢,E =200GPa 。
稳定安全系数规定为3=Wn 。
试校核其稳定性。
解:千斤顶螺杆简化为一端固定一端自由的压杆,故2μ=。
柔度应为:2500771001524pl i μλλ⨯===<=⨯应采用经验公式计算其临界力:由表中查出:304a MPa = 1.12b M P a =。
则:32304 1.1277218218100.05246244623.083150ej ej ej ej w a b MPaP A KNP n n P σλπσ=-=-⨯===⨯⨯⨯====>=工作所以满足稳定性要求。
15-6 10t 船用轻型吊货杆AB ,长为16cm ,截面为空心圆管,壁厚35Dt =,轴向压缩力P =222kN ,规定稳定安全系数5.5=Wn ,材料为A 3钢,E =210GPa ,吊杆两端均为铰支座。
试确定用杆的截面尺寸。
解:先按大柔度杆解()()4292222722101064351168.345810cr D D D EJ P l Nπππμ⎛⎫⎛⎫⨯⨯⨯-- ⎪ ⎪ ⎪⎝⎭⎝⎭==⨯=⨯7438.3458105.5 5.522210cr w P D n ⨯⨯>==⨯P347350D mmmm==1035Dt mm == 330d mm ∴=校核应用的公式是否对:22221350330120.264116000133120.26pD d i mmul i λλ-==-=⨯===>所以上面的计算有效。
15-7 图示托架中的AB 杆,直径d =40mm ,长l =800mm ,两端铰支,材料为A 3钢,试求 (a )托架的权限载荷maxQ ;(b )若工作载荷Q =70kN ,稳定安全系数Wn =2.0,问此托架是否安全? 解: (1)AB 杆1,10480018008010di mm l mmul i μλ====⨯===3A 钢100pλ=pλλ∴< 属于等杆2304 1.1280214.4214.440269.44cr cr cr ABa b MPaP A KN N σλπσ=-=-⨯===⨯⨯== 22900sin 600800600600800118.8900cr cr Q P P Q KN θ⨯=⨯-⨯==极限极限(2)118.8 1.70 2.070w Q n Q η===<=极限工作工作所以托架不安全。
15-8 两端固支的A 3钢管,长6m ,内径为60mm ,外径为70mm ,在C T20=时安装,此时管子不受力。
已知钢的线膨胀系数C/1105.126-⨯=α,弹性模量E =206GPa .当温度升高到多少度时,管子将失稳? 解:2222117060 2.3440.5600130.51002.3p J i D d cm A l i μλλ==-=-=⨯===>=属大柔度杆设温度t C ∆;则管子变形tl δα=∆ 伸长管子受压力crP P = 变形crP lEA∆=缩短 变形协调条件0δ+∆=或者δ=∆()222222646.4130.512.510cr P l El tl AEA EAt παλππλα-∆==∴∆===⨯⨯即升至2046.466.4T C =+=的管子失稳.15-9 有一结构ABCD ,由3根直径均为d 的圆截面钢杆组成如图,在B 点铰支,而在C 点和D 点固定,A 点为铰接。
π10=d L。
若此结构由于杆件在ABCD 平面内弹性失稳而丧失承载能力。
试确定作用于节点A 处的载荷P 的临界值。
解:AB 杆为铰支1μ=AC ,AD 杆为一端铰支一端固定0.7μ=AB 失稳此结构仍能继续承载,直到AC,AD 杆也失稳,此时整个结构才丧失承载能力。
由于对称()()cr cr AC ADP P =()()222220:2cos3036.12cos300.7cos30crcr cr ABAC y P P P EJEJEJll l ππ==+=+⨯=⎛⎫⨯ ⎪⎝⎭∑15-10 铰接杆系ABC 如图示,是由两根具有相同截面和同样材料的细长杆所组成,若由于杆件在ABC 平面内失稳而引起毁坏。
试确定载荷P 为最大时的θ角。
⎪⎭⎫⎝⎛<<20πθ。
解:当AB,BC 杆的轴力同时达到临界力时,P 最大。
两杆的临界力为:()()2222c o s s i n AB ACcr AB cr AC EJP P l EJP P l πθπθ====设BC 间距为L ,则cos ,sin ABAC lL l L ββ==代入上式222222cos sin sin sin A EJ P L EJP L πθβπθβ⎫=⎪⎪⎬⎪=⎪⎭ 消去P 得222222cos cos sin sin EJ EJL L ππβθβθ=即:2tg ctg θβ= ()2a r c t g c t gθβ∴= 15-11 某快锻水压机工作台油缸柱塞如图示。
已知油压力p =32 MPa ,柱塞直径d =120mm ,伸入油缸的最大行程l =1600mm ,材料为45钢,E =210Gpa 。
试求柱塞的工作安全系数。
解:工作压力()()2632100.12361.734P pA KN π==⨯⨯⨯=工作2.0μ= 1.6l m =()10.120.03442 1.6106.70.03J i d m A l i μλ====⨯∴===45钢96210108628010p p pEλπσλλ⨯===⨯∴>属细长杆2222922621010 5.7106.73210cr cr cr EE P P πσλσσππησλ∴=⨯⨯=====⨯⨯工作工作15-12蒸汽机车的连杆如图所示,截面为工字形,材料为A3钢,连杆所受最大输向压力为465kN。
连杆在摆动平面(xy平面)内发生弯曲时,两端可认为是固定支座,试确定其安全系数。
解:(1)xy平面内:()()()337421,3100119614096148512121.77551014096859614647052.391310059.252.39z l mmi J mm A mm i mml i μμλ===⎡⎤=⨯--⨯⎣⎦=⨯=⨯-⨯-=∴=⨯∴===3A 钢:100,106psλλ== xy ∴ 面内属短杆pλλ<()6623510647010152015203.27465cr s cr xyP A KN P mm P ση-∴==⨯⨯⨯=∴===工作(2)xz 面内:()33640.5,31001185142140859612124.0741025.102310024725.10y pl mmE i A J mm i mm liμμλλ===⎡⎤=⨯⨯+⨯-⨯⎣⎦=⨯∴=⨯∴===>所以属细长杆。
()229622200106470102472092091465cr cr xy E P A KN P P ππλη-⨯⨯∴==⨯⨯=∴==<工作所以不安全。
15-13钢结构压杆由两个85656⨯⨯等边铰钢组成,杆长1.5m ,两端铰支,P =150kN ,铰钢为A 3钢,计算临界应力的公式有:(1)欧拉公式。
(2)抛物线公式。
试确定压杆的临界应力及工作安全系数。
解:1, 1.5,150l m P KN μ===工作查表:56568⨯⨯角钢:244min 28.367223.63247.24223.63 1.6828.3671 1.589.30.0168z y z A cm J cm J cm J i cm A l i μλ=⨯=⨯=⨯⨯∴===⨯⨯∴===3A 钢:123eλλ=>所以采用抛物线公式计算:226432400.006822400.0068289.3185.6185.61028.36710 2.0715010cr cr a MPa b MPaa b MPaP P σλη-===-=-⨯=⨯⨯⨯⨯∴===⨯工作工作15-14 图示结构,用A 3钢制成,E =200GPa ,Pσ=200MPa ,试问当q =20N/mm 和q =40N/mm时,横梁截面B 的挠度分别为多少?BD 杆长2m ,截面为圆形,直径d =40mm 。
