随机信号分析第一章
合集下载
随机信号分析 第一章随机信号基础2
y
o
(x,y)
x
利用分布函数，对任意实数 x1 x 2 , y1 y2 则
P( x1 X x2 , y1 Y y2 ) F ( x2 , y2 ) F ( x2 , y1 ) F ( x1 , y2 ) F ( x1 , y1 )
y o
( x1, y2 ) ( x1, y1)
F ( x ) f ( t )dt
x
F(x)
=
0
x0
0 x 1
x
tdt tdt
0 1
x
0
1
(2 t )dt
1 x 2
x2
1
即
x0 0, x2 , 0 x 1 2 F ( x) x2 2x 1 , 1 x 2 2 1, x2
多维随机变量及其分布
由于从二维推广到多维一般无实质性的困难，我们重点 讨论二维随机变量 .
二维随机变量用（X，Y）表示下面着重讨论二维 r.v(X，Y),多维随机变量可类推。
二维随机变量（X,Y） X和Y的联合分布函数
一维随机变量X X的分布函数
F ( x ) P( X x )
F ( x , y) P ( X x , Y y) x, y
4．F ( x , y ) F ( x 0 , y ), F ( x , y ) F ( x , y 0 );
即F(x,y)对每个自变量都是右连续的。
5．对任意实数 x1 x2 , y1 y2
，有
F ( x2 , y2 ) F ( x2 , y1 ) F ( x1 , y2 ) F ( x1 , y1 ) 0.
随机信号分析第一章 概率论1
例 从一批灯泡中抽取一只灯泡，测试它的使用寿命， 这是个随机试验. 设t表示灯泡的使用寿命，则样本空间 S={t|t≥0}.
• 特殊事件
样本空间Ω和空集Φ 作为Ω的子集也看作事件. 由于Ω包含所有的基本事件，故在每次试验中，必 有一个基本事件e∊ Ω发生，即在试验中，事件S必 然发生；因此, Ω是必然事件. 又因在Φ 中不包含任何一个基本事件，故在任何一 次试验中,Φ 永远不会发生；因此,Φ 是不可能事件. 常用Ω ,Φ 分别表示必然事件与不可能事件. 必然事件与不可能事件可以说不是随机事件，但是 为了研究的方便，还是把它们作为随机事件的两个 极端情形来处理.
（b）试验的所有可能的结果不止一个，而且是事先 已知的； （c）每次试验总是恰好出现这些可能结果中的一个， 但究竟出现哪一个结果，试验之前是不能确切预言的
人们将满足上述（a）、（ b ）、（ c ）三个条件的试 验，称为随机试验，简称为试验，以字母E来表示.
随机试验的每一个可能的结果称为基本事件，也称 作样本点，用字母e表示. • 随机试验E的全体基本事件所构成的集合，称为E的 的样本空间，记为Ω. 例 将一枚质量均匀对称的硬币投掷两次，观察正反 面出现情况，这也是个随机试验. 故样本空间 S={(正，正)，(正，反)，(反，正)，(反，反)}.
在这个随机试验中，若设 A表示事件“第一次出现正面”.
在一次试验中，A发生当且仅当在这次试验中出现 基本事件 (正，正)，(正，反) 中的一个. 这样可以认为A是由(正，正)，(正，反)组成的， 而将A定义为它们组成的集合 A={(正，正)，(正，反)}. 又如 事件B表示“两次出现同一面”
都发生的对立事件是至少一个不发生；至少一个发 生的对立事件是都不发生. 对偶原理在事件的运算中经常用到，它可以推广到 更多个事件的情况，即
随机信号分析第一章
第1章 概率论基础
本章将复习与总结概率论的基本知识 也扩充一些新知识点，比如：
1) 利用冲激函数表示离散与混合型随机变量的 概率密度函数，
2) 随机变量的条件数学期望 3) 特征函数 4) 瑞利与莱斯分布 5) 随机变量的基本实验方法
合肥工1业/1大08学
1.1 概率论复习
合肥工2业/1大08学
1.1概率论复习
电子科技大学通信学院
合肥工60业/1大08学
1.4 随机变量数字特征
2020/6/8
合肥工业大学
61
1.2 随机变量要点回顾
2020/6/8
合肥工业大学
62
1.2 随机变量要点回顾
2020/6/8
合肥工业大学
63
1.2 随机变量要点回顾
2020/6/8
合肥工业大学
64
1.2 随机变量要点回顾
合肥工业大学
37
1.2 随机变量要点回顾
2020/6/8
合肥工业大学
38
1.2 随机变量要点回顾
2020/6/8
合肥工业大学
39
1.2 随机变量要点回顾
2020/6/8
合肥工业大学
40
1.2 随机变量要点回顾
2020/6/8
合肥工业大学
41
1.2 随机变量要点回顾
2020/6/8
合肥工业大学
54
1.3 随机变量的函数
2020/6/8
合肥工业大学
55
1.3 随机变量的函数
2020/6/8
合肥工业大学
56
1.3 随机变量的函数
2020/6/8
合肥工业大学
57
1.3 随机变量的函数
本章将复习与总结概率论的基本知识 也扩充一些新知识点，比如：
1) 利用冲激函数表示离散与混合型随机变量的 概率密度函数，
2) 随机变量的条件数学期望 3) 特征函数 4) 瑞利与莱斯分布 5) 随机变量的基本实验方法
合肥工1业/1大08学
1.1 概率论复习
合肥工2业/1大08学
1.1概率论复习
电子科技大学通信学院
合肥工60业/1大08学
1.4 随机变量数字特征
2020/6/8
合肥工业大学
61
1.2 随机变量要点回顾
2020/6/8
合肥工业大学
62
1.2 随机变量要点回顾
2020/6/8
合肥工业大学
63
1.2 随机变量要点回顾
2020/6/8
合肥工业大学
64
1.2 随机变量要点回顾
合肥工业大学
37
1.2 随机变量要点回顾
2020/6/8
合肥工业大学
38
1.2 随机变量要点回顾
2020/6/8
合肥工业大学
39
1.2 随机变量要点回顾
2020/6/8
合肥工业大学
40
1.2 随机变量要点回顾
2020/6/8
合肥工业大学
41
1.2 随机变量要点回顾
2020/6/8
合肥工业大学
54
1.3 随机变量的函数
2020/6/8
合肥工业大学
55
1.3 随机变量的函数
2020/6/8
合肥工业大学
56
1.3 随机变量的函数
2020/6/8
合肥工业大学
57
1.3 随机变量的函数
精品文档-随机信号分析基础(梁红玉)-第1章
第一章 随机变量基础
第一章 随机变量基础
1.1 概率基本术语 1.2 随机变量及其分布 1.3 随机变量函数及其分布 1.4 随机变量及其函数的数字特征 1.5 高斯随机变量
第一章 随机变量基础
第一章 随机变量基础
1.1.1 概率空间 1. 随机现象有两个主要特点： ① 个别试验的不确定性；
② 大量试验结果的统计规律性。 概率论和数理统计是描述和 研究随机现象统计规律性的数学学科， 它们研究大量随机现 象内在的统计规律、 建立随机现象的物理模型并预测随机现 象将要产生的结果。
第一章 随机变量基础
下面对一维实随机变量做简要说明。 (1) 样本ξk是样本空间上的点， 所对应的实数xk是某个 实数集R1上的点。 因此， 一维实随机变量X(ξ)就是从原样 本空间Ω到新空间R1的一种映射， 如图1-5所示。 (2) 随机变量X(ξ)总是对应一定的概率空间(Ω, F, P)。 为了书写简便， 没有特殊要求时不必每次写出随机变量X(ξ) 的概率空间(Ω, F, P)。 (3) 随机变量X(ξ)是关于ξ的单值实函数， 简写为X。 本书规定用大写英文字母X, Y, Z, …表示随机变量， 用 相应的小写字母x, y, z， …表示随机变量的可能取值， 用 R1表示一维实随机变量的值域。 简单地说， 随机变量实际上就是样本空间为一维实数域 R1其子集的概率空间。
推广到多个事件， 设A1, A2, …，AN为同一样本空间上 的一组事件， 若对任意的M(2≤M≤N)及任意M 个互不相同的
整数i1, i2, …， iM, 满足
P( Ai1 Ai2 AiM ) P( Ai1 )P( Ai2 )P( AiM )
(1-10)
第一章 随机变量基础
3.
若事件A1, A2, …，AN两两互斥(互不相容)， 即i j ，
第一章 随机变量基础
1.1 概率基本术语 1.2 随机变量及其分布 1.3 随机变量函数及其分布 1.4 随机变量及其函数的数字特征 1.5 高斯随机变量
第一章 随机变量基础
第一章 随机变量基础
1.1.1 概率空间 1. 随机现象有两个主要特点： ① 个别试验的不确定性；
② 大量试验结果的统计规律性。 概率论和数理统计是描述和 研究随机现象统计规律性的数学学科， 它们研究大量随机现 象内在的统计规律、 建立随机现象的物理模型并预测随机现 象将要产生的结果。
第一章 随机变量基础
下面对一维实随机变量做简要说明。 (1) 样本ξk是样本空间上的点， 所对应的实数xk是某个 实数集R1上的点。 因此， 一维实随机变量X(ξ)就是从原样 本空间Ω到新空间R1的一种映射， 如图1-5所示。 (2) 随机变量X(ξ)总是对应一定的概率空间(Ω, F, P)。 为了书写简便， 没有特殊要求时不必每次写出随机变量X(ξ) 的概率空间(Ω, F, P)。 (3) 随机变量X(ξ)是关于ξ的单值实函数， 简写为X。 本书规定用大写英文字母X, Y, Z, …表示随机变量， 用 相应的小写字母x, y, z， …表示随机变量的可能取值， 用 R1表示一维实随机变量的值域。 简单地说， 随机变量实际上就是样本空间为一维实数域 R1其子集的概率空间。
推广到多个事件， 设A1, A2, …，AN为同一样本空间上 的一组事件， 若对任意的M(2≤M≤N)及任意M 个互不相同的
整数i1, i2, …， iM, 满足
P( Ai1 Ai2 AiM ) P( Ai1 )P( Ai2 )P( AiM )
(1-10)
第一章 随机变量基础
3.
若事件A1, A2, …，AN两两互斥(互不相容)， 即i j ，
随机信号分析第一章2010
F XY ( x , y ) FY ( y | x ) = FX ( x ) p XY ( x , y ) pY ( y | x ) = p X ( x)
n维随机变量及其分布 维随机变量及其分布
定义 n维随机变量 ( X 维随机变量
1
, X
2
,L , X
n
)
的n维（联合）分布函数为 维 联合）分布函数为
+∞ −∞
p(x) ≥ 0
性质2 概率密度函数在整个取值区间积分为1 性质2：概率密度函数在整个取值区间积分为1，即
∫
p ( x ) dx = 1
x2 x1
性质3：概率密度函数在(x 区间积分， 性质 ：概率密度函数在(x1,x2)区间积分，得到该区 间的取值概率
P { x1 < X ≤ x 2 } =
1.1随机变量的概念 § 1.1随机变量的概念
抛硬币：可能出现正面或反面； 例1 抛硬币：可能出现正面或反面； 从一批产品中任取10件 例2 从一批产品中任取 件，抽到 的废品数可能是0,1,2,…,10中的一 的废品数可能是 中的一 个数； 个数； 掷色子：可能出现1,2,3,4,5,6点 例3 掷色子：可能出现 点
F XY ( x , y ) = P { X ≤ x , Y ≤ y }
(x,y)的二维联合概率密度，简称为二维概率密度 的二维联合概率密度，简称为二维概率密度 二维概率密度: 的二维联合概率密度
p XY
性质1： 性质 ：
∂ F XY ( x , y ) ( x, y) = ∂x∂y
2
二维概率密度具有以下性质： 二维概率密度具有以下性质：
F ( x1 , x 2 ,L , x n ) = P{ X
随机信号分析第一章习题讲解
1-9 已知随机变量X 的分布函数为20,0(),011,1X x F x kx x x <⎧⎪=≤≤⎨⎪>⎩求：①系数k ； ②X 落在区间(0.3,0.7)内的概率； ③随机变量X 的概率密度。
解：第①问 利用()X F x 右连续的性质 k ＝1第②问{}{}{}()()0.30.70.30.70.70.30.7P X P X F P X F =<<=<≤-=-第③问 201()()0X X xx d F x f x elsedx ≤<⎧==⎨⎩1-10已知随机变量X 的概率密度为()()xX f x kex -=-∞<<+∞（拉普拉斯分布），求：①系数k ②X 落在区间(0,1)内的概率 ③随机变量X 的分布函数 解： 第①问 ()112f x dx k ∞-∞==⎰ 第②问{}()()()211221x x P x X x F x F x f x dx <≤=-=⎰随机变量X 落在区间12(,]x x 的概率12{}P x X x <≤就是曲线()y f x =下的曲边梯形的面积。
{}{}()()1010101112P X P X f x dxe -<<=<≤==-⎰第③问()102102xx e x f x e x -⎧≤⎪⎪=⎨⎪>⎪⎩()00()110022111010222xx xxx x x x F x f x dxe dx x ex e dx e dxx e x -∞-∞---∞=⎧⎧≤≤⎪⎪⎪⎪==⎨⎨⎪⎪+>->⎪⎪⎩⎩⎰⎰⎰⎰1-11 某繁忙的汽车站，每天有大量的汽车进出。
设每辆汽车在一天内出事故的概率为0.0001，若每天有1000辆汽车进出汽车站，问汽车站出事故的次数不小于2的概率是多少？,(01)p q λ→∞→→∞→−−−−−−−−→−−−−−−−−→−−−−−−−−→n=1n ,p 0,np=n 成立，0不成立-分布二项分布泊松分布高斯分布汽车站出事故的次数不小于2的概率()()P(2)101k P k P k ≥=-=-= 答案0.1P(2)1 1.1k e -≥=-100.1n p ≥≤实际计算中，只需满足，二项分布就趋近于泊松分布()np!k e P X k k λλλ-=＝＝1-12 已知随机变量(,)X Y 的概率密度为(34)0,0(,)0x y XY kex y f x y -+⎧>>⎪=⎨⎪⎩,,其它求：①系数k ？②(,)X Y 的分布函数？③{01,02}P X X <≤<≤？第③问 方法一：联合分布函数(,)XY F x y 性质：若任意四个实数1212,,,a a b b ，满足1212,a a b b ≤≤，则121222111221{,}(,)(,)(,)(,)XY XY XY XY P a X a b Y b F a b F a b F a b F a b <≤<≤=+--{01,02}(1,2)(0,0)(1,0)(0,2)XY XY XY XY P X Y F F F F ⇒<≤<≤=+--方法二：利用(){(,)},XY DP x y D f u v dudv∈∈⎰⎰)(210{01,02},XY P X Y f x y dxdy <≤<≤=⎰⎰1-13 已知随机变量(,)X Y 的概率密度为101,(,)0x y xf x y ⎧<<<=⎨⎩,,其它 ①求条件概率密度(|)X f x y 和(|)Y f y x ？②判断X 和Y 是否独立？给出理由。
随机信号分析_第一章_概率论基础
1.2.2 全概率公式
假设样本空间S分为N个互斥事件Bn (n=1, 2, …, N), 即： Bi ∩ Bj = (i≠ j =1, 2, …, N) 及
i 1
Bi S
N
则
P[ A] P[ A | Bi ]P[ Bi ]
i 1
N
1.2.3 贝叶斯公式
P[ Bi | A] P[ Bi ]P[ A | Bi ] / P[ A] P[ Bi ]P[ A | Bi ] /( P[ Bi ]P[ A | Bi ])
f XY ( x, y)dxdy 1
则称(X, Y)为连续型的二维随机变量， FXY(x, y)为其连续型的联合分布函数； fXY(x, y)为(X, Y)的联合密度函数。
如果联合密度函数fXY(x, y)在点(x,y) 处连续，则
2 FXY ( x, y) f XY ( x, y) xy
F(b1,b2) - F(a1,b2) - F(b1,a2) + F(a1,a2) 0 y b2 a2 x a1 b1
离散型概率分布函数
Y
X
y1 y2 … yj … p11 p21 … pi1 … p12 p22 … pi2 … … p1j … … p2j … … … … … pij … … … …
1. 4 多维随机变量及其分布
n个随机变量X1 , X2 , … , Xn的总体 X=(X1 , X2 , … , Xn)为n维随机变量。 1.4.1 二维随机变量 设X, Y为定义在同一概率空间(S, £ , P)上的两个随机变量，则(X, Y) 称为二维 随机变量，对于任意x,y R ，令 FXY(x, y)= P[X<x, Y<y] 称FXY(x,y)为(X,Y)的二维联合分布函数。
随机信号分析(第3版)第一章 习题答案
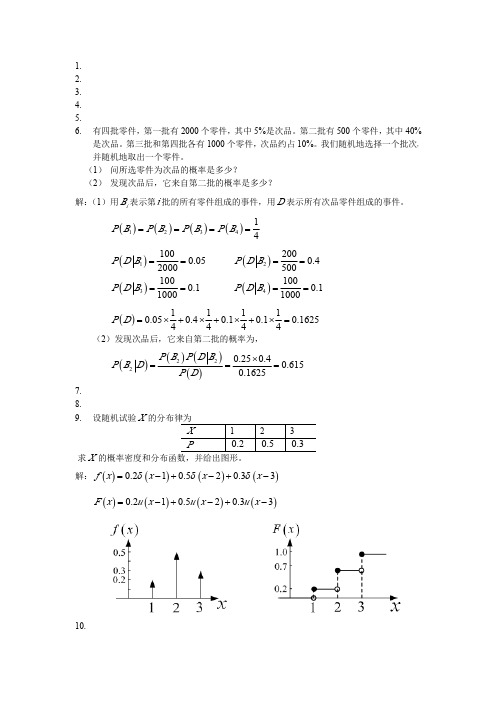
解： （1）用 Bi 表示第 i 批的所有零件组成的事件，用 D 表示所有次品零件组成的事件。
P ( B1 ) = P ( B2 ) = P ( B3 ) = P ( B4 ) =
100 = 0.05 2000 100 P ( D B3 ) = = 0.1 1000
1 4
P ( D B1 ) =
200 = 0.4 500 100 P ( D B4 ) = = 0.1 1000
22. 23. 24. 已知随机变量 X 服从 [0, a] 上的均匀分布。 随机变量 Y 服从 [ X , a] 上的均匀分布， 试求 （1） （2）
E (Y X ), (0 ≤ X ≤ a ) ； EY a+X 2
⎞ a+a/2 3 = a ⎟= 2 4 ⎠
解： （1）对 x ∈ [0, a ] 有， E (Y X ) =
1 −x f XY ( x, y ) = e 2π
2
+ y2 2
, ( x, y ) ∈ R 2 1 2 =−1， 1 2 − 2 , (u, v ) ∈ R 2
2
u+v 1 ⎧ x= ⎪ ⎪ 2 ，J = 2 由反函数 ⎨ 1 ⎪y = u −v ⎪ ⎩ 2 2
1 −u fUV ( u , v ) = e 4π 1 −u （2）由于, e 4π
2 2
（2） f ( x ) = 0.3δ ( x − 1) + 0.7δ ( x + 1)
E ( X ) = φ ′(0) / j = 1× 0.3 + ( −1) × 0.7 = −0.4 E ( X 2 ) = −φ ′′(0) = 12 × 0.3 + ( −1) × 0.7 = 1 Var ( X ) = E ( X 2 ) − E 2 ( X ) = 1 − 0.16 = 0.84
随机信号分析第一章 - 马氏过程
参考资料：•《概率论与数理统计》，工程数学，先修课教材•《随机信号分析》，朱华等编，北京理工大学出版社•《随机信号分析解题指南》，李永庆等编，北京理工大学出版社•《概率、随机变量与随机过程》，[美]A·帕普里斯著•研究生系列教材《随机过程》，张卓奎、陈慧婵编著，西安电子科技大学出版社第一章 随机过程马尔可夫过程的概念当随机过程在时刻1i t -所处的状态为已知的条件下，过程在时刻1()i i t t ->所处的状态，与过程在时刻1i t -以前所处的状态无关，而仅与过程在时刻1i t -的状态有关，则称该过程为马尔可夫过程。
这种特性称为随机过程的“无后效性”或马尔可夫性。
2i -i1i -2()i X t -()i X t 1()i X t -状态有限的马尔可夫链称为有限马尔可夫链。
规定一随机变量序列12,,,,n X X X ⋅⋅⋅⋅⋅⋅，可把此序列看作连续型随机过程()X t →采样→(),1,2,n n X X t n ==⋅⋅⋅称为随机变量序列12,,,,n X X X ⋅⋅⋅⋅⋅⋅ 也记作{(),1,2,,}X n n n =⋅⋅⋅⋅⋅⋅或{}n X ，简记为()X n 或n X 。
状态连续定义：若对于任意的n ，有1211(|,,,)(|)X n n n X n n F x x x x F x x ---⋅⋅⋅= （1）写成概率形式11221111{|,,,}{|}n n n n n n n n n n P X x X x X x X x P X x X x ------≤==⋅⋅⋅==≤=即，如果在112211,,,n n n n X x X x X x ----==⋅⋅⋅=条件下n X 的条件分布，等于仅在11n n X x --=条件下n X 的条件分布，则称此随机变量序列n X 为马尔可夫序列。
这一分布函数常称为转移分布。
概率论回顾：(|){|}F x y P X x Y y =≤=为在Y y =下X 的条件分布函数。
随机信号分析-1 随机过程(1)
X(ξ , t) 是随机过程的一个样本
X(ξ , t) 是一个随机变量 X(ξ , t) 是一个确定值
14
随机过程的定义
随机过程判断举例 例1.1 随机初相正弦波X(t)=A cos(ω0t+Φ )， A和ω0是正常数， Φ服从[0, 2π]上的均匀分布。判断其是否为随机过程. 从定义1的角度考虑： Φ是随机变量，每次观测其取值是随 机的，从而得到不同的样本函数，且该函数是时间函数； 从定义2的角度考虑，固定t时，X(t)是随机变量Φ的函数，也
18
随机过程的概率分布
根据定义2，对随机过程采样，可得多维随机变量。在满足 一定采样间隔要求下，随机过程的统计特性可由该多维随机 变量的统计特性反映；因此可将概率论中对随机变量的概率 统计特性的研究方法推广到随机过程的研究中。 随机过程的一维概率分布 定义3 设{X(t), t ∈T }是随机过程，对任意固定t1∈T 和实数x1 ∈R， 称Fx (x1 ; t1)=P {X(t1) ≤ x1} 为该过程的一维分布函数；若Fx
f X x1 , x2 ,, xn ; t1 , t2 , tn
1
2
n 2
1 ' 1 exp X C X 1 2 2 C
C是协方差矩阵，X=(x1 , x2 , …, xn）
24
随机过程的数字特征
有限维概率密度函数族可完全确定随机过程的全部统计特性， 但有时得到该函数族相当困难，甚至不可能 幸运的是，很多时候只需要掌握随机过程的几个统计值即可； 这些统计值即为随机过程的数字特征，有数学期望、均方值、 方差、相关函数等。 数字特征既能描述随机过程的重要特性，又便于实际测量； 对随机过程的数字特征的计算方法，是先把时间t固定，然 后用随机变量的分析方法来计算。
随机信号分析pdf第一章
x
−∞
⎧ ( x − m) 2 ⎫ 1 exp ⎨− ⎬ dx 2σ 2 ⎭ 2πσ ⎩
（1.3.16）
标准正态分布函数通常用Φ(x)表示，即
Φ ( x) = ∫
2 均匀分布
x
−∞
⎧ x2 ⎫ 1 exp ⎨− ⎬ dx 2π ⎩ 2⎭
（1.3.17）
如果随机变量 X 的概率密度函数为
⎧ 1 ⎪ f ( x) = ⎨ b − a ⎪ ⎩ 0
x≥0 x<0
其中 a、b 为常数，则称 X 服从韦伯分布，参数 a 称为尺度参数，b 称为形状参数，雷达的地杂波 的幅度特性通常可以用韦伯分布来描述，概率密度曲线如图 1.3(e)所示。 6 对数正态分布 如果随机变量 X 的概率密度为
⎧ 1 ⎧ ln 2 ( x / m) ⎫ exp ⎨− ⎪ ⎬ f ( x) = ⎨ x 2πσ 2σ2 ⎭ ⎩ ⎪ 0 ⎩
∫
x2
x1
f ( x)dx ，这说明随机变量 X 落在区间 ( x1 , x 2 ] 上的
概率等于图 1.2 中阴影区的面积。从这条性质我们也可以看出，对于连续型随机变量，有
P( X = x) = 0
f ( x)
0
x1
x2
x
图 1.2 随机变量 X 落在区间 ( x1 , x 2 ) 上的概率 对于离散型随机变量，由于它的概率分布函数是阶梯型，那么它的概率密度函数是一串 δ 函数 之和， δ 函数出现在随机变量的取值点，强度为取该值的概率。即
(1.3.15)
2
其中 m、σ为常数，则称 X 服从正态分布，正态分布通常也简记为 N (m, σ ) 。均值为 0，方差为 1 的正态分布 N (0,1) 称为标准正态分布。正态分布随机变量的概率密度是一个高斯曲线，所以又称 为高斯随机变量，概率密度曲线如图 1.3(a)所示。 正态分布函数，
随机信号分析第1章-随机变量与随机向量
（1）从盒子中任意选取一电阻器作为R的实验中， 样本空间S及其各基本实验结果出现的概率。
（2）经过分压器变换之后，随机变量V的值域空间
Rv和各基本结果的概率。
阻值（ ） 电阻器个数
500
100
30
200
40
+
12V
r0
R
V
E
_
500
15
1000
15
4
解（1）基本可能结果有4个，
s1 (R 100 ), s2 (R 200 ), s3 (R 500 ), s4 (R 1000 )
❖ 例 一个电子服务系统为5个用户服务。若一个用户 使用系统时，系统输出功率为0.6W，而且各用户 独立使用系统，使用概率均为0.3。
（1）求电子服务系统输出功率的概率；
（2）系统输出大于2W时，系统过载，求其过载概 率。
解（1）设输出功率为X，与使用系统的用户数有 关，且X=0.6K ,K取0，1，2，3，4，5，则输出功 率也相应的为0W，0.6W，1.2W，1.8W，2.4W， 3.0W 。输出功率X的概率等于使用系统的用户数K 的概率。在该系统中，使用的用户数K是一个二项 式分布的随机变量。
求（1）X的分布函数F(x);
（2） PX 1
解（1）
x
F (x) f ( )d
F (x) x 1e d 1 ex
2
2
x0
F (x) 0 1e d x 1e d 1 1 ex
2
02
2
（2）P X 1 1exdx 1 e1
12
2
x0
12
❖ 离散型随机变量的概率密度函数和分布函数
（3）F(x,y)是x，y的单增函数。
随机信号分析第一章
02
随机信号的统计描
述
概率密度函数
定义
概率密度函数（PDF） 是描述随机信号在各个 时刻取值概率分布的函 数。
性质
概率密度函数具有非负 性、归一化性质，即概 率密度函数在全域上的 积分等于1。
计算方法
可以通过直方图法、核 密度估计法等方法计算 概率密度函数。
概率分布函数
定义
概率分布函数（CDF）是描述随机信号取值小于或等 于某个值的概率的函数。
随机信号的特性
统计特性
随机信号的统计特性包括均值、 方差、概率分布等，这些特性描 述了信号的平均行为和不确定性 。
时间特性
随机信号的时间特性包括自相关 函数、互相关函数、功率谱密度 等，这些特性描述了信号在不同 时间点的相关性以及频率成分。
随机信号的应用
通信
在通信领域，随机信号可用 于扩频通信、无线通信等领 域，以提高通信的抗干扰能 力和保密性。
05
随机信号的采样定
理
采样定理的内容
采样定理定义
对于一个时间连续的模拟信号，如果以不高于其最高频率分量的频 率进行采样，则可以无失真地恢复原始信号。
采样定理的数学表达式
如果信号的最高频率为Fmax，则采样频率应不小于2Fmax。
采样定理的意义
采样定理是数字信号处理的基础，它确保了从离散样本中能够准确 重建原始信号。
雷达与声呐
在雷达与声呐领域，随机信 号可用于目标检测、测距、 定位等方面，以提高探测的 精度和可靠性。
地球物理学
在地球物理学领域，随机信 号可用于地震勘探、矿产资 源探测等方面，以揭示地球 内部结构和物质分布。
金融与经济
在金融与经济领域，随机信 号可用于股票价格分析、市 场预测等方面，以揭示市场 动态和经济发展趋势。
随机信号分析 第1章概率论
b
1.5随机变量函数
一个对机变量的函数Y=g(X)描述为：观察由实验得到实数x，然后完成由 Y=g(x)定义的算术运算。典型例子如下图所示：
y y y
x x
x
y=bx (a)线性变换
kx, x 0 y 0, x 0 (b)半波整流
y=x2 (c)平方律
为了说明求随机变量函数统计量的直接方法。考察上图a的情形，假设X 的概率密度函数已知，求Y的概率密度函数。
df ( y ) PY ( y ) | | PX [ x f ( y )] dy
1.6统计平均
对于离散随机变量X：定义统计平均（也叫期望，均值，集平均值）为
E[ X ] xi P( xi )
I 1
N
这一定义可以推广到X的函数的平均。例如，若Y=g(X),则
E[Y ] yi P( yi )
由于 Y y} { 的概率等于 X y / b}概率，即有 Y (Y y) P X (X y/b). { P 由概率密度函数定义直 接得到：
PY ( y )
d 1 PX ( X y / b) PX ( x y / b) dy |b|
Y的取值范围是X的取值范围乘以b。
b( x)
2. 概 率 密 度 函 数 定义 :
d f ( x) F ( x) , dx
性质 :
①
f ( x) 0
非负
②
a
f ( x)dx 1
归一性
③
b
f ( x)dx F (b) F (a) p[a X ( A) b]
区间性
离散分布 连续分布
p( x) P(x) (x - x i )
第一章 随机信号基础
样本空间，记为 S
2017/5/2
10/93
4. 随机事件（ Random Event ）
实验 E 中满足一定条件的样本点的集合称为随机
事件, 是S的子集。记为 A , B , …
每个样本点称为基本事件，样本空间S是必然事 件，Ø是不可能事件。
一 基本概念
5. 随机变量 Random Variable（R.V.）
2017/5/2 25/93
二 随机变量分布律
d) P x1 X x2 , y1 Y y2 FXY x2 , y2 FXY x1 , y2 FXY x2 , y1 FXY x1 , y1
e) 离散RV：
FXY x , y Pij u x xi , y y j
随机变量不同于普通变量，表现在两点上：
随机变量可以有多个取值，并且永远不能预知它到底
会取哪个值；
随机变量取值是有规律的，这种规律用概率特性来明
确表述；
因此，凡是讨论随机变量就必然要联系到它的取值范 围与概率特性。
2017/5/2
14/93
一 基本概念 (3）多维随机变量(随机向量)
e1· e2· X1(· )
p3
f X x Pi x xi
i 1
m
x1
f x p p2
1
x
30/93
x1
2017/5/2
x2
x3
二 随机变量分布律
2.二维
1）定义
X ,Y
f XY x , y 2 FXY x , y xy
联合概率密度：
称 f X x 或 fY y 为 f XY x, y 的边缘概率密度函数。
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
的理论与方法，必然是“张冠李戴”
t
无法得到正确的处理结果。
14
随着科学技术的进步，人们越来越发现，在自然界中所 遇到的大量信号均属于随机信号。如：
（1）－自由电子随机游动，在电阻上产生的“热噪声”。 （2）－某交叉路口每天24小时测量的噪音的分贝记录。 （3）－证卷交易所中，某股票每周涨落的记录。 （4）－反映人的生理、心理活动的“脑电波”。 (5)－反映地球物理特性的“地震信号”。 (6)－人说话时发出的“语音信号”。 （7）－雷达自动跟踪到的某飞行器的“运动轨迹”。 (8)－雷达接收到的目标信号的“幅度与相位”。
7
分析确定信号所用的数学工具有：微富积氏分变、换线、性拉代氏数变、换复、变等函等数
分析随机信号所用的数学工具有：随机概过率程论理论
上述的所有
数学工具
概率论研究的对象－－随机变量 X
随机过程理论研究的对象－－随机过程 X (t)
8
（一）课程的特点、地位、作用和任务：
20
教材及主要参考书
教材：随机信号分析基础（第4版） 王永德 王军 （编著）
电子工业出版社
参考教材：
李晓峰,周宁等编著 随机信号分析(第4版) 电子工业出版社
随机信号分析 赵淑清 郑薇（编著） 哈尔滨工业大学出版社
随机信号处理 陆光华 彭学愚 西安电子科技大学出版社
21
参考书籍
李晓峰,周宁等编著,随机信号分析(第4版)，电子工业出版社
29
30
1.1 概率的基本概念
定义(概率的统计定义) ：
在一定条件下,重复做 N 次实验, NA为 N 次实验中
事A发生的次数,如果随着
N
逐渐增大,频率
N A 逐渐稳定
N
在某一数值p附近,则数值p称为事件A在该条件下发生的
概率,记作
P(A.) p
注: (1) 频率具有稳定性 (2) 当试验次数N较大时,经常用频率代替概率
定义：设A、B为随机试验的两个事件，且P(A)>0，则 称
P(B | A) P(AB) / P(A), P(A) 0 (1.2.1)
为事件A发生的条件下事件B发生的条件概率。 类似地，P(B)>0
P(A | B) P(AB) / P(B), P(B) 0 (1.2.2)
35
1.2.2 乘法定理 设P(B)>0，则有 P(AB) P(A | B)P(B)
随机信号是通信、信号与信息处理、自动控制等学科 领域必须研究的信号形式。比如通信电子信息类专业的后 修课程中需要对随机信号进行处理的课程有：通信原理、 雷达原理、现代数字信号处理、信息论、图像信号处理、 语音信号处理、线性控制系统等等课程。
5
－课程的特点与研究方法－
学会用统计的观点来看研究对象－随机信号 由于随机信号是随机变化和不确定的，只有它的统计
12
根据信号的取值是否确定，可将信号分为确定信号和随机信号
确定性信号：可用确定的数学函数表示的信号，且信号的取值是确定的。 随机信号：给定一个时间值时，信号的取值不确定，只知其取某一数值的 概率。
调制信号
雷达接收机的噪声
鸟叫声
13
确定信号－－随时间做有规律的、已知的变化。可以用确定的时间函 数来描述。如：方波、锯齿波。人们可以准确地预测它 未来的变化，即：这次测出的是这种波形，下次测出的 还是这种波形。
若事件{A1},{A2},{A3}是统计独立的，则满足下列关系
P( A1A2 ) P( A1)P( A2 ) P( A1A3) P( A1)P( A3) P( A2 A3) P( A2 )P( A3)
P( A1A2 A3) P( A1)P( A2 )P( A3)
37
1.2.4 全概率公式
Radar： Radio Detection And Ranging
18
随机信号分析是一门研究随机变化过程的特 点与规律性的学科。
本课程主要介绍随机信号分析和处理的基本 概念、基本理论和基本方法及其应用。从分布 律、数字特征和特征函数引出随机信号的基本 概念，分别在时域和频域讨论随机信号的特点。
19
2
《信号与系统》与《随机信号分析》是电子信息 类专业两门主要的专业基础课，前者主要以分析确定 性的信号与系统为主要内容，后者则以分析随机信号 以及与系统的相互作用为主要内容。
随机信号分析是随机与信号分析的结合。随机性
的分析运用概率论的理论；信号分析运用信号与系统
理论，因此，本课程是概率论与信号与系统的结合 。
统计的概念； 模型的概念； 物理概念，注重数学推演结果和结论的物理意义
11
(三) 课程教学方法与手段：
结合多媒体教学手段以课堂教学为主，布置一 定量的作业。
(四) 课程与其它课程的联系：
该课程要在学生学习《高等数学》、《线性代 数》、《概率论与数理统计》课程后进行，也是 电子信息与通信工程等各专业课程的基础课。
22
罗鹏飞等,随机信号分析与处理,清华大学出版社
23
讲授总目录
绪论 第1章 概率论简介 第2章 随机信号概论 第3章 平稳随机过程 第4章 随机信号的功率谱密度 第5章 随机信号通过线性系统 第7章 窄带随机过程
24
课程的教学组织及时间安排
绪论 1 概率论基础 2 随机信号概论
3 平稳随机过程
它具有三个特点：重复性，明确性，随机性. 2、随机试验的样本点——随机试验的每一个可能
结果.
28
3.随机试验的样本空间（Ω或S Sample Space） ——随机试验的所有样本点构成的集合.
4.基本事件（Event）——Ω的单元素子集，即每个 样本点构成的集合.
5.随机事件——Ω的子集，常用F表示. 6.必然事件（Ω），包含所有样本点。 7.不可能事件（Φ），不包含任何样本点。
和处理的基本概念及它的基本理论和方法，从
而初步掌握处理随机现象的基本思想和方法，
培养学生运用概率论与随机过程分析方法解决
实际问题的能力。
建立：利用统计学概念，建立随机信号的系统
函数和数学模型，分析数学推演的结果和结论
的物理意义的思想。
10
本课程是一门专业技术基础课，不过多追求数学上的 严密，注重的是要掌握随机信号分析的基本原理和方 法，对复杂的理论和数学问题着重采用与实际的电子 工程技术问题相联系的途径和方法去处理。
若P(A)>0，则有 P(AB) P(B | A)P(A)
乘法定理可以推广到n个事件之积的情况。设 A1,A2,…, An为n个事件(n>=2)，且P(An| A1,A2,…, An-1)>0则有
P( A1A2... An ) P( A1)P( A2 | A1)P( A3 | A1A2 )... P( An | A1A2... An1)
称为随机试验 E 的概率空间。
32
1.1.2 概率的主要性质:
(1)P(Φ)=0，P(Ω)=1，逆不一定成立. (2)加法公式
若AB= Φ,则P(A+B)=P(A)+P(B) 即:若A1,A2,…,An两两互斥,则 P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An)
33
(3)P(A-B)=P(A)-P(AB)，P(Ω-A)=1-P(A). 若A是B的子事件,则P(B-A)=P(B)-P(A)； P(A)≤P(B);
3
随机信号分析与处理是一门研究随机信号 的特点与规律的学科，它广泛应用于雷达、 通信、自动控制、随机振动、地震信号处理、 图像处理、气象预报、生物电子等领域。近 几年来，随着现代科学技术，特别是信息科 学技术的发展，随机信号处理已是现代信号 处理的重要理论基础和有效方法之一。
4
随着现代化发展的需要，掌握这套方法，已不仅仅是 我们通信、信息类专业的要求，也已成为所有科技领域、 金融、管理、生物医学等许多专业的需要。
规律才是确定的，因此对随机信号而言，从描述方式、推 演方式到分析方法都是在统计意义上讨论与定义的。所以 必须学会用统计的观点来看所有随机的问题。
6
－课程的特点与研究方法－
学习时必须注重物理概念的理解 该课程是电子信息类和相关专业的一门专业基础课
程，不是一门数学课程，课程中用到的许多数学理论 是处理随机信号问题的数学工具。学习时除了注意处 理随机信号的方法外，更重要的是深入理解数学推演 结果、结论的物理意义。对一些复杂的数学推演的中 间步骤不必死记硬背，更不必深究其数学上的严密性， 重在掌握分析的思路与方法。
随机信号－－随时间做无规律的、未知的、“随机”的变化。无法用 确定的时间函数来描述，无法准确地预测它未来的变化。 这次测出的是这种波形，下次测出的会是另一种波形。
t
另外，信息在传输的过程中，不仅
传输的信号多数本身具有随机性，同
时它们还要受到传输系统（随机）噪
声的影响，使结果具有更加复杂的
随机性。如果使用经典的、确定信号
统原理》及从事统计信号处理研究 应用领域：雷达、通信、信号与信息处理、
自动控制、随机振动、地震信号处理、图像 处理、气象预报、生物电子等领域。
27
第1章 概率论简介
1.1 概率的基本概念
1.1 .1概率的基本概念 概率的概念与日常生活中事件出现的机会，
或者说几率相关。与概率统计定义相关的几个定义： 1、随机试验（Random Experiment 简称E）— —对随机现象进行的观察与科学实验.
(4)P(A+B)=P(A)+P(B)-P(AB), ， P(A+B+C)=P(A)+P(B)+P(C)-P(AB) -P(AC) P(BC)+P(ABC)