第四章部分习题解
现代控制理论习题解答(第四章)

第四章 控制系统的稳定性3-4-1 试确定下列二次型是否正定。
(1)3123212322212624)(x x x x x x x x x x v --+++= (2)232123222126410)(x x x x x x x x v ++---= (3)312321232221422410)(x x x x x x x x x x v --+++= 【解】: (1)04131341111,034111,01,131341111<-=---->=>⇒⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=P 二次型函数不定。
(2)034101103031,0110331,01,4101103031<-=--->=--<-⇒⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=P二次型函数为负定。
(3)017112141211003941110,010,1121412110>=---->=>⇒⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=P 二次型函数正定。
3-4-2 试确定下列二次型为正定时,待定常数的取值范围。
312321231221211242)(x x x x x x x c x b x a x v --+++=【解】:312321231221211242)(x x x x x x x c x b x a x v --+++=x c b a x T ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=1112121110212111,011,0111111>---->>c b a b aa 满足正定的条件为:⎪⎩⎪⎨⎧++>+>>1111111114410ca b c b a b a a3-4-3 试用李亚普诺夫第二法判断下列线性系统的稳定性。
;1001)4(;1111)3(;3211)2(;1110)1(x x x x x x x x ⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡---=⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡--=【解】: (1)设22215.05.0)(x x x v +=⎩⎨⎧≠≤==-=--=+=)0(0)0(0222221212211)(x x x x x x x x x x x x x v为半负定。
应用多元统计分析课后习题答案高惠璇第四章部分习题解答

其中β=(C'C)-1C'Y. 证明: Q( ) (Y C )(Y C ) ˆ C ˆ C )(Y C ˆ C ˆ C ) (Y C ˆ )(Y C ˆ ) ( ˆ )C C ( ˆ ) (Y C
ˆ) (1 R 2 ) ( y y ) 2 . ( 3 )残差平方和Q( i
i 1
13
第四章 回归分析
ˆ C(CC)1CY HY ˆ C 证明:(1)估计向量为 Y 1 n 1 ˆ 1 1 ˆ y ˆ i 1n Y 1n HY ( H 1n )Y y n i 1 n n n 1 1n Y y. n
解:样本的似然函数为
L(a, b, 2 )
1 2 2 2 exp [( y a ) ( y 2 a b ) ( y a 2 b ) ] 1 2 3 3 2 2 2 2 1
ˆ, 2 ) ˆ, b L(a
1 2 ˆ) 2 ( y a ˆ) 2 ] ˆ ˆ ˆ exp [( y a ) ( y 2 a b 2 b 2 3 3 2 2 1 2 2 1
3 似然比统计量的分子为
2
1 ˆ0 ( y1 y2 3 y3 ) a 11
ˆ0 , ˆ 0 ) (2 ) ( ˆ0 ) L( a
3 2
3 2 2
3 exp[ ]. 2
5
第四章 回归分析
似然比统计量为
2
ˆ0 , ˆ 0 ) ( L( a ˆ0 ) 2 ˆ, ˆ, b ˆ ) L( a
可得参数向量β和σ2的最大似然估计为:
ˆ (C C ) 1 C Y . 2 1 ˆ )(Y C ˆ) ˆ ( Y C n
第四章刚体运动习题详解
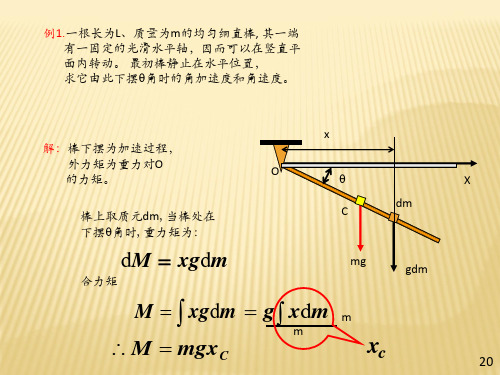
解:棒下摆为加速过程, 外力矩为重力对O 的力矩。
棒上取质元dm,当棒处在 下摆角时,重力矩为:
x
O
X
C
dm
dM xgdm
合力矩
mg
gdm
解:
因摩擦力产生的力矩是恒定的,故角速度均匀 减小。
0
0
t
0
0 t
dt t
0
f dS
r
σ
m πR2
R
dθ o
r
M J 1 mR2
2
dr
t 0mR2 / (2M ) (1) M ?
考虑面元dS对轴的摩擦力矩dM :
dM r0gdm r0g dS
26
t0mR2/(2M ) (1) dM r0g dS
mg 由(3)(4)(5)得
mgR sin
1 2
J02
1 2
J2
(5)
gh 2R2
cos2
g R
sin
1 2R
.
g 2
(h
4
3R)
M J
mgR 2mR2
g 2R
( 60 )
44
dt
O
X
C
即 d d
3g cos d d
mg
2L
θ
0
3gcos
2L
d
0
d
3g 2L
sin
1 2
2
3g sin
L
22
m 例2.质量为 、长为L的匀质细杆水平放置,一端
《理论力学》第四章 静力学应用专题习题解
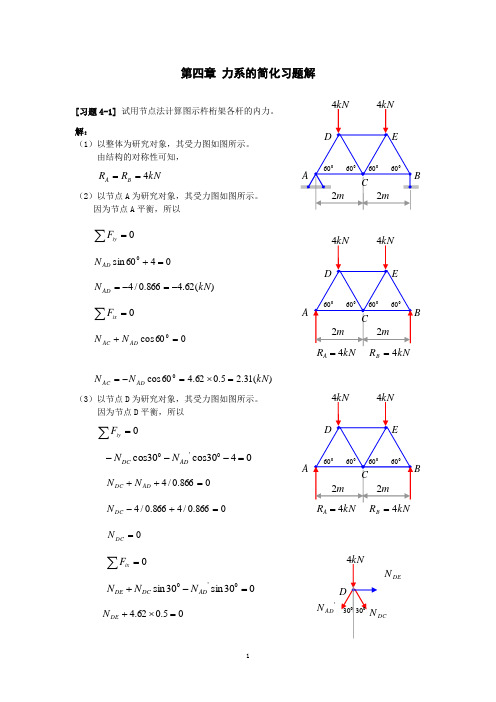
第四章 力系的简化习题解[习题4-1] 试用节点法计算图示杵桁架各杆的内力。
解:(1)以整体为研究对象,其受力图如图所示。
由结构的对称性可知, kN R R B A 4==(2)以节点A 为研究对象,其受力图如图所示。
因为节点A 平衡,所以0=∑iyF0460sin 0=+AD N)(62.4866.0/4kN N AD -=-=0=∑ixF060cos 0=+AD AC N N)(31.25.062.460cos 0kN N N AD AC =⨯=-= (3)以节点D 为研究对象,其受力图如图所示。
因为节点D 平衡,所以 0=∑iyF0430cos 30cos 0'0=---AD D C N N 0866.0/4=++AD D C N N 0866.0/4866.0/4=+-D C N0=DC N0=∑ixF030sin 30sin 0'0=-+AD D C D E N N N 05.062.4=⨯+DE NkN4)(akN4AB RkN 2AC23N A )(31.2kN N DE -=(4)根据对称性可写出其它杆件的内力如图所示。
[习题4-2] 用截面法求图示桁架指定杆件 的内力。
解:(a)(1)求支座反力以整体为研究对象,其受力图如图所示。
由对称性可知,kN R R B A 12==(2)截取左半部分为研究对象,其受力图 如图所示。
因为左半部分平衡,所以0)(=∑i CF M0612422843=⨯-⨯+⨯+⨯N 063243=⨯-++N )(123kN N =kN2AC23N A0=∑ixF0cos cos 321=++N N N αθ01252252421=+⋅+⋅N N012515221=+⋅+⋅N N0512221=++N N ……..(1) 0=∑iyF02812sin sin 21=--++αθN N025*******=+⋅+⋅N N02525121=+⋅+⋅N N052221=++N N0544221=++N N ……..(2) 05832=-N)(963.53/582kN N ==)(399.1652963.5252221kN N N -=-⨯-=--=解:(b )截取上半部分为研究对象,其受力图如图所示。
无机化学(周祖新)习题解答 第四章

无机化学(周祖新)习题解答第四章第四章酸碱平衡和溶解沉淀平衡习题解答(4)思考题1.强电解质的水溶液有强的导电性,但AgCl和BaSO4水溶液的导电性很弱,它们属于何种电解质?1.答:AgCl和BaSO4水溶液的导电性虽很弱,溶液中离子浓度很小,这是由于AgCl和BaSO4本身溶解度小,致使溶液中自由离子浓度小,导电性弱。
而AgCl和BaSO4(溶解部分)在溶液中还是全部解离的,所以是强电解质。
2.在氨水中加入下列物质时,NH3?H2O的解离度和溶液的pH将如何变化?⑴NH4Cl ⑵NaOH ⑶HAc ⑷加水稀释 2.NH3?H2ONH4++OH-⑴加入NH4Cl,氨水解离度下降,pH减小。
⑵加入NaOH,氨水解离度下降,pH增加。
⑶加入HAc,氨水解离度增加,pH减小。
⑷加水稀释,氨水解离度增加,pH减小。
3.下列说法是否正确?若有错误请纠正,并说明理由。
⑴酸或碱在水中的解离是一种较大的分子拆开而形成较小离子的过程,这是吸热反应。
温度升高将有利于电离。
⑵1×10-5 mol?L-1的盐酸溶液冲稀1000倍,溶液的pH值等于8.0。
⑶将氨水和NaOH溶液的浓度各稀释为原来1/2时,则两种溶液中OH-浓度均减小为原来的1/2。
⑷pH相同的HCl和HAc浓度也应相同。
⑸酸碱滴定中等当点即指示剂变色点。
⑹某离子被完全沉淀是指其在溶液中的浓度为0。
3.⑴错。
在解离即较大的分子拆开而形成较小离子的吸热反应的同时,较小离子与水分子的水合是是放热的,总反应的吸放热取决于两过程热效应的相对大小,有吸热也有放热,故温度升高不一定有利于解离。
⑵错。
在pH值远离7的时候,溶液每稀释10倍,pH近视增加一个单位,这是没有计算水解离出的H+,当pH接近7的时候,水解离出的H+就不能再忽略了,所以酸性溶液不管怎么稀释,只能越来越接近中性,不可能变为碱性。
⑶错。
NaOH溶液稀释为原来1/2时OH-浓度确实减小为原来的1/2;但氨水在稀释过程中,其解离平衡向右移动,会解离出更多的OH-,稀释一倍后,其OH-浓度大于原来的一半。
弹性力学(徐芝纶)第四章习题答案

第四章 习题解答4-14-2、解:本题为轴对称应力问题,相应的径向位移为: ()()()()()θ+θ+⎥⎦⎤⎢⎣⎡υ-+υ-+-υ-+υ+-=sin cos ln K I Cr 12Br 311r Br 12r A 1E 1u r (1) 轴对称应力通式为()()02ln 232ln 2122=+++-=+++=θθτσσr r C r B rAC r B r A由应力边界条件()()()()0,00,===-=====b r r b r r a r r a r r q θθτστσ并结合位移单值条件可知B=0,求得:22222222ab qa C a b qb a A -=--= 因半径的改变与刚体位移I ,K 无关,且为平面应变问题,将A 、B 、C 代入(1)式,并将υυυυ-→-→1,12EE 得:内半径的改变:()()()⎪⎪⎭⎫⎝⎛-+-+-=⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛--+-⎪⎭⎫ ⎝⎛-+-=∆=υυυυυυυυ11*111112222222222222a b a b Eqa a a b qa a a b q b a E u ar r外半径的改变:()()()2222222222221*11111a b ab E qa b a b qa b a b q b a Eu br r --=⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛--+-⎪⎭⎫ ⎝⎛-+-=∆=υυυυυυ 圆筒厚度的改变:()()()⎪⎪⎭⎫⎝⎛-++---=∆-∆=∆==υυυ112a b a b E qa u u R ar r b r r4-2另解:半径为r 的圆筒周长为r π2,受载后周长则为 ()θθεπεππ+=+1222r r r , 于是半径为 ()θε+1r ,半径的改变量则为:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+--⎪⎭⎫ ⎝⎛+--=⎪⎭⎫⎝⎛---=C r A C rA r E E r r r 212111*2222υυυσυυσυεθθ将对应的A 、C 及r=a,b 分别代入,可求出内外半径的改变及圆筒厚度的改变。
编译原理 龙书答案

第四章部分习题解答Aho:《编译原理技术与工具》书中习题(Aho)4.1 考虑文法S → ( L ) | aL → L, S | Sa)列出终结符、非终结符和开始符号解:终结符:(、)、a、,非终结符:S、L开始符号:Sb)给出下列句子的语法树i)(a, a)ii)(a, (a, a))iii)(a, ((a, a), (a, a)))c)构造b)中句子的最左推导i)S(L)(L, S) (S, S) (a, S) (a, a)ii)S(L)(L, S) (S, S) (a, S) (a, (L)) (a, (L, S)) (a, (S, S)) (a, (a, S) (a, (a, a))iii)S(L)(L, S) (S, S) (a, S) (a, (L)) (a, (L, S)) (a, (S, S)) (a, ((L), S)) (a, ((L, S), S)) (a, ((S, S), S)) (a, ((a, S), S))(a, ((a, a), S)) (a, ((a, a), (L))) (a, ((a, a), (L, S))) (a, ((a, a), (S, S))) (a, ((a, a), (a, S))) (a, ((a, a), (a, a)))d)构造b)中句子的最右推导i)S(L)(L, S) (L, a) (S, a) (a, a)ii)S(L)(L, S) (L, (L)) (L, (L, S)) (L, (L, a)) (L, (S, a)) (L, (a, a)) (S, (a, a)) (a, (a, a))iii)S(L)(L, S) (L, (L)) (L, (L, S)) (L, (L, (L))) (L, (L, (L, S))) (L, (L, (L, a))) (L, (L, (S, a))) (L, (L, (a, a))) (L, (S,(a, a))) (L, ((L), (a, a))) (L, ((L, S), (a, a))) (L, ((L, a), (a,a))) (L, ((S, a), (a, a))) (L, ((a, a), (S, S))) (S, ((a, a), (a,a))) (a, ((a, a), (a, a)))e)该文法产生的语言是什么解:设该文法产生语言(符号串集合)L,则L = { (A1, A2, …, A n) | n是任意正整数,A i=a,或A i∈L,i是1~n之间的整数}(Aho)4.2考虑文法S→aSbS | bSaS |a)为句子构造两个不同的最左推导,以证明它是二义性的S aSbS abS abaSbS ababS ababS aSbS abSaSbS abaSbS ababS ababb)构造abab对应的最右推导S aSbS aSbaSbS aSbaSb aSbab ababS aSbS aSb abSaSb abSab ababc)构造abab对应语法树d)该文法产生什么样的语言?解:生成的语言:a、b个数相等的a、b串的集合(Aho)4.3 考虑文法bexpr→bexpr or bterm | btermbterm→bterm and bfactor | bfactorbfactor→not bfactor | ( bexpr ) | true | falsea)试为句子not ( true or false)构造分析树解:b)试证明该文法产生所有布尔表达式证明:一、首先证明文法产生的所有符号串都是布尔表达式变换命题形式——以bexpr、bterm、bfactor开始的推导得到的所有符号串都是布尔表达式最短的推导过程得到true、false,显然成立假定对步数小于n的推导命题都成立考虑步数等于n 的推导,其开始推导步骤必为以下情况之一bexpr bexpr or btermbexpr btermbterm bterm and bfactorbexpr bfactorbfactor not bfactorbfactor ( bexpr )而后继推导的步数显然<n,因此由归纳假设,第二步句型中的NT推导出的串均为布尔表达式,这些布尔表达式经过or、and、not运算或加括号,得到的仍是布尔表达式因此命题一得证。
第4章理论力学习题解

4.1一质点受一与距离成反比的引力作用在一直线上运动,质点的质量为m ,比例系数为k ,如此质点从距原点O 为a 的地方由静止开始运动,求其到达O 点所需的时间。
解:质点受引力为:xk F -=,其运动微分方程为:xk tm-=d d v (1)即: x k xm -=d d v v分离变量积分:⎰⎰-=x axx k m d d 0v v vxa k m ln212=v)ln(2d d xa mk tx -==v (2)(v 与x 反向,取负值) )ln00ln ),0((∞→→>∴∈xa x xa a x令:y ayex aex xa y yyd 2d )ln(22---===,代入(2)式得;mk ty aey2d d 22-=-分离变量积分:)0:0:(∞→→y a x⎰⎰=-∞t yt mk y ea 0d 2d 22t mk a22π2=故到达O 点所需的时间为: km a t 2π=4.2一质点受力3K xa x F +-=作用,求势能)(x V 与运动微分方程的解。
解:C x a x x xa x x F x V ++=+--=-=⎰⎰2232K 21d )K (d )(适当选取势能零点,使0=C ,则222K 21)(xa x x V +=机械能 =++=2222K 2121xa x xm E 常量 (1)将(1)改写成2222K 242xa x E xm --= (2)质点运动微分方程:32K xa x xm +-= 22K 22xa x xmx +-=⇒ (3)(3)+(2)得22K 44)(2x E xx x m -=+ 即0)K(K 4d d 2222=-+E x mtx (4)(4)式通解:⎪⎪⎭⎫⎝⎛++=02 K2cos K θt m A Ex当0=x时,222K 21xa x E += 解得KK K)(2max 2a EE x -+=,KK 2aEA -=所以 ⎪⎪⎭⎫⎝⎛+-+=022K2cos KK Kθt m aE E x4.3若质点受有心力作用而在圆θcos 2a r =上运动时,则5228rh ma F -=,式中m 为质量,h 为速度矩。
《金属学原理》习题解答余永宁第四章

第4章 扩散1. 一块厚度为d 的薄板,在T 1温度下两侧的浓度分别为w 1,w 0(w 1>w 0),当扩散达到平稳态后,给出①扩散系数为常数,②扩散系数随浓度增加而增加,③扩散系数随浓度增加而减小等三种情况下浓度分布示意图。
并求出①种情况板中部的浓度。
解:一维扩散的平稳态有 D Cxd d =常数①扩散系数为常数时,d C /d x 也应为常数,故浓度分布是直线。
其中部的浓度C w w =−12②扩散系数随浓度增加而增加时,d C /d x 应随浓度增加而减小,浓度分布曲线是上凸的曲线。
③扩散系数随浓度增加而减小时,d C /d x 应随浓度增加而增加,浓度分布曲线是下凹的曲线。
2. 上题d =2mm,w 1=1.4%,w 0=0.15%。
在T 1温度下w 1和w 0浓度的扩散系数分别为D w 1=7.7×10-11m 2⋅s -1,D w 0=2.5×10-11m 2⋅s -1。
问板的两侧表面的浓度梯度的比值为多大?设w =0.8%≡ρ=60kg/m 3,问扩散流量为多少?(设扩散系数随浓度线性变化)解:①两侧表面的浓度梯度的比值:因 D C x D C xw w1010d d d d =,故 d d d d C x C x D D w w 100125770325===...②因扩散系数随浓度线性变化,设D =a+bC 因 D a bC D a bC 1100=+=+求得 010111011C C D D b C C C D D D a −−=−−−=扩散流量 J a bC C x =−+()d d 上式积分得 −=++Jx aC bC d22边界条件:x =l ,C =C 0;代入上式得:J a C C b C C l=−−+−[()()]10120221把a 和b 代入得J D D D C C C C D D C C C C l D D C C l =−−−−−+−−−=−−{()()()}()()110101*********10101212把重量百分数转化为体积浓度,因w =0.8%≡60kg/m3故 C C 130314086010501508601125=×=⋅=×=⋅−−.....kg m kg m 把浓度代入流量式子,最后得J =−−××⋅⋅=×⋅⋅−−−−−−−(..)(.).77251051125102102441011321621kg m s kg m s 3. 根据图4-5(b)和(c)给出的资料,计算x (Ni)=0.4以及x (Ni)=0.6两种合金在900°C 时的互扩散系数。
电路分析习题解答(第四章)
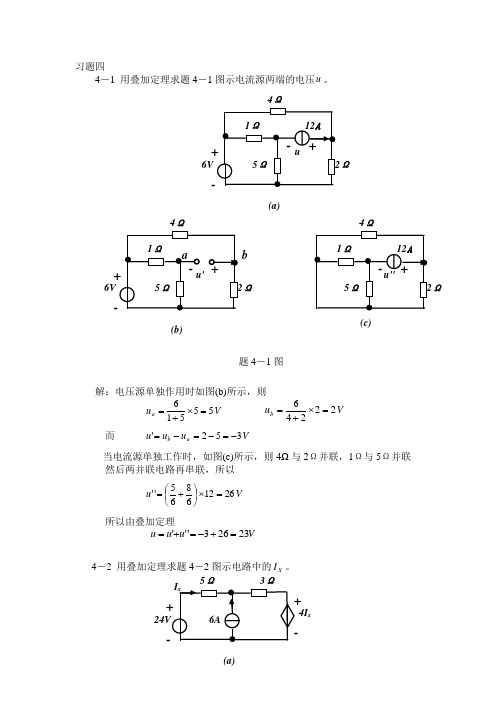
习题四4-1 用叠加定理求题4-1图示电流源两端的电压u 。
解:电压源单独作用时如图(b)所示,则V u a 55516=⨯+= V u b 22246=⨯+=而 V u u u a b 352'-=-=-=当电流源单独工作时,如图(c)所示,则4Ω与2Ω并联,1Ω与5Ω并联然后两并联电路再串联,所以V u 26126865''=⨯⎪⎭⎫⎝⎛+=所以由叠加定理V u u u 23263'''=+-=+=4-2 用叠加定理求题4-2图示电路中的X I 。
题4-1图 6V 4Ω Ω (b)b (c) 4Ω Ω5Ω 3Ω (a)4I x6V 4Ω Ω (a)解:电压源单独作用时的电路如图(b) 所示,则()24435''=++x x I I 解得 A I x 2'=电流源单独作用时的电路如图(c)所示,图中虚线为网孔电流,则 ()0''4''63''5=+++x x x I I I 解得 A I x 5.1''-= 所以 A I I I x x x 5.05.12'''=-=+=4-3 用叠加定理求题4-3图示电路中的独立电压源和独立电流源发出的功率。
5Ω 3Ω '(b) 4I 'x 4I ''x5Ω 3Ω I ''x(c) 题4-2图 题4-3图 2A 4Ω (a) 2V2A 4Ω 2i'(b) + - i''14Ω (c) u''1 2V解:电流源单独作用时的电路如图(b) 所示,则A i 2'1= 0'=i则 V i i u 824''1'1=-=电压源单独作用时的电路如图(b) 所示,则A i 5.042''1-=-= A i i 5.0''1''=-=则 V i u 122''''1=-=所以由叠加定理 A i i i 5.15.02''1'11=-=+=V u u u 918''1'11=+=+=可得电压源和电流源的功率分别为W i P V 3212-=-= W u P A 18212==4-4 题4-4图示电路中,R N 为电阻网络,由两个电流源供电。
建筑结构第四章习题解(杨鼎久主编第三版)

2
荷载效应组合的设计值——支座边剪力设计值 V=(g+q)ln /2=(66×5.56)/2kN=183.48kN (3)复核截面尺寸, hw/b=435/250=1.74<4 , 由式(4-8)得 0.25βcfcbh0=(0.25×1×14.3×250×440)N=388781N>V=183480N 截面尺寸满足要求。 (4)验算是否需要按计算配箍筋 由式(4-3)有 0.7ftbh0=0.7×1.43×250×435N=108859N<V=183480N 需要按计算配箍筋。 (5)计算箍筋数量 由式(4-5) Asv/s=(V-0.7ftbh0)/(fyvh0) =(183480-0.7×1.43×250×435)/(360×440) ㎜ =0.458 ㎜ 选 8,Asv1=50.3 ㎜2, n=2 , Asv=nAsv1 , 则 s=Asv/0.458=nAsv1/0.458=2×50.3/0.458=219 ㎜ 按表(4-1)要求,smax=200 ㎜,故取s=200 ㎜
9
⑥斜截面承载力计算 1)验算是否需要按计算配箍筋 由式(4-3)有 0.7ftbh0=0.7×1.43×250×465N=116366N<V=150000N 需要按计算配箍筋。 2)计算箍筋数量 由式(4-5) Asv/s=(V-0.7ftbh0)/(fyvh0) =(150000-0.7×1.43×250×465)/(360×465) ㎜ =0.201 ㎜ 选 6,Asv1=28.3 ㎜2, n=2 , Asv=nAsv1 , 则 s=Asv/0.201=nAsv1/0.252=2×28.3/0.201=281 ㎜ 按表(4-1)要求,smax=200 ㎜,故取s=200 ㎜ 3)验算最小配箍率 ρsv=nAsv1/(bs)=2×28.3/(250×200)=0.11%>0.24ft/fy=0.095% 故满足要求。
发电厂电气部分第四章习题解答

第四章电气主接线4—1 对电气主接线的基本要求是什么?答:对电气主接线的基本要求是:可靠性、灵活性和经济性.其中保证供电可靠是电气主接线最基本的要求。
灵活性包括:操作、调度、扩建的方便性。
经济性包括:节省一次投资,占地面积小,电能损耗少。
4-2 隔离开关与断路器的区别何在?对它们的操作程序应遵循哪些重要原则?答:断路器具有专用灭弧装置,可以开断或闭合负荷电流和开断短路电流,故用来作为接通和切断电路的控制电器.而隔离开关没有灭弧装置,其开合电流极小,只能用来做设备停用后退出工作时断开电路。
4—3 防止隔离开关误操作通常采用哪些措施?答:为了防止隔离开关误操作,除严格按照规章实行操作票制度外,还应在隔离开关和相应的断路器之间加装电磁闭锁和机械闭锁装置或电脑钥匙。
4-4 主母线和旁路母线各起什么作用?设置专用旁路断路器和以母联断路器或者分段断路器兼作旁路断路器,各有什么特点?检修出线断路器时,如何操作?答:主母线主要用来汇集电能和分配电能。
旁路母线主要用与配电装置检修短路器时不致中断回路而设计的。
设置旁路短路器极大的提高了可靠性。
而分段短路器兼旁路短路器的连接和母联短路器兼旁路断路器的接线,可以减少设备,节省投资。
当出线和短路器需要检修时,先合上旁路短路器,检查旁路母线是否完好,如果旁路母线有故障,旁路断路器在合上后会自动断开,就不能使用旁路母线。
如果旁路母线完好,旁路断路器在合上就不会断开,先合上出线的旁路隔离开关,然后断开出线的断路器,再断开两侧的隔离开关,有旁路短路器代替断路器工作,便可对短路器进行检修。
4-5 发电机—变压器单元接线中,在发电机和双绕作变压器之间通常不装设断路器,有何利弊?答:发电机和双绕组变压器之间通常不装设断路器,避免了由于额定电流或短路电流过大,使得在选择出口断路器时,受到制造条件或价格等原因造成的困难。
但是,变压器或者厂用变压器发生故障时,除了跳主变压器高压侧出口断路器外,还需跳发电机磁场开关,若磁场开关拒跳,则会出现严重的后果,而当发电机定子绕组本身发生故障时,若变压吕高压侧失灵跳闸,则造成发电机和主变压器严重损坏.并且发电机一旦故障跳闸,机组将面临厂用电中断的威胁。
第4章习题解答

第四章 机械振动和机械波4.1什么是简谐振动?分别从运动学和动力学两方面作出解释。
并说明下列运动是不是简谐振动;(1)小球在地面上做完全弹性的上下跳动;(2)小球在半径很大的光滑凹球面底部做小幅度的摆动; (3)曲柄连杆机构使活塞做往复运动。
4.2 若弹簧振子中弹簧本身的质量不可忽略,其振动周期是增加还是减小? 这相当于增加了系统的惯性,振动周期将增加。
4.3 将单摆拉到与竖直方向成ϕ角后,放手任其摆动,则ϕ是否就是其初相位?为什么?单摆的角速度是否是谐振动的圆频率?4.4判断以下说法是否正确?说明理由。
“质点作简谐振动时,从平衡位置运动到最远点需要1/4周期,因此走过该段距离的一半需时1/8周期。
”4.5两个相同的弹簧挂着质量不同的物体,当它们以相同的振幅做简谐运动时,问振动的能量是否相同?4.6什么是波动?振动与波动有什么区别和联系? 4.7试判断下列几种关于波长的说法是否正确. (1)在波传播方向上相邻两个位移相同点的距离; (2)在波传播方向上相邻两个运动速度相同点的距离; (3)在波传播方向上相邻两个振动相位相同点的距离。
4.8当波从一种媒质透入另一种媒质时,下面那些量会改变,哪些量不会改变:波长、频率、波速、振幅。
4.9有人认为频率不同、振动方向不同、相位差不恒定的两列波不能叠加,所以它们不是相干波,这种看法对不对?说明理由。
4.10 波的能量与振幅的平方成正比,两个振幅相同的相干波在空间叠加时,干涉加强的点的合振幅为原来的两倍,能量为原来的四倍,这是否违背能量守恒定律?4.11 一质点作简谐振动)7.0100cos(6ππ+=t x cm 。
某时刻它在23=x cm 处,且向X 轴负向运动,它要重新回到该位置至少需要经历的时间为( ) A 、s 1001 B 、s 2003 C 、s 501 D 、 s 503答案:(B)4.12 一个单摆,如果摆球的质量增加为原来的四倍,摆球经过平衡位置时的速度减为原来的一半,则单摆( )A 、频率不变,振幅不变;B 、频率不变,振幅改变;C 、频率改变,振幅不变;D 、频率改变,振幅改变; B4.13 以频率ν作简谐振动的系统,其动能和势能随时间变化的频率为( ) A 、2/ν B 、ν C 、ν2 D 、ν4 答案:(C)4.14 劲度系数为m N /100的轻弹簧和质量为10g 的小球组成的弹簧振子,第一次将小球拉离平衡位置4cm ,由静止释放任其运动;第二次将小球拉离平衡位置2cm 并给以2cm/s 的初速度任其振动。
博弈论第4章答案

R R M 4.1.a 标准式1↖2 L ’ R ’4,1 0,0 3,0 0,1 2,2 2,2纯战略纳什均衡:( L, L ’ ) ( R, R ’ )子博弈精炼纳什均衡:( L, L ’ ) ( R, R ’ )精炼贝叶斯纳什均衡:( L, L ’ )4.1.b 标准式1↖2 L ’ M ’ R ’1, 3 1, 2 4, 0 4, 0 0, 2 3, 3 2, 4 2, 4 2, 4纯战略纳什均衡:( R, M ’ )子博弈精炼纳什均衡:( R, M ’ )精炼贝叶斯均衡: 没有4.2标准式1↖2 L ’ R ’2,2 2,2 3,0 0,1 0,1 3,0六种纯战略组合,每种组合中都至少有一方存在偏离的动机,因此不存在纯战略纳什均衡,因此也就不存在纯战略精炼贝叶斯均衡。
求混合战略精炼贝叶斯均衡:设参与者1选择L 、M 、R 的概率分别为1,2,12(1)p p p p −−参与者2选择L ’和R ’的概率分别为,(1)q q −在给定参与者1的战略下,参与者2选择L ’和R ’的收益无差异,则: 1212120*1*1*0*p p p p p p +=+⇒=给定参与者2的战略,参与者1选择L 、M 、R 的收益无差异,则:12121212[3*0*(1)][0*3*(1)]2*(1)41:**,*112p q q p q q p p p p p p q +−=+−=−−====又 联立得 所以 L LML LM L RL4.3答案(见4.5)4.4表示方法第一个括号,逗号左边为type 1发送者信号,逗号右边为type 1发送者信号;第二个括号,逗号左边为接收到L 信号的反应,逗号右边为接收到R 信号的反应; P 为信号接收者对type 1发送L 的推断,q 为信号接收者对type 1发送R 的推断 (a )[(,),(,),1/2][(,),(,),1/2][(,),((1),),1/2][(,),(,),1,0]R R u u p R R d u p R R d u u p L R u d p q αα><+−===(b )[(,),(,),1/2,2/3][(,),(,),1,0][(,),(,),0,1]L L u u p q L R d u p q R L u d p q =<====中文版习题4.5答案(a )[(,),(,),1/3,1/2]R R u d p q >=(b )12121212[(,,),(,),1/3,1/2][(,,),(,),1/2,0]L L L u u p p q q L L R u d p p q q ==+<==+=。
第四章习题解答
4-13 试比较溢流阀、减压阀、顺序阀(内控外泄式)三者 之间的异同点。
解:参考答案如下表。
1) pY <pJ , pJ > pL ; 2) pY > pJ , pJ > pL ; 3) pY >pJ , pJ = pL ; 4) pY >pJ , pL =∞。
进口压力 出口压力 开启状况
1
pY
pL
全开
2
pY
pL
全开
3
pY
pJ = pL 开始关
4
pY
pJ
Hale Waihona Puke 关4-11 图示回路,负载压力为pL,减压阀调压力为pJ,溢流阀 调定压力为pY,且pY > pJ ,试分析泵的工作压力为多少?
4-8 如图所示,随着负载压力的增加,2个不同调定压力的减压阀串联后 的出口压力决定于哪个减压阀?为什么?另一个阀处什么状态?2个不同 调定压力的减压阀并联后的出口压力决定于哪个减压阀?为什么?另一 个阀处什么状态?
解答:减压阀控制的是出 口的压力,因此:
串联时: 1、当流体压力小于两个减压阀的压力调定值,出口压力等于
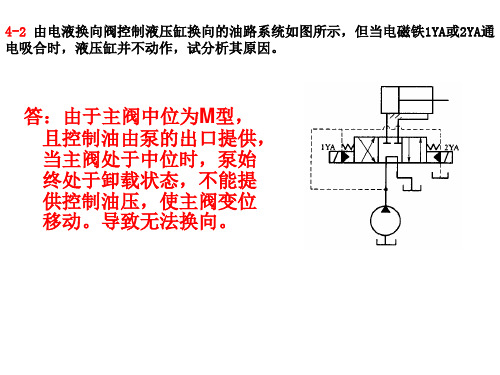
4-2 由电液换向阀控制液压缸换向的油路系统如图所示,但当电磁铁1YA或2YA通 电吸合时,液压缸并不动作,试分析其原因。
答:由于主阀中位为M型, 且控制油由泵的出口提供, 当主阀处于中位时,泵始 终处于卸载状态,不能提 供控制油压,使主阀变位 移动。导致无法换向。
4-3 如图所示,开启压力分别为0.2Mpa、0.3Mpa、0.4Mpa 的三个单向阀串联(如图a)或并联(如图b),当O点刚有 油液流过时,P点压力各为多少?
电力电子技术-第四章习题解析

直流-交流变换器(7)
第4章 习题(2)
第2部分:简答题 1.试说明PWM控制的基本原理。(略)
2.单极性和双极性PWM调制有什么区别?三相桥式PWM型逆变电路中,输
出相电压(输出端相对于直流电源中点的电压)和线电压SPWM波形各有几种
电平?
答:单极性PWM调制在调制信号的半个周期内载波只在正或负一种极性范围
分段同步调制优点:在输出频率高的频段采用较低的载波比,以使载 波频率不致过高,限制在功率开关器件允许的范围内。在输出频率低的频 段采用较高的载波比,以使载波频率不致过低而对负载产生不利影响。 7.什么是SPWM波形的规则化采样法?和自然采样法比规则采样法有什么 优点? 答:规则采样法是取三角波两个正峰值之间为一个采样周期,使每个脉冲 的中点都以相应的三角波中点为对称,在三角波的负峰值时刻对正弦信号 波采样得到一点,过该点作一水平直线和三角波交与两点,在这两个时刻 控制器件通断。规则采样法生成的SPWM波形与自然采样法接近,优点是 计算量大大减少。
刻(不含0和Л时刻)可以控制,可以消去的谐波有几种?
答:这是计算法中一种较有代表性的方法,为了减少谐波并简化控制,应 尽量使波形对称:首先,为消除偶次谐波,应使波形正负两半周期镜对称 ;其次,为消除谐波中余弦项,应使波形在半周期内前后1/4周期以π/2为 轴线对称。满足使波形四分之一周期对称后,再设法消去几种种特定频率 的谐波。 如果半个信号波周期内有10个开关时刻(不含0和Л时刻)可以控制,则可 以消去9种频率的谐波。
直流-交流变换器(7)
第4章 习题(2)
第1部分:填空题
1.PWM控制的理论基础是面积等效 原理,即冲量相等而形状不同的窄脉冲 加在具有惯性的环节上时,其效果基本相同。 2.根据“面积等效原理”,SPWM控制用一组等幅不等宽的脉冲(宽度按正弦 规律变化)来等效一个正弦波。 3.PWM控制就是对脉冲的宽度进行调制的技术;直流斩波电路得到的PWM 波是等效直流波形,SPWM控制得到的是等效正弦波形。 4.PWM波形只在单个极性范围内变化的控制方式称单极性控制方式,PWM 波形在正负极性间变化的控制方式称双极性控制方式,三相桥式PWM型逆 变电路采用双极性控制方式。 5.SPWM波形的控制方法:改变调制信号ur的幅值可改变基波幅值;改变调 制信号 ur 的频率可改变基波频率; 6.得到PWM波形的方法一般有两种,即计算法和调制法,实际中主要采用 调制法。 7.根据载波和信号波是否同步及载波比的变化情况,PWM调制方式可分为 同步调制和异步调制。一般为综合两种方法的优点,在低频输出时采用异步 调制方法,在高频输出时采用同步调制方法。
第4章 组合逻辑电路习题解答

习题4.1写出图所示电路的逻辑表达式,并说明电路实现哪种逻辑门的功能。
习题4.1图解:B A B A B A B A B A F ⊕=+=+= 该电路实现异或门的功能4.2分析图所示电路,写出输出函数F 。
习题4.2图 解:[]B A B BB A F ⊕=⊕⊕⊕=)(4.3已知图示电路及输入A 、B 的波形,试画出相应的输出波形F ,不计门的延迟.习题4.3图解:B A B A B A AB B AB A AB B AB A F ⊕=∙=∙∙∙=∙∙∙=4.4由与非门构成的某表决电路如图所示。
其中A 、B 、C 、D 表示4个人,L=1时表示决议通过。
(1) 试分析电路,说明决议通过的情况有几种。
(2) 分析A 、B 、C 、D 四个人中,谁的权利最大。
习题4.4图解:(1)ABD BC CD ABD BC CD L ++=∙∙=B AC & && & D L B A =1 =1 =1FF A B & && & & F B AABCD L ABCD L 0000 0001 0010 0011 0100 0101 0110 01110 0 0 1 0 0 1 11000 1001 1010 1011 1100 1101 1110 11110 0 0 1 0 1 1 1(3)根据真值表可知,四个人当中C 的权利最大。
4.5分析图所示逻辑电路,已知S 1﹑S 0为功能控制输入,A ﹑B 为输入信号,L 为输出,求电路所具有的功能。
习题4.5图解:(1)011011)(S S B S A S S B S A L ⊕⊕+⊕=⊕⊕∙⊕= (2)S 1S 0 L 00 01 10 11A+BB A +ABAB4.6试分析图所示电路的逻辑功能。
习题4.6图解:(1)ABC C B A F )(++=A BS 1S 0L =1 =1 &=1& & & & &FA BC电路逻辑功能为:“判输入ABC 是否相同”电路。
大学物理第四章习题解答
l
v v
O
以杆、摆锤和地球为整体,该系统在 摆动过程中机械能守恒,选择最低点 为重力势能零点。若刚好能完成一次
m/
A
m
/
v v 2
圆周运动,则系统在最高点的角速度 为0。
/ / 11 / 2 2 m gl 3m gl / 2 = + 2m / gl m l + m l ω0 + 23 2 2
解:有心力对地心的力矩为零, 有心力对地心的力矩为零, 卫星 m 对地心 o 角动量守恒
v 2 h2 r r 1
h1 m
mv1r1 = mv2 r2
卫星与地球系统机械能守恒: 1 2 GmM 1 2 GmM mv1 − = mv2 − 2 r1 2 r2
24
v1
r1 = R + h1 , r2 = R + h2
0
6
−t / τ
d ( − )]
t
τ
= ω 0 [t
−t / τ 6 + τe ]0
= 9[6 + 2(e −6 / 2 - e 0 )] = 36.9 rad
∆θ N= = 5.87 (圈) 2π
N ≠ ∆θ
6
4 − 9:一飞轮由一直径为30cm,厚度为2cm的圆盘和两个直径都为10cm ,长为8cm的共轴圆柱体组成,设飞轮的密度为7.8 ×103 kg / m 3,求飞轮 对轴的转动惯量。
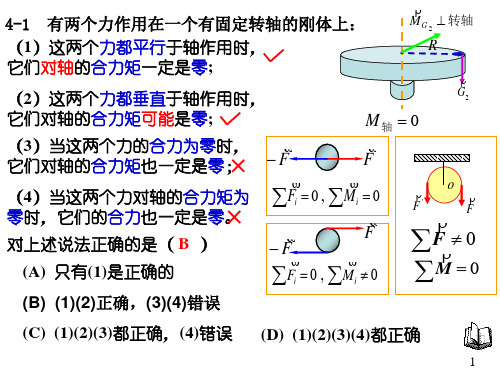
有两个力作用在一个有固定转轴的刚体上: 4-1 有两个力作用在一个有固定转轴的刚体上: 力都平行于轴作用时 (1)这两个力都平行于轴作用时, )这两个力都平行于轴作用时, 对轴的 一定是零 它们对轴 合力矩一定是 它们对轴的合力矩一定是零; 力都垂直于轴作用时 (2)这两个力都垂直于轴作用时, )这两个力都垂直于轴作用时, 它们对轴的合力矩可能是 合力矩可能 它们对轴的合力矩可能是零; 合力为零时 (3)当这两个力的合力为零时, )当这两个力的合力为零 它们对轴的合力矩也一定是零 合力矩也一定是 它们对轴的合力矩也一定是零; 4)当这两个力对轴的合力矩为 (4)当这两个力对轴的合力矩为 它们的合力也一定是零 合力也一定是 零时,它们的合力也一定是零。 对上述说法正确的是( 对上述说法正确的是( B ) (A) 只有 是正确的 只有(1)是正确的 (B) (1)(2)正确,(3)(4)错误 正确, 正确 错误 (C) (1)(2)(3)都正确,(4)错误 都正确, 错误 都正确
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章动态元件4.1 某电容FC2=,已知其初始电压0)0(=u,其电流i波形如题图4.1图所示。
8412340t/si/A题4.1图⑴求0≥t时的电容电压)(t u,并画出其波形。
⑵计算st2=时电容吸收的功率)2(p。
⑶计算st2=时电容的储能)2(w。
解:⑴⎰+=t dtt iCutu)(1)0()(,当10≤≤t时,tdttu t4821)(==⎰,当31≤<t时,4)1(21)(1=+=⎰udttu t,当43≤<t时,22421)3()(3-=+=⎰tdtutu t,当4>t时,Vutu6)4()(=+=,所以,0≥t时,443,311,622,4,4)(>≤<≤<≤≤⎪⎪⎩⎪⎪⎨⎧-=tttttttu,波形如图所示。
图 4.1⑵ )()()(t i t u t p = ,当s t 2=时,004)2()2()2(=⨯==i u p 。
⑶ ),(21)(2t Cu t w = 当s t 2=时,J w 164221)2(2=⨯⨯=。
4.2 某电感H L 4=,已知其初始电流0)0(=i ,其电压u 波形如题4.2图所示。
012342-2/u V/t s题4.2图⑴ 求0≥t 时的电感电流)(t i ,并画出其波形。
⑵ 计算s t 2=时电感吸收的功率)2(p 。
⑶ 计算s t 2=时电感的储能)2(w 。
解:⑴ ⎰==tdt t u L i t i 0)(1)0()(,当10≤≤t 时,t dt t i t5.0241)(0==⎰, 当31≤<t 时,5.0)1(01)(1=+=⎰i dt Lt i t,当43≤<t 时,25.0)2(41)3()(3+-=-+=⎰t dt i t i t,当4>t 时,A i t i 00)4()(=+=,所以,0≥t 时,443,3110,025.0,5.0,5.0)(>≤<≤<≤≤⎪⎪⎩⎪⎪⎨⎧+-=t t t t t t t i ,波形如图所示。
图 4.24.3 如题4.3图所示电路,已知电感电流;0,)1(5)(10≥-=-t A e t i t L 求0≥t 时电容电流)(t i c 和电压源电压)(t u s。
题4.3图解:电感电压t L e dtt di L t u 101100)()(-==,可知)()(t u t u C L =,C u 和)(t i C 参考非关联,则A e dtt du Ct i t C C 1010)()(-=-=,由KCL 可得t e i 10155--=,再由KVL 得t L s e t u i u 107010)(2-+=+=。
4.6 如题4.6图所示电路由一个电阻R 、一个电感L 和一个电容C 构成。
已知回路电流0,)2010()(2≥-=--t A e e t i t t ;电压V e e t u t t )205()(21--+-=,0≥t 。
若当0=t 时电路的总储能为25J ,试求R|、L 、C 的值。
题4.6图解:①不可能是电阻R ,所以≠)()(11t i t u 定值 ⑴ 若①是电容C ,则dt t du C t i )()(∙=,即C C ee e e tttt ,405201022=------为常数,显然不可能。
⑵ 若①是电感L ,则dt t di L t u )()(∙=,即5.0401020522==+-+-----L e e e e tt tt 显然成立,并且有H L 5.0=,当0=t 时,A i V u 10,1511-==,)2()1(,,25212111122⎪⎩⎪⎨⎧+==+=Ri u u Li Cu w 总,由上式⑴得0=u ,即得Ω=-=5.111i u R ,当 0≠t 时,C电容与之非关联,有⎰-=tdt t i Cu 01)(1,且由KVL 有11i R u u +=, F C dtt i Ri u Ct 1)(111=⇒+-=∴⎰。
综上所述,F C H L R 1,5.0,5.1==Ω=。
4.11 ⑴ 试确定如题4.11(a )图所示耦合线圈的同名端。
⑵ 如题4.11(b )图所示电路,已知开关S 突然断开时,电压表指针呈现正向偏转,试判断耦合电感的同名端,并说明理由。
M(b)题4.11图(a)解:⑴ 1和4是同名端,2和3是同名端。
⑵ 可知a 、d 或b 、c 是同名端。
当开关S 突然断开时,01<dt di ,而dt di M u 1±=都大于零,可知dtdi M u 1±=。
即a 与c 是异名端,所以有a 、d ,b 、c 是同名端。
4.12 写出如题4.2图所示三个电路端子上的电压、电流关系。
M +(a)2+-(b)题4.12图解:(a )⎪⎩⎪⎨⎧-=-=dt diM dt di L u dt di M dt di L u 12222111, (b )⎪⎩⎪⎨⎧-+=-+=dt diM dt di L i R u dt di M dt di L i R u 122222211111, (c )⎪⎩⎪⎨⎧-+=--+=dt di M dt di L dt di L u dt di M dt di M dt di L u u 122122211121⇒⎪⎩⎪⎨⎧+-=-+-+=dt diL dt di M L u dt di M L dt di M L L u 22122221211)()()2(. 4.14如题4.14图所示电路,已知tA i s sin =,求开路电压)(t u 。
题4.14图解:dtdiM u dt di M dt di u s H s s H 2516,6=+=,得t t u u t u H H cos 3cos 8)(56+=-== tVcos 11。
4.15 求题4.15图所示电路得等效电感。
∙2H 4H(a)题4.15图(a )解:列出VCR 关系有⎪⎩⎪⎨⎧+=+=)2(24)1(23122211dt di dt di u dt di dt di u ,由(2)可得dt di dt di 1221-=⇒,代入(1)得,dtdi dt didt di u 11112)21(23=-⨯+=,所以等效电感H L 2=。
(b )解:列出VCR 关系有⎪⎩⎪⎨⎧+=+=)2(39)1(36122211dt di dt di u dt di dt di u ,由(2)可得dt di dt di 1231-=⇒,代入(1)得,dtdi dt didt di u 11115)31(36=-⨯+=,且1u u =所以等效电感H L 5=。
(c )解:列出VCR 关系有⎪⎪⎪⎩⎪⎪⎪⎨⎧-=∙+=-∙+=dt di dt di u dt di dt di u dtdi dt di dt di u 13312232112613215,13232,i i i u u =+=,得+=1u u dt di dt di dt di i d dt di dt di u 212121264)(246+=--+=,所以可得dtdidt di 123=, dt di dt di 312=,故dtdi dt didt di u 11163164=⨯+=所以等效电感H L 6=。
4.19如题4.19图所示理想变压器电路,已知V U s 16=,试求负载L R 吸收的功率。
5ΩU 题4.19图解:电压电流参考方向如图所示。
i 1=-5i 2,i ,5132i -=所以 i 235i =- ,u 21110162i i u s +=-= , u 22232122152802,50805,51i i u u i u u u --=-=--=-=-=,u 34234435,5521651,5i u i u u u =---===, 16+,2555222i i -=所以,)17780(*55216,177400,17780432---==-=u A i A i P 5.251775.2*16*17740034==-=i u L w 。
4.20 如题4.20图所示理想变压器电路,tV u s cos 6=,试求电流)(1t i 。
解:电流电压的参考方向如图所示。
i 34432,5.0i i i ==对节点A,B,由KCL 得 i .321i i +=又有u u s 2=, 所以,u=t cos 3,i t u cos 35==,323212cos 3i i t i i i +=+=且对于最上方支路由VCR 得t i u u i s cos ,322=-=,所以,t i t i cos 2,cos 13==。
su 1Ωs i 图 4.204.21 如题4.21图所示理想变压器电路,tA t i s cos 2)(=,试求电压)(1t u 和)(2t u 。
2Ω图4.21解:电压电流方向如图所示。
t i u t i i i i s s cos 82,cos 42,5.02=====,t i i u i u u s cos 12)(22212=-+=+=,,cos 24't nu u == 所以,t i i u i u u s cos 20)2(22'1'1=--=-=。
4.22 如题4.22图所示理想变压器电路,A t i s )2sin(=,试求电压)(t u 。
22:1图 4.22解:232i i -= ,dt diU 4=,又dti i d dt di dt di U U s )(122)(3221231-=+-⨯== , V t dtdi t u )2cos(64)(1==∴。
4.23 如题4.23图所示理想变压器电路,V t u s )2sin(3=,试求电压)(1t u 。
题4.23图解:)(66,111111dtdudt du dt du i i u u u s c c s c -===-= ① 由理想变压器特性知 12122,5.0i i u u -==, 而,2,5.0122122i i i u u u c c =-=== dtdudt du i c 122612== ②由①②得 dtdu dt du dt du s 113)(6=-,123u u s =,所以, t t u 2sin 2)(1=。
