初中几何证明口诀
初中几何证明方法

初中几何证明方法
1. 直角三角形定理证明:利用勾股定理证明直角三角形的特征。
2. 等边三角形定理证明:通过三条边全等证明三角形的三个角都是60度。
3. 同位角证明:沿着一组平行线切割两条平行线,证明同位角相等。
4. 对顶角证明:利用两组平行线切割一条横线,证明对顶角相等。
5. 三角形内角和定理证明:通过将三角形分解成三个直角三角形,证明三角形的内角和为180度。
6. 圆的面积公式证明:通过四个等腰直角三角形的组合和排列得出圆的面积公式。
7. 相似三角形定理证明:通过两个三角形的对应角相等,证明两个三角形相似。
8. 等腰三角形定理证明:通过证明两个底角相等,证明等腰三角形的另外两条边相等。
9. 正方形定理证明:通过证明正方形的四个角都是直角且四条边相等,证明正方形的特征。
10. 角平分线定理证明:利用角平分线将一个角分成两个相等的角,证明相邻的角互补且对顶角相等。
初中几何学习记忆口诀

初中几何学习记忆口诀常见辅助线作法歌诀人说几何很困难,难点就在辅助线。
辅助线,如何添?把握定理和概念。
还要刻苦加钻研,找出规律凭经验图中有角平分线,可向两边作垂线。
角平分线平行线,等腰三角形来添。
线段垂直平分线,常向两端把线连。
要证线段倍与半,延长缩短可试验。
三角形中两中点,连接则成中位线。
三角形中有中线,延长中线加一倍。
梯形里面作高线,平移一腰试试看。
等积式子比例换,寻找相似很关键。
直接证明有困难,等量代换少麻烦。
斜边上面作高线,弦高公式是关键。
半径与弦长计算,弦心距来中间站。
圆上若有一切线,切点圆心半径连。
要想证明是切线,半径垂线仔细辨。
是直径,成半圆,想成直角径连弦。
弧有中点圆心连,垂径定理要记全。
圆周角边两条弦,直径和弦端点连。
要想作个外接圆,各边作出中垂线。
还要作个内切圆,内角平分线梦园。
如果遇到相交圆,不要忘作公共弦。
若是添上连心线,切点肯定在上面。
辅助线,是虚线,画图注意勿改变。
假如图形较分散,对称旋转去实验。
基本作图很关键,平时掌握要熟练。
解题还要多心眼,经常总结方法显。
切勿盲目乱添线,方法灵活应多变。
分析综合方法选,困难再多也会减。
虚心勤学加苦练,成绩上升成直线。
初中数学知识点几何部分总结大全1 过两点有且只有一条直线2 两点之间线段最短3 同角或等角的补角相等4 同角或等角的余角相等5 过一点有且只有一条直线和已知直线垂直6 直线外一点与直线上各点连接的所有线段中,垂线段最短7 平行公理经过直线外一点,有且只有一条直线与这条直线平行8 如果两条直线都和第三条直线平行,这两条直线也互相平行9 同位角相等,两直线平行10 内错角相等,两直线平行11 同旁内角互补,两直线平行12 两直线平行,同位角相等13 两直线平行,内错角相等14 两直线平行,同旁内角互补15 定理三角形两边的和大于第三边16 推论三角形两边的差小于第三边17 三角形内角和定理三角形三个内角的和等于180°18 推论1 直角三角形的两个锐角互余19 推论2 三角形的一个外角等于和它不相邻的两个内角的和20 推论3 三角形的一个外角大于任何一个和它不相邻的内角21 全等三角形的对应边、对应角相等22 边角边公理(SAS) 有两边和它们的夹角对应相等的两个三角形全等23 角边角公理( ASA)有两角和它们的夹边对应相等的两个三角形全等24 推论(AAS) 有两角和其中一角的对边对应相等的两个三角形全等25 边边边公理(SSS) 有三边对应相等的两个三角形全等26 斜边、直角边公理(HL) 有斜边和一条直角边对应相等的两个直角三角形全等27 定理1 在角的平分线上的点到这个角的两边的距离相等28 定理2 到一个角的两边的距离相同的点,在这个角的平分线上29 角的平分线是到角的两边距离相等的所有点的集合30 等腰三角形的性质定理等腰三角形的两个底角相等 (即等边对等角)31 推论1 等腰三角形顶角的平分线平分底边并且垂直于底边32 等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合33 推论3 等边三角形的各角都相等,并且每一个角都等于60°34 等腰三角形的判定定理如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)35 推论1 三个角都相等的三角形是等边三角形36 推论 2 有一个角等于60°的等腰三角形是等边三角形37 在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半38 直角三角形斜边上的中线等于斜边上的一半39 定理线段垂直平分线上的点和这条线段两个端点的距离相等40 逆定理和一条线段两个端点距离相等的点,在这条线段的垂直平分线上41 线段的垂直平分线可看作和线段两端点距离相等的所有点的集合42 定理1 关于某条直线对称的两个图形是全等形43 定理 2 如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线44定理3 两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上45逆定理如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称46勾股定理直角三角形两直角边a、b的平方和、等于斜边c的平方,即a^2 b^2=c^247勾股定理的逆定理如果三角形的三边长a、b、c有关系a^2 b^2=c^2 ,那么这个三角形是直角三角形48定理四边形的内角和等于360°49四边形的外角和等于360°50多边形内角和定理 n边形的内角的和等于(n-2)×180°51推论任意多边的外角和等于360°52平行四边形性质定理1 平行四边形的对角相等53平行四边形性质定理2 平行四边形的对边相等54推论夹在两条平行线间的平行线段相等55平行四边形性质定理3 平行四边形的对角线互相平分56平行四边形判定定理1 两组对角分别相等的四边形是平行四边形57平行四边形判定定理2 两组对边分别相等的四边形是平行四边形58平行四边形判定定理3 对角线互相平分的四边形是平行四边形59平行四边形判定定理4 一组对边平行相等的四边形是平行四边形60矩形性质定理1 矩形的四个角都是直角61矩形性质定理2 矩形的对角线相等62矩形判定定理1 有三个角是直角的四边形是矩形63矩形判定定理2 对角线相等的平行四边形是矩形64菱形性质定理1 菱形的四条边都相等65菱形性质定理2 菱形的对角线互相垂直,并且每一条对角线平分一组对角66菱形面积=对角线乘积的一半,即S=(a×b)÷267菱形判定定理1 四边都相等的四边形是菱形68菱形判定定理2 对角线互相垂直的平行四边形是菱形69正方形性质定理1 正方形的四个角都是直角,四条边都相等70正方形性质定理2正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角71定理1 关于中心对称的两个图形是全等的72定理2 关于中心对称的两个图形,对称点连线都经过对称中心,。
超级实用!初中几何证明口诀,别再说难了!

超级实用!初中几何证明口诀,别再说难了!
超级实用!初中几何证明口诀,别再说难了!
昨晚在微信群里和学生们聊Байду номын сангаас,好多初中生们都在说初中几何好难啊!怎么都得不了分,看着图形却证明不了,真是想哭了。
我就觉得纳闷了,初中几何很简单啊。只要掌握了下面的这些口诀,就轻松了。
是不是其实很简单,我将这些口诀分享在微信群里。学生一致要求我发出来分享给更多的人,让他们受益。
巧用顺口溜熟记初中数学公式和规律

巧用顺口溜熟记初中数学公式和规律数学公式和规律在初中阶段是非常重要的,它们是解题的基础和指导,也是理解数学概念和思维的关键。
然而,对于许多学生来说,记住这些公式和规律并不容易。
为了帮助学生更好地掌握数学知识,我整理了一些巧妙的顺口溜,通过这些顺口溜,学生能够轻松地记住一些重要的数学公式和规律。
一、顺口溜记代数公式:1. 一元二次方程求根法,b²-4ac你得掌握。
一大再小两个根,<0无实根,=0一个根。
2. x = (-b ± √(b²-4ac))/(2a)二次方程求解都留下。
3.(a+b)(a-b)=a²-b²平方差公式背下来。
4.a²-b²=(a-b)(a+b)平方差公式很容易。
5.二项式展开好简单,我的名字叫齐考公式。
(a+b)ⁿ = C(n,0)aⁿ + C(n,1)aⁿ⁻¹b + ... + C(n,n-1)abⁿ⁻¹ +C(n,n)bⁿ。
二、顺口溜记几何公式:1.长方形底乘高,得到面积的好帮手。
A=l×w,四边都相对。
2.正方形的面积,直接边长相乘。
A=s²,正方形停不住。
3.三角形面积公式,底边高你有。
A=1/2×b×h,底高更容易。
4.圆的面积公式,先半径,再面积。
A=πr²,记住吗?5.圆的弧长、扇形和正圆角,顺口溜心中藏。
L=2πr,S=1/2πr²,360度它很逆。
三、顺口溜记运算规律:1.交换律、结合律勿忘,运算啥都变得容。
a+b=b+a,a+(b+c)=(a+b)+ca×b=b×a,a×(b×c)=(a×b)×c。
2.分配律快记清,a×(b+c)=a×b+a×c(a+b)×c=a×c+b×c,加减乘除好朋友。
初中几何学习记忆口诀

初中几何学习记忆口诀常见辅助线作法歌诀人说几何很困难,难点就在辅助线。
辅助线,如何添?把握定理和概念。
还要刻苦加钻研,找出规律凭经验图中有角平分线,可向两边作垂线。
角平分线平行线,等腰三角形来添。
线段垂直平分线,常向两端把线连。
要证线段倍与半,延长缩短可试验。
三角形中两中点,连接则成中位线。
三角形中有中线,延长中线加一倍。
梯形里面作高线,平移一腰试试看。
等积式子比例换,寻找相似很关键。
直接证明有困难,等量代换少麻烦。
斜边上面作高线,弦高公式是关键。
半径与弦长计算,弦心距来中间站。
圆上若有一切线,切点圆心半径连。
要想证明是切线,半径垂线仔细辨。
是直径,成半圆,想成直角径连弦。
弧有中点圆心连,垂径定理要记全。
圆周角边两条弦,直径和弦端点连。
要想作个外接圆,各边作出中垂线。
还要作个内切圆,内角平分线梦园。
如果遇到相交圆,不要忘作公共弦。
若是添上连心线,切点肯定在上面。
辅助线,是虚线,画图注意勿改变。
假如图形较分散,对称旋转去实验。
基本作图很关键,平时掌握要熟练。
解题还要多心眼,经常总结方法显。
切勿盲目乱添线,方法灵活应多变。
分析综合方法选,困难再多也会减。
虚心勤学加苦练,成绩上升成直线。
初中数学知识点几何部分总结大全1 过两点有且只有一条直线2 两点之间线段最短3 同角或等角的补角相等4 同角或等角的余角相等5 过一点有且只有一条直线和已知直线垂直6 直线外一点与直线上各点连接的所有线段中,垂线段最短7 平行公理经过直线外一点,有且只有一条直线与这条直线平行8 如果两条直线都和第三条直线平行,这两条直线也互相平行9 同位角相等,两直线平行10 内错角相等,两直线平行11 同旁内角互补,两直线平行12 两直线平行,同位角相等13 两直线平行,内错角相等14 两直线平行,同旁内角互补15 定理三角形两边的和大于第三边16 推论三角形两边的差小于第三边17 三角形内角和定理三角形三个内角的和等于180°18 推论1 直角三角形的两个锐角互余19 推论2 三角形的一个外角等于和它不相邻的两个内角的和20 推论3 三角形的一个外角大于任何一个和它不相邻的内角21 全等三角形的对应边、对应角相等22 边角边公理(SAS) 有两边和它们的夹角对应相等的两个三角形全等23 角边角公理( ASA)有两角和它们的夹边对应相等的两个三角形全等24 推论(AAS) 有两角和其中一角的对边对应相等的两个三角形全等25 边边边公理(SSS) 有三边对应相等的两个三角形全等26 斜边、直角边公理(HL) 有斜边和一条直角边对应相等的两个直角三角形全等27 定理1 在角的平分线上的点到这个角的两边的距离相等28 定理2 到一个角的两边的距离相同的点,在这个角的平分线上29 角的平分线是到角的两边距离相等的所有点的集合30 等腰三角形的性质定理等腰三角形的两个底角相等 (即等边对等角)31 推论1 等腰三角形顶角的平分线平分底边并且垂直于底边32 等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合33 推论3 等边三角形的各角都相等,并且每一个角都等于60°34 等腰三角形的判定定理如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)35 推论1 三个角都相等的三角形是等边三角形36 推论 2 有一个角等于60°的等腰三角形是等边三角形37 在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半38 直角三角形斜边上的中线等于斜边上的一半39 定理线段垂直平分线上的点和这条线段两个端点的距离相等40 逆定理和一条线段两个端点距离相等的点,在这条线段的垂直平分线上41 线段的垂直平分线可看作和线段两端点距离相等的所有点的集合42 定理1 关于某条直线对称的两个图形是全等形43 定理 2 如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线44定理3 两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上45逆定理如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称46勾股定理直角三角形两直角边a、b的平方和、等于斜边c的平方,即a^2 b^2=c^247勾股定理的逆定理如果三角形的三边长a、b、c有关系a^2 b^2=c^2 ,那么这个三角形是直角三角形48定理四边形的内角和等于360°49四边形的外角和等于360°50多边形内角和定理 n边形的内角的和等于(n-2)×180°51推论任意多边的外角和等于360°52平行四边形性质定理1 平行四边形的对角相等53平行四边形性质定理2 平行四边形的对边相等54推论夹在两条平行线间的平行线段相等55平行四边形性质定理3 平行四边形的对角线互相平分56平行四边形判定定理1 两组对角分别相等的四边形是平行四边形57平行四边形判定定理2 两组对边分别相等的四边形是平行四边形58平行四边形判定定理3 对角线互相平分的四边形是平行四边形59平行四边形判定定理4 一组对边平行相等的四边形是平行四边形60矩形性质定理1 矩形的四个角都是直角61矩形性质定理2 矩形的对角线相等62矩形判定定理1 有三个角是直角的四边形是矩形63矩形判定定理2 对角线相等的平行四边形是矩形64菱形性质定理1 菱形的四条边都相等65菱形性质定理2 菱形的对角线互相垂直,并且每一条对角线平分一组对角66菱形面积=对角线乘积的一半,即S=(a×b)÷267菱形判定定理1 四边都相等的四边形是菱形68菱形判定定理2 对角线互相垂直的平行四边形是菱形69正方形性质定理1 正方形的四个角都是直角,四条边都相等70正方形性质定理2正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角71定理1 关于中心对称的两个图形是全等的72定理2 关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分73逆定理如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称74等腰梯形性质定理等腰梯形在同一底上的两个角相等75等腰梯形的两条对角线相等76等腰梯形判定定理在同一底上的两个角相等的梯形是等腰梯形77对角线相等的梯形是等腰梯形78平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等79 推论1 经过梯形一腰的中点与底平行的直线,必平分另一腰80 推论2 经过三角形一边的中点与另一边平行的直线,必平分第三边81 三角形中位线定理三角形的中位线平行于第三边,并且等于它的一半82 梯形中位线定理梯形的中位线平行于两底,并且等于两底和的一半 L=(a b)÷2 S=L×h83 (1)比例的基本性质如果a:b=c:d,那么ad=bc如果ad=bc,那么a:b=c:d84 (2)合比性质如果a/b=c/d,那么(a±b)/b=(c±d)/d85 (3)等比性质如果a/b=c/d=…=m/n(b d … n≠0),那么(a c … m)/(b d … n)=a/b86 平行线分线段成比例定理三条平行线截两条直线,所得的对应线段成比例87 推论平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例88 定理如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边89 平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形三边对应成比例90 定理平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似91 相似三角形判定定理1 两角对应相等,两三角形相似(ASA)92 直角三角形被斜边上的高分成的两个直角三角形和原三角形相似93 判定定理2 两边对应成比例且夹角相等,两三角形相似(SAS)94 判定定理3 三边对应成比例,两三角形相似(SSS)95 定理如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似96 性质定理1 相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比97 性质定理2 相似三角形周长的比等于相似比98 性质定理3 相似三角形面积的比等于相似比的平方99 任意锐角的正弦值等于它的余角的余弦值,任意锐角的余弦值等于它的余角的正弦值100任意锐角的正切值等于它的余角的余切值,任意锐角的余切值等于它的余角的正切值101圆是定点的距离等于定长的点的集合102圆的内部可以看作是圆心的距离小于半径的点的集合103圆的外部可以看作是圆心的距离大于半径的点的集合104同圆或等圆的半径相等105到定点的距离等于定长的点的轨迹,是以定点为圆心,定长为半106和已知线段两个端点的距离相等的点的轨迹,是着条线段的垂直平分线107到已知角的两边距离相等的点的轨迹,是这个角的平分线108到两条平行线距离相等的点的轨迹,是和这两条平行线平行且距离相等的一条直线109定理不在同一直线上的三点确定一个圆。
初中几何证明口诀

初中几何证明口诀在初中几何中,证明是学习的重要内容之一、通过证明,可以巩固和提高自己对几何知识的理解和应用能力。
以下是一些常用的初中几何证明口诀:1.三角形的内角和定理:三角形内角和为180度。
可以通过绘制平行线、共线线段等方法证明。
2.外角定理:三角形的外角等于其余两个内角的和。
可以通过绘制平行线等方法证明。
3.垂直角定理:垂直角相等。
可以通过绘制平行线、共线线段等方法证明。
4.同位角定理:同位角相等。
可以通过平行线等方法证明。
5.三角形的相似性定理:相似三角形的对应角相等,对应边成比例。
可以通过AA、SSS、SAS等方法证明。
6.圆周角定理:圆周角是圆心角的两倍。
可以通过绘制弧、使用同位角等方法证明。
7.弦切角定理:弦切角等于其对应的弧的一半。
可以通过绘制切线、弧等方法证明。
8.正方形的特性:正方形的四条边相等,四个角为直角。
可以通过对角线等方法证明。
9.等腰三角形的特性:等腰三角形的两边相等,两个底角相等。
可以通过绘制高线等方法证明。
10.平行四边形的特性:平行四边形的对边相互平行,对角线相互平分。
可以通过角平分线等方法证明。
11.三角形的中线定理:三角形的三个中线交于一点,且这点距离三个顶点的距离是各边长的一半。
可以通过线段等方法证明。
12.直角三角形的勾股定理:直角三角形的两个直角边的平方和等于斜边的平方。
可以通过平行四边形等方法证明。
13.外切圆定理:三角形的外接圆的圆心是三个顶点的垂直平分线的交点。
可以通过角平分线、圆心角等方法证明。
14.圆的切线定理:切线与半径垂直。
可以通过绘制切线、使用垂直角等方法证明。
15.纵横切割定理:两条平行线被一条截线切割,那么两个内角和为180度。
可以通过平行线等方法证明。
这些口诀可以帮助初中生记住一些重要的初中几何证明定理,并引导他们学习如何使用特定的几何性质进行证明。
同时,更重要的是理解定理的证明过程,培养逻辑思维能力和几何推理能力。
人教部编版初中数学几何知识常见辅助线顺口溜

人教部编版初中数学几何知识常见辅助线顺口溜三角形图中有角平分线,可向两边作垂线。
也可将图对折看,对称以后关系现。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看。
线段垂直平分线,常向两端把线连。
要证线段倍与半,延长缩短可试验。
三角形中两中点,连接则成中位线。
三角形中有中线,延长中线等中线。
四边形平行四边形出现,对称中心等分点。
梯形里面作高线,平移一腰试试看。
平行移动对角线,补成三角形常见。
证相似,比线段,添线平行成习惯。
等积式子比例换,寻找线段很关键。
直接证明有困难,等量代换少麻烦。
斜边上面作高线,比例中项一大片。
圆半径与弦长计算,弦心距来中间站。
圆上若有一切线,切点圆心半径连。
切线长度的计算,勾股定理最方便。
要想证明是切线,半径垂线仔细辨。
是直径,成半圆,想成直角径连弦。
弧有中点圆心连,垂径定理要记全。
圆周角边两条弦,直径和弦端点连。
弦切角边切线弦,同弧对角等找完。
要想作个外接圆,各边作出中垂线。
还要作个内接圆,内角平分线梦圆。
如果遇到相交圆,不要忘作公共弦。
内外相切的两圆,经过切点公切线。
若是添上连心线,切点肯定在上面。
要作等角添个圆,证明题目少困难。
辅助线,是虚线,画图注意勿改变。
假如图形较分散,对称旋转去实验。
基本作图很关键,平时掌握要熟练。
解题还要多心眼,经常总结方法显。
切勿盲目乱添线,方法灵活应多变。
分析综合方法选,困难再多也会减。
虚心勤学加苦练,成绩上升成直线。
七年级几何图形知识点口诀

七年级几何图形知识点口诀几何图形的认识是初中数学的重点,学习几何图形的知识点需要记住许多的定义、性质、公式等内容。
如何快速地记住几何图形的知识点,让学习变得更加轻松、高效呢?下面为大家介绍几个七年级几何图形知识点口诀。
1、三线两交一垂心,直角等腰又等边三线两交一垂心,指的是三角形内心、外心、垂心、重心所在的线段。
直角三角形中,两条直角边相等的三角形称为等腰直角三角形,两条直角边和斜边相等的三角形称为等边直角三角形。
2、相似三角形,全等三角形,都有一定的标准形相似三角形指的是形状相似但大小不同的三角形,全等三角形指的是形状和大小都相同的三角形。
每个三角形都有一定的标准形,例如直角三角形的标准形是3:4:5。
3、三角形内角和=180°,任意角度数都由它组成三角形内角和是指三角形内部各角度之和,等于180°,而任意角度数都可以用三角形内角和来表示。
4、平行四边形的对角线,相交于一点不三断平行四边形的对角线是指连接相邻角的线段。
两条对角线相交于一点,并且这个点不在对角线上。
5、圆心角是单位一度,对于弧度圆周角须提圆心角是以圆心为顶点的角,其度数等于扇形所对应的圆心角。
对于弧度的圆周角,需要进行相应的计算和转换。
6、圆的周长是2πr,面积是πr²,勾股圆周角在斜边圆的周长是指圆周上的长度,等于2πr,其中r为圆的半径。
圆的面积等于πr²。
勾股圆周角指的是以圆的直径为斜边的直角三角形所对应的圆心角。
以上就是七年级几何图形知识点口诀,可以通过记忆这些简单的口诀,快速掌握几何图形的知识点,轻松应对考试和做题。
当然,还需要多做习题和实践,加深对几何图形知识点的理解和应用。
(完整版)初中数学中常见公式口诀

(完整版)初中数学中常见公式口诀直角三角形- 勾股定理:直角三角形的两直角边的平方和等于斜边的平方。
- 正弦定理:a/sinA = b/sinB = c/sinC,其中a、b、c分别为三角形的边长,A、B、C分别为对应的内角。
- 余弦定理:c² = a² + b² - 2ab·cosC,其中a、b、c分别为三角形的边长,C为对应的内角。
圆- 圆的周长:C = 2πr,其中r为圆的半径。
- 圆的面积:A = πr²,其中r为圆的半径。
- 弧长公式:L = 2πr·(m/360°),其中L为弧长,r为圆的半径,m为对应的圆心角的度数。
反比例函数- 反比例函数的特点:y = k/x,其中k为常数。
- 两个变量间的比例关系:x1·y1 = x2·y2,其中x1、y1为第一组的值,x2、y2为第二组的值。
直线与平面- 平行线特征:对于两条直线l1和l2,如果有一条直线l3与l1和l2都平行,则l1和l2也平行。
- 垂直线特征:对于两条直线l1和l2,如果l1和l2的斜率乘积为-1,则l1和l2互相垂直。
- 平面的角的性质:平面上两直线平分同一角的直线互相平行。
平移、旋转、翻折- 平移变换:平移不改变图形的大小和形状,只改变图形的位置。
- 旋转变换:以某一点为中心,将图形按一定角度旋转,得到新的图形。
- 翻折变换:将图形关于直线对称,得到新的图形。
统计与概率- 均值:将一组数据相加,再除以数据的个数。
- 中位数:将一组数据按从小到大的顺序排列,位于中间位置的数。
- 众数:一组数据中出现次数最多的数。
- 百分比:百分之一表示1%,百分之十表示10%,以此类推。
以上是初中数学中常见的公式口诀,希望对你有所帮助!。
九年级知识点口诀

九年级知识点口诀代数与函数口诀:一元一次拆方程,消元结合求解法。
二元一次画平面,消元结合求解法。
二次方程分情况,求根公式有韦达。
二次函数开口看a,y轴交点看c。
直线与平面多方程,代入联立求交点。
函数图像开闭看头,单调性看斜率。
幂函数指数看正负,对称轴看指数。
几何与立体几何口诀:直角三角边边边,全等判定无尽言。
等腰三角底底底,等边三角三三三。
平行线副角相等,同位角竖角对顶。
相交线内角互补,同弧角同弦等。
圆心角是二倍弧,弦周角是六十大。
正多边形内角求解,(n-2)×180是关键。
体积单位立方为主,棱和面积都不丢。
概率与统计口诀:概率计算多方式,事件数拆分用概率。
排列组合求样本,全排除减概率。
求期望加加加平均,方差差差标准差。
直方图绘频数,折线图描数据。
箱形图展数据离散,饼图分析各部分。
数论与正整数口诀:最大公约数约约约,相乘除后大胆用。
最小公倍数积积积,相除除后安心求。
素数之间无约束,质因数打开又关口。
质因数分解是基础,约数个数数真多。
分数与小数转换先,无理数有时要算头。
代数运算口诀:加减乘除绝不迷,交换律结合律。
乘方连乘求大方,幂方乘方有技巧。
分数加减先通分,乘除也要约简。
多项式最高项最后,一元多项式都适用。
几何变换口诀:平移移移移,变量全加加加。
旋转逆时针是正,弧度用角度换。
缩放比例不迷茫,求点的坐标是关键。
镜像对称好学习,关于直线或点翻转。
这些知识点口诀,帮助九年级学习结实固。
记住它们,考试不发愁,学习进步更快速。
几何证明题解题口诀

几何证明题解题口诀
(作者:河南省唐河县刘军义)
几何做题很容易,证明过程写详细。
数学原理巧运用,前后贯通有条理!
题目信息不放过,必与结果有联系。
学科符号用恰当,统一规范又适宜:
因为所以单点对,大小符号尖相抵;
图形符号缩字同,角线名称字母替。
证理恰切书规范,美观整洁又得体!
解释:
1、题目信息:指题目中给的证明条件。
2、结果:指要证明的内容。
3、因为所以单点对:指“∵”和“∴”竖写时情况。
4、尖相抵:指“>”和“<”横写时的情况。
5、图形符号缩字同:指“□”“◇”“△”等代替图形名称时占
一个汉字的位置。
——作于2014年8月17日。
初中几何口诀大全

初中几何口诀大全初中几何口诀大全:1. 角的种类口诀:锐角钝角直角,加起来是180。
解析:锐角小于90度,钝角大于90度,直角等于90度。
锐角加钝角等于180度。
2. 三角形边长关系口诀:对边比底,中线比高,角平分线,比中线。
解析:三角形中,对边比底边长,中线比底边长的一半,角平分线分割对边比中线长。
3. 直角三角形三边关系口诀:勾股两边立,直角对边开。
解析:直角三角形中,勾股定理:直角边的平方等于两直角边平方和,即a²+ b² = c²。
4. 正多边形内角和口诀:正多边角内角和,等于(n-2)×180度。
解析:正多边形的内角和等于:(n-2)×180度,其中n为边的个数。
5. 圆的性质口诀:半径、直径、弦,关系记三半。
解析:圆的半径是直径的一半,弦是半径的两倍,直径是弦的两倍。
6. 三角形角平分线性质口诀:角平分线,平分角,边分比,比分角。
解析:三角形的角平分线将角平分为相等的两部分,边分比为两边的比例相等,比分角为角平分线角的比例相等。
7. 平行线性质口诀:平行线,对角等,内角和,180度。
解析:平行线对角相等,内角和等于180度,平行线的性质是几何学中的基础知识。
8. 三角形角度和口诀:三角角度和,等于180度。
解析:三角形的内角和等于180度,这是三角形的基本性质,任何三角形的内角和都等于180度。
以上就是初中几何口诀的大全,希望这些口诀能帮助你更好地记忆和理解几何知识,提高学习效率,顺利掌握初中几何的知识。
如果有任何疑问,欢迎继续咨询,我会尽力解答。
初中数学几何证明的口诀

初中数学几何证明的口诀初中数学几何证明的口诀在学习、工作乃至生活中,大家总免不了要接触或使用证明吧,证明是用以证明自己身份、经历或某事真实性的一种凭证。
想拟证明却不知道该请教谁?以下是小编收集整理的初中数学几何证明的口诀,希望对大家有所帮助。
初中数学几何证明的口诀三角形中两中点,连接则成中位线。
三角形中有中线,延长中线等中线。
平行四边形出现,对称中心等分点。
梯形里面作高线,平移一腰试试看。
平行移动对角线,补成三角形常见。
证相似,比线段,添线平行成习惯。
斜边上面作高线,比例中项一大片。
半径与弦长计算,弦心距来中间站。
弧有中点圆心连,垂径定理要记全。
圆周角边两条弦,直径和弦端点连。
弦切角边切线弦,同弧对角等找完。
如果遇到相交圆,不要忘作公共弦。
内外相切的两圆,经过切点公切线。
若是添上连心线,切点肯定在上面。
圆上若有一切线,切点圆心半径连。
切线长度的计算,勾股定理最方便。
要想证明是切线,半径垂线仔细辨。
是直径,成半圆,想成直角径连弦。
图中有角平分线,可向两边作垂线。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看。
线段垂直平分线,常向两端把线连。
等积式子比例换,寻找线段很关键。
直接证明有困难,等量代换少麻烦。
拓展延续:初中数学几何证明题做题技巧证明两线段相等1.两全等三角形中对应边相等。
2.同一三角形中等角对等边。
3.等腰三角形顶角的平分线或底边的高平分底边。
4.平行四边形的对边或对角线被交点分成的两段相等。
5.直角三角形斜边的中点到三顶点距离相等。
6.线段垂直平分线上任意一点到线段两段距离相等。
7.角平分线上任一点到角的两边距离相等。
8.过三角形一边的中点且平行于第三边的直线分第二边所成的线段相等。
9.同圆(或等圆)中等弧所对的弦或与圆心等距的两弦或等圆心角、圆周角所对的弦相等。
10.圆外一点引圆的两条切线的切线长相等或圆内垂直于直径的弦被直径分成的两段相等。
11.两前项(或两后项)相等的比例式中的两后项(或两前项)相等。
初中数学几何证明的口诀

初中数学几何证明的口诀数学几何证明是中学数学学习中的重要一环,通过证明可以深入理解几何定理和推理方法,并培养学生的逻辑思维和创造力。
然而,对于初学者来说,证明过程可能会显得复杂而困难。
为了帮助初中生更好地理解和掌握几何证明,下面将提供几个口诀,帮助他们记忆和应用。
一、相似三角形的证明在几何证明中,相似三角形是经常出现的题型。
相似三角形有一些重要的证明方法:1. 边比例法:两个三角形的对应边比例相等,则两个三角形相似。
2. 角对应法:两个三角形的对应角相等,则两个三角形相似。
3. 边角对应法:两个三角形有一个对应边比例相等,另外两个对应角相等,则两个三角形相似。
二、垂直性的证明证明两条线段或两条直线垂直的方法有:1. 互余角法:两条直线相交,且相交角互为余角,则两条直线垂直。
2. 垂直角法:两条直线相交,且形成的四个角中,两个相邻角为垂直角,则两条直线垂直。
三、平行性的证明证明两条线段或两条直线平行的方法有:1. 对顶角法:两条直线被一条直线截断,截断直线上的对顶角相等,则两条直线平行。
2. 平行线夹角法:两条直线被一条直线截断,截断直线上的内错角相等,则两条直线平行。
四、三角形形状与大小的证明证明三角形形状和大小的方法有:1. 等腰三角形证明:两条边相等的三角形,其对应的两个角也相等。
2. 直角三角形证明:一个角为直角的三角形,其余两个角为锐角或钝角。
3. 等边三角形证明:三条边相等的三角形,其对应的三个角也相等。
以上是初中数学几何证明中常见的口诀,通过记忆这些口诀,学生可以更好地理解和应用几何证明的方法。
当然,这些口诀只是一个指导,要想在实际学习中获得更好的成果,还需要多做几何证明的练习,不断提升自己的证明能力与思维能力。
祝愿大家在数学学习中取得好成绩!。
八年级数学证明题口诀

八年级数学证明题口诀在学习数学证明题中,学生们常常会遇到一定困难。
但是,如果熟记一些口诀,就能更轻松地进行证明。
以下是八年级学习数学证明题时要使用的口诀:“九章三层,证明不用猜,先识性质,推论结果得。
反证法论,反证口诀记,先找出假设,然后矛盾见。
比较法的威,两者定界必,让它们以某数类比,隐藏的答案即可见。
数学归纳法,找出规律很快,只要定义基本关系,自然的结果就可相知。
假设法非常强,把握难度来变短,先断定一结果,再推演步骤就行。
大师析证说,归纳恰好可,不论规律怎么变,结论不变它就拥有了。
图解结果来,形体给证明动力,可能比较复杂,它会让你看得见。
几何公式标,几何证明的必备,画图看对称,结论就很清楚”以上就是八年级学习数学证明题时应该记住的口诀,学生们可以根据这些口诀来记忆、理解和推导结论,更加深入理解数学证明中的思想,完成数学证明题。
首先,九章三层,证明不用猜,先识性质,推论结果得,指的是我们在进行数学证明时,应该先定义好问题的基本特征,根据这些基本特征来推导出结论,而不是猜想,这是一个正确的方法。
其次,反证法论,反证口诀记,先找出假设,然后矛盾见,这一段口诀提到了反证法,反证法也是数学证明题中常用的方法之一。
在进行反证时,我们需要明确假设,然后让假设产生矛盾,这样,就可以完成反证。
此外,比较法的威,两者定界必,让它们以某数类比,隐藏的答案即可见,比较法也是一种常用的数学证明方法。
它涉及到比较两个值,使用某种数学方程比较它们的大小,最终得出答案。
此外,数学归纳法,找出规律很快,只要定义基本关系,自然的结果就可相知,数学归纳法是一种从具体到抽象,从局部到整体的思维方式,它能让我们很快地发现规律,从而得出结论。
另外,假设法非常强,把握难度来变短,先断定一结果,再推演步骤就行,假设法也是一种常用的数学证明方法,它是通过引入假设,从而缩短推理步骤,得出正确结论。
接下来,大师析证说,归纳恰好可,不论规律怎么变,结论不变它就拥有了,大师析证法也是数学证明中常用的方法之一,它是定义一个归纳法,使得证明具有可推广性,无论规律怎么变,结论是不变的,因此,就可以拥有正确性。
初中几何口诀大全

初中几何口诀大全1.同位角平分线两两相交,外分则角相等,内分等分线。
2.外角等于两个非邻角和。
3.外角等于它的不相邻内角。
4.顶角平分线相交后,分出两等角。
5.三角形两边之和大于第三边,两边之差小于第三边。
6.三角形内角和为180度。
7.等边三角形的三个内角都是60度。
8.等腰三角形的底角相等。
9.三角形外角等于与它不相邻的两个内角。
10.直角三角形的斜边平方等于两直角边平方和。
11.两角互补,和为90度;两角互余,和为180度。
12.同位角互等则线平行,否则线相交。
13.平行线上的锐角互等,钝角互等,锐角对钝角补角。
14.平行线夹角相等,即使被截线分割。
15.相交线上的对顶角和为180度。
16.同位角、同旁内角互等,则直角外角相等。
17.平行线之间的距离是各个点与任一根线之距离相等。
18.平行线截被截线的对应线段成比例。
19.各边对顶角相等则四边形是平行四边形。
20.平行四边形的相邻角、对顶角互等。
21.任意一对对角线互相平分。
22.标定角互补,则四边形是菱形。
23.菱形的对角线互相垂直。
24.正方形的对角线互相重合,互相平分。
25.三角形的中位线互相平分,并且平分线的长度为相邻两边的一半。
26.四边形的对角线互相平分。
27.线段互相平分。
28.圆的半径互相平分。
29.圆心角的度数等于它所对的弧的度数。
30.弧等于半径乘弧所对的圆心角的度数。
31.同弧或同周角所对弧相等。
32.角的平分线与圆相交于其弦上,并且弧相等。
33.弧上及弦上的两点所对的弧相等,则这两弦相等。
34.线与圆相切,则切线垂直于半径。
35.在等腰三角形中,高、中线、以及角平分线互相重合。
36.等腰三角形的底角互等。
37.等腰直角三角形的斜边等于直角边乘根号2。
38.等边三角形的高等于边长的根号3除以2。
39.等腰梯形的两底边平行,且等长。
40.等腰梯形的高等于两底边的差的一半。
以上是一些初中几何口诀的大全参考内容,希望对你有帮助!。
初中几何口诀大全

初中几何口诀大全初中几何口诀如下:1.过两点有且只有一条直线。
2.两点之间线段最短。
3.同角或等角的补角相等。
4.同角或等角的余角相等。
5.过一点有且只有一条直线和已知直线垂直。
6.直线外一点与直线上各点连接的所有线段中,垂线段最短。
7.平行公理经过直线外一点,有且只有一条直线与这条直线平行。
8.如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
9.完全平方公式:首平方、尾平方、首尾两倍放中央、首尾括号带平方、尾项符号随中央。
10.因式分解:单项式除以单项式所得结果是多项式,多项式除以单项式所得结果是单项式。
11.单项式运算:加法、减法、乘法、除法混合运算时,先算乘除,后算加减。
12.一元一次不等式解题的一般步骤是:去分母、去括号、移项、时候要变号、同类项合并好,再把系数来除掉。
13.一元一次不等式组的解集:大大取较大,小小取较小;小大、大小取中间,大小、小大无处找。
14.数学归纳法:归纳递推时,首项正确是关键,假设必须两步全,归纳结论要全面。
15.完全平方公式:首平方、尾平方、首尾两倍放中央、首尾括号带平方、尾项符号随中央。
16.单项式运算:加法、减法、乘法、除法混合运算时,先算乘除,后算加减。
17.因式分解:多项式除以单项式所得结果是多项式,单项式除以单项式所得结果是单项式。
18.平面几何的基本概念:点、线、面、体;两点确定一条直线,两条平行线之间可以确定一个平面;两点之间线段最短;线段的中点到两端点的距离相等;垂线段最短;过一点可以画无数条直线和无数条垂线;线段的中点和线段的两个端点在同一直线上;三点确定一个平面;过一点可以画无数条直线和无数条垂线;过两点有且只有一条直线和一条垂线;过两点有且只有一条直线;过直线外一点有且只有一条直线和已知直线垂直;四个角中有一个直角时,其余三个角都是锐角。
19.立体几何的基本概念:点、线、面、体;一个物体占据一个位置,两个物体占据相对的位置;物体的各部分都是直的,并且各部分之间没有空隙;当一个物体占据一个位置时,其余物体不能同时占据这个位置;在一个平面内过一点可以画一条直线,过两点可以画两条直线;在空间中,过一点可以画一个平面,过两点可以画一个平面;两个平面平行时,它们没有公共点。
初中几何解题技巧口诀

初中几何解题技巧口诀
1、解决几何形运动问题,求空间位置要定位;
2、解决几何形空间问题,先求几何体的表面;
3、面积求解分三角形,体积积分球体中;
4、求几何体的表面积,可用三角形求和;
5、求几何体的体积,积分球体中心可计;
6、求向量的积分,将其分成三角形;
7、求多边形的面积,可以用叉积的方式;
8、求投影的几何性质,可以用叉积的方式;
9、求变换矩阵公式,向量积求导可以;
10、求三角形内接圆,便是内切圆即可求;
11、椭圆曲线跟踪求,可以用相似三角形;
12、构图交汇线求解,求投影即为求解;
13、求圆锥的奥林匹斯,可以用螺旋线的概念。
几何口诀
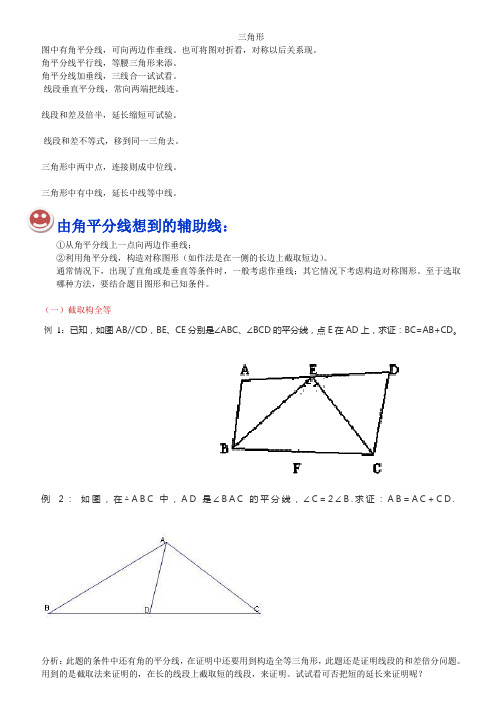
三角形图中有角平分线,可向两边作垂线。
也可将图对折看,对称以后关系现。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看。
线段垂直平分线,常向两端把线连。
线段和差及倍半,延长缩短可试验。
线段和差不等式,移到同一三角去。
三角形中两中点,连接则成中位线。
三角形中有中线,延长中线等中线。
由角平分线想到的辅助线:①从角平分线上一点向两边作垂线;②利用角平分线,构造对称图形(如作法是在一侧的长边上截取短边)。
通常情况下,出现了直角或是垂直等条件时,一般考虑作垂线;其它情况下考虑构造对称图形。
至于选取哪种方法,要结合题目图形和已知条件。
(一)截取构全等例1:已知,如图AB//CD,BE、CE分别是∠ABC、∠BCD的平分线,点E在AD上,求证:BC=AB+CD。
例2:如图,在△A B C中,A D是∠B A C的平分线,∠C=2∠B.求证:A B=A C+C D.例3.已知:如图1-3,AB=2AC,∠BAD=∠CAD,DA=DB,求证DC⊥AC例4已知:如图1-4,在△ABC中,∠C=2∠B,AD平分∠BAC,求证:AB-AC=CD(二)、角分线上点向角两边作垂线构全等过角平分线上一点向角两边作垂线,利用角平分线上的点到两边距离相等的性质来证明问题。
例3:如图2-1,已知AB>AD, ∠BAC=∠FAC,CD=BC。
求证:∠ADC+∠B=180例4:已知如图2-3,△ABC的角平分线BM、CN相交于点P。
求证:∠BAC的平分线也经过点P。
例5:如图∠AOP=∠BOP=15 ,PC//OA,PD⊥OA,如果PC=4,则PD=()例6:已知:如图2-6,在正方形ABCD中,E为CD 的中点,F为BC 上的点,∠FAE=∠DAE。
求证:AF=AD+CF。
例7:已知:如图2-7,在Rt△ABC中,∠ACB=90 ,CD⊥AB,垂足为D,AE平分∠CAB交CD于F,过F 作FH//AB交BC于H。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013.03.26 初中几何添加常见辅助线的口诀初中各学科口诀总汇 2013.12.03 初中各学科口诀总汇《初中数学口诀》 2013.03.31
圆上若有一切线,切点圆心半径连。
切线长度的计算,勾股定理最方便。
要想证明是切线,半径垂线仔细辨。
是直径,成半圆,想成直角径连弦。
九类差异导致初中三年后的天壤之别【收藏】中医药在线查询(点击药名) 2013.11.06 中医药在线查询(点击药名)高中各学科口诀总汇 2013.12.03
高中各学科口诀总汇
曾国藩《戒子书》 天道酬勤 地道酬善 商道酬信 业道酬精 人道酬诚
【转载】当你读完,你会放下好多事!【心灵悟语】2012-11-17 12:08:41 【转载】献给正在为未来打拼的人!【感悟哲理】2012-11-17
弦切角边切线弦,同弧对角等找完。
如果遇到相交圆,不要忘作公共弦。
内外相切的两圆,经过切点公切线。
若是添上连心线,切点肯定在上面。
平行四边形出现,对称中心等分点。
梯形里面作高线,平移一腰试试看。
平行移动对角线,补成三角形常见。
证相似,比线段,添线平行成习惯。
12:06:54 【转载】中国特色笑话18则2012-11-17 11:17:48 【转载】五类食品“害怕冰箱”!2012-11-17 11:01:36
【转载】家庭伦常道2012-11-17 10:43:37
2013.09.26 高中、初中物理化学实验大全【视频】初中数学常用的九种解题方法 2013.10.06
初中数学常用的九种解题方法【转载】小学初中高中分册整套教案学案(共376套全部永久免费下载) 2012.11.03
【转载】小学初中高中分册整套教案学案(共376套全部永久免费下载)九类差异导致初中三年后的天壤之别【收藏】 2013.03.04
图中有角平分线,可向两边作垂线。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看。
线段垂直平分线,常向两端把线连。
等积式子比例换,寻找线段很关键。
直接证明有困难,等量代换少麻烦。
初中几何证明口诀
三角形中两中点,连接则成中位线。
三角形中有中线,延长中线等中线。
《初中数学口诀》小学、初中、高中文言文在线阅读 2013.01.21 小学、初中、高中文言文在线阅读初中“物理+化学”学习记忆口诀N条 2013.03.28
初中“物理+化学”学习记忆口诀N条【转载】初中几何证明诀 2012.11.16 【转载】初中几何证明口诀高中、初中物理化学实验大全【视频】
斜边上面作高线,比例中项一大片。
半径与弦长计算,弦心距来中间站。
弧有中点圆心连,垂径定理要记全。
圆周角边两条弦,直径和弦端点连。
