平面几何四个重要定理
初中中平面几何重要定理汇总
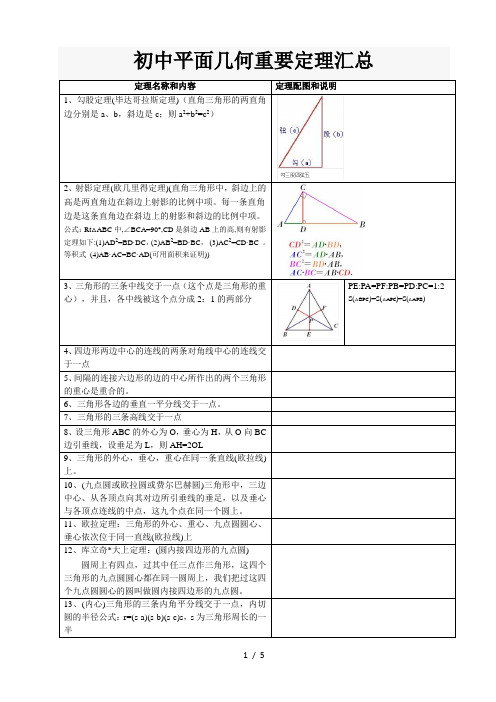
8、设三角形ABC的外心为O,垂心为H,从O向BC边引垂线,设垂足为L,则AH=2OL
9、三角形的外心,垂心,重心在同一条直线(欧拉线)上。
10、(九点圆或欧拉圆或费尔巴赫圆)三角形中,三边中心、从各顶点向其对边所引垂线的垂足,以及垂心与各顶点连线的中点,这九个点在同一个圆上。
29、塞瓦定理的逆定理:在△ABC的边BC,CA,AB上分别取点D,E,F,如果(AF:FB)(BD:DC)(CE:EA)=1那么直线AD,BE,CF相交于同一点。
30、塞瓦定理的逆定理的应用定理1:三角形的三条中线交于一点
31、塞瓦定理的逆定理的应用定理2:设△ABC的内切圆和边BC、CA、AB分别相切于点R、S、T,则AR、BS、CT交于一点。
14、(旁心)三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点
15、中线定理:(巴布斯定理)设三角形ABC的边BC的中点为P,则有AB2+AC2=2(AP2+BP2)
16、斯图尔特定理:P将三角形ABC的边BC内分成m:n,则有n×AB2+m×AC2=(m+n)AP2+mnm+nBC2
17、波罗摩及多定理:圆内接四边形ABCD的对角线互相垂直时,连接AB中点M和对角线交点E的直线垂直于CD
24、梅涅劳斯定理的逆定理:(略)
25、梅涅劳斯定理的应用定理1:设△ABC的∠A的外角平分线交边CA于Q、∠C的平分线交边AB于R,、∠B的平分线交边CA于Q,则P、Q、R三点共线。
26、梅涅劳斯定理的应用定理2:过任意△ABC的三个顶点A、B、C作它的外接ቤተ መጻሕፍቲ ባይዱ的切线,分别和BC、CA、AB的延长线交于点P、Q、R,则P、Q、R三点共线
平面几何的著名定理
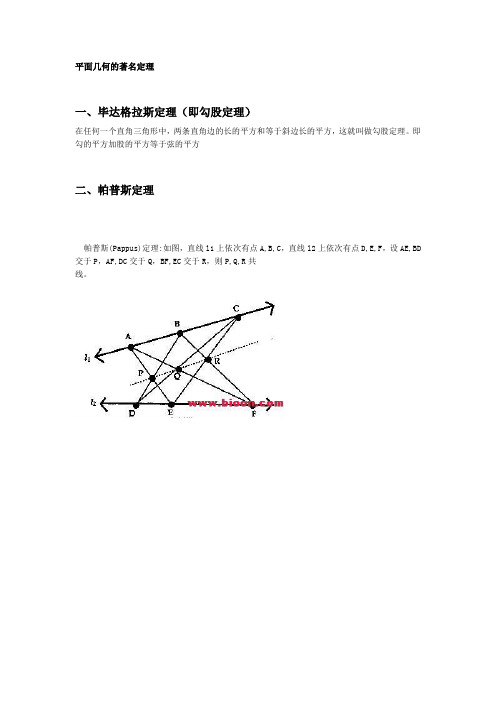
平面几何的著名定理一、毕达格拉斯定理(即勾股定理)在任何一个直角三角形中,两条直角边的长的平方和等于斜边长的平方,这就叫做勾股定理。
即勾的平方加股的平方等于弦的平方二、帕普斯定理帕普斯(Pappus)定理:如图,直线l1上依次有点A,B,C,直线l2上依次有点D,E,F,设AE,BD 交于P,AF,DC交于Q,BF,EC交于R,则P,Q,R共线。
三、影射定理(与相似三角形和比例有关)直角三角形射影定理(又叫欧几里德(Euclid)定理):直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项。
每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。
公式Rt△ABC中,∠BAC=90°,AD是斜边BC上的高,则有射影定理如下:(1)(AD)^2;=BD·DC,(2)(AB)^2;=BD·BC ,(3)(AC)^2;=CD·BC 。
等积式 (4)ABXAC=BCXAD(可用面积来证明)四、梅涅劳斯定理梅涅劳斯(Menelaus)定理(简称梅氏定理)是由古希腊数学家梅涅劳斯首先证明的。
它指出:如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点,那么(AF/FB)×(BD/DC)×(CE/EA)=1。
或:设X、Y、Z分别在△ABC的BC、CA、AB所在直线上,则X、Y、Z共线的充要条件是(AZ/ZB)*(BX/XC)*(CY/YA)=1 。
证明一过点A作AG∥BC交DF的延长线于G,则AF/FB=AG/BD , CE/EA=DC/AG。
三式相乘得:(AF/FB)×(BD/DC)×(CE/EA)=(AG/BD)×(BD/DC)×(DC/AG)=1证明二过点C作CP∥DF交AB于P,则BD/DC=FB/PF,CE/EA=PF/AF所以有AF/FB×BD/DC×CE/EA=AF/FB×FB/PF×PF/AF=1它的逆定理也成立:若有三点F、D、E分别在△ABC的边AB、BC、CA或其延长线上,且满足(AF/FB)×(BD/DC)×(CE/EA)=1,则F、D、E三点共线。
平面几何重要定理考点归纳

平面几何重要定理考点归纳1、勾股定理毕达哥拉斯定理2、射影定理欧几里得定理3、三角形的三条中线交于一点,并且,各中线被这个点分成2:1的两部分4、四边形两边中心的连线的两条对角线中心的连线交于一点5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。
6、三角形各边的垂直一平分线交于一点。
7、三角形的三条高线交于一点8、设三角形ABC的外心为O,垂心为H,从O向BC边引垂线,设垂足为L,则AH=2OL9、三角形的外心,垂心,重心在同一条直线欧拉线上。
10、九点圆或欧拉圆或费尔巴赫圆三角形中,三边中心、从各顶点向其对边所引垂线的垂足,以及垂心与各顶点连线的中点,这九个点在同一个圆上,11、欧拉定理:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线欧拉线上12、库立奇大上定理:圆内接四边形的九点圆圆周上有四点,过其中任三点作三角形,这四个三角形的九点圆圆心都在同一圆周上,我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。
13、内心三角形的三条内角平分线交于一点,内切圆的半径公式:r=s-as-bs-cs,s为三角形周长的一半14、旁心三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点15、中线定理:巴布斯定理设三角形ABC的边BC的中点为P,则有AB2+AC2=2AP2+BP216、斯图尔特定理:P将三角形ABC的边BC内分成m:n,则有n×AB2+m×AC2=m+nAP2+mnm+nBC217、波罗摩及多定理:圆内接四边形ABCD的对角线互相垂直时,连接AB中点M和对角线交点E的直线垂直于CD18、阿波罗尼斯定理:到两定点A、B的距离之比为定比m:n值不为1的点P,位于将线段AB分成m:n的内分点C和外分点D为直径两端点的定圆周上19、托勒密定理:设四边形ABCD内接于圆,则有AB×CD+AD×BC=AC×BD20、以任意三角形ABC的边BC、CA、AB为底边,分别向外作底角都是30度的等腰△BDC、△CEA、△AFB,则△DEF是正三角形21、爱尔可斯定理1:若△ABC和△DEF都是正三角形,则由线段AD、BE、CF的中心构成的三角形也是正三角形。
四个重要定理(梅涅劳斯_塞瓦_托勒密_西姆松)
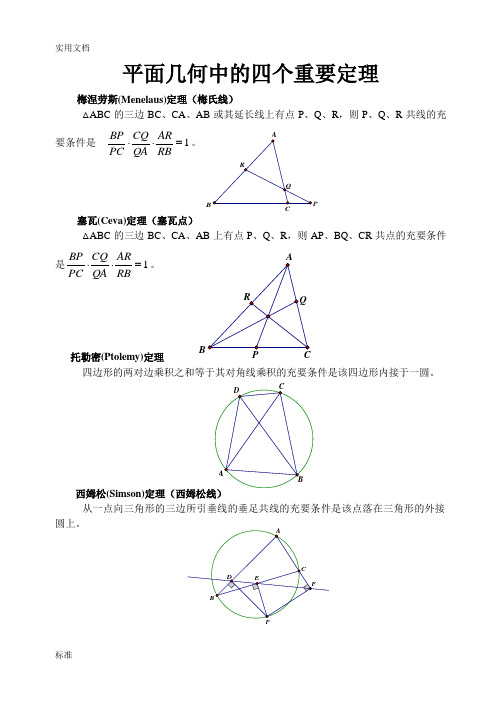
B平面几何中的四个重要定理梅涅劳斯(Menelaus)定理(梅氏线)△ABC 的三边BC 、CA 、AB 或其延长线上有点P 、Q 、R ,则P 、Q 、R 共线的充要条件是1=⋅⋅RBARQA CQ PC BP 。
塞瓦(Ceva)定理(塞瓦点)△ABC 的三边BC 、CA 、AB 上有点P 、Q 、R ,则AP 、BQ 、CR 共点的充要条件是1=⋅⋅RBARQA CQ PC BP 。
托勒密(Ptolemy)定理四边形的两对边乘积之和等于其对角线乘积的充要条件是该四边形内接于一圆。
西姆松(Simson)从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上。
例题:1、设AD 是△ABC 的边BC 上的中线,直线CF 交AD 于F 。
求证:FBAF 2ED AE =。
【分析】CEF 截△ABD→1FABFCB DC ED AE =⋅⋅(梅氏定理) 【评注】也可以添加辅助线证明:过A 、B 、D 之一作CF 的平行线。
2、过△ABC 的重心G 的直线分别交AB 、AC 于E 、F ,交CB 于D 。
求证:1FACFEA BE =+。
【分析】连结并延长AG 交BC 于M ,则M 为BC 的中点。
DEG 截△ABM→1DB MDGM AG EA BE =⋅⋅(梅氏定理)DGF 截△ACM→1DCMDGM AG FA CF =⋅⋅(梅氏定理)∴FA CF EA BE +=MDAG )DC DB (GM ⋅+⋅=MD GM 2MD 2GM ⋅⋅=1【评注】梅氏定理3、D 、E 、F 分别在△ABC 的BC 、CA 、AB 边上,λ===EACEFB AF DC BD ,AD 、BE 、CF 交成△LMN 。
求S △【分析】【评注】梅氏定理4、以△ABC 各边为底边向外作相似的等腰△BCE 、△CAF 、△ABG 。
求证:AE 、BF 、CG 相交于一点。
【分析】【评注】塞瓦定理5、已知△ABC 中,∠B=2∠C 。
初中数学平面几何基本定理

1. 中线定理(巴布斯定理)设△ABC 的边BC 的中点为P ,则有)(22222BP AP AC AB +=+; 中线长:222222a c b m a -+=2. 角平分线定理:三角形一个角的平分线分对边所成的两条线段与这个角的两边对应成比例.如△ABC 中,AD 平分∠BAC ,则ACAB DC BD =;(外角平分线定理) 3. 正弦定理:R Cc B b A a 2sin sin sin ===,(其中R 为三角形外接圆半径) 4. 余弦定理:C ab b a c cos 2222-+=5. 布拉美古塔(Brahmagupta )定理: 在圆内接四边形ABCD 中,AC ⊥BD ,自对角线的交点P 向一边作垂线,其延长线必平分对边6. 托勒密(Ptolemy )定理:圆内接四边形对角线之积等于两组对边乘积之和,即AC ·BD =AB ·CD +AD ·BC ,(逆命题成立) .(广义托勒密定理)AB ·CD +AD ·BC ≥AC ·BD7. 蝴蝶定理:AB 是⊙O 的弦,M 是其中点,弦CD 、EF 经过点M ,CF 、DE 交AB 于P 、Q ,则有:MP =QM .8. 欧拉(Euler )公式:设三角形的外接圆半径为R ,内切圆半径为r ,外心与内心的距离为d ,则d 2=R 2-2Rr .重心性质:①设G 为△ABC 的重心,连结AG 并延长交BC 于D ,则D 为BC 的中点,则1:2:=GD AG ; ②设G 为△ABC 的重心,则ABC ACG BCG ABG S S S S ∆∆∆∆===31③设G 为△ABC 的重心,过G 作DE ∥BC 交AB 于D ,交AC 于E ,过G 作PF ∥AC 交AB 于P ,交BC 于F ,过G 作HK ∥AB 交AC 于K ,交BC 于H ,则2;32=++===ABKH CA FP BC DE AB KH CA FP BC DE ④到三角形三顶点距离的平方和最小的点是重心,即222GC GB GA ++最小;⑤三角形内到三边距离之积最大的点是重心;反之亦然(即满足上述条件之一,则G 为△ABC 的重心).11. 垂心性质:(1)三角形任一顶点到垂心的距离,等于外心到对边的距离的2倍(2)垂心H 关于△ABC 的三边的对称点,均在△ABC 的外接圆上;(3)△ABC 的垂心为H ,则△ABC ,△ABH ,△BCH ,△ACH 的外接圆是等圆;(4)设O ,H 分别为△ABC 的外心和垂心, HCA BCO ABH CBO HAC BAO ∠=∠∠=∠∠=∠,,12. 内心:三角形的三条角分线的交点—内接圆圆心,即内心到三角形各边距离相等内心性质:(1)设I 为△ABC 的内心,则I 到△ABC 三边的距离相等,反之亦然(2)设I 为△ABC 的内心,则C AIB B AIC A BIC ∠+︒=∠∠+︒=∠∠+︒=∠2190,2190,219013. 外心:三角形的三条中垂线的交点——外接圆圆心,即外心到三角形各顶点距离相等;外心性质:(1)外心到三角形各顶点距离相等(2)设O 为△ABC 的外心,则A BOC ∠=∠2或A BOC ∠-︒=∠2360(3)∆=S abcR 4;(4)锐角三角形的外心到三边的距离之和等于其内切圆与外接圆半径之和14.其中a h 表示BC 边上的高,R 为外接圆半径,r 为内切圆半径,)(21c b a p ++= 1920·两条直线的平行和垂直(1)若111:l y k x b =+,222:l y k x b =+①121212||,l l k k b b ⇔=≠;②12121l l k k ⊥⇔=-.21·点到直线的距离d =(点00(,)P x y ,直线l :0Ax By C ++=).。
平面几何著名定理
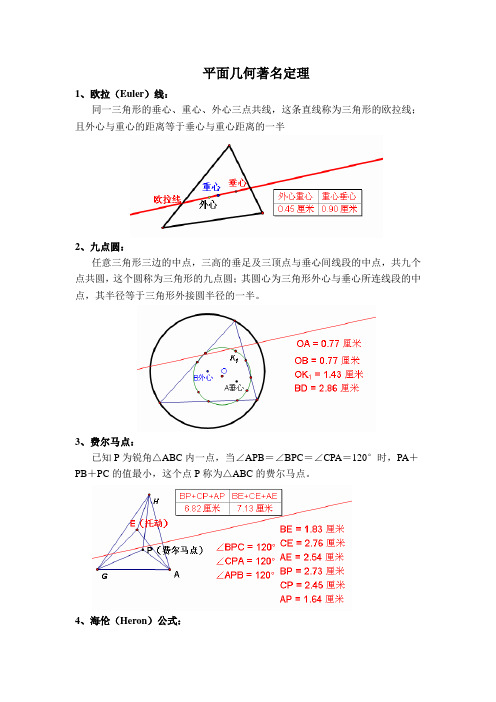
平面几何著名定理1、欧拉(Euler)线:同一三角形的垂心、重心、外心三点共线,这条直线称为三角形的欧拉线;且外心与重心的距离等于垂心与重心距离的一半2、九点圆:任意三角形三边的中点,三高的垂足及三顶点与垂心间线段的中点,共九个点共圆,这个圆称为三角形的九点圆;其圆心为三角形外心与垂心所连线段的中点,其半径等于三角形外接圆半径的一半。
3、费尔马点:已知P为锐角△ABC内一点,当∠APB=∠BPC=∠CPA=120°时,PA+PB+PC的值最小,这个点P称为△ABC的费尔马点。
4、海伦(Heron)公式:在△ABC 中,边BC 、CA 、AB 的长分别为a 、b 、c ,若p =21(a +b +c ), 则△ABC 的面积S =))()((c p b p a p p ---5、塞瓦(Ceva )定理:在△ABC 中,过△ABC 的顶点作相交于一点P 的直线,分别交边BC 、CA 、AB 与点D 、E 、F ,则1=⋅⋅FBAFEA CE DC BD ;其逆亦真6、密格尔(Miquel )点:若AE 、AF 、ED 、FB 四条直线相交于A 、B 、C 、D 、E 、F 六点,构成四个三角形,它们是△ABF 、△AED 、△BCE 、△DCF ,则这四个三角形的外接圆共点,这个点称为密格尔点。
7、葛尔刚(Gergonne )点:△ABC 的内切圆分别切边AB 、BC 、CA 于点D 、E 、F ,则AE 、BF 、CD 三线共点,这个点称为葛尔刚点。
8、西摩松(Simson )线:已知P 为△ABC 外接圆周上任意一点,PD ⊥BC ,PE ⊥ACPF ⊥AB ,D 、E 、F 为垂足,则D 、E 、F 三点共线,这条直线叫做西摩松线。
9、黄金分割:把一条线段(AB)分成两条线段,使其中较大的线段(AC)是原线段(AB)与较小线段(BC)的比例中项,这样的分割称为黄金分割11、笛沙格(Desargues)定理:已知在△ABC与△A'B'C'中,AA'、BB'、CC'三线相交于点O,BC与B'C'、CA与C'A'、AB与A'B'分别相交于点X、Y、Z,则X、Y、Z三点共线;其逆亦真。
平面几何四大定理

平面几何四个重要定理四个重要定理:梅涅劳斯(Menelaus)定理(梅氏成)△ ABC的三边BC、CA、AB或其延长线上有点P、Q、R,则P、Q、R共线的充妥条件是— = loPC QA RB室瓦(Ccva)定理(塞瓦点)A ABC 的三边BC、CA、AB 上有点P、Q、R,则AP、BQ、CR共点的充妥条件是BP CQ ARPC QA RBlo托勒密(Ptolemy)定理四边彩的两对边乘积之和等于其对角线乘积的充妾条件是该四边形内接于一圆。
西姆松(Simson)定理(西姆松线)从一点向三角形的三边所引垂线的垂足共线的充妄条件是该点落在三角形的外接网上。
例题:1.设AD是二ABC的边BC上的中线,直线XF交AD于F。
a. AE 2AF求'正: LC = 0ED FB【分析】CEF —— = 1 (梅氏定理)ED CB FA【评注】也叮以添加辅助线证明:过A、B、D之一作CF的平行践。
2.过^ABC的重心G的直经分别交AB、AC于E、F,交CB word于Po求证: BE CF —+ —EA FA【分析】连结异延长AG交BC于M,则M为BC的中点Oc 止BE AG DEG 裁zlABM— --------------EA GMCF AGPGF^AACM^--—FA Of 黑=1 (梅氏定理)U D罪=1 (梅氏定理)DC.BE 十CF _GM (DB + DC)_GM 2MD_[ EA+ FA AGMD 2GM MD~ 【评注】梅氏定理3.D、E、F分别在A ABC的BC、CA、AB边上,RD AF CF= 人,AD、BE、CF 交成ALMNoDC FB EA求S_LM*【分析】【评注】梅氏定理4. 以AABC各边为底边向外作相似的等膝zLBCE、ACAF.AABGo求证:AE、BF、CG相交于一点。
【分析】【评注】塞瓦定理5.已知ZiABC 中,ZB=2ZCo 求证:AC2=AB2+AB - BCo【分析】过A作BC的平行线交A ABC的外接圆于D,连结BPo 则CD=DA=AB, AC=BDo由,七勒密定理,AC - BP=AD - BC+CD - ABo【评注】托勒密定理6.已知正七边形A|A2A5A4A S A6A7O求证:+—!—o (第21届全苏数学竞赛)A | A 2 A j A j A]Aq【分析】【评注】托勒密定理7. AABC的BC边上的商AD的延长线交外接阅于P,作PE1AB于E,延长ED交AC延长残于F。
个人精心高中数学联赛竞赛平面几何四大定理及考纲

个人精心高中数学联赛竞赛平面几何四大定理及考纲Standardization of sany group #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#1、数学竞赛考纲二试1、平面几何基本要求:掌握高中数学竞赛大纲所确定的所有内容。
补充要求:面积和面积方法。
几个重要定理:梅涅劳斯定理、、、。
几个重要的极值:到三角形三顶点距离之和最小的点--。
到三角形三顶点距离的平方和最小的点--。
三角形内到三边距离之积最大的点--重心。
几何不等式。
简单的。
了解下述定理:在周长一定的n边形的集合中,正n边形的面积最大。
在周长一定的的集合中,圆的面积最大。
在面积一定的n边形的集合中,正n边形的周长最小。
在面积一定的简单闭曲线的集合中,圆的周长最小。
几何中的运动:反射、平移、旋转。
方法、方法。
平面、及应用。
2、代数在一试大纲的基础上另外要求的内容:周期函数与周期,带的函数的图像。
,三角形的一些简单的恒等式,三角不等式。
,一阶、二阶递归,法。
函数,求n次迭代,简单的函数方程。
n个变元的平均不等式,,及应用。
复数的指数形式,欧拉公式,,单位根,单位根的应用。
圆排列,有重复的排列与组合,简单的组合恒等式。
一元n次方程(多项式)根的个数,根与系数的关系,实系数方程虚根成对定理。
简单的初等数论问题,除初中大纲中所包括的内容外,还应包括,,欧几里得除法,非负最小完全剩余类,,,,,格点及其性质。
3、立体几何多面角,多面角的性质。
三面角、直三面角的基本性质。
正多面体,欧拉定理。
体积证法。
截面,会作截面、表面展开图。
4、平面解析几何直线的式,直线的,直线束及其应用。
二元一次不等式表示的区域。
三角形的。
圆锥曲线的切线和法线。
圆的幂和根轴。
5、其它。
集合的划分。
覆盖。
西姆松线的存在性及性质()。
及其逆定理。
一、平面几何1. 梅涅劳斯定理(Menelaus)定理(简称梅氏定理)是由数学家梅涅劳斯首先证明的。
它指出:如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点,那么(AF/FB)×(BD/DC)×(CE/EA)=1。
平面几何中几个重要定理的证明

证明:如图,过点C作AB的平行线,交EF于点G.
因为CG // AB,所以 ————(1)
因为CG // AB,所以 ————(2)
由(1)÷(2)可得 ,即得 .
注:添加的辅助线CG是证明的关键“桥梁”,两次运用相似比得出两个比例等式,再拆去“桥梁”(CG)使得命题顺利获证.
4.梅涅劳斯定理的逆定理及其证明
由于 DAE = BAM,所以 DAM = BAE,即 DAC = BAE。而 ABD = ACD,即 ABE = ACD,所以 ABE∽ ACD.即得
,即 ————(2)
由(1)+(2)得
.
所以AB·CD + BC·AD = AC·BD.
注:巧妙构造三角形,运用三角形之间的相似推得结论.这里的构造具有特点,不容易想到,需要认真分析题目并不断尝试.
三、托勒密定理
5.托勒密定理及其证明
定理:凸四边形ABCD是某圆的内接四边形,则有
AB·CD + BC·AD = AC·BD.
证明:设点M是对角线AC与BD的交点,在线段BD上找一点,使得 DAE = BAM.
因为 ADB= ACB,即 ADE = ACB,所以 ADE∽ ACB,即得
,即 ————(1)
五、欧拉定理
9.欧拉定理及其证明
定理:设ΔABC的重心、外心、垂心分别用字母G、O、H表示.则有G、O、H三点共线(欧拉线),且满足 .
证明(向量法):连BO并延长交圆O于点D。连接CD、AD、HC,设E为边BC的中点,连接OE和OC.则
———①
因为CD⊥BC,AH⊥BC,所以AH // CD.同理CH // DA.
另外,待定系数法在其中扮演了非常重要的角色,需注意掌握其用法.
平面几何中的几个重要定理

一.梅涅劳斯定理Menelaus (公元98年左右),希腊数学家、天文学家,梅涅劳斯定理包含在其几何著作《球论》里。
梅涅劳斯定理 设ABC ∆的三边AB CA BC ,,或它们的延长线与一条不经过其顶点的直线交于R Q P ,,三点(如图6),则1=⋅⋅RB AR QA CQ PC BP 。
梅涅劳斯定理逆定理 设R Q P ,,分别是ABC ∆的三边AB CA BC ,,上或它们延长线上三点,若有1=⋅⋅RBAR QA CQ PC BP , 则R Q P ,,三点在同一直线上。
设P 为三角形ABC 所在平面上一点,过点P 作PA 的垂线交直线BC 于D ,作PB 的垂线交直线CA 于E ,作PC 的垂线交AB 于F 。
求证:D,E,F 共线。
若三角形的三条外角平分线皆与对边所在直线相交,则三交点共线。
3.设ABC ∆的∠A 的外角平分线与BC 的延长线交于P,∠B 的平分线与AC 交于Q,∠C 的平分线和AB 交于R.求证: R Q P ,,三点在同一直线上。
AB C P Q R S AB C S P R Q 6 图A B CPQ R 7 图4.图8,过△ABC 的三个顶点A 、B 、C 作它的外接圆的切线,分别和BC 、CA 、AB 的延长线交于P 、Q 、R ,求证:P 、Q 、R 三点共线。
注: 直线PQR 叫做△ABC 的莱莫恩(Lemoine )线5.(戴沙格定理)设△ABC 和△C B A '''对应点的连线A A '、B B '、C C 'S ,这时如果对应边BC 和C B ''、CA 和A C ''、AB 和B A ''(或它们的延长线)相交,则它们的交点D 、E 、F 在同一直线上。
注:戴沙格定理是射影几何中的重要定理。
6(牛顿定理)设四边形ABCD 的一组对边AB 和CD 的延长线交于点E ,另一组对边 AD 和BC 的延长线交于点F ,则AC 的中点L 、BD 的中点M 及EF 的中点N ,三点共线。
平面几何的几个重要的定理

平面几何的几个重要的定理一、梅涅劳斯定理:1=⋅⋅=⋅⋅BAA C CBC B A h h h h h h RB AR QA CQ PC BP l C B A h h h 的垂线的长度,则:到直线、、分别是、、证:设注:此定理常运用求证三角形相似的过程中的线段成比例的条件;。
的交点,证明:与是的中点,是上,在点的平分线,是是斜边上的高,中,:若直角例CE //BF CK DE F AC D AK E ACK CE CK ABC ∠∆11PC BP R Q P AB CA BC ABC ABC l 1=⋅⋅RBARQA CQ ,则、、的延长线分别交于或它们、、的三边的顶点,并且与不经过:若直线定理∆∆CE//BF CKE FKB KE BK KC KF BE BK FC KF BE BK BC BP AC EP AC CK AE EK FC KF 1FCKFEK AE DA CD F E D ACK EPCK EP BC EBC CE BH 90HCB ACE HCB HBC ACE HBC ACKEBC BH B EBC ∴≅∴=====⋅⋅=∴⊥︒=∠+∠=∠+∠∠=∠∠=∠∠∆∆∆∆∆=依分比定理有:=即:=于是依梅涅劳斯定理有:、、和三点对于,则:上的高作为等腰三角形即:则:的平分线中,作在证:111111111111D B D A :C B C A BD AD :BC AC D C B A DC B A K 1=,试证:、、、和、、、线分别交这四条直线于引四条直线,另两条直】从点【练习注:此定理常用于证明三点共线的问题,且常需要多次使用 再相乘;共线;、、证明点引的垂线的垂足,、、向是从点、、的外接圆上;位于点例111111C B A AB CA BC P C B A ABC P .2∆三点共线;、、综上可得:也重合与的延长线上时,同在与类似地可证得当矛盾=这与于是可得即这时设必定重合,不然的话,与线段上,则同在与若的延长线上;线段上,或者同在或者同在与因此,或边上的点的个数也为三点中,位于、、由于在同一直线上的=,则:又得:,于是由定理交于与直线证:设直线R Q P R R AB R R BR AR BR AR BR AR BR AR ,BR BR ,AR AB AR AB ,AR AR R R AB R R AB AB R R 20ABC R Q P RBAR B R AR 1RB AR QA CQ 1BR AR QA CQ 1R AB PQ ''''''''''''''''''><-<->=⋅⋅=⋅⋅∆PC BP PC BP 三点共线;、、求证:,,这时若或边上的点的个数为三点中,位于、、三点,并且上或它们的延长线上的、、的三边分别是、、:设定理R Q P PC BP 20ABC R Q P AB CA BC ABC R Q P 21RBARQA CQ =⋅⋅∆∆ C BA1A 1B 1C 三点共线;、、依梅涅劳斯定理可知,=可得且将上面三条式子相乘,证:易得:111111111111111C B A 1BC AC AB CB CA BA 180PBA PCA ,PCB PAB ,PBC PAC PBA cos PB PABcos AP BC AC PAC cos AP PCAcos CP AB CB ,PCBcos CP PBCcos BP CA BA ⋅⋅︒=∠+∠∠=∠∠=∠∠⋅∠⋅-=∠⋅∠⋅-=∠⋅∠⋅-=直线上;在同一条、、的交点与,与,与,则、、上的切点分别为、、的内切圆在三边】设不等腰【练习Z Y X AB DE CA FD BC EF F E D AB CA BC ABC 2∆三点共线;、、,试证:的交点是与线,直的交点是与,直线的交点为和,直线相交于,,】已知直线【练习222211*********C B A B C A AC A C B BC C B A AB O CC BB AA 311111111111111111111111111111111111111D B D A :C B C A BD AD :BC AC 1C BD B D A C A BD BC AC AD 1LD D B K B BK BD LD 1BKKB C B LC LC BC 1LC C A K A AK AC LC 1AK KA D A LD LD AD BLB AL A L D A AD D A //AD 1==⋅⋅⋅=⋅⋅=⋅⋅=⋅⋅=⋅⋅即:得:将上面四条式子相乘可可得:和别用于,则把梅涅劳斯定理分相交与点与若,结论显然成立;证:若的证明练习∆∆三点共线、、可得的边上,由定理都不在、、又得:将上面三条式子相乘可==同理可得:=代人上式可得:又可得:所截,由定理被直线证:的证明练习Z Y X 2ABC Z Y X 1ZBAZYA CY XC BX BDEAZB AZ AF DC YA CY CEFBXC BX AF AE 1FBAFEA CE XC BX 1XFE ABC 2∆∆ =⋅⋅==⋅⋅共线、、,证明:、、的交点依次为和,和,和,和,记直线、、,在另一条上取点、、】在一条直线上取点【练习N M L N M L BC EF AF CD AF CD ED AB D F B A C E 4共线由梅涅劳斯定理可知可得:将上面的三条式子相乘应用梅涅劳斯定理有:,和,和,和们边上的点:对所得的三角形和在它的交点,和,和,和分别是直线、、证:设的证明练习222222222221111221111221111211211211111111222C ,B ,A 1BA CA CB AB AC BC 1CB AB OC CC AA OA 1BA CA OB BB CC OC 1AC BC BB OB OA AA )B ,C A (OAC ),A ,C B (OBC ),C ,B A (OAB B A AB C A AC C B BC C B A 3=⋅⋅=⋅⋅=⋅⋅=⋅⋅共线点得:将上面五条式子相乘可,则有点涅劳斯定理于五组三元,应用梅,对、、的交点分别为和,和,和证:记直线的证明练习N ,M ,L ,1VNUNUM WM WL VL 1UFVFWD UD VB WB 1UE VE WC UC VA WA 1WB VBUC WC VN UN 1YM WM VF UF WA VA 1UD WD WL VL VE UE )F ,D ,B (),E ,C ,A (),N ,C ,B (),F ,M ,A (),E ,D ,L (UVW W V U CD AB AB EF CD EF 4∴=⋅⋅=⋅⋅=⋅⋅=⋅⋅=⋅⋅=⋅⋅∆。
平面几何等几个重要定理

1.萊莫恩(Lemoine)線:設三角形ABC的∠A的外角平分線與BC的延長線交於P,∠B的平分線與AC交於Q,∠C的平分線和AB交於R。
求證P、Q、R三點共線。
註:直線PQR稱為三角形ABC的萊莫恩(Lemoine)線。
2.戴沙格定理:設三角形ABC和A'B'C'對應頂點的連線AA'、BB'、CC'交於一點S,這時如果對應邊BC和BC、CA和CA、AB和AB(或它們的延長線)相交,則它們的交點D、E、F在同直線上。
註:戴沙格定理是射影幾何中等一個重要定理。
3.牛頓定理:設四邊形ABCD的一組對邊AB和CD的延長線交於點E,另一組對邊AD和BC的延長線交於F,則AC中點L、BD中點M及EF中點N三點共線。
註:直線LMN稱為四方形ABCD的牛頓線。
4.斯特瓦爾特定理:設P為三角形ABC的邊BC上一點,且BP:PC=m:n,則有 nAB2 + m AC2 =(n+m)AP2 + mn BC2/(m+n)。
註:1.當m=n時,即P是BC的中點時,可得AB2 + m AC2 = 2( AP2 + BP2),此即三角形的中線定理,亦稱巴布斯定理。
2.當AP為三角形ABC中∠A的平分線時,則由角平線的性質得m/n=AB/AC。
此時BP =ac/(b+c),CP=ab/(b+c)。
所以AP2=4bcp(p-a)/(b+c)2。
這公式亦可用sinA/2,及三角形面積公式得到。
5.在三角形ABC中,設c>b,AD是∠A的平分線,E為BC上一點且BE=CD。
求證:AE2-AD2=(c-b)2。
6.設G為三角形的重心,M是平面上任意一點,求證:MA2+MB2+MC2=GA2+GB2+GC2+3MG2。
7.在三角形ABC的邊BC上任取一點D,設ADB和ADC的角平分線分別交AB、AC於E和E,求證AD、BE、CF交於一點。
8.已知AD是三角形ABC的邊BC上等高,P為AD上任意一點,直線BP、CP分別交AC、AB於E、F,求證∠FDA=∠ADE。
平面几何的几个重要的定理
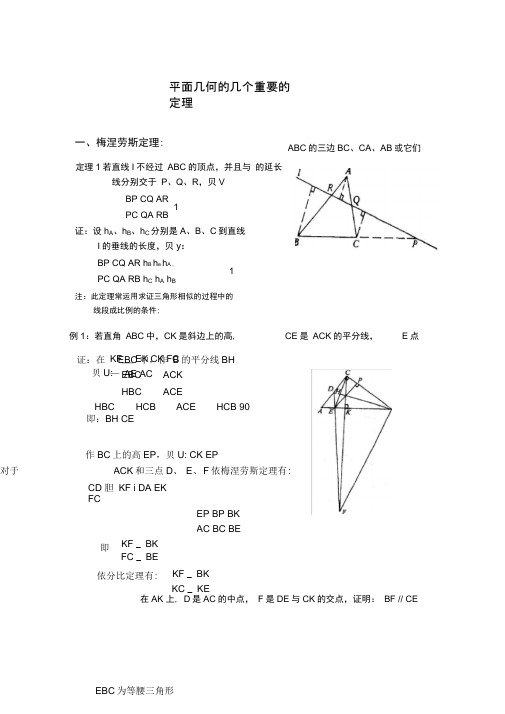
证:在 EBC 中,作 B 的平分线BH贝U: EBCACKHBCACE HBC HCB ACEHCB 90即:BH CE作BC 上的高EP ,贝U: CK EP对于ACK 和三点D 、 E 、 F 依梅涅劳斯定理有: CD 胆 KF i DA EKFCKF__ EK CK FC — AE AC EP BP BK AC BC BE即KF _ BK FC _ BE依分比定理有: KF _ BKKC _ KE平面几何的几个重要的定理一、梅涅劳斯定理:定理1若直线I 不经过 ABC 的顶点,并且与 的延长线分别交于 P 、Q 、R ,贝VBP CQ AR 1PC QA RB证:设h A 、h B 、h C 分别是A 、B 、C 到直线I 的垂线的长度,贝y : BP CQ AR h B h e h A , 1PC QA RB h C h A h B注:此定理常运用求证三角形相似的过程中的线段成比例的条件;在AK 上, D 是AC 的中点, F 是DE 与CK 的交点,证明: BF // CE例1:若直角 ABC 中,CK 是斜边上的高, CE 是 ACK 的平分线, E 点ABC 的三边BC 、CA 、AB 或它们EBC 为等腰三角形FKB CKE BF //CEA 1 C 1 A 1 D 1B 1C 1 B 1D 1【练习1从点K 引四条直线,另两条直 AC 和 A 1 > B 1> C 1> D 1,试证: --BC线分别交这四条直线于 A 、B 、C 、DAD BD依梅涅劳斯定理可知 A 1> B 1> 6三点共线; .下载可编辑.CA 、AB 上或它们的延长线上的P 、Q 、R 三点中,位于 ABC 边上的点的个数为 0或2,这时若 聖PC 定理2:设P 、Q 、R 分别是 ABC 的三边BC 、 三点,并且CQ AR QA RB1,求证:P 、Q 、R 三点共线;证:设直线PQ 与直线AB 交于R ',于是由定理BP CQ AR ' PC QA R ' B又 BP CQ AR PC QA RB由于在同一直线上的 ABC 边上的点的个数也为 0或2,AR AR 1,贝 U : - L =R B RBP 、Q 、R '三点中,位于因此R 与R '或者同在AB 线段上,或者同在 AB 的延长线上;若R 与R '同在AB 线段上,则R 与R '必定重合,不然的话, 设AR AR ',AR AR 'BR BR '这时AB AR AB AR ',即卩BR BR ',于是可得AR AR 这与 =——T 矛盾BR BR 类似地可证得当 R 与R'同在AB 的延长线上时, 综上可得:P 、Q 、R 三点共线;注:此定理常用于证明三点共线的问题,且常需要多次使用R 与R 也重合再相乘;例2点P 位于 ABC 的外接圆上;A 1>C 1是从点P 向BC 、CA 、AB 引的垂线的垂足,证明点A 1> B 1> BA 1 BP cos PBC CA 1 CP cos PCB CB 1 CP cos PCA AB 1 AP cos PAC AC 1 AP cos PABC i 共线;证:易得:PB cos PBABC 1将上面三条式子相乘,且 PAC PBC , PAB PCB , BA 1 CB 1 AC 1—1 , CA [ AB 1 BC 1PCAPBA 180可得【练习4在一条直线上取点E 、C 、B 、F 、D ,记直线AB 和ED ,【练习2】设不等腰 ABC 的内切圆在三边 BC 、CA 、AB 上的切点分别为 D 、E 、F ,则EF 与BC , FD 与CA ,DE与AB 的交点 X 、Y 、Z 在同一条 直线上;【练习3】已知直线 AA i ,BB 1,CC i 相交于0,直线AB 和 A 1B 1的交点为 C 2,直线 BC 与B 1C 1的交点是 A 2,直 线AC 与A i C i 的交点是B 2,试证:A 2、B 2、C 2三点共线;CD 和AF ,CD 和AF ,EF 和BC 的交点依次为 L 、M 、N ,证明:L 、M 、N 共线练习1的证明证:若AD // A 1D 1,结论显然成立; 若AD 与A 1 D 1相交与点AD LD LD BDLD j A 1K A 1D 1 AK BKBQ B 1K LD 1 将上面四条式子相乘可即:也:如 BC BD A 1C 1B 1C 1L ,则把梅涅劳斯定理分 LC AK A 1C 1 AC A 1K 得.AD 得: -ACA 1 D 1B 1 D 1LC 1别用于 A 1AL 和B 1BL 可得: BCLC L B 1KB 1C 1 LC BK 1BC A 1C 1 BD A 1D 1B 1D 1 B 1C 1证:ABC 被直线 XFE 所截,由定理 1可得:BXCE XCEA 又 AE AF 代人上式可得: BX FB XC CECY DC AZ EA同理可得: -YA AF ZBBD将上面三条式子相乘可得:BX 得: CY AZ d1XC YA ZB又 X 、 Y 、 Z 都不在 ABC 的边上 .,由定理 2可得 练习2的证明 X 、YAF FBZ 三点共线练习3的证明证:设A 2、B 2、C 2分别是直线 BC 和B 1C 1,对所得的三角形和在它 C 1 ,A 2 ),OAC 和(A 1, AA 1 OB 1 BC 2 1 AC? AC 和 A 1C 1, 们边上的点:OAB 和(A" C 1,B 2)应用梅涅劳斯定理有: OC 1 BB 1 CA 2 . OA CC 1 OB 1 BA 2 可得:B C 2 A B 2AC 2 CB 2 由梅涅劳斯定理可知 A 2 , B 2 ,C 2共线 AB 和A 1B 1的交点, B 1 ,C 2 ),OBC 和(B“ i OA 1 BB 1 BB 1 CA 2 将上面的二条式子相乘 1 AA 1 CA 2BA 2 1练习4的证明 CC 1 AB 2 i OC 1 CB 2 证:记直线 EF 和CD ,EF 和AB ,AB 和CD 的交点分别为 U 、V 、W ,对 UVW ,应用梅 涅劳斯定理于五组三元 点(L,D,E ),( A,M ,F ),(B,C,N ),( A,C,E ),( B,D,F ),则有UE VL WD VE WL UD WA UC VE VA WC UE,VA UF WM 1WA VF YM ,WB UD VF 1VB WD UF,UN WC VB1VN UC WB将上面五条式子相乘可得益晋赭1, 点L,M ,N 共线平面几何的几个重要定理塞瓦定理:设P 、Q 、R 分别是 ABC 的 BC 的充要条件是:聖3塑1PC QA RB------ 塞瓦定理CA 、AB 边上的点,则AP 、BQ 、CR 三线共点BMPACP SCMPSBCMSABMSACMSBCM以上三式相乘,得:C2竺=iPC QA RB证:先证必要性:设AP、BQ、CR相交于点M,贝BP S ABP S BMP S ABM PC S ACP S CMP S ACM同理:BQAARRBBP CQ AR再证充分性:若 ------------ 1,设AP与BQ相交于M,且直线CM交AB于R,PC QA RB由塞瓦定理有:圧竺翌1,PC QA R B于是:竺=纯R B RB因为R和R都在线段AB上,所以R必与R重合,故AP、BQ、CR相交于一点点M; 例1:证明:三角形的中线交于一点;证明:记ABC的中线AA,, BB,, CC,,我们只须证明型-BA1 1C, B A,C B, A而显然有:AC, C, B, BA, A1C,CB1B, AAC, BA, CB,即 1 1 1 1成立,ABC父于一点;C, B A,C B, A【练习1】证明:三角形的角平分线交于一点;【练习2】证明:锐角三角形的高交于一点;例2:在锐角ABC中,角C的平分线交于AB于L,从L作边AC和BC的垂线,垂足分别是M和N,设AN和BM的交点是P,证明:CP AB又 MC 即要证AMLAKCAM AL A K ACBNLBKCBK BC NB BL即要证AC 匹1BL 证:作CK AB下证CK 、BM 、AN 三线共点,且为P 点, 要证CK 、BM 、AN 三线共点,依塞瓦定理AM CN BK ,即要证:-1MC NB AK CN AM BK A K NBBBC BL FDA ,AD BC 故MN //BC ,可得 AME AM CDAD 、 CDE , Af ,于是AMBDFANF AE CD “ ,AN CECF 共点于P ,根据塞瓦定理可得:-BDDCAE AN CE ,BDBE、 AF BD BF CE AF , 1EA FBAE CD CE AM AN EDAAF BD BF FDA【练习创已知 CAN BCMABC 外有三点M 、N 、R ,且BAR ,CBM ABR , ACN ,证明:AM 、BN 、CR 三线共点;依三角形的角平分线定 理可知:昱ACCK 、BM 、AN 三线共点,且为P 点 CP AB例3.设AD 是 ABC 的高,且D 在BC 边上,若P 是AD 上任一点,BP 、CP 分别与AC 、 AB 交于 E 和 F ,贝U EDA = FDA证:过A 作AD 的垂线,与DE 、DF 的延长线分别 交于M 、N 。
四个重要定理(梅涅劳斯-塞瓦-托勒密-西姆松)

P 、Q R ,则P 、Q R 共线的充要条件是聖CQ ARj 。
PC QA RBBP CQ AR PC QA RB _ °平面几何中的四个重要定理梅涅劳斯(Menelaus )定理(梅氏线)△ABC 的三边BC CA AB 或其延长线上有点塞瓦(Ceva )定理(塞瓦点)△ABC 的三边 BC CA AB 上有点 P 、Q R ,贝U AP 、BQ CR 共点的充要条件是 托勒密(Ptolemy )定理四边形的两对边乘积之和等于其对角线乘积的充要条件是该四边形内接于一圆。
西姆松(Simson )定理(西姆松线)从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接 圆上。
例题:PA 1设AD是MBC的边BC上的中线,直线CF交AD于F。
求证:AE 2AFED。
AE DC RF【分析】CEF截△ARCH — .— .— =1 (梅氏定理)ED CR FA【评注】也可以添加辅助线证明:过A、R、D之一作CF的平行线。
2、过△ARC的重心G的直线分别交AB AC于E、F,交CR于D。
RE CF=1。
求证:EA FADEG截A ARM H REEAAGGMMDDR(梅氏定理)DGF截△ACM H =1 (梅氏定理)FA GM DCRE CF=GM (DR DC)=GM2MDEA FA AG MD 2GM MD【评注】梅氏定理3、D E、F分别在A ARC的RC CA AR边上,RD AFDC FRCEEAAD RE、CF交成△ LMN 求S A LM N O【分析】【评注】梅氏定理4、以A ARC各边为底边向外作相似的等腰A RCE A CAF A ARG 求证:AE、RF、CG相交【分析】连结并延长AG交RC于M,则M为RC的中点。
FLEM N【评注】塞瓦定理5、已知△ABC 中,/ B=2/ G 求证:AC^AB+ABBCo【分析】过A 作BC 的平行线交△ABC 的外接圆于D,连结BD 贝 U CD=DA=AB AC=BD由托勒密定理,AC BD=ADBC+CDAB【评注】托勒密定理求证:1 1 1A !A 2=A !A 3 A !A 4。
平面几何的几个重要的定理梅涅劳斯定理

平面几何的几个重要的定理一、梅涅劳斯定理:注:此定理常运用求证三角形相似的过程中的线段成比例的条件;注:此定理常用于证明三点共线的问题,且常需要多次使用 再相乘;共线;、、证明点的外接圆上位于点例111C B A ABC P .2∆平面几何的几个重要定理――――塞瓦定理塞瓦定理:1PC BP R Q PAB CA BC ABC ABC l 1=⋅⋅RBARQA CQ ,则、、的延长线分别交于或它们、、的三边的顶点,并且与不经过:若直线定理∆∆三点共线;、、依梅涅劳斯定理可知,=可得且将上面三条式子相乘,证:易得:111111111111111C B A 1BC AC AB CB CA BA 180PBA PCA ,PCB PAB ,PBC PAC PBAcos PB PABcos AP BC AC PAC cos AP PCAcos CP AB CB ,PCBcos CP PBCcos BP CA BA ⋅⋅︒=∠+∠∠=∠∠=∠∠⋅∠⋅-=∠⋅∠⋅-=∠⋅∠⋅-=Θ1:=⋅⋅∆RBARQA CQ PC BP CR BQ AP AB CA BC ABC R Q P 的充要条件是三线共点、、边上的点,则、、的分别是、、设;相交于一点点、、重合,故必与上,所以都在线段和因为=于是:,由塞瓦定理有:,于交,且直线相交于与,设再证充分性:若=以上三式相乘,得:同理:,则:相交于点、、证:先证必要性:设’’‘’‘’‘M CR BQ AP R R AB R R RB ARB R AR BR AR QA CQ PC BP R AB CM M BQ AP RB AR QA CQ PC BP RB ARQA CQ PC BP S S RB AR S S QA CQ S S S S S S PC BP M CR BQ AP BCMACMABMBCMACM ABMCMP BMP ACP ABP 111=⋅⋅=⋅⋅⋅⋅=====∆∆∆∆∆∆∆∆∆∆交于一点;:证明:三角形的中线例1ABCP P AN BM CK BLBCAC AL BLBCAC AL BLBCNB BK BKC BNL ACALAK AM AKC AML NBBKAK AM CNMC AKBKNB CN MC AM AN BM CK P AN BM CK ABCK ⊥∴∴=⋅=⋅=⇒∆≅∆=⇒∆≅∆=⋅==⋅⋅⊥点三线共点,且为、、理可知:依三角形的角平分线定即要证即要证明:又即要证:三线共点,依塞瓦定理、、要证点,三线共点,且为、、下证证:作1111ΘΘ平面几何的几个重要定理--托勒密定理托勒密定理:圆内接四边形中,两条对角线的乘积(两对角线所包矩形的面积)等于两组对边乘积之和(一组对边所包矩形的面积与另一组对边所包矩形的面积之和).即:;内接于圆,则有:设四边形BD AC BC AD CD AB ABCD ⋅=⋅+⋅一、直接应用托勒密定理 例1 如图2,P 是正△ABC 外接圆的劣弧上任一点 (不与B 、C 重合), 求证:PA=PB +PC . 四点共圆时成立;、、、上时成立,即当且仅当在且等号当且仅当相似和且又相似和则:,,使内取点证:在四边形D C B A BD E BDAC BC AD CD AB ED BE AC BC AD CD AB ED AC BC AD AD ED AC BC AED ABC EADBAC ADAE AC AB BE AC CD AB CDBE AC AB ACD ABE ACDABE CAD BAE E ABCD ⋅≥⋅+⋅∴+⋅=⋅+⋅∴⋅=⋅⇒=∴∆∆∴∠=∠=⋅=⋅⇒=∴∆∆∠=∠∠=∠)(Θ分析:此题证法甚多,一般是截长、补短,构造全等三角形,均为繁冗.若借助托勒密定理论证,则有PA·BC=PB·AC+PC·AB,∵AB=BC=AC.∴PA=PB+PC.二、完善图形借助托勒密定理例2证明“勾股定理”:在Rt△ABC中,∠B=90°,求证:AC2=AB2+BC2证明:如图,作以Rt△ABC的斜边AC为一对角线的矩形ABCD,显然ABCD是圆内接四边形.由托勒密定理,有AC·BD=AB·CD+AD·BC.①又∵ABCD是矩形,∴AB=CD,AD=BC,AC=BD.②把②代人①,得AC2=AB2+BC2.例3如图,在△ABC中,∠A的平分线交外接∠圆于D,连结BD,求证:AD·BC=BD(AB +AC).证明:连结CD,依托勒密定理,有AD·BC=AB·CD+AC·BD.∵∠1=∠2,∴ BD=CD.故 AD·BC=AB·BD+AC·BD=BD(AB+AC).三、构造图形借助托勒密定理例4若a、b、x、y是实数,且a2+b2=1,x2+y2=1.求证:ax+by≤1.证明:如图作直径AB=1的圆,在AB两边任作Rt△ACB和Rt△ADB,使AC=a,BC=b,BD=x,AD=y.由勾股定理知a、b、x、y是满足题设条件的.据托勒密定理,有AC·BD+BC·AD=AB·CD.∵CD≤AB=1,∴ax+by≤1.四、巧变原式妙构图形,借助托勒密定理例5已知a、b、c是△ABC的三边,且a2=b(b+c),求证:∠A=2∠B.分析:将a2=b(b+c)变形为a·a=b·b+bc,从而联想到托勒密定理,进而构造一个等腰梯形,使两腰为b,两对角线为a,一底边为c.证明:如图,作△ABC的外接圆,以 A为圆心,BC为半径作弧交圆于D,连结BD、DC、DA.∵AD=BC,∴∠ABD=∠BAC.又∵∠BDA=∠ACB(对同弧),∴∠1=∠2.依托勒密定理,有BC·AD=AB·CD+BD·AC.①而已知a2=b(b+c),即a·a=b·c+b2.②∴∠BAC=2∠ABC.五、巧变形妙引线借肋托勒密定理例6在△ABC中,已知∠A∶∠B∶∠C=1∶2∶4,分析:将结论变形为AC·BC+AB·BC=AB·AC,把三角形和圆联系起来,可联想到托勒密定理,进而构造圆内接四边形.如图,作△ABC的外接圆,作弦BD=BC,边结AD、CD.在圆内接四边形ADBC中,由托勒密定理,有AC·BD+BC·AD=AB·CD易证AB=AD,CD=AC,∴AC·BC+BC·AB=AB·AC,1.已知△ABC中,∠B=2∠C。
平面几何中的几个重要定理

平面几何中的几个重要定理自欧几里得的《几何原本》问世以来,初等几何以其新奇、美妙、丰富、完美的内容和形式引发了历代数学家们浓厚的兴趣.许多杰出的人物为了探索几何学中的奥秘而奉献了毕生的精力,他们发现了一个又一个新的定理,推动了几何学的迅速发展.为了纪念他们,人们以他们的名字来命名他们所获得的重要成果.这些优秀成果如同璀璨的明珠照亮了几何学的历程.这里我们介绍几何学中的几个重要定理以及它们在数学竞赛解题中的应用。
一、塞瓦定理塞瓦(G .Ceva 1647—1743),意大利著名数学家.塞瓦定理 设为三边所在直线外一点,连接分别和的边或三边的S ABC ∆CS BS AS ,,ABC ∆延长线交于(如图1),则.R Q P ,,1=⋅⋅RBARQA CQ PC BP 证明 (面积法)考虑到△ABS 与△ACS 有公共底边AS ,因此它们面积之比等于分别从顶点B 、C 向底边AS所引垂线长的比,而这个比又等于BP 与PC 之比,所以有P174同理可得三式相乘,即得··=··=1ABCSPQRBACSPQR1图与塞瓦定理同样重要的还有下面的定理.塞瓦定理逆定理 设为的边或三边的延长线上的三点(都在三边R Q P ,,ABC ∆R Q P ,,上或只有其中之一在边上),如果有,则三直线交于一点或互相平行. 1=⋅⋅RBARQA CQ PC BP CR BQ AP ,, 证明 因三点P 、Q 、R 中必有一点在三角形的边上,不妨假定P 点在BC 边上。
若BQ 与CR 相交,设交点为S ,又设AS 和BC 的交点为P’,由塞瓦定理,应有··=1与已知条件中的式子比较,得=但由于点P 和P’同在BC 边上,所以P 和P ’重合,即三直线AP 、BQ 、CQ 交于一点。
P175若BQ 与CR 平行,则=.把它代入已知条件的式子中,**=1,RB AB QC AC PC BP QA CQ QCAC∴;BQ//PA 。
平面几何四大定理

平面几何四个重要定理四个重要定理:梅涅劳斯(Menelaus)定理(梅氏线)△ABC得三边BC、CA、AB或其延长线上有点P、Q、R,则P、Q、R共线得充要条件就是.塞瓦(Ceva)定理(塞瓦点)△ABC得三边BC、CA、AB上有点P、Q、R,则AP、BQ、CR共点得充要条件就是。
托勒密(Ptolemy)定理四边形得两对边乘积之与等于其对角线乘积得充要条件就是该四边形内接于一圆。
西姆松(Simson)定理(西姆松线)从一点向三角形得三边所引垂线得垂足共线得充要条件就是该点落在三角形得外接圆上。
例题:1.设AD就是△ABC得边BC上得中线,直线CF交AD于F。
求证:。
【分析】CEF截△ABD→(梅氏定理)【评注】也可以添加辅助线证明:过A、B、D之一作C F得平行线。
2.过△ABC得重心G得直线分别交AB、AC于E、F,交CB于D。
求证:。
【分析】连结并延长AG交BC于M,则M为BC得中点。
DEG截△ABM→(梅氏定理)DGF截△ACM→(梅氏定理)∴===1【评注】梅氏定理3.D、E、F分别在△ABC得BC、CA、AB边上,,AD、BE、CF交成△LMN。
求S△LMN。
【分析】【评注】梅氏定理4.以△ABC各边为底边向外作相似得等腰△BCE、△CAF、△ABG。
求证:AE、BF、CG相交于一点。
【分析】【评注】塞瓦定理5.已知△ABC中,∠B=2∠C。
求证:AC2=AB2+AB·BC。
【分析】过A作BC得平行线交△ABC得外接圆于D,连结BD。
则CD=DA=AB,AC=BD。
由托勒密定理,AC·BD=AD·BC+CD·AB。
【评注】托勒密定理6.已知正七边形A1A2A3A4A5A6A7.求证:。
(第21届全苏数学竞赛)【分析】【评注】托勒密定理7.△ABC得BC边上得高AD得延长线交外接圆于P,作PE⊥AB于E,延长ED交AC延长线于F.求证:BC·EF=BF·CE+BE·CF。
平面几何中的几个重要定理.doc

S 二 CASS.1CBS=1平面几何中的几个重要定理自欧几里得的《几何原本》问世以来,初等几何以其新奇、美妙、丰富、完美的内容 和形式引发了历代数学家们浓厚的兴趣.许多杰出的人物为了探索几何学中的奥秘而奉献了 毕生的精力,他们发现了一个又一个新的定理,推动了几何学的迅速发展.为了纪念他们, 人们以他们的名字来命名他们所获得的重要成果.这些优秀成果如同璀璨的明珠照亮了儿何 学的历程.这里我们介绍儿何学中的儿个重要定理以及它们在数学竞赛解题中的应用。
一、塞瓦定理塞瓦(G. Ceva 1647—1743),意大利著名数学家.塞瓦定理 设S 为A/WC 三边所在直线外一点,连接AS,BS,CS 分别和\ABC 的边或三边的 延长线交于P,Q,R (如图1),则 竺.丝.坐=1.PC QA RB证明 (面积法)考虑到ACS 有公共底边AS,因此它们面积之比等于分别从顶点 B 、C 向底边AS 所引垂线长的比,而这个比乂等于BP 与PC 之比,所以有P174BP _ S^ABS PC Smcs同理可得CQ _ S 〉BCS QA S^BAS AR S^CAS . RB S^CBS三式相乘,即得BP . £Q . AR S 二A 〉- . S 隽usPC QA RB S iACS S^BASA平行.点或互相与塞瓦定理同样重要的还有下面的定理.塞瓦定理逆定理 设P,Q,R 为AABC 的边或三边的延长线上的三点(P,0R 都在三边证明 因三点P 、Q 、R 中必有一点在三角形的边上,不妨假定P 点在BC 边上。
若BQ 与CR 相交,设交点为S,又设AS 和BC 的交点为P',由塞瓦定理,应有BP CQ AR_ PC # QA # RB"1与已知条件中的式子比较,得BP BP , PC"PrC但由于点P 和P'同在BC 边上,所以P 和P'重合,即三直线AP 、BQ 、CQ 交于一点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【评注】面积法
9. O为△ABC内一点,分别以da、db、dc表示O到BC、CA、AB的距离,以Ra、Rb、Rc表示O到A、B、C的距离。
求证:(1)a·Ra≥b·db+c·dc;
(2)a·Ra≥c·db+b·dc;
(3)Ra+Rb+Rc≥2(da+db+dc)。
【分析】
【评注】面积法
10.△ABC中,H、G、O分别为垂心、重心、外心。
【分析】
【评注】平移变换
13. C是直径AB=2的⊙O上一点,P在△ABC内,若PA+PB+PC的最小值是 ,求此时△ABC的面积S。
【分析】
【评注】旋转变换
费马点 :已知O是△ABC内一点,∠AOB=∠BOC=∠COA=120°;P是△ABC内任一点,求证:PA+PB+PC≥OA+OB+OC。(O为费马点)
求证:H、G、O三点共线,且HG=2GO。(欧拉线△ABC中,AB=AC,AD⊥BC于D,BM、BN三等分∠ABC,与AD相交于M、N,延长CM交AB于E。
求证:MB//NE。
【分析】
【评注】对称变换
12. G是△ABC的重心,以AG为弦作圆切BG于G,延长CG交圆于D。求证:AG2=GC·GD。
求证: 。(第21届全苏数学竞赛)
【分析】
【评注】托勒密定理
7.△ABC的BC边上的高AD的延长线交外接圆于P,作PE⊥AB于E,延长ED交AC延长线于F。
求证:BC·EF=BF·CE+BE·CF。
【分析】
【评注】西姆松定理(西姆松线)
8. 正六边形ABCDEF的对角线AC、CE分别被内分点M、N分成的比为AM:AC=CN:CE=k,且B、M、N共线。求k。(23-IMO-5)
证明:连结BD交AC于H。对△BCD用塞瓦定理,可得
因为AH是∠BAD的角平分线,由角平分线定理,
可得 ,故 。
过C作AB的平行线交AG的延长线于I,过C作AD的平行线交AE的延长线于J。
则 ,
所以 ,从而CI=CJ。
又因为CI//AB,CJ//AD,故∠ACI=π-∠BAC=π-∠DAC=∠ACJ。
DEG截△ABM→ (梅氏定理)
DGF截△ACM→ (梅氏定理)
∴ = = =1
【评注】梅氏定理
3.D、E、F分别在△ABC的BC、CA、AB边上,
,AD、BE、CF交成△LMN。
求S△LMN。
【分析】
【评注】梅氏定理
4.以△ABC各边为底边向外作相似的等腰△BCE、△CAF、△ABG。求证:AE、BF、CG相交于一点。
又∠OCN=∠MAO,∴△OCN∽△MAO,于是 ,
∴AM·CN=AO·CO
同理,AQ·CP=AO·CO。
【评注】
15.(96全国竞赛)⊙O1和⊙O2与ΔABC的三边所在直线都相切,E、F、G、H为切点,EG、FH的延长线交于P。求证:PA⊥BC。
【分析】
【评注】
16.(99全国竞赛)如图,在四边形ABCD中,对角线AC平分∠BAD。在CD上取一点E,BE与AC相交于F,延长DF交BC于G。求证:∠GAC=∠EAC。
连结AC、BD,其交点为内切圆心O。设MN与⊙O切于K,连结OE、OM、OK、ON、OF。记∠ABO=φ,∠MOK=α,∠KON=β,则
∠EOM=α,∠FON=β,∠EOF=2α+2β=180°-2φ。
∴∠BON=90°-∠NOF-∠COF=90°-β-φ=α
∴∠CNO=∠NBO+∠NOB=φ+α=∠AOE+∠MOE=∠AOM
因此,△ACI≌△ACJ,从而∠IAC=∠JAC,即∠GAC=∠EAC。
已知AB=AD,BC=DC,AC与BD交于O,过O的任意两条直线EF和GH与四边形ABCD的四边交于E、F、G、H。连结GF、EH,分别交BD于M、N。求证:OM=ON。(5届CMO)
证明:作△EOH △E’OH‘,则只需证E’、M、H‘共线,即E’H‘、BO、GF三线共点。
【分析】
【评注】塞瓦定理
5. 已知△ABC中,∠B=2∠C。求证:AC2=AB2+AB·BC。
【分析】过A作BC的平行线交△ABC的外接圆于D,连结BD。则CD=DA=AB,AC=BD。
由托勒密定理,AC·BD=AD·BC+CD·AB。
【评注】托勒密定理
6.已知正七边形A1A2A3A4A5A6A7。
平面几何四个重要定理
———————————————————————————————— 作者:
———————————————————————————————— 日期:
ﻩ
竞赛专题讲座-平面几何四个重要定理ﻫ
重庆市育才中学瞿明强ﻫ
四个重要定理:
梅涅劳斯(Menelaus)定理(梅氏线)
△ABC的三边BC、CA、AB或其延长线上有点P、Q、R,则P、Q、R共线的充要条件是四个重要定理:
14.(95全国竞赛)菱形ABCD的内切圆O与各边分别交于E、F、G、H,在弧EF和弧GH上分别作⊙O的切线交AB、BC、CD、DA分别于M、N、P、Q。
求证:MQ//NP。
【分析】由AB∥CD知:要证MQ∥NP,只需证∠AMQ=∠CPN,
结合∠A=∠C知,只需证
△AMQ∽△CPN
← ,AM·CN=AQ·CP。
例题:
1. 设AD是△ABC的边BC上的中线,直线CF交AD于F。求证: 。
【分析】CEF截△ABD→ (梅氏定理)
【评注】也可以添加辅助线证明:过A、B、D之一作CF的平行线。
2. 过△ABC的重心G的直线分别交AB、AC于E、F,交CB于D。
求证: 。
【分析】连结并延长AG交BC于M,则M为BC的中点。
。
塞瓦(Ceva)定理(塞瓦点)
△ABC的三边BC、CA、AB上有点P、Q、R,则AP、BQ、CR共点的充要条件是 。
托勒密(Ptolemy)定理
四边形的两对边乘积之和等于其对角线乘积的充要条件是该四边形内接于一圆。
西姆松(Simson)定理(西姆松线)
从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上。
【分析】将C C‘,O O’,P P‘,连结OO’、PP‘。则△B OO’、△B PP‘都是正三角形。
∴OO’=OB,PP‘=PB。显然△BO’C‘≌△BOC,△BP’C‘≌△BPC。
由于∠BO’C‘=∠BOC=120°=180°-∠BO’O,∴A、O、O‘、C’四点共线。
∴AP+PP‘+P’C‘≥AC’=AO+OO‘+O’C‘,即PA+PB+PC≥OA+OB+OC。
