平面几何四大定理
平面几何四大神奇定理
【分析】
【评注】对称变换
12. G是△ABC的重心,以AG为弦作圆切BG于G,延长CG交圆于D。求证:AG2=GC·GD。
【分析】
【评注】平移变换
13. C是直径AB=2的⊙O上一点,P在△ABC内,若PA+PB+PC的最小值是 ,求此时△ABC的面积S。
【分析】
【评注】旋转变换
【评注】也可以添加辅助线证明:过A、B、D之一作CF的平行线。
2.过△ABC的重心G的直线分别交AB、AC于E、F,交CB 于D。
求证: 。
【分析】连结并延长AG交BC于M,则M为BC的中点。
DEG截△ABM→ (梅氏定理)
DGF截△ACM→ (梅氏定理)
∴ = = =1
【评注】梅氏定理
3.D、E、F分别在△ABC的BC、CA、AB边上,
费马点:已知O是△ABC内一点,∠AOB=∠BOC=∠COA=120°;P是△ABC内任一点,求证:PA+PB+PC≥OA+OB+OC。(O为费马点)
【分析】将C C',O O',P P',连结OO'、PP'。则△B OO'、△B PP'都是正三角形。
∴OO'=OB,PP'=PB。显然△BO'C'≌△BOC,△BP'C'≌△BPC。
,AD、BE、CF交成△LMN。
求S△LMN。
【分析】
【评注】梅氏定理
4.以△ABC各边为底边向外作相似的等腰△BCE、△CAF、△ABG。求证:AE、BF、CG相交于一点。
【分析】
【评注】塞瓦定理
5. 已知△ABC中,∠B=2∠C。求证:AC2=AB2+AB·BC。
数学竞赛-平面几何四个重要定理

【分析】
【评注】
16.(99 全国竞赛)如图,在四边形 ABCD 中,对角 线 AC 平分∠BAD。在 CD 上取一点 E,BE 与 AC 相交 于 F,延长 DF 交 BC 于 G。求证:∠GAC=∠EAC。
为
AM:AC=CN:CE=k,且 B、M、N 共线。
求
k。(23-IMO-5)
【分析】
【评注】面积法
9. O 为△ABC 内一点,分别以 da、db、dc 表示 O 到 BC、CA、AB 的距离,以 Ra、Rb、 Rc 表示 O 到 A、B、C 的距离。
求证:(1)a·Ra≥b·db+c·dc;
(2) a·Ra≥c·db+b·dc;
求证:MQ//NP。
∠AMQ=∠CPN,
【分析】由 AB∥CD 知:要证 MQ∥NP,只需证
结合∠A=∠C 知,只需证
△AMQ∽△CPN
←
,AM·CN=AQ·CP。
连结 AC、BD,其交点为内切圆心 O。设 MN 与⊙O 切于 K,连结 OE、OM、OK、ON、OF。 记∠ABO=φ,∠MOK=α,∠KON=β,则
费马点:
已知 O 是△ABC 内一点,∠AOB=∠BOC=∠COA=120°; P 是△ABC 内任一点,求证:PA+PB+PC≥OA+OB+OC。(O 为费马点)
【分析】将 C
C‘,O
O’, P
则△B OO’、△B PP‘都是正三角形。
P‘,连结 OO’、PP‘。
∴OO’=OB,PP‘=PB。显然△BO’C‘≌△BOC,△BP’C‘≌△BPC。
平面几何基本定理

.一.平面几何1. 勾股定理(毕达哥拉斯定理)(广义勾股定理)(1)锐角对边的平方,等于其他两边之平方和,减去这两边中的一边和另一边在这边上的射影乘积的两倍. (2)钝角对边的平方等于其他两边的平方和,加上这两边中的一边与另一边在这边上的射影乘积的两倍. 2. 射影定理(欧几里得定理)3. 中线定理(巴布斯定理)设△ABC 的边BC 的中点为P ,则有)(22222BP AP AC AB +=+; 中线长:222222a c b m a -+=4. 垂线定理:2222BD BC AD AC CD AB -=-⇔⊥高线长:C b B c A abcc p b p a p p a h a sin sin sin ))()((2===---=5. 角平分线定理:三角形一个角的平分线分对边所成的两条线段与这个角的两边对应成比例.如△ABC 中,AD 平分∠BAC ,则AC AB DC BD =;(外角平分线定理)角平分线长:2cos 2)(2Ac b bc a p bcp c b t a +=-+=(其中p 为周长一半)6. 正弦定理:R CcB b A a 2sin sin sin ===,(其中R 为三角形外接圆半径) 7. 余弦定理:C ab b a ccos 2222-+=8. 张角定理:AB DAC AC BAD AD BAC ∠+∠=∠sin sin sin9. 斯特瓦尔特(Stewart )定理:设已知△ABC 及其底边上B 、C两点间的一点D ,则有AB 2·DC +AC 2·BD -AD 2·BC =BC ·DC ·BD 10. 圆周角定理:同弧所对的圆周角相等,等于圆心角的一半.(圆外角如何转化?)11. 弦切角定理:弦切角等于夹弧所对的圆周角12. 圆幂定理:(相交弦定理:垂径定理:切割线定理(割线定理):切线长定理:)13. 布拉美古塔(Brahmagupta )定理: 在圆内接四边形ABCD中,AC ⊥BD ,自对角线的交点P 向一边作垂线,其延长线必平分对边14. 点到圆的幂:设P 为⊙O 所在平面上任意一点,PO =d ,⊙O 的半径为r ,则d 2-r 2就是点P 对于⊙O 的幂.过P 任作一直线与⊙O 交于点A 、B ,则PA ·PB = |d 2-r 2|.“到两圆等幂的点的轨迹是与此二圆的连心线垂直的一条直线,如果此二圆相交,则该轨迹是此二圆的公共弦所在直线”这个结论.这条直线称为两圆的“根轴”.三个圆两两的根轴如果不互相平行,则它们交于一点,这一点称为三圆的“根心”.三个圆的根心对于三个圆等幂.当三个圆两两相交时,三条公共弦(就是两两的根轴)所在直线交于一点.15. 托勒密(Ptolemy )定理:圆内接四边形对角线之积等于两组对边乘积之和,即AC ·BD =AB ·CD +AD ·BC ,(逆命题成立) .(广义托勒密定理)AB ·CD +AD ·BC ≥AC ·BD16. 蝴蝶定理:AB 是⊙O 的弦,M 是其中点,弦CD 、EF 经过点M ,CF 、DE 交AB 于P 、Q ,求证:MP =QM . 17. 费马点:定理1等边三角形外接圆上一点,到该三角形较近两顶点距离之和等于到另一顶点的距离;不在等边三角形外接圆上的点,到该三角形两顶点距离之和大于到另一点的距离.定理2 三角形每一内角都小于120°时,在三角形内必存在一点,它对三条边所张的角都是120°,该点到三顶点距离和达到最小,称为“费马点”,当三角形有一内角不小于120°时,此角的顶点即为费马点18. 拿破仑三角形:在任意△ABC 的外侧,分别作等边△ABD 、△BCE 、△CAF ,则AE 、AB 、CD 三线共点,并且AE =BF =CD ,这个命题称为拿破仑定理. 以△ABC 的三条边分别向外作等边△ABD 、△BCE 、△CAF ,它们的外接圆⊙C 1 、⊙A 1 、⊙B 1的圆心构成的△——外拿破仑的三角形,⊙C 1 、⊙A 1 、⊙B 1三圆共点,外拿破仑三角形是一个等边三角形;△ABC 的三条边分别向△ABC 的内侧作等边△ABD 、△BCE 、△CAF ,它们的外接圆⊙C 2 、⊙A 2 、⊙B 2的圆心构成的△——内拿破仑三角形,⊙C 2 、⊙A 2 、⊙B 2三圆共点,内拿破仑三角形也是一个等边三角形.这两个拿破仑三角形还具有相同的中心19. 九点圆(Nine point round 或欧拉圆或费尔巴赫圆):三角形中,三边中心、从各顶点向其对边所引垂线的垂足,以及垂心与各顶点连线的中点,这九个点在同一个圆上,九点圆具有许多有趣的性质,例如:(1)三角形的九点圆的半径是三角形的外接圆半径之半 (2)九点圆的圆心在欧拉线上,且恰为垂心与外心连线的中点(3)三角形的九点圆与三角形的内切圆,三个旁切圆均相切〔费尔巴哈定理〕20. 欧拉(Euler )线:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线(欧拉线)上.21. 欧拉(Euler )公式:设三角形的外接圆半径为R ,内切圆半径为r ,外心与内心的距离为d ,则d 2=R 2-2Rr .22. 锐角三角形的外接圆半径与内切圆半径的和等于外心到各边距离的和.23. 重心:三角形的三条中线交于一点,并且各中线被这个点分成2:1的两部分;)3,3(C B A C B A y y y x x x G ++++重心性质:(1)设G 为△ABC 的重心,连结AG 并延长交BC.于D ,则D 为BC 的中点,则1:2:=GD AG ;(2)设G 为△ABC 的重心,则ABC ACG BCG ABG S S S S ∆∆∆∆===31(3)设G 为△ABC 的重心,过G 作DE ∥BC 交AB 于D ,交AC 于E ,过G 作PF ∥AC 交AB 于P ,交BC 于F ,过G 作HK ∥AB 交AC 于K ,交BC 于H ,则2;32=++===ABKHCA FP BC DE AB KH CA FP BC DE (4)设G 为△ABC 的重心,则222222333GC AB GB CA GA BC +=+=+)(31222222CA BC AB GC GB GA ++=++22222223PG GC GB GA PC PB PA +++=++(P 为△ABC 内任意一点);④到三角形三顶点距离的平方和最小的点是重心,即222GC GB GA ++最小;⑤三角形内到三边距离之积最大的点是重心;反之亦然(即满足上述条件之一,则G 为△ABC 的重心).24. 垂心:三角形的三条高线的交点;)cos cos cos cos cos cos ,cos cos cos cos cos cos (Cc B b A a y C cy B b y A a C c B b A a x C c x B b x A a H C B A C B A ++++++++垂心性质:(1)三角形任一顶点到垂心的距离,等于外心到对边的距离的2倍(2)垂心H 关于△ABC 的三边的对称点,均在△ABC 的外接圆上;(3)△ABC 的垂心为H ,则△ABC ,△ABH ,△BCH ,△ACH 的外接圆是等圆;(4)设O ,H 分别为△ABC 的外心和垂心,HCA BCO ABH CBO HAC BAO ∠=∠∠=∠∠=∠,,25. 内心:三角形的三条角分线的交点—内接圆圆心,即内心到三角形各边距离相等),(cb a cy by ayc b a cx bx ax I CB AC B A ++++++++内心性质:(1)设I 为△ABC 的内心,则I 到△ABC 三边的距离相等,反之亦然 (2)设I为△ABC的内心,则C AIB B AIC A BIC ∠+︒=∠∠+︒=∠∠+︒=∠2190,2190,2190(3)三角形一内角平分线与其外接圆的交点到另两顶点的距离与到内心的距离相等;反之,若A ∠平分线交△ABC 外接圆于点K ,I 为线段AK 上的点且满足KI=KB ,则I 为△ABC 的内心(4)设I 为△ABC 的内心,,,,c AB b AC a BC === A ∠平分线交BC于D ,交△ABC 外接圆于点K ,则acb KD IK KI AK ID AI +=== (5)设I 为△ABC 的内心,,,,c AB b AC a BC ===I在AB AC BC ,,上的射影分别为F E D ,,,内切圆半径为r ,令)(21c b a p ++=①pr S ABC =∆;②c p CD CE b p BF BD a p AF AE -==-==-==;;;③CI BI AI p abcr ⋅⋅⋅=.26. 外心:三角形的三条中垂线的交点——外接圆圆心,即外心到三角形各顶点距离相等;2sin 2sin 2sin 2sin ,2sin 2sin 2sin 2sin 2sin 2sin (B A By AyC B A Cx Bx Ax O BA CB A +++++++外心性质:(1)外心到三角形各顶点距离相等(2)设O 为△ABC 的外心,则A BOC ∠=∠2或A BOC ∠-︒=∠2360(3)∆=S abc R 4;(4)锐角三角形的外心到三边的距离之和等于其内切圆与外接圆半径之和27. 旁心:一内角平分线与两外角平分线交点——旁切圆圆心;设△ABC 的三边,,,c AB b AC a BC ===令)(21c b a p ++=,分别与AB AC BC ,,外侧相切的旁切圆圆心记为C B A I I I ,,,其半径分别记为C B A r r r ,,旁心性质:(1),21,2190A C BI C BI A C BI C B A ∠=∠=∠∠-︒=∠(对于顶角B ,C 也有类似的式子) (2))(21C A I I I C B A ∠+∠=∠ (3)设A AI 的连线交△ABC 的外接圆于D ,则DC DB DI A ==(对于C B CI BI ,有同样的结论)(4)△ABC 是△I A I B I C 的垂足三角形,且△I A I B I C 的外接圆半径'R 等于△ABC 的直径为2R .28. 三角形面积公式C B A R Rabc C ab ah S a ABC sin sin sin 24sin 21212====∆)cot cot (cot 4222C B A c b a ++++=))()((c p b p a p p pr ---==,其中a h 表示BC 边上的.高,R 为外接圆半径,r 为内切圆半径,)(21c b a p ++=29. 三角形中内切圆,旁切圆和外接圆半径的相互关系;2sin 2cos 2cos 4,2cos 2sin 2cos 4,2cos 2cos 2sin 4;2sin 2sin 2sin 4CB A R rC B A R r C B A R r C B A R r c b a ====.1111;2tan2tan ,2tan 2tan ,2tan 2tan rr r r B A r r C A r r C B r r c b a c b a =++===30. 梅涅劳斯(Menelaus )定理:设△ABC 的三边BC 、CA 、AB或其延长线和一条不经过它们任一顶点的直线的交点分别为P 、Q 、R 则有1=⋅⋅RBARQA CQ PC BP .(逆定理也成立) 31. 梅涅劳斯定理的应用定理1:设△ABC 的∠A 的外角平分线交边CA 于Q ,∠C 的平分线交边AB 于R ,∠B 的平分线交边CA 于Q ,则P 、Q 、R 三点共线32. 梅涅劳斯定理的应用定理2:过任意△ABC 的三个顶点A 、B 、C 作它的外接圆的切线,分别和BC 、CA 、AB 的延长线交于点P 、Q 、R ,则P 、Q 、R 三点共线33. 塞瓦(Ceva )定理:设X 、Y 、Z 分别为△ABC 的边BC 、CA 、AB 上的一点,则AX 、BY 、CZ 所在直线交于一点的充要条件是AZ ZB ·BX XC ·CYYA=1 34. 塞瓦定理的应用定理:设平行于△ABC 的边BC 的直线与两边AB 、AC 的交点分别是D 、E ,又设BE 和CD 交于S ,则AS 一定过边BC 的中点M35. 塞瓦定理的逆定理:(略)36. 塞瓦定理的逆定理的应用定理1:三角形的三条中线交于一点,三角形的三条高线交于一点,三角形的三条角分线交于一点37. 塞瓦定理的逆定理的应用定理2:设△ABC 的内切圆和边BC 、CA 、AB 分别相切于点R 、S 、T ,则AR 、BS 、CT 交于一点.38. 西摩松(Simson )定理:从△ABC 的外接圆上任意一点P向三边BC 、CA 、AB 或其延长线作垂线,设其垂足分别是D 、E 、R ,则D 、E 、R 共线,(这条直线叫西摩松线Simson line )39. 西摩松定理的逆定理:(略)40. 关于西摩松线的定理1:△ABC 的外接圆的两个端点P 、Q关于该三角形的西摩松线互相垂直,其交点在九点圆上 41. 关于西摩松线的定理2(安宁定理):在一个圆周上有4点,以其中任三点作三角形,再作其余一点的关于该三角形的西摩松线,这些西摩松线交于一点42. 史坦纳定理:设△ABC 的垂心为H ,其外接圆的任意点P ,这时关于△ABC 的点P 的西摩松线通过线段PH 的中心. 43. 史坦纳定理的应用定理:△ABC 的外接圆上的一点P 的关于边BC 、CA 、AB 的对称点和△ABC 的垂心H 同在一条(与西摩松线平行的)直线上.这条直线被叫做点P 关于△ABC 的镜象线.44. 牛顿定理1:四边形两条对边的延长线的交点所连线段的中点和两条对角线的中点,三点共线.这条直线叫做这个四边形的牛顿线.45. 牛顿定理2:圆外切四边形的两条对角线的中点,及该圆的圆心,三点共线. 46. 笛沙格定理1:平面上有两个三角形△ABC 、△DEF ,设它们的对应顶点(A 和D 、B 和E 、C 和F )的连线交于一点,这时如果对应边或其延长线相交,则这三个交点共线. 47. 笛沙格定理2:相异平面上有两个三角形△ABC 、△DEF ,设它们的对应顶点(A 和D 、B 和E 、C 和F )的连线交于一点,这时如果对应边或其延长线相交,则这三个交点共线. 48. 波朗杰、腾下定理:设△ABC 的外接圆上的三点为P 、Q 、R ,则P 、Q 、R 关于△ABC 交于一点的充要条件是:弧AP +弧BQ +弧CR =0(mod2π) .49. 波朗杰、腾下定理推论1:设P 、Q 、R 为△ABC 的外接圆上的三点,若P 、Q 、R 关于△ABC 的西摩松线交于一点,则A 、B 、C 三点关于△PQR 的的西摩松线交于与前相同的一点.50. 波朗杰、腾下定理推论2:在推论1中,三条西摩松线的交点是A 、B 、C 、P 、Q 、R 六点任取三点所作的三角形的垂心和其余三点所作的三角形的垂心的连线段的中点. 51. 波朗杰、腾下定理推论3:考查△ABC 的外接圆上的一点P的关于△ABC 的西摩松线,如设QR 为垂直于这条西摩松线该外接圆的弦,则三点P 、Q 、R 的关于△ABC 的西摩松线交于一点.52. 波朗杰、腾下定理推论4:从△ABC 的顶点向边BC 、CA 、AB 引垂线,设垂足分别是D 、E 、F ,且设边BC 、CA 、AB的中点分别是L 、M 、N ,则D 、E 、F 、L 、M 、N 六点在同一个圆上,这时L 、M 、N 点关于关于△ABC 的西摩松线交于一点53. 卡诺定理:通过△ABC 的外接圆的一点P ,引与△ABC 的三边BC 、CA 、AB 分别成同向的等角的直线PD 、PE 、PF ,与三边的交点分别是D 、E 、F ,则D 、E 、F 三点共线. 54. 奥倍尔定理:通过△ABC 的三个顶点引互相平行的三条直线,设它们与△ABC 的外接圆的交点分别是L 、M 、N ,在△ABC 的外接圆上取一点P ,则PL 、PM 、PN 与△ABC 的三边BC 、CA 、AB 或其延长线的交点分别是D 、E 、F ,则D 、E 、F 三点共线.55. 清宫定理:设P 、Q 为△ABC 的外接圆的异于A 、B 、C 的两点,P 点的关于三边BC 、CA 、AB 的对称点分别是U 、V 、W ,这时,QU 、QV 、QW 和边BC 、CA 、AB 或其延长线的交点分别是D 、E 、F ,则D 、E 、F 三点共线.56. 他拿定理:设P 、Q 为关于△ABC 的外接圆的一对反点,点P 的关于三边BC 、CA 、AB 的对称点分别是U 、V 、W ,这时,.如果QU 、QV 、QW 和边BC 、CA 、AB 或其延长线的交点分别是D 、E 、F ,则D 、E 、F 三点共线.(反点:P 、Q 分别为圆O 的半径OC 和其延长线的两点,如果OC 2=OQ ×OP 则称P 、Q 两点关于圆O 互为反点)57. 朗古来定理:在同一圆周上有A 1、B 1、C 1、D 1四点,以其中任三点作三角形,在圆周取一点P ,作P 点的关于这4个三角形的西摩松线,再从P 向这4条西摩松线引垂线,则四个垂足在同一条直线上.58. 从三角形各边的中点,向这条边所对的顶点处的外接圆的切线引垂线,这些垂线交于该三角形的九点圆的圆心 59. 一个圆周上有n 个点,从其中任意n -1个点的重心,向该圆周的在其余一点处的切线所引的垂线都交于一点 60. 康托尔定理1:一个圆周上有n 个点,从其中任意n -2个点的重心向余下两点的连线所引的垂线共点.61. 康托尔定理2:一个圆周上有A 、B 、C 、D 四点及M 、N 两点,则M 和N 点关于四个三角形△BCD 、△CDA 、△DAB 、△ABC 中的每一个的两条西摩松线的交点在同一直线上.这条直线叫做M 、N 两点关于四边形ABCD 的康托尔线. 62. 康托尔定理3:一个圆周上有A 、B 、C 、D 四点及M 、N 、L三点,则M 、N 两点的关于四边形ABCD 的康托尔线、L 、N 两点的关于四边形ABCD 的康托尔线、M 、L 两点的关于四边形ABCD 的康托尔线交于一点.这个点叫做M 、N 、L 三点关于四边形ABCD 的康托尔点.63. 康托尔定理4:一个圆周上有A 、B 、C 、D 、E 五点及M 、N 、L 三点,则M 、N 、L 三点关于四边形BCDE 、CDEA 、DEAB 、EABC 中的每一个康托尔点在一条直线上.这条直线叫做M 、N 、L 三点关于五边形A 、B 、C 、D 、E 的康托尔线.64. 费尔巴赫定理:三角形的九点圆与内切圆和旁切圆相切. 65. 莫利定理:将三角形的三个内角三等分,靠近某边的两条三分角线相得到一个交点,则这样的三个交点可以构成一个正三角形.这个三角形常被称作莫利正三角形.66. 布利安松定理:连结外切于圆的六边形ABCDEF 相对的顶点A 和D 、B 和E 、C 和F ,则这三线共点.67. 帕斯卡(Paskal )定理:圆内接六边形ABCDEF 相对的边AB和DE 、BC 和EF 、CD 和FA 的(或延长线的)交点共线. 68. 阿波罗尼斯(Apollonius )定理:到两定点A 、B 的距离之比为定比m :n (值不为1)的点P ,位于将线段AB 分成m :n 的内分点C 和外分点D 为直径两端点的定圆周上.这个圆称为阿波罗尼斯圆.69. 库立奇*大上定理:(圆内接四边形的九点圆)圆周上有四点,过其中任三点作三角形,这四个三角形的九点圆圆心都在同一圆周上,我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆.70. 密格尔(Miquel )点: 若AE 、AF 、ED 、FB 四条直线相交于A 、B 、C 、D 、E 、F 六点,构成四个三角形,它们是△ABF 、△AED 、△BCE 、△DCF ,则这四个三角形的外接圆共点,这个点称为密格尔点.71. 葛尔刚(Gergonne )点:△ABC 的内切圆分别切边AB 、BC 、CA 于点D 、E 、F ,则AE 、BF 、CD 三线共点,这个点称为葛尔刚点.72. 欧拉关于垂足三角形的面积公式:O 是三角形的外心,M 是三角形中的任意一点,过M 向三边作垂线,三个垂足形成的三角形的面积,其公式: 222ABC D 4||R d R S S EF -=∆∆.二.集合1.元素与集合的关系U x A x C A ∈⇔∉,U x C A x A ∈⇔∉.2.德摩根公式();()U U U U U U C A B C A C B C A B C A C B==3.包含关系A B A A B B=⇔=U U A B C B C A ⇔⊆⇔⊆U A C B ⇔=ΦU C A B R ⇔=4.集合12{,,,}n a a a 的子集个数共有2n 个;真子集有2n–1个;非空子集有2n–1个;非空的真子集有2n–2个. 5.集合A 中有M 个元素,集合B 中有N 个元素,则可以构造M*N 个从集合A 到集合B 的映射;6.容斥原理()()card A B cardA cardB card A B =+-()()card A B C cardA cardB cardC card A B =++-()()()()card A B card B C card CA card ABC ---+.三.二次函数,二次方程1·二次函数的解析式的三种形式(1)一般式2()(0)f x ax bx c a =++≠;(2)顶点式2()()(0)f x a x h k a =-+≠;(3)零点式12()()()(0)f x a x x x x a =--≠. 2·解连不等式()N f x M <<常有以下转化形式()N f x M <<⇔[()][()]0f x M f x N --<⇔|()|22M N M Nf x +--<⇔()0()f x N M f x ->- ⇔11()f x N M N>--. 3·方程0)(=x f 在),(21k k 上有且只有一个实根,与0)()(21<k f k f 不等价,前者是后者的一个必要而不是充分条.件.特别地, 方程)0(02≠=++a c bx ax有且只有一个实根在),(21k k ,等价于0)()(21<k f k f ,或0)(1=k f 且22211k k a bk +<-<,或0)(2=k f 且22122k abk k <-<+. 4·闭区间上的二次函数的最值二次函数)0()(2≠++=a c bx ax x f 在闭区间[]q p ,上的最值只能在abx 2-=处及区间的两端点处取得,具体如下:(1)当a>0时,若[]q p abx ,2∈-=,则{}min max max ()(),()(),()2bf x f f x f p f q a =-=;[]q p abx ,2∉-=,{}max max ()(),()f x f p f q =,{}min min ()(),()f x f p f q =.(2)当a<0时,若[]q p abx ,2∈-=,则{}min ()min (),()f x f p f q =,若[]q p abx ,2∉-=,则{}max ()max (),()f x f p f q =,{}min ()min (),()f x f p f q =.5·一元二次方程的实根分布依据:若()()0f m f n <,则方程0)(=x f 在区间(,)m n 内至少有一个实根 .设q px x x f ++=2)(,则(1)方程0)(=x f 在区间),(+∞m 内有根的充要条件为0)(=m f 或2402p q pm ⎧-≥⎪⎨->⎪⎩; (2)方程0)(=x f 在区间(,)m n 内有根的充要条件为()()0f m f n <或2()0()0402f m f n p q p m n >⎧⎪>⎪⎪⎨-≥⎪⎪<-<⎪⎩或()0()0f m af n =⎧⎨>⎩或()0()0f n af m =⎧⎨>⎩; (3)方程0)(=x f 在区间(,)n -∞内有根的充要条件为()0f m <或2402p q pm ⎧-≥⎪⎨-<⎪⎩ . 6·定区间上含参数的二次不等式恒成立的条件依据 (1)在给定区间),(+∞-∞的子区间L (形如[]βα,,(]β,∞-,[)+∞,α不同)上含参数的二次不等式(,)0f x t ≥(t 为参数)恒成立的充要条件是min (,)0()f x t x L ≥∉.(2)在给定区间),(+∞-∞的子区间上含参数的二次不等式(,)0f x t ≥(t 为参数)恒成立的充要条件是(,)0()man f x t x L ≤∉.(3))(24>++=c bx ax x f 恒成立的充要条件是00a b c ≥⎧⎪≥⎨⎪>⎩或2040a b ac <⎧⎨-<⎩.四.简易逻辑1·真值表234·充要条件(1)充分条件:若p q ⇒,则p 是q 充分条件.(2)必要条件:若q p ⇒,则p 是q 必要条件.(3)充要条件:若p q ⇒,且q p ⇒,则p 是q 充要.条件.注:如果甲是乙的充分条件,则乙是甲的必要条件;反之亦然.五.函数1· 函数的单调性(1)设[]2121,,x x b a x x ≠∈⋅那么[]1212()()()0x x f x f x -->⇔[]b a x f x x x f x f ,)(0)()(2121在⇔>--上是增函数;[]1212()()()0x x f x f x --<⇔[]b a x f x x x f x f ,)(0)()(2121在⇔<--上是减函数.(2)设函数)(x f y =在某个区间内可导,如果0)(>'x f ,则)(x f 为增函数;如果0)(<'x f ,则)(x f 为减函数.2·如果函数)(x f 和)(x g 都是减函数,则在公共定义域内,和函数)()(x g x f +也是减函数; 如果函数)(u f y =和)(x g u =在其对应的定义域上都是减函数,则复合函数)]([x g f y =是增函数.3·奇偶函数的图象特征奇函数的图象关于原点对称,偶函数的图象关于y 轴对称;在对称区间上,奇函数的单调性相同,欧函数相反;,如果一个函数的图象关于原点对称,那么这个函数是奇函数;如果一个函数的图象关于y 轴对称,那么这个函数是偶函数,如果一个奇函数的定义域包括0,则必有f(0)=0;4若函数)(x f y =是偶函数,则)()(a x f a x f --=+;若函数)(a x f y +=是偶函数,则)()(a x f a x f +-=+. 5· 对于函数)(x f y =(R x ∈),)()(x b f a x f -=+恒成立,则函数)(x f 的对称轴是函数2ba x +=;两个函数)(a x f y +=与)(x b f y -= 的图象关于直线2ba x +=对称. 6·若)()(a x f x f +--=,则函数)(x f y =的图象关于点)0,2(a对称; 若)()(a x f x f +-=,则函数)(x f y =为周期为a 2的周期函数.7 多项式函数110()n n n n P x a x a xa --=+++的奇偶性 多项式函数()P x 是奇函数⇔()P x 的偶次项(即奇数项)的系数全为零.多项式函数()P x 是偶函数⇔()P x 的奇次项(即偶数项)的系数全为零. 8函数()y f x =的图象的对称性 (1)函数()y f x =的图象关于直线x a=对称()()f a x f a x ⇔+=- (2)()f a x f x ⇔-=.(2)函数()y f x =的图象关于直线2a b x +=对称()()f a mx f b mx ⇔+=- ()()f a b mx f mx ⇔+-=.9两个函数图象的对称性 (1)函数()y f x =与函数()y f x =-的图象关于直线0x =(即y 轴)对称.(2)函数()y f mx a =-与函数()y f b mx =-的图象关于直线2a bx m+=对称.(3)函数)(x f y =和)(1x f y -=的图象关于直线y=x 对称.10 若将函数)(x f y =的图象右移a 、上移b 个单位,得到函数b a x f y +-=)(的图象;若将曲线0),(=y x f 的图象右移a 、上移b 个单位,得到曲线0),(=--b y a x f 的图象.11 互为反函数的两个函数的关系a b f b a f =⇔=-)()(1.12若函数)(b kx f y +=存在反函数,则其反函数为])([11b x f ky -=-,并不是)([1b kx f y +=-,而函数)([1b kx f y +=-是])([1b x f ky -=的反函数.13 几个常见的函数方程 (1)正比例函数()f x cx =,()()(),(1)f x y f x f y f c +=+=. (2)指数函数()x f x a =,()()(),(1)0f x y f x f y f a +==≠. (3)对数函数()log a f x x =,()()(),()1(0,1)f xy f x f y f a a a =+=>≠.(4)幂函数()f x x α=,'()()(),(1)f xy f x f y f α==. (5)余弦函数()cos f x x =,正弦函数()sin g x x =,()()()()()f x y f x f y g x g y -=+,0()(0)1,lim 1x g x f x→==.14 几个函数方程的周期(约定a>0)(1))()(a x f x f +=,则)(x f 的周期T=a ; (2)0)()(=+=a x f x f ,或)0)(()(1)(≠=+x f x f a x f ,或1()()f x a f x +=-(()0)f x ≠,或[]1(),(()0,1)2f x a f x =+∈,则)(x f 的周期T=2a ;(3))0)(()(11)(≠+-=x f a x f x f ,则)(x f 的周期T=3a ;.(4))()(1)()()(212121x f x f x f x f x x f -+=+且1212()1(()()1,0||2)f a f x f x x x a =⋅≠<-<,则)(x f 的周期T=4a ;(5)()()(2)(3)(4)f x f x a f x a f x a f x a +++++++()()(2)(3)(4)f x f x a f x a f x a f x a =++++,则)(x f 的周期T=5a ;(6))()()(a x f x f a x f +-=+,则)(x f 的周期T=6a.六 指数与对数1·分数指数幂(1)m na=(0,,am n N *>∈,且1n >).(2)1mnm naa-=(0,,a m n N *>∈,且1n >).2·根式的性质(1)n a =.(2)当na =;当n 为,0||,0a a a a a ≥⎧==⎨-<⎩. 3·有理指数幂的运算性质(1) (0,,)r s r s a a a a r s Q +⋅=>∈.(2)()(0,,)r s rs a a a r s Q =>∈.(3)()(0,0,)rr r ab a b a b r Q =>>∈.注: 若a >0,p 是一个无理数,则a p表示一个确定的实数.上述有理指数幂的运算性质,对于无理数指数幂都适用. 4·指数式与对数式的互化式log b a N b a N =⇔=(0,1,0)a a N >≠>.5·对数的换底公式log log log m a m N N a=(0a >,且1a ≠,0m >,且1m ≠,0N >).推论log log m n a a nb b m=(0a >,且1a >,,0m n >,且1m ≠,1n ≠,0N >).6·对数的四则运算法则若a >0,a ≠1,M >0,N >0,则(1)log ()log log a a a MN M N=+;(2)log log log aa a MM N N=-; (3)log log ()na a M n M n R =∈. 7·设函数)0)((log )(2≠++=a c bx ax x f m ,记ac b 42-=∆.若)(x f 的定义域为R ,则0>a ,且0<∆;若)(x f 的值域为R ,则0>a ,且0≥∆.对于0=a 的情形,需要单独检验.8·对数换底不等式及其推广若0a>,0b >,0x >,1x a ≠,则函数log ()ax y bx = (1)当a b >时,在1(0,)a 和1(,)a+∞上log ()ax y bx =为增函数.,(2)当a b <时,在1(0,)a 和1(,)a +∞上log ()ax y bx =为减函数.推论:设1n m >>,0p >,0a >,且1a ≠,则(1)log ()log m p m n p n++<.(2)2log log log 2a a a m nm n +<. 9·平均增长率的问题如果原来产值的基础数为N ,平均增长率为p ,则对于时间x 的总产值y ,有(1)x y N p =+.39.数列的同项公式与前n 项的和的关系11,1,2n n n s n a s s n -=⎧=⎨-≥⎩( 数列{}n a 的前n 项的和为12n n s a a a =+++).七 数列1·等差数列的通项公式*11(1)()n a a n d dn a d n N =+-=+-∈;其前n项和公式为1()2n n n a a s +=1(1)2n n na d -=+211()22d n a d n =+-. 2·等比数列的通项公式1*11()n nna a a q q n N q-==⋅∈; 其前n 项的和公式为11(1),11,1n n a q q s q na q ⎧-≠⎪=-⎨⎪=⎩或11,11,1n n a a qq q s na q -⎧≠⎪-=⎨⎪=⎩.3·等比差数列{}n a :11,(0)n n a qa d a b q +=+=≠的通项公式为1(1),1(),11n n n b n d q a bq d b q d q q -+-=⎧⎪=+--⎨≠⎪-⎩;其前n 项和公式为(1),(1)1(),(1)111n n nb n n d q s d q db n q q q q +-=⎧⎪=-⎨-+≠⎪---⎩..八 三角函数1·常见三角不等式(1)若(0,)2x π∈,则sin tan x x x <<. (2) 若(0,)2x π∈,则1sin cos x x <+≤(3) |sin ||cos |1x x +≥.2·同角三角函数的基本关系式22sin cos 1θθ+=,tan θ=θθcos sin ,tan 1cot θθ⋅=.3·正弦、余弦的诱导公式212(1)sin ,sin()2(1)s ,nn n co απαα-⎧-⎪+=⎨⎪-⎩212(1)s ,s()2(1)sin ,nn co n co απαα+⎧-⎪+=⎨⎪-⎩;tan tan tan()1tan tan αβαβαβ±±=.22sin()sin()sin sin αβαβαβ+-=-(平方正弦公式);22cos()cos()cos sin αβαβαβ+-=-.sin cos a b αα+=)αϕ+(辅助角ϕ所在象限由点(,)a b 的象限决定,tan baϕ= ).5·半角正余切公式:sin sin tan ,cot 21cos 1cos αααααα==+- 6·二倍角公式sin 2sin cos ααα=.2222cos 2cos sin 2cos 112sin ααααα=-=-=-.22tan tan 21tan ααα=-. 7·最简单的三角不等式及其解集sin (||1)(2arcsin ,2arcsin ),x a a x k a k a k Z πππ>≤⇔∈++-∈sin (||1)(2arcsin ,2arcsin ),x a a x k a k a k Z πππ<≤⇔∈--+∈cos (||1)(2arccos ,2arccos ),x a a x k a k a k Zππ>≤⇔∈-+∈cos (||1)(2arccos ,22arccos ),x a a x k a k a k Zπππ<≤⇔∈++-∈tan ()(arctan ,),2x a a R x k a k k Zπππ>∈⇒∈++∈tan ()(,arctan ),2x a a R x k k a k Z πππ<∈⇒∈-+∈角的变形:2()()2()()()ααβαββαβαβααββ=-++=+--=+-8·三倍角公式3sin 33sin 4sin 4sin sin()sin()33ππθθθθθθ=-=-+3cos34cos 3cos 4cos cos()cos()33ππθθθθθθ=-=-+323tan tan tan 3tan tan()tan()13tan 33θθππθθθθθ-==-+-9·三角函数的周期公式函数sin()y x ωϕ=+,x ∈R 及函数cos()y x ωϕ=+,x ∈R(A,ω,ϕ为常数,且A ≠0,ω>0)的周期2T πω=;函数tan()y x ωϕ=+,,2x k k Z ππ≠+∈(A,ω,ϕ为常数,且A ≠0,ω>0)的周期T πω=.10·正弦定理 2sin sin sin a b cR A B C===.11余弦定理2222cos a b c bc A =+-;2222cos b c a ca B =+-;2222cos c a b ab C =+-.12·面积定理(1)111222a b c Sah bh ch ===(a b c h h h 、、分别表示a 、b 、c 边上的高).(2)111sin sin sin 222Sab C bc A ca B ===. (3)OABS ∆=.13·在三角形中有下列恒等式:①sin()sin A B C +=② tan tan tan tan .tan .tan A B C A B C ++=.14·简单的三角方程的通解sin (1)arcsin (,||1)kx a x k a k Z a π=⇔=+-∈≤. s 2arccos (,||1)co x a x k a k Z a π=⇔=±∈≤.tan arctan (,)x a x k a k Z a R π=⇒=+∈∈.特别地,有sin sin (1)()k k k Z αβαπβ=⇔=+-∈. s cos 2()co k k Z αβαπβ=⇔=±∈.tan tan ()k k Z αβαπβ=⇒=+∈.15·三角形内角和定理在△ABC 中,有()A B CC A B ππ++=⇔=-+222C A Bπ+⇔=-222()C A B π⇔=-+八 向量1·实数与向量的积的运算律设λ、μ为实数,那么 (1) 结合律:λ(μa )=(λμ)a ;(2)第一分配律:(λ+μ)a =λa +μa;(3)第二分配律:λ(a +b )=λa +λb .2·向量的数量积的运算律:(1) a ·b= b ·a (交换律);(2)(λa )·b=λ(a ·b )=λa ·b =a ·(λb );(3)(a +b )·c= a ·c +b ·c.3·平面向量基本定理如果e 1、e 2是同一平面内的两个不共线向量,那么对于这一平面内的任一向量,有且只有一对实数λ1、λ2,使得a=λ1e 1+λ2e 2. 不共线的向量e 1、e 2叫做表示这一平面内所有向量的一组基底. 4·向量平行的坐标表示 设a =11(,)x y ,b =22(,)x y ,且b≠0,则a b(b ≠0)12210x y x y ⇔-=.5·a 与b 的数量积(或内积)a ·b =|a ||b |cos θ.6·a ·b 的几何意义数量积a ·b 等于a 的长度|a |与b 在a 的方向上的投影|b |cos θ的乘积.7·平面向量的坐标运算(1)设a =11(,)x y ,b =22(,)x y ,则a+b=1212(,)x x y y ++. (2)设a =11(,)x y ,b =22(,)x y ,则a-b=1212(,)x x y y --. (3)设A11(,)x y ,B22(,)x y ,则2121(,)AB OB OA x x y y =-=--.(4)设a =(,),x y R λ∈,则λa=(,)x y λλ.(5)设a =11(,)x y ,b =22(,)x y ,则a ·b=1212()x x y y +.8·两向量的夹角公式cos θ=(a =11(,)x y ,b =22(,)x y ).9·平面两点间的距离公式,A Bd =||AB AB AB =⋅=11(,)x y ,B 22(,)x y ).10·向量的平行与垂直设a =11(,)x y ,b =22(,)x y ,且b ≠0,则A ||b ⇔b =λa12210x y x y ⇔-=.a ⊥b(a ≠0)⇔a ·b=012120x x y y ⇔+=.11·线段的定比分公式设111(,)P x y ,222(,)P x y ,(,)P x y 是线段12PP 的分点,λ是实数,且12PP PP λ=,则121211x x x y y y λλλλ+⎧=⎪⎪+⎨+⎪=⎪+⎩⇔121OP OP OP λλ+=+ ⇔12(1)OP tOP t OP =+-(11t λ=+). 12·三角形的重心坐标公式△ABC 三个顶点的坐标分别为11A(x ,y )、22B(x ,y )、33C(x ,y ),则△ABC 的重心的坐标是123123(,)33x x x y y y G ++++.13·点的平移公式''''x x h x x h y y k y y k⎧⎧=+=-⎪⎪⇔⎨⎨=+=-⎪⎪⎩⎩''OP OP PP ⇔=+ . 注:图形F 上的任意一点P(x ,y)在平移后图形'F 上的对应点为'''(,)Px y ,且'PP 的坐标为(,)h k .14·“按向量平移”的几个结论(1)点(,)P x y 按向量a =(,)h k 平移后得到点'(,)P x h y k ++.(2) 函数()y f x =的图象C 按向量a =(,)h k 平移后得到图象'C ,则'C 的函数解析式为()y f x h k =-+.(3) 图象'C 按向量a =(,)h k 平移后得到图象C ,若C 的解析式()y f x =,则'C 的函数解析式为()y f x h k =+-. (4)曲线C :(,)0f x y =按向量a =(,)h k 平移后得到图象'C ,则'C 的方程为(,)0f x h y k --=.(5) 向量m =(,)x y 按向量a =(,)h k 平移后得到的向量仍然为m =(,)x y .15·三角形五“心”向量形式的充要条件设O 为ABC ∆所在平面上一点,角,,A B C 所对边长分别为,,a b c ,则(1)O 为ABC ∆的外心222OA OB OC ⇔==.(2)O 为ABC ∆的重心0OA OB OC ⇔++=. (3)O 为ABC ∆的垂心.OA OB OB OC OC OA ⇔⋅=⋅=⋅.(4)O 为ABC ∆的内心0aOA bOB cOC ⇔++=. (5)O 为ABC ∆的A ∠的旁心aOAbOB cOC ⇔=+.九 不等式1·常用不等式:(1),a b R ∈⇒222a b ab +≥(当且仅当a =b 时取“=”号).(2),a b R +∈⇒2a b+≥(当且仅当a =b 时取“=”号).(3)3333(0,0,0).ab c abc a b c ++≥>>>(4)柯西不等式22222()()(),,,,.a b c d ac bd a b c d R ++≥+∈(5)b a b a b a +≤+≤-.2·极值定理已知y x ,都是正数,则有(1)若积xy 是定值p ,则当y x =时和y x +有最小值p 2;(2)若和y x +是定值s ,则当y x =时积xy 有最大值241s . 推广 已知R y x ∈,,则有xy y x y x 2)()(22+-=+(1)若积xy 是定值,则当||y x -最大时,||y x +最大; 当||y x -最小时,||y x +最小.(2)若和||y x +是定值,则当||y x -最大时, ||xy 最小;当||y x -最小时, ||xy 最大.3·一元二次不等式20(0)ax bx c ++><或2(0,40)a b ac ≠∆=->,如果a 与2axbx c ++同号,则其解集在两根之外;如果a 与2ax bx c ++异号,则其解集在两根之间.简言之:同号两根之外,异号两根之间.121212()()0()x x x x x x x x x <<⇔--<<; 121212,()()0()x x x x x x x x x x <>⇔--><或.4·含有绝对值的不等式当a> 0时,有22x a x a a x a <⇔<⇔-<<.22x a x a x a >⇔>⇔>或x a <-.75.无理不等式(1()0()0()()f x g x f x g x ≥⎧⎪>⇔≥⎨⎪>⎩. (2)2()0()0()()0()0()[()]f x f x g x g x g x f x g x ≥⎧≥⎧⎪>⇔≥⎨⎨<⎩⎪>⎩或. (32()0()()0()[()]f x g x g x f x g x ≥⎧⎪<⇔>⎨⎪<⎩.5·指数不等式与对数不等式(1)当1a >时,()()()()f x g x a a f x g x >⇔>;()0log ()log ()()0()()a a f x f x g x g x f x g x >⎧⎪>⇔>⎨⎪>⎩.(2)当01a <<时,()()()()f x g x a a f x g x >⇔<;()0log ()log ()()0()()a a f x f x g x g x f x g x >⎧⎪>⇔>⎨⎪<⎩十 直线方程1·斜率公式①2121y y kx x -=-(111(,)P x y 、222(,)P x y ).② k=tan α(α为直线倾斜角)2·直线的五种方程(1)点斜式 11()y y k x x -=- (直线l 过点111(,)P x y ,且斜率为k ).(2)斜截式y kx b =+(b 为直线l 在y 轴上的截距). (3)两点式 112121y y x x y y x x --=--(12y y ≠)(111(,)P x y 、222(,)P x y (12x x ≠)).(4)截距式 1x ya b+=(a b 、分别为直线的横、纵截距,0a b ≠、)(5)一般式 0Ax By C ++=(其中A 、B 不同时为0).5·两条直线的平行和垂直(1)若111:l y k x b =+,222:l y k x b =+ ①121212||,l l k k b b ⇔=≠;②12121l l k k ⊥⇔=-.(2)若1111:0l A x B y C ++=,2222:0l A x B y C ++=,且A 1、A 2、B 1、B 2都不为零,①11112222||A B C l l A B C ⇔=≠;②两直线垂直的充要条件是12120A A B B +=;即:12l l ⊥⇔12120A A B B +=.6·夹角公式(1)2121tan ||1k k k k α-=+.(111:l y k x b =+,222:l y k x b =+,121k k ≠-)(2)12211212tan ||A B A B A A B B α-=+. (1111:0l A x B y C ++=,2222:0l A x B y C ++=,12120A A B B +≠).直线12l l ⊥时,直线l 1与l 2的夹角是2π. 7·1l 到2l 的角公式(1)2121tan 1k k k k α-=+.(111:l y k x b =+,222:l y k x b =+,121k k ≠-)(2)12211212tan A B A B A A B B α-=+.(1111:0l A x B y C ++=,2222:0l A x B y C ++=,12120A A B B +≠).直线12l l ⊥时,直线l 1到l 2的角是2π.8·四种常用直线系方程(1)定点直线系方程:经过定点000(,)P x y 的直线系方程为00()y y k x x -=-(除直线0x x =),其中k 是待定的系数; 经过定点000(,)P x y 的直线系方程为00()()0A x x B y y -+-=,其中,A B 是待定的系数.(2)共点直线系方程:经过两直线1111:0l A x B y C ++=,2222:0l A x B y C ++=的交点的直线系方程为111222()()0A x B y C A x B y C λ+++++=(除2l ),其中λ是待定的系数.(3)平行直线系方程:直线y kx b =+中当斜率k 一定而b 变动时,表示平行直线系方程.与直线0Ax By C ++=平行的直线系方程是0Ax By λ++=(0λ≠),λ是参变量.(4)垂直直线系方程:与直线0Ax By C ++= (A ≠0,B ≠0)垂直的直线系方程是0Bx Ay λ-+=,λ是参变量.9·点到直线的距离d =(点00(,)P x y ,直线l:0Ax By C ++=).10·0Ax By C ++>或0<所表示的平面区域设直线:0l Ax By C ++=,若A>0,则在坐标平面内从左至右的区域依次表示Ax By C ++<,0Ax By C ++>,若A<0,则在坐标平面内从左至右的区域依次表示 0Ax By C ++>,0Ax By C ++<,可记为“x 为正开口对,X 为负背靠背“。
平面几何-五大定理及其证明

平面几何定理及其证明梅涅劳斯定理1 .梅涅劳斯定理及其证明 定理:一条直线与 ABC 的三边AB BC CA 所在直线分别交于点 D E 、F ,且D E 、F 均证明:如图,过点C 作AB 的平行线,交EF 于点G. 因为 CG // AB ,所以 CG CF --------------------- ( 1)AD FA因为 CG // AB ,所以 EC ( 2) DB BEC F ,即得 AD C FEC FA DB EC FA2.梅涅劳斯定理的逆定理及其证明定理:在 ABC 的边AB BC 上各有一点 D E ,在边 AC 的延长线上有一点 F ,若二、 塞瓦定理3 .塞瓦定理及其证明定理:在ABC 内一点P,该点与ABC 的三个顶点相连所在的 三条直线分别交 ABCE 边AB BC CA 于点D E 、F ,且D E 、F 三点均不是 ABC不是ABC 的顶点,则有AD BECF 1DB EC由(1)宁(2) DB可得兀AD BE CF DB EC FA1,那么,D E 、F 三点共线.证明:设直线EF 交AB 于点D ,则据梅涅劳斯定理有AD /BE CF 丽EC FA因为AD Bl CF DB EC FA1,所以有誥段AB 上,所以点D 与D 重合.即得D鴿.由于点D D 都在线 E 、F 三点共线.证明:运用面积比可得 ADDB S ADP S BDPS ADC S BDC根据等比定理有S ADP S ADCSADC S ADP S APCSSBDPBDCSBDCSBDPS的顶点,则有AD BE CF “1 DB EC FA .所以AD S A PC .同理可得BE SDB S BPCAPB, CFEC S APC FA SBPCS APB三式相乘得竺吏 DB EC CF i FA 4.塞瓦定理的逆定理及其证明 定理:在 ABC 三边AB BC CA 上各有一点 H 1,那么直线CD AE BF 三线共点. DE 、F ,且 D E 、 F 均不是 ABC 的顶点,AD BE若 DB EC证明:设直线AE 与直线BF 交于点P,直线CP 交AB 于点D ,则 据塞瓦定理有 AD Z DBBE EC CA1 -1,所以有 段AB 上,所以点D 与D 重合.即得 因为竺 DB EC CF FA AD DB D DDB •由于点D D 都在线 E 、F 三点共线.三、西姆松定理 5.西姆松定理及其证明 定理:从 ABC 外接圆上任意一点 F ,则D E 、F 三点共线. 证明:如图示,连接PC ,连接EF P 向BC CA AB 或其延长线引垂线, 垂足分别为DE、交BC 于点D ,连接P D• 因为PE 因为A 、 所以, 共圆. 所以, 即 PD BC 由于过点 F D E 、 四、 6 AE,PF AF,所以A 、F 、P 、E 四点共圆,可得B 、P 、C 四点共圆,所以 FEP = BCP 即 DEP = CDP + CEP = 180°。
平面几何四大定理

梅涅劳斯定理简介梅涅劳斯(Menelaus)定理(简称梅氏定理)是由古希腊数学家梅涅劳斯首先证明的。
它指出:如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点,那么(AF/FB)×(BD/DC)×(CE/EA)=1。
或:设X、Y、Z分别在△ABC的BC、CA、AB所在直线上,则X、Y、Z共线的充要条件是(AZ/ZB)*(BX/XC)*(CY/YA)=1证明一:过点A作AG∥BC交DF的延长线于G,则AF/FB=AG/BD , BD/DC=BD/DC , CE/EA=DC/AG。
三式相乘得:(AF/FB)×(BD/DC)×(CE/EA)=(AG/BD)×(BD/DC)×(DC/AG)=1证明二:过点C作CP∥DF交AB于P,则BD/DC=FB/PF,CE/EA=PF/AF 所以有AF/FB×BD/DC×CE/EA=AF/FB×FB/PF×PF/AF=1它的逆定理也成立:若有三点F、D、E分别在△ABC的边AB、BC、CA或其延长线上,且满足(AF/FB)×(BD/DC)×(CE/EA)=1,则F、D、E三点共线。
利用这个逆定理,可以判断三点共线。
证明三:过ABC三点向三边引垂线AA'BB'CC',所以AD:DB=AA':BB',BE:EC=BB':CC',CF:FA=CC':AA'所以(AF/FB)×(BD/DC)×(CE/EA)=1证明四:连接BF。
(AD:DB)〃(BE:EC)〃(CF:FA) =(S△ADF:S△BDF)〃(S △BEF:S△CEF)〃(S△BCF:S△BAF) =(S△ADF:S△BDF)〃(S △BDF:S△CDF)〃(S△CDF:S△ADF) =1此外,用定比分点定义该定理可使其容易理解和记忆:在△ABC的三边BC、CA、AB或其延长线上分别取L、M、N三点,又分比是λ=BL/LC、μ=CM/MA、ν=AN/NB。
平面几何基本定理总结

平面几何基本定理总结平面几何是研究二维图形、点、线和角度之间的关系和性质的数学分支。
它是数学中的基础学科,对于建立几何推理和解决实际问题具有重要意义。
在平面几何中,存在一些基本定理,它们为我们理解和运用几何知识提供了重要的依据。
本文将对平面几何的基本定理进行总结和概述。
一、点、线和角度1. 点:- 点是平面几何中最基本的概念,它没有长度、宽度和高度,只有位置。
- 点可以用大写字母表示,如A、B、C等。
2. 线:- 线是由一系列无限延伸的点组成的,它没有宽度。
- 线可以用小写字母表示,如AB、CD等。
3. 角度:- 角度是由两条射线共享一个端点而形成的图形,常用来表示两条线的夹角大小。
- 角度可以用小字母表示,如∠ABC、∠DEF等。
二、平面几何基本定理1. 直线的性质:- 直线上的任意两点可以确定一条直线。
- 一条直线上的所有点在同一条直线上。
2. 线段的性质:- 线段是由两个端点和它们之间的所有点组成的有限部分。
- 线段的长度可以通过两个端点的坐标计算得出。
3. 角度的性质:- 角度大小可以用度数或弧度来表示。
- 两条直线垂直时,它们所形成的角度为直角,即90度或π/2弧度。
- 两条直线平行时,它们所形成的角度为零度或零弧度。
4. 三角形的性质:- 三角形是由三条线段组成的图形。
- 三角形的内角和为180度或π弧度。
- 直角三角形中,直角的对边和斜边之间满足勾股定理:c² = a² +b²,其中c为斜边,a、b为直角边的长度。
5. 四边形的性质:- 四边形是由四条线段组成的图形。
- 平行四边形的对边互相平行且相等。
- 矩形是一种特殊的平行四边形,它的内角均为直角。
6. 圆的性质:- 圆是由等距离于圆心的所有点组成的图形。
- 圆心到圆上任意一点的距离称为半径。
- 圆的周长可以通过半径和圆周率π的乘积计算得出:周长= 2πr。
三、应用及实例平面几何的基本定理在各个领域都有广泛的应用,例如建筑、工程、地理测量等。
平面几何著名定理
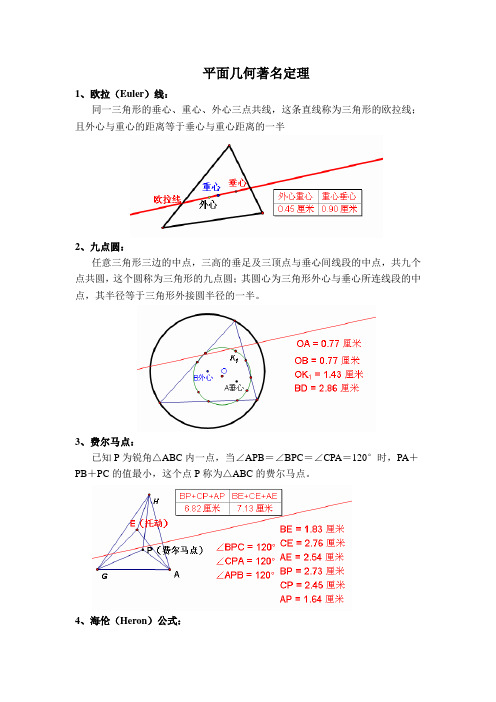
平面几何著名定理1、欧拉(Euler)线:同一三角形的垂心、重心、外心三点共线,这条直线称为三角形的欧拉线;且外心与重心的距离等于垂心与重心距离的一半2、九点圆:任意三角形三边的中点,三高的垂足及三顶点与垂心间线段的中点,共九个点共圆,这个圆称为三角形的九点圆;其圆心为三角形外心与垂心所连线段的中点,其半径等于三角形外接圆半径的一半。
3、费尔马点:已知P为锐角△ABC内一点,当∠APB=∠BPC=∠CPA=120°时,PA+PB+PC的值最小,这个点P称为△ABC的费尔马点。
4、海伦(Heron)公式:在△ABC 中,边BC 、CA 、AB 的长分别为a 、b 、c ,若p =21(a +b +c ), 则△ABC 的面积S =))()((c p b p a p p ---5、塞瓦(Ceva )定理:在△ABC 中,过△ABC 的顶点作相交于一点P 的直线,分别交边BC 、CA 、AB 与点D 、E 、F ,则1=⋅⋅FBAFEA CE DC BD ;其逆亦真6、密格尔(Miquel )点:若AE 、AF 、ED 、FB 四条直线相交于A 、B 、C 、D 、E 、F 六点,构成四个三角形,它们是△ABF 、△AED 、△BCE 、△DCF ,则这四个三角形的外接圆共点,这个点称为密格尔点。
7、葛尔刚(Gergonne )点:△ABC 的内切圆分别切边AB 、BC 、CA 于点D 、E 、F ,则AE 、BF 、CD 三线共点,这个点称为葛尔刚点。
8、西摩松(Simson )线:已知P 为△ABC 外接圆周上任意一点,PD ⊥BC ,PE ⊥ACPF ⊥AB ,D 、E 、F 为垂足,则D 、E 、F 三点共线,这条直线叫做西摩松线。
9、黄金分割:把一条线段(AB)分成两条线段,使其中较大的线段(AC)是原线段(AB)与较小线段(BC)的比例中项,这样的分割称为黄金分割11、笛沙格(Desargues)定理:已知在△ABC与△A'B'C'中,AA'、BB'、CC'三线相交于点O,BC与B'C'、CA与C'A'、AB与A'B'分别相交于点X、Y、Z,则X、Y、Z三点共线;其逆亦真。
平面几何四大定理

平面几何四个重要定理四个重要定理:梅涅劳斯(Menelaus)定理(梅氏成)△ ABC的三边BC、CA、AB或其延长线上有点P、Q、R,则P、Q、R共线的充妥条件是— = loPC QA RB室瓦(Ccva)定理(塞瓦点)A ABC 的三边BC、CA、AB 上有点P、Q、R,则AP、BQ、CR共点的充妥条件是BP CQ ARPC QA RBlo托勒密(Ptolemy)定理四边彩的两对边乘积之和等于其对角线乘积的充妾条件是该四边形内接于一圆。
西姆松(Simson)定理(西姆松线)从一点向三角形的三边所引垂线的垂足共线的充妄条件是该点落在三角形的外接网上。
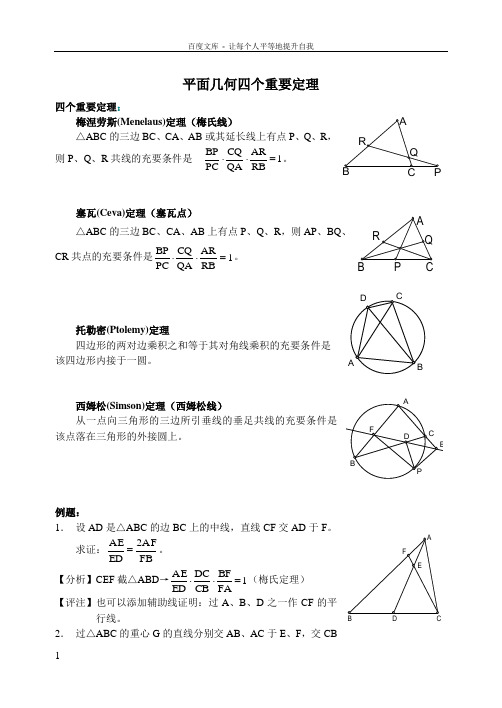
例题:1.设AD是二ABC的边BC上的中线,直线XF交AD于F。
a. AE 2AF求'正: LC = 0ED FB【分析】CEF —— = 1 (梅氏定理)ED CB FA【评注】也叮以添加辅助线证明:过A、B、D之一作CF的平行践。
2.过^ABC的重心G的直经分别交AB、AC于E、F,交CB word于Po求证: BE CF —+ —EA FA【分析】连结异延长AG交BC于M,则M为BC的中点Oc 止BE AG DEG 裁zlABM— --------------EA GMCF AGPGF^AACM^--—FA Of 黑=1 (梅氏定理)U D罪=1 (梅氏定理)DC.BE 十CF _GM (DB + DC)_GM 2MD_[ EA+ FA AGMD 2GM MD~ 【评注】梅氏定理3.D、E、F分别在A ABC的BC、CA、AB边上,RD AF CF= 人,AD、BE、CF 交成ALMNoDC FB EA求S_LM*【分析】【评注】梅氏定理4. 以AABC各边为底边向外作相似的等膝zLBCE、ACAF.AABGo求证:AE、BF、CG相交于一点。
【分析】【评注】塞瓦定理5.已知ZiABC 中,ZB=2ZCo 求证:AC2=AB2+AB - BCo【分析】过A作BC的平行线交A ABC的外接圆于D,连结BPo 则CD=DA=AB, AC=BDo由,七勒密定理,AC - BP=AD - BC+CD - ABo【评注】托勒密定理6.已知正七边形A|A2A5A4A S A6A7O求证:+—!—o (第21届全苏数学竞赛)A | A 2 A j A j A]Aq【分析】【评注】托勒密定理7. AABC的BC边上的商AD的延长线交外接阅于P,作PE1AB于E,延长ED交AC延长残于F。
关于平面几何的60条著名定理

关于平面几何的60条著名定理一些平面几何的著名定理1、勾股定理(毕达哥拉斯定理)2、射影定理(欧几里得定理)3、三角形的三条中线交于一点,并且,各中线被这个点分成2:1的两部分4、四边形两边中心的连线的两条对角线中心的连线交于一点5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。
6、三角形各边的垂直一平分线交于一点。
7、三角形的三条高线交于一点8、设三角形ABC的外心为O,垂心为H,从O向BC边引垂线,设垂足为L,则AH=2OL9、三角形的外心,垂心,重心在同一条直线(欧拉线)上。
10、(九点圆或欧拉圆或费尔巴赫圆)三角形中,三边中心、从各顶点向其对边所引垂线的垂足,以及垂心与各顶点连线的中点,这九个点在同一个圆上,11、欧拉定理:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线(欧拉线)上12、库立奇*大上定理:(圆内接四边形的九点圆)圆周上有四点,过其中任三点作三角形,这四个三角形的九点圆圆心都在同一圆周上,我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。
13、(内心)三角形的三条内角平分线交于一点,内切圆的半径公式:r=(s-a)(s-b)(s-c)s,s为三角形周长的一半14、(旁心)三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点15、中线定理:(巴布斯定理)设三角形ABC的边BC的中点为P,则有AB2+AC2=2(AP2+BP2)16、斯图尔特定理:P将三角形ABC的边BC内分成m:n,则有n×AB2+m×AC2=(m+n)AP2+mnm+nBC217、波罗摩及多定理:圆内接四边形ABCD的对角线互相垂直时,连接AB中点M和对角线交点E的直线垂直于CD 18、阿波罗尼斯定理:到两定点A、B的距离之比为定比m:n (值不为1)的点P,位于将线段AB分成m:n的内分点C和外分点D为直径两端点的定圆周上19、托勒密定理:设四边形ABCD内接于圆,则有AB×CD+AD×BC=AC×BD20、以任意三角形ABC的边BC、CA、AB为底边,分别向外作底角都是30度的等腰△BDC、△CEA、△AFB,则△DEF是正三角形,21、爱尔可斯定理1:若△ABC和△DEF都是正三角形,则由线段AD、BE、CF的中心构成的三角形也是正三角形。
平面四大公理

平面四大公理平面四大公理是欧几里得几何学的基础,它们是几何学中最基本的原理。
这四条公理被认为是自然、正确和不可证明的。
本文将详细介绍平面四大公理的内容和应用。
第一条公理:任意两点之间都可以画一条直线这条公理表明,平面上的任意两点之间都可以用一条直线相连。
这个公理看起来很简单,但它却是几何学中最基本的原理之一。
这条公理让我们可以在平面上画出各种形状和图形。
第二条公理:有限直线段可以无限延伸这条公理表明,一条有限的直线段可以延伸到任意长度。
这个公理也很容易理解,因为我们可以用一条尺子或者直尺来测量直线段的长度。
这条公理还表明了平面的无限性质,因为我们可以无限延伸直线段。
第三条公理:任意角度都可以构成这条公理表明,任意两条直线可以相交,并且相交的角度可以构成任意大小的角。
这个公理是几何学中最有争议的,因为它有时被看作是一个定理而不是一个公理。
但是,欧几里得认为这是一个基本的原理,因为我们可以通过它来定义角度的概念。
第四条公理:存在一条平行于给定直线的直线这条公理表明,如果给定一条直线和一点,那么存在一条通过这个点的直线,它与给定直线平行。
这个公理是几何学中最重要的原理之一,因为它让我们可以定义平行线的概念,从而可以进行各种几何证明。
除了这四条公理之外,欧几里得还提出了一些公理,例如角的和等于直角,以及两个直线平行的情况下,它们与第三条公理等价。
这些公理和定理在几何学中都有很重要的应用。
应用:平面四大公理在几何学中有广泛的应用,包括:1.在欧几里得几何学中,这些公理是证明各种定理的基础。
例如,我们可以用这些公理证明勾股定理。
2.这些公理也可以用于建立几何模型,例如建立建筑物、桥梁和运动场等。
3.这些公理还可以用于计算机图形学中,用于建立3D模型和计算机动画。
总结:平面四大公理是几何学中最基本的原理之一。
这些公理让我们可以在平面上进行各种形状和图形的构造和证明。
这些公理在数学、物理、计算机图形学等领域都有广泛的应用。
平面几何(4个定理)

例:已知△ABC中,∠B=2∠C。求证: AC2=AB2+AB·BC。
4.西姆松定理
从三角形ABC外接圆上一点P,作BC,AC,AB的垂 线,设垂足一次为L,M,N,则三点在一条直线上。( 逆定理也成立)
证明:若A、B、P、C四点共圆, 则∠PBN = ∠PCM。 因PL⊥ BC,PM ⊥ AC, PN ⊥ AB,有B、P、L、N 和M、P、L、C四点共圆,有 ∠PBN =∠PLN =∠PCM=∠PLM. 故L、M、N三点共线。
梅涅劳斯定理充分性证明
方法:同一法
梅涅劳斯定理
作用: 1.证明三点共线 2.导出线段比例
关键: 1.三角形 2.截线
2、塞瓦定理
设D、E、F分别是△ABC的BC,CA,AB边 上的点,则AD,BE,CF相交于一点O的充要 条件是
塞瓦定理必要性证明
法1:梅涅劳斯定理
塞瓦定理必要性证明
方法2:等高三角形 线段比=面积比
塞瓦定理充分性证明
塞瓦定理
作用: 1.证明三线共点 2.导出线段比例
关键: 1.三角形 2.共点
例:证明三角形的中线交于一点。
3、托勒密定理
证:作△ABE使∠BAE=∠CAD ∠ABE=∠ ACD,连接DE. 则△ABE∽△ACD BE/CD=AB/AC, 即BE·AC=AB·CD (1) △ABE∽△ACD得AD/AC=AE/AB, 又∠BAC=∠EAD,△ABC∽△AED. BC/ED=AC/AD,即ED·AC=BC·AD (2) (1)+(2),得AC(BE+ED)=AB·CD+AD·BC 又因为BE+ED≥BD
平面几何
三角பைடு நூலகம்五心
• 重心:中线 2:1 • 外心:垂直平分线 • 垂心:高线 • 内心:角平分线 • 旁心:两外角平分线第三内角平分线
关于平面几何的60条著名定理

关于平面几何的 60 条著名定理些平面几何的著名定理1、勾股定理(毕达哥拉斯定理)2、射影定理(欧几里得定理)3、三角形的三条中线交于一点,并且,各中线被这个点分成2:1 的两部分4、四边形两边中心的连线的两条对角线中心的连线交于5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。
6、三角形各边的垂直一平分线交于一点。
7、三角形的三条高线交于一点&设三角形ABC的外心为0,垂心为H 从0向BC边引垂线,设垂足为L,则AH=20L9、三角形的外心,垂心,重心在同一条直线(欧拉线)上。
10、(九点圆或欧拉圆或费尔巴赫圆)三角形中,三边中心、从各顶点向其对边所引垂线的垂足,以及垂心与各顶点连线的中点,这九个点在同一个圆上,11、欧拉定理:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线(欧拉线)上12、库立奇*大上定理:(圆内接四边形的九点圆)圆周上有四点,过其中任三点作三角形,这四个三角形的九点圆圆心都在同一圆周上,我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。
13、(内心)三角形的三条内角平分线交于一点,内切圆的半径公式:r=(s-a)(s-b)(s-c)s , s 为三角形周长的一半14、(旁心)三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点中线定理:(巴布斯定理)设三角形ABC的边BC的中点15、为P,则有AB2+AC2=2(AP2+BP2) 16、斯图尔特定理:P将三角形ABC的边BC内分成m:n,贝U有n×AB2+m×AC2=(m+n)AP2+mnm+nBC217、波罗摩及多定理:圆内接四边形ABCD勺对角线互相垂直时,连接AB中点M和对角线交点E的直线垂直于CD18、阿波罗尼斯定理:到两定点A、B 的距离之比为定比m:n (值不为1)的点P,位于将线段AB分成m:n的内分点C和外分点D为直径两端点的定圆周上19、托勒密定理:设四边形ABCD内接于圆,则有AB×CD+AD×BC=AC×BD 20、以任意三角形ABC 的边BC CA AB为底边,分别向外作底角都是30度的等腰^ BDC △ CEA △ AFB则^ DEF是正三角形,21、爱尔可斯定理1:若^ ABC和^ DEF都是正三角形,则由线段AD BE、CF的中心构成的三角形也是正三角形。
平面几何常用定理

11、欧拉定理:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线(欧拉线)上
12、库立奇*大上定理:(圆内接四边形的九点圆)
圆周上有四点,过其中任三点作三角形,这四个三角形的九点圆圆心都在同一圆周上,我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。
13、(内心)三角形的三条内角平分线交于一点,内切圆的半径公式:r=(s-a)(s-b)(s-c)ss为三角形周长的一半
28、塞瓦定理的应用定理:设平行于△ABC的边BC的直线与两边AB、AC的交点分别是D、E,又设BE和CD交于S,则S一定过边BC的中心M
29、塞瓦定理的逆定理:(略)
30、塞瓦定理的逆定理的应用定理1:三角形的三条中线交于一点
31、塞瓦定理的逆定理的应用定理2:设△ABC的内切圆和边BC、CA、AB分别相切于点R、S、T,则AR、BS、CT交于一点。
14、(旁心)三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点
15、中线定理:(巴布斯定理)设三角形ABC的边BC的中点为P,则有AB2+AC2=2(AP2+BP2)
16、斯图尔特定理:P将三角形ABC的边BC内分成m:n,则有n×AB2+m×AC2=(m+n)AP2+mnm+nBC2
32、西摩松定理:从△ABC的外接圆上任意一点P向三边BC、CA、AB或其延长线作垂线,设其垂足分别是D、E、R,则D、E、R共线,(这条直线叫西摩松线)
平面几何四大定理

平面几何四个重要定理四个重要定理:梅涅劳斯(Menelaus)定理(梅氏线)△ABC得三边BC、CA、AB或其延长线上有点P、Q、R,则P、Q、R共线得充要条件就是.塞瓦(Ceva)定理(塞瓦点)△ABC得三边BC、CA、AB上有点P、Q、R,则AP、BQ、CR共点得充要条件就是。
托勒密(Ptolemy)定理四边形得两对边乘积之与等于其对角线乘积得充要条件就是该四边形内接于一圆。
西姆松(Simson)定理(西姆松线)从一点向三角形得三边所引垂线得垂足共线得充要条件就是该点落在三角形得外接圆上。
例题:1.设AD就是△ABC得边BC上得中线,直线CF交AD于F。
求证:。
【分析】CEF截△ABD→(梅氏定理)【评注】也可以添加辅助线证明:过A、B、D之一作C F得平行线。
2.过△ABC得重心G得直线分别交AB、AC于E、F,交CB于D。
求证:。
【分析】连结并延长AG交BC于M,则M为BC得中点。
DEG截△ABM→(梅氏定理)DGF截△ACM→(梅氏定理)∴===1【评注】梅氏定理3.D、E、F分别在△ABC得BC、CA、AB边上,,AD、BE、CF交成△LMN。
求S△LMN。
【分析】【评注】梅氏定理4.以△ABC各边为底边向外作相似得等腰△BCE、△CAF、△ABG。
求证:AE、BF、CG相交于一点。
【分析】【评注】塞瓦定理5.已知△ABC中,∠B=2∠C。
求证:AC2=AB2+AB·BC。
【分析】过A作BC得平行线交△ABC得外接圆于D,连结BD。
则CD=DA=AB,AC=BD。
由托勒密定理,AC·BD=AD·BC+CD·AB。
【评注】托勒密定理6.已知正七边形A1A2A3A4A5A6A7.求证:。
(第21届全苏数学竞赛)【分析】【评注】托勒密定理7.△ABC得BC边上得高AD得延长线交外接圆于P,作PE⊥AB于E,延长ED交AC延长线于F.求证:BC·EF=BF·CE+BE·CF。
十大高中平面几何几何定理汇总及证明

v1.0可编辑可修改高中平面几何定理汇总及证明1.共边比例定理证明:分如下四种情况,分别作三角形高,由相似三角形可证SA PAB=(S\ PAM SA PMB)=(SAPAM/SXPMB1) X SAPMB=(AM/BM1) X SXPMB等高底共线,面积比=底长比)同理,SXQAB=(AM/BM1) X SXQMB所以,SXPAB/SXQAB=XPMB/S\QMB=PMQM等高底共线,面积比=底长比)定理得证!特殊情况:当PB// AC时,易知△ PAB与△ QAB的高相等,从而SX PAB=X QAB 反之,SX PAB=X QAB 贝U PB// AQ2.正弦定理在任意一个平面三角形中,各边和它所对角的正弦值的比相等且等于外接圆半径的2倍”,即卩a/sinA = b/sinB =c/sinC = 2r=R (r为外接圆半径,R为直径) 有公共边AB的两个三角形的顶点分别是P、Q, AB与PQ的连线交于点M则有以下比例式成立:△ PAB的面积:△ QAB的面积=PM QM.证明:A现将△ ABC做其外接圆,设圆心为Q我们考虑/C及其对边AB 设AB长度为c。
若/C为直角,贝U AB就是。
0的直径,即c= 2r。
•••sBC二1 (特殊角正弦函数值)•••盒皿若/C为锐角或钝角,过B作直径BC'交O 0于C',连接C'A,显然BC'= 2r=R。
若/C为锐角,贝U C'与C落于AB的同侧,此时/ C'= / C (同弧所对的圆周角相等)•••在Rt△ ABC'中有= =若/C为钝角,贝U C'与C落于AB的异侧,BC的对边为a,此时/ C'= / A,亦可推出sin匸■ - 5inA _。
考虑同一个三角形内的三个角及三条边,同理,分别列式可得a b c^A = ^B=^C=2r = R。
3.分角定理在厶ABC中,D是边BC上异于B,C或其延长线上的一点,连结则有BD/CD=(sin / BAD/sin / CAD)*(AB/AC)。
初中平面几何知识的60个定理

初中平面几何知识的60个定理1、勾股定理(毕达哥拉斯定理)小学都应该掌握的重要定理2、射影定理(欧几里得定理)重要3、三角形的三条中线交于一点,并且,各中线被这个点分成2:1的两部分重要4、四边形两边中心的连线的两条对角线中心的连线交于一点学习中位线时的一个常见问题,中考不需要,初中竞赛需要5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。
完全没有意义,学习解析几何后显然的结论,不用知道6、三角形各边的垂直一平分线交于一点。
重要7、从三角形的各顶点向其对边所作的三条垂线交于一点重要8、设三角形ABC的外心为O,垂心为H,从O向BC边引垂线,设垂足不L,则AH=2OL中考不需要,竞赛中很显然的结论9、三角形的外心,垂心,重心在同一条直线上。
高中竞赛中非常重要的定理,称为欧拉线10、(九点圆或欧拉圆或费尔巴赫圆)三角形中,三边中心、从各顶点向其对边所引垂线的垂足,以及垂心与各顶点连线的中点,这九个点在同一个圆上,高中竞赛中的常用定理11、欧拉定理:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线(欧拉线)上高中竞赛中会用,不常用12、库立奇*大上定理:(圆内接四边形的九点圆) 圆周上有四点,过其中任三点作三角形,这四个三角形的九点圆圆心都在同一圆周上,我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。
高中竞赛的题目,不用掌握13、(内心)三角形的三条内角平分线交于一点,内切圆的半径公式:r=(s-a)(s-b)(s-c)s,s为三角形周长的一半重要14、(旁心)三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点重要15、中线定理:(巴布斯定理)设三角形ABC的边BC的中点为P,则有AB^2+AC^2=2(AP^2+BP^2) 初中竞赛需要,重要16、斯图尔特定理:P将三角形ABC的边BC内分成m:n,则有n×AB^2+m×AC^2=(m+n)AP^2+mnm+nBC^2高中竞赛需要,重要17、波罗摩及多定理:圆内接四边形ABCD的对角线互相垂直时,连接AB中点M和对角线交点E的直线垂直于CD显然的结论,不需要掌握18、阿波罗尼斯定理:到两定点A、B的距离之比为定比m:n(值不为1)的点P,位于将线段AB分成m:n的内分点C和外分点D为直径两端点的定圆周上高中竞赛需要,重要19、托勒密定理:设四边形ABCD内接于圆,则有AB×CD+AD×BC=AC初中竞赛需要,重要20、以任意三角形ABC的边BC、CA、AB为底边,分别向外作底角都是30度的等腰△BDC、△CEA、△AFB,则△DEF是正三角形,学习复数后是显然的结论,不需要掌握21、爱尔可斯定理1:若△ABC和三角形△都是正三角形,则由线段AD、BE、CF的重心构成的三角形也是正三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平面几何四大定理平面几何四个重要定理四个重要定理:梅涅劳斯(Me nelau s)定理(梅氏线)△ABC 的三边BC 、CA 、AB 或其延长线上有点P 、Q 、R,则P、Q 、R共线的充要条件是 1RB ARQA CQ PC BP =⋅⋅。
塞瓦(Ceva)定理(塞瓦点)△ABC 的三边BC 、CA 、AB 上有点P 、Q 、R ,则AP 、BQ 、CR 共点的充要条件是1RBAR QA CQ PC BP =⋅⋅。
托勒密(Pto lemy)定理四边形的两对边乘积之和等于其对角线乘积的充要条件是该四边形内接于一圆。
西姆松(S imso n)定理(西姆松线)该点落在三角形的外接圆上。
例题:1. 设AD 是△A BC的边BC 上的中线,直线CF 交AD 于F 。
求证:FBAF 2ED AE =。
【分析】CEF 截△ABD →1FABFCB DC ED AE =⋅⋅(梅氏定理)【评注】也可以添加辅助线证明:过A 、B、D 之一作CF 的平行线。
2. 过△ABC 的重心G 的直线分别交AB 、AC 于E 、F,交CB 于平面几何四大定理D 。
求证:1FA CFEA BE =+。
【分析】连结并延长AG 交BC 于M,则M为BC 的中点。
DEG 截△AB M→1DB MDGM AG EA BE =⋅⋅(梅氏定理)D GF 截△AC M→1DCMDGM AG FA CF =⋅⋅(梅氏定理)∴FA CF EA BE +=MD AG )DC DB (GM ⋅+⋅=MDGM 2MD 2GM ⋅⋅=1 【评注】梅氏定理3. D 、E 、F 分别在△ABC 的BC 、C A、AB 边上,λ===EA CEFB AF DC BD ,A D、BE 、CF 交成△LMN 。
求S △LMN 。
【分析】【评注】梅氏定理4. 以△ABC 各边为底边向外作相似的等腰△B CE 、△CAF 、△ABG 。
求证:AE 、BF 、CG 相交于一点。
【分析】【评注】塞瓦定理5. 已知△ABC 中,∠B=2∠C。
求证:AC 2=AB 2+AB ·B C。
【分析】过A 作BC 的平行线交△ABC 的外接圆于D ,连结BD 。
则C D=DA=A B,AC =BD 。
由托勒密定理,AC ·BD=A D·B C+CD·AB 。
【评注】托勒密定理6. 已知正七边形A 1A 2A3A 4A 5A 6A 7。
求证:413121A A 1A A 1A A 1+=。
(第21届全苏数学竞赛) 【分析】【评注】托勒密定理7. △ABC 的BC 边上的高AD 的延长线交外接圆于P,作PE ⊥AB 于E,延长ED 交AC 延长线于F 。
求证:BC·E F=BF ·C E+BE·CF 。
【分析】【评注】西姆松定理(西姆松线)8. 正六边形AB CDEF 的对角线AC 、CE 分别被内分点M 、N分成的比为AM:AC=CN :CE=k,且B 、M 、N 共线。
求k(23-IMO-5) 【分析】【评注】面积法9. O 为△ABC 内一点,分别以d a 、d b 、d c 表示O 到BC 、CA 、DEA 7A 5A A 5AB 的距离,以R a 、R b 、R c表示O 到A、B 、C 的距离。
求证:(1)a·R a ≥b·d b +c·d c ;(2) a·R a ≥c·d b+b·d c ; (3) Ra +R b +R c ≥2(d a +d b +d c )。
【分析】【评注】面积法10. △A BC中,H、G 、O 分别为垂心、重心、外心。
求证:H、G 、O 三点共线,且HG =2GO 。
(欧拉线) 【分析】【评注】同一法11. △ABC 中,AB =A C,AD ⊥B C于D ,BM 、BN 三等分∠AB C,与AD 相交于M 、N,延长CM 交AB 于E 。
求证:MB//NE 。
【分析】【评注】对称变换 12. G 是△ABC 的重心,以A G为弦作圆切BG 于G,延长C G交圆于D 。
求证:AG 2=G C·GD 。
A【分析】【评注】平移变换13. C 是直径AB=2的⊙O 上一点,P 在△ABC 内,若PA +PB+PC 的最小值是7,求此时△AB C的面积S 。
【分析】【评注】旋转变换费马点:已知O是△ABC 内一点,∠AO B=∠BOC=∠C OA =120°;P 是△ABC 内任一【分析】将C−−−→−-)60,B (R 0C ',O −−−→−-)60,B (R 0O', P −−−→−-)60,B (R 0P ',连结OO '、PP'。
则△B OO'、△B PP'都是正三角形。
∴O O'=OB,PP' =PB 。
显然△BO'C '≌△BOC ,△BP'C'≌△BPC 。
由于∠BO 'C'=∠BO C=120°=180°-∠BO'O ,∴A、O 、O'、C'四点共线。
∴AP+PP'+P'C'≥A C'=AO+O O'+O'C',即PA+PB+PC ≥OA+OB+OC 。
14.(95全国竞赛) 菱形ABCD 的内切圆O 与各边分别交于E 、F、G、H,在弧EF 和弧GH 上分别作⊙O的切线交A B、BC 、CD、DA 分别于M 、N 、P 、Q 。
求证:MQ //NP。
【分析】由AB ∥CD 知:要证MQ ∥NP ,只需证∠AMQ=∠CP N,结合∠A=∠C 知,只需证 △AMQ ∽△C PN←CNCP AQ AM =,AM ·CN=AQ ·CP 。
连结A C、BD ,其交点为内切圆心O 。
设MN 与⊙O 切于K ,连结OE 、O M、OK 、O N、OF 。
记∠AB O=φ,∠MOK=α,∠KON=β,则 ∠EOM =α,∠FO N=β,∠EOF =2α+2β=180°-2φ。
∴∠BON =90°-∠NOF-∠COF=90°-β-φ=α∴∠CN O=∠NB O+∠NOB=φ+α=∠AOE+∠M OE=∠AOM又∠OCN=∠MA O,∴△OCN ∽△MAO ,于是CNAOCO AM =, ∴AM ·CN=AO·CO同理,AQ·CP=AO·CO 。
【评注】15.(96全国竞赛)⊙O 1和⊙O 2与ΔA都相切,E 、F 、G、H 为切点,EG 、F H的延长线交于P 求证:P A⊥BC。
【分析】BB 【评注】16.(99全国竞赛)如图,在四边形AB CD 中,对角线AC平分∠BA D。
在CD 上取一点E,BE 与A C相交于F ,延长DF 交BC 于G 。
求证:∠GA C=∠EA C。
证明:连结BD 交A C于H。
对△BCD 用塞瓦定理,可得1EC DE HD BH GB CG =⋅⋅因为AH 是∠BAD 的角平分线,由角平分线定理,可得AD AB HD BH =,故1ECDE AD AB GB CG =⋅⋅。
过C 作A B的平行线交AG 的延长线于I,过C 作AD 的平行线交AE 的延长线于J 。
则CJ ADEC DE ,AB CI GB CG ==, 所以1CJAD AD AB AB CI =⋅⋅,从而CI=CJ 。
又因为CI//AB,CJ //A D,故∠ACI =π-∠BAC =π-∠DA C=∠A CJ 。
因此,△ACI ≌△ACJ ,从而∠IAC =∠JA C,即∠G AC=∠EAC 。
已知AB =AD,BC=DC ,A C与BD 交于O ,过O的任意两条直线EF 和GH与四边形ABCD 的四边交于E、F 、G 、H 。
连结GF 、EH,分别交BD 于M 、N 。
求证:OM=ON 。
(5届CMO)证明:作△EOH −−→−)AC (S△E'OH',则只需证E '、M 、H'共线,即E 'H'、BO 、G F三线共点。
记∠BOG=α,∠G OE'=β。
连结E'F 交BO 于K 。
只需证'KE FKF 'H 'BH GBG 'E ⋅⋅=1(Ceva 逆定理)。
'KE FK F 'H 'BH GB G 'E ⋅⋅='OKE OFK F 'OH 'OBH OGB G 'OE S S S S S S ∆∆∆∆∆∆⋅⋅='OE OFsin OF sin OB sin OB sin 'OE ⋅βα⋅αβ=1 注:筝形:一条对角线垂直平分另一条对角线的四边形。
对应于99联赛2:∠E'O B=∠FO B,且E'H'、GF 、BO 三线共点。
求证:∠GOB =∠H'OB 。
事实上,上述条件是充要条件,且M在OB 延长线上时结论仍然成立。
证明方法为:同一法。
蝴蝶定理:P 是⊙O 的弦AB 的中点,过P点引⊙O 的两弦CD 、EF,连结DE 交AB 于M ,连结CF 交A B于N。
求证:MP=NP 。
【分析】设G H为过P 的直径,F −−→−)GH (S F'F,显然'∈⊙O 。
又P ∈GH,∴PF'=PF。
∵P F−−→−)GH (S PF',P A−−→−)GH (S PB,∴∠FPN =∠F'P M,PF=PF'。
又FF '⊥G H,A N⊥GH,∴FF'∥A B。
∴∠F'PM +∠MDF'=∠F PN+∠EDF' =∠EF F'+∠ED F'=180°,∴P 、M 、D 、F'四点共圆。
∴∠PF'M =∠PDE=∠P FN 。
∴△P FN ≌△PF'M,PN=PM 。
【评注】一般结论为:已知半径为R的⊙O 内一弦AB 上的一点P ,过P作两条相交弦CD 、E F,连CF 、ED 交AB 于M 、N ,已知OP=r,P 到AB 中点的距离为a,则22r R a 2PN 1PM 1-=-。
(解析法证明:利用二次曲线系知识) B。
