【解析版】【2014泰安市一模】山东省泰安市2014届高三第一轮复习质量检测 历史试题
山东省泰安市2014年春学期高三第一轮复习质量检测考试地理试卷(有答案)

山东省泰安市2014年春学期高三年级第一轮复习质量检测考试地理试卷(有答案)2014.3 本试卷分第I卷(选择题)和第II卷(非选择题)两部分。
第I卷1至6页。
第II卷7 至10页。
满分为100分。
考试用时90分钟。
第I卷(选择题共50分)注意事项:1.答第I卷前,考生务必将自己的姓名、准考证号、考试科目、试卷类型用铅笔涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
不能答在试卷上。
一、选择题(每小题2分,共50分,四个选项中,只有一个最符合题目要求)。
下表是泰山连续三个月21日的日出时刻(北京时间),据此完成第l一2题。
1.从a月21日到c月21日期间A.泰山昼长夜短且昼逐渐变长B.济南正午太阳高度先增大后减小C.地球公转速度逐渐加快D.太阳直射点位于北半球且向北移动2.下列现象可能出现在b月的是A.江淮地区适逢梅雨季节B.亚洲大陆被高压控制C.华北平原正值小麦播种期D.南非好望角附近炎热干燥读部分陆地沿某方向的自然植被依次分布状况和气候条件关系示意图,完成3—4题。
3.甲植被最可能是A.热带雨林B.常绿阔叶林C.常绿硬叶林D.温带草原4.形成图中自然带地域分异规律的基础是A.地形 B.水分 C.土壤 D.热量读某地地质剖面图和岩石圈物质循环示意图,完成5—6题。
5.图中④岩石类型属于右图中的A.甲 B.乙 C.丙 D.丁6.图中4种岩石或地质作用,按形成年代从早到晚排列正确的是A.①②④③ B.②④①③ C.③④②① D.②①④③下图是为研究某城市功能区而建立的地理信息系统(GIS)图层。
据图完成7—8题。
7.图中M地最适宜布局A.医院 B.学校 C.银行 D.居民住宅8.图中数字信息可以服务的对象最合适的是A.旅游部门 B.住房建设部门 C.消防部门 D.民政部门下图是北美洲部分地区某年1月30日8时海平面等压线图,读图完成9—10题。
2014泰安文科数学一模试题

泰安市2014届高三教学质量检测考试文 科 数 学本试卷分为选择题和非选择题两部分,共4页,满分150分.考试时间120分钟. 注意事项:1.答题前,考生务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号、县区和科类填写在答题卡上和试卷规定的位置上.2.第I 卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号,答案不能答在试卷上.3.第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不能 使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效.第Ⅰ卷(选择题 共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合要求的.1.设复数()(),2,1zz a bi a b R i P a b i =+∈=-+,若成立,则点在A.第一象限B.第二象限C.第三象限D.第四象限2.如果点()02P y ,在以点F 为焦点的抛物线24y x =上,则PF 等于A.1B.2C.3D.43.为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位 老人,结果如表:由()()()()()22n ad bc K a b c d a c b d -=++++算得()2250040270301609.96720030070430K ⨯⨯-⨯=≈⨯⨯⨯ 参照附表,得到的正确结论是A.在犯错误的概率不超过0.1%的前提下,认为“需要志愿者提供帮助与性别有关”B.在犯错误的概率不超过0.1%的前提下,认为“需要志愿者提供帮助与性别无关”C.有99%以上的把握认为“需要志愿者提供帮助与性别有关”D.有99%以上的把握认为“需要志愿者提供帮助与性别无关” 4.给定命题p :函数()()ln 11y x x =-+⎡⎤⎣⎦为偶函数;命题q :函数11x x e y e -=+为偶函数,下列说法正确的是 A.p q ∨是假命题 B.()p q ⌝∧是假命题 C.p q ∧是真命题 D.()p q ⌝∨是真命题 5.已知向量a ,b 的夹角为120°,且1,a b a b ⋅=--则的最小值为D.1 6.执行右面的程序框图,如果输入a=3,那么输出的n 的值为 A.2 B.3 C.4 D.5 7.将函数()2cos 2f x x x =-的图象向左平移m 个单位 2m π⎛⎫>- ⎪⎝⎭,若所得的图象关于直线6x π=对称,则m 的最小值为 A.3π- B.6π- C.0 D.12π 8.三棱柱的侧棱与底面垂直,且底面是边长为2的等边三角形,其正视 图(如图所示)的面积为8,侧视视图的面积为 A.8 B.4C.9.设直线x m =与函数()()24,2ln f x x g x x =+=的图象分别交于点M 、N , 则当MN 达到最小时m 的值为 A.14 B. 12 C.1 D.2 10.已知函数()()()2111f x x x a x a b ⎡⎤=-+++++⎣⎦的三个零点值分别可以 作为抛物线、椭圆、双曲线的离心率,则22a b +的取值范围是A.)+∞B.)+∞C.[)5,+∞D.()5,+∞【附表】泰安市2014届高三教学质量检测考试文 科 数 学第Ⅱ卷(非选择题 共100分)二、填空题:本大题共5小题,每小题5分,共25分.11.等比数列{}n a 的前n 项和为123,4,2,n S a a a 且成等差数列,若141a S ==,则 ▲ .12.在区间[]13-,上随机取一个数x ,则1x ≤的概率为 ▲ .13.已知12F F ,是双曲线E 的两个焦点,以线段12F F 为直径的圆与双曲线的一个公共点是M , 若1230MF F ∠=,则双曲线E 的离心率是 ▲ .14. 若3sin 52πββπ⎛⎫=<< ⎪⎝⎭,()22sin cos ,sin sin cos 2cos αβααααα+=+-则= ▲ .15.定义域为R 的函数()()()(]()2120,1f x f x f x x f x x x +=∈=-满足,且当时,,则当[]()2,1x f x ∈--时,的最小值为 ▲ .三、解答题:本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤.16.(本小题满分12分)在△ABC 中,角A 、B 、C 所对应的边分别为a 、b 、c ,且3cos .5b cC a a =+(I )求sinA ;(II)若10,a b BA BC == 求在上的投影.17.(本小题满分12分)已知四棱锥P-ABCD 中,底面ABCD 为直角梯形,//.=901,2,BC AD BAD PA AB BC AD PA ∠====⊥,且平面ABCD ,E 为AB 的中点.(I )证明:PC CD ⊥;(II )设F 为PA 上一点,且14AF AP =,证明:EF//平面PCD.18.(本小题满分12分) 某河流上的一座水利发电站,每年六月份的发电量Y (单位:万千瓦时)与该河流上游在六月份的降雨量X (单位:毫米)有关.据编译,当X=70时,Y=460;X 每增加10,Y 增加5.已知近20年的X 值为 140,110,160,70,200,160,140,160,220,200,110,160,160,200,140,110,160,220,140,160. (I )完成如下的频率分布表: (II )求近20年降雨量的中位数和 平均降雨量; (III )假定2014年六月份的降雨量 与近20年六月份降雨量的分布规律相同,并将频率视为概率,求2014年六月份该水车发电站 的发电量不低于520(万千瓦时)的概率. 19.(本小题满分12分) 已知数列{}1n a a t =中,(t 为非零常数),其前n 项和为12n n n S a S +=,满足. (I )求数列{}n a 的通项公式; (II )若对任意的()*1n n N a n n λ∈>+,都有成立,求实数λ的取值范围. 20.(本小题满分13分) 如图,A 、B 是椭圆()222210y x a b a b +=>>的两个顶点,它的短轴长 为1,其一个焦点与短轴的两个端点构成正三角形. (I )求椭圆方程; (II )若直线()0y kx k =>与椭圆相交于R 、S 两点.求四边形ARBS 的 面积的最大值. 21.(本小题满分14分) 已知函数()ln f x x mx =+,其中m 为常数. (I )当()1m f x =-时,求函数的单调区间; (II )若()(]0f x e 在区间,上的最大值为3m -,求的值; (III )令()()21f x g x f x x +'=-≥,若时,()1k g x x ≥+恒成立,求实数k 的取值范围.。
山东省泰安市2014届高三一模考试英语试题1

山东省泰安市2014届高三一模考试英语试题1高考英语2014-04-02 1541山东省泰安市2014届高三一模考试英语试题2014.03本试卷分第Ⅰ卷(选择题)和第1I卷(非选择题)两部分。
第Ⅰ卷1至2014页。
第Ⅱ卷11至14页。
满分为150分。
考试用时120分钟。
第Ⅰ卷(三部分,共20145分)第一部分听力(共两节,满分30分)第一节(共5 小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你将有2014秒钟的时间来回答有关小题和阅读下小,题。
每段对话仅读一遍。
1.What will the two speakers do first?A.Search for the new tie. B.Fix the shelf. C.Paint the shelf2.When does the conversation take place?A.OnFriday. B.On Saturday. C.On Sunday.3.What did the man say the book is about?A.Elephant hunting. B.A hunter’s life. C.Wild animals in Africa.4.How do the cat and the dog get along?A.In a friendly way. B.They often fight against each other.C.They don’t seem to like each other.5.What does the man think about the price of the car?A.Reasonable; B.Too high. C.Unbelievable.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
山东省2014届理科一轮复习试题选编38:算法初步(含解析)
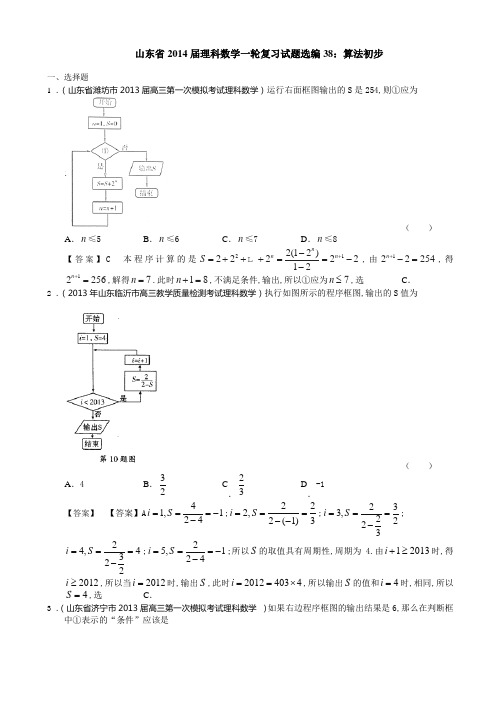
山东省2014届理科数学一轮复习试题选编38:算法初步一、选择题 1 .(山东省潍坊市2013届高三第一次模拟考试理科数学)运行右面框图输出的S 是254,则①应为( )A .n ≤5B .n ≤6C .n ≤7D .n ≤8【答案】C 本程序计算的是212(12)2222212n nn S +-=+++==-- ,由122254n +-=,得12256n +=,解得7n =.此时18n +=,不满足条件,输出,所以①应为7n ≤,选C . 2 .(2013年山东临沂市高三教学质量检测考试理科数学)执行如图所示的程序框图,输出的S 值为( )A .4B .32 C.23D .-1 【答案】 【答案】A 41,124i S ===--;222,2(1)3i S ===--;233,2223i S ===-;24,4322i S ===-;25,124i S ===--;所以S 的取值具有周期性,周期为 4.由12013i +≥时,得2012i ≥,所以当2012i =时,输出S ,此时20124034i ==⨯,所以输出S 的值和4i =时,相同,所以4S =,选 C .3 .(山东省济宁市2013届高三第一次模拟考试理科数学 )如果右边程序框图的输出结果是6,那么在判断框中①表示的“条件”应该是( )A .i≥3B .i≥4C .i≥5D .i≥6 【答案】D【解析】第一次循环,264,6410,2m s i =-+==+==;第二次循环,2262,10212,3m s i =-⨯+==+==;第三次循环,2360,12,4m s i =-⨯+===;第四次循环,2462,12210,5m s i =-⨯+=-=-==;第五次循环,2564,1046,6m s i =-⨯+=-=-==;此时满足条件输出6s =,所以条件应为,6i ≥选D .4 .(山东省泰安市2013届高三第二次模拟考试数学(理)试题)已知数列{}11,1,n n n a a a a n +==+中,若利用如图所示的程序框图计算并输出该数列的第10项,则判断框内的条件可以是( )A .11?n ≤B .10?n ≤C .9?n ≤D .8?n ≤【答案】C 5 .(山东省临沂市2013届高三5月高考模拟理科数学)执行如图所示的程序框图,输出的结果是( )A .11B .12C .13D .14【答案】C 第一次循环,1,2,123x y z ===+=;第二次循环,2,3,235x y z ===+=;第三次循环,3,5,358x y z ===+=;第四次循环,5,8,5813x y z ===+=,此时满足条件,输出13z =,选 C . 6 .(山东省泰安市2013届高三第一轮复习质量检测数学(理)试题)若程序框图如图所示,则该程序运行后输出k 的值是( )A .4B .5C .6D .7【答案】B第一次35116,1n k =⨯+==;第二次168,22n k ===;第三次84,32n k ===;第四次42,42n k ===;第五次21,52n k ===此时满足条件输出5k =,选 B . 7 .(山东省济南市2013届高三4月巩固性训练数学(理)试题)定义某种运算⊗,a b ⊗的运算原理如图 所示.设x x f ⊗=1)(.()f x 在区间[2,2]-上的最大值为. ( )A .-2B .-1C .0D .2【答案】D 8 .(山东省济宁市2013届高三4月联考理科数学)左图是某高三学生进入高中三年来的数学考试成绩茎叶图,第1次到14次的考试成绩依次记为1214,,,.A A A 右图是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是7.98.6 3 89.3 9 8 8 4 1 5 10.3 1 11.4 ( )A .7B .8C .9D .10【答案】D9 .(山东省滨州市2013届高三第一次(3月)模拟考试数学(理)试题)执行如图所示的程序框图,若输出结果为3,则可输入的实数x 值的个数为( )A .1B .2C .3D .4【答案】C 由题意知221,2log ,2x x y x x ⎧-≤=⎨>⎩.当2x ≤时,由213x -=,得24x =,解得2x =±.当2x >时,由2log 3x =,得8x =,所以输入的实数x 值的个数为3个,选 C .10.(山东省德州市2013届高三第二次模拟考试数学(理)试题)执行如图所示的程序框图,若输入n 的值为≤≥16,则输出s 的值为( )A .17B .16C .10D .9【答案】C 11.(山东省2013届高三高考模拟卷(一)理科数学)执行如图所示的程序框图,若输入5=p ,6=q ,则输出a ,i 的值分别为( )A .5,1B .30,3C .15.3D .30.6【答案】D 【解析】执行程序框图可知,当1=i 时,15⨯=a ;当2=i 时,25⨯=a ;;当6=i 时,65⨯=a ,即a 能被q 整除,退出循环,输出i a ,的值分别为30,6. 12.(山东省德州市2013届高三3月模拟检测理科数学)如图所示,程序框图运行后输出k 的值是( )A .4B .5C .6D .7【答案】B 第一次循环,35116,1n k =⨯+==;第二次循环,168,22n k ===; 第三次循环,84,32n k ===;第四次循环,42,42n k ===;第五次循环,21,52n k ===,此时输出5k =,选B . 13.(山东省菏泽市2013届高三第二次模拟考试数学(理)试题)阅读程序框图,若输出的S 的值等于16,那么在程序框图中的判断框内应填写的条件是( )A .i>5?B .i>6?C .i>7?D .i>8?【答案】A14.(山东省兖州市2013高三9月入学诊断检测数学(理)试题)右图给出的是计算111124620++++ 的值的一个框图,其中菱形判断框内应填入的条件是 ( )A .10>iB .10<iC .11>iD .11<i【答案】A15.(山东省莱钢高中2013届高三4月模拟检测数学理试题 )若右边的程序框图输出的S 是254,则条件①可为( )A .5n ≤B .6n ≤C .7n ≤D .8n ≤【答案】C16.(山东省枣庄市2013届高三3月模拟考试数学(理)试题)如图是一个算法的流程图,若输出的结果是31,则判断框中整数M 的值是( )A .3B .4C .5D .6【答案】B本程序计算的是21222AS =++++ ,即11122112A A S ++-==--,由121=31A +-得12=32A +,解得4A =,则15A +=时,条件不成立,所以4M =,选B . 17.(山东省莱芜五中2013届高三4月模拟数学(理)试题)执行如图所示的程序框图,则输出的结果为( )A .2B .1C .21 D .1-【答案】C 18.(山东省凤城高中2013届高三4月模拟检测数学理试题 )阅读如图所示的程序框图,运行相应的程序,则输出的结果是( )ABC.D.【答案】A19.(山东省文登市2013届高三3月二轮模拟考试数学(理))右面的程序框图中,若输出S 的值为126,则图中应填上的条件为( ) A .5n ≤ B .6n ≤C .7n ≤D .8n ≤【答案】B 20.(2012年山东理)(6)执行下面的程序图,如果输入a=4,那么输出的n 的值为( )C .4D .5【答案】:312,140,00=+==+==q p n ;716,541,11=+==+==q p n ;15114,2145,22=+==+==q p n ,q p n >=,3.答案应选 B .21.(山东省枣庄市2013届高三4月(二模)模拟考试数学(理)试题)右图是某算法的程序框图,则程序运行后输出的结果是( )A .6B .27C .124D .168【答案】B 22.(山东省潍坊市2013届高三第二次模拟考试理科数学)运行如图所示的程序,若结束时输出的结果不小于3,则t 的取值范围为( )A .14t ≥B .18t ≥C .14t ≤D .18t ≤ 【答案】B 第一次循环,2,2,211n x t a ===-=;第二次循环,4,4,413n x t a ===-=;第三次循环,6,8,633n x t a ===-=,此时满足条件输出83x t a =,由题意知833x t a =≥,解得81t ≥,即18t ≥,选B .23.(山东省济南市2013届高三3月高考模拟理科数学)阅读右边的程序框图,运行相应的程序,输出的结果为( )A .1311B .2113C .813D .138【答案】D第7题图第一次循环,112,1,2z x y =+===;第二次循环,123,2,3z x y =+===;第三次循环,235,3,5z x y =+===;第四次循环,358,5,8z x y =+===;第五次循环,5813,8,13z x y =+===;第六次循环,81321z =+=,不满足条件输出138y x =,选 D . 24.(山东省夏津一中2013届高三4月月考数学(理)试题)如图给出的是计算20121614121+⋅⋅⋅+++的值的程序框图,其中判断框内应填入的是( )A .2012i ≤B .i >2012C .1006≤iD .i >1006【答案】A 25.(山东省青岛即墨市2013届高三上学期期末考试数学(理)试题)如果执行下面的程序框图,输出的S=110,则判断框处为( )A .10<k ?B .11≥k ?C .10≤k ?D .11>k ?【答案】C【 解析】由程序可知该程序是计算(22)242(1)2k k S k k k +=+++==+ ,由(1)110S k k =+=得10k =,则当10k =时,110111k k =+=+=不满足条件,所以条件为10k ≤,选 C .26.(山东省莱芜市莱芜二中2013届高三4月模拟考试数学(理)试题)右图给出了一个程序框图,其作用是输入x 的值,输出相应的y 值.若要使输入的x 值与输出的y 值相等,则这样的x 值有( )A .1个B .2个C .3个D .4个【答案】C27.(山东威海市2013年5月高三模拟考试数学(理科))一算法的程序框图如右图所示,若输出的12y =,则输入的x 可能为 ( )A .1-B .1C .1或5D .1-或1【答案】 B . 二、填空题 28.(2013届山东省高考压轴卷理科数学)执行如右图的程序框图,那么输出S 的值是________.第5题图【答案】1-【解析】由框图知:12,1;1,2;,3;2S k S k S k ===-===2,4;1,5,S k S k ===-=不满足条件,输出S 的值是1-.29.(2013山东高考数学(理))执行右图的程序框图,若输入的ε的值为0.25,则输出的n 的值为_____.,10123,312,2F F n =+==-==,此时1110.253F =≤不成立.第二次循环,10235,523,3F F n =+==-==,此时1110.255F =≤成立,输出3n =. 30.(山东省济南市2013届高三上学期期末考试理科数学)已知程序框图如右图所示,则输出的i =________;【答案】9【 解析】第一次循环,133,5S i =⨯==;第二次循环,3515,7S i =⨯==;第三次循环,157105,9S i =⨯==;第四次循环,满足条件输出9i =. 31.(山东省德州市2013届高三上学期期末校际联考数学(理))执行如图所示程序框图,输出结果S=.【答案】1【解析】第一次循环1(1)2,3,2S T n =--===;第二次循环23(1)21,5,3S T n =--⨯===;第三次循环35(1)6,7,4S T n =--===;第四次循环47(1)61,9,5S T n =--⨯===,第五次循环,满足条件,输出1S =. 32.(2011年高考(山东理))执行右图所示的程序框图,输入2,3,5l m n ===,则输出的y 的值是______.【答案】解析:1406375278,y =++=278105173,17310568y y =-==-=.答案应填:68. 33.(山东省烟台市2013届高三3月诊断性测试数学理试题)执行如右图所示的程序框图,输出的S 值为___________【答案】10第一次循环,1,1,2i S i ==-=;第二次循环,22,123,3i S i ==-+==; 第三次循环,23,336,4i S i ==-=-=;第四次循环,24,6410,5i S i ==-+==,此时不满足条件,输出10S =. 34.(山东省菏泽市2013届高三5月份模拟考试数学(理)试题)执行如图所示的程序框图,输出S 的值为__________.【答案】-2 35.(山东省淄博市2013届高三复习阶段性检测(二模)数学(理)试题)执行如图所示的程序框图,若输出的结果是8,则输入的数是______.【答案】2或22- 由a b ≥得23x x ≥,解得1x ≤.所以当1x ≤时,输出2a x =,当1x >时,输出3b x =.所以当1x ≤时,由28a x ==,解得822x =-=-.若1x >,由38b x ==,得2x =,所以输入的数为2或22-. 36.(2010年高考(山东理))执行右图所示的程序框图,若输入10x =,则输出y 的值为_____________.【答案】54-【解析】当x=10时,y=110-1=42⨯,此时|y-x|=6; 当x=4时,y=14-1=12⨯,此时|y-x|=3;当x=1时,y=111-1=-22⨯,此时|y-x|=32;当x=12-时,y=115-1=-224⨯-(),此时|y-x|=3<14,故输出y 的值为54-.【命题意图】本题考查程序框图的基础知识,考查了同学们的试图能力.37.(山东省济南市2012届高三3月高考模拟题理科数学(2012济南二模))如果执行右面的程序框图,那么输出的S =______.【答案】 20【解析】第一次循环:2,220==+=k S ;第二次循环:3,642==+=k S ;第三次循环:4,1266==+=k S ;第四次循环:5,20812==+=k S ;第五次循环:输出20=S .38.(山东省莱芜市莱芜十七中2013届高三4月模拟数学(理)试题)执行如图的程序框图,如果输入的n 是4,则输出的p 是______【答案】3 39.(山东省青岛市2013届高三第一次模拟考试理科数学)某程序框图如右图所示,若3a=,则该程序运行后,输出的x 值为【答案】31 第一次循环,2317,2x n =⨯+==;第二次循环,27115,3x n =⨯+==;第三次循环,215131,4x n =⨯+==.此时不满足条件,输出31x =. 40.(2009高考(山东理))执行右边的程序框图,输入的T= .【答案】【解析】:按照程序框图依次执行为S=5,n=2,T=2; S=10,n=4,T=2+4=6;S=15,n=6,T=6+6=12;S=20,n=8,T=12+8=20;S=25,n=10,T=20+10=30>S,输出T=30 答案:30。
数学_2014年山东省泰安市高考数学一模试卷(文科)_(含答案)

2014年山东省泰安市高考数学一模试卷(文科)一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设复数z =a +bi(a, b ∈R),若z1+i =2−i 成立,则点P(a, b)在( )A 第一象限B 第二象限C 第三象限D 第四象限2. 如果点P(2, y 0)在以点F 为焦点的抛物线y 2=4x 上,则|PF|=( ) A 1 B 2 C 3 D 43. 为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老人,结果如表:由K 2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)算得,K 2=500×(40×270−30×160)2200×300×70×430≈9.967附表:A 在犯错误的概率不超过0.1%的前提下,认为“需要志愿者提供帮助与性别有关”B 在犯错误的概率不超过0.1%的前提下,认为“需要志愿者提供帮助与性别无关”C 有99%以上的把握认为“需要志愿者提供帮助与性别有关”D 有99%以上的把握认为“需要志愿者提供帮助与性别无关”4. 给定命题p :函数y =ln[(1−x)(1+x)]为偶函数;命题q :函数y =e x −1e x +1为偶函数,下列说法正确的是( )A p ∨q 是假命题B (¬p)∧q 是假命题C p ∧q 是真命题D (¬p)∨q 是真命题 5. 已知平面向量a →,b →的夹角为120∘,且a →⋅b →=−1,则|a →−b →|的最小值为( ) A √6 B √3 C √2 D 16. 执行所示的程序框图,如果输入a =3,那么输出的n 的值为( )A 2B 3C 4D 57. 将函数f(x)=√3sin2x −cos2x 的图象向左平移|m|个单位(m >−π2),若所得的图象关于直线x =π6对称,则m 的最小值为( )A −π3B −π6C 0D π128. 三棱柱的侧棱与底面垂直,且底面是边长为2的等边三角形.若三棱柱的正视图(如图所示)的面积为8,则侧视图的面积为( )A 8B 4C 4√3D √39. 设直线x =m 与函数f(x)=x 2+4,g(x)=2lnx 的图象分别交于点M 、N ,则当|MN|达到最小时m 的值为( ) A 14 B 12 C 1 D 210. 已知函数f(x)=(x −1)[x 2+(a +1)x +a +b +1]的三个零点值分别可以作为抛物线、椭圆、双曲线的离心率,则a 2+b 2的取值范围是( )A [√5, +∞)B (√5, +∞)C [5, +∞)D (5, +∞)二、填空题:本大题共5个小题,每小题5分,共25分.请把答案填在答题纸的相应位置. 11. 等比数列{a n }的前n 项和为S n ,且4a 1,2a 2,a 3成等差数列.若a 1=1,则S 4=________. 12. 在区间[−1, 3]上随机取一个数x ,则|x|≤1的概率为________.13. 已知F 1,F 2是双曲线E 的两个焦点,以线段F 1F 2为直径的圆与双曲线的一个公共点是M ,若∠MF 1F 2=30∘,则双曲线E 的离心率是________.14. 已知sinβ=35(π2<β<π),且sin(α+β)=cosα,则sin 2α+sinαcosα−2cos 2α等于________.15. 定义域为R 的函数f(x)满足f(x +1)=2f(x),且当x ∈(0, 1]时,f(x)=x 2−x ,则当x ∈[−2, −1]时,f(x)的最小值为________.三、解答题16. 在△ABC 中,角A 、B 、C 所对应的边分别为a 、b 、c ,且cosC =ba +3c5a . (1)求sinA ;(2)若a =8√2,b =10,求BA →在BC →上的投影.17. 已知四棱锥P −ABCD 中,底面ABCD 为直角梯形,BC // AD .∠BAD =90∘,且PA =AB =BC =1,AD =2,PA ⊥平面ABCD ,E 为AB 的中点. (1)证明:PC ⊥CD ;(2)设F 为PA 上一点,且AF →=14AP →,证明:EF // 平面PCD .18. 某河流上的一座水利发电站,每年六月份的发电量Y (单位:万千瓦时)与该河流上游在六月份的降雨量X (单位:毫米)有关.据统计,当X =70时,Y =460;X 每增加10,Y 增加5.已知近20年的X 值为:140,110,160,70,200,160,140,160,220,200,110,160,160,200,140,110,160,220,140,160.(1)完成如下的频率分布表: 近20年六月份降雨量频率分布表(2)求近20年降雨量的中位数和平均降雨量;(3)假定2014年六月份的降雨量与近20年六月份降雨量的分布规律相同,并将频率视为概率,求2014年六月份该水力发电站的发电量不低于520(万千瓦时)的概率. 19. 已知数列{a n }中,a 1=t (t 为非零常数),其前n 项和为S n ,满足a n+1=2S n . (1)求数列{a n }的通项公式;(2)若对任意的n ∈N ∗,都有λa n >n(n +1)成立,求实数λ的取值范围.20. 如图,A、B是椭圆y2a2+x2b2=1(a>b>0)的两个顶点,它的短轴长为1,其一个焦点与短轴的两个端点构成正三角形.(1)求椭圆方程;(2)若直线y=kx(k>0)与椭圆相交于R、S两点.求四边形ARBS面积的最大值.21. 已知函数f(x)=lnx+mx,其中m为常数.(I)当m=−1时,求函数f(x)的单调区间;(II)若f(x)在区间(0, e]上的最大值为−3,求m的值;(III)令g(x)=f(x)+2x −f′(x),若x≥1时,有不等式g(x)≥kx+1恒成立,求实数k的取值范围.2014年山东省泰安市高考数学一模试卷(文科)答案1. A2. C3. C4. B5. A6. C7. B8. C9. C10. D11. 1512. 1213. √3+114. −9515. −11616. 解:(1)在△ABC中,∵ cosC=ba +3c5a,∴ cosC=sinBsinA+3sinC5sinA,化简可得5sinAcosC=5sinB+3sinC,即5sinAcosC=5sin(A+C)+3sinC,即5sinAcosC=5sinAcosC+5cosAsinC+3sinC,∴ sinC(5cosA +3)=0,即5cosA +3=0, ∴ cosA =−35,sinA =45.(2)∵ a =8√2,b =10,cosC =b a+3c 5a,由余弦定理可得a 2+b 2−c 22ab=b a+3c 5a,解得:c =2.再由正弦定理可得bsinB =asinA , ∴ sinB =bsinA a=√22, ∴ cosB =√22. 故BA →在BC →上的投影为c ⋅cosB =2×√22=√2.17. 解:(1)连结AC , ∵ PA ⊥平面ABCD , ∴ PA ⊥CD ,取AD 中点G ,连结CG ,在直角梯形ABCD 中∠BAD =90∘,AB =BC =1,AD =2,BC // AD , ∴ AG =GD =GC =1,CG ⊥AD , ∴ CD ⊥AC ,∴ CD ⊥平面PAC , ∴ PC ⊥CD .(2)取AG 的中点H ,连结BG ,EH ,FH , ∵ E 为AB 的中点, ∴ EH // BG ,又BC =DG =1,BC // DG , ∴ 四边形BCDG 为平行四边形, ∴ GC // CD ,∵ AF →=14AP →,AH =14AD ,∴ FH // PD ,∴ 平面EFH // 平面PCD , ∴ EF // 平面PCD .18. 解:(1)近20年降雨量为110,160,220的频数分别为:3、7、2,由频数除以20得频率分别为320,720,220,频率分布表如图:(2)20个数从小到大排列为:70,110,110,110,140,140,140,140,160,160,160,160,160,160,160,200,200,200,220,220 中位数是160;平均降雨量x ¯=120(70+110×3+140×4+160×7+200×3+220×2)=156; (3)由已知可设 Y =12X +B ∵ X =70时,Y =460,∴ B =425, ∴ Y =12X +425.当Y ≥520时,由12X +425≥520,解得:X ≥190.∴ 发电量不低于520(万千瓦时)包含降雨量200和220两类,它们彼此互斥, ∴ 发电量低于520(万千瓦时)的概率P =320+220=14. 19. 解:(1)当n =1时,a 1=t ,当n ≥2时,a n =S n −S n−1=12a n+1−12a n ,即a n+1=3a n (n ≥2), 又a 1=t ≠0, ∴a n+1a n=3 (n ≥2),又a 2=2S 1=2t ,∴ 当n ≥2时,数列{a n }是以a 2为首项,3为公比的等比数列. ∴ a n =2t ⋅3n−2(n ≥2), 又∵ a 1=t 不适合上式,∴ a n ={t(n =1)2t ⋅3n−2(n ≥2);(2)当t >0时,λa n >n(n +1)成立,等价于λ大于n(n+1)a n的最大值.当n =1时,有λ>2t ,当n ≥2时,令b n =n(n+1)2t⋅3n−2, b n+1−b n =(n +1)(n +2)2t ⋅3n−1−n(n +1)2t ⋅3n−2=n+12t⋅3n−1(n +2−3n)=1−n 2t⋅3n−1<0.∴ 当n ≥2时,数列{a n }为递减数列, ∴ 当n ≥2时,b n ≤b 2=3t . ∴ 当t >0时,λ>3t .当t <0时,λa n >n(n +1)成立,等价于λ大于n(n+1)a n的最小值.当n =1时,有λ<2t ,当n ≥2时,令b n =n(n+1)2t⋅3n−2, b n+1−b n =(n +1)(n +2)2t ⋅3n−1−n(n +1)2t ⋅3n−2=n+12t⋅3n−1(n +2−3n)=1−n 2t⋅3n−1>0.∴ 当n ≥2时,数列{b n }为递增数列, ∴ 当n ≥2时,b n ≥b 2=3t . ∴ 当t <0时,λ<3t .综上所述,当t >0时,λ>3t;当t <0时,λ<3t.20. 解:(1)∵ A 、B 是椭圆y 2a 2+x 2b 2=1(a >b >0)的两个顶点, 它的短轴长为1,其一个焦点与短轴的两个端点构成正三角形, ∴ b =12,c =1⋅sin60∘=√32,∴ a =1,∴ 椭圆方程为x 214+y 2=0.(2)设点R 为(x 1, y 1),点S 为(x 2, y 2),直线y =kx 与曲线4x 2+y 2=1联立得(kx)2+4x 2=1,即(k 2+4)x 2−1=0, 设点R(x 1, y 1),S(x 2, y 2),联立{y =kx4x 2+y 2=1,得(kx)2+4x 2=1,即(k 2+4)x 2−1=0, ∴ x 1+x 2=0,x 1x 2=−1k 2+4,由题意知S四边形ARBS=S△RBS+S△RAS=14(2+k)|x1−x2|=14(2+k)√(x1+x2)2−4x1x2=14√(2+k)2⋅4k2+4=12√4+4k+k2k2+4=12√1+4k+4k≤12√1+2√k⋅4k=√22.当且仅当k=4k(k>0),即k=2时,取“=”号,∴ 四边形ARBS面积的最大值为√22.21. 解:(1)易知f(x)定义域为(0, +∞),当a=−1时,f(x)=−x+lnx,f′(x)=−1+1x,令f′(x)=0,得x=1.当0<x<1时,f′(x)>0;当x>1时,f′(x)<0.∴ f(x)在(0, 1)上是增函数,在(1, +∞)上是减函数.(2)∵ f′(x)=m+1x,x∈(0, e],①若m≥0,则f′(x)≥0,从而f(x)在(0, e]上增函数,∴ f(x)max=f(e)=me+1≥0,不合题意.②若m<0,则由f′(x)>0,即0<x<−1m由f′(x)<0,即−1m<x≤e.从而f(x)在(0, −1m )上增函数,在(−1m, e]为减函数,∴ f(x)max=f(−1m )=−1+ln(−1m)令−1+ln(−1m)=−3,∴ m=e−2,∵ −e2<−1e,∴ m=−e2为所求.(III)∵ g(x)=f(x)+2x −f′(x),f′(x)=m+1x,f(x)=lnx+mx,∴ g(x)=lnxx −1x,若x≥1时,有不等式g(x)≥kx+1恒成立,∴ k≤g(x)(x+1)=lnx+lnxx +1x+1,令ℎ(x)=(x)(x+1)=lnx+lnxx +1x+1,∴ ℎ′(x)=x−lnxx2>恒大于0,∴ ℎ(x)在[1, +∞)为增函数,∴ ℎ(x)min=ℎ(1)=2,∴ k≤2.。
2014届上学期泰安市高三年级考试 语文试题

2014届上学期泰安市高三年级考试语文试题2014届上学期泰安市高三年级考试语文试题2014.1本试卷分第卷和第卷两部分,共8页。
满分l50分。
考试用时150分钟。
注意事项:1.答题前,考生在答题卡上务必用直径0.5毫米黑色签字笔将自己的姓名、考试号填涂在答题卡和答题纸规定的位置上。
2.第卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,答案不能答在试卷上。
3.第卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试卷上。
第卷(选择题36分)一、(15分,每小题3分)1.下列词语中加点的字,读音全部正确的一项是A.蹿红(cun)缱绻(jun)跷跷板(qio)味同嚼蜡(jio)B.犄角(j)宽宥(yu)馏馒头(li)信手拈来(nin)C.馥郁(f)择菜(z)犟脾气(jing)蓬头跣足(xin)D.船舷(xin)肋骨(li)紧箍咒(g)敝帚自珍(zh)2.下列各句中,没有错别字的一句是A.宇宙浩翰,星汉灿烂。
70多亿人共同生活在我们这个星球上,应该守望相助、同舟共济、共同发展。
B.在公众看来,这些事无巨细的禁令,直指当前官场之积敝要害,既是防微杜渐,也是把“权力关进制度的笼子里”的一种表现。
C.你或许志得意满,也可能历经坎坷,不同的人有不同的际遇,时间诉说青春的美好,也镌刻着生命的衰竭。
D.收视率颇高的娱乐节目饱受垢病。
每当一类节目走红,跟风之作便犹如雨后春笋,且节目多为引进境外版权模式,缺乏创新。
3.下列各句中,加点的词语使用恰当一项是A.与愤青、小资一样,作为一种文化现象,“小清新”它所依照的现实背景、所展现的个性追求,却是值得人们重视的。
B.假哈佛校训在中国流行不是偶然。
谣言之所以流传,往往不是编造者有多高明,而是它反映了传播者的真实诉愿。
C.项羽出身贵族世家,天赋异禀,豪气干云,穿云裂石,是举世无伦的大英雄;刘邦则年逾四十,整日游手好闲,不谙劳作。
2014年山东省泰安市高考数学一模试卷(文科)

2014年山东省泰安市高考数学一模试卷(文科)学校:___________姓名:___________班级:___________考号:___________一、选择题(本大题共10小题,共50.0分)1.设复数z=a+bi(a,b∈R),若成立,则点P(a,b)在()A.第一象限B.第二象限C.第三象限D.第四象限【答案】A【解析】解:∵,∴z=(2-i)(1+i)=2+2i-i-i2=3+i,∴点P(3,1),显然在第一象限,故选:A由题意可得z=(2-i)(1+i),化简结合几何意义可得P的坐标,可得所在象限.本题考查复数的代数形式的乘除运算,涉及复数的几何意义,属基础题.2.如果点P(2,y0)在以点F为焦点的抛物线y2=4x上,则|PF|=()A.1B.2C.3D.4【答案】C【解析】解:抛物线y2=4x的准线方程为:x=-1,∵P到焦点F的距离等于P到准线的距离,点P(2,y0),∴P到焦点F的距离是|PF|=2+1=3.故选:C.确定抛物线y2=4x的准线方程,利用P到焦点F的距离等于P到准线的距离,即可求得结论.本题考查抛物线的性质,考查抛物线定义的运用即抛物线上的点到焦点的距离等于到准线的距离,属于基础题.3.为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了由算得,参照附表,得到的正确结论是()A.在犯错误的概率不超过0.1%的前提下,认为“需要志愿者提供帮助与性别有关”B.在犯错误的概率不超过0.1%的前提下,认为“需要志愿者提供帮助与性别无关”C.有99%以上的把握认为“需要志愿者提供帮助与性别有关”D.有99%以上的把握认为“需要志愿者提供帮助与性别无关”【答案】C【解析】解:由于K2=9.967>6.635,所以有99%的把握认为该地区的老年人是否需要帮助与性别有关.故选:C.K2=9.967,同临界值表进行比较,得到有多大把握认为老年人是否需要志愿者提供帮助与性别有关.本题考查独立性检验.利用观测值K2与临界值的大小来确定是否能以一定把握认为两个分类变量有关系.其方法是:K≥K0,解释为有[1-P(k2≥k0)]×100%的把握认为两个分类变量有关系;K<K0,解释为不能以[1-P(k2≥k0)]×100%的把握认为两个分类变量有关系.4.给定命题p:函数y=ln[(1-x)(1+x)]为偶函数;命题q:函数y=为偶函数,下列说法正确的是()A.p∨q是假命题B.(¬p)∧q是假命题C.p∧q是真命题D.(¬p)∨q是真命题【答案】B【解析】解:①∵函数y=ln[(1-x)(1+x)]的定义域是(-1,1),且∀x,有f(-x)=ln[(1+x)(1-x)]=f(x),∴f(x)是定义域上的偶函数,∴命题p正确.②∵函数y=,x∈R,∴f(-x)===-=-f(x),∴f(x)是定义域上的奇函数,∴命题q错误;∴p∨q是真命题,(¬p)∧q是假命题,p∧q是假命题,(¬p)∨q是假命题;故选:B.先判定命题p、命题q的真假,再判定各选项复合命题的真假即可.本题考查了函数的奇偶性判定以及复合命题的真假性判定问题,解题的关键是先判定命题p、q的真假性,是基础题.5.已知平面向量,的夹角为120°,且=-1,则|-|的最小值为()A. B. C. D.1【答案】A【解析】解:∵平面向量,的夹角为120°,∴=||•||cos120°==||•||=-1,∴||•||=2,则|-|==,当且仅当||=||=时取等号,故|-|的最小值为,故选:A.根据平面向量的数量积的应用,利用基本不等式即可求解.本题主要考查平面向量数量积的应用以及基本不等式的应用,利用数量积的定义求出向量长度之间的关系是解决本题的关键.6.执行所示的程序框图,如果输入a=3,那么输出的n的值为()A.2B.3C.4D.5【答案】C【解析】解:由程序框图得:程序第一次运行P=0+30=1,Q=2×1+1=3,n=1;第二次运行P=1+31=4,Q=2×3+1=7.n=2;第三次运行P=4+32=13,Q=2×7+1=15,n=3;第四次运行P=13+33=40,Q=2×15+1=31,n=4,不满足P≤Q,程序运行终止,输出n=4.故选:C.根据程序框图,依次计算运行的P、Q的值,直到条件P≤Q不满足,判断此时的n值,可得答案.本题考查了循环结构的程序框图,根据算法流程分别计算运行的结果是解答此类问题的常用方法.7.将函数f(x)=sin2x-cos2x的图象向左平移|m|个单位(m>-),若所得的图象关于直线x=对称,则m的最小值为()A. B. C.0 D.【答案】B【解析】解:把函数f(x)=sin2x-cos2x=2sin(2x-)的图象向左平移|m|个单位(m>-),可得函数y=2sin[2(x+|m|)-]=2sin(2x+2|m|-)的图象,再根据所得的图象关于直线x=对称,可得2×+2|m|-=kπ+,k∈z,故|m|=+,k∈z,故|m|的最小值为,结合m>-可得m的最小值为-,故选:B.根据函数y=A sin(ωx+φ)的图象变换规律,可得平移后所得函数y=2sin(2x+2|m|-)的图象,再根据所得的图象关于直线x=对称,可得2×+2|m|-=kπ+,k∈z,结合m>-可得m的最小值.本题主要考查函数y=A sin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,属于中档题.8.三棱柱的侧棱与底面垂直,且底面是边长为2的等边三角形.若三棱柱的正视图(如图所示)的面积为8,则侧视图的面积为()A.8B.4C.D.【答案】C【解析】解:由题意及正视图知,此几何体的高为4,底三角形的高及侧视图的边长侧视图应为矩形,底三角形的高是侧视图的边长所以侧视图的高为4,宽为,因此侧视图的面积为.故选C由题意及正视图知,此几何体的高为4,由此知求出底面三角形的高即得到侧视图的底边长,由于底面是边长为2的等边三角形,其长度易求,再求出侧视图的面积,选出正确选项本题考查由三视图求面积、体积,解题的关键是由三视图及题设条件想像出几何体的几何特征得出侧视图是一个长为4,宽为的矩形,从而计算出它的面积,本题考查了空间想像能力及根据图形计算的能力,三视图的考查是高考的热点,应注意总结此类题的做题规律9.设直线x=m与函数f(x)=x2+4,g(x)=2lnx的图象分别交于点M、N,则当|MN|达到最小时m的值为()A. B. C.1 D.2【答案】C【解析】解:当x=m时,|MN|=m2+4-2lnm,m>0,设f(m)=|MN|=m2+4-2lnm,则f'(m)=2m-=,由f'(m)>0得m>1,此时函数单调递增,由f'(m)<0得0<m<1,此时函数单调递减,即当m=1时,函数取得极小值,同时也是最小值为f(1)=1+4-2ln1=5.此时m=1.故选:C.当x=m时,|MN|=m2+4-2lnm,然后利用导数求出函数的最小值即可.本题主要考查函数最值的求法,利用导数研究函数的极值是解决本题的关键.10.已知函数f(x)=(x-1)[x2+(a+1)x+a+b+1]的三个零点值分别可以作为抛物线、椭圆、双曲线的离心率,则a2+b2的取值范围是()A.[,+∞)B.(,+∞)C.[5,+∞)D.(5,+∞)【答案】D【解析】解:令函数f(x)=(x-1)[x2+(a+1)x+a+b+1]=0,∴x=1是其中的一个根,所以f(x)=(x-1)[x2+(1+a)x+a+b+1]的另外两个零点分别是一个椭圆一个双曲线的离心率,故g(x)=x2+(1+a)x+a+b+1,有两个分别属于(0,1),(1,+∞)的零点,故有g(0)>0,g(1)<0,即a+b+1>0且2a+b+3<0,利用线性规划的知识,可确定a2+b2的取值范围是(5,+∞).故选:D.通过函数的零点即可推出a,b的关系利用线性规划求解a2+b2的取值范围即可.本题考查一元二次方程的根的分布与系数的关系,简单线性规划,考查计算能力.二、填空题(本大题共5小题,共25.0分)11.等比数列{a n}的前n项和为S n,且4a1,2a2,a3成等差数列.若a1=1,则S4= ______ .【答案】15【解析】解:∵2a2-4a1=a3-2a2,∴2q-4=q2-2q,q2-4q+4=0,q=2,∴a1=1,a2=2,a3=4,a4=8,∴S4=1+2+4+8=15.答案:15由题意知2a2-4a1=a3-2a2,即2q-4=q2-2q,由此可知q=2,a1=1,a2=2,a3=4,a4=8,于是得到S41+2+4+8=15.本题考查数列的应用,解题时要注意公式的灵活运用.12.在区间[-1,3]上随机取一个数x,则|x|≤1的概率为______ .【答案】【解析】解:在区间[-1,3]之间随机抽取一个数x,则-1≤x≤3,由|x|≤1得-1≤x≤1,∴根据几何概型的概率公式可知满足|x|≤1的概率为=,故答案为:.由条件知-1≤x≤3,然后解不等式的解,根据几何概型的概率公式即可得到结论.本题主要考查几何概型的概率的计算,根据不等式的性质解出不等式的是解决本题的关键,比较基础.13.已知F1,F2是双曲线E的两个焦点,以线段F1F2为直径的圆与双曲线的一个公共点是M,若∠MF1F2=30°,则双曲线E的离心率是______ .【答案】+1【解析】解:由题意,MF1⊥MF2,设|F1F2|=2c,∵∠MF1F2=30°,∴|MF1|=,|MF2|=c,∴2a=MF1-MF2=(-1)c.∴=.故答案为:.根据以线段F1F2为直径的圆与双曲线的一个公共点是M,可得MF1⊥MF2,利用∠MF1F2=30°,可得|MF1|,利用双曲线的定义及离心率的定义,可求双曲线E的离心率.本题考查了双曲线的性质以及定义,解题过程要灵活运用双曲线的定义,属于中档题.14.已知sinβ=(<β<π),且sin(α+β)=cosα,则sin2α+sinαcosα-2cos2α等于______ .【答案】-【解析】解:∵sinβ=(<β<π),∴cosβ=-.∵sin(α+β)=sinαcosβ+cosαsinβ=sinα(-)+cosα=cosα,∴-sinα=cosα,tanα=-.∴sin2α+sinαcosα-2cos2α====-,故答案为:-.由条件利用同角三角函数的基本关系求得cosβ=-,tanα=-.再根据sin2α+sinαcosα-2cos2α==,计算求得结果.本题主要考查同角三角函数的基本关系的应用,属于基础题.15.定义域为R的函数f(x)满足f(x+1)=2f(x),且当x∈(0,1]时,f(x)=x2-x,则当x∈[-2,-1]时,f(x)的最小值为______ .【答案】-【解析】解:当x∈[-2,-1]时,x+2∈[0,1],∴f(x+2)=(x+2)2-(x+2)=x2+3x+2,又f(x+1)=2f(x),∴f(x+2)=f[(x+1)+1]=2f(x+1)=4f(x),∴4f(x)=x2+3x+2(-2≤x≤-1),∴f(x)=(x2+3x+2)=-(-2≤x≤-1),∴当x=-时,f(x)取得最小值-;故答案为:-.根据题意,求出x∈[-2,-1]时f(x)的解析式,再求f(x)在区间[-2,-1]上的最小值即可.本题考查了函数的解析式以及在闭区间上的最值问题,是基础题.三、解答题(本大题共6小题,共74.0分)16.在△ABC中,角A、B、C所对应的边分别为a、b、c,且cos C=.(I)求sin A;(Ⅱ)若a=8,b=10,求在上的投影.【答案】解:(I)在△ABC中,∵cos C=,∴cos C=+,化简可得5sin A cos C=5sin B+3sin C,即5sin A cos C=5sin(A+C)+3sin C,即5sin A cos C=5sin A cos C+5cos A sin C+3sin C,∴sin C(5cos A+3)=0,即5cos A+3=0,∴cos A=-,sin A=.(Ⅱ)∵a=8,b=10,cos C=,由余弦定理可得=,解得:c=2.再由正弦定理可得,∴sin B==,∴cos B=.故在上的投影为c•cos B=2×=.【解析】(I)在△ABC中,由cos C=,利用正弦定理可得cos C=+,化简可得sin C (5cos A+3)=0,故有cos A=-,从而求得sin A的值.(Ⅱ)根据a=8,b=10,cos C=,由余弦定理求得c=2.再由正弦定理求得sin B=的值,可得cos B的值,从而求得在上的投影c•cos B 的值.本题主要考查正弦定理、余弦定理、三角恒等变换,一个向量在另一个向量上的投影的定义和求法,属于中档题.17.已知四棱锥P-ABCD中,底面ABCD为直角梯形,BC∥AD.∠BAD=90°,且PA=AB=BC=1,AD=2,PA⊥平面ABCD,E为AB的中点.(Ⅰ)证明:PC⊥CD;(Ⅱ)设F为PA上一点,且,证明:EF∥平面PCD.【答案】解:(Ⅰ)连结AC,∵PA⊥平面ABCD,∴PA⊥CD,取AD中点G,连结CG,在直角梯形ABCD中∠BAD=90°,AB=BC=1,AD=2,BC∥AD,∴AG=GD=GC=1,CG⊥AD,∴CD⊥AC,∴CD⊥平面PAC,∴PC⊥CD.(Ⅱ)取AG的中点H,连结BG,EH,FH,∵E为AB的中点,∴EH∥BG,又BC=DG=1,BC∥DG,∴四边形BCDG为平行四边形,∴GC∥CD,∵,AH=AD,∴FH∥PD,∴平面EFH∥平面PCD,∴EF∥平面PCD.【解析】(Ⅰ)连结AC,根据PA⊥平面ABCD,推断出PA⊥CD,取AD中点G,连结CG,在直角梯形ABCD中∠BAD=90°,AB=BC=1,AD=2,BC∥AD,进而求得AG=GD=GC=1,CG⊥AD,推断出CD⊥AC,进而可知CD⊥平面PAC,最后利用线面垂直的性质推断出PC⊥CD.(Ⅱ)取AG的中点H,连结BG,EH,FH,E为AB的中点,推断出EH∥BG,BC=DG=1,BC∥DG,判断出四边形BCDG为平行四边形,得出GC∥CD,根据已知,AH=AD,推断出FH∥PD,利用面面平行的判定定理判断出平面EFH∥平面PCD,进而可知EF∥平面PCD.本题主要考查了直线与平面平行,垂直的性质及判定定理的应用.作为基础,要求学生能熟练掌握.18.某河流上的一座水利发电站,每年六月份的发电量Y(单位:万千瓦时)与该河流上游在六月份的降雨量X(单位:毫米)有关.据统计,当X=70时,Y=460;X每增加10,Y增加5.已知近20年的X值为:140,110,160,70,200,160,140,160,220,200,110,160,160,200,140,110,160,220,140,160.(Ⅰ)完成如下的频率分布表:近20年六月份降雨量频率分布表(Ⅱ)求近20年降雨量的中位数和平均降雨量;(Ⅲ)假定2014年六月份的降雨量与近20年六月份降雨量的分布规律相同,并将频率视为概率,求2014年六月份该水力发电站的发电量不低于520(万千瓦时)的概率.【答案】解:(Ⅰ)近20年降雨量为110,160,220的频数分别为:3、7、2,由频数除以20得频率分别为,,,频率分布表如图:(Ⅱ)20个数从小到大排列为:70,110,110,110,140,140,140,140,160,160,160,160,160,160,160,200,200,200,220,220中位数是160;平均降雨量;(Ⅲ)由已知可设∵X=70时,Y=460,∴B=425,∴.当Y≥520时,由,解得:X≥190.∴发电量不低于520(万千瓦时)包含降雨量200和220两类,它们彼此互斥,∴发电量低于520(万千瓦时)的概率.【解析】(Ⅰ)由近20年X的值分别查出降雨量为110,160,220的频数,由频数除以20得频率分别为,,,然后填入频率分布表;(Ⅱ)直接把20个数值从小到大排列求中位数,由平均数公式求平均数;(Ⅲ)由已知可知发电量与降雨量呈一次函数关系,设出一次函数解析式,由X=70时,Y=460;X每增加10,Y增加5得到斜率和截距,再由Y≥520求得X的范围,从而可知2014年六月份的降雨量情况,进一步求得2014年六月份该水力发电站的发电量不低于520(万千瓦时)的概率.本题考查了古典概型及其概率公式,考查了离散型随机变量的分布列,考查了频率与概率之间的关系,是基础题.19.已知数列{a n}中,a1=t(t为非零常数),其前n项和为S n,满足a n+1=2S n.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)若对任意的n∈N*,都有λa n>n(n+1)成立,求实数λ的取值范围.【答案】解:(Ⅰ)当n=1时,a1=t,当n≥2时,,即a n+1=3a n(n≥2),又a1=t≠0,∴(n≥2),又a2=2S1=2t,∴当n≥2时,数列{a n}是以a2为首项,3为公比的等比数列.∴,又∵a1=t不适合上式,∴;(Ⅱ)当t>0时,λa n>n(n+1)成立,等价于λ大于的最大值.当n=1时,有>,当n≥2时,令,=<.∴当n≥2时,数列{a n}为递减数列,∴当n≥2时,.∴当t>0时,>.当t<0时,λa n>n(n+1)成立,等价于λ大于的最小值.当n=1时,有<,当n≥2时,令,=>.∴当n≥2时,数列{b n}为递增数列,∴当n≥2时,.∴当t<0时,<.综上所述,当t>0时,>;当t<0时,<.【解析】(Ⅰ)由数列递推式求出a2,再由a n=S n-S n-1(n≥2)整理得到(n≥2),由等比数列的通项公式求出n≥2时的通项,验证n=1时不成立,则数列{a n}的通项公式可求;(Ⅱ)把a n代入λa n>n(n+1),利用数学转化思想方法把不等式恒等变形,分离参数λ,然后对t分类,利用数列的函数特性求得t在不同范围内的最值,则实数λ的取值范围可求.本题是数列与不等式的综合题,考查了由数列递推式求数列的通项公式,考查了与数列有关的恒成立问题,体现了分类讨论的数学思想方法,是中高档题.20.如图,A、B是椭圆+=1(a>b>0)的两个顶点,它的短轴长为1,其一个焦点与短轴的两个端点构成正三角形.(Ⅰ)求椭圆方程;(Ⅱ)若直线y=kx(k>0)与椭圆相交于R、S两点.求四边形ARBS面积的最大值.【答案】解:(Ⅰ)∵A、B是椭圆+=1(a>b>0)的两个顶点,它的短轴长为1,其一个焦点与短轴的两个端点构成正三角形,∴b=,c=1•sin60°=,∴a=1,∴椭圆方程为.(Ⅱ)设点R为(x1,y1),点S为(x2,y2),直线y=kx与曲线4x2+y2=1联立得(kx)2+4x2=1,即(k2+4)x2-1=0,设点R(x1,y1),S(x2,y2),联立,得(kx)2+4x2=1,即(k2+4)x2-1=0,∴x1+x2=0,,由题意知S四边形ARBS=S△RBS+S△RAS==(2+k)===≤=.当且仅当k=(k>0),即k=2时,取“=”号,∴四边形ARBS面积的最大值为.【解析】(Ⅰ)由已知条件,分别求出b,c,a,由此能求出椭圆方程.(Ⅱ)设点R(x1,y1),S(x2,y2),联立,得(k2+4)x2-1=0,由S四边=S△RBS+S△RAS,利用韦达定理和均值定理能求出四边形ARBS面积的最大值.形ARBS本题考查椭圆方程的求法,考查四边形面积最大值的求法,解题时要认真审题,注意均值定理的合理运用.21.已知函数f(x)=lnx+mx,其中m为常数.(Ⅰ)当m=-1时,求函数f(x)的单调区间;(Ⅱ)若f(x)在区间(0,e]上的最大值为-3,求m的值;(Ⅲ)令g(x)=-f′(x),若x≥1时,有不等式g(x)≥恒成立,求实数k 的取值范围.【答案】解:(1)易知f(x)定义域为(0,+∞),当a=-1时,f(x)=-x+lnx,f′(x)=-1+,令f′(x)=0,得x=1.当0<x<1时,f′(x)>0;当x>1时,f′(x)<0.∴f(x)在(0,1)上是增函数,在(1,+∞)上是减函数.(2)∵f′(x)=m+,x∈(0,e],①若m≥0,则f′(x)≥0,从而f(x)在(0,e]上增函数,∴f(x)max=f(e)=me+1≥0,不合题意.②若m<0,则由f′(x)>0,即0<x<由f′(x)<0,即<x≤e.从而f(x)在(0,)上增函数,在(-,e]为减函数,∴f(x)max=f()=-1+ln()令-1+ln()=-3,∴m=e-2,∵-e2<,∴m=-e2为所求.(Ⅲ)∵g(x)=-f′(x),f′(x)=m+,f(x)=lnx+mx,∴g(x)=-,若x≥1时,有不等式g(x)≥恒成立,∴k≤g(x)(x+1)=lnx+++1,令h(x)=(x)(x+1)=lnx+++1,∴h′(x)=>恒大于0,∴h(x)在[1,+∞)为增函数,∴h(x)min=h(1)=2,∴k≤2.【解析】(Ⅰ)在定义域(0,+∞)内对函数f(x)求导,求其极大值,若是唯一极值点,则极大值即为最大值.(Ⅱ)在定义域(0,+∞)内对函数f(x)求导,对m进行分类讨论并判断其单调性,根据f(x)在区间(0,e]上的单调性求其最大值,并判断其最大值是否为-3,若是就可求出相应的最大值.(Ⅲ)首先求g(x),有不等式g(x)≥恒成立,转化为k≤g(x)(x+1),求g(x)(x+1)的最小值,问题得以解决.本题先通过对函数求导,求其极值,进而在求其最值,用到分类讨论的思想方法.。
【解析】高三第一轮复习质量检测 化学试题

山东省泰安市2014届高三第一轮复习质量检测化学试题2014.3本试卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,第I 卷1至5页,第Ⅱ卷5 至11页。
满分100分,考试时间90分钟。
相对原子质量:H 1 C 12 O 16 Na 23 S 32 Cl 35.5 Fe 56 Cu 64 I 127第I 卷 (选择题共46分)注意事项:1.答第I 卷前,考生务必将自己的姓名、考号、试卷类型、考试科目用铅笔涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,不能答在试卷上。
3.考试结束后,监考人员将本试卷和答题卡一并收回。
本卷共18小题。
1—8题每小题2分,9—18题每小题3分,共46分。
每小题只有一个....选项是符合题目要求的。
1.下列说法错误的是A .利用太阳能等清洁能源代替化石燃料,有利于节约资源、保护环境B .水泥厂、冶金厂常用高压电除去工厂烟尘,利用了胶体的性质C .橡胶、纤维、塑料都是高分子化合物D .日常生活中常用无水乙醇进行杀菌消毒2.有关化学用语表达正确的是[]222n CH CH CH --A .聚丙烯的结构简式:B .C1-的结构示意图:C .1021034646Pd Pd 和互为同位素D .过氧化氢电子式:3.全世界每年钢铁因锈蚀造成大量的损失。
某城市拟用如图方法保护埋在酸性土壤中的钢质管道,使其免受腐蚀。
关于此方法,下列说法不正确的是A .土壤中的钢铁易被腐蚀是因为在潮湿的土壤中形成了原电池B .金属棒M 的材料应该是比镁活泼的金属C .金属棒M 上发生反应:n M ne M -+-→D .这种方法称为牺牲阳极的阴极保护法 【答案】B 【解析】试题分析:A 、钢铁中含有石墨小颗粒,在潮湿的土壤中形成原电池,发生电化学腐蚀,正确;B 、若保护埋在酸性土壤中的钢质管道,金属棒M 的活泼性应大于Fe ,Fe 作正极免受腐蚀,错误;C 、金属棒M 作负极发生失电子反应:M - ne -=M n+,正确;D 、较活泼的M 作负极发生反应,Fe 作正极,受到保护,为牺牲阳极的阴极保护法,正确。
【2014泰安市一模】山东省泰安市2014届高三第一轮复习质量检测数学(理)

2014届泰安一模数学(理)试题2014.3一、选择题: 1.设复数()(),2,1z z a bi a b R i P a b i =+∈=-+,若成立,则点在 A.第一象限 B.第二象限 C.第三象限D.第四象限 2.如果点()02P y ,在以点F 为焦点的抛物线24y x =上,则PF 等于A.1B.2C.3D.43.为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老人,结果如表:由22()()()()()n ad bc K a b c d a c b d -=++++算得,22500(4027030160)9.96720030070430K ⨯⨯-⨯=≈⨯⨯⨯ 附表:参照附表,得到的正确结论是A.在犯错误的概率不超过0.1%的前提下,认为“需要志愿者提供帮助与性别有关”B.在犯错误的概率不超过0.1%的前提下,认为“需要志愿者提供帮助与性别无关”C.有99%以上的把握认为“需要志愿者提供帮助与性别有关”D.有99%以上的把握认为“需要志愿者提供帮助与性别无关”4.给定命题p :函数ln[(1)(1)]y x x =-+为偶函数;命题q :函数11x x e y e -=+为偶函数,下列正确是A.p q ∨是假命题 B.()p q ⌝∧是假命题C.p q ∧是真命题 D.()p q ⌝∨是真命题5.已知平面向量a,b 的夹角为120°,且1,a b a b ⋅=--则的最小值为 D.16.执行右面的程序框图,如果输入a=3,那么输出的n 的值为A.2 B.3 C.4D.57.将函数()2cos2f x x x -的图象向左平移m 个单位()2m π>-,若所得的图象关于直线6x π=对称,则m 的最小值为 A.3π- B.6π- C.0 D.12π8.如图矩形OABC 内的阴影部分是由曲线()sin ,(0,)f x x x π=∈及直线,(0,)x a a π=∈与x 轴 围成,向矩形OABC 内随机投掷一点,若落在阴影部分的概率为14,则a 的值是A.712πB.23πC.34πD.56π 9.某几何体的三视图如图所示,主视图和侧视图为全等的直角梯形,俯视图为直角三角形,则该几何体的表面积为A.6+ B. 16+ C.6+ D.16+10.已知函数2()(1)[(1)1]f x x x a x a b =-+++++的三个零点值分别可以作为抛物线、椭圆、双曲线的离心率,则22a b +的取值范围是A.)+∞ B.)+∞C.[5,)+∞ D.(5,)+∞二、填空题: 11.等比数列{}n a 的前n 项和为123,4,2,n S a a a 且成等差数列,若141a S ==,则 .12.从0,1,2,3,4,5,6,7,8,9,这10个数字中同时取4个不同的数,其和为偶数,则不同的取法为 .13.已知12F F ,是双曲线E 的两个焦点,以线段12F F 为直径的圆与双曲线的一个公共点是M ,若1230MF F ∠=, 则双曲线E 的离心率是 .14.已知3s i n ()52πββπ=<<,且sin()cos ,αβα+=则22sin sin cos 2cos αααα+-等于 . 15.定义域为R 的()f x 满足(1)2()f x f x +=,当(0,1]x ∈时,2()f x x x =-,则[]2,1x ∈--时,()f x 最小值为 .三、解答题: 16.在△ABC 中,角A 、B 、C 所对应的边分别为a 、b 、c ,且3cos .5b c C a a=+(I )求sinA ;(II )若10,a b BA BC ==求在上的投影.17.某班50位学生体育成绩的频率分布表如下:(I )估计成绩不低于80分的概率;(II )从成绩不低于80分的学生中随机选取3人,该3人中成绩在90分以上(含90分)的人数记为ξξ,求的数学期望.18.已知数列{}1n a a t =中,(t 为非零常数),其前n 项和为12n n n S a S +=,满足.(I )求数列{}n a 的通项公式; (II )若对任意的()*1n n N a n n λ∈>+,都有成立,求实数λ的取值范围.19.已知四棱锥P-ABCD 中,底面ABCD 为直角梯形, //BC AD ,=90BAD ∠,1PA AB BC ===,2AD =,PA ⊥面ABCD ,E 为AB 的中点.(I )证明:PC CD ⊥;(II )求二面角A-PD-C 的正切值;(III )设F 为PA 上一点,且14AF AP =,证明:EF//平面PCD.20.已知椭圆2241,x y O +=是坐标原点.(I )设椭圆在第一象限的部分曲线为C ,动点P 在C 上,C 在点P 处的切线与x 轴、y 轴的交点分别为G 、H ,以OG 、OH 为邻边作 OGMH ,求点M 的轨迹方程;(II )若椭圆与x 轴y 轴正半轴交于A 、B 两点,直线()0y kx k =>与椭圆交于R 、S 两点,求四边形ARBS 面积的最大值.21.已知函数()ln f x x mx =+,其中m 为常数.(I )当()1m f x =-时,求函数的单调区间;(II )若()(]0f x e 在区间, 上的最大值为3m -,求的值;(III )令()()2()1f x g x f x x x+'=-≥,若时,有不等式()1k g x x ≥+恒成立,求实数k 的取值范围.。
山东省2014届理科一轮复习试题选编28:直线与圆(含解析)

山东省2014届理科数学一轮复习试题选编28:直线与圆一、选择题1 .(山东省泰安市2013届高三第一轮复习质量检测数学(理)试题)直线()2110x a y +++=的倾斜角的取值范围是 ( )A .0,4π⎡⎤⎢⎥⎣⎦B .3[,)4ππ C .0,,42πππ⎡⎤⎛⎫⋃ ⎪⎢⎥⎣⎦⎝⎭D .3,,424ππππ⎡⎫⎡⎫⋃⎪⎪⎢⎢⎣⎭⎣⎭【答案】B直线的斜截式方程为221111y x a a =--++,所以斜率为211k a =-+,即21tan 1a α=-+,所以1tan 0α-≤<,解得34παπ≤<,即倾斜角的取值范围是3[,)4ππ,选 B . 2 .(山东省淄博市2013届高三复习阶段性检测(二模)数学(理)试题)在平面直角坐标系xoy 中,圆C的方程为228150x y x +-+=,若直线2y kx =+上至少存在一点,使得以该点为圆心,半径为1的圆与圆C 有公共点,则k 的最小值是 ( )A .43-B .54-C .35-D .53-【答案】A 因为圆C 的方程可化为:()2241x y -+=,所以圆C 的圆心为(4,0),半径为1.因为由题意,直线2y kx =+上至少存在一点00(,2)A x kx +,以该点为圆心,1为半径的圆与圆C 有公共点;所以存在0x R ∈,使得11AC ≤+成立,即min 2AC ≤. 因为min AC 即为点C 到直线2y kx =+,所以2≤,解得403k -≤≤.所以k 的最小值是43-,选A . 3 .(山东省文登市2013届高三3月二轮模拟考试数学(理))在平面直角坐标系xoy 中,圆C 的方程为228150x y x +-+=,若直线2y kx =-上至少存在一点,使得以该点为圆心,为半径的圆与圆C 有公共点,则k 的最大值为 ( )A .2B .43C .23D .3【答案】B4 .(山东省威海市2013届高三上学期期末考试理科数学)若直线y kx =与圆22(2)1x y -+=的两个交点关于直线20x y b ++=对称,则,k b 的值分别为 ( )A .1,42k b ==- B .1,42k b =-= C .1,42k b == D .1,42k b =-=- 【答案】A 因为直线y kx =与圆22(2)1x y -+=的两个交点关于直线20x y b ++=对称,则y kx =与直线20x y b ++=垂直,且20x y b ++=过圆心,所以解得1,42k b ==-,选A .5 .(山东省枣庄三中2013届高三上学期1月阶段测试理科数学)在圆x y x 522=+内,过点(25,23)有n条弦的长度成等差数列,最小弦长为数列的首项1a ,最大弦长为n a ,若公差为d∈[61,31],那么n 的取值集合为( )A .{4,5,6,7}B .{4,5,6}C .{3,4,5,6}D .{ 3.4.5,6,7}【答案】A【解析】圆的标准方程为22525()24x y -+=,所以圆心为5(,0)2,半径52r =,则最大的弦为直径,即5n a =,当圆心到弦的距离为32时,即点(25,23)为垂足时,弦长最小为4,即14a =,所以由1(1)n a a n d =+-得,1541111n a a d n n n --===---,因为1163d ≤≤,所以111613n ≤≤-,即316n ≤-≤,所以47n ≤≤,即4,5,6,7n =,选A . 6 .(山东省烟台市莱州一中2013届高三第三次质量检测数学(理)试题)若直线2x y -=被圆22()4x a y -+=所截得的弦长为,则实数a 的值为( )A .0或4B .1或3C .-2或6D .-1【答案】A 【解析】由圆的方程可知圆心坐标为(,0)a ,半径为2,因为弦AB的长为,所以圆心到直线的距离d ==.即圆心到直线20x y --=的距离d ,所以22a -=,解得4a =或0a =,选A .7 .(山东省济南市2013届高三3月高考模拟理科数学)已知直线0=++c by ax 与圆1:22=+y x O 相交于,A B 两点,且,3=AB 则OB OA ⋅ 的值是( )A .12-B .12C .34-D .0【答案】A在三角形OAB 中,1cos 2OAB ∠==-,所以23OAB π∠=,所以11cos 11()22OA OB OA OB OAB ⋅=⋅∠=⨯⨯-=- ,选A .8 .(山东省德州市2013届高三上学期期末校际联考数学(理))已知P 是直线:34110l x y -+=上的动点,P( )A .PB是圆222210x y x y+--+=的两条切线,C 是圆心,那么四边形PACB 面积的最小值是( )A B .CD .【答案】C【解析】圆的标准方程为22(1)(1)1x y -+-=,圆心为(1,1)C ,半径为1r =.根据对称性可知四边形PACB 面积等于1222APC S PA r PA ∆=⨯==要使四边形PACB 面积的最小值,则只需PC最小,此时最小值为圆心到直线:34110l x y -+=的距离1025d =,所以四边形PACB 面积的最小值为2APC S ∆===,选C,9 .(山东省兖州市2013高三9月入学诊断检测数学(理)试题)若函数21m y x x n n =-+的图象在点1(0,)M n处的切线l 与圆22:1C x y +=相交,则点(,)P m n 与圆C 的位置关系是( )A .圆内B .圆内或圆外C .圆上D .圆外【答案】D10.(山东省枣庄三中2013届高三上学期1月阶段测试理科数学)在直角坐标系中,30y +-=的倾斜角是 ( )A .6πB .3πC .65πD .32π 【答案】D【解析】直线的斜截式方程为3y =+,即直线的斜率tan k α==,所以23πα=,选 D . 11.(2013山东高考数学(理))过点(3,1)作圆22(1)1x y -+=的两条切线,切点分别为A ,B ,则直线AB的方程为 ( ) A .230x y +-= B .230x y --= C .430x y --= D .430x y +-=【答案】A 【解析】由图象可知,(1,1)A 是一个切点,所以代入选项知,,B D 不成立,排除.又AB 直线的斜率为负,所以排除C,选A 12.(山东省莱芜市莱芜二中2013届高三4月模拟考试数学(理)试题)若直线x-y=2被圆(x-a)2+y 2=4所截得的弦长为22,则实数a 的值为 ( ) A .-1或3 B .1或3 C .-2或6 D .0或4 【答案】D 13.(山东省莱芜市第一中学2013届高三12月阶段性测试数学(理)试题)若直线1x ya b+=通过点(cos sin )M αα,,则( )A .221a b +≤B .221a b +≥C .22111a b +≤ D .22111a b+≥ 【答案】解: D .由题意知直线1x ya b+=与圆221x y +=有交点,则22111a b +1,≥.另解:设向量11(cos ,sin ),(,)a b ααm =n =,由题意知cos sin 1a bαα+=由⋅≤m n m n可得cos sin 1a b αα=+ 14.(2013届山东省高考压轴卷理科数学)若直线10x y -+=与圆22()2x a y -+=有公共点,则实数a 取值范围是( )A .[-3,-1]B .[-1,3]C .[-3,l ]D .(-∞,-3] ⋃ [1.+∞)【答案】C 【解析】因为直线10x y -+=与圆22()2x a y -+=有公共点,所以圆心(,0)a 到直线10x y -+=的距离+12d a ≤≤≤即,所以-3a 1.15.(山东省夏津一中2013届高三4月月考数学(理)试题)若点()n m ,在直线01034=-+y x 上,则22n m +的最小值是 ( )A .2B .22C .4D .32 【答案】C 16.(山东省烟台市2013届高三上学期期末考试数学(理)试题)若与向量(1,1)v =平行的直线l 与圆221x y +=交于( ) A .B 两点,则A B 最大值为( )A .2B .C .4D .【答案】A【解析】因为直线l 与向量(1,1)v =平行,所以直线的斜率为1,当直线与圆相交时,A B 最大值为直径2,所以选A . 17.(山东省实验中学2013届高三第三次诊断性测试理科数学)已知两条直线2-=ax y 和01)2(3=++-y a x 互相平行,则a 等于( ) A .1或-3 B .-1或3 C .1或3 D .-1或3 【答案】A 【解析】因为直线2-=ax y 的斜率存在且为a ,所以(2)0a -+≠,所以01)2(3=++-y a x 的斜截式方程为3122y x a a =+++,因为两直线平行,所以32a a =+且122a ≠-+,解得1a =-或3a =,选A .18.(山东省实验中学2013届高三第三次诊断性测试理科数学)已知P(x,y)是直线)0(04>=++k y kx 上一动点,PA,PB 是圆C:0222=-+y y x 的两条切线, ( ) A .B 是切点,若四边形PACB 的最小面积是2,则k 的值为 ( )A .3B .212 C .22D .2【答案】D 【解析】由圆的方程得22(1)1x y +-=,所以圆心为(0,1),半径为1r =,四边形的面积2S S PBC ∆=,所以若四边形PACB 的最小面积是2,所以S PBC ∆的最小值为1,而12S PBC r PB ∆=,即PB 的最小值为2,此时PC 最小为圆心到直线的距离,此时d ===,即24k =,因为0k >,所以2k =19.(山东省莱芜市莱芜十七中2013届高三4月模拟数学(理)试题)点()2,1P -为圆()22125x y -+=内弦AB 的中点,则直线AB 的方程为 ( )A .10x y +-=B .230x y +-=C .30x y --=D .250x y --= 【答案】C 20.(山东省济南市2012届高三3月高考模拟题理科数学(2012济南二模))直线1l :kx +(1-k )y -3=0和2l :(k -1)x +(2k +3)y -2=0互相垂直,则k =( )A .-3或-1B .3或1C .-3或1D .-1或3【答案】C【解析】若1=k ,直线3:1=x l ,52:2=y l ,满足两直线垂直.若1≠k ,直线21l l ,的效率分别为321,121+-=-=k k k k k k ,由121-=⋅k k 得,3-=k ,综上1=k 或3-=k ,选 C .二、填空题21.(2013年山东临沂市高三教学质量检测考试理科数学)直线y=x 的任意点P 与圆22102240x y x y +--+=的任意点Q 间距离的最小值为_______.【答案】2 圆的标准方程为22(5)(1)2x y -+-=,所以圆心为(5,1),半径为2r =.圆心到直线y x =的距离为51222d -==,所以PQ 的最小值为2222d r -=-=.22.(2010年高考(山东理))已知圆C 过点(1,0),且圆心在x 轴的正半轴上,直线l:1y x =-被圆C 所截得的弦长为22,则过圆心且与直线l 垂直的直线方程为_______________.【答案】x+y-3=0【解析】由题意,设所求的直线方程为x+y+m=0,设圆心坐标为(a,0),则由题意知:22()+2=(a-1)2,解得a=3或-1,又因为圆心在x 轴的正半轴上,所以a=3,故圆心坐标为 (3,0),因为圆心(3,0)在所求的直线上,所以有3+0+m=0,即m=-3,故所求的直线方程为 x+y-3=0. 【命题意图】本题考查了直线的方程、点到直线的距离、直线与圆的关系,考查了同学们解决直线与圆问题的能力. 23.(山东省莱芜市莱芜二中2013届高三4月模拟考试数学(理)试题)设点(1,0)A ,(2,1)B ,如果直线1ax by +=与线段AB 有一个公共点,那么22a b +的最小值为_________【答案】15.24.(山东省2013届高三高考模拟卷(一)理科数学)如图放置的边长为2的正方形PABC 沿x 轴滚动.设顶点),(y x P 的轨迹方程是)(x f y =,则)(x f y =在其两个相邻零点间的图象与x 轴所围成的区域的面积为______.【答案】44π+【解析】由于本题是求两个相邻零点问的图象与x 轴所围成的区域的面积,所以为了简便,可以直接将P 点移到原点,开始运动,如图所示,当P 点第一次回到x 轴时经过的曲线是三段相连的圆弧,它与x 轴围成的区域面积为2221112[2222]244444ππππ⨯⨯+⨯⨯+⨯+⨯⨯=+().。
山东省泰安市2014届高三第一轮复习质量检测-语文(精)

山东省泰安市2014届高三第一轮复习质量检测-语文(精) 考试概况山东省泰安市2014届高三第一轮复习质量检测-语文(精)于20xx年xx月xx 日上午进行,考试时间为150分钟,试卷满分为150分,共分两部分:选择题和非选择题。
本次考试的选择题部分共40题,每题2分,共80分。
非选择题部分共2篇文章,分别为80分和40分,总计120分。
选择题部分选择题部分内容涵盖了高中三年语文学科的所有知识点,难度适中,题目形式多样,考查了考生的阅读理解和语文应用能力。
据考生反馈,选择题难度较前几年的模拟试卷略有下降,但对于一些偏生僻的字、词汇考查较为严格,需要考生具备丰富的语言积累和较强的语言应用能力。
总体来看,选择题部分难度适中,符合教材,考查内容全面,对于标准答案的解释较为详细,针对不同错误提供了不同的具体解释,便于帮助考生分清错误的原因和原因所在。
非选择题部分非选择题部分共分为两个部分,第一篇文章是阅读理解,共五个小题,每题16分,总计80分。
第二篇文章是作文,共40分。
第一篇文章第一篇文章选取了一篇以“城市绿化”为主的科普文章,围绕城市绿化的意义、作用和意识提升展开讨论,通过具体实例和数据分析展示城市绿化的重要性,结合社会现状呼吁人们加强绿化意识。
据考生反馈,阅读理解文章难度一般,文章属于科普类文章,语言简单易懂,内容丰富,针对性强,文章结构清晰,题目设计合理,适当考查了考生的语言理解能力、语言表达能力和实际应用能力。
第二篇文章第二篇文章是一篇议论性文本,选取的话题为“如何保障食品安全”,要求学生结合实际情况,针对食品安全问题展开讨论,提出自己的看法和建议。
据考生反馈,作文难度较大,选题很有实际意义,要求考生从多个角度分析问题,条理清晰,逻辑严谨。
但是作文不太注重对语言的修辞和文学性的要求,更注重实用性和个性表达,但是在使用语言上没有太多的限制。
通过本次考试,可以看出山东省泰安市2014届高三第一轮复习质量检测-语文(精)试卷整体难度适中,考查范围广泛,覆盖了语文学科的多个知识点。
山东省泰安市2014届高三历史第一轮复习质量检测试题(泰安市一模)(含解析)

高三第一轮复习质量检测历史试题2014.3 本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,共8页。
满分100分,考试时间为90分钟。
答卷前,考生务必将自己的某某、考号、考试科目、试卷类型用铅笔涂写在答题纸上。
考试结束后,监考人员将本试卷和答题纸一并收回。
第I卷(选择题45分)注意事项:1.第I卷共30小题.每小题1.5分,共45分。
在每小题所列的四个选项中,只有一项符合题目要求。
2.每小题选出答案后,用铅笔把答题纸上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后。
再选涂其他答案.不能答在试卷上。
1.斯塔夫里阿诺斯在《全球通史》中说:“中国人的姓总是位于个人的名字之前,而不像西方那样,位于个人的名字之后。
”中国人强调姓所反映的实质是A.男尊女卑思想严重 B.家族宗法观念浓厚C.个人观念淡漠D.专制王权强大【答案】B考点:宗法制。
本题考查学生对西周时期宗法制的准确理解,由材料可得出姓氏和血脉、家族相联在一起,中国人将姓置个人名字之前反映出家族宗法观念浓厚,而宗法制度是由氏族社会父系家长制演变而来的,是王族贵族按血缘关系分配国家权力,以便建立世袭统治的一种制度。
故B符合题意。
2.右图为《唐书》所载的830名进士的出身分布比例。
由此可见,唐代选官制度A.为选拔士族子弟而设立B.仍然是世卿世禄制度C.缩小了人才选拔的X围D.兼顾多个阶层但不完善【答案】D考点:科举制。
本题主要考查学生准确解读图片信息的能力,从图片中可以看出在唐代科举制选拔出的人才中世族子弟依然占据支配地位,下层民众所占比例较低,说明唐代的科举制尽管较九品中正制有很大的进步,但在人才选拔上依然不够公平、公正,仍然须进一步完善,故D项符合题意,ABC三项表述错误,与科举制本身的史实不符。
3.两千多年前雅典就产生了“三权分立”的国家组织形式:公民大会、五百人议事会、民众法庭。
1787年宪法规定美国行使相应权力的机构是A.总统、国会、最高法院B.议会、首相、上议院C.国会、总统、最高法院D.首相、议会、上议院【答案】C考点:古代雅典城邦公民大会、五百人议事会、民众法庭分别掌握的是立法权、行政权和司法权。
山东省泰安市2014高三一模(语文)

山东省泰安市2014高三一模(语文)高考语文2014-04-01 1943()泰安市高三第一轮复习质量检测语文试题注意事项:1.本试题分为选择题和非选择题两部分,共8页。
满分150分,答题时间150分钟。
2.答题前。
考生务必先将密封线内的项目填写清楚。
答第Ⅰ卷前先将自己的学校、姓名、考号、考试科目用铅笔涂写在答题卡上。
3.选择题的每小题选出答案后。
用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,不能答在试题纸或答题纸上。
4.非选择题写在答题纸对应区域内,严禁在试题纸或草稿纸上答题。
5.考试结束后,将试题纸、答题卡和答题纸一并交回。
第Ⅰ卷(选择题共36分)一、(15分,每小题3分)1.下列加点词语中每对读音都相同的一组是A.铺展/逮捕然诺/糯米潸然泪下/姗姗来迟B.坍塌/踏实阿谀/须臾逸兴遄飞/如椽巨笔C.凌驾/聆教分娩/婉约蹁跹起舞/骈拇枝指D.歃血/煞白摭谈/踯躅膘肥体壮/粗犷剽悍2.下列各组词语中没有错别字的一项是A.丹清构架晴空丽日虚无缥缈B.蓄志讲座危如垒卵添枝加叶C.静穆缱绻蓬头垢面了如指掌D.荧屏陨落不明就里押卷之作3.依次填入下列各句横线处的词语,最恰当的一组是①《孔子》与《刺陵》有如此票房奇迹,不单因为有好莱坞“灾难片大师”罗兰·艾默里奇作招牌,也受《独立日》影像印记影响,还有人们对“世界末日”的猎奇……②人们甚至觉得,《潜伏》中的两个虚构的人物应当续写情缘,实现他们自己那些在现实面前显得无奈的理想。
让如今的青年人意识到还有时间不能够的纯真感情。
③“毒豆角事件”本质上是利益的,导致公共利益虚置与错位。
因此,发现了“毒豆角”就查豆角,在海南发现的就追查海南的做法,都还只是治标不治本。
A.不止侵蚀纠葛 B.不只腐蚀瓜葛C.不止腐蚀瓜葛 D.不只侵蚀纠葛4.下列各句中,加点的成语使用恰当的一项是A.在东亚四强赛上,国足气冲斗牛,以30大比分大胜韩国足球队,打破了32年来逢韩必败的怪圈,令国人瞬间点燃对足球的热望。
【2014泰安市一模】山东省泰安市2014届高三第一轮复习质量检测英语试题Word版含答案

试卷类型:A高三第一轮复习质量检测英语试题2014.3 本试卷分第I卷(选择题)和第II卷(非选择题)两部分。
第I卷1至l0页。
第II卷11至12页。
满分为150分。
考试用时120分钟。
第I卷(共105分)注意事项:1.答第I卷前,考生务必将自己的姓名、准考证号、考试科目、试卷类型用铅笔涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
不能答在试卷上。
第一部分英语知识运用(共两节,满分55分)第一节语法和词汇知识(共10小题;每小题1.5分,满分15分)从A、B、C、D四个选项中,选出可以填入空白处的最佳选项,并在答题卡上将该项涂黑。
1.一W0uld it bother you if I turned up the radio?一___________.Lisa is sleeping.A.That’s all right B.I’m afraid soC.I suppose not D.It doesn’t matter2.The book is of great value,but____can be enjoyed unless you digest it.A.everything B.something C.nothing D.anything3.You’d better pull your car to the side of the road if you_____answer a phone call.A.must B.will C.can D.may4.My daughter reads a lot of books,_____from contemporary novels to ancient poems.A.having ranged B.range C.ranging D.to range5.They_____a rise in salary with the prices of food,petrol and housing increasing every day.A.are expected B.expected C.expect D.are expecting6.They regard it as their duty_______the best service to the customers.A.to provide B.providing C.provide D.Provided7.Many cities in the world have been polluted heavily,_______Beijing is an example.A.for which B.in which C.from which D.of which8.Children will act positively when they are praised,_____it is just a nod with smile.A.as though B.even if C.in case D.so that9.I’m afraid he is more of a talker than a doer,which is_______he never finishes anything.A.why B.when C.that D.where10.Scientists predict that by 2025,90%of all electronic communication______by mobile phone.A.will conduct B.will be conductedC.has conducted D.is conducted第二节完形填空(共30小题,1 l-20每小题1分,21-40每小题1.5分,满分40分) 阅读下面短文,掌握其大意,然后从11-40各题所给的四个选项(A、B、C和D)中选出最佳选项,并在答题卡上将该项涂黑。
山东省泰安市2014届高三第一轮复习质量检测英语1

山东省泰安市2014届高三第一轮复习质量检测英语1高考英语2014-03-23 1943()泰安市高三第一轮复习质量检测英语试题 2014.3本试卷分第I卷(选择题)和第II卷(非选择题)两部分。
第I卷1 至2014 页。
第II卷11至14页。
满分为150分。
考试用时120分钟。
第I卷(三部分,共20145分)注意事项:1. 答第I卷前, 考生务必将自己的姓名、准考证号、考试科目、试卷类型用铅笔涂写在答题卡上。
2. 每小题选出答案后, 用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动, 用橡皮擦干净后, 再选涂其他答案标号。
不能答在试卷上。
第一部分听力(共两节,满分30分)第一节(共5小题;每小题1.5分, 满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你将有1 0秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. What does the man mean?A. He wants to go to the park.B. He doesn’t know where to park the car.C. He wonders how to get to the park.2. What does the man usually do on Sunday evenings?A. He goes to the church.B. He reads the paper.C. He visits friends.3. Where do you suppose the conversation takes place?A. In a theatre.B. In the ticketoffice. C. In the church.4. What does the man mean?A. They are no t going too fast.B. They aren’t going to be on time.C. A good driver should learn to drive fast.5. What can we learn from the dialogue?A. The man went to t he club, which was unusual.B. The woman regularly visited the man at ten in the evening.C. The man takes some exercises regularly at the club.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
【2014泰安市一模】山东省泰安市2014届高三第一轮复习质量检测 政治试题 Word版含解析

本试卷分第I卷(选择题)和第II卷(非选择题)两部分,满分100分。
考试时间90分钟。
第I卷(选择题,共50分)注意事项:1.答第I卷前,考生务必将自己的姓名、考号填写在答题卡上。
2.选择题答案使用2B铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案的标号,非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写在答题纸规定位置,字体工整,笔迹清楚。
一、在下列各题的四个选项中,只有一项是最符合题目要求的。
每小题2分,共50分。
在四川双流的一些小区、临街商铺等地出现了储物柜一样的“绿箱子”。
这些箱子背后,是一种全新的消费模式——O2C(Office to customer),即从原产地(或基地)直接将产品送到消费者厨房的预订消费模式。
据此回答1—2题。
1.“O2C”消费模式的出现,帮助农场生产者有效回避了市场风险,避免生产浪费;帮助市民购买到价格合适、质量安全的新鲜蔬菜。
从生产与消费的关系看,这说明A.收入是消费的基础和前提 B.消费对生产具有重要反作用C.消费决定产业的优化升级 D.价格变动影响生产规模2.四川双流大学生创业园一群“90”后组成的创业团队,创新打造“种植管家”,连接蔬菜种植户和市民餐桌,短短一个月便吸引了600多家客户。
在日益严峻的就业形势下,四川双流大学生创业团队给我们的启示有①实施就业优先战略和积极的就业政策②劳动者要树立正确的就业观念③劳动者就业有利于使社会劳动力不断再生产④要提高劳动者的技能和素质实现自主就业A.①② B.①③ C.②④ D.③④3.上表主要说明A.消费心理影响人们的消费行为 B.收入预期影响人们当前的消费C.收入差距影响社会总体消费水平 D.消费能带动一个产业的出现和成长4.《中共中央关于全面深化改革若干重大问题的决定》指出:国有资本、集体资本、非公有资本等交叉持股、相互融合的混合所有制经济,是基本经济制度的重要实现形式,允许更多国有经济和其他所有制经济发展成为混合所有制经济。
山东省2014届理科数学一轮复习试题选编41:函数的极值与导数(教师版)

山东省2014届理科数学一轮复习试题选编41:函数的极值与导数一、选择题1 .(2012年高考(陕西文))设函数f(x)=2x+lnx 则 ( )A .x=12为f(x)的极大值点 B .x=12为f(x)的极小值点 C .x=2为 f(x)的极大值点 D .x=2为 f(x)的极小值点解析:22()x f x x -'=,令()0,f x '=得2x =,2x <时,()0f x '<,1()ln f x x x=+为减函数;2x >时,()0f x '>,1()ln f x x x=+为增函数,所以2x =为()f x 的极小值点,选 D .2 .(山东济南外国语学校2012—2013学年度第一学期高三质量检测数学试题(理科))若a>0,b>0,且函数224)(23---=bx ax x x f 在x=1处有极值,则ab 的最大值( )A .2B .3C .6D .9【答案】D 【解析】函数的导数为2'()1222f x x a x b =--,函数在1x =处有极值,则有'(1)1222f a b =--=,即6a b +=,所以6a b =+≥,即9ab ≤,当且仅当3a b ==时取等号,选D .3 .(2013浙江高考数学(理))已知e 为自然对数的底数,设函数)2,1()1)(1()(=--=k x e x f k x ,则( )A .当1=k 时,)(x f 在1=x 处取得极小值B .当1=k 时,)(x f 在1=x 处取得极大值C .当2=k 时,)(x f 在1=x 处取得极小值D .当2=k 时,)(x f 在1=x 处取得极大值【答案】 C 解:当2k =时,222()(1)(1)()2(1)(1)f x e x f x e x '=--⇒=--,且210e ->,所以当1x >时,()0f x '>,函数递增;当1x <时,()0f x '<,函数递减;所以当1x =时函数取得极小值;所以选C;4 .(山东省泰安市2013届高三第一轮复习质量检测数学(理)试题)设函数()()3402f x x x a a =-+<<有三个零点1x 、x 2、x 3,且123,x x x <<则下列结论正确的是 ( )A .11x >-B .20x <C .32x >D .201x <<【答案】D∵函数()()3402f x x x a a =-+<<, ∴f′(x)=3x 2﹣4.令f′(x)=0,得 x=±.∵当x <,'()0f x >;在(上,'()0f x <;在)+∞上,'()0f x >.故函数在(,-∞)上是增函数,在(上是减函数,在)+∞上是增函数.故(f是极大值,f 是极小值.再由 f (x)的三个零点为x 1,x 2,x 3,且123,x x x <<得 x 1<﹣,﹣<x 2,x 3>.根据f(0)=a>0,且f()=a ﹣<0,得>x 2>0.∴0<x 2<1.选D .5 .(山东师大附中2013届级高三12月第三次模拟检测理科数学)设函数()()3402f x x x a a =-+<<有三个零点123123,,x x x x x x <<、、且 则下列结论正确的是( )A .11x >-B .20x <C .201x <<D .32x >【答案】C 【解析】因为(3)150f a -=-<,(1)30f a -=+>,(0)0f a =>(1)30f a =-<,(2)0f a =>,所以函数的三个零点分别在(3,1),(0,1),(1,2)--之间,又因为123,x x x <<所以12331,012x x x -<<-<<<<,选C .6 .(2012年高考(大纲理))已知函数33y xx c =-+的图像与x 轴恰有两个公共点,则c = ( ) A .2-或2 B .9-或3 C .1-或1 D .3-或1【答案】 答案A【解析】因为三次函数的图像与x 轴恰有两个公共点,结合该函数的图像,可得极大值或者极小值为零即可满足要求.而2()333()(1)f x x x x '=-=-+,当1x =±时取得极值 由(1)0f =或(1)0f -=可得20c -=或20c +=,即2c =±.7 .(2013福建高考数学(文))设函数)(x f 的定义域为R ,)0(00≠x x 是)(x f 的极大值点,以下结论一定正确的是( )A .)()(,0x f x f R x ≤∈∀B .0x -是)(x f -的极小值点C .0x -是)(x f -的极小值点D .0x -是)(x f --的极小值点【答案】 D 【解析】本题考查的是函数的极值.函数的极值不是最值,A 错误;因为)(x f --和)(x f 关于原点对称,故0x -是)(x f --的极小值点,D 正确.8 .(2013湖北高考数学(文))已知函数()(ln )f x x x ax =-有两个极值点,则实数a 的取值范围是 ( )A .(,0)-∞B .1(0,)2C .(0,1)D .(0,)+∞【答案】B .ax x x f 21ln )('-+=,由()(ln )f x x x ax =-由两个极值点,得0)('=x f 有两个不等的实数解,即12ln -=ax x 有两个实数解,从而直线12-=ax y 与曲线x y ln =有两个交点. 过点(0,-1)作x y ln =的切线,设切点为(x 0,y 0),则切线的斜率01x k =,切线方程为110-=x x y . 切点在切线上,则0100=-=x x y ,又切点在曲线x y ln =上,则10ln 00=⇒=x x ,即切点为(1,0).切线方程为1-=x y . 再由直线12-=ax y 与曲线x y ln =有两个交点.,知直线12-=ax y 位于两直线0=y 和1-=x y 之间,如图所示,其斜率2a 满足:0<2a<1,解得0<a <21.9 .(2012年高考(重庆理))设函数()f x 在R 上可导,其导函数为()f x ',且函数(1)()y x f x '=-的图像如题(8)图所示,则下列结论中一定成立的是 ( ) A .函数()f x 有极大值(2)f 和极小值(1)f B .函数()f x 有极大值(2)f -和极小值(1)fC .函数()f x 有极大值(2)f 和极小值(2)f -D .函数()f x 有极大值(2)f -和极小值(2)f【答案】 【答案】D【解析】2,10x x <-->,由(1)()0()0x f x f x ''->⇒>,函数()f x 为增;21,10x x -<<->,由(1)()0()0x f x f x ''-<⇒<,函数()f x 为减; 12,10x x <<-<,由(1)()0()0x f x f x ''->⇒<,函数()f x 为减; 2,10x x >-<,由(1)()0()0x f x f x ''-<⇒>,函数()f x 为增.【考点定位】判断函数的单调性一般利用导函数的符号,当导函数大于0,则函数为增,当导函数小于0则函数递减.10.(2013辽宁高考数学(理))设函数()()()()()222,2,0,8x e e f x x f x xf x f x f x x '+==>满足则时,( )A .有极大值,无极小值B .有极小值,无极大值C .既有极大值又有极小值D .既无极大值也无极小值【答案】 D 解:由已知,2[()]x e x f x x '=(1) .在已知2()2()x e x f x xf x x'+=中令2x =,并将2(2)8e f =代入,得(2)0f '=;因为2()2()x e x f x x f x x'=-,两边乘以x 后令32()()2[()](2)x g x x f x e x f x '==- .求导并将(1)式代入,2()2x x x e x g x e e x x-'=-⋅=,显然(0,2)x ∈时,()0g x '<,()g x 减;(2,)x ∈+∞时,()0g x '>,()g x 增;并且由(2)式知(2)0g =,所以(2)0g =为()g x 的最小值,即()0g x ≥,所以3()0x f x '≥,在0x >时得()0f x '≥,所以()f x 为增函数,故没有极大值也没有极小值.二、填空题11.(山东省泰安市2013届高三上学期期末考试数学理)已知函数()f x 的定义域为[]1,5-,部分对应值如下表,()f x 的导函数()y f x '=的图像如图所示,给出关于()f x 的下列命题:①函数()2y f x x ==在时,取极小值②函数()[]0,1f x 在是减函数,在[]1,2是增函数,③当12a <<时,函数()y f x a =-有4个零点④如果当[]1,x t ∈-时,()f x 的最大值是2,那么t 的最小值为0,其中所有正确命题序号为_________.【答案】①③④【解析】由导数图象可知,当10x -<<或24x <<时,'()0f x >,函数递增.当02x <<或45x <<时,'()0f x <,函数递减.所以在2x =处,函数取得极小值,所以①正确,②错误.当12a <<时,由()0y f x a =-=得()f x a =.由图象可知,此时有四个交点,所以③正确.当[]1,x t ∈-时,()f x 的最大值是2,由图象可知0t ≥,所以t 的最小值为0,所以④正确.综上所有正确命题序号为①③④.三、解答题12.(2013届山东省高考压轴卷理科数学)已知函数f (x )=-13x 3+a2x 2-2x (a ∈R).(1)当a =3时,求函数f (x )的单调区间;(2)若对于任意x ∈[1,+∞)都有f ′(x )<2(a -1)成立,求实数a 的取值范围;(3)若过点⎝⎛⎭⎪⎫0,-13可作函数y =f (x )图象的三条不同切线,求实数a 的取值范围. 【答案】【解析】(1)当a =3时,f (x )=-13x 3+32x 2-2x ,得f ′(x )=-x 2+3x -2.因为f ′(x )=-x 2+3x -2=-(x -1)(x -2),所以当1<x <2时,f ′(x )>0,函数f (x )单调递增; 当x <1或x >2时,f ′(x )<0,函数f (x )单调递减.故函数f (x )的单调递增区间为(1,2),单调递减区间为(-∞,1)和(2,+∞).(2)方法一:由f (x )=-13x 3+a2x 2-2x ,得f ′(x )=-x 2+ax -2.因为对于任意x ∈[1,+∞)都有f ′(x )<2(a -1)成立,即对于任意x ∈[1,+∞)都有-x 2+ax -2<2(a -1)成立,即对于任意x ∈[1,+∞)都有x 2-ax +2a >0成立. 令h (x )=x 2-ax +2a ,要使h (x )对任意x ∈[1,+∞)都有h (x )>0成立,必须满足Δ<0,或⎩⎪⎨⎪⎧Δ≥0,a2≤1,h 1>0.即a 2-8a <0或⎩⎪⎨⎪⎧a 2-8a ≥0,a2≤1,1+a >0.所以实数a 的取值范围为(-1,8).方法二:由f (x )=-13x 3+a2x 2-2x ,得f ′(x )=-x 2+ax -2.因为对于任意x ∈[1,+∞)都有f ′(x )<2(a -1)成立,即对于任意x ∈[1,+∞)都有f ′(x )max <2(a -1).因为f ′(x )=-⎝ ⎛⎭⎪⎫x -a 22+a24-2,其图象开口向下,对称轴为x =a 2.①当a2<1,即a <2时,f ′(x )在[1,+∞)上单调递减,所以f ′(x )max =f ′(1)=a -3.由a -3<2(a -1),得a >-1,此时-1<a <2;②当a2≥1,即a ≥2时,f ′(x )在⎣⎢⎡⎦⎥⎤1,a 2上单调递增,在⎝ ⎛⎭⎪⎫a 2,+∞上单调递减,所以f ′(x )max =f ′⎝ ⎛⎭⎪⎫a 2=a24-2.由a 24-2<2(a -1),得0<a <8,此时2≤a <8.综上①②可得,实数a 的取值范围为(-1,8).(3)设点P ⎝ ⎛⎭⎪⎫t ,-13t 3+a 2t 2-2t 是函数y =f (x )图象上的切点,则过点P 的切线的斜率为k =f ′(t )=-t 2+at -2,所以过点P 的切线方程为y +13t 3-a2t 2+2t =(-t 2+at -2)(x -t ).因为点⎝⎛⎭⎪⎫0,-13在切线上,所以-13+13t 3-a 2t 2+2t =(-t 2+at -2)(0-t ),即23t 3-12at 2+13=0. 若过点⎝ ⎛⎭⎪⎫0,-13可作函数y =f (x )图象的三条不同切线,则方程23t 3-12at 2+13=0有三个不同的实数解. 令g (t )=23t 3-12at 2+13,则函数y =g (t )与t 轴有三个不同的交点.令g ′(t )=2t 2-at =0,解得t =0或t =a2.因为g (0)=13,g ⎝ ⎛⎭⎪⎫a 2=-124a 3+13,所以g ⎝ ⎛⎭⎪⎫a 2=-124a 3+13<0,即a >2.所以实数a 的取值范围为(2,+∞).13.(山东省青岛即墨市2013届高三上学期期末考试数学(理)试题)已知函数),1()1ln()1(2)1(2)(2+∞∈--+-+=x x a x a x x f .(1)23=x 是函数的一个极值点,求a 的值; (2)求函数)(x f 的单调区间; (3)当2=a 时,函数)0(,)(2>--=b b x x g ,若对任意⎥⎦⎤⎢⎣⎡++∈1,11,21e e m m ,e e m f m g 22|)()(|212+<-都成立,求b 的取值范围.【答案】解:(1)函数)1(1)1(2)1(2)(2--+-+=x n a x a x x f1)1(2)1(22)(--+-+='x a a x x f , 23=x 是函数的一个极值点0)23(='∴f解得:23=a(2)1)(21)1(2)1(22--=--+-+='x a x x x a a x f ),的定义域是(又∞+1)(x f),)的单调增区间为((时,函数当∞+≤∴11x f a 为增区间)为减区间,(,时,(当),11+∞〉a a a(3)当a=2时,由(2)知f(x)在(1,2)减,在(2,+∞)增.3)1(,11)11(,0)2(22-=++=+=e e f e e f f]3,0[]1,11[)(2-++=∴e e ex f y 的值域在为减函数在]1,11[)(2++--=e eb x x g])11(,1[]1,11[)(22b eb e e e x g y -+--+-++=∴)(的值域为在b>0成立,只要所以e e m g m f b e b e 22)()(0)1(,0)11(22122+〈-〈-+-〈-+-∴成立即可e e b e e b e e b e e 22222)1(3))1(3222222+〈+-+=+++-=-+---解得:0<b<214.(山东省泰安市2013届高三第一轮复习质量检测数学(理)试题)已知函数()()()()201,10.x fx a x b x c e f f =++==且 (I)若()f x 在区间[]0,1上单调递减,求实数a 的取值范围;(II)当a=0时,是否存在实数m 使不等式()224141x f x xe mx x x +≥+≥-++对任意x R ∈恒成立?若存在,求出m 的值,若不存在,请说明理由. 【答案】15.(山东省凤城高中2013届高三4月模拟检测数学理试题 )已知曲线32()f x x bx cx =++在点(1,(1)),(3,(3)A f B f --处的切线互相平行,且函数()f x 的一个极值点为0x =.(Ⅰ)求实数,c b 的值;(Ⅱ)若函数1()([,3])2y f x x =∈-的图象与直线y m =恰有三个交点,求实数m 的取值范围; (Ⅲ)若存在0[1,](x e e ∈ 2.71828)≈ ,使得0001()ln 6f x a x ax '+≤成立(其中()()f x f x '为的导数),求实数a 的取值范围【答案】(Ⅰ)2()32f x x bx c '=++,依题意有(1)(3)(0)0f f f ''-=⎧⎨'=⎩,即322760b c b cc -+=++⎧⎨=⎩,所以3,0.b c =-= (Ⅱ)322()3,()36f x x x f x x x '=-=-,由()0,02()0,02f x x x f x x ''><><<<得或,由得,所以函数()f x 在区间1[,0),(2,3]2-上递增,在区间(0,2)上递减 且17(),(0)0,(2)4,(3)028f f f f -=-==-=.所以函数()f x 的图象与直线y m =恰有三个交点,则708m -≤<,所以实数m 的取值范围为7[,0).8- (Ⅲ)依题意00001[1,],()ln ,6x e f x a x ax '∃∈+≤使得即200001ln 2x x a x ax -+≤成立, 设2min 1()ln (1),()02g x x a x a x g x '=+-+≤则,则min ()0g x ≤, ①当1a ≤时,由[1,],()0x e g x '∈>得函数()g x 在(1,)e 上递增,所以min 1()(1)(1)0,2g x g a ==-+≤得112a -≤≤②当1a e <<时,在(1,)a 上()0,g x '<在(,)a e 上()0,g x '>所以2min 1()()(1ln )02g x g a a a a ==---≤恒成立,所以1.a e <<③当a e ≥时,在[1,]e 上()0,g x '<所以函数是减函数,所以2min1()()02g x g e e a ae e ==-+--≤,222(1)e e a e -≥-, 又222(1)e ee e -<-,所以.a e ≥ 所以实数a 的取值范围为1[,).2-+∞16.(2013课标Ⅰ卷高考数学(文))(本小题满分共12分)已知函数2()()4x f x e ax b x x =+--,曲线()y f x =在点(0,(0))f 处切线方程为44y x =+. (Ⅰ)求,a b 的值;(Ⅱ)讨论()f x 的单调性,并求()f x 的极大值.【答案】【解析】(Ⅰ)()f x '=()24xeax a b x ++--.由已知得(0)f =4,(0)f '=4,故4b =,a b +=8,从而a =4,4b =;(Ⅱ)由(Ⅰ)知,()f x =24(1)4x e x x x +--,()f x '=4(2)24x e x x +--=14(2)()2x x e +-,令()f x '=0得,x =ln 2-或x =-2,∴当(,2)(ln 2,)x ∈-∞-⋃-+∞时,()f x '>0,当x ∈(-2,ln 2-)时,()f x '<0, ∴()f x 在(-∞,-2),(ln 2-,+∞)单调递增,在(-2,ln 2-)上单调递减.当x =-2时,函数()f x 取得极大值,极大值为2(2)4(1)f e --=-.17.(山东省烟台市2013届高三上学期期中考试数学试题(理科))已知函数)(ln )(R a x ax x f ∈+=.(1)求)(x f 的极值;(2)若函数)(x f 的图象与函数1)(=x g 的图象在区间],0(2e 上有公共点,求实数a 的取值范围【答案】解:(1))(x f 的定义域为),0(+∞,2)(ln 1)('x a x x f +-=,令0)('=x f 得a e x -=1, 当),0(1aex -∈时,,0)('>x f )(x f 是增函数;当),(1+∞∈-a e x 时,,0)('<x f )(x f 是减函数, ∴)(x f 在a e x -=1处取得极大值,11)()(--==a ae ef x f 极大值,无极小值(2)①当21e e a <-时,即1->a 时, 由(1)知)(x f 在),0(1ae-上是增函数,在],(21e e a -上是减函数,11max)()(--==∴a a e e f x f ,又当a e x -=时,0)(=x f ,当],0(aex -∈时,0)(<x f ;当],(2e e x a -∈时,0)(>x f ;)(x f 与图象1)(=x g 的图象在],0(2e 上有公共点, 11≥∴-a e ,解得1≥a ,又1->a ,所以1≥a②当21e e a ≥-时,即1-≤a 时,)(x f 在],0(2e 上是增函数, ∴)(xf 在],0(2e 上的最大值为222)(eae f +=, 所以原问题等价于122≥+ea ,解得22-≥e a . 又1-≤a ,∴无解. 综上,实数a 的取值范围是),1[+∞18.(山东省兖州市2013高三9月入学诊断检测数学(理)试题)已知函数f (x )=x 3+mx 2+nx -2的图象过点(-1,-6),且函数g (x )=()x f '+6x 的图象关于y 轴对称.(1)求m 、n 的值及函数y =f (x )的单调区间;(2)若a >0,求函数y =f (x )在区间(a -1,a +1)内的极值.【答案】(1)由函数f (x )的图象过点(-1,-6),得m -n =-3.① 由f (x )=x 3+mx 2+nx -2,得()x f '=3x 2+2mx +n ,则g (x )=()x f '+6x =3x 2+(2m +6)x +n .而g (x )的图象关于y 轴对称,所以-2m +62×3=0,解得 m =-3. 代入①得n =0.于是()x f '=3x 2-6x =3x (x -2)由()x f '>0得x >2或x <0,故f (x )的单调递增区间是(-∞,0),(2,+∞); 由()x f '<0,得0<x <2,故f (x )的单调递减区间是(0,2)(2)由(1)得()x f '=3x (x -2),令()x f '=0得x =0或x =2 当x 变化时,()x f ',f (x )的变化情况如下表:(0)=-2,当a =1时,f (x )在(a -1,a +1)内无极值;当1<a <3时,f (x )在(a -1,a +1)内有极小值f (2)=-6,无极大值; 当a ≥3时,f (x )在(a -1,a +1)内无极值.综上得,当0<a <1时,f (x )有极大值-2,无极小值; 当1<a <3时,f (x )有极小值-6,无极大值; 当a =1或a ≥3时,f (x )无极值19.(2012年高考(重庆理))(本小题满分13分,(Ⅰ)小问6分,(Ⅱ)小问7分.)设13()ln 1,22f x a x x x =+++其中a R ∈,曲线()y f x =在点(1,(1))f 处的切线垂直于y 轴. (Ⅰ) 求a 的值;(Ⅱ) 求函数()f x 的极值.【答案】解:(1)因()13ln 122f x a x x x =+++,故()21322a f x x x '=-+ 由于曲线()y f x =在点()()1,1f 处的切线垂直于y 轴,故该切线斜率为0,即()10f '=,从而13022a -+=,解得1a =- (2)由(1)知()()13ln 1022f x x x x x =-+++>, ()222113321222x x f x x x x --'=--+= ()2(31)(1)2x x f x x +-'∴=令()0f x '=,解得1211,3x x ==-(因213x =-不在定义域内,舍去),当()0,1x ∈时,()0f x '<,故()f x 在()0,1上为减函数;当()1,x ∈+∞时,()0f x '>,故()f x 在()1,+∞上为增函数; 故()f x 在1x =处取得极小值()13f =.20.(2013福建高考数学(理))已知函数()ln ()f x x a x a R =-∈(1)当2a =时,求曲线()y f x =在点(1,(1))A f 处的切线方程; (2)求函数()f x 的极值.【答案】解:函数()f x 的定义域为(0,)+∞,()1'=-af x x .(Ⅰ)当2=a 时,()2ln =-f x x x ,2()1(0)'=->f x x x,(1)1,(1)1'∴==-f f ,()∴=y f x 在点(1,(1))A f 处的切线方程为1(1)-=--y x , 即20+-=x y .(Ⅱ)由()1,0-'=-=>a x af x x x x可知: ①当0≤a 时,()0'>f x ,函数()f x 为(0,)+∞上的增函数,函数()f x 无极值;②当0>a 时,由()0'=f x ,解得=x a ;(0,)∈ x a 时,()0'<f x ,(,)∈+∞x a 时,()0'>f x()∴f x 在=x a 处取得极小值,且极小值为()ln =-f a a a a ,无极大值.综上:当0≤a 时,函数()f x 无极值当0>a 时,函数()f x 在=x a 处取得极小值ln -a a a ,无极大值.21.(山东省烟台市2013届高三上学期期中考试数学试题(理科))已知βα,是三次函数),(22131(23R b a bx ax x x f ∈++=)的两个极值点,且()1,0∈α,()2,1∈β,求动点()b a ,所在的区域面积S .【答案】解:由函数),(22131(23R b a bx ax x x f ∈++=)可得,b ax x x f 2)(2++=',由题意知,βα,是方程022=++b ax x 的两个根,且()1,0∈α,()2,1∈β,因此得到可 行域⎪⎩⎪⎨⎧>++='<++='>='0224)2(021)1(02)0(b a f b a f b f ,即⎪⎩⎪⎨⎧>++<++>020120b a b a b ,画出可行域如图.所以21=S22.(山东省寿光市2013届高三10月阶段性检测数学(理)试题)已知2()(2,),(),()()().x f x x a x a a x R g x e x f x g x -=++≤∈=Φ=⋅ (1) 当a=1时,求()x Φ的单调区间;(2) 求()g x 在点(0,1)处的切线与直线x=1及曲线()g x 所围成的封闭图形的面积;(3) 是否存在实数a,使()x Φ的极大值为3?若存在,求出a 的值,若不存在,请说明理由.【答案】解:(1)当a=1时,2()(1)x x x x e -Φ=++,2()().x x e x x -'Φ=-+当()0x 'Φ 时,01;()0x x 'Φ 当时,1x 或0x()x ∴Φ的单调递增区间为(0,1),单调递减区间为:(-∞,0),(1,+∞)(2)切线的斜率为0(0)|1,x x k g e -='==-=-∴切线方程为y=-x+1所求封闭图形面积为21011111[(1)](1)()|.0022x x x S e x dx e x dx e x x e---=--+=+-=-+-=-⎰⎰ (3)22()(2)()[(2)],x x x x x a e e x ax a e x a x ---'Φ=+-++=-+- 令()0,02.x x x a 'Φ===-得或列表如下:由表可知,()x Φ极大=2(2)(4)a a a e -Φ-=-设22()(4),()(3)0,a a a a e a a e μμ--'=-=-()a μ∴在(,2)-∞上是增函数,2()(2)23,(4)3,a a a e μμ-∴≤=-≠ 即∴不存在实数a,使()x Φ极大值为3.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三第一轮复习质量检测历史试题2014.3 本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,共8页。
满分100分,考试时间为90分钟。
答卷前,考生务必将自己的姓名、考号、考试科目、试卷类型用铅笔涂写在答题纸上。
考试结束后,监考人员将本试卷和答题纸一并收回。
第I卷(选择题45分)注意事项:1.第I卷共30小题.每小题1.5分,共45分。
在每小题所列的四个选项中,只有一项符合题目要求。
2.每小题选出答案后,用铅笔把答题纸上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后。
再选涂其他答案.不能答在试卷上。
1.斯塔夫里阿诺斯在《全球通史》中说:“中国人的姓总是位于个人的名字之前,而不像西方那样,位于个人的名字之后。
”中国人强调姓所反映的实质是A.男尊女卑思想严重 B.家族宗法观念浓厚C.个人观念淡漠D.专制王权强大【答案】B【解析】考点:宗法制。
本题考查学生对西周时期宗法制的准确理解,由材料可得出姓氏和血脉、家族相联在一起,中国人将姓置个人名字之前反映出家族宗法观念浓厚,而宗法制度是由氏族社会父系家长制演变而来的,是王族贵族按血缘关系分配国家权力,以便建立世袭统治的一种制度。
故B符合题意。
2.右图为《唐书》所载的830名进士的出身分布比例。
由此可见,唐代选官制度A.为选拔士族子弟而设立B.仍然是世卿世禄制度C.缩小了人才选拔的范围D.兼顾多个阶层但不完善【答案】D【解析】考点:科举制。
本题主要考查学生准确解读图片信息的能力,从图片中可以看出在唐代科举制选拔出的人才中世族子弟依然占据支配地位,下层民众所占比例较低,说明唐代的科举制尽管较九品中正制有很大的进步,但在人才选拔上依然不够公平、公正,仍然须进一步完善,故D项符合题意,ABC三项表述错误,与科举制本身的史实不符。
3.两千多年前雅典就产生了“三权分立”的国家组织形式:公民大会、五百人议事会、民众法庭。
1787年宪法规定美国行使相应权力的机构是A.总统、国会、最高法院B.议会、首相、上议院C.国会、总统、最高法院D.首相、议会、上议院【答案】C【解析】考点:古代雅典城邦公民大会、五百人议事会、民众法庭分别掌握的是立法权、行政权和司法权。
故选C。
4.英国通过《权利法案》、美国通过《1787年宪法》、德国通过《德意志帝国宪法》、法国通过《法兰西第三共和国宪法》确立了民主政治。
这反映了资产阶级民主政治的突出特点是A.法制化B.渐进性C.普选制D.反封建性【答案】A【解析】考点:代议制的特点。
本题主要考查学生运用所学知识解决问题的能力,从材料中不难看出英法美德四国资产阶级革命后均颁布宪法或类宪法以巩固革命的成果,捍卫资产阶级的统治和既得利益,因此这能体现出资产阶级民主政治确立过程中的法制化特征,故答案选A,BCD三项也是其重要特点但与材料主旨不符。
5.素有“民间思想家”之称的王康先生在接受采访时指出,“五四”的演员在中国,剧本和导演却是在国外。
这说明五四运动A.由外国领袖组织发动B.是十月革命在中国的翻版C.深受当时国际形势的影响D.受到世界各国的援助【答案】C【解析】考点:五四运动。
注意关键信息“剧本和导演却是在国外”,五四运动的导火线是巴黎和会上中国外交的失败,故选C项。
6.右面照片名为“Chinese Baby”(中文名为《上海南站日军空袭下的儿童》),于1937年出现在美国郝斯特报刊上,并迅速传遍世界各地。
这一照片的流传A.宣传了中国国共合作抗战的事实B.赢得了国际社会对中国抗战的同情C.丑化了中华民族在国际上的形象D.激化了美日两国在上海附近的矛盾【答案】B【解析】考点:抗日战争。
A项材料并未体现,材料只是说了日军的暴行;B项正确,材料中图片体现的是在日军轰炸下的中国的灾难形象,受到了国际进步势力的同情;C项明显错误;D项材料无法体现。
7.美国学者约翰.奈斯比特在他的著作《中国大趋势》一书中指出,民主的含义就是“人民说了算”、“人民是统治者”、“民主意味着人民统治国家”。
下列选项中最能反映这一观点的是A.中国共产党领导的多党合作和政治协商制度B.民族区域自治制度C.人民代表大会制度D.依法治国的方略【答案】C【解析】考点:人民代表大会制度。
本题主要考查人民代表大会制度。
材料中文字“人民说了算”“人民是统治者”“民主意味着人民统治国家”体现了人民当家作主,而题肢中体现体现人民当家作主的是人民代表大会制度,由此选择C。
8.1974年,为打击侵入我西沙群岛的南越当局,中国政府决定东海舰队“直接通过台湾海峡”驰援南海。
台湾蒋介石海军不仅没有阻拦、还友好地亮起“请通过”信号。
2008年马英九就任台湾地区领导人后,很快促成两岸直接“三通”。
这说明台湾国民党当局A.认同和坚持“一个中国”原则B.希望与共产党结成统一战线C.拥护“和平统一、一国两制”D.与共产党根本利益一致【答案】A【解析】考点:一个中国原则。
题干反映中国大陆与中国台湾在民族利益上是一致的,说明国民党当局认同和坚持“一个中国”原则,C项正确;“一国两制”是大陆所拥护的,台湾并没有;实事上,是中共希望与国民党结合统一战线,B项说法错误;与共产党的根本利益是一致的说法是错误,两个政党是不同的阶级政党,D项说法错误。
9.中国有句俗话:“远亲不如近邻”。
新时期中国的外交活动中,最能够体现上述思想的事件是A.以五大国之一的身份参加日内瓦会议B.发起参与亚太经合组织C.发起成立上海合作组织D.加入世贸组织【答案】C【解析】考点:新中国的外交。
“远亲不如近邻”体现的是加强与我国周边国家发展关系的思想。
上合组织的成立是我国加强与周边国家关系的重要的体现,其他各项都不是与周边国家的关系。
因此选C.10.保罗.约翰逊在《现代:从1919到2000年的世界》中写道:“(20世纪)80年代,人类刮起了一场巨大的求变之风……80年代成为当代史的分界线。
民主精神恢复了自信,开始广泛传播。
”这场“求变之风”对世界产生的深远影响是A.加快了西方政治民主化进程B.壮大了国际社会主义力量C.导致社会主义阵营瓦解D.改变了世界政治格局【答案】D【解析】考点:东欧剧变和苏联解体。
据材料可知:这场“求变之风”发生时间在80年代,其结果是“民主精神恢复了自信,开始广泛传播”(资本主义民主)所以可以断定这场“求变之风”就是20世纪80年代东欧和苏联社会主义国家的改革与剧变,其最终结果是导致东欧剧变苏联解体,进而引起世界格局的变化,故选D项。
11.“到1970年,欧洲不再是世界棋盘上的一个或两个卒子——东欧和西欧;中国也已不再是苏联的卫星国:美国发起的把中国排斥在联合国外的做法开始失败”。
最适合以上表述的主题是A.多极化趋势出现B.欧洲地理政治的变迁C.和平与发展成为时代主流D.欧盟增加新成员【答案】A【解析】考点:多极化趋势。
从题干中欧洲、中国的崛起对美苏的两极格局形成了冲击的信息可知这应是世界的多极化趋势。
BC两项表述不全面,D项不符合题干信息。
12.古代中国人对牛有着特殊情感:表现在很少吃牛肉,杨柳青年画等民间风情画很多以牛为题材,民间有“牛郎织女”、“太上老君骑牛入函谷关”等传说。
造成这一现象的关键原因是A.君主专制中央集权B.小农经济占主导地位C.封建统治者实施愚民政策D.佛教的广泛传播【答案】B【解析】考点:小农经济。
本题考查学生解读并获取历史信息的能力。
在自给自足的自然经济下,牛耕是重要的生产手段,牛在农业生产中的地位十分重要,故选B。
A项说的是政治制度;C项说的是文化政策,都与材料无关;D项材料未体现。
13.在西方人眼中,两千年前中国文明的“象征”是丝绸,一千年前中国文明的“象征”是瓷器,五百年前中国文明的“象征”是茶叶。
这主要表明古代中国①自然经济长时间内没有根本性突破②东西方的交流渠道不畅通③古代手工业发展水平世界领先④古代中国对外贸易一直居出超地位A.①②③B.②④C.①③D.②③④【答案】C【解析】考点:古代的手工业。
本题考查我国古代对外交流和手工业发展情况。
从丝绸到陶瓷到茶叶,对外交往中,中国主要输出手工业品,既说明我国古代手工业领先,也说明自然经济长期存在,没有根本性突破,故①③正确,因此答案为C;古代通过丝绸之路,我国手工业品大量外输,故②不正确;材料无法体现古代中国外贸出超还是入超,故④错误。
14.斯塔夫里阿诺斯指出:“人类的物质文化在过去的200年中发生的变化远甚于前5000年。
”这种现象出现的主要原因是①文艺复兴和启蒙运动解放了思想②地理大发现促进新旧大陆的联系③科学革命导致一系列新发明出现④两次工业革命极大地提高了生产力A.①②B.②③C.①④D.③④【答案】D【解析】考点:文艺复兴。
回答本题需注意“当代一历史学家”“在过去的200年中”这些关键信息和时间点,可以知道材料所指200年是19世纪、20世纪,根据所学知识,近代以来三次工业革命极大地推动了社会生产力和世界文明的进步,本题应选③④项,第①项文艺复兴兴起于14~17世纪,启蒙运动兴起时间17~18世纪;第②项地理大发现指新航路开辟,是在15~16世纪,时间上与本题不符合,可排除。
故选D。
15.张謇曾说:“我们儒家,有一句扼要而不可动摇的名言‘天地之大德日生’。
这句话的解释,就是说一切政治及学问最低的期望,要使得大多数的老百姓,都能得到最低水平线上的生活。
”因此,他把自己创办的纱厂命名为“大生”。
从这个角度看近代民族企业A.发展民族工业.救亡图存B.应大力发展重工业C.以轻工业为主,注重民生D.儒家思想指导商业【答案】C【解析】考点:民族工业的兴起。
依据材料中“天地之大德日生”,可以看出张謇创办大生纱厂的注重民生。
故从中可以看出近代民族工业以轻工业为主,注重民生。
故选C。
其他三项说法错误。
16.有学者指出,罗斯福新政“造成了资本主义的一次深刻变革或者是一种再生。
”这里的“变革”和“再生”主要是指①国家对经济的宏观调节成为一个重要的组成部分②第三产业蓬勃发展③“新经济”的出现④推行社会福利政策,逐步建立起“福利国家”制度A.①②④B.①④C.②③D.①②③④【答案】B【解析】考点:罗斯福新政。
②不对,第三产业蓬勃发展是指二战后第三次科技革命的作用,③不对,“新经济”的出现是在20世纪90年代美国;罗斯福新政开创了国家全面干预经济的模式,并且加强社会保障措施,因此①④正确。
17.苏俄的新经济政策和美国的罗斯福新政都是人类文明演进过程中的创举。
两者的根本相同点在于A.都注重从实际出发变革生产关系B.都将工作的重心转移到工业领域C.都强化了国家对经济的全面干预D.都对本国乃至世界产生深远影响【答案】A【解析】考点:新经济政策与罗斯福新政比较。
题干要说明的是苏俄新经济政策和美国罗斯福新政两者作为创举的根本相同点,两者本质上都是生产关系的局部调整,所以A符合题意。
