热力学方程

合集下载

工程热力学公式大全

工程热力学公式大全1.热力学第一定律：ΔU=Q-W其中，ΔU表示系统内能的变化，Q表示系统吸收的热量，W表示系统对外所做的功。

2.热力学第二定律（卡诺循环）：η=1-Tc/Th其中，η表示热机的热效率，Tc表示冷源温度，Th表示热源温度。

3.单级涡轮放大循环功率：W=h_1-h_2其中，h_1表示压缩机入口焓，h_2表示涡轮出口焓。

4.热力学性质之一：比热容C=Q/(m*ΔT)其中，C表示比热容，Q表示系统吸收的热量，m表示系统的质量，ΔT表示温度变化。

5.热力学性质之二：比焓变ΔH=m*C*ΔT其中，ΔH表示焓变，m表示系统的质量，C表示比热容，ΔT表示温度变化。

6.理想气体状态方程：PV=nRT其中，P表示气体的压力，V表示气体的体积，n表示气体的物质量，R表示气体常数，T表示气体的温度。

7.热机制冷效率：ε=(Qh-Qc)/Qh其中，ε表示热机的制冷效率，Qh表示热机吸收的热量，Qc表示热机传递给冷源的热量。

8.熵变表达式：ΔS=Q/T其中，ΔS表示熵变，Q表示系统吸收的热量，T表示温度。

9.热力学性质之三：比容变β=-(1/V)*(∂V/∂T)_P其中，β表示比容变，V表示体积，T表示温度，P表示压力。

10.工作物质循环效率η_cyc = W_net / Qin其中，η_cyc表示工作物质的循环效率，W_net表示净功，Qin表示输入热量。

这只是一小部分工程热力学公式的示例，实际上工程热力学涉及面较广，还有许多其他常用公式。

与热力学相关的公式使工程师能够更好地理解和解决与能量转换和热力学有关的问题，在工程设计和应用中起到重要的作用。

物理化学热力学基本方程

利用全微分条件，将其作用于(5.1)、(5.2)、(5.4)和(5.6)式，得到(5.8)~(5.11)式所给八个热力学偏导数的关系：
如果有全微分 df adx ( T ， p ) bdy / 则 S (a / y ) x (b / x ) y 必有
( T / V ) S ( p / S )V (V / S ) p ( p / T )V ( S / V ) T (V / T ) p ( S / p )T
p S T V V T
S V p T T p
G H TS
dG SdT V dp
V (G / p )T
当系统处于平衡态时，不仅描述该系统整体性质的宏观量不再随时间改变，而且这些宏观量之间还存在着函数关系。只有少数几个是独立态参量，其余宏观量则是态参量的函数。对于给定的系统，其态参量的数目是确定的，但选哪几个宏观量作为态参量则是任意的。
我们可以将(5.1)式看成以S和V为独立变量表示的全微分dU ,U=U(S,V), 于是写为
dU ( U / S ) V dS ( U / V ) S dV
可以与(5.1)式比较，得到两个偏导数：
T ( U / S )V
p (U / V ) S
(5.8)
H U p V U (U / V ) S V F U T S U ( U / S )V S G U pV TS
U ( U / V ) S V ( U / S )V S
这说明，只要已知以S，V为独立态参量时内能U的表达式U=U（S,V），就可以求得T，状态方程，p，H，F，G乃至系统的全部热力学量。所以内能U是以S、V为独立态参量的特性函数。同样可以证明焓H，自由能F和自由焓G分别是以(S,p)，(T,V)和(T,p) 为独立态参量的特性函数。

热力学函数的基本关系式

dG = －SdT + Vdp
S p
T
V T
p
麦克斯韦关系式：表示的是系统在同一状态的两种
变化率数值相等。 9
二阶混合偏导数
T p V S S V 麦氏方程记忆法：
T p
S
V S
p
① 对角乘积永远是pV，TS；
② 等式两边分母与外角标互换；
S p
T
V T
4
由四个热力学基本方程，分别加上相应的条件，可得到
8个派生公式：
dU = TdS－ pdV
U S
V
T
U V
S
p
dH = TdS + Vdp
T V H
S p
H p S
dA = －SdT－ pdV
A T
V
S
A V
T
p
dG = －SdT + Vdp
G T
P
S
G P
则
U T p p
V T T V
11
练习：由热力学基本方程出发证明，
H p
T
T
V T
p
V
证明：
dH＝TdS＋Vdp
定温下，等式两边除以dp
H p
T
T
S p
T
V
由麦克斯韦方程
S p
T
V T
p
返回
H p
T
T
V T
p
V
12
U T p p V T T V
S T p
T
T
定容
S CV T V T
S T V
15
T
V
5
2. 吉布斯 - 亥姆霍茨方程

热力学的计算和反应的热力学方程

热力学的计算和反应的热力学方程热力学是研究物质热力学性质和热力学变化规律的科学。

在化学领域中，热力学常被用于计算和分析化学反应的能量变化及其它热力学性质。

本文将介绍热力学的计算方法以及反应的热力学方程。

一、热力学计算方法1. 热力学第一定律热力学第一定律，也被称为能量守恒定律，表述了能量的守恒关系。

对于封闭系统而言，能量可以从一种形式转化为另一种形式，但能量的总量保持不变。

根据热力学第一定律，系统的能量变化可以通过以下公式进行计算：ΔE = Q - W其中，ΔE代表系统内能的变化，Q代表热量的变化，W代表对外做功的变化。

通过测量系统吸收或放出的热量以及对外做的功，可以计算出系统的能量变化。

2. 热力学第二定律热力学第二定律，也被称为熵增原理，表述了不可逆过程的方向性。

根据热力学第二定律，自发过程的熵增大于零，而不可逆过程的熵增等于零。

熵（S）是一个衡量系统混乱程度的物理量，熵增代表系统趋向于更大的混乱程度。

根据热力学第二定律，可以通过以下公式计算熵的变化：ΔS = Qrev/T其中，ΔS代表熵的变化，Qrev代表可逆过程的热量变化，T代表热力学温度。

通过测量可逆过程的热量变化，可以计算出系统熵的变化。

二、反应的热力学方程热力学方程被用于描述化学反应的热力学性质，如反应焓变、反应熵变和反应自由能变化等。

以下是常见的反应热力学方程：1. 反应焓变反应焓变（ΔH）指的是化学反应过程中系统吸热或放热的能量变化。

反应焓变可以通过测量反应物和产物的焓差来计算。

根据热力学计算中的化学方程式，可以通过以下公式计算反应焓变：ΔH = ΣnH(products) - ΣmH(reactants)其中，ΔH代表反应焓变，ΣnH(products)代表产物的摩尔焓，ΣmH(reactants)代表反应物的摩尔焓。

2. 反应熵变反应熵变（ΔS）指的是化学反应过程中系统熵的改变。

反应熵变可以通过测量反应物和产物的摩尔熵差来计算。

9热力学基本方程

推导热力学函数间关系时，也常用到麦克斯韦关系式
麦克斯韦关系式中不含：
S T
p
和
S
T
V
问题 S ?
T p
S ? T V
解：dH= TdS+Vdp
定压下，除以dT
H T S T p T p
得 S Cp
T p T
而
Cp
H T
p
同理可得：
G
G3
nRTln
p2 p1
28.314 373 .15 ln 50
101 .325
J 4.38
kJ 0
GT,p 4.38 kJ 0
由吉布斯函数判据可知，过程自发进行。
A G ( pV ) G nRT 4.38 kJ 28.314373103 kJ 10.58 kJ
1.15 热力学函数的基本关系式
定量，定组成的单相系统；纯物质是定组成的一种特例保持相平衡及化学平衡的系统
热力学基本方程的应用：
计算纯物质 p、V、T 变化过程的ΔA、ΔG
dA=－SdT－ pdV dG=－SdT+Vdp
AT
V2 V1
pdV
GT
p2 Vdp
p1
2. 麦克斯韦关系式
表明S、T、p、V 间的关系式
S p V T T V
p T S V V S
V S
p
T p
S
S p V T T V
S p
T
V T
p
几点结论：
麦克斯韦关系式表示：系统在同一状态的两种变化率数值相等
S p V T T V
S p
T
V T
p
该式提供了可由实验直接测定的量，替代不能直接测定的量

3.7 热力学基本方程及Maxwell关系式

恒T、p、W= 0： G 0
自发平衡
dGm α dGm β Sm α dT Vm α dp Sm β dT
Vm β dp
[Sm β Sm α ]dT [Vm β Vm α ]dp
dp Sm β Sm α
βαSm
dT Vm β Vm α
βαVm
又因 βαSm
βαHm T
dp dT
βαH m T βαVm
U
SV
H
A
pT
G
说明： 1. 等式右边只有四个物理量T，S， p，V
2. 十字交叉法：
对U来说，S，V分别表示dS和dV； dS对角线对应T，dV对角线对应p；箭头方向表示正负，指向为负，则为TdS和 –pdV
2. U、H、A、G的一阶偏导数关系式
U f (S,V ) H f (S, p) A f (T ,V ) G f (T , p)
p
S V
T
p T
V
V T
p
S p
T
T V
S
p S
V
T p
S
V S
p
S V
T
p T
V
V T
p
S p
T
说明：
1. 关系式中只有四个物理量T， S， p，V
2. 对角线乘积为 TS 与 pV
3. 等式两边的分母与下标互换
4. S和V为广度量，而T和p为强度量。同种性质的状态函数的分式，不取负号。
分析：利用克拉佩龙方程 dT T βαVm
dp 解：由克拉佩龙方程有 dT
T
βαH m
lsVm lsH m
dp
积分，得 lnT2
T1

热力学公式

1. 理想气体状态方程式nRT RT M m pV ==)/(或 RT n V p pV ==)/(m式中p ，V ，T 及n 单位分别为Pa ，m 3，K 及mol 。

m /V V n =称为气体的摩尔体积，其单位为m 3 · mol -1。

R =8.314510 J · mol -1 · K -1，称为摩尔气体常数。

此式适用于理想气体，近似地适用于低压的真实气体。

2. 气体混合物（1）组成摩尔分数 y B (或x B ) = ∑AA B /n n体积分数 /y B m,B B *=V ϕ∑*AVy Am ,A式中∑AA n 为混合气体总的物质的量。

Am,*V表示在一定T ，p 下纯气体A 的摩尔体积。

∑*AA m ,A V y 为在一定T ，p 下混合之前各纯组分体积的总和。

（2）摩尔质量∑∑∑===BBBB B BB mix //n M n m M y M式中 ∑=BB m m 为混合气体的总质量，∑=BB n n 为混合气体总的物质的量。

上述各式适用于任意的气体混合物。

（3） V V p p n n y ///B B B B *===式中p B 为气体B ，在混合的T ，V 条件下，单独存在时所产生的压力，称为B 的分压力。

*B V 为B 气体在混合气体的T ，p 下，单独存在时所占的体积。

3. 道尔顿定律p B = y B p ，∑=BB p p上式适用于任意气体。

对于理想气体V RT n p /B B =4. 阿马加分体积定律V RT n V /B B =*此式只适用于理想气体。

1. 热力学第一定律的数学表示式W Q U +=∆或 'amb δδδd δdU Q W Q p V W =+=-+规定系统吸热为正，放热为负。

系统得功为正，对环境作功为负。

式中 p amb 为环境的压力，W ’为非体积功。

上式适用于封闭体系的一切过程。

2. 焓的定义式3. 焓变（1） )(pV U H ∆+∆=∆式中)(pV ∆为pV 乘积的增量，只有在恒压下)()(12V V p pV -=∆在数值上等于体积功。

热力学方程

测定量
★定量计算的相关近似处理
以熔化平衡为例
dT dp
T Vm Hm
fusVm , fusHm不变 ln T2 T1
V fus m fus H m
( p2
p1 )
ln(1T /T1)T /T1 T
T1
V fus m fus Hm
p
问：滑冰运动员冰鞋下冰的熔点怎样变化？
§3.9 克拉佩龙方程
dT dp
Vm Sm
dT dp
T Vm Hm
这就是克拉佩龙方程，它表明纯物质两相平衡时，温度、压力两个变量中
只有一个是独立变量
§3.9 克拉佩龙方程
❖9.2 固-液平衡、固-固平衡积分式★凝聚相之间的两相平衡的定性讨论
Vm很小
熔化平衡：fusHm很大，dT/dp很小，外压对熔点的影响很小晶型转变平衡：trsHm较小，因而dT/dp比熔化平衡大
§3.8 热力学基本方程
❖8.1 热力学基本方程
dU Q W
非体积功为零时发生可逆变化：
dU TdS pdV
这是热力学第一与第二定律的联合公式，适用于组成恒定、不作非体
积功的封闭体系
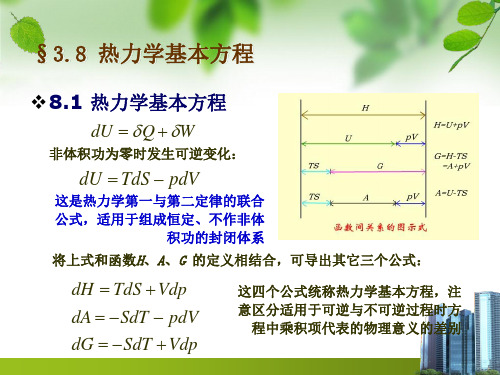
将上式和函数H、A、G 的定义相结合，可导出其它三个公式：
dH TdS Vdp dA SdT pdV dG SdT Vdp
克斯韦关系式
❖10.2 麦克斯韦关系式
z
f
(x, y) dz
z x
y
dx
z y
x
dy
Mdx
Ndy
M y
x
y
z x
y x
N x
y
x
ห้องสมุดไป่ตู้
z y
x

四个热力学基本方程

四个热力学基本方程
热力学是物理学一个分支，其最基本的特征是热量传递，真空无重力和
统一温度下不会发生热量移动。

热力学主要通过四个基本方程来描述物体内
热力学过程，它们分别是热力定律、热容定律、热运动定律和热量守恒定律。

首先是热容定律，它表示物体的温度随体积变化而变化，也就是说，如
果一个物体的温度扩大，其体积也会随之增大。

这一定律受到非Newton流
体模型的影响，例如对蒸汽来说，它的温度和大小成正比。

热力定律是热力学中一个重要的原理，它表明，物体吸收或释放热量时，伴随着一定的能量状态改变。

这种能量状态改变是由物体内部结构改变而引
起的，不同的热量模型会有不同的热能量状态改变。

接下来是热运动定律，它表明物质在热过程中会随着温度改变而出现不
同的运动现象。

例如，物体温度升高时，物质的动能就会升高，从而出现不
同的运动现象。

最后是热量守恒定律，它表明物质在发生热运动变化时，实际所发生的
能量是不变的。

这一定律受到反应热和潜热影响，因此热量异变是由这两种
能量变化共同作用所引起的。

总而言之，热力学的四个基本方程描述了热力学过程中物质所发生的特
性变化，而这些变化是由物质内部结构和外部条件共同决定的。

因此，广泛
使用热力学原理，能够更好地研究物质的性质，探究物质的热力学过程的变
化规律。

热力学函数的基本关系式

△S=QR/T; T △S= QR 故△G= △H- T △S=0- T △S= QR= WR=-RTlnP1/P2=5744Jmol-1 解法二： △G=∫ p1 p2Vdp = RTlnP2/P1=5744Jmol-1.
⑵等温等压相变△G 对于等温等压的可逆相变，直接可得（△G）T,P=0.对于非等温等压的非可逆相变或同温同压下两个相态的△G，可以通过设计可逆过程进行计算，也可根据G---P关系公式求算。
1.8 热力学函数的基本关系式
H
U、H、S、A、G 、 p、V、T H =U+pV，A =U-TS，G =H-TS 1. 热力学基本方程
U
pV
TS A pV
TS
G
δWr ′＝0时，则δWr＝－pdV，于是
一微小可逆过程
dU=δQr+δWr，
dS δ Qr T
δWr ′ ＝0时，则δWr＝－pdV，于是
=8586Jmol-1 故△G= △G1+ △G2 + △G3=8584Jmol-1 依Gibbs自由能减少原理，298K，1atm水不能经等温等压过程转变为同温同压的水蒸气，但其逆过程则是可以的。因此在298K， 1atm下液态水是稳定态。
⒊应用Gibbs--helmholtz方程求△G 将 G--H方程：｛э（△G/T）/эT｝P=- △H/T2
△S=0，△T=0，△H=0，
△G=0
⑵理气在等温等压的Gibbs自由能改变 △G = △H-T △S (△H=0) △S=-R∑nilnXi △G= RT∑nilnXi 其中ni为组分i的量，Xi为理想混合气中
为组分I的摩尔数。
⒌非等温等压两态的△G 若体系的两态温度，压力都不相等，根据G的定义：

第三章--热力学第一定律3(河北理工大学)

∆G (T2 ) − ∆G (T1 ) = − ∫ ∆SdT
T2 T1
§3.8 热力学第二定律在单组分系统相平衡中的应用
• 克拉佩龙方程 • 固-液平衡、固-固平衡积分式 • 液-气、固-气平衡的蒸气压方程——克-克方程 —— -
1. 克拉佩龙方程
恒温恒压T，p 可逆相变 B(α) ∆Gm=0 dGm(α) B’(α ) 可逆相变 ∆G’m=0 B(β) dGm(β) B’(β )
3. 液-气、固-气平衡的蒸气压方程—克-克方程
对于液-气两相平衡，并假设气体为1mol理想气体，将液体体积忽略不计，则
∆ vap H m dp ∆ vap H m = = dT TVm (g) T ( RT / p )
d ln p ∆ vap H m = dT RT 2
∆ 这就是Clausius-Clapeyron 方程， vap H m是摩尔气化热。
假定 ∆ vap H m 的值与温度无关，积分得：
∆ vap H m 1 1 p2 ln =− ( − ) p1 R T2 T1
这公式可用来计算不同温度下的蒸气压或摩尔蒸发热。
热力学第二定律的内容关联：热力学第二定律的内容关联：
卡诺循环热力学第二定律
热力学第一定律
熵，熵增原理
PVT
Ө $ m
恒容
$ Ө ∆ r Am Ө ∂( ) $ ∆ rU m T =− 2 ∂T T
• 麦克斯韦关系式
（不讲）
• 热力学函数关系式的推导和证明（不讲）
3. 由基本方程计算纯物质pVT变化的∆A, ∆G
恒温 dT=0时，从热力学基本方程 dA= – SdT – pdV dG= – SdT+Vdp 得 dAT= – pdV dGT= Vdp 对于理想气体，将pV=nRT代入积分，有 ∆AT = –nRT ln(V2 /V1) ∆GT = nRT ln(p2 /p1) 两者相等。

热力学热容和热传导方程

热力学热容和热传导方程热力学热容和热传导方程是研究物体热力学性质和热传导过程中的重要方程。

本文将就热力学热容和热传导方程的定义、特点以及应用进行讨论和探索。

一、热力学热容热力学热容是描述物体吸热能力的物理量，通常用符号C表示。

热容的定义是单位质量物质温度升高1摄氏度所需吸收的热量。

根据定义，热容可以用下式表示：C = dq / (m * dT)其中，C表示热容，dq表示吸收的热量，m表示质量，dT表示温度变化。

热容有两种不同的定义，分别是定压热容和定容热容。

定压热容表示在压强不变的情况下，单位质量物质温度升高1摄氏度所需吸收的热量，用符号Cp表示；定容热容表示在体积不变的情况下，单位质量物质温度升高1摄氏度所需吸收的热量，用符号Cv表示。

在实际应用中，定压热容和定容热容往往有一定的差别，因此需要根据实际情况进行选择。

例如，在气体热力学问题中，往往使用定压热容；而在固体热力学问题中，定容热容更为常用。

二、热传导方程热传导是指物体内部因温度差异而发生的热量传递过程。

热传导方程描述了热传导的数学规律，通常用符号∇·(k∇T) = ρc∂T/∂t来表示。

其中，∇表示梯度算子，k表示热传导系数，T表示温度，ρ表示密度，c表示热容，t表示时间。

热传导方程的形式可以根据不同情况进行推导和变形，常见的形式有一维稳态热传导方程、一维非稳态热传导方程以及三维热传导方程等。

这些方程在热传导问题的计算和分析中有着重要的应用。

热传导方程的求解可以通过数值方法或者解析方法进行，具体方法根据实际问题的复杂程度和求解精度来选择。

通过热传导方程的求解，可以研究物体的热传导特性以及温度分布的变化情况，对于工程设计和科学研究具有重要意义。

三、应用与展望热容和热传导方程的应用涵盖了多个领域。

在工程领域中，热容和热传导方程的研究可以用于热工系统的设计与优化，例如锅炉、换热器、冷却器等设备。

同时，研究热传导方程可以帮助我们了解材料的热传导性能，指导材料的选择与设计。

热力学基本方程PPT课件

如果取C(V )T nRT / (V nb)，就得范德华方程如果取C(V )T是硬球状态方程，就得硬球范德华方程
复习在热力学中常用到的偏导数关系式： 1. 由微分式求导数：导数的定义
f x y
lim
Δx 0
f ( x Δx, y) Δx
f (x, y)
Δf lim Δx0 Δx
y不变
V
4c S 3 V
1/ 3
p
U V
S
c S 3 V
4/3
T T (S,V )
27T 4
27T 3V
p
p(S,V )
p
256c3
,
T T (S,V ) S
64c3
如果已知的是U(T, V)，那么我们将得不到完整的其他热力学性质，比如不能由它推导出体系状态方程。
已知U(T ,V )
T
U S
V
H S
p
H G
V
p
S
p
T
p
U V
S
A V
T
S
A T
V
G T
p
(A/T) T V
U T2
,
(A/T)
(1/ T )
V
U
(G / T T
)
p
H T2
,
(G / T )
(1/T )
p
H
4.麦克斯韦关系式(Maxwell relations)
U V
T
dV
CV dT
U V
T
dV
类似的，焓的自然的独立变量是熵和压强，为方便起见，焓的独立变量也常取为温度和压强
dH TdS Vdp

物理化学1.15-1 热力学函数的基本关系式

§1.15 热力学函数的基本关系式
8个热力学函数：可直接测定
p、V、T、U 、H 、S、A、G
定 H ＝U＋pV 义式 A ＝U－TS
可求得
G ＝H－TS＝A＋pV
1.热力学基本方程
封闭系统 dU =δQ + δW
可逆过程
=δQr －pdV ＋ δWr′
δQr =TdS
dU = TdS －pdV ＋ δWr' δWr'＝0：
dA = －SdT－ pdV dG = －SdT + Vdp
G S T p

G p
T
V
证明：无相变和化学变化的封闭系统，在定温下其吉布斯自由能随压力的改变恒为正值。
证明：
dG = －SdT + Vdp
G ( p )T
V
>0
解： dG = －SdT + Vdp
S T2 nCV ,mdT nR ln V2 ,
T1
T
V1
A nRT ln V2 V1
应(用ቤተ መጻሕፍቲ ባይዱ()i封条i()i无i闭件i)非可系：体逆统积过，功程，。
可用于: (i)定量，定组成的单相系统;
(ii) 保持相平衡及化学平衡的系统.
8个派生公式： dU = TdS－ pdV dH = TdS + Vdp
U T S V U p V S
dU = TdS －pdV
dU=TdS－pdV
H=U+pV dH=dU+pdV+Vdp
A=U－TS dA=dU－TdS－SdT
dH=TdS+Vdp
dA= － SdT － pdV

热力学的四个基本方程

热力学的四个基本方程热力学的四个基本方程，嘿，听起来就有点高大上，对吧？这玩意儿跟我们生活息息相关，绝对不是天书。

想象一下，咱们平时喝的冰水、吃的热汤，这些都是热力学在背后默默发力。

第一条方程，咱叫它“内能”，这个词儿听起来有点生涩，其实就是物体内部的能量。

想象一下，你一口热汤下肚，热量可就进了你的肚子，这不就是内能的体现吗？简单来说，内能跟物体的温度、体积、物质状态关系密切。

你就想，越热的东西，内能越多。

这就是热力学的魔力，能量在转移、变化，像调皮的小孩儿，永远不肯呆在一个地方。

咱聊聊“熵”。

这玩意儿可神奇了，代表着无序的程度。

热量总是从高温区流向低温区，就像你从冰箱拿出来的可乐，慢慢变得温暖。

熵就像是时间的魔法，随着时间推移，系统的无序程度只会增加，不会减少。

生活中，这个熵真是个小捣蛋，每当你整理好的房间过几天又变得乱七八糟，嘿，熵在作怪呢！想要把东西整理好，简直比登天还难。

这就是熵的无情法则，提醒我们，生活有时候就是个不断增加无序的过程。

然后，我们再来说说“热量”，这个概念你肯定熟悉。

就是当你给某个物体加热，热量就往里灌。

这个时候，咱们要提到一个重要的关系——热量和温度的变化。

想象一下，冬天的早晨，你喝上一口热乎乎的茶，身体瞬间暖和起来，这就是热量在你体内发挥作用。

而这个热量又跟物体的质量和比热容有关系，像是不同种类的锅，烧水的速度可真不一样。

要是你用铁锅，水烧得飞快，要是用陶瓷锅，估计得等半天。

这不就是热量和材料的关系嘛，真是神奇！咱得提一提“气体状态方程”，这是热力学的终极武器。

气体的行为可复杂了，它们可不像固体和液体那样稳重。

气体分子像小兔子似的，四处乱窜。

这个方程通过温度、压力和体积把这些小家伙的行为联系起来。

想象一下，气球的气体，充得越满，气球的压力越大。

到哎呀，吹得太满就会爆炸，真是让人心惊胆战。

气体状态方程告诉我们，保持好气体的平衡，才能避免麻烦。

无论是喝汽水，还是打气球，这些都是热力学的绝妙应用。

热力学基本方程

热力学基本方程热力学是一门描述物理系统中能量、势能和熵之间关系的学科。

它的基本方程，也就是“热力学基本方程”，定义了这些量之间的联系。

热力学基本方程可以用来描述物质在不同物理状态和条件下的变化。

热力学基本方程是一个多元方程，由热力学定律组成：第一定律是能量守恒定律；第二定律是熵守恒定律；第三定律是势能守恒定律。

第一定律：热力学的第一定律宣称，在任何物理过程中，能量守恒，即能量不会消失，也不会出现。

由于能量守恒，物质在不同状态间的变化都会有特定的方法。

第二定律：热力学的第二定律宣称，由于能量不能在未受外力作用的情况下自发地流向热源或冷池，因此，熵在受外力作用的情况下不会减少，而是会增大。

第三定律：热力学的第三定律宣称，势能可以变化，而它的变化与系统的熵有关，当熵增加时，势能也会增加。

这三定律构成了热力学基本方程，用于说明物质在不同物理状态下的变化。

它解释了物质在不同状态间的转换和质量变化，以及在这些转换中的能量的流动方式。

此外，热力学基本方程还可以用来描述物质处于不同环境中的变化，如汽化、液化、固化等，也可以用来解释物质在受外力作用时的表现。

热力学基本方程的应用也非常广泛，它可以用来表示物理和化学反应的能量改变，也可以用来描述物质运动规律，还可以用来计算化学反应产物的分子量、活性能和自由能。

由于热力学基本方程具有如此强大的表达能力，它被广泛应用于热力学的各个分支中，包括绝热热力学，热压热力学，绝热变动热力学，精确热力学，化学动力学，流体力学，量子力学，共性热力学等。

热力学基本方程是一种强有力的理论，它引发了新的科学发现，让物理学和化学学者们有机会探索全新的物理和化学现象，为科学知识的发展做出了巨大贡献。

从上面可以看出，热力学基本方程是一个强大的热力学定律，它可以用来说明物质在不同状态、环境的变化，也可以描述物质的运动规律，为物理学和化学学的研究作出了巨大贡献。

它的应用也非常广泛，它也被用于各个热力学分支，被广泛应用于物理和化学反应的研究中。