物理化学热力学基本方程
物理化学知识点(全)
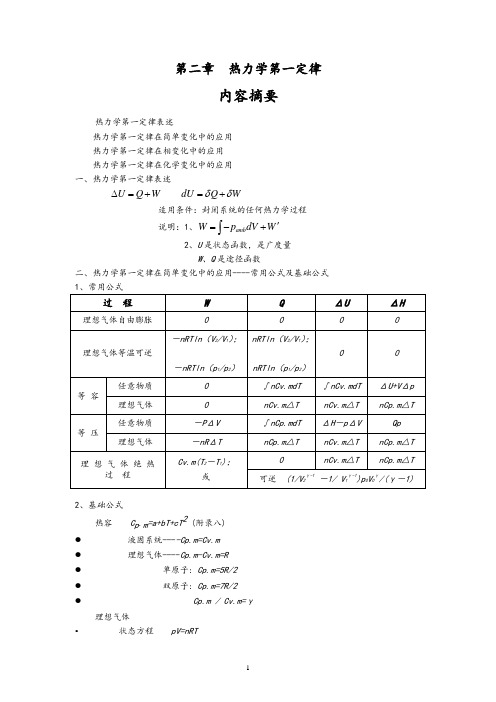
第二章热力学第一定律内容摘要热力学第一定律表述热力学第一定律在简单变化中的应用 热力学第一定律在相变化中的应用 热力学第一定律在化学变化中的应用 一、热力学第一定律表述U Q W ∆=+ dU Q W δδ=+适用条件:封闭系统的任何热力学过程 说明:1、amb W p dV W '=-+⎰2、U 是状态函数,是广度量W 、Q 是途径函数 二、热力学第一定律在简单变化中的应用----常用公式及基础公式 过 程WQΔUΔH理想气体自由膨胀理想气体等温可逆-nRTln (V 2/V 1); -nRTln (p 1/p 2) nRTln (V 2/V 1);nRTln (p 1/p 2)0 0等 容任意物质0 ∫nCv.mdT ∫nCv.mdT ΔU+V Δp 理想气体 0 nCv.m △T nCv.m △T nCp.m △T 等 压任意物质-P ΔV ∫nCp.mdT ΔH -p ΔV Qp 理想气体-nR ΔT nCp.m △TnCv.m △T nCp.m △T 理 想 气 体 绝 热过 程 Cv.m(T 2-T 1);或nCv.m △TnCp.m △T可逆 (1/V 2γ-1-1/ V 1γ-1)p 0V 0γ/(γ-1)2、基础公式热容 C p .m =a+bT+cT 2 (附录八) ● 液固系统----Cp.m=Cv.m ● 理想气体----Cp.m-Cv.m=R ● 单原子: Cp.m=5R/2 ● 双原子: Cp.m=7R/2 ● Cp.m / Cv.m=γ理想气体• 状态方程 pV=nRT• 过程方程 恒温:1122p V p V = • 恒压: 1122//V T V T = • 恒容: 1122/ / p T p T =• 绝热可逆: 1122 p V p V γγ= 111122 T p T p γγγγ--=111122 TV T V γγ--= 三、热力学第一定律在相变化中的应用----可逆相变化与不可逆相变化过程1、 可逆相变化 Q p =n Δ相变H m W = -p ΔV无气体存在: W = 0有气体相,只需考虑气体,且视为理想气体ΔU = n Δ相变H m - p ΔV2、相变焓基础数据及相互关系 Δ冷凝H m (T) = -Δ蒸发H m (T)Δ凝固H m (T) = -Δ熔化H m (T) Δ凝华H m (T) = -Δ升华H m (T)(有关手册提供的通常为可逆相变焓)3、不可逆相变化 Δ相变H m (T 2) = Δ相变H m (T 1) +∫Σ(νB C p.m )dT 解题要点: 1.判断过程是否可逆;2.过程设计,必须包含能获得摩尔相变焓的可逆相变化步骤;3.除可逆相变化,其余步骤均为简单变化计算.4.逐步计算后加和。
物理化学 0304热力学基本方程

1G= 5G 0
Vdp
G
H2O(s) T=263.15K p=101.325kPa
1G
H2O(l) T=263.15K p(l)=611Pa
等温可逆
5G
H2O(s) T=263.15K p(s)=552Pa
1G V l p
Pa V l 611 101326
p2 G=nRT ln p1
4
例:已知263.15K时H2O(s)和H2O(l)的饱和蒸气压分别为
H2O(l) 不可逆相变 解: T2=263.15K sl H m ( 263K ) (1)G 0 P=101.325kPa sl S m ( 263K ) G (2)有两种解法: H 1 可逆 S 1
A G S T V T p
dA SdT pdV dG SdT Vdp dU TdS pdV dA SdT pdV dH TdS Vdp dG SdT Vdp
U A p V S V T
解一:
G H TS
H2O(l) T2=273.15K P=101.325kPa S ( 273 K ) l m
263 S ( 263K )=S ( 273K ) m[C p ,m ( s ) C p ,m ( l )]ln 273
H (263K ) H (273K ) nC p,m T
各状态函数之间的关系
pV pV G
H U A
TS TS
H=PV+U A=U-TS G=H-TS =U+PV-TS =A+PV
9
dS Q r / T dU Q W dU TdS pdV
第三章 热力学第二定律重要公式

第三章 热力学第二定律1. 卡诺定理卡诺热机效率hc h c h 11T T Q Q Q W−=+=−=η 卡诺定理:工作于高温热源T h 与低温热源T c 之间的热机,可逆热机效率最大。
卡诺定理推论:所有工作于高温热源T h 与低温热源T c 之间的可逆热机,其热机效率都相等,与热机的工作物质无关。
卡诺循环中,热温商之和等于零0cch h =+T Q T Q 任意可逆循环热温商之和也等于零,即0R=⎟⎟⎠⎞⎜⎜⎝⎛∑i iiT Q 或 0δR =⎟⎠⎞⎜⎝⎛∫T Q 2. 热力学第二定律的经典表述克劳休斯说法:不可能把热由低温物体传到高温物体, 而不引起其他变化。
开尔文说法:不可能从单一热源吸热使之完全转化为功, 而不发生其他变化。
热力学第二定律的各种说法的实质:断定一切实际过程都是不可逆的。
各种经典表述法是等价的。
3. 熵的定义TQ S revδd =或∫=ΔB ArevδTQ S熵是广度性质,其单位为。
系统状态变化时,要用可逆过程的热温商来衡量熵的变化值。
1K J −⋅4. 克劳修斯不等式T QS δd irrev ≥ 或 ∫≥ΔB A ir rev δT Q S 等号表示可逆,此时环境的温度T 等于系统的温度,为可逆过程中的热量;不等号表示不可逆,此时T 为环境的温度,为不可逆过程中的热量。
Q δQ δ5. 熵增原理0)d (irrev≥绝热S 或0)(irrev≥Δ绝热S 等号表示绝热可逆过程,不等号表示绝热不可逆过程。
在绝热条件下,不可能发生熵减少的过程。
0)d (irrev≥孤立S 或0)(irrev≥Δ孤立S 等号表示可逆过程或达到平衡态,不等号表示自发不可逆过程。
可以将与系统密切相关的环境部分包括在一起,作为一个隔离系统,则有:0irrev sur sys iso ≥Δ+Δ=ΔS S S6. 熵变计算的主要公式计算熵变的基本公式: ∫∫∫−=+=δ=−=Δ2 12 12 1rev12d d d d TpV H T V p UTQ S S S 上式适用于封闭系统,一切非体积功过程。
物理化学公式大全

物理化学公式集热力学第一定律功:δW=δW e+δW f(1)膨胀功δW e=p外dV 膨胀功为正,压缩功为负。
(2)非膨胀功δW f=xdy非膨胀功为广义力乘以广义位移。
如δW(机械功)=fdL,δW(电功)=EdQ,δW(表面功)=rdA。
热Q:体系吸热为正,放热为负。
热力学第一定律:△U=Q—W 焓H=U+pV理想气体的内能和焓只是温度的单值函数。
热容C=δQ/dT(1)等压热容:C p=δQ p/dT=(∂H/∂T)p(2)等容热容:C v=δQ v/dT=(∂U/∂T)v常温下单原子分子:C v,m=C v,m t=3R/2常温下双原子分子:C v,m=C v,m t+C v,m r=5R/2等压热容与等容热容之差:(1)任意体系C p—C v=[p+(∂U/∂V)T](∂V/∂T)p(2)理想气体C p—C v=nR理想气体绝热可逆过程方程:pVγ=常数TVγ-1=常数p1-γTγ=常数γ=C p/ C v理想气体绝热功:W=C v(T1—T2)=(p1V1—p2V2)理想气体多方可逆过程:W=(T1—T2)热机效率:η=冷冻系数:β=-Q1/W可逆制冷机冷冻系数:β=焦汤系数:μJ-T==-实际气体的ΔH和ΔU:ΔU=+ΔH=+化学反应的等压热效应与等容热效应的关系:Q p=Q V+ΔnRT当反应进度ξ=1mol时,Δr H m=Δr U m+RT化学反应热效应与温度的关系:热力学第二定律Clausius不等式:熵函数的定义:dS=δQ R/T Boltzman熵定理:S=klnΩHelmbolz自由能定义:F=U—TS Gibbs自由能定义:G=H-TS热力学基本公式:(1)组成恒定、不作非膨胀功的封闭体系的热力学基本方程:dU=TdS-pdV dH=TdS+VdpdF=-SdT-pdV dG=-SdT+Vdp(2)Maxwell关系:==-(3)热容与T、S、p、V的关系:C V=T C p=TGibbs自由能与温度的关系:Gibbs-Helmholtz公式=-单组分体系的两相平衡:(1)Clapeyron方程式:=式中x代表vap,fus,sub。
物理化学热力学基本方程

利用全微分条件 ,将其作用于(5.1)、(5.2)、(5.4)和(5.6)式,得到(5.8)~(5.11)式所 给八个热力学偏导数的关系:
如果有全微分 df adx ( T , p ) bdy / 则 S (a / y ) x (b / x ) y 必有
( T / V ) S ( p / S )V (V / S ) p ( p / T )V ( S / V ) T (V / T ) p ( S / p )T
p S T V V T
S V p T T p
G H TS
dG SdT V dp
V (G / p )T
当系统处于平衡态时,不仅描述该系统整体性质的宏观量不再随时 间改变,而且这些宏观量之间还存在着函数关系。只有少数几个是 独立态参量,其余宏观量则是态参量的函数。对于给定的系统,其 态参量的数目是确定的,但选哪几个宏观量作为态参量则是任意的。
我们可以将(5.1)式看成以S和V为独立变量表示的全微分dU ,U=U(S,V), 于是写为
dU ( U / S ) V dS ( U / V ) S dV
可以与(5.1)式比较,得到两个偏导数:
T ( U / S )V
p (U / V ) S
(5.8)
H U p V U (U / V ) S V F U T S U ( U / S )V S G U pV TS
U ( U / V ) S V ( U / S )V S
这说明,只要已知以S,V为独立态参量时内能U的表达式U=U(S,V), 就可以求得T,状态方程,p,H,F,G乃至系统的全部热力学量。所 以内能U是以S、V为独立态参量的特性函数。同样可以证明焓H,自由 能F和自由焓G分别是以(S,p),(T,V)和(T,p) 为独立态参量的特性函数。
物理化学知识点总结 热力学计算及证明

热力学方法和计算到此为止,我们已经学习了八个热力学状态函数:p、V、T、U、H、S、A、G。
这八个状态函数中p、V、T、U、S有着明确的物理意义,而H、A、G是定义出来的状态函数,并没有明确的物理意义。
这八个状态函数可以构成许许多多热力学函数关系式一、热力学基本方程在非体积功为0的条件下,单组分单相封闭系统经过一个始态到达末态,根据热力学第一定律有。
dU=δQ r+δW r=δQ+δW式子中,δQ r和δW r是可逆过程的热和功,δQ和δW是不可逆过程的热和功。
在非体积功为0的条件下,对于单组分单相封闭系统的可逆过程有δQ r=TdS δW r=−pdV带入后可得到一项重要的公式:dU=TdS−pdV这项式子称为热力学第一定律和第二定律的联合表达式,适用于单相单组分封闭系统可逆过程与不可逆过程。
由焓的定义H=U+pV,两端同时微分得到dH=dU+pdV+Vdp再将dU=TdS−pdV带入上式,得到dH=TdS+Vdp由亥姆霍兹函数的定义A=U−TS,两端同时取微分得到dA=dU−TdS−SdT再将dU=TdS−pdV带入上式,得到dA=−SdT−pdV由吉布斯函数的定义G=H−TS,两端同时微分得到dG=dH−TdS−SdT再将dH=TdS+Vdp带入上式,得到dG=−SdT+Vdp这四个关系式,叫做封闭系统的热力学基本关系式,地位相当重要,务必准确推导和记忆。
严格地讲,这四个关系式只适用于封闭系统中无非体积功的可逆过程,但是我们知道一切实际过程都是不可逆过程,所以我们也可以将这四个关系式用到不可逆过程中,尽管有一些误差,但是完全可以忽略。
为了避免理解过于麻烦,咱不解释误差的来源。
二、对应系数关系式由此我们可以将U、(S,p)、A=A(T,V)、G=G(T,p),根据全微分的性质,可以得到dU=(ðUðS)VdS+(ðUðV)SdV dH=(ðHðS)pdS+(ðHðp)SdpdA=(ðAðT)VdT+(ðAðV)TdV dG=(ðGðT)pdT+(ðGðp)Tdp将上面四个全微分式,对应到四个基本表达式中,我们可以得到T =(ðU ðS )V =(ðH ðS )p p =−(ðU ðV )S =−(ðA ðV )TV =(ðH ðp )S =(ðG ðp )T S =−(ðA ðT)V =−(ðG ðT )p三、麦克斯韦关系式在数学上dz =Mdx +Ndy 是一个全微分的充要条件为(ðM ðy )x =(ðNðx )y我们再一次调出四个热力学基本关系式dU =TdS −pdV dH =TdS +Vdp dA =−SdT −pdV dG =−SdT+Vdp来导出麦克斯韦关系式:(ðS ðV )T =(ðp ðT )V (ðS ðp )T =−(ðVðT )p麦克斯韦关系式的意义在于:它能将不能直接测量出来的物理量(如:熵S ),换成可以直接测量出来的物理量(如T 、V 、p ),或者由状态方程求得的物理量。
物理化学第二章热力学第一定律主要公式及其适用条件

第二章 热力学第一定律主要公式及使用条件1. 热力学第一定律的数学表示式W Q U +=∆或 'a m b δδδd δd U Q W Q p V W=+=-+ 规定系统吸热为正,放热为负。
系统得功为正,对环境作功为负。
式中 p amb 为环境的压力,W ’为非体积功。
上式适用于封闭体系的一切过程。
2.焓的定义式3. 焓变(1) )(pV U H ∆+∆=∆式中)(pV ∆为pV 乘积的增量,只有在恒压下)()(12V V p pV -=∆在数值上等于体积功。
(2) 2,m 1d p H nC T ∆=⎰ 此式适用于理想气体单纯pVT 变化的一切过程,或真实气体的恒压变温过程,或纯的液体、固体物质压力变化不大的变温过程。
4.热力学能(又称内能)变 此式适用于理想气体单纯pVT 变化的一切过程。
5. 恒容热和恒压热V Q U =∆ (d 0,'0V W == p Q H =∆ (d 0,'0)p W ==6. 热容的定义式(1)定压热容和定容热容pVU H +=2,m 1d V U nC T ∆=⎰δ/d (/)p p p C Q T H T ==∂∂δ/d (/)V V V C Q T U T ==∂∂(2)摩尔定压热容和摩尔定容热容,m m /(/)p p p C C n H T ==∂∂,m m /(/)V V V C C n U T ==∂∂上式分别适用于无相变变化、无化学变化、非体积功为零的恒压和恒容过程。
(3)质量定压热容(比定压热容)式中m 和M 分别为物质的质量和摩尔质量。
(4) ,m ,m p V C C R -=此式只适用于理想气体。
(5)摩尔定压热容与温度的关系23,m p C a bT cT dT =+++式中a , b , c 及d 对指定气体皆为常数。
(6)平均摩尔定压热容21,m ,m 21d /()Tp p T C T T T C =-⎰7. 摩尔蒸发焓与温度的关系21vap m 2vap m 1vap ,m ()()d T p T H T H T C T ∆=∆+∆⎰ 或 v a p m v a p (/)p p H T C ∂∆∂=∆式中 vap ,m p C ∆ = ,m p C (g) —,m p C (l),上式适用于恒压蒸发过程。
物理化学公式全解

热力学第一定律功:δW =δW e +δW f(1)体积功 δW e =-p 外dV 体积功为正,压缩功为负。
(2)非体积功δW f =xdy非体积功为广义力乘以广义位移。
如δW (机械功)=fdL ,δW (电功)=EdQ ,δW (表面功)=rdA 。
热 Q :体系吸热为正,放热为负。
热力学第一定律: △U =Q+W 焓 H =U +pV 理想气体的内能和焓只是温度的单值函数。
热容 C =δQ/dT(1)等压热容:C p =δQ p /dT = (∂H/∂T)p (2)等容热容:C v =δQ v /dT = (∂U/∂T)v 常温下单原子分子:C v ,m =C v ,m t =3R/2常温下双原子分子:C v ,m =C v ,m t +C v ,m r =5R/2 等压热容与等容热容之差:(1)任意体系 C p —C v =[p +(∂U/∂V )T ](∂V/∂T )p (2)理想气体 C p —C v =nR 理想气体绝热可逆过程方程:pV γ=常数 TV γ-1=常数 p 1-γT γ=常数 γ=C p / C v 理想气体绝热功:W =C v (T 1—T 2)=11-γ(p 1V 1—p 2V 2) 理想气体多方可逆过程:W =1nR-δ(T 1—T 2) 热机效率:η=212T T T - 冷冻系数:β=-Q 1/W 可逆制冷机冷冻系数:β=121T T T -焦汤系数: μJ -T =H p T ⎪⎪⎭⎫⎝⎛∂∂=-()pT C p H ∂∂ 实际气体的ΔH 和ΔU :ΔU =dT T U V ⎪⎭⎫ ⎝⎛∂∂+dV V U T ⎪⎭⎫ ⎝⎛∂∂ ΔH =dT T H P ⎪⎭⎫⎝⎛∂∂+dp p H T ⎪⎪⎭⎫ ⎝⎛∂∂ 化学反应的等压热效应与等容热效应的关系:Q p =Q V +ΔnRT 当反应进度 ξ=1mol 时, Δr H m =Δr U m +∑BB γRT化学反应热效应与温度的关系:()()()dT B C T H T H 21T T m p B1m r 2m r ⎰∑∆∆,+=γ热力学第二定律Clausius 不等式:0TQS BAB A ≥∆∑→δ—熵函数的定义:dS =δQ R /T Boltzman 熵定理:S =kln Ω Helmbolz 自由能定义:F =U —TS Gibbs 自由能定义:G =H -TS 热力学基本公式:(1)组成恒定、不作非膨胀功的封闭体系的热力学基本方程:dU =TdS -pdV dH =TdS +Vdp dF =-SdT -pdV dG =-SdT +Vdp (2)Maxwell 关系:T V S ⎪⎭⎫⎝⎛∂∂=VT p ⎪⎭⎫ ⎝⎛∂∂Tp S ⎪⎪⎭⎫ ⎝⎛∂∂=-p T V ⎪⎭⎫ ⎝⎛∂∂ (3)热容与T 、S 、p 、V 的关系:C V =T VT S ⎪⎭⎫⎝⎛∂∂ C p =T p T S ⎪⎭⎫ ⎝⎛∂∂Gibbs 自由能与温度的关系:Gibbs -Helmholtz 公式 ()pT /G ⎥⎦⎤⎢⎣⎡∂∆∂T =-2T H ∆ 单组分体系的两相平衡: (1)Clapeyron 方程式:dT dp=mX m X V T H ∆∆ 式中x 代表vap ,fus ,sub 。
02-物理化学第二章 热力学第一定律
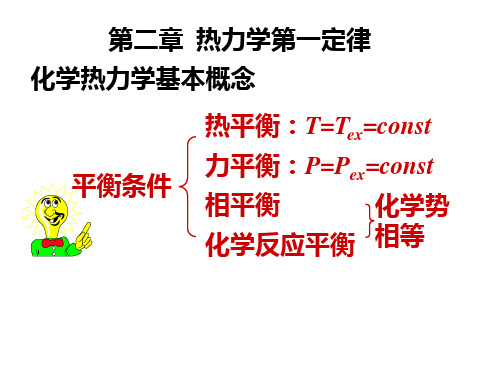
H
m
298
K
H1
H
2
r
H
m
298
K
298K
T
eCP,E fC P,F dT
T
298K gCP,G hCP,H dT
X = f(T,P)o=rf(T,V)… 双变量坐标
强度性质—— 与量n无关
整体 = 部分 (T、P)
广延性质—— 与量n成正比 整体 = ∑部分
强度量 = 广延量/广延量
本章任务:
计算能量变化:
状态函数 U、H + 过程量 Q、W 理想气体,纯物质的 U、H 性质
步骤: ㈠ 不需第一定律即能计算的Q和W ㈡ 第一定律及内能 ㈢ 用于计算过程热及焓 ㈣ 用于绝热功的计算
§2-1
热和功
过程量——计算时一定要看具体过程 2·1·1 热Q
显热的计算
用热容
QB n CB,mdT
利用手册中数据,只能计算恒压或恒容热
QP or V
n
C dT T2
T1
P or V ,m
2·1·2 功W
体积功的计算
2
W 1 PexdV
eg. 恒容过程 W = 0
等外压过程 Pex=constant
Ⅱ:192.5kPa
298.15K
352.15K
求:Q、W、△U、△H
解: Q=0
U n CV ,mdT
nCV ,m T2 T1 1.366kJ
H n CP,mdT
n CV ,m R T2 T1 1.814kJ
W U Q 1.366kJ
例2·5·2 1mol双原子理想气体于27℃, 101.325 kPa 状态下,受某恒定外压恒温 压缩到平衡,再由该状态恒容升温至 97 ℃,则压力升到 1013.25 kPa。求整个过 程的W、Q、 △U及△H。
物理化学公式大全

物理化学公式大全物理化学是研究物质的物理性质和化学性质之间的关系的学科。
以下是一些在物理化学中常用的公式:1.热力学方程:-理想气体状态方程:PV=nRT其中P为气体压强,V为气体体积,n为气体摩尔数,R为气体常数,T为气体温度。
-内能变化公式:ΔU=q+w其中ΔU为系统内能变化,q为系统吸取或放出的热量,w为系统对外界做的功。
-能量守恒定律:ΔE=q+w其中ΔE为系统总能量变化,q为系统吸取或放出的热量,w为系统对外界做的功。
2.动力学方程:-反应速率公式:r=k[A]^m[B]^n其中r为反应速率,k为反应速率常数,[A]和[B]分别为反应物A和B的浓度,m和n为反应物的反应级数。
- Arrhenius 公式:k = A * e^(-Ea/RT)其中 k 为反应速率常数,A 为 Arrhenius 常数,Ea 为活化能,R为气体常数,T 为反应温度。
3.量子力学方程:- 波函数公式:Ψ = Σcnφn其中Ψ 为波函数,cn 为系数,φn 为基态波函数。
- Schroedinger 方程:HΨ = EΨ其中H为哈密顿算符,Ψ为波函数,E为能量。
4.热力学方程:- 熵变公式:ΔS = q_rev / T其中ΔS 为系统熵变,q_rev 为可逆过程吸放热量,T 为温度。
- Gibbs 自由能公式:ΔG = ΔH - TΔS其中ΔG 为 Gibbs 自由能变化,ΔH 为焓变化,ΔS 为熵变化,T 为温度。
5.电化学方程:- Nerst 方程:E = E° - (RT / nF) * ln(Q)其中E为电池电势,E°为标准电势,R为气体常数,T为温度,n为电子数,F为法拉第常数,Q为电化学反应的反应物浓度比。
- Faraday 定律:nF = Q其中n为电子数,F为法拉第常数,Q为电荷数。
以上公式只是物理化学中的一小部分,这里列举的是一些常见的、基本的公式,实际上物理化学领域有非常多的公式和方程可供使用。
华东理工大学《物理化学》课件2.6 亥氏函数吉氏函数,热力学基本方程

dAT ,V d-W dAT ,V d-W R
AT ,V W AT ,V WR
不可逆程度
dAT ,V d-W
返回章首
不做非体积功时
W 0
dAT ,V ,W 0 0
dAT ,V ,W 0 0 AT ,V ,W 0 0
恒温恒容不做非体积功时,亥氏函数在可逆 中不变,在不可逆过程中减小,亥氏函数增大则是 不可能的。
不可逆程度
dAT ,V ,W 0
4.恒温恒压过程
T环dS d-Q 0
d-W d-W pdV d-W d( pV )
TdS dU d( pV ) d-W 0
dGT , p d-W 0
dGT , p d-W GT , p W dGT , p d-W R GT , p WR
T
p U A V S V T
S A G T V T p
返回章首
吉布斯–亥姆霍兹方程
(A/T) T V
U T2
,
(A/T)
(1/ T )
V
U
(G / T T
)
p
H T2
,
(G / T )
(1/T )
p
H
返回章首
4. 麦克斯韦关系式
dH
H S
dS p
H p
S
dp
dA A dT A dV
T V
V T
dG
G T
p
dT
G p
T
dp
dU TdS pdV dH TdS Vdp dA SdT pdV dG SdT Vdp
T U H S V S p
V
H p
S
G p
dZ MdX NdY
物理化学

热力学第一定律1、热力学第一定律:△U=Q+W2、体积功:(1)气体向真空膨胀:W=0(2)气体恒外压膨胀:W=—P外*△V(3)外压比内压差无限小膨胀:W=—∫p*dV 若气体为理想气体时,W=—nRTln(p1/p2)=—nRTln(v2/v1)(4)可逆相变的体积功:W=—nRT3、定容及定压下的热:(焓)△H=△U+△(PV)4、定压下:Q=△H=nCp,m*△T定容下:Q=△U=nCv,m*△T (Cp,m=Cv,m+R)5、理想气体的绝热过程:pV^γ=常数(γ=Cp,m/Cv,m)6、实际气体的节流膨胀(等焓膨胀)△H=07、定容与定压反应热:△H=△U+RT△n (Qp=Qv+RT△n)8、反应进度ζ:ζ=(n2-n1)/v9、任意一反应的反应焓等于产物生成焓之和减去反应物生成焓之和任意一反应的反应焓等于反应物燃烧焓之和减去产物燃烧焓之和10、反应焓与温度的关系(基尔霍夫方程):△H2-△H1=△Cp(T2-T1)热力学第二定律1、克劳休斯不等式:△S>=Q/T2、卡诺热机的效率:η=(T2-T1)/T23、定温过程的熵变:△S=nRln(p1/p2)4、定压熵变:△S=nCp,m*ln(T2/T1)5、定容熵变:△S=nCv,m*ln(T2/T1)6、绝热可逆过程为等熵过程(△S=0)7、定温定容系统:亥姆霍兹函数A=U—TS8、定温定压系统:吉布斯函数G=H—TS=A+pV (可逆相变:△G=0)9、热力学函数之间的关系:dU=TdS-p*dVdH=TdS+VdpdA=-SdT-p*dVdG=-SdT+Vdp10、吉布斯-亥姆霍兹公式:(△G/T2)-(△G/T1)=△H(1/T2-1/T1)。
物理化学重要概念公式总结

第一章 热力学第一定律一、基本概念系统与环境,状态与状态函数,广度性质与强度性质,过程与途径,热与功,内能与焓。
二、基本定律热力学第一定律:ΔU =Q +W 。
焦耳实验:ΔU =f (T ) ; ΔH =f (T )三、基本关系式1、体积功的计算 δW = -p e d V恒外压过程:W = -p e ΔV可逆过程: W =nRT 1221ln ln p p nRT V V =2、热效应、焓等容热:Q V =ΔU (封闭系统不作其他功)等压热:Q p =ΔH (封闭系统不作其他功)焓的定义:H =U +pV ; d H =d U +d(pV )焓与温度的关系:ΔH =⎰21d p T T T C3、等压热容与等容热容 热容定义:V V )(T U C ∂∂=;p p )(T HC ∂∂=定压热容与定容热容的关系:nR C C =-V p热容与温度的关系:C p =a +bT +c’T 2四、第一定律的应用1、理想气体状态变化等温过程:ΔU =0 ; ΔH =0 ; W =-Q =⎰-p e d V 等容过程:W =0 ; Q =ΔU =⎰T C d V ; ΔH =⎰T C d p 等压过程:W =-p e ΔV ; Q =ΔH =⎰T C d p; ΔU =⎰T C d V可逆绝热过程:Q =0 ; 利用p 1V 1γ=p 2V 2γ求出T 2,W =ΔU =⎰T C d V ;ΔH =⎰T C d p不可逆绝热过程:Q =0 ;利用C V (T 2-T 1)=-p e (V 2-V 1)求出T 2,W =ΔU =⎰T C d V ;ΔH =⎰T C d p2、相变化可逆相变化:ΔH =Q =n Δ_H ;W=-p (V 2-V 1)=-pV g =-nRT ; ΔU =Q +W3、热化学物质的标准态;热化学方程式;盖斯定律;标准摩尔生成焓。
摩尔反应热的求算:)298,()298(B H H m f B mr θθν∆=∆∑ 反应热与温度的关系—基尔霍夫定律:)(])([,p B C T H m p BB m r ∑=∂∆∂ν。
物理化学1-2章公式总结

(3)理想气体恒温混合 ∆S = −R∑ni ln yi
i =1 K
, 能用这个公式各气体的 对不同种分子的混合才 的 ∆ 分压在混合前后是改变 , 否则 S = 0 。 4 ( )单组分理想气体任意 过程 V2 T2 ∆S = SB − SA = nRln + nCV ,m ln V1 T1 p1 T2 V2 p2 = nRln + nC p,m ln = nC p,m ln + nCV ,m ln p2 T1 V1 p1
∂U ∂ H T = = ∂ S ∂ S
V
∂Z ∂ Z dZ = dY dX + ∂ X ∂Y
Y X
p
∂ A ∂ G S = − = − ∂T ∂T
V
p
麦克斯韦关系式 dZ = MdX + NdY
1.热力学基本定律 热力学基本定律
1.1热力学第一定律和热力学能 热力学第一定律和热力学能
①热力学第一定律的数学表达式 (封闭系统任何过程) ∆U = Q + W
dU = dQ + dW (封闭系统微小过程)
V2 V1
dW体积 = - p外dV,W体积 = -∫
p外dV
在封闭系统, W 在封闭系统, ' = 0的恒容过程中 ∆U = QV
T
V
p
12
V(β ) V (α )
∆U = ∆H − ∆( pV )
T2 T1
∆U = ∫ nCV ,mdT
pd = − p V ( β ) −V (α ) V
(
)
如涉及气体则液体或固体的体积可 , , 忽略 , 还可用 (g) = nRT pV 如气体可视为理想气体
物理化学公式

理气:pV=nRT , n = m /M ;分压或分体积;:B =c B RT =p y B ;压缩因子:Z = pV /RT 实/真 体积功:δW = -p 外dV热力学第一定律:∆ U = Q +W , d U =δQ +δW焓的定义: H =U + pV 热容:定容C V ,m = δQ V /dT = (∂ U m /∂ T )V 定压:C p ,m = δQ p /dT = (∂ H m /∂ T )P理气:C p ,m - C V ,m =R ;凝聚态:C p ,m - C V ,m ≈0体积膨胀系数:αV =(əV/əT )P /T等温压缩率:κV =-(əV/əP )T /T范德华方程:(P+a/Vm 2)(Vm -b)=RT,由(əP/əVm)Tc =0 ,(ə2P/əVm 2)Tc =0,可求a,b 波意尔温度T B :P →0 lim (ə(PVm )/əP )T B =0标准摩尔反应焓:∆ r H m θ = ∑ v B ∆ f H B θ (T ) = -∑ v B ∆ c H B θ (T )基希霍夫公式(适用于相变和化学反应过程)∆ r H m θ(T 2)= ∆ r H m θ(T 1)+∫T1T2∆ r C p ,m d T恒压摩尔反应热与恒容摩尔反应热的关系式Q p -Q V = ∆ r H m (T ) -∆ r U m (T ) =∑ v B (g)RT恒温过程d T =0, ∆ U =∆ H =0, Q =W非恒温过程,∆ U = n C V ,m ∆ T , ∆ H = n C p ,m ∆ T对于凝聚物质:∆ U ≈∆ H = n C p ,m ∆ T恒压过程:p 外=p =常数,无其他功W '=0(W = -p 外(V 2-V 1), ∆ H = Q p =∫T1T2 n C p ,m d T ,∆ U =∆ H -∆(pV ),Q =∆ U -W真空膨胀过程p 外=0,W =0,Q =∆ U理想气体结果:d T =0,W =0,Q =∆ U =0,∆ H =0恒容过程: W =0,Q V =∆ U = ∫T1n C V ,m d T,∆ H =∆ U +V ∆ p绝热可逆:W =∫V1V2-p d V = ∆ U =∫T1T2 n C V ,m d T ,∆ H =∆ U +∆ pV 。
物理化学1.15-1 热力学函数的基本关系式

8个热力学函数: 可直接测定
p、V、T、U 、H 、S、A、G
定 H =U+pV 义 式 A =U-TS
可求得
G =H-TS=A+pV
1.热力学基本方程
封闭系统 dU =δQ + δW
可逆过程
=δQr -pdV + δWr′
δQr =TdS
dU = TdS -pdV + δWr' δWr'=0:
dA = -SdT- pdV dG = -SdT + Vdp
G S T p
G p
T
V
证明:无相变和化学变化的封 闭系统,在定温下其吉布斯自 由能随压力的改变恒为正值。
证明:
dG = -SdT + Vdp
G ( p )T
V
>0
解: dG = -SdT + Vdp
S T2 nCV ,mdT nR ln V2 ,
T1
T
V1
A nRT ln V2 V1
应(用ቤተ መጻሕፍቲ ባይዱ()i封条i()i无i闭件i)非可系:体逆统积过,功程,。
可用于: (i)定量,定组成的单相系统;
(ii) 保持相平衡及化学平衡的系统.
8个派生公式: dU = TdS- pdV dH = TdS + Vdp
U T S V U p V S
dU = TdS -pdV
dU=TdS-pdV
H=U+pV dH=dU+pdV+Vdp
A=U-TS dA=dU-TdS-SdT
dH=TdS+Vdp
dA= - SdT - pdV
物理化学

二.一些基本过过程的 S , G, A的计算公式 W f 0
基本过程
S
V nRIn 2 V1
G
nRTIn P2 P1
A
A PdV V nRT dV nRTln 1 V V2
dV
T
③
dU T S dT S dV PdV TV VT T S P dV ④ dT T S T V VT
[
] [ ]
比较①与④对应系数应相等-------叫系数比较法
U V T S V T P P T
U T
V
1
T
U
V
这时要分别证
U V
T
?
U T
V
?
用前面介绍的二种方法在选一种证明,代入上式可得。现在证的例题都是 不符合特征变量,如果符合特征变量, 如: U
S
V
T ,直接用对应系数关系可得。
例题2:证明
C P CV T P
V T T
(1)全微分到偏微分法
从基本关系式 定温,对V微分
U V
dU TdS PdV
T
全微分
T S
V
T
P
偏微分 S
V
不易测量
T
由Maxwell关系
P T S V
V
T
U
V
T
T P
T
V
P
物理化学公式大全

物理化学公式大全物理化学是研究物质及其性质与能量变化之间关系的学科。
在物理化学的学习与研究过程中,掌握一些重要的公式是十分关键的。
下面是物理化学公式的大全,帮助你更好地理解和运用这些公式。
1. 热力学公式1.1 热力学第一定律dU = dq + dw其中,dU表示系统内能的变化,dq表示系统吸收的热量,dw表示系统对外界所做的功。
1.2 热力学第二定律(卡诺循环)η = 1 - Tc / Th其中,η表示卡诺循环的热效率,Tc表示循环过程中的低温热源温度,Th表示循环过程中的高温热源温度。
1.3 熵变ΔS = ∫dq / T其中,ΔS表示熵变,dq表示吸收的热量,T表示温度。
2. 电化学公式2.1 奥姆定律I = U / R其中,I表示电流强度,U表示电压,R表示电阻。
2.2 法拉第定律I = nFv其中,I表示电流强度,n表示电离物质的摩尔数,F表示法拉第常数,v表示电离的速率。
2.3 电解质溶液中浓度的关系c = n / V其中,c表示溶液的浓度,n表示溶质的物质的量,V表示溶液的体积。
3. 量子化学公式3.1 玻尔模型电子能级En = - 13.6 / n²其中,En表示第n个电子能级的能量。
3.2 库仑势能E = - (Z × e²) / (4πε₀r)其中,E表示两个带电粒子之间的库仑势能,Z表示电荷的量子数,e表示元电荷,ε₀表示真空介电常数,r表示两个带电粒子的距离。
4. 动力学公式4.1 反应速率常数k = A × e^(-Ea / RT)其中,k表示反应速率常数,A表示指前因子,Ea表示活化能,R 表示气体常数,T表示温度。
4.2 阿伦尼乌斯方程k = Z × f(ΔE)其中,k表示反应速率常数,Z表示碰撞频率,f(ΔE)表示碰撞激活因子,ΔE表示碰撞能量。
5. 其他公式5.1 时间-位移关系x = v₀t + 1/2at²其中,x表示位移,v₀表示初始速度,t表示时间,a表示加速度。
《物理化学》教学研讨——热力学基本方程记忆法

《物理化学》教学研讨——热力学基本方程记忆法
热力学基本方程是学习物理化学的一个重要概念,也是学生们在热力学学习中需要掌握的重要内容。
为了帮助学生们更好地掌握和记忆热力学基本方程,我们在教学研讨中提出了以下记忆方法:
1. 热力学基本方程的形式:dU = TdS - PdV
2. 记忆“T”和“S”在方程中的位置:T在dS前,S在dT后,可以看作是“TS”字母顺序的记忆。
3. 记忆“P”和“V”在方程中的位置:P在dV后,V在dP前,可以看作是“PV”字母顺序的记忆。
4. 利用“热”、“力”、“基”、“本”四个字的首字母记忆方程中的“dU”。
通过以上的记忆方法,学生们可以轻松地记忆热力学基本方程,从而更好地理解和掌握热力学学习中的相关知识。
同时,教师们也可以在教学中结合案例和实验等方式,帮助学生更深入地理解和应用热力学基本方程,提高学生的学习效果和能力。
- 1 -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
p S T V V T
S V p T T p
G H TS
dG SdT V dp
V (G / p )T
当系统处于平衡态时,不仅描述该系统整体性质的宏观量不再随时 间改变,而且这些宏观量之间还存在着函数关系。只有少数几个是 独立态参量,其余宏观量则是态参量的函数。对于给定的系统,其 态参量的数目是确定的,但选哪几个宏观量作为态参量则是任意的。
利用全微分条件 ,将其作用于(5.1)、(5.2)、(5.4)和(5.6)式,得到(5.8)~(5.11)式所 给八个热力学偏导数的关系:
如果有全微分 df adx ( T , p ) bdy / 则 S (a / y ) x (b / x ) y 必有
( T / V ) S ( p / S )V (V / S ) p ( p / T )V ( S / V ) T (V / T ) p ( S / p )T
我们可以将(5.1)式看成以S和V为独立变量表示的全微分dU ,U=U(S,V), 于是写为
dU ( U / S ) V dS ( U / V ) S dV
可以与(5.1)式比较,得到两个偏导数:
T ( U / S )V
p (U / V ) S
(5.8)
H U p V U (U / V ) S V F U T S U ( U / S )V S G U pV TS
U ( U / V ) S V ( U / S )V S
这说明,只要已知以S,V为独立态参量时内能U的表达式U=U(S,V), 就可以求得T,状态方程,p,H,F,G乃至系统的全部热力学量。所 以内能U是以S、V为独立态参量的特性函数。同样可以证明焓H,自由 能F和自由焓G分别是以(S,p),(T,V)和(T,p) 为独立态参量的特性函数。
如果选择的独立态参量适当,则只要知道一个态函数,就可以把全 部热力学量求出来,于是,我们将这样的态函数成为特性函数。
例如:已知以S,V为独立态参量时内能U的表达式U=U(S,V), 由(5.8)式可求得系统的温度T ( U / S ) V 和压强 p ( U / V ) S 显然后者是p,T,V之间的关系,即系统的状态方程。将已知的U=U(S,V) 和求得的T(S,V),p(S,V)一道代入H,G和F的定义式,可得:
(5.1)
dH T dS V dp
同理,交换基本方程中T和S的地位,得:
(5.2)
dF SdT pdV
F成为亥姆霍兹自由 能或称为自由能,定 义为
(5.4)
F U TS
交换T和S,p 和V的地位,可得:
dG SdT V dp
(5.6)
因此,当状态给定时, 态参量p,V,T及态函数U,S都有唯一 确定值,因而H,F和G也有唯一确定值。也就是说, H,F和G 都是态函数。因为U,S和V都是广延量, T,p是强度量,于是 G为吉布斯自由焓或简称自 上面所定义的H,F和G都是广延量,式(5.2)、(5.4)、(5.6)都是 由焓,定义为 均匀封闭流体系统的热力学基本方程,它们和(5.1)式等价。 G U pV T S H T S
T (H / S ) p
V (H / p ) S
T V p S S p
F U TS
dF SdT pdV
S ( F / T )V
p (F / V )T
S (G / T ) p
同样类似的,由 H H ( S , p ) ,F F (T , V ) ,G G (T , p ) 可以写出:
d H (H / S ) p d S (H / p ) S d V d F ( F / T )V d T ( F / V ) T d V d G (G / T ) p d T (G / p )T d p
热 力 学 原 理
勒让德变换
热 力 学 函 数
热力学基本方程
热 力 学 关 系
对于均匀封闭系统的热力学基本方程:
H称为焓,定 义为 H U pV 利用勒让德变换可将上式改写为另外三种等价形式,交换式中的p和V 的地位,即将 pdV d ( pV ) V dp 代入,则式子化为
dU T dS pdV
和(5.2),(5.4),(5.6)式比较,得到另外六个热力学偏导数:
T (H / S ) p
V (H / p ) S
(5.9)Байду номын сангаас(5.10) (5.11)
S ( F / T )V
S (G / T ) p
p (F / V )T
V (G / p )T
均匀封闭系的普遍热力学关系
热力学势 热力学基本方程 热力学偏导数 麦克斯韦关系
U
dU T dS pdV
T ( U / S )V
p (U / V ) S
T p V S S V
H U pV
dH T dS V dp
