一、三角形的等积变形
三角形等积变形

三角形的等积变形是指保持三角形面积不变的情况下,通过改变其形状而产生的变化。
以下是一些常见的三角形等积变形:1.直角三角形的等积变形:可以通过改变直角三角形的两条直角边的长度来实现等积变形。
例如,将直角三角形的两条直角边同时缩放,或保持一个直角边不变,将另一条直角边拉长或缩短,以使面积保持不变。
2.等边三角形的等积变形:等边三角形的边长相等,可以通过改变等边三角形的边长来实现等积变形。
可以将等边三角形的边长同时拉长或缩短,使得面积保持不变。
3.锐角三角形的等积变形:对于锐角三角形,可以通过改变其两条边长和夹角的关系来实现等积变形。
可以保持其中一条边不变,改变另一条边的长度和夹角的大小,以使面积保持不变。
4.钝角三角形的等积变形:钝角三角形也可以通过改变边长和夹角的关系来进行等积变形。
可以保持其中一条边不变,改变另一条边的长度和夹角的大小,使面积保持不变。
这些是一些常见的三角形等积变形的示例。
以下是一些额外的例子:1.等腰三角形的等积变形:等腰三角形的两条边相等,可以通过改变等腰三角形的边长和顶角的大小来实现等积变形。
可以保持其中一条边不变,改变另一条边的长度和顶角的大小,使面积保持不变。
2.不等边三角形的等积变形:对于不等边三角形,可以通过同时改变三条边的长度来实现等积变形。
保持三条边的比例关系不变,但同时拉长或缩短三条边的长度,使面积保持不变。
3.相似三角形的等积变形:相似三角形具有相似的形状但尺寸不同,可以通过改变相似三角形的比例尺寸来实现等积变形。
保持两个相似三角形的比例关系不变,但同时缩放整个三角形的尺寸,使面积保持不变。
第十讲 等积变换

◆ 孩子的未来 ◆第十讲 等积变换知识要点1.等积形:面积相等的两个图形称为等积形。
2.三角形的等积变形:三角形的等积变形指的是使三角形面积相等的变换。
3.三角形面积计算公式: S △=底×高÷24.三角形等积变形中常用到的几个重要性质: ⑴ 平行线间的距离处处相等。
⑵等底等高的两个三角形面积相等。
⑶底在同一条直线上并且相等,它们所对的角的度数是同一个,这样的两个三角形面积相等。
⑷若两个三角形的高(或底)相等,其中一个三角形的底(或高)是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍。
⑸若几个三角形的底边相等,并在两条平行线中的同一直线上,而且相等的底边所对的顶点在两条平行线中的另一条上,则这几个三角形面积相等。
5.解答三角形面积变形题目时常用到以下两条重要结论。
⑴等底等高的三角形面积相等。
⑵如果甲、乙两个三角形的高(底)相等,而甲的底(高)是乙的底(高)的几倍,则甲的面积一定是乙的面积的几倍。
典型例题例1 在三角形ABC 中(如图),3BD=DC ,阴影部分的面积是220dm 。
求三角形ABC 的面积。
ABC◆ 孩子的未来 我们的一切例2 在三角形ABC 中(如图),DC=2BD ,CE=3AE ,阴影部分的面积是20平方厘米。
求三角形ABC 的面积。
例3 △ABC 中,D 、E 为BC 边的三等分点,M 、N 分别为AE 、AC 的中点。
若22cm S MNC =∆,求=∆ABC S ?例4 下图长方形ABCD 的面积是32平方厘米,DE=3AE ,F 是CD 中点,求△BEF 的面积。
例5 已知三角形ABC 面积为8,2BD=AB ,BE=CE ,求三角形DBE 的面积。
图10-2D E C图10-3CFD 图10-4◆ 孩子的未来 我们的一切 ◆例6 右图中的三角形A 'B 'C '是把三角形ABC 的AB 延长1倍到B ',把BC 延长2倍到C ',把CA 延长3倍到A ',三角形A 'B 'C '的面积是三角形ABC 的多少倍?随堂小测1.求下列各图中阴影部分的面积。
【小升初专项训练】04 等积变形

第5讲等积变形第一关三角形的等积变形【例1】如图,在等腰直角三角形ABC中,已知AB的长是7厘米,那么这个直角三角形的面积为 平方厘米。
【答案】12.25【例2】如图,E、F分别是梯形ABCD两腰上的中点,已知阴影部分的面积是43c㎡,那么梯形ABCD 的面积是多少?【答案】172【例3】如图:三条直线互相平行,l1与l3之间的距离是7厘米,l2上AB=4厘米.求阴影部分三角形的面积是多少平方厘米? 【答案】14【例4】你能看出下面两个阴影部分A与B面积的大小关系吗?(两个长方形面积相等)【答案】A与B的面积相等【例5】如图,在斜边长为20cm的直角三角形ABC中去掉一个正方形EDFB,留下两个阴影部分直角三角形AED和DFC.若AD=8cm,CD=12cm,则阴影部分面积为多少?给出答案并说明你的计算依据.【答案】48【例6】如图,在直角三角形中有一个正方形,已知BD=10厘米,DC=7厘米,阴影部分的面积是多少?【答案】35平方厘米【例7】如图,梯形ABCD的面积是36,下底长是上底长的2倍,阴影三角形的面积是多少?【答案】16【例8】下图中阴影部分甲的面积与阴影部分乙的面积哪个大?【答案】图中甲乙的面积相等【例9】如图,在三角形ABC中,D是BC上靠近C的三等分点,E是AD中点,已知三角形ABC的面积为1,那么图中两个阴影三角形面积之和是多少?【答案】0.4【例10】已知△ABC面积为5,且BD=2DC,AE=ED,求阴影部分面积.要求写出关键的解题推理过程.【答案】2【例11】如图,将一个梯形分成四个三角形,其中两个三角形的面积分别为10与12.已知梯形的上底长度是下底的.请问:阴影部分的总面积是多少?【答案】23【例12】如图,已知梯形ABCD中,CD=10,梯形ABCD的高是4,那么阴影部分的面积是多少。
【答案】20【例13】(1)如图1,阴影部分的面积是多少?(2)如图2,一个长方形长4厘米,宽3厘米.A为长方形内的任意一点,阴影部分的面积是多少?【答案】(1)100;(2)6【例14】如图,在图中△ABE、ADF和四边形AECF面积相等.阴影部分的面积是多少?【答案】15【例15】如图,两个正方形(单位:厘米)中阴影部分的面积是多少平方厘米?【答案】8【例16】由面积为1,2,3,4的矩形拼成如图的长方形,图中阴影部分的面积为多少?【答案】【例17】如图所示,正方形ABCD的对角线BD长20厘米,BDFE是长方形.那么,五边形ABEFD的面积是多少平方厘米。
第十讲 等积变换

◆ 孩子的未来 ◆第十讲 等积变换知识要点1.等积形:面积相等的两个图形称为等积形。
2.三角形的等积变形:三角形的等积变形指的是使三角形面积相等的变换。
3.三角形面积计算公式: S △=底×高÷24.三角形等积变形中常用到的几个重要性质: ⑴ 平行线间的距离处处相等。
⑵等底等高的两个三角形面积相等。
⑶底在同一条直线上并且相等,它们所对的角的度数是同一个,这样的两个三角形面积相等。
⑷若两个三角形的高(或底)相等,其中一个三角形的底(或高)是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍。
⑸若几个三角形的底边相等,并在两条平行线中的同一直线上,而且相等的底边所对的顶点在两条平行线中的另一条上,则这几个三角形面积相等。
5.解答三角形面积变形题目时常用到以下两条重要结论。
⑴等底等高的三角形面积相等。
⑵如果甲、乙两个三角形的高(底)相等,而甲的底(高)是乙的底(高)的几倍,则甲的面积一定是乙的面积的几倍。
典型例题例1 在三角形ABC 中(如图),3BD=DC ,阴影部分的面积是220dm 。
求三角形ABC 的面积。
ABC◆ 孩子的未来 我们的一切例2 在三角形ABC 中(如图),DC=2BD ,CE=3AE ,阴影部分的面积是20平方厘米。
求三角形ABC 的面积。
例3 △ABC 中,D 、E 为BC 边的三等分点,M 、N 分别为AE 、AC 的中点。
若22cm S MNC =∆,求=∆ABC S ?例4 下图长方形ABCD 的面积是32平方厘米,DE=3AE ,F 是CD 中点,求△BEF 的面积。
例5 已知三角形ABC 面积为8,2BD=AB ,BE=CE ,求三角形DBE 的面积。
图10-2D E C图10-3CFD 图10-4◆ 孩子的未来 我们的一切 ◆例6 右图中的三角形A 'B 'C '是把三角形ABC 的AB 延长1倍到B ',把BC 延长2倍到C ',把CA 延长3倍到A ',三角形A 'B 'C '的面积是三角形ABC 的多少倍?随堂小测1.求下列各图中阴影部分的面积。
等积变形(附解答)

三角形的等积变形我们已经掌握了三角形面积的计算公式:三角形面积=底×高÷2这个公式告诉我们:三角形面积的大小,取决于三角形底和高的乘积.如果三角形的底不变,高越大(小),三角形面积也就越大(小).同样若三角形的高不变,底越大(小),三角形面积也就越大(小).这说明;当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状.本讲即研究面积相同的三角形的各种形状以及它们之间的关系.为便于实际问题的研究,我们还会常常用到以下结论:①等底等高的两个三角形面积相等.②底在同一条直线上并且相等,该底所对的角的顶点是同一个点或在与底平行的直线上,这两个三角形面积相等.③若两个三角形的高(或底)相等,其中一个三角形的底(或高)是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍.它们所对的顶点同为A点,(也就是它们的高相等)那么这两个三角形的面积相等.同时也可以知道△ABC的面积是△ABD或△AEC面积的3倍.例如在图中,△ABC与△DBC的底相同(它们的底都是BC),它所对的两个顶点A、D在与底BC平行的直线上,(也就是它们的高相等),那么这两个三角形的面积相等.例如图中,△ABC与△DBC的底相同(它们的底都是BC),△ABC的高是△DBC 高的2倍(D是AB中点,AB=2BD,有AH=2DE),则△ABC的面积是△DBC面积的2倍.上述结论,是我们研究三角形等积变形的重要依据.例1、用三种不同的方法,把任意一个三角形分成四个面积相等的三角形.方法2:如右图,先将BC二等分,分点D、连结AD,得到两个等积三角形,即△ABD与△ADC等积.然后取AC、AB中点E、F,并连结DE、DF.以而得到四个等积三角形,即△ADF、△BDF、△DCE、△ADE等积.例2、用三种不同的方法将任意一个三角形分成三个小三角形,使它们的面积比为及1∶3∶4.方法 1:如下左图,将BC边八等分,取1∶3∶4的分点D、E,连结AD、AE,从而得到△ABD、△ADE、△AEC的面积比为1∶3∶4.DE,从而得到三个三角形:△ADE、△BDE、△ACD.其面积比为1∶3∶4.当然本题还有许多种其他分法,同学们可以自己寻找解决.例3、如图,在梯形ABCD中,AC与BD是对角线,其交点O,求证:△AOB与△COD面积相等.证明:∵△ABC与△DBC等底等高,∴S△ABC=S△DBC又∵ S△AOB=S△ABC—S△BOCS△DOC=S△DBC—S△BOC∴S△AOB=S△COD.例4、如图,把四边形ABCD改成一个等积的三角形.分析本题有两点要求,一是把四边形改成一个三角形,二是改成的三角形与原四边形面积相等.我们可以利用三角形等积变形的方法,如右图,把顶点A移到CB的延长线上的A′处,△A′BD与△ABD面积相等,从而△A′DC面积与原四边形ABCD面积也相等.这样就把四边形ABCD等积地改成了三角形△A′DC.问题是A′位置的选择是依据三角形等积变形原则.过A 作一条和DB平行的直线与CB的延长线交于A′点.解:①连结BD;②过A作BD的平行线,与CB的延长线交于A′.③连结A′D,则△A′CD与四边形ABCD等积.例5、如图,已知在△ABC中,BE=3AE,CD=2AD.若△ADE的面积为1平方厘米.求三角形ABC的面积.解法1:连结BD,在△ABD中∵ BE=3AE,∴ S△ABD=4S△ADE=4(平方厘米).在△ABC中,∵CD=2AD,∴ S△ABC=3S△ABD=3×4=12(平方厘米).解法2:连结CE,如右图所示,在△ACE中,∵ CD=2AD,∴ S△ACE=3S△ADE=3(平方厘米).在△ABC中,∵BE=3AE∴ S△ABC=4S△ACE=4×3=12(平方厘米).例6、如下图,在△ABC中,BD=2AD,AG=2CG,BE=EF=FC=解:连结BG,在△ABG中,∴ S△ADG+S△BDE+S△CFG例7、如右图,ABCD为平行四边形,EF平行AC,如果△ADE的面积为4平方厘米.求三角形CDF的面积.解:连结AF、CE,∴S△ADE=S△ACE;S△CDF=S△ACF;又∵AC与EF平行,∴S△ACE=S△ACF;∴ S△ADE=S△CDF=4(平方厘米).例8、如右图,四边形ABCD面积为1,且AB=AE,BC=BF,DC=CG,AD=DH.求四边形EFGH的面积.解:连结BD,将四边形ABCD分成两个部分S1与S2.连结FD,有S△FBD=S △DBC=S1所以S△CGF=S△DFC=2S1.同理 S△AEH=2S2,因此S△AEH+S△CGF=2S1+2S2=2(S1+S2)=2×1=2.同理,连结AC之后,可求出S△HGD+S△EBF=2所以四边形EFGH的面积为2+2+1=5(平方单位).例9、如右图,在平行四边形ABCD中,直线CF交AB于E,交DA延长线于F,若S△ADE=1,求△BEF的面积.解:连结AC,∵AB//CD,∴S△ADE=S△ACE又∵AD//BC,∴S△ACF=S△ABF而 S△ACF=S△ACE+S△AEF∶S△ABF=S△BEF+S△AEF∴ S△ACE=S△BEF∴S△BEF=S△ADE=1.。
三角形的等积变形
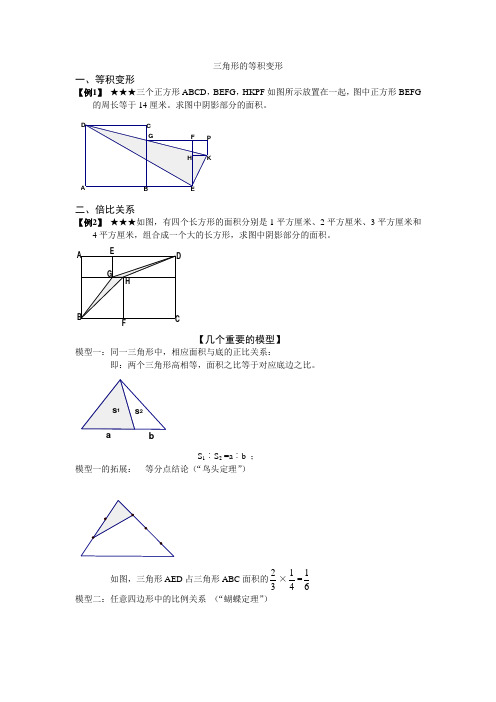
三角形的等积变形一、等积变形【例1】★★★三个正方形ABCD,BEFG,HKPF如图所示放置在一起,图中正方形BEFG 的周长等于14厘米。
求图中阴影部分的面积。
二、倍比关系【例2】★★★如图,有四个长方形的面积分别是1平方厘米、2平方厘米、3平方厘米和4平方厘米,组合成一个大的长方形,求图中阴影部分的面积。
【几个重要的模型】模型一:同一三角形中,相应面积与底的正比关系:即:两个三角形高相等,面积之比等于对应底边之比。
bS1︰S2 =a︰b ;模型一的拓展:等分点结论(“鸟头定理”)如图,三角形AED占三角形ABC面积的23×14=16模型二:任意四边形中的比例关系(“蝴蝶定理”)S 4S 3s 2s 1O DCBA①S 1︰S 2=S 4︰S 3 或者S 1×S 3=S 2×S 4 ②AO ︰OC=(S 1+S 2)︰(S 4+S 3) 模型三:梯形中比例关系(“梯形蝴蝶定理”)①S 1︰S 3=a 2︰b 2②S 1︰S 3︰S 2︰S 4= a 2︰b 2︰ab ︰ab ; ③S 的对应份数为(a+b )2模型四:相似三角形性质hh H cb a CB Aac b HC BA①a b c hA B C H=== ; ②S 1︰S 2=a 2︰A 2模型五:燕尾定理S △ABG :S △AGC =S △BGE :S △GEC =BE :EC ; S △BGA :S △BGC =S △AGF :S △GFC =AF :FC ; S △AGC :S △BCG =S △ADG :S △DGB =AD :DB ;F D CBAS 4S 3s 2s 1ba。
小学四年级奥数题三角形的等积变形及答案【三篇】

小学四年级奥数题三角形的等积变形及答案【三篇】【第一篇】1. 三角形把一个等边三角形分别分成8块和9块形状、大小都一样的三角形.分析分成8块的方法是:先取各边的中点并把它们连接起来,得到4个大小、形状相同的三角形,然后再把每一个三角形分成一半,得到如下左图所示的图形.分成9块的方法是:先把每边三等分,然后再把分点彼此连接起来,得到加上右图所示的符合条件的图形.2.比较比较下面两个积的大小:A=987654321×123456789,B=987654322×123456788.分析经审题可知A的第一个因数的个位数字比B的第一个因数的个位数字小1,但A的第二个因数的个位数字比B的第二个因数的个位数字大1.所以不经计算,凭直接观察不容易知道A和B哪个大.但是无论是对A或是对B,直接把两个因数相乘求积又太繁,所以我们开动脑筋,将A和B先进行恒等变形,再作判断.解: A=987654321×123456789=987654321×(123456788+1)=987654321×123456788+987654321.B=987654322×123456788=(987654321+1)×123456788=987654321×123456788+123456788.因为 987654321>123456788,所以 A>B.【第二篇】如图,四边形ABCD和四边形DEFG都是正方形,已知三角形AFH的面积为6平方厘米,求三角形CDH的面积.三角形面积答案:通常求三角形的面积,都是先求它的底和高.题目中没有一条线段的长度是已知的,所以我们只能通过创造等积的方法来求.直接找三角形HDC 与三角形AFH 的关系还很难,而且也没有利用"四边形ABCD和四边形DEFG 是正方形"这一条件.我们不妨将它们都补上梯形DEFH 这一块.寻找新得到大三角形CEF 和大直角梯形DEFA 之间的关系.经过验算,可以知道它们的面积是相等的.从而得到三角形 HDC与三角形AFH面积相等,也是6平方厘米.【第三篇】如下图,BE=2AB,BC=CD。
三角形等积变形

例5 如右图,已知在△ABC中,BE=3AE,CD=2AD.若△ADE 的面积为1平方厘米.求三角形ABC的面积.
解法1:连结BD,在△ABD 中 ∵ BE=3AE, ∴ S△ABD=4S△ADE=4 (平方厘米). 在△ABC中,∵CD=2AD, ∴ S△ABC=3S△ABD=3×4=12 (平方厘米).
上述结论,是我们研究三角形等积变形的 重要依据.
方法2:如右图,先将BC二等分,分点D、连结AD, 得到两个等积三角形,即△ABD与△ADC等 积.然后取AC、AB中点E、F,并连结DE、DF.以 而得到四个等积三角形,即△ADF、△BDF、 △DCE、△ADE等积.
例2 用三种不同的方法将任意一个三角形分成 三个小三角形,使它们的面积比为及 1∶3∶4.
三角形等积变形
我们已经掌握了三角形面积的计算公式: 三角形面积=底×高÷2
这个公式告诉我们:三角形面积的大小,取决 于三角形底和高的乘积.
①等底等高的两个三角形面积相等.
例如在右图中,若△ABD与 △AEC的底边相等 (BD=DE=EC=BC) ,它们所对的顶点同为A点, (也就是它们的高相等) 那么这两个三角形的面积 相等. 同时也可以知道△ABC 的面积是△ABD或 △AEC面积的3倍.
证明:∵△ABC与△DBC等 底等高, ∴S△ABC=S△DBC 又∵ S△AOB=S△ABC—S△BOC S△DOC=S△DBC— S△BOC ∴S△AOB=S△COD.
例4 如右图,把四边形ABCD改成一个等积的三角形
分析 本题有两点要求,一是把四边形改成一个三角形,二 是改成的三角形与原四边形面积相等.我们可以利用三角 形等积变形的方法,如右图, 把顶点A移到CB的延长线上的A′处, △A′BD与△ABD面积相等,从而 △A′DC面积与原四边形ABCD面积也 相等.这样就把四边形ABCD等积地 改成了三角形△A′DC.问题是A′位 置的选择是依据三角形等积变形原 则.过A作一条和DB平行的直线与 CB的延长线交于A′点. 解:①连结BD; ②过A作BD的平行线,与CB的 延长线交于A′. ③连结A′D,则△A′CD与四边形 ABCD等积.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、三角形的等积变形
①等底等高的两个三角形面积相等。
②底在同一条直线上并且相等,该底所对的角的顶点是同一个点或在与底平行的直线上,这两个
三角形面积相等。
③若两个三角形的高(或底)相等,其中一个三角形的底(或高)是另一个三角形的几倍,那么这个三
角形的面积也是另一个三角形面积的几倍。
【例1】
如右图,已知在△ABC中,BE=3AE,CD=2AD。
若△ADE的面积为1平方厘米。
求三角形ABC的面积。
二、鸟头模型
在△ABC中,D、E分别是AB、AC上的点如图⑴(或D在BA的延长线上,E在AC上),
则S△ABC∶S△ADE=(AB×AC)∶(AD×AE)
【例2】
如图,三角形ABC的面积是308,D,E,F分别为三角形三边上的点。
其中AD∶CD=5∶3,BF∶CF=4∶7,AE∶BE=1∶6。
问:阴影部分的小三角形的面积是多少
必备几何模型
【例3】
如图,三角形两边上的点都是各边上的五等分点。
问:阴影部分与空白部分的面积比为多少
三、相似三角形性质(沙漏模型):
①AD AE DE AF AB AC BC AG ===
②S△ADE∶S△ABC=AF2∶AG2
所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:
⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比;
⑵相似三角形的面积比等于它们相似比的平方;
【例4】
如图,在平行四边形ABCD中,直线CF交AB于E,交DA延长线于F,若S△ADE=1,求△BEF的面积。
四、蝴蝶模型
任意四边形中的比例关系(“蝴蝶定理”)
①S1×S3=S2×S4
②AO∶OC=(S1+S2)∶(S4+S3)
①S1∶S3=a2∶b2
②S1∶S2∶S3∶S4=a2∶ab∶b2∶ab
③梯形面积S的对于份数是(a+b)2
【例5】
如图面积为12平方厘米的正方形ABCD中,E、F是BC边上的三等分点,求阴影部分的面积。
【例6】
在直角梯形ABCD中,AB=15厘米,AD=12厘米,阴影部分的面积为15平方厘米。
梯形ABCD的面
积是多少平方厘米
测试题
1.如右图,在平行四边形ABCD 中,直线CF 交AB 于E ,交DA 延长线于F ,若S △ADE =1,求△BEF 的面积。
A . B .1
C .
D .2
2.(北京市第八届“迎春杯”数学竞赛决赛第一题第4题)如右图BE =
31BC ,CD =4
1
AC ,那么三角形AED 的面积是三角形ABC 面积的______。
D
E
C
B
A
A .1
2
B .
45
C .
23
D .
13
3.如图,已知长方形ADEF 的面积是16,三角形ADB 的面积是3,三角形ACF 的面积是4,那么三角
形ABC 的面积是____。
A
B
C
D E
F A.3 B.C.D.8
4.如图,四边形ABCD中,AC和BD相交于O点,三角形ADO的面积=5
,三角形DOC的面积=4,三角形AOB的面积=15,求三角形BOC的面积是多少
A.10 B.12 C.14 D.15
5.梯形ABCD的上底长为3厘米,下底长为9厘米,而三角形ABO的面积为12平方厘米。
则整个梯形的面积为多少
A.56 B.60 C.64 D.72
6.如下图,一个长方形被一些直线分成了若干个小块,已知三角形ADG的面积是11,三角形BCH的面积是23,求四边形EGFH的面积。
A.12 B.32 C.34 D.40。
