证明综合题训练
第十二章证明综合练习题.doc

第十二章综合练习班级姓名学号得分日期1.下列句子中,是命题的是( )A.今天的天气好吗B.作线段AB∥CD;C.连结A、B两点D.正数大于负数2.下列命题是真命题的是( )A.如果两个角不相等,那么这两个角不是对顶角;B.两互补的角一定是邻补角C.如果a2=b2,那么a=b;D.如果两角是同位角,那么这两角一定相等3.下列语句错误的是()A.同角的补角相等;B.同位角相等.C.垂直于同一条直线的两直线平行;D.两条直线相交有且只有一个交点.4.如图1,下列推理正确的是( )A.∵MA∥NB,∴∠1=∠3B.∵∠2=∠4,∴MC∥NDC.∵∠1=∠3,∴MA∥NBD.∵MC∥ND,∴∠1=∠35.如图1,AB∥CD,∠A=25°,∠C=45°,则∠E的度数是( )图1A.60°B.70°C.80°D.65°6.已知,如图AB‖DE,∠E=65°,则∠B+∠C=.7.如图,AB‖CD,AD,BC相交于点O,若∠BAD=35°,∠BOD=75°,则∠C=度.8.请把下列证明过程补充完整:图1已知:如图,DE ∥BC ,BE 平分∠ABC . 求证:∠1=∠3.证明:因为BE 平分∠ABC (已知),所以∠1=______( ). 又因为DE ∥BC (已知),所以∠2=_____( ).所以∠1=∠3( ). 9.已知:如图2,AD ∥BC ,∠B=∠D. 求证:AB ∥CD.10.已知:如图,AD ∥BC ,∠BAD =∠DCB . 求证:∠1=∠3.11.已知:A 、O 、B 在一直线上,OM 平分∠AOC ,ON 平分∠BOC. 求证:OM ⊥ON.12.今年五一节期间,王老板在其经营的服装店里卖出两件衣服,其中一件是裤子售价为168元,盈利20%,一件是夹克衫售价也是168元,但亏损20%,问王老板在这次的交易过程中是赚了还是亏了,赚了赚了多少?亏了亏了多少?还是不赚不亏?图 24321CAB第10题AOBCMN1 2。
专题2.10圆中的计算与证明的综合大题专项训练(50道)(举一反三)(苏科版)(原卷版)

专题2.10 圆中的计算与证明的综合大题专项训练(50道)【苏科版】考卷信息:本套训练卷共50题,题型针对性较高,覆盖面广,选题有深度,涵盖了圆中的计算与证明的综合问题的所有类型!一.解答题(共50小题)1.(2022秋•柯桥区月考)如图,D是⊙O弦BC的中点,A是⊙O上的一点,OA与BC交于点E,已知AO=8,BC=12.(1)求线段OD的长;(2)当EO=√2BE时,求DE的长.̂的中点,CE⊥AB于点E,BD交CE于点F.2.(2022•市中区校级一模)如图,AB是⊙O的直径,C是BD(1)求证:CF=BF;(2)若CD=6,AC=8,求⊙O的半径及CE的长.3.(2022秋•岱岳区期末)已知⊙O的直径为10,点A、点B、点C在⊙O上,∠CAB的平分线交⊙O于点D.(1)如图①,若BC为⊙O的直径,AB=6,求AC、BD、CD的长;(2)如图②,若∠CAB=60°,求BD的长.4.(2022•济宁)如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.(1)求证:BD=CD;(2)请判断B,E,C三点是否在以D为圆心,以DB为半径的圆上?并说明理由.5.(2022秋•辛集市期末)如图1,在△ABC中,AB=AC,⊙O是△ABC的外接圆,过点C作CD∥AB交⊙O于点D,连接AD,延长CD至点F,使BF=BC.(1)求证:BF∥AD;(2)如图2,当CD为直径,半径为1时,求弧BD,线段BF,线段DF所围成图形的面积.6.(2022•凤翔县一模)如图,⊙O的直径为AB,点C在⊙O上,点D,E分别在AB,AC的延长线上,DE⊥AE,垂足为E,CD与⊙O相切于点C.(1)求证:∠A=∠CDE;(2)若AB=4,BD=3,求CD的长.7.(2022秋•湛江校级月考)已知P A、PB分别切⊙O于A、B,E为劣弧AB上一点,过E点的切线交P A 于C、交PB于D.(1)若P A=6,求△PCD的周长.(2)若∠P=50°求∠DOC.8.(2022秋•仪征市校级月考)如图,⊙O是正方形ABCD与正六边形AEFCGH的外接圆.(1)正方形ABCD与正六边形AEFCGH的边长之比为;(2)连接BE,BE是否为⊙O的内接正n边形的一边?如果是,求出n的值;如果不是,请说明理由.9.(2022•高唐县二模)如图,在菱形ABCD中,对角线AC,BD交于点O,∠BAO=30°,AC=8.过点O作OH⊥AB于点H,以点O为圆心,OH为半径的半圆交AC于点M.(1)求图中阴影部分的面积;(2)点P是BD上的一个动点(点P不与点B,D重合),当PH+PM的值最小时,求PD的长度.10.(2022•黔东南州模拟)如图,已知AB是⊙O的直径,点C、D在⊙O上,∠D=60°且AB=6,过O 点作OE⊥AC,垂足为E.(1)求OE的长;(2)若OE的延长线交⊙O于点F,求弦AF、AC和弧CF围成的图形(阴影部分)的面积S.11.(2022秋•如东县期末)如图,CD是⊙O的直径,弦AB⊥CD于点E,∠DAB=30°,AB=4√3.(1)求CD的长;(2)求阴影部分的面积.12.(2022秋•松滋市期末)如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连接EO、FO,若DE=4√3,∠DP A=45°(1)求⊙O的半径.(2)若图中扇形OEF围成一个圆锥侧面,试求这个圆锥的底面圆的半径.13.(2022•沈阳)如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD(1)求证:BD平分∠ABC;(2)当∠ODB=30°时,求证:BC=OD.14.(2022•本溪)如图,△ABC中,AB=AC,点E是线段BC延长线上一点,ED⊥AB,垂足为D,ED 交线段AC于点F,点O在线段EF上,⊙O经过C、E两点,交ED于点G.(1)求证:AC是⊙O的切线;(2)若∠E=30°,AD=1,BD=5,求⊙O的半径.15.(2022•崇左)如图,正方形ABCD的边长为1,其中弧DE、弧EF、弧FG的圆心依次为点A、B、C.(1)求点D沿三条弧运动到点G所经过的路线长;(2)判断直线GB与DF的位置关系,并说明理由.̂=CD̂,16.(2022•凉山州二模)如图,AB是半圆的直径,C、D是半圆上的两点,且∠BAC=20°,AD 求:∠BCD的度数.17.(2022•白云区一模)如图,⊙O的半径OA⊥OC,点D在AĈ上,且AD̂=2CD̂,OA=4.(1)∠COD=°;(2)求弦AD的长;(3)P是半径OC上一动点,连接AP、PD,请求出AP+PD的最小值,并说明理由.(解答上面各题时,请按题意,自行补足图形)̂的中点,CE⊥AB于E,BD交CE于F.18.(2022•西湖区校级一模)如图,AB是⊙O的直径,C是BD(1)求证:CF=BF;(2)若CD=6,AC=8,求BE、CF的长.19.(2022•武昌区校级自主招生)如图,已知⊙O的直径为10,点A、B、C在⊙O上,∠CAB的平分线交⊙O于点D.(1)图①,当BC为⊙O的直径时,求BD的长.(2)图②,当BD=5时,求∠CDB的度数.20.(2022•东莞市校级模拟)如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F.(1)当∠E=∠F时,则∠ADC=°;(2)当∠A=55°,∠E=30°时,求∠F的度数;(3)若∠E=α,∠F=β,且α≠β.请你用含有α、β的代数式表示∠A的大小.21.(2022•鹿城区校级模拟)如图,△ABC中,AB>AC,AE是其外接圆的切线,D为AB上的点,且AD =AC=AE.求证:直线DE过△ABC的内心.22.(2022•鼓楼区校级模拟)如图,图1、图2、图3、…、图n分别是⊙O的内接正三角形ABC,正四边形ABCD、正五边形ABCDE、…、正n边形ABCD…,点M、N分别从点B、C开始以相同的速度在⊙O 上逆时针运动.(1)求图1中∠APN的度数是;图2中,∠APN的度数是,图3中∠APN的度数是.(2)试探索∠APN的度数与正多边形边数n的关系(直接写答案).23.(2022•温州一模)如图,在⊙O上依次有A、B、C三点,BO的延长线交⊙O于E,AÊ=CÊ,过点C 作CD∥AB交BE的延长线于D,AD交⊙O于点F.(1)求证:四边形ABCD是菱形;̂的长.(2)连接OA、OF,若∠AOF=3∠FOE,且AF=3,求劣弧CF24.(2022•岳麓区校级一模)如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连AD.(1)求证:AD=AN;(2)若AB=4√2,ON=1,求⊙O的半径.25.(2022•普陀区模拟)如图,在⊙O中,AD、BC相交于点E,OE平分∠AEC.(1)求证:AB=CD;(2)如果⊙O的半径为5,AD⊥CB,DE=1,求AD的长.26.(2022•乌鲁木齐一模)如图,四边形ABCD内接于⊙O,AB是⊙O的直径,点P在CA的延长线上,∠CAD=45°.(1)若AB=4,求弧CD的长;(2)若弧BC=弧AD,AD=AP,求证:PD是⊙O的切线.27.(2022•饶平县校级模拟)如图,⊙O中,弦CD与直径AB交于点H.(1)当∠B+∠D=90°时,求证:H是CD的中点;(2)若H为CD的中点,且CD=2√2,BD=√3,求AB的长.28.(2022•苏州模拟)如图,点A和动点P在直线l上,点P关于点A的对称点为Q,以AQ为边作Rt △ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O.点C在点P右侧,PC=4,过点CCD,作直线m⊥l,过点O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=32以DE,DF为邻边作矩形DEGF.设AQ=3x.(1)用关于x的代数式表示BQ=,DF=.(2)当点P在点A右侧时,若矩形DEGF的面积等于90,求AP的长.(3)当点P在点A右侧时,作直线BG交⊙O于点N,若BN的弦心距为1,求AP的长.29.(2022•福建模拟)如图1,△ABC中,AB=AC,⊙O是△ABC的外接圆,过点B作BE⊥AC,交⊙O 于点D,垂足为E,连接AD.(1)求证:∠BAC=2∠CAD;̂的中点,连接FG,若FG=2,CD (2)如图2,连接CD,点F在线段BD上,且DF=2DC,G是BC=2√2,求⊙O的半径.30.(2022•苏州模拟)如图,已知点D是△ABC外接圆⊙O上的一点,AC⊥BD于G,连接AD,过点B 作直线BF∥AD交AC于E,交⊙O于F,若点F是弧CD的中点,连接OG,OD,CD(1)求证:∠DBF=∠ACB;GE,试探究∠GOD与∠ADC之间的数量关系,并证明.(2)若AG=√62̂上一点,延长DA至点E,31.(2022•莱芜)如图,△ABC是⊙O的内接三角形,AC=BC,D为⊙O中AB使CE=CD.(1)求证:AE=BD;(2)若AC⊥BC,求证:AD+BD=√2CD.32.(2022•三明)如图①,②,在平面直角坐标系xOy中,点A的坐标为(4,0),以点A为圆心,4为半径的圆与x轴交于O,B两点,OC为弦,∠AOC=60°,P是x轴上的一动点,连接CP.(1)求∠OAC的度数;(2)如图①,当CP与⊙A相切时,求PO的长;(3)如图②,当点P在直径OB上时,CP的延长线与⊙A相交于点Q,问PO为何值时,△OCQ是等腰三角形?33.(2022•昆明)(1)如图(1),OA、OB是⊙O的两条半径,且OA⊥OB,点C是OB延长线上任意一点,过点C作CD切⊙O于点D,连接AD交OC于点E.求证:CD=CE;(2)若将图(2)中的半径OB所在直线向上平行移动交OA于F,交⊙O于B′,其他条件不变,那么上述结论CD=CE还成立吗?为什么?(3)若将图(3)中的半径OB所在直线向上平行移动到⊙O外的CF,点E是DA的延长线与CF的交点,其他条件不变,那么上述结论CD=CE还成立吗?为什么?34.(2022•襄城区模拟)如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连接AD.(1)求证:AD=AN;(2)若AB=8,ON=1,求⊙O的半径.35.(2022•台州校级模拟)某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.(1)请你补全这个输水管道的圆形截面.(2)若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.(3)在(2)的条件下,小明把一只宽12cm的方形小木船放在修好后的圆柱形水管里,已知船高出水面13cm,问此小船能顺利通过这个管道吗?36.(2022•泰州模拟)如图,BC是⊙O的直径,弦AD⊥BC,垂足为H,已知AD=8,OH=3.(1)求⊙O的半径;(2)若E是弦AD上的一点,且∠EBA=∠EAB,求线段BE的长.37.(2022•河北)图1是某学校存放学生自行车的车棚的示意图(尺寸如图所示),车棚顶部是圆柱侧面̂所在圆的圆心为O.车棚顶部是用一种的一部分,其展开图是矩形.图2是车棚顶部截面的示意图,AB帆布覆盖的,求覆盖棚顶的帆布的面积.(不考虑接缝等因素,计算结果保留π)38.(2022•咸宁模拟)小明学习了垂径定理,做了下面的探究,请根据题目要求帮小明完成探究.(1)更换定理的题设和结论可以得到许多真命题.如图1,在⊙O中,C是劣弧AB的中点,直线CD⊥AB于点E,则AE=BE.请证明此结论;(2)从圆上任意一点出发的两条弦所组成的折线,成为该圆的一条折弦.如图2,P A,PB组成⊙O的一条折弦.C是劣弧AB的中点,直线CD⊥P A于点E,则AE=PE+PB.可以通过延长DB、AP相交于点F,再连接AD证明结论成立.请写出证明过程;(3)如图3,P A.PB组成⊙O的一条折弦,若C是优弧AB的中点,直线CD⊥P A于点E,则AE,PE与PB之间存在怎样的数量关系?写出结论,不必证明.39.(2022•南开区一模)已知:如图1,在⊙O中,直径AB=4,CD=2,直线AD,BC相交于点E.(1)∠E的度数为;(2)如图2,AB与CD交于点F,请补全图形并求∠E的度数;(3)如图3,弦AB与弦CD不相交,求∠AEC的度数.40.(2022•安徽一模)如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.(1)判断△ABC的形状,并证明你的结论.(2)证明:P A+PB=PC.41.(2022•和平区一模)Rt△ABC中,∠ABC=90°,以AB为直径作⊙O交AC边于点D,E是边BC的中点,连接DE,OD.(Ⅰ)如图①,求∠ODE的大小;(Ⅱ)如图②,连接OC交DE于点F,若OF=CF,求∠A的大小.42.(2022•和平区二模)已知AB是⊙O的直径,AB=2,点C,点D在⊙O上,CD=1,直线AD,BC交于点E.(Ⅰ)如图1,若点E在⊙O外,求∠AEB的度数.(Ⅱ)如图2,若点E在⊙O内,求∠AEB的度数.43.(2022•南开区二模)如图,⊙O的直径AB的长为2,点C在圆周上,∠CAB=30°,点D是圆上一动点,DE∥AB交CA的延长线于点E,连接CD,交AB于点F.(Ⅰ)如图1,当∠ACD=45°时,请你判断DE与⊙O的位置关系并加以证明;(Ⅱ)如图2,当点F是CD的中点时,求△CDE的面积.44.(2022•红桥区二模)已知⊙O是△ABC的外接圆,过点A作⊙O的切线,与CO的延长线于点P,CP 与⊙O交于点D.(1)如图①,若AP=AC,求∠B的大小;(2)如图②,若AP∥BC,∠P=42°,求∠BAC的大小.45.(2022秋•镇海区期末)如图,在△ABC中,D在边AC上,圆O为锐角△BCD的外接圆,连结CO 并延长交AB于点E.(1)若∠DBC=α,请用含α的代数式表示∠DCE;(2)如图2,作BF⊥AC,垂足为F,BF与CE交于点G,已知∠ABD=∠CBF.①求证:EB=EG;②若CE=5,AC=8,求FG+FB的值.̂上任一点(点P与点A、B重合),46.(2022秋•虹口区校级期末)如图,等边△ABC内接于⊙O,P是AB连接AP、BP,过点C作CM∥BP交P A的延长线于点M.(1)求∠APC和∠BPC的度数;(2)求证:△ACM≌△BCP;(3)若P A=1,PB=2,求四边形PBCM的面积;̂的长度.(4)在(3)的条件下,求AB47.(2022秋•赣榆区期中)铁匠王老五要制作一个圆锥体模型,操作规则是:在一块边长为16cm的正方形纸片上剪出一个扇形和一个圆,使得扇形围成圆锥的侧面时,圆恰好是该圆锥的底面.他们首先设计了如图所示的方案一,发现这种方案不可行,于是他们调整了扇形和圆的半径,设计了如图所示的方案二.(两个方案的图中,圆与正方形相邻两边及扇形的弧均相切.方案一中扇形的弧与正方形的两边相切)请你帮助他算一算.(1)请说明方案一不可行的理由;(2)判断方案二是否可行?若可行,请确定圆锥的母线长l及其底面圆半径r;若不可行,请说明理由.48.(2022•浙江校级自主招生)如图,已知圆O的圆心为O,半径为3,点M为圆O内的一个定点,OM=√5,AB、CD是圆O的两条相互垂直的弦,垂足为M.(1)当AB=4时,求四边形ADBC的面积;(2)当AB变化时,求四边形ADBC的面积的最大值.49.(2022•浙江校级自主招生)如图,O为等边△ABC的外接圆,半径为2,点D在劣弧AB上运动(不与点A,B重合),连接DA,DB,DC.若点M,N分别在线段CA,CB上运动(不含端点),经过探究发现,点D运动到每一个确定的位置,△DMN的周长有最小值t,随着点D的运动,t的值会发生变化,求所有t值中的最大值.50.(2022•枣庄校级模拟)如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB.(1)求证:直线BF是⊙O的切线;(2)若点D,点E分别是弧AB的三等分点,当AD=5时,求BF的长和扇形DOE的面积;(3)填空:在(2)的条件下,如果以点C为圆心,r为半径的圆上总存在不同的两点到点O的距离为5,则r的取值范围为.。
苏科版2019七年级数学下册第12章证明综合练习题C(附答案)

苏科版2019七年级数学下册第12章证明综合练习题C(附答案)1.要证明命题“若a>b ,则a2>b2”是假命题,下列a ,b 的值能作为反例的是()A.a = 2 ,b = 1 B.a =-2 ,b =-1 C.a =-1 ,b =-2 D.a = 2 ,b =-1 2.下列命题中:有公共顶点和一条公共边的两个角一定是邻补角;垂线段最短;经过直线外一点,有且只有一条直线与这条直线平行;相等的角是对顶角;等角的余角相等,其中假命题的个数是A.0个B.1个C.2个D.3个3.下列四个命题是假命题的是( )A.平行线间距离处处相等B.两组对角分别相等的四边形是平行四边形C.一组对边平行且相等的四边形是平行四边形D.三角形的一个外角等于两个内角的和4.已知下列说法中:①相等的角是对顶角;②互补的角就是平角;③互补的两个角一定是一个锐角,另一个为钝角;④平行于同一条直线的两直线平行;⑤邻补角的平分线互相垂直.其中,正确的个数为()A.0 B.1个C.2个D.3个5.下列命题中:①三点确定一个圆;②三角形的外心到三角形三顶点的距离相等;③三角形的内心到三角形的三边的距离相等;④经过半径外端的直线是圆的切线,其中真命题的个数是( )A.1个B.2个C.3个D.4个6.下列命题的逆命题为真命题的是()A.对顶角相等B.两直线平行,同位角相等C.如果两个实数是正数,它们的积是正数D.等边三角形是锐角三角形7.把命题“同角的余角相等”用“如果…那么…”的形式写出来,下列写法正确的是()A.如果几个角是同一个角的余角,那么这几个角都相等B.如果一个角是这个角的余角,那么这两个角相等C.如果两个角是同角,那么同角的余角都相等D.如果两个角的和为90゜,那么这两个角可能相等8.已知下列命题,①若a>b,则ac>bc;②两直线平行,内错角相等;③直角三角形的两个锐角互余;④全等三角形的周长相等.其中原命题与逆命题均为真命题的有()A.1 B.2个C.3个D.4个9.下列语句中真命题有( )①点到直线的垂线段叫做点到直线的距离;②内错角相等;③两点之间线段最短;④过一点有且只有一条直线与已知直线平行;⑤在同一平面内,若两条直线都与第三条直线垂直,则这两条直线互相平行.A.5个B.4个C.3个D.2个10.把命题“如果a>b,那么ac>bc(c≠0)”的逆命题改写为“如果……,那么……”的形式:_________11.写出“两组对边分别相等的四边形是平行四边形”的逆命题_____.12.命题“经过直线上或直线外一点,有且只有一条直线与已知直线垂直”的条件是________________________,它是________命题(填“真”或“假”).13.命题“若a>b,则|a|>|b|”是______命题.(填“真”或“假”)14.完成下面的证明过程.已知:如图,∠1和∠D互余,∠C和∠D互余.求证:AB∥CD.证明:∵∠1和∠D互余(已知),∴∠1+∠D=90°(_____________).∵∠C和∠D互余(已知),∴∠C+∠D=90°(_____________),∴∠1=∠C(__________________),∴AB∥CD(________________________).15.命题“等角的余角相等”的条件是__________,结论是_________.16.命题“直角三角形的两个锐角互余”的逆命题是________.17.命題“等腰三角形两腰上的高线相等”的逆命题是______命題填“真”或“假”18.“如果a>0,b<0,那么ab<0”的逆命题是_______________________________________ 19.写出下列命题的逆命题,并判断真假性.(1)直角三角形的两锐角互余;(2)若a=b,则=;(3)如果a+b>0,那么a>0,b>0;(4)两个图形关于某条直线对称,则这两个图形一定全等.20.指出下列命题的条件和结论.(1)同位角相等,两直线平行;(2)同角的余角相等;(3)平行于同一条直线的两直线平行;(4)同旁内角不互补,两直线不平行.21.如图,点D,E 在△ABC的边BC上,连接AD,AE.下面有三个等式:①AB =AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,相构成以下三个命题:命题Ⅰ“如果①②成立,那么③成立”;命题Ⅱ“如果①③成立,那么②成立”;命题Ⅲ“如果②③成立,那么①成立”.(1)以上三个命题是真命题的为__________(直接作答);(2)请选择一个真命题进行证明(先写出所选命题,然后证明).22.先把下列两个命题分别改写成“如果……那么……”的形式,再判断该命题是真命题还是假命题,如果是假命题,举出一个反例.(1)同旁内角互补,两直线平行;(2)一个角的补角一定是钝角.23.指出下列命题的条件和结论.(1)两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行;(2)如果∠1=∠2,∠2=∠3,那么∠1=∠3;(3)锐角小于它的余角;(4)如果a+c=b+c,那么a=b.24.写出下列命题的逆命题,并判断真假.(1)若x=3,则x2=9;(2)三角形任何两边之和大于第三边;(3)面积相等的三角形全等.25.如图,AB∥CD,∠ABE=∠DCF.求证:∠E=∠F.答案1.C解:A、a=3,b=2,满足a>b,a2>b2,所以A选项不能作为证明原命题是假命题的反例;B、a=-2,b=-1,不满足a>b,所以B选项不能作为证明原命题是假命题的反例;C、a=-1,b=-2,满足a>b,但不满足a2>b2,所以C选项能作为证明原命题是假命题的反例;D、a=2,b=-1,满足a>b,但不满足a2>b2,所以D选项不能作为证明原命题是假命题的反例.故选C.2.C解:①有公共顶点和一条公共边的两个角一定是邻补角,是假命题,另一条边不一定互为反向延长线;②垂线段最短,是真命题;③经过直线外一点,有且只有一条直线与这条直线平行,是真命题;④相等的角是对顶角,是假命题,角平分线分成的两个角相等,但这两个角不是对顶角;⑤等角的余角相等,真命题;综上所述,假命题有2个.故选C.3.D解:平行线间距离处处相等,A是真命题;两组对角分别相等的四边形是平行四边形,B是真命题;一组对边平行且相等的四边形是平行四边形,C是真命题;三角形的一个外角等于与它不相邻的两个内角的和,D是假命题;故选:D.4.C解:①对顶角既要考虑大小,还要考虑位置,相等的角不一定是对顶角,故①错误;②互补的角不一定是邻补角,所以不一定是平角,故②错误;③互补的两个角也可以是两个直角,故③错误;④平行于同一条直线的两条直线平行,是平行公理,故④正确;⑤邻补角的平分线的夹角正好是平角的一半,是直角,所以互相垂直,故⑤正确.所以真命题有④⑤两个.故选C.5.B解:①三个不在一条直线上的点确定一个圆,故此选项错误;②三角形的外心到三角形三个顶点的距离相等,故此选项正确;③三角形的内心到三角形的三边的距离相等,故此项正确;④经过半径外端的直线且垂直半径的直线是圆的切线,故此项错误,综上所述,答案选B. 6.B解:A. 对顶角相等的逆命题是如果两个角相等,则它们是对顶角,是假命题;B. 两直线平行,同位角相等的逆命题是同位角相等,两直线平行,是真命题;C. 如果两个实数是正数,它们的积是正数的逆命题是如果两个实数相乘为正,那么这两个数是正数,是假命题;D. 等边三角形是锐角三角形的逆命题是锐角三角形都是等边三角形,是假命题.故选B.7.A解:命题“同角的余角相等”用“如果…那么…”的形式写出为:如果几个角是同一个角的余角,那么这几个角都相等.故选:A.8.B解:①若a>b,则ac>bc,只有当c>0时才成立,所以原命题是假命题;②:根据平行的性质得出“两直线平行,内错角相等”正确,再得出逆命题是“内错角相等,两直线平行”正确,所以其原命题与逆命题均为真命题;③:根据直角三角形的性质得出“直角三角形的两锐角互余”正确,再得出逆命题是“若一个三角形的两个锐角互余,则这个三角形是直角三角形”正确,所以其原命题与逆命题均为真命题;④:根据全等三角形的性质得出“全等三角形的周长相等”正确,是真命题,再得出逆命题“周长相等的三角形是全等三角形”错误,是假命题.故选B.9.D解:①点到直线的垂线段的长度叫做点到直线的距离,故错误,是假命题;②两直线平行,内错角相等,故错误,是假命题;③两点之间线段最短,正确,是真命题;④过直线外一点有且只有一条直线与已知直线平行,错误,是假命题;⑤在同一平面内,若两条直线都与第三条直线垂直,那么这两条直线互相平行,正确,是真命题. 真命题有2个,故选D.10.如果ac>bc(c≠0),那么a>b解:命题“如果a>b,那么ac>bc(c≠0)”的逆命题是“如果ac>bc(c≠0),那么a>b”.故答案为:如果ac>bc(c≠0),那么a>b.11.平行四边形是两组对边分别相等的四边形解:“两组对边分别相等的四边形是平行四边形”的逆命题是:“平行四边形是两组对边分别相等的四边形”.故答案为:“平行四边形是两组对边分别相等的四边形”.12.经过直线上或直线外一点作已知直线的垂线, 真解:命题“经过直线上或直线外一点,有且只有1条直线与已知直线垂直”的条件是经过直线上或直线外一点的的直线,它是真命题.故答案为:经过直线上或直线外一点的的直线;真.13.假解:∵3 >-5,但|3|<|-5|,∴命题“若a>b,则|a|>|b|”是假命题.故答案为:假.14.互余的定义;互余的定义;同角的余角相等;内错角相等,两直线平行.证明:∵∠1和∠D互余(已知),∴∠1+∠D=90°(互余的定义).∵∠C和∠D互余(已知),∴∠C+∠D=90°(_互余的定义),∴∠1=∠C(同角的余角相等),∴AB∥CD(内错角相等,两直线平行).15.两个角相等它们的余角也相等.解:“等角的余角相等”可改写成“如果两个角相等,那么它们的余角也相等”,所以:“等角的余角相等”的条件是:两个角相等;结论是:它们的余角也相等,故答案为:两个角相等;它们的余角也相等.16.如果三角形有两个锐角互余,那么这个三角形为直角三角形.解:逆命题为:如果三角形有两个锐角互余,那么这个三角形为直角三角形.故答案为:如果三角形有两个锐角互余,那么这个三角形为直角三角形.17.真解:等腰三角形两腰上的高线相等的逆命题是如果一个三角形两条边上的高线相等,那么这个三角形是等腰三角形,是真命题.故答案为:真.18.如果ab<0,那么a>0,b<0.解:“如果a>0,b<0,那么ab<0”的逆命题为“如果ab<0,那么a>0,b<0”.故答案为:如果ab<0,那么a>0,b<0.19.解:(1)直角三角形的两锐角互余的逆命题是两锐角互余的三角形是直角三角形,真命题;2)若a=b,则=的逆命题是若=,则a=b,真命题;(3)如果a+b>0,那么a>0,b>0的逆命题是若a>0,b>0,则a+b>0,真命题;(4)两个图形关于某条直线对称,则这两个图形一定全等的逆命题是若两个图形全等,则这两个图形关于某条直线对称,假命题.20.解:(1)该命题可以写成:如果同位角相等,那么两直线平行,所以命题的条件是同位角相等,结论是两直线平行;(2)该命题可以写成:如果两个角是同一个角的余角,那么这两个角相等,所以命题的条件是同角的余角,结论是相等;(3)该命题可以写成:如果两条件直线平行于同一条件直线,那么这两条直线平行,所以命题的条件是平行于同一条直线的两条直线,结论是平行;(4)该命题可以写成:如果同旁内角不互补,那么两直线不平行,所以命题的条件是同旁内角不互补,结论是两直线不平行.21.(1)Ⅰ,Ⅱ,Ⅲ;(2)证明解:(1)Ⅰ,Ⅱ,Ⅲ,故答案为:Ⅰ,Ⅱ,Ⅲ.(2)选择命题Ⅱ“如果①③成立,那么②成立”;证明:∵AB=AC,∴∠B=∠C,在△ABD 和△ACE 中,,∴△ABD≌△ACE(SAS),∴AD=AE.22.(1)见解析;(2)见解析.解:(1)如果两条直线被第三条直线所截得的同旁内角互补,那么这两条直线平行.是真命题.(2)如果一个角是另一个角的补角,那么这个角一定是钝角.是假命题.举反例不唯一,如:设∠1=60°,∠2=120°,∠1是∠2的补角,但∠1不是钝角.23.解:(1)条件:两条直线被第三条直线所截,同旁内角互补;结论:这两条直线平行(2)条件:∠1=∠2,∠2=∠3;结论:∠1=∠3(3)条件:一个角是锐角;结论:这个角小于它的余角(4)条件:a+c=b+c;结论:a=b24.解:(1)若x2=9,则x=3,是假命题;(2)如果两线段之和大于第三条线段,那么此三条线段可以组成三角形,是假命题;(3)如果三角形全等,那么它们的面积相等,是真命题.25.证明:∵AB∥CD,∴∠ABC=∠BCD.又∵∠ABE=∠DCF,∴∠ABC-∠ABE=∠BCD-∠DCF,即∠EBC=∠FCB,∴BE∥CF,∴∠E=∠F。
全等三角形的证明题综合
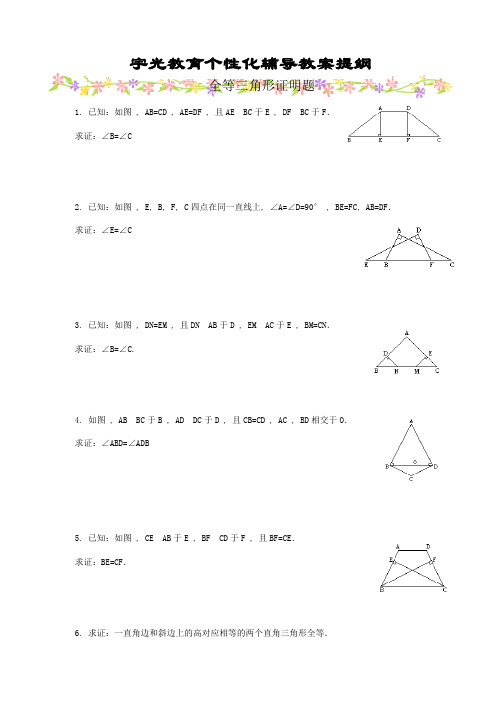
宇光教育个性化辅导教案提纲全等三角形证明题1. 已知:如图 , AB=CD , AE=DF , 且AE BC于E , DF BC于F.求证:∠B=∠C2. 已知:如图 , E, B, F, C四点在同一直线上, ∠A=∠D=90° , BE=FC, AB=DF.求证:∠E=∠C3. 已知:如图 , DN=EM , 且DN AB于D , EM AC于E , BM=CN.求证:∠B=∠C.4. 如图 , AB BC于B , AD DC于D , 且CB=CD , AC , BD相交于O.求证:∠ABD=∠ADB5. 已知:如图 , CE AB于E , BF CD于F , 且BF=CE.求证:BE=CF.6. 求证:一直角边和斜边上的高对应相等的两个直角三角形全等.7. 已知:如图 , AE , FC都垂直于BD , 垂足为E、F , AD=BC , BE=DF.求证:OA=OC.8. 已知:如图 , AB=CD , D、B到AC的距离DE=BF.求证:AB∥CD.9. 已知:如图 , OC=OD , AD OB于D , BC OA于C.求证:EA=EB.10. 如图 , 已知:∠ACB和∠ADB都是直角 , BC=BD , E是AB上任一点 , 求证:CE=DE.11. 已知:如图,∠A=∠D=90°,AC,BD交于O,AC=BD.求证:OB=OC.12. 已知:如图 , 四边形ABCD中, AB∥CD , AD∥BC.求证:△ABD≌△CDB13. 如图,已知:AD∥BC,AD=BC.求证:AB∥CD.14. 如图,已知:AC=DF,AC∥FD,AE=DB,求证:△ABC≌△DEF15. 已知:如图,点B,E,C,F在同一直线上,AB∥DE,且AB=DE,BE=CF. 求证:AC∥DF.16. 已知:如图,AD是BC上的中线 ,且DF=DE.求证:BE∥CF.17. 如图, △ABC中 , AD是从顶点A引出的一射线交BC于D , BE AD于E , CF AD于F , 且BE=CF , 求证:BD=DC18. 如图, AB, CD, EF交于O点, 且AC=BD, AC∥DB.求证:O是EF的中点.19. 已知:如图, AB⊥BC于B , EF⊥AC于G , DF⊥BC于D , BC=DF.求证:AC=EF.20. 已知:如图 , AD为CE的垂直平分线, EF∥BC.求证:△EDN≌△CDN≌△EMN.21. 已知:如图AB=CD,AD=BC 求证:AD∥BC22. 已知:如图, △ABC和△ADC有公共边AC , E是AC上一点 ,AB=AD , BE=DE.求证:∠ABC=∠ADC23. 已知:如图 , 点A、C、B、D在同一条直线上 , AC=BD , AM=CN , BM=DN 求证:AM∥CN , BM∥DN24. 已知:如图 , AB=AE , AC=AD , BC=DE , C , D在BE边上.求证:∠CAE=∠DAB.25. 已知:如图,四边形ABCD中,AD∥BC,AD=BC.求证:∠B=∠D.26. 已知:如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C.求证:AF=DE.27. 已知:如图 , E、D、B、F在同一条直线上, AD∥CB , ∠BAD=∠BCD , DE=BF.求证:AE∥CF28. 已知:如图 , AB=AC , AD=AE , 求证:△OBD≌△OCE29. 已知:如图, AE=BF , AD∥BC , AD=BC.AB、CD交于O点.求证:OE=OF.30. 已知:如图AC CD于C , BD CD于D , M是AB的中点 ,连结CM并延长交BD于点F.求证:AC=BF.32. 已知:如图 , AB=DC , BD=AC , AC , BD交于O.求证:△AOB≌△DOC.33. 如图 , 已知:AB=AC , BD=CD , E为AD上一点 ,求证:∠BED=∠CED34. 已知:如图 , AD=AE , BD=CE , AF BC , 且F是BC的中点.求证:∠D=∠E35. 已知:如图 , AB=CD , AD=BC ,O为BD中点 , 过O作直线分别与DA、BC的延长线交于E、F.求证:OE=OF36. 已知:如图, ∠1=∠2 , AB BC , AD DC , 垂足分别为B、D .求证:AB=AD.37. 假如两个三角形的两角和夹边上的高对应相等 , 那么这两个三角形全等.38. 如图在△ABC和△DBC中, ∠1=∠2 , ∠3=∠4 ,P是BC上任意一点.求证:PA=PD.39. 已知:如图 , E是AD上的一点 , AB=AC , AE=BD , CE=BD+DE.求证:∠B=∠CAE.40. 已知:如图 , AB=CD , BC=DA , E、F是AC上两点 , 且AE=CF.求证:BF=DE41. 已知:如图,∠1=∠2,BD=CD,求证:AD是∠BAC的平分线.42. 已知:如图,∠1=∠2,BE=C F,AC=DE,E、C在直线BF上.求证:∠A=∠D43. 已知:如图,点A、B、C、D在同一条直线上,AC=DB,AE=DF,EA⊥AD,FD⊥AD,垂足分别是A、D.求证:BE∥CF44. 如图:已知AE=CE,BE=DE,∠1=∠2 求证:AB=CD45. 已知:如图 , A、E、F、B在一条直线上 ,AC=BD , AE=BF , CF=DE.求证:AD=BC.46. 已知:如图 , 四边形 ABCD中, AD∥BC , F是AB的中点 ,DF交CB延长线于E , CE=CD.求证:∠ADE=∠EDC.47. 如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个能够直接到达A和B的点C,连结AC并延长到D,使CD=CA.连结BC并延长到E, 使EC=CB,连结DE,量出DE的长,就是A、B的距离.写出你的证明.48. 已知:如图,AM=BM,∠CMB=∠DMA,MC=MD.求证:AC=BD49. 已知:如图,AB=AC,AE平分∠BAC.求证:∠DBE=∠DCE.50. 已知:如图 , E、F是DA、BC延长线上的点 , AD=BC , AB=CD ,∠E=∠F.求证:EB∥DF.51. 假如两个三角形有两条边和其中一边上的中线对应相等 , 那么这两个三角形全等.52. 已知:如图 , OA=OE , OB=OF , 直线FA与BE交于C , AB和EF交于O ,求证:∠1=∠2.53. 已知:如图,AB=AC,AD=AE,∠BAC=∠DAE.求证:BD=CE54. 已知:如图,△ABC中,点E、F分别在AB、AC边上,点D是BC边中点,且EF∥BC,D E=DF.求证:∠B=∠C55. 已知:如图,AC、BD相交于O点,O是AC、BD的公共中点.求证:AB∥CD,AD∥BC.56. 已知:如图 , BC是△ABC和△DCB 的公共边 , AB=DC , AC=DB , AE、DF分别垂直BC于E , F.求证:AE=DF.57. 已知:如图 , AB=AC , EB=EC , AE的延长线交BC于D.求证:BD=CD.58. 如图:已知,AD=AB,AC=AE,∠DAB=∠CAE,求证:BE=CD59. 如图,△ABC中,∠ACB=90°,CE⊥AB于E,AD=AC,AF平分∠CAE交CE于F.求证:FD∥CB60. 已知:如图,D、E分别是△ABC的边AB,AC的中点,点F在DE的延长线上, 且EF=DE.求证:(1)BD=FC (2)AB∥CF61. 已知:如图,AC=AB,AE=AD,∠1=∠2.求证:∠3=∠462. 求证:全等三角形对应中线相等.63. 如图,已知:△ABC中,BE,CF分别为AC边和AB边上的高,在BE上截取BP=AC,延长CF,并截取CQ=AB.求证:AP=AQ.65. 已知:如图∠1=∠2 , ∠3=∠4.求证:AD=BC AC=BD.66. 已知:四边形ABCD中 , AC、BD交于O点 , AO=OC ,DC⊥垂足分别为A , C.求证:AD=BCBA⊥,ACAC67. 求证:三角形一边的两个端点 , 到这边上的中线的距离相等.68. 已知:如图 , AB=AD , DC=CB.求证:∠B=∠D69. 已知:如图,AB=DC,OC=OB,AB、CD交于点O.求证:AC=DB.70. 已知:如图, AB∥CD , ∠1=∠2 , O是AD的中点 , EF、AD交于O.求证:O也是EF的中点.71. 已知:如图, FB=CE , AB∥ED , AC∥FD.F、C在直线BE上.求证:AB=DE , AC=DF.72. 已知:如图, ∠1=∠2 , ∠3=∠4 , DE=CE.E是BC上的一点.求证:AE=BE73. 已知:如图AC∥BD , AE和BE分别平分∠CAB和∠DBA , CD过点E.求证AB=AC+BD74. 已知:如图, ∠1=∠2 , ∠3=∠4.求证:∠ADC=∠BCD75. 已知:如图:AB=CD , BE=CF , AF=DE.求证:△ABE≌△DCF76. 已知:如图 , AB=AC , AD=AE , BD=CE.求证:∠BAC=∠DAE.77. 如图 , 已知:DC=AB , DF=BE , CF=AE , 求证:AO=CO EO=FO.78. 已知:如图 , AB=DC , AD=BC , O是BD中点 , 过O的直线分别与DA、BC的延长线交于E、F.求证:OE=OF。
全等三角形证明题大综合
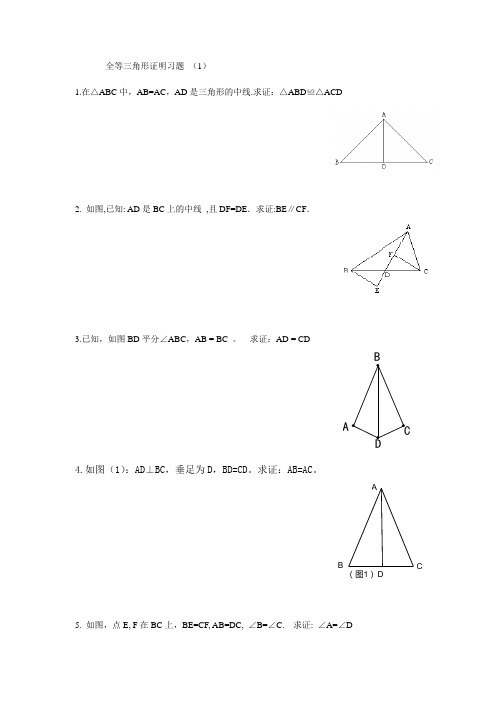
BA DC 全等三角形证明习题 (1)1.在△ABC 中,AB=AC ,AD 是三角形的中线.求证:△ABD ≌△ACD2. 如图,已知: AD 是BC 上的中线 ,且DF=DE .求证:BE ∥CF .3.已知,如图BD 平分∠ABC ,AB = BC 。
求证:AD = CD4.如图(1):AD ⊥BC ,垂足为D ,BD=CD 。
求证:AB=AC 。
5. 如图,点E, F 在BC 上,BE=CF, AB=DC, ∠B=∠C. 求证: ∠A=∠D(图1)D CBABDC E A6. 如图,AB=AD, BC=DE, ∠B=∠D . 问∠BAE 与∠DAC 相等吗?为什么?7. 已知:如图,∠1=∠2,BD=CD,求证:AD 是∠BAC 的平分线.8.如图所示在△ABC 中,AB=AC , D 是BD 的中点,求证:△9.如图(2):AC ∥EF ,AC=EF ,AE=BD 。
求证:△ABC ≌△EDF 。
CO ED BA F E DC B A10.已知:如图 , AB=AE , AC=AD , BC=DE , C , D 在BE 边上. 求证:∠CAE=∠DAB .11.已知:点D 在AB 上,点E 在AC 上,BE 和CD 相交于点O ,AB=AC , ∠B=∠C 。
求证: △ABE ≌△ACD12.如图:AC=DF ,AD=BE ,BC=EF 。
求证:∠C=∠F 。
13.如图:AB=AC ,DB=DC ,F 是AD 的延长线上的一点。
求证:BF=CF 。
DBEA OC FEB DAFD CBA14.如图,CE ⊥AB 于E , DF ⊥AB 于F , AF=BE , 且AC=BD , 求证:AC ∥BD15.如图,已知AB=DE ,BC=EF ,AF=DC ,则∠EFD=∠BCA ,请说明理由。
16.如图(6):CG=CF ,BC=DC ,AB=ED ,点A 、B 、C 、D 、E 在同一直线上。
专题01 勾股定理的证明综合题(原卷版)

专题01 勾股定理的证明(综合题)知识点:勾股定理的证明方法一:将四个全等的直角三角形拼成如图(1)所示的正方形. 图(1)中,所以. 方法二:将四个全等的直角三角形拼成如图(2)所示的正方形. 图(2)中,所以.方法三:如图(3)所示,将两个直角三角形拼成直角梯形. ,所以.一.选择题1.(2022春•龙凤区期中)如图,在四边形ABDE 中,AB ∥DE ,AB ⊥BD ,点C 是边BD 上一点,BC =DE =a ,CD =AB =b ,AC =CE =c.下列结论:易错点拨易错题专训①△ABC≌△CDE;②∠ACE=90°;③四边形ABDE的面积是(a+b)2;④(a+b)2﹣c2=2×ab;⑤该图可以验证勾股定理.其中正确的结论个数是( )A.5B.4C.3D.22.(2022秋•杏花岭区校级月考)下面四幅图中,不能证明勾股定理的是( )A.B.C.D.3.(2022春•威县期末)课堂上,王老师要求学生设计图形来证明勾股定理,同学们经过讨论,给出两种图形,能证明勾股定理的是( )A.①行,②不行B.①不行,②行C.①,②都行D.①,②都不行4.(2022•大观区校级开学)如图,“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的大正方形.若图中的直角三角形的一条直角边长为5,大正方形的边长为13,则中间小正方形的面积是( )A.144B.49C.64D.255.(2022春•交城县期中)勾股定理是一个古老的数学定理,它有很多种证明方法,如图所示四幅几何图形中,不能用于证明勾股定理的是( )A.B.C.D.6.(2022春•邕宁区期末)下面图形能够验证勾股定理的有( )A.4个B.3个C.2个D.1个7.(2022•邯郸三模)在证明勾股定理时,甲、乙两位同学分别设计了方案:甲:如图,用四个全等的直角三角形拼成,其中四边形ABDE和四边形CFGH均是正方形,通过用两种方法表示正方形ABDE的面积来进行证明;乙:两个全等的直角三角板ABC和直角三角板DEF,顶点F在BC边上,顶点C、D重合,通过用两种方法表示四边形ACBE的面积来进行证明.对于甲、乙两种方案,下列判断正确的是( )A.甲、乙均对B.甲对、乙不对C.甲不对,乙对D.甲、乙均不对8.(2021秋•无锡期末)如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3.若S1+S2+S3=18,则S2的值是( )A.B.6C.5D.9.(2020春•海陵区期末)“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=6,大正方形的面积为16,则小正方形的面积为( )A.8B.6C.4D.3二.填空题10.(2021秋•漳州期末)如图所示的四边形图案是用4个全等的直角三角形拼成的.已知四边形ABCD的面积为64,四边形EFGH的面积为9,若用x、y表示直角三角形的两直角边(x>y);下列四个结论:①x2+y2=64;②x﹣y=3;③x+y=;④2xy+9=64.其中正确的是 .(写出所有正确结论的序号)11.(2021秋•皇姑区期末)把图1中长和宽分别6和4的两个全等矩形沿对角线分成四个全等的直角三角形,将这四个全等的直角三角形拼成图2的正方形,则图2中小正方形ABCD的面积为 .12.(2021秋•迎泽区校级月考)“赵爽弦图”是由四个全等的直角三角形拼接而成.如图,若直角三角形的短直角边长为2,小正方形的面积为4,则大正方形边长为 .13.曾任美国总统的加菲尔德在《新英格兰教育日志》上发表了他提出的一个勾股定理的证明.如图,这就是他用两个全等的直角三角形拼出的图形.上面的图形整体上拼成一个直角梯形.所以它的面积有两种表示方法.既可以表示为 ,又可以表示为 .对比两种表示方法可得 .化简,可得a2+b2=c2.他的这个证明也就成了数学史上的一段佳话.三.解答题14.(2021秋•东坡区期末)勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,当两个全等的直角三角形如图摆放时,可以用“面积法”来证明.将两个全等的直角三角形按如图所示摆放,使点A、E、D 在同一条直线上.利用此图的面积表示式证明勾股定理.15.(2021春•利辛县期中)如图,小明用4个图1中的矩形组成图2,其中四边形ABCD,EFGH,MNPQ都是正方形,证明:a2+b2=c2.16.(2021春•滑县期末)如图是用硬纸板做成的四个全等的直角三角形,两直角边的长分别为a和b,斜边长为c.请你开动脑筋,用它们拼出正方形图案,要求拼图时直角三角形纸片不能互相重叠.(1)请你画出拼成的这个图形的示意图;(2)利用(1)中画出的图形证明勾股定理.17.(2021秋•汝州市期中)用四个全等的直角三角形拼成如图①所示的大正方形,中间也是一个正方形.它是美丽的弦图.其中四个直角三角形的直角边长分别为a,b(a<b),斜边长为c.(1)结合图①,求证:a2+b2=c2;(2)如图②,将这四个全等的直角三角形无缝隙无重叠地拼接在一起,得到图形ABCDEFGH.若该图形的周长为24,OH=3,求该图形的面积;(3)如图③,将八个全等的直角三角形紧密地拼接成正方形PQMN,记正方形PQMN、正方形ABCD、正方形EFGH的面积分别为S1、S2、S3,若S1+S2+S3=18,则S2= .18.(2022春•大观区校级期末)如图,对任意符合条件的直角三角形BAC,绕其锐角顶点逆时针旋转90°得△DAE,所以∠BAE=90°,且四边形ACFD是一个正方形,它的面积和四边形ABFE面积相等,而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和,根据图形写出一种证明勾股定理的方法.19.(2021秋•武汉月考)2000多年来,人们对直角三角形三边之间的关系的探究颇感兴趣,古往今来,下至平民百姓,上至帝王总统都愿意探究它,研究它的证明,新的证法不断出现.下面给出几种探究方法(由若干个全等的直角三角形拼成如图图形),试用面积法选择其中一种推导直角三角形的三边a、b、c 之间的数量关系(1)三边a、b、c之间的数量关系为 ;(2)理由: .20.(2018•保定二模)勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2证明:连接DB ,过点D 作BC 边上的高DF ,则DF =EC =b ﹣a∵S 四边形ADCB =S △ACD +S △ABC =b 2+ab .又∵S 四边形ADCB =S △ADB +S △DCB =c 2+a (b ﹣a )∴b 2+ab =c 2+a (b ﹣a )∴a 2+b 2=c 2请参照上述证法,利用图2完成下面的证明.将两个全等的直角三角形按图2所示摆放,其中∠DAB =90°.求证:a 2+b 2=c 2.。
相似证明及综合小题
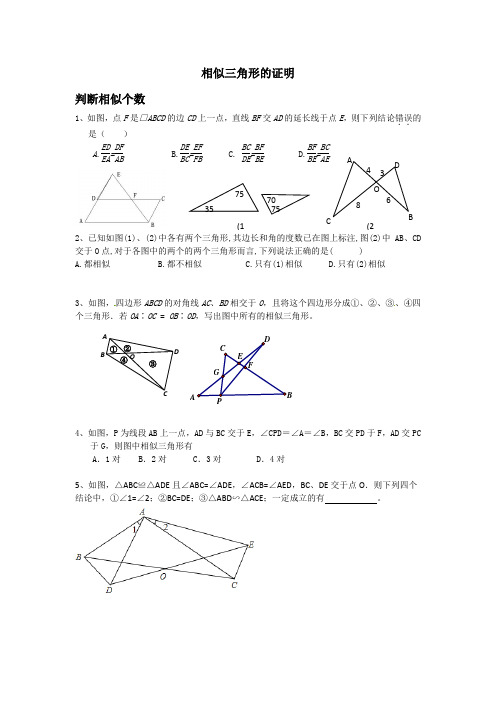
相似三角形的证明判断相似个数1、如图,点F 是□ABCD 的边CD 上一点,直线BF 交AD 的延长线于点E ,则下列结论错误..的是()A.ED EA =DF ABB.DE BC =EF FBC. BC DE =BF BED.BF BE =BCAE2、已知如图(1)、(2)中各有两个三角形,其边长和角的度数已在图上标注,图(2)中AB 、CD交于O 点,对于各图中的两个的两个三角形而言,下列说法正确的是( )A.都相似B.都不相似C.只有(1)相似D.只有(2)相似3、如图,四边形ABCD 的对角线AC 、BD 相交于O ,且将这个四边形分成①、②、③、④四个三角形.若OA ∶OC = OB ∶OD ,写出图中所有的相似三角形。
4、如图,P 为线段AB 上一点,AD 与BC 交于E ,∠CPD =∠A =∠B ,BC 交PD 于F ,AD 交PC于G ,则图中相似三角形有A .1对B .2对C .3对D .4对5、如图,△ABC ≌△ADE 且∠ABC=∠ADE ,∠ACB=∠AED ,BC 、DE 交于点O .则下列四个结论中,①∠1=∠2;②BC=DE ;③△ABD ∽△ACE ;一定成立的有。
AA B DO ① ②③④35757570(1 AB CDO4 3 68(2证明问题1、如图,已知等边三角形△AEC ,以AC 为对角线做正方形ABCD (点B 在△AEC 内,点D 在△AEC 外)。
连结EB ,过E 作EF ⊥ AB ,交AB 的延长线为F 。
(1)猜测直线BE 和直线AC 的位置关系,并证明你的猜想。
(2)证明:△BEF ∽△ABC ,并求出相似比。
2、已知:如图,在△ABC 中,AB=AC ,DE∥BC,点F 在边AC 上,DF 与BE 相交于点G ,且∠EDF=∠ABE.求证:(1)△DEF∽△BDE;(2)EF DB DF DG ⋅=⋅.3、如图,点P 是菱形ABCD 的对角线BD 上一点,连结CP 并延长,交AD 于E ,交BA 的延长线点F .问:(1) 图中△APD 与哪个三角形全等?并说明理由. (2) 求证:△APE ∽△FPA.(3) 猜想:线段PC 、PE 、PF 之间存在什么关系?并说明理由.B C以相似处理切割、动点存在问题、及最值问题1、如图,在Rt △ABC 内有边长分别为的三个正方形,则满足的关系式是( ) A 、 B 、 C 、 D 、2、一个铝质三角形框架三条边长分别为24cm 、30cm 、36cm ,要做一个与它相似的铝质三角形框架,现有长为27cm 、45cm 的两根铝材,要求以其中的一根为一边,从另一根上截下两段(允许有余料)作为另外两边.截法有() A.0种 B. 1种 C. 2种 D. 3种 3、如图,方格纸中每个小正方形的边长为1,△ABC 和△DEF的顶点都在方格纸的格点上.(1) 判断△ABC 和△DEF 是否相似,并说明理由;(2) P 1,P 2,P 3,P 4,P 5,D ,F 是△DEF 边上的7个格点,请在这7个格点中选取3个点作为三角形的顶点,使构成的三角形与△ABC 相似(要求写出2个符合条件的三角形,并在图中连结相应线段,不必说明理由).4、正方形ABCD 的边长为1cm ,M 、N 分别是BC 、CD 上两个动点,且始终保持AM ⊥MN ,当BM= cm 时,四边形ABCN 的面积最大,最大面积为cm 2.5、如图,在梯形ABCD 中,AB ∥CD ,AB =7,CD =1,AD =BC =5.点M ,N 分别在边AD ,BC上运动,并保持MN ∥AB ,ME ⊥AB ,NF ⊥AB ,垂足分别为E ,F . (1)求梯形ABCD 的面积; (2)求四边形MEFN 面积的最大值.(3)试判断四边形MEFN 能否为正方形,若能,求出正方形MEFN 的面积;若不能,请说明理由.,,a b c ,,a b c b a c =+b ac =222b ac =+22b a c ==ACBFEDP 1P 2 P 3P 4P 5C DABEFNM6、如图所示,E 是正方形ABCD 的边AB 上的动点, EF ⊥DE 交BC 于点F .(1)求证: ADE ∽BEF ;(2)设正方形的边长为4, AE =,BF =.当取什么值时, 有最大值?并求出这个最大值.7、如图(1),△ABC 与△EFD 为等腰直角三角形,AC 与DE 重合,AB =EF =9,∠BAC =∠DEF =90°,固定△ABC ,将△EFD 绕点A 顺时针旋转,当DF 边与AB 边重合时,旋转中止.不考虑旋转开始和结束时重合的情况,设DE 、DF (或它们的延长线)分别交BC (或它的延长线)于G 、H 点,如图(2).(1)问:始终与△AGC 相似的三角形有及;(2)设CG =x ,BH =y ,求y 关于x 的函数关系式(只要求根据2的情况说明理由); (3)问:当x 为何值时,△AGH 是等腰三角形?运用相似处理综合性小题∆∆x y xy1、如图,△ABC 中,点D 在线段BC 上,且△ABC ∽△DBA ,则下列结论一定正确的是() A .AB 2=BC ·BDB .AB 2=AC ·BDC .AB ·AD =BD ·BCD .AB ·AD =AD ·CD2、如图,在等边△ABC 中,D 为BC 边上一点,E 为AC 边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC 的边长为( )A .9B .12C .15D .183、如图,在等边△ABC 中,D 为BC 边上一点,E 为AC 边上一点,且∠ADB +∠EDC =120°,BD =3,CE =2,则△ABC 的边长为A .9B .12C .16D .184、如图,△ABC 为等边三角形,点E 在BA 的延长线上,点D 在BC 边上,且ED=EC .若△ABC 的边长为4,AE=2,则BD 的长为( ) A .2B .3C .15、如图,在Rt△ABC 中,,D 、E 是斜边BC 上两点,且∠DAE =45°,将△绕点顺时针旋转90后,得到△,连接,下列结论: ①△≌△;②△∽△; ③; ④其中一定正确的是 A .②④B .①③C .②③D .①④相似与函数问题AB AC=ADC A ︒AFB EF AED AEF ABE ACD BE DC DE +=222BE DC DE +=ABD C1、如图,O 为矩形ABCD 的中心,M 为BC 边上一点,N 为DC 边上一点,ON ⊥OM ,若AB=6,AD=4,设OM=x ,ON=y ,则y 与x 的函数关系式为。
定理证明与应用综合练习题

定理证明与应用综合练习题一、定理证明练习题1. 定理1:勾股定理证明:对于直角三角形ABC,若$$AB^2 + BC^2 = AC^2$$,则角C为直角。
证明思路:假设角C不是直角,即$$\angle C \neq 90^\circ$$。
根据余弦定理,有$$\cos C = \frac{AB^2 + BC^2 - AC^2}{2 \cdot AB \cdot BC}$$。
根据已知条件$$AB^2 + BC^2 = AC^2$$,将其代入上式,得$$\cosC = \frac{AC^2 - AC^2}{2 \cdot AB \cdot BC} = 0$$。
然而,余弦函数在0度到180度内都是正数,因此假设成立,角C为直角。
2. 定理2:平行线性质证明:若两个平行线被一条截线所交,那么同一侧的内角互补。
证明思路:设直线m和n为平行线,直线l为截线,交点为A。
要证明同一侧的内角互补,需证明$$\angle BAC + \angle CAD = 180^\circ$$。
根据平行线性质,$$\angle BAC = \angle BCA$$;根据同位角性质,$$\angle CAD = \angle ACD$$。
由于$$\angle BAC$$和$$\angle BCA$$为邻补角,角度之和为180度,同理$$\angle CAD$$和$$\angle ACD$$的度数之和也为180度。
因此,$$\angle BAC + \angle CAD = 180^\circ$$,证明完成。
二、应用练习题1. 问题:一块长方形田地的长是15米,宽是10米。
现在要在田地的四周围上一道铁丝网,如图所示。
请问需要多长的铁丝网?解答:根据长方形的性质,田地的周长为2(长 + 宽)。
周长 = 2(15 + 10) = 2(25) = 50米。
因此,需要50米的铁丝网。
2. 问题:某商店原价出售一件衣服为800元,现在打折出售,折扣为20%。
高中数学-推理与证明综合测试题

高中数学-推理与证明综合测试题一、选择题1.分析法是从要证明的结论出发,逐步寻求使结论成立的( )A.充分条件 B.必要条件 C.充要条件 D.等价条件答案:A2.结论为:n n x y +能被x y +整除,令1234n =,,,验证结论是否正确,得到此结论成立的条件可以为( )A.n *∈N B.n *∈N 且3n ≥ C.n 为正奇数 D.n 为正偶数答案:C3.在ABC △中,sin sin cos cos A C A C >,则ABC △一定是( )A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定答案:C4.在等差数列{}n a 中,若0n a >,公差0d >,则有4637a a a a >··,类经上述性质,在等比数列{}n b 中,若01n b q >>,,则4578b b b b ,,,的一个不等关系是( ) A.4857b b b b +>+ B.5748b b b b +>+ C.4758b b b b +>+D.4578b b b b +>+答案:B5.(1)已知332p q +=,求证2p q +≤,用反证法证明时,可假设2p q +≥,(2)已知a b ∈R ,,1a b +<,求证方程20x ax b ++=的两根的绝对值都小于1.用反证法证明时可假设方程有一根1x 的绝对值大于或等于1,即假设11x ≥,以下结论正确的是( ) A.(1)与(2)的假设都错误 B.(1)与(2)的假设都正确C.(1)的假设正确;(2)的假设错误 D.(1)的假设错误;(2)的假设正确答案:D6.观察式子:213122+<,221151233++<,222111712344+++<,L ,则可归纳出式子为( ) A.22211111(2)2321n n n ++++<-L ≥ B.22211111(2)2321n n n ++++<+L ≥ C.222111211(2)23n n n n -++++<L ≥ D.22211121(2)2321n n n n ++++<+L ≥答案:C7.如图,在梯形ABCD 中,()AB DC AB a CD b a b ==>,,∥.若EF AB ∥,EF 到CD 与AB 的距离之比为:m n ,则可推算出:ma mbEF m m+=+.试用类比的方法,推想出下述问题的结果.在上面的梯形ABCD 中,延长梯形两腰AD BC ,相交于O 点,设OAB △,OCD △的面积分别为12S S ,,EF AB ∥且EF 到CD 与AB 的距离之比为:m n ,则OEF △的面积0S 与12S S ,的关系是( )A.120mS nS S m n+=+B.120nS mS S m n +=+C.120m S n S S +=D.120n S m S S +=答案:C8.已知a b ∈R ,,且2a b a b ≠+=,,则( ) A.2212a b ab +<<B.2212a b ab +<<C.2212a b ab +<<D.2212a b ab +<<答案:B9.用反证法证明命题:若整系数一元二次方程20(0)ax bx c a ++=≠有有理根,那么a b c ,,中至少有一个是偶数时,下列假设中正确的是( ) A.假设a b c ,,都是偶数 B.假设a b c ,,都不是偶数C.假设a b c ,,至多有一个是偶数 D.假设a b c ,,至多有两个是偶数答案:B10.用数学归纳法证明(1)(2)()213(21)nn n n n n +++=-L L ····,从k 到1k +,左边需要增乘的代数式为( ) A.21k + B.2(21)k + C.211k k ++ D.231k k ++答案:B11.类比“两角和与差的正余弦公式”的形式,对于给定的两个函数,()2x xa a S x --=,()2x xa a C x -+=,其中0a >,且1a ≠,下面正确的运算公式是( ) ①()()()()()S x y S x C y C x S y +=+; ②()()()()()S x y S x C y C x S y -=-; ③()()()()()C x y C x C y S x S y +=-; ④()()()()()C x y C x C y S x S y -=+;A.①③ B.②④ C.①④ D.①②③④答案:D12.正整数按下表的规律排列则上起第2005行,左起第2006列的数应为( ) A.22005 B.22006C.20052006+D.20052006⨯答案:D二、填空题13.写出用三段论证明3()sin ()f x x x x =+∈R 为奇函数的步骤是 .答案:满足()()f x f x -=-的函数是奇函数, 大前提1 2 5 10 17 4 3 6 11 18 9 8 7 12 19 16 15 14 13 20 25 24 23 22 21333()()sin()sin (sin )()f x x x x x x x f x -=-+-=--=-+=-, 小前提所以3()sin f x x x =+是奇函数. 结论14.已知111()1()23f n n n *=++++∈N L ,用数学归纳法证明(2)2n nf >时,1(2)(2)k k f f +-等于 . 答案:111121222k k k ++++++L15.由三角形的性质通过类比推理,得到四面体的如下性质:四面体的六个二面角的平分面交于一点,且这个点是四面体内切球的球心,那么原来三角形的性质为 .答案:三角形内角平分线交于一点,且这个点是三角形内切圆的圆心16.下面是按照一定规律画出的一列“树型”图:设第n 个图有n a 个树枝,则1n a +与(2)n a n ≥之间的关系是 .答案:122n n a a +=+三、解答题17.如图(1),在三角形ABC 中,AB AC ⊥,若AD BC ⊥,则2AB BD BC =·;若类比该命题,如图(2),三棱锥A BCD -中,AD ⊥面ABC ,若A 点在三角形BCD 所在平面内的射影为M ,则有什么结论?命题是否是真命题.解:命题是:三棱锥A BCD -中,AD ⊥面ABC ,若A 点在三角形BCD 所在平面内的射影为M ,则有2ABC BCMBCD S S S =△△△·是一个真命题. 证明如下:在图(2)中,连结DM ,并延长交BC 于E ,连结AE ,则有DE BC ⊥. 因为AD ⊥面ABC ,,所以AD AE ⊥. 又AM DE ⊥,所以2AE EM ED =·. 于是22111222ABCBCM BCD SBC AE BC EM BC ED S S ⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭△△△·····.18.如图,已知PA ⊥矩形ABCD 所在平面,M N ,分别是AB PC ,的中点. 求证:(1)MN ∥平面PAD ;(2)MN CD ⊥.证明:(1)取PD 的中点E ,连结AE NE ,. N E ,∵分别为PC PD ,的中点.EN ∴为PCD △的中位线,12EN CD ∥∴,12AM AB =,而ABCD 为矩形, CD AB ∴∥,且CD AB =.EN AM ∴∥,且EN AM =.AENM ∴为平行四边形,MN AE ∥,而MN ⊄平面PAC ,AE ⊂平面PAD , MN ∴∥平面PAD .(2)PA ⊥∵矩形ABCD 所在平面,CD PA ⊥∴,而CD AD ⊥,PA 与AD 是平面PAD 内的两条直交直线, CD ⊥∴平面PAD ,而AE ⊂平面PAD , AE CD ⊥∴.又MN AE ∵∥,MN CD ⊥∴.19.求证:当一个圆和一个正方形的周长相等时,圆的面积比正方形的面积大.证明:(分析法)设圆和正方形的周长为l ,依题意,圆的面积为2π2πl ⎛⎫⎪⎝⎭·, 正方形的面积为24l ⎛⎫⎪⎝⎭.因此本题只需证明22π2π4l l ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭.要证明上式,只需证明222π4π16l l >,两边同乘以正数24l ,得11π4>.因此,只需证明4π>.∵上式是成立的,所以22π2π4l l ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭.这就证明了如果一个圆和一个正方形的周长相等,那么圆的面积比正方形的面积最大.20.已知实数a b c d ,,,满足1a b c d +=+=,1ac bd +>,求证a b c d ,,,中至少有一个是负数.证明:假设a b c d ,,,都是非负实数,因为1a b c d +=+=,所以a b c d ,,,[01]∈,,所以2a c ac +,2b cbd +, 所以122a cb dac bd ++++=≤, 这与已知1ac bd +>相矛盾,所以原假设不成立,即证得a b c d ,,,中至少有一个是负数.21.设()2x x a a f x -+=,()2x xa a g x --=(其中0a >,且1a ≠).(1)523=+请你推测(5)g 能否用(2)(3)(2)(3)f f g g ,,,来表示;(2)如果(1)中获得了一个结论,请你推测能否将其推广.解:(1)由3332332255(3)(2)(3)(2)22221a a a a a a a a a a f g g f -----+--+-+=+=··, 又55(5)2a a g --=,因此(5)(3)(2)(3)(2)g f g g f =+.(2)由(5)(3)(2)(3)(2)g f g g f =+,即(23)(3)(2)(3)(2)g f g g f +=+, 于是推测()()()()()g x y f x g y g x f y +=+.证明:因为()2x x a a f x -+=,()2x xa a g x --=(大前提).所以()()2x y x y a a g x y +-+-+=,()2y y a a g y --=,()2y ya a f y -+=,(小前提及结论)所以()()()()()()22222x x y y x x y y x y x y a a a a a a a a a a f x g y g x f y g x y ----+-++--+-+=+==+··.22.若不等式111123124an n n +++>+++L 对一切正整数n 都成立,求正整数a 的最大值,并证明结论.解:当1n =时,11111123124a ++>+++,即262424a>, 所以26a <.而a 是正整数,所以取25a =,下面用数学归纳法证明:11125123124n n n +++>+++L . (1)当1n =时,已证;(2)假设当n k =时,不等式成立,即11125123124k k k +++>+++L . 则当1n k =+时,有111(1)1(1)23(1)1k k k +++++++++L 111111112313233341k k k k k k k =++++++-+++++++L 251122432343(1)k k k ⎡⎤>++-⎢⎥+++⎣⎦. 因为2116(1)2323491883(1)k k k k k k ++=>+++++, 所以2116(1)2323491883(1)k k k k k k ++=>+++++, 所以112032343(1)k k k +->+++. 所以当1n k =+时不等式也成立. 由(1)(2)知,对一切正整数n ,都有11125123124n n n +++>+++L , 所以a 的最大值等于25.。
菱形的证明与计算综合训练题
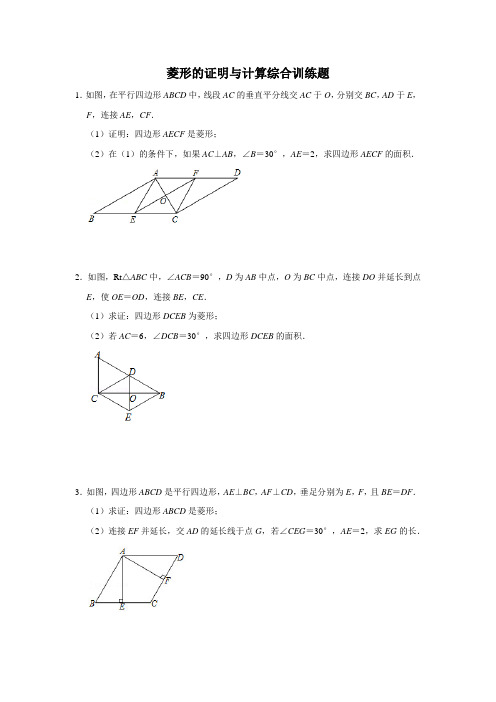
菱形的证明与计算综合训练题1.如图,在平行四边形ABCD中,线段AC的垂直平分线交AC于O,分别交BC,AD于E,F,连接AE,CF.(1)证明:四边形AECF是菱形;(2)在(1)的条件下,如果AC⊥AB,∠B=30°,AE=2,求四边形AECF的面积.2.如图,Rt△ABC中,∠ACB=90°,D为AB中点,O为BC中点,连接DO并延长到点E,使OE=OD,连接BE,CE.(1)求证:四边形DCEB为菱形;(2)若AC=6,∠DCB=30°,求四边形DCEB的面积.3.如图,四边形ABCD是平行四边形,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF.(1)求证:四边形ABCD是菱形;(2)连接EF并延长,交AD的延长线于点G,若∠CEG=30°,AE=2,求EG的长.4.如图,在Rt△ABC中,∠ACB=90°.CD⊥AB,AF平分∠CAB,交CD于点E,交BC 于点F.过点F作FG⊥AB交AB于点G,连接EG.(1)求证:四边形CEGF是菱形;(2)若∠B=30°,AC=6,求CE的长.5.四边形ABCD中,∠A=∠B=90°,点E在边AB上,点F在AD的延长线上,且点E 与点F关于直线CD对称,过点E作EG∥AF交CD于点G,连接FG,DE.(1)求证:四边形DEGF是菱形;(2)若AB=10,AF=BC=8,求四边形DEGF的面积.6.如图,在△ABC中,BD平分∠ABC交AC于D,作DE∥BC交AB于点E,作DF∥AB 交BC于点F.(1)求证:四边形BEDF是菱形;(2)若∠BDE=15°,∠C=45°,CD=,求DE的长.7.如图,在△ABC中,BD平分∠ABC交AC于D,EF垂直平分BD,分别交AB,BC,BD 于E,F,G,连接DE,DF.(1)求证:四边形BEDF是菱形;(2)若∠BDE=15°,∠C=45°,DE=2,求CF的长.8.如图,AM∥BN,C是BN上一点,BD平分∠ABN且过AC的中点O,交AM于点D,DE⊥BD,交BN于点E.(1)求证:△ADO≌△CBO.(2)求证:四边形ABCD是菱形.(3)若DE=AB=2,求菱形ABCD的面积.9.如图,在Rt△ABC中,∠ABC=90°,D、E分别是边BC,AC的中点,连接ED并延长到点F,使DF=ED,连接BE、BF、CF.(1)求证:四边形BFCE是菱形;(2)若BC=4,EF=2,求AD的长.10.如图,在△ABC中,CD平分∠ACB,CD的垂直平分线分别交AC、DC、BC于点E、F、G,连接DE、DG.(1)求证:四边形DGCE是菱形;(2)若∠ACB=30°,∠B=45°,ED=6,求BG的长.11.如图,在四边形ABCD中,AB∥CD,AB=BC=2CD,E为对角线AC的中点,F为边BC的中点,连接DE、EF.(1)求证:四边形CDEF为菱形;(2)连接DF交AC于点G,若DF=2,CD=,求AD的长.12.如图,在▱ABCD中,BD=AD,延长CB到点E,使BE=BD,连接AE.(1)求证:四边形AEBD是菱形;(2)连接DE交AB于点F,若DC=,DC:DE=1:3,求AD的长.13.如图,在△ABC中,AC=BC,点D,E,F分别是AB,AC,BC的中点,连接DE,DF.(1)求证:四边形DFCE是菱形;(2)若∠A=75°,AC=4,求菱形DFCE的面积.14.如图,▱ABCD中,E,F分别是边BC,AD的中点,∠BAC=90°.(1)求证:四边形AECF是菱形;(2)若BC=4,∠B=60°,求四边形AECF的面积.15.如图,在▱ABCD中,BC=2AB,E,F分别是BC,AD的中点,AE,BF交于点O,连接EF,OC.(1)求证:四边形ABEF是菱形;(2)若BC=8,∠ABC=60°,求OC的长.16.如图,在四边形ABCD中,AD∥BC,BA=BC,BD平分∠ABC.(1)求证:四边形ABCD是菱形;(2)过点D作DE⊥BD,交BC的延长线于点E,若BC=5,BD=8,求四边形ABED 的周长.17.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.(1)求证:四边形ABCD是菱形;(2)若AB=,BD=2,求OE的长.18.如图,在▱ABCD中,对角线BD平分∠ABC,过点A作AE∥BD,交CD的延长线于点E,过点E作EF⊥BC,交BC延长线于点F.(1)求证:四边形ABCD是菱形;(2)若∠ABC=45°,BC=2,求EF的长.19.如图,在△ABC中,∠ACB=90°,CD为边AB上的中线,点E与点D关于直线AC 对称,连接AE、CE.(1)求证:四边形AECD是菱形;(2)连接BE,若∠ABC=30°,AC=2,求BE的长.20.如图,在四边形ABCD中,AB∥CD,AB=AD,AC平分∠BAD.(1)求证:四边形ABCD是菱形;(2)若菱形ABCD的边长为13,对角线AC=24,点E、F分别是边CD、BC的中点,连接EF并延长,与AB的延长线相交于点G,求EG的长.21.如图,在平行四边形ABCD中,BE⊥AD,BF⊥CD,垂足分别为E,F,且AE=CF.(1)求证:平行四边形ABCD是菱形;(2)若DB=10,AB=13,求平行四边形ABCD的面积.22.在▱ABCD中,AE平分∠BAD,O为AE的中点,连接BO并延长,交AD于点F,连接EF,OC.(1)求证:四边形ABEF是菱形;(2)若点E为BC的中点,且BC=8,∠ABC=60°,求OC的长.23.已知,四边形ABCD中,AB∥CD,AB=2CD,E为AB的中点,AC为对角线,AC⊥BC.(1)求证:四边形AECD是菱形.(2)若∠DAE=60°,AE=2,求菱形AECD的面积.24.如图,在▱ABCD中,过AD的中点G作AD的垂直平分线,分别交CD的延长线和AB 于点E、F,连接AE、DF.(1)求证:四边形AFDE是菱形;(2)连接AC,若AE=2,AB=3,∠AED=60°,求AC的长.25.如图,四边形ABCD中,AD∥BC,AB⊥BC,三角形BDC为等边三角形,点E,F分别为BD,CD的中点.(1)求证:四边形AEFD是菱形;(2)若BC=2,求四边形ABCD的面积.26.如图,已知,在△ADE中,∠ADE=90°,点B是AE的中点,过点D作DC∥AE,DC=AB,连接BD,CE.(1)求证:四边形BDCE是菱形;(2)若AD=6,BD=5,求菱形BDCE的面积.27.如图,四边形ABCD中,AD∥BC,AB=AD=CD=BC.分别以B、D为圆心,大于BD长为半径画弧,两弧交于点M.画射线AM交BC于E,连接DE.(1)求证:四边形ABED为菱形;(2)连接BD,当CE=5时,求BD的长.28.在Rt△ABC中,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.(1)证明:四边形ADCF是菱形;(2)若AC=4,AB=5,求菱形ADCF的面积.29.如图,在▱ABCD中,AE平分∠BAD交BC于点E,过点B作BF⊥AE于点H,交AD 于点F,连接EF.(1)求证:四边形ABEF是菱形;(2)连接CF,若CE=1,CF=2,,求菱形ABEF的面积.30.如图,在△ABC中,∠ACB=90°,D,E分别是边AB,AC的中点,BC=BD,点F 在ED的延长线上,且BF∥CD.(1)求证:四边形CBFD为菱形;(2)连接CF,与BD相交于点O,若CF=,求AC的长.31.已知:如图,在等腰△ABC中,AB=BC,BO平分∠ABC交AC于点O,延长BO至点D,使OD=BO,连接AD,CD,过点D作DE⊥BD交BC的延长线于点E.(1)求证:四边形ABCD是菱形;(2)如果AB=2,∠BAD=60°,求DE的长.32.如图,在Rt△ABC中,∠ACB=90°,D,E分别是边AB,BC的中点,连接DE并延长到点F,使EF=DE,连接CF,BF.(1)求证:四边形CFBD是菱形;(2)连接AE,若CF=,DF=2,求AE的长.33.如图,在△ABC中,∠BAC=90°,AD是BC边上的中线,AE∥BC,CE∥AD.(1)求证:四边形ADCE是菱形;(2)连接BE,若∠ABC=30°,AC=2,求BE的长.34.如图,在▱ABCD中,BC=2CD,E,F分别是AD,BC的中点,连接EF.(1)求证:四边形EFCD是菱形;(2)连接AF,若AF=2,∠DEF=60°,则EF的长为;菱形EFCD的面积为.35.如图,Rt△ABC中,∠ABC=90°,D是AC的中点,连接BD,过点C作CE∥BD,过B作BE∥AC,两直线相交于点E.(1)求证:四边形DBEC是菱形;(2)若∠A=30°,BC=2,求四边形DBEC的面积.36.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC、BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E.(1)求证:四边形ABCD是菱形;(2)若AB=5,BD=6,求CE的长.37.如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.(1)求证:四边形ADCF是菱形;(2)若AC=12,AB=16,求菱形ADCF的面积.38.在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE∥DB交AB的延长线于点E,连接OE.(1)求证:四边形ABCD是菱形;(2)若∠DAB=60°,且AB=4,求OE的长.39.如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E 为AD的中点,连接BE.(1)求证:四边形BCDE为菱形;(2)连接AC,若AC平分∠BAD,BC=1,求AC的长.40.如图,平行四边形ABCD的两条对角线相交于O,且AC平分∠DAB.(1)求证:四边形ABCD是菱形;(2)若AC=8,BD=6,试求点O到AB的距离.41.如图,在△ABC中,∠C=90°,BD平分∠ABC交AC于点D,过D作DE∥BC交AB 于点E,DF∥AB交BC于点F,连接EF.(1)求证:四边形BFDE是菱形;(2)若AB=8,AD=4,求BF的长.42.如图,在△ABC中,∠BAC=90°,线段AC的垂直平分线交AC于D点,交BC于E 点,过点A作BC的平行线交直线ED于F点,连接AE,CF.(1)求证:四边形AECF是菱形;(2)若AB=CF,BC=6,求四边形AECF的面积.43.如图,在▱ABCD中,对角线AC,BD交于点O,E是AD上一点,连接EO并延长,交BC于点F.连接AF,CE,EF平分∠AEC.(1)求证:四边形AFCE是菱形;(2)若∠DAC=60°,AC=2,求四边形AFCE的面积.44.如图,在△ABC中,∠ABC=90°,BD为△ABC的中线.BE∥DC,BE=DC,连接CE.(1)求证:四边形BDCE为菱形;(2)连接DE,若∠ACB=60°,BC=4,求DE的长.45.如图,在△ABC中,BD平分∠ABC,BD的垂直平分线分别交AB,BD,BC于点E,F,G,连接DE,DG.(1)求证:四边形BGDE是菱形;(2)若∠ABC=30°,∠C=45°,ED=6,求CG的长.46.如图,在△ABC中,BA=BC,BD平分∠ABC交AC于点D,点E在线段BD上,点F 在BD的延长线上,且DE=DF,连接AE,CE,AF,CF.(1)求证四边形AECF是菱形;(2)若BF=BA,AD=4,DF=2,求BF的长.47.如图,△ABC中,BC=BA,作出△ABC关于AC对称的△ADC.(1)求证:四边形ABCD是菱形;(2)连接BD交AC于点O,取BC中点M,连接OM.若OA=6,S菱形ABCD=48,求OM的长.48.如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E,DF∥AB交BC于点F.(1)求证:四边形BEDF为菱形;(2)如果∠A=90°,∠C=30°,BD=12,求菱形BEDF的边长.49.已知:如图,平行四边形ABCD中,O为对角线AC、BD的交点,BD平分∠ABC.在OA上截取OE=OD,在OC上截取OF=OD.连结DE、EB、BF、FD.(1)求证:▱ABCD是菱形.(2)判断四边形BFDE的形状并证明.50.如图,四边形ABCD中,∠A=∠C=90°,DA=DC,过点D作DE∥BC交AB于点E,DF∥AB交BC于点F.(1)求证:四边形EBFD是菱形;(2)若BF=2,CF=1,求四边形EBFD的面积.51.如图,在▱ABCD中,CD=BD,DE平分∠BDC交BC于点O,交AB的延长线于点E,连接CE.(1)求证:四边形BECD是菱形;(2)如果AB=5,AD=6,求四边形BECD的面积.52.如图,在△ABC中,AB=AC,D,E分别是AB,BC的中点,BF∥DE,EF∥DB.(1)求证:四边形BDEF是菱形;(2)连接DF交BC于点M,连接CD,若BE=4,AC=2,求DM,CD的长.53.如图,在四边形ABCD中,AD=CD,BD⊥AC于点O,点E是DB延长线上一点,OE =OD,BF⊥AE于点F.(1)求证:四边形AECD是菱形;(2)若AB平分∠EAC,OB=3,BE=5,求EF和AD的长.54.如图,在△ABC中,AB=AC,D是BC的中点,点E,F在射线AD上,且DE=DF.(1)求证:四边形BECF是菱形;(2)若AD=BC=6,AE=BE,求菱形BECF的面积.55.如图,在△ABC中,BA=BC,BD平分∠ABC交AC于点D,点E在线段BD上,点F 在BD的延长线上,且DE=DF,连接AE,CE,AF,CF.(1)求证:四边形AECF是菱形;(2)若BA⊥AF,AD=4,BC=4,求BD和AE的长.56.如图,△ABC中,D,E分别是AC,AB的中点,DE=CE,过点B作BF∥CE,交DE的延长线于点F.(1)求证:四边形BCEF是菱形.(2)若BC=2,∠BCE=60°,求菱形BCEF的面积.57.如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E 为AD的中点,连接BE.(1)求证:四边形BCDE为菱形;(2)连接AC,若AC平分∠BAD,BC=4,求AC的长.58.在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC 交BE的延长线于点F.(1)证明四边形ADCF是菱形;(2)若AC=4,AB=5,求菱形ADCF的面积.59.如图,在▱ABCD中,BC=2AB,点E、F分别是BC、AD的中点,AE、BF交于点O,连接EF,OC.(1)求证:四边形ABEF是菱形;(2)若AB=4,∠ABC=60°,求OC的长.60.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.(1)求证:四边形ABCD是菱形;(2)若AB=2,BD=4,求OE的长.。
九年级数学第一章 证明综合检测题 试题

滕西中学九年级数学?第一章 证明?检测题班级 姓名 考号 一.选择题〔每一小题4分〕1.如图,△ABC 为直角三角形,∠C =90°,假设沿图中虚线剪去∠C ,那么∠1+∠2等于( )A .270°B .135°C .90°D . 315° 2.如图,将一个等腰直角三角形按图示方式依次翻折,假设DE =a ,那么下 列说法正确的个数有〔 〕①DC ′平分∠BDE ;②BC 长为a )22( ;③△B C ′D 是等腰三角形;④△CED 的周长等于BC 的长。
A . 1个; B .2个; C .3个; D .4个。
3.如图,△ABC 中,∠C=90°,AC=BC ,AD 平分∠CAB 交BC 于点D ,DE ⊥AB ,垂足为E ,且AB=6cm ,那么△DEB 的周长为〔 〕A .4cm B .6cm C .8 cm D .10cm 4.如图,EA ⊥AB ,BC ⊥AB ,EA=AB=2BC ,D 为AB 中点,有以下结论:(1)DE=AC ;(2)DE ⊥AC ;(3)∠CAB=30°;(4)∠EAF=∠ADE 。
其中结论正确的选项是〔 〕 A .(1),(3) B .(2),(3) C .(3),(4) D .(1),(2),(4)〔3〕 〔4〕 〔7〕 〔8〕 〔10〕 5、直角三角形的周长是4+26,斜边上中线长为2,那么这个三角形的面积为〔 〕 A.5B.2C.45ABC ABCB C DECE6等腰三角形底边长为7,一腰上的中线把其周长分成两局部的差为3,那么腰长是〔 〕 A .4 B .10 C .4或者10 D .以上答案都不对7.如图,△ABC 中,AB=AC ,点D 在AC 边上,且BD=BC=AD ,那么∠A 的度数为〔 〕 A .30° B .36° C .45° D .70°8.如图,在Rt △ABC 中,∠ACB=90°,AB=2BC ,在直线BC 或者AC 上取一点P ,使得△PAB 为等腰三角形,那么符合条件的点P 一共有〔 〕 A .1个 B .2个 C .3个 D .4个9.边长为2的等边三角形的内有一点0,那么0到三角形各边的间隔 之和为 ( ) A .3 B .23 C .2 D .4310.如图,△ABC 中,AD ⊥BC 于D ,BE ⊥AC 于E ,AD 与BE 相交于F ,假设BF=AC ,那么∠ABC 的大小是〔 〕A .40°B .45°C .50°D .60° 二.填空题〔每一小题4分〕 1.在△ABC 中,∠A =∠B =21∠C ,那么△ABC 是__________三角形。
平行线的有关证明综合题1
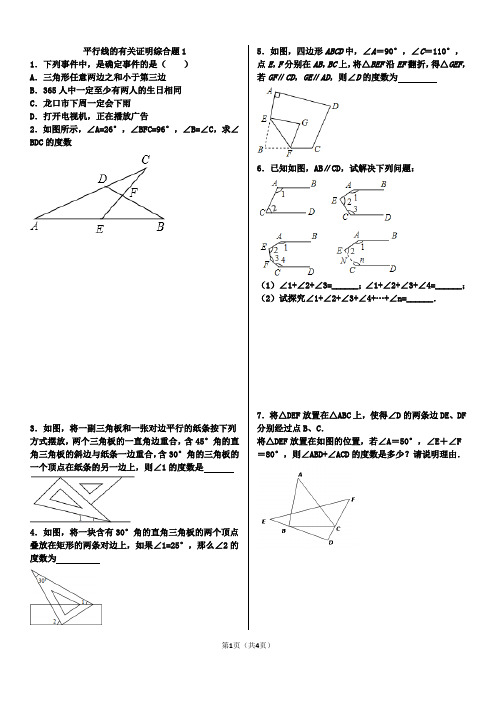
平行线的有关证明综合题11.下列事件中,是确定事件的是( ) A .三角形任意两边之和小于第三边 B .365人中一定至少有两人的生日相同 C .龙口市下周一定会下雨 D .打开电视机,正在播放广告2.如图所示,∠A=26°,∠BFC=96°,∠B=∠C ,求∠BDC 的度数3.如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含45°角的直角三角板的斜边与纸条一边重合,含30°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是4.如图,将一块含有30°角的直角三角板的两个顶点叠放在矩形的两条对边上,如果∠1=25°,那么∠2的度数为5.如图,四边形ABCD 中,∠A =90°,∠C =110°,点E ,F 分别在AB ,BC 上,将△BEF 沿EF 翻折,得△GEF ,若GF ∥CD ,GE ∥AD ,则∠D 的度数为6.已知如图,AB ∥CD ,试解决下列问题:(1)∠1+∠2+∠3=______;∠1+∠2+∠3+∠4=______; (2)试探究∠1+∠2+∠3+∠4+…+∠n=______.7.将△DEF 放置在△ABC 上,使得∠D 的两条边DE 、DF 分别经过点B 、C .将△DEF 放置在如图的位置,若∠A =50°,∠E +∠F =80°,则∠ABD+∠ACD 的度数是多少?请说明理由.7.如图,将△ABC的一角折叠,使点C落在△ABC内一点(1)若∠1=38°,∠2=26°,求∠C的度数;(2)试通过第(1)问,直接写出∠1、∠2、∠C三者之间的关系.9.如图所示,有一块直角三角板DEF(足够大),其中∠EDF=90°,把直角三角板DEF放置在锐角△ABC上,三角板DEF的两边DE、DF恰好分别经过B、C.(1)若∠A=40°,则∠ABC+∠ACB=______°,∠DBC+∠DCB=______°∠ABD+∠ACD=______°.(2)若∠A=55°,则∠ABD+∠ACD=______°.(3)请你猜想一下∠ABD+∠ACD与∠A所满足的数量关系______.10.已知关于x,y的方程组与方程x+y=3的解相同,求k的值11.某车间有60名工人,每人每天能生产螺栓16个或螺母24个,设有x名工人生产螺栓,y名工人生产螺母,每天生产的螺栓和螺母按1:2配套,求x,y值12.如图,直线y=x+1与直线y=mx﹣n相交于点M(1,b),则关于x,y 的方程组的解为.13.如图,△ABC中,AD⊥BC于点D,∠BAD=∠CAD,BE平分∠ABC交AC于E ,∠C=42°,若点F为线段BC 上的一点,当△EFC为直角三角形时,∠BEF的度数为.14.长方形ABCD中放置了6个形状、大小都相同的小长方形,所标尺寸如图所示,则图中阴影部分的面积是cm2.15.已知甲、乙两人从相距18km的两地同时出发,相向而行,1h相遇,如果甲比乙先走h,那么在乙出发后h两人相遇,求甲、乙两人的速度.16.如图,已知∠1=20°,∠2=25°,∠A=55°,求∠BDC的度数.21D17.如图,已知BE、CE分别是△ABC的内角、外角的平分线,∠A=40°,求∠E的度数.21、已知,如图,AB∥ED. 猜想∠B,∠D,∠BCD之间有什么等量关系?并证明你的结论.A BCE 22、已知,如图,AB∥ED. 猜想∠B,∠D,∠BCD之间有什么等量关系?并证明你的结论.A BCDE23、已知,如图,AB∥ED. 猜想∠B,∠D,∠BCD之间有什么等量关系?并证明你的结论.BE。
初中证明题综合题复习

初三综合题1.已知:如图,在直角梯形ABCD 中,∠ABC=90○,AD ∥BC ,DE ⊥AC 于点F ,交BC 于点G ,交AB 的延长线于点E ,且AE=AC 。
(1) 求证:AB=AF(2) 若∠ACB=30○,连接AG ,判断四边形AGCD 是什么特殊的四边形?并证明你的结论。
证明:(1)2.大海中有A 和B 两个岛屿,为测量它们之间的距离,在海岸线PQ 上点E 处测得 ∠AEP =74°,∠BEQ =30°;在点F 处测得∠AFP =60°,∠BF Q =60°,EF =1km .(1)判断AB 、AE 的数量关系,并说明理由;(2)求两个岛屿A 和B 之间的距离(结果精确到0.1km ).(参考数据:3≈1.73, sin74°≈0.96,cos74°≈0.28,tan74°≈3.49,sin76°≈0.97,cos76°≈0.24)3.烟台大樱桃闻名全国,今年又喜获丰收,某大型超市从大樱桃生产基地购进一批大樱桃,运输过程中质量损失5%。
(超市不负责其他费用)(1)如果超市把售价在进价的基础上提高5%,超市是否亏本?通过计算说明:(2)如果超市要获得至少20%的利润,那么大樱桃售价最低应提高百分之几?(结果精确到0.1%)4.已知:如图埋在直角梯形ABCD 中,∠ABC=90°,AD ∥BC ,DE ⊥AC 于点F ,交BC 于点G ,交AB 的延长线于点E ,且AE=AC 。
⑴求证:AB=AF⑵若∠ACB=30°,连接AG ,判断四边形AGCD 是什么特殊的四边形?并证明你的结论。
ABEFQP第195.儿童节前,某玩具商店根据市场调查,用2500元购进一批儿童玩具,上市后很快脱销,接着又用4500元购进第二批这种玩具,所购数量是第一批数量的1.5倍,但每套进价多了10元.(1)求第一批玩具每套的进价是多少元?(2)如果这两批玩具每套售价相同,且全部售完后总利润不低于25%,那么每套售价至少是多少元?解:6.某公司经过市场调研,决定从明年起对甲、乙两种产品实行“限产压库”,要求这两种产品全年共生产200件,这200件的总产值P(元)不低于1万元,且不超过1.1万元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
证明题综合训练
1、如图1,矩形MNPQ中,点E、F、G、H分别在NP、PQ、QM、MN上,若,
则称四边形EFGH为矩形MNPQ的反射四边形.图2、图3、图4中,四边形ABCD为矩形,且AB=4,BC=8.
理解与作图:
(1)在图2、图3中,点E、F分别
在BC、CD边上,试利用正方形网格
在图上作出矩形ABCD的反射四边形
EFGH.
计算与猜想:
(2)求图2、图3中反射四边形EFGH
的周长,并猜想矩形ABCD的反射四
边形的周长是否为定值?
启发与证明:
(3)如图4,为了证明上述猜想,小明同学尝试延长GF交BC的延长线于M,试利用小明同学给我们的启发,再添加适当的辅助线证明(2)中的猜想.
2、如图,在中,是边上的一点,是的中点,过点作的平行线交的延长线于,且,连结.
(1)求证:是的中点.(4分)
(2)如果,试判断四边形的形状,并证明你的结论.
3、如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连结BF。
(1)BD与CD有什么数量关系,并说明理由;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由。
2
4、如图,四边形ABCD 是矩形,对角线AC 、BD 相交于点O ,BE ∥AC 交DC 的延长线于
点E .
(1)求证:BD=BE ;
(2)若ÐD BC =30°,BO =4,求四边形ABED 的面积.
5、已知:如图,为平行四边形的对角线,为
的中点,于点,与分别交于点
. 求证 :(1)
⑵
6、已知,如图,在平行四边形ABCD 中,延长DA 到点E ,延长BC 到点F ,使得AE =CF ,连接EF ,分别交AB ,CD 于点M ,N ,连接DM ,BN .
(1)求证:△AEM ≌△CFN ;
(2)求证:四边形BMDN 是平行四边形.
7、如图,分别以Rt △ABC 的直角边AC 及斜边AB 向外作等边△ACD 、等边△ABE .已知∠BAC =30º,EF ⊥AB ,垂足为F ,连结DF .
(1)求证:AC =EF ;
(2)求证:四边形ADFE 是平行四边形.
8、已知:如图,在△ABC中,∠ACB=90°,点E为AB的中点,过点E作ED ⊥BC于D,F在DE的延长线上,且AF=CE,若AB=6,AC=2,求四边形ACEF
的面积.
11、已知:如图,四边形ABCD是平行四边形,DE//AC,交BC的延长线于
点E,EF⊥AB于点F,求证:AD=CF。
12、已知:如图,在□ABCD中,对角线AC交BD于点O,四边形AODE
是平行四边形。
求证:四边形ABOE、四边形DCOE都是平行四边形。
13、已知如图:在ABCD中,延长AB到E,延长CD到F,使BE=DF,则线段AC与EF是否互相平分?说明理由.
14、如图,菱形ABCD的对角线的长分别为2和5,P是对角线AC上任一点(点P不与点A、C重合),且PE∥BC交于E,PF∥CD交于AD于F,则阴
影部分的面积为____________。
4
15、矩形ABCD 的对角线相交于点O ,DE ∥AC ,CE ∥DB ,CE 、DE 交于点E ,
请问:四边形DOCE 是什么四边形?请说明理由.
16、如图,在四边形ABCD 中,AD ∥BC ,对角线AC 的中点为O ,过点O 作AC
的垂线分别与AD 、BC 相交于点E 、F ,连接AF .求证:AE=AF .
17、已知正方形ABCD 的边长为4,E 是CD 上一个动点,以CE 为一条直角边作等腰直角三角形CEF ,连结BF 、BD 、FD .
(1)BD 与CF 的位置关系是 .
(2)①如图1,当CE =4(即点E 与点D 重合)时,△BDF 的面积为 .
②如图2,当CE =2(即点E 为CD 的中点)时,△BDF 的面积为 .
③如图3,当CE =3时,△BDF 的面积为 .
(3)如图4,根据上述计算的结果,当E 是CD 上任意一点时,请提出你对△BDF
面积与正方形ABCD 的面积之间关系的猜想,并证明你的猜想.
18、已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.
①求证:CD=AN;
②若∠AMD=2∠MCD,求证:四边形ADCN是矩形.
19、如图,已知是等边三角形,点是延长线上的一个动点,以
为边作等边,过点作的平行线,分别交的延长线于点
,联结.
(1)求证:;
(2)如果BC =CD,判断四边形的形状,并说明理由.
20、如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是
对角线,过A点作AG∥DB交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90,求证四边形DEBF是菱形.
21、如图,在□ABCD中,∠ABD的平分线BE交AD于点E,∠CDB
的平分线DF交BC于点F,连接BD.
(1)求证:△ABE≌△CDF;
(2)若AB=DB,求证:四边形DFBE是矩形.
6
22、已知:如图10,D 是△ABC 的边AB 上一点,CN ∥AB ,DN 交AC 于点
M ,MA=MC .
(1)求证:CD=AN ;
(2)若∠AMD=2∠MCD ,求证:四边形ADCN 是矩形.
23、如图,△ABC 中,AB=AC ,AD 、AE 分别是∠BAC 和∠BAC 和外角的平分线, BE
⊥AE .
(1)求证:DA ⊥AE ;
(2)试判断AB 与DE 是否相等?并证明你的结论.
24、如图,在四边形ABCD 中,AD ∥BC ,对角线AC 的中点为O ,过点O 作
AC 的垂直平分线分别与AD 、BC 相交于点E 、F ,连接AF 。
求证:AE=AF 。
25、如图,等腰梯形ABCD 中,AB =CD ,AD ∥BC ,点E 、F 在BC 上,且BE =CF .
(1)求证:AE =DF ;
(2)若AD =EF ,试证明四边形AEFD 为矩形.
26、如图,AD∥FE,点B、C在AD上,∠1=∠2,BF=BC
⑴求证:四边形BCEF是菱形
⑵若AB=BC=CD,求证:△ACF≌△BDE
27、如图,将□ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
⑴求证:△ABF≌△ECF
⑵若∠AFC=2∠D,连接AC、BE.求证:四边形ABEC是矩形.
28、如图,△ABC是边长为1的等边三角形.取BC边中点E,作ED∥AB,EF
∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1,作E1D1∥FB,E1F1
∥EF,得到四边形E1D1FF1,它的面积记作S2.照此规律作下去,则S2011= .
29、如图,菱形ABCD的对角线的长分别为2和5,P是对角线AC上任一点(点P
不与点A、C重合),且PE∥BC交AB于E,PF∥CD交AD于F,则阴影部分的面
积是_______.
30、根据如图所示的(1),(2),(3)三个图所表示的规律,依次下去第个图中平行四边形的个数是()
A.3n B.3n(n+1) C.6n D.6n(n+1)
8
31、如图,DE 是△ABC 的中位线,M 是DE 的中点,CM 的延长线交AB 于点N ,则△DMN ∶四边形ANME 等于( )
A 、1∶5
B 、1∶4
C 、2∶5
D 、2∶7
32、已知:△ABC 中,AB =10
⑴如图①,若点D 、E 分别是AC 、BC 边的中点,求DE 的长;
⑵如图②,若点A 1、A 2把AC 边三等分,点B 1、B 2把BC 边三等分,求A 1B 1+A 2B 2的值; ⑶如图③,若点A 1、A 2、…、A 10把AC 边十一等分,点B 1、B 2、…、B 10把BC 边十一等分。
根据你所发现的规律,直接写出A 1B 1+A 2B 2+…+A 10B 10的结果。
33、已知:如图,在△ABC 中,AB =AC ,AD ⊥BC ,垂足为点D ,AN 是△ABC 外角∠CAM 的平分线,CE ⊥AN ,垂足为点E ,
(1)求证:四边形ADCE 为矩形;
(2)当△ABC 满足什么条件时,四边形ADCE 是一个正方形?并给出证明.
34、如图,△ABC 中,,以△ABC 的三边为边,在BC 的同一侧分别作三个等边三角形,即△ABD 、△BCE 、△ACF 。
求证:四边形ADEF 是矩形。
