第七章 气体动理论
第7章气体动理论习题解答

第7章 气体动理论7.1基本要求1.理解平衡态、物态参量、温度等概念,掌握理想气体物态方程的物理意义及应用。
2.了解气体分子热运动的统计规律性,理解理想气体的压强公式和温度公式的统计意义及微观本质,并能熟练应用。
3.理解自由度和内能的概念,掌握能量按自由度均分定理。
掌握理想气体的内能公式并能熟练应用。
4.理解麦克斯韦气体分子速率分布律、速率分布函数及分子速率分布曲线的物理意义,掌握气体分子热运动的平均速率、方均根速率和最概然速率的求法和意义。
5.了解气体分子平均碰撞频率及平均自由程的物理意义和计算公式。
7.2基本概念1 平衡态系统在不受外界的影响下,宏观性质不随时间变化的状态。
2 物态参量描述一定质量的理想气体在平衡态时的宏观性质的物理量,包括压强p 、体积V 和温度T 3 温度宏观上反映物体的冷热程度,微观上反映气体分子无规则热运动的剧烈程度。
4 自由度确定一个物体在空间的位置所需要的独立坐标数目,用字母i 表示。
5 内能理想气体的内能就是气体内所有分子的动能之和,即2iE RT ν= 6 最概然速率速率分布函数取极大值时所对应的速率,用p υ表示,p υ==≈其物理意义为在一定温度下,分布在速率p υ附近的单位速率区间内的分子在总分子数中所占的百分比最大。
7 平均速率各个分子速率的统计平均值,用υ表示,υ==≈8 方均根速率各个分子速率的平方平均值的算术平方根,用rms υ表示,rms υ==≈ 9 平均碰撞频率和平均自由程平均碰撞频率Z 是指单位时间内一个分子和其他分子平均碰撞的次数;平均自由程λ是每两次碰撞之间一个分子自由运动的平均路程,两者的关系式为:Zυλ==或λ=7.3基本规律1 理想气体的物态方程pV RT ν=或'm pV RT M=pV NkT =或p nkT =2 理想气体的压强公式23k p n ε=3 理想气体的温度公式21322k m kT ευ==4 能量按自由度均分定理在温度为T 的平衡态下,气体分子任何一个自由度的平均动能都相等,均为12kT 5 麦克斯韦气体分子速率分布律 (1)速率分布函数()dNf Nd υυ=表示在速率υ附近单位速率区间内的分子数占总分子数的百分比或任一单个分子在速率υ附近单位速率区间内出现的概率,又称为概率密度。
气体动理论

第十三章 气体动理论本章从理想气体的微观组成出发,假以统计性假设,推出理想气体的压强和温度公式,揭示了压强和温度的本质;提出了理想气体内能的概念,介绍了理想气体能量按自由度均分原理;阐述了理想气体的麦克斯韦速率分布率。
这称为气体动理论。
气体动理论的产生和发展凝聚了众多物理学家的智慧和心血。
早在1678年,胡克就提出了气体压强是由大量气体分子与器壁碰撞的结果的观点。
之后,在1738年,伯努利根据这一观点推导出压强公式,并且解释了玻意耳定律。
1744年,俄国的罗蒙诺索夫提出了热是分子运动表现的观点。
在19世纪中叶,气体动理论经克劳修斯、麦克斯韦和玻耳兹曼的努力而有了重大发展。
1858年,克劳修斯提出气体分子平均自由程的概念并导出相关公式。
1860年,麦克斯韦指出,气体分子的频繁碰撞并未使它们的速度趋于一致,而是达到稳定的分布,导出了平衡态气体分子的速率分布和速度分布。
之后,麦克斯韦又建立了输运过程的数学理论。
1868年,玻耳兹曼在麦克斯韦气体分子速率分布律中又引进重力场。
第一节理想气体状态方程一、状态参量1.状态参量概念如何描述系统的冷热变化规律,这就需要一些物理量。
假设气体的质量为 m ,其宏观状态一般可以用气体的压强p 、体积V 和温度T 三个物理量来描述。
如果在热力学过程中伴随着化学反应,还需要物质的量、摩尔质量 、物质各组分的质量等物理量来描述。
如果热力学系统处于磁场中,还需要电场强度E 、电极化矢量P 、磁场强度H 和磁化强度M 等物理量来描述。
选择几个描写系统状态的参量,称为状态参量。
2.状态参量分类按照不同的划分标准,状态参量可作如下划分:(1)按状态参量描写系统的性质划分可分为:V P E P H M几何参量:描述系统的空间广延性。
如体积 。
力学参量:描述系统的强度。
如压强 。
化学参量:描述系统的化学组分。
如各组分的质量,物质的量。
电磁参量:描述系统的电磁性质。
如电场强度 ,电极化强度 ,磁场强度 ,磁化强度 。
大学物理气体动理论

气体分子之间的相互作用力产生的势能, 由于气体分子之间的距离非常大,因此气 体分子的势能通常可以忽略不计。
分子动理论的基本假设
分子之间无相互作用力
气体分子之间不存在相互作用的力,它们之间只 存在微弱的范德华力。
分子运动速度服从麦克斯韦分布
气体分子的运动速度服从麦克斯韦分布,即它们 的速度大小和方向都是随机的。
分子碰撞的统计规律
分子碰撞的随机性
01
气体分子之间的碰撞是随机的,碰撞事件的发生和结果都是随
机的。
分子碰撞频率
02
单位时间内分子之间的碰撞次数与分子数密度、分子平均速度
和分子碰撞截面有关。
碰撞结果的统计规律
03
碰撞后分子的速度方向和大小的变化遵循一定的统计规律,可
以用概率密度函数来描述。
热现象的统计解释
大学物理气体动理论
• 引言 • 气体动理论的基本概念 • 气体动理论的基本定律 • 气体动理论的统计解释 • 气体动理论的应用 • 结论
01Biblioteka 引言主题简介气体动理论
气体动理论是通过微观角度研究气体 运动状态和变化的学科。它以分子运 动论为基础,探究气体分子运动的规 律和特性。
分子模型
气体动理论中,将气体分子视为弹性 小球,相互之间以及与器壁之间发生 弹性碰撞。通过建立分子模型,可以 更好地理解气体分子的运动特性。
对未来研究的展望
随着科学技术的发展,气体动理 论仍有很大的发展空间和应用前
景。
未来研究可以进一步探索气体分 子间的相互作用和气体在极端条 件下的行为,例如高温、高压或
低温等。
气体动理论与其他领域的交叉研 究也将成为未来的一个重要方向, 例如与计算机模拟、量子力学和
大学物理第六版第七章气体动理论基础总结

大学物理第六版第七章气体动理论基础总结
1. 气体分子模型:气体由大量无限小的分子组成,分子之间几乎没有相互作用,分子运动是无规则的。
2. 气体分子的运动:气体分子具有随机热运动,并遵循牛顿力学定律。
分子的速度和方向是随机的。
3. 气体的压强:气体分子与容器壁的碰撞会产生压强。
气体的压强与分子的速度、分子间平均自由程、分子总数等因素有关。
4. 理想气体状态方程:理想气体状态方程描述了气体的状态。
PV = nRT,其中P为气体压强,V为体积,n为物质的量,R为气体常数,T为温度。
5. 分子平均动能:气体分子的平均动能与气体的温度成正比。
分子平均动能与分子质量无关。
6. 温度和热力学温度:温度是描述物体热平衡状态的物理量。
热力学温度是温度的定量度量,它与分子平均动能的平方成正比。
7. 气体分子的速率分布:气体分子的速率分布服从麦克斯韦-波尔兹曼分布。
分子速率分布与温度相关,高温下分子速率分布图会变得更加平坦。
总结起来,第七章主要介绍了气体动理论的基本概念和定律,包括气体分子的运动、气体压强、气体状态方程、分子平均动能、温度和速率分布等内容。
大学物理学第7章气体动理论(Temperature)

4
研究对象:大量无规则热运动气体分子构成的系统 研究内容:物质与冷热有关的性质及这些性质的变化
对象特点:单个分子 无序性、偶然性、遵循力学规律 整体(大量分子):服从统计规律
mvx
l2
立直角坐标系。
a
O
-mvx
X
(2)选任意一个分子a作为研
究对象,求其对A1面的压力 Z
l1
分子“a” 的速度:
分子“ a”碰撞器壁A1面一次所受的冲量:
由牛顿第三定律可知,器壁A1面受分子碰撞一次所受的冲量:
23
分子“ a”相继碰撞器壁A1面两次所用的时间为: 单位时间内,分子“ a”与器壁A1面碰撞的次数为: 单位时间内,分子“ a”对器壁A1面的冲量即冲力为:
如压强 p、体积 V、温度 T等 .
平衡态:一定量的气体,在不受外界的影响下, 经过一 定的时间, 系统达到一个稳定的, 宏观性质不随时间变 化的状态称为平衡态 .(理想状态)
平衡态的特点
( p,V ,T )
p
*( p,V ,T )
o
V
1)单一性(
处处相等);
2)物态的稳定性---与时间无关;
3)自发过程的终点;
(2)在平衡态下,分子按位置的分布是均匀的 n dN N
则各处分子数密度是相同的。
dV V
(3) 分子速度指向任何方向的机会是一样, 或分子速度按方向的分布是均匀的。
vx2 vy2 vz2
各个方向的速度分量的平均值相等。
vx 2
v1 x 2
07 气体动理论答案(2016)

一.选择题 1、[ A ](基础训练2)下列各式中哪一式表示气体分子的平均平动动能?(式中M 为气体的质量,m 为气体分子质量,N 为气体分子总数目,n 为气体分子数密度,N A 为阿伏加得罗常量)(A)pV M m 23. (B) pV M Mmol23.(C) npV 23. (D) pV N M M A 23mol . 【解】:根据气体分子的平均平动动能:201322k m v kT ε==,==N p nkT kT V ,而=M N m,则333==222k pV mkT pV N Mε= 2、[ B ](基础训练5)一定量某理想气体按pV 2=恒量的规律膨胀,则膨胀后理想气体的温度(A) 将升高. (B) 将降低. (C) 不变. (D)升高还是降低,不能确定. 【解】:由于pV 2=恒量,又=pVC T,则有=VT C ',因此,体积膨胀,温度将降低。
3、[ C ](基础训练8)设某种气体的分子速率分布函数为f (v ),则速率分布在v 1~v 2区间内的分子的平均速率为 (A)⎰21d )(v v v v v f . (B) 21()d v v v vf v v ⎰.(C)⎰21d )(v v v v v f /⎰21d )(v v v v f . (D)⎰21d )(v v v v v f /()d f v v ∞⎰.【解】:速率分布在v 1~v 2区间内的分子的速率总和:⎰21d )(v v v v v f N ,速率分布在v 1~v 2区间内的分子数总和:21()d v v Nf v v ⎰,因此速率分布在v 1~v 2区间内的分子的平均速率:222111222111()()()()v v v v v v v v v v v v vdN vNf v dv vf v dvv dNNf v dvf v dv===⎰⎰⎰⎰⎰⎰4、[ B ](基础训练9)一定量的理想气体,在温度不变的条件下,当体积增大时,分子的平均碰撞频率Z 和平均自由程λ的变化情况是:(A) Z 减小而λ不变. (B)Z 减小而λ增大. (C) Z 增大而λ减小. (D)Z 不变而λ增大.【解】:根据分子的平均碰撞频率:n v d Z22π=,和平均速率公式:v =,在温度不变的条件下,平均速率不变,当体积增大时,分子数密度Nn V=减小,平均碰撞频率Z 减小。
物理学教程(第二版)上册课后答案7

物理学教程(第二版)上册课后答案7第七章 气体动理论7 -1 处于平衡状态的一瓶氦气和一瓶氮气的分子数密度相同,分子的平均平动动能也相同,则它们( )(A) 温度,压强均不相同 (B) 温度相同,但氦气压强大于氮气的压强(C) 温度,压强都相同 (D) 温度相同,但氦气压强小于氮气的压强分析与解 理想气体分子的平均平动动能23k /kT =ε,仅与温度有关.因此当氦气和氮气的平均平动动能相同时,温度也相同.又由物态方程nkT p =,当两者分子数密度n 相同时,它们压强也相同.故选(C).7-2 三个容器A 、B 、C 中装有同种理想气体,其分子数密度n 相同,方均根速率之比()()()4:2:1::2/12C 2/12B 2/12A =v v v ,则其压强之比C B A ::p p p 为( )(A) 1∶2∶4 (B) 1∶4∶8(C) 1∶4∶16 (D) 4∶2∶1 分析与解 分子的方均根速率为M RT /3=2v ,因此对同种理想气体有3212C 2B 2A ::::T T T =v v v ,又由物态方程nkT ρ,当三个容器中分子数密度n 相同时,得16:4:1::::321321==T T T p p p .故选(C).7 -3 在一个体积不变的容器中,储有一定量的某种理想气体,温度为0T 时,气体分子的平均速率为0v ,分子平均碰撞次数为0Z ,平均自由程为0λ ,当气体温度升高为04T 时,气体分子的平均速率v 、平均碰撞频率Z 和平均自由程λ分别为( ) (A)04,4,4λλZ Z ===0v v (B) 0022λλ===,,Z Z 0v v (C) 00422λλ===,,Z Z 0v v (D) 00,2,4λλ===Z Z 0v v 分析与解 理想气体分子的平均速率M RT π/8=v ,温度由0T 升至04T ,则平均速率变为0v 2;又平均碰撞频率v n d Z 2π2=,由于容器体积不变,即分子数密度n 不变,则平均碰撞频率变为0Z 2;而平均自由程n d 2π21=λ,n 不变,则λ也不变.因此正确答案为(B).7 -5 有一个体积为35m 1001⨯.的空气泡由水面下m050.深的湖底处(温度为C 0.4o )升到湖面上来.若湖面的温度为C 017o .,求气泡到达湖面的体积.(取大气压强为Pa 10013150⨯=.p )分析 将气泡看成是一定量的理想气体,它位于湖底和上升至湖面代表两个不同的平衡状态.利用理想气体物态方程即可求解本题.位于湖底时,气泡内的压强可用公式gh pp ρ+=0求出, 其中ρ为水的密度( 常取33m kg 100.1-⋅⨯=ρ).解 设气泡在湖底和湖面的状态参量分别为(p 1 ,V 1 ,T 1 )和(p 2 ,V 2 ,T 2 ).由分析知湖底处压强为gh ρp gh ρp p+=+=021,利用理想气体的物态方程222111T V p T V p =可得空气泡到达湖面的体积为()3510120121212m 1011.6-⨯=+==T p V T gh p T p V T p V ρ 7 -6 一容器内储有氧气,其压强为Pa 100115⨯.,温度为27 ℃,求:(1)气体分子的数密度;(2) 氧气的密度;(3) 分子的平均平动动能;(4) 分子间的平均距离.(设分子间均匀等距排列)分析 在题中压强和温度的条件下,氧气可视为理想气体.因此,可由理想气体的物态方程、密度的定义以及分子的平均平动动能与温度的关系等求解.又因可将分子看成是均匀等距排列的,故每个分子占有的体积为30d V=,由数密度的含意可知n V /10=,d 即可求出.解 (1) 单位体积分子数325m 1044.2⨯==kTp n (2) 氧气的密度3-m kg 30.1/⋅===RTpM V m ρ (3) 氧气分子的平均平动动能J 102162321k -⨯==./kT ε(4) 氧气分子的平均距离m 10453193-⨯==./n d通过对本题的求解,我们可以对通常状态下理想气体的分子数密度、平均平动动能、分子间平均距离等物理量的数量级有所了解.7-7 2.0×10-2 kg 氢气装在4.0×10-3 m 3 的容器内,当容器内的压强为3.90×105Pa 时,氢气分子的平均平动动能为多大?分析 理想气体的温度是由分子的平均平动动能决定的,即23k /kT =ε.因此,根据题中给出的条件,通过物态方程pV =Mm 'RT ,求出容器内氢气的温度即可得kε. 解 由分析知氢气的温度mRMpV T =,则氢气分子的平均平动动能为J 1089.3232322k -⨯='==Rm pVMk kT ε7 -8 某些恒星的温度可达到约1.0 ×108K ,这是发生聚变反应(也称热核反应)所需的温度.通常在此温度下恒星可视为由质子组成.求:(1) 质子的平均动能是多少? (2) 质子的方均根速率为多大?分析 将组成恒星的大量质子视为理想气体,质子可作为质点,其自由度 i =3,因此,质子的平均动能就等于平均平动动能.此外,由平均平动动能与温度的关系2/32/2kT m =v,可得方均根速率2v .解 (1) 由分析可得质子的平均动能为 J 1007.22/32/152k-⨯===kT m v ε (2) 质子的方均根速率为1-62s m 1058.13⋅⨯==mkT v 7 -9 日冕的温度为2.0 ×106K ,所喷出的电子气可视为理想气体.试求其中电子的方均根速率和热运动平均动能.解 方均根速率16e 2s m 105.93-⋅⨯==m kT v 平均动能J 10142317k -⨯==./kT ε7-10 在容积为2.0 ×10-3 m 3 的容器中,有内能为6.75 ×102J 的刚性双原子分子某理想气体.(1)求气体的压强;(2) 设分子总数为5.4×1022个,求分子的平均平动动能及气体的温度.分析 (1) 一定量理想气体的内能RT i M m E 2=,对刚性双原子分子而言,i =5.由上述内能公式和理想气体物态方程pV =νRT 可解出气体的压强.(2)求得压强后,再依据题给数据可求得分子数密度,则由公式p =nkT 可求气体温度.气体分子的平均平动动能可由23k /kT ε=求出.解 (1) 由RT i E 2ν=和pV =νRT 可得气体压强 Pa 1035.125⨯==iVE p (2) 分子数密度n =N/V ,则该气体的温度()()K 1062.3//2⨯===nk pV nk p T 气体分子的平均平动动能为J104972321k -⨯==./kT ε 7 -11 当温度为0C 时,可将气体分子视为刚性分子,求在此温度下:(1)氧分子的平均动能和平均转动动能;(2)kg 100.43-⨯氧气的内能;(3)kg 100.43-⨯氦气的内能.分析 (1)由题意,氧分子为刚性双原子分子,则其共有5个自由度,其中包括3个平动自由度和2个转动自由度.根据能量均分定理,平均平动动能kT 23kt =ε,平均转动动能kT kT ==22kr ε.(2)对一定量理想气体,其内能为RT i M mE 2'=,它是温度的单值函数.其中i 为分子自由度,这里氧气i =5、氦气i =3.而m '为气体质量,M 为气体摩尔质量,其中氧气13mol kg 1032--⋅⨯=M ;氦气13mol kg 100.4--⋅⨯=M .代入数据即可求解它们的内能.解 根据分析当气体温度为T=273 K 时,可得(1)氧分子的平均平动动能为J 107.52321kt -⨯==kT ε 氧分子的平均转动动能为J 108.32221kr -⨯==kT ε (2)氧气的内能为J 10 7.1J 27331.8251032100.42233⨯=⨯⨯⨯⨯⨯='=--RT i M m E (3)氦气的内能为J 10 3.4J 27331.823100.4100.42333⨯=⨯⨯⨯⨯⨯='=--RT i M m E 7 -12 已知质点离开地球引力作用所需的逃逸速率为gr v 2=,其中r 为地球半径.(1) 若使氢气分子和氧气分子的平均速率分别与逃逸速率相等,它们各自应有多高的温度;(2) 说明大气层中为什么氢气比氧气要少.(取r =6.40 ×106 m) 分析 气体分子热运动的平均速率M RTπ8=v ,对于摩尔质量M 不同的气体分子,为使v 等于逃逸速率v ,所需的温度是不同的;如果环境温度相同,则摩尔质量M 较小的就容易达到逃逸速率. 解 (1) 由题意逃逸速率gr 2=v ,而分子热运动的平均速率M RTπ8=v .当v v = 时,有RMrg T 4π= 由于氢气的摩尔质量13H mol kg 10022--⋅⨯=.M,氧气的摩尔质量12O mol kg 10232--⋅⨯=.M ,则它们达到逃逸速率时所需的温度分别为 K10891K,101815O 4H 22⨯=⨯=..T T (2) 根据上述分析,当温度相同时,氢气的平均速率比氧气的要大(约为4倍),因此达到逃逸速率的氢气分子比氧气分子多.按大爆炸理论,宇宙在形成过程中经历了一个极高温过程.在地球形成的初期,虽然温度已大大降低,但温度值还是很高.因而,在气体分子产生过程中就开始有分子逃逸地球,其中氢气分子比氧气分子更易逃逸.另外,虽然目前的大气层温度不可能达到上述计算结果中逃逸速率所需的温度,但由麦克斯韦分子速率分布曲线可知,在任一温度下,总有一些气体分子的运动速率大于逃逸速率.从分布曲线也可知道在相同温度下氢气分子能达到逃逸速率的可能性大于氧气分子.故大气层中氢气比氧气要少.7-13 容积为1 m 3 的容器储有1 mol 氧气,以v =10-1s m ⋅的速度运动,设容器突然停止,其中氧气的80%的机械运动动能转化为气体分子热运动动能.试求气体的温度及压强各升高了多少. 分析 容器作匀速直线运动时,容器内分子除了相对容器作杂乱无章的热运动外,还和容器一起作定向运动.其定向运动动能(即机械能)为221mv .按照题意,当容器突然停止后,80%定向运动动能转为系统的内能.对一定量理想气体内能是温度的单值函数,则有关系式:T R M m v m E Δ25%8021Δ2'=⋅'=成立,从而可求ΔT .再利用理想气体物态方程,可求压强的增量.解 由分析知T R M m m E Δ2528.0Δ2⋅'='=v ,其中m '为容器内氧气质量.又氧气的摩尔质量为12m ol kg 1023--⋅⨯=.M ,解得ΔT =6.16 ×10-2 K当容器体积不变时,由pV =M mRT 得Pa 51.0ΔΔ==T VRM m p7-14 有N 个质量均为m 的同种气体分子,它们的速率分布如图所示.(1) 说明曲线与横坐标所包围的面积的含义;(2) 由N 和0v 求a 值;(3) 求在速率0v /2到30v /2 间隔内的分子数;(4) 求分子的平均平动动能.题 7-14 图分析 处理与气体分子速率分布曲线有关的问题时,关键要理解分布函数()v f 的物理意义.()υd d N Nf =v ,题中纵坐标()v v d /d N Nf =,即处于速率v 附近单位速率区间内的分子数.同时要掌握()v f 的归一化条件,即()1d 0=⎰∞v v f .在此基础上,根据分布函数并运用数学方法(如函数求平均值或极值等),即可求解本题.解 (1) 由于分子所允许的速率在0 到20v 的范围内,由归一化条件可知图中曲线下的面积()N Nf S v ==⎰v v d 020即曲线下面积表示系统分子总数N .(2 ) 从图中可知,在0 到0v 区间内,()0/v v v a Nf =;而在0 到20v 区间,()αNf =v .则利用归一化条件有vv v vv ⎰⎰+=0020d d v v a a N(3) 速率在0v /2到30v /2间隔内的分子数为12/7d d Δ2/3000N a a N =+=⎰⎰v v v v v v v(4) 分子速率平方的平均值按定义为()v v f v v v d /d 0222⎰⎰∞∞==N N故分子的平均平动动能为20220302k 3631d d 212100v v v v v v v v v v m N a N a m m =⎥⎦⎤⎢⎣⎡+==⎰⎰ε 7-15 一飞机在地面时,机舱中的压力计指示为Pa100115⨯.,到高空后压强降为Pa101184⨯..设大气的温度均为27.0℃.问此时飞机距地面的高度为多少?(设空气的摩尔质量为2.89 ×10-2kg·mol -1) 分析 当温度不变时,大气压强随高度的变化主要是因为分子数密度的改变而造成.气体分子在重力场中的分布满足玻耳兹曼分布.利用地球表面附近气压公式()kT mgh p p /ex p 0-=,即可求得飞机的高度h .式中p 0 是地面的大气压强. 解 飞机高度为()()m 1093.1/ln /ln 300⨯===p p MgRT p p mg kT h7 -16 目前实验室获得的极限真空约为1.33×10-11Pa ,这与距地球表面1.0×104km 处的压强大致相等.而电视机显像管的真空度为1.33×10-3Pa ,试求在27 ℃时这两种不同压强下单位体积中的分子数及分子的平均自由程.(设气体分子的有效直径d =3.0×10-8cm)解 理想气体分子数密度和平均自由程分别为n =k T p ;pd kT λ2π2=,压强为1.33×10-11Pa 时,-39m 1021.3/⨯==kT p nm 108.7π282⨯==pd kT λ 从λ的值可见分子几乎不发生碰撞.压强为1.33×10-3Pa 时,3-17m 1021.3⨯==kT p n ,m 8.7π22==pd kT λ此时分子的平均自由程变小,碰撞概率变大.但相对显像管的尺寸而言,碰撞仍很少发生. 7-17 在标准状况下,1 cm 3中有多少个氮分子?氮分子的平均速率为多大?平均碰撞次数为多少?平均自由程为多大?(已知氮分子的有效直径m 1076.310-⨯=d )分析 标准状况即为压强Pa 10013.15⨯=p ,温度K 273=T .则由理想气体物态方程nkT p =可求得气体分子数密度n ,即单位体积中氮分子的个数.而氮气分子的平均速率、平均碰撞次数和平均自由程可分别由公式MRTv π8=,n v d Z 2π2=和nd 2π21=λ直接求出.解 由分析可知,氮分子的分子数密度为325m 1069.2-⨯==kTpn 即3cm 1中约有191069.2⨯个.氮气的摩尔质量为M =28 ×10-3kg·mol -1,其平均速率为MRTv π8==454 1s m -⋅则平均碰撞次数为-192s 107.7π2⨯==n v d Z平均自由程为m 106π2182-⨯==nd λ 讨论 本题主要是对有关数量级有一个具体概念.在通常情况下,气体分子平均以每秒几百米的速率运动着,那么气体中进行的一切实际过程如扩散过程、热传导过程等好像都应在瞬间完成,而实际过程都进行得比较慢,这是因为分子间每秒钟上亿次的碰撞导致分子的自由程只有几十纳米,因此宏观上任何实际过程的完成都需要一段时间.7-18 在一定的压强下,温度为20℃时,氩气和氮气分子的平均自由程分别为9.9×10-8m 和27.5×10-8m.试求:(1) 氩气和氮气分子的有效直径之比;(2) 当温度不变且压强为原值的一半时,氮气分子的平均自由程和平均碰撞频率. 分析 ( 1 ) 气体分子热运动的平均自由程()p d kT nd 22π2/π21==λ,因此,温度、压强一定时,平均自由程2/1d λ∝.(2) 当温度不变时,平均自由程p λ/1∝.解 (1) 由分析可知67.1//r 22r A N N A ==λλd d(2) 由分析可知氮气分子的平均自由程在压强降为原值的一半时,有m 105.527N N22-⨯=='λλ而此时的分子平均碰撞频率22222N N N N N 2π/8λM RT λZ ='=v将T =293K ,M N2 =2.8×10-2kg·mol -1代入,可得-18N s 1056.82⨯=Z。
第7章 气体动理论

碰后折回来需用的时间:
2x vx
t vxt 2x / vx 2x
一个分子在 t 时间内碰撞器壁的总冲量:
I1
2mv
x
t
2x / v x
mv
2 x
t
x
(3) N 个分子在 t 时间内
碰撞器壁的总冲量:
IN
N
mv
2 ix
t
x i 1
m x
t
N i 1
v2 ix
y
A1
vy
m
(4) I Ft P F / s
kr
1 2
mvc2x
1 2
mvc2y
1 2
mvc2z
1 2
J yc2y
1 2
J zc2z
1 2
J x c2x
2.能量均分定理(Boltzmann 假设)
t
1 2
mv2
3 2
kT
v
2 x
v
2 y
v
2 z
1 3
v2
1 2
mv
2 x
1 2
m
v
2 y
1 2
mvz2
1 ( 1 mv2 ) 32
1 kT 2
φ
确定刚体转轴的方位: 需要二个自由度(α,β);
β P(x,y,z)
α
γo
X
确定刚体绕转轴转过的角度, Z
需要一个自由度(φ);
刚体位置的确定共需要六个自由度。
3.气体分子模型自由度 ①单原子分子: 如氦原子 He 需要三个平动自由度 i=t=3;
②刚性双原子分子: 如氧气分子
O2
质心需要三个平动自由度;两原子连线方位需要
第7章 气体分子动理论

a
z
x
b
Δt 时间内与 A1 发生碰撞的次数:
t 2a vix
t 2a
vix
Δt 时间内分子 i 对 A1 的冲量:
t 2a
vix
2vix
t
a
vi2x
Δt 时间内所有分子对A1 的冲量:
I
N i 1
t
a
vi2x
t
a
N
vi2x
i 1
z
y
vix A1 c
x
O
b
a
F
p S A1
I t bc
k
玻耳兹曼常数
速率在 v ~ v + dv 间的分子数占总分子数的比率:
dNv f (v)dv 4 ( )3/ 2 v2ev2 / 2kT dv
N
2kT
速率在 v1 ~ v2 间的分子 数占总分子数的比率:
Nv v2 f (v)dv
N
v1
归一化条件:
0 f (v)dv 1
dv
v1 v2
abc
N i 1
vi2x
V
N
vi2x
i 1
p
V
N
vi2x
i 1
vx2
1 N
N
vi2x
i 1
其中 n N V
p
N
V
vx2
n vx2
1 3
n v 2
为气体分子数密度
1 v2
2
理想气体压强公式: p 2 n
3
§7.3 温度的微观本质
一、温度与理想气体分子平均平动动能的关系
p nkT p 2 n
第7章 气体分子动理论
大学物理(科学出版社,熊天信、蒋德琼、冯一兵、李敏惠)第七、八章习题解

第七章 气体动理论7–1 一定量的理想气体,在保持温度T 不变的情况下,使压强由P 1增大到P 2,则单位体积内分子数的增量为_________________。
解:由nkT P =,可得单位体积内分子数的增量为kTP P kT P n 12-=∆=∆ 7–2 一个具有活塞的圆柱形容器中贮有一定量的理想气体,压强为P ,温度为T ,若将活塞压缩并加热气体,使气体的体积减少一半,温度升高到2T ,则气体压强增量为_______,分子平均平动动能增量为_________。
解:设经加热和压缩后气体的压强为P ',则有TV P T PV 22/⨯'=所以P P 4='压强增量为P P P P 3=-'=∆由分子平均平动动能的计算公式kT 23=ε知分子平均平动动能增量为kT 23。
7–3 从分子动理论导出的压强公式来看,气体作用在器壁上的压强,决定于 和 。
解:由理解气体的压强公式k 32εn P =,可知答案应填“单位体积内的分子数n ”,“分子的平均平动动能k ε”。
7–4 气体分子在温度T 时每一个自由度上的平均能量为 ;一个气体分子在温度T 时的平均平动动能为 ;温度T 时,自由度为i 的一个气体分子的平均总动能为 ;温度T 时,m /M 摩尔理想气体的内能为 。
解:kT 21;kT 23;kT i2;RT i M m 27–5 图7-1所示曲线为处于同一温度T 时氦(原子量4)、氖(原子量20)和氩(原子量40)三种气体分子的速率分布曲线,其中曲线(a )是__________气分子的速率分布曲线; 曲线(c )是__________气分子的速率分布曲线。
解:在相同温度下,对不同种类的气体,分子质量大的,速率分布曲线中的最慨然速率p v 向量值减小方向迁移。
可得图7-1中曲线(a )是氩气分子的速率分布曲线,图7-1中曲线(c )是氦气分子的速率分布曲线。
7–6 声波在理想气体中传播的速率正比于气体分子的方均根速率。
2013第七章气体动理论答案 (1)

一. 选择题1. (基础训练2)[ C ]两瓶不同种类的理想气体,它们的温度和压强都相同,但体积不同,则单位体积内的气体分子数n ,单位体积内的气体分子的总平动动能(E K /V ),单位体积内气体的质量?的关系为: (A) n 不同,(E K /V )不同,??不同. (B) n 不同,(E K /V )不同,??相同. (C) n 相同,(E K /V )相同,??不同. (D) n 相同,(E K /V )相同,??相同. 【解】: ∵nkT p =,由题意,T ,p 相同∴n 相同;∵kTn V kTNVE k2323==,而n ,T 均相同∴V E k 相同 由RT M m pV =得m pMV RTρ==,∵不同种类气体M 不同∴ρ不同 2. (基础训练6)[ C ]设v 代表气体分子运动的平均速率,p v 代表气体分子运动的最概然速率,2/12)(v 代表气体分子运动的方均根速率.处于平衡状态下理想气体,三种速率关系为(A) p v v v ==2/12)( (B) 2/12)(v v v <=p(C) 2/12)(v v v <<p(D)2/12)(vvv>>p【解】:最概然速率:pv==算术平均速率:()v vf v dv∞==⎰2()v f v dv∞==⎰3.(基础训练7)[B]设图7-3所示的两条曲线分别表示在相同温度下氧气和氢气分子的速率分布曲线;令()2Opv和()2H p v分别表示氧气和氢气的最概然速率,则(A)图中a表示氧气分子的速率分布曲线;()2Opv/()2H p v=4.(B)图中a表示氧气分子的速率分布曲线;()2Opv/()2H p v=1/4.(C)图中b表示氧气分子的速率分布曲线;()2O p v/()2H p v=1/4.(D)图中b表示氧气分子的速率分布曲线;()2O p v/()2H p v= 4.【解】:理想气体分子的最概然速率pv=pv越小,又由氧气的摩尔质量33210(/)M kg mol-=⨯,氢气的摩尔质量3210(/)M kg mol-=⨯,可得()2Opv/()2H p v=1/4。
第七章 气体动理论(答案)

一、选择题[ C ]1、(基础训练2)两瓶不同种类的理想气体,它们的温度和压强都相同,但体积不同,则单位体积内的气体分子数n ,单位体积内的气体分子的总平动动能(E K /V ),单位体积内气体的质量ρ的关系为:(A) n 不同,(E K /V )不同,ρ 不同.(B) n 不同,(E K /V )不同,ρ 相同. (C) n 相同,(E K /V )相同,ρ 不同.(D) n 相同,(E K /V )相同,ρ 相同. 【提示】① ∵nkT p =,由题意,T ,p 相同,∴n 相同;② ∵kT n V kTNV E k 2323==,而n ,T 均相同,∴V E k 相同;③ RT M MpV mol=→RT pM V M mol ==ρ,T ,p 相同,而mol M 不同,∴ρ不同。
[ B ]2、(基础训练7)设图示的两条曲线分别表示在相同温度下氧气和氢气分子的速率分布曲线;令()2O p v 和()2H p v 分别表示氧气和氢气的最概然速率,则(A) 图中a 表示氧气分子的速率分布曲线;()2O p v /()2H p v = 4.(B) 图中a 表示氧气分子的速率分布曲线;()2O p v /()2H p v =1/4.(C) 图中b表示氧气分子的速率分布曲线;()2O p v /()2H p v =1/4.(D) 图中b表示氧气分子的速率分布曲线;()2O p v /()2H p v = 4.【提示】①最概然速率p v =p v 越小,故图中a 表示氧气分子的速率分布曲线;②23,3210(/)mol O M kg mol -=⨯, 23,210(/)mol H M kg mol -=⨯,得()()22Ov v p p H14=[ C ]3、(基础训练8)设某种气体的分子速率分布函数为f (v ),则速率分布在v 1~v 2区间内的分子的平均速率为(A)⎰21d )(v v v v v f . (B) 21()d v v v vf v v ⎰.(C)⎰21d )(v v v v v f /⎰21d )(v v v v f . (D)⎰21d )(v v v v v f /0()d f v v ∞⎰ .【提示】① f (v )d v ——表示速率分布在v 附近d v 区间内的分子数占总分子数的百分比;② ⎰21)(v v dv v Nf ——表示速率分布在v 1~v 2区间内的分子数总和;③21()v v vNf v dv ⎰表示速率分布在v 1~v 2区间内的分子的速率总和,因此速率分布在v 1~v 2区间内的分子的平均速率为22112211()()()()v v v v v v v v vNf v dv vf v dvNf v dvf v dv=⎰⎰⎰⎰[ B ]4、(基础训练9)一定量的理想气体,在温度不变的条件下,当体积增大时,分子的平均碰撞频率Z 和平均自由程λ的变化情况是:(A) Z 减小而λ不变. (B) Z 减小而λ增大. (C) Z 增大而λ减小. (D) Z 不变而λ增大.【提示】①2Z d n =,其中v =不变;N n V =,当V 增大时,n 减小; ∴Z 减小。
气体动理论

2 x
2 y
2 z
1 2
3
二、理想气体的压强公式
对压强的统计解释
气体的压强是由大量分子 在和器壁碰撞中不断给器 壁以力的作用所引起的, 压强是气体分子给容器壁 冲量的统计平均量。
例: 雨点对伞的持续作用。
压强公式的推导:
单位时间内分子a作用在A面上的作用力:
l3 l2 z
y
v a vx A
Fa 2mvx vx 2l
§1 气体的微观图像
一、原子(atom)
“假如在一次浩劫中所有的科学知识都被摧毁, 只剩下一句话留给后代,什么语句可用最少的 词包含最多的信息?我相信,这是原子假说,即 万物由原子(微小粒子)组成.”——费曼
道尔顿确立 了原子概念
原子是化学元素的基本单元
现代的仪器已可以观察和测量原子的大小 以及它们在物体中的排列情况, 例如 X 光 分析仪,电子显微镜, 扫描隧道显微镜等.
引言
气体动理论是从气体分子热运动的观点出发, 运用统计方法研究大量气体分子的宏观性质和统 计规律的科学,它是统计物理学最基本的内容。 本章将根据气体分子模型,研究气体的压强与温 度等宏观性质和分子速率分布规律与能量分布规 律等统计规律,从微观角度揭示这些性质和规律 的本质,同时穿插介绍这些理论的一些应用.
2 x
2 y
2 z
v y
o
vv x
2
2 x
2 y
2 z
v z
12
2 1x
12y
12z
22
2 2x
22y
2 2z
……
N112 N112x N112y N112z N222 N222x N222y N222z
……
07气体动理论2

EH 2 EO 2
i1 / 2 RT = = 1 :1 i2 / 2 RT
对1g氢气和1g氧气来说,都是双原子分子( i = 5), 但它们的摩尔数不同。
EH 2 EO 2
m1 M = 1 m2 M2
i1 RT M 32 2 = 2 = = 16 : 1 i2 RT M 1 2 2
3.理想气体的内能是 温度 的单值函数,平衡态时 能量按 自由度 均分, 理想气体分子的平均动能 , 1mol理想气体分子的内能
p = nkT
可知,V不变,P 要增大。
三、计算题
1.容积为10升的容器中储有 10克的氧气。若气体分子的方均 根速率 v 2 =600m ·s-1,则此气体的温度和压强各为多少? =600m· 由方均根速率公式 解: 解:由方均根速率公式
v2 =
3RT M
3 × 8.31 T ⇒ T = 462K 600 = −3 32 ×10 m pV = RT 由 M m 10 × 10 −3 p= RT = × 8.31× 462 可得 -3 −3 VM 10 × 10 × 32 ×10
B
dN/N表示dv间隔内的分子数占总分子数的百分比。所以 f (v)表示速率分布在v附近的单位速率间隔中的分子数占 总分子数的百分比。
2.若某种气体在温度 T2 时的最概然速率与它在温度 T1 时的 方均根速率相等,那么这两个温度之比 T1 : T2为: ( A )2 : 3 ; ( C )7 : 8 ; 解: 最概然速率 方均根速率 两者相等 可得 (B) 3 : 2 ; (D) 8 : 7
= 1.2 ×105 Pa
2.有N个气体分子,其速率分布如图所示,当 v>2v0时, 粒子的数目为零。求 : (1)常数a;
第七章 气体动理论答案

一.选择题1、(基础训练1)[ C ]温度、压强相同的氦气和氧气,它们分子的平均动能ε和平均平动动能w 有如下关系:(A) ε和w 都相等. (B) ε相等,而w 不相等.(C) w 相等,而ε不相等. (D) ε和w 都不相等. 【解】:分子的平均动能kT i2=ε,与分子的自由度及理想气体的温度有关,由于氦气为单原子分子,自由度为3;氧气为双原子分子,其自由度为5,所以温度、压强相同的氦气和氧气,它们分子的平均动能ε不相等;分子的平均平动动能kT w 23=,仅与温度有关,所以温度、压强相同的氦气和氧气,它们分子的平均平动动能w 相等。
2、(基础训练3)[ C ]三个容器A 、B 、C 中装有同种理想气体,其分子数密度n 相同,而方均根速率之比为()()()2/122/122/12::C B A v v v=1∶2∶4,则其压强之比A p ∶B p ∶C p 为:(A) 1∶2∶4. (B) 1∶4∶8. (C) 1∶4∶16. (D) 4∶2∶1. 【解】:气体分子的方均根速率:MRTv 32=,同种理想气体,摩尔质量相同,因方均根速率之比为1∶2∶4,则温度之比应为:1:4:16,又因为理想气体压强nkT p =,分子数密度n 相同,则其压强之比等于温度之比,即:1:4:16。
3、(基础训练8)[ C ]设某种气体的分子速率分布函数为f (v ),则速率分布在v 1~v 2区间内的分子的平均速率为 (A)⎰21d )(v v v v v f . (B) 21()d v v v vf v v ⎰.(C)⎰21d )(v v v v v f /⎰21d )(v v v v f . (D) ⎰21d )(v v v v v f /0()d f v v ∞⎰ .【解】:因为速率分布函数f (v )表示速率分布在v 附近单位速率间隔内的分子数占总分子数的百分率,所以⎰21d )(v v v v v f N 表示速率分布在v1~v2区间内的分子的速率总和,而21()d v v Nf v v ⎰表示速率分布在v 1~v 2区间内的分子数总和,因此⎰21d )(v v v v v f /⎰21d )(v v v v f 表示速率分布在v 1~v 2区间内的分子的平均速率。
第七章气体动理论7 –4 能量均分定律理想气体内能一自由度
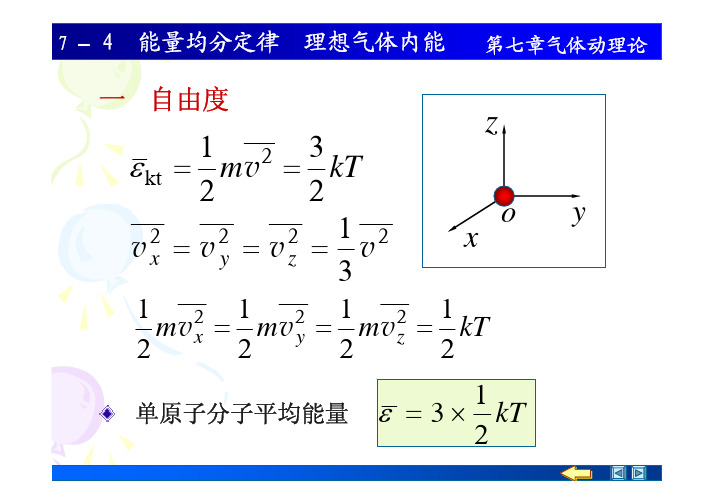
7 – 4能量均分定律 理想气体内能第七章气体动理论一 自由度1 2 3 ε kt = m v = kT 2 2 1 2 2 2 2 vx = v y = vz = v 3zoxy1 2 1 2 1 2 1 m v x = m v y = m v z = kT 2 2 2 21 单原子分子平均能量 ε = 3 × kT 27 – 4能量均分定律 理想气体内能 刚性双原子分子第七章气体动理论分子平均平动动能ε kt1 1 1 2 2 2 = m v Cx + m v Cy + m v Cz 2 2 2分子平均转动动能ε kr1 1 2 2 = Jω y + Jωz 2 27 – 4能量均分定律 理想气体内能 非刚性双原子分子第七章气体动理论分子平均能量ym2* Cε = ε kt + ε kr分子平均振动能量m1xz非刚性分子平均能量1 1 2 2 ε v = µ vCx + kx 2 2ε = ε kt + ε kr + ε v自由度 分子能量中独立的速度和坐标的二次 方项数目叫做分子能量自由度的数目, 简称自由 度,用符号 表示. i7 – 4能量均分定律 理想气体内能 自由度数目第七章气体动理论i=t+r+v平 动 转 动 振 动刚性分子能量自由度分子 自由度t 平动 r3 3 3转动 0 2 3i3 5 6总单原子分子 双原子分子 多原子分子7 – 4能量均分定律 理想气体内能第七章气体动理论二 能量均分定理(玻尔兹曼假设) 气体处于平衡态时,分子任何一个自由度的平均分定理 .1 kT ,这就是能量按自由度 均能量都相等,均为 2分子的平均能量i ε = kT 2三 理想气体的内能和摩尔热容 理想气体的内能 :分子动能和分子内原子间的 势能之和 . 1 mol 理想气体的内能i E = NAε = RT 27 – 4能量均分定律 理想气体内能第七章气体动理论m m i mol 理想气体的内能 E = RT M M 2理想气体内能变化 定体摩尔热容 定压摩尔热容 摩尔热容比m i dE = RdT M 2i CV ,m = R 2i+2 C p,m = R 2 Cp,m i + 2 = γ= CV ,m i。
麦克斯韦气体分子速率分布律

问题3:容器内N个分子的速率分布有什么规律? 1
7-6 麦克斯韦气体分子速率分布律
第七章 气体动理论
对某一分子,其任一时刻的速度具有偶然性,但大 量分子从整体上会出现一些统计规律。
1859年,麦克斯韦用概率论证明了在平衡态下,理 想气体分子速度分布是有规律的,这个规律叫麦克斯 韦速度分布律,若不考虑分子速度的方向,则叫麦克 斯韦速率分布律。
若要将气体分子按速率分布准确描述,则需要将
速率区间尽可能取小,当Δv→0时,即取dv为分子速
率区间,其相应分子数为dNv。
则任一速率区间(v→v+dv)间内的分子出现的概率
为
dN v
N
这概率在各速率区间是不同的,它应是速率 v 的函数,
并且与区间的大小dv成正比
dNv f (v)dv N
其中 f(v) 称为分子的速率分布函数。
第七章 气体动理论
v
4 3/2
a3/2
v3eav2 dv
0
利用积分公式 x e dx 3 ax2 1
0
2a2
v
4
1/2
a3/2
1 2a2
2
a
8kT
m
由
k R NA
和 M NAm
得: v 8kT 8RT 1.59 RT -平均速率
m M
一、速率分布函数
按统计假设,各种速率下的分子都存在,用某一 速率区间内分子数占总分子数的百分比,表示分子按 速率的分布规律。
1.将速率从 0→∞ 分割成很多相等的速率区间。 2
7-6 麦克斯韦气体分子速率分布律
一、速率分布函数
第七章 气体动理论
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 vx
2 vy
2 vz
1 2 v 3
二 理想气体压强公式 设 边长分别为 x、y 及 z 的长方体中有 N 个全 同的质量为 m 的气体分子,计算 A1 壁面所受压强 .
y x
A2
iy
0
A1 z
i
iz
z
ix
x y
1. 一个i分子碰撞一次给A1面的冲量
与A1面碰撞过程中,i分子受的冲量为 :
p
真 空膨 胀
p,V , T
( p ,V , T )
( p,V , T )
o
自发
p,V , T
V
平衡态的特点
p
( p ,V , T )
* ( p ,V , T )
o
1)单一性( 2)物态的稳定性;
V
p -V 图 上的每一点 表示一个平 衡态
p , T 处处相等);
内部气体分子仍在不断运动,发生能 3)动态平衡. 量交换,只是统计平均结果不变,是 一种动态平衡. 平衡条件: (1) 系统与外界在宏观上无能量和物质的交换; (2) 系统的宏观性质不随时间变化。
质点的运动状态 : 位矢r,速度v,加速度a
物态参量: 确定热力学系统状态的物理量 (宏观可测量量)
一 气体的物态参量(宏观量,可测量量)
1. 气体压强 p (力学量) : 单位面积上的正压力. 2 单位 : 1Pa 1N m
p,V , T
2. 体积 V (几何量) : 气体所能到达的最大空间. 单位: 1m3 103 L 103 cm3
N n V
2 x
1 N 2 2 v v ix x, N i 1
2 1 2 p nmv nmv , p n k 3 3 1 分子的平均平动动能 k mv 2
2
压强的物理意义 统计关系式 宏观可测量量
2 p n k 3
ek 微观统计平均值
压强正比于分子数密度 n 和分子平均平动动能 压强只有统计意义。 对少量分子或个别分子上述公式不成立!
小球在伽 尔顿板中的分 布规律 .
7-3
理想气体的压强公式
一 理想气体的微观模型 1)分子可视为质点; 直径
2 1 p n k , k mv 2 3 2
间距
r ~ 10 m, d r
; 2)除碰撞瞬间, 分子间无相互作用力; 短程力
3)弹性质点(碰撞均为完全弹性碰撞);
碰撞之后没有动能损失
ek
压强是大量分子对时间、对面积的统计平均结果 .
7-4 理想气体的平均分子动能和温度的关系 理想气体压强公式
理想气体状态方程
2 p n k 3
p nkT
1 3 2 k m v kT 2 2
宏观可测量量
分子平均平动动能
微观量的统计平均值
处于平衡态时的理想气体,其分子平均平动 动能与气体的温度成正比。
热现象是热运动的宏观表现 热运动是热现象的微观实质
研究对象特征
单个分子 —遵循力学规律, 具有偶然性、无序性 . 整体(大量分子)— 服从统计规律 .
周末的时候,每个同学去食堂吃饭具有偶然性和无序性; 一般11:00-12:00人最多,这就是统计规律
微观量:描述个别分子运动状态的物理量(不可 直接测量),如分子的 m , v 等 .
9
d ~ 10 m,
10
4)分子的运动遵从经典力学的规律 . 单个分子对器壁碰撞特性 : 偶然性 、不连续性. 大量分子对器壁碰撞的总效果 : 恒定的、持续 的力的作用 .
关于分子集体的统计性假设
1. 分子按位置的分布是均匀的 2. 分子各方向运动概率均等
(分子速度按方向的分布是均匀的)
dN N n dV V
kt
1 1 1 2 2 2 m vCx m vCy m vCz 2 2 2
分子平均转动动能
kr
1 1 2 2 J y Jz 2 2
刚性分子平均能量
kt kr
二 能量均分定理(玻尔兹曼假设)
1 kT ,这就是能量按自由度 均能量都相等,均为 2
均分定理 .
研究大量数目的粒子系统, 应用模型假设和统计方法揭示 宏观现象的微观本质.
特点:
1)具有可靠性; 2)知其然而不知其所以然; 3)应用宏观参量 .
特点:
1)揭示宏观现差,不可任意推广 .
热力学
相辅相成
气体动理学
第7章 气体动理论
7-1 平衡态
理想气体的物态方程 热力学第零定律
(分子数目太过巨大,如1m3的空气中,分子数目的量 级是1025,故无法直接测量)
宏观量:表示大量分子集体特征的物理量(可直 接测量), 如 p,V , T 等 .
微观量
统计平均
宏观量
二、热学的两种研究方法 热力学---宏观描述
通过实验和现象的总结, 给出宏观系统的热现象规律.
气体动理学---微观描述
2x vix
2 mvix 3.单位时间内所有N个分子对A1的总冲量 I x x i N
4.单位时间内整个气体对器壁的压强
A1受的平均冲力
N
2 mvix Fx I x x i
2 Fx 1 N mvix m N 2 mN 1 N 2 p vix vix , yz yz i x xyz i 1 V N i 1
分子的平均能量
气体处于平衡态时,分子任何一个自由度的平
i kT 2
转动
0
刚性分子能量自由度
分子 自由度
t 平动 r
3
i
3
总
单原子分子
双原子分子
多原子分子
3
3
2
3
5
6
三 理想气体的内能 理想气体的内能 :所有分子热运动动能和分子 内原子间的势能之和(温度的单值函数) .
i kT 2
1 mol 理想气体的内能
分子力 当r 当
F
r0
时,分
子力主要表现为斥力;
斥 力
r0 ~ 10
10
m
r r0 时,分子力
9
主要表现为引力.
引 力
o
r0
r
分子力
r 10 m , F 0
分子间的作用力是短程力
二
分子热运动 热运动:大量实验事实表明分子在作永不停息的 无规则运动 .
例 : 常温和常压下的氧分子热运动的平均速率v 450m/s, 氧分子每走过 ~ 107 m的路程就要和其他分子发生碰撞. 碰撞频率的量级为 z ~ 1010 次 / s.
N p kT nkT V
n:分子数密度 n N V 单位体积内的气体分子个数
pV NkT
k 1.3810 J K
气体摩尔数
NA 阿伏伽德罗常数
23
1
N N A
则
NA 6.02 1023 mol1
pV NA kT
R 摩尔气体常数
NA k R,
第二篇 热学
(与温度有关的物理规律)
热力学 统计物理
●
人物介绍
迈尔---能量转化思想
T2 卡诺 ---卡诺循环 1 T 1
麦克斯韦 ---麦克斯韦速度分布律 玻尔兹曼---气体动理论
Ludwig Boltzmann, 1844-1906, whose H theorem opened the door to an understanding of the macroscopic world on the basis of molecular dynamics.
温度 T 的物理意义
1 2 3 k m v kT 2 2
1) 温度是分子平均平动动能的量度 (反映热运动的剧烈程度).
k T
2)温度是大量分子的集体表现,个别分子无意义. 3)在同一温度下,各种气体分子平均平动动能均 相等.(与第零定律一致)
7-5 能量均分定量 理想气体的内能
力学中,怎样判断两个物体的运动快慢? 参考系---第三个物体 热学中,怎样判断两个物体的温度是不是相等?
48 C
A B
48 C
绝热板 A B
如果物体 A 和 B 分别与处于确定状态的物体 C 处 于热平衡状态,那么A和B之间也就处于热平衡. 热力学第零定律---温度相同的判定原则
7-2 物质的微观模型 统计规律性 一 分子线度和分子力 分子线度 分子平均间距 例 标准状态下氧分子 ~ 10 分子线度 直径 d 3 1010 m
y mvix A2 0 -mvix x
(-mvix ) - mvix -2mvix
器壁受的冲量为: 2mvix 2. 单位时间内i分子对A1面的冲量
A1
x
i分子相继与A1面碰撞的时间间隔 A1—A2—A1
vix 单位时间内i分子碰撞A1的次数(碰撞频率) 2x 2 v mv ix 单位时间内器壁受的冲量为: I 2mv ix ix ix 2x x
由于混沌效应,单个分子的运动具有偶然性和无序性.
统计规律性:对大量分子而言,在偶然、无序的 分子运动中,包含着一种规律性.
只抛一次,朝上朝下具有偶然性 抛硬币 抛1000次,朝上朝下的概率几乎相等
统计规律 对于由大 量分子组成的 热力学系统从 微观上加以研 究时,必须用 统计的方法 .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
