单缝和圆孔夫琅禾费衍射
圆孔的夫朗和费衍射
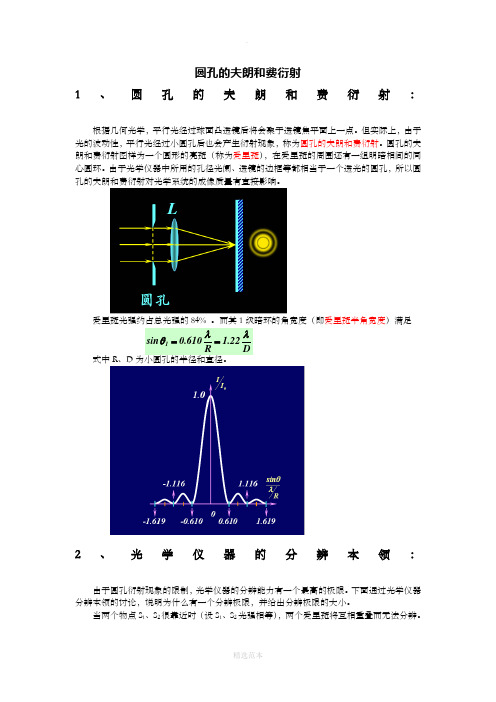
圆孔的夫朗和费衍射1、圆孔的夫朗和费衍射:根据几何光学,平行光经过球面凸透镜后将会聚于透镜焦平面上一点。
但实际上,由于光的波动性,平行光经过小圆孔后也会产生衍射现象,称为圆孔的夫朗和费衍射。
圆孔的夫朗和费衍射图样为一个圆形的亮斑(称为爱里斑),在爱里斑的周围还有一组明暗相间的同心圆环。
由于光学仪器中所用的孔径光阑、透镜的边框等都相当于一个透光的圆孔,所以圆孔的夫朗和费衍射对光学系统的成像质量有直接影响。
爱里斑光强约占总光强的84% 。
而其1级暗环的角宽度(即爱里斑半角宽度)满足D 22.1R610.0sin 1λλθ==式中R 、D 为小圆孔的半径和直径。
2、光学仪器的分辨本领:由于圆孔衍射现象的限制,光学仪器的分辨能力有一个最高的极限。
下面通过光学仪器分辨本领的讨论,说明为什么有一个分辨极限,并给出分辨极限的大小。
当两个物点S 1、S 2很靠近时(设S 1、S 2光强相等),两个爱里斑将互相重叠而无法分辨。
对一个光学仪器来说,若一个点光源产生的爱里斑的中央刚好与另一个点光源产生的爱里斑瑞的1级暗环相重合,这时两个爱里斑重合部分的光强约为单个爱里斑中央光强的80%左右,一般人眼刚好能分辨出这是两个光点的像。
因此,满足上述条件的两个点光源恰好能被该光学仪器所分辨。
这一条件称为瑞利分辨判据。
(见下图)恰能分辨时两光源发出的光线对透镜光心的夹角Δθ 称为最小分辨角,用δθ表示。
由上讨论可知,最小分辨角δθ等于爱里斑的半角宽度θ1:)D 22.1arcsin(1λθδθ==尤其当θ1 ~ 0D 22.1λδθ≈(或称分辨率),用R 表示:λδθ22.1D 1R ==讨论:⑴ 增大透镜的直径D 可提高镜头的分辨率。
光学天文望远镜的镜头孔径可达数米! ⑵ 设r 、d 为爱里斑的半径和直径,则:f 2d f r D 22.1===λδθ即:D f44.2d λ=f D称为镜头的相对孔径(越大越好)。
如照相机镜头上所标示的502:1字样,即表示镜头的焦距mm 50f =,而镜头的孔径mm 25D =。
单缝和圆孔夫琅禾费衍射介绍

三、入射光非垂直入射时光程差的计算
DB BC A
b(si n sin ) b
(中央明纹向下移动)
D
B
C
BC DA
b(si n sin )
(中央明纹向上移动)
D A
b
C
B
例1 在单缝衍射中,=600nm, a=0.60mm, f=60cm, 则(1)中央明纹宽度为多少?(2)两 个第三级暗纹之间的距离?
单缝和圆孔的夫琅 禾费衍射介绍
一、单缝夫琅禾费衍射
1.衍射装置及图样
单缝 透镜
衍射角
f
衍射屏
I
衍射图样
(1) 衍射条纹与狭缝平行。 (2)中心条纹很亮,两侧明条纹对称分布, 亮度减弱。 (3)中央亮斑的宽度为其他亮斑的两倍。
由惠更斯——菲涅耳原理:
单缝处波面看作无穷多个相干波源,屏上一点是 (无穷)多光束干涉的结果。
解 ⑴ 中央明纹的宽度
⑵第三级暗纹在屏上的位置
x3ftanf3a3l0
两个第三级暗纹之间的距离
x6l 7.2mm 0
例2 已知:一雷达位于路边d =15m处,射束与公路成 15°角,天线宽度a =0.20m,射束波长=30mm。
求:该雷达监视范围内公路长L =?
L
d
a
θ1
β
150
解:将雷达波束看成是单缝衍射的0级明纹
越大,
越大,衍射效应越明显.
1
二、用振幅矢量推导光强公式
1.振幅矢量法 将缝AB的面积S等分成N(很大)个等宽的窄带,
每个窄带宽度a/N.
每个窄带发的子波在P点振
A
幅近似相等,设为A1,相邻
窄带所发子波在P点引起的振
14-7单缝和圆孔夫琅禾费衍射

太原理工大学物理系
附: 1)若 BC a sin 2
半波带
将缝分为两个半波带
2
A
A1
p
半波带
B
C
o
/2
相邻两个半波带对应点光程差均是/2,每两个相邻 “半波带”发的光在 P处干涉相消形成暗纹。 若AB恰好被分成偶数个半波带,偶数个“半波带” 发的光在 P处干涉相消形成暗纹。即
2
附: 3) BC a sin n 2
(n整数)
缝分成整数个半波带.
(k 1, 2,3,)
n为偶数, BC a sin 2k
2
暗纹
n为奇数,BC a sin (2k 1)
BC 4) a sin m
2
(k 1, 2,3,) 明纹
平行光斜向下入射,衍射条纹将整体下移; 平行光斜向上入射,衍射条纹将整体上移。 太原理工大学物理系
本例即考点4,即ZP18,25 例1 在单缝衍射中,=600nm, a=0.60mm, 缝 后有一焦距f=60cm透镜, 则(1)中央明纹宽度 为多少?(2)两个第三级暗纹之间的距离? 解 ⑴ 中央明纹的宽度 ⑵第三级暗纹在屏上的位置 x3 f tan f 3 a 两个第三级暗纹之间的距离
4)在单缝衍射中,若使单缝和单缝后透镜分 别稍向上移,则衍射条纹将如何变化?
单缝上移衍射光束向上平移经透镜聚焦 后,位置不变条纹不变 单缝后的透镜上移衍射光束经透镜聚焦后, 位置随之上移条纹向上平移
衍射角
f
I
结论:单缝向上平移时,入射到单缝上,衍射条纹 将如何变化? f
对于屏上其它点P,由 于屏上位置不同,对应的 衍射角就不同,Ap的大小 也不同.
第43讲光的衍射现象单缝夫琅禾费衍射光学仪器的分辨本领

教学要求了解菲涅耳衍射、夫琅和费衍射、惠更斯-菲涅耳原理;理解光的衍射现象;单缝的夫琅和费衍射;圆孔的夫琅和费衍射、瑞利准则、分辨律;理解光学仪器的分辨本领。
15.1光的衍射现象惠更斯——菲涅耳原理15.1.1光的衍射现象及分类在讨论第六章时就已知道:孔隙(或障碍物)的线度与波长的比值直接影响着衍射现象,当孔隙(或障碍物)的线度与波长的数量级接近时,才能观察到明显的衍射现象。
对于光波,由于波长远小于一般孔隙(或障碍物)的线度,所以光的衍射现象通常不易观察到。
而光的直线传播却给人们留下了深刻的印象。
图15-1 光的衍射现象实验在实验室中,采用高亮度的激光或是普通的强点光源,同时屏幕的面积也足够大,则可以将光的衍射现象演示出来。
如图15-1(a)所示,E为屏幕,K是一个可调节的狭缝,S 为一单色点光源。
实验发现,当E,K,S三者位置固定的情况下,光通过宽缝时,是沿直线传播的,如图(a)所示。
若将缝的宽度减小到约10 4m及更小时,缝后几何阴影区的光屏上将出现衍射条纹,如图(b)所示,光斑的亮度也由原来的均匀分布变成一系列的明暗条纹(单色光源)或彩色条纹(白光光源),条纹的边缘也失去了明显的界限,变得模糊不清,这就是光的衍射现象。
衍射系统是由光源、衍射屏和接收屏组成,通常是根据三者相对位置的大小,把衍射现象分为两类。
一类是光源、接收屏(或两者之一)与衍射物之间的距离有限远。
这种衍射叫做菲涅耳衍射(或近场衍射),如图15-2(a )所示。
另一类是光源、接收屏与衍射物的距离都是无限远。
这种衍射称为夫琅禾费衍射(或远场衍射),如图15-2(b )所示。
在实验室中产生的夫琅禾费衍射通常利用两个会聚透镜来实现,如图15-2(c )。
由于夫琅和费衍射在实际应用和理论上都十分重要,而且这类衍射的分析与计算都比菲涅耳衍射简单,因此本节只讨论只讨论夫琅和费衍射。
15.1.2惠更斯——菲涅耳原理惠更斯原理指出:波阵面上的每一点都可以看成是发射子波的新波源,任何时刻子波的包迹即为新的波阵面。
§2.3 夫琅和费单缝、圆孔和矩孔衍射

(3)单缝衍射次最大位置的中心—高级衍射斑 在每两个相邻最小值之间有一次大值,这些次大值的位置可解 超越方程 u tgu 。见图3.3
图3.3超越方程 u
tgu 的图像解
3 sin 10 1.43 u 1.43 10 b 2b u 2.46 5 20 sin 20 2.46 u tgu b 2b 1 u ( j ) j0 sin ( j 1 ) 2 j0 2 b
2 I 0 A0
Ij 0 I j0
(2)
2
A0 2 j 1
3、解析法——光强分布的积分公式 菲涅耳衍射微分公式 近似: ① 在上式中的分母中
K ( ) A( x) i (t kr ) dE p C e dx r
r r0 C / r0 C C 1
sin u 0 u 0 sin 0 0
光强为最大,叠加的各个次波位相差为零,振幅叠加相互加强。
(2)单缝衍射最小值的位置中心(屏上这些点是暗的):
sin u 0 b sin j sin j j b u 0
j 1, 2
(2)分布图样.图3.7所示
2 A12 / A0 0.0175 2 2 A2 / A0 0.0042 2 2 A3 / A0 0.0016
I / I0
R sin
O 0.610
图3.7 夫琅禾费圆孔衍射光强分布
图3.8 夫琅禾费圆孔衍射光强三维分布图
4、爱里斑 爱里斑的半角宽度为:
条纹的位置及强度分布为
(1)
0 0 b sin 0 j sin j b sin 2 j / 2 b (2 j 1) b sin (2 j 1) / 2 sin j 0 2b
单缝和圆孔的夫琅禾费衍射介绍

明纹在屏上的位置
x f sin f (2k 1)
2a
k ax 1 3.5 0.5 3
f 2
第3级明 纹
(2)对应于 p点缝可分成多少个半波带?
asin (2k 1)
2
(23 1) 7
22
7个半波带
(3)将缝宽增加1倍,p 点将变为什么条纹?
y2 = u
-2 - o
··
··
2 u
-2.46π -1.43π
+1.43π +2.46π
u 1.43, 2.46, 3.47,…
相应 asin 1.43, 2.46, 3.47,…
三、入射光非垂直入射时光程差的计算
DB BC
b(sin sin)
“半波带”发的光在 P处干涉相消形成暗纹。
当asin=3/2时,可将缝分为3个半波带.
a
AA
A1
p
B
A2 C
o
B /2
相邻半波带的相对应点光程差均是/2,两个
“半波带”发的光在 P处干涉相消形成暗纹。第 3个“半波带”发的光在 P形成明纹。
一般情况下,可将缝分为k个半波带,当k为偶数 时,p点为暗纹,当k为奇数时,p点为明纹。
例3 在单缝衍射中,若使单缝和透镜分别 稍向上移,则衍射条纹将如何变化? 解:
o
⑴单缝上移衍射光束向上平移经透镜聚焦后, 位置不变条纹不变 ⑵透镜上移衍射光束经透镜聚焦后,位置随之 上移条纹向上平移
例4 在单缝夫琅和费衍射实验中,缝宽a=10,缝 后透镜焦距 f =40cm , 试求第一级明纹的角宽度,线 宽度以及中央明纹的线宽度。
2—3 夫琅和费单缝衍射

3、狭缝上所有次波在P 的叠加
积分过程见(附录2-1) b sinu u sin A A A0 sincu 令 p 0 u
2 sin u 2 2 2 2 Ap A0 A sin c u 0 2 u
I p I 0 sinc 2 u P点光强随θ的分布
16
三、强度公式的讨论 1、最大最小位置:
y2 = u
-
·
-2.46
·
-1.43
· 0
0
+1.43
+2.46
解得 :
相应 :
u 1.43, 2.46, 3.47, „
b sin 1.43 , 2.46 , 3.47 ,„
19
前几个次最大的位置
次最大序号 次最大位置 相对强度
u
1.43 2.46
(k 1, 2, ) 暗纹 (k 1, 2, ) 明纹 中央明纹
•正、负号表示衍射条纹对称分布于中央明纹的两侧 •对于任意衍射角,单缝不能分成整数个半波带,
在屏幕上光强介于最明与最暗之间。
方法一、菲涅耳半波带法
I / I0
明纹宽度
中央明条纹的角宽度 为中央两侧第一暗条纹 之间的区域:
3.47
4.48
sin
3 2b 5 2.46 b 2b 7 3.47 b 2b 9 4.48 b 2b 1.43 b
I I 0
1 2 3 4
0.047
0.017
0.008
0.005
1 sin k0 k 2 b
b
0
sin (2k 1)
2b
基于MATLAB的矩孔、单缝、圆孔夫琅和费衍射概诉

课程设计任务书学生姓名:专业班级:指导教师:工作单位:信息工程学院题目: 夫琅和费矩孔、单缝、圆孔衍射图样一、设计目的了解MA TLAB软件的基本知识,基本的程序设计,软件在高等数学和工程数学中的应用,学会使用软件进行数值计算和控制工程中的应用。
二、设计内容和要求1.绘制弗朗禾费矩孔、单缝和圆孔衍射图样,可以是二维的或三维的,也可以两种都有。
改变矩孔、单缝和圆孔的参数,比较衍射条纹的变化。
2. 学习Matlab语言的概况和Matlab语言的基本知识。
3.学习Matlab语言的程序设计。
三、初始条件计算机;Matlab软件。
四、时间安排1、2015年01月19日,任务安排,课设具体实施计划与课程设计报告格式的要求说明。
2、2015年01月20日,查阅相关资料,学习Matlab语言的基本知识,学习MATLAB语言的应用环境、调试命令,绘图功能函数等。
3、2015年01月21日至2015年01月22日,Matlab课程设计制作和设计说明书撰写。
4、2015年01月23日,上交课程设计成果及报告,同时进行答辩。
指导教师签名:2015年01 月19日系主任(或负责教师)签名:2015年01 月19日目录摘要 (I)1.设计的内容及要求 (1)1.1设计的目的 (1)1.2设计任务要求 (1)2.设计原理及设计思路 (1)2.1夫琅和费干涉理论 (1)2.1.1夫琅和费圆孔衍射 (2)2.1.2夫琅和费矩孔衍射 (2)2.1.3夫琅和费单缝衍射 (2)2.2设计思路 (3)3.仿真及分析 (4)4.心得和体会 (8)参考文献 (8)摘要物理光学理论较为复杂抽象,实验现象的演示对条件要求高。
采用MATLAB7.0强大的函数作图功能对矩孔、单缝、圆孔的夫琅和费衍射进行模拟,建立直观形象并且精确完整的理论模型,并附上程序代码,将干涉理论联系起来,分析衍射和干涉的本质。
从而加深对夫琅和费原理、概念、和图像的理解。
通过使用MATLAB编写程序,不仅理解了物理思想,而且了解了运用软件解决物理问题的方法。
夫琅禾费衍射实验报告

夫琅禾费衍射和菲涅尔衍射班级:物理1903 姓名:王高文 学号:41721176 同组人员:修为轩实验目的:测量单缝衍射的光强分布,验证光强分布理论;观察几类夫琅禾费衍射现象,加深对光的衍射现象和理论的理解。
实验原理:A 单缝衍射光强分布 202sin uI I u ,其中sin a u;a 为单缝宽度, 为光波波长,为衍射角。
当 =0时,u=0,此时光强为最大,这是中央零级亮条纹,称为主级强。
当sin ka时,u k ,这时 I =0,出现暗条纹。
实际上 很小,可以认为sin ,即暗条纹在ka的位置出现。
其他的亮条纹所在位置:sin 1.43, 2.46 3.47a a a,,,,次级强相对于主级强的强度分别为0.047,0.017,0.008...I I B 矩形孔衍射光强分布 22022sin sin I ,I,其中sin sin a b a b;,a 和b 为矩形孔边长, 为光波波长,a 和b 为衍射角。
C 圆孔衍射光强分布 2102J u I I u,式中, 1J u 为一阶贝塞尔函数;2sin a u;a 为圆孔半径, 为光波波长, 为衍射角。
根据贝塞尔函数的性质,当u=0时,即 =0时, 00I I I .这说明圆孔衍射的中心始终是一个亮点,并且强度取最大值,其他各级次强度极大值位置:'''123sin 0.819,sin 1.333,sin 1.84a a a,,,极小值位置123sin 0.610,sin 1.116,sin 1.619a a a,,,次级强相对主级强的相对强度分别为0.0175,0.0042,0.0016...I I D 双缝或双孔夫琅禾费衍射设狭缝宽度或圆孔半径为a,两狭缝或两圆孔的间距为d,双缝 220sin ()cos u I I u ,式中sin sin a b;, 为光波波长,为衍射角。
双孔 2120'2cos 'J I I,式中 1'J 为一阶贝塞尔函数;2sin 'a,sin b, 为光波波长, 为衍射角。
4-5 单缝和圆孔的夫琅禾费衍射

3) 任意相邻的半波带上的对应点的子波光程差为 , 2 π
,所以达到P点时将完全相互抵消。
4
R
A1
A
L
P
Q
BC a sin
B
A2
C
o
/2
讨论: 1) 半波带数为整数,且为偶数时
a sin 2k
2
k
干涉相消(暗纹)
2) 半波带数为整数,且为奇数时
a sin ( 2k 1)
15
I I0
1.43 2.46 a a
3
1.43
a
2
2.46
a
a
3
a
2
a
a
o
a
a
sin
16
二、圆孔的夫琅禾费衍射
中央是个明亮的圆斑,外围是一组同心的明环 17 和暗环。中央明区集中了光能的83.8%。
L2 D f
p
0 0
d
第一暗环对应的衍射角0称为艾里斑的半角 宽 (它标志着衍射的程度) ,理论计算得:
2
k
x kf a
sin k a
x k a sin a f
6
第一暗纹距中心的距离: 线度: x1 f
a
角度:
sin 1
a
a a (2)中央明纹:主极大(k = 1两暗纹之间)
第一暗纹的衍射角
1 arcsin
0 ,相当于到达屏上O点的各衍射子波的相位 相同,产生了最大的光强,是零级衍射斑的中心。
单孔衍射和圆孔衍射

显然,菲涅尔衍射是普遍情况,夫琅禾费衍射只是它的特例。
大学物理实验中心
实验目的:
1.观察单缝衍射和圆孔衍射现象; 2.学习掌握单缝和圆孔衍射规律,证明极小值
的位置与理论值一致。
大学物理实验中心
大学物理实验中心
数据记录:
表1 0.08mm单缝衍射
狭缝到屏幕的距离(D)=_________ (激光波长λ=532 × 10-6mm)
第一级(m=1)
第二级(m=2)
第三级(m=3)
条纹宽度(暗纹)
中心到暗条纹的距离y
计算狭缝宽度
|a - a0|/a0×100%
大学物理实验中心
数据记录:
表2 a=0.20mm圆孔衍射
圆孔到屏幕的距离(D)=_________ (激光波长λ=532 × 10-6mm)
第一级(m=1)
第二级(m=2)
第三级(m=3)
暗环直径(mm) (每级测3次)
暗环半径ym(mm)
ym=(直径3平均值) ×(1/2)
计算圆孔直径d(mm) (公式①②③)
|a - a0|/a0×100%
大学物理实验中心
数据处理:
1.利用各级别干涉条纹的数据,依据公式
d m D (m 1,2,3)
y
分别计算出狭缝距离d ,并计算出相对误差(表一)。
2.利用数据求出各级次的暗环直径平均值,再求出其相应的暗环半径 ymi
利用公式①、②、③分别计算出圆孔的直径d1,d2,d3;并求出其相对 误差。
大学物理实验中心
2.圆孔衍射 当光通过圆孔发生圆孔衍射,衍射图样是一组明暗相同 的圆环。中央明亮的圆斑——艾里斑,它集中了衍射光能的 83.5%。 如图,第一级暗环所对应的衍射角
单缝衍射和圆孔衍射
O
B
P
b
f
b 2
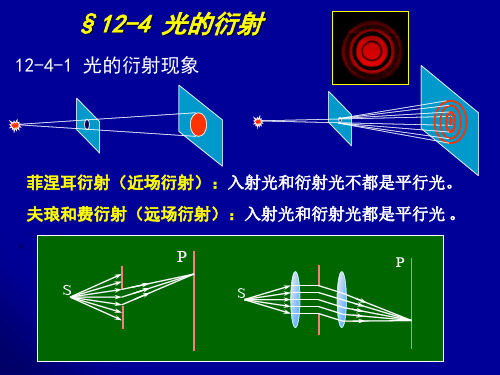
菲涅耳半波带:相邻两波带发出的子波之光
程差正好是 2 。
半波带个数与衍射角的关系: N b sin /2
•在衍射角 方向,狭缝被分成了偶数个
半波带,屏幕上p 点对应暗纹。
•在衍射角 方向,狭缝被分成了奇数个
半波带,屏幕上p点对应明纹。
1、夫琅禾费单缝衍射方程: b sin k
生振动的叠加。(菲聂耳提出“次波相干叠加”,对次波的振幅和相位做了补
充)
假设:S是某时刻的波前,dS是S上的任一面元
1. 次波在P点的振幅 A与距离 r 成反比。
2.振幅 A与面积元dS成正比。
3. 振幅 A 随 角增加而减小。
4.次波在p点的相位由光程差nr决定。
dS
n
S
r
dE CK() dS cos(t 2nr ) 振动方程
2
2b
3 x1 f tg f 2b
f
12-4-5 圆孔衍射 光学仪器的分辨本领
爱里斑:圆孔衍射的中央亮斑,其上集中了全部 衍射光能的84%。
D
艾里斑的半角宽度:
1.22 D
结论:圆孔直径 D 越小,艾里斑越大,衍射效果 越明显。
一般光学仪器中的透镜和光阑都相当于透光的圆孔,衍射效 应将直接影响成像质量。 虽然镜头的尺寸远比可见光波长大,衍射效应不明显,但要 想充分体现物体的精细结构还是会受到衍射效应的制约。 分辨两个靠的很近的物点的像,可用瑞利判据 瑞利判据:如果一个点像的衍射图样的中央最亮处刚好与另一 个点像的衍射图样的第一级暗环相重合,这时这两个物点恰好 能被这一光学仪器所分辨。
矩孔,单缝圆孔的弗朗禾费衍射
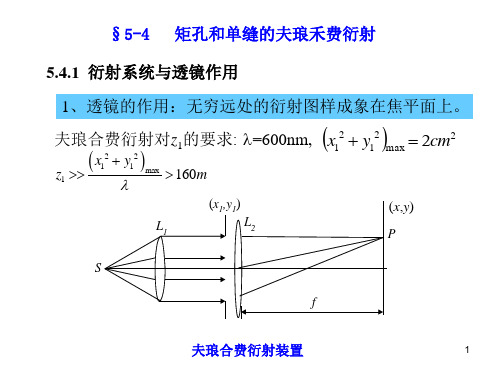
积分式表示孔径上各点子波的相干叠加。叠 加结果取决于各点发出的子波与中心点发出 子波的位相差。
5
夫琅合费衍射与傅立叶变换(1) 傅里叶变换的分类
傅里叶 变换
时间域 变换
空间域 变换
f(t)
(时间)频谱f(ω)
时间空间频率 可互相转化
f (z) (空间)频谱f (k)
f (x,y)
角谱f (kx,ky)
a
C
2 a
b
2 b
exp iklx1 my1 dx1dy1
22
16
E~ x, y
a
C
2 a
b
2 b
exp iklx1 my1 dx1dy1
22
a
b
C
2 a
exp
ik
lx1
dx1
2 b
exp
ik
my1
dy1
2
2
sin kla sin kmb Cab 2 2
kla kmb 2 2
2 2 r l r l f
v ky k y 1 y 1 y . y方向上的空间频率
2 2 r l r l f
f(x,y) 可 表 示 为 空 间 频 率 (u,v) 连 续 的 基 元 函 数
F(u,v)exp[i2(ux+vy)]的线性叠加; F(u,v)是这些基元函数
的权重,叫做函数f(x,y)的傅立叶变换或空间频谱.
E
x1
,
y1
exp
ik
x1
x f
y1
y f
dx1dy1
E x, y C
E
x1,
y1
exp
i
kx x1 k y y1
夫琅禾费圆孔衍射-精选

上式中D是圆孔的直径; 若上透图镜可L知2的,焦为距:为f,则艾里斑的线半径由
l f.tg1
由于1一般很小,故 tg1sin1。1 则:
l 1.22 f
D
数据处理
用测微目镜测出艾里斑的直径e,由已知衍射小孔 直径d=1mm,焦距f=70mm,可验证:
e 1.22 f
夫琅禾费圆孔衍射-精选源自实验目的观察夫郎和费圆孔衍射图样
实验步骤
把单缝衍射装置中的单缝以一小孔代替,应用 氦氖激光器,可以在透镜的焦平面上看到圆孔 衍射图样,衍射图样是一组同心的明暗相间的 圆环,可以证明以第一暗环为范围的中央亮斑 的光强占整个入射光束光强的84%,这个中央 光斑称为艾里斑。经计算可知,艾里斑的半角 宽度为:
a 公式的正确性(其中为孔的半径),本实验要求实 验环境很暗。
思考题
菲涅尔圆孔衍射图样的中心点可能是亮的,也可 能是暗的,而夫琅和费圆孔衍射的中心总是亮的。 这是为什么?
文档名
THE END!THANK YOU !
单缝和圆孔的夫琅禾费衍射

第八章 波动光学
(5)入射光非垂直入射时光程差的计算
DB BC
a(sin sin )
(中央明纹向下移动)
a
D
A
C
B A
BC DA
a(sin sin )
(中央明纹向上移动)
a
D
C
B
8 – 4 单缝和圆孔的夫琅禾费衍射
第八章 波动光学
例1 用单色平行光垂直照射到缝宽 a = 0.5mm的单
第八章 波动光学
例1 设人眼在正常照度下的瞳孔直径约为2mm, 而在可见光中,人眼最敏感的波长为550nm,问 (1)人眼的最小分辨角有多大? (2)若物体放在距人眼25cm(明视距离)处,则 两物点间距为多大时才能被分辨? 解(1)
1.22 5.5 10 m R 1.22 3
o
L
B
A
2
R
/2
A
b
a sin (2k 1)
B
A1
C
E
P
k 1,2,3,
B
A2
o
/2
8 – 4 单缝和圆孔的夫琅禾费衍射
R
第八章 波动光学
A1
A
C
L
E P
BC a sin
B
A2
o
/2
N
2
( N 个半波带) 中央明纹中心
a sin 0
a sin 2k k 干涉相消(暗纹) 2 k 个半波带 2 2k 1 a sin (2k 1)
22010 Hz 1 1.36103 m 1 2.44 2.44 0.00603 rad 2 D1 5510 m 2 1 . 57 10 m 2 (2) 2 2.44 2.44 0.0164 rad D2 2.33m
菲涅尔单缝和圆孔衍射

菲涅尔单缝和圆孔衍射一、背景介绍菲涅尔单缝和圆孔衍射是一种经典的光学现象,主要是研究光通过细缝或圆孔时所产生的衍射现象。
这种现象在物理学中被称为“菲涅尔衍射”。
菲涅尔衍射是由法国物理学家奥古斯丁·让·菲涅耳(Augustin-Jean Fresnel)在19世纪初提出的,自那以后便成为光学研究的重要领域之一。
菲涅尔衍射是一种由于细缝或圆孔对光波进行衍射造成的干涉现象。
它的本质是光的波动性,即当光通过一块缝或孔的时候,光波便会弯曲和扩散。
这种扩散过程会产生多条射线,并且它们会相互干涉形成一道明暗相间的衍射图样。
二、实验设计和原理1. 菲涅尔单缝衍射实验菲涅尔单缝衍射实验是以一块银色金属板为底板,上面放置一块透明的玻璃板,玻璃板上面贴着一条细缝的黑色条纹。
当经过该细缝的银光时,光线被分散,从而形成了一条由黑色和白色相间的光芒。
这里的黑色区域是由于光的干涉而形成的,而白色区域则是由于缝中光线通过的部分所形成的。
2. 菲涅尔圆孔衍射实验菲涅尔圆孔衍射实验是通过在一个透明的玻璃板上制作圆孔,然后从玻璃板的另一侧照射灯光,观察光线传播的过程。
当光线穿过圆孔时,它们会产生干涉,形成一定的衍射模式。
这种模式是由多个环形“光晕”组成的,其中心是亮的,外围是暗的。
三、实验步骤和结果1. 菲涅尔单缝衍射实验(1) 用压克力胶将一条宽度为0.1毫米,在长度方向上大约5毫米的细线粘在光滑的玻璃板上。
(2) 把细线面对一束点光源,光源要充分放大,使得光阑明显。
(3) 将近红外光线照射到缝线上,用镜头放大,观察缝线光的分光,当光源足够强大的时候,能够清晰地看到一系列相交、形状奇特的光带,光带有暗、光明之分。
2. 菲涅尔圆孔衍射实验(1) 在玻璃板上打一个直径为2毫米的小孔,又称“准光源”。
(2) 将准光源与白光灯光源距离相隔1.5米,然后通过玻璃板观察圆孔内的光线。
(3) 当光被圆孔散射后,形成的图案是一种光晕,其中心明亮、外围暗淡。
夫琅和费衍射实验

课程名称:物理光学实验
实验名称:夫琅禾费衍射实验
'0'0E()a a P C C ==⎰⎰,利用贝塞尔
消像差透镜
图4 夫琅禾费衍射光路图
使其探测面与透镜的距离为透镜焦距f(探测器靶面的位置与滑块
17.3mm,透镜距离滑块刻度为6mm);
“相机图像”预览功能,预览衍射图案。
调整CCD
光强适中(不饱和,也不过弱)。
记录CCD处的衍射图案;
打开软件,点击“圆孔方孔衍射”→“捕获衍射图案”,获取夫琅禾费圆孔衍射的实
图5
图6
图7 图8
图9 2.当D=300μm时的夫琅禾费圆孔衍射
图10
图11 图12
图13 L=500μm时的夫琅禾费方孔衍射
图14
图16
图17 L=300μm时的夫琅禾费方孔衍射
图18
图19 图20
图21
六、数据处理
同数据记录
七、结果陈述:
实验得到了夫琅禾费圆孔衍射和夫琅禾费方孔衍射的实验图像。
测量了夫琅禾费圆孔衍射和夫琅禾费方孔衍射的光强分布,发现实验值和理论值符合的很好,说明夫琅禾费衍射公式的正确性。
实验得到了夫琅禾费圆孔衍射和夫琅禾费方孔衍射虚焦时的图像。
高二物理竞赛课件:单缝和圆孔的夫琅禾费衍射

引起的光振动用一个小矢量来表示
∆x l l
4
用一个小矢量代表一个细带面元s = l x 对P 处光振动的贡献
= 0方向上各子波射线,到O点相位相同,光程相等,亮纹
在O点引起的光振动的振幅等 于各小矢量连成一条线, 即等
A
•P
于矢量A0的长度
式中 1 a sin
2
相位差 2 Δ 2 a sin
6
单缝夫琅禾费衍射光强分布
IP
I
0
(
sin
)2
缝宽a 一定时, 波长λ越大, 各级衍射角φ越大, 中央明条纹越宽
1 a sin k
2
IP
I0
A
p
o
BC
3π 2π π o π 2π 3π
3 2
aa
a
2 3
第一暗条纹对应衍射角:
0
arc sin
a
a
(4)两相邻暗条纹之间的亮条纹,称为次极大 1 = 1.43π,I1 =0.047I0
位置可以从式
AP
A0
s in
的微商为零求得
2 = 2.46π, I2 =0.016I0 3 = 3.47π, I3 =0.008I0
1
2
3
3π 2π π o π 2π 3π
3 2
2 3
s in
aa
a
aaa
9
光强分布的特点
(5)点O 到第一暗条纹中心的角距离,称为主极大的半角宽度0
⑹中央亮条纹的宽度等于各次极大的两倍,绝大部分光能 都落在了中央亮条纹上。
0
a
A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
d sin u ( ) 0 求得 位置:由 du u
2 2
得 tgu = u,由作图法可得次极大位置
y y1 = tgu
y2 = u
-2
-
o
·
2
·
u
·
-2.46π
·
-1.43π +1.43π
+2.46π
u 1.43, 2.46, 3.47,…
相应 a sin 1.43 , 2.46 , 3.47 ,… 太原理工大学物理系
太原理工大学物理系
2 2 x2 2 D a
例2 单缝衍射中,a=0.1mm,入射波长λ=500nm, 透镜焦距f=10cm,在屏上x=1.75mm的p点为明条纹
求:(1)p 点条纹级数 k ? 解 (1) x f tan
x tan 0.0175 f
很小
单缝衍射明纹的条件 a sin (2k 1) 明纹在屏上的位置
2 (n整数)
B
若A、B到达P点的光程差为
n
2
即波面AB可划分成n个半波带,即
BC a sin n
太原理工大学物理系
越大,AB分成的半波带数目越多,则每个半
波带越窄。因每个半波带面积相等,它们发出子 波在P点引起的光强度相同。 若AB恰好被分成偶数个半波带 暗纹 BC a sin 2k (k 1, 2,3, ) 2 则每两个相邻“半波带”发出的光在 P点会聚 2 干涉相消,形成暗纹。 若AB恰好被分成奇数个半波带
2
附: 3) BC a sin n 2
(n整数)
缝分成整数个半波带.
(k 1, 2,3, )
n为偶数, BC a sin 2k
2
暗纹
n为奇数,BC a sin (2k 1)
BC a sin m 4)
2
(k 1, 2,3, ) 明纹
sin u I I u
p 0
2
光强:中央明纹中心的光强最大 I = I0 2)暗纹
位置:在u≠0,sinu = 0处 条件:
a sin k
sin (/a), 2(/a), 3(/a),… 在sin坐标上暗纹是等间距的。 太原理工大学物理系
3)其他明纹
2
x f tan f sin f (2k 1)
2a
ax 1 k 3. 5 0 .5 3 f 2
第3级明纹
太原理工大学物理系
(2)对应于 p 点,缝可分成多少个半波带?
a sin (2k 1)
7个半波带
2
(2 3 1)
2
平行光斜向下入射,衍射条纹将整体下移; 平行光斜向上入射,衍射条纹将整体上移。 太原理工大学物理系
本例即考点4,即ZP18,25 例1 在单缝衍射中,=600nm, a=0.60mm, 缝 后有一焦距f=60cm透镜, 则(1)中央明纹宽度 为多少?(2)两个第三级暗纹之间的距离? 解 ⑴ 中央明纹的宽度 ⑵第三级暗纹在屏上的位置 x3 f tan f 3 a 两个第三级暗纹之间的距离
tan sin
x
f
f 2a
O
k 1, 2...
f k 1,2... 暗纹中心: x f tan f sin k a 3)其他明纹的线宽度:相邻暗纹中心间的距离
明纹中心: x f tan f sin (2k 1)
即中央明纹宽度为其他明纹宽度的两倍。 太原理工大学物理系
2 则总有一部分振动不能被抵消,会聚在屏上的 亮度介于明暗纹之间。
(m非整数) 缝不能分成整数个半波带.
综上可知,可得如下结论 太原理工大学物理系
△单缝衍射明、暗条纹条件 中央明纹中心
P119,式14.20,14.21及下第2行
0 (k 0)
2 (k 1, 2,3 )
2k+1个半波带
1 解: a sin 4 sin 30 4 4 2 2
0
4个半波带
练考点6,若缝宽a=4λ,单缝处波面可划分为4个 半波带,则衍射角φ=? (讨论P159) 26 作业P158 --23,28,
太原理工大学物理系
例 3B
在单缝夫琅和费衍射实验中,缝宽 a=10,
缝后透镜焦距 f =40cm , 试求第一级明纹的角宽度,
明纹中心(近似) a sin (2k 1) 暗纹中心 a sin 2k
2
(k 1, 2,3 )
2k个半波带
k=0为中央明纹,k=1,2,…分别称为第一,二,… 级明纹(或暗纹);正负表示对称。可见,单缝衍 射条纹是关于中央亮纹对称分布的。 太原理工大学物理系
P120 3.说明 1)中央明纹 半角宽度:k=1级暗纹所对应的衍射角
0, 0 光直线传播 a
3)a、λ一定,能看到条纹的最高级次
2 a sin
2
k
a (若k 不是整数, k 取整数部分) m m km (若km 为整数,则取km-1)
太原理工大学物理系
观察:单缝宽度变化,中央明纹宽度如何变化?
a减小,1增大,衍射效应越明显. 太原理工大学物理系
太原理工大学物理系
附: 1)若 BC a sin 2
半波带
2
将缝分为两个半波带
A
A1
p
半波带
B
C
o
/2
相邻两个半波带对应点光程差均是/2,每两个相邻 “半波带”发的光在 P处干涉相消形成暗纹。 若AB恰好被分成偶数个半波带,偶数个“半波带” 发的光在 P处干涉相消形成暗纹。即
2 x3 2 f tan 2 f 3
a
3l0 3.6mm
太原理工大学物理系
练考点3,即 13
解
x2 D tan
因
a sin 2
x2 tan 0.016 D
很小 tan sin
2 x2 D tan D sin D a 4 D 2 a 7.6 10 mm 2 x2
1 arcsin
a
或
1 sin 1
a
(1很小) (1很小)
角宽度:
21 2
。
a
线宽度: k=1和k= -1两个第一级暗纹间距离。
a
2 f l0 2 x1 2 f tan 1 2 f sin 1 a
太原理工大学物理系
讲考点2,教案附
2)其他条纹在屏幕上线位置 当 较小时,
三、圆孔夫琅禾费衍射 1.圆孔夫琅禾费衍射 光通过眼睛的瞳孔、望远镜、显微镜、照相 机所成的像都是光波通过圆孔的衍射图样。
4)单缝衍射的光强分布
x
f
O
k级亮纹合成(2k+1)个半波带;k级暗纹对应2k 个半波带.k越大,AB上波阵面分成的波带数就越多, 所以,每个半波带的面积就越小,在P点引起的光强 就越弱。因此,各级明纹随着级次的增加而亮度减弱。 太原理工大学物理系 P119图上面两行及P120第1行
4.讨论 1)波长变化对条纹的影响
7
2
(3)将缝宽增加1倍,p 点将变为什么条纹?
7 2a sin 2 14 7 2 2
第7级暗纹 思考:缝可分成的半波带数目为多少? 直接练ZP18,26,本次不练下例 作业P158 --23,28, 太原理工大学物理系 (讨论P159) 26
练考点 直接练 ZP18,26,本次不练下例
a sin 2k
2
k
sin k
a
a一定, sin ,λ越大,衍射效应越明显.
指出:白光照射,中央明纹为白色,每一级明纹 都成彩色(紫-红),称为衍射光谱。
对于高级次衍射条纹会发生重叠,条件
a sin (2k1 1) a sin (2k2 1)
对于屏上其它点P,由 于屏上位置不同,对应的 衍射角就不同,Ap的大小 也不同.
A
p
a sin 令 u
可以求出
A
i
sin u A A u
p 0
过程略
2
p点的光强
sin u I I u
p 0
太原理工大学物理系
2.衍射条纹的特点 1)中央明纹 位置:在 = 0处
通知:
各位同学: 上课前先到物理老师 处签到,并取回作业。
§14-7 单缝和圆孔的夫琅禾费衍射
△一、单缝夫琅禾费衍射
1.衍射装置及花样
单缝 衍射角 透镜 衍射屏
f
I
太原理工大学物理系
衍射图样 (1) S为线光源:衍射图样为一组与狭缝平行的 以中央明纹为中心,两侧对称分布的明暗相间 P117,图上段正数第2,4-7行画 的直条纹。 (2)中央明条纹很亮,两侧明条纹对称分布,亮 度减弱。 (3)中央明条纹的宽度为其它明条纹宽度的两倍。 解释: 由惠更斯——菲涅耳原理: 单缝处波面看作无穷多个相干的子波源,屏 上一点是 (无穷)多光束干涉的结果。 太原理工大学物理系
BC a sin 2k
太原理工大学物理系
2
(k 1, 2,3, )
暗纹
附: 2)BC
a sin 3
2
将缝分为3个半波带.
a
A
B
A
p
