青岛大学量子力学2017年考研真题考研试题硕士研究生入学考试试题
《量子力学》22套考研自测题+答案

算符,以保证它的本征值为
。
对一个量子体系进行某一力学量的测量时,所得到的测量值肯定
是
当中的某一个,测量结果一般来说是不确定的,除非
体系处于
。测量结果的不确定性来源于
。两个力
学量同时具有确定值的条件是
。
二、(本题 15 分)
1.设算符 aˆ 具有性质 aˆ 2 = 0,{aˆ, aˆ + }= 1 。求证:
ψ (1,2,),试证明交换算符 Pˆ12 是一个守恒量。 2.设Uˆ 是一个幺正算符,求证 Hˆ = i dUˆ ⋅Uˆ + 是厄米算符。
dt
3.设σ y 为 Pauli 矩阵, (1)求证: eiθσ y = cosθ + iσ y sinθ (2)试求:Treiθσ y
三、(本题 10 分)
求证:ψ (xyz) = x + y + z 是角动量平方算符 lˆ2 的本征值为 2 2 的本征
1 5
u
0
(
x)
+
1 2
u
2
(
x)
+
c3u
3
(
x)
式中 un (x) 是振子的第 n 个本征函数。
QQ:70499QQ:704999167
考研自测题精美汇总
HY制作
HY制作
HY制作
(1)试求 c3 的数值;(2)写出在 t 时刻的波函数;
(3)在 t = 0 时振子能量的期望值是多少? t = 1秒时呢?
HY制作
HY制作
HY制作
量子力学自测题(1)
一、简答与证明:(共 25 分) 1、什么是德布罗意波?并写出德布罗意波的表达式。 (4 分) 2、什么样的状态是定态,其性质是什么?(6 分) 3、全同费米子的波函数有什么特点?并写出两个费米子组成的全 同粒子体系的波函数。(4 分)
量子力学习题及解答

量子力学习题及解答第一章 量子理论基础1.1 由黑体辐射公式导出维恩位移定律:能量密度极大值所对应的波长m λ与温度T 成反比,即m λ T=b (常量);并近似计算b 的数值,准确到二位有效数字。
解 根据普朗克的黑体辐射公式dv e chv d kThv v v 11833-⋅=πρ, (1)以及 c v =λ, (2)λρρd dv v v -=, (3)(有,118)()(5-⋅=⋅=⎪⎭⎫ ⎝⎛-=-=kThc v v ehc cd c d d dv λλλπλλρλλλρλρρ这里的λρ的物理意义是黑体内波长介于λ与λ+d λ之间的辐射能量密度。
本题关注的是λ取何值时,λρ取得极大值,因此,就得要求λρ 对λ的一阶导数为零,由此可求得相应的λ的值,记作m λ。
但要注意的是,还需要验证λρ对λ的二阶导数在m λ处的取值是否小于零,如果小于零,那么前面求得的m λ就是要求的,具体如下:01151186'=⎪⎪⎪⎭⎫⎝⎛-⋅+--⋅=-kThc kT hc e kT hc e hcλλλλλπρ ⇒ 0115=-⋅+--kT hce kThc λλ ⇒ kThce kT hc λλ=--)1(5 如果令x=kThcλ ,则上述方程为x e x =--)1(5:这是一个超越方程。
首先,易知此方程有解:x=0,但经过验证,此解是平庸的;另外的一个解可以通过逐步近似法或者数值计算法获得:x=,经过验证,此解正是所要求的,这样则有xkhc T m =λ 把x 以及三个物理常量代入到上式便知K m T m ⋅⨯=-3109.2λ这便是维恩位移定律。
据此,我们知识物体温度升高的话,辐射的能量分布的峰值向较短波长方面移动,这样便会根据热物体(如遥远星体)的发光颜色来判定温度的高低。
1.2 在0K 附近,钠的价电子能量约为3eV ,求其德布罗意波长。
解 根据德布罗意波粒二象性的关系,可知E=hv ,λhP =】如果所考虑的粒子是非相对论性的电子(2c E e μ<<动),那么ep E μ22= 如果我们考察的是相对性的光子,那么E=pc注意到本题所考虑的钠的价电子的动能仅为3eV ,远远小于电子的质量与光速平方的乘积,即eV 61051.0⨯,因此利用非相对论性的电子的能量——动量关系式,这样,便有ph =λ nmm m E c hc E h e e 71.01071.031051.021024.1229662=⨯=⨯⨯⨯⨯===--μμ在这里,利用了m eV hc ⋅⨯=-61024.1以及,eVc e 621051.0⨯=μ最后,对Ec hc e 22μλ=作一点讨论,从上式可以看出,当粒子的质量越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强;同样的,当粒子的动能越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强,由于宏观世界的物体质量普遍很大,因而波动性极弱,显现出来的都是粒子性,这种波粒二象性,从某种子意义来说,只有在微观世界才能显现。
青岛大学818理论力学2016-2017年考研专业课真题试卷

1
青岛大学2017年硕士研究生入学考试试题
科目代码:818科目名称:理论力学
(共
5页)
请考生写明题号,将答案全部答在答题纸上,答在试卷上无效
一.选择题(每题5分,共55分)
1、楔形块、自重不计,并在光滑的mm 和nn 平面相接触,若其上分别作用有两个大小相等,方向相反,作用线相同的力F 和F',如图所示,则、两个刚体是否处于平衡状态?____
A .
、都不平衡B.
、都平衡C .
平衡,不平衡D.不平衡,
平衡2、如图,x 轴和y 轴的夹角为,设一力系在xy 平面内,对y 轴上的点和x 轴上的点有,且但已知OA =l 则点在x 轴的位置为____
A.
B.
C.
D.
3、如图所示若尖劈两侧与槽之间的摩擦角均为
,则欲使尖劈被打入后不致自动滑出,角应为多大?____
A.
B.
C.
D.
青岛大学考研专业课真题试卷
精都考研网(专业课精编资料、一对一辅导、视频网课)。
《量子力学》22套考研自测题+答案

⎜⎝ 0 3λ 3 + 2λ ⎟⎠ 的本征值至 λ 的二次项,本征矢至 λ 的一次
项。
五、(10 分)一体系由三个全同的玻色子组成, 玻色子之间无相互作
用. 玻色子只有两个可能的单粒子态. 问体系可能的状态有几
个? 它们的波函数怎样用单粒子波函数构成?
QQ:704999167
QQ:704999167
En
=
−
Z 2e2 2a
, ψ 100 =
1
⎜⎛
Z
⎟⎞ 3 /
2
− Zr
ea
π ⎝a⎠
,计算时,可利用积分公式
∫∞ xe−2ax dx = 1 。
0
4α 2
五、(本题 20 分)
设一维谐振子的能量本征函数为ψ n (x) ,求:
QQ:704999167
HY制作
HY制作
HY制作
量子力学自测题(5)
一、 填空题(本题 20 分)
1.Planck 的量子假说揭示了微观粒子
特性,Einstein 的光
量子假说揭示了光的
性。Bohr 的氢原子理论解决了经典
考研自测题精美汇总
电磁场理论和原子的
之间的矛盾,解决了原子的
的起源问题。
2.力学量算符必须是
10. n 为 Lz 的本征态,本征值为 n 。求在 L z 的本征态 n 下, Lx
和 Ly 的平均值。
11. 氢原子处于状态
⎜⎛
ψ
(r
,
s
z
)
=
⎜ ⎜
⎜− ⎝
1 2
R
21
Y 11
3 2 R 21 Y10
⎟⎞ ⎟ ⎟ ⎟
=
历年量子力学考研真题试卷

历年量子力学考研真题试卷历年量子力学考研真题试卷量子力学是现代物理学的重要分支,也是考研物理专业的必考内容之一。
历年来,考研真题试卷中的量子力学部分涵盖了许多重要的概念和原理,对于考生来说是一项重要的挑战。
本文将对历年的量子力学考研真题试卷进行回顾和分析,帮助考生更好地准备考试。
首先,我们来看一道经典的考研真题:2015年考研物理专业真题中的一道量子力学选择题。
题目如下:在一个一维无限深势阱中,一束波长为λ的平面波入射,其入射角为θ。
已知势阱宽度为a,求波函数在势阱内的形式。
这道题目考查了量子力学中的一维无限深势阱问题。
解答这道题目需要运用波函数的性质和边界条件来分析。
首先,我们可以根据波函数的性质得出波函数在势阱内的形式是一个定态波函数。
其次,根据边界条件,我们可以得到波函数在势阱两侧的形式是分别由入射波和反射波组成。
因此,波函数在势阱内的形式可以表示为:Ψ(x) = Ae^{ikx} + Be^{-ikx},其中A和B分别表示入射波和反射波的振幅,k 为波矢。
接下来,我们来看一道稍微复杂一些的考研真题:2018年考研物理专业真题中的一道量子力学计算题。
题目如下:考虑一个束缚在一维势阱中的粒子,势阱宽度为a。
已知粒子的质量为m,势阱内的势能为V_0,势阱外的势能为0。
求粒子在势阱内的能级。
这道题目考查了量子力学中的束缚态问题。
解答这道题目需要运用定态薛定谔方程和边界条件来分析。
首先,我们可以根据定态薛定谔方程得到粒子在势阱内的波函数形式。
其次,根据边界条件,我们可以得到波函数在势阱两侧的形式是分别由入射波和反射波组成。
因此,波函数在势阱内的形式可以表示为:Ψ(x) = Ae^{ikx} + Be^{-ikx},其中A和B分别表示入射波和反射波的振幅,k 为波矢。
然后,我们需要将波函数在势阱两侧的形式进行匹配,并利用边界条件得到粒子在势阱内的能级。
通过求解定态薛定谔方程,我们可以得到粒子在势阱内的能级为:E_n = \frac{n^2 \pi^2 \hbar^2}{2ma^2},其中n为能级的量子数。
青岛大学高分子物理2009-2017年考研初试真题

青岛大学2017年硕士研究生入学考试试题科目代码:833科目名称:高分子物理(共3页)
请考生写明题号,将答案全部答在答题纸上,答在试卷上无效
一、解释术语(20分)
1、构型和构象
2、均相成核和异相成核
3、蠕变和应力松弛
4、熵弹性和粘弹性
5、高分子合金和互穿聚合物网络(IPN)
二、单项选择题(10分)
1、下列聚合物中,刚性因子最大的是。
A、聚甲醛
B、聚乙烯
C、聚丙烯腈
2、塑料的使用温度范围是。
A、T b~Tg
B、Tg~T f
C、Tg~T d
3、PET试样经退火处理后,下列结构中不变的是。
A、结晶度
B、密度
C、构型
4、可用于描述非晶PS聚集态结构的模型是。
A、无规线团模型
B、缨状微束模型
C、插线板模型
5、分子量分别为4万和8万的两试样等数量混合的数均分子量为。
A、12万
B、6万
C、5.3万
6、一根橡胶带的初始拉伸模量为1.2×105Pa,在27℃下拉伸到原长的两倍所需应力为。
A、1.2×105Pa
B、7×104Pa
C、2.1×105Pa
1。
青岛大学2017年硕士研究生入学考试试题
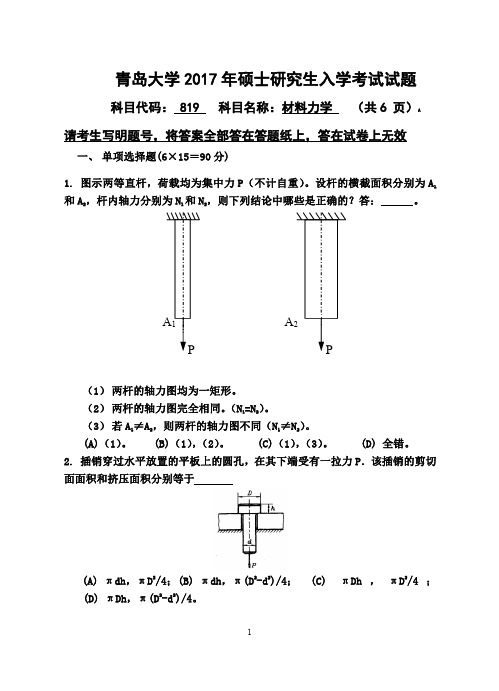
(应力单位:MPa)。答:
。
12. 将沸水倒人玻璃杯中,如杯子破裂,问杯的内外壁是否同时破裂? (A)同时破裂 (B)内壁先裂 (C)外壁先裂 (D)无法判定
4
13. 材料相同的四个直杆如图所示。其中哪一根杆变形能最大?
14.长度因数的物理意义是
。
(A)压杆绝对长度的大小;
(B)对压杆材料弹性模数的修正;
(D)压杆的许可载荷随着 A 的增加呈非线性变化。
二、 已知图示梁的载荷图,试作其剪力图和弯矩图 (14 分)
q=30kN/m A
C 1m
P=20kN
q=30kN/mBiblioteka D1m1m
E
B
1m
5
三、 图示桁架,各杆各截面的拉压刚度均为 EA,试计算节点 A 的水平位移。 ( 本题 15 分)
四、 图示钢杆,横截面面积 A=2500mm2 ,弹性模量 E=210GPa,轴向载荷 F=200kN。未加外载时,间隙δ=0.3 mm。试确定杆端的约束反力。 (本题 15 分)
9.弯曲与扭转组合变形圆轴表面 1、2、3、4 点的应力状态如图所示。其中哪个 是错误的?(图中的阴影面为自由表面)
3
10. 圆轴受扭时,轴表面各点处于
。
(A)单向应力状态。 (B) 各向等应力状态.
(C)三向应力状态. (D) 二向应力状态。
11. 绘出图示应力状态所对应的应力圆并求出图示斜面上的应力值σα和τα。
变为
。
(A) 1.82τ。 (B) 1.59τ。 (C) 1.35τ。 (D) 1.14τ。
4. 等强度梁各个横截面上的 (A) 最大正应力相等; (C) 最大剪应力相等;
。 (B) 最大正应力都等于许用正应力[σ]; (D) 最大剪应力都等于许用剪应力[τ]。
2017年青岛大学考研试题880数学基础综合

x2 f ( x1 ) f ( x2 ) 1 x x f 1 2 f (t )dt . 2 2 x2 x1 x1
1
8.(10 分)计算:
0
dx . (1 x )(1 x )
2
a a a a
1 ,
, s 线性表示.
11. (10 分) 若 A 2 A , 且 E A B 是可逆阵, 证明: 秩 ( AB ) A, B F nn , 秩 ( BA) . 12.(10 分)设 f ( x), g ( x) F [ x] ,且 f ( x), g ( x)) 1 ,则 a, b F ,且均 不为 0, ( f ( x) g ( x), af ( x) bg ( x)) 1 . 13.(10 分)设 F 是数域, A, B, E F nn ,且 AB A B ,
证明: ( A E )
1
EB .
14.(10 分)设 是数域 F 上的线性空间 V 的线性变换,且 2 ,证 明: (1) 的特征值只能是 0,1.
(2) Ker { ( ) V } .
15. (每小题 5 分,共 10 分)对于 R n 的线性变换,
6.(10 分)设 a, b 0, 函数 f ( x ) 0 ,且 f ( x) 在 [a, b] 上可积,
b a
xf ( x)dx 0. 试证明:
b a
x 2 f ( x)dx a(10 分)设 f ( x) 是 [a, b] 上连续的凸函数.试证:
3.(10 分)设 f ( x) 对 ( , ) 内一切 x 有 f ( x 2 ) f ( x)
青岛大学_815量子力学2017年_考研专业课真题试卷

科目代码: 815 科目名称: 量子力学 (共 1 页) 请考生写明题号,将答案全部答在答题纸上,答在试卷上无效 一、简答题(共 5 个小题,每个小题 6 分,共计 30 分) 1. 量子力学中力学量怎么表示?量子力学中力学量的测量原理是什么? 2. 简述氢原子的一级斯塔克效应、简单塞曼效应以及精细结构产生的原因? 3. 乌伦贝克和哥德斯密脱关于电子自旋的基本假设是什么? 4. 简述波函数的统计解释原理。 请问什么是微观粒子的束缚态、 定态和本征态? 5. 请用狄拉克符号写出本征值方程、薛定谔方程和力学量的平均值公式。 二、 (第 1 小题 10 分,共 20 分) 1. 一个微观粒子在一维无限深势阱中运动,势阱的形状如下:
ˆ 的作用,微扰矩阵元为 H H a,H H b ;a、b 都是实数。用 扰H 12 21 11 22
微扰公式求能量至二级修正值。
第1页
ˆ 五、 (本题共 20 分)求 S x
0 1 ˆ 0 及S y 2 1 0 2 i
第2页
0 u ( x) 0xa x 0,2. 若在上述势阱中运动粒子的状态为
2 x x 2 x A cos sin sin a a a
求粒子能量的几率分布和能量平均值。 三、 (20 分) 设氢原子处于状态 ( r , , )
1 3 R21 ( r )Y10 ( , ) R21 ( r )Y11 ( , ) , 2 2
求氢原子能量、角动量平方及角动量 Z 分量的可能值,这些可能值出现的几率 和这些力学量的平均值。 四、 (共 20 分)设一体系未受微扰作用时有两个能级: E 01及E 02 ,现在受到微
硕士学位研究生入学量子力学试卷

附件中国科学院-中国科技大学2000年招收攻读硕士学位研究生入学试卷 试卷名称:量子力学(理论型) 选做五题,毎题20分1、 一个质量为m 的粒子被限制在一维区域0x a ≤≤运动,0t =的波函数为(),012cos sin x x x t A a a ππψ⎡⎤⎛⎫⎛⎫==+⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ A 为常数。
(1) 后来某一时刻0t t =时波函数是什么?(2) 体系在0t t =和0t =时平均能量是多少? (3) 在0t t =时于势阱右半部(即2ax a ≤≤)发现粒子的几率是多少? 2、3、设粒子处于(),lm Y θϕ状态,计算角动量的x 分量和y 分量的方均差22,x y l l ∆∆4、记123,,σσσ为Pauli 矩阵,定义12,i σσσ±=±(1) 计算[][][]()233,,,,,,σσσσσσσ+-+-+和()2σ-, (2) 证明(ξ为常数 )332e e e ξσξσξσσ±±±=,证:[]3,2σσσ±±=± ()33322σσσσσσσ±±±±∴=±=±()()2233333322σσσσσσσσσσ±±±±==±=±反复利用即得()332nn σσσσ±±=± 两边同乘实数nξ得 ()332nn n nξσσσξσ±±=± 即()33322e ee e ξσξσξσξσσσ±±±±±==(3) 化简下面二式331112,e e e e ξσξσξσξσσσ--。
5、设0H 为一量子系统的能量算符,其本征态为0,1,2,⋅⋅⋅若体系受到微扰作用,微扰算符为ˆˆˆ,(H i A B λλ⎡⎤'=⎣⎦为实数),ˆA为厄密算符,ˆˆ,B C 为另外的厄密算符,且ˆˆˆ,.C i A B ⎡⎤=⎣⎦如在微扰作用前的基态0中,ˆˆˆ,,A B C 的平均值已知为000,,A B C ,试对微扰后的基态(非简并)计算厄密算符ˆB的平均值B ,精确到量级λ。
山东大学2017量子力学.docx

山东大学2017年硕士研究生入学考试
科目名称:量子力学考试时间: 三小时满分:150分
科目代码: 829 适用专业: 物理学院等相关专业
注意:①所有答案必须写在答题纸或答题卡上,写在本试题纸或草稿纸上均无效;
②本科目不允许使用计算器;③本试题纸须随答题纸一起装入试题袋中交回!
一、计算及证明(25分)
由基本对易关系[Xf p] = ih f计算[x,p n]以及[x n f p]的表达式,其中n为整数;
试证明:
d
[pJW]=_访疽3)
ox
d
/(P)
op
二、计算(25分)
已知束缚态波函数为寸(%),求动量p与动能T =球的几率分布函数的表达式。
对一维谐振子基态,波函数可以表示为:
p(x)=
算出动量P与动能r的儿率分布函数,并算出动能平均值。
三、计算(25分)
处于场强为B的均匀强磁场中的氢原子,不计自旋,其哈密顿量H
可近似记为:
p2 / 、eB .
H =^-+V(r)+—L z
2/1 2 卩c z
其中卩为氢原子质量,卩为其动量,e为电子电量,c为光速,£z为氢原
子轨道角动量。
求该氢原子的能级,并说明该磁场产生的物理效应。
四、计算(25分)
B
—个质量为m的粒子在三维势场:
1
V = —/c(x2+ y2 + z2 + Xxy)
中运动,式中k是正的常数,4是小量。
⑴ 写出2 = 0时,该势场下对应的本征态函数和本征能量,并指出各能级的简并度;
(2)用微扰论求基态能量至二级修正;
(3)用微扰论求第…激发态的能级的一级修正值。
青岛大学物理基础综合2013-2015,2017年考研初试真题

分)
10、以白光垂直照射在一块平面衍射光栅上,要求能在 30 度的衍射方向
观察到 600nm 的第二级主最大,并能在该处分辨波长差为 0.005nm 的两条
光谱线,但是 400nm的谱线在此缺级。试求:(1)光栅常数;(2)光栅的
总宽度;(3)光栅的缝宽;(4)用这块光栅总共能看到 590nm 的哪几条谱
1
6、如图所示一平行板电容器,两极板间距为 d , 板的面积为 S ,中间插入一块厚度为 t 、相对介电 常数为 r 的电介质平板(介质板贴近电容器的下 极板)。求:(1)未加入电介质之前电容器的电容; (2)加入电介质后的电容;(3)向上平移电介质, 是否改变电容器的电容?为什么?(15 分)
Fmax (M m)g mg
1 2kh (M m)g
(15 分)
4、如图所示,一长为 l ,质量为 M 的杆可绕支点 O 自由
转动。一质量为
m
、速度为
v
的子弹射入下端而不复出,
此后杆摆至水平位置又开始回落;设从子弹射入到停在杆
内为时极短。求:(1)子弹进入杆前的速度;(2)子弹刚
青岛大学目名称: 物理基础综合 (共 2 页)
请考生写明题号,将答案全部答在答题纸上,答在试卷上无效
1、已知质点的运动学方程为 r 2ti (2 t 2 )j ,式中 r 的单位为 m ,t 的单位为 s 。求:(1)质点的运动轨迹;(2) t 0 及 t 2s 时,质点的 位置矢量;(3)由 t 0 到 t 2s 内质点的位移 r ;(4) t 2s 时质点 的速度;(5) t 2s 时质点的加速度。 (15 分)
2、轻型飞机连同驾驶员总质量为 m ,飞机以 v0 的速率在水平跑道上着陆 后,驾驶员开始制动,若阻力与时间 t 成正比,即 f kt ,空气对飞机升 力不计,求:飞机任意时刻的加速度、速度,和其运动学方程。(以驾驶 员开始制动处为坐标原点)(15 分)
2017年青岛大学考研试题899工程热力学

12、绝热节流的温度效应可用一个偏导数来表征,这个量称为焦耳—汤姆逊系数。它是一个 状态的单值函数。实际气体节流后温度可能升高、降低或不变。 ( 13、工质在管道内作定熵流动时,各点对应的滞止参数都相同。 ( 14、工质经历可逆过程的熵变必然大于经历可逆过程的熵变。 ( ) ) ) )
8、一活塞气缸装置中,有温度为 30℃、压力为 400kPa 的空气。现在空气经历一个可逆定 温膨胀过程,过程中系统对外做膨胀功 15 kJ,外界对系统有 3 kJ 叶轮功的输入。问过程中 系统和外界的热交换量是 ( A 12kJ B 18kJ C ) 。 2.4kJ D 3.6kJ E 60kJ
9、 w c v dT 适用条件为( A 理想气体可逆过程 C 任何工质定容过程 A 渐缩喷管 B
1
D 压力下降,温度不定,熵增大 3、对一定大小气缸的活塞式压气机,因余隙容积的存在( A 使压缩每公斤气体的理论耗功增大,压气机生产量下降 B 使压缩每公斤气体的理论耗功增大,压气机生产量不变 C 使压缩每公斤气体的理论耗功不变,实际耗功增大,压气机生产量下降 D 使压缩每公斤气体的理论耗功不变,实际耗功增大,压气机生产量不变 4、抽气回热循环改善了朗肯循环,其根本原因在于( A 每公斤水蒸汽的作功量增加了 B 排气的热能得到了充分利用 C 水蒸汽的平均吸热温度提高了 D 水蒸汽的放热温度降低了 5、 一定质量的空气在无摩擦, 不导热的气缸和活塞中被缓慢地压缩, 这一过程是 ( A 可逆的 B 不可逆的 C 准平衡过程 D 不能确定 ) 。 ) 。 ) 。
6、1kg 工质经历一个不可逆过程从状态点 1 变化到状态点 2,过程中从外界环境中吸热 q, 环境温度恒定为 T。如果工质在状态点 1 和状态点 2 的熵,分别用 s1 和 s2 质在这个过程中的熵变△s 为( A △s<s2-s1 B △s>s2-s1 C E △s>s2-s1 +q/T 7、某绝热容器被隔板分为两半,其中一半盛有气体,另一半为真空。若该气体为理想气体, 则隔板抽开后气体的热力学能将( A 升高 B 降低 C ) 。 不变 ) 。 △s = s2-s1 D △s=s2-s1 +q/T 描述,那么工
《量子力学》22套考研自测题+答案

(2)求自旋角动量的 z 分量 sz 的平均值;
(3)求总磁矩 M = − e L − e s
2μ μ
的 z 分量 M z 的平均值。
12. s 、L 分别为电子的自旋和轨道角动量,J = s + L 为电子的总角动 量。证明:[ J , s ⋅ L ]=0;[ J 2 , Jα ]=0,α = x, y, z。 13.质量为 μ 的粒子受微扰后,在一维势场中运动,
QQ:704999167
HY制作
HY制作
HY制作
量子力学自测题(5)
一、 填空题(本题 20 分)
1.Planck 的量子假说揭示了微观粒子
特性,Einstein 的光
量子假说揭示了光的
性。Bohr 的氢原子理论解决了经典
考研自测题精美汇总
电磁场理论和原子的
之间的矛盾,解决了原子的
的起源问题。
2.力学量算符必须是
QQ:704999167
HY制作
HY制作
HY制作
量子力学自测题(3)
一、 简答题(每小题 5 分,共 40 分)
1.一粒子的波函数为ψ (r ) = ψ (x, y, z) ,写出粒子位于 x ~ x + dx 间的几
率。
考研自测题精美汇总
2.粒子在一维δ 势阱V (x) = −γ δ (x), (γ > 0),中运动,波函数为ψ (x) ,
ψ (1,2,),试证明交换算符 Pˆ12 是一个守恒量。 2.设Uˆ 是一个幺正算符,求证 Hˆ = i dUˆ ⋅Uˆ + 是厄米算符。
dt
3.设σ y 为 Pauli 矩阵, (1)求证: eiθσ y = cosθ + iσ y sinθ (2)试求:Treiθσ y
2017年青岛大学考研试题828有机化学

青岛大学2017年硕士研究生入学考试试题科目代码:828科目名称:有机化学(共7页)请考生写明题号,将答案全部答在答题纸上,答在试卷上无效一、选择题(每题3分,共60分)1.下列化合物(a)CH 3CH 2I (b)CH 3CH 2CH 2CH 3(c)CH 3CH 2Br (d)CH 3CH 3的沸点大小顺序为:(A)(a)>(b)>(d)>(c)(B)(b)>(d)>(c)>(a)(C)(a)>(c)>(b)>(d)(D)(d)>(c)>(b)>(a)2.下面各碳正离子中最不稳定的是:(A)Cl-C +HCH 2CH 3(B)C +H 2CH 2CH 2CH 3(C)CF 3C +HCH 2CH 3(D)CH 3OC +HCH 2CH 33.下列化合物酸性最强的是:4.乙苯在光照下一元溴化的主要产物是:5.1-甲基环己烯+HBr 反应的主要产物是:(A)1-甲基-1-溴代环己烷(B)顺-2-甲基溴代环己烷OHAOH NO 2BOHNO 2CDH 2O(C)反-2-甲基溴代环己烷(D)1-甲基-3-溴环己烷6.按S N 2历程反应,下列化合物活性次序是:Br1234BrBrBr (A)①>③>②>④(B)①>④>③>②(C)④>③>①>②(D)①>③>④>②7.的CCS 名称是:(A)(2Z,4E)-4-叔丁基-2,4-己二烯(B)(2E,4Z)-3-叔丁基-2,4-己二烯(C)(2Z,4E)-3-叔丁基-2,4-己二烯(D)(2E,4Z)-4-叔丁基-2,4-己二烯8.鉴别环丙烷、丙烯与丙炔需要的试剂是:(A)Br 2的CCl 4溶液,KMnO 4溶液(B)HgSO 4/H 2SO 4,KMnO 4溶液(C)AgNO 3的氨溶液,KMnO 4溶液(D)Br 2的CCl 4溶液,AgNO 3的氨溶液9.下列化合物中能形成分子内氢键是:10.用下列哪种方法可由1-烯烃制得伯醇:(A)H 2O(B)浓H 2SO 4,水解(C)①B 2H 6;②H 2O 2,OH -(D)冷、稀KMnO 4C CHCH 3C(CH 3)3C C HHCH 3OHOHNO 2NO 2ABOHCH 2OH COH COOHD11.下列哪个反应不能产生高收率的醇:12.具有R 构型的化合物为:13.顺-4-叔丁基环己醇的优势构象是:14.与HNO 2反应能放出N 2的是:(A)伯胺(B)仲胺(C)叔胺(D)都可以15.下列化合物能与NaHSO 3发生加成反应是:+ACB DCC Hg(OAc)2NaOH RMgXKOHH 2O +NaBH 4CH 2Cl H 2OOH 2O +CH 3CH CHCH 3CH 3BrBrC C CC CCH 3CH 3CH 3CH 3CH 3H H HH H HBrCl CH 2CH 3CH 2CH 3ACBDOHt-Bu (A)OH t-Bu (B)OHt-Bu(C)OHt-Bu(D)16.下列化合物中,不能发生羟醛缩合反应的是:17.蔗糖中,正确的描述是:(A)葡糖具有吡喃环,果糖具有呋喃环(B)葡糖具有呋喃环,果糖具有吡喃环(C)葡糖和果糖均为吡喃环(D)葡糖和果糖均为呋喃环18.酰胺与次卤酸钠的霍夫曼(Hoffmann)反应产物是:(A)生成少一个碳原子的酰胺(B)生成少一个碳原子的伯胺(C)生成多一个碳原子的酰胺(D)生成多一个碳原子的伯胺19.苯(a)、吡咯(b)、呋喃(c)、噻吩(d)的芳香性强弱次序是:(A)a>b>c>d(B)d>c>b>a(C)a>d>b>c(D)c>d>b>a20.蛋白质的一级结构是:(A)蛋白质填入到酶空腔的方式(B)分子所采取的结构形态(C)多肽链中氨基酸的组成和排列次序(D)折叠链所构成的一定形态二、填空题(每题3分,共30分)21.写出下列化合物的结构式。
青岛大学数学分析2009-2017年考研初试真题

, x ( 0, )
条件收敛。
n1 n
八、(满分 15 分)设 fn (x) , n 1,2,, 均在点 x b 连续,数列
{ fn (b)} 发散,求证 0 ,{ fn (x)} 在 (b , b ) 内非一致收敛。
九、(满分 10 分)确定幂级数 n2 xn1 的收敛域,并求其和函数。 n1
S
三、(满分 10 分)设曲线 C 的方程为 x 1 t 2 , y t t 2 ,求曲线 C
上在 t 2 对应的点 P 处的切线方程。 四、(满分 10 分)证明 f (x) sin 1 在 ( 0, 1) 内不一致连续。 x 五、(满分 10 分)设 f 在[ a , b ] 上连续,且有 f (a) , f (b) [ a , b ],
在一点 [a,b], 使得
b f (x)g(x)dx f ( )
b
g(x)dx .
a
a
6. (本题满分15分) 证明:广义积分 cos x dx 收敛,而 | cos x | dx 发散.
1x
1
x
7. (本题满分15分)
(x 1)n
讨论并指出级数
绝对收敛、条件收敛、发散的范围.
2. 计算 I = ∫∫ xdydz + 2 ydzdx + 3zdxdy ,其中 S 是圆柱面 x2 + y2 = 1被平
S
面 z = 0 和 z = 3 所截的部分之外侧.
2
青岛大学 2012 年硕士研究生入学考试试题
科目代码: 605 科目名称: 数学分析 (共 2 页) 请考生写明题号,将答案全部答在答题纸上,答在试卷上无效
青岛大学物理基础综合考研真题2015年、2017年

青岛大学2015年硕士研究生入学考试试题 科目代码: 913 科目名称: 物理基础综合 (共2页) 请考生写明题号,将答案全部答在答题纸上,答在试卷上无效1、质点由坐标原点出发时开始计时,沿x 轴运动,其速度12-=t v x 。
求:(1)瞬时加速度随时间的变化规律;(2)质点的运动学方程;(3)01=t到12=t 时间内质点的位移,以及运动的路程。
(15分)2、天平左端挂一定滑轮,一轻绳跨过滑轮,绳的两端分别系上质量为1m 、2m 的物体(21m m ≠)。
天平右端的托盘内放有砝码。
问天平托盘和砝码共重若干,才能保持天平平衡?不计滑轮和绳的质量及轴承摩擦,绳不伸长。
(15分)3、质量M 的物块与弹簧(劲度系数为k )原来处于静止,另一质量为m 的质点从离M 为h 的高度自由落下,m 和M 做完全非弹性碰撞。
证明:弹簧对地面的最大压力为gm M kh mg g m M F )(21)(max ++++= (15分)4、如图所示,一长为l ,质量为M 的杆可绕支点O 自由转动。
一质量为m 、速度为v 的子弹射入下端而不复出,此后杆摆至水平位置又开始回落;设从子弹射入到停在杆内为时极短。
求:(1)子弹进入杆前的速度;(2)子弹刚停在杆内时轴O 受杆的力。
(15分)5、空间有两块面积为S 的平行放置的金属平板A 和B ,两板长宽均比板间距离大得多,如图所示。
令每板带上A q 及B q 的电量,求每板表面的电荷密度。
(15分)6、半径为R 的金属球带电荷Q ,球外套一个同心球壳的均匀电介质,其内外半径分别为a 和b ,相对介电常数为r ε(如图所示)。
求:(1)介质球壳内外的电场强度E 和电位移D ;(2)导体球的电位。
(15分)7、把能量为E 的电子射入磁感应强度为B 的匀强磁场中,其速度矢量与B 成θ角,路径成螺旋线,其轴在B 的方向。
试求这螺旋线运动的周期T ,螺距h 和半径r 。
(15分)8、一长直导线中通有I 的电流,在与其相距d 处放有一矩形线圈,线圈以速度v 沿垂直长直导线的方向向右离开导线时,线圈中的感应电动势是多少?指出感应电流方向。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
青岛大学2017年硕士研究生入学考试试题
科目代码:815科目名称:量子力学(共1页)请考生写明题号,将答案全部答在答题纸上,答在试卷上无效
一、简答题(共5个小题,每个小题6分,共计30分)
1.量子力学中力学量怎么表示?量子力学中力学量的测量原理是什么?
2.简述氢原子的一级斯塔克效应、简单塞曼效应以及精细结构产生的原因?
3.乌伦贝克和哥德斯密脱关于电子自旋的基本假设是什么?
4.简述波函数的统计解释原理。
请问什么是微观粒子的束缚态、定态和本征态?
5.请用狄拉克符号写出本征值方程、薛定谔方程和力学量的平均值公式。
二、(第1小题10分,共20分)
1.一个微观粒子在一维无限深势阱中运动,势阱的形状如下:
00()0,x a u x x x a
<<⎧=⎨∞<>⎩求粒子的本征能量和本征波函数。
2.若在上述势阱中运动粒子的状态为
22cos sin sin x x x A a a a πππψ⎛⎫=+ ⎪⎝
⎭求粒子能量的几率分布和能量平均值。
三、(20分)设氢原子处于状态),()(2
3),()(21),,(11211021ϕθϕθϕθψ--=Y r R Y r R r ,求氢原子能量、角动量平方及角动量Z 分量的可能值,这些可能值出现的几率和这些力学量的平均值。
四、(共20分)设一体系未受微扰作用时有两个能级:0201E E 及,现在受到微扰H 'ˆ的作用,微扰矩阵元为b H H a H H ='='='='22
112112,;b a 、都是实数。
用微扰公式求能量至二级修正值。
第1页。
