《离散数学》期末考试题(E)
离散数学期末考试题及详细答案

离散数学期末考试题及详细答案一、选择题(每题5分,共20分)1. 在离散数学中,下列哪个概念用来描述元素与集合之间的关系?A. 并集B. 交集C. 子集D. 元素答案:D2. 布尔代数中,下列哪个运算符表示逻辑“与”?A. ∨B. ∧C. ¬D. →答案:B3. 下列哪个命题的否定是正确的?A. 如果今天是周一,则明天是周二。
B. 如果今天是周一,则明天不是周二。
答案:B4. 在图论中,一个图的顶点数为n,边数为m,下列哪个条件可以保证该图是连通的?A. m > nB. m ≥ nC. m = nD. m > n-1答案:D二、填空题(每题5分,共20分)1. 在集合论中,一个集合的幂集包含该集合的所有______。
答案:子集2. 如果一个函数f: A → B是单射的,那么对于任意的a1, a2 ∈ A,如果a1 ≠ a2,则f(a1) ≠ f(a2)。
这种性质称为函数的______。
答案:单射性3. 在图论中,一个图的直径是指图中任意两个顶点之间的最短路径的最大值。
如果一个图的直径为1,则该图被称为______。
答案:完全图4. 一个布尔表达式可以表示为一系列逻辑运算符和变量的组合。
布尔表达式(A ∧ B) ∨ (¬ A ∧ C)的真值表中,当A为真,B为假,C为真时,整个表达式的值为______。
答案:真三、简答题(每题10分,共30分)1. 请简述什么是图的哈密顿回路,并给出一个例子。
答案:哈密顿回路是图中的一个回路,它恰好访问每个顶点一次。
例如,在一个完全图中,任意一个顶点出发,依次访问其他顶点,最后回到出发点的路径就是一个哈密顿回路。
2. 请解释什么是二元关系,并给出一个二元关系的例子。
答案:二元关系是定义在两个集合上的一个关系,它关联了第一个集合中的元素和第二个集合中的元素。
例如,小于关系是实数集合上的一个二元关系,它关联了每一对实数,如果第一个数小于第二个数。
离散数学期末考试卷

离散数学期末考试卷一、选择题(每题2分,共20分)1. 在集合论中,下列哪个选项不是集合的基本运算?A. 并集B. 交集C. 差集D. 幂集2. 命题逻辑中,下列哪个命题不是合取命题?A. (p ∧ q)B. (p ∨ q)C. (p → q)D. (p ↔ q)3. 关系R在集合A上是自反的,这意味着:A. 对于所有a∈A,(a, a)∈RB. R是对称的C. R是传递的D. R是反对称的4. 在图论中,下列哪个不是图的基本概念?A. 顶点B. 边C. 路径D. 矩阵5. 布尔代数中,下列哪个操作不是基本操作?A. 与(AND)B. 或(OR)C. 非(NOT)D. 模(MOD)6. 函数f: A → B,下列哪个条件不是函数的一一对应的必要条件?A. 对于A中不同的元素,它们的函数值不同B. 对于B中的每个元素,A中至少有一个元素映射到它C. 对于A中的每个元素,B中只有一个元素映射到它D. A和B的元素数量相同7. 在组合数学中,下列哪个是排列的定义?A. 从n个不同元素中取出r个元素的所有可能组合B. 从n个不同元素中取出r个元素的所有可能排列C. 从n个元素中取出r个元素的所有可能组合,不考虑顺序D. 从n个元素中取出r个元素的所有可能排列,考虑顺序8. 逻辑等价是指两个命题:A. 总是同时为真或同时为假B. 在所有可能的真值分配下都具有相同的真值C. 只有在某些真值分配下具有相同的真值D. 至少在一个真值分配下具有相同的真值9. 递归函数的特点是:A. 只能通过迭代来实现B. 必须有一个或多个基本情况C. 只能通过递归调用自身来实现D. 不能包含任何循环结构10. 在证明中,归纳法的基本步骤是:A. 基础步骤和归纳步骤B. 假设步骤和证明步骤C. 假设步骤和归纳步骤D. 基础步骤和假设步骤二、填空题(每空2分,共20分)11. 集合{1, 2, 3}的幂集包含元素个数为______。
离散期末考试题

离散期末考试题一、选择题(每题3分,共30分)1. 在离散数学中,以下哪个概念用于描述两个集合之间的一一对应关系?A. 并集B. 交集C. 映射D. 子集2. 以下哪个命题的否定是正确的?A. 如果今天是周一,那么明天是周二。
B. 如果下雨,那么地面会湿。
C. 如果x > 0,则x² > 0。
D. 所有的鸟都会飞。
3. 在图论中,一个连通图是指图中任意两个顶点之间都存在一条路径。
以下哪个选项描述的不是连通图?A. 完全图B. 树C. 环D. 星形图4. 以下哪个逻辑运算符表示逻辑“或”?A. ∧B. ∨C. ¬D. →5. 在集合论中,以下哪个符号表示集合的差集?A. ∪B. ∩C. -D. ×6. 以下哪个命题是永真命题?A. p ∧ ¬pB. p ∨ ¬pC. p → ¬pD. ¬(p → ¬p)7. 在关系R中,如果对于任意的a, b ∈ A,都有(a, b) ∈ R和(b,a) ∈ R,则称R是对称的。
以下哪个关系不是对称的?A. 等价关系B. 子集关系C. 整除关系D. 朋友关系8. 在命题逻辑中,以下哪个等价于“p且q”?A. ¬p ∨ ¬qB. p ∧ qC. ¬p → ¬qD. ¬(p → ¬q)9. 在图论中,以下哪个术语描述的是一个图中没有环的子图?A. 路径B. 连通图C. 树D. 环10. 在集合论中,以下哪个符号表示集合的笛卡尔积?A. ×B. ∪C. ∩D. -二、填空题(每题2分,共20分)11. 如果集合A有n个元素,那么集合A的子集个数是________。
12. 在逻辑中,一个命题的________是当原命题为真时,它为假;当原命题为假时,它为真的命题。
13. 如果一个图的每个顶点的度数都是偶数,则该图一定存在________。
离散数学期末复习题(6套)

《离散数学》期末考试题(A)一、填空题(每小题3分,共15分)1.设}}{},,{{c b a A =,}}{},,{},{{c c b a B =,则)(=⋃B A ,)(=⋂B A ,)()(=A P .2.集合},,{c b a A =,其上可定义( )个封闭的1元运算,( )个封闭的2元运算,( )个封闭的3元运算.3.命题公式1)(↑∧q p 的对偶式为( ).4.所有6的因数组成的集合为( ).5.不同构的5阶根树有( )棵.二、单选题(每小题3分,共15分)1.设A , B 是集合,若A B A =-,则(A)B = ∅ (B) A = ∅ (C)=⋂B A ∅ (D)A B A =⋂2.谓词公式)())()((x R y yQ x P x ∧∃→∀中量词x ∀的辖域为(A))())()((x R y yQ x P x ∧∃→∀ (B))()(y yQ x P ∃→(C))())()((x R y yQ x P ∧∃→ (D))()(y yQ x P ∃→和)(x R3.任意6阶群的子群的阶一定不为(A)4 (B)6 (C)2 (D)34.设n 是正整数,则有限布尔代数的元素个数为(A)2n (B)4n (C)n 2 (D)2n5.对于下列序列,可构成简单无向图的度数序列为(A)3, 3, 4, 4, 5 (B)0, 1, 3, 3, 3 (C)1, 1, 2, 2, 3 (D)1, 1, 2, 2, 2三、判断题(每小题3分,共15分): 正确打“√”,错误打“×”.1. 设N N N :⨯→f ,)1,()(+=x x x f ,则f 是满射. () 2. 5男5女圆桌交替就座的方式有2880种. () 3. 设),(≤L 是格,对于L z y x ∈,,,若z x y x ⋅=⋅且z x y x +=+,则z y =. () 4. 任何树都至少2片树叶. ()5. 无向图G 有生成树的充要条件是G 为连通图. ( )四、(10分)设C B A ,,和D 是集合,证明)()()()(D B C A D C B A ⨯-⨯⊆-⨯-,并举例说明上式中不能将⊆改为 = .五、(15分)设N 是自然数集合,定义N 上的关系R 如下:y x R y x +⇔∈),(是偶数,1.证明R 是N 上的等价关系.2.求出N 关于等价关系R 的所有等价类.3.试求出一个N 到N 的函数f ,使得)}()(,N ,|),{(y f x f y x y x R =∈=.六、(10分)在实数集合R 中证明下列推理的有效性:因为R 中存在自然数,而所有自然数是整数,所以R 中存在整数.七、(10分)设R 是实数集合,令}0,R ,|),{(≠∈=a b a b a G ,定义G 上的运算如下: 对于任意G d c b a ∈),(),,(,),(),(),(b ad ac d c b a +=⋅,证明),(⋅G 是非Abel 群.八、(10分)若简单平面图G 的节点数7=n 且边数15=m ,则G 是连通图,试证明之.《离散数学》期末考试题(B)一、填空题(每小题3分,共15分)1.设,,},,{{b a b a A =∅},则-A ∅ = ( ),-A {∅} = ( ),)(A P 中的元素个数=|)(|A P ( ).2.设集合A 中有3个元素,则A 上的二元关系有( )个,其中有( )个是A 到A 的函数.3.谓词公式))()(())()((y P y Q y x Q x P x ⌝∧∃∧→∀中量词x ∀的辖域为( ), 量词y ∃的辖域为( ).4.设}24,12,8,6,4,3,2,1{24=D ,对于其上的整除关系“|”,元素( )不存在补元.5.当n ( )时,n 阶完全无向图n K 是平面图,当n 为( )时,n K 是欧拉图.二、单选题(每小题3分,共15分)1.设R 是集合A 上的偏序关系,1-R 是R 的逆关系,则1-⋃R R 是A 上的(A)偏序关系 (B)等价关系 (C)相容关系 (D)以上结论都不成立2.由2个命题变元p 和q 组成的不等值的命题公式的个数有(A)2 (B)4 (C)8 (D)163.设p 是素数且n 是正整数,则任意有限域的元素个数为(A)n p + (B)pn (C)n p (D)pn4.设R 是实数集合,≤是其上的小于等于关系,则(R, ≤)是(A)有界格 (B)分配格 (C)有补格 (D)布尔格5.3阶完全无向图3K 的不同构的生成子图有(A)2 (B)3 (C)4 (D)5 三、判断题(每小题3分,共15分): 正确打“√”,错误打“×”.1.若一个元素a 既存在左逆元l a ,又存在右逆元r a ,则r l a a =. ( )2.命题联结词→不满足结合律. ( )3.在Z 8 = {0,1,2,3,4,5,6,7}中,2关于“⋅8”的逆元为4. ( )4.整环不一定是域. ( )5.任何),(m n 平面图的面数2+-=n m r . ( )四、(10分)设B A f →:且C B g →:,若g f 是单射,证明f 是单射,并举例说明g 不一定是单射.五、(15分)设},,,{d c b a A =,A 上的关系)},(),,(),,(),,(),,(),,(),,(),,(),,{(c d b d a d c c b c a c c a b a a a R =,1.画出R 的关系图R G .2.判断R 所具有的性质.3.求出R 的关系矩阵R M .六、(10分)利用真值表求命题公式))(())((p q r r q p A →→↔→→=的主析取范式和主合取范式.七、(10分) 边数30<m 的简单平面图G ,必存在节点v 使得4)deg(≤v .八、(10分) 有六个数字,其中三个1,两个2,一个3,求能组成四位数的个数.《离散数学》期末考试题(C)一、填空题(每小题3分,共15分)1. 若n B m A ==||,||,则=⨯||B A ( ),A 到B 的2元关系共有( )个,A 上的2元关系共有( )个.2. 设A = {1, 2, 3}, f = {(1,1), (2,1), (3, 1)}, g = {(1, 1), (2, 3), (3, 2)}和h = {(1, 3), (2, 1), (3,1)},则( )是单射,( )是满射,( )是双射.3. 下列5个命题公式中,是永真式的有( )(选择正确答案的番号).(1)q q p p →→∧)(;(2))(q p p ∨→;(3))(q p p ∧→;(4)q q p p →∨∧⌝)(;(5)q q p →→)(.4. 设D 24是24的所有正因数组成的集合,“|”是其上的整除关系,则3的补元( ),4的补元( ),6的补元( ).5. 设G 是(7, 15)简单平面图,则G 一定是( )图,且其每个面恰由( )条边围成,G 的面数为( ).二、单选题(每小题3分,共15分)1. 设A , B , C 是集合,则下述论断正确的是( ).(A)若A ⊆ B , B ∈ C ,则A ∈ C . (B)若A ⊆ B , B ∈ C ,则A ⊆ C .(C)若A ∈ B , B ⊆ C ,则A ∈ C . (D)若A ∈ B , B ⊆ C ,则A ⊆ C .2. 设R ⊆ A ⨯ A ,S ⊆ A ⨯ A ,则下述结论正确的是( ).(A)若R 和S 是自反的,则R ⋂ S 是自反的.(B)若R 和S 是对称的,则S R 是对称的.(C)若R 和S 是反对称的,则S R 是反对称的.(D)若R 和S 是传递的,则R ⋃ S 是传递的.3.在谓词逻辑中,下列各式中不正确的是( ).(A))()())()((x xB x xA x B x A x ∀∨∀=∨∀(B))()())()((x xB x xA x B x A x ∀∧∀=∧∀(C))()())()((x xB x xA x B x A x ∃∨∃=∨∃(D)),(),(y x xA y y x yA x ∀∃=∃∀4. 域与整环的关系为( ).(A)整环是域 (B)域是整环 (C)整环不是域 (D) 域不是整环5.设G 是(n , m )图,且G 中每个节点的度数不是k 就是k + 1,则G 中度数为k 的节点个数为( ). (A)2n . (B)n (n + 1). (C)nk . (D)m k n 2)1(-+. 三、判断题(每小题3分,共15分): 正确打“√”,错误打“×”.1.设f : Z → Z ,x x x f 2||)(-=,则f 是单射. ( )2.设ϕ是群G 1到群G 2的同态映射,若G 1是Abel 群,则G 2是Abel 群. ( )3.设),(≤L 是格,对于L z y x ∈,,,若z x y x ⋅=⋅且z x y x +=+,则z y =. ( )4.元素个数相同的有限布尔代数都是同构的. ( )5.设G 是n (n ≥ 11)阶简单图,则G 或G 是非平面图. ( )四、(15分)设A 和B 是集合,使下列各式(1)A B A =⋂; (2)A B B A -=-;(3)A A B B A =-⋃-)()(成立的充要条件是什么,并给出理由.五、(10分) 设S 是实数集合R 上的关系,其定义如下∈=y x y x S ,|),{(R 且是3y x -是整数}, 证明: S 是R 上的等价关系. 六、(10分) 求谓词公式)))()(()(()(x xD y yC y B x xA ∀→∃⌝→→∃的前束范式.七、(10分) 若n 个人,每个人恰有3个朋友,则n 必为偶数,试证明之.八、(10分) 利用生成函数求解递归关系⎩⎨⎧=-+=-2)1(211a n a a n n .《离散数学》期末考试题(D)一、填空题(每小题3分,共15分)1. 设|A | = 5, |B | = 2, 则可定义A 到B 的函数( )个,其中有( )单射,( )个满射.2. 令G (x ): x 是金子,F (x ): x 是闪光的,则命题“金子都是闪光的,但闪光的未必是金子”符号化为( ).3. 设X 是非空集合,则X 的幂集P (X )关于集合的⋃运算的单位元是( ),零元是( ),P (X )关于集合的⋂运算的单位元是( ).4. 不同构的5阶无向树有( )棵.5. 对于n 阶完全无向图K n , 当n 为( )时是Euler 图,当n ≥ ( )时是Hamilton 图,当n ( )时是平面图.二、单选题(每小题3分,共15分)1. 幂集P (P (P (∅))) 为( )(A){{∅}, {∅, {∅}}}. (B){∅, {∅, {∅}}, {∅}}.(C){ ∅, {∅, {∅}}, {{∅}}, {∅}} (D){ ∅, {∅, {∅}}}.2. 设R 是集合A 上的偏序关系,则1-⋃R R 是( ).(A)偏序关系 (B)等价关系 (C)相容关系 (D)以上答案都不对3. 下列( )组命题公式是不等值的.(A))(B A →⌝与B A ⌝∧. (B) )(B A ↔⌝与)()(B A B A ∧⌝∨⌝∧.(C))(C B A ∨→与C B A →⌝∧)(. (D))(C B A ∨→与)(C B A ∨∧⌝.4.下列代数结构(G , *)中,( )是群.(A)G = {0, 1, 3, 5}, “*”是模7加法. (B) G = Q , “*”是数的乘法.(C)G = Z , “*”是数的减法. (D) G = {1, 3, 4, 5, 9}, “*”是模11乘法.5.4阶完全无向图4K 中含3条边的不同构的生成子图有(A)3 (B)4 (C)5 (D)2三、判断题(每小题3分,共15分): 正确打“√”,错误打“×”.1.函数的复合运算“ ”满足结合律. ( )2. {→⌝,}是最小功能完备联结词集合. ( )3. 实数集R 关于数的乘法运算“⋅”阿贝尔群. ( )4. 任意有限域的元素个数为2n . ( )5. 设G 是n (n 为奇数)简单图,则G 与G 中度数为奇数的节点个数相同. ( )四、(10分)设A 和B 是集合,使B B A =-成立的充要条件是什么,并给出理由.五、(10分) 设R 和S 是集合A 上的对称关系,证明S R 对称的充要条件是R S S R =.六、(15分)分别利用(1)等值演算法和(2)真值表求命题公式))(())((r q p p q r A ∨→→→∨⌝=的主析取范式和主合取范式.七、(10分) 设G 是(n , m )无向图,若n m ≥,证明G 中必存在圈.八、(10分) 在初始条件f (1) = c 下,求解递归关系bn n f n f +⎪⎭⎫ ⎝⎛=22)(,其中b ,c 为常数且kn 2=,k 为正整数.《离散数学》期末考试题(E)一、填空题(每小题3分,共15分)1.设A = {2, {3}, 4, a }, B = {1, 3, 4, {a }}, 则{3}( )A ,{a }( )B ,{{a }}( )B .2. 设A = {1, 2, 3, 4, 5}上的关系R = {(1, 2), (3, 4), (2, 2)}, S = {(4, 2), (2, 5), (3, 1), (1, 3)}, 则=S R { }, =R S { }, =R R { }.3. gcd(36, 48) = ( ),lcm(36, 48) = ( ).4.任意有限布尔代数)1,0,,,,(⋅+B 均与集合代数( )同构,其元素个数为( ).5. 不同构的5阶无向树有( )棵,不同构的5阶根树有( )棵.二、单选题(每小题3分,共15分)1. 在有理数集合Q 上定义运算“*”如下:对于任意x , y ∈ Q ,y x * = x + y – xy ,则Q 关于*的单位元是( ).(A)x . (B)y . (C)1. (D)0.2. 设A = {1, 2, 3}, 下图分别给出了A 上的两个关系R 和S ,则S R 是( )关系.(A)自反. (B)对称. (C)传递. (D)等价.3.令T (x ): x 是火车,B (x ): x 是汽车,F (x , y ): x 比y 快,则“某些汽车比所有的火车慢”符号化为( ).(A)()()),()()(y x H x T x y B y →∀∧∃.(B)()()),()()(y x H x T x y B y ∧∀→∃.(C)()()),()()(y x H x T y B y x ∧→∃∀.(D)()()),()()(y x H x T x y B y →∀→∃.4. 整数集合Z 关于数的加法“+”和数的乘法“⋅”构成的代数结构(Z, +, ⋅)是( ). 1 1 22 3 3G S G R(A)域(B)域和整环(C)整环(D) 有零因子环G≅,则称G为自补图. 5阶不同构的自补图5.设G是简单图,G是G的补图,若G个数为( ).(A)0. (B)1. (C)2. (D)3.三、判断题(每小题3分,共15分): 正确打“√”,错误打“×”.1. { ∅, {∅}} ∉P(P({∅})). ( )2. 非空1元及2元联结词集合的个数为29-1. ( )3. 群可分为Abel群和非Abel群. ( )4. 元素个数相同的有限域都是同构的. ( )5. 设G是简单图,则G或G是连通图. ( )四、(15分)设C,:, 若gf 是单射,证明f是单射,并举例说明g→:f→gBBA不一定是单射.五、(10分)设A = {a, b, c, d}上的关系R = {(a, b), (b, d), (c, c), (a, c)}, 画出R的关系图,并求出R的自反闭包r(R)、对称闭包s(R)和传递闭包t(R).六、(10分)用CP规则证明下列推理.⌝∨→∨(.⇒),(⌝),→pqssrqrqp→七、(10分)求谓词公式))xyByAxA∀→∨∀∧⌝∃的前束范式.zC((x()))(z(()八、(10分)任意6个人中,一定有3个人彼此认识或有3个人彼此不认识.《离散数学》期末考试题(F)一、填空题(每小题3分,共15分)1. 设A = {1, 2, 3, {1, 2}, {3}}, B = {2, {2,3}, {1}} , 则A–B = { }, B–A = { }, A⊕B = { }.2. 实数集合R关于加法运算“+”的单位元为( ), 关于乘法运算“⋅”的单位元为( ), 关于乘法运算“⋅”的零元为( ).3. 令Z(x): x是整数,O(x): x是奇数,则“不是所有整数都是奇数”符号化为( ).4. 有限域的元素个数为( ), 其中( )且( ).5. 设G 是(7, 15)简单平面图,则G 一定 ( )连通图,其每个面恰由( )条边围成,G 的面数为( ).二、单选题(每小题3分,共15分)1. 函数的复合运算“ ”满足( )(A)交换律. (B)结合律. (C)幂等律. (D)消去律.2. 设集合A 中有4个元素,则A 上的等价关系共有( )个.(A)13 (B)14 (C)15 (D)163.下列代数结构(G , *)中,( )是群.(A)G = {0, 1, 3, 5}, “*”是模7加法. (B) G = Q , “*”是数的乘法.(C)G = Z , “*”是数的减法. (D) G = {1, 3, 4, 5, 9}, “*”是模11乘法.4. 下列偏序集,( )是格.5. 不同构的(5, 3)简单无向图有( )个.(A)4 (B)5 (C)3 (D)2三、判断题(每小题3分,共15分): 正确打“√”,错误打“×”.1. 设A ,B ,C 是集合,若C A B A ⊕=⊕, 则B = C . ( )2. 逻辑联结词“→”满足结合律. ( )3. 设 (L , ≤)是偏序集,若L 的任意非空子集均存在上确界和下确界,则(L , ≤)是格.( )4. 在同构意义下,有限布尔代数只有,,,),((⋂⋃X P ∅, X ). ( )5. 设G 是简单图,则G 与G 中度数为奇数的节点个数相同. ( )四、(15分) 设C B g B A f →→:,:, 若g f 是满射,证明g 是满射,并举例说明f 不一定是满射.五、(10分) 在整数集合Z 上定义关系R 如下:对于任意∈y x , Z ,y y x x R y x +=+⇔∈22),(.判断R 是否具有自反性、反自反性、对称性、反对称性及传递性.六、(10分)利用真值表求命题公式)())(q p q p A ⌝→↔→⌝=的主析取范式和主合取范式.七、(10分)证明:在至少两个人的人群中,必有两个人有相同个数的朋友.八、(10分)将6阶完全无向图K 6的边随意地涂上红色或蓝色,证明:无论如何涂法,总存在红色的K 3或蓝色的K 3.(ps :答案见离散数学期末复习题(6套)答案文档)。
离散数学期末考试题及答案

离散数学期末考试题及答案1.选择题(每题3分,共30分)1. 下列命题中,属于复合命题的是:A. 3是一个奇数,且2是一个偶数B. 如果2是一个素数,那么4也是一个素数C. 不是所有奇数都是素数D. 存在一个整数x,使得x>5且x是一个偶数答案:D2. 已知命题p:草地是绿的,命题q:天空是蓝的。
下列表述可以表示p ∧ ¬q 的是:A. 草地是绿的,天空是蓝的B. 草地不是绿的,天空是蓝的C. 草地是绿的,天空不是蓝的D. 草地不是绿的,天空不是蓝的答案:B3. 设命题p表示“这个数是偶数”,q表示“这个数大于10”。
那么“这个数既是偶数又大于10”可以表示为:A. p ∧ qB. p ∨ qC. ¬p ∧ qD. ¬p ∨ q答案:A4. 下列以下列集合的方式描述,其中哪个是空集∅:A. {x | 0 ≤ x ≤ 1}B. {x | x是一个自然数,x > 10}C. {x | x是一个正偶数,x < 2}D. {x | x是一个负整数,x < -1}答案:C5. 设A = {a, b, c},B = {c, d, e},C = {a, c, e}。
则(A ∪ B) ∩ C等于:A. {a, b, c, d, e}B. {a, c, e}C. {c}D. 空集∅答案:B6. 假设U是全集,A、B、C是U的子集。
则(A ∪ B) ∩ C 的补集是:A. A ∩ B ∩ C的补集B. (A ∪ B) ∩ C的补集C. A ∪ (B ∩ C)的补集D. (A ∩ C) ∩ (B ∩ C)的补集答案:D7. 若关系R为集合A到集合B的一种映射,且|A| = 7,|B| = 4,则R包含的有序对数目为:A. 4B. 7C. 11D. 28答案:D8. 设A={1,2,3},B={4,5,6},则从A到B的映射总数为:A. 3B. 9C. 6D. 18答案:C9. 设A={a,b,c,d,e},则集合A的幂集的元素个数是:A. 2B. 5C. 10D. 32答案:D10. 若f:A→B为满射且g:B→C为单射,则(g ∘ f):A→C为:A. 双射B. 满射C. 单射D. 非单射且非满射答案:A2.简答题(每题10分,共20分)1. 请简要解释什么是关系R的自反性、对称性和传递性。
离散数学期末考试题及答案

离散数学期末考试题及答案一、选择题(每题2分,共20分)1. 在集合论中,空集表示为:A. {0}B. {1}C. {}D. Ø答案:D2. 命题逻辑中,下列哪个是合取命题的真值表?A. P | Q | P ∧ QB. P | Q | P ∨ QC. P ∧ Q | P ∨ QD. P ∧ Q | ¬(P ∨ Q)答案:A3. 函数f: A → B是单射的,那么f的逆函数:A. 一定存在B. 一定不存在C. 可能存在D. 以上都不对答案:C4. 关系R是自反的,那么对于所有a∈A,以下哪个命题一定为真?A. (a, a) ∈ RB. (a, a) ∉ RC. (a, a) ∈ R或(a, a) ∉ RD. (a, a) ∈ R且(a, a) ∉ R答案:A5. 在图论中,下列哪个不是图的基本术语?A. 顶点B. 边C. 子集D. 路径答案:C6. 命题p: “如果x是偶数,则x能被4整除”的否定是:A. 如果x是偶数,则x不能被4整除B. 如果x不是偶数,则x不能被4整除C. 如果x不是偶数,则x能被4整除D. 如果x是偶数,则x不能被4整除或x不是偶数答案:A7. 有向图G中,如果存在从顶点u到顶点v的有向路径,则称v是u 的:A. 祖先B. 后代C. 邻居D. 连接点答案:B8. 在命题逻辑中,下列哪个命题是永真命题?A. (P ∧ ¬P) ∨ (P ∨ ¬P)B. (P ∧ ¬P) ∧ (P ∨ ¬P)C. (P ∨ ¬P) ∧ (¬P ∨ P)D. (P ∧ ¬P) ∧ (¬P ∧ P)答案:C9. 以下哪个选项是等价命题?A. P ∧ (Q ∨ R) ≡ (P ∧ Q) ∨ (P ∧ R)B. P ∨ (Q ∧ R) ≡ (P ∨ Q) ∧ (P ∨ R)C. P ∨ ¬P ≡ ¬P ∧ PD. P ∧ ¬P ≡ ¬P ∨ P答案:A10. 树是无环连通图,以下哪个是树的属性?A. 至少有一个环B. 至少有两个顶点C. 至少有一个顶点D. 至少有一个边答案:B二、填空题(每空2分,共20分)11. 集合{1, 2, 3}的幂集含有__个元素。
离散数学期末试卷(4套附答案)

一、单项选择题(每小题3分,共30分)1.下列为两个命题变元p,q的最小项的是( ) A .p∧q∧⎤ pB .⎤ p∨qC .⎤ p∧qD .⎤ p∨p∨q 2.下列句子不是命题的是( ) A .中华人民共和国的首都是北京 B .张三是学生 C .雪是黑色的D .太好了!3.对于公式(∀x ) (∃y )(P (x )∧Q (y ))→(∃x )R (x ,y ),下列说法正确的是( ) A .y 是自由变元 B .y 是约束变元C .(∃x )的辖域是R(x , y )D .(∀x )的辖域是(∃y )(P (x )∧Q (y ))→(∃x )R (x ,y )4.7.集合A={1,2,…,10}上的关系R={(x ,y )|x +y =10,x ∈A ,y ∈A},则R 的性质是( )A .自反的B .对称的C .传递的、对称的D .反自反的、传递的 5.设论域为{l ,2},与公式)(x xA ∃等价的是( ) A.A (1)∨A (2)B. A (1)→A (2)C.A (1)D. A (2)→A (1)6. 下列关系矩阵所对应的关系具有反自反性的是( ) A .⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡001110101B .⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡101100001 C .⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡001100100D .⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡0010101017. 下列运算不满足...交换律的是( ) A .a *b =a+2bB .a *b =min(a ,b )C .a *b =|a -b |D .a *b =2ab8..设A 是奇数集合,下列构成独异点的是( ) A.<A ,+> B.<A ,-> C.<A ,×> D.<A ,÷> 9. 右图的最大入度是( ) A .0 B .1 C .2D .3第9题图拟题学院(系): 高密校区 适用专业: 学年 2学期 离散数学 (B卷) 试题标准答案10. 设有向图D 的节点数大于1,D=(V ,E )是强连通图,当且仅当( ) A. D 中至少有一条通路 B. D 中至少有一条回路C. D 中有通过每个结点至少一次的通路D. D 中有通过每个结点至少一次的回路 二、填空题(每空3分,共30分)1.设A ={1,2,3,4},B ={2,4,6},则A -B =________,A ⊕B =________。
大学期末离散数学试卷

一、选择题(每题2分,共20分)1. 下列命题中,正确的是()A. 逻辑真命题一定是逻辑假命题B. 逻辑假命题一定是逻辑真命题C. 逻辑真命题和逻辑假命题都是存在的D. 逻辑真命题和逻辑假命题都不存在2. 设A和B是两个集合,则下列命题中正确的是()A. A∩B = A∪BB. A∩B = A-BC. A∪B = A∩BD. A-B = A∩B3. 设A和B是两个集合,则下列命题中正确的是()A. A⊆B当且仅当A∩B = AB. A⊆B当且仅当A∩B = BC. A⊆B当且仅当A-B = ∅D. A⊆B当且仅当A∪B = B4. 下列命题中,不是逻辑等价命题的是()A. A→B与¬A∨BB. A∧B与A→BC. A∨B与B→AD. A→B与¬B∨A5. 设R是一个关系,下列命题中正确的是()A. R是等价关系当且仅当R是自反的、对称的和传递的B. R是等价关系当且仅当R是自反的、非对称的和传递的C. R是等价关系当且仅当R是非自反的、对称的和传递的D. R是等价关系当且仅当R是非自反的、非对称的和传递的6. 设P和Q是两个命题,则下列命题中正确的是()A. P∧Q的否定是P∨QB. P∧Q的否定是P∧QC. P∨Q的否定是P∧QD. P∨Q的否定是P∧Q7. 设R是一个偏序关系,下列命题中正确的是()A. R是自反的、反对称的和传递的B. R是自反的、对称的和传递的C. R是自反的、非对称的和传递的D. R是非自反的、对称的和传递的8. 设R是一个全序关系,下列命题中正确的是()A. R是自反的、反对称的和传递的B. R是自反的、对称的和传递的C. R是自反的、非对称的和传递的D. R是非自反的、对称的和传递的9. 设R是一个函数,下列命题中正确的是()A. R是单射当且仅当R是满射B. R是单射当且仅当R是自反的C. R是满射当且仅当R是自反的D. R是单射当且仅当R是反对称的10. 设R是一个关系,下列命题中正确的是()A. R是等价关系当且仅当R是自反的、对称的和传递的B. R是等价关系当且仅当R是自反的、非对称的和传递的C. R是等价关系当且仅当R是非自反的、对称的和传递的D. R是等价关系当且仅当R是非自反的、非对称的和传递的二、填空题(每题2分,共20分)1. 在集合A={1, 2, 3}中,A的子集个数是______。
国家开放大学电大本科《离散数学》2022-2023期末试题及答案(试卷号:1009)

国家开放大学电大本科《离散数学> 2022-2023期末试题及答案(试卷号:1009)一、单项选择题(每小题3分,本息共16分)1, 若集合A = <1,2,3},则下列表述正确的是〈 )•A. {1,2,3}€AB. AC(1,2}C. U,2,3}gAD. {1,2}£A2. 设 A = {1,2,3},B = (1,2,3,4},人到 B 的关系 R = {O ,>> |工 £ A ,了 £ B },则 R =().A. {<1,2>,V2,3>}B. {V1,1>,V1,2>,V1,3>,V1,4>,V1,5>}C. «1,1>,<2,1>)D. {<2,】>,V3,】>,V3,2>}3. 无向图G 的边数是10,则图G 的结点度数之和为(A. 10B. 20C. 30D. 54. 如图一所示,以下说法正确的是〈 )•A. e 是割点B. {a,e}是点割集C. (b.e}是点割集D. {d}是点割集5-设个体域为整数集,则公式Vx3y (x+y = 2)的解释可为().A. 任意整数工,对任意整数y 满足工+了 = 2B. 对任意整数工,存在整数y 满足工+了 = 2C. 存在一整数z,对任意整数y 满足工+了 = 2D. 存在一整数工,有整数了满足x+jr = 2则人 CHBUC )等于 _____ .7. 设 A = {1,2},B = <2,3},C=(3,4},从 A 到 B 的函数/= (VI,2>,V2,3>},从 B到 C 的函数 g = (V2,3>,V3,4>},则 Ran (g 0/)等于 ______ .8. 设G 是汉密尔顿图,S 是其结点集的一个子集,若S 的元素个数为6,则在G-S 中的连通分支数不超过 ________ .二、填空霆(每小题3分,本题共15分)9.设G是有8个结点的连通图,结点的度数之和为24,则可从G中删去 ________ 条边后使之变成树.10.设个体域D = {1,2, 3, 4},则谓词公式(VQ A S)消去量词后的等值式为H.将语句“昨夭下雨,今天仍然下雨.”翻译成命题公式.12. 将i 吾句“我们下午2点或者去礼堂看电彩或者去教室看书.”翻译成命飓公式. 得分评卷人13. 不存在集合A 与B,使得AEB 与AQB 同时成立.14. 如图二所示的图G 存在一条欧拉回路.15. 设 A = {l,2,3},R = (<x,y>l=£A<yCA 且 1+»=4}击={〈工,3>0£人,36人且 工=)},试求 R,S,R" ,r (S ).16. 设图 G = <VtE>»V=(v! 试(1) 画出G 的图形表示; (2) 写出其邻接矩阵; (3) 求出每个结点的度数; (4)画出图G 的补图的图形•17. 求-I (PVQ )VR 的析取范式与主合取范式•18. 试证明门 PVQ»P -*(i (n PVn Q)〉.(仅 一、单项选择题(每小题3分,本题共15分)1.C2. D3. B二、填空题(每小题3分,本题共15分)6. {b t c)7. {3,4)(或 C ) 8.6 9.5评卷人三、逻辑公式翻译(每小题6分,本题共12分)四、判断说明题(判断各题正误,并说明理由.每小题7分,本题共14 分)评卷人五、计算题(每小题12分,本题共36分)评卷人六、证明题(本题共8分)10.A(1)AA(2) AA(3) AA(4)三、逻辑公式翻译(每小题6分,本题共12分)11.设P:昨天下雨,Q:今天下雨. (2分)则命题公式为:PAQ. (6分)12.设P:我们下午2点去礼堂看电影,Q:我们下午2点去教室看书. (2分)则命题公式为门(P-Q). (6分)注:或者(1 PAQ)V(PAi Q)四、判断说明题(每小题7分,本题共14分)13.错误•(3分)例:设A = {a},B^{a,{a}}(5 分)则有AEB且AWB. (7分)说明:举出符合条件的反例均给分.14.正确. (3分)因为图G为连通的,且其中每个顶点的度数均为偶数. (7分)如果具体指出一条欧拉回路也同样给分.五、计算题(每小题12分,本题共36分)15.解:R = {V1,3>,V2,2>,V3,1>} (3分)S = {<1,1>,<2,2>,<3,3>} (6分)7?~* = (<3,1>,<2,2>,<1,3>} (9分)r(S) = (<l,l>,<2,2>,<3,3>} (12分)说明:对于每一个求解项,如果部分正确,可以给对应1分・16.解:(1)(2)邻接矩阵10 0.(3)deg(pi) = 2deg(v2)=2deg(v3)=Odcg(vj = 2 (9 分)(4)补图(12 分)17.解门(PVQ)VR«=>(-, PA-i Q)VR 析取范式(5分)PVR)A(n QVR) (7分)«((n PVK)V(QA-i Q))A(-| QVR) (9分) E((I P VK) V(QA-i Q))A((n QV^>V(P An P)) (10分)«(-i PVR VQ) A(" VR Vi Q) A(i QVk VP)A(i QVRV") ⑴分) «(PV-i QVR)A(i PVQVR)A(rPVi QVR) 主合取范式(12 分)六、证明题(本题共8分)18.证明:(Di PVQ P(1 分)<2)P P(附加前提) (3分)(3)Q T(l)(2)/ (5 分)(4)PAQ T(2)(3)/ (6 分)(5)n(i PV-i Q) T(4)E (7 分)(6)P^n (n PV-i Q) CP 规则(8 分)说明:(D因证明过程中,公式引用的次序可以不同,一般引用前提正确得1分,利用两个公式得出有效结论得1或2分,最后得出结论得2或1分.(2)可以用真值表验证.采用反证法可参照给分.。
离散数学期末考试题及答案

离散数学期末考试题及答案一、选择题(每题2分,共20分)1. 以下哪个选项是图的边数与顶点数的关系?A. 边数小于顶点数B. 边数等于顶点数C. 边数大于顶点数D. 边数与顶点数无固定关系答案:D2. 有限自动机的英文缩写是什么?A. FAB. PDAC. TMAD. NFA答案:A3. 布尔代数中,德摩根定律是指什么?A. ¬(A ∧ B) 等于¬ A ∨ ¬ BB. ¬(A ∨ B) 等于¬ A ∧ ¬ BC. A ∧ B 等于¬(A ∨ B)D. A ∨ B 等于¬(¬ A ∧ ¬B)答案:B4. 在命题逻辑中,以下哪个符号表示蕴含?A. ∧B. ∨C. →D. ↔答案:C5. 集合A = {1, 2, 3},B = {2, 3, 4},则A ∪ B等于:A. {1, 2, 3, 4}B. {1, 2, 3}C. {2, 3, 4}D. {1, 3, 4}答案:A6. 以下哪个选项是正确的递归定义?A. 一个数是偶数当且仅当它是2的倍数B. 一个数是偶数当且仅当它不是2的倍数C. 一个数是偶数当且仅当它是另一个偶数加1D. 以上都是正确的递归定义答案:A7. 有向图和无向图的主要区别是什么?A. 有向图的边有方向,无向图的边没有方向B. 有向图的顶点有方向,无向图的顶点没有方向C. 有向图的边可以相交,无向图的边不可以相交D. 有向图可以有环,无向图不可以有环答案:A8. 在命题逻辑中,以下哪个公式是矛盾的?A. A ∧ ¬ AB. A ∨ ¬ AC. A → BD. A ∧ B ∧ ¬ A答案:A9. 以下哪个是图的同义术语?A. 网络B. 矩阵C. 树D. 以上全部答案:A10. 以下哪个命题逻辑公式是有效的?A. (A → B) ∧ (B → A)B. (A ∧ B) → AC. (A ∨ B) → AD. (A ∧ B) → B答案:B二、填空题(每题2分,共20分)11. 在命题逻辑中,_________ 表示一个命题是真的,而 _________ 表示一个命题是假的。
大学离散数学期末考试题库和答案

大学离散数学期末考试题库和答案一、单项选择题(每题2分,共20分)1. 在集合论中,以下哪个符号表示“属于”?A. ∈B. ∉C. ⊆D. ⊂答案:A2. 如果A和B是两个集合,那么A∪B表示什么?A. A和B的交集B. A和B的并集C. A和B的差集D. A和B的补集答案:B3. 以下哪个命题是真命题?A. ∀x∈N, x^2 > xB. ∃x∈N, x^2 = x + 1C. ∀x∈N, x^2 ≥ xD. ∃x∈N, x^2 < x答案:C4. 在图论中,一个无向图的边数为E,顶点数为V,那么这个图的生成树的边数是多少?A. EB. V-1C. VD. E-1答案:B5. 以下哪个算法是用于解决旅行商问题(TSP)的?A. 动态规划B. 贪心算法C. 分支限界法D. 回溯法答案:D6. 在逻辑中,以下哪个符号表示“蕴含”?A. ∧B. ∨C. →D. ↔答案:C7. 以下哪个是二进制数?A. 1010B. 2A3C. 12BD. ZYX答案:A8. 在关系数据库中,以下哪个操作用于删除表中的行?A. SELECTB. INSERTC. UPDATED. DELETE答案:D9. 以下哪个是布尔代数的基本运算?A. 并集B. 交集C. 差集D. 所有以上答案:D10. 在离散数学中,以下哪个概念用于描述两个集合之间的关系?A. 函数B. 映射C. 序列D. 所有以上答案:D二、多项选择题(每题3分,共15分)11. 以下哪些是集合的基本运算?A. 并集B. 交集C. 差集D. 补集答案:ABCD12. 在图论中,以下哪些是图的基本类型?A. 无向图B. 有向图C. 完全图D. 二分图答案:ABCD13. 在逻辑中,以下哪些是命题逻辑的基本连接词?A. 与(∧)B. 或(∨)C. 非(¬)D. 蕴含(→)答案:ABCD14. 在关系数据库中,以下哪些是SQL的基本操作?A. SELECTB. INSERTC. UPDATED. DELETE答案:ABCD15. 在离散数学中,以下哪些是组合数学的基本概念?A. 排列B. 组合C. 二项式系数D. 图论答案:ABC三、填空题(每题3分,共30分)16. 如果集合A={1, 2, 3},集合B={2, 3, 4},那么A∩B=______。
离散数学期末考试题及答案

离散数学期末考试题及答案一、选择题(每题2分,共20分)1. 在集合论中,以下哪个选项不是集合的基本运算?A. 并集B. 交集C. 差集D. 乘法答案:D2. 命题逻辑中,以下哪个命题不是基本的逻辑连接词?A. 与(∧)B. 或(∨)C. 非(¬)D. 等于(=)答案:D3. 在图论中,一个图的度数之和等于边数的几倍?A. 1B. 2C. 3D. 4答案:B4. 以下哪个是布尔代数的基本定理?A. 德摩根定律B. 布尔代数的分配律C. 布尔代数的结合律D. 所有选项都是答案:D5. 以下哪个不是组合数学中的计数原理?A. 加法原理B. 乘法原理C. 排列D. 组合答案:C6. 在关系数据库中,以下哪个操作不是基本的数据库操作?A. 选择B. 投影C. 连接D. 排序答案:D7. 以下哪个是有限自动机的组成部分?A. 状态B. 转移C. 输入符号D. 所有选项都是答案:D8. 以下哪个命题逻辑表达式是真命题?A. (p ∧ ¬p) ∨ qB. (p ∨ ¬p) ∧ qC. (p → q) ∧ (q → p)D. (p → q) ∧ (¬p → ¬q)答案:D9. 以下哪个是归纳法证明的基本步骤?A. 基础步骤B. 归纳步骤C. 反证法D. 所有选项都是答案:B10. 以下哪个是图的遍历算法?A. 深度优先搜索(DFS)B. 广度优先搜索(BFS)C. Dijkstra算法D. 所有选项都是答案:A二、简答题(每题10分,共30分)1. 简述命题逻辑中的德摩根定律。
答案:德摩根定律是命题逻辑中描述否定命题的两个重要定律。
它们分别是:- ¬(p ∧ q) ≡ ¬p ∨ ¬q- ¬(p ∨ q) ≡ ¬p ∧ ¬q2. 解释什么是图的连通分量,并给出一个例子。
答案:图的连通分量是指图中最大的连通子图。
离散数学题库简答题e
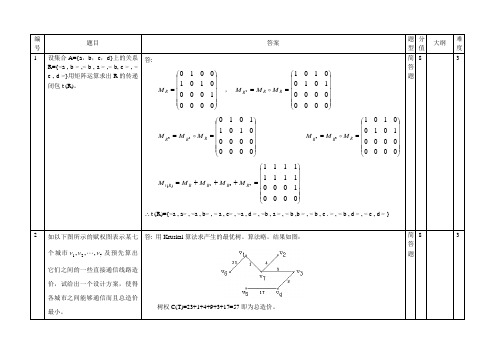
编号 题目答案题型 分值 大纲难度 11 设集合A={a ,b ,c ,d}上的关系R={<a , b > ,< b , a > ,< b, c > , <c ,d >}用矩阵运算求出R 的传递闭包t (R)。
答: ⎪⎪⎪⎪⎪⎭⎫⎝⎛=0000100001010010R M , ⎪⎪⎪⎪⎪⎭⎫⎝⎛==00000000101001012R R R M M M ⎪⎪⎪⎪⎪⎭⎫⎝⎛==000000000101101023R R R M M M ⎪⎪⎪⎪⎪⎭⎫⎝⎛==000000001010010134R R R M M M ⎪⎪⎪⎪⎪⎭⎫⎝⎛=+++=0000100011111111432)(R R R R R t M M M M M∴t (R)={<a , a> , <a , b> , < a , c> , <a , d > , <b , a > , < b ,b > , < b , c . > , < b , d > , < c , d > }简答题8 32如以下图所示的赋权图表示某七个城市721,,,v v v 及预先算出它们之间的一些直接通信线路造价,试给出一个设计方案,使得各城市之间能够通信而且总造价最小。
答: 用Kruskal 算法求产生的最优树。
算法略。
结果如图:树权C(T)=23+1+4+9+3+17=57即为总造价。
简答题833设<Z6,+6>是一个群,这里+6是模6加法,Z6={[0 ],[1],[2],[3],[4],[5]},试求出<Z6,+6>的所有子群。
答: 子群有<{[0]},+6>;<{[0],[3]},+6>;<{[0],[2],[4]},+6>;<{Z6},+6> 简答题8 34权数1,4,9,16,25,36,49,64,81,100构造一棵最优二叉树。
离散数学期末考试题及答案

离散数学期末考试题及答案一、单项选择题(每题2分,共20分)1. 集合{1, 2, 3}的子集个数是:A. 3B. 4C. 8D. 2^3答案:C2. 命题逻辑中,命题p∧(q∨¬p)的真值表中,真值个数为:A. 1B. 2C. 3D. 4答案:B3. 函数f: A→B中,若A={1, 2},B={a, b},则f是单射的必要条件是:A. |A| ≤ |B|B. |A| < |B|C. |A| = |B|D. |A| > |B|答案:B4. 以下哪个图是无向图?A. 有向图B. 无向图C. 完全图D. 树答案:B5. 在图论中,一个图的生成树是:A. 包含图中所有顶点的最小连通子图B. 包含图中所有边的最小连通子图C. 包含图中所有顶点和边的连通子图D. 包含图中所有顶点和边的无环子图答案:A6. 以下哪个命题是真命题?A. 所有偶数都是整数B. 所有整数都是偶数C. 所有奇数都是整数D. 所有整数都是奇数答案:A7. 在布尔代数中,以下哪个运算符表示逻辑与?A. ∨B. ∧C. ¬D. →答案:B8. 有限状态机中,状态的转移是由以下哪个决定的?A. 当前状态B. 输入符号C. 当前状态和输入符号D. 输出符号答案:C9. 以下哪个是图的遍历算法?A. 深度优先搜索B. 广度优先搜索C. 动态规划D. 分治算法答案:A10. 在集合论中,以下哪个符号表示集合的交集?A. ∪B. ∩C. ×D. ÷答案:B二、填空题(每题2分,共20分)1. 集合{1, 2, 3}的幂集是{∅, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}},其中包含元素个数最多的子集是_。
答案:{1, 2, 3}2. 在命题逻辑中,如果p和q都为真,则p∨q的真值为_。
答案:真3. 函数f: A→B中,若A={1, 2},B={a, b, c},则f是满射的必要条件是_。
《离散数学》期末练习题考试卷和答案

a , b, c , d , e, f , g,那么 所对应的 19. 设集合 A a , b , c , d , e , f , g , A 上有一个划分
等价关系 R 应有( )个序偶。 )。
20. 在有理数集合 Q 上定义二元运算*: a * b a b ab ,则 Q , * 的幺元是(
等价关系 R 应有( )个序偶。 )。
25. 在有理数集合 Q 上定义二元运算*: a * b a b ab ,则 Q , * 的幺元是(
26. 一个(
)称为布尔代数。
27.P Q P Q 的主析取范式是
。(写出一般
5
表示形式即可) 28.设集合 A a , b , c , d , R 是 A 上的二元关系,且 R a , b , b , a , b , c , c , d , a , c , 则 R 的传递闭包 t R 。
C. x x是正整数, x 5
D. x x是有理数, x 5
。
6.下面有关集合之间的包含和属于关系的说法,正确的是 Ⅰ. Ⅲ.
Ⅱ. , ,
Ⅳ.
a, b a, b, a, b
B.Ⅰ和Ⅲ
a, b a, b, a, b, c
二、填空题 1.设 A 为非空集合,且 A n ,则 A 上不同的二元关系的个数为 为 。 时, P Q 的真值为 1。 , A 上不同的映射的个数
2.设 P 、 Q 为两个命题,当且仅当
3. 在运算表中的空白处填入适当符号,使 a , b , c, * 成为群。 *
a a
a b c
4. 当 n 为 数时, K n n 3 必为欧拉图。
国家开放大学电大本科《离散数学》2024-2025期末试题及答案(试卷号:1009)

国家开放大学电大本科《离散数学》2024-2025期末试题及答案(试卷号:1009)一、单项选择题(每小题3分,本题共16分)若集合A = {1,2,3,4},则下列表述不正确的是( ).A.{2,3)€AB.AU{1,2,3,4}C. <1,2,3,4)QAD. 16A2.若无向图G的结点度数之和为20,则G的边数为( ).A.10B. 20C. 30D. 53.无向图G是棵树,结点数为10,则G的边数为( ).A. 5B. 10C.9D. 114.设A(x):x是人,B(x):x是学生,则命题“有的人是学生”可符号化为( )•A.Vx)(A(x)-*B(x»B.(3x)(A(x)AB(x))C.(Vx)(A(x)AB(x»D.-«(3x)(A(x)A -B(x»5.下面的推理正确的是( ).A.(l)(Vx)F(x)->G(x) 前提引入(2)F(>-)-*G(y) US(1).B.(1)( 3 x)F(x)-*G(x) 前提引入(2)F(y)-*G(y) US(1),C.(l)(3x)(F(x)->G(x»前提引入(2)F(y)-*G(x) ES(1).D.(l)(3x)(F(x)-*G(x)) 前提引入(2)F(y)-*G(y) ESQ).二、填空题(每小题3分,本题共15分)6.设A = {1,2),H = {1,2,3},则A到B上不同的函数个数为________________ .7.有&个结点的无向完全图的边数为 ____________ .8.若无向图G中存在欧拉路但不存在欧拉回路,则G的奇数度数的结点有________ 个.9.设G是有10个结点的无向连通图,结点的度数之和为30,则从G中删去条边后使之变成树.10.设个体域£> = {1,2,3,4},则谓词公式(*)人(了)消去量词后的等值式为三、逻辑公式翻译(每小题6分,本息共12分)11.将语句“昨天下甬“翻译成命题公式.12.将语句“小王今天上午或者去看电彩或者去打球”翻译成命JS公式.四、判断说明题(判断各题正误,并说明理由.每小题7分,本黑共14分)13.存在集合A与B,使得A6B与AUB同时成立.14.完全图K<是平面图.五、计算题(每小题12分,本题共36分)15.设偏序集VA,R>的哈斯图如下,B为A的子集,其中B = 试(1)写出R的关系表达式;(2)画出关系R的关系图;(3)求出B的最大元、极大元、上界.16.设图G — <V,E>,V={vj f v it v t,Vi»v s)»(v2, v3)»(v3»vs)}»试(1)画出G的图形表示;(2)写出其邻接矩阵;(3)求出每个结点的度数;(4)画出图G的补图的图形,17.求P TQ代R)的合取范式与主合取范式.六、证明题(本题共8分)18.设A.B是任意集合,试证明:若AXA=BXB,^ A = B.M答杖松标准(仅辩者)一、单项选择题(每小题3分,本题共15分)1. A2. A3. C4.B5. D二、填空题(每小题3分,本题共]5分)6.97.”3 — 1)/2(或庆)8.210. A(l) VA(2) V A(3) V A(4)三、 逻辑公式翻译(每小题6分,本题共】2分)H,设P :昨天下雨. 则命题公式为:P ,12. 设P :小王今天上午去看电影 Q :小王今天上午去打球 则命题公式为:r (PiQ ). 或者(rPAQ )V 〈PA rQ )四、 判断说明题(每小题7分,本题共14分)13. 正确.例:设 A = {a} t H — {a,{a}) 则有且ACI3.说明:举出符合条件的例均给分. 14. 正确.完全图K 〈是平面图, 如K,可以如下图示嵌入平面.(7分)五、计算题(每小题12分,本题共36分)15. (l )R = {Va ,a>,Vb,Q>,Vc,c>,Vd,d>・Va0>・Va ・c>,V&,d>,VQ,d >}. (4 分)(2)关系图(8分)(3)集合B 无最大元,极大元为6与c.无上界. 16, 解: (1)关系图(2分) (6分)(2分)(6分)(3分) (517. P TQAR) 5PV(QAR) 0(rPVQ 〉A(rPVR)合取范式<=>(-PVQ)V(K A rR)A(rPVR) 0("VQ)V(& A rR)A(" VR)V(QA -Q)D(rPVQVR)A(rPVQVA("VR VQ) A(-、PVR V -Q) c=>(-PVQV7?)A(-'PVQV-R)A(-PV-QVR) 主合取范式 六、证明题(本意共8分)18. 证明:V2(2)邻接矩阵bioir 101001001 1 00 0(6分)(3) deg(vi)=,3deg(v t )—2 <ieg(v 3)~2 deg顷)=1 deg(v s )=2 (4) 补图(9分)(】2分)(2分) (5分)(7分〉设x€A,则Vx,x>€AXA,(1 分)因AXA = BXB,故V X,X>€BXB,则有xGB, (3 分)因此AGB. (5分)设xQB,则Vx,x>€BXB,(6 分)因AXA-BXB,故Vx,x>eAXA,则有因此BWA. (7 分)故得A=B. (8分)。
离散数学期末考试题及答案

离散数学期末考试题及答案一、单项选择题(每题2分,共20分)1. 集合A={1,2,3},B={2,3,4},则A∩B=()。
A. {1,2,3}B. {2,3}C. {2,4}D. {1,4}答案:B2. 命题“若x>0,则x>1”的逆否命题是()。
A. 若x≤0,则x≤1B. 若x≤1,则x≤0C. 若x>1,则x>0D. 若x≤1,则x≤0答案:B3. 函数f: A→B的定义域是集合A,值域是集合B,则()。
A. A⊆BB. A⊂BC. A⊇BD. A⊃B答案:A4. 集合{1,2,3}与集合{3,2,1}是否相等?()。
A. 是B. 否C. 无法确定D. 以上都不对答案:A5. 命题p:“x>0”,则¬p为()。
A. x≤0B. x<0C. x=0D. x<0或x=0答案:A6. 命题“若x>0,则x>1”的逆命题是()。
A. 若x>0,则x>1B. 若x≤1,则x≤0C. 若x>1,则x>0D. 若x≤0,则x≤1答案:C7. 函数f: A→B的定义域是集合A,值域是集合B,则()。
A. A⊆BB. A⊂BC. A⊇BD. A⊃B答案:A8. 集合{1,2,3}与集合{3,2,1}是否相等?()。
A. 是B. 否C. 无法确定D. 以上都不对答案:A9. 命题p:“x>0”,则¬p为()。
A. x≤0B. x<0C. x=0D. x<0或x=0答案:A10. 命题“若x>0,则x>1”的逆命题是()。
A. 若x>0,则x>1B. 若x≤1,则x≤0C. 若x>1,则x>0D. 若x≤0,则x≤1答案:C二、填空题(每题2分,共20分)1. 集合A={1,2,3},B={2,3,4},则A∪B=______。
答案:{1,2,3,4}2. 命题“若x>0,则x>1”的逆否命题是:若x≤1,则x≤0。
离散数学期末考试试题(有几套带答案)

离散试卷及答案离散数学试题(A 卷及答案)一、证明题(10分) 1)(P ∧(Q ∧R))∨(Q ∧R)∨(P ∧R)R证明: 左端(P ∧Q ∧R)∨((Q ∨P)∧R)((P ∧Q)∧R))∨((Q ∨P)∧R)((P ∨Q)∧R)∨((Q ∨P)∧R)((P ∨Q)∨(Q ∨P))∧R ((P ∨Q)∨(P ∨Q))∧RT ∧R(置换)R2)x(A(x)B(x))xA(x)xB(x) 证明 :x(A(x)B(x))x(A(x)∨B(x))xA(x)∨xB(x)xA(x)∨xB(x)xA(x)xB(x)二、求命题公式(P ∨(Q ∧R))(P ∧Q ∧R)的主析取范式和主合取范式(10分)证明:(P ∨(Q ∧R))(P ∧Q ∧R)(P ∨(Q ∧R))∨(P ∧Q ∧R))(P ∧(Q ∨R))∨(P ∧Q ∧R) (P ∧Q)∨(P ∧R))∨(P ∧Q ∧R) (P ∧Q ∧R)∨(P ∧Q ∧R)∨(P ∧Q ∧R))∨(P ∧Q ∧R))∨(P ∧Q ∧R) m0∨m1∨m2∨m7 M3∨M4∨M5∨M6三、推理证明题(10分) 1)C ∨D, (C ∨D) E, E (A ∧B), (A ∧B)(R ∨S)R ∨S证明:(1) (C ∨D) E(2) E (A ∧B) (3) (C ∨D)(A ∧B)(4) (A ∧B)(R ∨S)(5) (C ∨D)(R ∨S)(6) C ∨D (7) R ∨S 2) x(P(x)Q(y)∧R(x)),xP(x)Q(y)∧x(P(x)∧R(x)) 证明(1)xP(x)(2)P(a) (3)x(P(x)Q(y)∧R(x)) (4)P(a)Q(y)∧R(a)(5)Q(y)∧R(a) (6)Q(y) (7)R(a) (8)P(a) (9)P(a)∧R(a) (10)x(P(x)∧R(x))(11)Q(y)∧x(P(x)∧R(x))四、设m 是一个取定的正整数,证明:在任取m +1个整数中,至少有两个整数,它们的差是m 的整数倍证明 设1a ,2a ,…,1+m a 为任取的m +1个整数,用m 去除它们所得余数只能是0,1,…,m -1,由抽屉原理可知,1a ,2a ,…,1+m a 这m +1个整数中至少存在两个数s a 和t a ,它们被m 除所得余数相同,因此s a 和t a 的差是m 的整数倍。
离散数学期末考试试卷

离散数学期末考试试卷一、选择题(每题2分,共20分)1. 集合A={1, 2, 3},集合B={2, 3, 4},请找出A与B的交集。
A. {1, 2}B. {2, 3}C. {1, 3}D. {4}2. 命题逻辑中,若P∨Q为真,P∧Q为假,以下哪个命题一定为真?A. P为真B. Q为真C. P为假D. 不能确定3. 以下哪个选项表示的是函数f(x) = x^2 + 3x + 2的值域?A. (-∞, +∞)B. [1, +∞)C. [0, +∞)D. (-∞, 1]4. 在图论中,一个图的度是指什么?A. 顶点的个数B. 边的个数C. 与顶点相连的边的个数D. 图的连通性5. 以下哪个命题是可满足的?A. ∀x P(x) → ∃x ¬P(x)B. ∃x P(x) ∧ ∀x ¬P(x)C. ∀x P(x) ∨ ∃x ¬P(x)D. ∀x ¬P(x) → ∃x P(x)...(此处省略其他选择题)二、简答题(每题10分,共20分)1. 简述什么是归纳推理,并给出一个具体的例子。
2. 解释什么是二元关系,并给出一个二元关系的例子。
三、证明题(每题15分,共30分)1. 证明:对于任意的自然数n,n^2 + 3n + 2总是大于等于n + 2。
2. 证明:如果一个图是连通的,并且每个顶点的度至少为1,那么这个图至少有一个环。
四、应用题(每题15分,共30分)1. 给定一个无向图,顶点集为{A, B, C, D, E},边集为{(A, B), (B,C), (C, D), (D, E), (E, A), (B, D)}。
请找出这个图的所有简单路径。
2. 假设有一个有限状态机,状态集合为{S1, S2, S3},初始状态为S1,接受状态为S3。
给定一个转换函数δ,其中δ(S1, a) = S2, δ(S2, b) = S3, δ(S3, a) = S1,以及一个输入字符串"ab",请确定这个有限状态机是否接受该字符串。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《离散数学》期末考试题(E)
一、填空题(每小题3分,共15分)
1.设A = {2, {3}, 4, a }, B = {1, 3, 4, {a }}, 则{3}( )A ,{a }( )B ,{{a }}( )B .
2. 设A = {1, 2, 3, 4, 5}上的关系R = {(1, 2), (3, 4), (2, 2)}, S = {(4, 2), (2, 5), (3, 1), (1, 3)}, 则=S R { }, =R S { }, =R R { }.
3. gcd(36, 48) = ( ),lcm(36, 48) = ( ).
4.任意有限布尔代数)1,0,,,,(⋅+B 均与集合代数( )同构,其元素个数为
( ).
5. 不同构的5阶无向树有( )棵,不同构的5阶根树有( )棵.
二、单选题(每小题3分,共15分)
1. 在有理数集合Q 上定义运算“*”如下:对于任意x , y ∈ Q ,y x * = x + y – xy ,则Q 关于*的单位元是( ).
(A)x . (B)y . (C)1. (D)0.
2. 设A = {1, 2, 3}, 下图分别给出了A 上的两个关系R 和S ,则S R 是( )关系.
(A)自反. (B)对称. (C)传递. (D)等价.
3.令T (x ): x 是火车,B (x ): x 是汽车,F (x , y ): x 比y 快,则“某些汽车比所有的火车慢”符号化为( ).
(A)()()),()()(y x H x T x y B y →∀∧∃.
(B)()()),()()(y x H x T x y B y ∧∀→∃.
(C)()()),()()(y x H x T y B y x ∧→∃∀.
G S G R
(D)()()),()()(y x H x T x y B y →∀→∃.
4. 整数集合Z 关于数的加法“+”和数的乘法“⋅”构成的代数结构(Z, +, ⋅)是( ).
(A)域 (B)域和整环 (C)整环 (D) 有零因子环
5.设G 是简单图,G 是G 的补图,若G G ≅,则称G 为自补图. 5阶不同构的自补图个数为( ).
(A)0. (B)1. (C)2. (D)3.
三、判断题(每小题3分,共15分): 正确打“√”,错误打“×”.
1. { ∅, {∅}} ∉ P (P ({∅})). ( )
2. 非空1元及2元联结词集合的个数为29-1. ( )
3. 群可分为Abel 群和非Abel 群. ( )
4. 元素个数相同的有限域都是同构的. ( )
5. 设G 是简单图,则G 或G 是连通图. ( )
四、(15分) 设C B g B A f →→:,:, 若g f 是单射,证明f 是单射,并举例说明g 不一定是单射.
五、(10分) 设A = {a , b , c , d }上的关系R = {(a , b ), (b , d ), (c , c ), (a , c )}, 画出R 的关系图,并求出R 的自反闭包r (R )、对称闭包s (R )和传递闭包t (R ).
六、(10分)用CP 规则证明下列推理.
s q p s r q r q p →⇒→→∨⌝∨⌝),(),(.
七、(10分) 求谓词公式))()(())()((z zC x A y yB x xA ∀→∧∀∨⌝∃的前束范式.
八、(10分)任意6个人中,一定有3个人彼此认识或有3个人彼此不认识.。
