奇妙的一笔画
小学数学竞赛:奇妙的一笔画.教师版解题技巧 培优 易错 难

所谓图的一笔画,指的就是:从图的一点出发,笔不离纸,遍历每条边恰好一次,即每条边都只画一次,不准重复.从图中容易看出:能一笔画出的图首先必须是连通图.但是否所有的连通图都可以一笔画出呢?下面,我们就来探求解决这个问题的方法.什么样的图形能一笔画成呢?这就是一笔画问题,它是一种有名的数学游戏.我们把一个图形中与偶数条线相连接的点叫做偶点.相应的把与奇数条线相连接的点叫做奇点. 一笔画问题:(1)能一笔画出的图形必须是连通的图形;(2)凡是只由偶点组成的连通图形.一定可以一笔画出.画时可以由任一偶点作为起点.最后仍回到这点; (3)凡是只有两个奇点的连通图形一定可以一笔画出.画时必须以一个奇点作为起点,以另一个奇点为终点; (4)奇点个数超过两个的图形,一定不能一笔画. 多笔画问题:我们把不能一笔画成的图,归纳为多笔画.多笔画图形的笔画数恰等于奇点个数的一半.事实上,对于任意的连通图来说,如果有2n 个奇点(n 为自然数),那么这个图一定可以用n 笔画成.模块一、判断奇偶点【例 1】 我们把一个图形上与偶数条线相连的点叫做偶点,与奇数条线相连的点叫做奇点.下图中,哪些点是偶点?哪些点是奇点?J O I H G FED CBA【考点】一笔画问题 【难度】2星 【题型】解答 【解析】 奇点: D H J O 偶点:A B C E F G I 【答案】奇点: D H J O 偶点:A B C E F G I【例 2】 同学们野营时建了9个营地,连接营地之间的道路如图所示,贝贝要给每个营地插上一面旗帜,要求相邻营地的旗帜色彩不同,则贝贝最少需要 种颜色的旗子,如果贝贝从某营地出发,不走重复路线就 (填“能”或“不能”)完成任务.【考点】一笔画问题 【难度】2星 【题型】填空 【关键词】华杯赛,六年级,初赛,第10题 【解析】 最少需要3种颜色的旗子。
因为中间的三点连成一个三角形,要使这三点所代表营地两粮相邻,要使相邻营地没有相同颜色的旗子,必须各插一种与其它两点不同颜色的旗子。
第五讲 神奇的一笔画
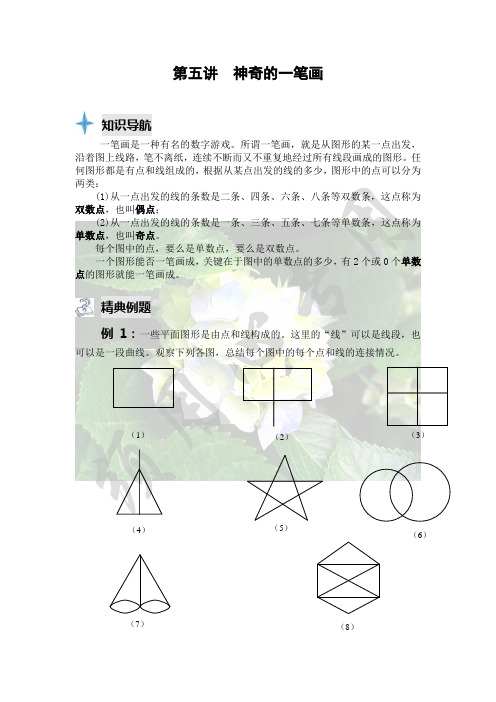
第五讲神奇的一笔画知识导航一笔画是一种有名的数字游戏。
所谓一笔画,就是从图形的某一点出发,沿着图上线路,笔不离纸,连续不断而又不重复地经过所有线段画成的图形。
任何图形都是有点和线组成的,根据从某点出发的线的多少,图形中的点可以分为两类:(1)从一点出发的线的条数是二条、四条、六条、八条等双数条,这点称为双数点,也叫偶点;(2)从一点出发的线的条数是一条、三条、五条、七条等单数条,这点称为单数点,也叫奇点。
每个图中的点,要么是单数点,要么是双数点。
一个图形能否一笔画成,关键在于图中的单数点的多少,有2个或0个单数点的图形就能一笔画成。
精典例题例1:一些平面图形是由点和线构成的。
这里的“线”可以是线段,也可以是一段曲线。
观察下列各图,总结每个图中的每个点和线的连接情况。
(1)(2)(3)(4)(5)(6)(7)(8)思路点拨首先在每一幅图中标出线与线相交的点,然后再将与每个点连接的线的条数数出来并标在旁边。
如果有单数条线与这个点连接,这个点就称之为单数点;如果有双数条线与这个点连接,这个点就称之为双数点。
模仿练习数一数,下图中有几个单数点,几个双数点。
单数点: 个 双数点: 个例2:下列图形中各有几个单数点?能一笔画成吗?思路点拨标出每幅图中的点,并将其归类为单数点或双数点,根据图中单数点的个数来判断其是否可以一笔画成。
单数点: 个 能不能一笔画: 单数点: 个 能不能一笔画: 单数点: 个 能不能一笔画:模仿练习( ) ( )( )( ) ( )( )例3:下图能不能一笔画成?如果能,应该怎样画?思路点拨有0个单数点或者2个单数点的图形才能一笔画。
第1个图形有 个单数点,是否可以一笔画,如果可以,在画的过程中应该从图上哪一处作为出发点,完成时笔尖又会停在哪呢?第2、3个图形呢?相信聪明的你们都能够发现这其中的奥妙,大胆来尝试吧!(1) (2) (5) (4) (模仿练习判断下列各图能否一笔画成,并说明理由。
1.3.1 奇妙的一笔画
调动学生积极性。
通过具体多次操练,以突破本课重点。
总结延伸
小结本课
小结:这节课你学会了什么?
学生总结,个别补充
学习成果
教学反思
课题
奇妙的一笔画
年级学科
六年信息技术
教材出版社
辽师大版
教者
单元章节
第三课
教学时间
40
教学目标
知识与
技能
掌握REPEAT重复命令的使用方法
过程与
方法
掌握REPEAT重复命令的使用方法
情感态度与价值观
培养学生动手操作能力。
内容分析
掌握REPEAT重复命令的使用方法
学情分析
学生对电脑知识的认知能力、实际操作能力、知识水平各不相同。
FD 30 BK 30 RT 90;FD 20 RT 90 FD 20 LT 90
FD 30 BK 30 RT 90;FD 20 RT 90 FD 20 LT 90
5、为小海龟画一个“跑道”吧!
学生倾听
学生操作,完成用重复命令画出一个正方形。
讨论并理解熟记重复命令。
学生操作并讨论如何确定角度。
学生讨论总结出画正多边形的公式。
3、画一个边长为25的正八边形。
指导学生得到画正多边形的公式:
REPEAT边数[FD边长RT 360/边数]
4、将下边的步骤用REPEAT命令表示出来,并画出相应的图形。
FD 30 BK 30 RT 90;FD 20 RT 90 FD 20 LT 90
FD 30 BK 30 RT 90;FD 20 RT 90 FD 20 LT 90
REPEAT重复次数[重复内容]
如:REPEAT 4[FD 60 RT 90]
小学奥数 奇妙的一笔画 精选练习例题 含答案解析(附知识点拨及考点)

所谓图的一笔画,指的就是:从图的一点出发,笔不离纸,遍历每条边恰好一次,即每条边都只画一次,不准重复.从图中容易看出:能一笔画出的图首先必须是连通图.但是否所有的连通图都可以一笔画出呢?下面,我们就来探求解决这个问题的方法.什么样的图形能一笔画成呢?这就是一笔画问题,它是一种有名的数学游戏.我们把一个图形中与偶数条线相连接的点叫做偶点.相应的把与奇数条线相连接的点叫做奇点. 一笔画问题:(1)能一笔画出的图形必须是连通的图形;(2)凡是只由偶点组成的连通图形.一定可以一笔画出.画时可以由任一偶点作为起点.最后仍回到这点; (3)凡是只有两个奇点的连通图形一定可以一笔画出.画时必须以一个奇点作为起点,以另一个奇点为终点; (4)奇点个数超过两个的图形,一定不能一笔画. 多笔画问题:我们把不能一笔画成的图,归纳为多笔画.多笔画图形的笔画数恰等于奇点个数的一半.事实上,对于任意的连通图来说,如果有2n 个奇点(n 为自然数),那么这个图一定可以用n 笔画成.模块一、判断奇偶点【例 1】 我们把一个图形上与偶数条线相连的点叫做偶点,与奇数条线相连的点叫做奇点.下图中,哪些点是偶点?哪些点是奇点?J O I H G FED CBA【考点】一笔画问题 【难度】2星 【题型】解答【解析】 奇点: D H J O 偶点:A B C E F G I 【答案】奇点: D H J O 偶点:A B C E F G I【例 2】 同学们野营时建了9个营地,连接营地之间的道路如图所示,贝贝要给每个营地插上一面旗帜,要求相邻营地的旗帜色彩不同,则贝贝最少需要 种颜色的旗子,如果贝贝从某营地出发,不走重复路线就 (填“能”或“不能”)完成任务.【考点】一笔画问题 【难度】2星 【题型】填空例题精讲知识点拨4-1-5.奇妙的一笔画【关键词】华杯赛,六年级,初赛,第10题【解析】最少需要3种颜色的旗子。
因为中间的三点连成一个三角形,要使这三点所代表营地两粮相邻,要使相邻营地没有相同颜色的旗子,必须各插一种与其它两点不同颜色的旗子。
小学奥数奇妙的一笔画题库教师版

奇妙的一笔画例题精讲所谓图的一笔画,指的就是:从图的一点出发,笔不离纸,遍历每条边恰好一次,即每条边都只画一次,不准重复.从图中容易看出:能一笔画出的图首先必须是连通图.但是否所有的连通图都可以一笔画出呢下面,我们就来探求解决这个问题的方法.什么样的图形能一笔画成呢这就是一笔画问题,它是一种有名的数学游戏.我们把一个图形中与偶数条线相连接的点叫做偶点.相应的把与奇数条线相连接的点叫做奇点.一笔画问题:(1)能一笔画出的图形必须是连通的图形;(2)凡是只由偶点组成的连通图形.一定可以一笔画出.画时可以由任一偶点作为起点.最后仍回到这点;(3)凡是只有两个奇点的连通图形一定可以一笔画出.画时必须以一个奇点作为起点,以另一个奇点为终点;(4)奇点个数超过两个的图形,一定不能一笔画.多笔画问题:我们把不能一笔画成的图,归纳为多笔画.多笔画图形的笔画数恰等于奇点个数的一半.事实上,对于任意的连通图来说,如果有2n个奇点(n为自然数),那么这个图一定可以用n笔画成.【例 1】我们把一个图形上与偶数条线相连的点叫做偶点,与奇数条线相连的点叫做奇点.下图中,哪些点是偶点哪些点是奇点【解析】奇点:J D H F偶点:A E B C G I【例 2】判断下列图a、图b、图c能否一笔画.【解析】图a能,因为有2个奇点,图b不能,因为图形不是连通的,图c能,因为因为图中全是奇点【例 3】下面图形能不能一笔画成若果能,应该怎样画【解析】图1能因为图中全是偶点,图2能因为图中全是偶点,图3不能因为有4个奇点.【例 4】下面的图形,哪些能一笔画出哪些不能一笔画出【解析】第1个能,2、3不能【例 5】下图中不能一笔画成,请你在下图中添加最少的线段,将其改成一笔画的图形,并画出路线图.【解析】不能一笔画出,因为图中有E H G F四个奇点,连结EH就可以使图形一笔画出.【例 6】下图中的线段表示小路,请你仔细观察,认真思考,能够不重复的爬遍小路的是甲蚂蚁还是乙蚂蚁该怎样爬【解析】要想不重复爬出,需要图形能一笔画出,由于图中有两个奇点,所以应该从奇点出发才能一笔画出图形,所以甲蚂蚁能够.【例 7】能否用剪刀从左下图中一次连续剪下三个正方形和两个三角形【解析】可以.【例 8】下图是儿童乐园的道路平面图,要使游客走遍每条路并且不重复,那么出、入口应设在哪里【解析】要想不重复,需要路线能一笔画出,由于图中有两个奇点,所以入口和出口应该分别放在两个奇点出,即F和I点.【例 9】邮递员叔叔向11个地点送信一次信,不走重复路,怎样走最合适【解析】不走重复路,一笔能画出路线图,图中有2个奇点,应该从奇点处出发,下面有一种参考路线:4-1-2-5-8-9-6-【例 10】观察下面的图,看各至少用几笔画成【解析】图(1)有8个奇点,所以要4笔画出,图(2)有12个奇点,所以要一笔画出,图(3)能一笔画出.【例 11】判断下列图形能否一笔画.若能,请给出一种画法;若不能,请加一条线或去一条线,将其改成可一笔画的图形.【解析】图(1)不能一笔画出,因为图中有4个奇点,连结BD,或者去掉BF都可以使图形能一笔画出.图(2)不能一笔画出,因为图中有4个奇点,去掉KL,或者BK都可以使图形能一笔画出.图(3)不能一笔画出,因为图中有4个奇点,去掉AB可以使图形能一笔画出.一个K(K>1)笔画最少要添加几条连线才能变成一笔画呢我们知道K笔画有2K个奇点,如果在任意两个奇点之间添加一条连线,那么这两个奇点同时变成了偶点.如左下图中的B,C两个奇点在右下图中都变成了偶点.所以只要在K笔画的2K个奇点间添加(K-1)笔就可以使奇点数目减少为2个,从而变成一笔画.【例 12】18世纪的哥尼斯堡城是一座美丽的城市,在这座城市中有一条布勒格尔河横贯城区,这条河有两条支流在城市中心汇合,汇合处有一座小岛A和一座半岛D,人们在这里建了一座公园,公园中有七座桥把河两岸和两个小岛连接起来(如图a).如果游人要一次走过这七座桥,而且对每座桥只许走一次,问如何走才能成功【解析】欧拉解决这个问题的方法非常巧妙.他认为:人们关心的只是一次不重复地走遍这七座桥,而并不关心桥的长短和岛的大小,因此,岛和岸都可以看作一个点,而桥则可以看成是连接这些点的一条线.这样,一个实际问题就转化为一个几何图形(如下图)能否一笔画出的问题了.而图B中有4个奇点显然不能一笔画出.【巩固】如下图所示,两条河流的交汇处有两个岛,有七座桥连接这两个岛及河岸.问:一个散步者能否一次不重复地走遍这七座桥【解析】能【例 13】右图是某展览厅的平面图,它由五个展室组成,任两展室之间都有门相通,整个展览厅还有一个进口和一个出口,问游人能否一次不重复地穿过所有的门,并且从入口进,从出口出【解析】将图形中的6个区域看成6个点,每个门看成连结他们的线段,显然6个点都是偶点,所以有人能一次不重复的走过所有的门.【巩固】右图是某展览馆的平面图,一个参观者能否不重复地穿过每一扇门如果不能,请说明理由.如果能,应从哪开始走【解析】不能【例 14】一条小虫沿长6分米,宽4分米,高5分米的长方体的棱爬行.如果它只能进不能退,并且同一条棱不能爬两次,那么它最多能爬多少分米【解析】8个定点都是奇点,所以至少需要4笔.多画长和高能保证总路程最长,为A-B-G-H-A-D-C-F-E-D总长为6×4+5×4 +4×1=48分米.【巩固】一只木箱的长、宽、高分别为5,4,3厘米(见右图),有一只甲虫从A点出发,沿棱爬行,每条棱不允许重复,则甲虫回到A点时,最多能爬行多少厘米【解析】最多34厘米【例 15】如图是某餐厅的平面图,共有五个小厅,相邻两厅之间有门相通,并且设有入口.请问你能否从入口进入一次不重复地穿过所有的门.如果可以,请指明穿行路线,如果不能,应关闭哪个门就可以办到【解析】可以将图中的五个小厅以及厅外的部分都抽象成点,为方便解题,给它们分别编号.这时,连通厅与厅之间的门就相当于各点之间的连线.于是题目中餐厅的平面图就抽象成为一个连通的图形,求穿形路线的问题就转化成一笔画的问题.在抽象出的图形中,我们可以找到四个奇点,即①、④、③和厅外,所以图形不能一笔画出也就是说,从入口进入不可能一次不重复的穿过所有的门.但根据一笔画问题的知识,只要关闭门,把③、④变为偶点,就可以办到,可行路线如下图:B【例 16】在3×3的方阵中每个小正方形的边长都是100米.小明沿线段从A点到B 点,不许走重复路,他最多能走多少米【解析】这道题大多数同学都采用试画的方法,实际上可以用一笔画原理求解.首先,图中有8 个奇点,在8 个奇点之间至少要去掉4 条线段,才能使这8 个奇点变成偶点;其次,从A点出发到B 点,A,B 两点必须是奇点,现在A,B 都是偶点,必须在与A,B 连接的线段中各去掉1 条线段,使A,B 成为奇点.所以至少要去掉6 条线段,也就是最多能走1800 米,走法如图【例 17】一个邮递员投递信件要走的街道如右图所示,图中的数字表示各条街道的千米数,他从邮局出发,要走遍各街道,最后回到邮局.怎样走才能使所走的行程最短全程多少千米【解析】图中共有8 个奇点,必须在8 个奇点间添加4 条线,才能消除所有奇点,成为能从邮局出发最后返回邮局的一笔画.在距离最近的两个奇点间添加一条连线,如左下图中虚线所示,共添加4 条连线,这4 条连线表示要重复走的路,显然,这样重复走的路程最短,全程30 千米.走法参考右下图(走法不唯一).。
小学奥数教程:奇妙的一笔画_全国通用(含答案)

所谓图的一笔画,指的就是:从图的一点出发,笔不离纸,遍历每条边恰好一次,即每条边都只画一次,不准重复.从图中容易看出:能一笔画出的图首先必须是连通图.但是否所有的连通图都可以一笔画出呢?下面,我们就来探求解决这个问题的方法.什么样的图形能一笔画成呢?这就是一笔画问题,它是一种有名的数学游戏.我们把一个图形中与偶数条线相连接的点叫做偶点.相应的把与奇数条线相连接的点叫做奇点. 一笔画问题:(1)能一笔画出的图形必须是连通的图形;(2)凡是只由偶点组成的连通图形.一定可以一笔画出.画时可以由任一偶点作为起点.最后仍回到这点; (3)凡是只有两个奇点的连通图形一定可以一笔画出.画时必须以一个奇点作为起点,以另一个奇点为终点; (4)奇点个数超过两个的图形,一定不能一笔画. 多笔画问题:我们把不能一笔画成的图,归纳为多笔画.多笔画图形的笔画数恰等于奇点个数的一半.事实上,对于任意的连通图来说,如果有2n 个奇点(n 为自然数),那么这个图一定可以用n 笔画成.模块一、判断奇偶点【例 1】 我们把一个图形上与偶数条线相连的点叫做偶点,与奇数条线相连的点叫做奇点.下图中,哪些点是偶点?哪些点是奇点?J O I H G FED CBA【考点】一笔画问题 【难度】2星 【题型】解答 【解析】 奇点: D H J O 偶点:A B C E F G I 【答案】奇点: D H J O 偶点:A B C E F G I【例 2】 同学们野营时建了9个营地,连接营地之间的道路如图所示,贝贝要给每个营地插上一面旗帜,要求相邻营地的旗帜色彩不同,则贝贝最少需要 种颜色的旗子,如果贝贝从某营地出发,不走重复路线就 (填“能”或“不能”)完成任务.【考点】一笔画问题 【难度】2星 【题型】填空 【关键词】华杯赛,六年级,初赛,第10题 【解析】 最少需要3种颜色的旗子。
因为中间的三点连成一个三角形,要使这三点所代表营地两粮相邻,要使相邻营地没有相同颜色的旗子,必须各插一种与其它两点不同颜色的旗子。
小学奥数—奇妙的一笔画

知识点拨
所谓图的一笔画,指的就是:从图的一点出发,笔不离纸,遍历每条边恰好一次,即每条边都只画一次, 不准重复.从图中容易看出:能一笔画出的图首先必须是连通图.但是否所有的连通图都可以一笔画出呢? 下面,我们就来探求解决这个问题的方法.
什么样的图形能一笔画成呢?这就是一笔画问题,它是一种有名的数学游戏. 我们把一个图形中与偶数条线相连接的点叫做偶点.相应的把与奇数条线相连接的点叫做奇点. 一笔画问题: (1)能一笔画出的图形必须是连通的图形; (2)凡是只由偶点组成的连通图形.一定可以一笔画出.画时可以由任一偶点作为起点.最后仍回到这点; (3)凡是只有两个奇点的连通图形一定可以一笔画出.画时必须以一个奇点作为起点,以另一个奇点为终点; (4)奇点个数超过两个的图形,一定不能一笔画. 多笔画问题: 我们把不能一笔画成的图,归纳为多笔画.多笔画图形的笔画数恰等于奇点个数的一半.事实上,对于 任意的连通图来说,如果有 2n 个奇点(n 为自然数),那么这个图一定可以用 n 笔画成.
【例 17】 下图中不能一笔画成,请你在下图中添加最少的线段,将其改成一笔画的图形,并画出路线图.
A
E
D
G
H
B
C
F
【例 18】 如图所示,某小区花园的道路为一个长 480 米,宽 200 米的长方形;一个边长为 260 米的菱形和十 字交叉的两条道路组成.一天,王大爷 A 处进入花园,走遍花园的所有道路并从 A 处离开.如果
【巩固】如下图所示,两条河流的交汇处有两个岛,有七座桥连接这两个岛及河岸.问:一个散步者能否一 次不重复地走遍这七座桥?
【例 21】 一个邮递员投递信件要走的街道如右图所示,图中的数字表示各条街道的千米数,他从邮局出发, 要走遍各街道,最后回到邮局.怎样走才能使所走的行程最短?全程多少千米?
4-1-4奇妙的一笔画

所谓图的一笔画,指的就是:从图的一点出发,笔不离纸,遍历每条边恰好一次,即每条边都只画一次,不准重复.从图中容易看出:能一笔画出的图首先必须是连通图.但是否所有的连通图都可以一笔画出呢?下面,我们就来探求解决这个问题的方法.什么样的图形能一笔画成呢?这就是一笔画问题,它是一种有名的数学游戏.我们把一个图形中与偶数条线相连接的点叫做偶点.相应的把与奇数条线相连接的点叫做奇点.一笔画问题:(1)能一笔画出的图形必须是连通的图形;(2)凡是只由偶点组成的连通图形.一定可以一笔画出.画时可以由任一偶点作为起点.最后仍回到这点;(3)凡是只有两个奇点的连通图形一定可以一笔画出.画时必须以一个奇点作为起点,以另一个奇点为终点;(4)奇点个数超过两个的图形,一定不能一笔画.多笔画问题:我们把不能一笔画成的图,归纳为多笔画.多笔画图形的笔画数恰等于奇点个数的一半.事实上,对于任意的连通图来说,如果有2n 个奇点(n 为自然数),那么这个图一定可以用n 笔画成.【例1】我们把一个图形上与偶数条线相连的点叫做偶点,与奇数条线相连的点叫做奇点.下图中,哪些点是偶点?哪些点是奇点?【解析】奇点:J D H F 偶点:A E B C G I【例2】判断下列图a 、图b 、图c 能否一笔画.图a NM L KFD E C BA图b O D CB A 图c G F E DC B A 【解析】图a 能,因为有2个奇点,图b 不能,因为图形不是连通的,图c 能,因为因为图中全是奇点【例3】下面图形能不能一笔画成?若果能,应该怎样画?例题精讲奇妙的一笔画【解析】图1能因为图中全是偶点,图2能因为图中全是偶点,图3不能因为有4个奇点.【例 4】下面的图形,哪些能一笔画出?哪些不能一笔画出?【解析】第1个能,2、3不能【例5】下图中不能一笔画成,请你在下图中添加最少的线段,将其改成一笔画的图形,并画出路线图.【解析】不能一笔画出,因为图中有E H G F四个奇点,连结EH就可以使图形一笔画出.【例6】下图中的线段表示小路,请你仔细观察,认真思考,能够不重复的爬遍小路的是甲蚂蚁还是乙蚂蚁?该怎样爬?【解析】要想不重复爬出,需要图形能一笔画出,由于图中有两个奇点,所以应该从奇点出发才能一笔画出图形,所以甲蚂蚁能够.【例7】能否用剪刀从左下图中一次连续剪下三个正方形和两个三角形?【解析】可以.【例8】下图是儿童乐园的道路平面图,要使游客走遍每条路并且不重复,那么出、入口应设在哪里?【解析】要想不重复,需要路线能一笔画出,由于图中有两个奇点,所以入口和出口应该分别放在两个奇点出,即F 和I 点.【例9】邮递员叔叔向11个地点送信一次信,不走重复路,怎样走最合适?【解析】不走重复路,一笔能画出路线图,图中有2个奇点,应该从奇点处出发,下面有一种参考路线:4-1-2-5-8-9-6-10-11-7-4-3【例10】观察下面的图,看各至少用几笔画成?【解析】图(1)有8个奇点,所以要4笔画出,图(2)有12个奇点,所以要一笔画出,图(3)能一笔画出.【例11】判断下列图形能否一笔画.若能,请给出一种画法;若不能,请加一条线或去一条线,将其改成可一笔画的图形.I H G F E D CB A图a H G I K L J F ED CB A图b D C H G E F B A 图c【解析】图(1)不能一笔画出,因为图中有4个奇点,连结BD ,或者去掉BF 都可以使图形能一笔画出.图(2)不能一笔画出,因为图中有4个奇点,去掉KL ,或者BK 都可以使图形能一笔画出.图(3)不能一笔画出,因为图中有4个奇点,去掉AB 可以使图形能一笔画出.一个K (K >1)笔画最少要添加几条连线才能变成一笔画呢?我们知道K 笔画有2K 个奇点,如果在任意两个奇点之间添加一条连线,那么这两个奇点同时变成了偶点.如左下图中的B ,C 两个奇点在右下图中都变成了偶点.所以只要在K 笔画的2K 个奇点间添加(K-1)笔就可以使奇点数目减少为2个,从而变成一笔画.【例12】18世纪的哥尼斯堡城是一座美丽的城市,在这座城市中有一条布勒格尔河横贯城区,这条河有两条支流在城市中心汇合,汇合处有一座小岛A 和一座半岛D ,人们在这里建了一座公园,公园中。
小学奥数奇妙的一笔画

所谓图的一笔画,指的就是:从图的一点出发,笔不离纸,遍历每条边恰好一次,即每条边都只画一次,不准重复.从图中容易看出:能一笔画出的图首先必须是连通图.但是否所有的连通图都可以一笔画出呢?下面,我们就来探求解决这个问题的方法.什么样的图形能一笔画成呢?这就是一笔画问题,它是一种有名的数学游戏.我们把一个图形中与偶数条线相连接的点叫做偶点.相应的把与奇数条线相连接的点叫做奇点.一笔画问题:(1)能一笔画出的图形必须是连通的图形;(2)凡是只由偶点组成的连通图形.一定可以一笔画出.画时可以由任一偶点作为起点.最后仍回到这点;(3)凡是只有两个奇点的连通图形一定可以一笔画出.画时必须以一个奇点作为起点,以另一个奇点为终点;(4)奇点个数超过两个的图形,一定不能一笔画.多笔画问题:我们把不能一笔画成的图,归纳为多笔画.多笔画图形的笔画数恰等于奇点个数的一半.事实上,对于任意的连通图来说,如果有2n个奇点(n为自然数),那么这个图一定可以用n笔画成.【例 1】我们把一个图形上与偶数条线相连的点叫做偶点,与奇数条线相连的点叫做奇点.下图中,哪些点是偶点?哪些点是奇点?【例 2】判断下列图a、图b、图c能否一笔画.N MLKFDECBA图bODCBAGFECBA【例 3】下面图形能不能一笔画成?若果能,应该怎样画?例题精讲奇妙的一笔画【例 4】下面的图形,哪些能一笔画出?哪些不能一笔画出?【例 5】下图中不能一笔画成,请你在下图中添加最少的线段,将其改成一笔画的图形,并画出路线图.【例 6】下图中的线段表示小路,请你仔细观察,认真思考,能够不重复的爬遍小路的是甲蚂蚁还是乙蚂蚁?该怎样爬?【例 7】能否用剪刀从左下图中一次连续剪下三个正方形和两个三角形?【例 8】下图是儿童乐园的道路平面图,要使游客走遍每条路并且不重复,那么出、入口应设在哪里?【例 9】邮递员叔叔向11个地点送信一次信,不走重复路,怎样走最合适?【例 10】观察下面的图,看各至少用几笔画成?【例 11】判断下列图形能否一笔画.若能,请给出一种画法;若不能,请加一条线或去一条线,将其改成可一笔画的图形.IFCA图aHGIK LJCADCHGFBA图c【例12】 18世纪的哥尼斯堡城是一座美丽的城市,在这座城市中有一条布勒格尔河横贯城区,这条河有两条支流在城市中心汇合,汇合处有一座小岛A 和一座半岛D ,人们在这里建了一座公园,公园中有七座桥把河两岸和两个小岛连接起来(如图a ).如果游人要一次走过这七座桥,而且对每座桥只许走一次,问如何走才能成功?【巩固】如下图所示,两条河流的交汇处有两个岛,有七座桥连接这两个岛及河岸.问:一个散步者能否一次不重复地走遍这七座桥?【例 13】 右图是某展览厅的平面图,它由五个展室组成,任两展室之间都有门相通,整个展览厅还有一个进口和一个出口,问游人能否一次不重复地穿过所有的门,并且从入口进,从出口出?【巩固】右图是某展览馆的平面图,一个参观者能否不重复地穿过每一扇门?如果不能,请说明理由.如果能,应从哪开始走?E CDB A【例 14】一条小虫沿长6分米,宽4分米,高5分米的长方体的棱爬行.如果它只能进不能退,并且同一条棱不能爬两次,那么它最多能爬多少分米?【巩固】一只木箱的长、宽、高分别为5,4,3厘米(见右图),有一只甲虫从A点出发,沿棱爬行,每条棱不允许重复,则甲虫回到A点时,最多能爬行多少厘米?【例 15】如图是某餐厅的平面图,共有五个小厅,相邻两厅之间有门相通,并且设有入口.请问你能否从入口进入一次不重复地穿过所有的门.如果可以,请指明穿行路线,如果不能,应关闭哪个门就可以办到?【例 16】在3×3的方阵中每个小正方形的边长都是100米.小明沿线段从A点到B点,不许走重复路,他最多能走多少米?【例 17】一个邮递员投递信件要走的街道如右图所示,图中的数字表示各条街道的千米数,他从邮局出发,要走遍各街道,最后回到邮局.怎样走才能使所走的行程最短?全程多少千米?。
小学奥数 奇妙的一笔画 精选例题练习习题(含知识点拨)

所谓图的一笔画,指的就是:从图的一点出发,笔不离纸,遍历每条边恰好一次,即每条边都只画一次,不准重复.从图中容易看出:能一笔画出的图首先必须是连通图.但是否所有的连通图都可以一笔画出呢?下面,我们就来探求解决这个问题的方法.什么样的图形能一笔画成呢?这就是一笔画问题,它是一种有名的数学游戏.我们把一个图形中与偶数条线相连接的点叫做偶点.相应的把与奇数条线相连接的点叫做奇点. 一笔画问题:(1)能一笔画出的图形必须是连通的图形;(2)凡是只由偶点组成的连通图形.一定可以一笔画出.画时可以由任一偶点作为起点.最后仍回到这点; (3)凡是只有两个奇点的连通图形一定可以一笔画出.画时必须以一个奇点作为起点,以另一个奇点为终点; (4)奇点个数超过两个的图形,一定不能一笔画. 多笔画问题:我们把不能一笔画成的图,归纳为多笔画.多笔画图形的笔画数恰等于奇点个数的一半.事实上,对于任意的连通图来说,如果有2n 个奇点(n 为自然数),那么这个图一定可以用n 笔画成.模块一、判断奇偶点【例 1】 我们把一个图形上与偶数条线相连的点叫做偶点,与奇数条线相连的点叫做奇点.下图中,哪些点是偶点?哪些点是奇点?J O I H G FED CBA【例 2】 同学们野营时建了9个营地,连接营地之间的道路如图所示,贝贝要给每个营地插上一面旗帜,要求相邻营地的旗帜色彩不同,则贝贝最少需要 种颜色的旗子,如果贝贝从某营地出发,不走重复路线就 (填“能”或“不能”)完成任务.【例 3】 判断下列图a 、图b 、图c 能否一笔画.图aNML KF DECBA 图bODCBA图cGFEDCBA例题精讲知识点拨4-1-5.奇妙的一笔画【例 4】 下面图形能不能一笔画成?若果能,应该怎样画?(1)(2)(3)【例 5】 下面的图形,哪些能一笔画出?哪些不能一笔画出?【例 6】 右图是某展览厅的平面图,它由五个展室组成,任两展室之间都有门相通,整个展览厅还有一个进口和一个出口,问游人能否一次不重复地穿过所有的门,并且从入口进,从出口出?【巩固】右图是某展览馆的平面图,一个参观者能否不重复地穿过每一扇门?如果不能,请说明理由.如果能,应从哪开始走?E CDB A【例 7】 下图中的线段表示小路,请你仔细观察,认真思考,能够不重复的爬遍小路的是甲蚂蚁还是乙蚂蚁?该怎样爬?乙甲【例 8】 能否用剪刀从左下图中一次连续剪下三个正方形和两个三角形?【例 9】 下图是儿童乐园的道路平面图,要使游客走遍每条路并且不重复,那么出、入口应设在哪里?IHGFEDC BA【例 10】 邮递员叔叔向11个地点送信一次信,不走重复路,怎样走最合适?【例 11】 观察下面的图,看各至少用几笔画成?(1)A ED HCF G B (2)(3)【例 12】 在3×3的方阵中每个小正方形的边长都是100 米.小明沿线段从A 点到B 点,不许走重复路,他最多能走多少米?【例 13】 有16个点排成的44 方阵。
新三第10讲-神奇的一笔画

神奇的一笔画古时候有一个国王,他不识字,却经常需要在重要文件上签名。
怎么办呢? 深思熟虑之后,他创造了一个双月图代表自己的签名。
后来,有个狡猾的大臣拿着模仿得一模一样的假冒签名向国王冒领财物时,却被精明的国王发觉了!你猜,国王是怎样发觉这位大臣的阴谋的呢?其实很简单。
国王的签名是一笔完成的。
旁人不知晓这个秘密,只注意模仿图形,而没有注意笔画的多少,因此画出的图形连接处有空隙,国王当然一眼就能看出这个签名是假冒的了。
所谓一笔画,是指在纸上连续不断,又不重复,笔画成某种图形。
正确理解这段话,要注意三点:1.一笔画图形必须是连通图形,即图形中的各部分必须是相连的而不能是分开的;2.每条线都要画到,但又不能重复;3.图形中的点可以重复通过。
一个图形能否一笔画成,关键在于图中奇点的多少。
任何图形都是由点和线组成的,图形中的点可以分成两大类:奇点(也叫单点)和偶点(也叫双点)。
从一点出发的线的条数是单数,这样的点称为奇点;从一点出发的线的条数是双数,这样的点称为偶点。
正确解答一笔画问题,要掌握两条规律:1.如果一个图中的奇点个数为0或2,那么,这个图形可以一笔画成。
当奇点的个数为。
时,可以从任何个偶点开始,最后仍回到这个点;当奇点的个数为2时,必须从某一奇点开始,最后到另一个奇点结束。
2.如果一个图中奇点个数不是0或2,那么这个图形不能一笔画成。
【例1】下面的各个图形都是由点和线组成的,请你仔细观察后回答后面的问题。
(1)与一条线相连的有哪些点?(2)与两条线相连的有哪些点?(3)与三条线相连的有哪些点?(4)与四条或四条以上的线相连的有哪些点?(5)若把与奇数条线相连的点叫奇点,把与偶数条线相连的叫偶点,那么有0个奇点(即全部是偶点)的图形有哪些? 有2个奇点的图形有哪些? 有3个或3个以上奇点的图形有哪些? 分析先找出图中的点,再数一数从这点出发的线有几条,根据从一个点出发的线的条数的多少就能确定这个点是奇点还是偶点了。
奇妙的一笔画教学设计(1)

《奇妙的一笔画》教学设计授课教师科目北师大版数学授课班级四年级(3)班课题名称奇妙的一笔画共1课时,第1课时单元教学目标1.经历从实际物体抽象出角、正方形、长方形和平行四边形的过程,初步发展空间概念。
2.结合生活情境,直观认识角、正方形、长方形和平行四边形;会借助三角板辨认直角、锐角和钝角;结合观察、操作活动,能够用学生自己语言描述长方形、正方形、平行四边形等图形,设计简单的图案,发展初步的审美意识。
3.了解用折、画、比、量等多种认识图形的方法,体会研究图形方法的多样性,激发对图形研究的好奇心。
单元教学内容前后联系教材分析本节课是在学生初步认识长方形、正方形、三角形等几何图形的基础上进行教学的,教材结合生活情境,引导学生从观察生活的实物开始,逐步抽象出角的几何图形。
这节课从图形到角的活动中学习新知,通过学生的实际操作,加深他们对角的认识,学生熟练地掌握这部分内容,将为学习更深的几何奠定基础。
学情分析学生已经初步认识了长方形、正方形和三角形,并且能准确地判断出各种图形,也就是说学生已经具备了相关角的感性认识。
但是,低年级学生的认知规律是以具体的形象思维为主,这部分内容对二年级学生来说比较抽象,接受起来较为困难。
角在生活中随处可见,如果让学生找这些图形,对学生来说一点也不困难,但是让学生抽象出角,说出角的特点,会比较困难,对于角的大小与边的长短无关这一知识点接受起来比较困难。
课题奇妙的一笔画教学目标1.知识技能:认识一笔画,能判断一个图形是否为一笔画,体会用数学知识解决问题的方法。
2.数学思考:生活中的许多问题,可以用数学方法来解决,但首先要通过抽象化和理想化建立数学模型。
3.问题解决:通过“一笔画”的数学问题,解决生活中的实际问题。
4.情感态度价值观:(1)通过探究“一笔画”规律的活动,锻炼学生克服困难的意志及勇于发表见解的好习惯。
(2)通过“一笔画”问题及其结论的了解,扩大学生知识视野,激发学生学习兴趣。
小学奥数:奇妙的一笔画.专项练习

所谓图的一笔画,指的就是:从图的一点出发,笔不离纸,遍历每条边恰好一次,即每条边都只画一次,不准重复.从图中容易看出:能一笔画出的图首先必须是连通图.但是否所有的连通图都可以一笔画出呢?下面,我们就来探求解决这个问题的方法.什么样的图形能一笔画成呢?这就是一笔画问题,它是一种有名的数学游戏. 我们把一个图形中与偶数条线相连接的点叫做偶点.相应的把与奇数条线相连接的点叫做奇点.一笔画问题:(1)能一笔画出的图形必须是连通的图形;(2)凡是只由偶点组成的连通图形.一定可以一笔画出.画时可以由任一偶点作为起点.最后仍回到这点;(3)凡是只有两个奇点的连通图形一定可以一笔画出.画时必须以一个奇点作为起点,以另一个奇点为终点;(4)奇点个数超过两个的图形,一定不能一笔画. 多笔画问题:我们把不能一笔画成的图,归纳为多笔画.多笔画图形的笔画数恰等于奇点个数的一半.事实上,对于任意的连通图来说,如果有2n 个奇点(n 为自然数),那么这个图一定可以用n 笔画成.模块一、判断奇偶点【例 1】 我们把一个图形上与偶数条线相连的点叫做偶点,与奇数条线相连的点叫做奇点.下图中,哪些点是偶点?哪些点是奇点?J O I H G FED CBA【例 2】 同学们野营时建了9个营地,连接营地之间的道路如图所示,贝贝要给每个营地插上一面旗帜,要求相邻营地的旗帜色彩不同,则贝贝最少需要 种颜色的旗子,如果贝贝从某营地出发,不走重复路线就 (填“能”或“不能”)完成任务.例题精讲知识点拨4-1-5.奇妙的一笔画【例 3】 判断下列图a 、图b 、图c 能否一笔画.图aNML KF DECBA 图bODCBA图cGFEDCBA【例 4】 下面图形能不能一笔画成?若果能,应该怎样画?(1)(2)(3)【例 5】 下面的图形,哪些能一笔画出?哪些不能一笔画出?【例 6】 右图是某展览厅的平面图,它由五个展室组成,任两展室之间都有门相通,整个展览厅还有一个进口和一个出口,问游人能否一次不重复地穿过所有的门,并且从入口进,从出口出?【巩固】右图是某展览馆的平面图,一个参观者能否不重复地穿过每一扇门?如果不能,请说明理由.如果能,应从哪开始走?E CDB A【例 7】 下图中的线段表示小路,请你仔细观察,认真思考,能够不重复的爬遍小路的是甲蚂蚁还是乙蚂蚁?该怎样爬?乙甲【例 8】 能否用剪刀从左下图中一次连续剪下三个正方形和两个三角形?【例 9】 下图是儿童乐园的道路平面图,要使游客走遍每条路并且不重复,那么出、入口应设在哪里?IHGFEDC BA【例 10】 邮递员叔叔向11个地点送信一次信,不走重复路,怎样走最合适?【例 11】 观察下面的图,看各至少用几笔画成?(1)A ED HCF GB (2)(3)【例 12】 在3×3的方阵中每个小正方形的边长都是100 米.小明沿线段从A 点到B 点,不许走重复路,他最多能走多少米?【例 13】 有16个点排成的44 方阵。
(小学奥数)奇妙的一笔画

所謂圖的一筆劃,指的就是:從圖的一點出發,筆不離紙,遍曆每條邊恰好一次,即每條邊都只畫一次,不准重複.從圖中容易看出:能一筆劃出的圖首先必須是連通圖.但是否所有的連通圖都可以一筆劃出呢?下麵,我們就來探求解決這個問題的方法.什麼樣的圖形能一筆劃成呢?這就是一筆劃問題,它是一種有名的數學遊戲. 我們把一個圖形中與偶數條線相連接的點叫做偶點.相應的把與奇數條線相連接的點叫做奇點.一筆劃問題:(1)能一筆劃出的圖形必須是連通的圖形;(2)凡是只由偶點組成的連通圖形.一定可以一筆劃出.畫時可以由任一偶點作為起點.最後仍回到這點;(3)凡是只有兩個奇點的連通圖形一定可以一筆劃出.畫時必須以一個奇點作為起點,以另一個奇點為終點;(4)奇點個數超過兩個的圖形,一定不能一筆劃.多筆劃問題:我們把不能一筆劃成的圖,歸納為多筆劃.多筆劃圖形的筆劃數恰等於奇點個數的一半.事實上,對於任意的連通圖來說,如果有2n 個奇點(n 為自然數),那麼這個圖一定可以用n 筆劃成.模組一、判斷奇偶點【例 1】 我們把一個圖形上與偶數條線相連的點叫做偶點,與奇數條線相連的點叫做奇點.下圖中,哪些點是偶點?哪些點是奇點? J O I HGFE DC B A例題精講知識點撥4-1-5.奇妙的一筆劃【例 2】同學們野營時建了9個營地,連接營地之間的道路如圖所示,貝貝要給每個營地插上一面旗幟,要求相鄰營地的旗幟色彩不同,則貝貝最少需要種顏色的旗子,如果貝貝從某營地出發,不走重複路線就(填“能”或“不能”)完成任務.【例 3】判斷下列圖a、圖b、圖c能否一筆劃.E【例 4】下麵圖形能不能一筆劃成?若果能,應該怎樣畫?(1)(2)(3)【例 5】下麵的圖形,哪些能一筆劃出?哪些不能一筆劃出?【例 6】 右圖是某展覽廳的平面圖,它由五個展室組成,任兩展室之間都有門相通,整個展覽廳還有一個進口和一個出口,問遊人能否一次不重複地穿過所有的門,並且從入口進,從出口出?【鞏固】右圖是某展覽館的平面圖,一個參觀者能否不重複地穿過每一扇門?如果不能,請說明理由.如果能,應從哪開始走?ECD B A【例 7】 下圖中的線段表示小路,請你仔細觀察,認真思考,能夠不重複的爬遍小路的是甲螞蟻還是乙螞蟻?該怎樣爬?乙甲【例 8】 能否用剪刀從左下圖中一次連續剪下三個正方形和兩個三角形?【例 9】 下圖是兒童樂園的道路平面圖,要使遊客走遍每條路並且不重複,那麼出、入口應設在哪里? I H GFE DC B A【例 10】 郵遞員叔叔向11個地點送信一次信,不走重複路,怎樣走最合適?【例 11】 觀察下麵的圖,看各至少用幾筆劃成?(1)AE DH C F G B(2)(3)【例 12】 在3×3的方陣中每個小正方形的邊長都是100 米.小明沿線段從A 點到B點,不許走重複路,他最多能走多少米?【例 13】 有16個點排成的44 方陣。
小学奥数4-1-5 奇妙的一笔画.专项练习及答案解析

所谓图的一笔画,指的就是:从图的一点出发,笔不离纸,遍历每条边恰好一次,即每条边都只画一次,不准重复.从图中容易看出:能一笔画出的图首先必须是连通图.但是否所有的连通图都可以一笔画出呢?下面,我们就来探求解决这个问题的方法.什么样的图形能一笔画成呢?这就是一笔画问题,它是一种有名的数学游戏. 我们把一个图形中与偶数条线相连接的点叫做偶点.相应的把与奇数条线相连接的点叫做奇点. 一笔画问题:(1)能一笔画出的图形必须是连通的图形; (2)凡是只由偶点组成的连通图形.一定可以一笔画出.画时可以由任一偶点作为起点.最后仍回到这点;(3)凡是只有两个奇点的连通图形一定可以一笔画出.画时必须以一个奇点作为起点,以另一个奇点为终点;(4)奇点个数超过两个的图形,一定不能一笔画. 多笔画问题:我们把不能一笔画成的图,归纳为多笔画.多笔画图形的笔画数恰等于奇点个数的一半.事实上,对于任意的连通图来说,如果有2n 个奇点(n 为自然数),那么这个图一定可以用n 笔画成.模块一、判断奇偶点【例 1】 我们把一个图形上与偶数条线相连的点叫做偶点,与奇数条线相连的点叫做奇点.下图中,哪些点是偶点?哪些点是奇点?J O I H G FED CBA【考点】一笔画问题 【难度】2星 【题型】解答 【解析】 奇点:D H J O 偶点:A B CEFG I【答案】奇点: D H J O 偶点:A B C E F G I【例 2】 同学们野营时建了9个营地,连接营地之间的道路如图所示,贝贝要给每个营地插上一面旗帜,要求相邻营地的旗帜色彩不同,则贝贝最少需要 种颜色的旗子,如果贝贝从某营地出发,不走重复路线就 (填“能”或“不能”)完成任务.例题精讲知识点拨4-1-5.奇妙的一笔画【考点】一笔画问题 【难度】2星 【题型】填空 【关键词】华杯赛,六年级,初赛,第10题【解析】 最少需要3种颜色的旗子。
因为中间的三点连成一个三角形,要使这三点所代表营地两粮相邻,要使相邻营地没有相同颜色的旗子,必须各插一种与其它两点不同颜色的旗子。
奇妙的一笔画(含详细解析)

所谓图的一笔画,指的就是:从图的一点出发,笔不离纸,遍历每条边恰好一次,即每条边都只画一次,不准重复.从图中容易看出:能一笔画出的图首先必须是连通图.但是否所有的连通图都可以一笔画出呢?下面,我们就来探求解决这个问题的方法.什么样的图形能一笔画成呢?这就是一笔画问题,它是一种有名的数学游戏.我们把一个图形中与偶数条线相连接的点叫做偶点.相应的把与奇数条线相连接的点叫做奇点. 一笔画问题:(1)能一笔画出的图形必须是连通的图形;(2)凡是只由偶点组成的连通图形.一定可以一笔画出.画时可以由任一偶点作为起点.最后仍回到这点; (3)凡是只有两个奇点的连通图形一定可以一笔画出.画时必须以一个奇点作为起点,以另一个奇点为终点; (4)奇点个数超过两个的图形,一定不能一笔画. 多笔画问题:我们把不能一笔画成的图,归纳为多笔画.多笔画图形的笔画数恰等于奇点个数的一半.事实上,对于任意的连通图来说,如果有2n 个奇点(n 为自然数),那么这个图一定可以用n 笔画成.模块一、判断奇偶点【例 1】 我们把一个图形上与偶数条线相连的点叫做偶点,与奇数条线相连的点叫做奇点.下图中,哪些点是偶点?哪些点是奇点?J O I H G FED CBA【考点】一笔画问题 【难度】2星 【题型】解答【解析】 奇点: D H J O 偶点:A B C E F G I 【答案】奇点: D H J O 偶点:A B C E F G I【例 2】 同学们野营时建了9个营地,连接营地之间的道路如图所示,贝贝要给每个营地插上一面旗帜,要求相邻营地的旗帜色彩不同,则贝贝最少需要 种颜色的旗子,如果贝贝从某营地出发,不走重复路线就 (填“能”或“不能”)完成任务.例题精讲知识点拨4-1-5.奇妙的一笔画【考点】一笔画问题【难度】2星【题型】填空【关键词】华杯赛,六年级,初赛,第10题【解析】最少需要3种颜色的旗子。
因为中间的三点连成一个三角形,要使这三点所代表营地两粮相邻,要使相邻营地没有相同颜色的旗子,必须各插一种与其它两点不同颜色的旗子。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4-1-5.奇妙的一笔画知识点拨所谓图的一笔画,指的就是:从图的一点出发,笔不离纸,遍历每条边恰好一次,即每条边都只画一次,不准重复.从图中容易看出:能一笔画出的图首先必须是连通图.但是否所有的连通图都可以一笔画出呢?下面,我们就来探求解决这个问题的方法.什么样的图形能一笔画成呢?这就是一笔画问题,它是一种有名的数学游戏.我们把一个图形中与偶数条线相连接的点叫做偶点.相应的把与奇数条线相连接的点叫做奇点.一笔画问题:(1)能一笔画出的图形必须是连通的图形;(2)凡是只由偶点组成的连通图形.一定可以一笔画出.画时可以由任一偶点作为起点.最后仍回到这点;(3)凡是只有两个奇点的连通图形一定可以一笔画出.画时必须以一个奇点作为起点,以另一个奇点为终点;(4)奇点个数超过两个的图形,一定不能一笔画.多笔画问题:我们把不能一笔画成的图,归纳为多笔画.多笔画图形的笔画数恰等于奇点个数的一半.事实上,对于任意的连通图来说,如果有2n个奇点(n为自然数),那么这个图一定可以用n笔画成.例题精讲模块一、判断奇偶点【例1】我们把一个图形上与偶数条线相连的点叫做偶点,与奇数条线相连的点叫做奇点.下图中,哪些点是偶点?哪些点是奇点?【考点】一笔画问题【难度】2星【题型】解答【解析】奇点:D H J O偶点:A B C E F G I【答案】奇点:D H J O偶点:A B C E F G I【例2】同学们野营时建了9个营地,连接营地之间的道路如图所示,贝贝要给每个营地插上一面旗帜,要求相邻营地的旗帜色彩不同,则贝贝最少需要种颜色的旗子,如果贝贝从某营地出发,不走重复路线就(填“能”或“不能”)完成任务.【考点】一笔画问题【难度】2星【题型】填空【关键词】2007年,第十二届,华杯赛,六年级,初赛,第10题【解析】最少需要3种颜色的旗子。
因为中间的三点连成一个三角形,要使这三点所代表营地两粮相邻,要使相邻营地没有相同颜色的旗子,必须各插一种与其它两点不同颜色的旗子。
不走重复路线不能完成插旗的任务,因为本题共有6各奇点。
【例3】判断下列图a、图b、图c能否一笔画.E【考点】一笔画问题【难度】2星【题型】解答【解析】图a能,因为有2个奇点,图a能b不能,因为图形不是连通的,图c能,因为因为图中全是奇点【答案】a能,a能,c能【例4】下面图形能不能一笔画成?若果能,应该怎样画?【考点】一笔画问题【难度】2星【题型】解答【解析】图1能因为图中全是偶点;图2能因为图中全是偶点;图3不能因为有4个奇点。
【答案】图1能因为图中全是偶点;图2能因为图中全是偶点;图3不能因为有4个奇点。
【例5】下面的图形,哪些能一笔画出?哪些不能一笔画出?【考点】一笔画问题【难度】2星【题型】解答【解析】第1个能,2、3不能【答案】第1个能,2、3不能【例6】右图是某展览厅的平面图,它由五个展室组成,任两展室之间都有门相通,整个展览厅还有一个进口和一个出口,问游人能否一次不重复地穿过所有的门,并且从入口进,从出口出?【考点】一笔画问题【难度】2星【题型】解答【解析】将图形中的6个区域看成6个点,每个门看成连结他们的线段,显然6个点都是偶点,所以有人能一次不重复的走过所有的门.【答案】能【巩固】右图是某展览馆的平面图,一个参观者能否不重复地穿过每一扇门?如果不能,请说明理由.如果能,应从哪开始走?ECDB A 【考点】一笔画问题【难度】2星【题型】解答【解析】不能【答案】不能【例7】下图中的线段表示小路,请你仔细观察,认真思考,能够不重复的爬遍小路的是甲蚂蚁还是乙蚂蚁?该怎样爬?【考点】一笔画问题【难度】2星【题型】解答【解析】要想不重复爬出,需要图形能一笔画出,由于图中有两个奇点,所以应该从奇点出发才能一笔画出图形,所以甲蚂蚁能够.【答案】甲蚂蚁【例8】能否用剪刀从左下图中一次连续剪下三个正方形和两个三角形?【考点】一笔画问题【难度】2星【题型】解答【解析】可以.【答案】可以【例9】下图是儿童乐园的道路平面图,要使游客走遍每条路并且不重复,那么出、入口应设在哪里?【考点】一笔画问题【难度】3星【题型】解答【解析】要想不重复,需要路线能一笔画出,由于图中有两个奇点,所以入口和出口应该分别放在两个奇点出,即F 和I 点.【答案】出口和入口应该分别放在F和I点【例10】邮递员叔叔向11个地点送信一次信,不走重复路,怎样走最合适?【考点】一笔画问题【难度】3星【题型】解答【解析】不走重复路,一笔能画出路线图,图中有2个奇点,应该从奇点处出发,下面有一种参考路线:4-1-2-5-8-9-6-10-11-7-4-3【答案】4-1-2-5-8-9-6-10-11-7-4-3【考点】一笔画问题【难度】3星【题型】解答【解析】图(1)有8个奇点,所以要4笔画出,图(2)有12个奇点,所以要一笔画出,图(3)能一笔画出.【答案】图(1)有8个奇点,所以要4笔画出,图(2)有12个奇点,所以要一笔画出,图(3)能一笔画出.【例12】在3×3的方阵中每个小正方形的边长都是100米.小明沿线段从A点到B点,不许走重复路,他最多能走多少米?【考点】一笔画问题【难度】3星【题型】解答【解析】这道题大多数同学都采用试画的方法,实际上可以用一笔画原理求解.首先,图中有8个奇点,在8个奇点之间至少要去掉4条线段,才能使这8个奇点变成偶点;其次,从A点出发到B点,A,B两点必须是奇点,现在A,B都是偶点,必须在与A,B连接的线段中各去掉1条线段,使A,B成为奇点.所以至少要去掉6条线段,也就是最多能走1800米,走法如图【答案】【例13】(2010年第8届走美杯3年级初赛第6题)有16个点排成的44方阵。
如图,请不间断地一笔画出6条直线经过每个点,且最后回到起点【考点】一笔画问题【难度】3星【题型】解答【解析】答案不唯一只使用横平竖直的线怎么都不够,因此尝试使用斜线进行构造。
【答案】答案不唯一【例14】一条小虫沿长6分米,宽4分米,高5分米的长方体的棱爬行.如果它只能进不能退,并且同一条棱不能爬两次,那么它最多能爬多少分米?【考点】一笔画问题【难度】3星【题型】解答【解析】8个定点都是奇点,所以至少需要4笔.多画长和高能保证总路程最长,为A -B -G -H -A -D -C -F -E -D 总长为6×4+5×4+4×1=48分米.【答案】48分米【巩固】一只木箱的长、宽、高分别为5,4,3厘米(见右图),有一只甲虫从A 点出发,沿棱爬行,每条棱不允许重复,则甲虫回到A点时,最多能爬行多少厘米?【考点】一笔画问题【难度】3星【题型】解答【解析】最多34厘米【答案】多34厘米模块二、调整奇偶点变一笔画【例15】判断下列图形能否一笔画.若能,请给出一种画法;若不能,请加一条线或去一条线,将其改成可一笔画的图形.F图aH图c【考点】一笔画问题【难度】3星【题型】解答【解析】图(1)不能一笔画出,因为图中有4个奇点,连结BD ,或者去掉BF 都可以使图形能一笔画出.图(2)不能一笔画出,因为图中有4个奇点,去掉KL ,或者BK 都可以使图形能一笔画出.图(3)不能一笔画出,因为图中有4个奇点,去掉AB 可以使图形能一笔画出.一个K (K >1)笔画最少要添加几条连线才能变成一笔画呢?我们知道K 笔画有2K 个奇点,如果在任意两个奇点之间添加一条连线,那么这两个奇点同时变成了偶点.如左下图中的B ,C 两个奇点【答案】【例16】如图是某餐厅的平面图,共有五个小厅,相邻两厅之间有门相通,并且设有入口.请问你能否从入口进入一次不重复地穿过所有的门.如果可以,请指明穿行路线,如果不能,应关闭哪个门就可以办到?【考点】一笔画问题【难度】4星【题型】解答【解析】可以将图中的五个小厅以及厅外的部分都抽象成点,为方便解题,给它们分别编号.这时,连通厅与厅之间的门就相当于各点之间的连线.于是题目中餐厅平面图就抽象成为一个连通的图形,如下:求穿形路线的问题就转化成一笔画的问题.在抽象出的图形中,我们可以找到四个奇点,即②、③、④和厅外,所以图形不能一笔画出也就是说,从入口进入不可能一次不重复的穿过所有的门.但根据一笔画问题的知识,只要关闭门,把③、④变为偶点,就可以办到,关闭B门,可行路线如上图。
【答案】关闭B门。
【例17】下图中不能一笔画成,请你在下图中添加最少的线段,将其改成一笔画的图形,并画出路线图.【考点】一笔画问题【难度】2星【题型】解答【解析】不能一笔画出,因为图中有E H G F四个奇点,连结EH就可以使图形一笔画出.【答案】连结EH就可以使图形一笔画出【例18】(2009“数学解题能力展示"读者评选活动四年级初赛6题)如图所示,某小区花园的道路为一个长480米,宽200米的长方形;一个边长为260米的菱形和十字交叉的两条道路组成.一天,王大爷A处进入花园,走遍花园的所有道路并从A处离开.如果他每分钟走60米,那么他从进入花园到走出花园最少要用分.【考点】一笔画问题【难度】4星【题型】填空【解析】根据一笔画的概念,因为道路图有四个奇点,所以王大爷是没法不重复地走完小区所有的道路回到A 【解析】的,但可以对道路图作一些处理,相当于王大爷通过走重复的道路,完成一笔画,如下图:道路的总路程为4803200326063600⨯+⨯+⨯=米,王大爷走完这些路要60分钟.【答案】60分钟【例19】(2009“数学解题能力展示"读者评选活动五年级初赛6题)某城市的交通系统由若干个路口(右图中线段的交点)和街道(右图中的线段)组成,每条街道都连接着两个路口.所有街道都是双向通行的,且每条街道都有一个长度值(标在图中相应的线段处).一名邮递员传送报纸和信件,要从邮局出发经过他所管辖的每一条街道最后返回邮局(每条街道可以经过不止一次).他合理安排路线,可以使得自己走过最短的总长度是.【考点】一笔画问题【难度】4星【题型】填空【解析】根据一笔画的有关概念,道路图中有6个奇点,邮递员不可能不重复地走遍所有街道并返回邮局.但【解析】可以对道路图作一些处理,相当于邮递员通过走重复的道路,完成一笔画,如下图:总路程为3102846⨯+⨯=.【答案】46【例20】18世纪的哥尼斯堡城是一座美丽的城市,在这座城市中有一条布勒格尔河横贯城区,这条河有两条支流在城市中心汇合,汇合处有一座小岛A和一座半岛D,人们在这里建了一座公园,公园中有七座桥把河两岸和两个小岛连接起来(如图a).如果游人要一次走过这七座桥,而且对每座桥只许走一次,问如何走才能成功?【考点】一笔画问题【难度】4星【题型】解答【解析】欧拉解决这个问题的方法非常巧妙.他认为:人们关心的只是一次不重复地走遍这七座桥,而并不关心桥的长短和岛的大小,因此,岛和岸都可以看作一个点,而桥则可以看成是连接这些点的一条线.这样,一个实际问题就转化为一个几何图形(如下图)能否一笔画出的问题了.而图B中有4个奇点显然不能一笔画出.【答案】不能【巩固】如下图所示,两条河流的交汇处有两个岛,有七座桥连接这两个岛及河岸.问:一个散步者能否一次不重复地走遍这七座桥?【考点】一笔画问题【难度】4星【题型】解答【解析】能【答案】能【例21】一个邮递员投递信件要走的街道如右图所示,图中的数字表示各条街道的千米数,他从邮局出发,要走遍各街道,最后回到邮局.怎样走才能使所走的行程最短?全程多少千米?【考点】一笔画问题【难度】5星【题型】解答【解析】图中共有8个奇点,必须在8个奇点间添加4条线,才能消除所有奇点,成为能从邮局出发最后返回邮局的一笔画.在距离最近的两个奇点间添加一条连线,如左下图中虚线所示,共添加4条连线,这4条连线表示要重复走的路,显然,这样重复走的路程最短,全程30千米.走法参考右下图(走法不唯一).【答案】30千米。
