物理化学 03-03相变过程熵变
合集下载
物理化学03章_热力学第二定律
Helmholtz自由能 Gibbs自由能
为什么要定义新函数？
热力学第一定律导出了热力学能这个状态函数， 为了处理热化学中的问题，又定义了焓。
热力学第二定律导出了熵这个状态函数，但用熵 作为判据时，系统必须是隔离系统，也就是说必须同 时考虑系统和环境的熵变，这很不方便。
通常反应总是在等温、等压或等温、等容条件下 进行，有必要引入新的热力学函数，利用系统自身状 态函数的变化，来判断自发变化的方向和限度。
§3.8 熵和能量退降
热力学第一定律表明：一个实际过程发生 后，能量总值保持不变。
热力学第二定律表明：在一个不可逆过程 中，系统的熵值增加。
能量总值不变，但由于系统的熵值增加， 说明系统中一部分能量丧失了作功的能力，这 就是能量“退降”。
能量 “退降”的程度，与熵的增加成正比
有三个热源 TA > TB > TC
从高“质量”的能贬值为低“质量”的能 是自发过程。
§3.9 热力学第二定律的本质和熵的统计意义
热力学第二定律的本质
热与功转换的不可逆性 热是分子混乱运动的一种表现，而功是分子 有序运动的结果。 功转变成热是从规则运动转化为不规则运动， 混乱度增加，是自发的过程； 而要将无序运动的热转化为有序运动的功就 不可能自动发生。
热力学第二定律的本质 气体混合过程的不可逆性 将N2和O2放在一盒内隔板的两边，抽去隔板， N2和O2自动混合，直至平衡。 这是混乱度增加的过程，也是熵增加的过程， 是自发的过程，其逆过程决不会自动发生。
热力学第二定律的本质
热传导过程的不可逆性
处于高温时的系统，分布在高能级上的分子 数较集中；
而处于低温时的系统，分子较多地集中在低 能级上。
这与熵的变化方向相同。
为什么要定义新函数？
热力学第一定律导出了热力学能这个状态函数， 为了处理热化学中的问题，又定义了焓。
热力学第二定律导出了熵这个状态函数，但用熵 作为判据时，系统必须是隔离系统，也就是说必须同 时考虑系统和环境的熵变，这很不方便。
通常反应总是在等温、等压或等温、等容条件下 进行，有必要引入新的热力学函数，利用系统自身状 态函数的变化，来判断自发变化的方向和限度。
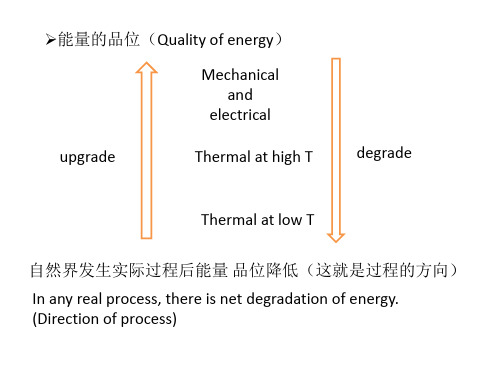
§3.8 熵和能量退降
热力学第一定律表明：一个实际过程发生 后，能量总值保持不变。
热力学第二定律表明：在一个不可逆过程 中，系统的熵值增加。
能量总值不变，但由于系统的熵值增加， 说明系统中一部分能量丧失了作功的能力，这 就是能量“退降”。
能量 “退降”的程度，与熵的增加成正比
有三个热源 TA > TB > TC
从高“质量”的能贬值为低“质量”的能 是自发过程。
§3.9 热力学第二定律的本质和熵的统计意义
热力学第二定律的本质
热与功转换的不可逆性 热是分子混乱运动的一种表现，而功是分子 有序运动的结果。 功转变成热是从规则运动转化为不规则运动， 混乱度增加，是自发的过程； 而要将无序运动的热转化为有序运动的功就 不可能自动发生。
热力学第二定律的本质 气体混合过程的不可逆性 将N2和O2放在一盒内隔板的两边，抽去隔板， N2和O2自动混合，直至平衡。 这是混乱度增加的过程，也是熵增加的过程， 是自发的过程，其逆过程决不会自动发生。
热力学第二定律的本质
热传导过程的不可逆性
处于高温时的系统，分布在高能级上的分子 数较集中；
而处于低温时的系统，分子较多地集中在低 能级上。
这与熵的变化方向相同。
物理化学相变过程熵变
s
dT
fus
H o-m
0K T
Tf
Tb
C
o-p ,m
(
l
) dT
vap
H
o-m
Tf
T
Tb
T
C
o-p ,m
(
g
) dT
Tb
T
pg g
S
o-m
T
4.标准摩尔反应熵的计算
r Sm（ T） B Sm（ B）
B
10
5.标准摩尔反应熵随温度的变化
例:分别计算298K和423K时甲醇合成反应的标准摩尔反应熵,
熵是度量系统无序度的函数
6
1. Nernst（1906）热定理
凝聚系统在恒温过程中的熵变，随温度趋于 0 K 而趋于零
lim T S 0（凝聚系统）
T 0 K
对于任意反应 A＋B→AB
在0K时 ΔrS(0K)=SAB(0K) －SA(0K) － SB(0K)=0 在温度为T时
r ST S AB T S A T SB T
423K,100kPa
423K,100kPa
r Sm 423K S1 S2 r Sm 298K S1
S 2
S1 S2
C 423K r p ,m
dT
CO(g)+2H2(g)
r
S
m
298K
CH3OH(g)
T 298 K
298K,100kPa
298K,100kPa
r
S
m
T
r
Q T
r
2、对于可逆过程，利用各种基础热力学数据计算其热温商
3、对于不可逆过程，则须在始末态之间设计一条可逆途径
2.6熵变的计算(物理化学)
nRT nRT (1)抗恒外压恒温过程： Q W p外 (V2 V1 ) p2 ( p p ) 2 1 8.314 300 (1 10 ) 2244.8 J 100
Q 2244.8 S环境＝ 7.48 JK 1 T 300
S孤立＝S系统＋S环境＝ 19.14－7.48＝ 11.66 JK1 0
f Hm V Hm
S气 S液 S固
四、可逆相变化过程中熵变的计算
例 1 mol冰在零度熔化成水，熔化热为6006.97 J/mol，求熵变。 解: 此过程是在等温等压条件下发生的正常相变。
S系统
Qr H 6006.97 21.99 JK 1 T T 273.2
终态混合气中各物质的分压 pA(终) p xA
S A nA R ln pA( 始） p A( 终 ) pD (终 ) p nA R ln p xA nA R ln p p xD
pD(终) p xD
Smix S A S D nA R ln x A nD R ln x D R ( nB ln x B )
Q 6006.97 S环境＝ 21.99 JK 1 T环境 237.2
S孤立＝S系统＋S环境＝0
这是一个可逆过程。
五、理想气体混合过程的熵变计算
理想气体在等温等压混合
A(T,p) (nA, VA) D(T,p) (nD, VD)
U 0,W 0, Q 0
A+D(T,p) (nA,+nD ,VA+VD)
S
T2
Qr
T
T1
T2
T1
CV dT T2 CV ln T T1
Q 2244.8 S环境＝ 7.48 JK 1 T 300
S孤立＝S系统＋S环境＝ 19.14－7.48＝ 11.66 JK1 0
f Hm V Hm
S气 S液 S固
四、可逆相变化过程中熵变的计算
例 1 mol冰在零度熔化成水，熔化热为6006.97 J/mol，求熵变。 解: 此过程是在等温等压条件下发生的正常相变。
S系统
Qr H 6006.97 21.99 JK 1 T T 273.2
终态混合气中各物质的分压 pA(终) p xA
S A nA R ln pA( 始） p A( 终 ) pD (终 ) p nA R ln p xA nA R ln p p xD
pD(终) p xD
Smix S A S D nA R ln x A nD R ln x D R ( nB ln x B )
Q 6006.97 S环境＝ 21.99 JK 1 T环境 237.2
S孤立＝S系统＋S环境＝0
这是一个可逆过程。
五、理想气体混合过程的熵变计算
理想气体在等温等压混合
A(T,p) (nA, VA) D(T,p) (nD, VD)
U 0,W 0, Q 0
A+D(T,p) (nA,+nD ,VA+VD)
S
T2
Qr
T
T1
T2
T1
CV dT T2 CV ln T T1
物理化学 第5章_相变热力学-3
=114.52 J· -1 K
18
4 相变过程自发性判据
(1):熵判据：把系统和环境看成是一个孤立系统， 用孤立系统的熵变作为判据来判断过程的自发性。
例5-1-5 求1.00mol过冷水在101325Pa及-10℃ 时凝固过程的△S。已知冰的质量熔化焓为334.7 J·-1，水和冰的质量热容分别为Cp(H2O,1) =4.184 g J·-1· -1，Cp(H2O,s) = 2.092J·-1· -1。 g K g K 解： H2O(1,263K)→H2O(s,263K) 这是一个不可逆相变过程。
= -1.00×8.314×630kJ= -5.24 kJ
Qp=ΔH = 58.5kJ58.5kJ
ΔU = Qp+W = (58.5-5.24)kJ = 53.3kJ53.26kJ
6
例：习题5-1：
解：
pV 50.663 103 100 103 n水 1.6377( mol) RT 8.314 373
解：根据相变热与温度的关系：
vap Hm (142.9 C ) vap Hm (100 C )
416.1 373.2
C
p,m
( g ) C p,m (1)dT
vap Hm (100 C ) Cp,m ( g) Cp,m (1)(T2 T1 )
vap Hm (142.9 C ) 40.63 (34.56 76.56 103 (416.1 373.2) ）
38.83kJ mol1
12
三、相变化过程熵变的计算 (1)可逆相变过程相变熵 可逆相变：是指在无限接近相平衡条件下进 行的相变化。 当相变发生在两相平衡共存的温度和压力下 时，称为可逆相变。 任何纯物质的可逆相变均具有恒温、恒压的 特点，根据熵变的定义式，对于恒温恒压的 可逆相变，相变熵为：
物理化学03热力学第二定律
Q1 Q2 T1 T2 综合卡诺定理及推论，有： Q1 T1
Q1 Q2 0 T1 T2
对无限小的循环, 有
不可逆 可逆
dQ1 dQ2 0 不可逆 可逆 T1 T2
小结: 对在两恒温热源间工作的热机 • 其热机效率小于(T1－T2)/T1是可能的, 大于则不可能, 等于时相 当于热机实际处在平衡状态; • 其热温商小于零是可能的, 大于则不可能, 等于时平衡. 上两式适合于任何物质，发生任何变化的循环过程。
•要解决过程的方向性的问题，必须依赖于热力 学第二定律。
99-11-24
3
§3-1 热力学第二定律
1. 自发过程与非自发过程
• 在一定的条件下，不需要消耗环境的作用就能 自动进行的过程，称为自发过程。 • 如水往低处流，冰熔化，墨水在清水中扩散， 常温下能自动进行的化学反应等等。 • 自发过程的逆过程是不能自动进行的，称为非 自发过程。 • 自发过程的共同特征是不可逆的。 [课堂讨论]：以气体真空膨胀为例，说明自发过 程是不可逆过程。
• 例：木炭在氧气中燃烧，热力学能转变为热，生成CO2， 其逆过程是CO2吸收相同的热量，转变为C和O2，是不违 反热力学第一定律的，但能否自动的进行呢？
99-11-24 2
同在能量守恒的前提下, 热的自发传递是单方向的; 功可全部转化为热, 而热转化为功却是有限制的.
• 热 从 高 温 传 向 低 温 • 功 转 化 为 热
1
任意不可逆过程的热温商之和一定小于其熵变.
dQ S T
>任意不可逆过程 =任意可逆过程
这就是克劳修斯不等式 , 不可逆时式中T仅为环境的温度. 当系统从始态1分别经可逆和不可逆途径到达末态2时, 系统状态函数熵的变化量是一样的, 不同的是热温商. 只有可 逆途径的热温商之和才与熵变量相等.
Q1 Q2 0 T1 T2
对无限小的循环, 有
不可逆 可逆
dQ1 dQ2 0 不可逆 可逆 T1 T2
小结: 对在两恒温热源间工作的热机 • 其热机效率小于(T1－T2)/T1是可能的, 大于则不可能, 等于时相 当于热机实际处在平衡状态; • 其热温商小于零是可能的, 大于则不可能, 等于时平衡. 上两式适合于任何物质，发生任何变化的循环过程。
•要解决过程的方向性的问题，必须依赖于热力 学第二定律。
99-11-24
3
§3-1 热力学第二定律
1. 自发过程与非自发过程
• 在一定的条件下，不需要消耗环境的作用就能 自动进行的过程，称为自发过程。 • 如水往低处流，冰熔化，墨水在清水中扩散， 常温下能自动进行的化学反应等等。 • 自发过程的逆过程是不能自动进行的，称为非 自发过程。 • 自发过程的共同特征是不可逆的。 [课堂讨论]：以气体真空膨胀为例，说明自发过 程是不可逆过程。
• 例：木炭在氧气中燃烧，热力学能转变为热，生成CO2， 其逆过程是CO2吸收相同的热量，转变为C和O2，是不违 反热力学第一定律的，但能否自动的进行呢？
99-11-24 2
同在能量守恒的前提下, 热的自发传递是单方向的; 功可全部转化为热, 而热转化为功却是有限制的.
• 热 从 高 温 传 向 低 温 • 功 转 化 为 热
1
任意不可逆过程的热温商之和一定小于其熵变.
dQ S T
>任意不可逆过程 =任意可逆过程
这就是克劳修斯不等式 , 不可逆时式中T仅为环境的温度. 当系统从始态1分别经可逆和不可逆途径到达末态2时, 系统状态函数熵的变化量是一样的, 不同的是热温商. 只有可 逆途径的热温商之和才与熵变量相等.
物理化学：2.08熵变的计算
对于非理想气体，也有类似公式，但 Cp、Cv 不是常数，要会推导（选择 适当的可逆途径）。
四、相变过程的熵变
体系的熵变量不仅与温度、压力、 体积的变化有关，还与物质发生熔 融、蒸发、升华等相变化过程有关；
因为物质在发生这些相变化时，有 热量的吸收或放出，故也应有熵的 变化。
潜热：
若相变过程是在恒温和恒压的平衡状 态下可逆地进行的，同时有热量的吸 收或放出，这种热量称为“潜热”。
vHm：摩尔气化热； Tb：正常沸点，P下沸点。
3） P下升华过程：
SSm = SHm / T
SHm：摩尔升化热； T：固、气可逆相变时的平衡温度。
说明：
1）熔化和气化时都需吸收热量，故熔化过 程和蒸发过程的熵都增加，即物质的液 态熵值比固态的要大，气态熵值比液态
的大：S气 S液 S固
T = 10.83C = 283.98 K
1kg 雪 水： S1 = 2.09 ln ( 273.15 / 263.15 ) + ( 334.4 / 273.15 ) + 4.18 ln ( 283.98 / 273.15 ) = 1.465 kJ/K
5 kg 水降温： S2 = 4.18 ln ( 283.98 / 303.15 ) = 1.365 kJ/K
解：Sm = S1 + S2 + S3 = Cp, m( l ) ln (T2/T1) – fHm/ Tf + Cp, m(s) ln (T1/T2) = – 35.45 J/Kmol
• 结果表明此自发过程之体系熵变为
– 35.45 J/Kmol < 0 体系熵变小于零，不能说其和自发过程矛盾，需 再计算相应的环境的熵变 Sm, 环。
物理化学课件第6讲-熵变的计算
S T
p
δQ / T T
p
nC p,m dT dT
T
p
nC p,m T
意义：T ↑ S ↑，且每升温1K，S 增加 nCp,m/T
则：
dS nCp,m dT T
dS S dT S dP T P P T
S T2 nCp,m dT
T T1
(1) 条件：等p简单变温
(2)
U
U
* A
U
* B
U
* C
H
H
* A
H
* B
H
* C
S
SA*
S
* B
SC*
∴ S SB
B
② 等T，p下不同理想气体的混合熵
T，nAp T，nBp T，nCp
…
抽去隔板
等T，p
nA+nB+nC+… T，p
nB：
T，p
SB
T，pB
SB
nBR ln
p pB
nBR ln
xB
∴ S SB (nBR ln xB)
但环境没有熵变，则： S（隔离） S（体系） 19.14 J K1 0
（2）为不可逆过程，自发的过程。
例2.如图有一绝热容器，其中一块用销钉固定的绝热隔板 将容器分为两部分，两边分别装有理想气体He和H2，状 态如图。若将隔板换作一块铝板，则容器内的气体(系
统)便发生状态变化。求此过程的(1)H；(2)S。
解：方法1
12m98o.2l HK，2Op(l)
等T, p, IR S = ?
298H.22OK(，g)p
Ⅰ 等 p, R
Ⅲ 等 p, R
373H.22OK，(l) p
03-2 熵变的计算
上页 下页
∆S = ∆S (O 2 ) + ∆S ( N 2 ) = 4.160J ⋅ K
∵ ∆ U＝0, W = 0， Q ＝0 为隔离系统， ∴ 为隔离系统，
−1
∆ S > 0, 此过程为自动发生的不 可逆过程
∆ S = − R Σ n B ln y B
(理想气体恒温混合 理想气体恒温混合) 理想气体恒温混合
上页 下页
环境的熵变
Q r (环 ) ∆S(环境 ) = T(环)
将环境看作一个巨大的热源： 将环境看作一个巨大的热源： T(环)=常数； 环 常数 常数； ＝－Q(系 由于 Q(环)＝－ 系) 环 ＝－ Q(环)＝ Qr(环) 环＝ 环
Q(系) ∆S(环境 ) = － T(环)
上页 下页
系统的熵变
上页 下页
说明: 说明:
尽管上式是在可逆的条件下得到的,但是 尽管上式是在可逆的条件下得到的 但是, 但是 不可逆时仍然成立 时仍然成立。 在不可逆时仍然成立。 不可逆 n, P1,V1,T1 ∆S 可逆 ∆ Sr n, P2,V2,T2
∆S =
∫
2
1
dU + pdV T
∆S = ∆Sr
(封闭系统 任意 封闭系统, 任意pVT变化 W’=0) 变化, 封闭系统 变化 上页 下页
解：
N2(g)：1mol ： T1=273K P1=100.0kPa
(1)等温可逆膨胀 等温可逆膨胀 (2) 自由膨胀
N2(g) ：1mol T2=273K P2=10.00kPa
上页 下页
(1) ∆S = ∫
2
1
dU + pdV = T
v2
pdV ∫ T v1
V2 p1 = nR ln = nR ln V1 p2
∆S = ∆S (O 2 ) + ∆S ( N 2 ) = 4.160J ⋅ K
∵ ∆ U＝0, W = 0， Q ＝0 为隔离系统， ∴ 为隔离系统，
−1
∆ S > 0, 此过程为自动发生的不 可逆过程
∆ S = − R Σ n B ln y B
(理想气体恒温混合 理想气体恒温混合) 理想气体恒温混合
上页 下页
环境的熵变
Q r (环 ) ∆S(环境 ) = T(环)
将环境看作一个巨大的热源： 将环境看作一个巨大的热源： T(环)=常数； 环 常数 常数； ＝－Q(系 由于 Q(环)＝－ 系) 环 ＝－ Q(环)＝ Qr(环) 环＝ 环
Q(系) ∆S(环境 ) = － T(环)
上页 下页
系统的熵变
上页 下页
说明: 说明:
尽管上式是在可逆的条件下得到的,但是 尽管上式是在可逆的条件下得到的 但是, 但是 不可逆时仍然成立 时仍然成立。 在不可逆时仍然成立。 不可逆 n, P1,V1,T1 ∆S 可逆 ∆ Sr n, P2,V2,T2
∆S =
∫
2
1
dU + pdV T
∆S = ∆Sr
(封闭系统 任意 封闭系统, 任意pVT变化 W’=0) 变化, 封闭系统 变化 上页 下页
解：
N2(g)：1mol ： T1=273K P1=100.0kPa
(1)等温可逆膨胀 等温可逆膨胀 (2) 自由膨胀
N2(g) ：1mol T2=273K P2=10.00kPa
上页 下页
(1) ∆S = ∫
2
1
dU + pdV = T
v2
pdV ∫ T v1
V2 p1 = nR ln = nR ln V1 p2
物理化学03章_热力学第二定律(二)
Ssys = 19.14 J K
Ssur = 0
1
(系统未吸热,也未做功)
Siso = Ssys + Ssur = 19.14 J K 1 > 0
(2)为不可逆过程.
例2:在273 K时,将一个 22.4 dm3 的盒子用隔板一分为二,
0.5 mol 0.5 mol O2 (g) N2 (g)
p1 V1 p2 V2 T2 p2 V2 ∵ = ∴ = T1 T2 T1 p1V1
V2 p2V2 ∴ S = nR ln + nCV ,m ln V1 p1V1
V2 p2 V2 = nR ln + nC V ,m ln + nC V ,m ln V1 p1 V1
p2 V2 ∴ S = nCV ,m ln + nC p ,m ln p1 V1
因为在可逆相变中压力恒定,所以可逆热即为相 因为在可逆相变中压力恒定, 变焓.又由于温度一定,所以, 变焓.又由于温度一定,所以,物质 B 由 α 相态 转化为 β 相态
p ,T B (α ) → B ( β )
的相变熵为: 的相变熵为:
β α H β α S = T
用上式,可计算正常熔点下的熔化熵, 用上式,可计算正常熔点下的熔化熵,正常 沸点下的蒸发熵等等. 沸点下的蒸发熵等等.
= TC S > 0
Q W
热源
R2
TC
1
W2
Q W2
TB热源做功能力低于TA
TB热源做功能力低于TA
其原因是经过了一个不可逆的热传导过程 功变为热是无条件的,而热不能无条件 地全变为功. 热和功即使数量相同,但"质量"不等, 功是"高质量"的能量. 高温热源的热与低温热源的热即使数量相 同,但"质量"也不等,高温热源的热"质量" 较高,做功能力强. 从高"质量"的能贬值为低"质量"的能 是自发过程.
物理化学解析化学反应的熵变与自由能变化
物理化学解析化学反应的熵变与自由能变化在物理化学领域中，解析化学反应的熵变与自由能变化是一项重要的研究内容。
熵变（ΔS）和自由能变化（ΔG）是描述化学反应中系统混乱程度和能量变化的重要物理量。
本文将对熵变和自由能变化的概念进行解析，并探讨它们与化学反应的关系。
1. 熵变的概念及含义熵（S）是描述系统无序程度的物理量，即系统的混乱程度。
熵变（ΔS）表示在化学反应中系统熵的增加或减少。
根据热力学第二定律，一个孤立系统的熵不断增加，因此熵变通常表示为正值。
熵变的计算可以通过以下公式求得：ΔS = S产物 - S反应物其中，S产物和S反应物分别表示反应产物和反应物的熵值。
2. 自由能变化的概念及计算自由能（G）是描述系统可逆过程中能量的物理量，是系统的稳定性指标。
自由能变化（ΔG）表示在化学反应中系统自由能的增加或减少。
自由能变化可以通过以下公式计算：ΔG = ΔH - TΔS其中，ΔH表示反应焓变，T表示绝对温度（Kelvin），ΔS表示熵变。
3. 熵变与自由能变化的关系熵变和自由能变化之间存在着密切的关系。
根据ΔG的计算公式，可以得知当ΔG<0时，化学反应是自发进行的；当ΔG>0时，化学反应是不可逆进行的；当ΔG=0时，化学反应处于平衡状态。
根据ΔG的公式，我们可以得出以下结论：- 当ΔH<0且ΔS>0时，自由能变化ΔG<0，反应是自发进行的。
- 当ΔH>0且ΔS<0时，自由能变化ΔG>0，反应是不可逆进行的。
- 当ΔH<0且ΔS<0时，自由能变化ΔG的正负取决于温度的影响。
4. 熵变与自由能变化在化学反应中的应用熵变和自由能变化是描述化学反应方向和速率的重要指标，具有广泛的应用：- 在工业生产中，通过熵变和自由能变化的计算，可以优化反应条件，提高反应产率和选择性。
- 在生物化学中，熵变和自由能变化对于描述酶催化反应的速率和选择性也具有重要作用。
第3章 熵变的计算
II
等温，等压，可逆
1mol H 2 O g 373.15 K，p o
S SⅠ SⅡ SⅢ 373.15 40.60 103 298.15 33 ln 298.15 373.15 373.15 118 J K 1 75 ln
等压 可逆
1mol H 2 O l 373.15 K，p o
S
理想气体混合物 A(g) + B(g) + C(g) + …
* * * U UA UB UC * * * H HA HB HC
S B nB R ln
p nB R ln xB n xB R ln xB nR xB ln xB pB
思考：因为 S > 0，该过程为自发过程；此推理正确吗？
3. 环境熵变的计算
环 境 系 统
环境通常由不发生相变及化学变化的物质 组成，即使环境与系统有功与热的交换，其 温度、压力并没有发生可觉察的变化。所以 认为 环境内部过程都是可逆过程
Samb
Qamb Tamb
Qsys Tamb
Qsys 为系统实际从环境得到的热； Qamb为环境实际由系统得到的热 两者绝对值相等，符号相反
O
3. 先恒压后恒容
V p S nC p ,m ln 2 nCV ,m ln 2 V1 p1
前提：设定理想气体的 CV,m和 Cp,m 均为常数
V1
V2
V
(4) 混合或传热过程 (理想气体/凝聚态物质)
混合过程：种类很多，都不可逆；所以，需要设计可逆过程； 总的原则：分别计算各个组分的熵变，然后加和
(1) 可逆相变 (恒温恒压可逆相变)
等温，等压，可逆
1mol H 2 O g 373.15 K，p o
S SⅠ SⅡ SⅢ 373.15 40.60 103 298.15 33 ln 298.15 373.15 373.15 118 J K 1 75 ln
等压 可逆
1mol H 2 O l 373.15 K，p o
S
理想气体混合物 A(g) + B(g) + C(g) + …
* * * U UA UB UC * * * H HA HB HC
S B nB R ln
p nB R ln xB n xB R ln xB nR xB ln xB pB
思考：因为 S > 0，该过程为自发过程；此推理正确吗？
3. 环境熵变的计算
环 境 系 统
环境通常由不发生相变及化学变化的物质 组成，即使环境与系统有功与热的交换，其 温度、压力并没有发生可觉察的变化。所以 认为 环境内部过程都是可逆过程
Samb
Qamb Tamb
Qsys Tamb
Qsys 为系统实际从环境得到的热； Qamb为环境实际由系统得到的热 两者绝对值相等，符号相反
O
3. 先恒压后恒容
V p S nC p ,m ln 2 nCV ,m ln 2 V1 p1
前提：设定理想气体的 CV,m和 Cp,m 均为常数
V1
V2
V
(4) 混合或传热过程 (理想气体/凝聚态物质)
混合过程：种类很多，都不可逆；所以，需要设计可逆过程； 总的原则：分别计算各个组分的熵变，然后加和
(1) 可逆相变 (恒温恒压可逆相变)
大学课程《物理化学》第二章(热力学第二定律)知识点汇总
B
VB ,m
V nB T , p ,n jB
H nB T , p ,n jB G nB T , p ,n jB
U B ,m
U nB T , p ,n jB
S nB T , p ,n jB
T2 p1 dT S S '1 S '2 nR ln C p p2 T1 T
dU TdS pdV
T p V S S V
dH TdS Vdp
( U )V T S
T V p S S p
S系统 S B S A
Qr
T
S孤立＝S系统 S环境 0
A
熵变的计算
总则
S环境
Q实际 T环境
理想气体等温过程的熵变
S S B S A
B
Qr
A
Q ( )r T T
Wmax Qr S T T
可逆相变过程的熵变
V2
V1
dG SdT Vdp B dnB
B
dU TdS pdV B dnB
B
U dU TdS pdV dnB nB S ,V ,n j B
B
U H F G nB S ,V ,n j B nB S , p ,n j B nB T ,V ,n j B B nB T , p ,n j B
B
dG SdT Vdp B dnB
B
纯理想气体的化学势
Gm Vm p T p T
VB ,m
V nB T , p ,n jB
H nB T , p ,n jB G nB T , p ,n jB
U B ,m
U nB T , p ,n jB
S nB T , p ,n jB
T2 p1 dT S S '1 S '2 nR ln C p p2 T1 T
dU TdS pdV
T p V S S V
dH TdS Vdp
( U )V T S
T V p S S p
S系统 S B S A
Qr
T
S孤立＝S系统 S环境 0
A
熵变的计算
总则
S环境
Q实际 T环境
理想气体等温过程的熵变
S S B S A
B
Qr
A
Q ( )r T T
Wmax Qr S T T
可逆相变过程的熵变
V2
V1
dG SdT Vdp B dnB
B
dU TdS pdV B dnB
B
U dU TdS pdV dnB nB S ,V ,n j B
B
U H F G nB S ,V ,n j B nB S , p ,n j B nB T ,V ,n j B B nB T , p ,n j B
B
dG SdT Vdp B dnB
B
纯理想气体的化学势
Gm Vm p T p T
物理化学 03-03相变过程熵变
2
将环境看作一个巨大的热源： 将环境看作一个巨大的热源： T(环)=常数；Qr(环)＝∆H(环) ； Q(环)＝－ 系) 常数； 环 ＝ ＝－Q(系 环 常数 环 环 ＝－
P121 例3.5.1
Q(系) ∆S (环境 )＝－ T (环)
∆H ( 263 K ) = ∆H ( 273 K ) + m ∆ C p ∆T＝－311.46kJ = Q( 系 )
-
§3.5 相变过程
1. 可逆相变
可逆相变—恒温恒压且无限接近平衡条件下进行的相变过程 恒温恒压且无限接近平衡条件下进行的相变过程
∆H 相变 Qr ∆ S＝ ＝ T相变 T相变
2. 不可逆相变
在始末态之间设计可逆途径
P121 例3.5.1
1
H2O(l) 263K 100kPa ∆1S
不可逆相变 ∆S(263K) ∆2S 可逆相变 ∆S(273K)
B
T δQ T δQ δQ r r = [S AB (0 K ) − S A (0 K ) − S B (0 K )] + ∫ −∫ −∫ r 0K T AB 0 K T A 0 K T B T
7
2.热力学第三定律
=
∫
Tf
C o--,m (s ) p T T
0K Tb
o ∆ fus H mdT + Tf
+∫ +∫
C o-,m ( l ) p
Tf T
dT +
o ∆ vap H m-
Tb
C o-,m ( g ) p
Tb
T
dT + ∆ pg S o- (T ) g m
4.标准摩尔反应熵的计算 4.标准摩尔反应熵的计算
将环境看作一个巨大的热源： 将环境看作一个巨大的热源： T(环)=常数；Qr(环)＝∆H(环) ； Q(环)＝－ 系) 常数； 环 ＝ ＝－Q(系 环 常数 环 环 ＝－
P121 例3.5.1
Q(系) ∆S (环境 )＝－ T (环)
∆H ( 263 K ) = ∆H ( 273 K ) + m ∆ C p ∆T＝－311.46kJ = Q( 系 )
-
§3.5 相变过程
1. 可逆相变
可逆相变—恒温恒压且无限接近平衡条件下进行的相变过程 恒温恒压且无限接近平衡条件下进行的相变过程
∆H 相变 Qr ∆ S＝ ＝ T相变 T相变
2. 不可逆相变
在始末态之间设计可逆途径
P121 例3.5.1
1
H2O(l) 263K 100kPa ∆1S
不可逆相变 ∆S(263K) ∆2S 可逆相变 ∆S(273K)
B
T δQ T δQ δQ r r = [S AB (0 K ) − S A (0 K ) − S B (0 K )] + ∫ −∫ −∫ r 0K T AB 0 K T A 0 K T B T
7
2.热力学第三定律
=
∫
Tf
C o--,m (s ) p T T
0K Tb
o ∆ fus H mdT + Tf
+∫ +∫
C o-,m ( l ) p
Tf T
dT +
o ∆ vap H m-
Tb
C o-,m ( g ) p
Tb
T
dT + ∆ pg S o- (T ) g m
4.标准摩尔反应熵的计算 4.标准摩尔反应熵的计算
《物理化学》教学提要 第五讲 熵变的计算
《物理化学》教学提要第五讲熵变的计算熵变是指热力学系统在定常过程中发生的熵的变化，即Δ
S=Sf-Si，其中Sf为终态熵，Si为初态熵。
2. 熵变的计算方法
(1) 对于理想气体的等温、等容和等压过程，熵变的计算公式分别为：
ΔS=q/T
ΔS=Cvln(Tf/Ti)
ΔS=Cpln(Tf/Ti)-Rln(Vf/Vi)
其中q为吸热量，T为热力学温度，Cv为定容热容，Cp为定压热容，R为气体常数，V为体积。
(2) 对于化学反应，熵变的计算公式为：
ΔS=∑nSf-∑mSi
其中n为生成物的系数，m为反应物的系数，S为标准熵。
(3) 对于固体和液体的物质状态变化，熵变的计算公式为：
ΔS=Cpln(Tf/Ti)
其中Cp为定压热容，T为热力学温度，f和i分别表示终态和初态。
3. 熵变的影响因素
熵变受到温度、压力、物质状态和化学反应等因素的影响。
一般来说，温度越高，熵变越大；压力越大，熵变越小；物质状态从固体到液体再到气体，熵变越大；而化学反应的熵变则与反应类型和反应
条件有关。
4. 熵定律
熵定律是指在孤立系统中，熵的增加是不可避免的。
这一定律对于热力学系统的稳定性和可逆性具有重要的理论和实际意义。
物理化学Ⅱ3.4 热力学第二定律和热力学第三定律(四)-熵变的计算(沈伟) 2
2019/10/15
物理化学II
5
热力学第二定律和第三定律
熵变的计算
（二）变温过程的熵变
体系：设计可逆（逐步加热）
恒压
Q可逆 CpdT
S
Q T2
可逆
T T1
T2 C pdT T T1
C
p
ln
T2 T1
恒容
Q可逆 CV dT
S
Q T2
可逆
T T1
T
0
C
p
d
ln
T
物理化学II
13
热力学第二定律和第三定律
熵变的计算
用积分法求熵值
以Cp / T为纵坐标， T为横坐标，求某物质 在40K时的熵值。
如图所示：
40
S 0 (Cp / T )dT
阴影下的面积， 就是所要求的该物质 的规定熵。
物理化学II
14
热力学第二定律和第三定律
熵变的计算
物理化学II
7
热力学第二定律和第三定律
熵变的计算
对物质的量一定从 p1,V1,T1 到 p2 ,V2 ,T2的过程。这种情 况一步无法计算，要分两步计算，有三种分步方法：
1. 先等温后等容 2. 先等温后等压 3. 先等压后等容
S nR ln(V2 ) T2 nCV ,mdT
V1
T1
如果要求某物质在沸点以上某温度T时的熵，则
积分不连续，要加上在熔点（Tf）和沸点（Tb）时的 相应熵，其积分公式可表示为：
2019/10/15
物理化学II
2
热力学第二定律和第三定律
熵变的计算
（一）等温过程的熵变
热力学第二定律-物理化学-课件-03
7
说明： 1.各种说法一定是等效的。若克氏说法不成 立，则开氏说法也一定不成立（证明见书48页）； 2.要理解整个说法的完整性切不可断章取义。如 不能误解为热不能转变为功，因为热机就是一种把 热转变为功的装置；也不能认为热不能完全转变为 功，因为在状态发生变化时，热是可以完全转变为 功的（如理想气体恒温膨胀即是一例） 3.热二律与热一律同样都是建立在无数客观事实基础 上的客观规律。至今还没有发现违背热二律的事实。
平衡
20
（2）真空膨胀 熵是状态函数，始终态相同，系统熵变也相同， 所以：
S sy 19.14 J K
1
S su
Q pra Tex
0
Sis Ssy Ssu 19.14 J K 1 0
自发过程
21
恒容变温
QV= dU = nCV,mdT
S
4
自发过程的定义
没有环境的影响下而能自动发生的过程 自发过程的特点 有方向的，有限度的，是不可逆过程。 要正确理解自发过程具有单向性（不可逆）的含义: 并不是其不能反向进行，环境对系统做功，可以使 系统复原，如利用水泵引水上山；利用空调机，可 以把热量从低温物体传到高温物体，但是一定在环 境中留下痕迹。 5
22
PVT均变化的ΔS的计算-理想气体
( p1 ,V1 , T1 ) ( p2 , V2 , T2 )
恒容 SV
S
( p ',V1 , T2 )
恒温 ST
T2 V2 S SV ST nCV ,m ln nR ln T1 V1
23
( p1 ,V1 , T1 ) ( p2 , V2 , T2 )
V2 p2 Qr Wr nRT ln nRT ln V1 p1 Qr V2 p2 S nR ln nR ln T V1 p1
说明： 1.各种说法一定是等效的。若克氏说法不成 立，则开氏说法也一定不成立（证明见书48页）； 2.要理解整个说法的完整性切不可断章取义。如 不能误解为热不能转变为功，因为热机就是一种把 热转变为功的装置；也不能认为热不能完全转变为 功，因为在状态发生变化时，热是可以完全转变为 功的（如理想气体恒温膨胀即是一例） 3.热二律与热一律同样都是建立在无数客观事实基础 上的客观规律。至今还没有发现违背热二律的事实。
平衡
20
（2）真空膨胀 熵是状态函数，始终态相同，系统熵变也相同， 所以：
S sy 19.14 J K
1
S su
Q pra Tex
0
Sis Ssy Ssu 19.14 J K 1 0
自发过程
21
恒容变温
QV= dU = nCV,mdT
S
4
自发过程的定义
没有环境的影响下而能自动发生的过程 自发过程的特点 有方向的，有限度的，是不可逆过程。 要正确理解自发过程具有单向性（不可逆）的含义: 并不是其不能反向进行，环境对系统做功，可以使 系统复原，如利用水泵引水上山；利用空调机，可 以把热量从低温物体传到高温物体，但是一定在环 境中留下痕迹。 5
22
PVT均变化的ΔS的计算-理想气体
( p1 ,V1 , T1 ) ( p2 , V2 , T2 )
恒容 SV
S
( p ',V1 , T2 )
恒温 ST
T2 V2 S SV ST nCV ,m ln nR ln T1 V1
23
( p1 ,V1 , T1 ) ( p2 , V2 , T2 )
V2 p2 Qr Wr nRT ln nRT ln V1 p1 Qr V2 p2 S nR ln nR ln T V1 p1
物理化学-03热力学第二定律
∫ (δQ
1
2
r
/T )
ΔS ≥
∫ ( δQ / T )
1
2
δQ dS ≥ T
>不可逆过程 = 可逆过程
克劳修斯不等式
6.熵判据——熵增原理1
(1) 对于一个绝热过程: Q=0 所以 dS ≥ 0 (>不可逆, =可逆) 绝热过程中,熵不可能减少 (2) 对于一个隔离系统 因为一个隔离系统与环境无能量交换 dS(隔)=dS(系)+dS(环) ≥0 (>不可逆, =可逆) Or: ΔS(隔)=ΔS(系)+ΔS(环) 0≥ (>不可逆, =可逆) 所以: dS(隔) ≥ 0 (>不可逆, =可逆) 判据 dS(隔) < 0 是不可能的 因此, 隔离系统的熵值永远不会减少.
ΔU = 0
Q1 = −W1 = ∫ pdV = nRT1 ln (V2 / V1 )
V1 V2
!V2 > V1 ,
Q1 > 0
体系吸热并对外作功
（2）绝热可逆膨胀 (2):p2 V 2 T1 to(3):p3 V3 T2
Q=0 W2 = ΔU 2 = nCV ,m (T2 − T1 )
! T2 < T1 ∴ 系统对外作功,W2 < 0
!T > 0 ∴0 < η < 1 ∴ 热不可以全部转化为功
因此，卡诺循环的热机效率： 只取决于高、低温热源的温度。
分 析 1）因为2－3, 4－1步为绝热过程Q＝0，所以与 热源无关； 2）η只与T1, T2有关，与工作介质无关，当T2一 定(常温)，T1越高（热的品位高）,η越高； 3）令卡诺循环的逆循环过程，外界作功(电功， 机械功)，从T2(低温)吸热Q2，向T1(高温) 放热Q2, 致冷； 4）卡诺循环是可逆循环，可逆过程系统对环境 作最大功，所以卡诺热机的η最大。
物理化学熵变的计算
理想气体等温等压
2012-8-30
上一内容
下一内容
回主目录
返回
10
2. 环境ΔS的计算
amb S dSamb
1 2
Qr T amb 1
2
一般环境常为大气 般环境常为大气
Tamb b A, Qamb b amb bH Qamb Qamb是环境与系统实际交换的热=-Qsys amb S Tamb
1mol He(g) 1mol H2(g) 300K 200K 101 3kPa 101 3kPa 101.3kPa 101.3kPa
解：求末态 过程特点：孤立系统， U = 0
U U ( He ) U ( H 2 )
3 5 n R T2 200 K n R T2 300 K 0 2 2
T， r， S (1)1 ( ) mol , 理气， 气 V1 1mol , 理气， 气 10V1 T，真空，S (2)1mol , 理气，V1 1mol , 理气， 10V1
解：(1)可逆膨胀 (此过程为可逆过程)
Wmax V2 Q 1 S1 ( ) R nR R ln l 19.14 19 14 J K T T V1
1
(此过程为 逆过程) (2) 真空膨胀 真空膨 (此过程为不可逆过程)
S2 19.14 J K
2012-8-30
上一内容
下一内容
回主目录
返回
13
例2：10mol理想气体，25℃时由1.000MPa 膨胀到 0.100MPa, 计算S, Q/T。假定过程为： (a)可逆膨胀； (b)自由膨胀； (c)抗恒外压0.100 0.100MPa MPa膨胀。 解 题中三个过程的始终态相同，故 解：题中三个过程的始终态相同，故 解： 题中三个过程的始终态相同 故S相同 S= nRln ln( (p1 / p2) = 191 JK-1 热不是状态函数，要分别计算三个过程的热： 理想气体定温过程 U=0，Q= -W W 理想气体定温过程，
《物理化学》第2章
热不是系统的状态函数，所以要分别计算三 个过程的热： 理想气体定温过程，U=0，Q= -W, 计算W即可
实际过程的热温商：
2．热由高温物体传向低温物体:
高温热源T2 Q’=Q1+W Q=W 做功W 吸热Q1 低温热源T1 冷冻机做功后，系统(两个热源)恢复原状，… 传热Q1
结果环境失去功W，得到热Q ，环境是否能恢复原状， 决定于热Q能否全部转化为功W而不引起任何其它变化 ?
3．化学反应:
Cd(s)+PbCl2(aq)=CdCl2(aq)+Pb(s)
用一闭合曲线代表任意可逆循环。在曲线上任 意取A，B两点，把循环分成AB和BA两个可逆过 程,即： A B A
根据任意可逆循环热温商的公式：
B
Qr
Qr Qr 0 T T B T A
B A
p T
Qr
热力学第二定律的提出
19世纪初,资本主义工业生产已经很发达,迫切需要解
决动力问题。当时人们已经认识到能量守恒原理,试图制
造第一类永动机已宣告失败,然而人们也认识到能量是可 以转换的。于是,人们就想到空气和大海都含有大量的能
量，应该是取之不尽的。有人计算若从大海中取热做功，
使大海温度下降1℃，其能量可供全世界使用100年…。于 是人们围绕这一设想，设计种种机器，结果都失败了。这 个问题的实质可归结为热只能从高温物体自动传向低温物 体，没有温差就取不出热来(即从单一热源吸热)。
环境中吸热全部变为功，但体积变大了，压力变小了。
3.“第二类永动机不可能造成”可用来判断过程的方
向。
热力学第二定律的提出是起源于热功转化的研究，寻找相
应的热力学函数需从进一步分析热功转化入手(热机效率)。
实际过程的热温商：
2．热由高温物体传向低温物体:
高温热源T2 Q’=Q1+W Q=W 做功W 吸热Q1 低温热源T1 冷冻机做功后，系统(两个热源)恢复原状，… 传热Q1
结果环境失去功W，得到热Q ，环境是否能恢复原状， 决定于热Q能否全部转化为功W而不引起任何其它变化 ?
3．化学反应:
Cd(s)+PbCl2(aq)=CdCl2(aq)+Pb(s)
用一闭合曲线代表任意可逆循环。在曲线上任 意取A，B两点，把循环分成AB和BA两个可逆过 程,即： A B A
根据任意可逆循环热温商的公式：
B
Qr
Qr Qr 0 T T B T A
B A
p T
Qr
热力学第二定律的提出
19世纪初,资本主义工业生产已经很发达,迫切需要解
决动力问题。当时人们已经认识到能量守恒原理,试图制
造第一类永动机已宣告失败,然而人们也认识到能量是可 以转换的。于是,人们就想到空气和大海都含有大量的能
量，应该是取之不尽的。有人计算若从大海中取热做功，
使大海温度下降1℃，其能量可供全世界使用100年…。于 是人们围绕这一设想，设计种种机器，结果都失败了。这 个问题的实质可归结为热只能从高温物体自动传向低温物 体，没有温差就取不出热来(即从单一热源吸热)。
环境中吸热全部变为功，但体积变大了，压力变小了。
3.“第二类永动机不可能造成”可用来判断过程的方
向。
热力学第二定律的提出是起源于热功转化的研究，寻找相
应的热力学函数需从进一步分析热功转化入手(热机效率)。
物理化学03-03相变过程熵变
T Qr 0K T B
7
2.热力学第三定律
planck说法: 0K时纯物质凝聚态熵值为零。
修正的planck说法:0K时纯物质完美晶体的熵值为零。
S
* m
完美晶体,OK
0
完美晶体:所有质点均 处于最低能级,规则地排列在
点阵结构中,形成一种唯一的排布状态.
COCOCOCOCO…
15
T
Tb
T
C
o-p ,m
(
g
) dT
Tb
T
pg g
S
o-m
T
4.标准摩尔反应熵的计算
r Sm（ T） B Sm（ B）
B
10
5.标准摩尔反应熵随温度的变化
例:分别计算298K和423K时甲醇合成反应的标准摩尔反应熵,
反应方程式为: CO(g)+2H2(g) →CH3OH(g) CO(g) 、2H2(g) 、CH3OH(g)的Cp,m分别为:29.04、29.29、 51.25J·K-1·mol-1
T(环)=常数；Qr(环)＝ΔH(环) ； Q(环)＝－Q(系)
P121
例3.5.1
S
(环境)＝－
Q(系) T (环)
H ( 263K ) H ( 273K ) mC pT＝－311.46kJ Q( 系 )
S
(环境)＝－
Q(系) T (环)
＝1.184kJ
K
1
S(隔离)＝S(系统)＋S(环境)＝45J K 1 0
S H nR ln p1 9.275J K 1
T
p2
5
§3.6 热力学第三定律和 化学变过程熵变的计算
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
T Q T Q Qr r S AB 0 K S A 0 K S B 0 K r 0K T AB 0 K T A 0 K T B T
6
2.热力学第三定律
planck说法: 0K时纯物质凝聚态熵值为零。
§3.5 相变过程
1. 可逆相变
可逆相变—恒温恒压且无限接近平衡条件下进行的相变过程
H 相变 Qr S＝ ＝ T相变 T相变
2. 不可逆相变
在始末态之间设计可逆途径
P121 例3.5.1
0
H2O(l) 263K 100kPa
Δ1S
不可逆相变 ΔS(263K) Δ2S 可逆相变 ΔS(273K)
(2)
恒温恒压 恒温变压 B(g) B(l) B(g) p1=25.664kPa p1=101kPa 可逆相变 p1=101kPa
H n vap H m 0 2.5104 kJ dV 0 W 0
Q U H ( pVg pVl ) H pVg H nRT 2.5104kJ 0.1 8.314 308.66 10 3 kJ 2.2538kJ
r S T S AB T S A T S B T
T Q T Q T Q r r S AB 0 K S A 0 K S B 0 K r 0K 0K 0K T AB T A T B
p1 H 1 S nR ln 9.275J K T p2
4
§3.6 热力学第三定律和 化学变过程熵变的计算
熵的物理意义
T2 理想气体恒压过程 : S nC p,m ln T1
T , S 即S 高温 S 低温
p1 p , S 即S 低压 S 高压 理 想气 体 恒 温过 程 : S nR ln p2 理想气体恒温混合 : S＝ RnB ln yB 0
S B S B ( T ) S B ( 0 K ) S B ( T )
S (B,T)
o m
T
C p,m T
0K
dT
条件: 纯固体（完美晶体） ，po 100 kPa， 0 K T 间无相变
8
求某气体在温度为T时的标准熵
o -o -o -Sm ( T ) Sm ( 0 K ) S m ( 0K T )
1
环境的熵变
S (隔离 )＝S (系统)＋S (环境)
Qr (环) S (环 境)＝ 1 T (环)
2
将环境看作一个巨大的热源： T(环)=常数；Qr(环)＝ΔH(环) ； Q(环)＝－Q(系)
P121 例3.5.1
Q(系) S (环 境)＝ － T ( 环)
H ( 263K ) H ( 273K ) mC p T＝－ 311.46kJ Q( 系 )
Q(系) S (环 境)＝ － ＝1.184kJ K 1 T (环)
S (隔离)＝S(系统)＋S (环境)＝45J K
1
0
2
ΔS的计算及利用其判断过程的方向与限度
Q r 1、 计 算 S的 基 本 公 式 为 ： S＝ T
2、对于可逆过程，利用各种基础热力学数据计算其热温商 3、对于不可逆过程，则须在始末态之间设计一条可逆途径 求其ΔS 4、由多组分物质组成的理想气体系统，可分别求出每种组分 之ΔS，则系统总的ΔS等于各组分ΔS之和 5、利用ΔS判断过程的方向及限度有两种方法：
Tf
-Co p ,m s
0K Tb
T T
o - fuCo p ,m ( l )
Tf T
dT
o - vap H m
Tb
-Co p ,m ( g )
Tb
T
o -dT pg S g m T
H2O(s) 263K 100kPa 可逆降温 H2O(s) 273K 100kPa
可逆升温
H2O(l) 273K 100kPa
263 273 2 S mC p ( s ) ln 1 S mC p ( l ) ln 273 263 S ( 263K )＝S ( 273K ) 1 S 2 S fus H ( 273K ) 263 ＝ m[C p ( s ) C p ( l )]ln ＝－ 1.139kJ K 1 273K 273
S
B
A
Q T
ir 不可逆过程 r 可逆过程
>0可能发生的不可逆过程 =0平衡（可逆）过程 <0不可能发生的过程
dS(隔离)
3
ex3.28
解:设乙醚全部蒸发
nRT 0.1 8.314 308.66 (1) P2 Pa 25.664kPa 3 V 10 10 P2<101.325kPa 说明假设合理
修正的planck说法:0K时纯物质完美晶体的熵值为零。
* 完美晶体 Sm ,OK 0
完美晶体:所有质点均 处于最低能级,规则地排列在
点阵结构中,形成一种唯一的排布状态.
COCOCOCOCO… COCOOCCOCO…
7
3.规定熵和标准熵 以热力学第三定律为基础,我们可以求得任何状 态下纯物质的相对熵,称为该物质在指定状态下的 规定熵.如果指定状态为标准状态,则其规定熵称为 该物质的标准熵
S 混合前 S 混合后
: Sg Sl S s 相变过程 : 由计算知
熵是度量系统无序度的函数
5
1. Nernst（1906）热定理
凝聚系统在恒温过程中的熵变，随温度趋于 0 K 而趋于零
T 0 K
lim T S 0（凝聚系统）
对于任意反应 A＋B→AB 在0K时 ΔrS(0K)=SAB(0K) －SA(0K) － SB(0K)=0 在温度为T时