同步BUCK中的开关损耗计算
BUCK同步整流MOS损耗

基于Buck同步整流电路中功率MOSFETS管参数的优化 华晓辉1 林维明21 2)福州大学电气工程与自动化学院 福州 3500021)Email :hxh_1889@ 2) Email :weiming @摘 要 本文是分析BUCK 同步整流电路中开关管与整流管的损耗模型,以两支管的损耗最小为目标,并以输入电压IN V =5V ,输出电压OUT V =1.8V ,开关频率s f =5MHZ为例,用MATLAB 工具对其进行优化计算,得出该条件下器件物理参数。
关键词 SR-Buck, MOSFET 损耗模型 , MATLAB 优化1.引言MOSFET 现已成为高频开关变换器、微处理器与半导体存储器等先进集成电路(IC)中最主要的器件单元,它尺寸小、功耗低、并与数字电路的主流工艺兼容。
近年来,使用MOSFET 的模拟IC 逐渐已成为主流,改变了以往主要使用双极型器件的局面。
GENFET MOSFET 器件就采用了Genera l Semiconductor 公司的0.35um 深槽工艺制造出了每平方英寸含200M 单元,集成度提高了4倍,更加适合了移动电话机,笔记本电脑,PDA 以及其它的无线电产品的应用。
因此在高功率密度集成Buck 同步整流电路中,确定MOSFET 的损耗模型,优化电路中主开关管与同步整流管的最小损耗模型显得十分重要。
2.寄生参数随着器件尺寸的不断减小,电路模拟程序中的器件模型也越来越复杂,以保证模拟结果的精确度;然而电路的模拟精确度不仅与器件模型有关,还与给定的器件模型参数有关。
功率MOSFET 的常用等效模型如图1,其中dson R 为导通电阻,Cgs 及Cds 和Cgd 为MOSFET 的寄生电容[1],它们的值是非线性的与施加在MOSFET 上的栅极的电压有关。
为简化分析,在此的模型的优化过程中忽略了引线电感等,并使器件工作在线形放大区。
在图1中:Cgov W Cox L W Cgd Cgs ⋅+⋅⋅==2 (1)Cgs 、Cgd 分别是栅极与源极、栅极与漏极之间的电容,Cgov 是栅极与源极、漏极之间的重叠电容[2];图1 MOSFET 常用等效电路模型Cox =ox ox T /97.3ε 是每单位面积的氧化层的电容,其中o ε是真空介电 常数,ox T 为栅极氧化层的厚度,ox ε为栅极氧化层的介电常数。
buck电路 开关损耗 开关频率 导通损耗

buck电路开关损耗开关频率导通损耗【深入探究Buck电路的开关损耗与导通损耗】1. 引言:Buck电路是一种常用的降压型DC-DC转换器,广泛应用于各种电子设备中。
Buck电路通过开关频率的控制,将高压输入电源转换为所需的低压输出电源。
然而,在Buck电路的工作过程中,会产生开关损耗与导通损耗,这两种损耗对电路的效率和性能有重要影响。
2. 开关损耗:开关损耗是指在Buck电路的开关元件(如MOSFET)开关过程中产生的能量损耗。
在每个开关周期内,当MOSFET从导通状态切换到关断状态时,会出现导通损耗和关断损耗。
导通损耗主要由MOSFET的导通电阻和开关电压之间的功率损耗导致,关断损耗则是由于MOSFET在关断过程中的开关电压和关断电流之间的功率损耗引起。
3. 导通损耗:导通损耗是指在Buck电路的开关元件导通状态下产生的能量损耗。
当MOSFET处于导通状态时,会因为导通电阻而产生功率损耗。
导通电阻主要受到MOSFET的导通电阻和电流大小的影响,通过减小导通电阻和控制合理的电流大小,可以降低导通损耗。
4. 开关频率:在Buck电路中,开关频率的选择对开关损耗和导通损耗有着重要的影响。
较高的开关频率可以减少每个开关周期的时间,从而降低了开关损耗;而较低的开关频率则能减少开关元件切换的频率,降低导通损耗。
在选择开关频率时,需要权衡开关损耗和导通损耗之间的关系,以达到最佳的效果。
5. 个人观点和理解:Buck电路的开关损耗与导通损耗是在电路设计中需要重视的问题。
通过合理选择开关频率,能够在一定程度上平衡这两种损耗,从而提高Buck电路的效率和性能。
为了降低开关损耗,可以采用功率金属氧化物半导体场效应管(MOSFET)来替代传统的二极管开关,因为MOSFET具有更低的导通电阻。
选择合适的开关频率也是关键,需考虑电路工作条件和所需的输出电压范围。
通过精心设计和优化Buck电路,在保证稳定输出电压的前提下,可以最大程度地降低开关损耗和导通损耗,提高电路效率和性能。
buck mos管开通关断损耗计算公式

buck mos管开通关断损耗计算公式Buck MOS管是一种常见的功率开关器件,广泛应用于电力电子领域。
在使用过程中,我们经常需要计算其开通关断损耗,以评估器件的性能和效率。
本文将介绍关于Buck MOS管开通关断损耗计算的公式和相关知识。
一、Buck MOS管的工作原理Buck MOS管是一种由金属氧化物半导体材料制成的场效应管。
它具有良好的导电特性和控制性能,适用于高频开关电源和DC/DC 变换器等应用场合。
Buck MOS管的工作原理可简单描述为:当控制信号施加在栅极上时,栅极与源极之间的电场会改变沟道的导电特性,从而控制电流的流动。
当栅极施加正向电压时,电场会吸引电子到沟道中,使其导电;当栅极施加负向电压时,电场会阻挡电子流动,使其截断。
二、开通损耗的计算公式开通损耗是指在MOS管开通过程中,由于电流流动而产生的功率损耗。
开通损耗的计算公式如下:P_on = (V_in - V_out) * I_out其中,P_on为开通损耗,V_in为输入电压,V_out为输出电压,I_out为输出电流。
该公式的计算基于以下假设:忽略了开关管的导通电阻和开关管的内部电源电压降。
三、关断损耗的计算公式关断损耗是指在MOS管关断过程中,由于电流截断而产生的功率损耗。
关断损耗的计算公式如下:P_off = V_out * I_out其中,P_off为关断损耗,V_out为输出电压,I_out为输出电流。
同样地,该公式的计算也基于了忽略了开关管的导通电阻和开关管的内部电源电压降。
四、开通关断损耗的影响因素开通关断损耗的大小取决于多个因素,如输入电压、输出电压、输出电流、开关频率等。
1. 输入电压和输出电压:开通损耗与输入电压和输出电压之间的差异成正比,而关断损耗则仅与输出电压成正比。
2. 输出电流:开通损耗和关断损耗都与输出电流成正比。
当输出电流增大时,开通关断的功率损耗也会增加。
3. 开关频率:开通关断损耗与开关频率成正比。
开关电源的设计及计算
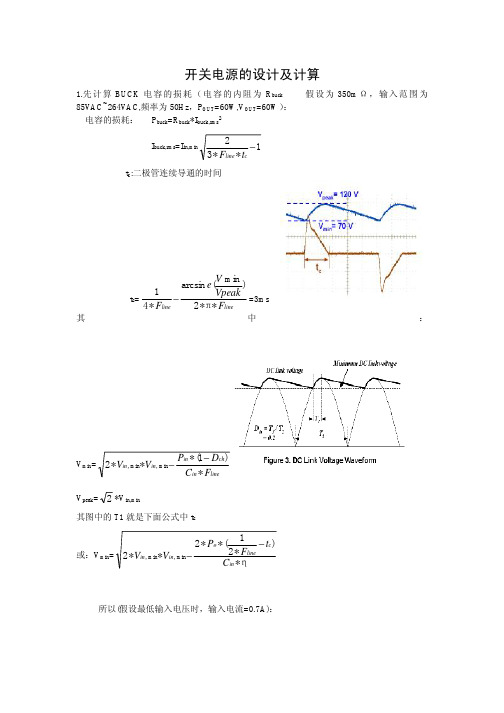
开关电源的设计及计算1.先计算BUCK 电容的损耗(电容的内阻为R buck 假设为350m Ω,输入范围为85VAC~264VAC,频率为50Hz ,P OUT =60W,V OUT =60W ):电容的损耗:P buck =R buck *I buck,rms 2I buck,rms =I in,min1**32−cline t F t c :二极管连续导通的时间t c =linelineF VpeakV e F **2)min(arcsin *41π−=3ms其中:V min =linein ch in in in F C D P V V *)1(***2min ,min ,−−V peak =2*V in,min其图中的T1就是下面公式中t c或:V min =η*)*21(**2**2min ,min ,in c line o in in C t F P V V −−所以(假设最低输入电压时,输入电流=0.7A):I buck,rms =I in,min1**32−cline t F =0.7*13*50*32−=1.3A P buck =350m*1.32=0.95W第一步计算电容损耗是为了使用其中的t c 值,电容的容量一般通用范围选2~3μ/W ,固定电压为1μ/W2.输入交流整流桥的计算(假设V TO =0.7V,R d =70m Ω)在同一个时间内有两个二极管同时导通,半个周期内两个二极管连续导通I d,rms =c line in t F I **3min ,=m3*50*37.0=1.04AP diodes =2*(V TO *2min ,in I +R d *I d,rms 2)=2*(0.7*27.0+70m*1.042)=640mW 一个周期内桥堆损耗为:P BR=2*P diodes =2*640m=1.28W桥堆功耗超过1.5W 时,我个人认为应加散热器(特别是电源的使用环境温度较高时)变压器和初级开关MOS :反激式开关电源有两种模式CCM 和DCM ,各有优缺点。
buck电路 开关损耗 开关频率 导通损耗

标题:深度剖析Buck电路中的开关损耗与导通损耗在电源系统中,Buck电路是一种常见的降压开关电源,其工作稳定、效率高、成本低,因而受到了广泛的应用。
然而,在实际应用中,Buck电路的开关损耗和导通损耗是影响其效率和稳定性的重要因素。
本文将全面探讨Buck电路中的开关损耗和导通损耗,从简单到深入地剖析其原理和影响因素。
1. 核心概念Buck电路是一种电源降压转换器,通过开关管(MOSFET)的开关动作,将输入电压转换为输出电压。
在其工作过程中,开关管的导通和关断会产生开关损耗和导通损耗。
2. 开关损耗开关损耗是由开关管的导通和关断动作引起的能量损失。
主要包括导通时的通态损耗和关断时的反向恢复损耗。
导通时,开关管处于导通状态,存在导通电压降和导通电流,由此产生的功率损耗即为通态损耗;而在关断过程中,由于开关管内外部电感和电容的能量存储和释放,产生反向恢复损耗。
3. 导通损耗在Buck电路中,导通损耗是由开关管和二极管的导通引起的能量损耗。
在导通状态下,由于开关管和二极管内阻的存在,以及导通时的通态电压降和导通电流,会产生导通损耗。
4. 影响因素开关频率是影响Buck电路开关损耗和导通损耗的关键因素之一。
较高的开关频率会减小开关管和二极管的导通和关断时间,从而减小损耗。
然而,较高的开关频率也会导致开关管和二极管的开关损耗增加。
5. 个人观点在实际应用中,合理设计Buck电路的开关频率和开关管、二极管的参数是至关重要的。
在追求高效率和稳定性的需要综合考虑开关损耗和导通损耗,以达到最佳的性能和成本效益。
总结通过本文对Buck电路中的开关损耗和导通损耗的深入剖析,我们了解到了其工作原理和影响因素。
在实际应用中,我们应该综合考虑开关频率、开关管、二极管的参数等因素,以最大程度地降低损耗、提高效率和稳定性。
结语Buck电路中的开关损耗和导通损耗是影响其性能的重要因素,我们需要深入理解和合理设计,以应对不同的应用场景和要求。
buck电路开关损耗计算

buck电路开关损耗计算
Buck电路是一种常用的直流-直流(DC-DC)转换器,用于将输入电压降低到所需的输出电压。
在Buck电路中,开关损耗是一个重要的考虑因素,它会影响电路的效率。
开关损耗主要由两部分组成:开通损耗(Turn-on Loss)和关断损耗(Turn-off Loss)。
开通损耗发生在开关从关断状态转换到开通状态时,而关断损耗发生在开关从开通状态转换到关断状态时。
开通损耗和关断损耗的计算通常涉及到开关的电压和电流波形,以及开关的转换时间。
然而,为了简化计算,我们可以使用一种近似方法,即假设开关的电压和电流波形是矩形的。
在这种近似方法下,开通损耗(E_on)和关断损耗(E_off)可以分别用以下公式计算:
E_on = I_avg * V_in * t_on
E_off = I_avg * V_out * t_off
其中:
I_avg 是开关的平均电流。
V_in 是输入电压。
V_out 是输出电压。
t_on 是开通时间。
t_off 是关断时间。
总开关损耗(E_total)则是开通损耗和关断损耗之和:
E_total = E_on + E_off
请注意,这些公式仅适用于简化的近似计算,并且假设了电压和电流波形是矩形的。
在实际应用中,开关损耗的计算可能需要更复杂的模型和方法。
此外,还需要注意,开关损耗只是Buck电路总损耗的一部分。
其他损耗还包括导通损耗、电感损耗和电容损耗等。
因此,在计算电路的总效率时,需要综合考虑所有损耗。
buck电路 开关损耗 开关频率 导通损耗

【buck电路:深度评估与全面探讨】随着电子技术的迅猛发展,各种高效能、低功耗的电源系统逐渐成为现代电子设备中不可或缺的组成部分。
在这其中,buck电路作为一种常见的降压转换器,被广泛应用于各种电子设备中,以提供稳定、高效的电源输出。
然而,在实际应用中,buck电路的开关损耗和开关频率等问题一直备受关注。
本文将深入分析buck电路的工作原理、开关损耗、开关频率及其影响因素,并提供个人观点和理解。
一、buck电路的工作原理1.工作原理简介在buck电路中,输入电压通过开关器件(MOSFET或IGBT)的控制,经过电感和电容等元件的作用,输出为较低的电压。
其中,通过控制开关器件的导通和关断,实现对输出电压的调节。
2.工作原理详解–输入电压经过控制开关器件后,会形成交替导通和关断的工作状态,实现电能的转换和输出。
–通过电感和电容等元件的协同作用,实现对电压的稳定输出,并且能够在一定程度上提高效率和响应速度。
二、开关损耗对buck电路的影响1.开关损耗的概念在buck电路中,由于开关器件进行导通和关断时会产生一定的能量损耗,这部分损耗即为开关损耗。
它主要包括开关器件导通时的导通损耗和关断时的反向恢复损耗。
2.开关损耗的计算–导通损耗:P sw,on=I sw2×R on–反向恢复损耗:P sw,off=Q rr×V DS×f s w3.开关损耗的影响因素–开关频率–开关器件的导通/关断速度–开关器件的导通/关断损耗特性三、开关频率对buck电路的影响1.开关频率的作用开关频率是指开关器件在单位时间内的开关次数,它直接影响着buck电路的工作性能和效率。
常见的开关频率包括几十千赫兹至几百千赫兹,不同的频率对buck电路的影响也不尽相同。
2.开关频率与效率的关系–高频率:可以减小输出滤波器元件的尺寸和成本,但会增加开关损耗和开关器件的损耗,影响整体效率。
–低频率:能够降低开关损耗,但需要更大尺寸的滤波器元件,导致成本提高并且功耗增加。
BUCK同步整流MOS损耗

基于Buck同步整流电路中功率MOSFETS管参数的优化 华晓辉1 林维明21 2)福州大学电气工程与自动化学院 福州 3500021)Email :hxh_1889@ 2) Email :weiming @摘 要 本文是分析BUCK 同步整流电路中开关管与整流管的损耗模型,以两支管的损耗最小为目标,并以输入电压IN V =5V ,输出电压OUT V =1.8V ,开关频率s f =5MHZ为例,用MATLAB 工具对其进行优化计算,得出该条件下器件物理参数。
关键词 SR-Buck, MOSFET 损耗模型 , MATLAB 优化1.引言MOSFET 现已成为高频开关变换器、微处理器与半导体存储器等先进集成电路(IC)中最主要的器件单元,它尺寸小、功耗低、并与数字电路的主流工艺兼容。
近年来,使用MOSFET 的模拟IC 逐渐已成为主流,改变了以往主要使用双极型器件的局面。
GENFET MOSFET 器件就采用了Genera l Semiconductor 公司的0.35um 深槽工艺制造出了每平方英寸含200M 单元,集成度提高了4倍,更加适合了移动电话机,笔记本电脑,PDA 以及其它的无线电产品的应用。
因此在高功率密度集成Buck 同步整流电路中,确定MOSFET 的损耗模型,优化电路中主开关管与同步整流管的最小损耗模型显得十分重要。
2.寄生参数随着器件尺寸的不断减小,电路模拟程序中的器件模型也越来越复杂,以保证模拟结果的精确度;然而电路的模拟精确度不仅与器件模型有关,还与给定的器件模型参数有关。
功率MOSFET 的常用等效模型如图1,其中dson R 为导通电阻,Cgs 及Cds 和Cgd 为MOSFET 的寄生电容[1],它们的值是非线性的与施加在MOSFET 上的栅极的电压有关。
为简化分析,在此的模型的优化过程中忽略了引线电感等,并使器件工作在线形放大区。
在图1中:Cgov W Cox L W Cgd Cgs ⋅+⋅⋅==2 (1)Cgs 、Cgd 分别是栅极与源极、栅极与漏极之间的电容,Cgov 是栅极与源极、漏极之间的重叠电容[2];图1 MOSFET 常用等效电路模型Cox =ox ox T /97.3ε 是每单位面积的氧化层的电容,其中o ε是真空介电 常数,ox T 为栅极氧化层的厚度,ox ε为栅极氧化层的介电常数。
BUCK型开关电源中的损耗与效率的计算

在BUCK型开关电源中,如果没有损耗,那效率就是100%,但这是不可能的,BUCK型开关电源中主要的损耗是导通损耗和交流开关损耗,导通损耗主要是指MOS管导通后的损耗和肖特基二极管导通的损耗(是指完全导通后的损耗,因为导通不是瞬间导通,有个从线性区到非线性区的过程),在MOS管导通时,由于存在导通电阻,那么流过电流就必然存在导通损耗,而肖特基导通损耗是指在MOS 管关闭期间,由于电感的电流不能突变加上电感反冲现象,会产生与MOS管导通时的相反电压方向,从而使肖特基导通,流过的电流会在肖特基上产生损耗。
由于MOS管在导通的时候,流过其的电流不是瞬间达到最大,此时电流有个从零逐渐上升到最大的过程,此时MOS管漏源(DS)之间的电压也是从Vdc逐渐下降到零,MOS管关闭的时候也存在此情况,只是与打开的时候过程相反,那么在这逐渐的过程中就会产生损耗,这就是交流开关损耗,交流开关损耗包括MOS管打开和关闭损耗,交流开关损耗与开关的频率成正比,因为一开一关的次数越多,损耗自然就大了。
在忽略交流开关损耗的情况下,假设输入电压Vdc,输出电压为Vo,MOS管导通时间为Ton,关闭时间为Toff,整个周期为T,即T=Ton+Toff。
在MOS管导通期间流过的平均电流为Io,由于电感电流不能突变,那么在MOS管关闭期间流过肖特基的平均电流也为Io,在MOS管和肖特基导通期间产生的压差基本为1V,那么导通损耗=P(mos管)+P(肖特基)=1*Io*Ton/T+1*Io*Toff/T=1*Io。
那么此时的效率E=Po/(Po+Plosse)=(Vo*Io)/(Vo*Io)+(1*Io)=Vo/Vo+1。
在考虑交流开关损耗的时候,基本交流开关损耗可以分两种情况来考虑,第一种情况是MOS管导通期间,电流开始上升的时候电压同时开始下降,MOS管关闭期间电流开始下降的时候电压同时上升,此种情况也是最理想的情况(一般实际情况很难达到),那么在此情况下,交流开关损耗=整个开关周期的导通损耗+整个开关周期的关断损耗=(时间从0到Ton,流过电流和电压剩积的积分)*(Ton/T)+(时间从0到Toff,流过电流和电压剩积的积分)*(Toff/T)=Io*Vdc/6*(Ton/T)+Io*Vdc/6*(Toff/T)。
开关损耗计算公式

开关损耗计算公式1.开关损耗的概念开关电源作为一种常见的电源类型,其在使用过程中会伴随着损耗。
而其中重要的一种就是开关损耗,这种损耗是由于开关管在反复进行开关过程中,会产生电感、电容、二极管等等的反向电流,从而产生能量损耗,这些损耗就是开关损耗。
2.开关损耗的分类开关损耗可分为导通损耗和开关损耗两种。
导通损耗是指开关管导通时的损耗,其大小取决于开关管的导通电阻及电源电压;而开关损耗是指开关管有明显的反向阻抗及电子载流子的迁移,从而在反向断路时产生的损耗,其大小取决于开关管的开关频率及负载电容。
3.开关损耗的计算公式开关损耗的计算公式为:Psw=0.5fvho*(Eon+Eoff)*Iload其中,Psw代表开关损耗功率,f为开关频率,vho为开关管输出电压幅值,Eon为开管损失,Eoff为关管损失,Iload为负载电流。
4.各项参数的解释开关损耗公式中的各项参数解释如下:(1)fvho:开关管输出电压幅值,由于开关管导通时,肯定有较小的电压掉电,因此这里要用输出电压的幅值来计算。
(2)Eon:开关管开启损耗,是指开关管在导通时产生的损耗,由于导通阻抗的存在,电流只能通过少量的电阻降,因此产生一定的损耗。
(3)Eoff:开关管关闭损耗,是指开关管在关断时产生的损耗,因为关断过程中会出现电容放电、电感储能等现象,所以会产生相应的能量损耗。
(4)Iload:负载电流,开关管所控制的负载电流,与电路中电阻和电容等元器件有关。
5.开关损耗的影响因素(1)开关频率:开关频率越高,开关管的损耗就越大,这是由于开关管在高频率下会出现更多的反向电流。
(2)开关管特性:开关管的导通阻抗、关断速度等特性,都会对开关损耗产生影响。
(3)电源电压:电源电压高,开关损耗也会随之增大。
6.如何降低开关损耗为了降低开关损耗,可以从以下几个方面入手:(1)选择适合的开关管型号,如IGBT、MOS、SBD等,根据具体场合,选用性价比高的产品。
BUCK型开关电源中的损耗与效率的计算

在BUCK型开关电源中,如果没有损耗,那效率就是100%,但这是不可能的,BUCK型开关电源中主要的损耗是导通损耗和交流开关损耗,导通损耗主要是指MOS管导通后的损耗和肖特基二极管导通的损耗(是指完全导通后的损耗,因为导通不是瞬间导通,有个从线性区到非线性区的过程),在MOS管导通时,由于存在导通电阻,那么流过电流就必然存在导通损耗,而肖特基导通损耗是指在MOS 管关闭期间,由于电感的电流不能突变加上电感反冲现象,会产生与MOS管导通时的相反电压方向,从而使肖特基导通,流过的电流会在肖特基上产生损耗。
由于MOS管在导通的时候,流过其的电流不是瞬间达到最大,此时电流有个从零逐渐上升到最大的过程,此时MOS管漏源(DS)之间的电压也是从Vdc逐渐下降到零,MOS管关闭的时候也存在此情况,只是与打开的时候过程相反,那么在这逐渐的过程中就会产生损耗,这就是交流开关损耗,交流开关损耗包括MOS管打开和关闭损耗,交流开关损耗与开关的频率成正比,因为一开一关的次数越多,损耗自然就大了。
在忽略交流开关损耗的情况下,假设输入电压Vdc,输出电压为V o,MOS管导通时间为Ton,关闭时间为T off,整个周期为T,即T=Ton+Toff。
在MOS管导通期间流过的平均电流为Io,由于电感电流不能突变,那么在MOS管关闭期间流过肖特基的平均电流也为Io,在MOS管和肖特基导通期间产生的压差基本为1V,那么导通损耗=P(mos管)+P(肖特基)=1*Io*Ton/T+1*Io*Toff/T=1*Io。
那么此时的效率E=Po/(Po+Plosse)=(Vo*Io)/(Vo*Io)+(1*Io)=Vo/Vo+1。
在考虑交流开关损耗的时候,基本交流开关损耗可以分两种情况来考虑,第一种情况是MOS管导通期间,电流开始上升的时候电压同时开始下降,MOS管关闭期间电流开始下降的时候电压同时上升,此种情况也是最理想的情况(一般实际情况很难达到),那么在此情况下,交流开关损耗=整个开关周期的导通损耗+整个开关周期的关断损耗=(时间从0到T on,流过电流和电压剩积的积分)*(Ton/T)+(时间从0到T off,流过电流和电压剩积的积分)*(Toff/T)=Io*Vdc/6*(Ton/T)+Io*Vdc/6*(Toff/T)。
同步BUCK中的开关损耗计算
- output inductor power losses - PCB traces power losses
Iin(Vs, Io, Vgs) := Io ⋅ D(Vs, Io, Vgs)
- input current
PQ(Vs, Io, Vgs) := PQ1(Vs, Io, Vgs) + PQ2(Vs, Io, Vgs)
Qtt(10 ⋅ V) = 25.22 ncoul
Rdsu(Vgs) := ⎡⎢5 ⋅ mΩ + 10.5 ⋅ V ⋅ mΩ ⎤⎥ ⋅ 1.4
⎣
(Vgs − VthU) ⎦
- Rdson at 125 C
16 14 12 10 Rdsu( Vgs) 8 mΩ 6 4 2 0
2 3 4 5 6 7 8 9 10 11 12 Vgs
The author, and/or Texas Instruments Inc are not responsible for any issue as the result of use of this software!
One Phase of Synchronous Buck Converter used as an Example in this File
- internal gate resistor of FET - external gate resistor - source output resistor of driver
Rdn := 1 ⋅ ohm
- sink output resistor of driver
IgU1(Vs, Io, Vgs, Rdp) :=
Qtb(4.5 ⋅ V) = 27.65 ncoul
同步buck电路的功耗计算

同步buck电路的功耗计算
要计算同步buck电路的功耗,我们可以考虑以下几个方面:
1. 导通损耗(Switching Losses):导通损耗是由于开关管(如MOSFET)在导通状态下产生的功耗。
它可以通过开关管的导通电阻和开关频率来计算。
一般情况下,导通损耗与电流大小成正比。
2. 关断损耗(Conduction Losses):关断损耗是由于开关管在关闭状态下产生的功耗。
它取决于开关管的关断速度、关断电压以及开关频率。
一般情况下,关断损耗与电流大小和关断速度成正比。
3. 开关损耗(Switching Losses):开关损耗是由于开关管在切换过程中产生的功耗。
它主要取决于开关管的切换频率、输入电压范围和输出电流。
开关损耗与切换频率成正比。
4. 输出滤波器损耗(Output Filter Losses):输出滤波器损耗是由于输出电感和输出电容器中的电流产生的功耗。
它与输出电流和输出电压纹波有关。
综上所述,同步buck电路的总功耗可以通过将上述各个功耗项相加来计算。
具体的计算公式和参数需要根据实际电路的设计和特性来确定。
1。
MOS在开关电路中的应用与计算

小於0.6V,此時diode無法導通,所有電流均
流經RDS,在t3階段,溝道電阻線性下降到 RDS(ON),MOS完全導通。啟開損耗為:
(t1
*VF
+ t2
*VF
+
t3
* VF
+
IO
*1.1* RDS (O 2
) )IO * FSW
關閉損耗:如圖所示,L-side MOS關閉過程為開啟逆過程,則L-side MOS關閉損耗與開啟損耗相同。 驅動損耗:和H-side MOS一樣,其驅動損耗為
ID線性增加到Io,VDS基本不變,所以此段時間內功耗為: E t2-t1=Io*VDS* (t2-t1)/2
t2-t3期間, Io不變,VDS基本呈線 性下降,所以此段時間內功耗為:
E t3-t2=Io*VDS* (t3-t2)/2
所以開通時開關損耗為Psw(on)=Io*VDS* (t3-t1)*Fsw/2
= RDS (O
)
*
I
2 O
*D
+
1 2
IO
*VDS
* (tr
+
tf
) * FSW
+ QG *VG * FSW
2:Low-side MOS損耗(PL) 導通損耗:Pon=Irms2*Rds(on)*(1-D)
開啟損耗:L-side MOS 由於是D端為負壓, 開啟前期DS間電流會從寄生diode流過,和H-
下面以IRF6337(H)和IRF6618(L)的参数表为例来说明下MOS选取应该注 意的参数几个参数.
MOS好坏的判断
量测之前,先把GS两端短路放电,然后用欧姆表量测DSG任意两端电 阻为M欧级,假若先量测GS,再量测DS两端电阻,其阻值会明显 变小或者通路。
BucK功率损耗分析

电感损耗是指电感均方根电流 IRMS 在电感电阻 DCR 上产生之压降造成的损耗
电感电流 iL(t)的分段函数:(为了书写方便下面令 Io_design=Io)
iL
(t
)
=
⎪⎪⎨⎧IoIo+−∆∆I2oIo−+
∆Io t1 ∆Io
t,t ∈[0,t1] t,t ∈[t1,T
]
⎩ 2 T − t1
5
Pcap = 1 Coss *(Vds)2 * f 2
b)Switching loss 开启过程损耗。指在 MOSFET 开启过程中逐渐下降的漏源电 VDS 与逐渐上升的负载电流(即 漏源电流) IDS 交叉重叠部分造成的损耗
VDS 方程
v = −Vin *t +Vin tr
ID
方程 i =
Id tr
=
6
T
3
(Vin − Vo) * Io* Vo f * Lo
(Irms)2 = 2 * (Vin − Vo)* Io* Vo
3
f * Lo
Pinductor = (Irms)2 * R DC * KTH
8
6.3 MOFET,Schottky 损耗 6.3-1 High side MOSFET 损耗 6.3-2 Schottky 损耗
电感电流 iL(t)的分段函数:
电感电流波形
iL
(t
)
=
⎧ ⎪ ⎨ ⎪ ⎩
ILMAX * dT − ILMAX d'T
t, *
t
+
I
LMAX
,
t
t ∈[0,t1] ∈[t1, t2]
Irms =
同步整流buck损耗计算

同步整流buck损耗计算
同步整流buck变换器是一种常见的DC-DC变换器拓扑,用于将输入电压转换为较低的输出电压。
在这种拓扑中,损耗主要来自开关管的导通和关断损耗、二极管的正向压降损耗以及电感和电容元件的损耗。
首先,我们来计算开关管的损耗。
在导通状态下,开关管的损耗与导通电流和开关管的导通压降有关。
在关断状态下,开关管的损耗与开关频率、关断时的反向恢复电压以及开关管的反向恢复时间有关。
这些参数需要根据具体的开关管型号和工作条件来计算。
其次,二极管的损耗也需要考虑。
二极管的损耗与正向电流和正向压降有关。
在buck变换器中,二极管的损耗在整流过程中起着重要作用。
需要根据具体的二极管型号和工作条件来计算。
此外,电感元件和电容元件也会产生一定的损耗。
电感元件的损耗主要来自于电感的等效串联电阻产生的焦耳热损耗,而电容元件的损耗则主要来自于等效串联电阻产生的损耗。
这些损耗需要根据具体的元件参数和工作条件来计算。
综上所述,同步整流buck变换器的损耗计算涉及到开关管、二极管、电感元件和电容元件的损耗计算,需要考虑到多个因素。
在实际工程中,可以通过仿真软件进行损耗计算和分析,以优化设计方案,提高转换效率。
同时,也可以根据具体的应用场景和要求,选择合适的元件和工作参数,以降低整体损耗,提高系统性能。
buck同步整流电路mosfet损耗的计算

buck同步整流电路mosfet损耗的计算1. 引言1.1 背景介绍随着科技的不断发展,电子设备在我们生活中扮演着越来越重要的角色。
在许多电子设备中,直流电源是必不可少的组成部分。
而在直流电源中,buck同步整流电路是一种常见且有效的电路拓扑结构,广泛应用于各种领域中。
在buck同步整流电路中,mosfet作为电路的关键元件,承担着整流和开关的功能。
而mosfet在工作过程中会产生一定的损耗,影响整个电路的效率和性能。
对mosfet的损耗进行准确的计算和分析,对于优化整流电路的性能至关重要。
本文将重点研究buck同步整流电路中mosfet的损耗问题。
通过分析mosfet损耗的来源、计算方法、影响因素以及优化方法,希望能为电子设备的设计和性能优化提供一定的参考。
通过深入了解mosfet的损耗问题,可以更好地理解整流电路的性能特点,为未来的研究和发展方向提供指导。
本文旨在全面探讨mosfet损耗对整流电路的影响,并为未来在这一领域开展更深入的研究工作提供借鉴和参考。
1.2 问题提出在实际工程中,buck同步整流电路是一种常见的电源转换电路,它能够将输入电压转换为稳定的输出电压,广泛应用于电子设备中。
在buck同步整流电路中,mosfet器件的损耗问题一直是制约其性能的一个重要因素。
问题提出:mosfet器件在buck同步整流电路中存在着较大的损耗,这些损耗主要包括导通损耗和开关损耗。
导通损耗是mosfet器件在导通状态下的功耗,开关损耗是mosfet器件在切换过程中由于开关过程中的导通电阻带来的功耗。
这些损耗不仅会导致mosfet器件发热严重,影响整流电路的稳定性和效率,还会影响整个系统的性能表现。
如何减小mosfet器件的损耗,提高整流电路的效率和稳定性,成为了当前研究的焦点之一。
为了解决mosfet器件损耗的问题,需要对其损耗进行深入的研究和分析,探讨其来源和计算方法,寻找影响其损耗的因素,并提出相应的优化方法,以提高整流电路的性能和效率。
buck电路计算实例

buck电路计算实例下面是一个Buck(降压)电路的计算实例:假设我们有以下参数:输入电压 Vin = 12V输出电压 Vout = 5V输出电流 Iout = 2A开关频率 f = 200 kHz效率η = 90%首先,我们可以使用以下公式计算Duty Cycle(占空比):D = Vout / Vin在这个例子中,D = 5V / 12V ≈ 0.4167接下来,我们需要计算开关管的导通时间和断开时间:Ton = (D * 1/f) / (1 - D)Toff = (1/f) / (1 - D)根据给定的频率,我们可以得到:Ton ≈ (0.4167 * 1/200kHz) / (1 - 0.4167) ≈ 3.57μsToff ≈ (1/200kHz) / (1 - 0.4167) ≈ 2.38μs然后,我们可以计算开关管上的平均功率损耗:Psw = (Ton * Vout * (1 - D) + Toff * Vin * D) * Iout其中,第一项表示开关管在导通期间的功率损耗,第二项表示开关管在断开期间的功率损耗。
代入数值进行计算:Psw ≈ (3.57μs * 5V * (1 - 0.4167) + 2.38μs * 12V * 0.4167) * 2A ≈ 11.76 mW接下来,我们可以计算输出功率:Pout = Vout * Iout代入数值进行计算:Pout = 5V * 2A = 10W由于给定了效率,我们可以计算输入功率:Pin = Pout / η代入数值进行计算:Pin = 10W / 0.9 ≈ 11.11W最后,我们可以计算效率:η = Pout / Pin代入数值进行计算:η= 10W / 11.11W ≈ 0.9001 或约为 90%这个计算实例展示了如何计算Buck电路的一些重要参数,包括Duty Cycle、开关管导通时间和断开时间、功率损耗、输入功率和效率。
BUCK型开关电源中的损耗与效率的计算

BUCK型开关电源中的损耗与效率的计算BUCK(降压)型开关电源是一种常见的电源系统,广泛应用于各种电子设备中。
计算BUCK型开关电源的损耗与效率是非常重要的,可以帮助我们了解电源系统的性能和优化设计。
本文将详细介绍如何计算BUCK型开关电源的损耗与效率。
1.BUCK型开关电源的工作原理工作原理如下:-当输入电压大于输出电压时,开关管关闭,电感储存能量;-当输入电压小于输出电压时,开关管打开,电感释放能量,使输出电流继续供电。
2.BUCK型开关电源的损耗2.1静态损耗静态损耗主要包括开关管的导通损耗和电感元件的电流损耗。
- 开关管的导通损耗可以通过导通电流和开关管的导通电阻来计算,即 P1 = I(on) * R(on)。
- 电感元件的电流损耗可以通过电感电流和电感的电阻来计算,即P2 = I(lm)² * R(lm)。
2.2动态损耗动态损耗主要包括开关管的开关损耗和反馈电路的功耗。
- 开关管的开关损耗可以通过开关频率、开关管的导通电阻和电容负载来计算,即 P3 = f * V(in) * I(C) * (t(on) + t(off)),其中 f为开关频率,V(in)为输入电压,I(C)为电容负载电流,t(on)和t(off)为开关管的导通时间和关断时间。
- 反馈电路的功耗主要来自反馈控制电路,可以通过电压和电流来计算,即 P4 = V(fbk) * I(fbk)。
总的损耗为 P(total) = P1 + P2 + P3 + P43.BUCK型开关电源的效率输出功率可以通过输出电压和输出电流来计算,即 P(out) = V(out) * I(out)。
输入功率可以通过输入电压和输入电流来计算,即 P(in) = V(in) * I(in)。
4.优化BUCK型开关电源的设计为了提高BUCK型开关电源的效率,可以采取以下措施:-选择低导通电阻的开关管,减少导通损耗。
-选择低电阻的电感元件,减少电流损耗。
BuckBoost电路的开关损耗分析
电力传动与控制课程设计任务书2017-2018学年第一学期第12周-14周注:1、此表一组一表二份,课程设计小组组长一份;任课教师授课时自带一份备查。
2、课程设计结束后与“课程设计小结”、“学生成绩单”一并交院教务存档。
目录1、概述 (2)2 主电路拓扑和控制方式 (3)2.1 Buck/Boost主电路的构成 (3)2.2 电感电流连续时的工作原理及基本关系 (4)3、主电路参数的计算 (7)4、 MATLAB仿真 (8)5、Buck/Boost电路的开关损耗分析 (9)6、结论 (9)7、心得 (10)1、概述直流-直流变流电路的功能是将直流电变为另一固定电压或可调电压的直流电,包括直接直流变流电路和间接直流变流电路。
其中,直接直流变流电路又叫斩波电路,它包括降压斩波电路(Buck Chopper)、升压斩波电路(Boost Chopper)、升降压斩波电路(Buck/Boost)、Cuk斩波电路、Sepic斩波电路和Zeta斩波电路共六种基本斩波电路。
Buck/Boost升降压斩波电路同时具有Buck斩波电路和Boost斩波电路的特点,能对直流电直接进行降压或者升压变换,应用广泛。
本文将对Buck/Boost升降压斩波电路进行详细的分析。
2 主电路拓扑和控制方式2.1 Buck/Boost主电路的构成Buck/Boost变换器的主电路与Buck或Boost变换器所用元器件相同,也由开关管、二极管、电感、电容等构成,如图1所示。
与Buck和Boost不同的是电感L在中间,不在输出端也不在输入端,且输出电压极性与输入电压极性相反。
开关管也采用PWM控制方式。
Buck/Boost变换器也由电感电流连续和断续两种工作方式,但在实际应用中,往往要求电流不断续,即电流连续,当电路中电感值足够大时,就能使得电路工作在电流连续的状态下。
因此为了分析方便,现假设电感足够大,则在一个周期内电流连续。
图1 Buck/Boost主电路结构图电流连续时有两个开关模态,即V导通时的模态1,等效电路见图2(a);V 关断时的模态2,等效电路见图2(b)(a)V导通(b)V关断,VD续流图2 Buck/Boost不同模态等效电路2.2 电感电流连续时的工作原理及基本关系电感电流连续工作时的工作主要波形见图3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
δIo( Vs , 40 ⋅ A , Vgs) = 26.109 A
IQ1rms( Vs , Io , Vgs) := ⎡D( Vs , Io , Vgs) ⋅ ⎛ Io + ⎢ ⎜
1 12
⎣
⎝
⋅ δIo( Vs , Io , Vgs) Kt( Io) 1.4
2⎞⎤
0.5
⎥ ⎠⎦
- high-side FET RMS current
2
2
- output inductor power losses - PCB traces power losses - input current - conduction losses in FETs Total Conduction Power Losses
Ploss ( Vs , Io , Vgs) := PQ1( Vs , Io , Vgs) + PQ2( Vs , Io , Vgs) + PLo( Vs , Io , Vgs) + Ppcb( Vs , Io , Vgs) PQ1( Vs , Iomax , Vgs) = 1.309 W PQ2( Vs , Iomax , Vgs) = 2.319 W PQ1( Vs , 0 ⋅ A , Vgs) = 0.037 W PQ2( Vs , 0 ⋅ A , Vgs) = 0.073 W
Conduction losses per FET PQ11( Vs , Io , Vgs) := PQ21( Vs , Io , Vgs) := 1 Nu 1 Nl ⋅ PQ1( Vs , Io , Vgs) ⋅ PQ2( Vs , Io , Vgs) PQ11( Vs , Iomax , Vgs) = 1.309 W PQ21( Vs , Iomax , Vgs) = 1.16 W
Rpcb := 0 ⋅ mΩ
Nl := 2 RdsU( 7 ⋅ V) = 9.94 mΩ
- number of low FETs RdsU_25( Vgs) := RdsL_25( Vgs) := Rdsu( Vgs) 1.4 Rdsl( Vgs) 1.4 - Rdson at 25 C
RdsU( 12 ⋅ V) = 8.47 mΩ - Rdson at 125 C RdsL( 12 ⋅ V) = 2.071 mΩ
PHASE
7
8
Vout
EN/PG
L_FET
3
PWM
LGATE
5
2V to 13V Pulse
GND
4
Control FET (U_FET): HAT2168N: Parameters taken from Data Sheet gU := 0.5 ⋅ V 35 ⋅ A gU = 0.014 V A 1 gU = 70 S - Forward Transconductnace
VthL := 2.2 ⋅ V Qgs1b := 6 ⋅ ncoul Qgs2b := 6 ⋅ ncoul Qgsb := Qgs1b + Qgs2b Qgsb = 12 ncoul Qgdb := 5.9 ⋅ ncoul Qtb ( Vgs) := Qgsb + Qgdb + Qtb ( 4.5 ⋅ V) = 27.65 ncoul Rdsl( Vgs) := ⎢ 2.55 ⋅ mΩ + 30 ⋅ ncoul 4⋅V ⋅ ( Vgs − 3.2 ⋅ V) - Charge at Vgs Qtb ( 7 ⋅ V) = 46.4 ncoul - Rdson at 125 C Qtb ( 10 ⋅ V) = 68.9 ncoul Qtb ( 12 ⋅ V) = 83.9 ncoul
2⎞⎤ 0.5
1 12
⎣
⎝
⋅ δIo( Vs , Io , Vgs)
⎥ ⎠⎦
- low-side FET RMS current
PQ2( Vs , Io , Vgs) := IQ2rms( Vs , Io , Vgs) ⋅ RdsL( Vgs) ⋅ δIo( Vs , Io , Vgs) 2 δIo( Vs , Io , Vgs) 2 1 12 ⋅ δIo( Vs , Io , Vgs)
Iirms( Vs , Io , Vgs) := ⎛ Io + ⎜
2
⎝
⎠
- inductor RMS current
Iirms( Vs , Iomax , Vgs) = 33.33 A ICorms( Vs , Io , Vgs) := 1 2⋅ 3 ⋅ δIo( Vs , Io , Vgs) - output capacitor RMS current (for 1-phase buck)
Qtt ( 5 ⋅ V) = 11.72 ncoul
⎡ ⎣
10.5 ⋅ V ⋅ mΩ ⎤
( Vgs − VthU) ⎦
⎥ ⋅ 1.4
- Rdson at 125 C
16 14 12 10 Rdsu( Vgs) mΩ 8 6 4 2 0 2 3 4 5 6 7 Vgs 8 9 10 11 12
Synchronous FET (L_FET): HAT2166N: Parameters taken from Data Sheet gL := 0.5 ⋅ V 35 ⋅ A gL = 0.014 V A 1 gL = 70 S - Forward Transconductnace
D( Vs , Io , Vgs) 12
⎣
⋅ δIo( Vs , Io , Vgs)
2⎤
0.5
⎥ - input capacitor RMS current ⎦
PLo( Vs , Io , Vgs) := Iirms( Vs , Io , Vgs) ⋅ Ri ⋅ Kt( Io) Ppcb( Vs , Io , Vgs) := Iirms( Vs , Io , Vgs) ⋅ Rpcb ⋅ Kt( Io) Iin( Vs , Io , Vgs) := Io ⋅ D( Vs , Io , Vgs) PQ ( Vs , Io , Vgs) := PQ1( Vs , Io , Vgs) + PQ2( Vs , Io , Vgs)
ICorms( Vs , Iomax , Vgs) = 7.39 A
ICorms( Vs , 0 ⋅ A , Vgs) = 6.971 A
2
ICinrms( Vs , Io , Vgs) := ⎡D( Vs , Io , Vgs) ⋅ ( 1 − D( Vs , Io , Vgs) ) ⋅ Io + ⎢
⎝
⎠
Vs − Io ⋅ ( RdsU( Vgs) − RdsL( Vgs) ) ⋅ D( Vs , Iomax , Vgs) = 0.119 δIo( Vs , Io , Vgs) :=
Kt( Io) 1.4
[ Vs − Io ⋅ ( RdsU( Vgs) + Ri) − Vo] ⋅ D( Vs , Io , Vgs) Lo ⋅ fs - inductor ripple current
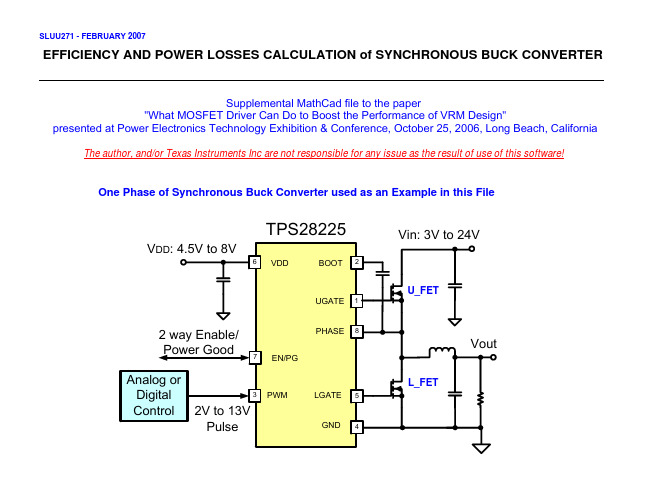
SLUU271 - FEBRUARY 2007
EFFICIENCY AND POWER LOSSES CALCULATION of SYNCHRONOUS BUCK CONVERTER
Supplemental MathCad file to the paper "What MOSFET Driver Can Do to Boost the Performance of VRM Design" presented at Power Electronics Technology Exhibition & Conference, October 25, 2006, Long Beach, California The author, and/or Texas Instruments Inc are not responsible for any issue as the result of use of this software!
PLo( Vs , Iomax , Vgs) = 0.56 W Ppcb( Vs , Iomax , Vgs) = 0 W Ploss ( Vs , Iomax , Vgs) = 4.188 W
- inductor conduction losses - PCB conduction losses - Total Conduction Power Losses
Qgst := Qgs1t + Qgs2t
Vgs := 2.3 ⋅ V , 2.4 ⋅ V .. 12 ⋅ V Qtt ( Vgs) := Qgst + Qgdt + Qtt ( 4.5 ⋅ V) = 10.37 ncoul Rdsu( Vgs) := ⎢ 5 ⋅ mΩ + 27 ⋅ ncoul 10 ⋅ V ⋅ ( Vgs − 0.4 ⋅ V − 3 ⋅ V) - Charge at Vgs Qtt ( 7 ⋅ V) = 17.12 ncoul Qtt ( 10 ⋅ V) = 25.22 ncoul Qtt ( 12 ⋅ V) = 30.62 ncoul
PQ1( Vs , Io , Vgs) := IQ1rms( Vs , Io , Vgs) ⋅ RdsU( Vgs) ⋅ IQ2rms( Vs , Io , Vgs) := ⎡( 1 − D( Vs , Io , Vgs) ) ⋅ ⎛ Io + ⎢ ⎜
2Байду номын сангаас
2
- high-side FET static losses
One Phase of Synchronous Buck Converter used as an Example in this File
TPS28225
