习题2 答案
结构力学课后习题答案(2)
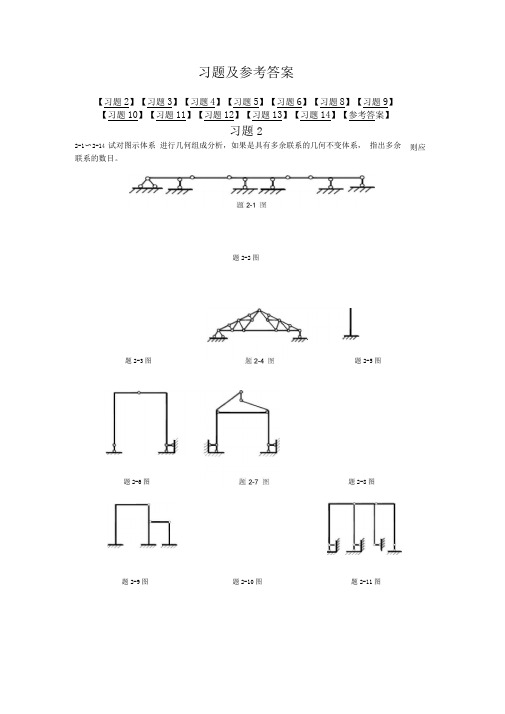
习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1〜2-14 试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,指出多余则应联系的数目。
题2-2图题2-3图题2-5图题2-6图题2-8图题2-9图题2-10图题2-11图题4-1图4-2 作图示刚架的M 图。
3-1 试作图示多跨静定梁的M 及Q 图。
习题(a)1.5m 1 2m I2.5m | 1.5m l 4.5m题3-1(b)3-2 试不计算反力而绘出梁的M 图。
4m40kN(a) 5kN/mM(b )4-1 作图示刚架的M 、Q 、N 图。
2kN /m2kN • m (a)2kN 题3-2习题4(b ) (c )4-3 4-4 4-54m(a)(d)作图示三铰刚架的M图。
M=4Pa2a(b)4kN4m 4m(c)珂10kN/m4m(e)题4-2图CE0.5m ]m2J 0.5m7mB7m(a)题4-3作图示刚架的M图。
(a)I 盒lUlUUW已知结构的M图,试绘出荷载。
10kN/m1.5m题4-4图urm*~ G3mC7.35m 7.35m(b)m6Nn m220kN40kN/m4m(b)C_PaPaPaa4-6 检查下列刚架的M图,并予以改正。
5-15-2 题4-5图(b)P(d)(e) (f)(c)题4-6图习题5图示抛物线三铰拱轴线方程4 f1kN/mx)x,(h)试求D截面的内力。
20kN10m题5-1图K15m j 5ml=30m带拉杆拱,拱轴线方程 y ,求截面的弯矩。
题5-3图习题66-1 判定图示桁架中的零杆。
6-2 6-3 6-4 6-5 用结点法计算图示桁架中各杆内力。
(b) (c)m题6-2用截面法计算图示桁架中指定各杆的内力。
3m [ 3m3m I 3m题6-3试求图示组合结构中各链杆的轴力并作受弯杆件的用适宜方法求桁架中指定杆内力。
习题二和上机答案

习题二⒉1描述以下四个概念的区别:头指针变量,头指针,头结点,首结点(第一个结点)。
解:头指针变量和头指针是指向链表中第一个结点(头结点或首结点)的指针;在首结点之前附设一个结点称为头结点;首结点是指链表中存储线性表中第一个数据元素的结点。
若单链表中附设头结点,则不管线性表是否为空,头指针均不为空,否则表示空表的链表的头指针为空。
2.2简述线性表的两种存储结构有哪些主要优缺点及各自使用的场合。
解:顺序存储是按索引直接存储数据元素,方便灵活,效率高,但插入、删除操作将引起元素移动,降低了效率;而链式存储的元素存储采用动态分配,利用率高,但须增设表示结点之间有序关系的指针域,存取数据元素不如顺序存储方便,但结点的插入和删除十分简单。
顺序存储适用于线性表中元素数量基本稳定,且很少进行插入和删除,但要求以最快的速度存取线性表中的元素的情况;而链式存储适用于频繁进行元素动态插入或删除操作的场合。
2.3 在头结点为h的单链表中,把值为b的结点s插入到值为a的结点之前,若不存在a,就把结点s插入到表尾。
Void insert(Lnode *h,int a,int b){Lnode *p,*q,*s;s=(Lnode*)malloc(sizeof(Lnode));s->data=b;p=h->next;while(p->data!=a&&p->next!=NULL){q=p;p=p->next;}if (p->data==a){q->next=s;s->next=p;}else{p->next=s;s->next=NULL;}}2.4 设计一个算法将一个带头结点的单链表A分解成两个带头结点的单链表A和B,使A中含有原链表中序号为奇数的元素,而B中含有原链表中序号为偶数的元素,并且保持元素原有的相对顺序。
Lnode *cf(Lnode *ha){Lnode *p,*q,*s,*hb;int t;p=ha->next;q=ha;t=0;hb=(Lnode*)malloc(sizeof(Lnode));s=hb;while(p->next!=NULL){if (t==0){q=p;p=p->next;t=1;}else{q->next=p->next;p->next=s->next; s->next=p; s=p;p=p->next; t=0;}}s->next=NULL;return (hb);}2.5设线性表中的数据元素是按值非递减有序排列的,试以不同的存储结构,编写一算法,将x插入到线性表的适当位置上,以保持线性表的有序性。
复变函数论第三版课后习题答案 2

第一章习题解答(一)1.设z =z 及Arcz 。
解:由于3i z e π-==所以1z =,2,0,1,3Arcz k k ππ=-+=±。
2.设121z z =,试用指数形式表示12z z 及12z z 。
解:由于6412,2i i z e z i e ππ-==== 所以()64641212222i i iiz z e eee πππππ--===54()146122611222ii i i z e e e z e πππππ+-===。
3.解二项方程440,(0)z a a +=>。
解:12444(),0,1,2,3k ii z a e aek πππ+====。
4.证明2221212122()z z z z z z ++-=+,并说明其几何意义。
证明:由于2221212122Re()z z z z z z +=++2221212122Re()z z z z z z -=+-所以2221212122()z z z z z z ++-=+其几何意义是:平行四边形对角线长平方和等于于两边长的和的平方。
5.设z 1,z 2,z 3三点适合条件:0321=++z z z ,1321===z z z 。
证明z 1,z 2,z 3是内接于单位圆1=z 的一个正三角形的顶点。
证 由于1321===z z z,知321z z z ∆的三个顶点均在单位圆上。
因为33331z z z ==()[]()[]212322112121z z z z z z z z z z z z +++=+-+-=21212z z z z ++=所以, 12121-=+z z z z ,又)())((122122112121221z z z z z z z z z z z z z z +-+=--=-()322121=+-=z z z z故 321=-z z ,同理33231=-=-z z z z ,知321z z z ∆是内接于单位圆1=z 的一个正三角形。
习题参考答案2-电阻应变式

浙江大学电气工程学院10192091 现代传感器技术赵梦恋,吴晓波 2008-2009学年冬学期2008年12月二、电阻应变式传感器(2) 习 题2-1一丝绕应变计的灵敏系数为2,初始阻值100Ω,试求当试件受力后的应变为31.810-⨯时该应变计的电阻变化ΔR 。
答:Ω=⨯⨯⨯=⋅⋅=∆-36.0108.121003εK R R2-2一试件受力后的应变为3102-⨯;丝绕应变计的灵敏系数为2,初始阻值120Ω,温度系数C61050-⨯-,线膨胀系数为C 61014-⨯;试件的线膨胀系数为C61012-⨯。
试求:温度升高20℃时,应变计输出的相对误差和相对热输出。
答:()t S t Ra t K t Rββ∆=∆+-⋅∆ =()C C C C20101410122201050666⨯⨯-⨯⨯+⨯⨯---- =31008.1-⨯-()43104.521008.1/--⨯-=⨯-=∆=KR R tt ε2-3在悬臂梁的上下方各贴一片电阻为120Ω的金属应变片R 1和R 2。
若应变片的灵敏系数k =2,电源电压U =2V ,当悬臂梁顶端受到向下的力F 时,电阻R 1和R 2的变化值ΔR 1 =ΔR 2 =0.48Ω,试求电桥的输出电压。
答:ACD U OR 4UR 311R R +∆22R R -∆1R 1R ()2R 2R120124R R U U R R ⎛⎫∆∆∆=- ⎪⎝⎭20.480.4844120120mV ⎡⎤⎛⎫=--= ⎪⎢⎥⎝⎭⎣⎦解析:参见PPT P23~24,关于电阻应变计的测量电路。
理解电桥的测量原理和计算方法。
F2-4图为一直流应变电桥,图中U =4V ,1234120R R R R ====Ω,试求:① 1R 为金属应变片,其余为外接电阻,当1R 的增量为1 1.2R ∆=Ω时,电桥输出电压U O 。
② 1R 、2R 都是应变片,且批号相同,感应应变的极性和大小都相同,其余为外接电阻,电桥输出电压U O 。
电气CAD习题答案2

电气CAD练习题:一.名词解释1.图层:在建筑电气CAD绘图软件中,图层可以假想成一张透明的纸。
一张图纸应该有N 张透明的图层而组成。
2.图层管理:图层管理包括图层名、图层颜色、图层线型、图层线宽四部分。
3、绘图设置:绘图设置包括绘图单位的设置和绘图区域的设置。
4、精确绘图的辅助工具:2006版精确绘图的辅助工具有栅格、捕捉、正交模式、对象捕捉、极轴追踪、DYN动态输入5、构造线的绘制方式:构造线的绘制方式有水平方式、垂直方式、角度方式、二等分方式、偏移方式。
6、圆弧的绘制方法:1)三点法;2)起点、端点、半径法;3)起点、端点、角度法;4)起点、圆心、长度法;5)起点、端点、方向法7、矩形的绘制方法:有规则矩形、倒角矩形、圆角矩形8、对象选择方法:有直接选择、窗口方式、交叉方式、快速选择命令。
9、阵列对象的方法:有矩形阵列和环形阵列。
10、文字设置:文字设置有文字样式、文字字体、文字高度、加粗、倾斜、下划线、设置堆叠文字、文字颜色。
11、尺寸标注应遵循的规划:1)图中所标注的尺寸数据应以实际设计的物体尺寸为依据,与绘制比例及绘图的准确度无关。
2)图样中的尺寸一般以mm为单位,不需要标注单位的代号或名称。
如果使用其他单位,则必须在图中注明计算单位的代号或名称,如cm、 m等。
3)尺寸标注要简明,一个尺寸只标一次,并应标在反映该结构最清晰的图形上。
4)图样中所标注的尺寸为该图样所表示的物体的最后完工尺寸,否则应该另加说明。
5)在绘制机械图时,文字应采用长仿宋字体,数字采用阿拉伯数字。
12、五角星中点样式的设置方法:[格式]/[点样式]/选择第四个交叉“×”13、五角星中等分点的设置方法:命令:DIVIDE,菜单中[绘图]/[点]/[定数等分]/选择要等分的对象/输入等分数目,即可。
14、样条曲线操作方法:点击“样条曲线”图标,鼠标左键点击第一点,第二点……N点,鼠标右键确定,ENTER两次完成。
数据库系统基础教程(第二版)课后习题答案2

Database Systems: The Complete BookSolutions for Chapter 2Solutions for Section 2.1Exercise 2.1.1The E/R Diagram.Exercise 2.1.8(a)The E/R DiagramKobvxybzSolutions for Section 2.2Exercise 2.2.1The Addresses entity set is nothing but a single address, so we would prefer to make address an attribute of Customers. Were the bank to record several addresses for a customer, then it might make sense to have an Addresses entity set and make Lives-at a many-many relationship.The Acct-Sets entity set is useless. Each customer has a unique account set containing his or her accounts. However, relating customers directly to their accounts in a many-many relationship conveys the same information and eliminates the account-set concept altogether.Solutions for Section 2.3Exercise 2.3.1(a)Keys ssNo and number are appropriate for Customers and Accounts, respectively. Also, we think it does not make sense for an account to be related to zero customers, so we should round the edge connecting Owns to Customers. It does not seem inappropriate to have a customer with 0 accounts;they might be a borrower, for example, so we put no constraint on the connection from Owns to Accounts. Here is the The E/R Diagram,showing underlined keys andthe numerocity constraint.Exercise 2.3.2(b)If R is many-one from E1 to E2, then two tuples (e1,e2) and (f1,f2) of the relationship set for R must be the same if they agree on the key attributes for E1. To see why, surely e1 and f1 are the same. Because R is many-one from E1 to E2, e2 and f2 must also be the same. Thus, the pairs are the same.Solutions for Section 2.4Exercise 2.4.1Here is the The E/R Diagram.We have omitted attributes other than our choice for the key attributes of Students and Courses. Also omitted are names for the relationships. Attribute grade is not part of the key for Enrollments. The key for Enrollements is studID from Students and dept and number from Courses.Exercise 2.4.4bHere is the The E/R Diagram Again, we have omitted relationship names and attributes other than our choice for the key attributes. The key for Leagues is its own name; this entity set is not weak. The key for Teams is its own name plus the name of the league of which the team is a part, e.g., (Rangers, MLB) or (Rangers, NHL). The key for Players consists of the player's number and the key for the team on which he or she plays. Since the latter key is itself a pair consisting of team and league names, the key for players is the triple (number, teamName, leagueName). e.g., JeffGarcia is (5, 49ers, NFL).Database Systems: The Complete BookSolutions for Chapter 3Solutions for Section 3.1Exercise 3.1.2(a)We can order the three tuples in any of 3! = 6 ways. Also, the columns can be ordered in any of 3! = 6 ways. Thus, the number of presentations is 6*6 = 36.Solutions for Section 3.2Exercise 3.2.1Customers(ssNo, name, address, phone)Flights(number, day, aircraft)Bookings(ssNo, number, day, row, seat)Being a weak entity set, Bookings' relation has the keys for Customers and Flights and Bookings' own attributes.Notice that the relations obtained from the toCust and toFlt relationships are unnecessary. They are:toCust(ssNo, ssNo1, number, day)toFlt(ssNo, number, day, number1, day1)That is, for toCust, the key of Customers is paired with the key for Bookings. Since both include ssNo, this attribute is repeated with two different names, ssNo and ssNo1. A similar situation exists for toFlt.Exercise 3.2.3Ships(name, yearLaunched)SisterOf(name, sisterName)Solutions for Section 3.3Exercise 3.3.1Since Courses is weak, its key is number and the name of its department. We do not have arelation for GivenBy. In part (a), there is a relation for Courses and a relation for LabCourses that has only the key and the computer-allocation attribute. It looks like:Depts(name, chair)Courses(number, deptName, room)LabCourses(number, deptName, allocation)For part (b), LabCourses gets all the attributes of Courses, as:Depts(name, chair)Courses(number, deptName, room)LabCourses(number, deptName, room, allocation)And for (c), Courses and LabCourses are combined, as:Depts(name, chair)Courses(number, deptName, room, allocation)Exercise 3.3.4(a)There is one relation for each entity set, so the number of relations is e. The relation for the root entity set has a attributes, while the other relations, which must include the key attributes, have a+k attributes.Solutions for Section 3.4Exercise 3.4.2Surely ID is a key by itself. However, we think that the attributes x, y, and z together form another key. The reason is that at no time can two molecules occupy the same point.Exercise 3.4.4The key attributes are indicated by capitalization in the schema below:Customers(SSNO, name, address, phone)Flights(NUMBER, DAY, aircraft)Bookings(SSNO, NUMBER, DAY, row, seat)Exercise 3.4.6(a)The superkeys are any subset that contains A1. Thus, there are 2^{n-1} such subsets, since each of the n-1 attributes A2 through An may independently be chosen in or out.Solutions for Section 3.5Exercise 3.5.1(a)We could try inference rules to deduce new dependencies until we are satisfied we have them all.A more systematic way is to consider the closures of all 15 nonempty sets of attributes.For the single attributes we have A+ = A, B+ = B, C+ = ACD, and D+ = AD. Thus, the only new dependency we get with a single attribute on the left is C->A.Now consider pairs of attributes:AB+ = ABCD, so we get new dependency AB->D. AC+ = ACD, and AC->D is nontrivial. AD+ = AD, so nothing new. BC+ = ABCD, so we get BC->A, and BC->D. BD+ = ABCD, giving usBD->A and BD->C. CD+ = ACD, giving CD->A.For the triples of attributes, ACD+ = ACD, but the closures of the other sets are each ABCD. Thus, we get new dependencies ABC->D, ABD->C, and BCD->A.Since ABCD+ = ABCD, we get no new dependencies.The collection of 11 new dependencies mentioned above is: C->A, AB->D, AC->D, BC->A, BC->D, BD->A, BD->C, CD->A, ABC->D, ABD->C, and BCD->A.Exercise 3.5.1(b)From the analysis of closures above, we find that AB, BC, and BD are keys. All other sets either do not have ABCD as the closure or contain one of these three sets.Exercise 3.5.1(c)The superkeys are all those that contain one of those three keys. That is, a superkey that is not a key must contain B and more than one of A, C, and D. Thus, the (proper) superkeys are ABC, ABD, BCD, and ABCD.Exercise 3.5.3(a)We must compute the closure of A1A2...AnC. Since A1A2...An->B is a dependency, surely B is in this set, proving A1A2...AnC->B.Exercise 3.5.4(a)Consider the relationThis relation satisfies A->B but does not satisfy B->A.Exercise 3.5.8(a)If all sets of attributes are closed, then there cannot be any nontrivial functional dependenc ies. For suppose A1A2...An->B is a nontrivial dependency. Then A1A2...An+ contains B and thus A1A2...An is not closed.Exercise 3.5.10(a)We need to compute the closures of all subsets of {ABC}, although there is no need to think about the empty set or the set of all three attributes. Here are the calculations for the remaining six sets: A+ = AB+ = BC+ = ACEAB+ = ABCDEAC+ = ACEBC+ = ABCDEWe ignore D and E, so a basis for the resulting functional dependencies for ABC are: C->A and AB->C. Note that BC->A is true, but follows logically from C->A, and therefore may be omitted from our list.Solutions for Section 3.6Exercise 3.6.1(a)In the solution to Exercise 3.5.1 we found that there are 14 nontrivial dependencies, including the three given ones and 11 derived dependencies. These are: C->A, C->D, D->A, AB->D, AB-> C, AC->D, BC->A, BC->D, BD->A, BD->C, CD->A, ABC->D, ABD->C, and BCD->A.We also learned that the three keys were AB, BC, and BD. Thus, any dependency above that does not have one of these pairs on the left is a BCNF violation. These are: C->A, C->D, D->A, AC->D, and CD->A.One choice is to decompose using C->D. That gives us ABC and CD as decomposed relations. CD is surely in BCNF, since any two-attribute relation is. ABC is not in BCNF, since AB and BC are its only keys, but C->A is a dependency that holds in ABCD and therefore holds in ABC. We must further decompose ABC into AC and BC. Thus, the three relations of the decomposition are AC, BC, and CD.Since all attributes are in at least one key of ABCD, that relation is already in 3NF, and no decomposition is necessary.Exercise 3.6.1(b)(Revised 1/19/02) The only key is AB. Thus, B->C and B->D are both BCNF violations. The derived FD's BD->C and BC->D are also BCNF violations. However, any other nontrivial, derived FD will have A and B on the left, and therefore will contain a key.One possible BCNF decomposition is AB and BCD. It is obtained starting with any of the four violations mentioned above. AB is the only key for AB, and B is the only key for BCD.Since there is only one key for ABCD, the 3NF violations are the same, and so is the decomposition.Solutions for Section 3.7Exercise 3.7.1Since A->->B, and all the tuples have the same value for attribute A, we can pair the B-value from any tuple with the value of the remaining attribute C from any other tuple. Thus, we know that R must have at least the nine tuples of the form (a,b,c), where b is any of b1, b2, or b3, and c is any of c1, c2, or c3. That is, we can derive, using the definition of a multivalued dependency, that each of the tuples (a,b1,c2), (a,b1,c3), (a,b2,c1), (a,b2,c3), (a,b3,c1), and (a,b3,c2) are also in R.Exercise 3.7.2(a)First, people have unique Social Security numbers and unique birthdates. Thus, we expect the functional dependencies ssNo->name and ssNo->birthdate hold. The same applies to children, so we expect childSSNo->childname and childSSNo->childBirthdate. Finally, an automobile has a unique brand, so we expect autoSerialNo->autoMake.There are two multivalued dependencies that do not follow from these functional dependencies. First, the information about one child of a person is independent of other information about that person. That is, if a person with social security number s has a tuple with cn,cs,cb, then if there isany other tuple t for the same person, there will also be another tuple that agrees with t except that it has cn,cs,cb in its components for the child name, Social Security number, and birthdate. That is the multivalued dependencyssNo->->childSSNo childName childBirthdateSimilarly, an automobile serial number and make are independent of any of the other attributes, so we expect the multivalued dependencyssNo->->autoSerialNo autoMakeThe dependencies are summarized below:ssNo -> name birthdatechildSSNo -> childName childBirthdateautoSerialNo -> autoMakessNo ->-> childSSNo childName childBirthdatessNo ->-> autoSerialNo autoMakeExercise 3.7.2(b)We suggest the relation schemas{ssNo, name, birthdate}{ssNo, childSSNo}{childSSNo, childName childBirthdate}{ssNo, autoSerialNo}{autoSerialNo, autoMake}An initial decomposition based on the two multivalued dependencies would give us {ssNo, name, birthDate}{ssNo, childSSNo, childName, childBirthdate}{ssNo, autoSerialNo, autoMake}Functional dependencies force us to decompose the second and third of these.Exercise 3.7.3(a)Since there are no functional dependencies, the only key is all four attributes, ABCD. Thus, each of the nontrvial multivalued dependencies A->->B and A->->C violate 4NF. We must separate out the attributes of these dependencies, first decomposing into AB and ACD, and then decomposing the latter into AC and AD because A->->C is still a 4NF violation for ACD. The final set of relations are AB, AC, and AD.Exercise 3.7.7(a)Let W be the set of attributes not in X, Y, or Z. Consider two tuples xyzw and xy'z'w' in the relation R in question. Because X ->-> Y, we can swap the y's, so xy'zw and xyz'w' are in R. Because X ->-> Z, we can take the pair of tuples xyzw and xyz'w' and swap Z's to get xyz'w and xyzw'. Similarly, we can take the pair xy'z'w' and xy'zw and swap Z's to get xy'zw' and xy'z'w.In conclusion, we started with tuples xyzw and xy'z'w' and showed that xyzw' and xy'z'w must also be in the relation. That is exactly the statement of the MVD X ->-> Y-union-Z. Note that the above statements all make sense even if there are attributes in common among X, Y, and Z.Exercise 3.7.8(a)Consider a relation R with schema ABCD and the instance with four tuples abcd, abcd', ab'c'd, and ab'c'd'. This instance satisfies the MVD A->-> BC. However, it does not satisfy A->-> B. For example, if it did satisfy A->-> B, then because the instance contains the tuples abcd and ab'c'd, we would expect it to contain abc'd and ab'cd, neither of which is in the instance.Database Systems: The Complete BookSolutions for Chapter 4Solutions for Section 4.2Exercise 4.2.1class Customer {attribute string name;attribute string addr;attribute string phone;attribute integer ssNo;relationship Set<Account> ownsAcctsinverse Account::ownedBy;}class Account {attribute integer number;attribute string type;attribute real balance;relationship Set<Customer> ownedByinverse Customer::ownsAccts}Exercise 4.2.4class Person {attribute string name;relationship Person motherOfinverse Person::childrenOfFemalerelationship Person fatherOfinverse Person::childrenOfMalerelationship Set<Person> childreninverse Person::parentsOfrelationship Set<Person> childrenOfFemaleinverse Person::motherOfrelationship Set<Person> childrenOfMaleinverse Person::fatherOfrelationship Set<Person> parentsOfinverse Person::children}Notice that there are six different relationships here. For example, the inverse of the relationship that connects a person to their (unique) mother is a relationship that connects a mother (i.e., a female person) to the set of her children. That relationship, which we call childrenOfFemale, is different from the children relationship, which connects anyone -- male or female -- to their children.Exercise 4.2.7A relationship R is its own inverse if and only if for every pair (a,b) in R, the pair (b,a) is also in R. In the terminology of set theory, the relation R is ``symmetric.''Solutions for Section 4.3Exercise 4.3.1We think that Social Security number should me the key for Customer, and account number should be the key for Account. Here is the ODL solution with key and extent declarations.class Customer(extent Customers key ssNo){attribute string name;attribute string addr;attribute string phone;attribute integer ssNo;relationship Set<Account> ownsAcctsinverse Account::ownedBy;}class Account(extent Accounts key number){attribute integer number;attribute string type;attribute real balance;relationship Set<Customer> ownedByinverse Customer::ownsAccts}Solutions for Section 4.4Exercise 4.4.1(a)Since the relationship between customers and accounts is many-many, we should create a separate relation from that relationship-pair.Customers(ssNo, name, address, phone)Accounts(number, type, balance)CustAcct(ssNo, number)Exercise 4.4.1(d)Ther is only one attribute, but three pairs of relationships from Person to itself. Since motherOf and fatherOf are many-one, we can store their inverses in the relation for Person. That is, for each person, childrenOfMale and childrenOfFemale will indicate that persons's father and mother. The children relationship is many-many, and requires its own relation. This relation actually turns out to be redundant, in the sense that its tuples can be deduced from the relationships stored with Person. The schema:Persons(name, childrenOfFemale, childrenOfMale)Parent-Child(parent, child)Exercise 4.4.4Y ou get a schema like:Studios(name, address, ownedMovie)Since name -> address is the only FD, the key is {name, ownedMovie}, and the FD has a left side that is not a superkey.Exercise 4.4.5(a,b,c)(a) Struct Card { string rank, string suit };(b) class Hand {attribute Set theHand;};For part (c) we have:Hands(handId, rank, suit)Notice that the class Hand has no key, so we need to create one: handID. Each hand has, in the relation Hands, one tuple for each card in the hand.Exercise 4.4.5(e)Struct PlayerHand { string Player, Hand theHand };class Deal {attribute Set theDeal;}Alternatively, PlayerHand can be defined directly within the declaration of attribute theDeal. Exercise 4.4.5(h)Since keys for Hand and Deal are lacking, a mechanical way to design the database schema is to have one relation connecting deals and player-hand pairs, and another to specify the contents of hands. That is:Deals(dealID, player, handID)Hands(handID, rank, suit)However, if we think about it, we can get rid of handID and connect the deal and the player directly to the player's cards, as:Deals(dealID, player, rank, suit)Exercise 4.4.5(i)First, card is really a pair consisting of a suit and a rank, so we need two attributes in a relation schema to represent cards. However, much more important is the fact that the proposed schema does not distinguish which card is in which hand. Thus, we need another attribute that indicates which hand within the deal a card belongs to, something like:Deals(dealID, handID, rank, suit)Exercise 4.4.6(c)Attribute b is really a bag of (f,g) pairs. Thus, associated with each a-value will be zero or more (f,g) pairs, each of which can occur several times. We shall use an attribute count to indicate the number of occurrences, although if relations allow duplicate tuples we could simply allow duplicate (a,f,g) triples in the relation. The proposed schema is:C(a, f, g, count)Solutions for Section 4.5Exercise 4.5.1(b)Studios(name, address, movies{(title, year, inColor, length,stars{(name, address, birthdate)})})Since the information about a star is repeated once for each of their movies, there is redundancy. To eliminate it, we have to use a separate relation for stars and use pointers from studios. That is: Stars(name, address, birthdate)Studios(name, address, movies{(title, year, inColor, length,stars{*Stars})})Since each movie is owned by one studio, the information about a movie appears in only one tuple of Studios, and there is no redundancy.Exercise 4.5.2Customers(name, address, phone, ssNo, accts{*Accounts})Accounts(number, type, balance, owners{*Customers})Solutions for Section 4.6Exercise 4.6.1(a)We need to add new nodes labeled George Lucas and Gary Kurtz. Then, from the node sw (which represents the movie Star Wars), we add arcs to these two new nodes, labeled direc tedBy and producedBy, respectively.Exercise 4.6.2Create nodes for each account and each customer. From each customer node is an arc to a node representing the attributes of the customer, e.g., an arc labeled name to the customer's name. Likewise, there is an arc from each account node to each attribute of that account, e.g., an arc labeled balance to the value of the balance.To represent ownership of accounts by customers, we place an arc labeled owns from each customer node to the node of each account that customer holds (possibly jointly). Also, we placean arc labeled ownedBy from each account node to the customer node for each owner of that account.Exercise 4.6.5In the semistructured model, nodes represent data elements, i.e., entities rather than entity sets. In the E/R model, nodes of all types represent schema elements, and the data is not represented at all. Solutions for Section 4.7Exercise 4.7.1(a)<STARS-MOVIES><STAR starId = "cf" starredIn = "sw, esb, rj"><NAME>Carrie Fisher</NAME><ADDRESS><STREET>123 Maple St.</STREET><CITY>Hollywood</CITY></ADDRESS><ADDRESS><STREET>5 Locust Ln.</STREET><CITY>Malibu</CITY></ADDRESS></STAR><STAR starId = "mh" starredIn = "sw, esb, rj"><NAME>Mark Hamill</NAME><ADDRESS><STREET>456 Oak Rd.<STREET><CITY>Brentwood</CITY></ADDRESS></STAR><STAR starId = "hf" starredIn = "sw, esb, rj, wit"><NAME>Harrison Ford</NAME><ADDRESS><STREET>whatever</STREET><CITY>whatever</CITY></ADDRESS></STAR><MOVIE movieId = "sw" starsOf = "cf, mh"><TITLE>Star Wars</TITLE><YEAR>1977</YEAR></MOVIE><MOVIE movieId = "esb" starsOf = "cf, mh"><TITLE>Empire Strikes Back</TITLE><YEAR>1980</YEAR></MOVIE><MOVIE movieId = "rj" starsOf = "cf, mh"><TITLE>Return of the Jedi</TITLE><YEAR>1983</YEAR></MOVIE><MOVIE movieID = "wit" starsOf = "hf"><TITLE>Witness</TITLE><YEAR>1985</YEAR></MOVIE></STARS-MOVIES>Exercise 4.7.2<!DOCTYPE Bank [<!ELEMENT BANK (CUSTOMER* ACCOUNT*)><!ELEMENT CUSTOMER (NAME, ADDRESS, PHONE, SSNO)> <!A TTLIST CUSTOMERcustId IDowns IDREFS><!ELEMENT NAME (#PCDA TA)><!ELEMENT ADDRESS (#PCDA TA)><!ELEMENT PHONE (#PCDA TA)><!ELEMENT SSNO (#PCDA TA)><!ELEMENT ACCOUNT (NUMBER, TYPE, BALANCE)><!A TTLIST ACCOUNTacctId IDownedBy IDREFS><!ELEMENT NUMBER (#PCDA TA)><!ELEMENT TYPE (#PCDA TA)><!ELEMENT BALANCE (#PCDA TA)>]>Database Systems: The CompleteBookSolutions for Chapter 5Solutions for Section 5.2Exercise 5.2.1(a)PI_model( SIGMA_{speed >= 1000} ) (PC)Exercise 5.2.1(f)The trick is to theta-join PC with itself on the condition that the hard disk sizes are equal. That gives us tuples that have two PC model numbers with the same value of hd. However, these two PC's could in fact be the same, so we must also require in the theta-join that the model numbers be unequal. Finally, we want the hard disk sizes, so we project onto hd.The expression is easiest to see if we write it using some temporary values. We start by renaming PC twice so we can talk about two occurrences of the same attributes.R1 = RHO_{PC1} (PC)R2 = RHO_{PC2} (PC)R3 = R1 JOIN_{PC1.hd = PC2.hd AND PC1.model <> PC2.model} R2R4 = PI_{PC1.hd} (R3)Exercise 5.2.1(h)First, we find R1, the model-speed pairs from both PC and Laptop. Then, we find from R1 those computers that are ``fast,'' at least 133Mh. At the same time, we join R1 with Product to connect model numbers to their manufacturers and we project out the speed to get R2. Then we join R2 with itself (after renaming) to find pairs of different models by the same maker. Finally, we get our answer, R5, by projecting onto one of the maker attributes. A sequence of steps giving the desired expression is: R1 = PI_{model,speed} (PC) UNION PI_{model,speed} (Laptop)R2 = PI_{maker,model} (SIGMA_{speed>=700} (R1) JOIN Product)R3 = RHO_{T(maker2, model2)} (R2)R4 = R2 JOIN_{maker = maker2 AND model <> model2} (R3)R5 = PI_{maker} (R4)Exercise 5.2.2Here are figures for the expression trees of Exercise 5.2.1 Part (a)Part (f)Part (h). Note that the third figure is not really a tree, since it uses a common subexpression. We could duplicate the nodes to make it a tree, but using common subexpressions is a valuable form of query optimization. One of the benefits one gets from constructing ``trees'' for queries is the ability to combine nodes that represent common subexpressions.Exercise 5.2.7The relation that results from the natural join has only one attribute from each pair of equated attributes. The theta-join has attributes for both, and their columns are identical.Exercise 5.2.9(a)If all the tuples of R and S are different, then the union has n+m tuples, and this number is the maximum possible.The minimum number of tuples that can appear in the result occurs if every tuple of one relation also appears in the other. Surely the union has at least as many tuples as the larger of R and that is, max(n,m) tuples. However, it is possible for every tuple of the smaller to appear in the other, so it is possible that there are as few as max(n,m) tuples in the union.Exercise 5.2.10In the following we use the name of a relation both as its instance (set of tuples) and as its schema (set of attributes). The context determines uniquely which is meant.PI_R(R JOIN S) Note, however, that this expression works only for sets; it does not preserve the multipicity of tuples in R. The next two expressions work for bags.R JOIN DELTA(PI_{R INTERSECT S}(S)) In this expression, each projection of a tuple from S onto the attributes that are also in R appears exactly once in the second argument of the join, so it preserves multiplicity of tuples in R, except for those thatdo not join with S, which disappear. The DELTA operator removes duplicates, as described in Section 5.4.R - [R - PI_R(R JOIN S)] Here, the strategy is to find the dangling tuples of R and remove them.Solutions for Section 5.3Exercise 5.3.1As a bag, the value is {700, 1500, 866, 866, 1000, 1300, 1400, 700, 1200, 750, 1100, 350, 733}. The order is unimportant, of course. The average is 959.As a set, the value is {700, 1500, 866, 1000, 1300, 1400, 1200, 750, 1100, 350, 733}, and the average is 967. H3>Exercise 5.3.4(a)As sets, an element x is in the left-side expression(R UNION S) UNION Tif and only if it is in at least one of R, S, and T. Likewise, it is in the right-side expressionR UNION (S UNION T)under exactly the same conditions. Thus, the two expressions have exactly the same members, and the sets are equal.As bags, an element x is in the left-side expression as many times as the sum of the number of times it is in R, S, and T. The same holds for the right side. Thus, as bags the expressions also have the same value.Exercise 5.3.4(h)As sets, element x is in the left sideR UNION (S INTERSECT T)if and only if x is either in R or in both S and T. Element x is in the right side(R UNION S) INTERSECT (R UNION T)if and only if it is in both R UNION S and R UNION T. If x is in R, then it is in both unions. If x is in both S and T, then it is in both union. However, if x is neither in R nor in both of S and T, then it cannot be in both unions. For example, suppose x is not in R and not in S. Then x is not in R UNION S. Thus, the statement of when x is in the right side is exactly the same as when it is in the left side: x is either in R or in both of S and T.Now, consider the expression for bags. Element x is in the left side the sum of the number of times it is in R plus the smaller of the number of times x is in S and the number of times x is in T. Likewise, the number of times x is in the right side is the smaller ofThe sum of the number of times x is in R and in S.The sum of the number of times x is in R and in T.A moment's reflection tells us that this minimum is the sum of the number of times x is in R plus the smaller of the number of times x is in S and in T, exactly as for the left side.Exercise 5.3.5(a)For sets, we observe that element x is in the left side(R INTERSECT S) - T。
现代控制理论习题答案(2)

第二章2-3 已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=452100010A ,试用拉氏反变换求e At 解:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=-4521001s s s A sI ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-+--+-----+--+--+---+--+-----+--+--+---+-------+--+--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---+---=--2413)1(12818)1(32414)1(22212)1(12415)1(32212)1(22212)1(12212)1(321)1(2522)4(21454)2()1(1)(2222222222221s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s A sI ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-+--+-----+--+--+---+--+-----+--+--+---+-------+--+--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---+---=--2413)1(12818)1(32414)1(22212)1(12415)1(32212)1(22212)1(12212)1(321)1(2522)4(21454)2()1(1)(2222222222221s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s A sI[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+---++--+---+--+---++-=-=--t t t tt t t t t t t t t t t t t t t t t t t t tt At e e te e e te e e te e e te e e te e te e e e te e e te e te A sI L e 2222222221143883442224532222232)(2-4 用三种方法计算以下矩阵指数函数e At , (1) ⎥⎦⎤⎢⎣⎡-=0410A 解:(1)化为约旦标准型04412=+=⎥⎦⎤⎢⎣⎡-=-λλλλA I j j 2,221-==λλ⎥⎦⎤⎢⎣⎡-=j j T 2211 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=-j j T 412141211⎥⎥⎦⎤⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+--+=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=Λ=------t t t t e e e e j e e j e e j j e e j j T T e jt jt jtjt jt jt jt jt jt jtAt 2cos 2sin 22sin 212cos )(21))()(41)(21412141210221122222222221(2)拉普拉斯变换⎥⎦⎤⎢⎣⎡-=-s s A sI 41 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+++-+=⎥⎦⎤⎢⎣⎡-+=--4444144141)(222221s s s s s s s s s A sI[]⎥⎥⎦⎤⎢⎢⎣⎡-=-=--t t t t A sI L e At 2cos 2sin 22sin 212cos )(11(3)凯莱-哈密顿定理⎥⎥⎦⎤⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡---t t e e j j e e j j jt jt jt jt 2sin 212cos 4141212121212222110αα⎥⎥⎦⎤⎢⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡=+=t t t t t t A I e At 2cos 2sin 22sin 212cos 04102sin 2110012cos 10αα(2) ⎥⎦⎤⎢⎣⎡=1411A解:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++-+-+=Φ----)(21)()(41)(21)(3333tt tt t t tt e e e e e e e e t2-5 下列矩阵是否满足状态转移矩阵的条件,如果满足,试求出与子对应的A 阵(2)⎥⎥⎦⎤⎢⎢⎣⎡-=Φ--t t e e t 220)1(211)( (4)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++-+-+=Φ----)(21)()(41)(21)(3333tt tt t t tt e e e e e e e e t 状态转移矩阵的条件()()(0)()()()t A t It t ττΦ=ΦΦ=ΦΦ=Φ+ 求取A 的方法:1(())()()()()()t L t sI A t A t t A A t -=Φ=-Φ=Φ=Φ=Φ解(2)此矩阵是状态转移矩阵1)(210)211(211))((--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++-=ΦA sI s s s s t L⎥⎦⎤⎢⎣⎡+-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+++=-20110)121(2121)2()(s s s ss s s s A sI ⎥⎦⎤⎢⎣⎡-=2010A(4)此矩阵是状态转移矩阵1)(14113)(1(1)3111(21)3111)3111(41)3111(21))((--=⎥⎦⎤⎢⎣⎡-----+=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-++-++--++--++=ΦA sI s s s s s s s s s s s s t L )⎥⎦⎤⎢⎣⎡----=-1411s s A sI ⎥⎦⎤⎢⎣⎡=1411A2-6 求下列状态空间表达式的解[]xy u x x 01100010=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=解:⎥⎦⎤⎢⎣⎡=0010A ⎥⎦⎤⎢⎣⎡-=-s s A sI 01 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡=--s s s s s s A sI 1011011)(221[]⎥⎦⎤⎢⎣⎡=-=--101)(11t A sI L e At ⎥⎥⎦⎤⎢⎢⎣⎡+++=⎥⎥⎦⎤⎢⎢⎣⎡+⎥⎦⎤⎢⎣⎡+=⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡+=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=-Φ+=⎰⎰⎰t t t t t t d t t d t t d Bu t x e t x t t tAt 1212111111010111101)()()(220000ττττττ2-7 试证本章2-3,在特定控制作用下,状态方程式(2-25)的解,式(2-30),式(2-31)和式(2-32)成立(2)0)0(),()(x x t k t u ==δBKe x e d BK e x e d BK e x e t x At At t A Attt A At +=+=+=⎰⎰+---000)(00)(0)()()(ττδττδττ(3)0)0(),(1)(x x t K t u =⨯=(4)0)0(),(1)(x x t Kt t u =⨯=2-9根据系统的方框图可得212121112x x y u x xku x x+=-=+-=[]⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡212121121000101x x y u k x x x x[]⎥⎦⎤⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎪⎪⎪⎪⎭⎫⎝⎛+-++=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛++=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-+=-=--------1101111011)1(1110)1(1101)(111111t t At e e s s s s s s L s s s s L s s L A sI L e⎥⎦⎤⎢⎣⎡-==--110)(T T ATe e eT G⎥⎦⎤⎢⎣⎡-=100k B ⎥⎦⎤⎢⎣⎡-+--=⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡+--=⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡-==------⎰⎰T e T k e k k T eT e k dt e e B dt e H T TT TTT T TAT)1(0)1(1001011001100当T=0.1时⎥⎦⎤⎢⎣⎡-==--110)1.0()(1.01.0ee G T G ⎥⎦⎤⎢⎣⎡-+--==--1.0)9.0(0)1()1.0()(1.01.0e k e k H T H当T=1时⎥⎦⎤⎢⎣⎡-==--110)1()(11e e G T G ⎥⎦⎤⎢⎣⎡--==--10)1()1.0()(11kee k H T H 2-11根据上面的模拟结构图,求去连续的状态方程,进而化成离散状态方程。
《随机过程及其在金融领域中的应用》习题二答案

0
sin
ux
f
xdx
0
sin
ux
f
xdx
0
0
sin
u
x
f
xdx
sin ux 0
f
x dx
0
令其中一式中的 x t
0
sin
ut
f
t
d
t
0
sin
ux
f
xdx
0
sin ut 0
证明:
X u
eiux f xdx
cos ux i sin ux f xdx
cos ux
f
xdx
i
sin
ux
f
xdx
(a)充分性:
当f
x
f
x时,sin ux
f
x
为奇函数
,
则i
c o vY Y, E Y 2 E Y 2 3 80
故(X,Y)的协方差矩阵为
cov X , X cov Y , X
1
cov X ,Y cov Y ,Y
18 0
0
3 80
4、已知二维随机变量(X,Y)服从联合正态分布,且
dFX
x
e tx f xdx
etxexdx etxdx
热力学课后习题02答案

第2章 热力学第一定律2-1 定量工质,经历了下表所列的4个过程组成的循环,根据热力学第一定律和状态参数的特性填充表中空缺的数据。
过程 Q/ kJ W/ kJ△U/ kJ1-2 0 100 -1002-3-11080 -1903-4 300 90 210 4-1 20 -60802-2 一闭口系统从状态1沿过程123到状态3,对外放出47.5 kJ 的热量,对外作功为30 kJ ,如图2-11所示。
(1) 若沿途径143变化时,系统对外作功为6 kJ ,求过程中系统与外界交换的热量; (2) 若系统由状态3沿351途径到达状态1,外界对系统作功为15 kJ ,求该过程与外界交换的热量;(3) 若U 2=175 kJ ,U 3=87.5 kJ ,求过程2-3传递的热量,及状态1的热力学能U 1。
图2-11 习题2-2解:(1)根据闭口系能量方程,从状态1沿途径123变化到状态3时,12313123Q U W −=∆+,得1347.5kJ 30kJ 77.5kJ U −∆=−−=−从状态1沿途径143变化到状态3时,热力学能变化量13U −∆保持不变,由闭口系能量方程14313143Q U W −=∆+,得14377.5kJ 6kJ 71.5kJ Q =−+=−,即过程中系统向外界放热71.5kJ(2)从状态3变化到状态1时,()31133113U U U U U U −−∆=−=−−=−∆,由闭口系能量方程35131351Q U W −=∆+,得35177.5kJ 15kJ 62.5kJ Q =−=,即过程中系统从外界吸热92.5kJ(3)从状态2变化到状态3体积不变,323232323232Q U W U pdV U −−−=∆+=∆+=∆∫,因此23233287.5kJ 175kJ 87.5kJ Q U U U −=∆=−=−=−由1331187.577.5kJ U U U U −∆=−=−=−,得1165kJ U =2-3 某电站锅炉省煤器每小时把670t 水从230℃加热到330℃,每小时流过省煤器的烟气的量为710t ,烟气流经省煤器后的温度为310℃,已知水的质量定压热容为 4.1868 kJ/(kg ·K),烟气的质量定压热容为1.034 kJ/(kg ·K),求烟气流经省煤器前的温度。
《现代控制理论》课后习题答案2

( sI − A) −1 =
1 adj( sI − A) det( sI − A)
(1)
式(1)中的 adj( sI − A) 和 det( sI − A) 可分别写成以下形式:
adj( sI − A) = H n −1s n −1 + H n − 2 s n − 2 + " + H 0 det( sI − A) = s + an −1s
故
Φ (t ) = α 0 (t ) I + α1 (t ) A + α 2 (t ) A2
⎡ −2tet + e 2t ⎢ = ⎢ −2(1 + t )et + 2e 2t ⎢ −2(2 + t )et + 4e 2t ⎣
(3t + 2)et − 2e 2t (3t + 5)et − 4e 2t (3t + 8)et − 8e 2t
n n −1
(2) (3) (4)
+ " + a0
,可得 将式(1)两边分别左乘 det( sI − A)( sI − A) ,并利用式(2)和(3)
Is n + an −1 Is n −1 + " + a0 I = H n −1s n + ( H n − 2 − AH n−1 ) s n − 2 + " + ( H 0 − AH1 )s − AH 0
e jt = a0 (t ) + a1 (t ) j , e − jt = a0 (t ) − a1 (t ) j
而
e jt = cos t + j sin t , e− jt = cos t − j sin t 因此, a0 (t ) = cos t , a1 (t ) = sin t 。由此得到状态转移矩阵 ⎡ cos t sin t ⎤ Φ (t ) = e At = a0 (0) I + a1 (t ) A = ⎢ ⎥ ⎣ − sin t cos t ⎦
操作系统课后习题答案2

2. 进程和线程的管理例题解析例试说明进程和程序之间的区别和联系。
解进程和程序是既有区别又有联系的两个概念。
进程是动态的,程序是静态的。
程序是一组有序的指令集合,是一个静态的概念;进程则是程序及其数据在计算机上的一次执行,是一个动态的集合。
离开了程序,进程就失去了存在的意义,但同一程序在计算机上的每次运行将构成不同的进程。
程序可看作是电影的胶片,进程可以看作电影院放电影的过程。
一个进程可以执行多个程序,如同一个电影院的一场电影可放映多部影片。
一个程序可被多个进程执行,如同多个影院同时利用一个电影的胶片放映同一部电影。
程序可以长期保存,进程只能存在于一段时间。
程序是永久存在的,而进程有从被创建到消亡的生命周期。
例举例说明多道程序系统失去了封闭性和再现性。
解例如,有两个循环程序A和B,共享一个变量N。
程序A每执行一次时,都要做N:=N+1操作;程序B则每执行一次时,都要执行print(N)操作,然后再将N的值置成“0”。
程序A 和B在多道程序系统中同时运行。
假定某时刻变量N的值为n,可能出现下述三种情况:N:=N+1 在print(N)和N:=0之前,此时得到N值变化过程为n+1、n+1、0;N:=N+1 在print(N)和N:=0之后,此时得到N值变化过程为n 、0 、1;N:=N+1 在print(N)之后和N:=0之前,此时得到N值变化过程为n、n+1、0。
所以,在A、B程序多次执行过程中,虽然其每次执行时的环境和初始条件都相同,但每次得到的结果却不一定相同。
例为什么将进程划分成执行、就绪和阻塞三个基本状态解根据多道程序执行的特点,进程的运行是走走停停的。
因此进程的初级状态应该是执行和等待状态。
处于执行状态的进程占用处理机执行程序,处于等待状态的进程正在等待处理机或者等待其它某种事件的发生。
但是,当处理机空闲时,并不是所有处于等待状态的进程都能放到处理机上执行,有的进程即使分配给它处理机,它也不能执行,因为它的执行的条件没有得到满足。
《概率论与数理统计》课后习题答案2

1. 试分别给出随机变量的可能取值为可列、有限的实例.解 用X 表示一个电话交换台每小时收到呼唤的次数,X 的全部可能取值为可列的 0,1,2,3,…,;用Y 表示某人掷一枚骰子出现的点数,Y 的全部可能取值为有限个 1,2,3,4,5,6 ;2. 试给出随机变量的可能取值至少充满一个实数区间的实例.解 用X 表示某灯泡厂生产的灯泡寿命(以小时记),X 的全部可能取值为区间 (0,+∞)3. 设随机变量X 的分布函数()F x 为()F x = 2 1, >20, 2A x xx ⎧-⎪⎨⎪≤⎩ 确定常数A 的值,计算(04)P X ≤≤.解 由(20)(2),F F +=可得10, =44AA -= (04)(04)(4)(0)0.75P X P X F F ≤≤=<≤=-=.4.试讨论:A 、B 取何值时函数()arctan3xF x A B =+ 是分布函数. 解 由分布函数的性质,有()()0,1F F -∞=+∞=,可得0,211,,21,2A B A B A B πππ⎧⎛⎫+-= ⎪⎪⎪⎝⎭⇒==⎨⎛⎫⎪+= ⎪⎪⎝⎭⎩于是()11arctan ,.23xF x x π=+-∞<<+∞1.设10个零件中有3个不合格. 现任取一个使用,若取到不合格品,则丢弃重新抽取一个,试求取到合格品之前取出的不合格品数X 的概率分布.解 由题意知,X 的取值可以是0,1,2,3.而X 取各个值的概率为{}{}70,103771,10930P X P X ====⨯= {}{}32772,1098120321713.10987120P X P X ==⨯⨯===⨯⨯⨯= 因此X 的概率分布为012 377711030120120X ⎡⎤⎢⎥⎢⎥⎣⎦2.从分别标有号码1 ,2 ,… ,7的七张卡片中任意取两张, 求余下的卡片中最大号码的概率分布.解 设X 为余下的卡片的最大号码 ,则X 的可能取值为5、6、7,且1{5}21P X ==5{6}21P X ==15{7}21P X ==即所求分布为567 1515212121X ⎡⎤⎢⎥⎢⎥⎣⎦ 3.某人有n 把外形相似的钥匙,其中只有1把能打开房门,但他不知道是哪一把,只好逐把试开.求此人直至将门打开所需的试开次数的概率分布.解 设此人将门打开所需的试开次数为X ,则X 的取值为1,2,3,...,k n =,事件{}{}1X k k k ==-前次未打开,第次才打开,且{}11P X n ==, {}11121n P X n n n-==⋅=-,… …,{}()121112111,2,....,n n n k P X k n n n k n k k n n ---+==⋅⋅⋅⋅--+-+== 故所需试开次数的分布为12~111X n nn ⎡⎤⎢⎥⎢⎥⎣⎦ ... n .... 4.随机变量X 只取1 、2 、3共三个值,并且取各个值的概率不相等且组成等差数列,求X 的概率分布.解 设{}{}{}1,2,3P X a P X b P X c ======,则由题意有1a b c c b b a ++=⎧⎨-=-⎩解之得2313a c b ⎧+=⎪⎪⎨⎪=⎪⎩设三个概率的公差为d ,则11,33a d c d =-=+,即X 的概率分布为 12 3111333X d d⎡⎤⎢⎥⎢⎥-+⎢⎥⎣⎦,103d << 5.设随机变量X 的全部可能取值为1 ,2 ,… ,n ,且()P X k = 与k 成正比,求X 的概率分布.解 由题意,得{}() 1,2,,k P X k p ck k n ====其中c 是大于0的待定系数.由11nkk p==∑,有12....1nk k cp c c n c ==+++=∑ 即()112n n c +=,解之得 ()21c n n =+.把()21c n n =+代入k p ,可得到X 的概率分布为{}()2,1,2,...,.1kP X k k n n n ===+6.一汽车沿街道行驶时须通过三个均设有红绿灯的路口.设各信号灯相互独立且红绿两种信号显示的时间相同,求汽车未遇红灯通过的路口数的概率分布.解 设汽车未遇红灯通过的路口数为X ,则X 的可能值为0,1,2,3.以()1,2,3i A i =表示事件“汽车在第i 个路口首次遇到红灯”,则123,,A A A 相互独立,且()()1,1,2,32i i P A P A i ===.对0,1,2,3k =,有{}()1102P X P A ==={}()()()1212211142P X P A A P A P A ===== {}()123311282P X P A A A ==== {}()123311382P X P A A A ==== 所以汽车未遇红灯通过的路口数的概率分布为012 311112488X ⎡⎤⎢⎥⎢⎥⎣⎦7.将一颗骰子连掷若干次,直至掷出的点数之和超过3为止.求掷骰子次数的概率分布.解 设掷骰子次数为X ,则X 可能取值为1,2,3,4,且31{1}62P X === 141515{2}6666612P X ==⨯+⨯+=;115111117{3}6666666216P X ==⨯⨯+⨯+⨯=; 1111{4}666216P X ==⨯⨯=所以掷骰子次数X 的概率分布为123 415171212216216X ⎡⎤⎢⎥⎢⎥⎣⎦ 8.设X 的概率分布为试求(1)X 的分布函数并作出其图形;(2) 计算{11}P X -≤≤ ,{0 1.5}P X ≤≤ ,{2}P X ≤ . 解(1)由公式 (){}()k kx xF X P X x p x ≤=≤=-∞<<+∞∑,得()0,00.2,010.5,120.6,231,3x x F X x x x <⎧⎪≤<⎪⎪=≤<⎨⎪≤<⎪≥⎪⎩(2) {}11(1)(10)0.500.5P X F F -≤≤=---=-= {}0 1.5(1.5)(00)0.500.5P X F F ≤≤=--=-={}2(2)0.6P X F ≤==9.设随机变量X 的分布函数为010.210()0.70212x x F x x x <-⎧⎪-≤<⎪=⎨≤<⎪⎪≥⎩,,,,试求(1) 求X 的概率分布;(2) 计算1322P X ⎧⎫-<≤⎨⎬⎩⎭,{1}P X ≤- ,{03}P X ≤< ,{1|0}P X X ≤≥解 (1)对于离散型随机变量,有{}()()0P X k F k F k ==--,因此,随机变量X 的概率分布为10 2 0.20.50.3X -⎡⎤⎢⎥⎣⎦ (2) 由分布函数计算概率,得13310.52222P X F F ⎧⎫⎛⎫⎛⎫-<≤=--=⎨⎬ ⎪ ⎪⎩⎭⎝⎭⎝⎭;{}()110.2P X F ≤-=-=;{}()0330(00)10.20.8P X F F ≤<=---=-=; {}{}{}{}{}1,0100010.50.625.00.8P X X P X X P X P X P X ≤≥≤≥=≥≤≤===≥10.已知随机变量X 服从0—1分布,并且{0}P X ≤=0.2,求X 的概率分布 . 解 X 只取0与1两个值,{0}P X =={0}P X ≤-{0}P X <=0.2,{1}1{0}0.8P X P X ==-==11.已知{}P X n == nP ,n =1,2,3,⋯,求P 的值 .解 因为1{}1,n P X n ∞===∑ 有 11=,1n n pp p∞==-∑解此方程,得0.5p =. 12.商店里有5名售货员独立地售货.已知每名售货员每小时中累计有15分钟要用台秤.(1) 求在同一时刻需用台秤的人数的概率分布;(2) 若商店里只有两台台秤,求因台秤太少而令顾客等候的概率.解 (1) 由题意知,每名售货员在某一时刻使用台秤的概率为150.2560p ==, 设在同一时刻需用台秤的人数为X , 则()~5,0.25X B , 所以{}550.250.75(0,1,2,3,4,5)kk k P X k C k -===(2) 因台秤太少而令顾客等候的概率为{}{}55553320.250.75k k k k k P X P X k C -==>===∑∑332445550.250.750.250.750.250.1035C C =++≈13.保险行业在全国举行羽毛球对抗赛,该行业形成一个羽毛球总队,该队是由各地区的部分队员形成.根据以往的比赛知,总队羽毛球队实力较甲地区羽毛球队强,但同一队中队员之间实力相同,当一个总队运功员与一个甲地区运动员比赛时,总队运动员获胜的概率为0.6,现在总队、甲队双方商量对抗赛的方式,提出三种方案:(1)双方各出3人; (2)双方各出5人; (3)双方各出7人.3种方案中得胜人数多的一方为胜利.问:对甲队来说,哪种方案有利?解 设以上三种方案中第i 种方案甲队得胜人数为(1,2,3),i X i =则上述3种方案中,甲队胜利的概率为(1){}331322(0.4)(0.6)0.352k k k k P X C -=≥=≈∑(2){}552533(0.4)(0.6)0.317k k k k P X C -=≥=≈∑(3){}773744(0.4)(0.6)0.290kk k k P X C -=≥=≈∑因此第一种方案对甲队最为有利.这和我们的直觉是一致的。
《误差理论与数据处理》习题2及解答

(mm)
② 重复测量 10 次,计算其算术平均值为: x = 26.2025(mm). 取与①相同的置信度,则测量结果为:26.2025±3σ= 26.2025±0.0015 (mm). ③ 若无该仪器测量的标准差资料,则依 10 次重复测量数据计算标准差和表示测量结 果。选参考值 x0 = 26.202,计算差值 ∆x i = x i − 26.202 、 ∆ x 0 和残差ν i 等列于表中。 序 1 2 3 4 5 6 7 8 9 10 号
∑ν
i =1
i
n( n − 1)
= 1.253
0.0008 5× 4
= 0.000224 (mm)
σx =
σ
n
=
0.000255 5
= 0.000114 ; σ x =
'
σ'
n
=
0.000224 5
= 0.0001
⑤求单次测量的极限误差和算术平均值的极限误差 因假设测量值服从正态分布,并且置信概率 P=2Φ(t)=99%,则Φ(t)=0.495,查附录
∆ x0 = 1 10 ∑ ∆xi = 0.0005 10 i =1
νi
0 +0.0003 +0.0003 0 +0.0001 -0.0003 -0.0002 0 +0.0001 -0.0003
ν i2
0 9×10 9×10 0 1×10
微机原理习题答案2

《微机原理》习题2 (P40)参考答案2.1为什么说计算机只能“识别”二进制数,并且计算机内部数的存储及运算也都采用二进制?解:因为二进制是计算机刚出现时就奠定的计算机内的进位记数制,之所以选用它来表示计算机内的信息,是因为两个状态的物理器件容易制造和实现,将这两个状态抽象为数字就可用0、1来表示;此外,采用二进制的运算规则较为简单,容易实现。
2.2在进位记数制中,“基数”和“位权(或权)”的含义是什么?一个以b为基数的任意进制数N,它按位权展开式求值的一般通式是如何描述的?解:在进位记数制中,常常要用“基数”(或称底数)来区别不同的数制,而进位制的基数就是该进位制所用的字符或数码的个数。
在一个进位记数制中,每一位都有特定的权,称为位权或简称权。
每个位权由基数的 n次幂来确定。
数N的按位权展开式的一般通式为:N=±(ki×b i)式中,ki为第i位的数码;b为基数;b i为第位的位权;n为整数的总位数;m 为小数的总位数。
2.3将下列十进制数分别转化为二进制数。
(1)147 (2)4095 (3)0.625 (4) 0.15625解:(1) 147 D=10010011 B(2) 4095 D=111111111111 B(3) 0.625 D=0.101 B(4) 0.15625 D=0.00101 B2.4将下列二进制数分别转换为BCD码。
(1)1011 (2) 0.01 (3) 10101.101 (4) 11011.001解:(1) 1011 B=1×23+0×22+1×21+ 1×20=11 D=(0001 0001)BCD(2) 0.01 B=1×2-2=0.25 D=(0.0010 0101)BCD(3) 10101.101 B =1×24+1×22+1×20+1×2-1+1×2-3 =21.625 D=(0010 0001.0110 0010 0101)BCD(4) 11011.001B=1×24+1×23+1×21+1×20+1×2-3=27.125D=(0010 0111.0001 0010 0101)BCD2.5将下列二进制数分别转换为八进制数和十六进制数。
尿液沉渣显微镜检查习题2

尿液沉渣显微镜检查习题21.10 ml尿标本经离心处理弃去上清液后,应保留多少沉渣作镜检A.0.1 mlB.0.2 mlC.0.4 mlD.0.5 mlE.1.0 ml【参考答案】B2.尿沉渣镜检时,正确的叙述是A.首先用低倍视野观察B.检查细胞应观察10个低倍视野C.检查管型应观察10个高倍视野D.检查管型应观察20个高倍视野E.检查结晶用低倍视野报告【参考答案】A3.尿中出现大量非均一性红细胞提示红细胞来自A.膀胱B.尿道C.肾脏D.输尿管E.前列腺【参考答案】C4.非肾性血尿的变形红细胞应A.≤30%B.≤40%C.≤50%D.≤60%E.≤70%【参考答案】C5.肾移植后出现排斥反应,尿中会出现大量A.中性粒细胞B.嗜酸性粒细胞C.移行上皮细胞D.红细胞E.淋巴细胞【参考答案】E6.闪光细胞主要见于A.急性肾小球肾炎B.急性肾小管肾炎C.急性肾盂肾炎D.尿道炎E.膀胱炎【参考答案】C7.关于尿中肾小管上皮细胞,错误的叙述是A.来自肾小管立方上皮B.略小于中性粒细胞C.胞质内可见小空泡D.胞质内可见脂肪滴E.胞质内可见含铁血黄素颗粒【参考答案】B8.肾盂上皮细胞又称为A.肾小管上皮细胞B.大圆上皮细胞C.尾形上皮细胞D.小圆上皮细胞E.鳞状上皮细胞【参考答案】C9.女性尿中出现较多而无明显临床意义的细胞是A.红细胞B.脓细胞C.鳞状上皮细胞D.尾形上皮细胞E.肾小管上皮细胞【参考答案】C10.管型形成的必备条件不包括A.原尿中有足够的T—H蛋白B.远曲小管有浓缩及酸化尿液的能力C.尿流缓慢,有局部性尿积滞D.有可供交替使用的肾单位E.近曲小管功能障碍【参考答案】E11.正常人剧烈运动后,尿液中可偶见A.透明管型B.红细胞管型C.白细胞管型D.颗粒管型E.蜡样管型【参考答案】A12.提示肾单位内有出血的是A.透明管型B.红细胞管型C.白细胞管型D.颗粒管型E.蜡样管型【参考答案】B13.提示肾脏有实质性病变的是A.红细胞0~1/HPFB.白细胞l~3/HPFC.鳞状上皮细胞2~5/HPFD.透明管型0~1/LPFE.颗粒管型0~3/LPF【参考答案】E14.有关管型的临床意义,错误的叙述是A.透明管型可见于心力衰竭B.红细胞管型可见于输尿管结石C.白细胞管型可见于肾盂肾炎D.脂肪管型可见于肾病综合征E.蜡样管型可见于慢性肾衰竭【参考答案】B15.粘液纤维状物粘附于非晶形尿酸盐或磷酸盐,所形成的一种圆柱体称为A.粘液丝B.纤维丝C.管型D.假管型E.类圆柱体【参考答案】D16.尿液呈白色混浊,pH8.5,离心后出现白色颗粒状沉淀,此沉淀可能为A.尿酸结晶B.非晶形尿酸盐C.磷酸盐结晶D.亮氨酸结晶E.磺胺结晶【参考答案】C17.急性溶血患者的尿液中易见A.胆红素结晶B.胱氨酸结晶C.酪氨酸结晶D.含铁血黄素颗粒E.胆固醇结晶【参考答案】D18.患者,女,35岁。
课后习题答案 (2)

第1章一、单项选择题1.对项目而言,“一次性”是指( A )。
A.每个项目都有明确的起止时间 B.项目周期短 C.项目将在未来不能确定的时候完成 D.项目随时可能取消 2.项目是一系列( D )的活动和任务。
A.具有特定目标 B.具有明确开始和终止日期 C.消耗资源 D.以上皆是 3.下列属于项目的是(C )。
A、生产线上生产汽车B、管理一个公司C、修建一座水库D、信息系统的维护二、多项选择题1.项目管理的基本特性有( ABCDE )。
A、目的性B、独特性C、普遍性D、创新性E、集成性 2.以下关于项目和日常运营说法正确的是( ABCD )。
A、项目中存在较多创新性、一次性的工作和活动B、日常运营中存在较多确定性、程序性、常规性和不断重复的工作或活动C、项目的环境是相对不确定的D、项目的组织形式多数是团队性的E、运营工作的组织管理模式主要是基于过程和活动的管理系统为主三、简答题1. 什么是项目?项目有哪些特点?答:项目是一个组织为实现既定的目标,在既定的资源和要求的约束下,为实现某种目的而相互联系的一次性工作任务。
项目具有目的性、独特性、一次性、制约性、过程性、不确定性、组织的临时性与开放性、成果的不可挽回性等特点。
2. 什么是项目管理?项目管理有哪些特点?答:项目管理是运用各种知识、技能、方法与工具,为满足或超越项目有关各方对项目的要求与期望所开展的各种计划、组织、领导和控制等方面的活动。
项目管理具有普遍性、目的性、独特性、创新性和集成性等特点。
四、论述题1. 项目与日常运营有哪些不同点?答:(1)根本目的和作用不同:项目的根本目的是为创造具有某种独特性的新成果。
但是运营的根本目的是通过使用特定项目的成果开展周而复始的日常工作从而获得相应的回报。
(2)结果和回收模式不同:项目工作的结果是人们获得的创新性成果,运营工作的结果是通过开展周而复始的运营活动不断获得收益并最终收回项目和运营投入。
(3)工作性质与内容不同:一般在日常运营中存在着大量的确定性、程序性、常规性和不断重复的工作或活动,而在项目中则存在较多创新性、一次性和具有不确定性的工作或活动。
双子叶生药习题答案2

双子叶植物生药I(蓼科、毛茛科、木兰科、罂粟科、十字花科)自测题:一、名词解释1. 星点:2. 云锦花纹:3. 过桥杆:二、填空题1.蓼科植物多为,单叶互生,茎节处常具膜质。
花两性,花,常宿存。
果为或,常包于内。
2.毛茛科植物的主要形态特征是:草本或藤本,单叶或复叶,通常无。
雄蕊和心皮多数,,排列在花托上。
果为或。
3.木兰科植物的主要形态特征为木本,稀为藤本,体内常具而有香气。
单叶互生,节上有明显。
花被,雄蕊和雌蕊多数分离,排列在花托上。
果为或。
4.十字花科植物的主要形态特征是:草本,单叶互生,花序为,花冠,雄蕊,雌蕊二心皮,侧膜胎座,具,果为。
5.罂粟科植物的主要形态特征是:草本,体内常含或。
果为,裂或裂。
6.去尽外皮的大黄表面颜色为,大黄气,味,嚼之有感,并使唾液。
7.大黄根茎髓部较,有环列或散在。
8.黄连为科植物、和的干燥根茎。
所含的主要有效成分为。
9.味连根茎显微特征为:皮层,可见;中柱鞘;维管束型,断续,髓部。
10.黄连细粉1g,加甲醇10,置水浴上加热至沸腾,放冷。
取上清液5滴,加稀盐酸1与漂白粉少量,显色。
11白芍为科的。
主产于省、省。
功效为,,。
12.将下列植物学名译成中文名,并写出其所属的科名及药用部位名1.2.3.4.5.6.三、选择题(一)单选题1.药材横断面可见“星点”的是( )A.大黄的根茎B.大黄的根C.何首乌的根茎D.何首乌的根2.韧皮部外侧组织中散有异型维管束,薄壁细胞含草酸钙簇晶,此药材是( )A.大黄B. 何首乌C.商陆D.牛膝3.黄连断面在紫外灯下木质部显( )A.天蓝色荧光B.紫色荧光C.金黄色荧光D.红棕色荧光4.大黄髓部的“星点”为异型维管束,其类型为( )A.外木型维管束B.外韧型维管束C.周木型维管束D.周韧型维管束5.五味子的主要有效成分为( )A.木脂素类B.有机酸类C.挥发油D.脂肪酸6.厚朴的主产地是( )A.四川、湖北、浙江B.山西、山东C.吉林、辽宁D.甘肃、青海7.取黄连细粉1g,加甲醇10,置水浴上加热至沸腾,放冷,取上清液5滴,加稀盐酸1与漂白粉少许,显樱红色。
图论习题答案2

w
而 (G ) (Gi ) (最外面的平面被重复 1 计算 1次)
i 1
w
(G ) (G ) (G ) 2 1 1
第四次作业
• 四(1).求K2n和Kn,n中不同的完备匹配的个数 • 解:K2n:(2n-1)!! • Kn,n:n!
第五次作业
第五次作业
在C '中,在点vh 1处,缺ih色,但ih 1色重复出现,由引理5.2可知, E ih E ih1 所导出的子图中含vh 1的连通片为一个奇圈C1,又因为边 vh 1vh 2为ih 1色,所以vh 2 C1。 第三步:着色调整 : 在奇圈C1上保持vh 1vh 2边着色不变,对其他的 边ih和ih 1交换,得到边着色C' '。 则在C' '中,vh 1处增加了一个ih色,而vh 2处减少了一个ih色,C1上其 他顶关联边的颜色数不变,则C' ' 也是个最佳边着色。在C' '中,在点 vh 2处,缺ih色,但ih 2色重复出现,,由引理5.2可知,E ih E ih2 所导 出的子图中含vh 2的连通片为一个奇圈C 2,又因为边vh 2 vh 3为ih 2色, 所以vh 3 C 2。
第四次作业
四(20).设A1 , A 2 ,..., A m 是集合S的子集, (A1 , A 2 ,..., A m )的不同代表 系是指S的一个子集{a1 , a2 ,..., am }, 其中ai A i , i 1,2,..., m, 且i j 时,ai a j , 求证: (A1 , A 2 ,..., A m )有不同代表系的充要条件是对 {1,2,..., m}的任意子集J, | A i || J | 。
实验室安全知识习题2单选

201.[单项选择题]用于有机玻璃的粘合的三氯甲烷〔氯仿〕,应注意:不可接触人体B.可以接触人体C.无所谓D.特殊情况可以参考答案:A[单项选择题]进行照明设施的接电操作,应采取的防触电措施为:湿手操作B.切断电源C.站在金属登子或梯子上D.戴上手套参考答案:B[单项选择题]受污染的移液管放在()消毒灭菌,再用自来水冲洗及去离子水冲净。
适宜的消毒剂中浸泡和高压消毒锅中;B.高压消毒锅中;C.适宜的消毒剂中浸泡参考答案:A[单项选择题]大多数氧化剂和〔〕都能发生剧烈反响,放出有毒气体。
强酸B.弱酸C.碱参考答案:A205.[单项选择题]化学药品库中的一般药品应如何分类?A.按生产日期分类B.按有机、无机两大类,有机试剂再细分类存放C.随意摆放D.按购置日期分类参考答案:A[单项选择题]剧毒物品保管人员应做到:A.日清月结B.帐物相符C.手续齐全D.以上都对参考答案:D207.[单项选择题]对实验室危险药品的使用规那么,以下哪一项不对()绝不允许把各种化学药品任意混合,以免发生意外事故可燃性试剂不能用明火加热,必须用水浴、油浴、沙浴或可调电压的电热套加热使用不挥发药品时,试剂瓶盖可敞口至实验结束D.取用钾、钠和白磷等必须使用镊子参考答案:C208.[单项选择题]防止毒物危害的最正确方法是〔〕。
穿工作服B.佩戴呼吸器具C.使用无毒或低毒的代替品A.参考答案:C[单项选择题]过滤除菌操作时,滤器和过滤瓶等装置使用前用什么设备进行消毒灭菌?烘箱B.高压灭菌锅C.加热真空烘箱D.微波炉参考答案:B210.[单项选择题]如果睡觉时被烟火呛醒,正确的做法是〔〕。
寻找逃生通道B.往床底下钻C.找衣服穿或抢救心爱的东西参考答案:A[单项选择题]黄磷自燃应如何扑救用高压水枪用高压灭火器C.用雾状水灭火或用泥土覆盖D.以上都对参考答案:C[单项选择题]对α源的防护主要是:内照射防护B.外照射防护C.不用防护参考答案:A[单项选择题]转基因植物的平安性包括:〔〕食品平安性;B.生态平安性;C.食品平安性和生态平安性;D.人类健康平安性。
习题2及解答

习题 21.设p 、q 都是素数,且7p +q ,pq +11也都为素数,求()()22pqp q q p ++的值.【答案】若p 、q 都是奇数,则7p +q 为偶数,它不是素数,故p 、q 中有一个为偶数.情形一 设p 为偶数,则p =2,此时由7p +q 为素数,知q 为奇素数,若q ≠3,则q ≡1或2(mod3) . 若q ≡1 (mod3),则 7p +q =14+q ≡0(mod3), 矛盾;若q ≡2(mod3),则pq +11=2q +11≡4+11≡0(mod3),亦矛盾,所以q =3,此时7p +q =17,pq +11=17,都是素数,故 (p 2+q p )( q 2+p q )=(22+32)( 32+23)=221. 情形二 设q 为偶数,则q =2,同上讨论可知p =3,此时(p 2+q p )( q 2+p q )=(32+23)( 22+32)=221.综上可知,所求的值为221.2.设12345p p p p p <<<<是5个素数,且12345p p p p p ,,,,成等差数列.求5p 的最小值. 【答案】设d 为公差,则p 1,p 1+d ,p 1+2d ,p 1+3d ,p 1+4d 都是素数. 若2d ,即d 为奇数,则p 1+d ,p 1+2d 中有一个为偶数,它不是素数.若3d ,则p 1+d ,p 1+2d ,p 1+3d 中有一个为3的倍数(它们构成模3的一个完系),矛盾. 若5d ,则p 1,p 1+d ,…,p 1+4d 中有一个为5的倍数只能是p 1=5,这时公差d 是6的倍数. 而5,11,17,23,29是5个成等差的素数数列,所以,p 5最小为29.3.对每个正整数n ,用()S n 表示n 在十进制表示下各数码之和.证明:对任意正整数m ,存在正整数n ,使得()()3S n mS n =.【答案】注意到,对任意正整数k ,(1008)k S 个=9,于是,设1008k 个=3n ,则n =336k 个,故S (n )=3k +6,这样,对任意正整数m ,取k =3m -2,就有S (n )=mS (3n ).说明 由S (3n )≡3n (mod9),故要求3|S (n ),进而3|n ,所以在先确定3n 时,要寻找一个9的倍数(例如1002k 个作为3n 就不能满足条件) .另外,在S (2n )与S (n )之间没有上述性质,事实上,可证:S (2n )≤2S (n );S (n )≤5S (2n ).4.求最大的正整数k ,使得存在正整数n ,满足2|31kn+. 【答案】注意到,当n 为偶数时,设n =2m ,有3n =9m ≡1(mod8), 当n =2m +1时,3n =9m ×3≡3(mod8),所以,对任意正整数n ,有3n +1=2或4(mod8), 故k ≤2.又22|31+1,所以,所求k 的最大值为2.5.设n 为正整数.证明:存在十进制表示中只出现数码0和1的正整数m ,使得|n m .【答案】考虑数列 1,11,111,…,111n+个,其中必有两个数对模n 同余(因为任何整数除以n 所得的余数只能为0,1,2,…,n -1,共n 种情况),它们的差(大的减小的)就是符合要求的m .6.设n 为是一个正奇数.证明:存在一个十进制表示中每个数码都是奇数的正整数m ,使得|n m . 【答案】如果(5,n )=1,那么由上题的结论,知存在m =11i 个0j 个,使得n |m ,而n 为奇数,结合5n ,知(n ,10)=1,故n |11i 个.命题获证.如果5|n ,设5α|n ,那么可写n =5α·n 1,其中5n 1.利用2.2节例5的结论,可知存在一个α位的正整数m 1,使得5α|m 1,且m 1的每个数码都是奇数,这时,考虑数m 1, 11m m ,…,111n m m +1个,这里11i m m 个表示i 个m 1连写形成的十进制数(故上面所列的数都是5α的倍数),则存在1≤i <j ≤n 1+1,使得 11j m m 个≡11i m m 个(mod n 1),结合(n 1,10)=1,可知n 1|11j-i m m 个,于是记m =11j-i m m 个,则m 中的每个数码都是奇数,且5α|m ,n 1|m ,而 (5α,n 1)=1, 故5α·n 1|m ,即n |m . 命题获证.7.证明:对每个正整数n ,数19817n⨯+都是合数. 【答案】若n 为偶数,则 19×8n +17≡1×(-1)n +2≡0(mod3);若n ≡1(mod4),写n =4k +1,则19×8n +17=19×642k ×8+17≡6×(-1)2k ×8+4≡0(mod13);若n ≡3(mod4),则 19×8n +17=19×642k +1×8+17≡(-1)×(-1)2k +1×3+2≡0(mod5) . 所以,对任意正整数n ,数19×8n +17是合数.8.Fibonaccia 数列{}n F 定义如下:121F F ==,21n n n F F F ++=+,n =1,2,…. (1)证明:该数列任意连续10项之和是11的倍数;(2)求最小的正整数k ,使得该数列中任意连续k 项之和是12的倍数. 【答案】考虑数列{F n }中每一项除以11(或12)所得的余数. ⑴{F n (mod11)}:1,1,2,3,5,-3,2,-1,1,0,1,1,…,所以{F n (mod11)}是以10为周期的纯周期数列,因此{F n }中任意连续10项之和≡1+1+2+3+5+(-3) +2+ (-1)+1+0=11≡0(mod11), 命题获证.⑵{F n (mod12)}:1,1,2,3,5,-4,1,-3,-2,-5,5,0,1,1,…是以12为周期的纯周期数列.直接验证,可求出满足条件的最小正整数k =36.说明 若k 是满足⑵的最小正整数,而n 是满足⑵的正整数,则k |n (这个结论请读者证明) .因此,找到满足条件的n =36 ({F n (mod12) }的每个周期内各数之和≡4(mod12))后,只需验证36的正因数不合要求,就能断言36是符合条件的最小正整数.9.设整数a 、b 满足:2221|a b +.证明:22441|a b +.【答案】先分别证明:⑴若a 2+b 2≡0(mod3),则a ≡b ≡0(mod3) ; ⑵若a 2+b 2≡0(mod7),则a ≡b ≡0(mod7) .这只需注意到,对任意整数x ,都有x 2≡0或1(mod3), 及 x 2≡0,1,2或4(mod7), 即可证出.现在由21|a 2+b 2可推出21|a ,21|b ,故212|a 2+b 2,所以命题成立.10.正整数a 、b 、c 满足:222c a b ab =++.证明:c 有一个大于5的素因子.【答案】我们分别证明: ⑴若2|c ,则2|a ,2|b ; ⑵若3|c ,则3|a ,3|b ; ⑶若5|c ,则5|a ,5|b . ⑴的证明是平凡的.⑵的证明只需注意到 c 2=a 2+ab +b 2=(a -b ) 2+3ab ,就容易证出. 对于⑶,由条件,知 4c 2=4a 2+4ab +4b 2=3a 2+(a +2b )2, 而对任意整数x ,知 x 2≡0,1,4(mod5), 于是,由 3x 2+y 2≡0 (mod5), 可知 x 2≡y 2≡0 (mod5), 即 x ≡y ≡0 (mod5).因此,由5|c ,知 3a 2+(a +2b )2≡0 (mod5), 故 a ≡a +2b ≡0(mod5), 可得 a ≡b ≡0(mod5), 所以⑶成立.回到原题,当c 是2、3或5的倍数时,c 2=a 2+ab +b 2两边可分别约去22、32或52后,等式的形式保持不变.所以c 有一个大于5的素因子.11.将整数1,2,…,9填入一个3×3的表格,每格一个数,使得每行、每列及每条对角线上各数之和都是9的倍数.(1)证明:该表格中正当中那个方格内的数是3的倍数;(2)给出一个正当中方格内所填数为6的满足条件的放置方法.【答案】⑴设表格中第i 行、第j 列的方格上所填的数为a ij ,1≤i ≤3,1≤j ≤3, 则 a 11+a 22+a 33≡a 13+a 22+a 31≡a 12+a 22+a 32≡a 21+a 22+a 23≡0(mod9), 于是它们求和后,得(a 11+a 12+a 13+a 21+a 22+a 23+a 31+a 32+a 33)+3a 22≡0(mod9), 即 3a 22+(1+2+…+9)≡0(mod9), 故 9|3a 22, 即 3|a 22,从而表格中正当中的格子内所填数为3的倍数. ⑵下表给出的例子是中间格为612.下面的算式给出了一种判别一个数是否为19的倍数的方法:每次去掉该数的最后一位数字,将其两倍与剩下的数相加,依此类推,直到数变为20以内的数为止,若最后一个数为19,则最初的那个数为19的倍数,否则原数不是19的倍数. 6 7 9 4 4 8 6 8 0 2 4 6 8 4 8 7 6 1 2 1 9 4 4 9 7 6 12 4 5 0 9 1 8 4 6 8 16 6 2 4 1 0例如上面判定了67944为19的倍数,而44976不是19的倍数.(1)试证明:上面的判别方法是正确的;(2)请给出判别一个数是否为29的倍数的类似方法. 【答案】一般地,设数10n n a a a -是一个十进制表示下的n +1位数,则若它是19的倍数,那么1011n n a a a -+a 0=10n n a a a -≡0(mod19),故 2011n n a a a -+2a 0≡0(mod19), 即 11n n a a a -+2a 0≡0(mod19),这表明每次操作后的结果都是19的倍数. 另一方面,若 11n n a a a -+2a 0≡0(mod19), 则 1011n n a a a -+20a 0≡0(mod19), 这表明 1011n n a a a -+a 0≡0(mod19),即 10n n a a a -≡0(mod19),所以,每次操作后的结果是19的倍数,则操作前该数也是19的倍数. 所以,题给的判别方法是正确的.对于29而言,类似的判别方法是:每次去掉最后一位,将它的3倍与剩下的数相加,以此类推,直到变为30以内的数为止.若最后的结果为29,则原数是29的倍数,否则原数不是29的倍数.13.能否将2010×2010的方格表的每个方格染成黑色或白色,使得关于表格的中心对称的方格颜色不同,且每行、每列中黑格数与白格数都各占一半? 【答案】不能做到.事实上,若存在满足条件的染色方式,我们在黑格中都写上+1,白格中都写上-1,并依表格的中心所在的两条方格线将表格分为4块,左上角那块中各数之和设为A ,右上角那块为B ,左下角那块为C ,右下角那块为D .由条件,可知A ,B ,C ,D 都是10052个奇数之和,故A ,B ,C ,D 都为奇数,且A =-D ,B =-C (因为关于表格的中心对称的方格不同色),而且A +B =A +C =0(这里用到每行、每列中黑、白格数各占一半).所以,A -C =A +C =0,这要求A =C =0,但A 、C 都是奇数,矛盾.14.标号为1,2,…,100的火柴盒中有一些火柴,如果每次提问允许问其中任意15盒中所有火柴数之和的奇偶性.那么要确定1号盒中火柴数的奇偶性,至少需要提问几次? 【答案】至少需要3次提问.先证“3次提问是足够的” .例如: 第一次为:a 1,a 2,…,a 15;第二次为:a 1,a 2,…,a 8,a 16,a 17,…,a 22; 第三次为:a 1,a 9,a 10,…, a 22.其中a i 表示第i 盒中火柴的数目.这样,3个答案之和的奇偶性与a 1的奇偶性相同(其余每盒在3次提问中恰好出现2次) .因此,经3次提问可确定a 1的奇偶性.再证“至少需要3次提问” .如果提问只有两次,且两次中都出现a 1,那么在两次提问中必有a i 和a j ,使得a i 只在第1次提问中出现,而a j 只在第二次提问中出现,这样同时改变a 1、a i 、 a j 的奇偶性,每次答案是相同的,从而不能确定a 1的奇偶性.如果两次中都不出现a 1,在a 1都不出现时,改变a 1的奇偶性;在a 1只出现一次时,改变a 1与a i (这里a i 是与a 1同时出现的某个火柴盒)的奇偶性,那么两次答案仍是相同的,不能确定a 1的奇偶性. 综上可知,至少需要提问3次.15.求所有的正整数n ,使得可以在一个n ×n 的方格表的每个方格内写上+1或-1,满足:每个标号为+1的方格的相邻格中恰有一个标号是-1,而每个标号为-1的方格的相邻格中恰有一个标号是+1. 【答案】用a ij 表示第i 行、第j 列上的方格内所填的数.如果存在符合要求的填法,那么我们不妨设a 11=1(否则改变表格中所有数的符号再讨论),此时a 21与a 22中恰好有一个为-1,不妨设a 21=-1(否则将表格的第2行与第2列互换后再讨论),则a 12=1,进一步讨论,知a 22=-1,a 13=1,…,可知第1行中的数都是1,第2行中的数都是-1,进而,第3行中的数都是-1,第4行中的数都是1,依此递推,知当且仅当i ≡1(mod3)时,第i 行中的数都是1,而其余每行中的数都是-1.如果,n ≡0(mod3),那么第n 行的数为-1,该行上的每个方格中相邻方格上的书都是-1,不合要求,直接验证可知其余情况都合要求. 所以,当且仅当3n ,n >1时,存在符合要求的填法.16.设12100a a a ,,…,是1,2,…,100的一个排列,令12i i b a a a =++…+,i =1,2,…,100,记i r 为i b 除以100所得的余数.证明:12100r r r ,,…,中至少有11个不同的数.【答案】若r 1,r 2,…,r 100中只有10个不同的数,则对i =1,2,…,99,r i +1-r i 只有102-9=91(这里减去9是因为r i +1=r i 时所得的值都是零)种不同取值.但是在模100的意义下,r i +1-r i 依次为a 2,a 3,…,a 100,共有99种不同的取值,矛盾.所以r 1,r 2,…,r 100中至少有11个不同的值.17.求所有满足下述条件的正整数a 的个数:存在非负数0122001x x x x ,,,…,,使得0xa =200112x x x a a a +++.【答案】若a 是一个满足条件的数,则0x a >1,故a >1.此时,对 0x a =1x a +2x a +…+2001x a 两边模a -1,知 1≡200111++个(mod a -1),所以 a -1|2000.另一方面,若a >1满足a -1|2000,则我们在x 1,x 2,…,x 2001中取a 个数为0,a -1个为1,a -1个为2,…,a -1个为k -1,这里k =20001a -,并取x 0=k ,就有0x a =1x a +2x a +…+2001x a . 所以,当且仅当a >1且a -1|2000时,a 为满足条件的数,这样的a 共有20个.18.设m 、n 为正整数,m >1.证明:()21|mm n -的充要条件是()221|21mn--. 【答案】若m (2m -1)|n ,设n =m (2m -1)k ,则 2n-1=(21)2m m k--1=()()212mmk--1=()21mk -A ,其中 A =()222mmk -+()232mmk -+…+()12mk +1.注意到 2mk -1=()2km -1≡1k -1≡0(mod2m -1), 所以 ()21m -2|2n -1.反过来,若()21m -2|2n -1,我们先证m |n .若否,设n =mq +r ,0<r <m ,则由 2n ≡1(mod2m -1),知 (2m )q ·2 r ≡1(mod2m -1), 故 2 r ≡1(mod2m -1), 但是 1≤2 r -1<2m -1. 所以2m -12 r -1,矛盾.因此m |n .现设n =mq ,则 2n -1=(2m -1)×B ,其中 B =(2m )q -1+(2m )q -2+…+2m +1, 由 (2m -1)2|2n -1, 知 2m -1|B ,又 B =1 q -1+1 q -2+…+1=q (mod 2m -1), 所以 2m -1|q , 从而 m (2m -1)|n . 命题获证.19.设正整数a 、b 互素,p 为奇素数.证明:1p p a b a b p a b ⎛⎫⎪⎝⎭++,=或+. 【答案】记A =p pa b a b ++=a p -1―a p -2b +…―ab p -2+b p -1,结合p 为奇数及b ≡―a (mod a +b ),知A ≡111p p p p a a a ---+++个=pa p -1(mod a +b ).而 (a ,b )=1, 故 (a ,a +b )=1,所以 (a +b ,p pa b a b++)=(a +b ,A )=(a +b ,pa p -1)=(a +b ,p )=1或p .20.求最小的正整数a ,使得对任意整数x ,都有()13565|5139x x ax ++.【答案】由条件,知65|(18+9a )(取x =1),而(9,65)=1,故65|a +2, 即a ≥63.当a =63时,利用Fermat 小定理知:对任意整数x ,都有5x 13+13x 5+9ax ≡13x +9ax ≡(3+(-1)×3)x ≡0(mod5 ); 5x 13+13x 5+9ax ≡5x +9ax ≡(5+9×(-2))x ≡0(mod13 ). 所以 65|5x 13+13x 5+9ax . 综上可知,所求的最小正整数a =63.21.是否存在整数a 、b 、c ,使得方程20ax bx c ++=和()()()21110a x b x c +++++=都有两个整数根?【答案】不存在这样的整数a 、b 、c .事实上,若a 、b 、c 满足条件,我们不妨设a 为偶数(否则用-(a +1)、-(b +1)、-(c +1)代替a 、b 、c 讨论),由条件,结合韦达定理知-b a 与ca都是整数,故b 、c 都是偶数,所以a +1、b +1、c +1都是奇数.此时,对任意整数x ,有(a +1)x 2+(b +1)x +(c +1)≡x 2+x +1=x (x +1)+1≡1(mod2)(最后一步用到x 与x +1中有一个偶数).这表明方程(a +1)x 2+(b +1)x +(c +1)=0没有整数根,矛盾.22.求所有的正整数组(x ,y ,z ,w ),使得x !+y !+z !=w !. 【答案】不妨设x ≤y ≤z <w ,则w ≥z +1,若z ≥3,则w !≥(z +1)·(z !)≥z !+y !+x !, 矛盾,故 z ≤2.若z =1,则x =y =z =1,此时w !=3,不存在这样的w ,故z =2. 此时w ≥3,故 w !≡0(mod3),所以 x !+y !≡1(mod3), 而 x ≤y ≤2, 故只能是 x =y =2, 此时 w =3,故 (x ,y ,z ,w )=(2,2,2,3).23.求满足下述条件的整数数组(a ,b )的组数:0≤a ,b ≤36,且()220mod37a b +=.【答案】注意到,a 2+b 2≡a 2-36b 2(mod37),故由条件知 37|a 2-36b 2, 即 37|(a -6b )(a +6b ),所以 37|a -6b 或37|a +6b .因此,对每个1≤b ≤36,可知恰有两个a (a ≡±6b (mod37)) 满足条件, 而b =0时,由a 2+b 2≡0(mod37)知a =0. 所以,满足条件的(a ,b )共有2×36+1=73(组).24.设m 、n 为正整数,且22|mn m n m ++.证明:m 是一个完全平方数.【答案】有条件可设m 2+n 2+m =kmn ,k 为正整数,这样,关于n 的一元二次方程n 2-kmn +m 2+m =0①有正整数解,故△=(km ) 2-4(m 2+m )=m (k 2m -4m -4)是一个完全平方数.若m 为奇数,则(m ,k 2m -4m -4)=(m ,-4)=1,故由△为完全平方数知m 为完全平方数.若m 为偶数,则由①知n 为偶数 (否则①的左边为奇数,矛盾),故4|n 2,4|kmn ,4|m 2,从而由①知4|m .设m =4m 1,则△=16 m 1(k 2m 1-m 1-1),所以,m 1(k 2m 1-m 1-1)是一个完全平方数,这时(m 1,k 2m 1-m 1-1) =(m 1,-1)=1. 故m 1是完全平方数,所以m =4m 1也是完全平方数,命题获证.25.证明:若正整数n 可以表示为三个正整数的平方和的形式,则2n 也可以表示为三个正整数的平方和的形式.【答案】设n =x 2+y 2+z 2,x ≥y ≥z 为正整数,则n 2=(x 2+y 2+z 2) 2=(x 2+y 2) 2+2(x 2+y 2) z 2+z 4 =(x 2+y 2-z 2) 2+4(x 2+y 2) z 2=(x 2+y 2-z 2) 2+(2xz ) 2+(2yz ) 2.注意到,x 2+y 2-z 2>0,知n 2可表为3个正整数的平方和.26.求所有的正整数n ,使得n 的三次方根等于n 去掉最后三位数字后得到的正整数.【答案】设n =1000x +y ,这里x 为正整数,y 为整数,且0≤y ≤999.依题意知x 3=1000x +y .1000x ≤x 3<1000x +1000=1000(x +1), 故 x 2≥1000,x 3+1≤1000(x +1), 得 x 2≥1000,x 2-x +1≤1000. 所以 32≤x <33, 故 x =32, 这样 y =768, 所以 n =32 768.27.证明:存在无穷多个整数n ,使得数n 、n +1、n +2都可以表示为两个整数(不必不同)的平方和.例如:22000=+,22101=+,22211=+,故n =0即为一个满足条件的整数. 【答案】只需寻找正整数l ,使得l 2-1=x 2+y 2有正整数解.令x =2m 2,y =2m ,及l =2m 2+1,就有l 2-1=x 2+y 2.所以,对任意正整数m ,取 n =(2m 2+1) 2-1=4m 4+4m 2, 则 n =(2m 2) 2+(2m ) 2, n +1=(2m 2+1) 2+02, n +2=(2m 2+1) 2+12.28.求最小的正整数n ,使得在十进制表示下3n 的末三位数字是888. 【答案】由条件,知n 3≡888(mod1000),故n 3≡888(mod8),n 3≡888(mod125), 由前者知n 为偶数,设n =2m ,则m3≡111(mod125),因此m3≡111≡1(mod5) .注意到当m=0,1,2,3,4(mod5)时,对应地m3≡0,1,3,2,4(mod5),所以,由m3≡1(mod5)知m≡1(mod5),可设m=5k+1,这时m3=(5k+1) 3=125k 3+75k2+15k+1≡111(mod125),故75k2+15k≡110(mod125),从而15k2+3k≡22(mod25),既有15k2+3k+3≡0(mod25),故5k2+k+1≡0(mod25) .这要求5k2+k+1≡0(mod25),故5│k+1.可设k+1=5l,得5k2+k+1=5×(5l-1) 2+5l,=125l2-50l+5(l+1)≡0(mod25),故5│l+1.可设l+1=5r,因此n=2m=10k+2=10(5l-1)+2=50l-8=50(5r-1)-8=250r-58.结合n为正整数,可知n≥250-58=192.又1922=7077888符合要求,故满足条件的最小正整数为192.29.设正整数n>1,证明:数21n-既不是完全平方数,也不是完全立方数.【答案】由于n≥2,故2n-1≡-1(mod4),而完全平方数≡0或1(mod4),故2n-1不是完全平方数.另一方面,若存在n>1及正整数x,使得2n-1=x3,则2n=(x+1)(x 2-x+1),由于x 2-x+1=x(x-1)+1,其中x(x-1)为偶数(两个相邻整数中有一个为偶数),故x 2-x+1为奇数,这要求x 2-x+1=1,进而x=1,导出n=1,矛盾.故2n-1不是一个完全平方数.30.设a、b、c a、b、c都是完全平方数.【答案】先证:对任意正整数a a为完全平方数.qp,p、q为正整数,且(p,q)=1,则a=22qp,此时由a为正整数,知p2|q2,但(p,q)=1,故p=1,即a=q2.m,m为整数,则)2=(m2即a+b+m 2-c,n ,n 为正有理数,则 ab =(n 2=n 2-2c ,c =m 可知a ,b 也都是完全平方数.31.已知正整数c 是一个奇合数.证明:存在正整数a ,使得13ca ≤-,且()2218a c -+是一个完全平方数.【答案】通过凑完全平方式来处理.由条件可设c =pq ,3≤p ≤q ,p 、q 都是奇数,现在需要寻找a ,使得(2a -1) 2+8pq 是一个完全平方式,一个自然的取法是:2a -1=2q -p ,则(2a -1)2+8pq =(2q -p ) 2+8pq =(2q +p ) 2,a =12(2q -p +1)=q -12p -≤q -1=c p -1≤3c-1,符合题中的要求.32.设整数a 、b 满足:对任意正整数n ,数2na b •+都是完全平方数.证明:a =0.【答案】若a ≠0,注意到在a <0时,n 充分大后,数2n a +b <0,与2n a +b 为完全平方数矛盾,故a >0.现在设2n a +b ≡x 2n ,x n 为正整数,则对任意正整数n ,有x n <x n +1.由于 4x 2n -x 2n +2=4(2n a +b )-(2n +2a +b )=3b , 故 3│b │=│2x n -x n +2│·│2x n +x n +2│,而 2x n +x n +2随着n 的增大而增大,故只能是│2x n -x n +2│=0, 即 │b │=0,但这时2n a 与2n +1a 都要是完全平方数,这是不可能的,矛盾.所以a =0.33.求不能表示为42的正倍数与一个合数之和的最大正整数.【答案】对任意不能表示为42的正倍数与一个合数之和的正整数n ,考虑n 除以42所得的余数r .若r =0或r 为合数,则n ≤42.下面考虑r =1或r 为素数的情形.若 r ≡1(mod5),则 84+r ≡0(mod5), 此时 n <3×42=126;若 r ≡2(mod5),则 4×42+r ≡0(mod5), 此时 n <5×42=210;若 r ≡3(mod5),则 42+r ≡0(mod5), 此时 n <2×42=84;若 r ≡4(mod5),则 3×42+r ≡0(mod5), 此时 n <4×42=168;若 r ≡0(mod5),则 r =5,此时由于5,47,89,131,173都是素数,故n 最大为215. 综上可知,所求最大正整数为215.34.求一个正整数n ,使得数n ,n +1,…,n +20中每个数都与30030不互素. 【答案】由于30 030=2×3×5×7×11×13,所以若取N =210k ,则N 与N ±r 都与30 030不互素,这里r 为2,3,…,10中的数.现在考虑数N ±1,我们取k ,使得210k ≡1(mod11)且210k ≡-1(mod13),前者要求k ≡1(mod11),设k =11m +1,后者要求 210(11m +1)≡-1(mod13),解得 m ≡4(mod13),所以,令k =45,则所得的21个数9440,9441,…,9460与30 030都不互素,因此取n =9440即可.35.是否存在连续13个正整数,其中每个数都是2、3、5、7、11中的某个数的倍数?连续14个呢?【答案】注意到,114,115,…,126这13个数都是合数,每个数都是2、3、5、7、11中某个数的倍数,因此存在13个符合要求的数.下证:没有连续14个正整数,使得其中每个数都是2、3、5、7、11中某个数的倍数.事实上,若存在这样的14个数,考虑其中的7个奇数,设它们为a ,a +2,…,a +12.由于若两个奇数都是3的倍数,则它们的差至少为6,故这7个奇数中至多有1个数为11的倍数.同样可证这7个奇数中至多有2个数是5的倍数;至多有1个数为7的倍数;至多有1个数为11的倍数.由假设,这7个数都是3、5、7、11中某个数的倍数,故这7个奇数中分别有3个为3的倍数,2个为5的倍数,1个为7的倍数,1个为11的倍数,并且不出现一个数同时是3、5、7、11中某两个数的倍数.但是,这时要求a 、a +6、a +12为3的倍数;a 、a +10或者a +2、a +12中有一组数为5的倍数.必有一个数同为3和5的倍数,矛盾.36.设p 为素数,a 、n 都是正整数,且23p p n a +=.证明:n =1.【答案】当p =2时,a n =13,知a =13,n =1.当p >2时,由p 为素数,可知p 为奇数,此时2p +3 p =(2+3)(2 p -1-2 p -2×3+…-2×3 p -2+3p -1) ,故 5|a n ,即5|a .若n >1,则52|a n ,这时,应有2 p -1-2p -2×3+…-2×3 p -2+3p -1≡0(mod5) .利用3≡-2(mod5),p 为奇数及上式,知2 p -1-2p -2×3+…-2×3 p -2+3p -1≡11112222p p p p p -----++个=p ·2 p -1≡0(mod5), 所以5|p ,而p 为素数,故p =5,这导致a n =25+35=275=52×11,n 只能为1,矛盾.因此n =1.37.圆周上排列着2000个点,在某个点上标上数1,按顺时针方向数两个点,在其上标数2,再数3个点标数3,依此继续,标出数1,2,…,2000.这样,有些点上没有标数,有些点上所标的数不止一个.问:被标上2000的那个点上所标的数中最小的是多少?【答案】等价于求最小的正整数n ,使得1+2+…+n ≡1+2+…+2000(mod2000) . ①即(1)2n n +≡1000(mod2000), 等价于 n (n +1)≡2000(mod4000),这要求 2000|n (n +1) .注意到 (n ,n +1)=1,而 2000=24×53,所以24|n ,53|n +1;或者53|n ,24|n +1;或者n 与n +1中有一个为2000的倍数.分别求得n 最小为624,1375,1999,其中满足①的最小的数为624.所以,被标上2000的那个点上所标的数中最小的那个是624.38.圆周上有800个点,依顺时针方向标号为1,2,…,800,它们将圆周分为800个间隙.现在选定某个点,将其染上红色,然后进行下述操作:如果第k 号点染成了红色,那么依顺时针方向转过k 个间隙,将所到达的点染成红色.问:依此规则,圆周上最多有多少个点被染成了红色?证明你的结论.【答案】等价于求在模800的意义下,数列a ,2a ,22a ,23a ,…中,出现的不同的数的个数的最大值,这里a 在1,2,…,800中取值.注意到,当2n 2m (mod800)时 ,2n a 2m a (mod800)不一定成立;反过来,当2n a 2m a (mod800)成立时,2n 2m (mod800) 一定成立.因此,数列a ,2a ,22a ,…在模800的意义下,不同元素个数的最大值在a =1时可以取到,因此,只需求1,2,22,…在模800的意义下不同元素的个数.由于800=25×52,而n ≥5时有 2n ≡0(mod25),另外{2n (mod25)}为2,4,8,16,7,14,3,6,12,-1,-2,-4,-8,-16,-7,-14,-3,-6,-12,1,…故{2n (mod25)}中恰好有20个不同元素.结合{2n (mod25)}为2,4,8,16,0,0,…,可得{2n (mod800)}中恰好有20+4=24(个)不同的数.所以,圆周上至多有24个点染成了红色.39.设m 为正整数,且()2mod4m ≡.证明:至多存在一对正整数(a ,b ),使得m ab =,且05441a b m <-<++【答案】如果能确定a +b 的值(视m 为常数),那么利用韦达定理的逆定理,可知至多只有一组正整数(a ,b )满足条件.由条件,知(a +b ) 2=(a -b ) 2+4ab 满足1+4m ≤(a +b ) 2<5+4+1m 4m =4+1m 2) 2,即 4+1m a +b 4+1m 2,所以 41411141121m m m a b m m m +++++⎡⎡++++⎪⎣⎣⎩或,若4为整数;或4+1,若4不是整数. 总之,a +b 只能取值于某两个连续正整数.而ab =m ≡2(mod4),可知a 、b 一奇一偶,即a +b 为奇数.这样我们知道a +b 的值唯一确定,命题获证.40.设n 是一个大于10的正整数,且n 的每个数码都为1、3、7或9.证明:n 有一个大于10的素因子.【答案】用反证法,若n 的每个素因子都不大于10,利用条件,知n 为奇数,且n 不是5的倍数,故存在非负整数i 、j ,使得 n =3i ·7j ,考虑3i 与7 j 除以20所得的余数,对i =0,1,2,…, j =0,1,2,…,分别依次有 {3i (mod20)}:1,3,9,7,1,3,…;{7 j (mod20)}:1,7,9,3,1,7,….这两个都是以4为周期循环的数列,因此 3i ·7j ≡ab (mod20),这里a 、b 都为1,3,7或9.分别计算,可知 3i ·7j ≡1,3,7或9 (mod20),这表明,所有形如3i ·7j 的数的十位数字都为偶数,但n 的每一位数字都是1,3,7或9,矛盾. 所以,n 有一个大于10的素因子.41.求所有的素数对(p ,q ),使得|1p qpq p q ++.【答案】由条件可知p ≠q ,利用对称性,不妨设p <q .若p =2,则q q +5≡0(mod q ),知q =5.直接验证,可知(p ,q )=(2,5)符合要求.若p >2,则p ,q 都为奇素数.由条件知p p +1≡0(mod q ),故p 2p ≡1(mod q ),利用Fermat 小定理,有p q -1≡1(mod q ),于是, p (2p ,q -1)≡1(mod q ) . ①注意到,2|(2p ,q -1),而(2p ,q -1) |2p ,故只有下面的两种情形.情形一 (2p ,q -1) =2,则由①知p 2≡1(mod q ),导致q |p +1或q |p -1,这与p ≤q -2矛盾. 情形二 (2p ,q -1) =2p ,则由①知q ≡1(mod p ),于是0≡p p +q q +1=2(mod p ),导致p =2,矛盾.综上可知,满足条件的(p ,q )=(2,5)或(5,2) .42.设()22010f n n n n ⋯=1++++.证明:对任意整数m ,若2≤m ≤2010,则不存在正整数n ,使得()|m f n .【答案】若存在2≤m ≤2010,使得对某个正整数n ,有m |f (n ) .则由于f (1)=2011为素数(这里2011为2011去验证),故n ≠1,此时可写f (n )=201111n n --. 对m 的素因子p ,由m |f (n )知n 2011≡1(mod p ),而由Fermat 小定理知n p -1≡1(mod p ),所以,有 (2011,1)p n -≡1(mod p ).结合 p -1<2011,及2011为素数,可得(2011,p -1)=1,于是n ≡1(mod p ),从而 0≡f (n )≡1+12+…+12010=2011(mod p ),要求 p =2011,这与m ≤2010矛盾.所以命题成立.43.是否存在整数x 、y ,使得2012201120102010442011x y y y -=++?【答案】不存在这样的整数x ,y .若不然,则有x 2012+1=(4y 2010+2011)( y +1) . ①注意到,4y 2010+2011≡3(mod4),这表明①式右边有模4余3的素因子,故存在素数p ,使得p ≡3(mod4), 且 x 2012+1≡0(mod p ) .由于2012为偶数,利用2.3节例2的结论知x 2012+1的每一个奇素因子都≡1(mod4),矛盾.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、名词解释(每题3分,共12分)1、庄票:庄票是由钱庄签发的载有一定金额并由其负责兑现的一种票据,分即期和远期两种,即期庄票贝票即付,远期庄票到期付现。
2、袁头币:币面镌有袁世凯头像的银元。
辛亥革命后,北洋政府于1914年颁布《国币条例》,实行银本位制,当年十二月及次年二月先后由天津造币总厂及江南造币厂开铸,每枚重7钱2分,原订成色为纯银九成,后改为八九成。
3、信交风潮: 1921年上海发生的一次金融风潮。
是由投机商人发行信托公司股票,在交易所上市买卖,并暗中哄抬价格,牟取暴利。
当时一些商人见有利可图,争相招募股份,纷起组织,成立交易所达100多家,信托公司10多家,股票大量上市,形成投机狂潮,信交事业一时畸形发展,最终纷纷倒闭。
4、善后大借款:是袁世凯窃踞大总统职位以后,为筹集军费以消灭南方各省势力而借办理善后为名向外国银行团举借的巨额长期借款。
1913年4月,袁世凯政府同5国银行团签署了“善后大借款”的合同。
该合同规定:借款金额2500万英镑(合银元24827万元),年息5厘,折扣84,期限47年,用途为偿指定的借款、垫款、赔款和军政费用等6项;中国以全部盐税、部分关税和直隶、河南、山东、江苏4省的中央税为担保;
借款由汇丰、东方汇理、华俄道胜、横滨正金、德华
5家银行承担。
二、判断(正确的打“√”,错误的打“×”。
每题1分,共10分)1、库平是政府征税时使用的标准。
(√ ) 2、漕平是征收漕银折色使用的平。
(√ ) 3、清朝,各地铸造银锭的机构是银炉,又叫炉房。
(√ )4、中国第一家正式开业的证券交易所是1905年成立的上海从业公所。
(× )5、1910年,清政府颁布《币制则例》,将银元的铸造权收归中央,开始铸造“大清银币”,称为国币。
(√)6、“汇划”就是钱庄业的票据清算。
(√ )7、“逆汇”是票号汇兑业务的一种业务,是存款、放款、汇兑相结合。
(√ ) 8、票号的组织形式一般是独资或合资,均负有限责任。
(× )9、最早入侵中国的美国银行是花旗银行。
(√ ) 10、北洋政府时期,除中国银行、交通银行代表国家发行纸币外,各省地方银行、
私营银行也发行纸币。
(√)三、单选(每题1分,共10分) 1、最早入侵中国的外国银行是英国的( A ) A、丽如银行B、汇丰银行 C、汇隆银行 2、第一个将总行设在中国领土上的外国银行是( A ) A、
汇丰银行 B、法兰西银行 C、汇隆银行3、第一批流通于中国市场的外国钞票是( A ) A、丽如银行发行的纸币 B、汇丰银行发行的纸币 C、汇隆银行发行的纸币 4、北洋政府规定国家中央银行为( A ) A、中国银行 B、交通银行 C、中国通商银行 5、我国第一家私人资本银行是( B ) A、中国通商银行 B、信成银行 C、信义银行6、中国银行的前身是( A ) A、户部银行 B、中国通商银行 C、交通银行7、我国最早铸造的银元是( A ) A、光绪元宝 B、袁头币 C、金圆券 8、我国最早铸造铜元的是( B ) A、准两广总督张之洞 B、两广总督李鸿章 C、两广总督张之洞9、交通银行成立于1908年,这是一家(B )A、清政府独资银行B、官商合资银行C、商股银行10、票号吸收的存款( A )
A、以公款为主
B、以私款为主
C、以公款和私款为主四、多项选择(每题2分,共20分) 1、宝银的成色,全国统一、公认的标准有( ABCD ) A、纯银 B、足银 C、纹银
D、标
准银 E、虚银 2、宝银的重量标准是“平”,全国主要的平有( ABCD ) A、库平 B、关平 C、漕平 D、市平 E、仓平 3、清末发生在上海的三次大的金融风潮是( ABC ) A、1883年的上海金融风潮 B、贴票风潮 C、橡皮股票风潮D、信交风潮 E、挤兑风潮 4、当铺的日常业务是(ABC )A、存款B、放款 C、签发银铺票 D、委托收款E、办理结算 5、外国银行对中国的经济侵略与掠夺的手段有( ABCD ) A、垄断国际汇兑 B、吸收存款,办理放款,控制中国金融市场C、发行钞票,侵略中国主权 D、通过借款控制中国的财政E、广泛设立营业网点6、制钱的落后性表现在( ABD ) A、统治者对制钱贬值,以此对人民实行超经济剥削B、分散铸造的政策,造成制钱纷繁杂乱 C、集中铸造的政策,造成制钱品种单一
D、制钱的流通有很大的局限性
E、制钱的流通毫无局限性7、典当业由盛而衰的主要原因是( ABC ) A、银行的兴起 B、钱庄、票号的发展 C、官银钱号的设立 D、抵押放款业务大大萎缩E、经营方式不适应8、“北四行”是指( ABCE ) A、金城银行 B、盐业银行
C、中南银行
D、浙江实业银行
E、大陆银行 9、“南三行”是指( ABC ) A、上海商业储蓄银行 B、浙江实业银行 C、浙江兴业银行 D、新华信托储蓄银行 E、广东银行 10、1845年,清室内务府设立的官银号是( ABCDE ) A、天元 B、天亨 C、天利 D、天贞 E、西天元五、简答(每题7分,共28分)1、清末外国银行利用哪些手段控制中国金融市场?答:(1)垄断国际汇兑,操纵外汇牌价;(2)吸收存款,办理贷款,控制中国的金融市场;(3)发行钞票,侵犯中国的主权; (4)通过借款控制中国的财政。
2、中国银行业是在什么历史背景下兴起的?有什么特点?答:中国银行业是在帝国主义侵略的日益加深以及因为这种侵略的刺激所形成的近代产业的发展中产生的。
其特点是:(1)中国的银行业不是直接由工业资本发展而产生,它是间接地由民族自救和民族工业的发展造成的;(2)中国封建经济下的金融机构钱庄和票号,没有直接演变为近代的新式银行;(3)中国的银行业一产生就分为官僚资本和民族资本两类银行。
3、“京钞风潮”及其产生的原因?答:由于中交两行滥发钞票,导致银行实力不断削弱,信用基础日益动摇。
在这种情形之下,袁世凯的心腹、长期
控制交通银行实权、时任总统府秘书长的梁士诒和段祺瑞的亲信徐树铮密度发行不兑现纸币。
但消息走漏,风声所及,市场震动,挤兑风潮迅速在京、津等地发生。
1916年5月,北洋政府以国务院的名义悍然下令中、交两行停止钞票兑现和存款付现。
于是京、津两地两行完全停止兑付,外地也开始停兑。
这些钞票当时人们称为京钞。
京钞停止兑现以后,人们纷纷抛出纸币,抢购商品,致使物价上涨,币值下跌,投机盛行,交易停顿,市场混乱。
这就是20世纪初发生在京、津等地的京钞风潮。
产生的原因:(1)北洋军阀之间连年内战,大量军费开支,导致财政不支,于是大量发行不兑现纸币,以弥补军费不足和财政空虚;
(2)中交两行为北洋政府垫款和发行钞票外,还为北洋政府开出担保空头存单,向其他商业银行借款,到期无力偿还,但又不得不兑现,以致头寸日紧;(3)英美帝国主义从中操纵破坏。
企图破坏中国的财政金融,作为策划国际共管中国的口实,于是指使它们控制的海关、邮电部门拒收两行钞票,外国银行也向两行挤提存款。
4、国际银团的侵略活动主要有哪些?答:国际银团以贷款和投资对中国进行经济掠夺:(1)1911年5月,英、法、德、美四国银行团同清政府签订了《粤汉川汉铁路借款合同》。
借款金额600
万英镑(合银4540万两),以两湖的厘金、盐税收入担保,4国享有两湖境内两路的修筑权以及两路在延伸时继续借款和修筑的优先权。
(2)1911年5月,英、法、德、美四国银行团同清政府签订了《币制实业借款合同》。
借款金额1000万英镑,年息5厘,折扣95,期限45年,并规定4国参与中国币制改革和在东北三省进行农垦、畜牧、森林、矿产资源的开发。
这触犯了日、俄在东北的利益,后几经争吵,4国银团接受日、俄参加。
4国银行团变成了6国银行团。
(3)1913年4月,袁世凯政府同英、法、德、日、俄五国银行团签订了“善后大借款”的合同。
借款金额2500万英镑(合银元24827万元),年息5厘,折扣84,期限47年,借款到期的利息是4285万英镑,大大超过本金。
它们通过这笔借款攫取了中国关税、盐税收入的保管权。
关盐两税,在中国财政收入中占极大比重,帝国主义控制了这两税,也就控制了中国财政。
六、论述(20分)钱庄、票号发展的原因是什么?为什么辛亥革命后钱庄能继续存在,票号却消亡?答:1、钱庄发展的原因:鸦片战争后,随着沿海沿江城市的陆续对外开放,中外交往日渐频繁,商品经济迅速发展,钱庄的数量和资本额大幅度增长、业务扩大,活动中心逐渐转移到上海。
2、票号发展
的原因:(1)鸦片战争以后,打破了中国的封闭式的自然经济,通商口岸的开放,商品经济的发展,票号本身就起源于汇兑,资金调拨的频率和数量逐年增加,给票号提供了发展机会;(2)农民运动给清政府解送现银增加了困难,票号长期为清政府汇解公款,得到清政府的信任,这就为票号能够扩大业务扩张机构创造了有利条件;(3)票号同清朝地方政府官吏紧密地勾结在一起,垄断官款汇兑,壮大了自己的资金实力。
3、钱庄的继续发展的原因:辛亥革命前夕,随着大量资金涌入上海,为钱庄增添了资金力量,钱庄趋向于稳定,进而发展。
究其原因:(1)第一次世界大战中,中国民族资本主义、工商业的发展需要钱庄的支持,而商号同钱庄有来往久长,同银行打交道的不多;(2)一些银行还依靠钱庄代理收解,存款于钱庄,钱庄在业务中领用银行的钞券,增加了资金实力;(3)外国银行仍然接受庄票以支持钱庄。
4、票号衰亡的原因:(1)中国近代银行的兴起,官银钱号的设立,同票号展开了竞争;(2)票号保守,不思变革,组织制度、用人机制和经营方式都很死板,无法同银行竞争;(3)清政府灭亡,票号失去靠山。
