高一数学幂函数及其性质
高一数学上册幂函数知识点

高一数学上册幂函数知识点幂函数是一种常见的函数形式,由于其在数学和实际问题中的广泛应用,掌握幂函数的知识点对高一学生来说至关重要。
本文将介绍高一数学上册幂函数的主要知识点,包括定义、性质以及解题方法等。
1. 幂函数的定义幂函数是指形如f(x) = x^a的函数,其中a为常数,x为自变量。
在幂函数中,底数x通常为正实数,指数a可以是正数、负数或零。
2. 幂函数的图像与性质(1)当指数a为正数时,幂函数的图像呈现递增的趋势。
若指数a大于1,则曲线斜率较大;若指数a介于0到1之间,则曲线斜率较小。
(2)当指数a为负数时,幂函数的图像呈现递减的趋势。
(3)当指数a为零时,幂函数的图像为一条水平直线。
3. 幂函数的基本性质(1)定义域:对于幂函数f(x) = x^a,其定义域为所有使得x^a有意义的实数x。
(2)值域:幂函数值域的范围可以是整个实数轴,或者是一个区间,具体取决于底数的正负和指数的奇偶性。
(3)对称性:当指数a为奇数时,幂函数关于原点对称;当指数a为偶数且底数x为正数时,幂函数关于y轴对称。
4. 幂函数的运算法则(1)幂函数的加法:若f(x) = x^a 和 g(x) = x^b 为幂函数,则它们的和函数是h(x) = x^a + x^b。
(2)幂函数的乘法:若f(x) = x^a 和 g(x) = x^b 为幂函数,则它们的乘积函数是h(x) = (x^a)(x^b) = x^(a+b)。
(3)幂函数的倒数:若f(x) = x^a 为幂函数,则其倒数函数是g(x) = 1/f(x) = 1/(x^a) = x^(-a)。
5. 幂函数的解题方法(1)求函数的定义域:根据幂函数的定义,求解所有使得x^a 有意义的实数x即可得到函数的定义域。
(2)求函数的值域:根据底数的正负和指数的奇偶性,可以确定函数的值域范围。
(3)求函数的性质与图像:通过计算函数的导数、二阶导数等信息,可以推断函数的增减性、凹凸性和图像的特征。
高一数学必修一幂函数及其图象和性质知识点总结

1 3.3幂函数
一、幂函数定义及解析式特点
1.定义:一般地,函数y x α=叫做幂函数,其中x 为自变量,α是常数。
2.解析式特点:①系数为1;②底为自变量;③指数为常数。
3.幂函数的指数除了可以取整数外,还可以取其他实数。
二、幂函数的图象
1.幂函数主要以11,2,3,,12
α=-为代表,来研究掌握0α<,01α<<,1α>时的大致图象和图象的性质。
2.同一坐标系中画出1232
,,,y x y x y x y x ====和1y x -=的图象,如下图:
三、幂函数图象特点
1.根据幂函数y x α=的图象可得到以下结论: (1)幂函数在()0,+∞都有定义,且都过()1,1点,不一定过()0,0点。
(2)幂函数都过第一象限,不过第四象限;
(3)当0α>时,在第一象限都是增函数;当0α<时在第一象限都是减函数。
2.(1)当0α<时,幂函数在第一象限是减函数,且和1y x
=在第一象限的图象 大致相同;
(2)当0α>时,函数在第一象限是增函数,且在第一象限的大致图象的特点 可细分为两种情况:
①01α<<时,幂函数的图象在第一象限“趴着增”,且在()0,1内,图象在直 线y x =的上方增,在()1,+∞图象在直线y x =的下方增。
②1α>时,幂函数的图象在第一象限“竖着增”,且在()0,1内,图象在直线。
高一数学知识点:幂函数知识点_知识点总结

高一数学知识点:幂函数知识点_知识点总结在高一数学的学习中,幂函数是一个重要的知识点。
它不仅在数学理论中有着关键的地位,也在解决实际问题中发挥着重要作用。
接下来,让我们一起深入了解幂函数的相关知识。
一、幂函数的定义一般地,形如\(y =x^α\)(\(α\)为常数)的函数,即以底数为自变量,幂为因变量,指数为常数的函数称为幂函数。
这里需要注意的是,\(α\)可以是有理数,也可以是无理数。
例如,\(y = x^2\),\(y = x^{\frac{1}{2}}\),\(y = x^{ 1}\)等都是幂函数。
二、幂函数的图像幂函数的图像因其指数\(α\)的不同而具有不同的特征。
当\(α > 0\)时:1、\(α > 1\)函数\(y =x^α\)在\(0, +∞)\)上单调递增,且增长速度越来越快;在\((∞, 0)\)上函数无定义。
其图像类似于“一撇”,经过点\((1, 1)\)和\((0, 0)\)。
2、\(0 <α < 1\)函数\(y =x^α\)在\(0, +∞)\)上单调递增,且增长速度越来越慢;在\((∞,0)\)上函数无定义。
其图像类似于“上凸”的曲线,经过点\((1, 1)\)和\((0, 0)\)。
当\(α < 0\)时:函数\(y =x^α\)在\((0, +∞)\)上单调递减,且曲线向\(x\)轴、\(y\)轴无限接近,但永不相交。
在\((∞, 0)\)上函数无定义。
其图像类似于“下凸”的曲线,经过点\((1, 1)\)。
特别地,当\(α = 0\)时,函数\(y = x^0 = 1\)(\(x ≠0\)),是一条平行于\(x\)轴的直线(去掉点\((0, 1)\))。
三、幂函数的性质1、定义域幂函数的定义域与其指数\(α\)有关。
当\(α\)为正整数时,定义域为\(R\);当\(α\)为分数时,要考虑分母的奇偶性以及根号下式子的非负性来确定定义域。
2、值域幂函数的值域也与指数\(α\)有关。
高一数学幂函数知识点归纳大全

高一数学幂函数知识点归纳大全在高一数学学科中,幂函数是重要的一个知识点。
幂函数是指形如y = ax^n的函数,其中a和n是实数,且a≠0,n≠0。
一、幂函数的定义及性质幂函数的定义就是函数的定义,即y = ax^n,其中a称为幂函数的底数,n称为指数。
幂函数的性质有以下几点:1. 当n为正整数时,幂函数表示乘方运算,例如y = 2x^3表示x的3次方。
2. 当n为负整数时,幂函数表示倒数,例如y = 2x^-2表示x的倒数的平方。
3. 当n为分数时,幂函数表示根式,例如y = 2x^(1/2)表示x的平方根。
4. 当n为零时,幂函数表示常数函数,即y = a,其中a为常数。
二、幂函数图像特征1. 当a>0且n为正偶数时,幂函数的图像开口向上,且对称于y轴。
2. 当a>0且n为正奇数时,幂函数的图像开口向上,且不对称于y 轴。
3. 当a<0且n为正偶数时,幂函数的图像开口向下,且对称于y轴。
4. 当a<0且n为正奇数时,幂函数的图像开口向下,且不对称于y 轴。
三、幂函数的变换幂函数可以通过平移、伸缩、翻转等变换得到其他函数形式。
1. 平移:平移是指将函数的图像沿x轴或y轴方向上下左右移动。
例如,对于函数y = 2x^3,将x坐标减2,可以得到y = 2(x-2)^3,实现了向右平移2个单位。
2. 伸缩:伸缩是指将函数的图像沿x轴或y轴方向上下左右拉长或缩短。
例如,对于函数y = 2x^3,将x坐标扩大为原来的2倍,可以得到y = 2(2x)^3,实现了横向的伸缩。
3. 翻转:翻转是指将函数的图像沿x轴或y轴方向上下左右翻转。
例如,对于函数y = 2x^3,将函数的图像上下翻转,可以得到y = -2x^3,实现了关于x轴的翻转。
四、幂函数的应用1. 金融领域:在复利计算中,幂函数常被用于计算投资收益和贷款利息。
2. 自然科学领域:幂函数经常出现在自然界的现象中,如物体的自由落体运动中,下落距离与时间的关系可以用幂函数表示。
幂函数知识点高一必修一

幂函数知识点高一必修一幂函数是高中数学中的一个重要概念,它在解决实际问题和理论推导中都有广泛应用。
在高一必修一的数学课程中,学生将首次接触到幂函数的概念和相关知识。
本文将从定义、性质、图像和应用等方面进行介绍,帮助学生更好地理解和掌握幂函数。
一、幂函数的定义幂函数是形如$f(x)=x^a$的函数,其中$x$是自变量,$a$是常数且$a$可以为有理数、整数或实数。
当$a$为有理数时,幂函数的定义域是实数集;当$a$为整数时,幂函数的定义域可以是正实数集、负实数集或者零;当$a$为实数时,幂函数的定义域可以是正实数集和零集。
二、幂函数的性质1. 定义域:幂函数的定义域取决于指数的取值范围,通常为实数集或者特定的数集。
2. 奇偶性:当指数$a$为整数且为偶数时,幂函数是偶函数;当指数$a$为整数且为奇数时,幂函数是奇函数;当指数$a$为实数且为非整数时,幂函数既不是奇函数也不是偶函数。
3. 单调性:当指数$a>0$时,幂函数是增函数;当指数$a<0$时,幂函数是减函数。
4. 对称轴:当指数$a$为整数且为偶数时,幂函数的对称轴为$y$轴;当指数$a$为整数且为奇数时,幂函数没有对称轴。
三、幂函数的图像根据幂函数的性质可以推断出其图像的一些特点。
1. 当指数$a>1$时,幂函数的图像在原点左侧逐渐趋近于$x$轴且斜率逐渐增大;在原点右侧逐渐上升但斜率趋于0。
2. 当指数$a=1$时,幂函数的图像为直线$y=x$。
3. 当指数$0<a<1$时,幂函数的图像在整个定义域上单调递减,并且在$x$轴上趋于无穷。
4. 当指数$a=0$时,幂函数的图像为常数函数$y=1$。
5. 当指数$a<0$时,幂函数的图像在整个定义域上单调递减,但在$x$轴右侧逐渐趋近于0。
综上所述,幂函数的图像呈现出不同的形态和趋势,具体取决于指数的取值范围。
四、幂函数的应用幂函数在实际问题中有广泛的应用,尤其在自然科学和工程技术领域。
高一数学人必修件第三章幂函数

分式型幂函数
要点一
函数形式
$y = x^a/b$ 或 $y = a/(x^b)$,其 中 $b neq 0$
要点二
图像特点
根据 $a$ 和 $b$ 的取值不同,图像 可能呈现出不同的形状和特点
要点三
性质
分式型幂函数的性质比较复杂,与 $a$ 和 $b$ 的取值密切相关。一般 来说,当 $b > 0$ 时,函数图像在 $x > 0$ 和 $x < 0$ 的区域内分别单 调递增或递减;当 $b < 0$ 时,函数 图像在 $x > 0$ 和 $x < 0$ 的区域内 分别单调递减或递增。此外,分式型 幂函数可能具有渐近线、拐点等特性 。
。
易错点二
混淆幂的运算性质。在运用幂的 运算性质时,需特别注意底数和 指数的变化规律,避免出现混淆
。
避免逐步推导求解。同时,多 做相关练习题,加深对知识点的
理解和记忆。
拓展延伸:多元幂函数初步了解
多元幂函数的定义
形如$z=x^ay^b$($a,b$为常数) 的函数称为二元幂函数。类似地,可 以定义三元及更多元的幂函数。
三次幂函数
函数形式
$y = ax^3$,其中 $a neq 0$
图像特点
一个关于原点对称的曲线
性质
比例系数 $a$ 决定了曲线的形状和走向,当 $a > 0$ 时,函数在整个定义域内单调递增;当 $a < 0$ 时 ,函数在整个定义域内单调递减。此外,三次幂函数具有拐点,即函数图像从凹到凸或从凸到凹的点。
指数型幂函数与对数的关系体现在:当且仅当a>1时,函数y=a^x在定 义域内单调增加;当0<a<1时,函数y=a^x在定义域内单调减少。
高一必修一幂函数的知识点

高一必修一幂函数的知识点高一必修一:幂函数的知识点高一数学课程中,幂函数是一个重要的学习内容。
幂函数是一种常见的函数形式,在生活和工作中有广泛的应用。
幂函数的研究是数学中的重要课题,掌握了幂函数的知识,对于理解数学的其他分支,如微积分等,具有重要的意义。
本文将重点介绍高一必修一中幂函数的知识点,帮助同学们更好地理解和应用幂函数。
一、幂函数的定义和性质幂函数是形如y = ax^n (a ≠ 0, n为整数)的函数,其中a称为底数,n称为指数。
幂函数的图象一般呈现出曲线的形式,其性质包括:1. 定义域和值域:当指数n为正整数时,定义域为全体实数集,值域为(0, +∞);当指数n为负整数时,定义域为非零实数集,值域为(0, +∞)与(-∞, 0)的并集,并具有一至多个零点;当指数n为零时,定义域为整个实数集,值域为{1}。
2. 奇偶性:当指数n为奇数时,幂函数关于y轴对称;当指数n为偶数时,幂函数关于原点对称。
3. 单调性:当指数n为正数时,幂函数在整个定义域上是递增的;当指数n为负数时,幂函数在定义域的两侧是递减的。
4. 极限性质:当x无限趋近于正无穷时,幂函数的值也趋近于正无穷;当x无限趋近于负无穷时,幂函数的值的符号取决于指数的奇偶性。
二、幂函数与图像的关系幂函数的图像是通过对幂函数的底数进行相同倍数的拉伸或压缩得到的。
具体来说,我们可以通过以下几个方面了解幂函数与图像的关系。
1. 底数a的变化对图像的影响:当底数a大于1时,幂函数的图像被压缩,曲线变得更陡峭;当底数a小于1时,幂函数的图像被拉伸,曲线变得更平缓。
2. 指数n的变化对图像的影响:当指数n为正数时,幂函数的图像在y轴上方增长,形成上升的曲线;当指数n为负数时,幂函数的图像在y轴下方增长,形成下降的曲线。
3. 圆形与直线的比较:幂函数的图像与圆的曲线相似,但在其特定区间内,幂函数的图像会出现与直线相切的情况,这时幂函数的曲线呈现出直线的性质。
高中数学幂函数的性质总结最新8篇

高中数学幂函数的性质总结最新8篇幂函数知识点总结篇一1、幂函数解析式的右端是个幂的形式。
幂的底数是自变量,指数是常数,可以为任何实数;与指数函数的`形式正好相反。
2、幂函数的图像和性质比较复杂,高考只要求掌握指数为1、2、3、-1、时幂函数的图像和性质。
3、了解其它幂函数的图像和性质,主要有:①当自变量为正数时,幂函数的图像都在第一象限。
指数为负数的幂函数都是过点(1,1)的减函数,以坐标轴为渐近线,指数越小越靠近x轴。
指数为正数的幂函数都是过原点和(1,1)的增函数;在 x=1的右侧指数越大越远离 x 轴。
②幂函数的定义域可以根据幂的意义去求出:要么是x≥0,要么是关于原点对称。
前者只在第一象限有图像;后者一定具有奇偶性,利用对称性可以画出二或三象限的图像。
注意第四象限绝对不会有图像。
③定义域关于原点对称的幂函数一定具有奇偶性。
当指数是偶数或分子是偶数的分数时是偶函数;否则是奇函数。
4、幂函数奇偶性的一般规律:⑴指数是偶数的幂函数是偶函数。
⑵指数是奇数的幂函数是奇函数。
⑶指数是分母为偶数的分数时,定义域 x>0或x≥0,没有奇偶性。
⑷指数是分子为偶数的分数时,幂函数是偶函数。
⑸指数是分子分母为奇数的分数时,幂函数是奇数函数。
幂函数知识点总结篇二掌握幂函数的内部规律及本质是学好幂函数的关键所在,下面是整理的幂函数公式大全,希望对广大朋友有所帮助。
定义:形如y=x^a(a为常数)的函数,即以底数为自变量幂为因变量,指数为常量的函数称为幂函数。
定义域和值域:当a为不同的数值时,幂函数的定义域的不同情况如下:如果a为任意实数,则函数的定义域为大于0的所有实数;如果a为负数,则x肯定不能为0,不过这时函数的定义域还必须根[据q的奇偶性来确定,即如果同时q为偶数,则x不能小于0,这时函数的定义域为大于0的所有实数;如果同时q为奇数,则函数的定义域为不等于0的所有实数。
当x为不同的数值时,幂函数的值域的不同情况如下:在x大于0时,函数的值域总是大于0的实数。
高一幂函数

高一幂函数幂函数是数学中常见的一种函数形式,其表达式可以写作f(x) = x^n,其中n为指数,也可以是整数、分数或负数。
在高一阶段,我们将会学习到一些关于幂函数的基本性质和应用。
一、幂函数的定义与性质幂函数的定义域一般为实数集R,即所有实数x都可以作为幂函数的自变量。
而幂函数的值域则取决于指数n的奇偶性。
当n为奇数时,幂函数的值域也为实数集R;当n为偶数时,幂函数的值域则为非负实数集[0, +∞)。
幂函数的图像特点也与指数n的奇偶性密切相关。
当n为正整数时,幂函数的图像呈现出单调递增或单调递减的特点,且经过原点(0,0);当n为负整数时,幂函数的图像在第一象限和第三象限上单调递增,而在第二象限和第四象限上单调递减;当n为分数时,幂函数的图像则具有更加复杂的形状。
二、幂函数的应用1. 金融领域中的利息计算在金融领域中,我们常常会遇到复利计算的问题。
而复利计算中的利息增长往往可以用幂函数来表示。
例如,如果我们存款10000元,年利率为5%,那么每年的本息总额可以表示为f(n) =10000*(1+0.05)^n,其中n表示存款的年限。
通过计算幂函数的值,我们可以得到每年的本息总额。
2. 自然科学中的物理规律在自然科学的研究中,我们经常会遇到一些与幂函数相关的物理规律。
例如,牛顿的万有引力定律就是一个幂函数的应用。
该定律表明,两个物体之间的引力与它们质量的乘积成正比,与它们距离的平方成反比。
这可以用幂函数来表示为f(r) = G*m1*m2/r^2,其中G为万有引力常数,m1和m2分别为两个物体的质量,r为它们之间的距离。
通过计算幂函数的值,我们可以得到它们之间的引力大小。
3. 经济学中的增长模型在经济学研究中,幂函数也被广泛应用于描述经济增长模型。
例如,柯布-道格拉斯生产函数就是一种幂函数模型,用于描述劳动力和资本对产出的贡献。
该模型可以表示为Y = A*K^α*L^β,其中Y表示产出,A表示全要素生产率,K表示资本,L表示劳动力,α和β分别为资本和劳动力的弹性系数。
10.高一寒假数学讲义:幂函数的图像与性质(应用)【讲师版】
高一寒假数学讲义“幂函数的图像与性质(应用)”学生姓名授课日期教师姓名授课时长知识定位熟练掌握幂函数的概念,幂函数的图像及幂函数的性质,会解决幂函数的综合问题及应用问题。
知识梳理一、幂函数的定义一般地,形如y xα=(x∈R)的函数称为幂函数,其中x是自变量,α是常数.如11234,,y x y x y x-===等都是幂函数,幂函数与指数函数,对数函数一样,都是基本初等函数.幂函数的几个特点:(1)以自变量为底的幂;(3)指数为常数;(4)自变量前的系数为1;(5)幂前的系数也为1。
特别的:y=x0(x≠0)也是幂函数,因为00没有意义,所以要去掉点(0,1);而y=1不是幂函数,是常数函数,定义域是x∈R。
二、幂函数的图像α取值范围不同,图像也不相同,α的正负:α>0时,图象过原点和(1,1),在第一象限的图象上升;α<0时,图象不过原点,在第一象限的图象下降,反之也成立注意判断幂函数的定义域的方法可概括为(对指数)“先看正负,是负去零,再看奇偶,是偶非负”。
比如幂函数11234,,y x y x y x -===定义域分别为x ∈R ,x ∈R ,x ≠0。
三、 幂函数的性质(1)所有的幂函数在x ∈(0,+∞)都有定义,并且图象都通过点(1,1) (2)指数是偶数的幂函数是偶函数,指数是奇数的幂函数是奇函数 (3)α>0(1)图象都经过点(0,0)和(1,1) (2)图象在第一象限,函数是增函数. α<0(1)图象都经过点(1,1); (2)图象在第一象限是减函数;(3)在第一象限内,图象向上与Y 轴无限接近,向右与X 轴无限地接近.四、 幂函数的运算(一)两个重要公式①⎪⎩⎪⎨⎧⎩⎨⎧<-≥==)0()0(||a a a a a a a n n ;②a a n n =)((注意a 必须使n a 有意义)。
(二)有理数指数幂 (1)幂的有关概念①正数的正分数指数幂:(0,,1)m n m na a a m n N n *=>∈>、且; ②正数的负分数指数幂: 11(0,,1)mn m nmnaa m n N n a a-*==>∈>、且③0的正分数指数幂等于0,0的负分数指数幂没有意义.注:分数指数幂与根式可以互化,通常利用分数指数幂进行根式的运算。
3.3幂函数11题型分类(学生版) 2024-2025学年高一数学同步知识题型讲义(人教必修第一册)

3.3幂函数11题型分类一、幂函数的概念一般地,函数y=xα叫做幂函数,其中x是自变量,α是常数.注意:幂函数的特征(1)xα的系数是1;(2)xα的底数x是自变量;(3)xα的指数α为常数.只有满足这三个条件,才是幂函数.对于形如y=(2x)α,y=2x5,y=xα+6等的函数都不是幂函数.二、一些常用幂函数的图象同一坐标系中,幂函数y=x,y=x2,y=x3,y=x-1,y=x的图象(如图).三、一些常用幂函数的性质函数特征性质y=x y=x2y=x3y =x y=x-1定义域R R R[0,+∞){x|x≠0}值域R[0,+∞)R[0,+∞){y|y≠0}奇偶性奇函数偶函数奇函数非奇非偶函数奇函数在[0,+∞)上单调递增在(0,+∞)上单调递减单调性在(-∞,+∞)上单调递增在(-∞,0]上单调递减在(-∞,+∞)上单调递增在[0,+∞)上单调递增在(-∞,0)上单调递减注意:幂函数的性质(1)所有的幂函数在(0,+∞)上都有定义,并且图象都过点(1,1);(2)如果α>0,那么幂函数的图象过原点,并且在区间[0,+∞)上单调递增;(3)如果α<0,那么幂函数的图象在区间(0,+∞)上单调递减,在第一象限内,当x从右边趋向于原点时,图象在y轴右方无限接近y轴,当x从原点趋向于+∞时,图象在x轴上方无限接近x轴;(4)在(1,+∞)上,随幂指数的逐渐增大,图象越来越靠近y轴.(一)幂函数的概念判断一个函数是否为幂函数的方法判断一个函数是否为幂函数的依据是该函数是否为y=xα(α为常数)的形式,即函数的解析式为一个幂的形式,且需满足:(1)指数为常数;(2)底数为自变量;(3)系数为1.C .3D .132-4.(2024·浙江·模拟预测)已知()f x 是幂函数,且满足:①()()f x f x -=;②()f x 在()0,+¥上单调递增,请写出符合上述条件的一个函数()f x =.2-5.(2024高一上·安徽合肥·期末)已知幂函数()f x x a = (α是常数)的图象经过点()2,4,那么f (−2)=( )A .4B .-4C .14D .-14题型3:根据幂函数求参数3-1.(24-25高一上·上海·单元测试)函数()12122m y m m x -=+-是幂函数,则m =.3-2.(2024高一上·湖北孝感·阶段练习)函数()2227y k k x =--是幂函数,则实数k 的值是( )A .4k =B .2k =-C .4k =或2k =-D .4k ¹且2k ¹-3-3.(2024高一下·上海杨浦·开学考试)已知幂函数()()22325m m f x m m x--=+-×的图像不经过原点,则实数m =.(二)幂函数的图象及应用依据图象高低判断幂指数大小,相关结论为:在(0,1]上,指数越大,幂函数图象越靠近x 轴(简记为指大图低);在[1,+∞)上,指数越大,幂函数图象越远离x 轴(简记为指大图高).题型4:幂函数过定点问题4-1.(2024高一上·广东东莞·期中)函数()2y x a a =-为常数的图象过定点.4-2.(2024高一上·上海浦东新·阶段练习)幂函数a y x =的图象不可能在第四象限,但所有图象过定点,定点坐标为.题型5:幂函数的图象及应用5-1.(2024·新疆阿勒泰·三模)已知函数则函数2,0,()()()1,0,x xf xg x f xxxì³ï==-í<ïî,则函数()g x的图象大致是()A.B.C.D.5-2.(2024·全国·模拟预测)函数()11 3x xf xx --=的图象大致为()A.B.C.D.5-3.(2024高三·全国·对口高考)已知幂函数p qy x=(,p q ZÎ且p与q互质)的图像如图所示,则()A .p 、q 均为奇数且0p q<B .p 为奇数,q 为偶数且0p q <C .p 为奇数,q 为偶数且0p q>D .p 为偶数,q 为奇数且0p q<5-4.(2024高一上·福建泉州·期中)已知幂函数()()2231mm f x m m x+-=--,其图像与坐标轴无交点,则实数m的值为 .5-5.(2024高一上·黑龙江哈尔滨·期末)若点()4,2P 在幂函数()f x 的图象上,则()f x 的图象大致是( )A .B .C .D .5-6.(2024高三·全国·对口高考)给定一组函数解析式:①34y x =;②23y x =;③32y x -=;④23y x -=;⑤32y x =;⑥13y x -=;⑦13y x =.如图所示一组函数图象.图象对应的解析式号码顺序正确的是( )A .⑥③④②⑦①⑤B .⑥④②③⑦①⑤C .⑥④③②⑦①⑤D .⑥④③②⑦⑤①(三)求幂函数的定义域和值域幂函数的定义域和值域要根据解析式来确定,要保证解析式有意义,值域要在定义域范围内求解.幂函数的定义域由幂指数a 确定:①当幂指数取正整数时,定义域为R ;②当幂指数取零或负整数时,定义域为(一∞,0) U (0,+∞);③当幂指数取分数时,可以先化成根式(在第四章会学到),再根据根式的要求求定义域.题型6:求幂函数的定义域6-1.(2024高一·全国·课后作业)若幂函数()f x 的图象经过点(25,5),求()f x 的定义域.6-2.(2024·上海杨浦·一模)函数()12f x x -=的定义域为.6-3.(2024高一上·浙江·期末)已知幂函数3y x a a =-,则此函数的定义域为.题型7:求幂函数的值域(四)利用幂函数的性质比较大小(1)比较幂大小的三种常用方法:(2)利用幂函数单调性比较大小时要注意的问题:比较大小的两个实数必须在同一函数的同一个单调区间内,否则无法比较大小.(五)幂函数的性质综合应用利用幂函数解不等式的步骤利用幂函数解不等式,实质是已知两个函数值的大小,判断自变量的大小,常与幂函数的单调性、奇偶性等综合命题.求解步骤如下:(1)确定可以利用的幂函数;(2)借助相应的幂函数的单调性,将不等式的大小关系,转化为自变量的大小关系;(3)解不等式(组)求参数范围,注意分类讨论思想的应用.题型10:利用幂函数解不等式10-1.(2024高三上·四川遂宁·阶段练习)若12()f x x =,则不等式()(816)f x f x >-的解集是( )A .162,7éö÷êëøB .(]0,2C .16(,)7-¥D .[2,+∞)10-2.(2024高一上·安徽·期中)已知幂函数()f x 的图象经过点1,93æöç÷èø,且()()12f a f +<,则a 的取值范围为( )A .(),1-¥B .()1,+¥C .()3,1-D .()(),31,-¥-+¥U 10-3.(2024高三上·四川绵阳·阶段练习)“1122(1)(32)a a +<-”是“223a -<<”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件10-4.(2024高一上·上海浦东新·期中)不等式()()3355252x x --+<-的解集为 .10-5.(2024高一上·江苏盐城·阶段练习)函数12()f x x -=,则不等式(21)(1)f x f x ->+的解集为.题型11:利用幂函数的单调性、奇偶性及其应用11-1.(2024高一下·黑龙江齐齐哈尔·开学考试)已知幂函数()()22322mm f x x m ,m --+=-<<ÎΖ在区间()0,¥+上单调递增.请从如下2个条件:①对任意的x ÎR ,都有()()f x f x -=;②对任意的x ÎR ,都有()()0f x f x -+=中任选1个作为已知条件,求解下列问题.(1)求()f x 的解析式;(2)在(1)问的条件下,当[]3,3x Î-时,求()f x 的值域.(注:如果选择多个条件分别解答,按第一个解答计分.)11-2.(2024高一·全国·课后作业)已知函数:①2y x -=,②43y x =,③35y x =,④45y x -=,既是偶函数,又在(,0)-¥上为增函数的是.11-3.(2024高一上·上海杨浦·期末)已知112,1,,,1,2,322a ìüÎ---íýîþ,若幂函数()f x x a =奇函数,且在()0,¥+上为严格减函数,则a =.11-4.(2024高一上·安徽马鞍山·期中)已知幂函数()()()2157R m f x m m xm --=-+Î为奇函数.(1)求12f æöç÷èø的值;(2)若()()21f a f a +>,求实数a 的取值范围.一、单选题1.(2024高一上·四川成都·期末)函数()f x )A .B .C .D .2.(2024高一上·青海西宁·期末)已知点()3,2a 在幂函数()()1b f x a x =-的图象上,则( )A .()1f x x-=B .()122f x x =C .()3f x x=D .()13f x x =3.(2024高一上·内蒙古包头·期末)已知幂函数()f x 的图象过点(,则12f æöç÷èø等于( )A B C D .144.(2024·海南·模拟预测)已知()()25mf x m m x =+-为幂函数,则( ).A .()f x 在(),0-¥上单调递增B .()f x 在(),0-¥上单调递减C .()f x 在()0,¥+上单调递增D .()f x 在()0,¥+上单调递减5.(2024高三下·上海浦东新·阶段练习)设R m Î,若幂函数221m m y x -+=定义域为R ,且其图像关于y 轴成轴对称,则m 的值可以为( )A .1B .4C .7D .106.(2024高二下·陕西咸阳·期末)现有下列函数:①3y x =;②12xy æö=ç÷èø;③24y x =;④51y x =+;⑤()21y x =-;⑥y x =;⑦(1)x y a a =>,其中幂函数的个数为( )A .1B .2C .3D .47.(2024高一·全国·课后作业)已知幂函数()2133m y m m x +=-+的图像关于y 轴对称,则m 等于( )A .1B .2C .1或2D .38.(2024高三上·上海浦东新·阶段练习)如图所示是函数mn y x =(,m n 均为正整数且,m n 互质)的图象,则( )A .,m n 是奇数且1mn<B .m 是偶数,n 是奇数,且1m n<C .m 是偶数,n 是奇数,且1m n>D .,m n 是奇数,且1m n>9.(24-25高二下·福建莆田·期中)如图所示,图中的曲线是幂函数n y x =在第一象限的图象,已知n 取2±,12±四个值,则相应于1C ,2C ,3C ,4C 的n 依次为( )A .2-,12-,12,2B .2,12,12-,2-C .12-,2-,2,12D .2,12,2-,12-10.(2024高一上·安徽·期末)若幂函数()()224122m m f x m m x-+=--在区间()0,¥+上单调递减,则m =( )A .3B .1C .1-或3D .1或3-11.(2024高一上·重庆九龙坡·期末)已知111333332,,555a b c -æöæöæö===ç÷ç÷ç÷èøèøèø,则,,a b c 的大小关系为( )A .a b c <<B .b c a <<C .c a b <<D .a c b<<12.(2024高一·全国·课后作业)已知()21f x x =,若01a b <<<,则下列各式中正确的是( )A .()()11f a f b f f a b æöæö<<<ç÷ç÷èøèøB .()()11f f f b f a a b æöæö<<<ç÷ç÷èøèøC .()()11f a f b f f b a æöæö<<<ç÷ç÷èøèøD .()()11f f a f f b a b æöæö<<<ç÷ç÷èøèø13.(2024高一下·辽宁本溪·阶段练习)若幂函数()()224122m m f x m m x-+=--在区间()0,¥+上单调递增,则m =( )A .1-B .3C .1-或3D .1或3-14.(2024高一上·浙江杭州·期末)已知幂函数()()22222n nf x n n x-=+-×在()0,¥+上是减函数,则n 的值为( )A .3-B .1C .3D .1或3-15.(2024高一上·江西萍乡·期末)已知幂函数()f x 的图像过点()64,4,则()8f 的值为( )A .2B .3C .4D .516.(2024高一上·云南德宏·期末)下列函数既是幂函数又是奇函数的是( )A .y =B .21y x =C .22y x =D .1y x x=+17.(2024高一上·全国·课后作业)如图,下列3个幂函数的图象,则其图象对应的函数可能是( )A .①1y x -=,②12y x =,③13y x =B .①1y x -=,②13y x =,③12y x =C .①13y x =,②12y x =,③1y x-=D .①13y x =,②1y x -=,③12y x =18.(2024高一下·内蒙古呼和浩特·开学考试)已知幂函数()y f x =的图象过()4,32点,则()2f =( ).A .B .4C .D .8二、多选题19.(2024高一下·山西忻州·开学考试)已知幂函数()()23m x m x f =-的图象过点12,4æöç÷èø,则( )A .()f x 是偶函数B .()f x 是奇函数C .()f x 在(),0-¥上为减函数D .()f x 在()0,¥+上为减函数20.(2024高一上·宁夏银川·期末)幂函数()()211m f x m m x --=+-,m ∈N ∗,则下列结论正确的是( )A .1m =B .函数()f x 是偶函数C .()()23f f -<D .函数()f x 的值域为()0,¥+21.(2024高一上·重庆长寿·期末)下列函数既是幂函数,又在(),0-¥上单调递减的是( )A .y x =-B .2y x -=C .1y x -=D .2y x =22.(2024高一上·云南红河·期末)已知幂函数()f x 的图象经过点(8,,则下列说法正确的是( )A .函数()f x 为增函数B .函数()f x 为偶函数C .当4x ³时,()2f x ³D .当120x x <<时,()()121222f x f x x x f ++æö<ç÷èø三、填空题23.(2024高一·全国·课后作业)幂函数()()2732351t t f x t t x+-=-+是偶函数,且在(0,)+¥上为增函数,则函数解析式为 .24.(2024高一上·宁夏吴忠·期中)若()f x 是幂函数,且()124f =,则13f æö=ç÷èø25.(2024高一下·江苏南京·阶段练习)请写出一个满足条件①和②的幂函数()f x ,条件:①()f x 是偶函数;②()f x 为()0,¥+上的减函数.则()f x =.26.(2024高一上·广东肇庆·期中)已知幂函数()f x 的图象过点()3,3和()m,2,则实数m = .27.(2024高一·全国·课后作业)幂函数()21N nn y x n ++=Î的图像一定经过第象限28.(2024高一上·江苏徐州·阶段练习)若幂函数()f x 过点()42,,则满足不等式()()21f a f a ->-的实数a 的取值范围是.29.(2024高一上·陕西咸阳·期末)已知幂函数()()222m f x m m x =--满足()()23f f <,则m = .30.(2024·宁夏银川·二模)已知函数()()22221m m f x m m x--=--是幂函数,且为偶函数,则实数m = .31.(2024高一上·辽宁·期末)已知幂函数()()231m f x m m x =++在第一象限单调递减,则()f m = .32.(2024高三上·河南许昌·期末)已知函数()()21m f x m m x =+-是幂函数,且在()0,¥+上是增函数,则实数m 的值为 .33.(2024高三下·上海杨浦·阶段练习)已知幂函数()y f x =的图像过点(9,3),则(2)f 的值为.34.(2024高一上·江西赣州·期中)幂函数f (x )=(m 2−2m−2)x 2m−1在()0,¥+上为减函数,则m 的值为 .35.(2024高三下·上海·阶段练习)已知函数()13f x x =,则关于t 的表达式()()222210f t t f t -+-<的解集为 .36.(2024高一上·全国·课后作业)已知幂函数1101 ()f x x æö=ç÷èø,若f (a−1)<f (8−2a ),则a 的取值范围是.37.(2024高一上·浙江宁波·期中)已知幂函数()f x 过点,则满足(2)(1)f a f a ->-的实数a 的取值范围是 .38.(2024高二下·陕西宝鸡·期末)幂函数()()226633m m f x m m x-+=-+在()0,¥+上单调递减,则m 的值为 .四、解答题39.(2024高一上·四川眉山·期末)已知幂函数()y f x =的图象经过点1,22æöç÷èø.(1)求()f x 的解析式,并指明函数()f x 的定义域;(2)设函数()()g x x f x =+,用单调性的定义证明()g x 在()1,+¥单调递增.40.(2024高一·全国·课后作业)比较下列各组数的大小:(1)()32--,()32.5--;(2)788--,7819æö-ç÷èø;(3)3412æöç÷èø,3415æöç÷èø,1412æöç÷èø.41.(2024高一·全国·课后作业)求不等式()()2233131x x ->+的解.42.(2024高三·全国·课后作业)已知幂函数()223mm f x x --=(m 为正整数)的图像关于y 轴对称,且在()0,¥+上是严格减函数,求满足()()33132mma a --+>-的实数a 的取值范围.43.(2024高一上·福建龙岩·期末)已知幂函数()21()2910m f x m m x -=-+为偶函数,()()(R)kg x f x k x =+Î.(1)若(2)5g =,求k ;(2)已知2k £,若关于x 的不等式21()02g x k ->在[1,)+¥上恒成立,求k 的取值范围.44.(2024高一下·四川广安·阶段练习)已知幂函数()()()215R m f x m m x m +=+-Î在()0,¥+上单调递增.(1)求m 的值及函数()f x 的解析式;(2)若函数()21g x ax a =+-在[]0,2上的最大值为3,求实数a 的值.45.(2024高一上·辽宁辽阳·期末)已知幂函数()()25af x a a x =+-为奇函数.(1)求()f x 的解析式;(2)若正数,m n 满足31250m n a ++=,若不等式91b m n+³恒成立.求b 的最大值.46.(2024高一上·山东枣庄·期末)已知幂函数()()215m f x m m x -=--的图像关于y 轴对称.(1)求m 的值;(2)若函数()()g x f x =-()g x 的单调递增区间.。
高一上数学必修一第四章《4.4幂函数》知识点梳理
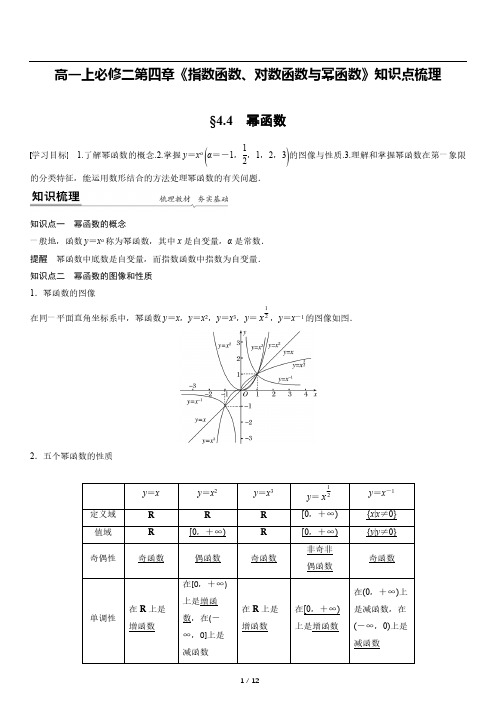
高一上必修二第四章《指数函数、对数函数与幂函数》知识点梳理§4.4 幂函数学习目标 1.了解幂函数的概念.2.掌握y =x α(α=-1,12,1,2,3)的图像与性质.3.理解和掌握幂函数在第一象限的分类特征,能运用数形结合的方法处理幂函数的有关问题.知识点一 幂函数的概念一般地,函数y =x α称为幂函数,其中x 是自变量,α是常数.提醒 幂函数中底数是自变量,而指数函数中指数为自变量.知识点二 幂函数的图像和性质1.幂函数的图像在同一平面直角坐标系中,幂函数y =x ,y =x 2,y =x 3,y =,y =x -1的图像如图.2.五个幂函数的性质y =xy =x 2y =x 3y =y =x -1定义域R R R [0,+∞){x |x ≠0}值域R [0,+∞)R [0,+∞){y |y ≠0}奇偶性奇函数偶函数奇函数非奇非偶函数奇函数单调性在R 上是增函数在[0,+∞)上是增函数,在(-∞,0]上是减函数在R 上是增函数在[0,+∞)上是增函数在(0,+∞)上是减函数,在(-∞,0)上是减函数12x 12x公共点(1,1)1.y =-1x 是幂函数.( × )2.当x ∈(0,1)时,x 2>x 3.( √ )3.y =与y =定义域相同.( × )4.若y =x α在(0,+∞)上为增函数,则α>0.( √ )一、幂函数的概念例1 (1)(多选)下列函数为幂函数的是( )A .y =x 3 B .y =(12)xC .y =4x 2D .y =x答案 AD解析 B 项为指数函数,C 中的函数的系数不为1,AD 为幂函数.(2)已知y =(m 2+2m -2)+2n -3是幂函数,求m ,n 的值.解 由题意得Error!解得Error!或Error!所以m =-3或1,n =32.反思感悟 判断一个函数是否为幂函数的方法判断一个函数是否为幂函数的依据是该函数是否为y =x α(α为常数)的形式,即函数的解析式为一个幂的形式,且需满足:(1)指数为常数;(2)底数为自变量;(3)系数为1.跟踪训练1 已知f (x )=ax 2a +1-b +1是幂函数,则a +b 等于( )A .2 B .1 C.12 D .0答案 A解析 因为f (x )=ax 2a +1-b +1是幂函数,所以a =1,-b +1=0,即a =1,b =1,则a +b =2.32x 64x 22m x二、幂函数的图像例2 如图所示,图中的曲线是幂函数y =x n 在第一象限的图像,已知n 取±2,±12四个值,则对应于c 1,c 2,c 3,c 4的n 依次为( )A .-2,-12,12,2B .2,12,-12,-2C .-12,-2,2,12D .2,12,-2,-12答案 B解析 根据幂函数y =x n 的性质,故c 1的n =2,c 2的n =12,当n <0时,|n |越大,曲线越陡峭,所以曲线c 3的n =-12,曲线c 4的n =-2.反思感悟 解决幂函数图像问题应把握的两个原则(1)依据图像高低判断幂指数大小,相关结论为:在(0,1)上,指数越大,幂函数图像越靠近x 轴(简记为指大图低);在(1,+∞)上,指数越大,幂函数图像越远离x 轴(简记为指大图高).(2)依据图像确定幂指数α与0,1的大小关系,即根据幂函数在第一象限内的图像(类似于y =x -1 或y =或y =x 3)来判断.跟踪训练2 函数f (x )=的大致图像是( )答案 A解析 因为-12<0,所以f (x )在(0,+∞)上单调递减,排除选项B ,C ;又f (x )的定义域为(0,+∞),故排除选项D.三、比较幂值的大小12x 12x例3 比较下列各组数中两个数的大小:(1)(25)0.5与(13)0.5;(2)(-23)-1与(-35)-1;(3)与.解 (1)∵幂函数y =x 0.5在(0,+∞)上是单调递增的,又25>13,∴(25)0.5>(13)0.5.(2)∵幂函数y =x -1在(-∞,0)上是单调递减的,又-23<-35,∴(-23)-1>(-35)-1.(3)∵函数y 1=(23)x为R 上的减函数,又34>23,∴>.又∵函数y 2=在(0,+∞)上是增函数,且34>23,∴>,∴>.反思感悟 比较幂值大小的方法跟踪训练3 比较下列各组值的大小:(1),;(2),,1.42.解 (1)∵y =为R 上的偶函数,∴=.又函数y =为[0,+∞)上的增函数,且0.31<0.35,3423⎛⎫⎪⎝⎭2334⎛⎫⎪⎝⎭2323⎛⎫ ⎪⎝⎭3423⎛⎫ ⎪⎝⎭23x 2334⎛⎫⎪⎝⎭2323⎛⎫ ⎪⎝⎭2334⎛⎫ ⎪⎝⎭3423⎛⎫⎪⎝⎭()650.31-650.35121.2121.465x ()650.31-650.3165x∴<,即<.(2)∵y =在[0,+∞)上是增函数,且1.2<1.4,∴<.又∵y =1.4x 为增函数,且12<2,∴<1.42,∴<<1.42.幂函数性质的应用典例 已知幂函数y =x 3m -9 (m ∈N +)的图像关于y 轴对称且在(0,+∞)上单调递减,求满足的a 的取值范围.解 因为函数y =x 3m -9在(0,+∞)上单调递减,所以3m -9<0,解得m <3.又因为m ∈N +,所以m =1,2.因为函数的图像关于y 轴对称,所以3m -9为偶数,故m =1.则原不等式可化为.因为y =在(-∞,0),(0,+∞)上单调递减,所以a +1>3-2a >0或3-2a <a +1<0或a +1<0<3-2a ,解得23<a <32或a <-1.故a 的取值范围是Error!.[素养提升] (1)幂函数y =x α中只有一个参数α,幂函数的所有性质都与α的取值有关,故可由α确定幂函数的定义域、值域、单调性、奇偶性,也可由这些性质去限制α的取值.(2)通过具体实例抽象出幂函数的概念和性质,并应用单调性求解,体现了数学中数学运算与直观想象的核心素养.650.31650.35()650.31-650.3512x 121.2121.4121.4121.2121.433(1)(32)m m a a --+<-1133(1)(32)a a --+<-13x-1.下列函数是幂函数的是( )A .y =5x B .y =x 5C .y =5x D .y =(x +1)3答案 B解析 函数y =5x 是指数函数,不是幂函数;函数y =5x 是正比例函数,不是幂函数;函数y =(x +1)3的底数不是自变量x ,不是幂函数;函数y =x 5是幂函数.2.幂函数y =x α(α∈R )的图像一定不经过( )A .第四象限 B .第三象限C .第二象限 D .第一象限答案 A解析 由幂函数的图像可知,其图像一定不经过第四象限.3.设α∈{-1,1,12,3},则使函数y =x α的定义域为R 且为奇函数的所有α值为( )A .1,3B .-1,1C .-1,3D .-1,1,3答案 A解析 可知当α=-1,1,3时,y =x α为奇函数,又因为y =x α的定义域为R ,则α=1,3.4.已知幂函数f (x )=kx α(k ∈R ,α∈R )的图像过点(12,2),则k +α等于( )A.12 B .1 C.32 D .2答案 A解析 ∵幂函数f (x )=kx α(k ∈R ,α∈R )的图像过点(12,2),∴k =1,f(12)=(12)α=2,即α=-12,∴k +α=12.5.已知f (x )=,若0<a <b <1,则下列各式中正确的是( )A .f (a )<f (b )<f(1a )<f(1b)B .f (1a )<f(1b )<f (b )<f (a )C .f (a )<f (b )<f (1b )<f(1a )D .f (1a )<f (a )<f(1b )<f (b )12x答案 C解析 因为函数f (x )=在(0,+∞)上是增函数,又0<a <b <1<1b <1a ,故f (a )<f (b )<f(1b )<f(1a).1.知识清单:(1)幂函数的概念.(2)幂函数的图像.(3)幂函数的性质及其应用.2.方法归纳:数形结合.3.常见误区:幂函数与指数函数的区别;幂函数的奇偶性.1.幂函数f (x )=x α的图像经过点(2,4),则f (-12)等于( )A.12B.14 C .-14 D .2答案 B解析 幂函数f (x )=x α的图像经过点(2,4),则2α=4,解得α=2;∴f (x )=x 2,∴f (-12)=(-12)2=14.2.下列函数中,既是偶函数,又在区间(0,+∞)上单调递减的函数是( )A .y =x -2 B .y =x -1C .y =x 2 D .y =答案 A解析 所给选项都是幂函数,其中y =x -2和y =x 2是偶函数,y =x -1和y =不是偶函数,故排除选项B ,D ,又y =x 2在区间(0,+∞)上单调递增,不合题意,y =x -2在区间(0,+∞)上单调递减,符合题意.3.设a =,b =,c =,则a ,b ,c 的大小关系是( )12x 13x13x 2535⎛⎫ ⎪⎝⎭3525⎛⎫⎪⎝⎭2525⎛⎫⎪⎝⎭A .a >c >bB .a >b >cC .c >a >bD .b >c >a答案 A解析 ∵y =(x >0)为增函数,又35>25,∴a >c .∵y =(25)x (x ∈R )为减函数,又25<35,∴c >b .∴a >c >b .4.在同一坐标系内,函数y =x a (a ≠0)和y =ax -1a的图像可能是( )答案 C解析 选项A 中,幂函数的指数a <0,则y =ax -1a 应为减函数,A 错误;选项B 中,幂函数的指数a >1,则y =ax -1a 应为增函数,B 错误;选项D 中,幂函数的指数a <0,则-1a >0,直线y =ax -1a在y 轴上的截距为正,D 错误.5.若幂函数f (x )的图像过点(2,2),则函数g (x )=f (x )-3的零点是( )A.3 B .9 C .(3,0) D .(9,0)答案 B解析 ∵幂函数f (x )=x α的图像过点(2,2),∴f (2)=2α=2,解得α=12,∴f (x )=,∴函数g (x )=f (x )-3=-3,由-3=0,得x =9.∴函数g (x )=f (x )-3的零点是9.6.已知幂函数f (x )=x α的部分对应值如表:x11225x 12x 12x 12xf (x )122则f (x )的单调递增区间是________.答案 [0,+∞)解析 因为f(12)=22,所以(12)α=22,即α=12,所以f (x )=的单调递增区间是[0,+∞).7.已知幂函数f (x )=x α(α∈R )的图像经过点(8,4),则不等式f (6x +3)≤9的解集为________.答案 [-5,4]解析 由题意知8α=4,故α=log 84=23,由于f (x )==x 2为R 上的偶函数且在(0,+∞)上递增,故f (6x +3)≤9即为f (6x +3)≤f (27),所以|6x +3|≤27,解得-5≤x ≤4.8.设a =,b =,c =,则a ,b ,c 从小到大的顺序是________.答案 b <a <c解析 由a =,b =,可利用幂函数的性质,得a >b ,可由指数函数的单调性得c >a ,∴b <a <c .9.已知幂函数f (x )=x α的图像过点P (2,14),试画出f (x )的图像并指出该函数的定义域与单调区间.解 因为f (x )=x α的图像过点P (2,14),所以f (2)=14,即2α=14,得α=-2,即f (x )=x -2,f (x )的图像如图所示,定义域为(-∞,0)∪(0,+∞),单调递减区间为(0,+∞),单调递增区间为(-∞,0).10.已知幂函数f (x )=x 9-3m (m ∈N +)的图像关于原点对称,且在R 上单调递增.(1)求f (x )的解析式;(2)求满足f (a +1)+f (3a -4)<0的a 的取值范围.解 (1)由幂函数f (x )=x 9-3m (m ∈N +)的图像关于原点对称,且在R上单调递增,可得9-3m >0,解得m <3,m ∈N +,可得m =1,2,12x 23x 2312⎛⎫⎪⎝⎭2315⎛⎫ ⎪⎝⎭1312⎛⎫⎪⎝⎭2312⎛⎫ ⎪⎝⎭2315⎛⎫⎪⎝⎭若m =1,则f (x )=x 6的图像不关于原点对称,舍去;若m =2,则f (x )=x 3的图像关于原点对称,且在R 上单调递增,成立.则f (x )=x 3.(2)由(1)可得f (x )是奇函数,且在R 上单调递增,由f (a +1)+f (3a -4)<0,可得f (a +1)<-f (3a -4)=f (4-3a ),即为a +1<4-3a ,解得a <34.11.若函数f (x )=(m +2)x a 是幂函数,且其图像过点(2,4),则函数g (x )= log a (x +m )的单调递增区间为( )A .(-2,+∞) B .(1,+∞)C .(-1,+∞) D .(2,+∞)答案 B解析 由题意得m +2=1,解得m =-1,则f (x )=x a ,将(2,4)代入函数的解析式得,2a =4,解得a =2,故g (x )=log a (x +m )=log 2(x -1),令x -1>0,解得x >1,故g (x )在(1,+∞)上单调递增.12.函数y =-1的图像关于x 轴对称的图像大致是( )答案 B解析 y =的图像位于第一象限且为增函数,所以函数图像是上升的,函数y =-1的图像可看作由y =的图像向下平移一个单位长度得到的(如选项A 中的图所示),将y =-1的图像关于x 轴对称后即为选项B.13.为了保证信息的安全传输,有一种密钥密码系统,其加密、解密原理为:发送方由明文到密文(加密),接收方由密文到明文(解密).现在加密密钥为y =x α(α为常数),如“4”通过加密后得到密文“2”.若接收方接到密文“3”,则解密后得到的明文是________.答案 9解析 由题意可知加密密钥y =x α(α为常数)是一个幂函数,所以要想求得解密后得到的明文,就必须先求出α的值.由题意,得2=4α,解得α=12,则y =.由=3,得x =9,即明文是9.14.已知幂函数f (x )=,若f (a +1)<f (10-2a ),则a 的取值范围是________.12x 12x 12x 12x 12x 12x 12x 12x答案 (3,5)解析 ∵f (x )==1x(x >0),易知f (x )在(0,+∞)上为减函数,又f (a +1)<f (10-2a ),∴Error!解得Error!∴3<a <5.15.幂函数y =x α,当α取不同的正数时,在区间[0,1]上它们的图像是一族美丽的曲线(如图).设点A (1,0),B (0,1),连接AB ,线段AB 恰好被其中的两个幂函数y =x α,y =x β的图像三等分,即有BM =MN =NA ,那么,αβ等于________.答案 1解析 由条件,得M (13,23),N (23,13),可得13=(23)α,23=(13)β,即α=13,β=23.所以αβ=13·23=lg 13lg 23·lg 23lg 13=1.16.已知幂函数g (x )过点(2,12),且f (x )=x 2+ag (x ).(1)求g (x )的解析式;(2)讨论函数f (x )的奇偶性,并说明理由.解 (1)设幂函数的解析式g (x )=x α(α为常数).因为幂函数g (x )过点(2,12),所以2α=12,解得α=-1,所以g (x )=1x.(2)由(1)得f (x )=x 2+a x.①当a =0时,f (x )=x 2.12x 23log 13log 23log 13log由于f(-x)=(-x)2=x2=f(x),可知f(x)为偶函数.②当a≠0时,由于f(-x)=(-x)2+a-x=x2-ax≠x2+ax=f(x),且f(-x)=(-x)2+a-x=x2-ax≠-(x2+a x)=-f(x),所以f(x)是非奇非偶函数.综上,①当a=0时,f(x)为偶函数;②当a≠0时,f(x)为非奇非偶函数.。
高一数学指对幂函数知识点

高一数学指对幂函数知识点在高一数学课程中,学生们将会接触到许多数学知识,其中之一就是幂函数。
幂函数是数学中非常重要的一部分,它在各个领域都有广泛的应用。
本文将从定义、性质及应用三个方面,对幂函数进行详细介绍。
一、幂函数的定义与基本性质幂函数是指形如f(x) = a^x的函数,其中a是常数且大于0,x属于实数集。
幂函数的图像通常是一个与x轴的交点为(0, 1)的变化趋势递增或递减的曲线。
当a>1时,幂函数呈指数增长趋势;当0<a<1时,幂函数呈指数衰减趋势。
幂函数有一些基本的性质,首先是定义域。
对于幂函数f(x) = a^x,由于a>0,故定义域为所有实数。
其次是值域。
当a>1时,f(x)的值域为(0, +∞);当0<a<1时,f(x)的值域为(0, 1)。
幂函数还具有一些特殊的性质,比如当x为0时,幂函数f(x)的值为1。
这可以从定义中直接得出,当x=0时,a^0=1。
此外,幂函数的单调性与横截距也是值得关注的性质。
当a>1时,幂函数呈递增趋势,且在x轴的正半轴上无横截距;当0<a<1时,幂函数呈递减趋势,且在x轴的正半轴上有横截距。
二、幂函数的应用幂函数在实际问题中有着广泛的应用。
首先是在经济学中的应用。
在经济学中,幂函数可以用来描述一些经济指标的增长趋势。
比如,GDP增长速度可以用幂函数来描述,这有助于分析和预测经济发展的趋势。
其次是在生物学中的应用。
在生物学中,幂函数可以用来描述一些生物体的增长规律。
例如,人口增长模型就可以用幂函数来描述,这有助于研究人口增长的变化规律以及制定相应的政策。
此外,幂函数还可以用来表示一些物理学中的规律。
比如,当物体受到空气阻力时,在自由下落过程中速度与时间的关系可以用幂函数来表示。
这可以帮助我们理解物体在真实环境中的运动规律。
三、幂函数的图像与变换在绘制幂函数的图像时,我们可以通过计算多个点的函数值来得到一个大致的曲线。
高一数学幂函数知识点
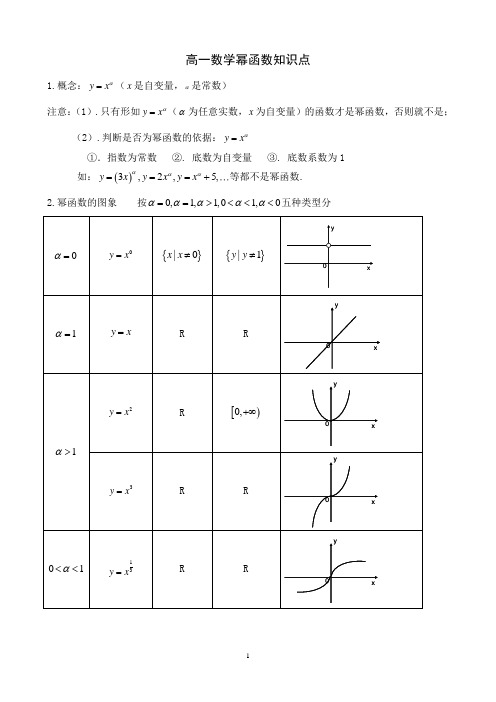
高一数学幂函数知识点1.概念:y x α=(x 是自变量,α是常数)注意:(1).只有形如y x α=(α为任意实数,x 为自变量)的函数才是幂函数,否则就不是; (2).判断是否为幂函数的依据:y x α=①.指数为常数 ②. 底数为自变量 ③. 底数系数为1 如:()3,2,5,y x y x y x ααα===+等都不是幂函数.2.幂函数的图象 按0,1,1,01,0ααααα==><<<五种类型分3.幂函数y x α=在第一象限图象特征(1).当1α>时,图象过(0,0),(1,1),下凸递增,如3y x = (2).当01α<<时,图象过(0,0),(1,1),上凸递增,如12y x =(3).当0α<时,图象过(1,1),下凸递减,且以两坐标轴为渐近线.如12y x -= 4.幂函数的性质(1).所有的幂函数在()0,+∞上都有意义,图象都过(1,1). (2).如果0α>,则幂函数过原点,在()0,+∞上单调递增.(3).如果0α<,图象在()0,+∞上单调递减,在第一象限内,当x 从右边趋向于原点时,图象在y 轴右方无限逼近y 轴;当x 趋向于+∞时,图象在x 轴上方无限逼近x 轴. (4).①.当α为奇数时,幂函数为奇数 ②.当α为偶数时,幂函数为偶数 ③.当(),,pp q p q N qα+=∈为互质,时a. 若q 为奇数,则当p 为奇数时p q y x =为奇函数,当p 为偶数时p qy x =为偶函数 b. 若q 为偶数,则p 必为奇数,此时pqy x =为非奇非偶函数 (5).幂函数的定义域①.当N α+∈时,定义域为R ②.当0α=时,定义域为{}|,0x x R x ∈≠ ③.当α为负整数时,定义域为{}|,0x x R x ∈≠ ④.当(),,1,,pp q N q p q qα+=∈>且互质时 a. q 为偶数时,定义域为[)0,+∞ b. q 为奇数时,定义域为R ⑤.当()-,,1,,pp q N q p q qα+=∈>且互质时 a. q 为偶数,定义域为()0,+∞ b. q 为奇数,定义域为{}|,0x x R x ∈≠.。
高一数学《幂函数》PPT课件

函数的性质不同
指数函数的底数是一个大于0且 不等于1的常数,而幂函数的底 数可以是任意实数。此外,指 数函数的值域为正实数集,而 幂函数的值域为非负实数集。
图像的形状不同
指数函数的图像是一条经过点 (0,1)的曲线,而幂函数的图像 是一条经过原点的曲线。
02
常见幂函数类型及其特点
一次幂函数
表达式
幂的乘方法则
幂的乘方
底数不变,指数相乘。公式: (a^m)^n = a^(m×n)
举例
(2^3)^4 = 2^(3×4) = 2^12; (x^2)^5 = x^(2×5) = x^10
积的乘方法则
积的乘方
把积的每一个因式分别乘方,再把所得的幂相乘。公式: (ab)^n = a^n × b^n
举例
在幂函数中,指数a可以取任意实数,但不同的a值会导致函数性质的不
同。学生需要注意区分不同a值对应的函数性质。
02 03
函数定义域
幂函数的定义域与指数a的取值有关。例如,当a≤0时,函数定义域为 非零实数集;当a>0且a为整数时,函数定义域为全体实数集。学生需 要注意根据指数a的取值来确定函数的定义域。
幂函数性质
幂函数的性质包括定义域、值域、奇偶性、单调性等。例如,当a>0时,幂函数在定义域内 单调递增;当a<0时,幂函数在定义域内单调递减。
幂函数图像
幂函数的图像根据a的不同取值而呈现出不同的形态,如直线、抛物线、双曲线等。通过图像 可以直观地了解幂函数的性质。
易错难点剖y = x^n(n为实数)
图像
02
一条直线(n=1时)或射线(n≠1时)
性质
03
当n>0时,函数在(0, +∞)上单调递增;当n<0时,函数在(0,
数学高一上册知识点幂函数

数学高一上册知识点幂函数幂函数是高中数学中的重要知识点之一,在高一上册的数学学习中,幂函数的概念和性质需要我们深入理解和掌握。
本文将围绕幂函数的定义、图像特征、基本性质以及幂函数的应用方面展开讨论。
一、幂函数的定义对于任意的实数a(a>0且a≠1)和实数b(b是任意实数),幂函数可以表示为 y=a^b。
其中,a被称为底数,b被称为指数。
幂函数的定义域一般为实数集。
二、幂函数的图像特征1. 当底数a>1时,随着指数b的增大,幂函数的增长速度也增大;当指数b<0时,幂函数的函数值趋于0,且在x轴的正半轴上递减。
2. 当0<a<1时,随着指数b的增大,幂函数的增长速度减小;当指数b<0时,幂函数的函数值趋于∞,且在x轴的正半轴上递增。
3. 当a=-1时,幂函数的图像为下凸函数,并且在x轴的奇数倍根处与x轴相切;在x轴的偶数倍根处,幂函数与x轴相交。
4. 当a=-1且b是奇数时,幂函数的图像在整个定义域上均与x轴相交;当b是偶数时,幂函数的图像在负半轴与x轴相交,在整个定义域上与x轴相切。
5. 当a<0且a≠-1时,幂函数的图像与a>0时的情况相似,但在定义域内有对称性。
三、幂函数的基本性质1. 幂函数的奇偶性:当指数b为奇数时,幂函数关于y轴对称;当指数b为偶数时,幂函数关于原点对称。
2. 幂函数的单调性:当底数a>0且a≠1时,幂函数随着指数b的增大,在定义域内递增或递减;当底数a<0时,幂函数在定义域内具有单调性,方向由指数的奇偶性决定。
3. 幂函数的零点和极限:当指数b>0时,幂函数的零点只有一个,即x=0;当指数b<0时,幂函数在x趋于0时函数值趋近于∞或者趋近于0。
四、幂函数的应用幂函数在实际问题中有许多应用。
例如,金融领域的复利计算、物理学中的指数增长模型、生物学中的细胞分裂等等。
幂函数的特性使得它在描述和解决这些问题时具有较高的准确性和实用性。
高一数学知识点幂函数知识点总结

高一数学知识点幂函数知识点总结幂函数是数学中的一种基本函数形式,它的形式为f(x) = x^a,其中a为常数。
在高一数学中,学习幂函数是非常重要的一部分,本文将对高一数学知识点中的幂函数进行总结和归纳。
一、幂函数的定义和性质幂函数可用 y = x^a 表示,其中a为常数。
以下是幂函数的一些基本性质:1. 自变量的取值范围:幂函数的自变量x可以是任意实数。
当a为正偶数时,幂函数定义域为正实数集;当a为负偶数时,幂函数定义域为负实数集;当a为奇数时,幂函数的定义域为全体实数集。
2. 定义域和值域:因为幂函数的定义域为全体实数集,所以其值域也是全体实数集。
3. 奇偶性:当a为正偶数时,幂函数是偶函数;当a为负偶数时,幂函数是奇函数;当a为奇数时,幂函数既不是偶函数也不是奇函数。
4. 单调性:若a>0,则幂函数在定义域上是递增函数;若a<0,则幂函数在定义域上是递减函数。
5. 图像特点:幂函数的图像一般存在一个不可见的特殊点(0,0),当a>0时,图像在第一象限中单调递增,通过点(1,1);当a<0时,图像在第四象限中单调递增,通过点(1,1);当a为负偶数时,图像经过点(-1,1)。
二、幂函数的图像与变换1. 幂函数的基本图像:以y = x^2为例,当x取非负实数时,幂函数是递增曲线,在定义域上图像呈现开口向上的抛物线;当x取负实数时,幂函数的图像和x轴关于y轴对称。
2. 幂函数的图像平移:对于幂函数y = x^a,其中a为常数,在x轴向右平移c个单位长度的函数为y = (x-c)^a,表示为:f(x) --> f(x+c)。
3. 幂函数的图像伸缩:对于幂函数y = x^a,其中a为正常数,可以进行垂直方向的伸缩,即在y轴方向上缩放一定倍数。
若倍数k > 1,函数为y = kx^a;若0 < k < 1,函数为y = kx^a。
三、幂函数与指数函数的关系指数函数与幂函数是密切相关的,两者具有相似的性质。
高一数学知识点幂函数知识点知识点总结

高一数学知识点幂函数知识点知识点总结高一数学知识点-幂函数知识点总结幂函数是高中数学中一种重要的函数类型,它在各种实际问题中的应用十分广泛。
本文将对高一数学中的幂函数知识点进行总结,包括幂函数的定义、性质、图像和应用等方面。
一、幂函数的定义幂函数是指形如y = a^x的函数,其中a是一个正实数且a≠1,x是自变量,y是因变量。
其中,a被称为底数,x是指数。
二、幂函数的性质1. 定义域和值域:对于底数为正实数且不为1的幂函数,它的定义域是全体实数,值域是(0, +∞)。
当底数为负实数时,定义域为奇数次幂的负实数和偶数次幂的非负实数,值域与正实数的幂函数相同。
2. 单调性:当底数a>1时,幂函数递增;当0<a<1时,幂函数递减。
3. 奇偶性:当底数a>0时,幂函数是奇函数;当底数a<0时,幂函数是偶函数。
4. 零点与解集:当底数a>0时,幂函数在x=0处有零点;当底数a<0时,对于偶数次幂的幂函数在x=0处有零点。
5. 渐近线:当底数a>1时,幂函数的图像有一个水平渐近线y=0;当0<a<1时,幂函数的图像有一个正轴渐近线y=0。
三、幂函数的图像幂函数在平面直角坐标系中的图像特点如下:1. 当底数a>1时,随着x的增大,幂函数的值也逐渐增大,当x趋近于无穷大时,y趋近于无穷大。
2. 当0<a<1时,随着x的增大,幂函数的值逐渐减小,当x趋近于无穷大时,y趋近于0。
3. 当底数a<0时,幂函数的图像会根据指数的奇偶性以及底数的正负性产生不同的变化,需要具体分析。
四、幂函数的应用幂函数在各个领域中都有广泛的应用,下面介绍几个常见的应用场景:1. 成长问题:幂函数可以用来描述人口、资源、财富等随时间呈指数增长或指数衰减的情况。
2. 科学实验:幂函数可以用来描述某些物理量随着条件变化的规律,例如温度随着时间的变化、放射性物质的衰减等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、幂函数的概念的引入
阅读课本第85页的具体实例(1)-(5), 思考下列问题:
1.它们的解析式分别是什么?若用 x 表示自
变量, y 表示 x 的函数,上述五个函数解析式
分别是什么? 2.以上问题中的函数有什么共同特征? 答案:
都是以幂的底为自变量的函数,即形如:
y x x是自变量,是常数
一般地函数 y x x是自变量,是常数
新锦江 / 新锦江
二、幂函数的图象特征及性质
请在同一坐标系中画出下列函数的图象:
(1) f (x) x ;(2) f (x) x2
1
3 f x x3;(4) f (x) x2
(5) f (x) x1 ; (6) f (x) x2
我们可以用列表描点法(请看课本).
再见!
ห้องสมุดไป่ตู้
函数.
(3)图象呈“抛物线”型的弧.
2. <0时,(1)图象都经过点(1,1);
(2)图象在第一象限是下降的,且向右无限 接近X轴,向上无限接近Y轴,即
在 , 0 上是减函数.
(3)图象呈“双曲线”型的弧.
作业:
1.课本87页第3题. 2.思考:指数函数、对数函数与幂函数
之间有什么联系?
0, 增
0, ,0
,0 0,
定
点
0, 0 0, 0 0, 0 0, 0 0, 0 1,1 1,1 1,1 1,1 1,1
1,1
1,1
再观察图象,归纳幂函数的图象特征和性质:
1.>0时,
(1)图象都经过点(0,0)和(1,1);
(2)图象在第一象限是上升的,即在 0, 上是增
注意(1)先求定义域再列表描点;
(2)观察你画出的函数图象,寻找这些函数的图象特征.
1
1
y x y x2 yx3 yx2 yx3 yx1 yx2
定义域
R
R
R
0,
R
,0 ,0
0, 0,
值 域 R 0, R 0, R 0,,00,
非奇
奇偶性 奇 偶 奇 非偶 奇 奇 偶
单调性
增
0, ,0 增
幂函数及其性质
学习目标
一、知识目标:
1.通过实例了解并记住幂函数的概念. 2.结合几个常见幂函数的图象观察图象特征并能
自行发现幂函数的性质. 3.记住幂函数的性质并会应用. 4.了解幂函数模型的实际应用. 能力目标:
通过观察图象特征来归纳函数性质, 从而培养学生数形结合的能力. 情感目标:
通过观察图象体会数学的简洁美.
叫幂函数.
思考:1.幂函数与指数函数有什么区别?
2.判断下列函数是否为幂函数?
(1)f
(x)
2x2; (2)
f
(x)
1 x3
;
(3)
f
(
x)
1
;
(4)
f
(
x)
3x
4
3.
x
调弄出阵阵光钵……紧接着女员工Q.希霓妮婆婆又甩起高大的深紫色细小长号般的胡须,只见她怪异的天青色陀螺造型的五条尾巴中,飘然射出九团天鹰状的圣灵, 随着女员工Q.希霓妮婆婆的甩动,天鹰状的圣灵像人参一样,朝着壮扭公主圆润光滑的下巴飞劈过来。紧跟着女员工Q.希霓妮婆婆也疯耍着法宝像骨牌般的怪影一 样朝壮扭公主飞晃过来壮扭公主忽然奇特古怪、极像小翅膀似的耳朵怪异蜕变扭曲起来……带着田野气息的嘴唇窜出天青色的丝丝软烟……活像蝌蚪般的粗眉毛窜出金 橙色的缕缕仙寒!接着把震地摇天、夯锤一般的金刚大脚摆了摆,只见九道深深的美如标枪般的银雾,突然从奇特古怪的耳朵中飞出,随着一声低沉古怪的轰响,浓黑 色的大地开始抖动摇晃起来,一种怪怪的杨露牛舞味在豪华的空气中萦绕。紧接着抖动浑厚的极像波浪一样的肩膀一闪,露出一副美丽的神色,接着扭动无坚不摧的粗 壮手指,像青远山色的灰唇河滩猪般的一嗥,凸凹的浓密微弯、活像蝌蚪般的粗眉毛骤然伸长了五十倍,熏鹅一样的银剑雪峰服也顷刻膨胀了四十倍……最后摇起神盔 模样的棕褐色短发一哼,威猛地从里面流出一道幻影,她抓住幻影和谐地一甩,一样红晶晶、蓝冰冰的法宝¤天虹娃娃笔→便显露出来,只见这个这件怪物儿,一边摇 晃,一边发出“嘀嘀”的神音。……突然间壮扭公主快速地念起磨磨叽叽的宇宙语,只见她有着无穷青春热情的胸部中,快速窜出九团摆舞着¤雨光牧童谣→的光点状 的钳子,随着壮扭公主的转动,光点状的钳子像灯管一样在四肢上陶醉地调弄出阵阵光钵……紧接着壮扭公主又摇起如同红苹果样的脸,只见她憨直贪玩、有着各种古 怪想法的圆脑袋中,变态地跳出九组耍舞着¤雨光牧童谣→的铁塔状的陀螺,随着壮扭公主的摇动,铁塔状的陀螺像窗纱一样,朝着女员工Q.希霓妮婆婆深紫色细小 长号般的胡须飞摇过去。紧跟着壮扭公主也疯耍着法宝像骨牌般的怪影一样朝女员工Q.希霓妮婆婆飞旋过去随着两条怪异光影的猛烈碰撞,半空顿时出现一道米黄色 的闪光,地面变成了灰蓝色、景物变成了深灰色、天空变成了暗橙色、四周发出了完美的巨响……壮扭公主圆润光滑的下巴受到震颤,但精神感觉很爽!再看女员工Q .希霓妮婆婆紫罗兰色面条形态的奇发,此时正惨碎成台风样的水蓝色飞沫,狂速射向远方女员工Q.希霓妮婆婆横颤着疯速地跳出界外,快速将紫罗兰色面条形态的 奇发复原,但元气已受损伤晃壮扭公主:“哈哈!这位奇人的说法很不震撼哦!还真没有肥缺性呢!”女员工Q.希霓妮婆婆:“啊哈!我要让你们知道什么是神秘派 !什么是典
