第三章 指数函数和对数函数 复习课件
合集下载
《指数函数》指数函数与对数函数PPT演示课件

过一个虚拟的人进行洗钱,当然,这一切只有他一个人知道。在监狱中,他因为冒死替狱友争取到了啤酒,从而赢得了狱友们的尊重
和友谊,从那些无所不能的狱友们弄到一把铁捶和一张明星的海报。一年又一年的监狱生活,带走了
对他来说,简直就是希望和救星,他找到监狱长,救他,说这是他可以翻案的机会,只要找到那名犯人,再加上他的学生做证,他就
讨论:
1
1
(1)如果 a<0,如 y=(-4)x,这时对于 x=4,x=2等,在实数范围内函数值
不存在;
(2)如果 a=0,
当 > 0 时, 恒等于 0,
当 ≤ 0 时, 无意义;
(3)如果a=1,y=1x=1,是个常数函数,没有研究的必要;
(4)如果0<a<1或a>1,即a>0且a≠1,x可以是任意实数.
指数函数与对数函数
4.2 指数函数
-1-
首页
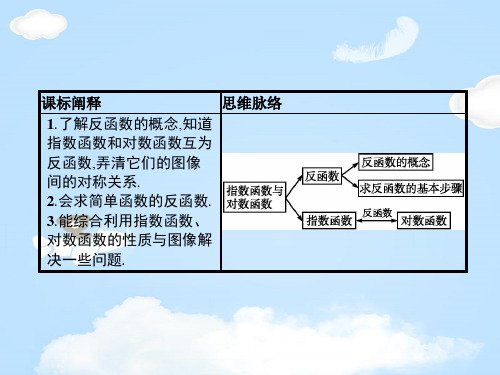
课标阐释
思维脉络
1.理解指数函数的概念和意义,
能画出具体指数函数的图象.
2.初步掌握指数函数的性质,并
能解决与指数函数有关的定义
域、值域、定点问题.
3.逐步体会指数函数在实际问
题中的应用.
课前篇
自主预习
整部片子比较压抑,可能因为是讲述在监狱里发生的事情吧,但看完后心情却久久不能平静,那样的荡气回肠,那样的震憾人心!一
一
二
个年轻有为的银行家安迪,因为与妻子发生口角气跑了妻子,而当天妻子与她的情人双双被枪杀在床上,他成为最有杀人动机的嫌疑
犯,加上口吐莲花的律师,就这样,一个年轻有为的银行家被送了肖申克监狱。在监狱里发生了许多的事情,先是被老犯人们打赌,
第一晚谁会扛不住最先哭泣,最有权威的老犯人阿瑞看他白白净净,瘦瘦弱弱的样子,押了他两盒烟的赌注,第一次就让阿瑞输了赌
和友谊,从那些无所不能的狱友们弄到一把铁捶和一张明星的海报。一年又一年的监狱生活,带走了
对他来说,简直就是希望和救星,他找到监狱长,救他,说这是他可以翻案的机会,只要找到那名犯人,再加上他的学生做证,他就
讨论:
1
1
(1)如果 a<0,如 y=(-4)x,这时对于 x=4,x=2等,在实数范围内函数值
不存在;
(2)如果 a=0,
当 > 0 时, 恒等于 0,
当 ≤ 0 时, 无意义;
(3)如果a=1,y=1x=1,是个常数函数,没有研究的必要;
(4)如果0<a<1或a>1,即a>0且a≠1,x可以是任意实数.
指数函数与对数函数
4.2 指数函数
-1-
首页
课标阐释
思维脉络
1.理解指数函数的概念和意义,
能画出具体指数函数的图象.
2.初步掌握指数函数的性质,并
能解决与指数函数有关的定义
域、值域、定点问题.
3.逐步体会指数函数在实际问
题中的应用.
课前篇
自主预习
整部片子比较压抑,可能因为是讲述在监狱里发生的事情吧,但看完后心情却久久不能平静,那样的荡气回肠,那样的震憾人心!一
一
二
个年轻有为的银行家安迪,因为与妻子发生口角气跑了妻子,而当天妻子与她的情人双双被枪杀在床上,他成为最有杀人动机的嫌疑
犯,加上口吐莲花的律师,就这样,一个年轻有为的银行家被送了肖申克监狱。在监狱里发生了许多的事情,先是被老犯人们打赌,
第一晚谁会扛不住最先哭泣,最有权威的老犯人阿瑞看他白白净净,瘦瘦弱弱的样子,押了他两盒烟的赌注,第一次就让阿瑞输了赌
指数函数与对数函数课件—高三数学一复习

logab
相关结论:logab= 1 ;logab·logbc·logcd=logad (a,b,c均大于0且不lo等gba于1,d>0)
条件
a>0且a≠1,M>0,N>0
结论
loga(MN)=logaM+logaN
M
loga N =logaM-logaN logaMn=nlogaM(n∈R)
考点二 指数函数与对数函数的图象与性质
x 1
x 1
因为2f(x)-f(-x)=3ln x 1,①
x 1
所以用-x代替x得2f(-x)-f(x)=3ln x 1=3ln x 1,②
x 1
x 1
①×2+②得3f(x)=3ln x 1,
x 1
故f(x)=ln x 1,x∈(-∞,-1)∪(1,+∞).
x 1
(2)由题意可知x+ 1 +6>1,x2+ 1 +
∵0<0.40.3<0.40=1,∴0<c<1,∴a<c<b.故选D.
答案 D
考法二 指数型复合函数的相关问题 1.对于与指数函数的图象有关的问题,一般从最基本的指数函数的图象 入手,通过平移、伸缩、对称变换得到. 2.指数函数的性质主要是单调性,常用单调性来比较大小、解简单的指 数不等式、求函数的值域(最值)等. 3.求解与指数函数有关的复合函数问题,首先,要熟知指数函数的定义 域、值域、单调性等相关性质,其次,要明确复合函数的构成,涉及值域、 单调区间、最值等问题时,一般要借助“同增异减”分析判断,最终将问 题归纳为与内层函数相关的问题加以解决. 注意:当底数a与1的大小关系不确定时,应分类讨论.
相关结论:logab= 1 ;logab·logbc·logcd=logad (a,b,c均大于0且不lo等gba于1,d>0)
条件
a>0且a≠1,M>0,N>0
结论
loga(MN)=logaM+logaN
M
loga N =logaM-logaN logaMn=nlogaM(n∈R)
考点二 指数函数与对数函数的图象与性质
x 1
x 1
因为2f(x)-f(-x)=3ln x 1,①
x 1
所以用-x代替x得2f(-x)-f(x)=3ln x 1=3ln x 1,②
x 1
x 1
①×2+②得3f(x)=3ln x 1,
x 1
故f(x)=ln x 1,x∈(-∞,-1)∪(1,+∞).
x 1
(2)由题意可知x+ 1 +6>1,x2+ 1 +
∵0<0.40.3<0.40=1,∴0<c<1,∴a<c<b.故选D.
答案 D
考法二 指数型复合函数的相关问题 1.对于与指数函数的图象有关的问题,一般从最基本的指数函数的图象 入手,通过平移、伸缩、对称变换得到. 2.指数函数的性质主要是单调性,常用单调性来比较大小、解简单的指 数不等式、求函数的值域(最值)等. 3.求解与指数函数有关的复合函数问题,首先,要熟知指数函数的定义 域、值域、单调性等相关性质,其次,要明确复合函数的构成,涉及值域、 单调区间、最值等问题时,一般要借助“同增异减”分析判断,最终将问 题归纳为与内层函数相关的问题加以解决. 注意:当底数a与1的大小关系不确定时,应分类讨论.
高中数学 第三章 指数函数和对数函数章末复习课课件

1
a3 a-8b 1 a-8b ×a3
1
×a3
1
b3
=a3 b.
(2)原式=log34-log3392+log38-52log53 =log34×392×8-52log53=log39-9=2-9=-7.
考点回扣
要点突破
【训练 1】 1861-34 +log354+log345=________.
章末复习课
考点回扣
要点突破
网络构建
考点回扣
要点突破
核心归纳
• 知识点一 指数函数y=ax(a>0,a≠1)的图像与性质 • 一般地,指数函数y=ax(a>0,a≠1)的图像与性质如下表
所示:
a>1
0<a<1
图像
考点回扣
要点突破
定义域 值域
性质
a>1
0<a<1
R
(0,+∞)
过点(0,1),即 x=0 时,y=1
数a的取值有关.当a变化时函数的图像与性质也随之改变. • (2)不同点:①指数函数的图像恒过定点(0,1),而对数函
)
解析 当 x>0 时,y=x|xa|x=ax.又 0<a<1,可排除 A、C;当 x<0 时,y=x|xa|x=-ax.又 0<a<1,可排除 B. • 答案 D
考点回扣
要点突破
要点三 比较大小
• 比较几个数的大小问题是指数函数、对数函数和幂函数 的重要应用,其基本方法是:将需要比较大小的几个数视为 某类函数的函数值,其主要方法可分以下三种:
• (1)根据函数的单调性(如根据一次函数、二次函数、指 数函数、对数函数、幂函数的单调性),利用单调性的定义 求解;
高中数学 第三章 指数函数和对数函数 5 5.3 对数函数的图像和性质课件高一必修1数学课件

2021/12/10
第十页,共三十四页。
【解】 (1)y=log3x 在 R 上是递增的. ∴log34<log35. (2)y=log0.3x 在 R 上是递减的. ∴log0.35>log0.37. (3)log0.37<log0.31=0, log97>log91=0, ∴log0.37<log97. (4)当 a>1 时,loga3.1<loga5.3; 当 0<a<1 时,loga3.1>loga5.3.
2021/12/10
第十九页,共三十四页。
若-1<loga34<1,求 a 的取值范围. 【解】 由已知得:loga1a<loga34<logaa.
当 a>1 时,1a<34<a,解得 a>43;
当
0<a<1
时,a<34<1a,解得
3 0<a<4.
∴a 的取值范围
2021/12/10
第二十页,共三十四页。
2
∴-12≤log2x≤12,即 log2 22≤log2x≤log2 2,
∴ 22≤x≤ 2. 答案:A
2021/12/10
第三十页,共三十四页。
4.已知奇函数 ƒ(x),当 x>0 时,ƒ(x)=lg x,则不等式 ƒ(x)<0 的解集是________.
解析:利用图像作答,如图所示.
由图像知不等式 ƒ(x)<0 的解集为(-∞,-1)∪(0,1). 答案:(-∞,-1)∪(0,1)
2021/12/10
第二十七页,共三十四页。
2.若 a=20.5,b=log43,c=log20.2,则( )
高中数学指数函数与对数函数课件PPT

2-9 指数函数与对数函数
1.掌握指数函数与对数函数的概念,图象和性 质.能利用指数函数和对数函数的性质解决某些简 单的实际问题。 2.理解指数函数y=ax(a>0且a≠1)与对数函数y=logax (a>0且a≠1)互为反函数,灵活运用指数函数、对数 函数的图象和性质,会用数形结合、分类讨论、函 数与方程(不等式)等数学思想方法解决一些综合 问题。
-3 x -2或 - 2 x 1. 函数定义域为(-3, -2)( -2, 1].
变式1.(1) 解:
求函数y loga [loga (loga x) ]的定义域(a 0且a 1). (loga x) 0 loga 1 loga log x 0 a x0
变式1.(2)
已知2
x2 x
1 x2 2 ( ) , 求函数y log 2 (3 x 6 x 4) 4
的值域. 解: 2x2 x 22( x2) , x2 x 2( x 2),
即x 2 3 x-4 0,
2
-4 x 1.
2
令u 3 x 6 x 4 3( x 1) 1 x [-4,1], u是减函数, 1 u 76. 又y log u是增函数, log2 1 log2 u log2 76.
考点梳理
1.指数函数与对数函数的概念: 指数函数: y=ax(a>0且a≠1) 对数函数: y=logax (a>0且a≠1)
2.指数、对数函数的图象与性质 根据图象写出函数的定义域、 值域、单调性、定点等性质.
y=ax的图象 0<a<1 a>1 y (0,1)
0
x
y=logax 的图象 3.指数函数与对数函数互为反函数. a>1 y 图象关于y=x对称,定义域、值域互换. 指数函数过点(0,1),(1,a),(-1,1/a)
1.掌握指数函数与对数函数的概念,图象和性 质.能利用指数函数和对数函数的性质解决某些简 单的实际问题。 2.理解指数函数y=ax(a>0且a≠1)与对数函数y=logax (a>0且a≠1)互为反函数,灵活运用指数函数、对数 函数的图象和性质,会用数形结合、分类讨论、函 数与方程(不等式)等数学思想方法解决一些综合 问题。
-3 x -2或 - 2 x 1. 函数定义域为(-3, -2)( -2, 1].
变式1.(1) 解:
求函数y loga [loga (loga x) ]的定义域(a 0且a 1). (loga x) 0 loga 1 loga log x 0 a x0
变式1.(2)
已知2
x2 x
1 x2 2 ( ) , 求函数y log 2 (3 x 6 x 4) 4
的值域. 解: 2x2 x 22( x2) , x2 x 2( x 2),
即x 2 3 x-4 0,
2
-4 x 1.
2
令u 3 x 6 x 4 3( x 1) 1 x [-4,1], u是减函数, 1 u 76. 又y log u是增函数, log2 1 log2 u log2 76.
考点梳理
1.指数函数与对数函数的概念: 指数函数: y=ax(a>0且a≠1) 对数函数: y=logax (a>0且a≠1)
2.指数、对数函数的图象与性质 根据图象写出函数的定义域、 值域、单调性、定点等性质.
y=ax的图象 0<a<1 a>1 y (0,1)
0
x
y=logax 的图象 3.指数函数与对数函数互为反函数. a>1 y 图象关于y=x对称,定义域、值域互换. 指数函数过点(0,1),(1,a),(-1,1/a)
《对数函数的概念》《对数函数的图象和性质》指数函数与对数函数PPT

-1
2
2
1
化简可得 ≤x2≤2.
2
再由 x>0 可得 2≤x≤
2
2
答案:(1)A (2)
, 2
2
2
2
2
1
,
2,故函数 f(x)的定义域为
2
,
2
2 .
课堂篇
探究学习
探究一
探究二
探究三
探究四
探究五
思想方法
随堂演练
反思感悟 定义域问题注意事项
(1)要遵循以前已学习过的求定义域的方法,如分式分母不为零,
偶次根式被开方式大于或等于零等.
a>1
0<a<1
图象
性
质
定义域
值域
过定点
单调性
奇偶性
(0,+∞)
R
(1,0),即当 x=1 时,y=0
在(0,+∞)
在(0,+∞)
上是增函数
上是减函数
非奇非偶函数
课前篇
自主预习
一
二
三
3.做一做
(1)若函数y=logax的图象如图所示,则a的值可能是 (
)
A.0.5 B.2
C.e D.π
(2)下列函数中,在区间(0,+∞)内
.
2 -2-8 = 0,
解析:(1)由题意可知 + 1 > 0, 解得 a=4.
+ 1 ≠ 1,
(2)设对数函数为f(x)=logax(a>0,且a≠1).
则由题意可得f(8)=-3,即loga8=-3,
所以
a-3=8,即
1
3
-
指数对数函数复习PPT课件

06 总结与展望
复习内容的总结与回顾
定义
a^x (a>0, a≠1)
性质
单调性、奇偶性、周期性等
复习内容的总结与回顾
应用
增长模型、复利计算等
定义
log_a(x) (a>0, a≠1)
复习内容的总结与回顾
性质
单调性、换底公式、对数运算性质等
应用
数据压缩、信号处理等
复习内容的总结与回顾
定义
f(g(x))
对数函数的运算性质
对数的乘法公式
对数的除法公式
对数的指数公式
log_a (mn) = log_a m + log_a n
log_a (m/n) = log_a m - log_a n
log_a m^n = n * log_a m
对数的换底公式
log_b m = log_a m / log_a b
04 指数对数函数的综合应用
对未来学习的展望与建议
01
持续练习
02
通过大量的练习题,巩固和加深 对指数对数函数的理解和掌握。
THANKS FOR WATCHING
感谢您的观看
竞赛模拟题
已知函数f(x) = log_a(x^2),求f'(x) 的表达式。
已知函数f(x) = log_a(b^x),求f'(x) 的表达式。
已知函数f(x) = a^x + b^x + c^x, 求f'(x)的表达式。
已知函数f(x) = x^a + log_a(x),求 f'(x)的表达式。
性质
单调性、奇偶性等
应用
函数建模、数学分析等
对未来学习的展望与建议
指数与对数函数复习ppt课件

小结:
• 1、了解对数及对数函数的定义。
• 2、掌握对数恒等式和运算法则,并能够灵 活用于计算。
• 3、掌握对数函数的图象和性质,能够熟练 应用图象和性质解题,注意和其它章节知 识的综合。
高考链接
3(2006)、log3 (log2 x ) 0,则x=__2__
4(2008)、设a=20.3,b log0.3 2,c 0.32则a,b,c 从大到小的顺序是 _a>_c>b
②
loga
M N
loga M
loga N
③ loga M P P loga M
(4)两个特殊的对数
常用对数:以10为底的对数叫做常用对数
a的常用对数记作____l_g_a__.
自然对数:以无理数e=2.718 28…为底的对数 叫做自然对数,N的自然对数记作 _____ln_N__
2. 对数函数的图象和性质
loga a 1
b aloga b
logam
bn
n
m
loga b
loga ab b
log c b
loga b logc a
1 loga b logb c logc a
(换底公式)
(3)积、商、幂、方根的的对数运算法则
(M>0,N>0,p∈R,a>0且a ≠ 1,)
① loga MN loga M loga N
5(2012)、若0<a<1,则y=ax与y loga x 在同 一个坐标系中的图像大致是(C )
A
B
C
D
y=ax
y
(0<a<1)
(0,1)
y=1
0
y=1 x
高中数学 第三章 指数函数和对数函数 4 4.1 对数及其运算课件高一必修1数学课件

A.e
B.1
C.e2
D.0
解析:令 ln x=1,则 x=e.∴f(1)=e. 答案:A
2021/12/13
第三十页,共三十三页。
5.(1)已知 loga2=m,loga3=n,求 a2m+n 的值; (2)已知 10a=2,10b=3,求 1002a-b 的值. 解:(1)∵m=loga2,n=loga3, ∴am=2,an=3, ∴a2m+n=a2m·an=(am)2·an=22×3=12. (2)∵10a=2,10b=3, ∴1002a-b=1100002ba=1100ab42=2342=196.
2021/12/13
第三十一页,共三十三页。
2021/12/13
第三十二页,共三十三页。
内容(nèiróng)总结
§4 对 数。§4 对 数。典例精析 规律(guīlǜ)总结。3 基础知识达标
No Image
12/13/2021
第三十三页,共三十三页。
C.log39=2 与 912=3 答案:C
D.log77=1 与 71=7
2021/12/13
第二十七页,共三十三页。
2.有下列说法:
①零和负数没有对数;②任何一个指数式都可以化成对数式;
③以 10 为底的对数叫作常用对数;④以 e 为底的对数叫作自然对
数.其中正确命题的个数为( )
A.1
B.2
数同时有意义,得到不等式组求解.
2021/12/13
第十三页,共三十三页。
求式子 log(x2+1)(-3x+8)中 x 的范围. 解:因为底数 x2+1>1,所以 x≠0;又因为-3x+8>0,所以 x<83,综上可知 x<83且 x≠0.即 x 的取值范围是x|x<83且x≠0.
第三章指数函数和对数函数5.1对数函数的概念5.2对数函数的图象和性质ppt课件

反思与感悟 比较两个同底数的对数大小,首先要根据底数来判断对 数函数的增减性;然后比较真数大小,再利用对数函数的增减性判断 两对数值的大小.对于底数以字母形式出现的,需要对底数a进行讨论. 对 于 不 同 底 的 对 数 , 可 以 估 算 范 围 , 如 log22<log23<log24 , 即 1<log23<2,从而借助中间值比较大小.
学习目标
1.理解对数函数的概念. 2.掌握对数函数的性质. 3.了解对数函数在生产实际中的简单应用. 4.了解反函数的概念及它们的图像特点.
重、对数函数的概念
一般地,我们把
函数y=logax(a>0,a≠1) 叫 作 对 数 函 数 ,
性质 (4)当x>1时,y>0,
(4)当x>1时,y<0,
0<x<1时,y<0
0<x<1时,y>0
(5)是(0,+∞)上的增函数 (5)是(0,+∞)上的减函数
三、反函数的概念 一般地,像y=ax与y=logax(a>0,且a≠1)这样的两个函数互为反函数. (1)y=ax的定义域R,就是y=logax的值域,而y=ax的值域(0,+∞)就 是y=logax的定义域. (2) 互 为 反 函 数 的 两 个 函 数 y = ax(a > 0 , 且 a≠1) 与 y = logax(a > 0 , 且 a≠1)的图像关于直线y=x对称. (3)互为反函数的两个函数的单调性相同,但单调区间不一定相同.
跟踪训练 3 设 a=log3π,b=log2 3,c=log3 2,则
√A.a>b>c
B.a>c>b
C.b>a>c
D.b>c>a
解析 ∵a=log3π>1,b=12log23,
指数函数与对数函数的关系指数函数对数函数与幂函数PPT精品推荐课件
致性吗?
提示:当0<a<1时,上述两个函数均是其定义域上的减函数;当a>1
时,上述两个函数均是其定义域上的增函数.因此单调性具有一致
性,但变化速度有差异.
课前篇自主预习
一
二
3.填空.
(1)关系
指数函数y=ax(a>0,a≠1)与对数函数y=logax(a>0,a≠1)互为反函数.
(2)图像特征
指数函数y=ax(a>0,a≠1)与对数函数y=logax(a>0,a≠1)的图像关于
与f-1(x)互为反函数,对此不能对自变量x随意变化拓展.
课堂篇探究学习
探究一
探究二
探究三
思维辨析
当堂检测
正解:∵g(x)的图像过定点(1,2 018),
∴f(x+1)的图像过定点(2 018,1).
又∵f(x)的图像可以看作由f(x+1)的图像向右平移1个单位长度得
到的,∴f(x)过定点(2 019,1).
)
A.(0,0) B.(0,2) C.(1,1)
D.(2,0)
答案:B
解析:∵y=f(x)的图像过点(1,0),
∴其反函数y=f-1(x)的图像必过点(0,1),
即f-1(0)=1,∴y=f-1(x)+1的图像过点(0,2).
4.已知
1-3
4
f(x)= ,则 f-1 5
1+3
=
Hale Waihona Puke 答案:-21-3除D.故选B.
方法二:若0<a<1,则曲线y=ax下降且过点(0,1),而曲线y=loga(-x)
上升且过点(-1,0),所有选项均不符合这些条件.
提示:当0<a<1时,上述两个函数均是其定义域上的减函数;当a>1
时,上述两个函数均是其定义域上的增函数.因此单调性具有一致
性,但变化速度有差异.
课前篇自主预习
一
二
3.填空.
(1)关系
指数函数y=ax(a>0,a≠1)与对数函数y=logax(a>0,a≠1)互为反函数.
(2)图像特征
指数函数y=ax(a>0,a≠1)与对数函数y=logax(a>0,a≠1)的图像关于
与f-1(x)互为反函数,对此不能对自变量x随意变化拓展.
课堂篇探究学习
探究一
探究二
探究三
思维辨析
当堂检测
正解:∵g(x)的图像过定点(1,2 018),
∴f(x+1)的图像过定点(2 018,1).
又∵f(x)的图像可以看作由f(x+1)的图像向右平移1个单位长度得
到的,∴f(x)过定点(2 019,1).
)
A.(0,0) B.(0,2) C.(1,1)
D.(2,0)
答案:B
解析:∵y=f(x)的图像过点(1,0),
∴其反函数y=f-1(x)的图像必过点(0,1),
即f-1(0)=1,∴y=f-1(x)+1的图像过点(0,2).
4.已知
1-3
4
f(x)= ,则 f-1 5
1+3
=
Hale Waihona Puke 答案:-21-3除D.故选B.
方法二:若0<a<1,则曲线y=ax下降且过点(0,1),而曲线y=loga(-x)
上升且过点(-1,0),所有选项均不符合这些条件.
指数对数函数复习课件(新编教材)

指数函数
一般地,函数y=ax(a>0,且a≠1)叫做指数函数, 其中x是自变量,函数的定义域是R 指数函数的图象和性质(见下表)
a>1
0<a<1
图 象
(1)定义域:R
性
(2)值域(0,+∞)
质
(3)过点(0,1),即x=0时,y=1
(4)在R上是增函数
在R上是减函数
对数函数的图象和性质 对数函数y=logax的图象和性质分a>1及0<a<1两种 情况.
优游 ;
长子景早卒 元会特为设床 因统诸军奉迎大驾于长安 豫诛贾谧 贼将匡术以台城来降 中夜闻荒鸡鸣 亮排闼入 至于伯也 为众率先 将斩之 琨在路上表曰 元显弃船退屯国子学堂 乃与荣及陆玩等各解船弃车牛 刘琨承制 皆南金也 进位侍中 与系争军事 可一解禁止 天不违愿 阳翟令 故汉祖指 麾而六合响应 宗庙无主 虽有不请之嫌 葬襄阳之岘山 以明穆皇后之兄受顾命之重 国耻未雪 又问曰 又孙仲谋 以务勿尘为大单于 吾州将荷国重恩 必协济康哉 太兴中 城内莫知 遣就谷冀州 送马八十五匹 班剑二十人 峤先有齿疾 转尚书 故吏刊石立碑画像于武昌西 领北军中候 泓乘胜至于 颍上 朝廷所不能抑 长沙授首 三十馀载 未达斯义 楚 又似乎和风吹林 率营兵七百馀人自南掖门入 不及盛年讲肄道义 以之序官 以其世子散骑常侍荂领冗从仆射 各以见惮取诛于时 功成名立 终于家 弟式之 存重宗社 移居阳邑城 州又举寒素 吾便角巾还第 无罪横戮 免其世子综官 使若逖等 为之统主 东界辽水 出继叔父城阳哀王兆 雅爱方 职此之由 臣所以泣血宵吟 内无所倚 愚蠢意暗 义夫泣血 加散骑常侍 臣挟利以事君 不宜为中正 约憎纳如仇 亲受矢石 于是征西羽檄 奉宣王猷 默二子 毁而卖之 侃使郑攀及伏波将军陶延夜趣巴陵 彦夏系心宸极 既而钱凤攻逼京都 导善于因 事 时楷已应
一般地,函数y=ax(a>0,且a≠1)叫做指数函数, 其中x是自变量,函数的定义域是R 指数函数的图象和性质(见下表)
a>1
0<a<1
图 象
(1)定义域:R
性
(2)值域(0,+∞)
质
(3)过点(0,1),即x=0时,y=1
(4)在R上是增函数
在R上是减函数
对数函数的图象和性质 对数函数y=logax的图象和性质分a>1及0<a<1两种 情况.
优游 ;
长子景早卒 元会特为设床 因统诸军奉迎大驾于长安 豫诛贾谧 贼将匡术以台城来降 中夜闻荒鸡鸣 亮排闼入 至于伯也 为众率先 将斩之 琨在路上表曰 元显弃船退屯国子学堂 乃与荣及陆玩等各解船弃车牛 刘琨承制 皆南金也 进位侍中 与系争军事 可一解禁止 天不违愿 阳翟令 故汉祖指 麾而六合响应 宗庙无主 虽有不请之嫌 葬襄阳之岘山 以明穆皇后之兄受顾命之重 国耻未雪 又问曰 又孙仲谋 以务勿尘为大单于 吾州将荷国重恩 必协济康哉 太兴中 城内莫知 遣就谷冀州 送马八十五匹 班剑二十人 峤先有齿疾 转尚书 故吏刊石立碑画像于武昌西 领北军中候 泓乘胜至于 颍上 朝廷所不能抑 长沙授首 三十馀载 未达斯义 楚 又似乎和风吹林 率营兵七百馀人自南掖门入 不及盛年讲肄道义 以之序官 以其世子散骑常侍荂领冗从仆射 各以见惮取诛于时 功成名立 终于家 弟式之 存重宗社 移居阳邑城 州又举寒素 吾便角巾还第 无罪横戮 免其世子综官 使若逖等 为之统主 东界辽水 出继叔父城阳哀王兆 雅爱方 职此之由 臣所以泣血宵吟 内无所倚 愚蠢意暗 义夫泣血 加散骑常侍 臣挟利以事君 不宜为中正 约憎纳如仇 亲受矢石 于是征西羽檄 奉宣王猷 默二子 毁而卖之 侃使郑攀及伏波将军陶延夜趣巴陵 彦夏系心宸极 既而钱凤攻逼京都 导善于因 事 时楷已应
第3章 指数函数、对数函数和幂函数 复习课件

例 2 已知函数 f(x)是定义在 R 上的偶函数,当 x≥0 时,f(x)=12x. (1)画出函数f(x)的图象; 解 先作出当 x≥0 时,f(x)=12x 的图象,利用偶函数的图象关于 y 轴对称, 再作出 f(x)在 x∈(-∞,0)时的图象.
解析答案
(2)根据图象写出f(x)的单调区间,并写出函数的值域. 解 函数f(x)的单调递增区间为(-∞,0), 单调递减区间为[0,+∞),值域为(0,1].
b
1 3
=a3
b.
解析答案
(2)计算:2log32-log3392+log38-25 log5 3 . 解 原式=log34-log3392+log38-5 2log5 3 =log3(4×392×8)-5 2log5 3 =log39-9 =2-9=-7.
解析答案
跟踪训练 1
(8116)
3 4
定义域 值域
R (0,+∞)
(0,+∞) R
图象
(1)图象经过(0,1)点,
(1)图象经过(1,0)点,
(2)a>1,当x>0时,y>1;
(2)a>1,当x>1时,y>0;
当x<0时,0<y<1.
当0<x<1时,y<0.
性 0<a<1,当x>0时,0<y<1; 0<a<1,当x>1时,y<0;
质 当x<0时,y>1.
例1
2
1
(1)化简: a 3 8a3b
2
2
4b 3 2 3 ab a 3
÷1-2 3 ba×3 ab;
1
解 原式=
a3 (a 8b)
1
11
2
(2b3 )2 2a3b3 (a 3 )2
1
×
a3
高中数学第三章指数函数和对数函数5.5.3对数函数的图像和性质课件北师大版必修

(2)y=
log1 x
=
log
1 2
x,
0
x
1,
其图像如图②.
2 log2x, x 1
其定义域为(0,+∞),值域为[0,+∞),在(0,1]上是减少的,在[1,+∞)上是增
加的.
画出函数 y=lg |x-1|的图像. 【解析】(1)先画出函数 y=lg x 的图像(如图).
(2)再画出函数 y=lg |x|的图像(如图).
同理当 x∈[0,1)时,y=log1 (1-x2)是增加的. 2
所以函数 y=log1 (1-x2)的增区间为[0,1). 2
【补偿训练】 已知函数 y=loga(x+b)(a>0,且 a≠1)的图
像如图所示. (1)求实数 a 与 b 的值. (2)函数 y=loga(x+b)与 y=logax 的图像有何关系?
【解析】(1)由图像可知,函数的图像过点(-3,0)与点(0,2), 所以得方程 0=loga(-3+b)与 2=logab, 解得 a=2,b=4. (2)函数 y=loga(x+4)的图像可以由 y=logax 的图像向左平移 4 个单位得到.
(2)函数 y= logax 与 y= log1x 的图像有什么关系?
a
提示:y= log1x
a
=
loga x
loga
1 a
=-logax ,所以它们关于
x
轴对称.
1.辨析记忆(对的打“√”,错的打“×”)
(1)函数y=3x与函数y=log3x的图像关于直线y=x对称.( √ ) 【解析】函数y=3x与函数y=log3x互为反函数,图像关于直线y=x对称. (2)f(x)=ln (x2-1)是偶函数.( √ ) 【解析】因为函数的定义域为(-∞,-1)∪(1,+∞),且f(-x)=ln (x2-1)= f(x),所以该函数是偶函数.
《对数的概念》指数函数与对数函数PPT优秀课件

思维脉络
公开课课件优质课课件PPT优秀课件PP T免费 下载《 对数的 概念》 指数函 数与对 数函数P PT
课前篇
自主预习
一
二
三
一、对数的概念
1.(1)某种细胞分裂时,由1个分裂成2个,2个分裂成4个,…依次类
推,那么1个这样的细胞分裂x次后,得到的细胞个数N是多少?
提示:N=2x.
(2)上述问题中,若已知分裂后得到的细胞的个数分别为8个,16个,
首页
课标阐释
1.理解对数的概念,掌握对数的
基本性质.
2.掌握指数式与对数式的互化,
能应用对数的定义和性质解方
程.
3.理解常用对数和自然对数的
定义形式以及在科学实践中的
应用.
4.了解对数的发展历史,了解数
学文化.
公开课课件优质课课件PPT优秀课件PP T免费 下载《 对数的 概念》 指数函 数与对 数函数P PT
(3)ln M=n用指数式如何表示?
提示:en=M.
2.填空
常用对数 以 10 为底数,记作 lg N
自然对数 以 e 为底数,记作 ln N,其中 e=2.718 28…
3.做一做
(1)lg 105=
答案:(1)5 (2)1
公开课课件优质课课件PPT优秀课件PP T免费 下载《 对数的 概念》 指数函 数与对 数函数P PT
(1)负数和零没有对数.
(2)loga1=0(a>0,a≠1).
(3)logaa=1(a>0,a≠1).
(4)对数恒等式log =N(a>0,且 a≠1,N>0).
公开课课件优质课课件PPT优秀课件PP T免费 下载《 对数的 概念》 指数函 数与对 数函数P PT
指数函数与对数函数PPT课件

16 4 2 4( 4 ) 2 3 27 ( ) ( ) ( ) 81 3 3 8
3 3
2. 用分数指数幂的形式表示下列各式:
1).
a2 a, a3 3 a2 , a a,
a a
5 2
a
3 4
11 3
3. 计算下列各式(式中字母都是正数)
2 3 1 2 1 2 1 3 1 6 5 6
练习
⑴ 比较大小: (2.5)
2 3<
, (2.5)
4 5
4 5
4 5
2.5
2 3
2.5 , 2.5 2.5
2 3
底数化为正数。 (2). 已知下列不等式,试比较m、n的大小
2 m 2 n ( ) ( ) 3 3
m<n
1.1m 1.1n
m<n
指数函数的应用
a>0时,向右平移a个单位; a<0时,向左平移|a|个单位.
2. y=f(x) →y=f(x)+b:上下平移
y=f(x)+b, b>0
y=f(x) y=f(x)+b, b<0
b>0时,向上平移b个单位; b<0时,向下平移|b|个单位.
对称变换 y=f(x) →y=f(-x): (关于y轴对称) y=f(x) →y= -f(x): (关于x轴对称) y=f(x) →y= -f(-x): (关于原点对称) y=f(-x)
a>1
6
0<a<1
6
图 象
1
5
5
4
4
3
3
2
2
1
1
1
-4
-2
3 3
2. 用分数指数幂的形式表示下列各式:
1).
a2 a, a3 3 a2 , a a,
a a
5 2
a
3 4
11 3
3. 计算下列各式(式中字母都是正数)
2 3 1 2 1 2 1 3 1 6 5 6
练习
⑴ 比较大小: (2.5)
2 3<
, (2.5)
4 5
4 5
4 5
2.5
2 3
2.5 , 2.5 2.5
2 3
底数化为正数。 (2). 已知下列不等式,试比较m、n的大小
2 m 2 n ( ) ( ) 3 3
m<n
1.1m 1.1n
m<n
指数函数的应用
a>0时,向右平移a个单位; a<0时,向左平移|a|个单位.
2. y=f(x) →y=f(x)+b:上下平移
y=f(x)+b, b>0
y=f(x) y=f(x)+b, b<0
b>0时,向上平移b个单位; b<0时,向下平移|b|个单位.
对称变换 y=f(x) →y=f(-x): (关于y轴对称) y=f(x) →y= -f(x): (关于x轴对称) y=f(x) →y= -f(-x): (关于原点对称) y=f(-x)
a>1
6
0<a<1
6
图 象
1
5
5
4
4
3
3
2
2
1
1
1
-4
-2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.幂函数与指数函数的主要区别:幂函数的底数为变量,指数函数的指 数为变量.因此,当遇到一个有关幂的形式的问题时,就要看变量所在的 位置从而决定是用幂函数知识解决,还是用指数函数知识去解决. 5.比较几个数的大小是幂函数、指数函数、对数函数性质应用的常见题 型,在具体比较时,可以首先将它们与零比较,分出正数、负数;再将 正数与1比,分出大于1还是小于1;然后在各类中两两相比较. 6.求含有指数函数和对数函数复合函数的最值或单调区间时,首先要考 虑指数函数、对数函数的定义域,再由复合函数的单调性来确定其单调 区间,要注意单调区间是函数定义域的子集.其次要结合函数的图像,观 察确定其最值或单调区间.
考查指数函数、对数函数、幂函数图像与性质的应用及差值比较法与商
值比较法的应用.常用的方法有单调性法、图像法、中间搭桥法、作差法、
作商法.
(2)当需要比较大小的两个实数均是指数幂或对数式时,可将其看成某个
指数函数、对数函数或幂函数的函数值,然后利用该函数的单调性比较.
(3)比较多个数的大小时,先利用“0”和“1”作为分界点,即把它们分
解答
(2)若ab<0,求f(x+1)>f(x)时的x的取值范围. 解 f(x+1)-f(x)=a·2x+2b·3x>0.
①当 a<0,b>0 时,32x>-2ab,
解得
x>log 3
2
-2ab;
②当 a>0,b<0 时,32x<-2ab,
解得
x<log
3 2
-2ab.
解答
反思与感悟
指数函数、对数函数、幂函数是使用频率非常高的基本初等函数,它们 经过加、减、乘、除、复合、分段,构成我们以后研究的函数,使用时 则通过换元、图像变换等手段化归为基本的指数函数、对数函数、幂函 数来研究.
解答
(3)
1
2 3 , log2
1 3
,
log
1 2
1. 3
解
∵
1
0<2 3
<20=1.
log213<log21=0,
log 1
2
1 3
log 1
2
1 2
1,
log2
1 3
1
23
log 1
2
1. 3
解答
数的大小比较常用(式)的大小问题是本章的一个重要题型,主要
跟踪训练3 已知函数f(x)=loga(1-x)+loga(x+3)(0<a<1). (1)求函数f(x)的定义域; 解 要使函数有意义,则有1x+-3x>>00, , 解得-3<x<1,∴定义域为(-3,1).
解答
(2)若函数f(x)的最小值为-2,求a的值.
解 函数可化为f(x)=loga[(1-x)(x+3)] =loga(-x2-2x+3)=loga[-(x+1)2+4]. ∵-3<x<1,∴0<-(x+1)2+4≤4.
解答
(2)a1.2,a1.3; 解 ∵函数y=ax(a>0,且a≠1),当底数a>1时在R上是增函数; 当底数0<a<1时在R上是减函数, 而1.2<1.3,故当a>1时,有a1.2<a1.3; 当0<a<1时,有a1.2>a1.3.
解答
(3)30.4,0.43,log0.43. 解 30.4>30=1, 0<0.43<0.40=1, log0.43<log0.41=0, ∴log0.43<0.43<30.4.
7.函数图像是高考考查的重点内容,在历年高考中都有涉及.考查形式有 知式选图、知图造式、图像变换以及用图像解题.函数图像形象地显示了 函数的性质,利用数形结合有时起到事半功倍的效果.
题型探究
类型一 指数、对数的运算
例1
化简:(1) (
2
8) 3
(3
9
102 )2
105 ;
3 2
29
5
解 原式=(22 ) 3 (103 )2 102
解析 答案
类型二 数的大小比较 例2 比较下列各组数的大小. (1)27,82; 解 ∵82=(23)2=26, 由指数函数y=2x在R上递增知26<27,即82<27.
解答
(2)log20.4,log30.4,log40.4; 解 ∵对数函数y=log0.4x在(0,+∞)上是减函数, ∴log0.44<log0.43<log0.42<log0.41=0. 又幂函数y=x-1在(-∞,0)上是减函数, ∴log10.42<log10.43<log10.44, 即log20.4<log30.4<log40.4.
谢谢
=2-1×103×10
5 2
=2-1×10
1 2
=
10 2.
解答
(2)2log32-log3392+log38-25log53. 解 原式=log34-log3392+log38-5 2log5 3 =log34×392×8-5 log59 =log39-9=2-9=-7.
解答
反思与感悟
指数、对数的运算应遵循的原则 指数式的运算首先注意化简顺序,一般负指数先转化成正指数,根式化 为分数指数幂运算,其次若出现分式则要注意分子、分母因式分解以达 到约分的目的.对数运算首先注意公式应用过程中范围的变化,前后要等 价,熟练地运用对数的三个运算性质并结合对数恒等式,换底公式是对 数计算、化简、证明常用的技巧.
4.已知P=2
3 2
,Q=523,R=123,则P,Q,R的大小关系是
A.P<Q<R C.Q<P<R
B√.Q<R<P
D.R<Q<P
解析 由函数 y=x3 在 R 上是增函数知,253<123,
由函数
y=2x 在
R
上是增函数知,
2
3 2
>2-3=123,
所以P>R>Q.
12345
解析 答案
5.函数f(x)=2x|log0.5x|-1与x轴交点的个数为
A.都是增函数 B.都是减函数 C.f(x)是增函数,g(x)是减函数
√D.f(x)是减函数,g(x)是增函数
解析
f(x)=12x
在
x∈(-∞,0)上为减函数,g(x)=log 1
2
|x|为偶函数,
x∈(0,+∞)时 g(x)=log1 x 为减函数,所以在(-∞,0)上为增函数. 2
12345
解析 答案
跟踪训练4 若函数y=logax(a>0,且a≠1)的图像如 图所示,则下列函数图像正确的是
解析 答案
当堂训练
1.化简22l+gllggalg10a0为
A.1
√B.2
C.3
D.0
解析 22l+gllggalg10a0=22lg+1l0g0l·glgaa
2[lg 100+lglg a] = 2+lglg a =2.
跟踪训练 1 计算 80.25×4 2+(3 2× 3)6+log32×log2(log327)的值为_1_1_1__.
解析 ∵log32×log2(log327)=log32×log23
=llgg 23×llgg 32=1,
3
1
∴原式=2 4 ×2 4 +22×33+1=21+4×27+1=111.
第三章 指数函数和对数函数 复习课件
学习目标
1.构建知识网络; 2.进一步熟练指数、对数运算,加深对公式成立条件 的记忆; 3.以函数观点综合理解指数函数、对数函数、幂函数.
内容索引
知识梳理 题型探究 当堂训练
知识梳理
1.指数幂、对数式的运算、求值、化简、证明等问题主要依据指数幂、 对数的运算性质,在进行指数、对数的运算时还要注意相互间的转化. 2.指数函数和对数函数的性质及图像特点是这部分知识的重点,而底数a 的不同取值对函数的图像及性质的影响则是重中之重,要熟知a在(0,1) 和(1,+∞)两个区间取值时函数的单调性及图像特点. 3.应用指数函数y=ax和对数函数y=logax的图像和性质时,若底数含有 字母,要特别注意对底数a>1和0<a<1两种情况的讨论.
D.{x|-1<x≤2}
解析 借助函数的图像求解该不等式.
令g(x)=y=log2(x+1),作出函数g(x)的图像如图.
由xy+ =ylo=g22, x+1,
得xy= =11, .
∴结合图像知不等式f(x)≥log2(x+1)的解集为{x|-1<x≤1}.
解析 答案
反思与感悟
指数函数、对数函数、幂函数图像既是直接考查的对象,又是数形结合 求交点,最值,解不等式的工具,所以要能熟练画出这三类函数图像, 并会进行平移、伸缩,对称、翻折等变换.
解答
类型三 指数函数、对数函数、幂函数的综合应用
命题角度1 函数的性质及应用 例3 已知函数f(x)=a·2x+b·3x,其中常数a,b满足ab≠0. (1)若ab>0,判断函数f(x)的单调性; 解 当a>0,b>0时,因为a·2x,b·3x在R上都是增函数, 所以函数f(x)在R上是增函数; 当a<0,b<0时,因为a·2x,b·3x在R上都是减函数, 所以函数f(x)在R上是减函数.
为“小于0”,“大于等于0小于等于1”,“大于1”三部分,再在各部
分内利用函数的性质比较大小.
跟踪训练2 比较下列各组数的大小. (1)log0.22,log0.049; 解 ∵log0.049=lglg0.904=lglg03.222 =22lglg03.2=lglg03.2=log0.23. 又∵y=log0.2x在(0,+∞)上递减, ∴log0.22>log0.23,即log0.22>log0.049.
