利用MATLAB 实现极点配置、设计状态观测器(现代控制)
利用MATLAB设计状态观测器

利用MATLAB 设计状态观测器本节将介绍用MATLAB 设计状态观测器的若干例子。
我们将举例说明全维状态观测器和最小阶状态观测器设计的MATLAB 方法。
------------------------------------------------[例1] 考虑一个调节器系统的设计。
给定线性定常系统为Cxy Bu Ax x =+=& 式中]01[,10,06.2010=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=C B A且闭环极点为)2,1(==i s i μ,其中4.28.1,4.28.121j j −−=+−=μμ期望用观测-状态反馈控制,而不是用真实的状态反馈控制。
观测器的期望特征值为821−==μμ试采用MATLAB 确定出相应的状态反馈增益矩阵K 和观测器增益矩阵e K 。
[解]对于题中给定的系统,可利用如下MATLAB Program 1来确定状态反馈增益矩阵K和观测器增益K。
矩阵eMATLAB Program 1% Pole placement and design of observer ------% ***** Design of a control system using pole-placement% technique and state observer. Solve pole-placement% problem *****% ***** Enter matrices A,B,C,and D *****A=[0 1;20.6 0];B=[0;1]C=[1 0];D=[0];% ***** Check the rank of the controllability matrix Q *****Q=[B A*B];Rank(Q)ans=2% ***** Since the rank of the controllability matrix Q is 2, % arbitrary pole placement is possible *****% ***** Enter the desired characteristic polynomial by% defining the following matrix J and computingpoly(J) *****J=[-1.8+2.4*i 0;0 -1.8-2.4*i];Poly(J)ans=1.000 3.6000 9.0000% ***** Enter characteristic polynomial Phi *****Phi=polyvalm(poly(J),A);% ***** State feedback gain matrix K can be given by ***** K=[0 1]*inv(Q)*PhiK=29.6000 3.6000% ***** The following program determines the observer matrix Ke *****% ***** Enter the observability matrix RT and check its rank *****RT=[C’ A’*C’];rank(RT)ans=2% ***** Since the rank of the observability matrix is 2, design of% the observer is possible *****% **** Enter the desired characteristic polynomial by defining % the following matrix J0 and entering statement poly(JO) *****JO=[-8 0;0 -8];Poly(JO)ans=1 16 64% ***** Enter characteristic polynomial Ph ***** Ph=polyvalm(ply(JO),A);% ***** The observer gain matrix Ke is obtained from ***** Ke=Ph*(inv(RT’))*[0;1]Ke=16.000084.60000求出的状态反馈增益矩阵K 为[]6.36.29=K观测器增益矩阵e K 为⎥⎦⎤⎢⎣⎡=6.8416e K 该观测-状态反馈控制系统是4阶的,其特征方程为0=+−+−C K A sI BKA sI e通过将期望的闭环极点和期望的观测器极点代入上式,可得5764.3746.1306.19)8)(4.28.1)(4.28.1(2342++++=+++−+=+−+−s s s s s j s j s C K A sI BK A sI e这个结果很容易通过MATLAB得到,如MATLAB Program 2所示(MATLAB Program 2是K已MATLAB Program1的继续。
现代控制理论的MATLAB实现

现代控制理论的MATLAB实现现代控制理论是控制工程中一门重要的学科,它研究如何设计和分析控制系统以满足一定的性能指标。
MATLAB是一种功能强大的科学计算和工程仿真软件,广泛应用于控制系统设计与分析。
本文将介绍现代控制理论的一些常见方法在MATLAB中的实现。
1.线性系统的状态空间表示线性系统的状态空间表示是现代控制理论的核心内容之一、在MATLAB中,可以使用`ss`命令创建线性系统的状态空间模型。
例如,假设存在一个二阶线性时不变系统,其传递函数为:可以使用以下代码将其转换为状态空间模型:```matlabnum = [1];den = [1, 1, 1];sys = tf(num, den);ss_sys = ss(sys);```2.线性系统的传递函数表示传递函数是描述线性系统输入输出关系的一种常用表示方法。
在MATLAB中,可以使用`tf`命令创建线性系统的传递函数模型。
例如,假设存在一个二阶线性时不变系统,其状态空间描述为:```matlabA=[0,1;-1,-1];B=[0;1];C=[1,0];D=0;ss_sys = ss(A, B, C, D);```可以使用以下代码将其转换为传递函数模型:```matlabtf_sys = tf(ss_sys);```3.常见控制器的设计与分析现代控制理论中常用的控制器设计方法包括PID控制器、根轨迹法、频率域分析等。
在MATLAB中,可以使用`pid`命令创建PID控制器,并使用`rlocus`命令绘制根轨迹图。
例如,创建一个PID控制器:```matlabKp=1;Kd=0.1;pid_controller = pid(Kp, Ki, Kd);```绘制根轨迹图:```matlabsys = tf([1], [1, 1, 1]);rlocus(sys);```4.系统的频率响应分析频率响应分析是现代控制理论中常用的系统性能评估方法之一、在MATLAB中,可以使用`bode`命令绘制系统的频率响应曲线。
现代控制理论基础实验指导书200

现代控制理论基础实验指导书实验一:控制系统模型转换一、实验目的1.掌握控制系统模型转换,并使用计算机仿真软件验证。
2.学习并会简单应用MATLAB软件。
二、实验器材[1] 微型计算机[2] MATLAB软件三、实验要求与任务1.设系统的零极点增益模型为,求系统的传递函数及状态空间模型。
解:在MATLAB软件中,新建m文件,输入以下程序后保存并运行。
%Example 1%k=6;z=[-3];p=[-1,-2,-5];[num,den]=zp2tf(z,p,k)[a,b,c,d]=zp2ss(z,p,k)其中:zp2tf函数——变零极点表示为传递函数表示zp2ss函数——变零极点表示为状态空间表示记录实验结果,并给出系统的传递函数及状态空间模型。
2.给定离散系统状态空间方程求其传递函数模型和零极点模型,并判断其稳定性。
解:在MATLAB软件中,新建m文件,输入以下程序后保存并运行。
%Example 2%a=[ 0 0 ; 0 0 0; ;0 0 0];b=[1;0;1;0];c=[0,0,0,1];d=[0];[num,den]=ss2tf(a,b,c,d)[z,p,k]=ss2zp(a,b,c,d)pzmap(p,z)title('Pole-zero Map')其中:ss2tf函数——变状态空间表示为传递函数表示ss2zp函数——变状态空间表示为零极点表示pzmap ——零极点图记录实验结果,并给出系统的传递函数模型和零极点模型;绘出图形,并判断系统稳定性。
3.已知系统的传递函数为,求系统的零极点增益模型及状态空间模型。
tf2zp函数——变系统传递函数形式为零极点增益形式tf2ss函数——变系统传递函数形式为状态空间表示形式编写程序,记录实验结果,并给出系统的状态空间模型和零极点模型。
4.已知系统状态空间表达式为ss2tf函数——变状态空间表示为传递函数表示ss2zp函数——变状态空间表示为零极点表示编写程序,记录实验结果,并给出系统传递函数模型和零极点模型。
利用matlab实现极点配置、设计状态观测器(现代控制)

实 验 报 告实验名称 利用MATLAB 实现极点配置、设计状态观测器系 专业 自动化 班 姓名 学号 授课老师 预定时间实验时间实验台号一、目的要求1、掌握状态反馈和输出反馈的概念及性质。
2、掌握利用状态反馈进行极点配置的方法。
学会用MATLAB 求解状态反馈矩阵。
3、掌握状态观测器的设计方法。
学会用MATLAB 设计状态观测器。
4、熟悉分离定理,学会设计带有状态观测器的状态反馈系统。
二、原理简述1、状态反馈和输出反馈设线性定常系统的状态空间表达式为Cxy Bu Ax x =+=如果采用状态反馈控制规律u= r-Kx ,其中 r 是参考输入,则状态反馈闭环系统的传递函数为:B BK A sIC G k 1)]([---=2、极点配置如果 SISO 线性定常系统完全能控,则可通过适当的状态反馈, 将闭环系统极点配置到任意期望的位置。
MATLAB 提供的函数acker( )是用Ackermann 公式求解状态反馈阵K 。
该函数的调用格 式为K=acker(A,B,P)其中A 和B 分别为系统矩阵和输入矩阵。
P 是期望极点构成的向量。
MATLAB 提供的函数place( )也可求出状态反馈阵K 。
该函数的调用格式为 K=place(A,B,P)函数place( )还适用于多变量系统极点配置,但不适用含有多重期望极点的问题。
函数acker( )不适用于多变量系统极点配置问题,但适用于含有多重期望极点问题。
三、仪器设备PC 计算机,MATLAB 软件⎣[y1=lsim(G,u,t); plot(t,y1,':',t,y2,'-')蓝色为配置前,绿色为配置后题5-3 某系统状态空间描述如下[]010100134326100x x u y x⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦= 设计全维状态观测器,要求状态观测器的极点为[]123---。
程序>> A=[0 1 0;0 0 1;-4 -3 -2];B=[1;3;-6]'; C=[1 0 0]; D=0;p=[-1 -2 -3]; L=(acker(A',C',p))' 结果:L = 40 -10。
现代控制理论MATLAB编程

现代控制理论实验报告姓名:班级:学号:目录一.实验设备二.实验目的三.实验步骤一、实验设备PC计算机1台,MATLAB软件1套。
二、实验目的1。
学习系统状态空间表达式的建立方法、了解系统状态空间表达式与传递函数相互转换的方法;2。
通过编程、上机调试、掌握系统状态空间表达式与传递函数相互转换方法;3。
学习MATLAB的使用方法。
三、实验步骤1、根据所给系统的结构图写出死循环系统的传递函数,若K=10,T=0。
1时阶跃输出下的系统输出响应,并采用MATLAB编程.2、在MATLAB接口下调试程序,并检查是否运行正确.3、给出定二阶系统结构图:图为二阶系统结构图(1)求二阶系统的闭环循环传递函数ɸ(s )=)(1)(s G s G +=K S TS K++2(2)若K=10,T=0。
1,仿真给出阶跃下的系统输出响应把K T 代入方程得Φ(S)= =1)MATLAB 命令得出的系统响应曲线在MATLAB 上输入下列指令:〉> num=[100];>> den=[1,10,100];>> step (num,den)程序运行后显示的时域动态响应曲线(如图2)图为 时域动态响应曲线2)、用进行Simulink 进行仿真启动Simulink并打开一个空白的模块编辑窗口,画出所需模块,并给出正确参数,将画出的所有模块链接起来(如图1),构成一个原系统的框图描述(如图3).选择仿真控制参数,启动仿真过程。
仿真结果示波器显示如图4。
图3二阶系统的Simulink(仿真)图4仿真结果示波器显示(仿真输出)(3) 调整比例系数K,使之从零开始增加。
同时,观察仿真曲线的变化,并给出过阻尼、临界、欠阻尼的条件。
当K=0时的仿真曲线当K=1时的仿真曲线当K=2.5时的仿真曲线当K=3。
5时的仿真曲线当K=4时的仿真曲线根据调整比例系数K,使之从零开始增加,同时观察仿真曲线的变化,得出以下结论;过阻尼的条件:K>2.5时;临界阻尼条件:K=2.5时;欠阻尼的条件:K<2。
基于matlab的状态观测器设计

基于MATLAB 的状态观测器设计预备知识: 极点配置基于状态反馈的极点配置法就是通过状态反馈将系统的闭环极点配置到期望的极点位置上,从而使系统特性满足要求。
1. 极点配置原理假设原系统的状态空间模型为:⎩⎨⎧=+=Cxy Bu Ax x 若系统是完全可控的,则可引入状态反馈调节器,且:Kx u input -=这时,闭环系统的状态空间模型为:⎩⎨⎧=+-=Cxy Bu x )BK A (x 2. 极点配置的MATLAB 函数 在MATLAB 控制工具箱中,直接用于系统极点配置的函数有acker()和place()。
调用格式为:K=acker(A,C,P) 用于单输入单输出系统其中:A ,B 为系统矩阵,P 为期望极点向量,K 为反馈增益向量。
K=place(A,B,P)(K,prec,message)=place(A,B,P)place()用于单输入或多输入系统。
Prec 为实际极点偏离期望极点位置的误差;message 是当系统某一非零极点偏离期望位置大于10%时给出的警告信息。
3. 极点配置步骤:(1)获得系统闭环的状态空间方程;(2)根据系统性能要求,确定系统期望极点分布P ;(3)利用MATLAB 极点配置设计函数求取系统反馈增益K ; (4)检验系统性能。
已知系统模型如何从系统的输入输出数据得到系统状态?初始状态:由能观性,从输入输出数据确定。
不足:初始状态不精确,模型不确定。
思路:构造一个系统,输出逼近系统状态称为是的重构状态或状态估计值。
实现系统状态重构的系统称为状态观测器。
观测器设计状态估计的开环处理:但是存在模型不确定性和扰动!初始状态未知!应用反馈校正思想来实现状态重构。
通过误差来校正系统:状态误差,输出误差。
基于观测器的控制器设计系统模型若系统状态不能直接测量,可以用观测器来估计系统的状态。
L是观测器增益矩阵,对偏差的加权。
真实状态和估计状态的误差向量误差的动态行为:的极点决定了误差是否衰减、如何衰减?通过确定矩阵L来保证。
实验 6 极点配置与全维状态观测器的设计

实验 6 极点配置与全维状态观测器的设计一、实验目的1. 加深对状态反馈作用的理解。
2. 学习和掌握状态观测器的设计方法。
二、实验原理在MATLAB 中,可以使用acker 和place 函数来进行极点配置,函数的使用方法如下:K = acker(A,B,P) A,B为系统系数矩阵,P为配置极点,K为反馈增益矩阵。
K = place(A,B,P) A,B为系统系数矩阵,P为配置极点,K为反馈增益矩阵。
[K,PREC,MESSAGE] = place(A,B,P) A,B为系统系数矩阵,P为配置极点,K为反馈增益矩阵,PREC 为特征值,MESSAGE 为配置中的出错信息。
三、实验内容1.已知系统(1)判断系统稳定性,说明原因。
(2)若不稳定,进行极点配置,期望极点:-1,-2,-3,求出状态反馈矩阵k。
(3)讨论状态反馈与输出反馈的关系,说明状态反馈为何能进行极点配置?(4)使用状态反馈进行零极点配置的前提条件是什么?1.(1)(2)代码:a=[-2 -1 1;1 0 1;-1 0 1];b=[1,1,1]';p=[-1,-2,-3]';K=acker(a,b,p)K =-1 2 4(3)讨论状态反馈与输出反馈的关系, 说明状态反馈为何能进行极点配置?在经典控制理论中,一般只考虑由系统的输出变量来构成反馈律,即输出反馈。
在现代控制理论的状态空间分析方法中,多考虑采用状态变量来构成反馈律,即状态反馈。
从状态空间模型输出方程可以看出,输出反馈可视为状态反馈的一个特例。
状态反馈可以提供更多的补偿信息,只要状态进行简单的计算再反馈,就可以获得优良的控制性能。
(4)使用状态反馈配置极点的前提是系统的状态是完全可控的。
2.已知系统设计全维状态观测器,使观测器的极点配置在12+j,12-j 。
(1)给出原系统的状态曲线。
(2)给出观测器的状态曲线并加以对比。
(观测器的初始状态可以任意选取)观察实验结果,思考以下问题:(1)说明反馈控制闭环期望极点和观测器极点的选取原则。
实验2 利用MATLAB判断系统的稳定性

G=Gt' (3)极点配置状态反馈系统的实现 根据(2)中的运行结果,用 SIMULINK 搭建仿真模型,实现极点配置状态反馈系统,绘制 系统的单位阶跃响应曲线
Step 1
x2 1 s Integrator 4
3
Gain 9
1 Gain 11
3 Gain 12
x1 1 s
Integrator 5
2 Gain 10
x
0 2
1 3
x
0 1u
y 1 0
K=
31
G=
9
7
三
:
示
波
器
图
形
四: a:
b
:
五:
(2)实验体会。
1:带有状态观测器的状态反馈系统在不同初始条件下更加稳定,反馈平稳,图像更加平缓, 稳定性更强。 2:初始状态值越大,系统稳定性 越低,、反馈时间越长,系统平稳所需时间越长。
[z,p,k]=ss2zp(A,B,C,D,1)
z= -4.3028 -0.6972
p= -1.6506 -0.1747 + 1.5469i -0.1747 - 1.5469i
k= 1
二:已知系统的状态方程和输出方程如下,用状态反馈使闭环系统的极点为-2+j、-2-j,
由于状态变量不能量测,设计状态观测器使观测器的极点为-6,-6
2 Gain 4
4 Out 4
Scope
4.实验报告: (1)写出将实验内容的程序和运行结果。
0 1 0 1
x 一:)判定系统的稳定性
0
0
1
x
现代控制工程MATLAB实验指导书V

昆明理工大学机电学院机械工程专业研究生实验《现代控制工程》MATLA实验指导书昆明理工大学机电工程学院现代控制工程》MATLAB 实验指导书一、MATLAB 简介1 MATLAB 概述MATLAB 是MA Trix LABoratory 的缩写,早期主要用于现代控制中复杂的矩阵、向量的各种运算。
由于MA TLAB 提供了强大的矩阵处理和绘图功能,很多专家因此在自己擅长的领域用它编写了许多专门的MATLAB 工具包( toolbox ),如控制系统工具包( control systems toolbox );系统辨识工具包( system identification toolbox );信号处理工具包( signal processing toolbox );鲁棒控制工具包( robust control toolbox );最优化工具包(optimization toolbox )等等。
由于MA TLAB 功能的不断扩展,所以现在的MATLAB 已不仅仅局限与现代控制系统分析和综合应用,它已是一种包罗众多学科的功能强大的“技术计算语言( TheLanguage of Technical Computing )”。
MathWorks 公司于1992 年推出了具有划时代意义的MATLAB 4.0 版本,并推出了交互式模型输入与仿真系统SIMULINK ,它使得控制系统的仿真与CAD 应用更加方便、快捷,用户可以方便地在计算机上建模和仿真实验。
1997 年MathWorks 推出的MA TLAB 5.0 版允许了更多的数据结构,1999 年初推出的MA TLAB 5.3 版在很多方面又进一步改进了MATLAB 语言的功能。
2000 年底推出的MATLAB 6.0 。
最新版本是MA TLAB7.0 。
MATLAB 以矩阵作为基本编程单元,它提供了各种矩阵的运算与操作,并有较强的绘图功能。
MATLAB 集科学计算、图像处理、声音处理于一身,是一个高度的集成系统,有良好的用户界面,并有良好的帮助功能。
现代控制理论实验内容

现代控制理论实验一一、实验目的:1.熟悉MATLAB,掌握Simulink 工具的使用方法;2.根据传递函数设计出对应的能控、串联结构图;3.掌握极点配置状态反馈方法设计控制器技术;4.学会设计全维观测器。
二、实验内容: 已知系统传递函数)3)(2()1(6)(+++=s s s s s W 1. 用Simulink 对该系统进行实现(1)能控性实现(2)串联实现2. 以上述系统的串联实现为基础,实验研究:(1)系统在初始条件作用下的状态响应和输出响应(2)系统在阶跃输入信号作用下的状态响应和输出响应(3)分析系统在状态空间坐标原点的稳定性3. 以上述系统的能控实现为基础,设计状态反馈控制器要求:系统输出的最大超调量8.16%=δ,调节时间1=s t 秒仿真分析系统的实际工作效果,由系统输出的实际阶跃响应曲线计算最 大超调量、调节时间、稳态误差等系统的性能参数分析该系统在输出比例控制下是否会存在稳态误差?状态反馈控制下是否会存在稳态误差?分析出现这种差异的原因,讨论消除状态反馈稳态误差的方 法。
4. 以上述系统的串联实现为基础,设计系统的全维状态观测器,观测器极点全为-4。
仿真分析在原系统和观测器系统初始条件相同和不同时,观测状态与原状态变量的差值随时间变化的情况,例如改变观测器极点配置到-9,结果有何不同?5. 结合以上 3、4 的结果,应用观测状态实现状态反馈控制对比分析实际状态反馈与观测状态反馈系统控制效果的异同三、实验装置:1.微型计算机2.实验平台采用MATLAB 及Simulink 工具四、实验数据及分析1.(1)能控性实现根据状态空间表达式直接写出系统的能控标准I 型:[]066,100560100010=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=y u x x输出响应:(2)串联实现输出响应:2.(1)初始条件下的状态响应和输出响应:状态响应:输出响应:(2)阶跃信号作用下的状态响应和输出响应:状态响应:输出响应:分析系统在坐标原点的稳定性:在(1)中设置的初始值为1,1,1,由状态响应曲线可以看出X1并不能最终稳定在零点,其他两条输出曲线虽可稳定,但系统仍可认为在原点处是不稳定的。
利用MATLAB设计状态观测器
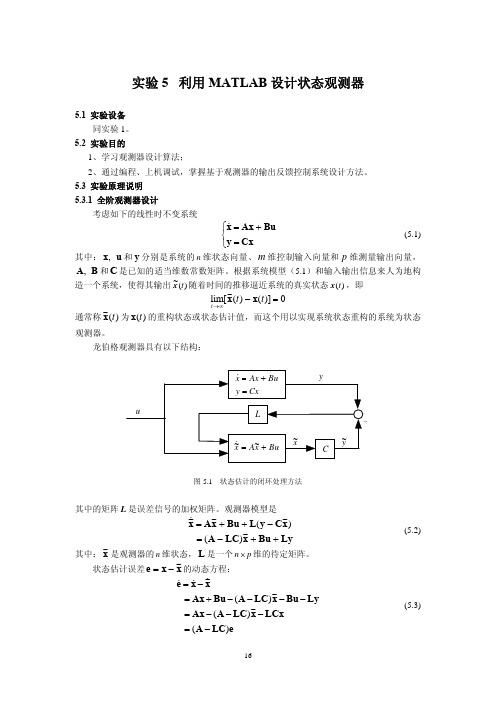
x%
+
⎢ ⎢
0
⎥ ⎥
u
+
⎢⎢147.3875⎥⎥
y
⎜⎝ ⎢⎣1.244 0.3965 −3.145⎥⎦ ⎢⎣544.3932⎥⎦
⎟⎠ ⎢⎣1.244⎥⎦ ⎢⎣544.3932⎥⎦
⎡ −16.855 = ⎢⎢−147.3875
⎣⎢−543.1492
1 0 0.3965
0 ⎤ ⎡ 0 ⎤ ⎡ 16.855 ⎤
统(5.9)具有任意给定的极点,这样的矩阵 L 可以应用全阶观测器的设计方法来设计。矩
阵 L 也称为是系统的降阶观测器增益矩阵。
对于降阶观测器的设计,使用 MATLAB 软件中的函数
L=(acker(Abb’,Aab’,V))’ 或
L=(place(Abb’,Aab’,V))’
可以得到观测器的增益矩阵 L 。其中的 V 是由降阶观测器的期望极点所组成的向量。
确定所需要的观测器增益矩阵。例如,对于单输入单输出系统,观测器的增益矩阵可以由函
数
L=(acker(A’,C’,V))’ 得到。其中的 V 是由期望的观测器极点所构成的向量。类似的,也可以用
L=(place(A’,C’,V))’ 来确定一般系统的观测器矩阵,但这里要求 V 不包含相同的极点。
5.3.2 降阶观测器设计
实验 5 利用 MATLAB 设计状态观测器
5.1 实验设备
同实验 1。
5.2 实验目的
1、学习观测器设计算法;
2、通过编程、上机调试,掌握基于观测器的输出反馈控制系统设计方法。
5.3 实验原理说明
5.3.1 全阶观测器设计
考虑如下的线性时不变系统
⎧x& = Ax + Bu
《现代控制理论》实验报告

.现代控制理论实验报告组员:院系:信息工程学院专业:指导老师:年月日实验1 系统的传递函数阵和状态空间表达式的转换[实验要求]应用MATLAB 对系统仿照[例1.2]编程,求系统的A 、B 、C 、阵;然后再仿照[例1.3]进行验证。
并写出实验报告。
[实验目的]1、学习多变量系统状态空间表达式的建立方法、了解系统状态空间表达式与传递函数相互转换的方法;2、通过编程、上机调试,掌握多变量系统状态空间表达式与传递函数相互转换方法。
[实验内容]1 设系统的模型如式(1.1)示。
p m n R y R u R x DCx y Bu Ax x ∈∈∈⎩⎨⎧+=+= (1.1)其中A 为n ×n 维系数矩阵、B 为n ×m 维输入矩阵 C 为p ×n 维输出矩阵,D 为传递阵,一般情况下为0,只有n 和m 维数相同时,D=1。
系统的传递函数阵和状态空间表达式之间的关系如式(1.2)示。
D B A SI C s den s num s G +-==-1)()()(()( (1.2)式(1.2)中,)(s num 表示传递函数阵的分子阵,其维数是p ×m ;)(s den 表示传递函数阵的按s 降幂排列的分母。
2 实验步骤① 根据所给系统的传递函数或(A 、B 、C 阵),依据系统的传递函数阵和状态空间表达式之间的关系如式(1.2),采用MATLA 的file.m 编程。
注意:ss2tf 和tf2ss 是互为逆转换的指令;② 在MATLA 界面下调试程序,并检查是否运行正确。
③ [1.1] 已知SISO 系统的状态空间表达式为(1.3),求系统的传递函数。
,2010050010000100001043214321u x x x x x x x x ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡ []⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=43210001x x x x y (1.3)程序:A=[0 1 0 0;0 0 -1 0;0 0 0 1;0 0 5 0]; B=[0;1;0;-2]; C=[1 0 0 0]; D=0;[num,den]=ss2tf(A,B,C,D,1)程序运行结果:num =0 -0.0000 1.0000 -0.0000 -3.0000 den =1.0000 0 -5.0000 0 0从程序运行结果得到:系统的传递函数为:24253)(ss s S G --= ④ [1.2] 从系统的传递函数式求状态空间表达式。
现代控制实验--状态反馈器和状态观测器的设计

现代控制实验--状态反馈器和状态观测器的设计-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN状态反馈器和状态观测器的设计一、实验设备PC 计算机,MATLAB 软件,控制理论实验台,示波器二、实验目的(1)学习闭环系统极点配置定理及算法,学习全维状态观测器设计法;(2)掌握用极点配置的方法(3)掌握状态观测器设计方法(4)学会使用MATLAB工具进行初步的控制系统设计三、实验原理及相关知识(1)设系统的模型如式所示若系统可控,则必可用状态反馈的方法进行极点配置来改变系统性能。
引入状态反馈后系统模型如下式所示:(2)所给系统可观,则系统存在状态观测器四、实验内容(1)某系统状态方程如下10100134326x x u •⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦[]100y x =理想闭环系统的极点为[]123---.(1)采用 Ackermann 公式计算法进行闭环系统极点配置;代码:A=[0 1 0;0 0 1;-4 -3 -2];B=[1; 3; -6];P=[-1 -2 -3];K=acker(A,B,P)Ac=A-B*Keig(Ac)(2)采用调用 place 函数法进行闭环系统极点配置;代码:A=[0 1 0;0 0 1;-4 -3 -2];B=[1;3;-6];eig(A)'P=[-1 -2 -3];K=place(A,B,P)eig(A-B*K)'(3)设计全维状态观测器,要求状态观测器的极点为[]---123代码:a=[0 1 0;0 0 1;-4 -3 -2];b=[1;3;-6];c=[1 0 0];p=[-1 -2 -3];a1=a';b1=c';c1=b';K=acker(a1,b1,p);h=(K)'ahc=a-h*c(2)已知系统状态方程为:10100134326x x u •⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦[]100y x =(1)求状态反馈增益阵K ,使反馈后闭环特征值为[-1 -2 -3];代码:A=[0 1 0;0 0 1;4 -3 -2];b=[1;3;-6];p=[-1 -2 -3];k=acker(A,b,p)A-b*keig(A-b*k)(2)检验引入状态反馈后的特征值与希望极点是否一致。
实验五利用MATLAB求解极点配置问题

现代控制理论第四次上机实验报告实验五 利用MATLAB 求解极点配置问题实验目的:1、学习极点配置状态反馈控制器的设计算法;2、通过编程、上机调试,掌握系统极点配置设计方法。
实验步骤:1、极点配置状态反馈控制器的设计,采用MA TLAB 的m-文件编程;2、在MA TLAB 界面下调试程序,并检查是否运行正确。
实验要求:1、 在运行以上程序的基础上,针对状态空间模型为[]01034132x x u y x⎡⎤⎡⎤=+⎢⎥⎢⎥--⎣⎦⎣⎦=的被控对象设计状态反馈控制器,使得闭环极点为-4和-5,并讨论闭环系统的稳态性能。
先判断系统能控性:>> A = [0 1 ;-3 -4];B = [0;1];Tc=ctrb(A,B)n=size(A);if rank(Tc)==n(1)disp('The system is controlled')elsedisp('The system is not controlled')endTc =0 11 -4The system is controlled再求状态反馈器:>> A = [0 1 ;-3 -4];B = [0;1];J = [-4 -5];K = place(A,B,J)K =17.0000 5.0000即状态反馈控制器为:状态反馈闭环系统状态空间表达式:A1=A-BK=[0 1;-20 -9]配置极点前:>> A=[0 1 ;-3 -4];B=[0;1];C=[3 2];D=0;step(A,B,C,D)得到波形:配置极点后:A变为A1>> A=[0 1 ;-20 -9];B=[0;1];C=[3 2];D=0;step(A,B,C,D)得到波形:由上述两图对比可知,配置极点后,系统动态性能变好,但是稳态误差变大。
2、 分析极点配置对稳态性能有何影响?如何消除对稳态性能的负面影响?答:配置极点后动态性能变好,但是稳态误差不能消除。
基于MATLAB的状态观测器设计

基于MATLAB 的状态观测器设计预备知识: 极点配置基于状态反馈的极点配置法就是通过状态反馈将系统的闭环极点配置到期望的极点位置上,从而使系统特性满足要求。
1. 极点配置原理假设原系统的状态空间模型为:⎩⎨⎧=+=Cxy Bu Ax x 若系统是完全可控的,则可引入状态反馈调节器,且:Kx u input -=这时,闭环系统的状态空间模型为:⎩⎨⎧=+-=Cxy Bu x )BK A (x 2. 极点配置的MATLAB 函数 在MATLAB 控制工具箱中,直接用于系统极点配置的函数有acker()和place()。
调用格式为:K=acker(A,C,P) 用于单输入单输出系统其中:A ,B 为系统矩阵,P 为期望极点向量,K 为反馈增益向量。
K=place(A,B,P)(K,prec,message)=place(A,B,P)place()用于单输入或多输入系统。
Prec 为实际极点偏离期望极点位置的误差;message 是当系统某一非零极点偏离期望位置大于10%时给出的警告信息。
3. 极点配置步骤:(1)获得系统闭环的状态空间方程;(2)根据系统性能要求,确定系统期望极点分布P ;(3)利用MATLAB 极点配置设计函数求取系统反馈增益K ; (4)检验系统性能。
已知系统模型如何从系统的输入输出数据得到系统状态?初始状态:由能观性,从输入输出数据确定。
不足:初始状态不精确,模型不确定。
思路:构造一个系统,输出逼近系统状态称为是的重构状态或状态估计值。
实现系统状态重构的系统称为状态观测器。
观测器设计状态估计的开环处理:但是存在模型不确定性和扰动!初始状态未知!应用反馈校正思想来实现状态重构。
通过误差来校正系统:状态误差,输出误差。
基于观测器的控制器设计系统模型若系统状态不能直接测量,可以用观测器来估计系统的状态。
L是观测器增益矩阵,对偏差的加权。
真实状态和估计状态的误差向量误差的动态行为:的极点决定了误差是否衰减、如何衰减?通过确定矩阵L来保证。
基于MATLAB平台的现代控制理论研究

c mp e e so fs se c n e t n he c mb n to fmo e c nr lt o n o r h n in o y t m o c p ,a d t o i ain o d m o to he r a d MATL y AB
wilo ti o d ta h n f c . l b an a g o e c i g ef t e
C ia 2 R rl f c, uuC u t R rl o e C m ayLm t , uuJl 3 20 C ia h ; . ua O e F y ony ua P wr o p n iid F y in1 10 , h ) n f i e i n
Absr c Mo e c n r lt e r sa mp ra tp oe so lb sc c u s n t e rl td s e i l t a t: d m o to h oy i n i ot n r f sina a i o re i h ea e p ca —
能观 测 性 的基 本 性 质 , 以及 对 稳 定性 的分 析 和 系统
数学 圈 。M T A A L B语 言能 用简单 的命令 给 出状 态 空 间模 型 以及 能控 性 和能 观测 性 , 析 系 统 稳定 性 时 分
的综合 , 也就 是状态 反馈 和状 态观 测器 的设计 , 同时 掌握 最优控 制 的问题 。 在本 门课 程 的学 习过 程 中 , 用 的数 学 工 具 最 应
收 稿 日期 :0 0 9 .0 2 1 46 2
也 可用直 观 的图形来 描述 系统 的稳定 性 。我 们要 改 变传 统 中过分 突 出数 学分 析和 变换 而掩 盖 本 质 内容 的缺 点 , 学 生 明确 分 析 目的 , 住 重 点 , 高 分 析 使 抓 提 问题 的能力 , 实现数学 概念 、 理概 念 和工 程 概念 的 物 统 一 , 导 学生 学 习使用 计 算 机 进行 实 际 的 分析 和 引 处 理 , 现理论 与实 际 的紧密结 合 , 分培 养 学生 利 实 充 用理 论分 析 问题 、 解决 问题 的能 力 。 针 对 以上 的思路 , 在 教 学 过程 中 针对 本 门课 拟 程 本 科 阶段 教 学 大 纲提 出的 重点 问题 , 状 态空 间 如 模 型 , 统 的求 解 问 题 , 系 以及 系 统 的 能 控 性 和 能 观 性, 系统 的李雅 普诺 夫稳定 性分 析 , 系统 的极 点 配置 和观测 器 设计 等 主要 问题 建立 MA L B平 台 , 示 TA 演 相 应 的概念定 理方 法 , 深学生 对抽 象 问题 的理 解 。 加
现代控制理论状态反馈和状态观测器的设计实验报告

现代控制理论状态反馈和状态观测器的设计实验报告本次实验是关于现代控制理论中状态反馈与状态观测器的设计与实现。
本次实验采用MATLAB进行模拟与仿真,并通过实验数据进行验证。
一、实验目的1、学习状态反馈控制的概念、设计方法及其在实际工程中的应用。
3、掌握MATLAB软件的使用方法。
二、实验原理1、状态反馈控制状态反馈控制是指将系统状态作为反馈控制的输出,通过对状态反馈控制器参数的设计,使系统的状态响应满足一定的性能指标。
状态反馈控制的设计步骤如下:(1) 确定系统的状态方程,即确定系统的状态矢量、状态方程矩阵和输出矩阵;(2) 设计状态反馈控制器的反馈矩阵,即确定反馈增益矩阵K;(3) 检验状态反馈控制器性能是否满足要求。
2、状态观测器(1) 确定系统的状态方程;(2) 设计观测器的状态估计矩阵和输出矩阵;(3) 检验观测器的状态估计精度是否符合标准。
三、实验内容将简谐信号加入单个质点振动系统,并对状态反馈控制器和状态观测器进行设计与实现。
具体实验步骤如下:1、建立系统状态方程:(1)根据系统的物理特性可得单自由度振动系统的运动方程为:m¨+kx=0(2)考虑到系统存在误差、干扰等因素,引入干扰项,得到系统状态方程:(3)得到系统状态方程为:(1)观察系统状态方程,可以发现系统状态量只存在于 m 行 m 到 m 行 n 之间,而控制量只存在于 m 行 1 到 m 行 n 之间,满足可控性条件。
(2)本次实验并未给出状态变量的全部信息,只给出了系统的一维输出,因此需要设计状态反馈器。
(3)我们采用极点配置法进行状态反馈器设计。
采用 MATLAB 工具箱函数,计算出极点:(4) 根据极点求解反馈矩阵,得到状态反馈增益矩阵K:(1)通过矩阵计算得到系统的可观性矩阵:(2)由若干个实测输出建立观测器,可将观测器矩阵与可观测性矩阵组合成 Hankel 矩阵,求解出状态观测器系数矩阵:(3)根据系统的状态方程和输出方程,设计观测方程和状态估计方程,如下:4、调试控制器和观测器(1)经过上述设计步骤,将反馈矩阵和观测矩阵带入 MATLAB 工具箱函数进行仿真。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
订 线
实 验 报 告
实验名称 利用MATLAB 实现极点配置、设计状态观测器
系 专业 自动化 班 姓名 学号 授课老师 预定时间
实验时间
实验台号
一、目的要求
1、掌握状态反馈和输出反馈的概念及性质。
2、掌握利用状态反馈进行极点配置的方法。
学会用MATLAB 求解状态反馈矩阵。
3、掌握状态观测器的设计方法。
学会用MATLAB 设计状态观测器。
4、熟悉分离定理,学会设计带有状态观测器的状态反馈系统。
二、原理简述
1、状态反馈和输出反馈
设线性定常系统的状态空间表达式为Cx
y Bu Ax x
=+=
如果采用状态反馈控制规律u= r-Kx ,其中 r 是参考输入,则状态反馈闭环系统的传递函数为:
B BK A sI
C G k 1)]([---=
2、极点配置
如果 SISO 线性定常系统完全能控,则可通过适当的状态反馈, 将闭环系统极点配置到任意期望的位置。
MATLAB 提供的函数acker( )是用Ackermann 公式求解状态反馈阵K 。
该函数的调用格 式为
K=acker(A,B,P)
其中A 和B 分别为系统矩阵和输入矩阵。
P 是期望极点构成的向量。
MATLAB 提供的函数place( )也可求出状态反馈阵K 。
该函数的调用格式为 K=place(A,B,P)
函数place( )还适用于多变量系统极点配置,但不适用含有多重期望极点的问题。
函数acker( )不适用于多变量系统极点配置问题,但适用于含有多重期望极点问题。
三、仪器设备
PC 计算机,MATLAB 软件
[0410x y ⎢=⎢⎢--⎣=理想闭环系统的极点为(1)采用直接计算法进行闭环系统极点配置;(2)采用Ackermann
订 线
y1=lsim(G,u,t); plot(t,y1,':',t,y2,'-')
蓝色为配置前,绿色为配置后
题5-3 某系统状态空间描述如下
[]010100134326100x x u y x
⎡⎤⎡⎤
⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦
= 设计全维状态观测器,要求状态观测器的极点为[]123---。
程序>> A=[0 1 0;0 0 1;-4 -3 -2];
B=[1;3;-6]'; C=[1 0 0]; D=0;
p=[-1 -2 -3]; L=(acker(A',C',p))' 结果:L = 4
0 -10。
