利用MATLAB 实现极点配置、设计状态观测器(现代控制系统)

利用MATLAB设计状态观测器

利用MATLAB 设计状态观测器本节将介绍用MATLAB 设计状态观测器的若干例子。

我们将举例说明全维状态观测器和最小阶状态观测器设计的MATLAB 方法。

------------------------------------------------[例1] 考虑一个调节器系统的设计。

给定线性定常系统为Cxy Bu Ax x =+=& 式中]01[,10,06.2010=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=C B A且闭环极点为)2,1(==i s i μ，其中4.28.1,4.28.121j j −−=+−=μμ期望用观测-状态反馈控制，而不是用真实的状态反馈控制。

观测器的期望特征值为821−==μμ试采用MATLAB 确定出相应的状态反馈增益矩阵K 和观测器增益矩阵e K 。

[解]对于题中给定的系统，可利用如下MATLAB Program 1来确定状态反馈增益矩阵K和观测器增益K。

矩阵eMATLAB Program 1% Pole placement and design of observer ------% ***** Design of a control system using pole-placement% technique and state observer. Solve pole-placement% problem *****% ***** Enter matrices A,B,C,and D *****A=[0 1;20.6 0];B=[0;1]C=[1 0];D=[0];% ***** Check the rank of the controllability matrix Q *****Q=[B A*B];Rank(Q)ans=2% ***** Since the rank of the controllability matrix Q is 2, % arbitrary pole placement is possible *****% ***** Enter the desired characteristic polynomial by% defining the following matrix J and computingpoly(J) *****J=[-1.8+2.4*i 0;0 -1.8-2.4*i];Poly(J)ans=1.000 3.6000 9.0000% ***** Enter characteristic polynomial Phi *****Phi=polyvalm(poly(J),A);% ***** State feedback gain matrix K can be given by ***** K=[0 1]*inv(Q)*PhiK=29.6000 3.6000% ***** The following program determines the observer matrix Ke *****% ***** Enter the observability matrix RT and check its rank *****RT=[C’ A’*C’];rank(RT)ans=2% ***** Since the rank of the observability matrix is 2, design of% the observer is possible *****% **** Enter the desired characteristic polynomial by defining % the following matrix J0 and entering statement poly(JO) *****JO=[-8 0;0 -8];Poly(JO)ans=1 16 64% ***** Enter characteristic polynomial Ph ***** Ph=polyvalm(ply(JO),A);% ***** The observer gain matrix Ke is obtained from ***** Ke=Ph*(inv(RT’))*[0;1]Ke=16.000084.60000求出的状态反馈增益矩阵K 为[]6.36.29=K观测器增益矩阵e K 为⎥⎦⎤⎢⎣⎡=6.8416e K 该观测-状态反馈控制系统是4阶的，其特征方程为0=+−+−C K A sI BKA sI e通过将期望的闭环极点和期望的观测器极点代入上式，可得5764.3746.1306.19)8)(4.28.1)(4.28.1(2342++++=+++−+=+−+−s s s s s j s j s C K A sI BK A sI e这个结果很容易通过MATLAB得到，如MATLAB Program 2所示(MATLAB Program 2是K已MATLAB Program1的继续。

matlab的自动控制原理实现

第 5 章 MATLAB在自动控制原理中的应用
对象名称 tf对象 (传递函数) 属性名称 den 意义传递函数分母系数属性值的变量类型由行数组组成的单元阵列
num
variable k
传递函数分子系数
传递函数变量增益极点
由行数组组成的单元阵列
s、z、p、k、z-1中之一二维矩阵由行数组组成的单元阵列
第 5 章 MATLAB在自动控制原理中的应用
第5章 MATLAB在自动控制原理的应用
5.1 控制系统模型 5.2 控制系统的时域分析
5.3 控制系统的根轨迹
5.4 控制系统的频域分析 5.5 系统的状态空间分析函数 5.6 极点配置和观测器设置 5.7 最优控制系统设计
x
p

i
x
D Dd
第 5 章 MATLAB在自动控制原理中的应用
2. 连续系统与采样系统之间的转换函数函数名 c2d 功能调用格式 sysd = c2d(sysc,Ts,method)
连续系统转换为采样系统
d2c
d2d
采样系统转换为连续系统
采样系统改变采样频率
sysc = d2c(sysd,method)
第 5 章 MATLAB在自动控制原理中的应用
2．LTI模型的复杂模型组合对复杂系统的任意组合，在MATLAB中，则采用集成的软件包，让机器自动去完成复杂的组合，人们只要输入各环节的LTI模型和相应的联接矩阵与输入矩阵，指定输出变量，软件包会自动判别输入的模型表述方式，作出相应的运算并最后给出组合后系统的状态方程。在求解过程中，主要涉及append( )函数和connect( )函数。通常，由以下五个步骤来完成： ①对方框图中的各个环节进行编号，建立它们的对象模型。 ②利用append函数命令建立无连接的状态空间模型。 sap=append(s1,s2,…,sm) ③按规定写出系统的互联接矩阵q 互联矩阵q中的每一行由组合系统的一个输入编号和构成该输入的其它输出编号组成，其中该行的第一个元素为该输入的编号，接下来的元素则由构成该输入的其它子框的输出编号组成，如果为负反馈，则编号应取负号。 ④选择组合系统中需保留的对外的输入和输出端的编号并列出。 Inputs=[i1,i2, …] outputs=[j1, j2,…] ⑤用connect命令生成组合后的系统。

基于Matlab的高阶阶系统单位阶跃响应主导极点分析

基于Matlab的高阶阶系统单位阶跃响应主导极点分析1. 引言在控制系统的设计和分析中，经常会遇到高阶阶系统。

高阶阶系统的单位阶跃响应主导极点分析是一项重要的任务。

通过分析系统的主导极点，可以对系统的动态性能进行评估，并在必要时进行控制器的调整和优化。

Matlab是一种强大的数值计算和编程环境，支持矩阵计算、绘图和数据分析等功能。

本文将介绍在Matlab中对高阶阶系统进行单位阶跃响应主导极点分析的方法和步骤。

2. 单位阶跃响应主导极点分析方法单位阶跃响应主导极点分析是通过分析系统的单位阶跃响应以及极点的位置来评估系统的动态特性。

主导极点是决定系统响应快慢的关键因素。

在Matlab中，可以使用控制系统工具箱中的函数来进行单位阶跃响应主导极点分析。

以下是一套基本的步骤：1.定义系统传递函数：在Matlab中，可以使用tf函数定义系统的传递函数。

例如，对于一个二阶系统，可以定义如下：sys = tf([b0 b1 b2], [a0 a1 a2]);其中b0, b1, b2和a0, a1, a2分别是系统的分子和分母多项式的系数。

2.绘制单位阶跃响应曲线：使用step函数可以绘制系统的单位阶跃响应曲线。

例如：step(sys);该命令将绘制系统的单位阶跃响应曲线。

3.分析主导极点：观察单位阶跃响应曲线，可以确定系统的主导极点。

主导极点是响应曲线上最快的极点。

4.评估系统的动态性能：根据主导极点的位置和单位阶跃响应曲线的特点，可以评估系统的动态性能。

例如，主导极点越远离虚轴，系统的动态响应速度越快。

5.进行控制器调整和优化：根据动态性能评估结果，可以对控制器进行调整和优化，以满足设计要求。

3. 实例分析为了更好地理解基于Matlab的高阶阶系统单位阶跃响应主导极点分析的方法，我们将介绍一个实例。

假设有一个三阶系统，传递函数为：G(s) = (s+2) / ((s+1)(s+3))我们可以在Matlab中进行如下操作：b = [12];a = conv([11], [13]);sys = tf(b, a);step(sys);运行上述代码后，将绘制出系统的单位阶跃响应曲线。

基于matlab gui的控制系统界面设计毕业设计论文

基于MATLAB GUI的控制系统界面设计摘要：MATLAB语言是一种十分有效的工具，能容易地解决在系统仿真及控制系统设计领域的教学与研究中遇到的问题，它可以将使用者从频繁的底层编程中解放出来，把有限的宝贵时间更多地华仔解决科学问题上。

MATLABA GUI是MATLAB人际交互界面。

由于GUI本身提供了windows基本控件的支持，并且具有良好的时间驱动机制，同时提供了MATLAB数学库的接口，所以GUI对于控制系统仿真的平台设计显得十分合适。

GUI对于每个用户窗口生成.fig和.m 文件。

前者负责界面的设计信息，后者负责后台代码的设计。

本文界面设计主要基于MATLAB GUI平台，结合控制系统基础理论和MATLAB控制系统工具箱，实现了用于控制系统界面的设计。

主要包括：进行常规控制环节（比如PID）的图形界面设计，能够在已知传输函数的情况下，输出常用响应曲线。

关键词：控制系统；MATLAB GUI；计算机设计Control system based on MATLAB GUI interface designAbstract: MATLAB language is a very effective tool,and can be easily resolved in the system simulation and control system of teaching in the field of computer-aided design and research problems,it could be the bottom of the user from tedious programming liberate the limted spend more valuable time to solve scientific problems. The MATLAB GUI is the interative interface.As the GUI itself provides the basic control windows support,and has a good mechanism for event-driven,while providing the MATLAB Math Library interface,the GUI for control system simulation platform for the design of it is suitable. GUI window generated for each user.Figand .M file. The former is responsible for the design of the interfaceinformation,which is responsible for the design of the background code.Research done in this article is mainly based on MATLAB GUI platform,the basis of combination of control syetem theory and MATLAB Control System Toolbox,the realization of control systems for computer-aided analysis and design software.Mainly includes:routine control links,such as PID,graphical interface design,can in the known transfer function of the case,the output respnonse curve is commonly used.Key words: Control System;MATLAB GUI;Computer design目录1 概述 (1)1.1 本文研究的目的以及意义 (1)1.2 已了解的本课题国内外研究现状 (1)1.3 本课题研究内容 (3)2 控制系统与MATLAB语言 (3)2.1 控制系统理论基础 (3)2.1.1 控制系统的古典理论与现代理论 (3)2.1.2 控制系统理论的基本内容 (4)2.2 MATLAB语言与控制系统工具箱 (4)2.2.1 MATLAB软件介绍 (5)2.2.2 控制系统工具箱介绍 (7)3 MATLAB简介及应用 (9)3.1 MATLAB GUI (9)3.2 图形用户界面设计工具的启动 (10)3.2.1图形用户界面设计工具的启动方式 (10)3.2.2 菜单方式 (10)3.2.3 图形用户界面设计窗口 (13)3.3 图形用户界面开发环境(GUIDE) (14)3.4 控件对象及属性 (16)3.5 菜单设计 (18)3.5.1 建立用户菜单 (18)3.5.2 菜单对象常用属性 (18)3.5.3 快捷菜单 (18)3.5.4 对话框设计 (19)3.5.5 公共对话框 (19)3.6 GUI程序设计 (19)4 GUI控制系统界面 (20)4.1 GUI控制系统界面设计 (20)4.1.1 具体设计步骤 (20)4.2 具体实现过程 (23)4.2.1 运行效果 (23)4.2.2 实现代码 (24)[参考文献] (25)附录 (26)谢辞 (29)1 概述1.1 本文研究的目的以及意义自动控制原理是自动控制专业和自动化专业的主要课程之一[3]，是研究自动控制技术的基础理论课，是必修的专业基础课程。

利用matlab实现极点配置、设计状态观测器(现代控制)

实验报告实验名称利用MATLAB 实现极点配置、设计状态观测器系专业自动化班姓名学号授课老师预定时间实验时间实验台号一、目的要求1、掌握状态反馈和输出反馈的概念及性质。

2、掌握利用状态反馈进行极点配置的方法。

学会用MATLAB 求解状态反馈矩阵。

3、掌握状态观测器的设计方法。

学会用MATLAB 设计状态观测器。

4、熟悉分离定理，学会设计带有状态观测器的状态反馈系统。

二、原理简述1、状态反馈和输出反馈设线性定常系统的状态空间表达式为Cxy Bu Ax x =+=如果采用状态反馈控制规律u= r-Kx ，其中 r 是参考输入，则状态反馈闭环系统的传递函数为：B BK A sIC G k 1)]([---=2、极点配置如果 SISO 线性定常系统完全能控，则可通过适当的状态反馈, 将闭环系统极点配置到任意期望的位置。

MATLAB 提供的函数acker( )是用Ackermann 公式求解状态反馈阵K 。

该函数的调用格式为K=acker(A,B,P)其中A 和B 分别为系统矩阵和输入矩阵。

P 是期望极点构成的向量。

MATLAB 提供的函数place( )也可求出状态反馈阵K 。

该函数的调用格式为 K=place(A,B,P)函数place( )还适用于多变量系统极点配置，但不适用含有多重期望极点的问题。

函数acker( )不适用于多变量系统极点配置问题，但适用于含有多重期望极点问题。

三、仪器设备PC 计算机，MATLAB 软件⎣[y1=lsim(G,u,t); plot(t,y1,':',t,y2,'-')蓝色为配置前，绿色为配置后题5-3 某系统状态空间描述如下[]010100134326100x x u y x⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦= 设计全维状态观测器，要求状态观测器的极点为[]123---。

程序>> A=[0 1 0;0 0 1;-4 -3 -2];B=[1;3;-6]'; C=[1 0 0]; D=0;p=[-1 -2 -3]; L=(acker(A',C',p))' 结果：L = 40 -10。

利用MATLAB 实现极点配置、设计状态观测器(现代控制)

订线实验报告实验名称利用MATLAB 实现极点配置、设计状态观测器系专业自动化班姓名学号授课老师预定时间实验时间实验台号一、目的要求1、掌握状态反馈和输出反馈的概念及性质。

2、掌握利用状态反馈进行极点配置的方法。

学会用MATLAB 求解状态反馈矩阵。

3、掌握状态观测器的设计方法。

学会用MATLAB 设计状态观测器。

4、熟悉分离定理，学会设计带有状态观测器的状态反馈系统。

二、原理简述1、状态反馈和输出反馈设线性定常系统的状态空间表达式为Cxy Bu Ax x=+=如果采用状态反馈控制规律u= r-Kx ，其中 r 是参考输入，则状态反馈闭环系统的传递函数为：B BK A sIC G k 1)]([---=2、极点配置如果 SISO 线性定常系统完全能控，则可通过适当的状态反馈, 将闭环系统极点配置到任意期望的位置。

MATLAB 提供的函数acker( )是用Ackermann 公式求解状态反馈阵K 。

该函数的调用格式为K=acker(A,B,P)其中A 和B 分别为系统矩阵和输入矩阵。

P 是期望极点构成的向量。

MATLAB 提供的函数place( )也可求出状态反馈阵K 。

该函数的调用格式为 K=place(A,B,P)函数place( )还适用于多变量系统极点配置，但不适用含有多重期望极点的问题。

函数acker( )不适用于多变量系统极点配置问题，但适用于含有多重期望极点问题。

三、仪器设备PC 计算机，MATLAB 软件[0410x y ⎢=⎢⎢--⎣=理想闭环系统的极点为（1）采用直接计算法进行闭环系统极点配置；（2）采用Ackermann订线y1=lsim(G,u,t); plot(t,y1,':',t,y2,'-')蓝色为配置前，绿色为配置后题5-3 某系统状态空间描述如下[]010100134326100x x u y x⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦= 设计全维状态观测器，要求状态观测器的极点为[]123---。

matlab设计状态反馈矩阵运行步骤

matlab设计状态反馈矩阵运行步骤步骤1：定义系统模型我们需要定义系统的状态空间模型。

状态空间模型由系统的状态方程和输出方程组成。

我们可以使用matlab中的tf函数或ss函数来创建系统模型。

例如，如果我们有一个传递函数为G(s)的系统模型，我们可以使用tf函数将其转换为状态空间模型：```G = tf([1],[1 2 1]);sys = ss(G);```在这个例子中，我们创建了一个传递函数为1/(s^2 + 2s + 1)的系统模型，并将其转换为状态空间模型。

步骤2：选择反馈增益矩阵接下来，我们需要选择反馈增益矩阵K。

反馈增益矩阵的选择决定了状态反馈的效果。

一般来说，我们可以使用极点配置方法来选择反馈增益矩阵。

极点配置方法可以使系统的极点移动到我们期望的位置，从而改变系统的响应特性。

在matlab中，我们可以使用place函数来进行极点配置。

place函数需要输入系统模型、期望的极点位置和对应的增益矩阵，然后返回一个满足极点配置要求的反馈增益矩阵。

例如，如果我们希望系统的极点位于-1和-2处，我们可以使用以下代码选择反馈增益矩阵：```desired_poles = [-1 -2];K = place(sys.A, sys.B, desired_poles);```在这个例子中，我们将系统模型的A矩阵和B矩阵作为输入，以及期望的极点位置，然后使用place函数计算反馈增益矩阵K。

步骤3：计算闭环系统的状态空间模型有了反馈增益矩阵K之后，我们可以计算闭环系统的状态空间模型。

闭环系统的状态空间模型由系统的A矩阵、B矩阵、C矩阵和D矩阵组成。

我们可以使用matlab中的feedback函数来计算闭环系统的状态空间模型。

feedback函数需要输入系统模型、反馈增益矩阵和反馈信号的位置，然后返回闭环系统的状态空间模型。

例如，如果我们希望将反馈信号加到系统的输入端，我们可以使用以下代码计算闭环系统的状态空间模型：```feedback_sys = feedback(sys, K, 1);```在这个例子中，我们将系统模型、反馈增益矩阵和反馈信号的位置作为输入，然后使用feedback函数计算闭环系统的状态空间模型。

现代控制理论MATLAB编程

现代控制理论实验报告姓名：班级:学号：目录一．实验设备二．实验目的三．实验步骤一、实验设备PC计算机1台,MATLAB软件1套。

二、实验目的1。

学习系统状态空间表达式的建立方法、了解系统状态空间表达式与传递函数相互转换的方法；2。

通过编程、上机调试、掌握系统状态空间表达式与传递函数相互转换方法;3。

学习MATLAB的使用方法。

三、实验步骤1、根据所给系统的结构图写出死循环系统的传递函数，若K=10，T=0。

1时阶跃输出下的系统输出响应,并采用MATLAB编程.2、在MATLAB接口下调试程序，并检查是否运行正确.3、给出定二阶系统结构图:图为二阶系统结构图（1）求二阶系统的闭环循环传递函数ɸ(s ）=)(1)(s G s G +=K S TS K++2（2)若K=10，T=0。

1，仿真给出阶跃下的系统输出响应把K T 代入方程得Φ（S)= =1）MATLAB 命令得出的系统响应曲线在MATLAB 上输入下列指令：〉> num=［100]；>> den=［1，10，100]；>> step （num,den)程序运行后显示的时域动态响应曲线（如图2)图为时域动态响应曲线2）、用进行Simulink 进行仿真启动Simulink并打开一个空白的模块编辑窗口,画出所需模块,并给出正确参数，将画出的所有模块链接起来（如图1）,构成一个原系统的框图描述(如图3）.选择仿真控制参数，启动仿真过程。

仿真结果示波器显示如图4。

图3二阶系统的Simulink(仿真）图4仿真结果示波器显示（仿真输出）（3) 调整比例系数K，使之从零开始增加。

同时，观察仿真曲线的变化,并给出过阻尼、临界、欠阻尼的条件。

当K=0时的仿真曲线当K=1时的仿真曲线当K=2.5时的仿真曲线当K=3。

5时的仿真曲线当K=4时的仿真曲线根据调整比例系数K，使之从零开始增加，同时观察仿真曲线的变化，得出以下结论；过阻尼的条件：K>2.5时；临界阻尼条件：K=2.5时；欠阻尼的条件：K<2。

现代控制理论实验五、状态反馈控制器设计河南工业大学

河南工业大学《现代控制理论》实验报告专业: 自动化班级: F1203 姓名: 蔡申申学号:201223910625完成日期：2015年1月9日成绩评定:一、实验题目：状态反馈控制器设计二、实验目的1. 掌握状态反馈和输出反馈的概念及性质。

2. 掌握利用状态反馈进行极点配置的方法。

学会用MATLAB 求解状态反馈矩阵。

3. 掌握状态观测器的设计方法。

学会用MATLAB 设计状态观测器。

三、实验过程及结果1. 已知系统u x x ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=111100020003.[]x y 3333.02667.04.0= （1）求解系统的零点、极点和传递函数，并判断系统的能控性和能观测性。

A=[-3 0 0;0 2 0;0 0 -1];B=[1;1;1];C=[0.4 0.266 0.3333];[z p k]=ss2zp(A,B,C,0)系统的零极点：z =1.0017-1.9997p =-3-12k =0.9993[num den]=ss2tf(A,B,C,0)num =0 0.9993 0.9973 -2.0018den =1 2 -5 -6系统的传递函数：G1=tf(num,den)G1 =0.9993 s^2 + 0.9973 s - 2.002-----------------------------s^3 + 2 s^2 - 5 s - 6Continuous-time transfer function.Uc=ctrb(A,B); rank(Uc)ans =3满秩，系统是能控的。

Vo=obsv(A,C); rank(Vo)ans =3满秩，系统是能观的。

（2）分别选取K=[0 3 0]，K=[1 3 2]，K=[0 16 /3 –1/3]（实验中只选取其中一个K为例）为状态反馈矩阵，求解闭环系统的零点、极点和传递函数，判断闭环系统的能控性和能观测性。

基于matlab的状态观测器设计

基于MATLAB 的状态观测器设计预备知识：极点配置基于状态反馈的极点配置法就是通过状态反馈将系统的闭环极点配置到期望的极点位置上，从而使系统特性满足要求。

1. 极点配置原理假设原系统的状态空间模型为：⎩⎨⎧=+=Cxy Bu Ax x 若系统是完全可控的，则可引入状态反馈调节器，且：Kx u input -=这时，闭环系统的状态空间模型为：⎩⎨⎧=+-=Cxy Bu x )BK A (x 2. 极点配置的MATLAB 函数在MATLAB 控制工具箱中，直接用于系统极点配置的函数有acker()和place()。

调用格式为：K=acker(A,C,P) 用于单输入单输出系统其中：A ，B 为系统矩阵，P 为期望极点向量，K 为反馈增益向量。

K=place(A,B,P)(K,prec,message)=place(A,B,P)place()用于单输入或多输入系统。

Prec 为实际极点偏离期望极点位置的误差；message 是当系统某一非零极点偏离期望位置大于10%时给出的警告信息。

3. 极点配置步骤：（1）获得系统闭环的状态空间方程；（2）根据系统性能要求，确定系统期望极点分布P ；（3）利用MATLAB 极点配置设计函数求取系统反馈增益K ；（4）检验系统性能。

已知系统模型如何从系统的输入输出数据得到系统状态？初始状态：由能观性，从输入输出数据确定。

不足：初始状态不精确，模型不确定。

思路：构造一个系统，输出逼近系统状态称为是的重构状态或状态估计值。

实现系统状态重构的系统称为状态观测器。

观测器设计状态估计的开环处理：但是存在模型不确定性和扰动！初始状态未知！应用反馈校正思想来实现状态重构。

通过误差来校正系统：状态误差，输出误差。

基于观测器的控制器设计系统模型若系统状态不能直接测量，可以用观测器来估计系统的状态。

L是观测器增益矩阵，对偏差的加权。

真实状态和估计状态的误差向量误差的动态行为：的极点决定了误差是否衰减、如何衰减？通过确定矩阵L来保证。

实验 6 极点配置与全维状态观测器的设计

实验 6 极点配置与全维状态观测器的设计一、实验目的1. 加深对状态反馈作用的理解。

2. 学习和掌握状态观测器的设计方法。

二、实验原理在MATLAB 中，可以使用acker 和place 函数来进行极点配置，函数的使用方法如下：K = acker(A,B,P) A，B为系统系数矩阵，P为配置极点，K为反馈增益矩阵。

K = place(A,B,P) A，B为系统系数矩阵，P为配置极点，K为反馈增益矩阵。

[K,PREC,MESSAGE] = place(A,B,P) A，B为系统系数矩阵，P为配置极点，K为反馈增益矩阵，PREC 为特征值，MESSAGE 为配置中的出错信息。

三、实验内容1.已知系统（1）判断系统稳定性，说明原因。

（2）若不稳定，进行极点配置，期望极点：-1，-2，-3，求出状态反馈矩阵k。

（3）讨论状态反馈与输出反馈的关系，说明状态反馈为何能进行极点配置？（4）使用状态反馈进行零极点配置的前提条件是什么？1.（1）（2）代码：a=[-2 -1 1;1 0 1;-1 0 1];b=[1,1,1]';p=[-1,-2,-3]';K=acker(a,b,p)K =-1 2 4（3）讨论状态反馈与输出反馈的关系, 说明状态反馈为何能进行极点配置?在经典控制理论中,一般只考虑由系统的输出变量来构成反馈律，即输出反馈。

在现代控制理论的状态空间分析方法中,多考虑采用状态变量来构成反馈律，即状态反馈。

从状态空间模型输出方程可以看出，输出反馈可视为状态反馈的一个特例。

状态反馈可以提供更多的补偿信息，只要状态进行简单的计算再反馈，就可以获得优良的控制性能。

(4)使用状态反馈配置极点的前提是系统的状态是完全可控的。

2.已知系统设计全维状态观测器，使观测器的极点配置在12+j，12-j 。

（1）给出原系统的状态曲线。

（2）给出观测器的状态曲线并加以对比。

（观测器的初始状态可以任意选取）观察实验结果，思考以下问题：（1）说明反馈控制闭环期望极点和观测器极点的选取原则。

实验2 利用MATLAB判断系统的稳定性

G=Gt' （3）极点配置状态反馈系统的实现根据（2）中的运行结果，用 SIMULINK 搭建仿真模型，实现极点配置状态反馈系统，绘制系统的单位阶跃响应曲线
Step 1
x2 1 s Integrator 4
3
Gain 9
1 Gain 11
3 Gain 12
x1 1 s
Integrator 5
2 Gain 10

x

0 2
1 3
x

0 1u
y 1 0
K=
31
G=
9
7
三
：
示
波
器
图
形
四： a:
b
：
五：
（2）实验体会。
1：带有状态观测器的状态反馈系统在不同初始条件下更加稳定，反馈平稳，图像更加平缓，稳定性更强。 2：初始状态值越大，系统稳定性越低，、反馈时间越长，系统平稳所需时间越长。
[z,p,k]=ss2zp(A,B,C,D,1)
z= -4.3028 -0.6972
p= -1.6506 -0.1747 + 1.5469i -0.1747 - 1.5469i
k= 1
二：已知系统的状态方程和输出方程如下，用状态反馈使闭环系统的极点为-2+j、-2-j，
由于状态变量不能量测，设计状态观测器使观测器的极点为-6，-6
2 Gain 4
4 Out 4
Scope
4.实验报告：（1）写出将实验内容的程序和运行结果。
0 1 0 1

x 一：）判定系统的稳定性

0
0
1

x

利用MATLAB设计状态观测器—现代控制理论实验报告

实验六利用MATLAB设计状态观测器*******学号1121*****实验目的：1、学习观测器设计算法；2、通过编程、上机调试，掌握基于观测器的输出反馈控制系统设计方法。

实验原理：1、全阶观测器模型：()()x Ax Bu L y Cx A LC x Bu Ly =++-=-++由极点配置和观测器设计问题的对偶关系，也可以应用MATLAB 中极点配置的函数来确定所需要的观测器增益矩阵。

例如，对于单输入单输出系统，观测器的增益矩阵可以由函数L=(acker(A ’,C ’,V))’得到。

其中的V 是由期望的观测器极点所构成的向量。

类似的，也可以用L=(place(A ’,C ’,V))’来确定一般系统的观测器矩阵，但这里要求V 不包含相同的极点。

2、降阶观测器模型：ˆˆˆw AwBy Fu =++ b x w Ly =+基于降阶观测器的输出反馈控制器是：ˆˆˆˆ()[()]()b a bb a b w A FK w B F K K L y u K w K K L y=-+-+=--+对于降阶观测器的设计，使用MATLAB 软件中的函数L=(acker(Abb ’,Aab ’,V))’或L=(place(Abb ’,Aab ’,V))’可以得到观测器的增益矩阵L 。

其中的V 是由降阶观测器的期望极点所组成的向量。

实验要求1．在运行以上例程序的基础上，考虑图6.3所示的调节器系统，试针对被控对象设计基于全阶观测器和降阶观测器的输出反馈控制器。

设极点配置部分希望的闭环极点是1,2223j λ=-±，希望的观测器极点是（a ）对于全阶观测器，18μ=-和 28μ=-；（b ）对于降阶观测器，8μ=-。

比较系统对下列指定初始条件的响应：（a ）对于全阶观测器： 1212(0)1,(0)0,(0)1,(0)0x x e e ====（b ）对于降阶观测器：121(0)1,(0)0,(0)1x x e ===进一步比较两个系统的带宽。

利用MATLAB设计状态观测器

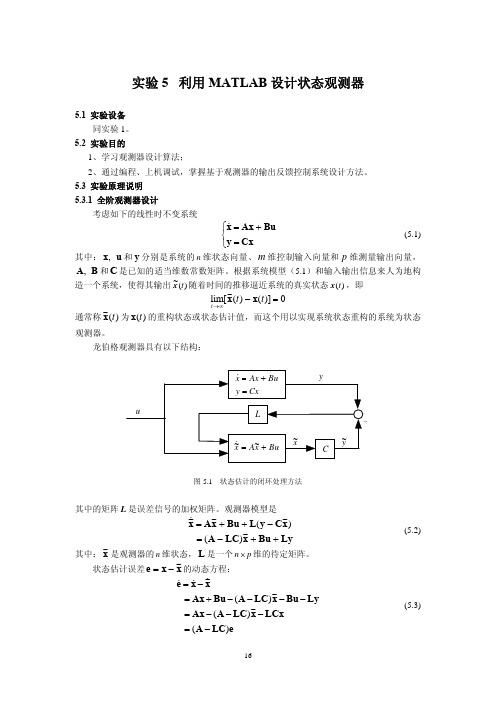
x%
+
⎢ ⎢
0
⎥ ⎥
u
+
⎢⎢147.3875⎥⎥
y
⎜⎝ ⎢⎣1.244 0.3965 −3.145⎥⎦ ⎢⎣544.3932⎥⎦
⎟⎠ ⎢⎣1.244⎥⎦ ⎢⎣544.3932⎥⎦
⎡ −16.855 = ⎢⎢−147.3875
⎣⎢−543.1492
1 0 0.3965
0 ⎤ ⎡ 0 ⎤ ⎡ 16.855 ⎤
统（5.9）具有任意给定的极点，这样的矩阵 L 可以应用全阶观测器的设计方法来设计。矩
阵 L 也称为是系统的降阶观测器增益矩阵。
对于降阶观测器的设计，使用 MATLAB 软件中的函数
L=(acker(Abb’,Aab’,V))’ 或
L=(place(Abb’,Aab’,V))’
可以得到观测器的增益矩阵 L 。其中的 V 是由降阶观测器的期望极点所组成的向量。
确定所需要的观测器增益矩阵。例如，对于单输入单输出系统，观测器的增益矩阵可以由函
数
L=(acker(A’,C’,V))’ 得到。其中的 V 是由期望的观测器极点所构成的向量。类似的，也可以用
L=(place(A’,C’,V))’ 来确定一般系统的观测器矩阵，但这里要求 V 不包含相同的极点。
5.3.2 降阶观测器设计
实验 5 利用 MATLAB 设计状态观测器
5.1 实验设备
同实验 1。
5.2 实验目的
1、学习观测器设计算法；
2、通过编程、上机调试，掌握基于观测器的输出反馈控制系统设计方法。
5.3 实验原理说明
5.3.1 全阶观测器设计
考虑如下的线性时不变系统
⎧x& = Ax + Bu

实验五利用MATLAB求解极点配置问题

现代控制理论第四次上机实验报告实验五利用MATLAB 求解极点配置问题实验目的：1、学习极点配置状态反馈控制器的设计算法；2、通过编程、上机调试，掌握系统极点配置设计方法。

实验步骤：1、极点配置状态反馈控制器的设计，采用MA TLAB 的m-文件编程；2、在MA TLAB 界面下调试程序，并检查是否运行正确。

实验要求：1、在运行以上程序的基础上，针对状态空间模型为[]01034132x x u y x⎡⎤⎡⎤=+⎢⎥⎢⎥--⎣⎦⎣⎦=的被控对象设计状态反馈控制器，使得闭环极点为-4和-5，并讨论闭环系统的稳态性能。

先判断系统能控性：>> A = [0 1 ;-3 -4];B = [0;1];Tc=ctrb(A,B)n=size(A);if rank(Tc)==n(1)disp('The system is controlled')elsedisp('The system is not controlled')endTc =0 11 -4The system is controlled再求状态反馈器：>> A = [0 1 ;-3 -4];B = [0;1];J = [-4 -5];K = place(A,B,J)K =17.0000 5.0000即状态反馈控制器为：状态反馈闭环系统状态空间表达式：A1=A-BK=[0 1;-20 -9]配置极点前：>> A=[0 1 ;-3 -4];B=[0;1];C=[3 2];D=0;step(A,B,C,D)得到波形：配置极点后：A变为A1>> A=[0 1 ;-20 -9];B=[0;1];C=[3 2];D=0;step(A,B,C,D)得到波形：由上述两图对比可知，配置极点后，系统动态性能变好，但是稳态误差变大。

2、分析极点配置对稳态性能有何影响？如何消除对稳态性能的负面影响？答：配置极点后动态性能变好，但是稳态误差不能消除。

Matlab控制系统设计工具箱的状态反馈控制指南

Matlab控制系统设计工具箱的状态反馈控制指南引言：状态反馈控制是控制系统设计中常用的一种方法。

它通过测量系统状态，并将其反馈回控制器中，以调节系统的输出。

Matlab控制系统设计工具箱提供了一些强大的功能和工具，使得状态反馈控制的设计变得更加简单和方便。

本文将探讨Matlab控制系统设计工具箱中的状态反馈控制设计，并提供一些实例进行演示和说明。

一、Matlab控制系统设计工具箱简介Matlab控制系统设计工具箱是Matlab提供的一个用于控制系统设计与分析的工具。

它集成了多种控制系统设计和分析方法，包括状态反馈控制、PID控制、根轨迹设计等。

其中，状态反馈控制是一个重要且常用的设计方法，可以用来改善系统的稳定性、响应速度和鲁棒性。

二、Matlab控制系统设计工具箱中的状态反馈控制设计1. 系统模型的建立在进行状态反馈控制设计之前，我们首先需要建立被控对象的数学模型。

这个模型可以通过系统的物理特性、传递函数或差分方程等方式得到。

在Matlab中，我们可以使用tf或zpk函数来建立连续或离散的传递函数模型，并使用ss函数建立状态空间模型。

2. 系统的可控性和可观性分析在进行状态反馈控制设计之前，我们需要对系统进行可控性和可观性分析。

可控性是指系统是否可以通过状态反馈方式对其进行控制；可观性是指系统是否可以通过测量其输出对系统的状态进行估计。

在Matlab中，我们可以使用ctrb和obsv函数来进行可控性和可观性分析。

3. 构造状态反馈控制器构造状态反馈控制器的目标是通过选择适当的反馈矩阵来使系统在闭环下具有所需的性能指标。

在Matlab中，我们可以使用place函数来通过极点配置的方式构造状态反馈控制器，也可以使用lqr函数来进行基于线性二次调节器的控制器设计。

4. 系统的闭环分析在构造状态反馈控制器之后，我们需要对闭环系统进行性能分析。

通常，我们可以通过计算系统的特征根来评估系统的稳定性和响应速度。

基于MATLAB的状态观测器设计

基于MATLAB 的状态观测器设计预备知识：极点配置基于状态反馈的极点配置法就是通过状态反馈将系统的闭环极点配置到期望的极点位置上，从而使系统特性满足要求。

1. 极点配置原理假设原系统的状态空间模型为：⎩⎨⎧=+=Cxy Bu Ax x 若系统是完全可控的，则可引入状态反馈调节器，且：Kx u input -=这时，闭环系统的状态空间模型为：⎩⎨⎧=+-=Cxy Bu x )BK A (x 2. 极点配置的MATLAB 函数在MATLAB 控制工具箱中，直接用于系统极点配置的函数有acker()和place()。

调用格式为：K=acker(A,C,P) 用于单输入单输出系统其中：A ，B 为系统矩阵，P 为期望极点向量，K 为反馈增益向量。

K=place(A,B,P)(K,prec,message)=place(A,B,P)place()用于单输入或多输入系统。

Prec 为实际极点偏离期望极点位置的误差；message 是当系统某一非零极点偏离期望位置大于10%时给出的警告信息。

3. 极点配置步骤：（1）获得系统闭环的状态空间方程；（2）根据系统性能要求，确定系统期望极点分布P ；（3）利用MATLAB 极点配置设计函数求取系统反馈增益K ；（4）检验系统性能。

已知系统模型如何从系统的输入输出数据得到系统状态？初始状态：由能观性，从输入输出数据确定。

不足：初始状态不精确，模型不确定。

思路：构造一个系统，输出逼近系统状态称为是的重构状态或状态估计值。

实现系统状态重构的系统称为状态观测器。

观测器设计状态估计的开环处理：但是存在模型不确定性和扰动！初始状态未知！应用反馈校正思想来实现状态重构。

通过误差来校正系统：状态误差，输出误差。

基于观测器的控制器设计系统模型若系统状态不能直接测量，可以用观测器来估计系统的状态。

L是观测器增益矩阵，对偏差的加权。

真实状态和估计状态的误差向量误差的动态行为：的极点决定了误差是否衰减、如何衰减？通过确定矩阵L来保证。

现代控制理论状态反馈和状态观测器的设计实验报告

现代控制理论状态反馈和状态观测器的设计实验报告本次实验是关于现代控制理论中状态反馈与状态观测器的设计与实现。

本次实验采用MATLAB进行模拟与仿真，并通过实验数据进行验证。

一、实验目的1、学习状态反馈控制的概念、设计方法及其在实际工程中的应用。

3、掌握MATLAB软件的使用方法。

二、实验原理1、状态反馈控制状态反馈控制是指将系统状态作为反馈控制的输出，通过对状态反馈控制器参数的设计，使系统的状态响应满足一定的性能指标。

状态反馈控制的设计步骤如下：(1) 确定系统的状态方程，即确定系统的状态矢量、状态方程矩阵和输出矩阵；(2) 设计状态反馈控制器的反馈矩阵，即确定反馈增益矩阵K；(3) 检验状态反馈控制器性能是否满足要求。

2、状态观测器(1) 确定系统的状态方程；(2) 设计观测器的状态估计矩阵和输出矩阵；(3) 检验观测器的状态估计精度是否符合标准。

三、实验内容将简谐信号加入单个质点振动系统，并对状态反馈控制器和状态观测器进行设计与实现。

具体实验步骤如下：1、建立系统状态方程：（1）根据系统的物理特性可得单自由度振动系统的运动方程为：m¨+kx=0（2）考虑到系统存在误差、干扰等因素，引入干扰项，得到系统状态方程：（3）得到系统状态方程为：（1）观察系统状态方程，可以发现系统状态量只存在于 m 行 m 到 m 行 n 之间，而控制量只存在于 m 行 1 到 m 行 n 之间，满足可控性条件。

（2）本次实验并未给出状态变量的全部信息，只给出了系统的一维输出，因此需要设计状态反馈器。

（3）我们采用极点配置法进行状态反馈器设计。

采用 MATLAB 工具箱函数，计算出极点：(4) 根据极点求解反馈矩阵，得到状态反馈增益矩阵K：（1）通过矩阵计算得到系统的可观性矩阵：（2）由若干个实测输出建立观测器，可将观测器矩阵与可观测性矩阵组合成 Hankel 矩阵，求解出状态观测器系数矩阵：（3）根据系统的状态方程和输出方程，设计观测方程和状态估计方程，如下：4、调试控制器和观测器（1）经过上述设计步骤，将反馈矩阵和观测矩阵带入 MATLAB 工具箱函数进行仿真。

自动控制原理MATLAB仿真实验指导书(4个实验)

自动控制原理MATLAB仿真实验实验指导书电子信息工程教研室实验一典型环节的MA TLAB仿真一、实验目的1．熟悉MATLAB桌面和命令窗口，初步了解SIMULINK功能模块的使用方法。

2．通过观察典型环节在单位阶跃信号作用下的动态特性，加深对各典型环节响应曲线的理解。

3．定性了解各参数变化对典型环节动态特性的影响。

二、SIMULINK的使用MATLAB中SIMULINK是一个用来对动态系统进行建模、仿真和分析的软件包。

利用SIMULINK功能模块可以快速的建立控制系统的模型，进行仿真和调试。

1．运行MA TLAB软件，在命令窗口栏“>>”提示符下键入simulink命令，按Enter键或在工具栏单击按钮，即可进入如图1-1所示的SIMULINK仿真环境下。

2．选择File菜单下New下的Model命令，新建一个simulink仿真环境常规模板。

图1-1 SIMULINK仿真界面图1-2 系统方框图3．在simulink仿真环境下，创建所需要的系统。

以图1-2所示的系统为例，说明基本设计步骤如下：1）进入线性系统模块库，构建传递函数。

点击simulink下的“Continuous”，再将右边窗口中“Transfer Fen”的图标用左键拖至新建的“untitled”窗口。

2）改变模块参数。

在simulink仿真环境“untitled”窗口中双击该图标，即可改变传递函数。

其中方括号内的数字分别为传递函数的分子、分母各次幂由高到低的系数，数字之间用空格隔开；设置完成后，选择OK，即完成该模块的设置。

3）建立其它传递函数模块。

按照上述方法，在不同的simulink的模块库中，建立系统所需的传递函数模块。

例：比例环节用“Math”右边窗口“Gain”的图标。

4）选取阶跃信号输入函数。

用鼠标点击simulink下的“Source”，将右边窗口中“Step”图标用左键拖至新建的“untitled”窗口，形成一个阶跃函数输入模块。