机器人的位姿描述与坐标变换
合集下载
第3章 位姿描述和齐次变换

ZB ZA YB
P
AP
XB
OA
YA
A
参考坐标系{A}
机器人研究所
4
第1节 位置和姿态的表示
位置描述(Description of Position)
px A p p y pz
Ap
zA
{A}
p
A
p
:p点在坐标系{A}中的表示,
xA
oA
yA
也称作位置矢量。
图1 位置表示
齐次的,将其等价为齐次变换形式:
A A p B R | A pBo B p 0 0 0 | 1 1 1
A A B p B R p A pBo A
直角坐标
齐次坐标
等价于
p A BT
B
p
11
齐次变换
机器人研究所
22
第3节 齐次坐标变换
机器人研究所14坐标变换复合变换compositetransform机器人研究所15例21已知坐标系b的初始位姿与a重合首先b相对于坐标系a的zb0和旋转矩阵求它在坐标系a中的描述坐标变换机器人研究所16例21已知坐标系b的初始位姿与a重合首先b相对于坐标系a的zb0和旋转矩阵求它在坐标系a中的描述坐标变换机器人研究所17例21已知坐标系b的初始位姿与a重合首先b相对于坐标系a的zb0和旋转矩阵求它在坐标系a中的描述坐标变换机器人研究所18例21已知坐标系b的初始位姿与a重合首先b相对于坐标系a的zb0和旋转矩阵求它在坐标系a中的描述3030086605303030050866坐标变换机器人研究所19例21已知坐标系b的初始位姿与a重合首先b相对于坐标系a的zb0和旋转矩阵求它在坐标系a中的描述坐标变换机器人研究所20例21已知坐标系b的初始位姿与a重合首先b相对于坐标系a的zb0和旋转矩阵求它在坐标系a中的描述0866051211098050866坐标变换第第33节节齐次坐标变换齐次坐标变换旋转变换通式第三章位姿描述和齐次变换机器人研究所22齐次坐标变换齐次坐标和齐次变换坐标变换式中对于点是非齐次的将其等价为齐次变换形式
P
AP
XB
OA
YA
A
参考坐标系{A}
机器人研究所
4
第1节 位置和姿态的表示
位置描述(Description of Position)
px A p p y pz
Ap
zA
{A}
p
A
p
:p点在坐标系{A}中的表示,
xA
oA
yA
也称作位置矢量。
图1 位置表示
齐次的,将其等价为齐次变换形式:
A A p B R | A pBo B p 0 0 0 | 1 1 1
A A B p B R p A pBo A
直角坐标
齐次坐标
等价于
p A BT
B
p
11
齐次变换
机器人研究所
22
第3节 齐次坐标变换
机器人研究所14坐标变换复合变换compositetransform机器人研究所15例21已知坐标系b的初始位姿与a重合首先b相对于坐标系a的zb0和旋转矩阵求它在坐标系a中的描述坐标变换机器人研究所16例21已知坐标系b的初始位姿与a重合首先b相对于坐标系a的zb0和旋转矩阵求它在坐标系a中的描述坐标变换机器人研究所17例21已知坐标系b的初始位姿与a重合首先b相对于坐标系a的zb0和旋转矩阵求它在坐标系a中的描述坐标变换机器人研究所18例21已知坐标系b的初始位姿与a重合首先b相对于坐标系a的zb0和旋转矩阵求它在坐标系a中的描述3030086605303030050866坐标变换机器人研究所19例21已知坐标系b的初始位姿与a重合首先b相对于坐标系a的zb0和旋转矩阵求它在坐标系a中的描述坐标变换机器人研究所20例21已知坐标系b的初始位姿与a重合首先b相对于坐标系a的zb0和旋转矩阵求它在坐标系a中的描述0866051211098050866坐标变换第第33节节齐次坐标变换齐次坐标变换旋转变换通式第三章位姿描述和齐次变换机器人研究所22齐次坐标变换齐次坐标和齐次变换坐标变换式中对于点是非齐次的将其等价为齐次变换形式
机器人的位姿描述与坐标变换

0
1
0
⎥ ⎥
⎢⎣− sinθ 0 cosθ ⎥⎦
Zi Zj
θ
θ Xi
Xj
Yi Y j
⎡cosθ − sinθ 0⎤
j i
R(Zi
,θ
)
=
⎢⎢sinθ
cosθ
0⎥⎥
⎢⎣ 0
0 1⎥⎦
Zi Zj
θ
Xi Xj
Yj
θ
Yi
⎡1 0
0⎤
j i
R(
X
i
,θ
)
=
⎢⎢0
cosθ
−
sinθ
⎥ ⎥
⎢⎣0 sinθ cosθ ⎥⎦
¥ ¥假设机器人的连杆和关节都是刚体¥ ¥
位置矢量
⎡x0 ⎤
P o '
o
=
⎢ ⎢
y0
⎥ ⎥
⎢⎣ z0 ⎥⎦
Z b Z'
O' Y' t n X' O
X Y
姿态矢量
O' O
R
=
[
O' O
X
OO'Y
⎡cos(∠X ' X )
O' O
Z
]3×3
=
⎢ ⎢
cos(∠X
'Y
)
⎢⎣cos(∠X ' Z )
单位主矢量
cos(∠Y ' X ) cos(∠Y 'Y ) cos(∠Z ' Z )
cos(∠Z ' X )⎤
cos(∠Z
'Y
)
⎥ ⎥
cos(∠Z ' Z ) ⎥⎦
姿态矩阵R的特点:
机器人学技术基础课程-位姿描述和齐次变换

2、齐次变换在研究空间机构动力学、机器人控制算法、计算 机视觉等方面也得到广泛应用。
位姿描述与齐次变换
1 刚体位姿的描述 2 坐标变换 3 齐次坐标系和齐次变换 4 齐次变换矩阵的运算 5 变换方程
2.1 刚体位姿的描述
为了完全描述一个刚体在空间的位姿,通常将刚体与某 一坐标系固连,坐标系的原点一般选在刚体的特征点上,如 质心、对称中心等。
YˆB ZˆA
ZˆB Xˆ A ZˆB YˆA
ZˆB ZˆA
XB n
2.1.4 旋转矩阵的意义
若坐标系B可由坐标系A,通过绕A的某一坐标轴获得,则绕 x,y,z三轴的旋转矩阵分别为:
1 0 0
c 0 s
c s 0
R(x, ) 0
Ay
y
所以: A Axaˆx Ayaˆy Azaˆz
2.1.2 方位的描述
矢量: A Axaˆx Ayaˆy Azaˆz
模的计算: | A | Ax2 Ay2 Az2
z
Az
A
方向角与方向余弦:, ,
o
Ay
Ax
y
x
cos Ax = A aˆx , cos Ay = A aˆy , cos Az A aˆz
两矢量的叉积又可表示为:
aˆx aˆy aˆz A B Ax Ay Az
Bx By Bz
2.1.2 方位的描述
空间物体B的方位(Orientation)可由某个固接于此物体的坐标系{B}的三 个单位主矢量[xB,yB,zB]相对于参考坐标系A的方向余弦组成的3x3矩阵描述.
BAR n o a a
位姿描述与齐次变换
1 刚体位姿的描述 2 坐标变换 3 齐次坐标系和齐次变换 4 齐次变换矩阵的运算 5 变换方程
2.1 刚体位姿的描述
为了完全描述一个刚体在空间的位姿,通常将刚体与某 一坐标系固连,坐标系的原点一般选在刚体的特征点上,如 质心、对称中心等。
YˆB ZˆA
ZˆB Xˆ A ZˆB YˆA
ZˆB ZˆA
XB n
2.1.4 旋转矩阵的意义
若坐标系B可由坐标系A,通过绕A的某一坐标轴获得,则绕 x,y,z三轴的旋转矩阵分别为:
1 0 0
c 0 s
c s 0
R(x, ) 0
Ay
y
所以: A Axaˆx Ayaˆy Azaˆz
2.1.2 方位的描述
矢量: A Axaˆx Ayaˆy Azaˆz
模的计算: | A | Ax2 Ay2 Az2
z
Az
A
方向角与方向余弦:, ,
o
Ay
Ax
y
x
cos Ax = A aˆx , cos Ay = A aˆy , cos Az A aˆz
两矢量的叉积又可表示为:
aˆx aˆy aˆz A B Ax Ay Az
Bx By Bz
2.1.2 方位的描述
空间物体B的方位(Orientation)可由某个固接于此物体的坐标系{B}的三 个单位主矢量[xB,yB,zB]相对于参考坐标系A的方向余弦组成的3x3矩阵描述.
BAR n o a a
机器人运动学

58
斯坦福机器人反向运动学方程求解
• 已知斯坦福机器人的运动学方程为T6=A1A2A3A4A5A6, 以及T6 矩阵与各杆参数a、α、d,求关节变量θ1~θ6 , 其中θ3= d3。
• 求θ1:
59
斯坦福机器人反向运动学方程求解
• 求θ1:
• “+”号对应右肩位姿,“-”号对应左肩位姿。60
斯坦福机器人反向运动学方程求解
2 机器人运动学
• • • • 齐次坐标及动坐标系、对象物位姿的描述 齐次变换 机器人连杆坐标系及其齐次变换矩阵 机器人运动学方程及其求解
1
齐次坐标及动坐标系、对象物位姿的描述 • • • • • 点的直角坐标描述 点的齐次坐标描述 坐标轴方向的齐次坐标描述 动坐标系位姿的齐次坐标描述 对象物位姿的齐次坐标描述
n cos30 cos60 cos90 0 T 0.866 0.500 0.000 0
P 2 1 cos90 0 T 0.500 0.866 0.000 0 a 0.000 0.000 1.000 0
2
点的直角坐标描述
式中:Px、Py、Pz是点P在坐标 系{A}中的三个位置坐标分量。
点的直角坐标描述
3
点的齐次坐标描述
• 齐次坐标的表示不是惟一的,将其各元素同 乘一非零因子ω后,仍然代表同一点P,即
4
坐标轴方向的齐次坐标描述
坐标轴方向的描述
5
• 4 1列阵[a b c w]T中第四个元素不为零,则表示空 间某点的位置; • 4 1列阵[a b c w]T 中第四个元素为零,且满足 a2 + b2 + c2 = 1,则表示某轴(矢量)的方向。
44
正向运动学方程求解
2-2.1位姿描述

这是绕Z轴的旋转.其它两轴只要把坐标次序调换可得上页结果.
上海电机学院 机械学院
旋转矩阵的几何意义: 1) 可以表示固定于刚体上的坐标系{B}相对于参考坐标系 的姿态. 2) 可作为坐标变换矩阵.它使得坐标系{B}中的点的坐标 变换成{A}中点的坐标 . 3) 可作为算子,将{B}中的矢量或物体变换到{A}中.
px A P py pz
齐次坐标
px p y pz 1
注意: 齐次坐标的表示不是惟一的。
P px
py
p z 1 a b c
T
T
上海电机学院 机械学院
位姿描述——齐次坐标
规定: (1) (4×1)列阵[a b c ω]T中第四个元素不为零,则表示空间某点的 位置; (2) (4×1)列阵[a b c 0]T中第四个元素为零,且a2+b2+c2=1,则表示 某轴(矢量)的方向; (2)矢量(坐标轴)方向的齐次坐标 X、Y、Z三个坐标轴方向的齐次坐标为:
0 1 Rot( x, ) 0 cos 0 sin cos 0 sin Rot ( y , ) cos sin 0 0 sin cos sin 1 0 Rot ( z , ) 0 cos 0 sin cos 0 0 0 1
动系位姿 采用齐次坐标后可将原来 的3×4的非方阵转化为 4×4的方阵。
1 0 A 0 0 0 1 0 0 0 100 0 0 1 0 0 1
上海电机学院 机械学院
位姿描述——刚体位姿的描述
机器人的每一个连杆均可视为一个刚体。 1 2 3
上海电机学院 机械学院
旋转矩阵的几何意义: 1) 可以表示固定于刚体上的坐标系{B}相对于参考坐标系 的姿态. 2) 可作为坐标变换矩阵.它使得坐标系{B}中的点的坐标 变换成{A}中点的坐标 . 3) 可作为算子,将{B}中的矢量或物体变换到{A}中.
px A P py pz
齐次坐标
px p y pz 1
注意: 齐次坐标的表示不是惟一的。
P px
py
p z 1 a b c
T
T
上海电机学院 机械学院
位姿描述——齐次坐标
规定: (1) (4×1)列阵[a b c ω]T中第四个元素不为零,则表示空间某点的 位置; (2) (4×1)列阵[a b c 0]T中第四个元素为零,且a2+b2+c2=1,则表示 某轴(矢量)的方向; (2)矢量(坐标轴)方向的齐次坐标 X、Y、Z三个坐标轴方向的齐次坐标为:
0 1 Rot( x, ) 0 cos 0 sin cos 0 sin Rot ( y , ) cos sin 0 0 sin cos sin 1 0 Rot ( z , ) 0 cos 0 sin cos 0 0 0 1
动系位姿 采用齐次坐标后可将原来 的3×4的非方阵转化为 4×4的方阵。
1 0 A 0 0 0 1 0 0 0 100 0 0 1 0 0 1
上海电机学院 机械学院
位姿描述——刚体位姿的描述
机器人的每一个连杆均可视为一个刚体。 1 2 3
机器人运动学坐标变换

xi cos x j sin y j 0 z j yi sin x j cos y j 0 z j zi 0 x j 0 y j 1 z j
2017年2月19日星期日
工 业 机 器 人
第3章
3.2.1 直角坐标变换
工 业 机 器 人
第3章
3.1.1 机器人位姿的表示
姿态可h o p(x,y,z) h
o yh y
3.1 机器人的位姿描述
z
余弦值组成3×3的姿态
矩阵来描述。
cos(x , x h ) cos(x , yh ) cos(x , z h ) R cos(y , x h ) cos(y , yh ) cos(y , z h ) cos(z , x h ) cos(z , yh ) cos(z , z h )
2017年2月19日星期日
工 业 机 器 人
R
x , ij
第3章
3.2.1 直角坐标变换
2、旋转变换
②绕x轴旋转α角的 旋转变换矩阵为:
机器人运动学
zi
3.2 齐次变换及运算
zj
α
0 0 1 0 cos sin 0 sin cos
xj
yj oi oj
xi x j cos y j sin yi x j sin y j cos zi z j
xi
yi
xj
2017年2月19日星期日
工 业 机 器 人
第3章
3.2.1 直角坐标变换
2、旋转变换
机器人运动学
3.2 齐次变换及运算
① 绕z轴旋转θ角 若补齐所缺的有些项,再作适当变形,则有:
(优选)机器人位姿描述详解.

R
B
p
A B
R
B
p
A p C p A pCo
Ap
A B
R
B
p
A pBo
24
旋转部分 平移部分
三、齐次坐标和齐次变化
齐次坐标
a P b
c
直角坐标
x
P
y z
齐次坐标
非零的比例因子
a x
b y
c z
25
1)点的齐次坐标:
P x y z T
0
P 2 3 4 1T , P 4 6 8 2T
5
2、方位的描述
为了规定空间某刚体B的方位,设一坐标系{B}与此刚 体固连。用坐标系{B}的三个单位主矢量 , xB, y相B 对zB 于{A}的方向余弦组成的3x3矩阵来表示刚体B相对于 坐标系{A}的方位。
BAR AxB A yB AzB
r11 r12 r13
A B
R
r21
r22
r23
A p BAR B p cos( yA, xB )
cos( yA, yB )
cos(
yA
,
zB
)
pBy
18
cos(zA, xB ) cos(zA, yB ) cos(zA, zB ) pBz
绕一个坐标轴旋转的转动矩阵
ZA ZB
q q
XA
X
B
1)RX
YB YA
ZA ZB
ZA ZB
q
已知点P在B坐标系的坐标:
B P [x B y B zB ]T
求点P在A坐标系的坐标:
AP [x A y A zA ]T
15
ZB
ZA
3位姿变换Trans-Matrix

cos z R sin z 0
与o-xyz之间的方位关系,即旋
0 0 1
sin z cos z 0
从
ob xb yb zb
到O-xyz的坐标变换
由
x x0 Rx b
x u cos z v sin z 得 y u sin z v cos z w z
x x0 Rxb
例题: 如图3-4所示,b 系
坐标原点与基坐标系 O-xyz 原 点重合, x 轴与 xb 轴之间的夹 角为θz,另外轴zb与轴z重合, 求表示 b 系相对于 O-xyz 的位 置矢量 x0 和方位矩阵 R,并求 空间一点从 b 系到 O-xyz 的坐 标变换。 z 解: (1)x0为零。
四、齐次坐标变换
1、 齐次坐标 将三维直角坐标系中点矢量(a,b,c)T用四维列向量 U=(x,y,z,w)T来表示,其中w是比例因子,且令a=x/w, b=y/w, c=z/w,则称(x,y,z,w)T为三维空间点(a,b,c)T的齐次坐标。 当取w=1,则(a,b,c)T的一个齐次坐标为(a,b,c,1)T。 例:
又称此矩阵为旋转矩阵
(4)R矩阵正交性:
由于n、o、a为三个坐标轴的单位矢量,于是有 n o 0, a o 0, na 0 n n 1, o o 1, a a 1 因此矩阵R是正交矩阵。 (5)刚体位姿描述: R P 用4× 4的齐次矩阵来表示刚体位姿 T 013 1 称此矩阵 为刚体位 姿矩阵
c s 0 s c 0 0 cb 0 0 1 sb 0 sb 1 0 0 cg 1 0 0 cb 0 sg 0 sg cg
与o-xyz之间的方位关系,即旋
0 0 1
sin z cos z 0
从
ob xb yb zb
到O-xyz的坐标变换
由
x x0 Rx b
x u cos z v sin z 得 y u sin z v cos z w z
x x0 Rxb
例题: 如图3-4所示,b 系
坐标原点与基坐标系 O-xyz 原 点重合, x 轴与 xb 轴之间的夹 角为θz,另外轴zb与轴z重合, 求表示 b 系相对于 O-xyz 的位 置矢量 x0 和方位矩阵 R,并求 空间一点从 b 系到 O-xyz 的坐 标变换。 z 解: (1)x0为零。
四、齐次坐标变换
1、 齐次坐标 将三维直角坐标系中点矢量(a,b,c)T用四维列向量 U=(x,y,z,w)T来表示,其中w是比例因子,且令a=x/w, b=y/w, c=z/w,则称(x,y,z,w)T为三维空间点(a,b,c)T的齐次坐标。 当取w=1,则(a,b,c)T的一个齐次坐标为(a,b,c,1)T。 例:
又称此矩阵为旋转矩阵
(4)R矩阵正交性:
由于n、o、a为三个坐标轴的单位矢量,于是有 n o 0, a o 0, na 0 n n 1, o o 1, a a 1 因此矩阵R是正交矩阵。 (5)刚体位姿描述: R P 用4× 4的齐次矩阵来表示刚体位姿 T 013 1 称此矩阵 为刚体位 姿矩阵
c s 0 s c 0 0 cb 0 0 1 sb 0 sb 1 0 0 cg 1 0 0 cb 0 sg 0 sg cg
[课件](工业机器人)位姿描述与齐次变换PPT
位姿描述与齐次变换PPT](https://img.taocdn.com/s3/m/711ba841caaedd3383c4d3c4.png)
六、齐次表达
根据几何学知识,上面第四小节中给定点的绝对位置为:
Ap b a b a b a c s cs b a
写成三维形式,有:
a a a c s 0a Apbbbs c 0b
3. 试按照运动顺序计算相关基本变换矩阵相乘结果
c s 0 a
Tra(An a,A sb,A0)Ro(zA t,)s0
c
0
0 b 1 0
0
1
4. 计算结果比较
两种方法结果相同!但后一种方法简单!
问题:是否仅仅按照运动变换顺序将相关的基本变 换矩阵相乘,即可以得到齐次变换阵?
0 0 0 0 0 10
O B 在A中位置,记作 A pOB
B在
A 中姿态,记作
A B
R
。
分成两块,不便于记忆!
齐次变换矩阵
若写成如下齐次形式,有:
c s 0 aa
A 1ps0 0
c
0 0
0 1 0
A 中的位置,然后与
b
A坐标原点值相加即可
得到该点绝对位置。
OA
由几何法,得:
aacbs 写成矩阵形式
b as bc
Y A
YB
b
b
XB a
OB
a
X A
a
XA
相
a c sa 对
bs cb
坐 标 值
b 1 0b 1 0B A 0R
Ap 1OBB 1pA BTB 1p
七、齐次变换矩阵
1. 构成:分为4块。左上角是姿态矩阵,为一单位正交 矩阵;右上角为对象坐标系原点位置值;左下角为 三个0 0 0,简记为0;右下角为1。
根据几何学知识,上面第四小节中给定点的绝对位置为:
Ap b a b a b a c s cs b a
写成三维形式,有:
a a a c s 0a Apbbbs c 0b
3. 试按照运动顺序计算相关基本变换矩阵相乘结果
c s 0 a
Tra(An a,A sb,A0)Ro(zA t,)s0
c
0
0 b 1 0
0
1
4. 计算结果比较
两种方法结果相同!但后一种方法简单!
问题:是否仅仅按照运动变换顺序将相关的基本变 换矩阵相乘,即可以得到齐次变换阵?
0 0 0 0 0 10
O B 在A中位置,记作 A pOB
B在
A 中姿态,记作
A B
R
。
分成两块,不便于记忆!
齐次变换矩阵
若写成如下齐次形式,有:
c s 0 aa
A 1ps0 0
c
0 0
0 1 0
A 中的位置,然后与
b
A坐标原点值相加即可
得到该点绝对位置。
OA
由几何法,得:
aacbs 写成矩阵形式
b as bc
Y A
YB
b
b
XB a
OB
a
X A
a
XA
相
a c sa 对
bs cb
坐 标 值
b 1 0b 1 0B A 0R
Ap 1OBB 1pA BTB 1p
七、齐次变换矩阵
1. 构成:分为4块。左上角是姿态矩阵,为一单位正交 矩阵;右上角为对象坐标系原点位置值;左下角为 三个0 0 0,简记为0;右下角为1。
第3章 机器人位姿的数学描述与坐标变换

x=a(1-cos) , y=a(1-sinθ)
第3章 机器人位姿的数学描述与坐标变换
3.1 机器人位姿的数学描述
#假设机器人的连杆和关节都是刚体 (1)首先,建立一个参考坐标系; (2)然后,在刚体上任意建立一个刚体坐标系。
Z Z'
O' Y'
O
X'
X Y
第3章 机器人位姿的数学描述与坐标变换
刚体位置:
,
)
=
?
j i
R(,q
,
)
=
R(Z
,
)
R(Y
,q
)R(Z
,
)
绕动坐标轴依次转动时,每 个旋转矩阵要从左往右乘。
Z2
Zj
Zi (Z1)
q
q
Yj
(Y2 )
q Y1
Yi
Xi
X1 X2 X j
第3章 机器人位姿的数学描述与坐标变换
cos − sin 0 cosq 0 sinq cos − sin 0
R(Z
i
,q
)
=
s
inq
cosq
0
0
0 1
Zi Zj
q Xi
Xj
Yj q
Yi
第3章 机器人位姿的数学描述与坐标变换
1 0
0
j i
R(
X
i
,q
)
=
0
cosq
−
s in q
0 sinq cosq
cosq 0 sinq
j i
R(Yi
,q
)
=
0
1
0
− sinq 0 cosq
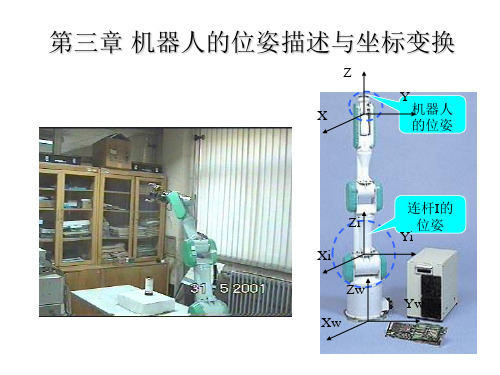
3机器人的位姿描述与坐标变换
利用旋转矩阵的正交性质:
假设:
整理得:
旋转变换通式
讨论:
(1)
(2)
(3)
例:坐标系B原来与A重合,将坐标系B绕过原点O的轴线
转动
,求旋转矩阵
解答:
1)
2)
3)带入旋转通式得:
2、等效转轴与等效转角
转轴和转角
旋转矩阵
1
2?
1)将方程两边矩阵的主对角线元素分别相加,则
2)将方程两边矩阵的非对角线元素成对相减得:
►绕多个坐标轴旋转的转动矩阵
1)、绕固定坐标系旋转
2)、绕运动坐标系旋转
ZYZ欧拉角
注意:多个旋转矩阵连乘时,次序不同则含义不同。1)绕新的动坐标轴依次转动时,每个旋转矩阵要从左往右乘,即旋转矩阵的相乘顺序与转动次序相同;2)绕旧的固定坐标轴依次转动时,每个旋转矩阵要从右往左乘,即旋转矩阵的相乘顺序与转动次序相反。
解:
1)
2)
Z
i
X
i
Y
i
P
坐标系j由坐标系i旋转而成
求点P在i坐标系的坐标:
已知点P在j坐标系的坐标:
P
☺
►姿态矢量矩阵
坐标系j相对于i的方位
旋转矩阵的性质:
旋转矩阵
►绕一个坐标轴旋转的转动矩阵
1)RX
2)RY
3)RZ
转动矩阵的特点:(1) 主对角线上有一个元素为1,其余均为转角的余弦/正弦;(2) 绕轴转动的次序与元素1所在的行、列号对应;(3) 元素1所在的行、列,其它元素均为0;(4) 从元素1所在行起,自上而下,先出现的正弦为负,后出现的为正,反之依然。
2、变换矩阵T的相乘 ★矩阵相乘的顺序一般不可换,特殊可换的情况为变换都是同参考系下的平移或绕同一坐标轴的旋转。
假设:
整理得:
旋转变换通式
讨论:
(1)
(2)
(3)
例:坐标系B原来与A重合,将坐标系B绕过原点O的轴线
转动
,求旋转矩阵
解答:
1)
2)
3)带入旋转通式得:
2、等效转轴与等效转角
转轴和转角
旋转矩阵
1
2?
1)将方程两边矩阵的主对角线元素分别相加,则
2)将方程两边矩阵的非对角线元素成对相减得:
►绕多个坐标轴旋转的转动矩阵
1)、绕固定坐标系旋转
2)、绕运动坐标系旋转
ZYZ欧拉角
注意:多个旋转矩阵连乘时,次序不同则含义不同。1)绕新的动坐标轴依次转动时,每个旋转矩阵要从左往右乘,即旋转矩阵的相乘顺序与转动次序相同;2)绕旧的固定坐标轴依次转动时,每个旋转矩阵要从右往左乘,即旋转矩阵的相乘顺序与转动次序相反。
解:
1)
2)
Z
i
X
i
Y
i
P
坐标系j由坐标系i旋转而成
求点P在i坐标系的坐标:
已知点P在j坐标系的坐标:
P
☺
►姿态矢量矩阵
坐标系j相对于i的方位
旋转矩阵的性质:
旋转矩阵
►绕一个坐标轴旋转的转动矩阵
1)RX
2)RY
3)RZ
转动矩阵的特点:(1) 主对角线上有一个元素为1,其余均为转角的余弦/正弦;(2) 绕轴转动的次序与元素1所在的行、列号对应;(3) 元素1所在的行、列,其它元素均为0;(4) 从元素1所在行起,自上而下,先出现的正弦为负,后出现的为正,反之依然。
2、变换矩阵T的相乘 ★矩阵相乘的顺序一般不可换,特殊可换的情况为变换都是同参考系下的平移或绕同一坐标轴的旋转。
第二章_位姿描述和齐次变换(2010-09)

Px Puvw ix ix ( Pu iu Pv jv Pw kw )
Py Puvw j y j y ( Pu iu Pv jv Pw k w )
x
Pw P Pv o
(O')
v y
Pu
Pz Puvw jz jz ( Pu iu Pv jv Pw k w )
acr cos(
mn mn
)
位置描述(position)---点在坐标系的位置
一旦建立了一个坐标系,我们就能够用某个3×1位置矢量来确定该空 间内任一点的位置。对于直角坐标系{A},空间任一点p的位置可用3×1的 列矢量AP表示。其中,px、py、pz入是点p在坐标系{A}中的三个坐标分量。 Ap的上标A代表参考坐标系{A}。我们称Ap为位置矢量,见图2.1。
T
解2:用分步计算的方法 ① R(x, 90°)
1 0 0 1 1 P ' 0 0 - 1 2 3 0 1 0 3 2
(2-14)
② R(z, 90°)
0 - 1 0 1 3 P '' 1 0 0 3 1 0 0 1 2 2
(2.10)
旋转矩阵
设固定参考坐标系直角坐标为ΣOxyz,动坐标系为ΣO´uvw, 研究旋转变换情况。
① 初始位置时,动静坐标系重合,O、O´ 重合,如图。各轴 对应重合,设P点是动坐标系ΣO´uvw中的一点,且固定不变。 则P点在ΣO´uvw中可表示为:
z
Puvw Pu iu Pv ju Pw k w
在机器人工作台上加装一电视摄像机摄像机可见到固联着6dof关节机器人的机座坐标系原点它也可以见到被操作物体立方体的中心如果在物体中心建一局部坐标系则摄像机所见到的这个物体可由齐次变换矩阵t来表示如果摄像机所见到的机座坐标系为矩阵t处它的xyz轴分别与机座坐标系的yxz轴平行
Py Puvw j y j y ( Pu iu Pv jv Pw k w )
x
Pw P Pv o
(O')
v y
Pu
Pz Puvw jz jz ( Pu iu Pv jv Pw k w )
acr cos(
mn mn
)
位置描述(position)---点在坐标系的位置
一旦建立了一个坐标系,我们就能够用某个3×1位置矢量来确定该空 间内任一点的位置。对于直角坐标系{A},空间任一点p的位置可用3×1的 列矢量AP表示。其中,px、py、pz入是点p在坐标系{A}中的三个坐标分量。 Ap的上标A代表参考坐标系{A}。我们称Ap为位置矢量,见图2.1。
T
解2:用分步计算的方法 ① R(x, 90°)
1 0 0 1 1 P ' 0 0 - 1 2 3 0 1 0 3 2
(2-14)
② R(z, 90°)
0 - 1 0 1 3 P '' 1 0 0 3 1 0 0 1 2 2
(2.10)
旋转矩阵
设固定参考坐标系直角坐标为ΣOxyz,动坐标系为ΣO´uvw, 研究旋转变换情况。
① 初始位置时,动静坐标系重合,O、O´ 重合,如图。各轴 对应重合,设P点是动坐标系ΣO´uvw中的一点,且固定不变。 则P点在ΣO´uvw中可表示为:
z
Puvw Pu iu Pv ju Pw k w
在机器人工作台上加装一电视摄像机摄像机可见到固联着6dof关节机器人的机座坐标系原点它也可以见到被操作物体立方体的中心如果在物体中心建一局部坐标系则摄像机所见到的这个物体可由齐次变换矩阵t来表示如果摄像机所见到的机座坐标系为矩阵t处它的xyz轴分别与机座坐标系的yxz轴平行
机器人运动学

R3
Z
三个平移自由度 T1, T2, T3
三个旋转自由度 R1, R2, R3
T3
T1
T2
Y R2
X
2019/3/31
R1
2.2 刚体位姿描述
方位描述
第三章
机器人运动学
利用固定于物体的坐标系描述方位 (orientation)。方位又称为姿 态 (pose)。
在刚体 B上设置直角坐标系 {B} ,利用与 {B} 的坐标轴平行 的三个单位矢量表示B的姿态。
A
p R ( x , ) p
B
zB
zA
Bp
P
yB
{A}
1 0 R ( x , ) 0 c 0 s
c R ( y , ) 0 s 0 s 1 0 , 0 c
0 s c
s c 0 0 0 1
2019/3/31
i A iB A jB r11 r12
第三章
机器人运动学
2.2 刚体位姿描述
位置与姿态的表示 相对于参考坐标系{A},坐标系{B}的原点位置和坐标轴的 方位可以由位置矢量和旋转矩阵描述。刚体B在参考坐标 系{A}中的位姿利用坐标系{B}描述。
{ B}
当表示位置时 当表示方位时
zA
iB
jB
A
kA 坐标系{B}的三个单位主矢量在坐标系{A}中的描述:
pBo
kB
yA
{ A iB , A jB , A k B }
坐标系{B}相对于坐标系{A}的姿态描述:
A B
O
R { iB , jB , k B }
A A A
机器人学--坐标转换

1
p px py pz T ,n nx ny nz T ,o ox oy oz T ,a ax ay az T
Robotics 数学基础
2.4 物体的变换 及逆变换
3.变换方程初步 {B}:基坐标系 {T}:工具坐标系 {S}:工作台坐标系 {G}:目标坐标系
或工件坐标系 满足方程
A P
1
A B
R
0
A
PB 1
0
B P
1
P点在{A}和{B}中的位置矢量分别增广为:
(2-14)
AP Ax A y Az 1T ,BP Bx B y Bz 1T
而齐次变换公式和变换矩阵变为:
A P ABTB P,
ABT
A B
R
0
A
PB0 1
(2-15,16)
Robotics 数学基础
ny
oy
ay
0
fx
f
yvers
f z s
fy fyvers c
fz fyvers fxs 0
nz 0
oz 0
az 0
0 1
fx
f z v ers 0
f y s
fy fzvers fxs 0
fz fzvers c 0
0 1
将上式对角线元素相加,并简化得
nx
oy
az
(
f
2 x
f
2 y
f
2023最新整理收集 do
something
机器人技术数学基础
Mathematic Preparation for Robotics
2.1 位置和姿态的表示 2.2 坐标变换 2.3 齐次坐标变换 2.4 物体的变换及逆变换 2.5 通用旋转变换
第1章位姿几何基础资料

0 0 0 1
c 表示 cos
s 表示 sin
点绕过原点任意轴的一般旋转变换
旋转算子为
kX kX vers c kY kX vers kZ s kZ kX vers kY s 0
Rot(k, ) kX kY vers kZ s kY kY vers c kZ kY vers kX s 0
u = [0 0.866 0.5 0]T
矢量 v:cos=0.866,cos=0,cos=0.5
v = [0.866 0 0.5 0]T
矢量 w:cos=0.866,cos=0.5,cos=0
w = [0.866 0.5 0 0]T
四、齐次变换
连杆的运动是由转动和平移组成的,引入齐次坐标变换矩阵描 述刚体运动。
算子左、右乘规则
若相对固定坐标系进行变换,则算子左乘;
若相对动坐标系进行变换,则算子右乘。 已知坐标系C和变换T:绕z轴旋转90,并沿x轴方 向平移10, 当相对基系和动系进行变换时,坐标 系C的位置?
已知坐标系C和变换T:绕z轴旋转90,并沿x轴方向平移10 当以基系进行变换时 左乘坐标系C,得新坐标系位置为P=TC:
类似地,对三维空间中坐标点[x,y,z] 例如齐次坐标(1 2 3 1)、(2 4 6 2)、(3 6 9 3) 均表示笛卡尔坐标下的空间点(1 2 3) 取w = 1,为齐次坐标的规格化形式,即
P = [PX PY PZ 1]T
━ w≠0时表示唯一点,点的坐标分别为 x=a/w y=b/w z=c/w
机器人手部的位置和姿态 机器人手部的位置和姿态用固连于手部的动系 {B}的位姿来表示。 手部的中心点为动系原点OB
关节轴为ZB轴,单位矢量a为接近矢量指向朝外。 手指的连线为YB轴,单位矢量o为姿态矢量,指向可 任意选定。
c 表示 cos
s 表示 sin
点绕过原点任意轴的一般旋转变换
旋转算子为
kX kX vers c kY kX vers kZ s kZ kX vers kY s 0
Rot(k, ) kX kY vers kZ s kY kY vers c kZ kY vers kX s 0
u = [0 0.866 0.5 0]T
矢量 v:cos=0.866,cos=0,cos=0.5
v = [0.866 0 0.5 0]T
矢量 w:cos=0.866,cos=0.5,cos=0
w = [0.866 0.5 0 0]T
四、齐次变换
连杆的运动是由转动和平移组成的,引入齐次坐标变换矩阵描 述刚体运动。
算子左、右乘规则
若相对固定坐标系进行变换,则算子左乘;
若相对动坐标系进行变换,则算子右乘。 已知坐标系C和变换T:绕z轴旋转90,并沿x轴方 向平移10, 当相对基系和动系进行变换时,坐标 系C的位置?
已知坐标系C和变换T:绕z轴旋转90,并沿x轴方向平移10 当以基系进行变换时 左乘坐标系C,得新坐标系位置为P=TC:
类似地,对三维空间中坐标点[x,y,z] 例如齐次坐标(1 2 3 1)、(2 4 6 2)、(3 6 9 3) 均表示笛卡尔坐标下的空间点(1 2 3) 取w = 1,为齐次坐标的规格化形式,即
P = [PX PY PZ 1]T
━ w≠0时表示唯一点,点的坐标分别为 x=a/w y=b/w z=c/w
机器人手部的位置和姿态 机器人手部的位置和姿态用固连于手部的动系 {B}的位姿来表示。 手部的中心点为动系原点OB
关节轴为ZB轴,单位矢量a为接近矢量指向朝外。 手指的连线为YB轴,单位矢量o为姿态矢量,指向可 任意选定。
3位姿变换Trans-Matrix

csb cg s sg ssb cg c sg cb cg
RPY逆变换
r11 r12 由 R(g , b , ) r21 r22 r31 r32
r13 r23 r33
求 g、b 和
c cb R(g , b , ) s cb sb
p xb w
u
yb
ob
v
点p在基坐标系和刚体坐 标系的位置矢量分别为
x x y z u xb v w
x0 o x y xb
坐标变换
x与xb之间的变换关系为
x x0 un vo wa
从坐标xb到基坐标x的一般变换关系式
其中C=cos,S=sin,v=1-cos 当给定旋转变换矩阵R(k,),也可以确定矢量k和转角:
r11 r12 r13 R(k , ) r r r 21 22 23 r31 r32 r33
1 r 11 r22 r33 1 cos 2 r32 r23 k 1 r13 r31 2 sin r21 r12
又称此矩阵为旋转矩阵
(4)R矩阵正交性:
由于n、o、a为三个坐标轴的单位矢量,于是有 n o 0, a o 0, na 0 n n 1, o o 1, a a 1 因此矩阵R是正交矩阵。 (5)刚体位姿描述: R P 用4× 4的齐次矩阵来表示刚体位姿 T 013 1 称此矩阵 为刚体位 姿矩阵
方向余弦矩阵为
cos( x, xb ) cos( x , yb ) cos( x, zb ) R [n o a] cos( y , x ) cos( y , y ) cos( y , z ) b b b cos( z, xb ) cos( z, yb ) cos( z, z b )
第2章 位子描述和齐次变换(1)

zB
坐标系{A}和{B}有共同的坐标原点,但方 位不同,旋转矩阵 B R 用来描述坐标系{B}相对于 {A}的方位。同一点P在坐标系{A}中的描述Ap与 在坐标系{B}中的描述Bp满足:
xB
A A p = BR B
A
zA
Bp
o
yA
p
xA
yB
——坐标旋转方程
A
图2.4 坐标旋转
B 旋转矩阵 B R 描述坐标系{B}相对于{A}的方位,而 A R 用于描述{A}相 对于{B}的方位。两个旋转矩阵满足如下关系:
A B
A C
B T = AT CT = B
R⋅ B pCo + A pBo
1
o
齐次变换矩阵相乘不满足交换律:变换矩阵“右乘” 注意:齐次变换矩阵相乘不满足交换律:变换矩阵“右乘”,表示 运动是相对于运动坐标系而言的;变换矩阵“左乘” 运动是相对于运动坐标系而言的;变换矩阵“左乘”,表示运动是相 对于固定坐标系而言的。 对于固定坐标系而言的。
B A
A A R = B R -1 = B RT
一般变换(复合变换) 2.2.3 一般变换(复合变换) 坐标系{A}和{B}的方位不同, 原点也不重合,任意点P在坐标系{A} 和{B}中的描述Ap和 Bp满足: :
zA oA xA
Ap
zC zB
Bp
oB xC
yB yC
Ap Bo
A
p= R
A B
B
p + pBo
S E
O B
T
0
B 6
T
T 相对于物体被定位。末端执行器位姿的描述
O S
6 E
T
S E
y
有两种方式,一种是相对于物体的描述,一种是 相对于机械手的描述。由于两种方式描述的是同 一个点,我们可以把这两个描述等同起来,得到
坐标系{A}和{B}有共同的坐标原点,但方 位不同,旋转矩阵 B R 用来描述坐标系{B}相对于 {A}的方位。同一点P在坐标系{A}中的描述Ap与 在坐标系{B}中的描述Bp满足:
xB
A A p = BR B
A
zA
Bp
o
yA
p
xA
yB
——坐标旋转方程
A
图2.4 坐标旋转
B 旋转矩阵 B R 描述坐标系{B}相对于{A}的方位,而 A R 用于描述{A}相 对于{B}的方位。两个旋转矩阵满足如下关系:
A B
A C
B T = AT CT = B
R⋅ B pCo + A pBo
1
o
齐次变换矩阵相乘不满足交换律:变换矩阵“右乘” 注意:齐次变换矩阵相乘不满足交换律:变换矩阵“右乘”,表示 运动是相对于运动坐标系而言的;变换矩阵“左乘” 运动是相对于运动坐标系而言的;变换矩阵“左乘”,表示运动是相 对于固定坐标系而言的。 对于固定坐标系而言的。
B A
A A R = B R -1 = B RT
一般变换(复合变换) 2.2.3 一般变换(复合变换) 坐标系{A}和{B}的方位不同, 原点也不重合,任意点P在坐标系{A} 和{B}中的描述Ap和 Bp满足: :
zA oA xA
Ap
zC zB
Bp
oB xC
yB yC
Ap Bo
A
p= R
A B
B
p + pBo
S E
O B
T
0
B 6
T
T 相对于物体被定位。末端执行器位姿的描述
O S
6 E
T
S E
y
有两种方式,一种是相对于物体的描述,一种是 相对于机械手的描述。由于两种方式描述的是同 一个点,我们可以把这两个描述等同起来,得到
04-机器人课程-运动学

1、机器人运动学
1.5机器人微分运动及速度
机器人的微分运动是研究机器人关节变量的微小变化与机器人手部位姿的微小变化 之间的微分关系。如果已知两者之间的微分关系,就可以解决机器人微分运动的两 类基本问题:一类是在已知机器人各个关节变量的微小变化时求机器人手部位姿的 微小变化;另一类是在已知机器人手部位姿的微小变化时求机器人各个关节变量相 应的微小变化。机器人的微分运动对机器人控制、误差分析、动力分析和保证工作 精度具有十分重要的意义。
1、机器人运动学
1.3齐次变换及运算
1.3.1 直角坐标变换 在机器人中建立直角坐标系后,机器人的手部和各活动杆件之间相对位 置和姿态就可以看成是直角坐标系之间的坐标变换。
1、机器人运动学
1.3齐次变换及运算
平移变换 设坐标系{i}和坐标系{j}具有相同的姿态,但两者的坐标原点不重合,如图3-7所 示。 若用矢量Pij表示坐标系{i}和坐标系{j}原点之间的矢量,则坐标系{j}就可以看成 是由坐标系{i}沿矢量Pij平移变换而来的,所以称矢量Pij为平移变换矩阵,它是一个 3×1的矩阵
1.1、机器人位姿描述
机器人的位姿主要是指机器人手部在空间的位置和姿态,有 时也会用到其他各个活动杆件在空间的位置和姿态。需要先 了解的与机器人运动相关的一些基础知识。 机器人的机构运动简图、机器人的自由度、机器人的坐标系、 机器人的工作空间、机器人的位姿
1、机器人运动学
1.2机器人的位姿
所谓机器人的位姿主要就是指机器人手部在空间的位置和姿态。有了机器 人坐标系,机器人手部和各个活动杆件相对于其他坐标系的位置和姿态就 可以用一个3×1的位置矩阵和一个3×3的姿态矩阵来描述。如图3-2所示, 机器人手部的坐标系{H}相对于机座坐标系{O}位置就可以用坐标系{H}的 原点OH在坐标系{O}三个坐标分量xOH、yOH、zOH、组成3×1的位置矩阵来 表示
机器人的空间描述与坐标变换

BPCBTCP APA BTBPA BTC BTCP
(2-24) (2-25)
{A}
{C}
{B}
CP
AP
OC
OB OA
图2-10 复合坐标变换
根据坐标变换的定义得
CATABTCBT
(2-26)
11
例2-3已知点u=7i+3j+2k,先对它进行绕Z轴旋转90o 的变换得点v,再对点v进行绕Y轴旋转90o的变换得 点w,求v和w。
f fxifyjfzk
以 f 为 Z 轴建立与{A}固连的坐标系{C}用n、o和f表示坐标系{C}三个坐标
轴的单位矢量,在坐标系{A}下表示为
ZA
n nxi ny j nzk o oxi oy j ozk f fxi fy j fzk
A C
R
n n
x y
ox oy
f f
x y
B
P
BAR
BP
(2-6)
图2-4旋转变换
B
Z
T A
式(2-6)即为我们要求的旋转变换关系,该变换是通过两个坐
标系之间的旋转变换实现的。
5
3.复合变换
如果两个坐标系之间即存在平移
又存在旋转,如何计算同一个空间点
在两个坐标系下描述的变换关系?
{A}
{C} {B}
BP AP
OB
为了得到位置矢量BP和AP之 间的变换关系,我们建立一个中 间坐标系{C}。
c90 0 s90 1
0
0
CAR
0
1
0
0
c 30
s 30
s90 0 c90 0 s 30 c 30
0 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
j i
R (a , ) R( Z , ) R( X , a )
Xi
Xm
Xj
cos sin j i R (a , ) 0
sin cos 0
0 1 0 0 cos a 0 1 0 sin a
0 cos sin sin a cos a 0
Yj
xi
Xi
yi
Yi
xj
Xj
xi x j cos(X i , X j ) y j cos(X i , Y j ) z j cos(X i , Z j ) i P yi x j cos(Yi , X j ) y j cos(Yi , Y j ) z j cos(Yi , Z j ) z x cos(Z , X ) y cos(Z , Y ) z cos(Z , Z ) j i j j i j j i j i
T
5 21 7
2、坐标旋转(坐标系原点相同)
Zj Zi P
坐标系j由坐标系i旋转而成 已知点P在j坐标系的坐标:
Yj
j
P [x j
yj
z j ]T
Yi Xi Xj
求点P在i坐标系的坐标:
i
P [ xi
yi
zi ]T
Zj
Zi
zi
P
yj
zj
Yj
xi
Xi
yi
Yi
xj
Xj
☺ 关于(Yi , X j )?
Z2 Z i (Z1 )
j f
R(Z i ,j )
j i
R(Y1 , )
R(Z 2 , f )
Zj
R(j , , f ) R ( Z , j ) R (Y , ) R ( Z , f )
Yj (Y2 )
f j
ZYZ欧拉角jY1 YifXi
X1 X 2 X j
cos j j R(j , , f ) i sin j 0
3、坐标变换综合(平移+旋转)
Zj Zc P
Pi RPj P
旋转部分 平移部分
Zi
Oj i
j i
Oj i
Pj
X Z b Z' O' O n X' Y' t
Y
刚体姿态:
O' O ' R [O OX O' O
Y
单位主矢量
cos(X ' X ) cos(Y ' X ) cos(Z ' X ) cos(X 'Y ) cos(Y 'Y ) cos(Z 'Y ) O' Z ] O 33 cos(X ' Z ) cos(Y ' Z ) cos(Z ' Z )
►绕多个坐标轴旋转的转动矩阵 1)、绕固定坐标系旋转
坐标系 ( X i , Yi , Z i ) 坐标系( X m , Ym , Z m ) 坐标系 ( X j , Y j , Z j )
Zi Zm Zj
R( X i ,a )
R ( Z i , )
j i
R (a , ) ?
a a
Yj Ym Yi
sin j cos j 0
0 cos 0 0 1 sin
0 sin cos f sin f 1 0 0 cos 0
sin f cos f 0
0 0 1
cosj cos cosf sin j sin f sin j cos cosf cosj sin f sin sin f
3)RZ
Zi Z
j
Yj Yi
Xi
Xj
cos(X i , X j ) cos(X i , Y j ) cos(X i , Z j ) x j i P cos(Yi , X j ) cos(Yi , Y j ) cos(Yi , Z j ) y j cos(Z , X ) cos(Z , Y ) cos(Z , Z ) z i j i j i j j
证明: 1)绕运动坐标系旋转
R(Z i ,j )
坐标系 ( X i , Yi , Z i )
Z2 Zj Z i (Z1 )
R(Y1 , ) R(Z 2 , f ) 坐标系 ( X 1 , Y1 , Z 1 ) 坐标系 ( X 2 , Y2 , Z 2 )
坐标系 ( X j , Y j , Z j )
1) Pm mjR Pj R ( Z i , ) Pj 2) Pi m iR P m R( X i , a) P m R ( X i , a ) R ( Z i , ) Pj
Xj
适用的机器人类型举例(有旋转关节)
例1: 已知坐标系B初始位姿与A重合,首先B相对于坐标系A的Z 轴转30度, 假设点P在 坐标系B的描述为PB={3,7,0}T,求它在坐标 系A中的描述PA.
cos(X i , X j ) cos(X i , Y j ) cos(X i , Z j ) x j i P cos(Yi , X j ) cos(Yi , Y j ) cos(Yi , Z j ) y j cos(Z , X ) cos(Z , Y ) cos(Z , Z ) z i j i j i j j
cos(X ' X ) cos(Y ' X ) cos(Z ' X ) cos(X 'Y ) cos(Y 'Y ) cos(Z 'Y ) O' O' O' O' R [ X Y Z ] O O O O 33 cos(X ' Z ) cos(Y ' Z ) cos(Z ' Z ) 姿态矩阵R的特点:
Xi
X1 X 2 X j
2)、绕固定坐标系旋转
( X i , a) ( Z i , )
坐标系 ( X i , Yi , Z i )
Zi Zm Zj
坐标系( X m , Ym , Z m )
j i
坐标系 ( X j , Y j , Z j )
a a
Xi Xm Yj Ym Yi
R?
证明与讨论:
cosj cos sin f sin j cosf sin j cos sin f cosj cosf sin sin f
cosj sin sin j sin cos
注意:多个旋转矩阵连乘时,次序不同则含义不同。
1)绕新的动坐标轴依次转动时,每个旋转矩阵要从左往右 乘,即旋转矩阵的相乘顺序与转动次序相同; 2)绕旧的固定坐标轴依次转动时,每个旋转矩阵要从右往 左乘,即旋转矩阵的相乘顺序与转动次序相反。
X
Z b Z' O' Y' t O n X'
Y
i
P R P
旋转矩阵
j i
j
坐标系j相对 于i的方位
旋转矩阵的性质:
j i
R R R
i j
1
i j
T
►绕一个坐标轴旋转的转动矩阵
Zi Z
j
Zi Zj
Yj
Yi Y j
Yi Xi Xi X
j
Xj
1)RX
Zi Zj
2)RY
Yj
Xi Xj Yi
sin cos a cos cos a sin a
sin sin a cos sin a cos a
2)、绕运动坐标系旋转
坐标系 ( X i , Yi , Z i ) 坐标系 ( X 1 , Y1 , Z1 ) 坐标系 ( X 2 , Y2 , Z 2 ) 坐标系 ( X j , Y j , Z j )
0 1 0 cos j R ( X , ) i i 0 sin sin cos 0
Zi Zj
cos 0 j R ( Y , ) i i sin
0 sin 1 0 0 cos
R是单位正交阵
O' O
R 1
刚体的位置和姿态:
' {O'} {O O R, O' O
P}
Zj
例:某刚体j在参考系i中的 位置 姿态
oj oi
P?
Oj Oi
Oj
Yj Xj Zi
R?
6
10
Oi
Xi
Yi
3-2 坐标变换(点的映射)
1、坐标平移(坐标系方位相同)
已知点P在j坐标系的坐标,平移j至i,求 点P在i坐标系的坐标。
Xi Xj Yi Yj
Zi
Zj Yj
cos sin j R ( Z , ) i i 0
sin cos 0
0 0 1
Xi
Xj
Yi
0 1 0 cos j R ( X , ) i i 0 sin
sin cos
yi x j cos(Yi , X j )
yi x j cos(Yi , X j ) y j cos(Yi , Y j ) yi x j cos(Yi , X j ) y j cos(Yi , Y j ) z j cos(Yi , Z j )
Zj
Zi
zi
P
zj
yj
适用的机器人类型举例(有平移关节)
Z1 X1
Y1 Z2 X2
Y2
Z3 X3
