数值传热学陶文铨主编第二版习题答案

合集下载

数值传热学习题答案(汇总版)

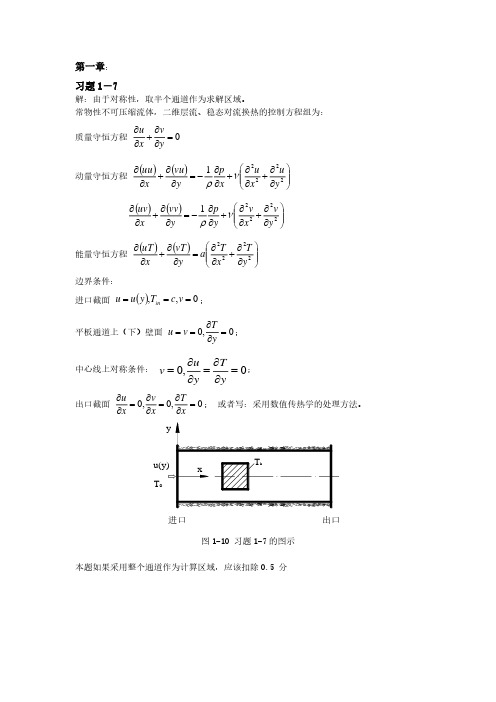
e
(uu) −(uu) dydt =
n t + t s e w t
e
w
u u 2[ y n − s ]dxdt y
将
(uu )e = (uu )E +(uu) P
2
, (uu )w =
(uu )W +(uu )P ,
第一章：习题 1－7
解：由于对称性，取半个通道作为求解区域。常物性不可压缩流体，二维层流、稳态对流换热的控制方程组为：质量守恒方程
u v + =0 x y
动量守恒方程
2u 2u (uu ) (vu ) 1 p + =− 2v (uv) (vv) 1 p + =− + + 2 2 x y y y x
2krP kr k kr k TP = P + TE + P − TW + rP rS r r 2 r 2
令
1 kr ， rP 1 krw ， a P = a E + aW ， b r aE = k P + = e aW = k − = r 2 r r 2 r
t t t t (uu)tE − (uu)W uN − 2u P + uS yt = 2 xt 2 y
整理得离散方程为：
t (uu)tE − (uu)W
4x
t t t uN + uS − 2uP − =0 y 2
2—3：
u 1 (u 2 ) 2u 解：由 u = x = 2 x = y 2 得：
v = 0,
u T = = 0； y y

数值传热学(陶文铨)第二章习题答案

p1 p2
（1）
p 2 p x2 x 2 x i 2 x i 2 2!
p 2 p x2 p3 p2 x 2 x i 2 x i 2 2!
（2）式（2）-（1）得
p p1 p 3 x i 2 2 x
2-11.解：对于均分网格用泰勒级数展开法，用 2 点分别表示 1,3,4 处热流量得
（i+1,n）= （i,n）+
(1)
x
( x)
i ,n
2 x 2
i ,n
(( x) )2 2!
（i-1,n）= （i,n）+
(2) 式（1）-（2）得：
x
( x)
i ,n
2 x 2
i ,n
(( x) )2 2!
（i+1,n）- （i-1,n）=
即
krp k krp k 2k rpTp ( )Te ( )T r s r r r 2 r 2 w p
化简后得
2krp
r
Tp
kre kr S Te w Tw rp r r r 2
计算结果与控制容积积分法一致。 2-9.解：对于均分网格用泰勒级数展开法分别表示 1 和 3 点处的压力值
（1）对 T 随 r 由 Tw 变到 Te 的过程进行积分
（2）可化为
rk
dT dr
e

w
S 2 r 2 w
e
（3）取 T 随 r 呈分段线性的变化，则（3）式中
Tw
Tp Tw 2 Tp Te 2
（4）
Te
（5）
dT Te Tp r dr e
（6）

数值传热学第5章作业答案

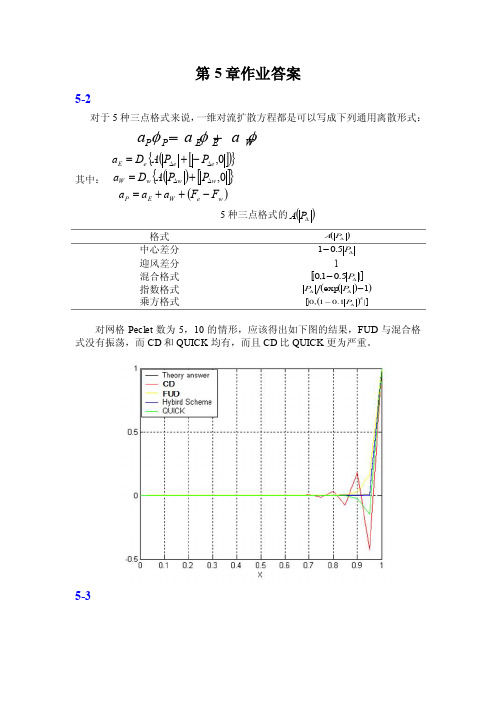
第5章作业答案5-2对于5种三点格式来说，一维对流扩散方程都是可以写成下列通用离散形式：P P E E W Wa a a φφφ=+ 其中： [](){}()[]{}()w e W E P w w w W e e e E F F a a a P P A D a P P A D a -++=+=-+=∆∆∆∆0,0,5种三点格式的()∆P A格式()∆P A迎风差分 1混合格式 []|5.01,0|∆-P 指数格式 ()()1exp -∆∆P P对网格Peclet 数为5，10的情形，应该得出如下图的结果，FUD 与混合格式没有振荡，而CD 和QUICK 均有，而且CD 比QUICK 更为严重。

5-3不同网格∆P 数下各系数计算结果如下∆P E aW a 0P a P a 0.1 28.53 31.53 2 62.05910 0 3255-5 四个节点之值如下一阶迎风混合格式乘方格式二阶迎风（边界一阶）二阶迎风（边界二阶）1φ 94.26 73.96 79.01 58.57 91.122φ 147.61 91.10 115.13 76.65 144.19 3φ 82.14 72.40 74.19 69.33 81.34 4φ 126.99 85.31 102.70 87.38 124.505-7不计扩散项，采用QUICK 离散i 控制容积的非稳态与对流项得：12117338n nn n n ni i i i i i x utφφφφφφ+--+--++∆=-∆ （(0)u >采用离散扰动分析法，对i+1得到扰动为78n i u t ρε∆，对i-1 得到扰动为38ni u t xε∆-∆，符号不变原则要求：0832≥∆Γ∆+∆∆-ninin i x t x t u εερερ，由此得：38≤=Γ∆∆P xu ρ5-9根据三阶迎风格式的定义：⎪⎩⎪⎨⎧<∆--+->∆+-+=∂∂-++--+0,62360,6632112211u x u xx i i i i i i i i φφφφφφφφφ仿照QUICK 格式，令三阶迎风格式的控制容积右界面上的值的形式为：⎪⎩⎪⎨⎧<+--+>+--+=0,220,22u a u a EEE P E P WP E E P e φφφφφφφφφφφ同理可以写出w φ的计算式。

数值传热学第六章答案 (2)

数值传热学第六章答案简介本文档将为读者提供《数值传热学》第六章的答案。

第六章主要涉及热对流传热的数值计算方法，包括网格划分、边界条件、离散方法等内容。

通过本文档，读者将了解如何使用数值方法解决热对流传热问题，并学会应用这些方法进行实际计算。

问题回答1. 简述热对流传热的数值计算方法。

热对流传热的数值计算方法主要包括三个步骤：网格划分、边界条件设置和离散方法。

网格划分是指将传热区域划分为若干个离散的小单元，每个单元内部温度变化均匀。

常见的网格划分方法有结构化网格和非结构化网格。

结构化网格适用于简单几何形状，易于处理；非结构化网格则适用于复杂几何形状。

边界条件设置是指给定物体表面的边界条件，如温度或热流密度。

边界条件的设置需要根据实际问题来确定，可以通过实验或经验公式来获取。

离散方法是指将传热控制方程进行离散化，通常使用有限差分法或有限元法。

有限差分法将控制方程离散化为代数方程组，而有限元法则通过近似方法将方程离散化。

2. 什么是结构化网格和非结构化网格？它们在热对流传热计算中有何不同？结构化网格是指由规则排列的矩形或立方体单元组成的网格。

在结构化网格中，每个单元与其相邻单元之间的联系都是固定的，因此易于处理。

结构化网格适用于简单几何形状，如长方体或圆柱体。

非结构化网格是指由不规则形状的三角形、四边形或多边形组成的网格。

在非结构化网格中，每个单元与其相邻单元之间的联系可能是不确定的，需要使用邻接表来表示网格拓扑关系。

非结构化网格适用于复杂几何形状，如复杂流体流动中的腔体或障碍物。

在热对流传热计算中，结构化网格和非结构化网格的主要区别在于网格的配置方式和计算复杂度。

结构化网格由正交单元组成，计算稳定性较高，但对于复杂几何形状的处理能力较差。

非结构化网格可以灵活地适应复杂几何形状，但计算复杂度较高。

3. 如何设置边界条件？边界条件的设置是热对流传热计算中非常重要的一步，它决定了计算结果的准确性和可靠性。

数值传热学陶文铨主编第二版习题答案

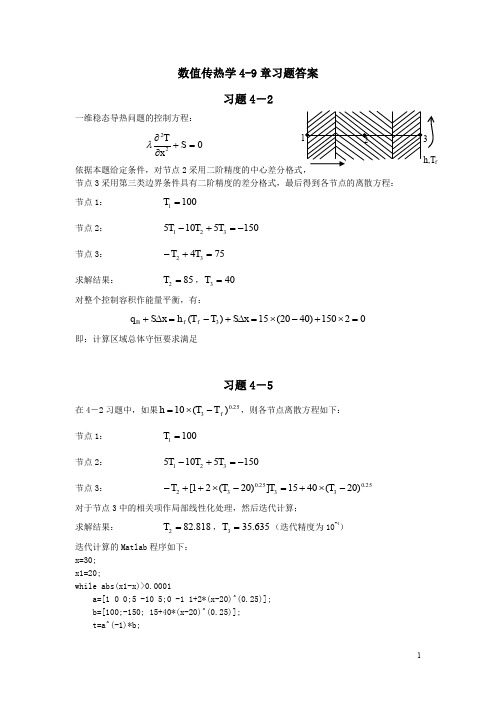
依据本题给定条件，对节点 2 采用二阶精度的中心差分格式，节点 3 采用第三类边界条件具有二阶精度的差分格式，最后得到各节点的离散方程：节点 1：节点 2：节点 3：求解结果：
T1 100
5T1 10T2 5T3 150 T2 4T3 75
T2 85 ， T3 40
习题 4-12 的 Matlab 程序
%代数方程形式 AiTi=CiTi+1+BiTi-1+Di mdim=10;%计算的节点数 x=linspace(1,3,mdim);%生成 A、C、B、T 数据的基数； A=cos(x);%TDMA 的主对角元素 B=sin(x);%TDMA 的下对角线元素 C=cos(x)+exp(x); %TDMA 的上对角线元素 T=exp(x).*cos(x); %温度数据 %由 A、B、C 构成 TDMA coematrix=eye(mdim,mdim); for n=1:mdim coematrix(n,n)=A(1,n); if n>=2 coematrix(n,n-1)=-1*B(1,n); end if n<mdim coematrix(n,n+1)=-1*C(1,n); end end %计算 D 矢量 D=(coematrix*T')'; %由已知的 A、B、C、D 用 TDMA 方法求解 T %消元 P(1,1)=C(1,1)/A(1,1); Q(1,1)=D(1,1)/A(1,1); for n=2:mdim P(1,n)=C(1,n)/(A(1,n)-B(1,n)*P(1,n-1)); Q(1,n)=(D(1,n)+B(1,n)*Q(1,n-1))/(A(1,n)-B(1,n)*P(1,n-1)); end %回迭 Tcal(1,mdim)=Q(1,mdim); for n=(mdim-1):-1:1 Tcal(1,n)=P(1,n)*Tcal(1,n+1)+Q(1,n); end Tcom=[T;Tcal]; %绘图比较给定 T 值和计算 T 值 plot(Tcal,'r*') hold on plot(T)

西安交通大学数值传热学大作业

5
数值传热学论文
能量方程： u 边界条件：
T T 2T 2T v ( 2 2 ) x y x y
T ( x, Tp ) T ( x,0)
(4)
(5) (6) (7) (8) (9) (10)
u( x, Tp ) u( x,0)
v( x, T v( x, 0 ) p )
图 2 网格划分
百叶窗翅片通道内周期性充分发展流动与换热的控制方程如下：连续性方程：动量方程： u
u v 0 x y
(1) (2) (3)
u u 1 p 2 u 2u v v( 2 2 ) x y x x y u v v 1 p 2v 2v v v( 2 2 ) x y y x y
2
数值传热学论文
主要符号表
f
Nu m
摩擦因数平均 Nusselt 数 Prandtl（普朗特）数雷诺数竖直平板和封闭方腔壁面间的距离,热扩散系数（定义 u r ）表面换热系数导热系数温度平均温度内部翅片的温度 W/(m2℃) W/(m℃) ℃ ℃ ℃ m/s m m m Pa W/m2
数值传热学论文
数值传热学大作业
1
数值传热学论文
百叶窗翅片流动换热的数值模拟
（西安交通大学能源与动力工程学院，710049，西安）摘要：针对具有一定倾斜角度的流动和换热已经进入周期性充分发展的百叶窗换热问题，在稳态、层流、常物性和翅片温度恒定的条件下，采用 SIMPLER 算法，对百叶窗的一个翅片单元进行了数值模拟计算。在翅片倾角θ =25°，雷诺数 Re 在 10 到 500 范围内变化时，得到了平均 Nusselt 数与阻力系数 f 的计算结果。计算结果表明：随着 Re 的增大，平均 Nusselt 数逐渐增大，f 却随之逐渐减少。关键词：百叶窗；周期性发展；数值模拟；SIMPLER 算法

数值传热学陶文铨第四章作业

4-1解：采用区域离散方法A 时；网格划分如右图。

内点采用中心差分123278.87769.9T T T === 22d T T=0dx - 有 i+1i 122+T 0i i T T T x ---=∆ 将2点,3点带入321222+T 0T T T x --=∆ 即321209T T -+= 432322+T 0T T T x --=∆4321322+T 0T T T x --=∆ 即4321209T T T -+-= 边界点4（1）一阶截差由x=1 1dT dx =，得 4313T T -= （2）二阶截差 11B M M q x x x T T S δδλλ-=++V 所以 434111. 1.36311T T T =++ 即 43122293T T -=采用区域离散方法B 22d T T=0dx - 由控制容积法 0w e dT dT T x dT dT ⎛⎫⎛⎫--∆= ⎪ ⎪⎝⎭⎝⎭ 所以代入2点4点有322121011336T T T T T ----= 即 239028T T -= 544431011363T T T T T ----= 即 34599 02828T T T -+=对3点采用中心差分有 432322+T 013T T T --=⎛⎫ ⎪⎝⎭ 即 2349901919T T T -+= 对于点5 由x=1 1dT dx =，得 5416T T -= （1）精确解求左端点的热流密度由 ()21x x e T e e e -=-+ 所以有 ()220020.64806911x x x x dTe e q e e dx e e λ-====-+=-=++ （2）由A 的一阶截差公式（3）由B 的一阶截差公式（4）由区域离散方法B 中的一阶截差公式：通过对上述计算结果进行比较可得：区域离散B 有控制容积平衡法建立的离散方程与区域离散方程A 中具有二阶精度的格式精确度相当！ 4-3解：将平板沿厚度方向3等分，如图由题可知该导热过程可看作无限大平板的一维稳态有源导热问题，则控制方程为x=0， T 0=75℃x=0.1 dT =h(T-T )dx f λ-1点，2点采用中心差分有21022+T 0T T S xλ-+=∆ （1） 32122+T 0T T S x λ-+=∆ （2）右端点采用一阶截差的离散231f hx T T T x h λλ⎡⎤+⎢⎥⎣⎦=⎛⎫+ ⎪⎝⎭V （3）右端点采用二阶截差的离散代入（1）（2）（3）得1223132280.62 5.67625T T T T T T T -=--=-= 解得123278.87769.9T T T ===代入（4）得解得 12380.6380.6675.1T T T ===精确解 22d T +S=0dxλ （4） x=0， T 0=75℃ （5） x=0.1 dT =h(T-T )dxf λ- （6）代入数据积分的将 x 1=10.13⨯，x 2=20.13⨯, x 3=0.1T 1=80.56 T 2=80.56 T 3=75.1通过比较可得右端点采用二阶截差的离散更接近真实值。

陶文铨老师_数值传热学_热流问题的数值计算02

热流问题的数值计算
Numerical Simulations of Thermal & Fluid Problems
第二章一维导热问题的数值解
主讲陶文铨
西安交通大学能源与动力工程学院热流中心 CFD-NHT-EHT CENTER 2007年10月23日, 西安
1/62
第二章一维导热问题的数值解 2.1 一维稳态导热 2.2 边界条件及源项的处理 2.3 一维非稳态导热 2.4 代数方程的求解方法 2.5 一维非稳态导热通用程序介绍 2.6 数值计算举例
A= B=
δ xiΔxi S hiδ x )T f TM 1−1 + +( q －第二类条件 T = λ λ M1 hiδ x +1 λ hT f －第三类条件
δ xiΔxi S δ x TM 1−1 + + A λ λ h －第三类条件 TM 1 = B iδ x +1 λ 此式适合于两种边界条件
0
－第二类条件
22/62
（3）区域离散方法B 区域离散方法B的边界节点的控制容积为零，只要令以上公式中的
Δx = 0 即得方法B中的相应公式：
0 TM1−1 −TM1 qB +λ + ΔxiS = 0 δx qB iδ x 第二类边界－ TM 1 = TM 1−1 + λ hiδ x )T f TM 1−1 + ( λ TM 1 = 第三类边界－控制容积为零 hiδ x 1+ λ 离散方法B公式具有二阶截差的精度。
边界节点不同截差离散对数值计算结果的影响
26/62
离散方法B，内部取3点，内部结点 T2 , T3 , T4 用二阶截差离散，边界节点 T5 按前述公式 TM 1 = TM 1−1 +

陶文铨老师_数值传热学_热流问题的数值计算03

主讲陶文铨西安交通大学能源与动力工程学院热流中心CFD-NHT-EHT CENTER2007年11月20日,西安第三章多维导热问题热流问题的数值计算Numerical Simulations of Thermal & Fluid Problems=xΔP Pa T+极坐标均可以表示成为：2.解决的一种方案为写出适合于三种坐标系中系数的通用表达式，特引进两个辅助变量：（1）x –方向标尺因子，scaling factor ，x-方向的距离表示成为sx x δi 。

对直角、圆柱坐标规定1;sx ≡（2）y-方向引入一个名义半径，R 。

对直角坐标R ＝1，据此，东西导热距离为：sx xδi 东西导热面积为：R /y sxΔ对圆柱与极坐标R ＝r 。

3.1.3三种二维正交坐标系中离散方程的统一表达式按这种方式编制程序时，只要设置一个变量MODE，它按以下方式取值，程序即可自动处理三种坐标系。

3.2附加源项法3.2.1第二、三类边界条件的处理方法1. 补充以边界节点代数方程的方法2. 附加源项法3.2.2附加源项法的实施细则1. 处理第二类边界条件的附加源项法2. 处理第三类边界条件的附加源项法3. 附加源项法的实施步骤3.2.3 附加源项法与补充节点法的对比对第二，第三类边界条件问题，边界温度未知，x缺点：对多维问题显著增加了求解的节点数目。

对20X20的二维区域，增加了内点的23％。

寻找不增加结点数目而又能使内节点的代数方程封闭的方法对多维问题具有重要意义。

2. 附加源项法（additional source term method,ASTM)区域的热量折算成与边界相邻的第一个控制容积的源将由第二类、第三类边界条件所规定的进入计算项；切断内点与边界点的联系，从而将未知的边界点温度从内点离散方程中排除。

W =B q y VΔΔfTC S V Δ(2)令该边界上的导热系数为零；(3)按常规方法建立内接点的离散方程，并在内接点区域求解方程组；(4)在内点区域求解方程组; 获得收敛解后按Newton 冷却公式或Fourier 定律确定边界温度。

热学第二版习题答案

热学第二版习题答案热学第二版习题答案【篇一：热工测试课后练习答案】1-1、测量方法有哪几类，直接测量与间接测量的主要区别是什么？(p1-2) 答：测量的方法有：1、直接测量；2、间接测量；3、组合测量。

直接测量与间接测量的主要区别是直接测量中被测量的数值可以直接从测量仪器上读得，而间接测量种被测量的数值不能直接从测量仪器上读得，需要通过直接测得与被测量有一定函数关系的量，然后经过运算得到被测量的数值。

1-2、简述测量仪器的组成与各组成部分的作用。

(p3-4) 答：测量仪器由感受器、中间器和效用件三个部分组成。

1、感受器或传感器：直接与被测对象发生联系（但不一定直接接触），感知被测参数的变化，同时对外界发出相应的信号；2、中间器或传递件：最简单的中间件是单纯起“传递”作用的元件，它将传感器的输出信号原封不动地传递给效用件；3、效用件或显示元件：把被测量信号显示出来，按显示原理与方法的不同，又可分模拟显示和数字显示两种。

1-3、测量仪器的主要性能指标及各项指标的含义是什么？（p5-6）答：测量仪器的主要性能指标有：精确度、恒定度、灵敏度、灵敏度阻滞、指示滞后时间等。

1、精确度：表示测量结果与真值一致的程度，它是系统误差与随机误差的综合反映；2、恒定度：仪器多次重复测试时，其指示值的稳定程度，通常以读数的变差来表示；3、灵敏度：以仪器指针的线位移或角位移与引起这些位移的被测量的变化值之间的比例来表示。

4、灵敏度阻滞：又称感量，是以引起仪器指针从静止到作极微小移动的被测量的变化值。

5、指示滞后时间：从被测参数发生变化到仪器指示出该变化值所需的时间。

1-4、说明计算机测控系统基本组成部分及其功能。

（p6-7）答：计算机测控系统基本组成部分有：传感器、信号调理器、多路转换开关、模/数（a/d）和数/模（d/a）转换及微机。

1、信号调理器：完成由传感器输出信号的放大、整形、滤波等，以保证传感器输出信号成为a/d转换器能接受的信号；2、实现多路信号测量，并由它完成轮流切换被测量与模/数转换器的连接；3、采样保持器：保证采样信号在a/d转换过程中不发生变化以提高测量精度；4、a/d转换器：将输入的模拟信号换成计算机能接受的数字信号；5、d/a转换器：将输入的数字信号换成计算机能接受的模拟信号。

数值方法(第2版)答案

C语言编程习题第二章习题2-25.用二分法编程求6x4 -40x2+9=0 的所有实根。

#include <stdio.h>#include <math.h>#define N 10000double A,B,C;double f(double x){return (A*x*x*x*x+B*x*x+C);}void BM(double a,double b,double eps1,double eps2){int k;double x,xe;double valuea = f(a);double valueb = f(b);if (valuea > 0 && valueb > 0 || valuea <0 && valueb < 0) return;printf("Finding root in the range: [%.3lf, %.3lf]\n", a, b);for(k=1;k<=N;k++) {x=(a+b)/2;xe=(b-a)/2;if(fabs(xe)<eps2 || fabs(f(x))<eps1) {printf("The x value is:%g\n",x);printf("f(x)=%g\n\n",f(x));return;}if(f(a)*f(x)<0) b=x;else a=x;}printf("No convergence!\n");}int main(){double a,b,eps1,eps2,step,start;printf("Please input A,B,C:\n");scanf("%lf %lf %lf",&A,&B,&C);printf("Please input a,b, step, eps1,eps2:\n");scanf("%lf %lf %lf %lf %lf",&a,&b,&step,&eps1,&eps2);for (start=a; (start+step) <= b; start += step) { double left = start;double right = start + step;BM(left, right, eps1, eps2);}return 0;}运行：Please input A,B,C:6 -40 9Please input a,b, step, eps1,eps2:-10 10 1 1e-5 1e-5Finding root in the range: [-3.000, -2.000]The x value is:-2.53643f(x)=-0.00124902Finding root in the range: [-1.000, 0.000]The x value is:-0.482857f(x)=0.00012967Finding root in the range: [0.000, 1.000]The x value is:0.482857f(x)=0.00012967Finding root in the range: [2.000, 3.000]The x value is:2.53643f(x)=-0.00124902有时若把判别语句if(fabs(xe)<eps2 || fabs(f(x))<eps1)改为if(fabs(xe)<eps2 && fabs(f(x))<eps1)会提高精度，对同一题运行结果：Finding root in the range: [-3.000, -2.000]The x value is:-2.53644f(x)=-4.26496e-007Finding root in the range: [-1.000, 0.000]The x value is:-0.482861f(x)=-7.3797e-006Finding root in the range: [0.000, 1.000]The x value is:0.482861f(x)=-7.3797e-006Finding root in the range: [2.000, 3.000]The x value is:2.53644f(x)=-4.26496e-007习题2-35. 请用埃特金方法编程求出x=tgx在4.5（弧度）附近的根。

(完整版)数值传热学陶文铨主编第二版习题答案

数值传热学4-9章习题答案习题4－2一维稳态导热问题的控制方程：022=+∂∂S xTλ依据本题给定条件，对节点2节点3采用第三类边界条件具有二阶精度的差分格式，最后得到各节点的离散方程：节点1：1001=T 节点2：1505105321-=+-T T T 节点3：75432=+-T T 求解结果：，852=T 403=T 对整个控制容积作能量平衡，有：2150)4020(15)(3=⨯+-⨯=∆+-=∆+x S T T h x S q f f B 即：计算区域总体守恒要求满足习题4－5在4－2习题中，如果，则各节点离散方程如下：25.03)(10f T T h -⨯=节点1：1001=T 节点2：1505105321-=+-T T T 节点3：25.03325.032)20(4015])20(21[-⨯+=-⨯++-T T T T 对于节点3中的相关项作局部线性化处理，然后迭代计算；求解结果：，（迭代精度为10-4）818.822=T 635.353=T 迭代计算的Matlab 程序如下：x=30;x1=20;while abs(x1-x)>0.0001a=[1 0 0;5 -10 5;0 -1 1+2*(x-20)^(0.25)]; b=[100;-150; 15+40*(x-20)^(0.25)]; t=a^(-1)*b;x1=x;x=t(3,1);endtcal=t习题4-12的Matlab程序%代数方程形式A i T i=C i T i+1+B i T i-1+D imdim=10;%计算的节点数x=linspace(1,3,mdim);%生成A、C、B、T数据的基数；A=cos(x);%TDMA的主对角元素B=sin(x);%TDMA的下对角线元素C=cos(x)+exp(x); %TDMA的上对角线元素T=exp(x).*cos(x); %温度数据%由A、B、C构成TDMAcoematrix=eye(mdim,mdim);for n=1:mdimcoematrix(n,n)=A(1,n);if n>=2coematrix(n,n-1)=-1*B(1,n);endif n<mdimcoematrix(n,n+1)=-1*C(1,n);endend%计算D矢量D=(coematrix*T')';%由已知的A、B、C、D用TDMA方法求解T%消元P(1,1)=C(1,1)/A(1,1);Q(1,1)=D(1,1)/A(1,1);for n=2:mdimP(1,n)=C(1,n)/(A(1,n)-B(1,n)*P(1,n-1));Q(1,n)=(D(1,n)+B(1,n)*Q(1,n-1))/(A(1,n)-B(1,n)*P(1,n-1)); end%回迭Tcal(1,mdim)=Q(1,mdim);for n=(mdim-1):-1:1Tcal(1,n)=P(1,n)*Tcal(1,n+1)+Q(1,n);endTcom=[T;Tcal];%绘图比较给定T值和计算T值plot(Tcal,'r*')hold onplot(T)n gin th a r e 结果比较如下，由比较可知两者值非常切合（在小数点后8位之后才有区别）：习题4-14充分发展区的温度控制方程如下：)(1rTr r r x T uc p ∂∂∂∂=∂∂λρ对于三种无量纲定义、、进行分析如下w b w T T T T --=Θ∞∞--=ΘT T T T w ww T T T T --=Θ∞1）由得：wb wT T T T --=Θww b T T T T +Θ-=)(由可得：T x T x T x T T T x T w b w w b ∂∂Θ-+∂∂Θ=∂+Θ-∂=∂∂)1(])[(rT r T T r T T T r T w w b w w b ∂∂Θ-+∂Θ∂-=∂+Θ-∂=∂∂)1()(])[(由与无关、与无关以及、的表达式可知，除了均匀的情况外，该无量b T r Θx x T ∂∂rT∂∂w T 纲温度定义在一般情况下是不能用分离变量法的；2）由得：∞∞--=ΘT T T T w ∞∞+Θ-=T T T T w )(由可得：T xT x T T T x T w w ∂∂Θ=∂+Θ-∂=∂∂∞∞])[(rT r T T r T T T r T w w w ∂∂Θ+∂Θ∂-=∂+Θ-∂=∂∂∞∞∞)(])[(由与无关、与无关以及、的表达式可知，在常见的四种边界条件中除了b T r Θx x T ∂∂rT ∂∂轴向及周向均匀热流的情况外，有，则该无量纲温度定义是可以用分const q w =0=∂∂rT w离变量法的；3）由得：wwT T T T --=Θ∞ww T T T T +Θ-=∞)(由可得：T xT x T T T x T w w w ∂∂Θ-=∂+Θ-∂=∂∂∞)1(])[(r T T r T T T r T w w w -+∂Θ∂-=∂+Θ-∂=∂∂∞∞1()(])[(同2）分析可知，除了轴向及周向均匀热流const q w =温度定义是可以用分离变量法的；习题4－181）采用柱坐标分析，写出统一的稳态柱坐标形式动量方程：S r r r r r r x x w r v r r r u x +∂∂∂∂+∂∂∂∂+∂∂∂∂=∂∂+∂∂+∂∂(1)(1)()(1)(1)(θφλθφλφλφρθφρφρ、和分别是圆柱坐标的3个坐标轴，、和分别是其对应的速度分量，其中x r θu v w 是管内的流动方向；x 对于管内的层流充分发展有：、，；0=v 0=w 0=∂∂xu并且方向的源项：x x pS ∂∂-=方向的源项：r r pS ∂∂-=方向的源项：θθ∂∂-=pr S 1由以上分析可得到圆柱坐标下的动量方程：方向：x 0)(1)(1=∂∂-∂∂∂∂+∂∂∂∂x pu r r r u r r r θλθλ方向：r 0=∂∂r p 方向：θ0=∂∂θp 边界条件：，R r =0=u ，；对称线上，0=r 0=∂∂r u 0=∂∂θu 不考虑液体的轴向导热，并简化分析可以得到充分发展的能量方程为：)(1(1θλθλρ∂∂∂∂+∂∂∂∂=∂∂Tr r r T r r r x T uc p 边界条件：，；，R r =w q r T =∂∂λ0=r 0=∂∂rT，πθ/0=0=∂∂-θλT2）定义无量纲流速：dxdp R uU 2-=λ并定义无量纲半径：；将无量纲流速和无量纲半径代入方向的动量方程得：R r /=ηx 0))1((1)1((122=∂∂-∂-∂∂∂+∂-∂∂∂xp U dx dp R R R R U dx dp R RR R θληλθηηλληηη上式化简得：011(1(1=+∂∂∂∂+∂∂∂∂θηθηηηηηU U 边界条件：，1=η0=U ，；对称线上，0=η0=∂∂ηU 0=∂∂θU定义无量纲温度：λ/0R q T T b-=Θ其中，是折算到管壁表面上的平均热流密度，即：；0q Rq q wπ=0由无量纲温度定义可得：bT Rq T +Θ=λ0将表达式和无量纲半径代入能量方程得：T η(1)(100θληλθηηλληηηρ∂Θ∂∂∂+∂Θ∂∂∂=∂∂R q R R R R q R R R x T uc b p 化简得：（1）)1(1)(10θηθηηηηηρ∂Θ∂∂∂+∂Θ∂∂∂=∂∂x T u c q R b p 由热平衡条件关系可以得：mm m b m p b p p RU U q R u u R q A u u dx dT A u c x T u c x T uc 020221221)(===∂∂=∂∂ππρρρ将上式代入式（1）可得：)1(1)(12θηθηηηηη∂Θ∂∂∂+∂Θ∂∂∂=m U U 边界条件：，；，0=η0=∂Θ∂η1=ηR q q w πη10==∂Θ∂，；，0=θ0=∂Θ∂θπθ=0=∂Θ∂θ单值条件：由定义可知：且： 0/0=-=ΘλR q T T b b b ⎰⎰Θ=ΘAAb UdAUdA 即得单值性条件：=Θ⎰⎰AA UdAUdA 3）由阻力系数及定义有：f Re 228)(21/Re ⎪⎭⎫ ⎝⎛=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=D D U D u u dx dp D f e m e m me νρ且：m W b m W b m W R q T T D T T q Nu ,0,,0~2)/(2Θ=-=-=λλ5－21．一维稳态无源项的对流－扩散方程如下所示：（取常物性）xx u 22∂∂Γ=∂∂φφρ边界条件如下：LL x x φφφφ====,;,00上述方程的精确解如下： 11)/(00--=--⋅Pe L x Pe L e e φφφφΓ=/uL Pe ρ2．将分成20等份，所以有：L ∆=P Pe 20 1 2 3 4 5 6……………………… 17 18 19 20 21对于中心差分、一阶迎风、混合格式和QUICK 格式分别分析如下：1）中心差分中间节点： 2)5.01()5.01(11-∆+∆++-=i i i P P φφφ20,2 =i 2）一阶迎风中间节点： ∆-∆++++=P P i i i 2)1(11φφφ20,2 =i 3）混合格式当时，中间节点： 1=∆P 2)5.01()5.01(11-∆+∆++-=i i i P P φφφ 20,2 =i 当时，中间节点： 10,5=∆P 1-=i i φφ20,2 =i 4）QUICK 格式*12111)35(8122121⎥⎦⎤⎢⎣⎡---++++++=+--∆∆-∆∆+∆i i i i i i i P P P P P φφφφφφφ2≠i*1111)336(8122121⎥⎦⎤⎢⎣⎡--++++++=+-∆∆-∆∆+∆i i i i i i P P P P P φφφφφφ2=i 数值计算结果与精确解的计算程序如下：%except for HS, any other scheme doesnt take Pe<0 into consideration %expression of exact solutiony=dsolve('a*b*Dy=c*D2y','y(0)=y0,y(L)=yL','x')y=subs(y,'L*a*b/c','t')y=simple(subs(y,'a*b/c*x','t*X'));ysim=simple(sym(strcat('(',char(y),'-y0)','/(yL-y0)')))y=sym(strcat('(',char(ysim),')*(yL-y0)','+y0'))% in the case of Pe=0y1=dsolve('D2y=0','y(0)=y0,y(L)=yL','x')y1=subs(y1,'-(y0-yL)/L*x','(-y0+yL)*X')%grid Pe number tt=[1 5 10];%dimensionless length m=20;%mdim is the number of inner node mdim=m-1;X=linspace(0,1,m+1);%initial value of variable during calculation y0=1;yL=2;%cal exact solution for n=1:size(tt,2) t=m*tt(1,n); if t==0 yval1(n,:)=eval(y1); else yval1(n,:)=eval(y); end end%extra treatment because max number in MATLAB is 10^308if max(isnan(yval1(:))) yval1=yval1'; yval1=yval1(:);indexf=find(isnan(yval1)); for n=1:size(indexf,1) if rem(indexf(n,1),size(X,2))==0 yval1(indexf(n),1)=yL; else yval1(indexf(n),1)=y0; endendyval1=reshape(yval1,size(X,2),size(yval1,1)/size(X,2));yval1=yval1';end%CD solutiond=zeros(size(tt,2),mdim);a=repmat([1],size(tt,2),mdim);for n=1:size(tt,2)t=tt(1,n);b(n,:)=repmat([0.5*(1-0.5*t)],1,mdim);c(n,:)=repmat([0.5*(1+0.5*t)],1,mdim);d(n,1)=0.5*(1+0.5*tt(1,n))*y0;d(n,mdim)=0.5*(1-0.5*tt(1,n))*yL;endc(:,1)=0;b(:,mdim)=0;%numerical cal by using TDMA subfuctionyval2=TDMA(a,b,c,d,mdim);yval2=[repmat([1],size(tt,2),1),yval2,repmat([2],size(tt,2),1)]; Fig(1,X,yval1,yval2,tt);title('CD Vs. Exact Solution')% FUS solutiond=zeros(size(tt,2),mdim);a=repmat([1],size(tt,2),mdim);for n=1:size(tt,2)t=tt(1,n);b(n,:)=repmat([1/(2+t)],1,mdim);c(n,:)=repmat([(1+t)/(2+t)],1,mdim);d(n,1)=(1+tt(1,n))/(2+tt(1,n))*y0;d(n,mdim)=1/(2+tt(1,n))*yL;endc(:,1)=0;b(:,mdim)=0;%numerical cal by using TDMA subfuctionyval3=TDMA(a,b,c,d,mdim);yval3=[repmat([1],size(tt,2),1),yval3,repmat([2],size(tt,2),1)]; Fig(2,X,yval1,yval3,tt);title('FUS Vs. Exact Solution')% HS solutiond=zeros(size(tt,2),mdim);a=repmat([1],size(tt,2),mdim);for n=1:size(tt,2)t=tt(1,n);if t>2b(n,:)=repmat([0],1,mdim);c(n,:)=repmat([1],1,mdim);d(n,1)=y0;elseif t<-2b(n,:)=repmat([1],1,mdim);c(n,:)=repmat([0],1,mdim);d(n,mdim)=yL;elseb(n,:)=repmat([0.5*(1-0.5*t)],1,mdim);c(n,:)=repmat([0.5*(1+0.5*t)],1,mdim);d(n,1)=0.5*(1+0.5*t)*y0;d(n,mdim)=0.5*(1-0.5*t)*yL;endendc(:,1)=0;b(:,mdim)=0;% numerical cal by using TDMA subfuctionyval4=TDMA(a,b,c,d,mdim);yval4=[repmat([1],size(tt,2),1),yval4,repmat([2],size(tt,2),1)]; Fig(3,X,yval1,yval4,tt);title('HS Vs. Exact Solution')%QUICK Solutiond=zeros(size(tt,2),mdim);a=repmat([1],size(tt,2),mdim);for n=1:size(tt,2)t=tt(1,n);b(n,:)=repmat([1/(2+t)],1,mdim);c(n,:)=repmat([(1+t)/(2+t)],1,mdim);d(n,1)=(1+tt(1,n))/(2+tt(1,n))*y0;d(n,mdim)=1/(2+tt(1,n))*yL;endc(:,1)=0;b(:,mdim)=0;%numerical cal by using TDMA subfuctionyval5=zeros(size(tt,2),mdim);yval5com=yval5+1;counter=1;%iterativewhile max(max(abs(yval5-yval5com)))>10^-10if counter==1yval5com=TDMA(a,b,c,d,mdim);endfor nn=1:size(tt,2)for nnn=1:mdimif nnn==1d(nn,nnn)=((6*yval5com(nn,nnn)-3*y0-3*yval5com(nn,nnn+1))*tt(1,nn))/(8*(2+tt(1,nn)))+((1+tt(1,nn))/(2+tt(1,nn))*y0);elseif nnn==2d(nn,nnn)=((5*yval5com(nn,nnn)-3*yval5com(nn,nnn+1)-yval5com(nn,nnn-1)-y0)*tt(1,nn))/(8*(2+tt(1,nn)));elseif nnn==mdimd(nn,nnn)=((5*yval5com(nn,nnn)-3*yL-yval5com(nn,nnn-1)-yval5com(nn,nnn-2))*tt(1,nn))/(8*(2+tt(1,nn)))+(1/(2+tt(1,nn))*yL);elsed(nn,nnn)=((5*yval5com(nn,nnn)-3*yval5com(nn,nnn+1)-yval5com(nn,nnn-1)-yval5com(nn,nnn-2))*tt(1,nn))/(8*(2+tt(1,nn)));endendendyval5=TDMA(a,b,c,d,mdim);temp=yval5;yval5=yval5com;yval5com=temp;counter=counter+1;endyval5=yval5com;yval5=[repmat([1],size(tt,2),1),yval5,repmat([2],size(tt,2),1)];Fig(4,X,yval1,yval5,tt);title('QUICK Vs. Exact Solution')%-------------TDMA SubFunction------------------function y=TDMA(a,b,c,d,mdim)%form a b c d resolve yval2 by using TDMA%eliminationp(:,1)=b(:,1)./a(:,1);q(:,1)=d(:,1)./a(:,1);for n=2:mdimp(:,n)=b(:,n)./(a(:,n)-c(:,n).*p(:,n-1));q(:,n)=(d(:,n)+c(:,n).*q(:,n-1))./(a(:,n)-c(:,n).*p(:,n-1));end%iterativey(:,mdim)=q(:,mdim);for n=(mdim-1):-1:1y(:,n)=p(:,n).*y(:,n+1)+q(:,n);end%-------------ResultCom SubFunction------------------function y=ResultCom (a,b,c)for n=1:max(size(c,2))y(2*n-1,:)=a(n,:);y(2*n,:)=b(n,:);end%-------------Fig SubFunction------------------function y=Fig(n,a,b,c,d)figure(n);plot(a,b);hold onplot(a,c,'*');str='''legend(';for n=1:size(d,2)if n==size(d,2)str=strcat(str,'''''Pe=',num2str(d(1,n)),''''')''');elsestr=strcat(str,'''''Pe=',num2str(d(1,n)),''''',');endendeval(eval(str));a n d A l l t h i n g s i n t h ei r b e i n g a r e g 13精确解与数值解的对比图，其中边界条件给定，。

数值传热学第二章部分习题参考答案

习题2－4 [解]1．先用控制容积积分法得出离散方程：以r 乘式01=+⎪⎭⎫⎝⎛S dr dT rk dr d r ，并对图2-2所示的控制容积P 作积分： wewe dr dT rk dr dT rk dr dr dT rk dr d r r⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎰1 2-4-1 ()E P e eT T dT dr r δ-⎛⎫=⎪⎝⎭ 2-4-1-1 ()P W w wT T dT dr r δ-⎛⎫= ⎪⎝⎭2-4-1-2将式（2-4-1-1）、式（2-4-1-2）代入式（2-4-1）可以得到：()()W P wP E e ewT T x rk T T x rk dr dr dT rk dr d r r-⎪⎭⎫⎝⎛--⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎰δδ1 2-4-2 222ee wP w r r rSdr S Sr r -==∆⎰2-4-3根据式（2-4-2）、式（2-4-3）可以得到：P E W P e w e w rk rk rk rk T T T Sr r x x x x δδδδ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+=++∆ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦2-4-4令e E x rk a ⎪⎭⎫ ⎝⎛=δ，wW x rk a ⎪⎭⎫⎝⎛=δ，W E P a a a +=，P b Sr r =∆，式（2-4-4）可以写成b T a T a T a W W E E P P ++=的形式。

2. 再用Taylor 展开法导出022=++S drdTr k dr T d k的离散方程。

将点E T 对点P T 作Taylor 展开，有：()() +++=!2222e Pe P P E x dr Td x drdTT T δδ 2-4-5再将点W T 对点P T 作Taylor 展开，有：()() ++-=!2222wPw P P W x dr Td x drdTT T δδ 2-4-6根据式（2-4-5）、式（2-4-6）可以计算出dr dT ，22drTd ()[]()()[]()[]()()[]()()[]222222w e e w We P w e E w x x x x T x T x x T x dr dT δδδδδδδδ+---= 2-4-7 ()()()[]()()[]()()[]()222222we e w We P w e E w x x x x T x T x x T x dr T d δδδδδδδδ+++-= 2-4-8 将式（2-4-7）、式（2-4-8）代入上面的非守恒型方程，整理成（并考虑到常物性、均分网格）：222P P P P E W P kr kr kr k k T T T r rS r r r ⎡⎤⎡⎤=++-+∆⎢⎥⎢⎥∆∆∆⎣⎦⎣⎦2-4-9 令12e P E kr ra k r r ⎡⎤=+=⎢⎥∆∆⎣⎦，12w P W kr r a k r r⎡⎤=-=⎢⎥∆∆⎣⎦，W E P a a a +=，P b r rS =∆式（2-4-9）也可以写成b T a T a T a W W E E P P ++=的形式。

数值传热学部分习题问题详解2

习题4－2一维稳态导热问题的控制方程：022=+∂∂S xTλ 依据本题给定条件，对节点2采用二阶精度的中心差分格式，节点3采用第三类边界条件具有二阶精度的差分格式，最后得到各节点的离散方程：节点1： 1001=T节点2： 1505105321-=+-T T T 节点3：75432=+-T T求解结果：852=T ，403=T对整个控制容积作能量平衡，有：02150)4020(15)(3=⨯--⨯=∆+-=∆+x S T T h x S q f f B即：计算区域总体守恒要求满足习题4－5在4－2习题中，如果25.03)(10f T T h -⨯=，则各节点离散方程如下：节点1： 1001=T节点2： 1505105321-=+-T T T节点3：25.03325.032)20(4015])20(21[-⨯+=-⨯++-T T T T对于节点3中的相关项作局部线性化处理，然后迭代计算；求解结果：818.822=T ，635.353=T （迭代精度为10-4）迭代计算的Matlab 程序如下：x=30; x1=20;while abs(x1-x)>0.0001a=[1 0 0;5 -10 5;0 -1 1+2*(x-20)^(0.25)]; b=[100;-150; 15+40*(x-20)^(0.25)]; t=a^(-1)*b; x1=x; x=t(3,1); end tcal=t习题4-14充分发展区的温度控制方程如下：)(1rTr r r x T uc p ∂∂∂∂=∂∂λρ 对于三种无量纲定义w b w T T T T --=Θ、∞∞--=ΘT T T T w 、w w T T T T --=Θ∞进行分析如下1）由wb wT T T T --=Θ得：w w b T T T T +Θ-=)(由T 可得：x T x T x T T T x T w b w w b ∂∂Θ-+∂∂Θ=∂+Θ-∂=∂∂)1(])[(rT r T T r T T T r T w w b w w b ∂∂Θ-+∂Θ∂-=∂+Θ-∂=∂∂)1()(])[( 由b T 与r 无关、Θ与x 无关以及x T ∂∂、rT∂∂的表达式可知，除了w T 均匀的情况外，该无量纲温度定义在一般情况下是不能用分离变量法的； 2）由∞∞--=ΘT T T T w 得：∞∞+Θ-=T T T T w )(由T 可得：xT x T T T x T w w ∂∂Θ=∂+Θ-∂=∂∂∞∞])[(rT r T T r T T T r T w w w ∂∂Θ+∂Θ∂-=∂+Θ-∂=∂∂∞∞∞)(])[( 由b T 与r 无关、Θ与x 无关以及x T ∂∂、rT∂∂的表达式可知，在常见的四种边界条件中除了轴向及周向均匀热流const q w =的情况外，有0=∂∂rT w离变量法的；3）由wwT T T T --=Θ∞得：w w T T T T +Θ-=∞)(由T 可得： xT x T T T x T w w w ∂∂Θ-=∂+Θ-∂=∂∂∞)1(])[(rT r T T r T T T r T w w w w ∂∂Θ-+∂Θ∂-=∂+Θ-∂=∂∂∞∞)1()(])[( 同2）分析可知，除了轴向及周向均匀热流const q w =的情况外，有0=∂∂rT w，该无量纲温度定义是可以用分离变量法的；习题4－181）采用柱坐标分析，写出统一的稳态柱坐标形式动量方程：S r r r r r r x x w r v r r r u x +∂∂∂∂+∂∂∂∂+∂∂∂∂=∂∂+∂∂+∂∂)(1)(1)()(1)(1)(θφλθφλφλφρθφρφρ x 、r 和θ分别是圆柱坐标的3个坐标轴，u 、v 和w 分别是其对应的速度分量，其中x 是管内的流动方向；对于管内的层流充分发展有：0=v 、0=w ，0=∂∂xu；并且x 方向的源项：x p S ∂∂-= r 方向的源项：r pS ∂∂-=θ方向的源项：θ∂∂-=pr S 1 由以上分析可得到圆柱坐标下的动量方程： x 方向： 0)(1)(1=∂∂-∂∂∂∂+∂∂∂∂x pu r r r u r r r θλθλ r 方向：0=∂∂r pθ方向：0=∂∂θp边界条件： R r =，0=u0=r ，0=∂∂r u ；对称线上，0=∂∂θu 不考虑液体的轴向导热，并简化分析可以得到充分发展的能量方程为：)(1)(1θλθλρ∂∂∂∂+∂∂∂∂=∂∂Tr r r T r r r x T uc p 边界条件： R r =，w q r T =∂∂λ；0=r ，0=∂∂rTπθ/0=，0=∂∂-θλT2）定义无量纲流速：dxdp R uU 2-=λ并定义无量纲半径：R r /=η；将无量纲流速和无量纲半径代入x 方向的动量方程得：0))1((1))1((122=∂∂-∂-∂∂∂+∂-∂∂∂xp U dx dp R R R R U dx dp R RR R θληλθηηλληηη 上式化简得：01)1(1)(1=+∂∂∂∂+∂∂∂∂θηθηηηηηU U 边界条件：1=η，0=U0=η，0=∂∂ηU ；对称线上，0=∂∂θU定义无量纲温度：λ/0R q T T b-=Θ其中，0q 是折算到管壁表面上的平均热流密度，即：Rq q wπ=0；由无量纲温度定义可得： b T Rq T +Θ=λ将T 表达式和无量纲半径η代入能量方程得：)(1)(100θληλθηηλληηηρ∂Θ∂∂∂+∂Θ∂∂∂=∂∂R q R R R R q R R R x T uc b p 化简得：)1(1)(10θηθηηηηηρ∂Θ∂∂∂+∂Θ∂∂∂=∂∂x T u c q R b p （1）由热平衡条件关系可以得：mm m b m p b p p RU U q R u u R q A u u dx dT A u c x T u c x T uc 020221221)(===∂∂=∂∂ππρρρ 将上式代入式（1）可得：)1(1)(12θηθηηηηη∂Θ∂∂∂+∂Θ∂∂∂=m U U 边界条件： 0=η，0=∂Θ∂η；1=η，R q q w πη10==∂Θ∂0=θ，0=∂Θ∂θ；πθ=，0=∂Θ∂θ单值条件：由定义可知：0/0=-=ΘλR q T T b b b 且： ⎰⎰Θ=ΘAAb UdAUdA即得单值性条件：0=Θ⎰⎰AA UdAUdA 3）由阻力系数f 及Re 定义有：228)(21/Re ⎪⎭⎫ ⎝⎛=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=D D U D u u dx dp D f e m e m me νρ 且：m W b m W b m W R q T T D T T q Nu ,0,,0~2)/(2Θ=-=-=λλ5－21．一维稳态无源项的对流－扩散方程如下所示：xx u 22∂∂Γ=∂∂φφρ （取常物性）边界条件如下：L L x x φφφφ====,;,00上述方程的精确解如下：11)/(00--=--⋅PeL x Pe L e e φφφφ Γ=/uL Pe ρ 2．将L 分成20等份，所以有：∆=Pe 20图示如下：1 2 3 4 5 6 ………… …………… 17 18 19 20 21 对于中心差分、一阶迎风、混合格式和QUICK 格式分别分析如下： 1）中心差分中间节点： 2)5.01()5.01(11-∆+∆++-=i i i P P φφφ 20,2Λ=i2）一阶迎风中间节点： ∆-∆++++=P P i i i 2)1(11φφφ 20,2Λ=i3）混合格式当1=∆P 时，中间节点：2)5.01()5.01(11-∆+∆++-=i i i P P φφφ20,2Λ=i当10,5=∆P 时，中间节点： 1-=i i φφ 20,2Λ=i 4） QUICK 格式*12111)35(8122121⎥⎦⎤⎢⎣⎡---++++++=+--∆∆-∆∆+∆i i i i i i i P P P P P φφφφφφφ 2≠i *1111)336(8122121⎥⎦⎤⎢⎣⎡--++++++=+-∆∆-∆∆+∆i i i i i i P P P P P φφφφφφ 2=i 5－3乘方格式：⎪⎪⎩⎪⎪⎨⎧<-≤≤--+≤≤->=∆∆∆∆∆∆∆∆10,010,)1.01(100,)1.01(10,055P P P P P P P P D a e E当1.0=∆P 时有：951.0)1.01.01()1.01(55=⨯-=-=∆P D a eE因为：301.0/3)()()()()()(===Γ=Γ=∆eee e e e e e e P u x u u x D ρδρρδ 所以：5297.2830951.0951.0=⨯==e E D a由系数关系式∆=-P D a D a eEw W 可得： 53.3130)951.01.0()(=⨯+=⨯+=∆w eEW D D a P a 且： 205.01.010=⨯=∆∆=txa P p ρ 当采用隐式时1=f ，因此可得：0597.62253.315297.280=++=++=P W E P a fa fa a同理可得当10=∆P 时有：0=E a ，3=W a ，5=P a5－5二维稳态无源项的对流－扩散问题的控制方程：)()()()(yy x x y v x u ∂∂Γ∂∂+∂∂Γ∂∂=∂∂+∂∂φφφρφρφφ 对于一阶迎风、混合、乘方格式的通用离散方程：S S N N W W E E P P a a a a a φφφφφ+++=其中：[]0,)(e e e E F P A D a -+=∆ []0,)(w w w W F P A D a +=∆ []0,)(n n n N F P A D a -+=∆ []0,)(s s s S F P A D a +=∆5－71）QUICK 格式的界面值定义如下：⎪⎪⎩⎪⎪⎨⎧-+=-+=)36(81)36(81WW P W w W E P e φφφφφφφφ0>u 对（5－1）式dxdx d d dx u d )()(φφρΓ=积分可得： w e w e dxd dx d u u )()()()(φφφρφρΓ-Γ=-对流项采用QUICK 格式的界面插值，扩散项采用线性界面插值，对于0>u 及均分网格有：)]()([]))(36())(36[(81x x u u W P w P E e w WW P W e W E P ∆-Γ-∆-Γ=-+--+φφφφρφφφρφφφ 整理得：WW w W w e w E e e P w e w e u u u x u x x x u u φρφρρφρφρρ)(81])(43)(81[])(83[)]()(83)(43[-++∆Γ+-∆Γ=∆Γ+∆Γ+-上式即为QUICK 格式离散得到的离散方程；2）要分析QUICK 格式的稳定性，则应考虑非稳平流方程：xut ∂∂-=∂∂φφ 在t ∆时间间隔内对控制容积作积分：⎰⎰⎰⎰∆+∆+∂∂-=∂∂t t t e w e w tt tdxdt x u dtdx xφφ得：dt u dx tt tw e e wttt ⎰⎰∆+∆+--=-)()(φφφφφ随时间变化采用阶梯显式，随空间变化采用QUICK 格式得：t u x WW P W W E P tP t t P ∆+---+-=∆-∆+)]3636(81[)(φφφφφφφφ整理得：xu t ni n i n i n i ni n i ∆+-+-∆---++87332111φφφφφφ对于初始均匀零场，假设在),(n i 点有一个扰动n i ε；对1+i 点写出QUICK 格式的离散方程：xu tni n i n i n i n i n i ∆+-+-∆--+++++8733121111φφφφφφ可得：ni n i xt u εφ∆∆=++8711 对1-i 点分析可得：ni n i xt u εφ∆∆-=+-8311 由于扩散对扰动的传递恒为正，其值为ni x t ερ2∆Γ∆，所以根据符号不变原则有： 0)/)83(2≥∆Γ∆+∆∆-ni n i n i xt x t u εερε 整理得到QUICK 格式的稳定性条件为：38≤∆P 5－91）三阶迎风格式采用上游两个节点和下游一个节点的值来构造函数界面插值形式，所以定义如下：⎩⎨⎧<++=>++=00u c b a u c b a EEE P e W P E e φφφφφφφφ根据上述定义，在0>u 时对控制容积内的对流项作积分平均可得：])()([1)(11WW W P E e w w e c b c a b a xxdx x x φφφφφφφ--+-+∆=-∆=∂∂∆⎰由表2－1式可知三阶迎风格式的差分格式：xxni n i n i n i ni ∆+-+=∂∂--+1221264211,φφφφφ 由控制容积积分法得到的对流项离散格式应与Taylor 离散展开得到的离散格式具有相同的形式和精度，所以比较可得：61,65,31-===c b a所以三阶迎风格式的函数插值定义为：⎪⎪⎩⎪⎪⎨⎧<-+=>-+=06165310616531u u EE E P e W P E e φφφφφφφφ2）由上述分析可知，得到的三阶迎风格式的插值定义与给出节点上导数表达式的定义在形式上显然是一致的；6－1二维直角坐标中不可压缩流体的连续方程及动量方程如下：⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧+∂∂∂∂+∂∂∂∂+∂∂-=∂∂+∂∂+∂∂+∂∂∂∂+∂∂∂∂+∂∂-=∂∂+∂∂+∂∂=∂∂+∂∂)3()()()()()()2()()()()()()1(0vu S y y v x x v y p y vv x vu t v S y y u x x u x p y uv x uu tu y v x u ηηρρρηηρρρ假设常粘性，则0==v u S S ；对公式（2）及（3）分别对y x ,求偏导得：⎪⎪⎩⎪⎪⎨⎧∂∂+⎪⎪⎭⎫ ⎝⎛∂∂∂∂+⎪⎪⎭⎫ ⎝⎛∂∂∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂⎪⎪⎭⎫⎝⎛∂∂∂∂+∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂33222233)()()()()()(y v x v y y p y y vv y x vu y t v y y u x x u x p x y uv x x uu x t u x ηηρρρηηρρρ 两式相加得并变换积分顺序有：⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛∂∂+∂∂∂∂+⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛∂∂+∂∂∂∂+⎪⎪⎭⎫⎝⎛∂∂+∂∂-=⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂∂∂+⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂∂∂+⎪⎪⎭⎫ ⎝⎛∂∂+∂∂∂∂y v x u yy v x u xy p x p x v u x u v y v v y y v u y u v x u u x y v x u t 2222222222ηηρρ利用连续方程有：⎪⎪⎭⎫ ⎝⎛∂∂+∂∂-=⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛∂∂+∂∂∂∂+⎪⎪⎭⎫ ⎝⎛∂∂+∂∂∂∂2222y p x p x v u y v v y y u v x u u x ρ ⎪⎪⎭⎫ ⎝⎛∂∂+∂∂-=⎥⎦⎤⎢⎣⎡∂∂∂∂-∂∂∂∂+∂∂+∂∂+∂∂∂∂22222222222y p xp y v x u y v x u y v x u x v y u ρ 最后即得：⎥⎦⎤⎢⎣⎡∂∂∂∂-∂∂∂∂=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂x v y u y v x u y p x p ρ222226－4假设5*=P p ，则有：5105*-=-=e u 5.3)05(7.0*=-⨯=n v由连续性条件有：s w n e v u v u +=+按SIMPLE 算法有：'''*5)(P E P e e e p p p d u u +-=-+= '''*7.05.3)(P n P n n n p p p d v v +=-+=将上两式代入连续性方程中有：20507.05.35''+=+++-P P p p计算得：06.42'=P p所以：06.4706.425'*=+=+=P P P p p p06.371006.47=-=-=E P e p p u 94.32)006.47(7.0)(7.0=-⨯=-=N P n p p v6－5假设250*3=p ，150*6=p ，所以各点的流量为：⎪⎪⎪⎩⎪⎪⎪⎨⎧-=-⨯==-⨯=-=-⨯=-=-⨯==-⨯=11)15040(1.020)150250(2.024)25010(1.04)270250(2.010)250275(4.0*****E DC B A Q Q Q Q Q 上述流量满足动量方程，但并不满足连续性方程，所以对流量修正：⎪⎪⎪⎩⎪⎪⎪⎨⎧-⨯+-=-⨯+=-⨯+-=-⨯+-=-⨯+=)(1.011)(2.020)(1.024)(2.04)(4.010'6'5'6'3'3'4'2'3'3'1p p Q p p Q p p Q p p Q p p Q ED C B A 对节点3作质量守恒有：B DC A Q Q Q Q +=+即得：)(2.04)(2.020)(1.024)(4.010'2'3'6'3'3'4'3'1p p p p p p p p -⨯+--⨯+=-⨯+--⨯+对节点3作质量守恒有：F E D Q Q Q =+即得：20)(1.011)(2.020'6'5'6'3=-⨯+--⨯+p p p p联立求解上两式有：70.48'3-=p ，13.69'6-=p修正后的压力为：3.20170.48250'3*33=-=+=p p p 87.8013.69150'6*66=-=+=p p p修正后的流量为：⎪⎪⎪⎩⎪⎪⎪⎨⎧-=-⨯==-⨯=-=-⨯=-=-⨯==-⨯=09.4)87.8040(1.009.24)87.803.201(2.013.19)3.20110(1.074.13)2703.201(2.048.29)3.201275(4.0ED C B A Q Q Q Q Q由)(76p p C Q F F -=。

《传热学》2版辅导资料思考题参考答案

2．参见附图，圆筒壁内侧t1<t2，请判断壁内温度分布应该是两图中哪一个？并说明理由，设导热系数等于常数。
回答：导热系数等于常数的一维导热方程是（3-1-15），于是温度梯度可以写作(dt/dr) =c/r。可见，温度梯度与径向坐标成反比，即半径小的圆筒壁内侧的温度梯度一定大于外侧的温度梯度。所以附图(b)是正确的。
回答：非稳态导热问题遵循两个基本规律，一个是能量守恒定律，一个是傅里叶定律。在对物体内的任意微元体积做热平衡分析时，切记傅里叶定律中的热流密度和温度梯度均代表瞬时值，傅里叶定律的规律仍成立。
3．应用傅里叶定律时有哪些限制？
回答：限制条件是：（1）纯导热物体（非纯导热物体以当量或表观导热系数描述之）；（2）各向同性（各向异性物体须在导热主轴坐标系中运用傅里叶定律）；（3）非超短时间、超大热流密度或超低温度的导热问题。
3．凸状轴呈对称图形，如果侧面绝热且导热系数为常数，其一维稳态温度分布呈什么？
回答：在一维、稳态、无内热源且常物性条件下，热流量为常数，即A(x)dt/dx=常数。这表明导热的截面积A与温度梯度成反比。只有在等截面情况下，温度梯度才是常量。
回答：导热系数随温度变化时，函数关系一般是写作=0（1＋b t）的形式。但是一般来说0却并不代表0℃时该材料的导热系数。参见附图，这是因为0实际上是该式适用温度区间内近似线性关系的延长线与纵轴的交点。它一般不会正好与=f（t）曲线在0℃时的数值相等。
写为=0＋bt时，0未变，而b相当于原式中的0b。
8．已知某个确定的热流场q=f(x, y)，能否由此唯一地确定物体的温度场？或者还需要补充什么条件？反过来，从温度场能否唯一地确定热流场？
回答：导热问题中若全部边界条件都是第二类（包括绝热），将无法唯一地得到温度场的确定解。而对给定的温度场，却可以根据傅里叶定律唯一地确定热流场。因为一个物体若均匀地提升相同温度，其热流场将不会发生任何改变。即一个热流场可以对应无穷多个温度场。所以，导热问题必须至少具有一个温度参考点，才能唯一地确定其解。

数值传热学绪论热流问题的数值计算课件01

注意
1.4数值传热学及常用的数值方法
1.4.1数值传热学求解问题的基本思想:
把原来在空间与时间坐标中连续的物理量的场，用一系列有限个离散点（称为节点）上的值的集合来代替，通过一定的原则建立起这些离散点上变量值之间关系的代数方程（称为离散方程），求解的建立起来的代数方程以获得所求解变量的近似值。如图1-7所表示（见下页）。
1.3控制方程的数学分类及基对数值解的影响
1.3.1偏微分方程的3种类型
双曲型(hyperbolic)；抛物型（parabolic）；椭圆型（elliptic）.
1.3.2椭圆型方程
描写物理学中一类稳态问题，这种物理问题的变量与时间无关而需要在空间的一个闭区域内来求解。如图1-4所示。各节点上的代数方程必须联立求解，而不能先解得区域中某一部分上的值后再去确定其余地区上的值。
u-动量方程:
v-动量方程:
w-动量方程:
流体的第2 分子黏度
流体的动力粘度
矢量形式为：
其中
为3个动量方程的广义
源项，其表达式为：
对粘性为常数的不可压缩流体
于是式（1-6）简化成为：
1.1.3能量守恒方程
对图1-1所示的微元体应用能量守恒定律：
[微元体内热力学能的增加率]=[进入微元体的净热流量]+[体积力与表面力对微元体做的功]
再引入导热Fourier定律，可得出用流体比焓h及温度T表示的能量方程：
导热系数
耗散函数
流体的内热源
为由于粘性作用机械能转换为热能的部分，其计算式如下：
对不可压流体有：
1.1.4控制方程的通用形式
1.1.5几点说明:
1. 式（1-4）是三维非稳态Navier-Stokes方程，无论对层流或湍流都是适用的。

数值传热学答案

例题3-3：算例的matlab程序clear%************一维非稳态热传导方程的数值解法与解析解对比程序**************** %****************************前处理（定义网格与节点）********************x=linspace(0,1,11);t=linspace(0,0.2,101);%****************************前处理（定义边界）************************** % 初值条件for i=1:11if i*0.1<=0.5T(i+1,1)=2*i*0.1;elseT(i+1,1)=2*(1-i*0.1);endend% 边界条件T(1,:)=0;T(11,:)=0;%****************************求解器（差分算法）*************************F=input('please input 网格fourier数：F=')%采用时间一阶向前差分，空间的的二阶中心差分的显式离散格式for j=2:101for i=2:10T(i,j)=F*(T(i+1,j-1)+T(i-1,j-1))+(1-2*F)*T(i,j-1);endend%****************************后处理（结果输出）*************************%输出x和T的关系的二维图形axis([0 1 0 0.6]);plot(x,T([1:11],41),':*r',x,T([1:11],21),':*b',x,T([1:11],11),':*k')hold on%**************************与解析解进行比较**************************%方程的解析解：T(x,t)=(8/pi^2)*exp(-((pi^2)*t))*sin(pi*x)%*******************************************************************axis([0 1 0 0.6]);y1=(8/pi^2)*exp(-(pi^2)*0.192)*sin(pi*x);% t=0.192y2=(8/pi^2)*exp((-pi^2)*0.096)*sin(pi*x);% t=0.096y3=(8/pi^2)*exp((-pi^2)*0.048)*sin(pi*x);% t=0.048xlabel('x');ylabel('T');title('一维非稳态热传导方程的数值解法与解析解');plot(x,y1,'r',x,y2,'b',x,y3,'k')3-9.试证明扩散项的中心差分格式具有守恒性。

数值传热学习题解答(汇总版)

习题1－7解：由于对称性，取半个通道作为求解区域。

常物性不可压缩流体，二维层流、稳态对流换热的控制方程组为：质量守恒方程0=∂∂+∂∂yv x u 动量守恒方程 ()()⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂−=∂∂+∂∂22221y u x u x py vu x uu νρ ()()⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂−=∂∂+∂∂22221y v x v y p y vv x uv νρ 能量守恒方程 ()()⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=∂∂+∂∂2222y T xT a y vT x uT 边界条件：进口截面 ()0,,===v c T y u u in ；平板通道上（下）壁面 0,0=∂∂==yTv u ；中心线上对称条件： 0,0u T v y y∂∂===∂∂；出口截面0,0,0=∂∂=∂∂=∂∂xT x v x u ；或者写：采用数值传热学的处理方法。

图1-10 习题1-7的图示本题如果采用整个通道作为计算区域，应该扣除0.5 分2-3.解：由u x u ∂∂=()xuu ∂∂21=η22y u ∂∂得：其守恒形式为：()xuu ∂∂=2η22y u ∂∂ 对方程两端在t ∆时间间隔内对其控制容积积分得：()dxdydt x uu t t t nsew ⎰⎰⎰∆+∂∂=⎰⎰⎰∆+∂∂t t t e w n s dydxdt y u 222η()()[]dxdt y u y u dydt uu uu s n t t t ewtt t w e n s ][2⎪⎪⎭⎫ ⎝⎛∂∂−⎪⎪⎭⎫ ⎝⎛∂∂=−⎰⎰⎰⎰∆+∆+η 将()()2)(PE e uu uu uu +=, ()()()2P W w uu uu uu +=,()n PN n y u u y u δ−=⎪⎪⎭⎫ ⎝⎛∂∂，()sSP s y u u y u δ−=⎪⎪⎭⎫ ⎝⎛∂∂。

y y y s n ∆==)()(δδ 带入，得：xdt y u u u ydt uu uu t t t S P N tt tW E ∆∆+−=∆⎥⎦⎤⎢⎣⎡−⎰⎰∆+∆+]2[22)()(η t x yu u u t y uu uu tSt P t N t W t E ∆∆∆+−=∆∆−222)()(η整理得离散方程为：()()0242=∆−+−∆−yu u u xuu uu t P t S t N tWt E η2—3：解：由2221()u 2u u ux x y η∂∂∂===∂∂∂得：原方程的守恒形式为： 222()2u ux yη∂∂=∂∂ 对方程两端在t ∆时间间隔内对其控制容积积分，把可积的部分积出后得：22()t tsne wtu u dtdy +∆−⎰⎰= 2t te wtn s u u dtdx y y η+∆⎡⎤⎛⎫⎛⎫∂∂−⎢⎥ ⎪ ⎪∂∂⎝⎭⎝⎭⎣⎦⎰⎰选定2u 随y 而变化的型线，这里取为阶梯式，即在控制容积内沿y 方向不变，则2222()=y ()t tt ts ne we w ttu u dtdy u u dt +∆+∆−∆−⎰⎰⎰选定2u 随t 而变化的规律，这里采用阶梯式显式，则22()t tewty u u dt +∆∆−⎰= ()()22t t e w u u t y ⎡⎤−∆∆⎢⎥⎣⎦选定uy∂∂随x 而变化的型线，这里取为阶梯式，即在控制容积内沿x 方向不变，则22t tt t e wtt n s n s u u u u dtdx x dt y y y y ηη+∆+∆⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫∂∂∂∂−=∆−⎢⎥⎢⎥ ⎪ ⎪ ⎪ ⎪∂∂∂∂⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦⎰⎰⎰ 选定uy∂∂随t 而变化的规律，这里采用阶梯显式，则 2t ttn s u u x dt y y η+∆⎡⎤⎛⎫⎛⎫∂∂∆−⎢⎥ ⎪ ⎪∂∂⎝⎭⎝⎭⎣⎦⎰= 2t t n s u u t x y y η⎡⎤⎛⎫⎛⎫∂∂−∆∆⎢⎥ ⎪ ⎪∂∂⎢⎥⎝⎭⎝⎭⎣⎦进一步选取u 随x,y 分段线性变化，则2222E Pe u u u += ， 222w 2W P u u u +=()nt PtN ty uu y u δ−=⎪⎪⎭⎫ ⎝⎛∂∂n ， ()stSt p ts y u u y u δ−=⎪⎪⎭⎫ ⎝⎛∂∂。

数值传热学习题答案

数值传热学习题答案【篇一：习题解答】s=txt>1.1 什么是汇编语言？汇编语言的特点是什么？答：为了克服机器语言难以记忆、表达和阅读的缺点，人们采用具有一定含义的符号作为助忆符，用指令助忆符、符号地址等组成的符号指令称为汇编格式指令(或汇编指令)。

汇编语言是汇编指令集、伪指令集和使用它们规则的统称。

① 55h，70h，70h，65h，72h② 53h，6ch，6fh，77h③ 43h，6fh，6dh，70h，75h，74h，65h，72h ④ 57h，68h，61h，74h 1.7 求下列带符号十进制数的8位基2码补码。

① +127② ?2③ ?128④ +2 答：汇编语言的特点是：（1）执行速度快。

（2）程序短小。

（3）可以直接控制硬件。

（4）可以方便地编译。

（5）辅助计算机工作者掌握计算机体系结构。

（6）程序编制耗时，可读性差。

（7）程序可移植性差。

1.2 把下列十进制数转换成二进制数、八进制数、十六进制数。

①127② 1021 ③ 0.875④ 6.25 答：① 1111111b；177q；7fh ② 1111111101；1775q；3fdh ③0.111 b；0.7q；0.eh ④ 110.01b；6.2q；6.4h1.3 把下列二进制数转换成十进制数。

① 1001.11 ② 101011.10011 ③ 111.011④1011.1答：① 9.75d ② 43.59375d③ 7.375d④ 11.5d1.4 把下列八进制数转换成十进制数。

① 573.06 ② 75.23 ③ 431.7④ 123.45 答：① 379.09375d ② 61.296875d③ 281.875④ 83.5781251.5 把下列十六进制数转换成十进制数。

① 0d5.f4 ② 8ba.7c ③ 0b2e.3a④ 6ec.2d 答：① 213.953125d ② 2234.484375③ 2862.2265625 ④1772.175781251.6 把下列英文单词转换成ascii编码的字符串。

数值传热学陶文铨主编第二版习题答案

数值传热学习题答案(汇总版)

数值传热学(陶文铨)第二章习题答案

数值传热学第5章作业答案

数值传热学 第六章答案 (2)

数值传热学陶文铨主编第二版习题答案

西安交通大学数值传热学大作业

数值传热学陶文铨第四章作业

陶文铨老师_数值传热学_热流问题的数值计算02

陶文铨老师_数值传热学_热流问题的数值计算03

热学第二版习题答案

数值方法(第2版)答案

(完整版)数值传热学陶文铨主编第二版习题答案

数值传热学第二章部分习题参考答案

数值传热学部分习题问题详解2

《传热学》2版 辅导资料 思考题参考答案

数值传热学绪论热流问题的数值计算课件01

数值传热学答案

数值传热学习题解答(汇总版)

数值传热学习题答案

数值传热学第六章答案 (2)

《传热学》2版辅导资料思考题参考答案