小学解方程方法及答案
第十讲 一元一次方程的解法
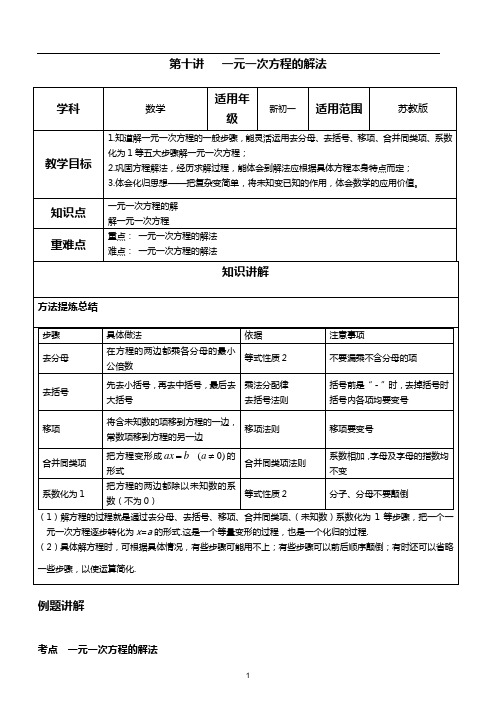
第十讲 一元一次方程的解法知识讲解方法提炼总结步骤 具体做法依据 注意事项去分母在方程的两边都乘各分母的最小公倍数等式性质2不要漏乘不含分母的项 去括号先去小括号,再去中括号,最后去大括号乘法分配律 去括号法则 括号前是“-”时,去掉括号时括号内各项均要变号 移项将含未知数的项移到方程的一边,常数项移到方程的另一边 移项法则移项要变号合并同类项 把方程变形成b ax = )0(≠a 的形式合并同类项法则 系数相加,字母及字母的指数均不变系数化为1把方程的两边都除以未知数的系数(不为0)等式性质2分子、分母不要颠倒(1)解方程的过程就是通过去分母、去括号、移项、合并同类项、(未知数)系数化为1等步骤,把一个一元一次方程逐步转化为x =a 的形式.这是一个等量变形的过程,也是一个化归的过程.(2)具体解方程时,可根据具体情况,有些步骤可能用不上;有些步骤可以前后顺序颠倒;有时还可以省略一些步骤,以使运算简化.例题讲解考点 一元一次方程的解法学科数学适用年级新初一适用范围苏教版教学目标1.知道解一元一次方程的一般步骤,能灵活运用去分母、去括号、移项、合并同类项、系数化为1等五大步骤解一元一次方程;2.巩固方程解法,经历求解过程,能体会到解法应根据具体方程本身特点而定;3.体会化归思想——把复杂变简单,将未知变已知的作用,体会数学的应用价值。
知识点 一元一次方程的解 解一元一次方程重难点重点: 一元一次方程的解法 难点: 一元一次方程的解法例 1:(1)解方程4x -15=9(2)解方程2x =5x -21【课堂练习】5. 解方程 (1)32x=9-x (2) 313131+=-x x例 2:解方程 -3(x +1)=9【解析】方法一:1、先将方程左边去括号。
2、观察去括号后的方程,与上次课学习过的方程一样吗?方法二:方程两边同除以-3,得到与上次课同类的方程。
【答案】略。
例 3:解方程2(2x +1)=1-5(x -2)【答案】略【课堂练习】1、解下列方程:(1)()()13315+=+x x (2)()()914322+-=-x x (3)()16328=-+x (4)()x x -=-10620 2、某班在绿化校园的活动中共植树130棵,有5位学生每人种了2棵,其余学生每人种了3棵。
五年级 解方程 -含答案

解方程买糖的故事有个小男孩,有一天妈妈带着他到杂货店去买东西,老板看到这个可爱的小孩,就打开一罐糖果,要小男孩自己拿一把糖果。
但是这个男孩却没有任何动作。
几次的邀请之后,老板亲自抓了一大把糖果放进他的口袋中。
回到家中,母亲好奇地问小男孩,为什么没有自己去抓糖果而要老板抓呢?小男孩回答很妙:“因为我的手比较小呀!而老板的手比较大,所以他拿的一定比我拿的多很多!”启示:这是一个聪明的孩子,他知道自己的有限,而更重要的,他也知道别人比自己强。
凡事不只靠自己的力量,学会适时地依靠他人,是一种谦卑,更是一种聪明。
例1 解方程:6x-3=15 例2 解方程:2x+9x=11例3 解方程:3x-83=65例4 解方程:16.8÷x=30%1例5 解方程:6.7x -60.3=7610 例6 解方程:(200-x)÷5=30例7 25% + 10x =54 例8 x- 15%x = 68例9 70%x + 20%x= 3.6 例10 x ÷356=4526÷2513A 档(巩固专练)1 . x+32=76 2.15x =303.3x+9=27 4.9x-40=55.x-0.8x=6 6.3x+23=18754x-x=16 8.20%x-8=89.x +72x =43 10. 0.8x -4=1.611.5x ÷0.2%=10 12.x -0.25x =3B 档(提升精练)1.23x-14x=18 2.99 x =100- x3.26×1.5= 2x+10 4.4×8+2x=365.53x-90=16 6.90y-90=90-90y7.32-22x =10 8.88-4x=80-2x9.25% + 10x =54 10. x- 15%x = 6811.70%x + 20%x= 3.6 12.x ÷356=4526÷2513C 档(跨越导练)1.x ÷5+9=21 2.0.273÷x=0.353.3(x+3)=50-x+3 4.150×2+3x=6905.45x-50=40-45x 6.0.5×16-16×0.2=4x7.2(x+x+0.5)=9.8 8.(0.5+x)+x=9.8÷29.23(x- 4.5) = 7 10.x×(16+38)=131211.12x- 25%x = 10 12.0.36×5-34x =35解方程答案例1 【答案】x=3【解析】6x-3=156x-3+3=15+36x=186x÷6=18÷6x=3例2 【答案】x=1 【解析】2x+9x=11(2+9)x=1111x=11例3 【答案】x=58 45例4 【答案】x=56【解析】16.8÷x=30%0.3x=16.80.3x÷0.3=16.8÷0.3x=56例5 【答案】x=10【解析】 6.7x-60.3=7 6 106.7x-60.3+60.3=6.7+60.36.7x=676.7x÷6.7=67÷6.7x=10例6 【答案】x=50(200-x)÷5×5=30×5200-x=150x+150=200x+150-150=200-150x=50例7 【答案】x=11 200例8 【答案】x=17 20例9 【答案】x=4例10 【答案】x=421A档(巩固专练)1 【答案】x=44【解析】x+32=76x+32-32=76-32x=442 【答案】x=2【解析】15x=3015x÷15=30÷15x=23 【答案】x=6【解析】3x+9=273x+9-9=27-93x÷3=18÷3x=64 【答案】x=5【解析】9x-40=59x-40+40=5+409x=459x÷9=45÷9x=55 【答案】x=30【解析】x-0.8x=6(1-0.8)x=60.2x=60.2x÷0.2=6÷0.2x=306 【答案】x=52 97 【答案】x=648 【答案】x=809 【答案】x=7 1210 【答案】x=711 【答案】x=1 25012 【答案】x=4B档(提升精练)1 【答案】x=2【解析】23x-14x=18(23-14)x=189x=189x÷9=18÷9x=22 【答案】x=1【解析】99 x =100- x99x+x=100(99+1)x=100100x=100x=13 【答案】x=14.5【解析】26×1.5=2x+102x+10=392x+10-10=39-102x=292x÷2=29÷2x=14.54 【答案】x=2【解析】4×8+2x=362x+32=362x+32-32=36-322x=4x=25 【答案】x=2【解析】53x-90=1653x-90+90=16+9053x=10653x÷53=106÷53x=26 【答案】y=1【解析】90y-90=90-90y90y+90y=90+90180y=180180y÷180=180÷180y=17 【答案】x=1【解析】32-22 x =1022x=32-1022x÷22=22÷22x=18 【答案】x=4【解析】88-4x=80-2x88-4x+4x=80-2x+4x88=2x+8088-80=2x+80-802x÷2=8÷2x=49 【答案】x=11 20010 【答案】x=17 2011 【答案】x=412 【答案】x=421C档(跨越导练)1 【答案】x=60【解析】x÷5+9=21x÷5+9-9=21-9x÷5=12x÷5×5=12×5x=602 【答案】x=0.78【解析】0.273÷x=0.350.35x=0.2730.35x÷0.35=0.273÷0.35x=0.783 【答案】x=11【解析】3(x+3)=50-x+33x+9=53-x3x+x+9-9=53-9-x+x4x=44x=114 【答案】x=130【解析】150×2+3x=690300+3x-300=690-3003x=3903x÷3=390÷3x=1305 【答案】x=1【解析】45x-50=40-45x45x-50+45x+50=40-45x+45x+5090x=9090x÷90=90÷90x=16 【答案】x=1.2【解析】0.5×16-16×0.2=4x8-3.2=4x4x=4.84x÷4=4.8÷4x=1.27 【答案】x=2.2【解析】2(x+x+0.5)=9.82x+0.5=4.92x+0.5-0.5=4.9-0.52x=4.42x÷2=4.4÷2x=2.28 【答案】x=2.2【解析】(0.5+x)+x=9.8÷20.5+2x=4.90.5+2x-0.5=4.9-0.52x=4.42x÷2=4.4÷2x=2.29 【答案】x=1510 【答案】x=211 【答案】x=4012 【答案】x=8 5。
人教版五年级数学上册期末总复习解方程的计算技巧附答案

人教版五年级数学上册2.解方程的计算技巧一、仔细审题,填一填。
(第2小题3分,其余每小题4分,共15分) 1.当x=0.8时,2x=(),x2=()。
2.在里填上“>”“<”或“=”。
当x=4.5时,3×(x-4)0.4;当x=7时,(8+x)÷53;当x=5.2时,8x-3x10.5。
3.在里填上合适的数,使每个方程的解是x=6。
+x=24.5x-=5.9×x=30.6x÷=40 4.若x=2是方程3x+4a=22的解,则a=()。
二、下面解方程的过程对吗?对的画“√”,错的画“×”并改正。
(每小题4分,共12分)1.3x-15=45改正:解:3x÷3-15=45÷3x-15=15x-15+15=15+15x=30()2.6(x-2.4)=12改正:解:6x-2.4=126x-2.4+2.4=12+2.46x=14.4x= 2.4()3. 2.5x+3.3=24.6改正:解:2.5x+3.3÷3=24.6÷32.5x+1.1=8.22.5x+1.1-1.1=8.2-1.12.5x=7.1x= 2.84()三、不计算,把每组方程中代表数值最大的字母圈出来。
(每小题3分,共12分)四、解方程。
(每小题3分,共18分)9.4x-0.4x=8.1×221x-5×14=148x-20=6x-4 4-3x=5-5x3(18-x)=30 3(2x-3)=18五、聪明的你,答一答。
(共43分)1.如果x+3=9.6与mx=23.1有相同的解,求m的值。
(7分)2.已知x+x+x+x+x+y+y=36,x+x+y=15,求x和y的值。
(7分)3.已知式子(42-2a)÷5。
(1)当a是多少时,式子的结果是0?(7分)(2)当a是多少时,式子的结果是2?(7分)(3)当a是多少时,式子的结果是a?(7分)4.如果a+b=56.8,a-b=19.6,求a和b的值。
六年级数学解方程答题技巧+解方程应用题练习(有答案)

同学们学习了用字母表示数和解简易方程,还开始试着运用简易方程来解决一些实际问题。
列方程解应用题是一个难点,这一部分内容融入了等式的性质,以及四则运算各部分的关系,有助于同学们对所学的算术知识进行巩固和加深理解。
如何应用方程来解应用题呢?同学们不妨看看下面的一些技巧。
一、首先是审题,确定未知数。
审题,理解题意。
就是全面分析已知数与已知数、已知数与未知数的关系。
特别要把牵涉到的一些概念术语弄清,如同向、相向、增加到、增加了等,并确立未知数。
即用x表示所求的数量或有关的未知量。
在小学阶段同学们遇到的应用题并不十分复杂,一般只需要直接把要求的数量设为未知数,如:“学校图书馆里科技书的本数比文艺书的2倍多47本,科技书有495本,文艺书有多少本?”在这道题目中只有“文艺书的数量”不知道,所以只要设“文艺书的数量”为未知数x就可以了。
二、寻找等量关系,列出方程是关键。
“含有未知数的等式称为方程”,因而 “等式”是列方程必不可少的条件。
所以寻找等量关系是解题的关键。
如上题中“科技书得本数比文艺书的2倍多47本”这是理解本题题目意思的关键。
仔细审题发现“文艺书本数的2倍加上47本就是科技书的本数”故本题的等量关系为:文艺书本数的2倍+47=科技书的本数。
上题中的方程可以列为:“2x+47=495”三、解方程,求出未知数得值。
解方程时应当注意把等号对齐。
如:2x+47=4952x+47-47=495-47 ←应将“2x”看做一个整体。
2x=4482x÷2=448÷2x=224四、检验也是列方程解应用题中必不可少的。
检验并写出答案.检验时,一是要将所求得的未知数的值代入原方程,检验方程的解是否正确;二是检查所求得的未知数的值是否符合题意,不符合题意的要舍去,保留符合题意的解.1)将求得的方程的解代入原方程中检验。
如果左右两边相等,说明方程解正确了。
如上题的检验过程为:检验:把x=224代入原方程。
小学解方程方法及答案

小学解方程方法及答案 Ting Bao was revised on January 6, 20021小学四年级解方程的方法详解方程:含有未知数的等式叫做方程。
如4x-3=21,6x-2(2x-3)=20方程的解:使方程成立的未知数的值叫做方程的解。
如上式解得x=6解方程:求方程的解的过程叫做解方程。
解方程的依据:方程就是一架天平,“=”两边是平衡的,一样重!1. 等式性质:(1)等式两边同时加上或减去同一个数,等式仍然成立;(2)等式两边同时乘以或除以同一个非零的数,等式仍然成立。
2. 加减乘除法的变形:(1) 加法:a + b = 和则 a = 和-b b = 和-a例:4+5=9 则有:4=9-5 5=9-4(2) 减法:被减数a –减数b = 差则:被减数a = 差+减数b 被减数a-差 = 减数b 例:12-4=8 则有:12=8+4 12-8=4(3) 乘法:乘数a ×乘数b = 积则:乘数a = 积÷乘数b 乘数b= 积÷乘数a 例:3×7=21 则有:3=21÷7 7=21÷3(4) 除法:被除数a ÷除数b = 商则:被除数a= 商×除数b 除数b=被除数a ÷商例:63÷7=9 则有:63=9×7 7=63÷9解方程的步骤:1、去括号:(1)运用乘法分配律;(2)括号前边是“-”,去掉括号要变号;括号前边是“+”,去掉括号不变号。
2、移项:法1——运用等式性质,两边同加或同减,同乘或同除;法2——符号过墙魔法,越过“=”时,加减号互变,乘除号互变。
注意两点:(1)总是移小的;(2)带未知数的放一边,常数值放另一边。
3、合并同类项:未知数的系数合并;常数加减计算。
4、系数化为1:利用同乘或同除,使未知数的系数化为1。
5、写出解:未知数放在“=”左边,数值(即解)放右边;如x=66、验算:将原方程中的未知数换成数,检查等号两边是否相等!注意:(1)做题开始要写“解:”(2)上下“=”要始终对齐【例1】x-5=13 x-5=13法1 解: x-5+5=13+5 法2 解: x=13+5x=18 x=18【例2】3(x+5)-6=18 3(x+5)-6=18法1 解: 3x+3×5-6=18 法2 解: 3x+3×5-6=183x+15-6=18 3x+15-6=183x+9=18 3x+9=183x+9-9=18-9 3x=18-93x=9 3x=93x÷3=9÷3 x=9÷3x=3 x=3【例3】3(x+5)-6=5(2x-7)+2解: 1.去括号: 3x+3×5-6=5×2x-5×7+23x+15-6=10x-35+23x+9=10x-332.移项: 33+9=10x-3x (注意:移小的,如-33, 3x)3.合并同类项: 42=7x4.系数化为1: 42÷7=7x÷76=x5.写出解: x=66.验算:3×(6+5)-6=5(2x6-7)+23×11-6=5×5+227=27√解方程练习(写出详细过程):4+x=7 x+6=9 4+x=7+54+x-2=7 x-6=9 17-x=9x-6=9+3 9+3=17-x 16+2x =24+x4x=16 15=3x 4x+2=1824-x =15+2x 2+5x=18+3x 6x-2=3x+103(x+6) =2+5x 2(2x-1)=3x+10 30-4(x-5)=2x-162(x+4) -3=2+5x 100-3(2x-1)=3-4x 30+4(x-5)=2x-2620x-50=50 28+6 x =88 32-22 x =1024-3 x =3 10 x ×(5+1)=60 99 x =100- x 36÷ x=18 x÷6=12 56-2 x =2036÷ x-2=16 x÷6+3=9 56-3x =20-x 4y+2=6 x+32=76 3x+6=1816+8x=40 2x-8=8 4x-3×9=298x-3x=105 x-6×5=42+2x 2x+5=7 × 32(x+3)+3=13 12x-9x=9 6x+18=4856x-50x=30 5x=15(x-5) 78-5x=2832y-29y=3 5(x+5)=15 89 – 9x =80 100-20x=20+30x 55x-25x=60 76y÷ 76=123y÷ 23=23 4x-20=0 80y+20=100-20y 53x-90=16 2x+9x=11 12(y-1)=2480÷ 5x=100 7x÷ 8=14 65x+35=10019y+y=40 25-5x=15 79y+y=8042x+28x=140 3x-1=8-2x 90y-90=90-90y 80y-90=70÷ 30 78y+2y=160 88-4x=80-2x 9÷(4x)=1 20x=40 – 10x 65y-30=100 51y-y=100 85y+1=y+86 45x-50=40-45x二、列方程解应用题:(一)口算:a+2a= 3c+5c= 4m-2m= X+3x=5x-x= 6x-2x= = +=(二)用方程表示数量关系:1.火车每小时行120千米,汽车每小时a千米,火车每小时比汽车快6千米。
小升初数学《解方程》完整知识点讲解与专项练习题及答案

小升初《解方程》专题知识点整理+列方程解应用题专项训练《解方程》知识点列方程解应用题题型汇总练习1、0.3乘以14的积比这个数的3倍少0.6,求这个数是多少?2、甲数比乙数多34,甲数是乙数的3倍,甲乙各是多少?3、今年10月份,李明家用电131度,王强家用电120度,王强家少缴电费5.5元。
平均每度电多少元?4、长方形养鸡场的栅栏长400米,长是宽的3倍,求养鸡场的面积是多少?5、鸡兔同笼,头共有20个,腿共有56条,鸡兔各有多少只?6、鸡兔数量相同,鸡腿比兔腿少30条,鸡兔各有多少只?7、爷爷比小明大52岁,今天爷爷的年龄是小明的5倍,爷爷和小明今年各是多少岁?8、甲乙两地相距360km,张三由甲地开往乙地,李四以45km/时的速度由乙地开往甲地,3个小时后,两人相距15km,张三的速度是多少千米?9、沈阳与北京相距约700km,土豆与地瓜分别从沈阳和北京出发,相向而行,土豆每小时行驶80km,地瓜每小时行驶70km。
土豆出发5个小时后,地瓜才出发,在经过多少小时才能相遇?10、长方形养鸡场的一个长面靠墙,栅栏长400米,长是宽的2倍,养鸡场的面积是多少?11、甲乙两人骑自行车,同时从相距65km的两地相向而行,甲车每小时行驶17.5km,1小时候,两人相距32.5km,乙车每小时行驶多少千米?12、一个三层书架共有书159本,第一层比第二层的4倍少2本,第三层比第二层的3倍多1本。
第三层书架有多少本书?13、土豆和地瓜同时分别从两地相向而行,8小时相遇。
如果他们每小时多行2.5km,那么就6小时相遇。
问两地相距多少千米?14、甲有书的本数是乙有书的本数的3倍,甲、乙两人平均每人有82本书,求甲、乙两人各有书多少本?15、汽车从甲地到乙地,去时每小时行60千米,比计划时间早到1小时;返回时,每小时行40千米,比计划时间迟到1小时。
求甲乙两地的距离?16、一把直尺和一把小刀共1.9元,4把直尺和6把小刀共9元,每把直尺和每把小刀各多少元?17、三个连续的一位小数的和是1.5,这三个小数分别是多少?18、甲乙两个书架,若从甲书架取出8本放入乙书架,两个书架的本数就一样多;如果从乙书架取出13本放入甲书架,甲书架的书就是乙书架的2倍。
小学数学列不定方程解应用题(含答案)

列不定方程解应用题知识框架一、知识点说明 历史概述不定方程是数论中最古老的分支之一.古希腊的丢番图早在公元3世纪就开始研究不定方程,因此常称不定方程为丢番图方程.中国是研究不定方程最早的国家,公元初的五家共井问题就是一个不定方程组问题,公元5世纪的《张丘建算经》中的百鸡问题标志着中国对不定方程理论有了系统研究.宋代数学家秦九韶的大衍求一术将不定方程与同余理论联系起来.考点说明在各类竞赛考试中,不定方程经常以应用题的形式出现,除此以外,不定方程还经常作为解题的重要方法贯穿在行程问题、数论问题等压轴大题之中.在以后初高中数学的进一步学习中,不定方程也同样有着重要的地位,所以本讲的着重目的是让学生学会利用不定方程这个工具,并能够在以后的学习中使用这个工具解题。
重难点(1) 根据题目叙述找到等量关系列出方程 (2) 根据解不定方程方法解方程 (3) 找到符合条件的解例题精讲一、不定方程与数论【例 1】 把2001拆成两个正整数的和,一个是11的倍数(要尽量小),一个是13的倍数(要尽量大),求这两个数.【考点】列不定方程解应用题【解析】 这是一道整数分拆的常规题.可设拆成的两个数分别为11x 和13y ,则有:11132001x y +=,要让x 取最小值,y 取最大值. 可把式子变形为:2001111315312132122153131313x x x x y x -⨯+-++===-+,可见12213x+是整数,满足这一条件的x 最小为7,且当7x =时,148y =. 则拆成的两个数分别是71177⨯=和148131924⨯=.【答案】则拆成的两个数分别是77和1924.【巩固】 甲、乙二人搬砖,甲搬的砖数是18的倍数,乙搬的砖数是23的倍数,两人共搬了300块砖.问:甲、乙二人谁搬的砖多?多几块?【考点】列不定方程解应用题【解析】 设甲搬的是18x 块,乙搬的是23y 块.那么1823300x y +=.观察发现18x 和300都是6的倍数,所以y 也是6的倍数.由于3002313y <÷≈,所以y 只能为6或12. 6y =时18162x =,得到9x =;12y =时1824x =,此时x 不是整数,矛盾.所以甲搬了162块,乙搬了138块,甲比乙搬得多,多24块.【答案】甲比乙搬得多,多24块【例 2】 用十进制表示的某些自然数,恰等于它的各位数字之和的16倍,则满足条件的所有自然数之和为___________________.【考点】列不定方程解应用题【解析】 若是四位数abcd ,则()161636<1000a b c d ⨯+++⨯≤,矛盾,四位以上的自然数也不可能。
小学解方程方法及答案

小学解方程方法及答案Newly compiled on November 23, 2020小学四年级解方程的方法详解方程:含有未知数的等式叫做方程。
如4x-3=21,6x-2(2x-3)=20方程的解:使方程成立的未知数的值叫做方程的解。
如上式解得x=6解方程:求方程的解的过程叫做解方程。
解方程的依据:方程就是一架天平,“=”两边是平衡的,一样重!1. 等式性质:(1)等式两边同时加上或减去同一个数,等式仍然成立;(2)等式两边同时乘以或除以同一个非零的数,等式仍然成立。
2. 加减乘除法的变形:(1) 加法:a + b = 和则 a = 和-b b = 和-a例:4+5=9 则有:4=9-5 5=9-4(2) 减法:被减数a –减数b = 差则:被减数a = 差+减数b 被减数a-差 = 减数b例:12-4=8则有:12=8+4 12-8=4(3) 乘法:乘数a ×乘数b = 积则:乘数a = 积 ÷乘数b 乘数b= 积 ÷乘数a例:3×7=21则有:3=21÷7 7=21÷3(4) 除法:被除数a ÷除数b = 商则:被除数a= 商 ×除数b 除数b=被除数a ÷商例:63÷7=9 则有:63=9×7 7=63÷9解方程的步骤:1、去括号:(1)运用乘法分配律;(2)括号前边是“-”,去掉括号要变号;括号前边是“+”,去掉括号不变号。
2、移项:法1——运用等式性质,两边同加或同减,同乘或同除;法2——符号过墙魔法,越过“=”时,加减号互变,乘除号互变。
注意两点:(1)总是移小的;(2)带未知数的放一边,常数值放另一边。
3、合并同类项:未知数的系数合并;常数加减计算。
4、系数化为1:利用同乘或同除,使未知数的系数化为1。
5、写出解:未知数放在“=”左边,数值(即解)放右边;如x=66、验算:将原方程中的未知数换成数,检查等号两边是否相等!注意:(1)做题开始要写“解:”(2)上下“=”要始终对齐【例1】x-5=13 x-5=13法1 解: x-5+5=13+5 法2 解: x=13+5x=18 x=18【例2】3(x+5)-6=18 3(x+5)-6=18法1 解: 3x+3×5-6=18 法2 解: 3x+3×5-6=183x+15-6=18 3x+15-6=183x+9=18 3x+9=183x+9-9=18-9 3x=18-93x=9 3x=93x÷3=9÷3 x=9÷3x=3 x=3【例3】3(x+5)-6=5(2x-7)+2解: 1.去括号: 3x+3×5-6=5×2x-5×7+23x+15-6=10x-35+23x+9=10x-332.移项: 33+9=10x-3x (注意:移小的,如-33, 3x)3.合并同类项: 42=7x4.系数化为1: 42÷7=7x÷76=x5.写出解: x=66.验算:3×(6+5)-6=5(2x6-7)+23×11-6=5×5+227=27√解方程练习(写出详细过程):4+x=7 x+6=9 4+x=7+54+x-2=7 x-6=9 17-x=9x-6=9+3 9+3=17-x 16+2x =24+x4x=16 15=3x 4x+2=1824-x =15+2x 2+5x=18+3x 6x-2=3x+103(x+6) =2+5x 2(2x-1)=3x+10 30-4(x-5)=2x-162(x+4) -3=2+5x 100-3(2x-1)=3-4x 30+4(x-5)=2x-26 20x-50=50 28+6 x =88 32-22 x =1024-3 x =3 10 x ×(5+1)=60 99 x =100- x36÷ x=18 x÷6=12 56-2 x =2036÷ x-2=16 x÷6+3=9 56-3x =20-x4y+2=6 x+32=76 3x+6=1816+8x=40 2x-8=8 4x-3×9=298x-3x=105 x-6×5=42+2x 2x+5=7 × 32(x+3)+3=13 12x-9x=9 6x+18=4856x-50x=30 5x=15(x-5) 78-5x=2832y-29y=3 5(x+5)=15 89 – 9x =80 100-20x=20+30x 55x-25x=60 76y÷ 76=1 23y÷ 23=23 4x-20=0 80y+20=100-20y 53x-90=16 2x+9x=11 12(y-1)=2480÷ 5x=100 7x÷ 8=14 65x+35=10019y+y=40 25-5x=15 79y+y=8042x+28x=140 3x-1=8-2x 90y-90=90-90y 80y-90=70÷ 30 78y+2y=160 88-4x=80-2x 9÷(4x)=1 20x=40 – 10x 65y-30=100 51y-y=100 85y+1=y+86 45x-50=40-45x 二、列方程解应用题:(一)口算:a+2a= 3c+5c= 4m-2m= X+3x=5x-x= 6x-2x= = +=(二)用方程表示数量关系:1.火车每小时行120千米,汽车每小时a千米,火车每小时比汽车快6千米。
六年级解方程解题方法及练习题(有答案)

小学数学六年级解方程的方法及巩固练习题一、如何教好解方程首先得让学生理解和掌握好“天平平衡的道理”或“等式的基本性质”。
即:等式的两边都加上或减去相同的数,左右两边仍然相等等式的两边都乘上或除以相同的数(0除外),左右两边仍然相等。
然后灵活运用这一规律,在不改变等式平衡的前提下,把未知数一边的已知数全部想办法去掉,最终留下的就是“未知数等于多少”的解。
但是出现得一些特殊的方程,运用等式的基本性质来解学生理解比较困难,我们就应该采取特殊的方法,让孩子容易接受。
二、用字母表示数的方法1、数字和字母、字母和数字相乘时,乘号可以记作“。
”,或者可以省略不写,省略乘号时,数字必须写在字母的前面。
2、当“1”与任何字母相乘时,“1”省略不写。
3、在同一个问题中,同一个字母表示同一个量,不同的量用不同的字母表示。
4、数与数之间的运算符号不能省略。
三、方程的相关知识点:知识要点等式:表示相等关系的式子叫做等式。
方程:含有未知数的等式叫做方程。
使方程左右两边相等的未知数的值叫方程的解。
求方程的解的过程叫解方程。
式与方程的关系:所有的方程都是等式,但等式不一定是方程。
四、解方程的依据1、四则运算各部分间的关系:加法:加数+加数=和,和–加数=加数减法:被减数-减数=差;差 + 减数=被减数被减数–差 = 减数乘法:因数X因数=积;积÷ 因数 = 因数除法:被除数÷除数=商;除数X 商 = 被除数被除数÷ 商 = 除数2、等式的基本性质:(1):等式两边都加上(或减去)同一个数,左右两边仍然相等。
(2):等式两边都乘以(或除以)同一个不等于0的数,左右两边仍然相等。
3、比例的基本性质:两个外项的积等于两个内项的积。
五、方程的基本类型1、x + A = B类型。
X是加数。
2、x - A = B类型。
X是被减数。
3、A – X = B 类型, X是减数。
4、A X = B 类型, X是因数。
小学五年级数学思维训练(奥数)《巧解方程》讲解及练习题(含答案)

巧解方程专题简析:学习解方程。
首先,我们要对方程进行观察,将能够先计算的部分先计算或合并,使其化简,然后再求出x的值。
例1:解方程:6x+9x-13=17分析与解答方程左边的6x与9x可以合并为15x,因此,可以将原方程转化成15x-13=17,从而顺利地求出方程的解。
解:6x+9x-13=17,15x-13=1715x=30x= 2随堂练习:解方程7.5x-4.1x+1.8=12例2 解方程:8x-16=4x分析与解答方程胡两边都有X,运用等式的性质,我们先将方程两边同时减去4x,然后再方程两边同时加上16变为8x-4x=16.8x-16=4x解:8x-4x=164x= 16x=4随堂练习:解方程10x-7=4.5x+20.5 16-2x=6x例3 解方程:4(4x-11)=3(22-2x)分析与解答第一步先运用乘法分配律去掉括号;第二步,运用等式的性质,便未知数和已知数分别在等号的两边;第三步把等号两边的未知数与数合并;第四步求出方程的解4(4x-11)=3(22-2x)解:16x-44=66-6x 去括号16x+6x=66+44 等式的性质22x=110x=5随堂练习解方程7(2x-6)=84 15(22-x)+2=68x例4 解方程:x÷3=(2x-11) ÷5分析与解答我们先根据等式的性质,在方程的两边同时乘3和5的最小公倍数,然后再运用前面的方法进行求解。
解:x÷3×15=(2x-11)÷5×155x=3(2x-11)5x=6x-33x=33随堂练习:解方程:2x÷3=(2x-5)÷2 (3x-0.5)÷2=2x÷3拓展应用1、解方程5x+0.7x-3x=10-1.92、解方程7(2x-6)=843、解方程5(x-8)=3x4、解方程5.9x-9=4.2x+2.95、解方程9(2x-3)-2=5(2x-1)6、解方程:x÷5+0.5=x÷47、在下面的□内填入相同的数,使等式成立。
80道解方程带答案 有过程

1、已知A,B是方程x^2+2x-5=0的两个实数根,求(A^2+2AB+2A)(B^2+2AB+2B)的值.由A,B是方程x^2+2x-5=0的两个实数根得:AB=-5,A+B=-2A^2+2AB+2A)(B^2+2AB+2B)=AB(A+2B+2)(B+2A+2)=-5(-2+B+2)(-2+A+2)=-5AB=252、1/2(x+y+z)方+1/2(x-y-z)(x-y+z)-z(x+y),其中x-y=6,xy=21.要详细步骤化简得:1/2(x+y+z)方+1/2(x-y-z)(x-y+z)-z(x+y)=1/2[(x+y)方+2z(x+y)+z方]+1/2[(x-y)方-z方]-z(x+y)=1/2(x+y)方+1/2(x-y)方=x方+y方由x-y=6,xy=21得,x方+y方=(x-y)方+2xy=783、a^2-ab+2b^2=3 求2ab-2a^2-4b^2-7的值2ab-2a^2-4b^2-7=2(ab-a^2-2b^2)-7=-2(a^2-ab+2b^2)-7=(-2)*3-7=-6-7=-134、若A=2x^2+3xy-2x-3,B=-x^2+xy+2,且3A+6B的值与x无关,求y的值解:3A+6B=6x^2+9xy-6x-9-6x^2+6xy+12=15xy-6x+3=x(15y-6)+35、9x+6x^2 -3(x-2/3x^2).其中x=-29x+6x²-3(x-2/3x²)=9x+6x²-3x+2x²=8x²+6x=8×(-2)²+6×(-2)=32-12=206、1/4(-4x^2+2x-8)-(1/2x-1),其中x=1/21/4(-4x²+2x-8)-(1/2x-1)=-x²+1/2x-2-1/2x+1=-x²-1=-(1/2)²-1=-1/4-1=-5/47、3x'y-[2x'y-(2xyz-x'z)-4x'z]-xyz,其中x=-2,y=-3,z=1,:3x'y-[2x'y-(2xyz-x'z)-4x'z]-xyz=3x'y-2x'y+2xyz-x'z+4x'z-xyz=x'y-xyz+3x'z=4*(-3)-2*3*1+3*4*1=-12-6+12=-68、(5a^2-3b^2)+(a^2+b^2)-(5a^2+3b^2),其中a=-1,b=1=5a^2-3b^2+a^2+b^2-5a^2-3b^2=a^2-5b^2=(-1)^2-5*1^2=1-5=-49、2(a^2b+ab^2)-2(a^2 b-1)-2ab^2 -2其中a=-2,b=2=2a^2b+2ab^2-2a^2b+2-2ab^2-2=010、(X-2分之1Y-1)(X-2分之1Y+1)-(X-2分之1Y-1)的平方其中X=1.7,Y=3.9(先化简再求值)[(X-2分之1Y)-1][(X+2分之1Y)+1]-(X-2分之1Y-1)平方=(X+2分之1Y)平方-1-(X-2分之1Y)平方+2(X-2分之1Y)-1 =(X+2分之1Y)平方-(X-2分之1Y)平方+2(X-2分之1Y)-2 =2XY+2X-Y-2=3.9*2.4+1.4=10.7611、(5a^2-3b^2)+(a^2+b^2)-(5a^2+3b^2),其中a=-1,b=1=5a^2-3b^2+a^2+b^2-5a^2-3b^2=a^2-5b^2=(-1)^2-5*1^2=1-5=-412、2(a^2b+ab^2)-2(a^2 b-1)-2ab^2 -2其中a=-2,b=2=2a^2b+2ab^2-2a^2b+2-2ab^2-2=013、9x+6x² -3(x-2/3x²) ,x=-2.=9x+6x²-3x+2x²=8x²+6x=8×(-2)²+6×(-2)=32-12=2014、1/4(-4x²+2x-8)-(1/2x-1) ,x=1/2.=-x²+1/2x-2-1/2x+1=-x²-1=-(1/2)²-1=-1/4-1=-5/415、2a-(3a-2b+2)+(3a-4b-1) ,a=b=1.=2a-3a+2b-2+3a-4b-1=(2-3+3)a+(2-4)b+(-2-1)=2a-2b-3=-316、5-(1-x)-1-(x-1),x=4=5-1+x-1-x+1=417、2x-(x+3y)-(-x-y)-(x-y),x=2,y=1=2x-x+3y+x+y-x+y=x+5y=718、9x+6x² -3(x-2/3x²) ,x=-2.=9x+6x²-3x+2x²=8x²+6x=8×(-2)²+6×(-2)=32-12=2019、1/4(-4x²+2x-8)-(1/2x-1) ,x=1/2=-x²+1/2x-2-1/2x+1=-x²-1=-(1/2)²-1=-1/4-1=-5/420、(x+5y)(x+4y) - (x-y)(x+y) 其中x=1 y= -1x^2+9xy+20y^2-x^2+y^2=21y^2+9xy=21-9=1221、已知A,B是方程x^2+2x-5=0的两个实数根,求(A^2+2AB+2A)(B^2+2AB+2B)的值.由A,B是方程x^2+2x-5=0的两个实数根得:AB=-5,A+B=-2A^2+2AB+2A)(B^2+2AB+2B)=AB(A+2B+2)(B+2A+2)=-5(-2+B+2)(-2+A+2)=-5AB=2522、1/2(x+y+z)方+1/2(x-y-z)(x-y+z)-z(x+y),其中x-y=6,xy=21.要详细步骤化简得:1/2(x+y+z)方+1/2(x-y-z)(x-y+z)-z(x+y)=1/2[(x+y)方+2z(x+y)+z方]+1/2[(x-y)方-z方]-z(x+y)=1/2(x+y)方+1/2(x-y)方=x方+y方由x-y=6,xy=21得,x方+y方=(x-y)方+2xy=7823、a^2-ab+2b^2=3 求2ab-2a^2-4b^2-7的值2ab-2a^2-4b^2-7=2(ab-a^2-2b^2)-7=-2(a^2-ab+2b^2)-7=(-2)*3-7=-6-7=-1324、若A=2x^2+3xy-2x-3,B=-x^2+xy+2,且3A+6B的值与x无关,求y的值解:3A+6B=6x^2+9xy-6x-9-6x^2+6xy+12=15xy-6x+3=x(15y-6)+325、9x+6x^2 -3(x-2/3x^2).其中x=-29x+6x² -3(x-2/3x²)=9x+6x²-3x+2x²=8x²+6x=8×(-2)²+6×(-2)=32-12=2026、1/4(-4x^2+2x-8)-(1/2x-1),其中x=1/21/4(-4x²+2x-8)-(1/2x-1)=-x²+1/2x-2-1/2x+1=-x²-1=-(1/2)²-1=-1/4-1=-5/427、3x'y-[2x'y-(2xyz-x'z)-4x'z]-xyz,其中x=-2,y=-3,z=1,:3x'y-[2x'y-(2xyz-x'z)-4x'z]-xyz=3x'y-2x'y+2xyz-x'z+4x'z-xyz=x'y-xyz+3x'z=4*(-3)-2*3*1+3*4*1=-12-6+12=-628、(5a^2-3b^2)+(a^2+b^2)-(5a^2+3b^2),其中a=-1,b=1 =5a^2-3b^2+a^2+b^2-5a^2-3b^2=a^2-5b^2=(-1)^2-5*1^2=1-5=-429、2(a^2b+ab^2)-2(a^2 b-1)-2ab^2 -2其中a=-2,b=2=2a^2b+2ab^2-2a^2b+2-2ab^2-2=030、(X-2分之1Y-1)(X-2分之1Y+1)-(X-2分之1Y-1)的平方其中X=1.7,Y=3.9(先化简再求值)[(X-2分之1Y)-1][(X+2分之1Y)+1]-(X-2分之1Y-1)平方=(X+2分之1Y)平方-1-(X-2分之1Y)平方+2(X-2分之1Y)-1=(X+2分之1Y)平方-(X-2分之1Y)平方+2(X-2分之1Y)-2=2XY+2X-Y-2=3.9*2.4+1.4=10.7631.(3X+2Y)+(4X+3Y)其中X=5,Y+3解:原式=3X+2Y+4X+3Y=7X+5Y当X=5,Y=3时原式=5*7+(-3)*5+2032.(5a^2-3b^2)+(a^2+b^2)-(5a^2+3b^2),其中a=-1,b=1 =5a^2-3b^2+a^2+b^2-5a^2-3b^2=a^2-5b^2=(-1)^2-5*1^2=1-5=-433、2(a^2b+ab^2)-2(a^2 b-1)-2ab^2 -2其中a=-2,b=2=2a^2b+2ab^2-2a^2b+2-2ab^2-2=034、2a-(3a-2b+2)+(3a-4b-1) =(),a=b=1=2a-3a+2b-2+3a-4b-1=(2-3+3)a+(2-4)b+(-2-1)=2a-2b-3=-335、5-(1-x)-1-(x-1),x=11=5-1+x-1-x+1=436、2x-(x+3y)-(-x-y)-(x-y),x=y=2=2x-x+3y+x+y-x+y=x+5y=1237、求2(a-b-54)+3(a+b),a=2,b=4=5a+b-108=5*2+4-108=-9438、求a+b-2(a-b+1),a=b=1=-a+3b-2=-1+3-2=039、(a+b)(a-b)+a(2b-a),a=1.5,b=-2=a²-b²+2ab-a²=2ab-b²∴当时,原式=2×1.5×(-2)-(-2)²=-6-4=-1040、9x+6x^2-3(x-2/3x^2),其中x=-29x+6x^2-3x+11/3x^2=6x+29/3x^2=6*(-2)+29/3*(-2)=-12-58/3=-94/341、1/4(-4x^2+2x-8)-(1/2x-1),其中x=1/2-x^2+1/2x-2-1/2x+1=-1/2^2+1/4-2-1/4+1=1/4-1=-3/442、(5a^2-3b^2)+(a^2+b^2)-(5a^2+3b^2),其中a=-1,b=15a^2-3b^2+a^2+b^2-5a^2-3b^2=5-3+1+1-5-3=-6+2=-443、2(a^2b+ab^2)-2(a^2b-1)-2ab^2-2,其中a=-2,b=22a^2*2b+2ab^2-2a^2*2b*2-2ab^2-2=8*4-4*4-8*4*2+4*4-2=-1844、2(x+5)(x-4)-3(x-6)(x+1),其中x=22(x+5)(x-4)-3(x-6)(x+1)=2*(x^2+x-20)-3*(x^2-5x-6)=2x^2+2x-40-3x^2+15x+18=-x^2+17x-22=-2^2+17*2-22=-4+34-22=845、1/3(-3ax+3)-(-ax^2-1/2ax-1),其中a=-2,x=3=-ax+1+ax²+1/2ax+1=ax²-0.5ax+2=-2×3²-0.5×(-2)×3+2=-18+3+2=-1346、5x的2平方+4-3x的2平方-5x-2x的2平方-5+6x,其中x=-3=(5x²-3x²-2x²)+(6x-5x)+(4-5)=x-1=-3-1=-447、b<a<0<c<1化简:│a+b│-│b-1│-│a-c│-│1-c│原式=-(a+b)+(b-1)+(a-c)-(1-c)=-a-b+b-1+a-c-1+c=-248、3x平方y-【2x平方y-3(2xy-x平方y)-xy】,其中x=负1,y=负2=3x平方y-2x平方y+6xy-3x平方y+xy=-2x平方y+7xy=-2*1*(-2)+7*(-1)*(-2)=4+14=1849、【(a^2-b^2)/a】除以【(a-2ab-b^2)/(a)】,其中a=3,b=2〔[(a^2-b^2)/a〕/[(a-(2ab-b^2)/a]=〔[(a^2-b^2)/a〕/{[(a^2-(2ab-b^2)]/a}=[(a^2-b^2)/a〕/[(a^2-2ab+b^2)/a]=[(a-b)(a+b)/a]/[(a-b)^2/a]=[(a-b)(a+b)/a][a/(a-b)^2]=(a+b)/(a-b) 因为a=3,b=2=(3+2)/(3-2)=550、(2x+3y)²-(2x+y)(2x-y)其中x=3/1 y=负的2/1 (2x+3y)²-(2x+y)(2x-y)=4x²+12xy+9y²-4x²+y²=12xy+10y²当x=1/3 y=-1/2时,上式得:12×(1/3)×(-1/2)+10×(-1/2)²=-2+2.5=0.551、3a²-4ab+b²-a²+3ab-2b²,其中a=0.9,b=-1原式=(3-1)a²+(1-2)b²+(-4+3)ab=2a²-b²-ab当a=0.9,b=-1时原式=2*0.9²-(-1)²-(-1)*0.9=1.62-1+0.9=1.5252、1/4(a-b)²-9(a-b)-1/2(a-b)²+5(a-b),其中a=1,b=-1 原式=(1/4-1/2)(a-b)²+(-9+5)(a-b)= -1/4(a-b)²-4(a-b)当a=1,b=-1时原式=1/4*【1-(-1)】²-4*【1-(-1)】=1/4*4-4*2=1-8=-753、(X-3)(X^2+6X+9)-(X+3)(x^2+2x-15),其中X=-3原式=(X-3)(X+3)²-(X+3)(X+5)(X-3)=(X-3)(X+3)(X+3)-(X+3)(X+5)(X-3)=(X-3)(X+3)(x+3-x-5)=-2(X-3)(X+3)因为X=-3所以该式=054、3b-[1-(5a²-b)+2(a²-2b)],其中b=½,a=﹣2=3b-1+5a^2-b-2a^2+4b=3a^2+6b-1=12+3-1=14 2、3、55、﹣½(2x²+6x-4)-4(¼x²+1-x),其中x=5=-x^2-3x+2-x^2-4+4x=-2x^2+x-2=-50+5-2=-4756、3x²y-[2xy²-2(xy-1.5x²y)+xy]+3xy²,其中x=﹣3,y=﹣2 =3x^2y-2xy^2+2xy-3x^2y-xy+3xy^2=xy^2+xy=-12+6=-657、2a²b-(2a³+5a²b-3ab²-2a³-4a²b+2ab²),a=-2,b=1 原式=2a²b-(2a³+5a²b-3ab²-2a³-4a²b+2ab²)=2a²b-a³-5a²b+3ab²+2a³+4a²b-2ab²)=a²b-ab²当a=-2,b=1时原式=4-2=258、(1)9x+6x²-3(x-2/3x-2²),其中X=-2=9x+6x²-3x+2x+12 =6x²+8x+12其中X=-2=6*(-2)²+8*(-2)+12 =24-16+12=2059、1/4(-4x²-2x-8)-(1/2x-1),其中X=1/2=-x²-1/2x-2-1/2x+1=-x²-x-1其中X=1/2=-(1/2)²-1/2-1=-1/4-1/2-1=-7/460、(5a²-3b²)+(a²+b²)-(5a²+3b²),其中a=-1,b=161、=5a²-3b²+a²+b²-5a²-3b²=a²-5b²其中a=-1,b=1=(-1)²-5*1²=1-5=-4 62、2(a²b+ab²)-2(a²b-1)-2ab²-2,其中a=-2,b=2=2a²b+2ab²-2a²b+2-2ab²-2=062、(5a^2-3b^2)+(a^2+b^2)-(5a^2+3b^2)。
8.一元二次方程解法及应用(解答题)

8.一元二次方程解法及应用(解答题)解答题58.(2009仙桃)解方程:2420x x ++=. 【关键词】一元二次方程 【答案】解:242x x +=- ()2244242222x x x x x ++=-++=+==∴122, 2.x x ==59.(2009年山西省)解方程:2230x x --= 【关键词】解一元二次方程【答案】解:移项,得223x x -=,配方,得()214x -=, ∴12x -=±,∴1213x x =-=,.60.(2009年赤峰市)某工厂今年3月份的产值为100万元,由于受国际金融风暴的影响,5月份的产值下降到81万元,求平均每月产值下降的百分率。
61.(2009年常德市)常德市工业走廊南起汉寿县太子庙镇,北至桃源县盘塘镇创元工业园.在这一走廊内的工业企业2008年完成工业总产值440亿元,如果要在2010年达到743.6亿元,那么2008年到2010年的工业总产值年平均增长率是多少?《常德工业走廊建设发展规划纲要(草案)》确定2012年走廊内工业总产值要达到1200亿元,若继续保持上面的增长率,该目标是否可以完成? 【关键词】年平均增长率【答案】设2008年到2010年的年平均增长率为 x ,则 2440(1)743.6x += 化简得 : 2(1) 1.69x +=, 120.330% 2.3x x ===-,(舍去)2743.6(10.3)1256.6841200⨯+=> 答:2008年到2010年的工业总产值年平均增长率为 30%,若继续保持上面的增长率, 在2012年将达到1200亿元的目标.62.(2009武汉)17.解方程:2310x x --=.【关键词】解一元二次方程【答案】解:131a b c ==-=- ,,,224(3)41(1)13b ac ∴-=--⨯⨯-=,123322x x +-∴==.(2009年上海市)20.解方程组:21220y x x xy -=⎧⎨--=⎩,①.②【关键词】解二元二次方程组 【答案】⎩⎨⎧=-=01y x 或⎩⎨⎧==32y x63.(2009年义乌)解方程2220x x --=。
解方程配方法练习题加答案

解方程配方法练习题加答案1. 题目:2x + 3 = 7解答:Step 1: 将等式转化为2x = 7 - 3= 4Step 2: 将2x除以2,得到x = 4/2= 2答案:x = 22. 题目:3y - 4 = 5y + 10解答:Step 1: 将等式转化为3y - 5y = 10 + 4= -2y = 14Step 2: 将-2y除以-2,得到y = 14/-2= -7答案:y = -73. 题目:4z + 8 = 2z - 6解答:Step 1: 将等式转化为4z - 2z = - 6 - 8= 2z = -14Step 2: 将2z除以2,得到z = -14/2= -7答案:z = -74. 题目:5a + 10 = 2(a + 4)解答:Step 1: 将等式转化为5a + 10 = 2a + 8Step 2: 将2a移到等式左边,得到5a - 2a = 8 - 10 = 3a = -2Step 3: 将3a除以3,得到a = -2/3答案:a = -2/35. 题目:6b - 5 = 2(b + 3)解答:Step 1: 将等式转化为6b - 2b = 5 - 6= 4b = -1Step 2: 将4b除以4,得到b = -1/4答案:b = -1/46. 题目:7c + 2 = 3(c - 1)解答:Step 1: 将等式转化为7c - 3c = 3 - 2= 4c = 1Step 2: 将4c除以4,得到c = 1/4答案:c = 1/47. 题目:8d - 7 = 10 - 3d解答:Step 1: 将等式转化为8d + 3d = 10 + 7 = 11d = 17Step 2: 将11d除以11,得到d = 17/11答案:d = 17/118. 题目:9e + 12 = 5(e - 2)解答:Step 1: 将等式转化为9e - 5e = 5(-2) - 12 = 4e = -10 - 12= 4e = -22Step 2: 将4e除以4,得到e = -22/4答案:e = -11/29. 题目:10f + 3 = 2 - 4f解答:Step 1: 将等式转化为10f + 4f = 2 - 3= 14f = -1Step 2: 将14f除以14,得到f = -1/14答案:f = -1/1410. 题目:11g - 9 = 6g + 7解答:Step 1: 将等式转化为11g - 6g = 7 + 9= 5g = 16Step 2: 将5g除以5,得到g = 16/5答案:g = 16/5通过以上题目的解答,我们可以看到解方程题目配合相应的方法可以得到正确的解答。
小学生解方程练习题答案

小学生解方程练习题答案解方程是数学学科中的重要内容,也是小学数学的一部分。
小学生学习解方程的目的是培养他们的逻辑思维和解决问题的能力。
本文将为小学生解方程练习题提供答案,帮助他们更好地掌握解方程的方法。
一、一步解一元一次方程1. 例题:求解方程2x + 3 = 9。
解答:为了消去3,我们可以执行逆运算,即减去3。
方程两边执行同样操作,得到2x = 6。
此时,我们需要消去2,所以将方程两边都除以2,得到x = 3。
因此,方程的解为x = 3。
2. 例题:求解方程4y - 7 = 9。
解答:为了消去-7,我们可以执行逆运算,即加上7。
方程两边执行同样操作,得到4y = 16。
此时,我们需要消去4,所以将方程两边都除以4,得到y = 4。
因此,方程的解为y = 4。
二、两步解一元一次方程1. 例题:求解方程2x + 3 = 7x - 5。
解答:首先,我们要将方程变形为x在一边、常数在另一边的形式。
将方程写为2x - 7x = -5 - 3,整理后得到-5x = -8。
接下来,为了消去-5,我们需要将方程两边都除以-5,得到x = 8/5。
因此,方程的解为x =8/5。
2. 例题:求解方程3y - 2 = 4y + 1。
解答:首先,我们要将方程变形为y在一边、常数在另一边的形式。
将方程写为3y - 4y = 1 + 2,整理后得到-y = 3。
接下来,为了消去-1,我们需要将方程两边都乘以-1,得到y = -3。
因此,方程的解为y = -3。
三、应用解一元一次方程1. 例题:班级里有30个学生,男生与女生的比例是3:2,试求男生和女生各有多少人?解答:设男生的人数为3x,女生的人数为2x,根据题意得到3x +2x = 30。
将方程整理为5x = 30,解得x = 6。
因此,男生的人数为3x = 18,女生的人数为2x = 12。
2. 例题:Tony的年龄是Tom的3倍,两年前他们的年龄之和是25岁,试求Tony和Tom的年龄各是多少?解答:设Tom的年龄为x,Tony的年龄为3x。
人教版5年级数学上册《解方程的办法》附答案

⼈教版5年级数学上册《解⽅程的办法》附答案⼈教版5年级数学上册9.解⽅程的⽅法⼀、仔细审题,填⼀填。
(每空1分,共13分)1.含有()的()叫⽅程。
2.等式两边加上或()同⼀个数,左右两边仍然()。
3.在⾥填上“>”“<”或“=”。
(1)当x=14时,3x+3.845,3x-3.845。
(2)当x=2.5时,5x+3x20,5x+320。
(3)当x=5时,(6x+3)÷6 5, (6x-3)÷6 5。
4.在()⾥填上含有字母的式⼦。
(1)学校器材室有212根跳绳,借出x根,还剩()根。
(2)李⽼师买回x⽀钢笔,每⽀6元,付出100元,应找回()元。
(3)⼤象重3200千克,⽐马体重的3倍多y千克,马重()千克。
⼆、⽕眼⾦睛,判对错。
(对的在括号⾥画“√”,错的画“×”)(每⼩题3分,共15分)1.等式的两边同时除以⼀个相同的数,等式两边仍然相等。
() 2.x=8是⽅程。
() 3.含有未知数的式⼦叫⽅程。
() 4.7x=0,x的值是0,所以此⽅程⽆解。
() 5.等式不⼀定是⽅程。
()三、仔细推敲,选⼀选。
(将正确答案的序号填在括号⾥)(每⼩题3分,共9分)1.下⾯不是⽅程的是()。
A.x-8>6B.0.8y=1C.a+3b=8D.5=2y 2.⽅程x+3.8=10的解是()。
A.13.8B.x=13.8C.x=6.2D.6.2 3.下列⽅程中,()的解与⽅程0.4x+0.5=0.6的解相同。
A.4x=1.1B.4x=1C.0.4x=1.1D.0.9x=0.6四、解⽅程,带☆的要检验。
(每⼩题4分,共24分)x+9.87=13.4312.4x-5.6x=0.347(x-8)=5.6☆6.8x+4.7=6.74(x-1.8)÷4=2.8☆8x-4×8=16五、看图列⽅程,并求解。
(每⼩题3分,共12分)1.2.3.4.六、⽤⽅程表⽰下⾯的数量关系,并求⽅程的解。
(完整版)小学解方程方法及答案

小学四年级解方程的方法详解方程:含有未知数的等式叫做方程。
如4x-3=21 , 6x-2(2x-3)=20方程的解:使方程成立的未知数的值叫做方程的解。
如上式解得x=6解方程:求方程的解的过程叫做解方程。
解方程的依据:方程就是一架天平,“=”两边是平衡的,一样重!1. 等式性质:(1)等式两边同时加上或减去同一个数,等式仍然成立;(2)等式两边同时乘以或除以同一个非零的数,等式仍然成立。
2. 加减乘除法的变形:(1)加法:a + b =二和则a ==和一b b =和一a例:4+5=9则有:4=9-55=9-4⑵减法:被减数 a -减数b =差贝被减数a =差+减数b被减数a —差=减数b 例:12-4=8则有:12=8+412-8=4⑶乘法:乘数a 1 X乘数b =积则:乘数a =积宁乘数b乘数b=积—•乘数a 例: 3 X 7=21则有:3=21-77=21 -3⑷除法:被除数a宁除数b =商贝被除数a=商X除数b除数b=被除数a宁商例:63 - 7=9则有:63=9 X 77=63-9解方程的步骤:1、去括号:(1)运用乘法分配律;(2)括号前边是“―”,去掉括号要变号; 括号前边是“ + ”,去掉括号不变号。
2、移项:法1――运用等式性质,两边同加或同减,同乘或同除;法2 ―- 符号过墙魔法,越过“=”时,加减号互变,乘除号互变。
注意两点:(1)总是移小的;(2)带未知数的放一边,常数值放另一边。
3、合并同类项:未知数的系数合并;常数加减计算。
4、系数化为1:利用同乘或同除,使未知数的系数化为1。
5、写出解:未知数放在“=”左边,数值(即解)放右边;如x=6&验算:将原方程中的未知数换成数,检查等号两边是否相等!注意:(1 )做题开始要写“解:”(2)上下“=”要始终对齐【例1】法1解:x-5+5=13+5x=18法2解:x=13+5x=18例2】3(x+5)-6=183(x+5)-6=18法 1 解:3x+3X 5-6=18法 2 解:3x+3X5-6=183x+15-6=183x+15-6=183x+9=183x+9=183x+9-9=18-93x=18-93x=93x=93x - 3=9 - 3x=9 宁3x=3x=3例 3 】3(x+5)-6=5(2x-7)+2解:1.去括号:3x+3 X 5-6=5 X 2x-5 X 7+23x+15-6=10x-35+23x+9=10x-332. 移项:33+9=10x-3x (注意:移小的,3. 合并同类项:42=7x4. 系数化为1 : 42 - 7=7x - 76=x5. 写出解:x=66. 验算:3X (6+5)-6=5(2x6-7)+23X11-6=5X5+227=27V-33, 3x)4+x-2=7 x-6=9 17-x=9x-6=9+3 9+3=17-x 16+2x =24+x4x=16 15=3x 4x+2=1824-x =15+2x 2+5x=18+3x 6x-2=3x+103(x+6) =2+5x 2(2x-1)=3x+10 30-4(x-5)=2x-16 2(x+4) -3=2+5x 100-3(2x-1)=3-4x 30+4(x-5)=2x-26 20x-50=50 28+6 x =88 32-22 x =1024-3 x =3 10x ( 5+1 ) =60 99 x =100- x36 十x=18 x 七=12 56-2 x =20x £+3=9 56-3x =20-x36 十x-2=164y+2=6 x+32=76 3x+6=1816+8x=40 2x-8=8 4x-3 >9=298x-3x=105 x-6 >5=42+2x 2x+5=7 > 3 2(x+3)+3=13 12x-9x=9 6x+18=4856x-50x=30 5x=15 (x-5 )78-5x=2832y-29y=3 5(x+5)=15 89 -9x =80100-20x=20+30x 55x-25x=60 76y十76=153x-90=162x+9x=11 12(y-1)=24、列方程解应用题:一)口算: a+2a= 3c+5c= 5x-x= 6x-2x=(二)用方程表示数量关系:1 .火车每小时行 120 千米,汽车每小时 a 千米,火车每小时比汽车快 6 千米80*5x=100 7x *8=14 65x+35=10019y+y=40 25-5x=15 79y+y=8042x+28x=140 3x-1=8-2x 90y-90=90-90y80y-90=70 *30 78y+2y=160 88-4x=80-2x9* ( 4x )=1 20x=40 -10x 65y-30=10051y-y=100 85y+1=y+86 45x-50=40-45x4m-2m=X+3x= 1.5x-x=3.6x+1.4x=2. 男生人数比女生少16人,男生56人,女生x人。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学四年级解方程的方法详解
方程:含有未知数的等式叫做方程。
如4x-3=21,6x-2(2x-3)=20
方程的解:使方程成立的未知数的值叫做方程的解。
如上式解得x=6
解方程:求方程的解的过程叫做解方程。
解方程的依据:方程就是一架天平,“=”两边是平衡的,一样重!
1. 等式性质:(1)等式两边同时加上或减去同一个数,等式仍然成立;
(2)等式两边同时乘以或除以同一个非零的数,等式仍然成立。
2. 加减乘除法的变形:
(1) 加法:a + b = 和则 a = 和-b b = 和-a
例:4+5=9 则有:4=9-5 5=9-4
(2) 减法:被减数a –减数b = 差则:
被减数a = 差+减数b 被减数a-差= 减数b 例:12-4=8则有:12=8+4 12-8=4
(3) 乘法:乘数a ×乘数b = 积则:
乘数a = 积÷乘数b 乘数b= 积÷乘数a 例:3×7=21则有:3=21÷7 7=21÷3
(4) 除法:被除数a ÷除数b = 商则:
被除数a= 商×除数b 除数b=被除数a ÷商例:63÷7=9 则有:63=9×7 7=63÷9
解方程的步骤:
1、去括号:(1)运用乘法分配律;(2)括号前边是“-”,去掉括号要变号;括号前边是“+”,去掉括号不变号。
2、移项:法1——运用等式性质,两边同加或同减,同乘或同除;法2——符号过墙魔法,越过“=”时,加减号互变,乘除号互变。
注意两点:(1)总是移小的;(2)带未知数的放一边,常数值放另一边。
3、合并同类项:未知数的系数合并;常数加减计算。
4、系数化为1:利用同乘或同除,使未知数的系数化为1。
5、写出解:未知数放在“=”左边,数值(即解)放右边;如x=6
6、验算:将原方程中的未知数换成数,检查等号两边是否相等!
注意:(1)做题开始要写“解:”(2)上下“=”要始终对齐
【例1】
x-5=13 x-5=13
法1 解:x-5+5=13+5 法2 解:x=13+5
x=18 x=18
【例2】
3(x+5)-6=18 3(x+5)-6=18
法1 解: 3x+3×5-6=18 法2 解:3x+3×5-6=18
3x+15-6=18 3x+15-6=18
3x+9=18 3x+9=18
3x+9-9=18-9 3x=18-9
3x=9 3x=9
3x÷3=9÷3 x=9÷3
x=3 x=3
【例3】
3(x+5)-6=5(2x-7)+2
解: 1.去括号:3x+3×5-6=5×2x-5×7+2
3x+15-6=10x-35+2
3x+9=10x-33
2.移项:33+9=10x-3x (注意:移小的,如-33, 3x)
3.合并同类项:42=7x
4.系数化为1:42÷7=7x÷7
6=x
5.写出解:x=6
6.验算:3×(6+5)-6=5(2x6-7)+2
3×11-6=5×5+2
27=27√
解方程练习(写出详细过程):
4+x=7 x+6=9 4+x=7+5
4+x-2=7 x-6=9 17-x=9
x-6=9+3 9+3=17-x 16+2x =24+x
4x=16 15=3x 4x+2=18
24-x =15+2x 2+5x=18+3x 6x-2=3x+10
3(x+6) =2+5x 2(2x-1)=3x+10 30-4(x-5)=2x-16
2(x+4) -3=2+5x 100-3(2x-1)=3-4x 30+4(x-5)=2x-26
20x-50=50 28+6 x =88 32-22 x =10
24-3 x =3 10 x ×(5+1)=60 99 x =100- x
36÷ x=18 x÷6=12 56-2 x =20
36÷ x-2=16 x÷6+3=9 56-3x =20-x
4y+2=6 x+32=76 3x+6=18
16+8x=40 2x-8=8 4x-3×9=29
8x-3x=105 x-6×5=42+2x 2x+5=7 × 3 2(x+3)+3=13 12x-9x=9 6x+18=48
56x-50x=30 5x=15(x-5)78-5x=28
32y-29y=3 5(x+5)=15 89 – 9x =80 100-20x=20+30x 55x-25x=60 76y÷ 76=1 23y÷ 23=23 4x-20=0 80y+20=100-20y
53x-90=16 2x+9x=11 12(y-1)=24
80÷ 5x=100 7x÷ 8=14 65x+35=100
19y+y=40 25-5x=15 79y+y=80
42x+28x=140 3x-1=8-2x 90y-90=90-90y 80y-90=70÷ 30 78y+2y=160 88-4x=80-2x 9÷(4x)=1 20x=40 – 10x 65y-30=100 51y-y=100 85y+1=y+86 45x-50=40-45x
二、列方程解应用题:
(一)口算:
a+2a= 3c+5c= 4m-2m= X+3x=
5x-x= 6x-2x= 1.5x-x= 3.6x+1.4x=
(二)用方程表示数量关系:
1.火车每小时行120千米,汽车每小时a千米,火车每小时比汽车快6千米。
______ ___
2.男生人数比女生少16人,男生56人,女生x人。
_____________________
3.苹果树和梨树共38棵,苹果树x棵,梨树15课。
___________________
(三)列方程解应用题
1.画出线段图:
①女生比男生的2倍多2人。
②小明年龄比弟弟年龄的2倍少5岁。
2.上海野生动物园是中国首家野生动物园,截至2004年,一共有成年东北虎和白虎16只,东北虎的只数是白虎的7倍。
你能提出什么问题?
3.校园里的杨树和柳树共有36棵,杨树的棵树是柳树的2倍。
杨树和柳树各有多少棵?
4.小宝家养了一些兔子,其中白兔的只数是黑兔的3倍,白兔比黑兔多12只。
白兔和黑兔各有多少只?
5.用一根长54厘米的铁丝围成一个长方形,要使长是宽的2倍,围成的长方形的长和宽各应是多少厘米?面积是多少平方厘米?
6.甲、乙两个工程队共同铺铁路,16天共铺2144米。
甲队每天铺70米,乙队每天铺多少米?
7. 妈妈去超市买了3千克苹果和2千克橙子,共花了19.6元。
苹果每千克4.8元,橙子每千克多少元?
8 甲、乙两艘轮船同时从一个码头向相反的方向开出,甲船每小时行23.5千米,乙船每小时行21.5 千米。
航行几小时后两船相距315千米?
9. 下列方程中哪些是正确的?
两地相距40千米,甲、乙两人同时从两地对面走来,3小时后两人相距10千米。
已知甲每小时行5.5千米,那么乙每小时行多少千米?
解:设乙每小时行X千米。
(1)(5.5 +X)×3=10 ()
(2)5.5×3+3X=40-10 ()
(3)40-3X-5.5×3=10 ()
(4)5.5×3+3X=40 ()
(5)3X+3×5.5+10=40 ()。
