SPSS统计分析1：正态分布检验

合集下载

SPSS学习系列19. 正态性检验

19. 正态性检验实际中，经常需要检验数据是否服从正态分布。

一、Kolmogorov-Smirnov(K - S) 单样本检验这是一种分布拟合优度检验，即将一个变量的累积分布函数与特定分布进行比较。

有数据文件：对“数学成绩”“英语成绩”做正态性检验。

1.【分析】——【非参数检验】——【单样本】，打开“单样本非参数检验”窗口，【目标】界面勾选“自动比较观察数据和假设数据”2.【字段】界面，勾选“使用定制字段分配”，将要检验的变量“数学成绩”“英语成绩”选入【检验字段】框，3. 【设置】界面，选择“自定义检验”，勾选“检验观察分布和假设分布（Kolmogorov-Smimov检验）”点【选项】，打开“Kolmogorov-Smimov检验选项”子窗口，选择“正态分布”，勾选“使用样本数据”，点【确定】回到原窗口，点【运行】得到结果说明：样本量大于50用Kolmogorov-Smirnov检验，样本量小于50用Shapiro-Wilk检验；原假设H0：服从正态分布；H1：不服从正态分布。

P值<0.05, 拒绝原假设H0；P值>0.05, 接受原假设H0, 即服从正态分布；本例中，“数学成绩”、“英语成绩”的P值都>0.05, 故服从正态分布。

双击上面结果可以看到更详细的检验结果：注：类似的操作也可以检验数据是否服从“二项、均匀、指数、泊松”等分布。

二、用“旧对话框”进行上述检验1.【分析】——【非参数检验】——【旧对话框】——【1-样本K-S】，打开“单样本Kolmogorov-Smirnov检验”窗口，将要检验的变量选入【检验变量列表】框，【检验分布】勾选“常规”，2.点【精确】，打开“精确检验”窗口，勾选“精确”，“仅渐进法”——只计算检验统计量的渐近分布的近似概率值，而不计算确切概率，适用用样本量较大，P值远离α=0.05，节省计算时间，否则可能结果偏差较大；“Monte Carlo”——利用模拟抽样方法求得P值的近似无偏估计，适合大样本数据，节省计算时间；“精确”——计算精确的概率值（P值）。

SPSS统计分析1：正态分布检验.

正态分布检验一、正态检验的必要性[1]当对样本是否服从正态分布存在疑虑时，应先进行正态检验；如果有充分的理论依据或根据以往积累的信息可以确认总体服从正态分布时，不必进行正态检验。

当然，在正态分布存疑的情况下，也就不能采用基于正态分布前提的参数检验方法，而应采用非参数检验。

二、图示法1、P-P图以样本的累计频率作为横坐标，以安装正态分布计算的相应累计概率作为纵坐标，把样本值表现为直角坐标系中的散点。

如果资料服从整体分布，则样本点应围绕第一象限的对角线分布。

2、Q-Q图以样本的分位数作为横坐标，以按照正态分布计算的相应分位点作为纵坐标，把样本表现为指教坐标系的散点。

如果资料服从正态分布，则样本点应该呈一条围绕第一象限对角线的直线。

Q-Q图为佳，效率较高。

以上两种方法以3、直方图判断方法：是否以钟形分布，同时可以选择输出正态性曲线。

4、箱式图判断方法：观测离群值和中位数。

5、茎叶图类似与直方图，但实质不同。

三、计算法1、峰度（Kurtosis）和偏度（Skewness）（1）概念解释峰度是描述总体中所有取值分布形态陡缓程度的统计量。

这个统计量需要与正态分布相比较，峰度为0表示该总体数据分布与正态分布的陡缓程度相同；峰度大于0表示该总体数据分布与正态分布相比较为陡峭，为尖顶峰；峰度小于0表示该总体数据分布与正态分布相比较为平坦，为平顶峰。

峰度的绝对值数值越大表示其分布形态的陡缓程度与正态分布的差异程度越大。

峰度的具体计算公式为：注：SD就是标准差σ。

峰度原始定义不减3，在SPSS中为分析方便减3后与0作比较。

偏度与峰度类似，它也是描述数据分布形态的统计量，其描述的是某总体取值分布的对称性。

这个统计量同样需要与正态分布相比较，偏度为0表示其数据分布形态与正态分布的偏斜程度相同；偏度大于0表示其数据分布形态与正态分布相比为正偏或右偏，即有一条长尾巴拖在右边，数据右端有较多的极端值；偏度小于0表示其数据分布形态与正态分布相比为负偏或左偏，即有一条长尾拖在左边，数据左端有较多的极端值。

spss-数据正态分布检验-Q

spss 数据正态分布检验 Q-Q图学习交流 2009-02-08 14:40 阅读1378 评论9字号：大中小把自己学习spss的一点理解拿出来晒一晒，要是不对大家可以留言啊，一定要讨论啊。

要观察某一属性的一组数据是否符合正态分布，可以有两种方法（目前我知道这两种，并且这两种方法只是直观观察，不是定量的正态分布检验）：1：在spss里的基本统计分析功能里的频数统计功能里有对某个变量各个观测值的频数直方图中可以选择绘制正态曲线。

具体如下：Analyze-----Descriptive Statistics-----Frequenc ies，打开频数统计对话框，在Statistics里可以选择获得各种描述性的统计量，如：均值、方差、分位数、峰度、标准差等各种描述性统计量。

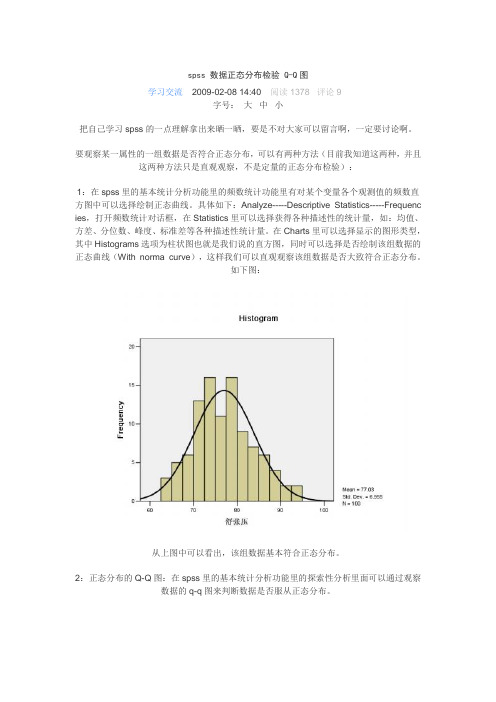
在Charts里可以选择显示的图形类型，其中Histograms选项为柱状图也就是我们说的直方图，同时可以选择是否绘制该组数据的正态曲线（With norma curve），这样我们可以直观观察该组数据是否大致符合正态分布。

如下图：从上图中可以看出，该组数据基本符合正态分布。

2：正态分布的Q-Q图：在spss里的基本统计分析功能里的探索性分析里面可以通过观察数据的q-q图来判断数据是否服从正态分布。

具体步骤如下：Analyze-----Descriptive Statistics-----Explore打开对话框，选择Plots选项，选择Normality plots with tests选项，可以绘制该组数据的q-q图。

图的横坐标为改变量的观测值，纵坐标为分位数。

若该组数据服从正态分布，则图中的点应该靠近图中直线。

纵坐标为分位数，是根据分布函数公式F(x)=i/n+1得出的.i为把一组数从小到大排序后第i 个数据的位置，n为样本容量。

若该数组服从正态分布则其q-q图应该与理论的q-q图（也就是图中的直线）基本符合。

对于理论的标准正态分布，其q-q图为y=x直线。

spss判断是否符合正态分布

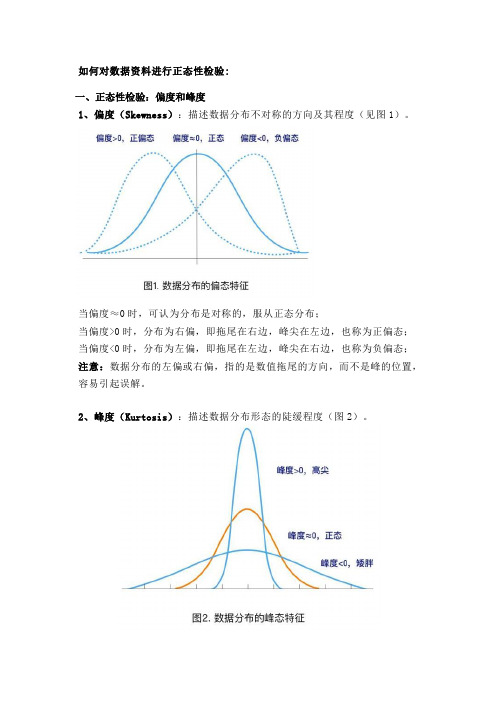
如何对数据资料进行正态性检验:一、正态性检验：偏度和峰度1、偏度（Skewness）：描述数据分布不对称的方向及其程度（见图1）。

当偏度≈0时，可认为分布是对称的，服从正态分布；当偏度>0时，分布为右偏，即拖尾在右边，峰尖在左边，也称为正偏态；当偏度<0时，分布为左偏，即拖尾在左边，峰尖在右边，也称为负偏态；注意：数据分布的左偏或右偏，指的是数值拖尾的方向，而不是峰的位置，容易引起误解。

2、峰度（Kurtosis）：描述数据分布形态的陡缓程度（图2）。

当峰度≈0时，可认为分布的峰态合适，服从正态分布（不胖不瘦）；当峰度>0时，分布的峰态陡峭（高尖）；当峰度<0时，分布的峰态平缓（矮胖）；利用偏度和峰度进行正态性检验时，可以同时计算其相应的Z评分（Z-score），即：偏度Z-score=偏度值/标准误，峰度Z-score=峰度值/标准误。

在α=0.05的检验水平下，若Z-score在±1.96之间，则可认为资料服从正态分布。

了解偏度和峰度这两个统计量的含义很重要，在对数据进行正态转换时，需要将其作为参考，选择合适的转换方法。

3、SPSS操作方法以分析某人群BMI的分布特征为例。

(1) 方法一选择Analyze → Descriptive Statistics → Frequencies将BMI选入Variable(s)框中→点击Statistics →在Distribution框中勾选Skewness和Kurtosis(2) 方法二选择Analyze → Descriptive Statistics → Descriptives将BMI选入Variable(s)框中→点击Options →在Distribution框中勾选Skewness和Kurtosis4、结果解读在结果输出的Descriptives部分，对变量BMI进行了基本的统计描述，同时给出了其分布的偏度值0.194（标准误0.181），Z-score = 0.194/0.181 = 1.072，峰度值0.373（标准误0.360），Z-score = 0.373/0.360 = 1.036。

spss_数据正态分布检验方法及意义

spss 数据正态分布检验方法及意义判读要观察某一属性的一组数据是否符合正态分布，可以有两种方法（目前我知道这两种，并且这两种方法只是直观观察，不是定量的正态分布检验）：1：在spss里的基本统计分析功能里的频数统计功能里有对某个变量各个观测值的频数直方图中可以选择绘制正态曲线。

具体如下：Analyze-----Descriptive S tatistics-----Frequencies，打开频数统计对话框，在Statistics里可以选择获得各种描述性的统计量，如：均值、方差、分位数、峰度、标准差等各种描述性统计量。

在Charts里可以选择显示的图形类型，其中Histograms选项为柱状图也就是我们说的直方图，同时可以选择是否绘制该组数据的正态曲线（With nor ma curve），这样我们可以直观观察该组数据是否大致符合正态分布。

如下图：从上图中可以看出，该组数据基本符合正态分布。

2：正态分布的Q-Q图：在spss里的基本统计分析功能里的探索性分析里面可以通过观察数据的q-q图来判断数据是否服从正态分布。

具体步骤如下：Analyze-----Descriptive Statistics-----Explore打开对话框，选择Plots选项，选择Normality plots with tests选项，可以绘制该组数据的q-q 图。

图的横坐标为改变量的观测值，纵坐标为分位数。

若该组数据服从正态分布，则图中的点应该靠近图中直线。

纵坐标为分位数，是根据分布函数公式F(x)=i/n+1得出的.i为把一组数从小到大排序后第i个数据的位置，n为样本容量。

若该数组服从正态分布则其q-q图应该与理论的q-q图（也就是图中的直线）基本符合。

对于理论的标准正态分布，其q-q图为y=x直线。

非标准正态分布的斜率为样本标准差，截距为样本均值。

如下图：如何在spss中进行正态分布检验1(转)(2009-07-22 11:11:57)标签：杂谈一、图示法1、P-P图以样本的累计频率作为横坐标，以安装正态分布计算的相应累计概率作为纵坐标，把样本值表现为直角坐标系中的散点。

SPSS学习笔记-正态性检验

如何在spss中进行正态分布检验一、图示法1、P-P图以样本的累计频率作为横坐标，以安装正态分布计算的相应累计概率作为纵坐标，把样本值表现为直角坐标系中的散点。

如果资料服从整体分布，则样本点应围绕第一象限的对角线分布。

2、Q-Q图以样本的分位数作为横坐标，以按照正态分布计算的相应分位点作为纵坐标，把样本表现为指教坐标系的散点。

如果资料服从正态分布，则样本点应该呈一条围绕第一象限对角线的直线。

以上两种方法以Q-Q图为佳，效率较高。

3、直方图判断方法：是否以钟形分布，同时可以选择输出正态性曲线。

4、箱式图判断方法：观测离群值和中位数。

5、茎叶图类似与直方图，但实质不同。

二、计算法1、偏度系数（Skewness）和峰度系数（Kurtosis）计算公式：g1表示偏度，g2表示峰度，通过计算g1和g2及其标准误σg1及σg2然后作U检验。

两种检验同时得出U<U0.05=1.96，即p>0.05的结论时，才可以认为该组资料服从正态分布。

由公式可见，部分文献中所说的“偏度和峰度都接近0……可以认为……近似服从正态分布”并不严谨。

2、非参数检验方法非参数检验方法包括Kolmogorov-Smirnov检验（D检验）和Shapiro- Wilk（W检验）。

SAS中规定：当样本含量n≤2000时，结果以Shapiro – Wilk（W检验）为准，当样本含量n >2000时，结果以Kolmogorov – Smirnov（D检验）为准。

SPSS中则这样规定：（1）如果指定的是非整数权重，则在加权样本大小位于3和50之间时，计算Shapiro-Wilk统计量。

对于无权重或整数权重，在加权样本大小位于3和5000之间时，计算该统计量。

由此可见，部分SPSS教材里面关于“Shapiro – Wilk适用于样本量3-50之间的数据”的说法是在是理解片面，误人子弟。

（2）单样本Kolmogorov-Smirnov检验可用于检验变量（例如income）是否为正态分布。

spss正态分布检验方法

spss正态分布检验方法SPSS正态分布检验方法。

SPSS（Statistical Package for the Social Sciences）是一种统计分析软件，广泛应用于社会科学、生物医学、教育研究等领域。

在数据分析过程中，正态分布检验是一项重要的统计方法，用于检验数据是否符合正态分布。

本文将介绍在SPSS中进行正态分布检验的方法及步骤。

SPSS正态分布检验方法主要包括两种统计检验，Shapiro-Wilk 检验和Kolmogorov-Smirnov检验。

Shapiro-Wilk检验是一种较为常用的正态性检验方法，适用于样本量较小（通常小于50）的情况。

在SPSS中，进行Shapiro-Wilk检验的步骤如下：1. 打开SPSS软件，导入需要进行正态分布检验的数据文件。

2. 选择“分析”菜单中的“描述统计”选项，然后在弹出的对话框中选择“探索性数据分析”。

3. 在“探索性数据分析”对话框中，将需要进行正态性检验的变量移动到“因子”框中。

4. 点击“统计”按钮，在弹出的对话框中勾选“Shapiro-Wil k”复选框。

5. 点击“确定”按钮，SPSS将输出Shapiro-Wilk检验的结果，包括统计量W和显著性水平。

Kolmogorov-Smirnov检验适用于样本量较大的情况，其原理是通过比较累积分布函数来检验数据是否符合正态分布。

在SPSS中进行Kolmogorov-Smirnov检验的步骤如下：1. 打开SPSS软件，导入需要进行正态分布检验的数据文件。

2. 选择“分析”菜单中的“非参数检验”选项，然后在弹出的对话框中选择“单样本K-S检验”。

3. 在“单样本K-S检验”对话框中，将需要进行正态性检验的变量移动到“测试变量列表”框中。

4. 点击“确定”按钮，SPSS将输出Kolmogorov-Smirnov检验的结果，包括统计量D和显著性水平。

在进行正态分布检验时，需要注意以下几点：1. 正态性检验是基于样本数据进行的统计推断，结果受样本量的影响。

(可视化整理)spss统计分析-实例分析

众数（Mode）统计学名词，在统计分布上具有明显集中趋势点的数值，代表数据的一般水平（众数可以不存在或多于一个）。修正定义：是一组数据中出现次数最多的数值，叫众数，有时众数在一组数中有好几个。用M表示。理性理解：简单的说，就是一组数据中占比例最多的那个数。
全距也称为极差，是数据的最大值与最小值之间的绝对差。在相同样本容量情况下的两组数据，全距大的一组数据要比全距小的一组数据更为分散。计算公式：最大值－最小值。
1.2 描述分析
计算基本描述统计量的操作
（1）分析—描述统计—描述（2）将分析变量选择到变量框中（3）单击选项按钮指定基本统计量
1.2 描述分析
1.2.2 应用例一
案例1－3：计算人均住房面积的基本描述统计量，并对本市户口和外地户口家庭的情况进行比较。操作步骤：
• 调用命令Analyze\Descriptive Statistics \Descriptives
1.1频数分析
1.1频数分析
输出结果
1.1 频数分析＿例1
例1－1 分析住房状况调查数据中户主的从业状况和目前所住房屋的产权情况思路：利用频数分布表及图形条件：都是分类变量，直接分析步骤：
• 调用命令：
• Analyze\Descriptive Statistics\Frequencies
常用统计量：均值、中位数、众数
1.2 描述分析
刻画离散程度的统计量
离散程度是指一组数据远离其“中心值”的程度。
如果数据都紧密地集中在“中心值”的周围，数据的离散程度较小，说明这个“中心值”对数据的代表性好；相反，如果数据仅是比较松散地分布在“中心值”的周围，数据的离散程度较大，则此“中心值”说明数据特征是不具有代表性的。

正交试验设计的spss分析报告

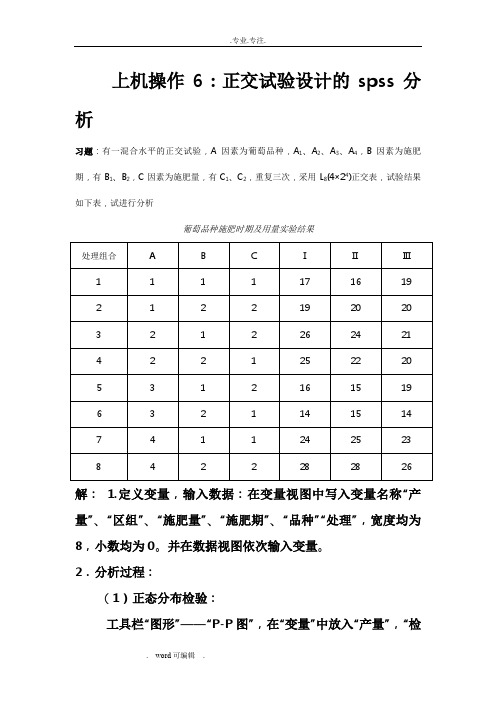
上机操作6：正交试验设计的spss分析习题：有一混合水平的正交试验，A因素为葡萄品种，A1、A2、A3、A4，B因素为施肥期，有B1、B2，C因素为施肥量，有C1、C2，重复三次，采用L8(4×24)正交表，试验结果如下表，试进行分析葡萄品种施肥时期及用量实验结果解： 1.定义变量，输入数据：在变量视图中写入变量名称“产量”、“区组”、“施肥量”、“施肥期”、“品种”“处理”，宽度均为8，小数均为0。

并在数据视图依次输入变量。

2．分析过程：（1）正态分布检验：工具栏“图形”——“P-P图”，在“变量”中放入“产量”，“检验分布”为“正态”，“确定”。

（2）方差齐性检验：a.工具栏“分析”——“比较均值”——“单因素ANOVA”。

b.在“因变量”中放入“产量”，在“固定因子”中放入“品种”。

c.点击“选项”，在“统计量”中点击“方差同质性检验”，“继续”。

d.“确定”。

工具栏“分析”——“比较均值”——“单因素ANOVA”。

e.在“因变量”中放入“产量”，在“固定因子”中放入“施肥期”。

f.点击“选项”，在“统计量”中点击“方差同质性检验”，“继续”。

g.“确定”。

在“因变量”中放入“产量”，在“固定因子”中放入“施肥量”。

h.点击“选项”，在“统计量”中点击“方差同质性检验”，“继续”。

i.“确定”。

在“因变量”中放入“产量”，在“固定因子”中放入“处理”。

点击“选项”，在“统计量”中点击“描述性”和“方差同质性检验”，“继续”。

j.“确定”。

（3）显著性差异检验：a.工具栏“分析”——“常规线性模型”——“单变量”。

b.在“因变量”中放入“产量”，在“固定因子”中分别放入“施肥期”、“施肥量”、“品种”“区组”。

c.点击“模型”，“定制”，将“施肥期”、“施肥量”、“品种”、“区组”放入“模型”下。

在“建立项”中选择“主效应”，“继续”。

d.点击“两两比较”，将“施肥期”、“施肥量”、“品种”放入“两两比较检验”中，点击“假定方差齐性”中的“Duncan”。

spss 数据正态分布检验-两种方法

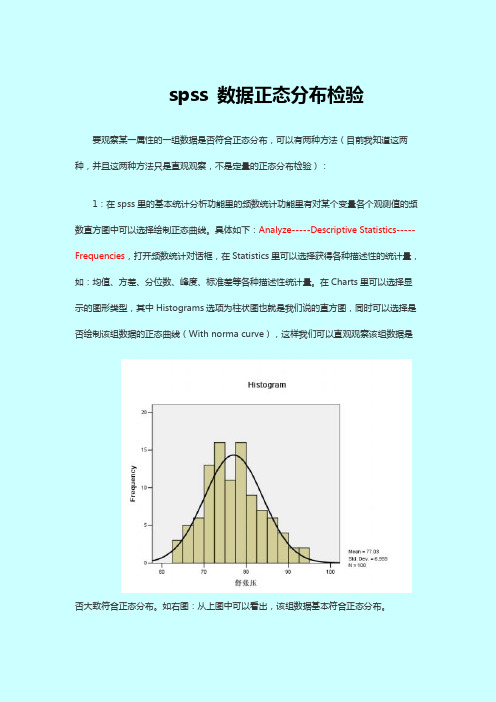
spss 数据正态分布检验要观察某一属性的一组数据是否符合正态分布，可以有两种方法（目前我知道这两种，并且这两种方法只是直观观察，不是定量的正态分布检验）：1：在spss里的基本统计分析功能里的频数统计功能里有对某个变量各个观测值的频数直方图中可以选择绘制正态曲线。

具体如下：Analyze-----Descriptive Statistics-----Frequencies，打开频数统计对话框，在Statistics里可以选择获得各种描述性的统计量，如：均值、方差、分位数、峰度、标准差等各种描述性统计量。

如右图：从上图中可以看出，该组数据基本符合正态分布。

2：正态分布的Q-Q图：在spss里的基本统计分析功能里的探索性分析里面可以通过观察数据的q-q图来判断数据是否服从正态分布。

具体步骤如下：Analyze-----Descriptive Statistics-----Explore打开对话框，选择Plots选项，选择Normality plots with tests选项，可以绘制该组数据的q-q图。

图的横坐标为改变量的观测值，纵坐标为分位数。

若该组数据服从正态分布，则图中的点应该靠近图中直线。

纵坐标为分位数，是根据分布函数公式F(x)=i/n+1得出的.i为把一组数从小到大排序后第i个数据的位置，n为样本容量。

若该数组服从正态分布则其q-q图应该与理论的q-q图（也就是图中的直线）基本符合。

对于理论的标准正态分布，其q-q图为y=x直线。

非标准正态分布的斜率为样本标准差，截距为样本均值。

正态分布检验的3大步骤及结果处理spss

正态分布检验的3⼤步骤及结果处理spss7. NormalityBelow, I describe five steps for determining and dealing with normality. However, the bottom line is that almost no one checks their data for normality; instead they assume normality, and use the statistical tests that are based upon assumptions of normality that have more power (ability to find significant results in the data).First, what is normality A normal distribution is a symmetric bell-shaped curve defined by two things: the mean (average) and variance (variability).Second, why is normality important The central idea behind statistical inference is that as sample size increases, distributions will approximate normal. Most statistical tests rely upon the assumption that your data is “normal”. Tests that rely upon the assumption or normality are called parametric tests. If your data is not normal, then you would use statistical tests that do not rely upon the assumption of normality, call non-parametric tests. Non-parametric tests are less powerful than parametric tests, which means the non-parametric tests have less ability to detect real differences or variability in your data. In other words, you want to conduct parametric tests because you want to increase your chances of finding significant results.Third, how do you determine whether data are “normal” There are three interrelated approaches to determine normality, and all three should be conducted.First, look at a histogram with the normal curve superimposed. A histogram provides useful graphical representation of the data. SPSS can also superimpose the theoretical “normal” distribution onto the histogram of your data so that you can compare your data to the normal curve. To obtain a histogram with thesuperimposed normal curve:1. Select Analyze --> Descriptive Statistics --> Frequencies.2. Move all variables into the “Variable(s)” window.3. Click “Charts”, and click “Histogram, with normal curve”.4. Click OK.Output below is for “system1”. Notice the bell-shaped black line superimposed on the distribution.All samples deviate somewhat from normal, so the question is how much deviation from the black line indicates “non-normality”? Unfortunately, graphical representations like histogram provide no hard-and-fast rules. After you have viewed many (many!) histograms, over time you will get a sense for the normality of data. In my view, the histogram for “system1” shows a fairly normal distribution.Second, look at the values of Skewness and Kurtosis. Skewness involves the symmetry of the distribution.Skewness that is normal involves a perfectly symmetric distribution. A positively skewed distribution has scores clustered to the left, with the tail extending to the right. A negatively skewed distribution has scores clustered to the right, with the tail extending to the left. Kurtosis involves the peakedness of the distribution.Kurtosis that is normal involves a distribution that is bell-shaped and not too peaked or flat. Positive kurtosis is indicated by a peak. Negative kurtosis is indicated by a flat distribution. Descriptive statistics about skewness and kurtosis can be found by using either the Frequencies, Descriptives, or Explore commands. I like to use the “Explore” command because it provides other useful information about normality, so1. Select Analyze --> Descriptive Statistics --> Explore.2. Move all variables into the “Variable(s)” window.3. Click “Plots”, and un click “Stem-and-leaf”4. Click OK.Descriptives box tells you descriptive statistics about the variable, including the value of Skewness and Kurtosis, with accompanying standard error for each. Both Skewness and Kurtosis are 0 in a normaldistribution, so the farther away from 0, the more non-normal the distribution. The question is “how much”skew or kurtosis render the data non-normal? This is an arbitrary determination, and sometimes difficult to interpret using the values of Skewness and Kurtosis. Luckily, there are more objective tests of normality, described next.Third, the descriptive statistics for Skewness and Kurtosis are not as informative as established tests for normality that take into account both Skewness and Kurtosis simultaneously. The Kolmogorov-Smirnov test (K-S) and Shapiro-Wilk (S-W) test are designed to test normality by comparing your data to a normaldistribution with the same mean and standard deviation of your sample:1. Select Analyze --> Descriptive Statistics --> Explore.2. Move all variables into the “Variable(s)” window.3. Click “Plots”, and un click “Stem-and-leaf”, and click “Normality plots with tests”.4. Click OK.“Test of Normality” box gives the K-S and S-W test results. If the test is NOT significant, then the data are normal, so any value above .05 indicates normality. If the test is significant (less than .05), then the data are non-normal. In this case, both tests indicate the data are non-normal. However, one limitation of the normality tests is that the larger the sample size, the more likely to get significant results. Thus, you may get significant results with only slight deviations from normality. In this case, our sample size is large (n=327) so thesignificance of the K-S and S-W tests may only indicate slight deviations from normality. You need to eyeball your data (using histograms) to determine for yourself if the data rise to the level of non-normal.“Normal Q-Q Plot” provides a graphical way to determine the level of normality. The black line indicates the values your sample should adhere to if the distribution was normal. The dots are your actual data. If the dots fall exactly on the black line, then your data are normal. If they deviate from the black line, your data are non-normal. In this case, you can see substantial deviation from the straight black line.Fourth, if your data are non-normal, what are your options to deal with non-normality You have four basic options.a.Option 1 is to leave your data non-normal, and conduct the parametric tests that rely upon theassumptions of normality. Just because your data are non-normal, does not instantly invalidate theparametric tests. Normality (versus non-normality) is a matter of degrees, not a strict cut-off point.Slight deviations from normality may render the parametric tests only slightly inaccurate. The issue isthe degree to which the data are non-normal.b.Option 2 is to leave your data non-normal, and conduct the non-parametric tests designed for non-normal data.c.Option 3 is to conduct “robust” tests. There is a growing branch of statistics called “robust” tests thatare just as powerful as parametric tests but account for non-normality of the data.d.Option 4 is to transform the data. Transforming your data involving using mathematical formulas tomodify the data into normality.Fifth, how do you transform your data into “normal” data There are different types of transformations based upon the type of non-normality. For example, see handout “Figure 8.1” on the last page of this document that shows six types of non-normality (e.g., 3 positive skew that are moderate, substantial, and severe; 3 negative skew that are moderate, substantial, and severe). Figure 8.1 also shows the type of transformation for each type of non-normality. Transforming the data involves using the “Compute” function to create a new variable (the new variable is the old variable transformed by the mathematical formula):1. Select Transform --> Compute Variable2. Type the name of the new variable you wan t to create, such as “transform_system1”.3. Select the type of transformation from the “Functions” list, and double-click.4. Move the (non-normal) variable name into the place of the question mark “?”.5. Click OK.The new variable is reproduced in the last column in the “Data view”.Now, check that the variable is normal by using the tests described above.If the variable is normal, then you can start conducting statistical analyses of that variable.If the variable is non-normal, then try other transformations.。

spss操作步骤讲解系列--正态性检验

正态分布及spss中的检验方法1.基本理论正态分布：又称高斯分布或上帝分布，分布形态，呈现最好和最坏的较少，较多的集中在一般如果是图形展示类似钟形。

一般问卷数据可以采用中心极限定理：在收集数据时只要收集的数据，次数足够大，数据将会趋向于正态分布，因此一般认为问卷数据满足近似正态分布。

正态性检验方法：K-S和S-W较严格和准确，但因为对数据的要求较为严格。

图形法p-p和q-q图，还有描述统计分析的偏度和峰度，非参数检验的单样本K-S检验。

图1探索方法勾选2.描述统计探索分析方法探索性分析方法的操作第一步：将数据导入spss软件后，点击分析、描述统计、探索。

图2探索性操作第一步第二步、进入图中对话框后，点击图，勾选直方图和含检验的正态性图，点击继续、确定。

图3探索性第二步然后正态性检验的结果就出来了（在正态检验中重要的是正态性检验表中的结果）。

图4探索性检验结果展示将结果粘贴复制到Excel表格中，后将整理好的结果粘贴复制到Word文档进行，由于p<0.05，表明本次数据不满足正态分布。

图5探索结果整理3.p-p图操作步骤第一步、将数据导入spss软件中，p-p图操作：点击分析、描述统计、p-p 图。

图6p-p操作步骤第一步进入图中框中后，将变量放入对应的对话框中点击确定。

图7p-p图勾选情况然后p-p图结果就出来了（根据图中点是否均匀的分布在对角线上，来判断是否满足近似正态）。

图8p-p图结果展示将p-p图结果放入Word文档中进行分析，从图中可以看出，点均分布在对角线附近，表明数据满足正态分布。

图9p-p结果整理4.Q-Q图操作步骤Q-Q图操作第一步：首先将数据导入spss中，点击分析、描述统计、Q-Q图。

图10Q-Q图操作步骤一第二步、进入图中对话框后，将对应变量放入对应框中，点击确定。

图11Q-Q图勾选情况然后Q-Q图结果就出来了（根据图中点是否均匀的分布在对角线上，来判断是否满足近似正态）。

spss_数据正态分布检验方法及意义

如何在spss中进行正态分布检验1(转)标签：一、图示法1、P-P图以样本的累计频率作为横坐标，以安装正态分布计算的相应累计概率作为纵坐标，把样本值表现为直角坐标系中的散点。

如果资料服从整体分布，则样本点应围绕第一象限的对角线分布。

2、Q-Q图以样本的分位数作为横坐标，以按照正态分布计算的相应分位点作为纵坐标，把样本表现为指教坐标系的散点。

如果资料服从正态分布，则样本点应该呈一条围绕第一象限对角线的直线。

以上两种方法以Q-Q图为佳，效率较高。

3、直方图判断方法：是否以钟形分布，同时可以选择输出正态性曲线。

4、箱式图判断方法：观测离群值和中位数。

5、茎叶图类似与直方图，但实质不同。

二、计算法1、偏度系数（Skewness）和峰度系数（Kurtosis）计算公式：g1表示偏度，g2表示峰度，通过计算g1和g2及其标准误σg1及σg2然后作U检验。

两种检验同时得出U<=，即p>的结论时，才可以认为该组资料服从正态分布。

由公式可见，部分文献中所说的“偏度和峰度都接近0……可以认为……近似服从正态分布”并不严谨。

2、非参数检验方法非参数检验方法包括Kolmogorov-Smirnov检验（D检验）和Shapiro- Wilk（W检验）。

SAS中规定：当样本含量n≤2000时，结果以Shapiro –Wilk（W检验）为准，当样本含量n >2000时，结果以Kolmogorov –Smirnov（D检验）为准。

SPSS中则这样规定：（1）如果指定的是非整数权重，则在加权样本大小位于3和50之间时，计算Shapiro-Wilk统计量。

对于无权重或整数权重，在加权样本大小位于3 和5000 之间时，计算该统计量。

由此可见，部分SPSS教材里面关于“Shapiro –Wilk适用于样本量3-50之间的数据”的说法是在是理解片面，误人子弟。

（2）单样本Kolmogorov-Smirnov 检验可用于检验变量（例如income）是否为正态分布。

spss正态分布检验方法

spss正态分布检验方法SPSS正态分布检验方法。

SPSS（Statistical Package for the Social Sciences）是一种统计分析软件，广泛应用于社会科学、生物医学等领域的数据分析。

在进行数据分析时，我们经常需要对数据的分布进行检验，其中正态分布检验是一种常见的方法。

本文将介绍如何在SPSS中进行正态分布检验，以及如何解释检验结果。

首先，在SPSS中打开需要进行正态分布检验的数据文件。

在数据文件打开后，选择“分析”菜单中的“描述统计”选项，然后再选择“探索”子菜单。

在弹出的对话框中，将需要进行正态分布检验的变量移动到右侧的“变量”框中，然后点击“统计”按钮。

在“统计”对话框中，勾选“正态性”选项。

这里还可以选择其他统计量，比如偏度和峰度，以便进行更全面的正态分布检验。

点击“确定”后，SPSS将生成正态分布检验的结果。

正态分布检验的结果包括了多个统计量，其中最常用的是K-S检验（Kolmogorov-Smirnov test）和Shapiro-Wilk检验。

K-S检验是一种非参数检验，适用于任意分布的正态性检验；而Shapiro-Wilk检验对样本量有要求，适用于小样本数据的正态性检验。

在SPSS的输出结果中，我们可以看到这两种检验的统计量和p值，以及对应的判定标准。

在解释正态分布检验的结果时，我们需要关注p值的大小。

通常情况下，如果p值大于0.05，我们就可以接受原假设，即数据符合正态分布；反之，如果p值小于0.05，我们就需要拒绝原假设，认为数据不符合正态分布。

需要注意的是，正态分布检验并不是一种绝对的判定，而是基于统计学的推断，因此在解释结果时要慎重。

除了p值，我们还可以关注统计量的数值。

在K-S检验中，统计量D越小，说明数据与正态分布的偏差越小；在Shapiro-Wilk检验中，统计量W越接近1，也说明数据与正态分布的拟合程度越高。

因此，通过统计量的数值，我们也可以初步判断数据的正态性。

SPSS统计分析1：正态分布检验

当然，在正态分布存疑的情况下，也就不能采用基于正态分布前提的参数检验方法，而应采用非参数检验。

二、图示法1、P-P图以样本的累计频率作为横坐标，以安装正态分布计算的相应累计概率作为纵坐标，把样本值表现为直角坐标系中的散点。

如果资料服从整体分布，则样本点应围绕第一象限的对角线分布。

2、Q-Q图以样本的分位数作为横坐标，以按照正态分布计算的相应分位点作为纵坐标，把样本表现为指教坐标系的散点。

如果资料服从正态分布，则样本点应该呈一条围绕第一象限对角线的直线。

以上两种方法以Q-Q图为佳，效率较高。

3、直方图判断方法：是否以钟形分布，同时可以选择输出正态性曲线。

4、箱式图判断方法：观测离群值和中位数。

5、茎叶图类似与直方图，但实质不同。

三、计算法1、峰度（Kurtosis）和偏度（Skewness）（1）概念解释峰度是描述总体中所有取值分布形态陡缓程度的统计量。

峰度的绝对值数值越大表示其分布形态的陡缓程度与正态分布的差异程度越大。

峰度的具体计算公式为：注：SD就是标准差σ。

峰度原始定义不减3，在SPSS中为分析方便减3后与0作比较。

偏度与峰度类似，它也是描述数据分布形态的统计量，其描述的是某总体取值分布的对称性。

SPSS软件正态性检验

行变量输出格式行变量数据值升序排序行变量数据值降序排序
2、结果解释
SPSS统计分析
练习2-9 某药厂观察9只小鼠口服高山红景天醇提物（RSAE）后在乏氧条件下的生存时间（分钟）如下：49.1,60.8，63.3，63.6，63.6，65.6， 65.8，68.6，69.0 求其均值、中位数和众数。
Q-Q作图对话框设置
SPSS统计分析
检验分布类型
定义所检验的分布参数根据样本数据估计总体参数
转换自然对数变换标准化值差分变换季节差分变换
2、结果解释
Normal Q-Q Plot of 血清总胆固醇
7
6
5
Deviation from Normal
4
3
2
2
3
4
5
6
7
Observed Value
选择汇总方式以某个分类变量分组汇总分别对各变量进行汇总
SPSS统计分析
单击Define按钮,打开单式箱式图定义对话框，选择作图。
观察单位标记（标记极端值、离群值）
SPSS统计分析
单击Define按钮,打开复式箱式图定义对话框，选择作图。
分类变量
观察单位标记（标记极端值、离群离）
SPSS统计分析
535453.5 2
SPSS统计分析
第三讲正态性检验
主要内容
3.1 P-P图法 3.2 Q-Q图法 3.3 直方图、箱式图与茎叶图法 3.4 计算法
SPSS统计分析
3.1 P-P图法
两种P-P图：正态P-P图和正态去势P-P图（累计概率残差图）
正态P-P图是以样本的累计频率作为横坐标, 以按照正态分布计算的相应累计概率作为纵坐标，把样本值表现为直角坐标系的散点，所描绘的图形。

spss数据正态分布检验

spss数据正态分布检验一、Z检验第一步：录入数据;1．命名“变量视图”；2．“数据视图”中输入数据；第二步：进行分析;第三步：设置变量；第四步：得到结果：二、相关系数检验在一项研究中,一个学生想检查生活意义和心理健康是否相关;同意参与这项研究的30个学生测量了生活意义和心理健康;生活意义的得分范围是10-70分更高的得分表示更强的生活意义,心理健康的得分范围是5-35分更高的得分表示更健康的心理状态;在研究中基本的兴趣问题也可以用研究问题的方式表示,例如例题：生活意义和心理健康相关吗相关系数数据的例子ParticipantMeaninginLifeWell-being ParticipantMeaninginLifeWell-being13519 26527 31419 43535 56534 63334 75435 82028 92512 105821 113018 123725 135119 145025 153029 167031 172512 185520 196131 205325 216032 223512 233528 245020 253924 266834 275628 281912 295635 306035说明：变量participant包含在数据中,但不用输入SPSS;在spss中输入数据及分析步骤1：生成变量1．打开spss;2．点击“变量视图”标签;在spss中将生成两个变量,一个是生活意义,另一个是心理健康;变量分别被命名为meaning和wellbeing;3．在“变量视图”窗口前两行分别输入变量名称meaning 和wellbeing;步骤2：输入数据1．点击“数据视图”,变量meaning 和wellbeing 出现在数据视图前两列;2．将两个变量的数据分别输入;如图;步骤3：分析数据1．从菜单栏中选择“分析>相关>双变量>……”打开“双变量”对话框,变量meaning 和wellbeing 出现在对话框的左边;2．选择变量meaning 和wellbeing,点击向右箭头按钮,把变量移到“变量”框中;3．点击“确定”;步骤4：解释结果二元相关性的输出结果显示如下：相关性 wellbei ng meaningwellbei ng Pearson 相关性1 .549 显着性双侧.002N3030 meaning Pearson 相关性.549 1显着性双侧.002同样的结果在相关生活意义和相关性显SPSS生成了一个输出表,标记为“相关性”,其中包括我们研究问题的答案,即变量meaning和wellbeing之间是否相关;注意在表格中meaning和wellbeing出现了两次,一次在行,一次在列这表明SPSS生成的表格中出现了冗余;相关系数值和原假设检验的p值位于变量meaning和wellbeing相交处;表格中显示meaning和wellbeing的相关性是,相应的p值是小于,原假设被拒绝,在meaning和wellbeing的总体中存在正相关相关系数右边的两个星号暗示了在水平上相关性是统计显着的,因为p值为小于;剩下的两个单元格显示了1的相关性,一个完美的正相关;即变量meaning和wellbeing自身与自身的相关性;三、独立样本T检验例题：临床心理学家想调查认知行为治疗和精神分析治疗对抑郁症的相对有效性;30名患有抑郁症的病人随机分配接受两个疗法;其中15人接受行为治疗,另外15人接受精神分析治疗,经过两个月的治疗后,记录下每个病人抑郁症得分;在本研究中,自变量是治疗方法认知行为治疗与精神分析治疗,因变量是抑郁症,较高的分数表示更高的抑郁水平抑郁水平的分数变化范围为10~70;在研究中基本的兴趣问题也可以用研究问题的方式表示,例如：“在接受认知行为治疗与精神分析治疗的病人中,抑郁症水平的均值是否存在差异呢”T检验用来检验两组数据的均值;所以,零假设假设两组数据的均值相等：原假设指出两组的抑郁症分数均值在总体上是相等的：H0：μ精神分析=μ认知行为对立假设指出两组的抑郁症分数均值在总体上是不等的：H1：μ精神分析≠μ认知行为数据在下表列出了30个参与者的数据;接受精神分析治疗的参与者标记为“1”,接受认知行为治疗的标记为“2”;独立样本t检验例子的数据Participan Therap Depressio Participan Therap Depressiot y n t y n1 1 57 162 472 1 61 17 2 423 1 67 18 2 594 1 63 19 2 375 l 51 20 2 356 1 55 21 2 427 1 45 22 2 388 1 62 23 2 499 1 41 24 2 6110 l 36 25 2 4311 1 55 26 2 4712 1 57 27 2 4913 1 70 28 2 3714 l 62 29 2 4115 1 58 30 2 48说明：变量participant包含在数据中,但不用输入SPSS;步骤1：生成变量1．打开SPSS;2．点击变量视图标签;在SPSS中将生成两个变最,一个是不同治疗方法的组别自变量,另一个是抑郁症分数因变量;这些变量将各自被命名为therapy治疗方法和depression抑郁症;3．在变量视图窗口前两行分别输入变量名称therapy和depression详见图表4．为变量therapy建立变量值标签,1=“精神分析治疗”,2=“认知行为治疗”;步骤2：输入数据1．点击数据视图标签;变量therapy和depression出现在数据视图窗口的前两列;2．参照图表6-1,为每个参与者输入两个变量的数据;对第一个参与者,为变量therapy和depression分别输人数值1和57;依次输入全部30个参与者的数据;对therapy,注意到前15个参与者为1精神分析治疗,后15个参步骤3：分析数据1．从菜单栏中选择分析>比较均值>独立样本T检验见图;打开独立样本T检验对话框,变量therapy和depression出现在对话框的左边;2．选择因变量depression,点击向右箭头按钮把变量移到检验变量框;3．选择自变量therapy,点击向右箭头按钮把变量移到分组变量框中;在分组变量框中,两个在括号内的问号出现在therapy的右边见图;这些问号表示原先的数字分配到两个治疗样本中也就是l、2;这些数字需要通过点击定义组来输入;4．点击定义组;5．定义组对话框被打开,在组1表示精神分析治疗样本的数字的右边输入“1”,并且在“组2”表示认知行为治疗样本的数字的右边输入“２”;6．点击继续;7．点击确定;结果显示在查看窗口中;步骤4：解释结果组统计量表输出的第一个表格显示每个治疗组的描述统计量,包括样本量、平均值、标准差和标准误差;注意到认知行为治疗样本的抑郁分数均值均值=比精神分析治疗样本均值=的低;我们稍后将会考虑这两组之间的差异对具有统计显着性而言是否足够大;独立样本检验表第二个表格“独立样本检验表”显示在“均值相等的t检验”之后的“假设方差相等”栏中的结果;方差方程的Levene检验“方差方程的Levene检验”检验两个治疗组的总体方差是否相等,这是独立样本t检验的一个假设;SPSS使用个由Levene开发的方法来检验总体相等的假设;Levene检验的原假设和对立假设是：H0：σ2精神分析=σ2认知行为两组的总体方差相等H1：σ2精神分析≠σ2认知行为两组的总体方差不相等T检验四、相依样本T检验在对某种程度上相关的两个样本的均值进行比较时,我们可以使用相依样本t检验也称为配对样本t检验,重复测量t检验,匹配样本t检验等;在相依样本t检验中．两个样本可能包含同一个人在两个不同时刻进行侧量或者两个有联系的人分别测量的结果例如,双胞胎的IQ,妻子与丈夫的沟通质量;准确定义相依样本t检验的关健在于记住两样本间要在某方面存在自然联系．下面给出一个相依样本t检验的例子;一个国家选举机构的工作人员负责通过民意调查来决定经济和国家安全哪个议题对于选民更重要;有25个选民被调查以确定两个议题的重要性等级,每个议题用1-7的等级表示1=一点也不重要,7=极其重要;自变量是投票议题经济、国家安全,因变量是重要性等级;在研究中,基本的兴趣问题也可以用研究问题的方式表示,例如,“对选民来说经济重要性等级和国家安全是否存在不同”数据步骤1：生成变量1．打开spss;2．点击变量视图标签;在spss中将生成的两个变量,分别用于经济等级和国家安全;两个变量分别命名为economy和security;3．在变量视图窗口前两行分别输入变量名称economy和security;见图;步骤2：输入数据1．点击数据视图标签;变量economy和security出现在数据视图窗口的两列;2．为每个参与者输入两个变量的数据;对第一个参与者,为变量economy和security分别输入等级5和7;依次输入全部25个参与者的数据;步骤3：分析数据1．从菜单栏中选择分析>比较均值>配对样本T检验;打开配对样本T检验对话框,变量economy和security出现在对话框的左边;2．选择因变量economy和security,点击向右箭头按钮把变量移到成对变量框中;3．点击确定;在spss中运行相依样本t检验程序,结果显示在“查看”视窗中;步骤4：解释结果成对样本统计量输出的第一个表格“成对样本统计量”显示了economy和security的描述统计量、包括样本量、平均值、标准差和标准误差;请注意,经济的平均重要性等级均值=比国家安全均值=的高;我们稍后将会考虑这两个平均等级之间的差异对是否大到足以具有统计显着性;成对样本相关系数表格“成对样本相关系数”除了提到这个相关性等于25个参与者对于经济和国家安全的等级之间的皮尔逊相关系数外,对于解释配对样本t检验不是重要的;成对样本检验表格“成对样本检验”为我们的研究问题提供了答案,就是经济和国家安全的重要性等级间是否存在差异;原假设的检验是以t的形式显示的,这里五、χ2独立性检验一双因素卡方检验双因素卡方检验法常用来检验两个因素是否互相独立;如果不是互相独立,就是互相联系;做出零假设H0,两个因素互相独立,没有联系；备择假设H1两个因素不互相独立;如果p﹥或,接受原假设,互相独立；相反,如果p﹤或,拒绝原假设,说明两事件有联系;小拒绝大接受A2×2表卡方检验例子一位研究员想调查性格类型个性内向的人、个性外向的人和休闲运动的选择逛游乐园、休息一天是否有关系;他对100名答应参与这项研究的人做了性格测试,并且基于测试的分值把他们分为性格内向的人和性格外向的人,然后要求每个参与者在逛游乐园和休息一天两者之中选择更喜欢的休闲方式;图表5-1描述了每个参与者的性格类型和选择的休闲方式：因为性格类型和休闲方式都有两个水平,得到四个单元,当前的例子为2×2卡方表;分析：零假设为2×2列联表中列一“性格类型”与列二“休闲方式”之间独立;如果p<,则拒绝零假设；如果p>,则接受零假设;步骤1：生成变量1．打开spss;2．点击变量视图标签;在SPSS中将生成三个变量,一个是不同的性格类型,一个是休闲方式,一个是频数;这三个变量分别命名为personality,activity和frequency;3．在变量视图窗口前三行分别输入变量名称personality,activity和frequency;4．为分类变量personality和activity建立变量值标签,对于personality,l=“内向”,2=“外向”;对于activity,1=“逛游乐园”,2=“休息”;步骤2：输入数据接下来,我们在spss中输入数据;χ2独立性检验有两种不同的数据输入方法：加权方法和个体观测值方法;当数据在每个单元的频数统计出来时,应采用加权方法;由于在我们的例子中,单元中的频数已经被统计出来如图表1,我们将采用加权方法来输入数据;在我们的例子中,内向性格和外向性格的人可以进择逛游乐园和休息中的一个,于是产生了四种不同情况内向／逛游乐园、内向／休息、外向／逛游乐园、外向／休息;由于我们采用加权方法来输人数据,我们需要在数据视窗窗口为这四种情况的每一种创建单独的一行;用加权方法建立的数据文件结构如图表所示;输入数据1．点击数据视图标签;变量personality,activity和frequency出现在数据视图窗口的前三列;按照图表,第一种情况对应于内向1且选择逛游乐园1的人,总共有12个人,这些值应该被输入数据视图窗口的第一行;2．在数据视图窗口的第一行对personality,activity和frequency 分别输入l,1和12,在数据视图窗口的2～4行输入剩下的三种情况在第2行输入l,2和28,在第3行输入2,1和43,在第4行输入2,2和17;图表中给出了完整的数据文件;步骤3：分析数据在执行χ2检验之前,我们首先需要对frequency进行加权;加权表明给定变量的值表示观测总次数,而不仅仅是一个分数值;例如,对frequency 进行加权时,frequency取值为12代表12个人,而不是分数为12;对frequency进行加权1．在菜单栏中选择“数据>加权个案”;2．打开加权个案对话框;选择“加权个案”并选择变量frequency,点击向右箭头按钮,把frequency移到“频率变量”框中;3．点击“确定”;这表示在每个类别中频数的取值12,28,43和17对应于每个单元的所有参与者,而不仅仅是一个分数;通过对frequency进行加权,现在我们可以在SPSS中执行χ2独立性检验;执行χ2独立性检验1．在菜单栏中选择“分析>描述统计>交叉表”;打开交叉表对话框,变量personality,activity和frequency出现在对话框的左侧;2．选择personality,点击向右箭头按钮〔,把变量移到“行”框;3．选择activity,点击向右箭头按钮,把变量移到“列”框中;4．点击;打开“交叉表：统计量”对话框,选择“卡方”;5．点击“继续”;6．点击“单元格”;打开“交叉表：单元显示”对话框,在“计数”下选择“观察值”“期望值”；在“百分比”下选择“行”;7．点击“继续”;8．点击“确定”;步骤4：解释结果案例处理摘要案例有效的缺失合计N 百分比N 百分比N 百分比personalityactivity 100 % 0 .0% 100 %personalityactivity交叉制表B r×c列联表的卡方检验当列联表不是2×2交叉表的时候,要判断总体的变量是否彼此独立,这时候自由度：df=r-1c-1;列联表形式r×c如：应用语言学实验方法一书83页的例子;分析：零假设为：列一“第一语言背景”与列二“冠词错误频数”之间独立;如果p<,则拒绝零假设,反之,则接受零假设;小拒绝,大接受经过计算,结果如下：p=接受原假设,即：在spss中的计算方法;步骤1：建立变量变量视图中同样输入“错误类型”、“语言背景”和“频数”三行;然后,分别对“错误类型”和“语言背景”标签赋值;步骤2：输入数据在数据视图中输入数据;注意按照列联表的对应情况,分别为“错误类型”和“语言背景”中输入1~4、1~2的值;并将它们在列联表中的频数值,输入第三列“频数”中;步骤3：分析数据因为“频数”一列中的数值是频率数,所以先为它加权;执行χ2独立性检验1．在菜单栏中选择“分析>描述统计>交叉表”;2．选择“语言背景”,点击向右箭头按钮〔,把变量移到“行”框;3．选择“错误类型”,点击向右箭头按钮,把变量移到“列”框中;4．点击“确定”;步骤4：解释结果交叉表线性和线性组合 1 .174有效案例中的N 100单元格.0%的期望计数少于5;最小期望计数为;二单因素χ2检验法单因素χ2检验法是将收集到的数据按频数分组,然后检验频数的分布是否与某个概率分布模式拟合;例如,在某英语测验中,已测得各分数段的频数,要检验分数的频数分布是否与正态分布、均匀分布或其他分布拟合;我们以应用语言学实验方法一书中的例子79页,说明如何用spss进行单因素χ2分析;注意：单因素卡方检验的零假设不是“独立性”假设,我们可以将它变换成类似独立性问题的假设;在本例中,三组学生的选择问题如果是“独立”的,就是它们之间互不影响,选择方面均匀分布,各占1/3;即：“专业倾向没有差别”;统计结果中,如果p<,拒绝零假设=有差别；如果p>,接受原假设=无差别;Spss中的实现：步骤1：建立变量1．打开spss;2．点击变量视图标签;3．在变量视图窗口前三行分别输入变量名称“类别”,“人数”;4．为分类变量“类别”建立变量值标签,对于“类别”,l=“文学”,2=“语言学”,3=“外语”;结果如下：步骤2：输入数据1．点击数据视图标签;变量“类别”和“人数”出现在数据视图窗口中;2．在数据视图窗口的第一行“类别”中分别输入l,2和3,在“人数”输入48,42和30;步骤3：分析数据在执行χ2检验之前,我们首先需要对“人数”进行加权;加权表明给定变量的值表示观测总次数,而不仅仅是一个分数值;取值为48代表48个人,而不是分数为48;对“人数”进行加权1．在菜单栏中选择“数据>加权个案”;2．打开加权个案对话框;选择“加权个案”并选择变量“人数”,点击向右箭头按钮,把“人数”移到“频率变量”框中;3．点击“确定”;执行χ2检验1．在菜单栏中选择“分析>非参数检验>旧对话框>卡方”;打开卡方对话框,变量“类别”和“人数”出现在对话框的左侧;2．选择“人数”,点击向右箭头按钮〔,把变量移到“检验变量列表”框;3．选择“选项”,出现“卡方检验：选项”;勾选“描述性”,然后点;4．点击“确定”;步骤4：解释结果描述性统计量N 均值标准差极小值极大值人数120卡方检验频率人数观察数期望数残差304248总数120检验统计量人数卡方 4.200adf 2 渐近显着性.122个单元.0%具有小于5的期望频率;单元最小期望频率为;。