北航飞控大作业
飞行控制系统大作业

《飞行控制系统》课程实验报告班级 0314102学号 ********* 姓名孙旭东成绩南京航空航天大学2017年4月(一)飞机纵向飞行控制系统的设计与仿真1、分析飞机纵向动力学模态,求飞机的长周期与短周期阻尼与自然频率。
在MATLAB环境下导入数据文件,输入damp(alon),得出结果:Eigenvalue Damping Freq. (rad/s)-2.29e+000 + 4.10e+000i 4.88e-001 4.69e+000-2.29e+000 - 4.10e+000i 4.88e-001 4.69e+000-3.16e-002 1.00e+000 3.16e-002-7.30e-003 + 3.35e-002i 2.13e-001 3.42e-002-7.30e-003 - 3.35e-002i 2.13e-001 3.42e-002长周期的根为 -7.30e-003 + 3.35e-002i 和 -7.30e-003 - 3.35e-002i阻尼为 2.13e-001自然频率为 3.42e-002(rad/s)短周期的根为 -2.29e+000 + 4.10e+000i 和 -2.29e+000 - 4.10e+000i阻尼为 4.88e-001自然频率为 4.69e+000(rad/s)2、对升降舵及油门单位阶跃输入下的飞机自然特性进行仿真,画出相应的状态曲线。
sys=ss(alon,blon,clon,dlon)[y,t]=step(sys,500)subplot(221)plot(t,y(:,1,1))xlabel('t(s)')ylabel('\Deltau(m/s)')subplot(222)plot(t,y(:,1,2))xlabel('t(s)')ylabel('\Deltau(m/s)')subplot(223)plot(t,y(:,2,1))xlabel('t(s)')ylabel('\Delta\alpha(deg)')subplot(224)plot(t,y(:,2,2))xlabel('t(s)')ylabel('\Delta\alpha(deg)')200400600-10-505t(s)∆q (d e g /s )200400600-4-2024t(s)∆q (d e g /s )200400600-150-100-50050t(s)∆θ(d e g )0200400600-50050100t(s)∆θ(d e g )200400600-2000200400t(s)∆u (m /s )0200400600-6-4-2t(s)∆α(d e g )200400600-2000200400t(s)∆u (m /s )0200400600-2024t(s)∆α(d e g )subplot(221) plot(t,y(:,3,1)) xlabel('t(s)')ylabel('\Deltaq(deg/s)') subplot(222) plot(t,y(:,3,2)) xlabel('t(s)')ylabel('\Deltaq(deg/s)') subplot(223) plot(t,y(:,4,1)) xlabel('t(s)')ylabel('\Delta\theta(deg)') subplot(224) plot(t,y(:,4,2)) xlabel('t(s)')ylabel('\Delta\theta(deg)')subplot(121) plot(t,y(:,5,1)) xlabel('t(s)')ylabel('\Deltah(m)') subplot(122) plot(t,y(:,5,2)) xlabel('t(s)')ylabel('\Deltah(m)')2004006004t(s)∆h (m )200400600-2.5-2-1.5-1-0.54t(s)∆h (m )以上各图为升降舵及油门单位阶跃输入下的飞机自然特性行仿真,左边一列为升降舵的阶跃输入,右边一列为油门的阶跃输入。
北航计算机控制系统大作业

计算机控制系统大作业姓名:陈启航学号: 教师:周锐 日期:2016年6月1日综合习题1已知: 44)(+=s s D , 1) 试用 Z 变换、一阶向后差分、向前差分、零极点匹配、Tustin 变换和预修正的Tustin (设关键频率=4)变换等方法将D(s)离散化,采样周期分别取为 和 ;2) 将 D(z)的零极点标在Z 平面图上 3) 计算D (j ω)和各个D(e j ωT )的幅频和相频特性并绘图,w 由0~ 20ra d ,计算40 个点,应包括=4 点,每个T 绘一张图(Z 变换方法单画)4) 计算 D(s)及T=,T= 时D(z)的单位脉冲响应,运行时间为4 秒 5) 结合所得的结果讨论分析各种离散化方法的特点 6) 写出报告,附上结果。
解:(1) Z 变换法:a.离散化: T =0.1s 时,D (z )=4zz −0.6703;T =0.4s 时,D (z )=4zz −0.2019;b.D (z )的零极点c. D (jω)和D(e jωT )幅频相频特性曲线 连续系统: T =0.1s 时 T =0.4s 时d. D(s)和D(z)单位脉冲响应D(s)单位脉冲响应:D(z)单位脉冲响应:T=0.1s时T=0.4s时(2)各种离散化方法:a.离散化后的D(z)1、一阶向后差分:T=0.1s时D(z)=0.2857z z−0.7143T=0.4s时D(z)=0.6154z z−0.38462、一阶向前差分:T=0.1s时D(z)=0.4 z−0.6T=0.4s时D(z)=1.6 z+0.63、零极点匹配T=0.1s时D(z)=0.1648(z+1) z−0.6703T=0.4s时D(z)=0.3991(z+1) z−0.20194、Tustin变换T=0.1s时D(z)=0.1667(z+1) z−0.6667T=0.4s时D(z)=0.4444(z+1)5、预修正的Tustin变换(设关键频率=4)T=0.1s时D(z)=0.1685(z+1) z−0.6629T=0.4s时D(z)=0.5073(z+1) z+0.0146b.D(z)的零极点1、一阶向后差分2、一阶向前差分3、零极点匹配4、Tustin变换5、预修正的Tustin变换(设关键频率=4)c. D(jω)和D(e jωT)幅频相频特性曲线1、一阶向后差分T=0.1s时T=0.4s时2、一阶向前差分T=0.1s时T=0.4s时3、零极点匹配T=0.1s时T=0.4s时4、Tustin变换T=0.1s时T=0.4s时5、预修正的Tustin变换(设关键频率=4)T=0.1s时T=0.4s时d. D(s)和D(z)单位脉冲响应1、一阶向后差分T=0.1s时T=0.4s时2、一阶向前差分T=0.1s时T=0.4s时3、零极点匹配T=0.1s时T=0.4s时4、Tustin变换T=0.1s时T=0.4s时5、预修正的Tustin变换(设关键频率=4)T=0.1s时T=0.4s时二、实验结果分析和总结:在本题中,当采样周期T=时所有离散方法的都会出现频率混叠现象,使得采样信号失真。
北航航空工程大型通用软件应用大作业样本

航空科学与工程学院《航空工程大型通用软件应用》大作业机翼结构设计与分析组号第3组小组成员11051090 赵雅甜11051093 廉佳11051100 王守财11051108 刘哲11051135 张雄健11051136 姜南6月目录一 CATIA部分....................................... 错误!未定义书签。
( 一) 作业要求..................................... 错误!未定义书签。
( 二) 作业报告..................................... 错误!未定义书签。
1、三维模型图................................... 错误!未定义书签。
2、工程图....................................... 错误!未定义书签。
二 FLUENT部分...................................... 错误!未定义书签。
( 一) 作业要求..................................... 错误!未定义书签。
( 二) 作业报告..................................... 错误!未定义书签。
1、计算方法和流程............................... 错误!未定义书签。
2、网格分布图................................... 错误!未定义书签。
3、气动力系数................................... 错误!未定义书签。
4、翼型表面压力曲线............................. 错误!未定义书签。
5、翼型周围压力云图............................. 错误!未定义书签。
飞控大作业(蔡云鹏)
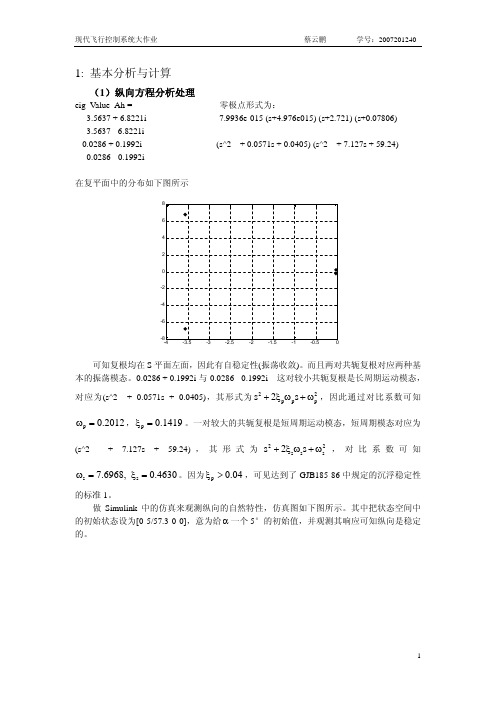
1: 基本分析与计算(1)纵向方程分析处理eig_Value_Ah = 零极点形式为: -3.5637 + 6.8221i -7.9936e-015 (s+4.976e015) (s+2.721) (s+0.07806) -3.5637 - 6.8221i ---------------------------------------------------------------------- -0.0286 + 0.1992i (s^2 + 0.0571s + 0.0405) (s^2 + 7.127s + 59.24) -0.0286 - 0.1992i在复平面中的分布如下图所示可知复根均在S 平面左面,因此有自稳定性(振荡收敛)。
而且两对共轭复根对应两种基本的振荡模态。
-0.0286 + 0.1992i 与-0.0286 - 0.1992i 这对较小共轭复根是长周期运动模态,对应为(s^2 + 0.0571s + 0.0405),其形式为22p p s 2s p +ξω+ω,因此通过对比系数可知,。
一对较大的共轭复根是短周期运动模态,短周期模态对应为p 0.2012ω=p 0.1419ξ=(s^2 + 7.127s + 59.24),其形式为2s s s s 2s 2+ξω+ω,对比系数可知。
因为s s 7.6968, 0.4630ω=ξ=p 0.04ξ>,可见达到了GJB185-86中规定的沉浮稳定性的标准1。
做Simulink 中的仿真来观测纵向的自然特性,仿真图如下图所示。
其中把状态空间中的初始状态设为[0 5/57.3 0 0],意为给α一个5°的初始值,并观测其响应可知纵向是稳定的。
上图中右图是空速V 的响应,左图是迎角α的响应。
可以看出其纵向自然特性是随着时间而自稳定的。
在讨论纵向操纵性时,给定升降舵偏角一个幅值为5=°e δ,宽度为1秒的一个脉冲,其中脉冲可用signal builder 来构造,Simulink 框图和各状态变量的响应的输出如下图所示:Vαqθ可见,,,V q αθ在升降舵受到脉冲干扰后,其均随时间而收敛,其中空速V 和仰俯角θ的变换范围较大,其稳定所需时间较长。
北航研究生飞行力学大作业

1.1.2 体轴系下的质心动力学方程
与风轴系下质心加速度类似:
2
飞行力学计算实习作业
~ E E VCB aCB WBBVCB 0 r q u u 0 p v v r 0 w w q p vr wq u ur v wp uq vp w
力 fW 分为可控力 AW 和重力 mgW ,可控力分为气动力和推力
D TxW AW C Ty 1 0 cos W 0 sin W cos W sin W 0 cos W sin W 0 0 sin W 0 1 0 0 0 cos W g
于是
~W E E CW aCW LWEWE LEW VCW V
又
~W ~W WW LWEWE LEW
则
1
飞行力学计算实习作业
~W E E VCW V aCW WW CW rW 0 0 rW pW qW V VrW VqW qW V V 0 0 pW 0 0 0
2
飞行力学计算实习作业
第 1 章 在平面地球假设条件下推导方程
1.1 质心动力学方程推导
1.1.1 风轴系下质心动力学方程。
基于大地平面假设、无风( w 0 ) ,取 FW 为动系,质心 C 为动点。由于质心 C 始 终与 FW 原点重合, 因此 r w 0 , 进而 aCW aOW 。 其中 aCW 为 C 点的绝对加速度在 FW 下 的表示。 由于绝对速度在风轴系中有
V
于是加速度为:
E CW
【VIP专享】北航飞机飞行操纵系统大作业

飞机飞行操纵系统实验报告教师:于黎明班级:130326姓名:xxx学号:130312xx一、飞机操纵系统传动机构的发展历史1、简单机械操纵系统驾驶员通过机械传动装置直接偏转舵面,舵面上的气动铰链力矩通过机械传动装置使驾驶员获得力和位移的感觉。
机械传动装置直接带动舵面,有软式和硬式两种基本型式。
软式传动装置由钢索和滑轮组成,特点是重量轻,容易绕过障碍,但是弹性变形和摩擦力较大。
硬式传动装置由传动拉杆和摇臂组成,优点是刚度大,操纵灵活。
软式和硬式可以混合使用。
2、可逆助力操纵系统在大型高速飞机上,舵面上的气动铰链力矩很大,虽然用气动补偿的方法可以减小力矩,但很难在高低速范围内达到同样效果。
40年代末出现了液压助力系统,舵面由液压助力器驱动,驾驶员通过中央操纵机构、机械传动装置控制助力器的伺服活门,间接地使舵面偏转。
它同时通过杠杆系统把舵面一部分气动载荷传给中央操纵机构,使驾驶员获得操纵力的感觉,构成所谓“机械反馈”,这就是可逆助力操纵系统。
3、不可逆助力操纵系统可逆助力操纵系统虽可解决杆力过大的问题,但在超音速飞机上还会出现杆力反向变化的问题。
由于杆力反向变化,会使驾驶员产生错觉而无法正确驾驶飞机。
为此,须把可逆助力操纵系统中的机械反馈取消,即舵面气动载荷全部由液压助力器承受。
为了使驾驶员获得操纵力感觉,在系统中增加了人工载荷机构(通常是弹簧的)以及其他改善操纵特性的装置,形成不可逆助力操纵系统。
在高空超音速飞行时,由于空气密度减小,飞机容易发生频率很高的俯仰和横侧振荡,驾驶员来不及作出反应。
为了克服振荡,在超音速飞机上普遍安装自动增稳装置,如俯仰阻尼器和方向阻尼器等。
4、电传操纵系统靠电信号传递飞行员的操纵指令,提高了响应速度性,并减轻了重量和体积。
消除了机械传动结构的非线性因素,改善了机械操纵直接固定在机体上面而引起的人机诱发振荡,改善了飞机的操纵品质,对飞机的结构变化的影响不敏感,可以降低和减少维护工作量以及更容易与自动飞行控制系统相结合。
飞控大作业

《飞行控制系统》课程实验报告班级 0314103学号 031410329 姓名嵇程成绩南京航空航天大学2017年4月《飞行控制系统》课程实验(8学时)一、目标通过本实验,学生能够掌握基本的飞行控制系统的结构,设计的方法,仿真验证方法及控制性能的分析,加深对课堂教学内容的理解。
二、环境在windows操作系统下,matlab/simulink下进行设计与仿真。
三、内容(一)飞机纵向飞行控制系统的设计与仿真(4学时)1、飞机纵向自然特性的分析与仿真,包括短周期模态,长周期模态的分析,求解阻尼与自然频率,分析开环响应特性。
2、飞机俯仰角控制系统的设计;3、飞机速度控制系统的设计;4、飞机纵向运动的仿真与分析(二)飞机侧向飞行控制系统的设计与仿真(4学时)1、飞机纵向自然特性的分析与仿真,包括滚转模态,荷兰滚及螺旋模态的分析,求解阻尼与自然频率,分析开环响应特性。
2、飞机滚转角控制系统的设计;3、飞机航向控制系统的设计;4、飞机侧向航向协调控制仿真与分析四.要求1.在matlab下进行编程,系统设计与仿真;2.撰写实验报告,要求给出设计的参数,实验结果及曲线。
3.报告封面采用模板给定格式。
4.报告需提交打印稿,沿左侧装订。
(一)飞机纵向俯仰角与速度控制系统设计 某飞机的纵向线性小扰动方程为:lon lon xA xB u =+& 其中 状态[]T x u q h αθ=∆∆∆∆∆,控制量[]T e T u δδ=∆∆ 问题:1、 分析飞机纵向动力学模态,求飞机的长周期与短周期阻尼与自然频率。
输入:[W n ,z,p]=damp(alon)%系统的自然频率、阻尼比和闭环极点输出:W n z p 2.7127 2.7127 0.0708 0.0708 0.0030 0.3890 0.3890 0.0875 0.0875 1.0000 -1.0553 + 2.4990i -1.0553 - 2.4990i -0.0062 + 0.0706i -0.0062 - 0.0706i -0.0030 + 0.0000i表1-1-1p 1p 2ζ W n 长周期 -0.0062 + 0.0706i -0.0062 - 0.0706i 0.0875 0.0708 短周期 -1.0553+2.4990i -1.0553 - 2.4990i0.3890 2.7127表1-1-22、 对升降舵及油门单位阶跃输入下的飞机自然特性进行仿真,画出相应的状态曲线。
北航航空发动机原理大作业

北航航空发动机原理大作业航空发动机是飞机最核心的部件之一,它负责提供动力以便飞机能够在空中顺利飞行。
北航航空发动机原理大作业旨在深入研究航空发动机的工作原理,包括结构、工作循环、燃烧过程以及相关技术等方面。
本文将围绕这些内容进行详细的阐述。
航空发动机的结构一般包括压缩机、燃烧室、涡轮和喷管等组成部分。
首先,压缩机负责将来自外界的空气加压,使其增加密度,为燃烧提供充足的氧气。
然后,在燃烧室中燃烧燃料与氧气的混合物,产生高温高压的燃气。
接着,燃气驱动涡轮旋转,通过轴向流动推动涡轮转子。
最后,高速的喷气流通过喷管喷出,产生向后的推力,推动飞机向前飞行。
航空发动机的工作循环一般采用布雷顿循环。
该循环由四个过程组成:进气、压缩、燃烧和排气。
在进气过程中,空气被压缩机压缩,增加了密度和温度。
接着,燃料被喷射到燃烧室中,与压缩空气混合燃烧,释放出大量的热能。
然后,燃烧产生的高温高压气体驱动涡轮旋转,将一部分动能转化为机械功,用于驱动压缩机和其他系统工作。
最后,燃烧产物通过喷口排出,形成喷气流,产生推力。
航空发动机的燃烧过程是发动机组成中较为重要的一个环节。
燃烧室是燃烧过程的主要场所,其中燃料与空气发生充分混合和燃烧。
燃烧的质量和稳定性直接关系到发动机的性能和效率。
为了实现燃烧的充分,燃烧室通常具有特殊的结构设计,如喷嘴、涡流室和火花塞等。
喷嘴的作用是将燃料细小雾化,并与空气充分混合,以促进燃烧。
涡流室则通过旋转气流的方式,使燃料和氧气更好地混合,并提高燃烧效率。
火花塞则在适当的时间点产生火花,引燃燃料,使燃烧开始。
航空发动机还涉及到多种相关技术。
例如,超音速进气技术可以通过进气道中的激波冷却进气空气并提高压力,提高发动机的性能。
燃烧室冷却技术可以通过将冷却剂喷射到燃烧室壁面,降低燃烧室温度,延长发动机寿命。
另外,航空发动机还涉及到调节和控制系统,如油门控制、温度控制和故障监测等,以确保发动机的正常运行和安全性。
北航计算机控制系统大作业

计算机控制系统大作业姓名:陈启航学号: 教师:周锐 日期:2016年6月1日综合习题1已知: 44)(+=s s D , 1) 试用 Z 变换、一阶向后差分、向前差分、零极点匹配、Tustin 变换和预修正的Tustin (设关键频率=4)变换等方法将D(s)离散化,采样周期分别取为0.1s 和 0.4s ;2) 将 D(z)的零极点标在Z 平面图上 3) 计算D (j ω)和各个D(e j ωT )的幅频和相频特性并绘图,w 由0~ 20ra d ,计算40 个点,应包括=4 点,每个T 绘一张图(Z 变换方法单画)4) 计算 D(s)及T=0.1,T=0.4 时D(z)的单位脉冲响应,运行时间为4 秒5) 结合所得的结果讨论分析各种离散化方法的特点 6) 写出报告,附上结果。
解:(1) Z 变换法:a.离散化: T =0.1s 时,D (z )=4zz −0.6703;T =0.4s 时,D (z )=4zz −0.2019;b.D (z )的零极点c. D (jω)和D(e jωT )幅频相频特性曲线 连续系统:T=0.1s时T=0.4s时d. D(s)和D(z)单位脉冲响应D(s)单位脉冲响应:D(z)单位脉冲响应:T=0.1s时T=0.4s时(2)各种离散化方法:a.离散化后的D(z)1、一阶向后差分:T=0.1s时D(z)=0.2857zT=0.4s时D(z)=0.6154z z−0.38462、一阶向前差分:T=0.1s时D(z)=0.4 z−0.6T=0.4s时D(z)=1.6 z+0.63、零极点匹配T=0.1s时D(z)=0.1648(z+1) z−0.6703T=0.4s时D(z)=0.3991(z+1)4、Tustin变换T=0.1s时D(z)=0.1667(z+1) z−0.6667T=0.4s时D(z)=0.4444(z+1) z−0.11115、预修正的Tustin变换(设关键频率=4)T=0.1s时D(z)=0.1685(z+1) z−0.6629T=0.4s时D(z)=0.5073(z+1) z+0.0146b.D(z)的零极点1、一阶向后差分2、一阶向前差分3、零极点匹配4、Tustin变换5、预修正的Tustin变换(设关键频率=4)c. D(jω)和D(e jωT)幅频相频特性曲线1、一阶向后差分T=0.1s时T=0.4s时2、一阶向前差分T=0.1s时T=0.4s时3、零极点匹配T=0.1s时T=0.4s时4、Tustin变换T=0.1s时T=0.4s时5、预修正的Tustin变换(设关键频率=4)T=0.1s时T=0.4s时d. D(s)和D(z)单位脉冲响应1、一阶向后差分T=0.1s时T=0.4s时2、一阶向前差分T=0.1s时T=0.4s时3、零极点匹配T=0.1s时T=0.4s时4、Tustin变换T=0.1s时T=0.4s时5、预修正的Tustin变换(设关键频率=4)T=0.1s时T=0.4s时二、实验结果分析和总结:在本题中,当采样周期T=0.4s时所有离散方法的都会出现频率混叠现象,使得采样信号失真。
飞行动力学与控制大作业

飞行动力学及控制大作业报告院(系)航空科学及工程学院专业名称飞行器设计学号学生姓名目录一.飞机本体动态特性计算分析 (1)1.1 飞机本体模型数据 (1)1.2 模态分析 (2)1.3 传递函数 (2)1.4 升降舵阶跃输入响应 (2)1.5 频率特性分析 (3)1.6 短周期飞行品质分析 (3)二.改善飞行品质的控制器设计 (4)2.1 SAS控制率设计 (4)2.1.1 控制器参数选择 (4)2.1.2 数值仿真验证 (7)2.2 CAS控制率设计 (8)三.基于现代控制理论的飞行控制设计方法 (9)3.1 特征结构配置问题描述 (9)3.1.1 特征结构的可配置性 (9)3.1.2 系统模型 (10)3.2 系统的特征结构配置设计 (10)3.2.1 设计过程 (10)3.2.2 具体的设计数据 (11)3.2.3 结果与分析 (12)四. 附录 (13)一. 飞机本体动态特性计算分析1.1 飞机本体模型数据本文选取F16飞机进行动态特性分析及控制器设计,飞机的纵向状态方程形式如下:.x =Ax +Bu y =Cx(1.1) 状态变量为:[]T u q αθ=x控制变量为:e δ=u 基准状态选择为120,2000V m s H m ==的定直平飞。
选取状态向量()Tu q αθ=x ,控制量为升降舵偏角,则在此基准状态下线化全量方程所得到的矩阵数据如下:-0.0312 -1.1095 -9.8066 -0.5083-0.0013 -0.6543 0 0.9185 0 0 0 1.00000 -0.3828 0 -0.6901⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦Α (1.2)[]-0.0167-0.00140-0.0956T =B (1.3)[]1.000057.295857.295857.2958diag =C (1.4) 1.2 模态分析矩阵A 的特征值算出为:对应的特征向量如下:由系统特征值可知,系统具有两对共轭复根,也即具有两种运动模态:长周期模态及短周期模态,其对应的模态频率及阻尼比如下:表一 飞机长短周期模态特征可以看出,在此飞行状态下,飞机纵向具有明显的长周期模态,但不具备明显的短周期的模态特征,模态频率过低,需要使用纵向增稳系统,改善阻尼比和自然频率。
北航计算机控制系统大作业,DOC

计算机控制系统大作业姓名:陈启航j)和各个D()个点,应包括=点,每个T时,时,b.的零极点c.和幅频相频特性曲线连续系统:时时d.和单位脉冲响应单位脉冲响应:单位脉冲响应:时时(2)各种离散化方法:a.离散化后的1、一阶向后差分:时时2、一阶向前差分:时时3、零极点匹配时时4、Tustin变换时时5、预修正的Tustin变换(设关键频率=4)时时b.的零极点1、一阶向后差分2、一阶向前差分3、零极点匹配4、Tustin变换5、预修正的Tustin变换(设关键频率=4)c.和幅频相频特性曲线1、一阶向后差分时时2、一阶向前差分时时3、零极点匹配时时4、Tustin变换时时5、预修正的Tustin变换(设关键频率=4)时时d.和单位脉冲响应1、一阶向后差分时时2、一阶向前差分时时3、零极点匹配时时4、Tustin变换时时5、预修正的Tustin变换(设关键频率=4)时时二、实验结果分析和总结:⑤Tustin变换法采样周期较小的情况下,在低频段范围内,s域与z域的频率近似保持线性,所以在此范围内Tustin变换频率失真较小。
但随着频率的升高,Tu stin变换频率范围变得很窄,高频失真严重。
所以主要应用于低频环节离散化。
⑥修正Tustin变换法由于此方法只能保证在指定频率点附近时的频率特性与原系统相近,但在其他频率点附近无法保证不失真,故其多用在要求在某些特征频率处离散前后频率特性保持不变的场合。
综合习题2计算机伺服控制系统设计1.已知:1)被控对象为一个带有均质圆盘负载的直流力矩电机,其伺服系统方框图如下:2)D/A输出5v,电机转速其中,电机传递函数为角速率;模拟控制其由KG1,KG2,KG3组成,数字控·电机传函·电机启动电压·测速机传递系数·电位计最大转角为,输出·功放·采样周期.设计要求:,电机启动:,电机转速)设计状态反馈增益,使系统闭环极点,)设)求离散控制率)将进行实现,配置适当的比例因子。
北航智能控制模糊控制作业

智能控制及应用大作业一——双输入—单输出系统的模糊控制姓名:学号:2011-10-14题目要求以双输入—单输出系统为例,画出模糊控制算法程序流程图,计算出模糊控制器的查询表。
假设控制器输入为误差e和误差变化率ec,输出为控制量u,其基本论域分别为[e min,e max],[ec min,ec max],[u min,u max],对应的语言变量E、EC和U的论域为{-6,-5,…,-1,0,1,…,5,6},E、EC和U都选7个语言值{NB,NM,NS,Z,PS,PM,PB},各语言值的隶属函数采用三角函数,其分布可用表1表示,控制规则如表2所示。
注意:u的去模糊化要采用与你的学号ID的奇偶性对应的方法,设ID=奇数者用最大隶属度法,ID=偶数者用重心法;要有计算查询表时的必要计算步骤,不能只给出最后结果。
表2模糊控制规则表程序设计与程序流程图1、模糊算法的选择模糊蕴含用求交法,输出量的清晰化计算用最大隶属度法。
于是有输出量的模糊集合'U 为:491'491''491''491''491''''')]([)]([])[()()()(=======→→=→⨯⨯=⨯=⨯=i ii iEC iE i i i i i i i i i i iCU U U EC EC U E EU EC E EC E R EC E R EC E U2、程序结构说明利用Matlab 编写该模糊算法,并且计算出模糊控制器的查询表。
程序按照上面的控制算法,先计算模糊关系隶属度矩阵R 。
通过上面的式子,根据每一条控制规则,查找相对应的赋值表当中的向量值。
如第一条法则:If E=NB and EC=NB, then U=NB.则找到E 中NB 对应的行向量和EC 中NB 对应的行向量,然后将第一个行向量转置后与第二个行向量按照乘法法则对应取小值,生成新的矩阵。
北航计算机控制系统大作业精编版

北航计算机控制系统大作业公司内部编号:(GOOD-TMMT-MMUT-UUPTY-UUYY-DTTI-计算机控制系统大作业姓名:陈启航学号:教师:周锐日期:2016年6月1日综合习题1已知: 44)(+=s s D , 1) 试用 Z 变换、一阶向后差分、向前差分、零极点匹配、Tustin 变换和预修正的Tustin (设关键频率=4)变换等方法将D(s)离散化,采样周期分别取为0.1s 和 0.4s ;2) 将 D(z)的零极点标在Z 平面图上3) 计算D (j ω)和各个D(e j ωT )的幅频和相频特性并绘图,w 由0~ 20rad ,计算40 个点,应包括=4 点,每个T 绘一张图(Z 变换方法单画)4) 计算 D(s)及T=0.1,T=0.4 时D(z)的单位脉冲响应,运行时间为4 秒5) 结合所得的结果讨论分析各种离散化方法的特点6) 写出报告,附上结果。
解:(1)Z变换法:a.离散化:T=0.1s时,j(j)=4jj−0.6703;T=0.4s时,j(j)=4jj−0.2019;b.j(j)的零极点c.j(jj)和j(j jjj)幅频相频特性曲线连续系统:T=0.1s时T=0.4s时d.j(j)和j(j)单位脉冲响应j(j)单位脉冲响应:j(j)单位脉冲响应:T=0.1s时T=0.4s时(2)各种离散化方法:a.离散化后的j(j)1、一阶向后差分:T=0.1s时j(j)=0.2857j j−0.7143T=0.4s时j(j)=0.6154j j−0.38462、一阶向前差分:T=0.1s时D(z)=0.4j−0.6T=0.4s时D(z)=1.6j+0.63、零极点匹配T=0.1s时D(z)=0.1648(j+1) j−0.6703T=0.4s时D(z)=0.3991(j+1) j−0.20194、Tustin变换T=0.1s时D(z)=0.1667(j+1) j−0.6667T=0.4s时D(z)=0.4444(j+1) j−0.11115、预修正的Tustin变换(设关键频率=4)T=0.1s时D(z)=0.1685(j+1) j−0.6629T=0.4s时D(z)=0.5073(j+1) j+0.0146b.D(z)的零极点1、一阶向后差分2、一阶向前差分3、零极点匹配4、Tustin变换5、预修正的Tustin变换(设关键频率=4)c.j(jj)和j(j jjj)幅频相频特性曲线1、一阶向后差分T=0.1s时T=0.4s时2、一阶向前差分T=0.1s时T=0.4s时3、零极点匹配T=0.1s时T=0.4s时4、Tustin变换T=0.1s时T=0.4s时5、预修正的Tustin变换(设关键频率=4)T=0.1s时T=0.4s时d.j(j)和j(j)单位脉冲响应1、一阶向后差分T=0.1s时T=0.4s时2、一阶向前差分T=0.1s时T=0.4s时3、零极点匹配T=0.1s时T=0.4s时4、Tustin变换T=0.1s时T=0.4s时5、预修正的Tustin变换(设关键频率=4)T=0.1s时T=0.4s时二、实验结果分析和总结:在本题中,当采样周期T=0.4s时所有离散方法的都会出现频率混叠现象,使得采样信号失真。
北航现代控制理论结课大作业

1. 控制系统任务的物理描述为了满足飞机品质的要求,飞机的纵向运动和横侧向运动都需要有能够连续工作的阻尼器,以用来调整飞机的飞行姿态,防止其出现不必要的俯仰和倾斜。
维持飞机纵向运动的阻尼器称为俯仰阻尼器,维持飞机横侧向运动的阻尼器称为偏航阻尼器。
本次课程大作业旨在通过运用Matlab 的经典控制系统设计工具对某型飞机偏航阻尼器进展控制系统的设计。
2. 控制系统对象的数学模型巡航状态下,某型飞机侧向运动的状态空间模型为:111121314111222122232421221313233343132234142434441424()1()()()()2()()()3()()4t x t a a a a b b t x t a a a a b b u t a a a a b b u t x t t a a a a b b x t t x x x x ••••⎡⎤⎢⎥⎢⎥⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦ 1111213141221222324234()()()()()()x t c c c c y t x t c c c c y t x t x t ⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦式中: 1()x t :侧滑角〔单位为rad 〕2()x t :偏航角速度〔单位为/rad s 〕3()x t :滚转角速度〔单位为/rad s 〕4()x t :倾斜角〔单位为rad 〕输入向量及输出向量分别为:1()u t :方向舵偏角〔单位为rad 〕2()u t :副翼偏角〔单位为rad 〕1()y t :偏航角速度〔单位为/rad s 〕2()y t :倾斜角〔单位为rad 〕设飞机巡航飞行时的速度为0.8马赫,高度为40000英尺,此时模型的参数为:0.055800.99680.08020.04150.598000.11500.031803.050000.38800.4650000.0805 1.00000A --⎡⎤⎢⎥--⎢⎥=⎢⎥--⎢⎥⎣⎦ 0.007290.00000.475000.007750.15300.1430000B ⎡⎤⎢⎥-⎢⎥=⎢⎥⎢⎥⎣⎦0 1.000000 1.0C ⎡⎤=⎢⎥⎣⎦0000D ⎡⎤=⎢⎥⎣⎦首先输入飞机状态空间模型参数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
*****
飞控
1. 攻角 2°干扰 解题思路概括:根据已知量求出传递函数,在 simulink 里搭建模型并仿真。再将得到的 结果导入工作空间,在 matlab 里画出仿真曲线。 传递函数:
V ( s) 0.0057 s 2 0.0049875s 0.3110271 0 ( s) ( s 2 1.464472s 8.945125)( s 2 0.0121326s 0.001546684) ( s) s 3 0.891605s 2 0.0145294s 0.032175324 2 0 ( s) ( s 1.464472s 8.945125)( s 2 0.0121326s 0.001546684)
搭建 simulink 仿真结构图:
12031180
*****
飞控
短周期 10 秒
12031180
*****
飞控
长周期 200s 仿真曲线
12031180
*****
飞控
仿真曲线生成代码: subplot(311) plot(t2,V2,'m'); grid; xlabel('t/s'); ylabel('V/m/s') title('V 受舵偏 1°的变化曲线--10 秒'); subplot(312) plot(t2,alpha2,'b'); grid; xlabel('t/s'); ylabel('alpha/rad') title('alpha 受舵偏 1°的变化曲线--10 秒'); subplot(313) plot(t2,sita2,'r'); grid; xlabel('t/s'); ylabel('sita/rad') title('sita 受舵偏 1°的变化曲线--10 秒');
%%%%%%% subplot(411) plot(t2,gama2,'m');
12031180
*****
飞控
grid; xlabel('t/s'); ylabel('伽马/rad') title('伽马受舵偏 1°的变化曲线--10 秒'); subplot(412) plot(t2,q2,'b'); grid; xlabel('t/s'); ylabel('q/rad/s') title('俯仰角速度 q 受舵偏 1°的变化曲线--10 秒'); subplot(413) plot(t2,H2,'r'); grid; xlabel('t/s'); ylabel('H/m') title('高度 H 受舵偏 1°的变化曲线--10 秒'); subplot(414) plot(t2,delta2,'g'); grid; xlabel('t/s'); ylabel('delta/rad') title('舵偏变化曲线--10 秒');
( s) 8.42892s 0.134992 2 0 ( s) ( s 1.464472s 8.945125)( s 2 0.0121326s 0.001546684)
用 simulink 搭建模型,如下图:
12031180
*****
飞控
10s 短周期仿真曲线:
V ( s ) e ( s ) [( ( s ) e ( s ) ( s ) e ( s )
s s 1)( 1) 1.44 7251.4 s 2 0.0714 s 2 0.493 ) 2( ) s 1][( ) 2( ) s 1] 0.063 0.063 4.27 4.27 s s 2 0.0713 1.68( 1)[( ) 2( ) s 1] 248.5 0.068 0.068 s 2 0.0714 s 2 0.493 [( ) 2( ) s 1][( ) 2( ) s 1] 0.063 0.063 4.27 4.27 s s 4.85( 1)( 1) 0.0098 1.371 s 2 0.0714 s 2 0.493 [( ) 2( ) s 1][( ) 2( ) s 1] 0.063 0.063 4.27 4.27 24.142(
( s) ( s) ( s) e ( s) e ( s) e ( s) q( s) ( s) s e ( s) e ( s)
1 1 H ( s ) tan V ( s ) V0 ( s ) V ( s ) V0 s s
200s 仿真曲线:
仿真曲线生成代码: %攻角 2°干扰 200 仿真 subplot(311)控
plot(t,V,'m'); grid; xlabel('t/s'); ylabel('V/m/s') title('V 受攻角 2°干扰的变化曲线'); subplot(312) plot(t,alpha,'g'); grid; xlabel('t/s'); ylabel('alpha/°') title('alpha 受攻角 2°干扰的变化曲线'); subplot(313) plot(t,sita,'r'); grid; xlabel('t/s'); ylabel('sita/°') title('sita 受攻角 2°干扰的变化曲线'); 2. 1°舵偏 解题思路概括:根据已知量求出传递函数,在 simulink 里搭建模型并仿真。再将得到的 结果导入工作空间,在 matlab 里画出仿真曲线。 传递函数:
