初中-数学-人教版-第四章实数本章测试(一)

合集下载

【期末复习提升卷】浙教版2022-2023学年七上数学第4章代数式测试卷1(解析版)

【期末复习提升卷】浙教版2022-2023学年七上数学第4章代数式测试卷1（解析版）一、选择题（本大题有10小题，每小题3分，共30分）下面每小题给出的四个选项中，只有一个是正确的. 1．a −2a = （） A ．3a B ．a C ．−a D ．-2 【答案】C【解析】 a −2a =−a . 故答案为：C.2．已知等式 13ax =4a ，则下列等式中不一定成立的是（）A ．13ax −4a =0B ．13ax −b =4a −bC ．ax =12aD ．13x =4【答案】D【解析】A 、如果 13ax =4a 移项得 13ax −4a =0 ，原变形成立，故此选项不符合题意；B 、如果 13ax =4a ，那么两边同时减b 得 13ax −b =4a −b ，原变形成立，故此选项不符合题意； C 、如果 13ax =4a ，那么两边同时乘以3得 ax =12a ，原变形成立，故此选项不符合题意；D 、如果 13ax =4a ，当a≠0时，两边同时除以a 得 13x =4 ，这里必须a≠0，原变形不一定成立，故此选项符合题意. 故答案为：D.3．代数式 x 2 ， s t ， 1x+y ，20%•x ， √ab ， √2 ab ， 2a+b 3中，多项式有（）个A ．0B ．1C ．2D ．3 【答案】B【解析】多项式有：2a+b 3，共1个，故答案为：B.4．若﹣3a 2b x 与﹣3a y b 是同类项，则y x 的值是（） A ．1 B ．2 C ．3 D ．4 【答案】B【解析】∵﹣3a 2b x 与﹣3a y b 是同类项， ∴x=1，y=2， ∴y x =21=2. 故答案为：B.5．根据语句“x 的5倍与y 的和”，列出的代数式为（） A ．x +5+y B ．x +5y C ．5(x +y) D ．5x +y 【答案】D【解析】x 的5倍与y 的和，列代数式为：5x +y ，故答案为：D.6．若 m <0 ， n >0 ， m +n <0 ，则 m ， n ， −m ， −n 这四个数的大小关系是（） A ．−m >n >−n >m B ．m >n >−n >−m C ．m >−n >n >−m D ．−m >n >m >−n 【答案】A【解析】∵m ＜0，n ＞0， ∴n ＞m m+n ＜0， ∴-m ＞n ， ∴-m ＞n ＞-n ， ∴-m ＞n ＞-n ＞m. 故答案为：A.7．对于任意实数a 和b ，如果满足 a 3+b 4=a+b 3+4+23×4那么我们称这一对数a ，b 为“友好数对”，记为（a ，b ）.若（x ，y ）是“友好数对”，则2x ﹣3[6x+（3y ﹣4）]＝（） A ．﹣4 B ．﹣3 C ．﹣2 D ．﹣1 【答案】C【解析】∵（x ，y ）是“友好数对”， ∴x 3+y 4=x+y 3+4+23×4， ∴x 3+y 4=x+y 7+16，整理得： 16x +9y =14 ， ∴2x −3[6x +(3y −4)] = −16x −9y +12 = −(16x +9y)+12 = −14+12 =-2故答案为：C. 8．一个关于a ，b 的多项式，除常数项为1外，其余各项次数都是4，系数为﹣1，并且各项都不相同，这个多项式最多有（）项？ A ．3 B ．5 C ．6 D ．7 【答案】C【解析】∵一个关于a ，b 的多项式，除常数项为1外，其余各项次数都是4，系数为﹣1，并且各项都不相同，∴这个多项式可能为：-a 4-b 4-ab 3-a 2b 2-a 3b+1， ∴这个多项式最多有6项. 故答案为：C.9．如图①，在五环图案内，分别填写数字a ，b ，c ，d ，e ，其中a ，b ，c 表示三个连续偶数（a ＜b ＜c ），d ，e 表示两个连续奇数（d ＜e ），且满足a+b+c ＝d+e 如图②2+4+6＝5+7.若b ＝﹣12，则d 2−e 2的结果为（）A ．﹣72B ．72C ．﹣56D ．56 【答案】B【解析】∵a ，b ，c 表示三个连续偶数，b=-12， ∴a=-14，c=-10， ∴a+b+c=-36，∵d ，e 表示两个连续奇数， ∴d=-19，e=-17， ∴d 2-e 2=361-289=72，所以则d 2-e 2的结果为72. 故答案为：B.10．如图，在一个长方形中放入三个正方形，从大到小正方形的边长分别为 a 、 b 、 c ，则右上角阴影部分的周长与左下角阴影部分周长差为（）A ．a+bB ．b +cC ．2aD ．2b【答案】D【解析】设重叠部分的小长方形的长与宽分别为 x,y ，如图，在图上依次表示阴影部分的各边的长，所以右上角阴影部分的周长与左下角阴影部分周长差为：2(a+b−x−c)+2(b+c−y)−2(b−x)−2(a−y)=2a+2b−2x−2c+2b+2c−2y−2b+2x−2a+2y=2b.故答案为：D.二、填空题（本大题有6小题，每小题4分，共24分）要注意认真看清题目的条件和要填写的内容，尽量完整地填写答案.11．单项式−3x2y的次数是.【答案】3【解析】单项式−3x2y的次数是：2+1=3，故填：3.12．写出一个含有字母x、y的三次单项式，这个单项式可以是.【答案】x2y（答案不唯一）【解析】∵这个单项式中要含有字母x、y，且次数是3，∴这个单项式可以是x2y（答案不唯一）.故答案为：x2y（答案不唯一）.13．已知铅笔每支m元，橡皮每块n元，若买两支铅笔和三块橡皮，则一共需付款元．【答案】(2m+3n)【解析】一共需付款(2m+3n)元，故答案为：(2m+3n)．14．如图，是某广场用地板铺设的部分图案，中央是一块正六边形的地板砖，周围是正三角形和正方形的地板砖.从里向外的第 1 层包括 6 个正方形和 6 个正三角形，第2 层包括6 个正方形和18 个正三角形，依此递推，第50 层中含有正三角形个数为个.【答案】594【解析】根据题意分析可得：从里向外的第1层包括6个正三角形.第2层包括18个正三角形.此后，每层都比前一层多12个.依此递推，第50层中含有正三角形个数是6+12×49=594个.故答案为：594.15．如图，将边长为10的正方形的四个角向内翻折，使得翻折的四个三角形无缝连接，若中间没有重叠的空白部分是边长为4的正方形，则折痕AB的长是．【答案】√58【解析】如图，取线段a 、b ，{a +b =10a −b =4， ∴{a =7b =3， ∴AB=√a 2+b 2=√72+32=√58.（解法二：最大的正方形面积100，最小的正方形面积16，所以8个三角形的面积和为84，则4个黑色三角形面积和为42，以AB 为边的正方形面积,16+42=58，得出AB=√58）故答案为： √58 . 16．有4个不同的整数m 、n 、p 、q 满足（5﹣m ）（5﹣n ）（5﹣p ）（5﹣q ）＝9，那么m+n+p+q ＝ . 【答案】20【解析】因为（5﹣m ）（5﹣n ）（5﹣p ）（5﹣q ）＝9，每一个因数都是整数且都不相同，那么只可能是﹣1，1，﹣3，3，由此得出m 、n 、p 、q 分别为6、4、8、2，所以，m+n+p+q ＝20. 故答案为：20.三、解答题（本题有8小题，第17～19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分）解答应写出文字说明，证明过程或推演步骤. 17．求值：（1）已知 5x −2y =3 ，求 15x −6y −8 的值.（2）已知 a −b =5，−ab =3 ，求 (7a +4b +ab)−6(56b +a −ab) 的值.【答案】（1）解： 15x −6y −8=3(5x −2y)−8 ，当 5x −2y =3 时，原式 =3×3−8=1 ，（2）解：原式 =7a +4b +ab −5b −6a +6ab ， =a −b +7ab ，∵−ab =3，∴ab =−3，当 a −b =5 ， ab =−3 时，原式 =5−21=−16 .18．已知A =2a 2+3ab −2a −1，B =−a 2+12ab +23．（1）化简A +2B ．（2）当a =−1，b =−2时，求（1）中式子的值．（3）若（1）中式子的值与a 的取值无关，求b 的值．【答案】（1）解：∵A =2a 2+3ab −2a −1，B =−a 2+12ab +23，∴A+2B=2a 2+3ab −2a −1+2(−a 2+12ab +23)=2a 2+3ab −2a −1−2a 2+ab +43=4ab −2a +13；（2）解：∵a =−1，b =−2，∴4ab −2a +13=4×(−1)×(−2)−2×(−1)+13=1013；（3）解：∵4ab −2a +13=(4b −2)a +13，4ab −2a +13的值与a 的取值无关， ∴4b -2=0， ∴b=12．19．定义：若a +b =2，则称a 与b 是关于1的平衡数．（1）3与是关于1的平衡数，5−x 与是关于1的平衡数（用含x 的代数式表示）（2）若a =2x 2−3(x 2+x)+4，且a 与b 是关于1的平衡数，请求出b ．（用含x 的代数式表示）【答案】（1）-1；x -3（2）解：∵a =2x 2−3(x 2+x)+4=2x 2−3x 2−3x +4=−x 2−3x +4 a 与b 是关于1的平衡数， ∴−x 2−3x +4+b =2，∴b =2−(−x 2−3x +4)=2+x 2+3x −4=x 2+3x −2．【解析】（1）∵2-3=-1，∴3与-1是关于1的平衡数， ∵2-（5-x ）=x -3，∴5-x 与x -3是关于1的平衡数，故答案为：-1，x -3； 20．小丽暑假期间参加社会实践活动，从某批发市场以批发价每个m 元的价格购进80个手机充电宝，然后每个加价n 元到市场出售．（1）求售出80个手机充电宝的总售价为多少元？（结果用含m ，n 的式子表示）（2）由于开学临近，小丽在成功售出50个充电宝后，决定将剩余充电宝按售价8折出售，并很快全部售完．相比不采取降价销售，实际销售少盈利多少元？（结果用含m 、n 的式子表示）【答案】（1）解：∵从某批发市场以批发价每个m 元的价格购进80个手机充电宝，然后每个加价n 元到市场出售．∴每一个的售价为（m+n ）元，∴售出80个手机充电宝的总售价为80（m+n ）=（80n+80m ）元. （2）解：原售价=80(m+n)，实际售价=50(m+n)+30(m+n)×0.8 =74(m+n)，∴少盈利=80(m+n)-74(m+n) =(6m+6n)元.21．先阅读材料，再解决问题． ⑴ √13=√12=1 ⑴ √13+23=√32=3⑴ √13+23+33=√62=6⑴ √13+23+33+43=√102=10 …根据上面的规律，解决问题：（1）√13+23+33+43+53+63 = = （2）√13+23+33+⋯+n 3 （用含n 的代数式表示）．【答案】（1）√212；21 （2）解： √13+23+33+⋯+n 3 =1+2+3+…+n= n(n+1)222．已知多项式x 3－3xy 2－4的常数项是a ，次数是b（1）则a ＝，b ＝，并将这两数在数轴上所对应的点A 、B 表示出来（2）数轴上在B 点右边有一点C 到A 、B 两点的距离和为11，求点C 在数轴上所对应的数（3）若A 点、B 点同时沿数轴向正方向运动，A 点的速度是B 点速度的2倍，且3秒后，2OA ＝OB ，求点B 的速度.【答案】（1）-4；3；（2）解：设点C 在数轴上所对应的数为x ， ∵C 在B 点右边， ∴x ＞3．根据题意得x -3+x -（-4）=11，解得x=5，即点C 在数轴上所对应的数为5（3）解：设B 速度为v ，则A 的速度为2v ， 3秒后点，A 点在数轴上表示的数为（-4+6v ），B 点在数轴上表示的数为3+3v ，当A 还在原点O 的左边时，由2OA=OB 可得-2（-4+6v ）=3+3v ，解得v= 13；当A 在原点O 的右边时，由2OA=OB 可得2（-4+6v ）=3+3v ，v= 119．即点B 的速度为 13 或 119【解析】（1）∵多项式x 3-3xy 2-4的常数项是a ，次数是b ， ∴a=-4，b=3，点A 、B 在数轴上如图所示：（023．阅读材料：材料1：如果一个四位数为 abcd̅̅̅̅̅̅̅ （表示千位数字为 a ，百位数字为 b ，十位数字为 c ，个位数字为 d 的四位数，其中 a 为1~9的自然数， b 、 c 、 d 为0~9的自然数），我们可以将其表示为： abcd̅̅̅̅̅̅̅=1000a +100b +10c +d ；材料2：把一个自然数（个位不为0）各位数字从个位到最高位倒序排列，得到一个新的数，我们称该数为原数的兄弟数，如数“123”的兄弟数为“321”.（1）四位数 x5y3̅̅̅̅̅̅̅= ；（用含 x ， y 的代数式表示）（2）设有一个两位数 xy̅̅̅̅ ，它的兄弟数与原数的差是45，请求出所有可能的数 xy ̅̅̅̅ ；（3）设有一个四位数 abcd̅̅̅̅̅̅̅ 存在兄弟数，且 a +d =b +c ，记该四位数与它的兄弟数的和为 S ，问 S 能否被1111整除？试说明理由. 【答案】（1）1000x+10y+503（2）解：由题意得， xy̅̅̅̅ 的兄弟数为 yx ̅̅̅̅ ， ∵两位数 xy̅̅̅̅ 的兄弟数与原数的差为45， ∴yx ̅̅̅̅ - xy ̅̅̅̅ =45， ∴10y+x -（10x -y ）=45， ∴y -x=5，∵x ，y 均为1～9的自然数， ∴xy̅̅̅̅ 可能的数为16或27或38或49. （3）解：S 能被1111整除，理由如下： ∵abcd̅̅̅̅̅̅̅ =1000a+100b+10c+d ， ∴它的兄弟数为 dcba̅̅̅̅̅̅̅ =1000d+100c+10b+a ， ∵a+d=b+c ，∴S= abcd ̅̅̅̅̅̅̅ + dcba̅̅̅̅̅̅̅ =1000a+100b+10c+d+1000d+100c+10b+a =1001a+110b+110c+1001a =10001a+110（b+c ）+1001d=10001a+110（a+d）+1001d=1111a+1111d=1111（a+d），∵a，d为1～9的自然数，∴1111（a+d）能被1111整除，即S能被1111整除.̅̅̅̅̅̅̅=1000x+5×100+10y+3=1000x+10y+503.【解析】（1）解：x5y3故答案为：1000x+10y+503；24．对于有理数a，b，n，d，若|a﹣n|+|b﹣n|＝d，则称a和b关于n的“相对关系值”为d，例如，|2﹣1|+|3﹣1|＝3，则2和3关于1的“相对关系值”为3.（1）﹣4和6关于2的“相对关系值”为；（2）若a和3关于1的“相对关系值”为7，求a的值；（3）若a0和a1关于1的“相对关系值”为1，a1和a2关于2的“相对关系值”为1，a2和a3关于3的“相对关系值”为1，…，a30和a31关于31的“相对关系值”为1.①a0+a1的最大值为▲ ；②直接写出所有a1+a2+a3+…+a30的值.（用含a0的式子表示）【答案】（1）10（2）解：∵a和3关于1的“相对关系值”为7，∴|a﹣1|+|3﹣1|＝7.∴|a﹣1|＝5.解得a＝﹣4或6，答：a的值为﹣4或6；（3）解：①3；②30a0+465或525﹣30a0【解析】（1）由“相对关系值”的意义可得，﹣4和6关于2的“相对关系值”为|﹣4﹣2|+|6﹣2|＝6+4＝10，故答案为：10；（3）①根据题意得，|a0﹣1|+|a1﹣1|＝1，分为四种情况：当a0≥1，a1≥1时，有a0﹣1+a1﹣1＝1，则a0+a1＝3；当a0≥1，a1＜1时，有a0﹣1+1﹣a1＝1，则a0﹣a1＝1，得a0+a1＝1+2a1＜3；当a0＜1，a1≥1时，有1﹣a0+a1﹣1＝1，则a1﹣a0＝1，得a0+a1＝1+2a0＜3；当a0＜1，a1＜1时，有1﹣a0+1﹣a1＝1，则a0+a1＝1＜3；由上可知，a0+a1的最大值为3；故答案为3；②分为3种情况，当a0＝0，时a1＝1，a2＝2，•••，a30＝30，∴a1+a2+a3+…+a30＝1+2+•••+30＝465；当a0＝1时，a1＝0，则，|a1﹣2|+|a2﹣2|≠1，此种情形，不存在.当0＜a0＜1时，|a0﹣1|+|a1﹣1|＝1，|a1﹣2|+|a2﹣2|＝1，|a2﹣3|+|a3﹣3|＝1，…，|a29﹣30|+|a30﹣30|＝1，∴1＜a1＜2，2＜a2＜3，…，29＜a29＜30，∴1﹣a0+a1﹣1＝1，即a1﹣a0＝1；2﹣a1+a2﹣2＝1，即a2﹣a1＝1；同理可得：a3﹣a2＝1，…，a30﹣a29＝1，∴a1＝1+a0，a2＝1+a1＝2+a0，a3＝1+a2＝3+a0，…，a30＝1+a29＝30+a0，∴a1+a2+a3+…a30＝1+a0+2+a0+3+a0+…+30+a0＝30a0+（1+2+3+ (30)＝30a0+（1+30）× 302＝30a0+465；当1＜a0≤2，1≤a1＜2时，a0+a1＝3，a2﹣a1＝1，a3﹣a2＝1，…，a31﹣a30＝1，∴a1＝3﹣a0，a2＝4﹣a0，a3＝5﹣a0，…，a30＝32﹣a0，∴a1+a2+a3+…+a30＝3﹣a0+4﹣a0+5﹣a0+…+32﹣a0＝（3+4+5+…+32）﹣30a0＝（3+32）× 302﹣30a0＝525﹣30a0，综上所述：a1+a2+a3+…+a30的值为30a0+465或525﹣30a0.。

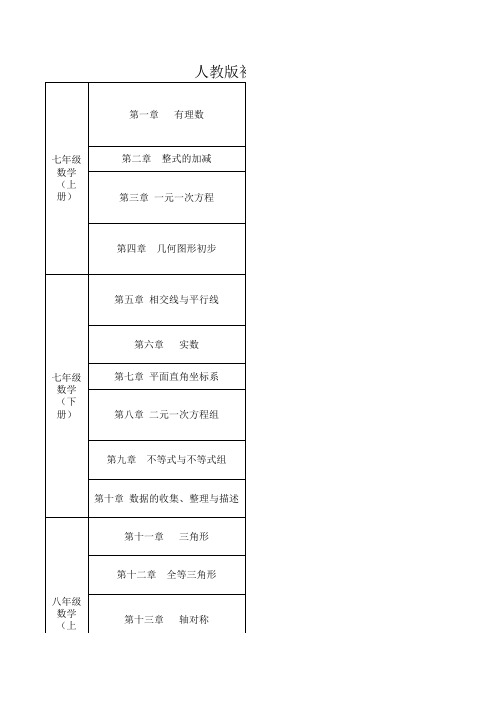
人教版初中数学全目录

初中数学目录七年级上册第一章有理数1.1 正数和负数1.2 有理数1.3 有理数的加减法实验与探究填幻方阅读与思考中国人最先使用负数1.4 有理数的乘除法观察与猜想翻牌游戏中的数学道理1.5 有理数的乘方第二章整式的加减法2.1 整式阅读与思考数字1与字母X的对话2.2 整式的加减信息技术应用电子表格与数据计算第三章一元一次方程3.1 从算式到方程阅读与思考“方程”史话3.2 解一元一次方程（一） ----合并同类项与移项实验与探究无限循环小数3.3 解一元一次方程（二） ----去括号与去分母3.4 实际问题与一元一次方程第四章几何图形初步4.1 几何图形阅读与思考几何学起源4.2 直线、射线、线段阅读与思考长度的测量4.3 角4.4 课题学习设计制作长方体形状的包装纸盒七年级下册第五章相交线与平行线5.1 相交线观察与猜想看图时的错觉5.2 平行线及其判定5.3 平行线的性质信息技术应用探索两条直线的位置关系5.4 平移第六章实数6.1 平方根6.2 立方根6.3 实数阅读与思考为什么根号2不是有理数第七章平面直角坐标系7.1 平面直角坐标系阅读与思考用经纬度表示地理位置7.2 坐标方法的简单应用第八章二元一次方程组8.1 二元一次方程组8.2 消元----解二元一次方程组8.3 实际问题与二元一次方程组8.4 三元一次方程组的解法阅读与思考一次方程组的古今表示与解法第九章不等式与不等式组9.1 不等式阅读与思考用求差法比较大小9.2 一元一次不等式9.3 一元一次不等式组第十章数据的收集、整理与描述10.1 统计调查实验与探究瓶子中有多少粒豆子10.2 直方图信息技术应用利用计算机画统计图10.3 课题学习从数据谈节水八年级上册第十一章三角形11.1 与三角形有关的线段11.2 与三角形有关的角11.3 多边形及其内角和第十二章全等三角形12.1 全等三角形12.2 三角形全等的判定12.3 角的平分线的性质第十三章轴对称13.1 轴对称13.2 画轴对称图形13.3 等腰三角形13.4 课题学习最短路径问题第十四章整式的乘法与因式分解14.1 整式的乘法14.2 乘法分式14.3 因式分解第十五章分式15.1 分式15.2 分式的运算15.3 分式方程八年级下册第十六章二次根式16.1 二次根式16.2 二次根式的乘除16.3 二次根式的加减第十七章勾股定理17.1 勾股定理17.2 勾股定理的逆定理第十八章平行四边形18.1 平行四边形18.2 特殊的平行四边形第十九章一次函数19.1 函数19.2 一次函数19.3 课题学习选择方案第二十章数据的分析20.1 数据的集中趋势20.2 数据的波动程度20.3 课题学习体质健康测试中的数据分析九年级上册第二十一章一元二次方程21.1 一元二次方程21.2 解一元二次方程21.3 实际问题与一元二次方程第二十二章二次函数22.1 二次函数的图像和性质22.2 二次函数与一元二次方程22.3 实际问题与二次函数第二十三章旋转23.1 图形的旋转23.2 中心对称23.3 课题学习图案设计第二十四章圆24.1 圆的有关性质24.2 点和圆、直线和圆的位置关系24.3 正多边形和圆24.4 弧长和扇形面积第二十五章概率初步25.1 随机事件和概率25.2 用列举法求概率25.3 用频率估计概率九年级下册第二十六章反比例函数26.1 反比例函数信息技术应用探索反比例函数的性质26.2 实际问题与反比例函数阅读与思考生活中的反比例函数第二十七章相似27.1 图形的相似27.2 相似三角形观察与猜想奇妙的分形图形27.3 位似信息技术应用探索位似的性质第二十八章锐角三角函数28.1 锐角三角函数阅读与思考一张古老的“三角函数表”28.2 解直角三角形及其应用阅读与思考山坡的高度第二十九章投影与视图29.1 投影29.2 三视图阅读与思考视图的产生与应用29.3课题学习制作立体模型。

人教版初中数学章节目录(新版)

20.3 课题学习体质健康测试中的数据分析
21.1 一元二次方程 21.2 解一元二次方程 21.3 实际问题与一元二次方程 22.1 二次函数的图像与性质 22.2 二次函数与一元二次方程 22.3 实际问题与二次函数 23.1 图形的旋转 23.2 中心对称 23.3 课题学习图案设计 24.1 圆的有关性质 24.2 点和圆、直线和圆的位置关系 24.3 正多边形和圆 24.4 弧长和扇形面积 25.1 随机事件与概率 25.2 用列举法求概率 25.3 用频率估计概率 26.1 反比例函数 26.2 实际问题与反比例函数 27.1 图形的相似 27.2 相似三角形 27.3 位似 28.1 锐角三角函数 28.2 解直角三角形及其应用 29.1 投影 29.2 三视图
第十二章全等三角形第十三章轴对称
八年级数学（上册）
第十三ห้องสมุดไป่ตู้ 轴对称
第十四章整式的乘除与因式分解
第十五章分式
八年级数学（下册）
第十六章二次根式第十七章勾股定理第十八章平行四边形第十九章一次函数
第二十章数据的分析
第二十一章一元二次方程
九年级数学（上册）
第二十二章二次函数第二十三章旋转第二十四章圆
第二十五章概率初步
第二十六章反比例函数
九年级数学
（下册)
第二十七章相似第二十八章锐角三角函数
第二十九章投影与视图
九年级数学
（下册)
第二十九章投影与视图
人教版初中数学目录
1.1 正数和负数 1.2 有理数 1.3 有理数的加减法 1.4 有理数的乘除法 1.5 有理数的乘方 2.1 整式 2.2 整式的加减 3.1 从算式到方程 3.2 解一元一次方程（一）----合并同类项与移项 3.3 解一元一次方程（二）----去括号与去分母 3.4 实际问题与一元一次方程 4.1 几何图形 4.2 直线、射线、线段 4.3 角 4.4 课题学习设计制作长方体形状的包装纸盒 5.1 相交线 5.2 平行线及其判定 5.3 平行线的性质 5.4 平移 6.1 平方根 6.2 立方根 6.3 实数 7.1 平面直角坐标系 7.2 坐标方法的简单应用 8.1 二元一次方程组 8.2 消元----解二元一次方程组 8.3 实际问题与二元一次方程组 8.4 三元一次方程组的解法 9.1 不等式 9.2 一元一次不等式 9.3 一元一次不等式组 10.1 统计调查 10.2 直方图 10.3 课题学习从数据谈节水 11.1 与三角形有关的线段 11.2 与三角形有关的角 11.3 多边形及其内角和 12.1 全等三角形 12.2 全等三角形的判定 12.3 角的平分线的性质 13.1 轴对称 13.2 轴对称图形 13.3 等腰三角形

初中数学苏科版八年级上册第4章实数4.1 平方根-章节测试习题(9)

章节测试题1.【答题】估计的值（）A. 在1和2之间B. 在2和3之间C. 在3和4之间D. 在4和5之间【答案】C【分析】本题考查了算术平方根大小的估计．【解答】∵2＜＜3，∴3＜＜4，∴在在3和4之间．选：C．2.【答题】规定用符号[m]表示一个实数m的整数部分，例如：[]＝0，[3.14]＝3.按此规定[＋1]的值为（）A. 3B. 4C. 5D. 6【答案】B【分析】本题考查了算术平方根大小的估计．【解答】根据，则，即，根据题意可得：=4．3.【答题】25的算术平方根是（）A. 5B. -5C. ±5D.【答案】A【分析】本题考查了算术平方根．【解答】∵（5）2=25，∴25的算术平方根是5．选A．4.【答题】估计在（）A. 0～1之间B. 1～2之间C. 2～3之间D. 3～4之间【答案】C【分析】本题考查了算术平方根估计大小．【解答】∵4＜5＜9，∴，∴，选C．5.【答题】若，则m＋n的值是（）A. -1B. 0C. 1D. 2【答案】A【分析】本题考查了平方根．【解答】根据“几个非负数的和为0，这几个数为0”，则m-1＝0，n＋2＝0，∴m＝1，n＝-2，∴m＋n＝-1．6.【答题】4的算术平方根是（）A. 16B. 2C. -2D. ±2【答案】B【分析】本题考查了算术平方根．【解答】∵22＝4，∴4的算术平方根是2，选择B．7.【答题】若a是（-4）2的平方根，b的一个平方根是2，则a＋b的值是（）A. 8B. 0C. 8或0D. 4或-4【答案】C【分析】本题考查了平方根．【解答】a是（-4）2的平方根，则a为±4，b的一个平方根是2，b为4，所以a＋b为8或08.【答题】如果一个数的平方根是这个数本身，那么这个数是（）A. 1B. -1C. 0D. ±1【答案】C【分析】本题考查了平方根．【解答】只有0的平方根只有它本身，负数没有平方根，1的平方根是±19.【答题】下列各式表示正确的是（）A. B.C. D.【答案】C【分析】本题考查了平方根．【解答】；，，故只有C正确．10.【答题】下列说法正确的是（）A. a2的平方根是aB. 的平方根是±3C. 16的四次方根是±2D. 只有正数才有平方根【答案】C【分析】本题考查了平方根．【解答】a2的平方根是±a，故A错；，3的平方根是，故B错；0也有平方根，故D错，因此选C．11.【答题】25的算术平方根是（）A. B. 5 C. -5 D. ±5【答案】B【分析】本题考查了算数平方根．【解答】根据算术平方根的定义求解，，选B．12.【答题】有下列各数：49，，0，-4，-|-3|，-（-3），-（-5）2．其中有平方根的数共有（）A. 3个B. 4个C. 5个D. 6个【答案】B【分析】本题考查了平方根．【解答】有平方根的数是49，，0，-（-3），共4个．13.【答题】下列说法错误的是（）A. 5是25的算术平方根B. 是的一个平方根C. （-4）2的平方根是-4D. 0的平方根和算术平方根都是0【答案】C【分析】本题考查了算术平方根．【解答】一个正数的平方根有两个，是成对出现的．14.【答题】下列说法正确的是（）A. 任何数的平方根都有两个B. 只有正数才有平方根C. 一个正数的平方根的平方是它本身D. a2的平方根是a【答案】C【分析】本题考查了平方根．【解答】A，B都可以是0，D，也可以是-a，C是对的15.【答题】4的平方根是（）A. 2B. 16C. ±2D. ±16【答案】C【分析】本题考查了平方根．【解答】本题考查了平方根的定义．掌握平方根的定义是解题的关键．选项A是4的算术平方根；选项B是4的平方，选项C是4的平方根，选C．16.【答题】的平方根是（）A. B. C. D.【答案】D【分析】本题考查了平方根．【解答】∵，，∴的平方根是．17.【答题】下列各数的算术平方根比本身大的数是（）A. B. 0 C. 1 D. （-1）2【答案】A【分析】本题考查了算术平方根．【解答】算术平方根的计算，得数大于本身．18.【答题】如果x的算术平方根是9，那么x的值是（）A. 3B. 18C. 81D. 【答案】C【分析】本题考查了算术平方根．【解答】因为81的算术平方根是9，所以x的值是81．19.【答题】若x是49的算术平方根，则x等于（）A. 7B. -7C. 49D. -49 【答案】A【分析】本题考查了算术平方根．【解答】因为72＝49，所以49的算术平方根是7．20.【答题】下列各式中，正确的是（）A. B. C. D.【答案】B【分析】本题考查了平方根．【解答】选项A、C、D的计算结果均为3，只有B选项正确．。

初中数学鲁教版(五四制)七年级上册第四章实数5 用计算器开方-章节测试习题(1)

章节测试题1.【答题】计算：≈______(精确到百分位).【答案】2.92【分析】利用计算器按照以上步骤按键即可得出结果．【解答】解：故答案为：2.【答题】使用课本介绍的学生计算器，计算，结果是______（精确到0.01）．【答案】8.62【分析】先用计算器算出的结果，再加上π的值即可，注意精确的位数．【解答】解：原式=+π≈5.477+3.141≈8.62故答案为8.623.【答题】利用计算器计算：=______．【答案】－8.406【分析】先用计算器得到π≈3.142，≈2.236，然后代入原式进行加减运算即可．【解答】解：原式≈0.5﹣3.142+2.236﹣8=﹣8.4064.【答题】利用计算器计算：≈______．（精确到0.01）．【答案】2.13【分析】首先熟练应用计算器，然后对计算器给出的结果，根据有效数字的概念用四舍五入法取近似数即可解决问题．【解答】解：根据题意用计算器解：≈2×1.710﹣1.286≈2.135.【答题】用计算器计算：=______（结果保留4个有效数字）．【答案】2.646【分析】首先熟练应用计算器，然后对计算器给出的结果，根据有效数字的概念用四舍五入法取近似数即可求解．【解答】解：根据题意在计算器计算：=2.6457，∵结果保留4个有效数字，∴=2.6466.【答题】已知，（n≥3），请用计算器计算当n≥3时，A、B的若干个值，并由此归纳出当n≥3时，A、B间的大小关系为______．【答案】A＜B【分析】从n=3开始，分别计算出n=3、4、5、6时的A、B的值，然后根据变化规律即可作出判断．【解答】解：n=3时，A=﹣≈0.3178，B=1﹣0=1，∴A＜B，n=4时，A=﹣≈0.2679，B=﹣1≈0.4142，∴A＜B，n=5时，A=﹣≈0.2361，B=﹣≈0.3178，∴A＜B，n=6时，A=﹣≈0.2134，B=﹣≈0.2679，A＜B，以此类推，随着n的增多，A在不断变小，而B的变化比A慢两个数，∴当n≥3时，A、B间的大小关系为：A＜B．故答案为：A＜B．7.【答题】（Ⅰ）若x与3﹣2x互为相反数，则=______．（Ⅱ）用计算器计算：=______．（保留三个有效数字）．【答案】-1,12.6【分析】（1）由于x与3﹣2x互为相反数，由此得到x=3﹣2x=0，解方程求出x 代入即可求解；（2）用计算器计算即可求出近似值．【解答】解：（1）由题意知，x=3﹣2x=0，∴=﹣1∴=﹣=1；（2）=12.68.【答题】选做题（从下面两题中只选做一题，如果做了两题的，只按第（Ⅰ）题评分）（Ⅰ）分解因式：2x2﹣2y2=______（Ⅱ）用计算器计算：=______（保留三位有效数字）．【答案】2（x+y）（x﹣y）,10.2【分析】（Ⅰ）先提取公因式2，再根据平方差公式进行二次分解即可求得答案．（Ⅱ）首先利用二次根式的乘法求得答案，再利用计算机求解即可求得答案．【解答】解：（Ⅰ）2x2﹣2y2=2（x2﹣y2）=2（x+y）（x﹣y）；（Ⅱ）=≈10.247≈10.2故答案为：（Ⅰ）2（x+y）（x﹣y），（Ⅱ）10.29.【答题】用计算器比较：5，4，3的大小（用小于符号连接）______．【答案】3＜4＜5【分析】先用计算器对无理数进行估算，再进行比较即可．【解答】解：∵5≈5×1.414=7.07，4≈4×1.732=6.88，3≈3×2.236=6.708，6.708＜6.88＜7.07，∴3＜4＜5．10.【答题】用计算器求的值，结果保留五个有效数字，得______．【答案】44.788【分析】本题要求同学们能熟练应用计算器，会用科学记算器进行计算．【解答】解：∵≈44.7883914，∴保留五个有效数字为44.77811.【答题】已知A=n﹣，B=3﹣2（n为正整数）．当n≤5时，有A＜B；请用计算器计算当n≥6时，A、B的若干个值，并由此归纳出当以n≥6时，A、B间的大小关系为A______B．【答案】＞【分析】本题要求同学们能熟练应用计算器，会用科学记算器进行计算．并根据结果归纳规律．【解答】解：根据题意，计算可得：当n=6时，A=5.5，B≈5.35；当n=7时，A=6.5，B≈5.94；当n=8时，A=7.5，B≈6.49．由此可得：n≥6时，A、B问的大小关系为A＞B．故答案为A＞B．12.【答题】用计算器计算：≈______．（结果精确到0.1）【答案】44.8【分析】首先熟悉计算器的求算术平方根的键，然后即可利用计算器求出结果，根据有效数字的概念用四舍五入法取近似数即可．【解答】解：根据题意用计算器运算得≈44.8（结果精确到0.1）．13.【答题】用计算器计算：（结果保留4个有效数字）______，＝______，＝______．【答案】177.2,±0.7861,0.08159【分析】首先熟悉计算器的求算术平方根的键，然后即可利用计算器求出结果，根据有效数字的概念用四舍五入法取近似数即可．【解答】解：故答案为：方法总结：有效数字：从左边第一个不是零的数字算起，到末尾数字为止都是有效数字.14.【答题】用计算器计算：（1）≈______；（2）≈______.（结果精确到0.0001）.【答案】44.8776,－12.6285【分析】首先熟悉计算器的求算术平方根、立方根的键，然后即可利用计算器求出结果，根据有效数字的概念用四舍五入法取近似数即可．【解答】直接利用计算器的“”和“”键进行开方计算，即可得到=44.8776，=-12.6285.故答案为：44.8776；-12.628515.【答题】用科学记算器计算，按键顺序的结果是______．【答案】－3【分析】了解计算器的使用，很容易得出结果【解答】原题是计算的值，根据按键顺序的结果是﹣3故答案为：-3.16.【题文】用计算器求下列各式的值（精确到0.001）：(1) ； (2) ； (3) .【答案】(1)28.284； (2)0.762； (3)49.000.【分析】先利用计算器求值，然后按要求取近似值即可．【解答】解：（1）≈28.284；（2）≈0.762；（3）≈49.000．方法总结：本题考查了用计算器进行数的开方，解题的关键是按要求取近似值．17.【题文】请同学们做完上面考题后，再认真检查一遍，估计一下你的得分情况．如果你全卷得分低于65分，则本题的5个小题得分将计入全卷总分，但计入后全卷总分不超过65分；如果你全卷得分已经达到或超过65分，则本题可不做，得分不计入全卷总分．（1）计算：（﹣2）+（﹣3）= ，（﹣2）×5= ，（﹣3）2= ；（2）用计算器计算：= ，= ，≈；（保留三位小数）（3）合并同类项：3a+2b+5a﹣8b= ；（4）如图，直线AB、CD相交于点O，OP平分∠BOD，若∠AOC=60°，则∠AOD= °，∠DOP= 度．（5）解方程：3x﹣7=x+1（写出过程）．【答案】见解答【分析】（1）根据有理数的混合运算法则即可求解；（2）利用计算器求解；（3）根据合并同类项的法则即可求解；（4）首先利用对顶角的性质，然后利用角平分线的性质即可求解；（5）利用解一元一次方程的一般步骤即可求解．【解答】解：（1）①（﹣2）+（﹣3）=﹣5，②（﹣2）×5=﹣10，③（﹣3）2=9；（2）要根据要求保留三位小数，=1.1，=3，≈1.414；（3）3a+2b+5a﹣8b=（3a+5b）+（2b﹣8b）=8a﹣6b；（4）∠AOD=（180°﹣∠AOC）=（180°﹣60°）=120°，∵∠AOC与∠DOB互为对顶角，OP平分∠BOD，∴∠DOP=∠BOD=30°；（5）解：移项，得3x﹣x=1+7合并，得2x=8∴x=4．18.【题文】求一个正数的算术平方根，有些数可以直接求得，如，有些数则不能直接求得，如，但可以通过计算器求得．还有一种方法可以通过一组数的内在联系，运用规律求得，请同学们观察下表：n 16 0.16 0.0016 1600 160000 …4 0.4 0.04 40 400 …（1）表中所给的信息中，你能发现什么规律？（请将规律用文字表达出来）（2）运用你发现的规律，探究下列问题：已知≈1.435，求下列各数的算术平方根：①0.0206；②206；③20600．【答案】见解答【分析】（1）从被开方数和算术平方根的小数点的移动位数考虑解答；（2）根据（1）中的规律解答即可．【解答】解：（1）被开方数扩大或缩小102n倍，非负数的算术平方根就相应的扩大或缩小10n倍；或者说成被开方数的小数点向左或向右移动2n位，算术平方根的小数点就向左或向右移动n位；（2）=0.1435；=14.35；=143.5．19.【题文】用计算器计算：2+（结果精确到0.001）.【答案】3.312【分析】首先熟悉计算器的求算术平方根和立方根的键，然后利用计算器求出结果，根据有效数字的概念用四舍五入取近似数即可.【解答】解：2+≈2+4.5826-3.2711≈3.31220.【题文】计算：（结果精确到1）．【答案】9【分析】首先根据用计算器求一个数的立方根的方法，求出的值是多少；然后应用四舍五入法，将结果精确到1即可．【解答】解：≈9。

2023-2024学年人教B版数学必修第二册同步测试(解析版)4.1.1实数指数幂及其运算

第四章 4.1.1实数指数幂及其运算A 级基础巩固一、选择题1．化简4(3(－5)2)3的结果为( )A ．5B ． 5C ．－ 5D ．－52．若2＜a ＜3，化简(2－a )2＋4(3－a )4的结果是( ) A ．5－2a B ．2a －5 C ．1D ．－13．(多选题)下列各式运算正确的是( ) A ．(－a 2b )2·(－ab 2)3＝－a 7b 8 B ．(－a 2b 3)3÷(－ab 2)3＝a 3b 3 C ．(－a 3)2·(－b 2)3＝a 6b 6D ．[－(a 3)2·(－b 2)3]3＝a 18b 184．如果x ＝1＋2b ，y ＝1＋2－b ，那么用x 表示y 等于( ) A ．x ＋1x －1B ．x ＋1xC ．x －1x ＋1D ．x x －15．若m ＜0，n ＞0，则m n 等于( ) A ．－m 2n B ．－m 2n C ．－(mn )2 D ．m 2n二、填空题6．64－23的值是____．7．计算：2－12＋(－4)02＋12－1－(1－5)0＝____．8．(1)4(x －4)4＝____； (2)7(x －7)7＝____．三、解答题 9．化简下列各式： (1)4x 14(－3x 14y 13)6x －12 y －23 ； (2)(3a 2b )·a b 4ab 3．10．若代数式2x －1＋2－x 有意义，化简4x 2－4x ＋1＋24(x －2)4．B 级素养提升一、选择题1．(多选题)在下列根式与分数指数幂的互化中，不正确的是( ) A ．(－x )0.5＝－x (x ≠0) B ．6y 2＝y 13C ．⎝⎛⎭⎫x y －34＝4⎝⎛⎭⎫y x 3(xy ≠0)D ．x －13＝－3x2．下列式子中，错误的是( ) A ．(27a 3) 13÷0.3a －1＝10a 2B ．(a 23－b 23 )÷(a 13＋b 13)＝a 13－b 13C ．[(22＋3)2(22－3)2] 12＝－1D ．4a 3a 2a ＝24a 113．若(3－2x )－34有意义，则实数x 的取值范围是( )A ．(－∞，＋∞)B ．(－∞，32)∪(32，＋∞)C ．(－∞，32)D ．(32，＋∞)4．化简3a a 的结果是( ) A ．a B ．a 12C ．a 2D ．a 13二、填空题5．已知a ＋1a ＝7，则a 2＋a －2＝____，a －a －1＝____．6．计算49－12＋3×⎝⎛⎭⎫1343233＝____． 7．若10x＝2,10y＝3，则10(3x -4y )2＝____．三、解答题 8．化简：a 43 －8a 13b4b 23 ＋23ab ＋a 23÷(1－23b a)×3a ． 9．根据已知条件求下列值：(1)已知x ＝12，y ＝23，求x ＋y x －y －x －y x ＋y的值；(2)已知a ，b 是方程x 2－6x ＋4＝0的两根，且a ＞b ＞0，求a －ba ＋b的值．第四章 4.1.1实数指数幂及其运算A 级基础巩固一、选择题1．化简4(3(－5)2)3的结果为( B )A ．5B ． 5C ．－ 5D ．－5[解析] 原式＝4(352)3＝(523)34＝523 ×34＝512 ＝5．2．若2＜a ＜3，化简(2－a )2＋4(3－a )4的结果是( C ) A ．5－2a B ．2a －5 C ．1 D ．－1[解析] ∵(2－a )2＝|2－a |＝a －2．4(3－a )4＝|3－a |＝3－a ，∴原式＝a －2＋3－a ＝1，故选C ．3．(多选题)下列各式运算正确的是( ABD ) A ．(－a 2b )2·(－ab 2)3＝－a 7b 8 B ．(－a 2b 3)3÷(－ab 2)3＝a 3b 3 C ．(－a 3)2·(－b 2)3＝a 6b 6D ．[－(a 3)2·(－b 2)3]3＝a 18b 18[解析] 对于A ，(－a 2b )2·(－ab 2)3＝a 4b 2·(－a 3b 6)＝－a 7b 8，故A 正确；对于B ，(－a 2b 3)3÷(－ab 2)3＝－a 6b 9÷(－a 3b 6)＝a 6－3b 9－6＝a 3b 3，故B 正确；对于C ，(－a 3)2·(－b 2)3＝a 6·(－b 6)＝－a 6b 6，故C 错误；对于D ，易知正确，故选ABD ．4．如果x ＝1＋2b ，y ＝1＋2－b ，那么用x 表示y 等于( D ) A ．x ＋1x －1B ．x ＋1xC ．x －1x ＋1D ．x x －1[解析] 由x ＝1＋2b ，得2b ＝x －1，y ＝1＋2－b ＝1＋12b ＝1＋1x －1＝xx －1．5．若m ＜0，n ＞0，则m n 等于( A ) A ．－m 2n B ．－m 2n C ．－(mn )2D ．m 2n[解析] ∵m ＜0，∴m ＝－m 2， ∴m n ＝－m 2n ，故选A ．二、填空题6．64－23的值是__116__．[解析] 64－23＝(26)－23＝2－4＝116．7．计算：2－12＋(－4)02＋12－1－(1－5)0＝．[解析] 2－12＋(－4)02＋12－1－(1－5)0＝12＋12＋2＋1－1＝22． 8．(1)4(x －4)4＝__⎩⎪⎨⎪⎧x －4，x ≥4，4－x ，x ＜4__；(2)7(x －7)7＝__x －7__．[解析] 当化简偶次根式时，需判断根式内式子的取值范围．三、解答题 9．化简下列各式： (1)4x 14(－3x 14y 13)6x －12 y －23；(2)(3a 2b )·a b 4ab 3．[解析] (1)原式＝⎝⎛⎭⎫－4×3×16·x 14 ＋14 ＋12y 13 ＋23＝－2xy ． (2)原式＝a 23＋12 －14b 13－1－34＝a 1112b －1712．10．若代数式2x －1＋2－x 有意义，化简4x 2－4x ＋1＋24(x －2)4． [解析] 由2x －1＋2－x 有意义，则⎩⎪⎨⎪⎧2x －1≥0，2－x ≥0，即12≤x ≤2．故4x 2－4x ＋1＋24(x －2)4＝(2x －1)2＋24(x －2)4＝|2x －1|＋2|x －2| ＝2x －1＋2(2－x )＝3．B 级素养提升一、选择题1．(多选题)在下列根式与分数指数幂的互化中，不正确的是( ABD ) A ．(－x )0.5＝－x (x ≠0) B ．6y 2＝y 13C ．⎝⎛⎭⎫x y －34 ＝4⎝⎛⎭⎫y x 3(xy ≠0)D ．x －13＝－3x[解析] 对于A ，若x ＜0，－x 无意义，故A 错误；对于B ，当y ＜0时，6y 2≠y 13，故B 错误；对于C ，由分数指数幂可得xy ＞0，则⎝⎛⎭⎫x y －34＝⎝⎛⎭⎫y x 34＝4⎝⎛⎭⎫y x 3，故C 正确；对于D ，x －13＝1x 13＝13x，故D 错误．2．下列式子中，错误的是( C ) A ．(27a 3) 13÷0.3a －1＝10a 2B ．(a 23 －b 23 )÷(a 13 ＋b 13 )＝a 13 －b 13 C ．[(22＋3)2(22－3)2] 12＝－1D ．4a 3a 2a ＝24a 11[解析] 对于A ，原式＝3a ÷0.3a －1＝3a 20.3＝10a 2，故A 正确；对于B ，原式＝(a 13－b 13)(a 13＋b 13)a 13 ＋b 13＝a 13 －b 13 ，故B 正确；对于C ，原式＝[(3＋22)2(3－22)2] 13 ＝(3＋22)(3－22)＝1.这里注意3＞22，a 13(a ＞0)是正数，故C 错误；对于D ，原式＝ 4a3a52＝4a ·a 56＝a 1124 ＝24a 11，故D 正确． 3．若(3－2x )－34有意义，则实数x 的取值范围是( C )A ．(－∞，＋∞)B ．(－∞，32)∪(32，＋∞)C ．(－∞，32)D ．(32，＋∞)[解析]要使(3－2x ) －34有意义，需使3－2x ＞0，即x ＜32．4．化简3a a 的结果是( B ) A ．a B ．a 12 C ．a 2 D ．a 13[解析] 原式＝3aa 12＝3a 32＝a 12．二、填空题5．已知a ＋1a＝7，则a 2＋a －2＝__47__，a －a －1＝．[解析] 因为a ＋1a ＝7，则(a ＋1a )2＝a 2＋1a 2＋2＝49，变形可得a 2＋1a 2＝47；(a －a －1)2＝(a ＋a －1)2－4＝49－4＝45所以a －a －1＝±35． 6．计算49－12＋3×⎝⎛⎭⎫1343233＝__17__． [解析]原式＝7－1＋23×7－3×233＝7－1＝17．7．若10x ＝2,10y＝3，则10(3x -4y )2＝9．[解析] 由10x＝2,10y＝3，得1032x ＝(10x) 32 ＝232，102y ＝(10y )2＝32，∴10(3x -4y )2＝1032 x 102y ＝23232＝229．三、解答题 8．化简：a 43 －8a 13b4b 23＋23ab ＋a 23÷(1－23b a)×3a ． [解析] 原式＝a 13 (a －8b )4b 23 ＋2a 13 b 13 ＋a 23 ÷a 13 －2·b 13 a 13·a 13 ＝a 13(a 13－2b 13)(a 23＋2a 13b 13＋4b 23)4b 23 ＋2a 13 b 13 ＋a 23 ·a 13a 13 －2b 13 ·a 13 ＝a 13 ·a 13 ·a 13＝A ．9．根据已知条件求下列值：(1)已知x ＝12，y ＝23，求x ＋y x －y －x －y x ＋y的值；(2)已知a ，b 是方程x 2－6x ＋4＝0的两根，且a ＞b ＞0，求a －ba ＋b的值． [解析] (1)x ＋y x －y－x －y x ＋y＝(x ＋y )2x －y －(x －y )2x －y ＝4xy x －y ．将x ＝12，y ＝23代入上式得：原式＝4 12×2312－23＝4 13－16＝－2413＝－83． (2)∵a ，b 是方程x 2－6x ＋4＝0的两根，∴⎩⎪⎨⎪⎧a ＋b ＝6ab ＝4，∵a ＞b ＞0，∴a ＞b ． ∴⎝⎛⎭⎪⎫a －b a ＋b 2＝a ＋b －2ab a ＋b ＋2ab ＝6－246＋24＝210＝15， ∴a －b a ＋b＝15＝55．。

(人教版)初一数学下册实数测试题及答案解析

一、选择题1．已知: []x 表示不超过x 的最大整数，例: ][3.93, 1.82⎡⎤=-=-⎣⎦，令关于k 的函数()][1k 44k k f +⎡⎤=-⎢⎥⎣⎦ (k 是正整数)，例：()][313344f +⎡⎤=-⎢⎥⎣⎦=1，则下列结论错误．．的是（） A ．()10f = B ．()()4f k f k += C ．()()1f k f k +≥ D ．()0f k =或12．设[x]表示最接近x 的整数（x≠n+0.5，n 为整数），则[1]+[2]+[3]+…+[36]=（） A ．132B ．146C ．161D ．6663．若实数p ，q ，m ，n 在数轴上的对应点的位置如图所示，且满足0p q m n +++=，则绝对值最小的数是（）A ．pB ．qC ．mD ．n4．如图，A 、B 、C 、D 是数轴上的四个点，其中最适合表示10的点是（）A ．点AB ．点BC ．点CD ．点D5．将尺寸如图的4块完全相同的长方形薄木块（厚度忽略不计）进行拼摆，恰好可以不重叠地摆放在如图的甲、乙两个方框内．已知小木块的宽为2，图甲中阴影部分面积为19，则图乙中AD 的长为（）A ．2192+B ．194+C ．2194+D ．192+6．如图，四个有理数m ，n ，p ，q 在数轴上对应的点分别为M ，N ，P ，Q ，若n+p=0，则m ，n ，p ，q 四个有理数中，绝对值最大的一个是（）A ．pB ．qC ．mD ．n7．现定义一种新运算“*”，规定a *b ＝ab ＋a －b ，如1*3＝1×3＋1－3，则(－2*5)*6等于( ) A ．120B ．125C ．－120D ．－1258．下列说法中，正确的个数是（）．（1）64-的立方根是4-；（2）49的算术平方根是7±；（3）2的立方根为32；（4）7是7的平方根．A ．1B ．2C ．3D ．49．如图，数轴上,A B 两点表示的数分别为1,2--，点B 关于点A 的对称点为点C ，则点C 所表示的数是（）A ．12B 21C ．22D 2210．已知f(1)=2 (取12⨯的末位数字)，f(2)=6 (取2?3的末位数字)，f(3)=2 (取34⨯的末位数字)，…，则()()()()f 1f 2f 3f 2021++++的值为（）A ．4036B ．4038C ．4042D ．4044二、填空题11．在数轴上，点M ，N 分别表示数m ，n ，则点M ，N 之间的距离为|m ﹣n |．（1）若数轴上的点M ，N 分别对应的数为222M ，N 间的距离为 ___，MN 中点表示的数是 ___．（2）已知点A ，B ，C ，D 在数轴上分别表示数a ，b ，c ，d ，且|a ﹣c |＝|b ﹣c |＝23|d ﹣a |＝1（a ≠b ），则线段BD 的长度为 ___．12．观察下列等式：1﹣12＝12，2﹣25＝85，3﹣310＝2710，4﹣417＝6417，…，根据你发现的规律，则第20个等式为_____． 13．观察下列各式： 225-85425⨯25225-253310-27103910⨯3103310-31021n n n -+_____．14．对于任意有理数a ，b ，规定一种新的运算a ⊙b ＝a （a +b ）﹣1，例如，2⊙5＝2×（2+5）﹣1＝13．则（﹣2）⊙6的值为_____15．a ※b 是新规定的这样一种运算法则：a ※b=a+2b ，例如3※（﹣2）=3+2×（﹣2）=﹣1．若（﹣2）※x=2+x ，则x 的值是_____．16．若[x ]表示不超过x 的最大整数．如[π]＝3，[4]＝4，[﹣2.4]＝﹣3．则下列结论： ①[﹣x ]＝﹣[x ]；②若[x ]＝n ，则x 的取值范围是n ≤x ＜n +1； ③x ＝﹣2.75是方程4x ﹣[x ]+5＝0的一个解； ④当﹣1＜x ＜1时，[1+x ]+[1﹣x ]的值为1或2．其中正确的结论有 ___（写出所有正确结论的序号）．17．定义一种新运算a b ※，其规则是：当a b >时，2a b a b =-※，当a b =时，a b a b =+※，当a b <时，2a b b a =-※，若()21x -=※，则x =____________．18．如图，半径为1的圆与数轴的一个公共点与原点重合，若圆在数轴上做无滑动的来回滚动，规定圆向右滚动的周数记为正数，向左滚动周数记为负数，依次滚动的情况如下（单位：周）：﹣3，﹣1，＋2，﹣1，＋3，＋2，则圆与数轴的公共点到原点的距离最远时，该点所表示的数是_______．19．已知M 是满足不等式27a -<<的所有整数的和，N 是52的整数部分，则M N +的平方根为__________．20．对任意两个实数a ，b 定义新运算：a ⊕b=()()a a b b a b ≥⎧⎨⎩若若＜，并且定义新运算程序仍然是先做括号内的，那么（5⊕2）⊕3=___．三、解答题21．我们知道，正整数按照能否被2整除可以分成两类：正奇数和正偶数，小华受此启发，按照一个正整数被3除的余数把正整数分成了三类：如果一个正整数被3除余数为1，则这个正整数属于A 类，例如1，4，7等；如果一个正整数被3除余数为2，则这个正整数属于B 类，例如2，5，8等；如果一个正整数被3整除，则这个正整数属于C 类，例如3，6，9等．（1）2020属于类（填A ，B 或C ）；（2）①从A 类数中任取两个数，则它们的和属于类（填A ，B 或C ）； ②从A 、B 类数中任取一数，则它们的和属于类（填A ，B 或C ）；③从A 类数中任意取出8个数，从B 类数中任意取出9个数，从C 类数中任意取出10个数，把它们都加起来，则最后的结果属于类（填A ，B 或C ）；（3）从A 类数中任意取出m 个数，从B 类数中任意取出n 个数，把它们都加起来，若最后的结果属于C 类，则下列关于m ，n 的叙述中正确的是（填序号）． ①2m n +属于C 类；②m n -属于A 类；③m ，n 属于同一类．22．如图1，把两个边长为1的小正方形沿对角线剪开，所得的4个直角三角形拼成一个面积为2的大正方形．由此得到了一种能在数轴上画出无理数对应点的方法．（1）图2中A 、B 两点表示的数分别为___________，____________；（2）请你参照上面的方法：①把图3中51⨯的长方形进行剪裁，并拼成一个大正方形．在图3中画出裁剪线，并在图4的正方形网格中画出拼成的大正方形，该正方形的边长a =___________．（注：小正方形边长都为1，拼接不重叠也无空隙）②在①的基础上，参照图2的画法，在数轴上分别用点M 、N 表示数a 以及3a -．（图中标出必要线段的长）23．观察下列各式：21131222-=⨯；21241333-=⨯；21351444-=⨯；……根据上面的等式所反映的规律，（1）填空：21150-=______；2112019-=______；（2）计算：2222111111112342019⎛⎫⎛⎫⎛⎫⎛⎫---⋅⋅⋅- ⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭24．对于实数a ，我们规定：用符号⎡⎤⎣⎦a a ⎡⎣a 为a 的根整数，例如：93⎡=⎣，10⎡⎣=3．(1)仿照以上方法计算：4⎡⎣=______；26⎡⎤⎣⎦=_____．(2)若1x ⎡=⎣，写出满足题意的x 的整数值______．如果我们对a 连续求根整数，直到结果为1为止．例如：对10连续求根整数2次103⎡=⎣→3⎡⎣=1，这时候结果为1．(3)对100连续求根整数，____次之后结果为1．(4)只需进行3次连续求根整数运算后结果为1的所有正整数中，最大的是____． 25．我们知道，正整数按照能否被2整除可以分成两类：正奇数和正偶数，小华受此启发，按照一个正整数被3除的余数把正整数分成了三类：如果一个正整数被3除余数为1，则这个正整数属于A 类，例如1，4，7等；如果一个正整数被3除余数为2，则这个正整数属于B 类，例如2，5，8等；如果一个正整数被3整除，则这个正整数属于C 类，例如3，6，9等．（1）2020属于类（填A ，B 或C ）；（2）①从A 类数中任取两个数，则它们的和属于类（填A ，B 或C ）； ②从A 、B 类数中任取一数，则它们的和属于类（填A ，B 或C ）；③从A 类数中任意取出8个数，从B 类数中任意取出9个数，从C 类数中任意取出10个数，把它们都加起来，则最后的结果属于类（填A ，B 或C ）；（3）从A 类数中任意取出m 个数，从B 类数中任意取出n 个数，把它们都加起来，若最后的结果属于C 类，则下列关于m ，n 的叙述中正确的是（填序号）．①2m n +属于C 类；②m n -属于A 类；③m ，n 属于同一类．26．阅读下面的文字,解答问题:是无理数,而无理数是无限不循环小数,的小数部分我们不可能全部写出来,而121.请解答下列问题：_______，小数部分是_________；(2)的小数部分为a b ，求a b +(3)已知:100x y +=+，其中x 是整数,且01y ＜＜，求24x y -的平方根． 27．观察下列各式： (x －1)(x+1)=x 2－1 (x －1)(x 2+x+1)=x 3－1 (x －1)(x 3+x 2+x+1)=x 4－1 ……（1）根据以上规律，则(x －1)(x 6+x 5+x 4+x 3+x 2+x+1)=__________________．（2）你能否由此归纳出一般性规律(x －1)(x n +x n －1+x n －2+…+x+1)=____________．（3）根据以上规律求1+3+32+…+349+350的结果． 28．阅读下面的文字，解答问题的小数部分我们不可能全部11，将这个数减去其整数部分，差就是小数部分．23， ∴22）请解答：（1整数部分是，小数部分是．（2a b ，求|a ﹣b（3）已知：x +y ，其中x 是整数，且0＜y ＜1，求x ﹣y 的相反数． 29．探究与应用：观察下列各式： 1+3＝ 2 1+3+5＝ 2 1+3+5+7＝ 2 1+3+5+7+9＝ 2 ……问题：（1）在横线上填上适当的数；（2）写出一个能反映此计算一般规律的式子；（3）根据规律计算：（﹣1）+（﹣3）+（﹣5）+（﹣7）+…+（﹣2019）．（结果用科学记数法表示）30．我们知道，任意一个正整数x 都可以进行这样的分解：x m n =⨯（m ，n 是正整数，且m n ≤），在x 的所有这种分解中，如果m ，n 两因数之差的绝对值最小，我们就称m n ⨯是x 的最佳分解，并规定：()=nf x m．例如：18可分解成118⨯，29⨯或36⨯，因为1819263->->-，所以36⨯是18的最佳分解，所以()311862f == （1）填空：()6f = ；()16=f ；（2）一个两位正整数t （10t a b =+，19a b ≤≤≤，a ，b 为正整数），交换其个位上的数字与十位上的数字得到的新数减去原数所得的差为54，求出所有的两位正整数；并求()f t 的最大值；（3）填空：①()22357f ⨯⨯⨯= ；②()42357f ⨯⨯⨯= ；【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【分析】根据新定义的运算逐项进行计算即可做出判断. 【详解】A. ()f 1=][11144+⎡⎤-⎢⎥⎣⎦=0-0=0，故A 选项正确，不符合题意； B. ()f k 4+=][k 41k 444+++⎡⎤-⎢⎥⎣⎦=][k 1k 1144+⎡⎤+-+⎢⎥⎣⎦=][k 1k 44+⎡⎤-⎢⎥⎣⎦，()f k =][k 1k 44+⎡⎤-⎢⎥⎣⎦，所以()()f k 4f k +=，故B 选项正确，不符合题意；C. ()f k 1+=k 11k 1k 2k 14444+++++⎡⎤⎡⎤⎡⎤⎡⎤-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦，()f k = ][k 1k 44+⎡⎤-⎢⎥⎣⎦，当k=3时，()f 31+=323144++⎡⎤⎡⎤-⎢⎥⎢⎥⎣⎦⎣⎦=0，()f 3= ][31344+⎡⎤-⎢⎥⎣⎦=1，此时()()f k 1f k +<，故C 选项错误，符合题意； D.设n 为正整数，当k=4n 时，()f k =4n 14n 44+⎡⎤⎡⎤-⎢⎥⎢⎥⎣⎦⎣⎦=n-n=0，当k=4n+1时，()f k =4n 24n 144++⎡⎤⎡⎤-⎢⎥⎢⎥⎣⎦⎣⎦=n-n=0，当k=4n+2时，()f k =4n 34n 244++⎡⎤⎡⎤-⎢⎥⎢⎥⎣⎦⎣⎦=n-n=0，当k=4n+3时，()f k =4n 44n 344++⎡⎤⎡⎤-⎢⎥⎢⎥⎣⎦⎣⎦=n+1-n=1，所以()f k 0=或1，故D 选项正确，不符合题意，故选C. 【点睛】本题考查了新定义运算，明确运算的法则，运用分类讨论思想是解题的关键.2．B解析：B 【详解】分析：先计算出1.52，2.52，3.52，4.52，5.52，即可得出中有2个1，4个2，6个3，8个4，10个5，6个6，从而可得出答案．详解：1.52=2.25，可得出有2个1； }2.52=6.25，可得出有4个2； 3.52=12.25，可得出有6个3； 4.52=20.25，可得出有8个4； 5.52=30.25，可得出有10个5；则剩余6个数全为6.故=1×2+2×4+3×6+4×8+5×10+6×6=146. 故选B.点睛本题考查了估算无理数的大小.3．C解析：C 【分析】根据0p q m n +++=，并结合数轴可知原点在q 和m 之间，且离m 点最近，即可求解．【详解】解：∵0p q m n +++= 结合数轴可得：()-=p q m n ++，即原点在q 和m 之间，且离m 点最近， ∴绝对值最小的数是m ，故选：C ．【点睛】本题考查实数与数轴，解题的关键是明确数轴的特点，利用数形结合的思想解答．4．D解析：D 【分析】根据<4即可得到答案．【详解】∵9<10<16，∴<4，∴的点是点D，故选：D．【点睛】此题考查利用数轴表示实数，实数的大小比较，正确比较实数是解题的关键．5．C解析：C【分析】设木块的长为x，结合图形知阴影部分的边长为x-2，根据其面积为19得出（x-2）2=19，利用平方根的定义求出符合题意的x的值，由AD=2x可得答案．【详解】解：设木块的长为x，根据题意，知：（x-2）2=19，则2x-=∴2x=（舍去）x=22则24==，BC x故选：C．【点睛】本题主要考查算术平方根，解题的关键是结合图形得出木块长、宽与阴影部分面积间的关系．6．B解析：B【分析】根据n+p=0可以得到n和p互为相反数，原点在线段PN的中点处，从而可以得到绝对值最大的数．【详解】解：∵n+p=0，∴n和p互为相反数，∴原点在线段PN的中点处，∴绝对值最大的一个是Q点对应的q．故选B．【点睛】本题考查了实数与数轴及绝对值．解题的关键是明确数轴的特点．7．D解析：D【详解】根据题目中的运算方法a *b =ab +a -b ，可得（-2*5）*6=（-2×5-2-5）*6=-17*6=-17×6+（-17）-6=-125．故选D ．点睛：本题主要考查了新定义运算，根据题目所给的规律（或运算方法），利用有理数的混合法则计算正确是解题关键．8．C解析：C 【详解】4-，故（1）对；根据算术平方根的性质，可知49的算术平方根是7，故（2）错；根据立方根的意义，可知23）对；7的平方根．故（4）对；故选C.9．D解析：D 【分析】设点C 的坐标是x ，根据题意列得12x=-，求解即可. 【详解】解：∵点A 是B ，C 的中点． ∴设点C 的坐标是x ，1=-，则2x =-∴点C 表示的数是2-．故选：D. 【点睛】此题考查数轴上两点的中点的计算公式：两点的中点所表示的数等于两点所表示的数的平均数，正确掌握计算公式是解题的关键.10．C解析：C 【分析】先计算部分数的乘积，观察运算结果，发相规律，每运算5次后结果重复出现，求出f(1)+f(2)+f(3)+f(4)+f(5)和，再求2021次运算重复的次数，用除数5，商和余数表示2021=5×404+1，说明重复404次和f(2021)=2的结果，（f(1)+f(2)+f(3)+f(4)+f(5)）×10+2计算结果即可．【详解】解：f(1)=2， f(2)=6，f(3)=2，f(4)=0，f(5)=0，f(6)=2，f(7)=6，f(8)=2，f(9)=0，f(10)=0，f(11)=2，每5次运算一循环，f(1)+f(2)+f(3)+f(4)+f(5)=2+6+2+0+0=10， 2021=5×404+1，()()()()f 1f 2f 3f 2021++++=10×404+2=4040+2=4042．故选：C ．【点睛】本题考查新定义运算，读懂题目的含义与要求，掌握运算的方法，观察部分运算结果，从中找出规律，用规律解决问题是解题关键．二、填空题 11．2 【分析】（1）直接根据定义，代入数字求解即可得到两点间的距离；根据两点之间的距离得出其一半的长度，然后结合其中一个端点表示的数求解即可得中点表示的数；（2）先根据|a ﹣c|＝|b ﹣c|与a≠解析：2 【分析】（1）直接根据定义，代入数字求解即可得到两点间的距离；根据两点之间的距离得出其一半的长度，然后结合其中一个端点表示的数求解即可得中点表示的数；（2）先根据|a ﹣c |＝|b ﹣c |与a ≠b 推出C 为AB 的中点，然后根据题意分类讨论求解即可．【详解】解：（1）由题意，M ，N 间的距离为(222==； ∵2MN =， ∴112MN =，由题意知，在数轴上，M 点在N 点右侧， ∴MN 的中点表示的数为1；（2）∵1a c b c -=-=且ab ，∴数轴上点A 、B 与点C 不重合，且到点C 的距离相等，都为1， ∴点C 为AB 的中点，2AB =， ∵213d a -=， ∴32d a -=，即：数轴上点A 和点D 的距离为32，讨论如下：1>若点A位于点B左边：①若点D在点A左边，如图所示：此时，37222 BD AD AB=+=+=；②若点D在点A右边，如图所示：此时，31222 BD AB AD=-=-=；2>若点A位于点B右边：①若点D在点A左边，如图所示：此时，31222 BD AB AD=-=-=；②若点D在点A右边，如图所示：此时，37222 BD AD AB=+=+=；综上，线段BD的长度为12或72，故答案为：2；21；12或72．【点睛】本题考查数轴上两点间的距离，以及与线段中点相关的计算问题，理解数轴上点的特征以及两点间的距离表示方法，灵活根据题意分类讨论是解题关键．12．20﹣．【分析】观察已知等式，找出等式左边和右边的规律，再归纳总结出一般规律，由此即可得出答案．【详解】观察已知等式，等式左边的第一个数的规律为，第二个数的规律为：分子为，分母为等式右边的解析：20﹣208000= 401401．【分析】观察已知等式，找出等式左边和右边的规律，再归纳总结出一般规律，由此即可得出答案．【详解】观察已知等式，等式左边的第一个数的规律为1,2,3,，第二个数的规律为：分子为1,2,3,，分母为222112,215,3110,+=+=+=等式右边的规律为：分子为3331,2,3,，分母为222112,215,3110,+=+=+= 归纳类推得：第n 个等式为32211n n n n n -=++（n 为正整数）当20n =时，这个等式为322202020201201-=++，即20800020401401-= 故答案为：20800020401401-=．【点睛】本题考查了实数运算的规律型问题，从已知等式中归纳类推出一般规律是解题关键． 13．n ．【分析】根据已知等式，可以得出规律，猜想出第n 个等式，写出推导过程即可．【详解】解：＝n ．故答案为：n ．【点睛】此题主要考查了平方根的性质，利用已知得出数字之间的规律是解决问题的关解析：【分析】根据已知等式，可以得出规律，猜想出第n 个等式，写出推导过程即可．【详解】故答案为：【点睛】此题主要考查了平方根的性质，利用已知得出数字之间的规律是解决问题的关键． 14．-9【分析】直接利用已知运算法则计算得出答案．【详解】（﹣2）⊙6＝﹣2×（﹣2+6）﹣1＝﹣2×4﹣1＝﹣8﹣1＝﹣9．故答案为﹣9．【点睛】此题考察新定义形式的有理数计算，解析：-9【分析】直接利用已知运算法则计算得出答案．【详解】（﹣2）⊙6＝﹣2×（﹣2+6）﹣1＝﹣2×4﹣1＝﹣8﹣1＝﹣9．故答案为﹣9．【点睛】此题考察新定义形式的有理数计算，正确理解题意是解题的关键，依据题意正确列代数式计算即可.15．4【解析】根据题意可得（﹣2）※x=﹣2+2x，进而可得方程﹣2+2x=2+x，解得：x=4.故答案为：4．点睛：此题是一个阅读理解型的新运算法则题，解题关键是明确新运算法则的特点，然后直接根解析：4【解析】根据题意可得（﹣2）※x=﹣2+2x，进而可得方程﹣2+2x=2+x，解得：x=4.故答案为：4．点睛：此题是一个阅读理解型的新运算法则题，解题关键是明确新运算法则的特点，然后直接根据新定义的代数式计算即可.16．②④【分析】根据若表示不超过的最大整数，①取验证；②根据定义分析；③直接将代入，看左边是否等于右边；④以0为分界点，分情况讨论．【详解】解：①当x＝2.5时，[﹣2.5]＝﹣3，﹣[2.5]解析：②④【分析】根据若[]x 表示不超过x 的最大整数，①取 2.5x 验证；②根据定义分析；③直接将 2.75-代入，看左边是否等于右边；④以0为分界点，分情况讨论．【详解】解：①当x ＝2.5时，[﹣2.5]＝﹣3，﹣[2.5]＝﹣2，∴此时[﹣x ]与﹣[x ]两者不相等，故①不符合题意；②若[x ]＝n ，∵[x ]表示不超过x 的最大整数，∴x 的取值范围是n ≤x ＜n +1，故②符合题意；③将x ＝﹣2.75代入4x ﹣[x ]+5，得：4×（﹣2.75）﹣（﹣3）+5＝﹣3≠0，故③不符合题意；④当﹣1＜x ＜1时，若﹣1＜x ＜0，[1+x ]+[1﹣x ]＝0+1＝1，若x ＝0，[1+x ]+[1﹣x ]＝1+1＝2，若0＜x ＜1，[1+x ]+[1﹣x ]＝1+0＝1；故④符合题意；故答案为：②④．【点睛】本题主要考查取整函数的定义，是一个新定义类型的题，解题关键是准确理解定义求解． 17．或﹣5【分析】根据新定义运算法则，分情况讨论求解即可．【详解】解：当x ＞﹣2时，则有，解得：，成立；当x=﹣2时，则有，解得：x=3，矛盾，舍去；当x ＜﹣2时，则有，解得：x=﹣5，成立解析：12-或﹣5 【分析】根据新定义运算法则，分情况讨论求解即可．【详解】解：当x ＞﹣2时，则有()22(2)1x x -=--=※，解得：12x =-，成立；当x =﹣2时，则有()2(2)1x x -=+-=※，解得：x =3，矛盾，舍去；当x ＜﹣2时，则有()22(2)1x x -=⨯--=※，解得：x =﹣5，成立，综上，x =12-或﹣5，故答案为：12-或﹣5．【点睛】本题考查新定义下的实数运算、解一元一次方程，理解新定义运算法则，运用分类讨论思想正确列出方程是解答的关键．18．﹣8π．【分析】根据每次滚动后，所对应数的绝对值进行解答即可．【详解】解：半径为1圆的周长为2π，滚动第1次，所对应的周数为0﹣3＝﹣3（周），滚动第2次，所对应的周数为0﹣3﹣1＝﹣4解析：﹣8π．【分析】根据每次滚动后，所对应数的绝对值进行解答即可．【详解】解：半径为1圆的周长为2π，滚动第1次，所对应的周数为0﹣3＝﹣3（周），滚动第2次，所对应的周数为0﹣3﹣1＝﹣4（周），滚动第3次，所对应的周数为0﹣3﹣1＋2＝﹣2（周），滚动第4次，所对应的周数为0﹣3﹣1＋2﹣1＝﹣3（周），滚动第5次，所对应的周数为0﹣3﹣1＋2﹣1＋3＝0（周），滚动第6次，所对应的周数为0﹣3﹣1＋2﹣1＋3＋2＝2（周），所以圆与数轴的公共点到原点的距离最远是﹣4周，即该点所表示的数是﹣8π，故答案为：﹣8π．【点睛】题目主要考察数轴上的点及圆的滚动周长问题，确定相应滚动周数是解题关键．19．±3【分析】先通过估算确定M、N的值，再求M+N的平方根．【详解】解：∵，∴，∵，∴，∵，∴，∴a的整数值为：-1，0，1，2，M=-1+0+1+2=2，∵，∴，N=7解析：±3【分析】先通过估算确定M 、N 的值，再求M+N 的平方根．【详解】解：∵< ∴221， ∵∴23<，∵a <∴23a -<<，∴a 的整数值为：-1，0，1，2，M=-1+0+1+2=2， ∵∴78<，N=7，M+N=9，9的平方根是±3；故答案为：±3．【点睛】本题考查了算术平方根的估算，用“夹逼法”估算算术平方根是解题关键．20．【分析】根据“⊕”的含义，以及实数的运算方法，求出算式的值是多少即可．【详解】(⊕2)⊕3=⊕3=3，故答案为3．【点睛】本题考查了定义新运算，以及实数的运算，要熟练掌握，解答此题的关解析：【分析】根据“⊕”的含义，以及实数的运算方法，求出算式的值是多少即可．【详解】2)⊕3=3，故答案为3．【点睛】本题考查了定义新运算，以及实数的运算，要熟练掌握，解答此题的关键是要明确：在进行实数运算时，和有理数运算一样，要从高级到低级，即先算乘方、开方，再算乘除，最后算加减，有括号的要先算括号里面的，同级运算要按照从左到右的顺序进行．另外，有理数的运算律在实数范围内仍然适用．三、解答题21．（1）A；（2）①B；②C；③B；（3）①③．【分析】÷，结合计算结果即可进行判断；（1）计算20203（2）①从A类数中任取两个数进行计算，即可求解；②从A、B两类数中任取两个数进行计算，即可求解；③根据题意，从A类数中任意取出8个数，从B类数中任意取出9个数，从C类数中任意取出10个数，把它们的余数相加，再除以3，即可得到答案；（3）根据m，n的余数之和，举例，观察即可判断．【详解】解：（1）根据题意，÷=，∵202036731∴2020被3除余数为1，属于A类；故答案为：A．（2）①从A类数中任取两个数，如：（1+4）÷3=1…2，（4+7）÷3=3…2，……∴两个A类数的和被3除余数为2，则它们的和属于B类；②从A、B类数中任取一数，与①同理，如：（1+2）÷3=1，（1+5）÷3=2，（4+5）÷3=3，……∴从A、B类数中任取一数，则它们的和属于C类；③从A类数中任意取出8个数，从B类数中任意取出9个数，从C类数中任意取出10个数，把它们的余数相加，则⨯+⨯+=，8192026÷=，∴26382∴余数为2，属于B类；故答案为：①B；②C；③B．（3）从A类数中任意取出m个数，从B类数中任意取出n个数，余数之和为：m×1+n×2=m+2n，∵最后的结果属于C类，∴m+2n能被3整除，即m+2n属于C类，①正确；②若m=1，n=1，则|m-n|=0，不属于B类，②错误；③观察可发现若m+2n属于C类，m，n必须是同一类，③正确；综上，①③正确．故答案为：①③．【点睛】本题考查了新定义的应用和有理数的除法，解题的关键是熟练掌握新定义进行解答． 22．（1）2-，2；（2）①图见解析，5；②见解析【分析】（1）根据图1得到小正方形的对角线长，即可得出数轴上点A 和点B 表示的数（2）根据长方形的面积得正方形的面积，即可得到正方形的边长，再画出图象即可；（3）从原点开始画一个长是2，高是1的长方形，对角线长即是a ，再用圆规以这个长度画弧，交数轴于点M ，再把这个长方形向左平移3个单位，用同样的方法得到点N ．【详解】（1）由图1知，小正方形的对角线长是2，∴图2中点A 表示的数是2-，点B 表示的数是2，故答案是：2-，2；（2）①长方形的面积是5，拼成的正方形的面积也应该是5，∴正方形的边长是5，如图所示：故答案是：5；②如图所示：【点睛】本题考查无理数的表示方法，解题的关键是理解题意，模仿题目中给出的解题方法进行求解．23．（1）49515050⨯；2018202020192019⨯；（2）10102019. 【分析】（1）根据已知数据得出规律，2111111n n n ⎛⎫⎛⎫-=-+ ⎪⎪⎝⎭⎝⎭，进而求出即可；（2）利用规律拆分，再进一步交错约分得出答案即可．【详解】解：（1）21150-=49515050⨯； 2112019-=2018202020192019⨯；（2）2222111111112342019⎛⎫⎛⎫⎛⎫⎛⎫---⋅⋅⋅- ⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭=1324352018202022334420192019⨯⨯⨯⨯⨯⨯⨯⨯…… =1202022019⨯ =10102019. 【点睛】此题主要考查了实数运算中的规律探索，根据已知运算得出数字之间的变化规律是解决问题的关键．24．（1）2；5；（2）1，2，3；（3）3；（4）255【分析】（1（2）根据定义可知x ＜4，可得满足题意的x 的整数值；（3）根据定义对120进行连续求根整数，可得3次之后结果为1；（4）最大的正整数是255，根据操作过程分别求出255和256进行几次操作，即可得出答案．【详解】解：（1）∵22=4， 62=36，52=25,∴56，∴，，故答案为2，5；（2）∵12=1，22=4，且＝1，∴x=1，2，3，故答案为1，2，3；（3）第一次：，第二次：，第三次：，故答案为3；（4）最大的正整数是255，理由是：∵，，，∴对255只需进行3次操作后变为1，∵，，，，∴对256只需进行4次操作后变为1，∴只需进行3次操作后变为1的所有正整数中，最大的是255，故答案为255．【点睛】本题考查了估算无理数的大小的应用，主要考查学生的阅读能力和猜想能力，同时也考查了一个数的平方数的计算能力．25．（1）A；（2）①B；②C；③B；（3）①③．【分析】÷，结合计算结果即可进行判断；（1）计算20203（2）①从A类数中任取两个数进行计算，即可求解；②从A、B两类数中任取两个数进行计算，即可求解；③根据题意，从A类数中任意取出8个数，从B类数中任意取出9个数，从C类数中任意取出10个数，把它们的余数相加，再除以3，即可得到答案；（3）根据m，n的余数之和，举例，观察即可判断．【详解】解：（1）根据题意，÷=，∵202036731∴2020被3除余数为1，属于A类；故答案为：A．（2）①从A类数中任取两个数，如：（1+4）÷3=1…2，（4+7）÷3=3…2，……∴两个A类数的和被3除余数为2，则它们的和属于B类；②从A、B类数中任取一数，与①同理，如：（1+2）÷3=1，（1+5）÷3=2，（4+5）÷3=3，……∴从A、B类数中任取一数，则它们的和属于C类；③从A类数中任意取出8个数，从B类数中任意取出9个数，从C类数中任意取出10个数，把它们的余数相加，则⨯+⨯+=，8192026÷=，∴26382∴余数为2，属于B类；故答案为：①B；②C；③B．（3）从A类数中任意取出m个数，从B类数中任意取出n个数，余数之和为：m×1+n×2=m+2n，∵最后的结果属于C类，∴m+2n能被3整除，即m+2n属于C类，①正确；②若m=1，n=1，则|m-n|=0，不属于B类，②错误；③观察可发现若m+2n属于C类，m，n必须是同一类，③正确；综上，①③正确．故答案为：①③．【点睛】本题考查了新定义的应用和有理数的除法，解题的关键是熟练掌握新定义进行解答．26．(1) 4；(2)1;(2) ±12．【分析】（1（2a、b的值，再代入求出即可；（3的范围，求出x、y的值，再代入求出即可．【详解】解：（1）∵45，∴4，故答案为4；（2）∵2＜3，∴-2，∵34，∴b=3，∴；（3）∵100＜110＜121，∴1011，∴110＜111，∵，其中x是整数，且0＜y＜1，∴x=110，，∴+10=144，的平方根是±12．【点睛】键．27．（1）x7－1；（2）x n+1－1；（3）51312-．【分析】（1）仿照已知等式写出答案即可；（2）先归纳总结出规律，然后按规律解答即可；（3）先利用得出规律的变形，然后利用规律解答即可．【详解】解：（1）根据题意得：(x－1)(x6+x5+x4+x3+x2+x+1)=x7-1；（2）根据题意得：（x-1）（x"+x"-1+.…+x+1）=x"+1-1；（3）原式=12×（3-1）(1+3+32+···+349+350)=12×（x50+1-1）=51312-故答案为：（1）x7－1；（2）x n+1－1；（3）51312-．【点睛】本题考查了平方差公式以及规律型问题，弄清题意、发现数字的变化规律是解答本题的关键．28．（1）7；（2）5；（3）【分析】（1（2）分别确定出a、b的值，代入原式计算即可求出值；（3）根据题意确定出等式左边的整数部分得出y的值，进而求出y的值，即可求出所求．【详解】解：（1）∵78，∴7．故答案为：7．（2）∵34，∴3a，∵23，∴b＝2∴=5（3）∵23∴11＜12，∵，其中x是整数，且0﹤y＜1，∴x＝11，y＝，∴x-y＝＝【点睛】本题考查的是无理数的小数部分和整数部分及其运算．估算无理数的整数部分是解题关键．29．（1）2、3、4、5；（2）第n个等式为1+3+5+7+…+（2n+1）＝n2；（3）﹣1.008016×106．【分析】(1) 根据从1开始连续n各奇数的和等于奇数的个数的平方即可得到.(2) 根据规律写出即可.(3) 先提取符号，再用规律解题.【详解】解：（1）1+3＝221+3+5＝321+3+5+7＝421+3+5+7+9＝52……故答案为：2、3、4、5；（2）第n 个等式为1+3+5+7+…+（2n+1）＝2(1)n +（3）原式＝﹣（1+3+5+7+9+ (2019)＝﹣10102＝﹣1.0201×106．【点睛】本题考查数字变化规律，解题的关键是找到第一个的规律，然后加以运用即可.30．（1）23，1；（2）两位正整数为39，28，17，()f t 的最大值为47；（3）①2021；②2021【分析】（1）仿照样例进行计算即可；（2）由题设可以看出交换前原数的十位上数字为a ，个位上数字为b ，则原数可以表示为10a+b ，交换后十位上数字为b ，个位上数字为a ，则交换后数字可以表示为10b+a ，根据“交换其个位上的数字与十位上的数字得到的新数减去原数所得的差为54”确定出a 与b 的关系式，进而求出所有的两位数，然后求解确定出()f t 的最大值即可；（3）根据样例分解计算即可．【详解】解：（1）61623=⨯=⨯，∵6132->-，∴()263f =； 161162844=⨯=⨯=⨯∵1618244->->-，∴()161f =，故答案为：23；1；（2）由题意可得：交换后的数减去交换前的数的差为：10109()54b a a b b a +--=-=，∴6b a -=，∵19a b ≤≤≤，∴93b a ==，或82b a ==，或71b a ==，，∴t 为39，28，17；∵39＝1×39＝3×13，∴()33913f =； 28＝1×28＝2×14＝4×7，∴()28f ＝47； 17＝1×17，∴()11717f =； ∴()f t 的最大值47．（3）①∵223572021⨯⨯⨯=⨯∴()220235721f ⨯⨯⨯=； ②423574042⨯⨯⨯=⨯∴()4402023574221f ⨯⨯⨯==；故答案为：2021；2021 【点睛】本题主要考查了有理数的运算，理解最佳分解的定义，并将其转化为有理数的运算是解题的关键．。

初中数学鲁教版(五四制)七年级上册第四章实数1 无理数-章节测试习题(4)

章节测试题1.【答题】下列各数为无理数的是（）①-3.14159；②2.5；③2π；④；⑤A. ①②③B. ②③④C. ①④⑤D. ③④【答案】D【分析】本题考查了无理数．【解答】根据无理数的定义可得，只有③④是无理数，选D．2.【答题】下列各数中为无理数的是（）A. B. - C. 3.1415926 D.【答案】B【分析】本题考查了无理数．【解答】根据无理数的概念，无限不循环小数是无理数，及三种一般特点：开方开不尽的数，含有π的倍数的数，有规律但不循环的数，可知-是无理数．选：B．3.【答题】下列各数中，是无理数的（）A. πB. 0C.D. -【答案】A【解答】A选项中，π是无理数，故此选项正确；B选项中，0是有理数，故此选项错误；C选项中，=2，是有理数，故此选项错误；D选项中，是有理数，故此选项错误；选A.4.【答题】下列各式化简后，结果为无理数的是（）A. B. C. D.【答案】D【分析】本题考查了无理数．【解答】=8，=4，=3，=2，无理数为．选D．5.【答题】在实数：3.14159，，1.010010001，，，π，，中，无理数有（）A. 4个B. 1个C. 3个D. 2个【答案】D【解答】=4，，∴在实数：3.14159，，1.010010001，，，π，，中，无理数有π，，共2个．选D．6.【答题】下列说法正确的是（）A. 任何一个实数都可以用分数表示B. 无理数化为小数形式后一定是无限小数C. 无理数与无理数的和是无理数D. 有理数与无理数的积是无理数【答案】B【分析】本题考查了无理数与有理数．【解答】A.∵实数不都可以用分数表示，例如：无理数∴本选项错误．B. ∵无理数化为小数形式后一定是无限小数，∴本选项正确．C. ∵无理数与无理数的和不一定是无理数，例如：∴本选项错误．D. ∵有理数与无理数的积不一定是无理数，例如：∴本选项错误．选B．7.【答题】下列实数是无理数的是（）A. B. - C. 0 D. -1.010101 【答案】B【分析】本题考查了无理数．【解答】试题解析：是无理数．选B．8.【答题】下列4个数：，π，（）0，其中无理数是（）A. B. C. π D. （）0【答案】C【分析】本题考查了无理数．【解答】π是无理数，选C．9.【答题】下列各数中为无理数的是（）A. -1B. 3.14C. πD. 0【答案】C【分析】本题考查了无理数．【解答】π是圆周率，是无限不循环小数，所以π是无理数10.【答题】在下列各数：0.51525354…，，0.2，，中，无理数的个数是（）A. 2个B. 3个C. 4个D. 5个【答案】B【分析】本题考查了无理数．【解答】无理数是指无限不循环小数，本题中只有和是无理数，=0．9，=3．考点：无理数的判定11.【答题】下列实数中，无理数是（）A. 0B.C. -2D.【答案】B【分析】本题考查了无理数．【解答】解：0，-2，是有理数，数无理数，选B.12.【答题】下列各数中（相邻两个1之间有1个0）是无理数的有（）A. 2个B. 3个C. 4个D. 6个【答案】A【分析】本题考查了无理数．【解答】是无理数．选A．13.【答题】在实数中，无理数有（）A. 1个B. 2个C. 3个D. 4个【答案】A【分析】本题考查了无理数．【解答】无限不循环小数是无理数，所以无理数有：，共1个，选A．14.【答题】在以下实数1.212，1.010010001…，，，中无理数有（）A. 4个B. 3个C. 2个D. 1个【答案】B【分析】本题考查了无理数．【解答】解：无理数有：1.010010001…，，共3个．选B．15.【答题】在下列实数中，无理数是（）A. B. C. D. 0.2020020002【答案】C【分析】本题考查了无理数．【解答】为无理数，、、0.2020020002为有理数．选C．16.【答题】下列实数，0.010010001...中，无理数有______个．【答案】3【分析】本题考查了无理数．【解答】根据无理数的定义可得：，0.010010001..是无理数，共3个，故答案为：3．17.【答题】在，，，，，3.14，0.101001（相邻两个1之间的0的个数逐次加1中，无理数有______个．【答案】4【分析】本题考查了无理数．【解答】根据无理数的意义，可知，，，0.101001（相邻两个1之间的0的个数逐次加1）是无理数．共4个．故答案为：4．18.【题文】有下列各数：，3．1415，，0，，，1．3030030003……（每两个3之间多一个0）中，回答下列问题：（1）写出其中的无理数；（2）写出其中的整数；（3）按从小到大排列，并用“＜”连接．【答案】（1）无理数为：，1．3030030003……（每两个3之间多一个0）（2）整数为：，0，（3）【分析】按照无理数，整数的概念进行分类，再进行大小比较即可．【解答】（1）无理数为：（2）整数为：（3）大小关系为：19.【答题】下列各数：，，，，，0.101001…（每两个1之间的0逐渐增加一个），中，无理数有（）个．A. 3B. 4C. 2D. 1【答案】A【分析】本题考查了无理数．【解答】根据无限不循环小数是无理数，可知，，0.101001…（每两个1之间的0逐渐增加一个），共3个．选：A．20.【答题】下列实数中，是无理数的为（）A. 0B.C. -D. 3.14【答案】B【分析】本题考查了无理数．【解答】是无理数．选B.。

初中数学六年级上册 LJ

第一章丰富的图形世界1生活中的立体图形2展开与折叠3截一个几何体4从三个方向看物体的形状本章检测专项综合全练（一）第二章有理数及其运算1有理数2数轴3绝对值4有理数的加法5有理数的减法6有理数的加减混合运算7有理数的乘法8有理数的除法9有理数的乘方10科学记数法11有理数的混合运算12近似数13用计算器进行运算本章检测专项综合全练（一）期中测试（一）期中测试（二）第三章整式及其加减第四章一元一次方程期末测试答案全解全析第五章基本平面图形1线段、射线、直线2比较线段的长短3角4角的比较5多边形和圆的初步认识本章检测第六章整式的乘除1同底数幂的乘法2幂的乘方与积的乘方3同底数幂的除法4零指数幂与负整数指数幂5整式的乘法6平方差公式7完全平方公式8整式的除法本章检测期中复习专题整合期中测试第七章相交线与平行线1两条直线的位置关系2探索直线平行的条件3平行线的性质4用尺规作角本章检测第八章数据的收集与整理1数据的收集2普查和抽样调查3数据的表示4统计图的选择本章检测第九章变量之间的关系1用表格表示变量之间的关系2用表达式表示变量之间的关系3用图象表示变量之间的关系本章检测期末复习专题整合期末测试答案全解全析第一章三角形1认识三角形2图形的全等3探索三角形全等的条件4三角形的尺规作图5利用三角形全等测距离本章检测第二章轴对称1轴对称现象2探索轴对称的性质3简单的轴对称图形4利用轴对称进行设计本章检测第三章勾股定理1探索勾股定理2一定是直角三角形吗3勾股定理的应用举例本章检测期中复习专题整合期中测试第四章实数1无理数……第五章位置与坐标第六章一次函数期末测试答案全解全析第七章二元一次方程组1二元一次方程组2解二元一次方程组3二元一次方程组的应用4二元一次方程与一次函数5三元一次方程组本章检测第八章平行线的有关证明1定义与命题2证明的必要性3基本事实与定理4平行线的判定定理5平行线的性质定理6三角形内角和定理本章检测第九章概率初步1感受可能性2频率的稳定性3等可能事件的概率本章检测期中复习专题整合期中测试第十章三角形的有关证明1全等三角形2等腰三角形3直角三角形4线段的垂直平分线5角平分线本章检测第十一章一元一次不等式与一元一次不等式组1不等关系2不等式的基本性质3不等式的解集4一元一次不等式5一元一次不等式与一次函数6一元一次不等式组本奄检测期末复习专题整合期末测试答案全解全析初中数学八年级上册LJ（鲁教版）五四制第一章因式分解1 因式分解2提公因式法3公式法本章检测专项综合全练（一）第二章分式与分式方程1 认识分式2分式的乘除法3分式的加减法4分式方程本章检测专项综合全练（二）第三章数据的分析1 平均数2中位数与众数3从统计图分析数据的集中趋势4数据的离散程度本章检测期中测试（一）期中测试（二）第四章图形的平移与旋转1 图形的平移2图形的旋转3中心对称4图形变化的简单应用本章检测第五章平行四边形1 平行四边形的性质2平行四边形的判定3三角形的中位线4 多边形的内角和与外角和本章检测专项综合全练（三）期末测试（一）期末测试（二）答案全解全析初中数学五四制八年级下册LJ（鲁教版）第六章特殊平行四边形1菱形的性质与判定2矩形的性质与判定3正方形的性质与判定本章检测第七章二次根式1二次根式2二次根式的性质3二次根式的加减4二次根式的乘除本章检测期中复习专题整合期中测试第八章一元二次方程1一元二次方程2用配方法解一元二次方程3用公式法解一元二次方程4用因式分解法解一元二次方程5一元二次方程的根与系数的关系6一元二次方程的应用本章检测第九章图形的相似1成比例线段2平行线分线段成比例3相似多边形4探索三角形相似的条件5相似三角形判定定理的证明6黄金分割7利用相似三角形测高8相似三角形的性质9利用位似放缩图形本章检测期末复习专题整合期末测试初中数学九年级上册LJ（鲁教版）五四制第一章反比例函数1反比例函数2反比例函数的图象与性质3反比例函数的应用本章检测专项综合全练（一）专项综合全练（二）第二章直角三角形的边角关系1锐角三角函数230°，45°，60°角的三角函数值3用计算器求锐角的三角函数值4解直角三角形5三角函数的应用6利用三角函数测高本章检测专项综合全练（三）第三章二次函数1对函数的再认识2二次函数3二次函数y=ax2的图象与性质4二次函数y=ax2+bx+c的图象与性质期中测试（一）期中测试（二）5确定二次函数的表达式6二次函数的应用7二次函数与一元二次方程本章检测专项综合全练（四）第四章投影与视图1投影2视图本章检测期末测试（一）期末测试（二）答案全解全析初中数学五四制九年级下册LJ（鲁教版）第五章圆1 圆2圆的对称性3垂径定理4圆周角和圆心角的关系5确定圆的条件6直线和圆的位置关系7切线长定理8正多边形和圆期中测试（一）期中测试（二）9弧长及扇形的面积10圆锥的侧面积本章检测专项综合全练（一）专项综合全练（二）专项综合全练（三）第六章对概率的进一步认识1 用树状图或表格求概率2生活中的概率3用频率估计概率本章检测专项综合全练（四）期末测试（一）期末测试（二）答案全解全析初中语文六年级上册LJ（鲁教版）五四制第一单元第1课走一步，再走一步第2课生命生命第3课在山的那边第4课生命的意义第5课童趣第6课《论语》十则单元检测专项综合全练（一）第二单元第7课风筝第8课祖父、后园和我第9课冬夜的灯光第10课散步第11课诗两首第12课《世说新语》两则单元检测第三单元第13课春第14课济南的冬天第15课海滨仲夏夜第16课秋天第17课奔落的雪原第18课古代诗歌五首单元检测专项综合全练（二）期中测试（一）期中测试（二）第四单元第19课莺第20课看云识天气第21课斜塔上的实验第22课月亮上的足迹第23课科学24小时第24课山市单元检测专项综合全练（三）第五单元第25课皇帝的新装第26课郭沫若诗两首第27课女娲造人第28课盲孩子和他的影子第29课《伊索寓言》两则第30课古代寓言两则单元检测专项综合全练（四）期末测试（一）期末测试（二）答案全解全折初中语文六年级下册LJ（鲁教版）五四制第一单元第1课理想第2课短文两篇第3课人生寓言(节选)第4课我的信念第5课小溪流的歌第6课为学单元检测第二单元第7课从百草园到三味书屋第8课爸爸的花儿落了第9课胆小鬼第10课未选择的路一第11课十三岁的际遇第12课伤仲永单元检测第三单元第l3课黄河颂第14课最后一课第15课艰难的国运与雄健的国民第16课土地的誓言第17课失根的兰花第18课木兰诗单元检测期中复习专题整合期中测试第l9课伟大的悲剧第20课荒岛余生第21课登上地球之巅第22课真正的英雄第23课追求人类更大的自由第24课短文两篇单元检测第五单元第25课珍珠鸟第26课鹤群翔空第27课绿色蝈蝈第28课马第29课森林中的绅士第30课狼单元检测期末复习专题整合期末测试答案全解全析初中语文七年级上册LJ（鲁教版）第一单元1 社戏2 安塞腰鼓3 竹影4 观舞记——献给印度舞蹈家卡拉5 看戏6 12 技单元检测第二单元7 日稼先8 闻一多先生的说和做9 纪念白求恩10 音乐巨人贝多芬11 福楼拜家的星期天12 孙权劝学单元检测第三单元13 最出色的球员14 我打败了男子汉15 我的梦想16 门外观球18 纪昌学射单元检测第四单元19 向沙漠进军20 罗布泊，消逝的仙湖21 旅鼠之谜22 大雁归来23 死海不死24 枯叶蝴蝶单元检测第五单元25 桃花源记26 短文两篇27 核舟记28 卖油翁29 推敲30杜甫诗三首单元检测期中复习专题整合期中测试期末复习专题整合期末测试答案全解全析初中语文五四制七年级下册LJ（鲁教版）第一单元第1课云南的歌会第2课端午的鸭蛋第3课吆喝第4课春酒第5课俗世奇人第6课绝唱单元检测第二单元第7课雪第8课雷电颂第9课短文两篇第10课心田上的百合花开第11课海燕第12课雨之歌单元检测第三单元第13课事物的正确答案不止一个第14课应有格物致知精神第15课谈读书第16课不求甚解第17课怀疑与学问第18课中国人失掉自信力了吗单元检测第四单元第19课与朱元思书第20课五柳先生传第21课马说第22课送东阳马生序（节选）第23课诗词曲五首单元检测第五单元第24课小石潭记第25课岳阳楼记第26课醉翁亭记第27课满井游记第28课诗五首单元检测期中复习专题整合期中测试期末复习专题整合期末测试第一单元第1课藤野先生第2课我的母亲第3课4我的第一本书第4课列夫·托尔斯泰第5课再塑生命单元检测第二单元第6课敬业与乐业第7课最后一次演讲第8课悼念玛丽·居里第9课傅雷家书两则第10课致女儿的信单元检测第三单元第11课故乡第12课孤独之旅第13课我的叔叔于勒第l4课心声第15课白色鸟单元检测第四单元第16课陈涉世家第17课唐雎不辱使命第18课隆中对第19课出师表第20课词五首单元检测第五单元第21课公输第22课《孟子》两章第23课鱼我所欲也第24课《庄子》故事两则第25课扁鹊见蔡桓公单元检测期中复习专题整合期中测试期末复习专题整合期末测试答案全解全析第一单元第1课沁园春雪第2课雨说第3课星星变奏曲第4课外国诗两首第5课桂林山水歌单元检测第二单元第6课谈生命第7课那树第8课地下森林断想第9课人生第10课落叶单元检测第三单元第11课孔乙己第12课蒲柳人家（节选）第13课变色龙第14课热爱生命（节选）单元检测期中复习专题整合期中测试第四单元第15课晏子使楚第16课童区寄传第17课西门豹治邺第18课陌上桑单元检测第五单元第19课诫子书第20课西湖游记两则第21课墨池记第22课少年中国说单元检测期末复习专题整合期末测试答案全解全析第一单元第1课诗两首第2课中国的土地第3课我用残损的手掌第4课祖国啊，我亲爱的祖国第5课外国诗两首单元检测第二单元第6课威尼斯商人（节选）第7课变脸（节选）第8课枣儿第9课音乐之声（节选）第10课陈毅市长（节选）单元检测第三单元第11课智取生辰纲第12课杨修之死第13课范进中举第14课香菱学诗单元检测第四单元第15课触龙说赵太后第16课捕蛇者说第17课卖柑者言第18课黄生借书说单元检测第五单元第19课曹刿论战第20课邹忌讽齐王纳谏第21课愚公移山第22课《诗经》两首单元检测期中复习专题整合期中测试期末复习专题整合期末测试答案全解全析初中英语六年级上册LJ（鲁教版）五四制Unit l Good morning!Section ASection B＆Self Check单元检测Unit 2 What’S this in English7Section A 。

数学分析课本-习题及答案01

第一章实数集与函数习题§1实数1、设a 为有理数，x 为无理数。

证明：（1）a+ x 是无理数；（2）当a ≠0时，ax 是无理数。

2、试在数轴上表示出下列不等式的解：（1）x （2x -1）>0；（2）|x-1|<|x-3|；（3）1-x -12-x ≥23-x 。

3、设a 、b ∈R 。

证明：若对任何正数ε有|a-b|<ε，则a = b 。

4、设x ≠0，证明|x+x1|≥2，并说明其中等号何时成立。

5、证明：对任何x ∈R 有（1）|x-1|+|x-2|≥1；（2）|x-1|+|x-2|+|x-3|≥2。

6、设a 、b 、c ∈+R （+R 表示全体正实数的集合）。

证明 |22b a +-22c a +|≤|b-c|。

你能说明此不等式的几何意义吗7、设x>0，b>0，a ≠b 。

证明x b x a ++介于1与ba 之间。

8、设p 为正整数。

证明：若p 不是完全平方数，则p 是无理数。

9、设a 、b 为给定实数。

试用不等式符号（不用绝对值符号）表示下列不等式的解：（1）|x-a|<|x-b|；（2）|x-a|< x-b ；（3）|2x -a|<b 。

§2数集、确界原理1、用区间表示下列不等式的解：（1）|1-x|-x ≥0；（2）| x+x1|≤6；（3）（x-a ）（x-b ）（x-c ）>0（a ，b ，c 为常数，且a<b<c ）；（4）sinx ≥22。

2、设S 为非空数集。

试对下列概念给出定义：（1）S 无上界；（2）S 无界。

3、试证明由（3）式所确定的数集S 有上界而无下界。

4、求下列数集的上、下确界，并依定义加以验证：（1）S={x|2x <2}；（2）S={x|x=n ！，n ∈+N }；（3）S={x|x 为（0，1）内的无理数}；（4）S={x|x=1-n21，n ∈+N }。

人教版数学七年级下册-第六章《实数》单元测试(含答案)

第六章《实数》单元测试姓名：班级：座号：一、单选题（共8题；共32分）1. 9的算术平方根是（）A. 81B. ±81C. 3D. ±32. -8的立方根是（）A. B. C.D.3.在，1.01001000100001，2 ，3.1415，- ，，0，，这些数中，无理数共有（）A. 2个B. 3个C. 4个D. 5个4.下列说法中错误的是( )A. 0的算术平方根是0B. 36的平方根为±6C.D. -4的算术平方根是-25.已知a2=25， =7，且|a+b|=a+b，则a﹣b的值为（）A. 2或12B. 2或﹣12C. ﹣2或12D. ﹣2或﹣126.，则a与b的关系是（）A. B. a与b相等 C. a与b互为相反数 D. 无法判定7.下列计算或说法：①±3都是27的立方根；②=a；③的立方根是2；④=±4，其中正确的个数是（）A. 1个B. 2个C. 3个 D. 4个8.下列六种说法正确的个数是（）①无限小数都是无理数；②正数、负数统称实数；③无理数的相反数还是无理数；④无理数与无理数的和一定还是无理数；⑤无理数与有理数的和一定是无理数；⑥无理数与有理数的积一定仍是无理数．A. 1B. 2C. 3 D . 4二、填空题（共24分）1.算术平方根等于本身的实数是________.2.﹣125的立方根是________．3.比较大小：﹣π________﹣3.14（选填“＞”、“=”、“＜”）．4.某正数的平方根是n+l和n﹣5，则这个数为________．5.已知一个正数的两个平方根是x﹣7和3x﹣1，则x的值是________．6.方程（x﹣1）3﹣8=0的根是 ________7.若=2﹣x，则x的取值范围是________；若3+ 的小数部分是m，3﹣的小数部分是n，则m+n=________．三、求下列各式中x的值（共10分）（1）（2x﹣1）2=9 （2）2x3﹣6=四、解答题（共10分）1.已知某数的平方根是a+3和2a﹣15，求1﹣7a的立方根。

(完整版)人教版初中数学目录(四年制)

人教版（五四制）初中数学目录六年级上册第一章分数乘法1.1 分数乘法 1.1.1 分数与整数相乘；1.1.2 一个数乘分数；1.1.3 混合运算及运算定律1.2 倒数的认识1.3 分数乘法的应用第二章分数除法2.1 分数除法2.1.1分数除法的意义；2.1.2分数除以整数；2.1.3一个数除以分数2.2 混合运算2.3 分数除法的应用2.4 比2.4.1比的意义；2.4.2比的基本性质；2.4.3比的应用第三章圆的初步认识3.1 认识圆3.2 圆的周长3.3 圆的面积3.4 扇形第四章百分数4.1 百分数的意义和写法4.2 百分数和小数、分数的互化4.2.1 百分数与小数互化；4.2.2 百分数与分数互化4.3 百分数的应用4.3.1一般的百分数问题；4.3.2折扣；4.3.3税率；4.3.4 利率4.4 扇形统计图第五章圆柱和圆锥5.1 圆柱 5.1.1圆柱的认识；5.1.2圆柱的表面积；5.1.3圆柱的体积5.2 圆锥 5.2.1圆锥的认识；5.2.2圆锥的体积第六章比例6.1 比例的意义和基本性质6.1.1比例的意义；6.1.2比例的基本性质；6.1.3解比例6.2 正比例和反比例的意义6.2.1成正比例的量；6.2.2成反比例的量6.3 比例的应用6.3.1比例尺；6.3.2用比例解决问题六年级下册第七章有理数7.1 正数和负数7.2 有数7.2.1有理数；7.2.2数轴；7.2.3相反数；7.2.4绝对值7.3 有理数的加减法7.3.1有理数的加法；7.3.2有理数的减法7.4 有理数的乘除法7.4.1有理数的乘法；7.4.2有理数的除法7.5 有理数的乘方7.5.1乘方；7.5.2科学计数法；7.5.3近似数第八章整式的加减8.1 整式8.2 整式的加减第九章图形认识初步9.1 多姿多彩的图形9.2 直线、射线、线段9.3 角第十章数据的收集、整理与描述10.1 统计调查10.2 直方图七年级上册第十一章一元一次方程11.1 从算式到方程11.2 解一元一次方程（一）11.3 解一元一次方程（二）11.4 一元一次方程与实际问题第十二章：相交线与平行线12.1 相交线12.2 平行线及其判定12.3 平行线的性质12.4 平移第十三章：实数13.1 平方根13.2 立方根13.3 实数第十四章平面直角坐标系14.1 平面直角坐标系14.2 平面直角坐标系的简单应用七年级下册第十五章二元一次方程组15.1 二元一次方程组15.2 消元——解二元一次方程组15.3 二元一次方程组与实际问题15.4 三元一次方程组的解法第十六章不等式及不等式组16.1 不等式16.1.1不等式及其解集；16.1.2不等式的性质16.2 一元一次不等式16.3 一元一次不等式组第十七章三角形17.1 与三角形有关的线段17.1.1三角形的边17.1.2三角形的高、中线和角平分线17.1.3三角形的稳定性17.2 与三角形有关的角17.2.1三角形的内角；17.2.2 三角形的外角17.3 多边形及其内角和17.3.1 多边形；17.3.2 多边形的内角和第十八章全等三角形18.1 全等三角形18.2 三角形全等的判定18.3 角的平分线的性质第十九章数据的分析19.1 数据的集中趋势19.1.1平均数；19.1.2中位数和众数19.2 数据的波动程度19.3 课题学习体质健康测试中的数据分析八年级上册第二十章轴对称20.1 轴对称20.2 画轴对称图形20.2.1作轴对称图形；20.2.2 用坐标表示轴对称20.3 等腰三角形20.3.1等腰三角形；20.3.2等边三角形第二十一章整式的乘法与因式分解21.1 整式的乘法21.1.1同底数幂的乘法21.1.2幂的乘方21.1.3积的乘方21.1.4整式的乘法21.2 乘法公式21.2.1平方差公式21.2.2完全平方公式21.3 因式分解21.3.1提公因式法21.3.2 公式法第二十二章分式22.1 分式22.1.1从分数到分式22.1.2分式的基本性质22.2 分式的运算22.2.1分式的乘除22.2.2分式的加减22.2.3整数指数幂22.3 分式方程第二十三章二次根式23.1 二次根式23.2 二次根式的乘除22.3 二次根式的加减八年级下册第二十章四一次函数24.1 变量与函数24.1.1变量与函数24.2 一次函数24.2.1正比例函数；24.2.2一次函数24.3 用函数观点看方程（组）与不等式24.3.1 一次函数与一元一次方程24.3.2 一次函数与一元一次不等式24.3.3 一次函数与二元一次方程组第二十五章一元二次方程25.1 一元二次方程25.2 降次------解一元二次方程25.2.1配方法25.2.2公式法25.2.3 因式分解法25.3 实际问题与一元二次方程第二十六章勾股定理26.1 勾股定理26.2 勾股定理的逆定理第二十七章四边形27.1 平行四边形27.1.1 平行四边形的性质27.1.2 平行四边形的判定27.2 特殊的平行四边形27.2.1 矩形27.2.2 菱形27.2.3 正方形27.3 梯形九年级上册第二十八章二次函数28.1二次函数的图象和性质28.1.1二次函数28.1.2二次函数y=ax²的图象和性质28.1.3二次函数y=a(x-h)²+k的图象和性质 28.1.4二次函数y=ax²+bx+c的图象和性质28.2二次函数与一元二次方程28.3二次函数与实际问题第二十九章反比例函数29.1 反比例函数29.1.1反比例函数29.1.2反比例函数的图象和性质29.2 反比例函数与实际问题第三十章旋转30.1图形的旋转30.2中心对称30.2.1中心对称30.2.2中心对称图形30.2.3关于原点对称的点的坐标30.3 课题学习图案设计第三十一章圆31.1圆的有关性质31.1.1圆31.1.2垂直于弦的直径31.1.3弧、弦、圆心角31.1.4圆周角31.2点和圆、直线和圆的位置关系31.2.1点和圆的位置关系31.2.2直线和圆的位置关系31.2.3圆和圆的位置关系31.3正多边形和圆31.4弧长和扇形面积第三十二章概率初步32.1随机事件与概率32.1.1随机事件32.1.2概率32.2用列举法求概率32.3用频率估计概率九年级下册第三十三章相似33.1图形的相似33.2相似三角形33.3位似第三十四章锐角三角形函数34.1锐角三角函数34.2解直角三角形第三十五章投影与视图35.1投影35.2三视图35.3课题学习制作立体模型。

人教版初中数学目录(新课标)

第二十九章投影与视图 29.1 投影 29.2 三视图阅读与思考视图的产生与应用 29.3 课题学习制作立体模型数学活动小结复习题 29
20.3 课题学习体质健康测试中的数据分析
数学活动小结复习题 20
10.1 平方根 10.2 立方根 10.3 实数
上八
年
级
上九
年
级
上
---------------------------------
--------------------------------
第十一章一次函数
第二十一章二次根式
11.1 变量与函数
11.2 一次函数 11.3 用函数观点看方程与不等式第十二章数据的描述
20.1 数据的代表 20.2 数据的活动信息技术应用用计算机求几种统计量阅读与思考数据波动的几种度量
26.1 二次函数 26.2 用函数观点看一元二次方程 26.3 实际问题与二次函数第二七章相似 27.1 图形的相似 27.2 相似三角形 27.3 位似第二十八章锐角三角函数 28.1 锐角三角函数 28.2 解直角三角形数学活动小结复习题 28
16.1 分式 16.2 分式的运算 16.3 分式方程第十七章反比例函数 17.1 反比例函数 17.2 实际问题与反比例函数第十八章勾股定理
18.1 勾股定理阅读与思考勾股定理的证明 18.2 勾股定理的逆定理第十九章四边形 19.1 平行四边形 19.2 特殊的平行四边形 19.3 梯形 19.4 课题学习重心，第二十章数据的分析
初中人教版数学目录
七
年
级
-------------------------------第一章有理数
1.1 正数和负数 1.2 有理数 1.3 有理数的加减法 1.4 有理数的乘除法

初中数学总复习分章节测试题与答案(完整版)

2012年第一章有理数的概念一、选择题：1．下列命题中，正确的是（）Ａ有限小数是有理数Ｂ无限小数是无理数Ｃ数轴上的点与有理数一一对应Ｄ数轴上的点与实数一一对应2．四位同学画数轴如下图所示，你认为正确的是（）A B C D3．下列说法正确的是（） A 绝对值较大的数较大 B 绝对值较大的数较小 C 绝对值相等的两数相等 D 相等两数的绝对值相等4．若a 与b 互为相反数，则下列式子成立的是（） A 0=-b a B 1=+b a C 0=+b a D .0=ab5．数轴上原点和原点左边的点表示的数是（） A 负数 B 正数 C 正数或零 D 负数或零6．下列比较中，正确的是（）A331212-<<- B212313-<<- C 210->-> D 201-><- 7．a--是一个（）Ａ正数Ｂ负数Ｃ正数或零Ｄ负数或零8．下列命题中正确的是（）Ａ 3和－是互为相反数Ｂ 3和－3是互为倒数Ｃ绝对值为3的数是－3Ｄ－3的绝对值是39．数x 由四舍五入得到的近似数是35．0，数x 不可能是（）Ａ 35．049 Ｂ 34．974Ｃ 35．052 Ｄ 34．95910．若a 为实数，下列代数式中，一定是负数的是（）Ａ 2a - Ｂ 2)1(+-a Ｃ a - Ｄ )1(+--a11．若)(21++n m b a ·)(35212b a b a m n =-，则n m +的值为（）Ａ 1 Ｂ 2 Ｃ 3 Ｄ－312．据6月4日《苏州日报》报道，今年苏州市商品房销售量迅速增加，1～4月商品房销售金额高达1 711 000 00O 元，这个数用科学计数法表示是（）A 1.711×610B 1.711×910C 1.711×1010D 1711×61013．在0，1-，1，2的四个数中，最小的数是（） A. 0 B 1- C 1 D. 214．张玲身高h ，由四舍五入后得到的近似数为1.5米，正确表示h 的值是（） A 1.43米 B 1.56米 C 1.41≤ h ≤ 1.51 D 1.41≤ h <1.55 二、填空题：14．2001年3月，国家统计局公布我国总人口为129533万人．如果以亿为单位保留两位小数，可以写成约为____________亿人；15．计算：)3()20()100(---⨯-＝；16．2)1(-的相反数是_______；17．已知5,10=-=b a ，代数式)(b a --的值是； 18．如果ba b a ><<,0,0，那么0____b a -；如果ba b a <<<,0,0，那么___b a -0；19．21的倒数的相反数的3次幂等于；20．把3729000-用科学记数法可表示为； 21．41030.3⨯有个有效数字，它精确到位； 22．方程275=+x 的解的2003次幂是； 23．若0<m ，则_____=+m m ，若0>m ，则______=+m m ，若0=m ，则______=+m m ；24．0)4(|3||2|2=+-+-++z y x ，则.____=+zy x x 25．观察下列算式：21＝2；22＝4；23＝8；24＝16；25＝32；26＝64；27＝128；28＝256；……通过观察，用你所发现的规律写出811的末位数字是；26．已知：1＋3＝22；1＋3＋5＝32；1＋3＋5＋7＝42；1＋3＋5＋7＋9＝52； ……… 根据前面各式的规律，可猜测：1＋3＋5＋7＋…＋_____12=+n ；27．观察下列等式：41314313121321211211－＝；－＝；－＝⨯⨯⨯; ……。

人教版七年级数学下册15.实数全章复习与巩固(提高)巩固练习及答案.doc

【若缺失公式、图片现象属于系统读取不成功，文档内容齐全完整，请放心下载。

】【巩固练习】一.选择题1．已知a 、b 是实数，下列命题结论正确的是（） A ．若a ＞b ，则2a ＞2bB ．若a ＞｜b ｜，则2a ＞2bC ．若｜a ｜＞b ，则2a ＞2b D ．若3a ＞3b ，则2a ＞2b 2.下列式子表示算术平方根的是（）． ①()233-= ②()()2515--= ③93104-=- ④ 255-= ⑤ 0.010.1±=± ⑥ ()20a a a =≥A ．①②④B ．①④⑥C ．①⑤⑥D ．①②⑥ 3. 下列说法正确的有（）①无限小数不一定是无理数； ②无理数一定是无限小数； ③带根号的数不一定是无理数； ④不带根号的数一定是有理数. A ①②③ B ②③④ C ①③④ D ①②④4. 下列语句、式子中 ① 4是16的算术平方根，即.416=±②4是16的算术平方根，即.416=③－7是49的算术平方根，即.7)7(2=-④7是2(7)-的算术平方根，即.7)7(2=-其中正确的是（）A. ①③B. ②③C. ②④D. ①④ 5. （2015•南京）估计介于（）A ．0.4与0.5之间B ．0.5与0.6之间C ．0.6与0.7之间D ．0.7与0.8之间6.下列运算中正确的是（）4913=12622-82==）（C. 24±=D. ∣32-∣＝23- 7. 已知:a a 则，且,68.2868.82.62333=-=＝（） A.2360 B.－2360 C.23600 D.－23600 8. －2781 ） A ．0 B ．6C ．6或－12D ．0或6 二.填空题9. 下列命题中正确的有 (填序号)(1)若,b a >那么b a 22>; (2)两数的和大于等于这两数的差;(3)若,b a >那么22b a >; (4)若,b a > c b >则c a >;(5))()(c b a c b a ++=++ (6)一个数越大,这个数的倒数越小; (7)有理数加有理数一定是有理数; (8)无理数加无理数一定是无理数; (9)无理数乘无理数一定是无理数; 10.（2015•庆阳）若﹣2xm ﹣n y 2与3x 4y2m+n是同类项，则m ﹣3n 的立方根是．11. 若22)3(-=a ，则a ＝，若23)3(-=a ，则a ＝ .12. 已知 :===00236.0,536.136.2,858.46.23则 . 13. 若x x -+有意义，则=+1x ________.14. 阅读下列材料：设0.30.333x ==…①，则10 3.333x =…②，则由②－①得：93x =，即13x =.所以0.30.333= (1)=3.根据上述提供的方法把下列两个数化成分数. 0.7＝ 1.3＝；15. 方程 361(12)164x +-=的解x ＝ _________ . 16. 若,19961995a a a =-+-则21995-a 的值等于_________.三.解答题17. （2015春•和平区期末）已知一个正数的两个平方根分别为a 和2a ﹣9 （1）求a 的值，并求这个正数；（2）求17﹣9a 2的立方根．18. 如图所示，已知A 、B 两点的坐标分别为(5,0)A -，(2,1)B -．（1）求△OAB 的面积和△ACB 的面积（结果保留一位小数）；（2）比较点A 所表示的数与－2.4的大小．19. 把下列无限循环小数化成分数：（1）0.6•（2）0.23••（3）0.107••20．细心观察右图，认真分析各式，然后解答问题：()()212211122===+，S ； ()()223312222===+，S； ()()234413322===+，S； ……，……；（1）请用含n(n 为正整数)的等式表示上述变化规律；（2）观察总结得出结论：三角形两条直角边与斜边的关系，用一句话概括为：；（3）利用上面的结论及规律，请作出等于7的长度；（4）你能计算出210232221S S S S ++++ 的值吗？【答案与解析】一.选择题1. 【答案】B ；【解析】B 答案表明,||||a b a b >>且，故2a ＞2b . 2. 【答案】D ；【解析】算术平方根的专用记号是“a ”根号前没有“－”或“±”号. 3. 【答案】A ； 4. 【答案】C ；【解析】算术平方根是平方根中符号为正的那个. 5.【答案】C ．【解析】∵ 2.235，∴﹣1≈1.235，∴≈0.617，∴介于0.6与0.7之间.6. 【答案】D ；7. 【答案】D ；O.....S 5S 4S 3S 2S 1111111A 6A 5A 4A 3A 2A 1【解析】2.868向右移动1位，23.6应向右移动3位得23600，考虑到符号，a ＝－23600. 8. 【答案】A ；【解析】819=，9的算术平方根是3，故选A. 二.填空题 9. 【答案】（1），（4），（5），（7）； 10.【答案】2. 【解析】若﹣2xm ﹣n y 2与3x 4y2m+n是同类项，∴，解方程得：．∴m ﹣3n=2﹣3×（﹣2）=8．8的立方根是2．故答案为：2． 11.【答案】3±39【解析】正数的平方根有2个，实数有一个与它符号相同的立方根. 12.【答案】0.04858【解析】23.6向左移动4位，4.858向左移动2位得0.04858. 13.【答案】1；【解析】x ≥0，－x ≥0，得x ＝0，所以=+1x 1. 14.【答案】74;93；【解析】设x ＝0.777……，10x ＝7.777……，9x ＝7, x ＝79.设y ＝1.333……，10y ＝13.333……，9y ＝12, y ＝43. 15.【答案】18；【解析】()31255112,12,6448x x x +=+==. 16.【答案】1996；1996a -a ≥1996，原式＝a －19951996a -a 1996a -1995，两边平方得21995-a ＝1996. 三.解答题17.【解析】解：（1）由平方根的性质得，a+2a ﹣9=0，解得a=3，∴这个正数为32=9；（2）当a=3时，17﹣9a 2=﹣64， ∵﹣64的立方根﹣4， ∴17﹣9a 2的立方根为﹣4． 18.【解析】解：（1）∵ (5,0)A ，(2,1)B -，∴ ||5OA =BC ＝1，AC ＝OA －OC 52．∴ 115||||51 1.122OAB S OA BC ∆===≈． 115||||(52)110.1222ACB S AC BC ∆==⨯⨯=-≈．（2）点A 表示的实数为5-5 2.24-≈-． ∵ 2.24＜2.4，∴ －2.24＞－2.4，即 5 2.4>- 19.【解析】解：(1) 设0.6x •= ① 则10x ＝6.6•② ②－①得 9x ＝6∴6293x ==，即20.63•=(2) 设0.23x ••= ① 则10023.23x ••= ② ②－①，得 99x ＝23∴2399x =，即230.2399••=. (3) 设0.107x ••= ① 则1000107.107x ••= ② ②－①，得 999x ＝107，∴107999x =，即1070.107999••=. 20.【解析】解：（1）()2,112nS n n n =+=+．（2）直角三角形中，两条直角边的平方和等于斜边的平方．（3）略．22222222123101231055(4)22224S S S S ⎛⎫⎛⎫⎛⎫⎛⎫++++=+++= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭初中奥数题试题一一、选择题（每题1分，共10分）1．如果a，b都代表有理数，并且a＋b=0，那么 ( )A．a，b都是0 B．a，b之一是0C．a，b互为相反数 D．a，b互为倒数2．下面的说法中正确的是 ( )A．单项式与单项式的和是单项式B．单项式与单项式的和是多项式C．多项式与多项式的和是多项式D．整式与整式的和是整式3．下面说法中不正确的是 ( )A. 有最小的自然数 B．没有最小的正有理数C．没有最大的负整数 D．没有最大的非负数4．如果a，b代表有理数，并且a＋b的值大于a－b的值，那么 ( )A．a，b同号 B．a，b异号 C．a＞0 D．b＞05．大于－π并且不是自然数的整数有 ( )A．2个 B．3个 C．4个 D．无数个6．有四种说法：甲．正数的平方不一定大于它本身；乙．正数的立方不一定大于它本身；丙．负数的平方不一定大于它本身；丁．负数的立方不一定大于它本身。

(完整版)初中数学教材章节-人教版

七年级上册（人教版）第一章有理数1、正数和负数2、有理数（有理数、数轴、相反数、绝对值）3、有理数的加减法（加法法则、交换律、结合律）4、有理数的乘除（倒数、交换律、结合律、分配律）5、有理数的乘方（幂、近似数）第二章整式的加减1、整式（单项式、多项式）2、整式的加减（同类项、合并同类项）第三章一元一次方程1、从算式到方程（一元一次方程、等式的性质）2、解一元一次方程-合并同类项与移项3、解一元一次方程-去括号去分母4、实际问题与一元一次方程第四章几何图形的初步1、几何图形（立体图形、平面图形、三视图、点线面体）2、直线、射线、线段（相交）3、角（度、分、秒、角的比较与运算、角平分线、余角、补角）4、课题设计-设计制作长方形形状的包装纸盒七年级下册第五章相交线与平行线1、相交线（邻补角、对顶角、垂线、同位角、内错角、同旁内角）2、平行线及其判定（3个判定）3、平行线的性质（3个性质、命题、定理、证明）4、平移第六章实数1、平方根（算术平方根）；2、立方根；3、实数（无理数）第七章平面直角坐标系1、平面直角坐标系（有序数对、坐标系、原点、横轴、纵轴）2、坐标方法的简单应用（位置、平移）第八章二元一次方程组1、二元一次方程组2、消元-解二元一次方程组3、实际问题与二元一次方程组4、三元一次方程组的解法第九章不等式1、不等式（解集、不等式的性质3个）2、一元一次不等式3、一元一次不等式组第十章数据的收集、整理与描述1、统计调查（全面调查、抽样调查、简单随机抽样）2、直方图（组距、频数）；3、课题学习-从数据谈节水八年级上册第十一章三角形1、与三角形有关的线段（三边关系、高、中线、角平分线、重心、稳定性）2、与三角形有关的角（内角和、外角）3、多边形及其内角和（多边形、内角和、外角和360°）第十二章全等三角形1、全等三角形（全等形、性质、）2、三角形全等的判定（SSS 、SAS 、AAS 、ASA 、HL ）3、角的平分线的性质第十三章轴对称1、轴对称（对称点、垂直平分线、对称轴、垂直平分线的性质）2、画轴对称图形3、等腰三角形（性质、等边三角形、30°的直角三角形）4、课题学习-最短路径的问题第十四章整式的乘法与因式分解1、整式的乘法（同底数幂的乘法、幂的乘方、积的乘方、单项式/多项式×单项式/多项式）2、乘法公式（平方差、完全平方公式）3、因式分解（分解因式、提公因式法、公式法）第十五章分式1、分式（分数-分式、性质、约分、最简分式、通分、最简公分母）2、分式的运算（乘除法则、加减法则、整数指数幂）3、分式的方程（检验）八年级下册第十六章二次根式1、二次根式（()的区别与22a a 、代数式）2、二次根式的乘除（最简二次根式）3、二次根式的加减（同类二次根式）第十七章勾股定理1、勾股定理2、勾股定理的逆定理第十八章平行四边形1、平行四边形（性质、判定、三角形中位线）2、特殊的平行四边形（矩形、直角三角形的中线、菱形、正方形）第十九章一次函数1、函数（变量、函数、解析式、图像）2、一次函数（正比例函数、一次函数、待定系数法、一次函数与方程/不等式）3、课题学习-选择方案第二十章数据的分析1、数据的集中趋势（平均数、中位数、众数）2、数据的波动程度（方差）3、课题学习-体质健康测试中的数据分析九年级上册第二十一章一元一次方程1、一元一次方程（定义、根）2、解一元一次方程（配方法、公式法、判别式、因式分解法、根与系数的关系）3、实际问题与一元二次方程第二十二章二次函数1、二次函数的图象和性质2、二次函数与一元一次方程3、实际问题与二次函数第二十三章旋转1、图形的旋转2、中心对称（关于原点对称的点的坐标）3、课题学习-图形设计第二十四章圆1、圆的有关性质（圆心、半径、弦、等圆、垂直弦的直径、圆心角、圆周角）2、点和圆、直线和圆的位置关系3、正多边形和圆4、弧形和扇形面积第二十五章概率初步1、随机事件与概率2、用列举法求概率3、用频率估计概率九年级下册第二十六章反比例函数1、反比例函数（图像、性质）2、实际问题与反比例函数第二十七章相似1、图形的相似（相似比）2、相似三角形（判定、性质、应用）3、位似（位似图形、位似中心）第二十八章锐角三角函数1、锐角三角函数2、解直角三角形及其应用第二十九章投影与视图1、投影（平行投影、中心投影、正投影）2、三视图3、课题学习-制作立体模型。

初中数学专题训练--实数--《有理数》本章测试

《有理数》本章测试与巩固练习一、选择题：1．下列说法正确的是（）（A ）整数包括正整数和负整数（B ）分数包括正分数和负分数（C ）1是最小的有理数（D ）符号相反的数互为相反数2．c b a -,,表示的数如图所示，则c b a -,,由小到大的顺序为（）（A ）b c a ,,- （B ）c a b -,, （C ）c b a -,, （D ）a c b ,,-3．若a a -=，则a 一定是（）（A ）正数（B ）负数（C ）非负数（D ）非正数4．一个数的倒数的相反数是524，则这个数是（）（A ）522- （B ）522 （C ）225- （D ）2255．计算200020032003)1(1)1()1(-+-÷-+-的值为（）（A ）0 （B ）1 （C ）－1 （D ）2二、填空题：1．若赢利2 000元记作＋2 000元，则亏损800元记作__________； 2．计算____2123____,59=+-=--； 3．存折中有4 500元，取出1 300元，又存入800元，则存折中还有___________元； 4．_________的倒数是它本身；5．近似数51060.9⨯精确到________位，有效数字是_________。

三、解答题：1．在数轴上表示下列各数，并按从大到小的顺序用“＞”把这些数连接起来：3-，－5，213，－2.5，2)2(--，－（－1），0 2．按括号内的要求，用四舍五入法对下列各数取近似数：（1）2.879（精确到百分位）（2）9.527（精确到0.1）（3）0.036 403（保留3个有效数字）（4）17 249（精确到千位） 3．计算：（1）314)14.0(314+-+⎪⎭⎫ ⎝⎛- （2）2)2()2(3---⨯（3）－65×4－（－2.5）÷（－0.1）（4）⎪⎭⎫⎝⎛++-÷51312160（5）942)1(2125.0-⨯⎪⎭⎫⎝⎛-÷- （6）)3()4()2(8102-⨯---÷+-4．某公路检修组乘汽车沿公路检修，约定前进为正，后退为负。

人教版七年级数学下册第第六章实数第4课-实数(1)——无理数、有理数

17. 填空： (1)小于的 10 非负整数有________0_，__1_，__2_，__3___________； (2)在数轴上离原点的距离是的 5 点表示的数是__5_或__-__5_； (3)比较大小：22 ____>____π； (4)请你写出一7个大于0而小于2的无理数：____2____.
10. 无限不循环小数叫做__无__理__数__.
11. (2020期末)在0.25，π ，7，1 中，无理数有(
2 12
B
)
A.1个
B．2个
C．3个
D．4个
12. 如图，在数轴上标有字母的各点中，与实数 5 对应的点可能是( C )
A.A
B．B
C．C
D．D
13. 下列说法正确的是( C ) A.无限小数都是无理数 B.带根号的数都是无理数 C.无理数都是无限小数 D.不循环的小数都是无理数
负有理数负无理数
6. (例3)下列说法正确的是( D ) A.正整数和负整数统称整数 B.正数、0、负数统称有理数 C.开方开不尽的数和π统称无理数 D.有理数、无理数统称为实数
7. 下列说法错误的是( D ) A.有理数和无理数统称实数 B.实数包括正实数、0、负实数 C.整数和分数统称有理数 D.无理数包括正无理数、0、负无理数
14. 与数轴上的点一一对应的数是( D )
A.整数
B．有理数
C.无理数
D．实数
15. 有四个实数：3，－ 2 ，π， 5 ，其中最大的是( C )
A.3
B．－ 2
C．π
D. 5
16. 把下列各数分类：
π，－3.14，0，0.101 001…， 9,- 3 8,22 .

初中数学鲁教版(五四制)七年级上册第四章实数2 平方根-章节测试习题

章节测试题1.【答题】有下列说法：（1）无理数就是开方开不尽的数；（2）无理数是无限不循环小数；（3）无理数包括正无理数、零、负无理数；（4）无理数都可以用数轴上的点来表示．其中正确的说法的个数是（）A. 1B. 2C. 3D. 4【答案】B【分析】根据无理数的定义以及实数的分类即可作出判断．【解答】解：（1）π是无理数，而不是开方开不尽的数，则命题错误；（2）无理数就是无限不循环小数，则命题正确；（3）0是有理数，不是无理数，则命题错误；（4）正确；选B.2.【答题】已知是169的平方根，且，则的值是( )A. 11B. ±11C. ±15D. 65或【答案】D【分析】先解出x，然后代入到求出y.【解答】解：∵x是169的平方根，∴x=±13当x=13时，2×13+3y=169，解得：y=；当x=－13时，2×（－13）+3y=169，解得：y=65综上所述：y=65或．选D.3.【答题】若a是（-4）2的平方根，b的一个平方根是2，则代数式a＋b的值为( )A. 8B. 0C. 8或0D. 4或－4【答案】C【分析】先依据平方根的定义和性质求得a、b的值，然后依据有理数的加法法则求解即可．【解答】∵a是（-4）2的平方根，∴a=±4，∵b的一个平方根是2，∴b=4,∴a+b=8或0.选C.4.【答题】的平方根是( )A.B.C.D. ±【答案】D【分析】利用定义直接计算结果.【解答】解：∵（±）2=∴的平方根是±.选D.5.【答题】下列说法中不正确的是( )A.-是2的平方根B. 是2的平方根C. 2的平方根是D. 2的算术平方根是【答案】C【分析】根据定义直接计算.【解答】解： A. -是2的平方根，正确；B. 是2的平方根，正确；C. 2的平方根是±，故原选项不正确；D. 2的算术平方根是，正确.选C.6.【答题】的算术平方根是( )A.B.C.D. ±【答案】C【分析】根据定义直接计算.【解答】解：的算术平方根是．选C.7.【答题】若一个自然数的算术平方根是x，则下一个自然数的算术平方根是( )A. x+1B. x2+1C.D.【答案】D【分析】先求出这个数，然后根据算术平方根的定义再求出它的下一个自然数的算术平方根即可．【解答】一个自然数的算术平方根是x，则这个自然数是则它后面一个数的算术平方根是.选D.8.【答题】下列说法中错误的是( )A. 是0.25的一个平方根B. 正数a的两个平方根的和为0C. 的平方根是D. 当x≠0时，－x2没有平方根【答案】C【分析】根据各个选项中的说法可以判断是否正确，从而可以解答本题．【解答】A选项中，因为“”，所以A中说法正确；B选项中，因为“正数的两个平方根互为相反数，而互为相反数的两数和为0”，所以B中说法正确；C选项中，因为“的平方根是”，所以C中说法错误；D选项中，因为“当时，的值是负数，而负数没有平方根”，所以D中说法正确；选C.9.【答题】9的平方根是( )A. ±3B. ±C. 3D.【答案】A【分析】根据定义直接计算.【解答】∵，∴9的平方根是±3.选A.10.【答题】下列说法：①任何数都有算术平方根；②一个数的算术平方根一定是正数；③a2的算术平方根是a；④(π－4)2的算术平方根是π－4；⑤算术平方根不可能是负数．其中不正确的有( )A. 2个B. 3个C. 4个D. 5个【答案】C【分析】①②③④⑤分别根据平方根和算术平方根的概念即可判断．【解答】①因为“负数没有算术平方根”，所以①中说法错误；②因为“0的算术平方根是0，不是正数”，所以②中说法错误；③因为“的算术平方根是”，所以③中说法错误；④因为“的算术平方根是”，所以④中说法错误；⑤因为“算术平方根都是非负数”，所以⑤中说法正确.选C.方法总结：关于“一个数的算术平方根”需注意以下几点：（1）正数的算术平方根是正数，0的算术平方根是0，负数没有算术平方根；即只有非负数才有算术平方根，且算术平方根都是非负数；（2）.11.【答题】下列计算正确的是( )A. ＝±3B. |－3|＝－3C. ＝3D. －32＝9【答案】C【分析】原式各项利用算术平方根，绝对值的代数意义，以及有理数的乘方运算法则计算得到结果，即可做出判断．【解答】A选项中，因为，所以A中计算错误；B选项中，因为，所以B中计算错误；C选项中，因为，所以C中计算正确；D选项中，因为，所以D中计算错误；选C.12.【答题】2的算术平方根是( )A. ±B.C. －D. 2【答案】B【分析】由算术平方根的定义可直接得出结果. 【解答】2的算术平方根是.选B.13.【答题】的平方根是( )A. 4B. 2C.D. ±【答案】D【分析】根据平方根的定义直接得出结果.【解答】因为=2，2的平方根是±，选D.14.【答题】“的平方根是”，用数学式子可以表示为( )A.B.C.D.【答案】B【分析】根据一个正数的平方根有两个，且它们互为相反数可以得到答案．【解答】∵，∴的平方根是，即.选B.15.【答题】的平方根是( )A.B.C.D.【答案】D【分析】根据平方根的定义直接得出结果.【解答】∵，∴的平方根是.故选D.16.【答题】下列说法中不正确的是( )A. 是2的平方根B. 是2的算术平方根C. 2的平方根是D. 2的算术平方根是【答案】C【分析】根据珏根和算术平方根的定义可得结果.【解答】A. ∵=2，∴是2的平方根，故正确；B. ∵=2，∴是2的算术平方根，故正确；C. ∵=2，∴2的平方根是，故不正确；D∵=2，∴2的算术平方根是，故正确；选C.17.【答题】下列运算正确的是（）A.B.C.D.【答案】A【分析】A、B选项可根据绝对值定义即可判定； C、D选项依据算术平方根的定义即可判定．【解答】A. ∵，故正确；B. ∵，故不正确；C. ∵，故不正确；D. ∵，故不正确；选A.18.【答题】若a是的平方根，b的一个平方根是2，则代数式a＋b的值为( )A. 8B. 0C. 8或0D. 4或－4【答案】C【分析】先依据平方根的定义和性质求得a、b的值，然后依据有理数的加法法则求解即可．【解答】∵若a是的平方根，∴a=±4.∵b的一个平方根是2，∴b=4.∴a+b=4+4=8或a+b=-4+4=0.选C.方法总结：本题考查了平方根的意义，如果个一个数x的平方等于a，即x2=a,那么这个数x叫做a的平方根.正数a有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根.19.【答题】下列各式中，正确的个数是( )①；②；③的平方根是；④的算术平方根是；⑤是的平方根.A. 1个B. 2个C. 3个D. 4个【答案】A【分析】根据相关定义即可得出结果.【解答】①∵，故①不正确；②，故②不正确；③∵没有平方根，故③不正确；④∵的算术平方根是，故④不正确；⑤∵，∴是的平方根，故⑤正确.选A.20.【答题】若实数a满足,则=( )A. 2aB. 0C. －2aD. －a【答案】C【分析】根据|a|=-a，即可确定a的范围，再根据二次根式的性质即可化简．【解答】根据绝对值的性质，由|a|=-a，可知a≤0，然后根据二次根式的性质，可知=-a，即可知=|a-（-a）|=|2a|=-2a.选C.。