C语言实现树的遍历
数据结构c语言课设-二叉树排序

题目:二叉排序树的实现1 内容和要求1)编程实现二叉排序树,包括生成、插入,删除;2)对二叉排序树进展先根、中根、和后根非递归遍历;3)每次对树的修改操作和遍历操作的显示结果都需要在屏幕上用树的形状表示出来。
4)分别用二叉排序树和数组去存储一个班(50 人以上)的成员信息(至少包括学号、姓名、成绩3 项),比照查找效率,并说明在什么情况下二叉排序树效率高,为什么?2 解决方案和关键代码2.1 解决方案:先实现二叉排序树的生成、插入、删除,编写DisplayBST函数把遍历结果用树的形状表示出来。
前中后根遍历需要用到栈的数据构造,分模块编写栈与遍历代码。
要求比照二叉排序树和数组的查找效率,首先建立一个数组存储一个班的成员信息,分别用二叉树和数组查找,利用clock〔〕函数记录查找时间来比照查找效率。
2.2关键代码树的根本构造定义及根本函数typedef struct{KeyType key;} ElemType;typedef struct BiTNode//定义链表{ElemType data;struct BiTNode *lchild, *rchild;}BiTNode, *BiTree, *SElemType;//销毁树int DestroyBiTree(BiTree &T){if (T != NULL)free(T);return 0;}//清空树int ClearBiTree(BiTree &T){if (T != NULL){T->lchild = NULL;T->rchild = NULL;T = NULL;}return 0;}//查找关键字,指针p返回int SearchBST(BiTree T, KeyType key, BiTree f, BiTree &p) {if (!T){p = f;return FALSE;}else if EQ(key, T->data.key){p = T;return TRUE;}else if LT(key, T->data.key)return SearchBST(T->lchild, key, T, p);elsereturn SearchBST(T->rchild, key, T, p);}二叉树的生成、插入,删除生成void CreateBST(BiTree &BT, BiTree p){int i;ElemType k;printf("请输入元素值以创立排序二叉树:\n");scanf_s("%d", &k.key);for (i = 0; k.key != NULL; i++){//判断是否重复if (!SearchBST(BT, k.key, NULL, p)){InsertBST(BT, k);scanf_s("%d", &k.key);}else{printf("输入数据重复!\n");return;}}}插入int InsertBST(BiTree &T, ElemType e){BiTree s, p;if (!SearchBST(T, e.key, NULL, p)){s = (BiTree)malloc(sizeof(BiTNode));s->data = e;s->lchild = s->rchild = NULL;if (!p)T = s;else if LT(e.key, p->data.key)p->lchild = s;elsep->rchild = s;return TRUE;}else return FALSE;}删除//某个节点元素的删除int DeleteEle(BiTree &p){BiTree q, s;if (!p->rchild) //右子树为空{q = p;p = p->lchild;free(q);}else if (!p->lchild) //左子树为空{q = p;p = p->rchild;free(q);}else{q = p;s = p->lchild;while (s->rchild){q = s;s = s->rchild;}p->data = s->data;if (q != p)q->rchild = s->lchild;elseq->lchild = s->lchild;delete s;}return TRUE;}//整棵树的删除int DeleteBST(BiTree &T, KeyType key) //实现二叉排序树的删除操作{if (!T){return FALSE;}else{if (EQ(key, T->data.key)) //是否相等return DeleteEle(T);else if (LT(key, T->data.key)) //是否小于return DeleteBST(T->lchild, key);elsereturn DeleteBST(T->rchild, key);}return 0;}二叉树的前中后根遍历栈的定义typedef struct{SElemType *base;SElemType *top;int stacksize;}SqStack;int InitStack(SqStack &S) //构造空栈{S.base = (SElemType*)malloc(STACK_INIT_SIZE *sizeof(SElemType));if (!S.base) exit(OVERFLOW);S.top = S.base;S.stacksize = STACK_INIT_SIZE;return OK;}//InitStackint Push(SqStack &S, SElemType e) //插入元素e为新栈顶{if (S.top - S.base >= S.stacksize){S.base = (SElemType*)realloc(S.base, (S.stacksize + STACKINCREMENT)*sizeof(SElemType));if (!S.base) exit(OVERFLOW);S.top = S.base + S.stacksize;S.stacksize += STACKINCREMENT;}*S.top++ = e;return OK;}//Pushint Pop(SqStack &S, SElemType &e) //删除栈顶,应用e返回其值{if (S.top == S.base) return ERROR;e = *--S.top;return OK;}//Popint StackEmpty(SqStack S) //判断是否为空栈{if (S.base == S.top) return TRUE;return FALSE;}先根遍历int PreOrderTraverse(BiTree T, int(*Visit)(ElemType e)) {SqStack S;BiTree p;InitStack(S);p = T;while (p || !StackEmpty(S)){if (p){Push(S, p);if (!Visit(p->data)) return ERROR;p = p->lchild;}else{Pop(S, p);p = p->rchild;}}return OK;}中根遍历int InOrderTraverse(BiTree T, int(*Visit)(ElemType e)) {SqStack S;BiTree p;InitStack(S);p = T;while (p || !StackEmpty(S)){if (p){Push(S, p);p = p->lchild;}else{Pop(S, p);if (!Visit(p->data)) return ERROR;p = p->rchild;}}return OK;}后根遍历int PostOrderTraverse(BiTree T, int(*Visit)(ElemType e)) {SqStack S, SS;BiTree p;InitStack(S);InitStack(SS);p = T;while (p || !StackEmpty(S)){if (p){Push(S, p);Push(SS, p);p = p->rchild;}else{if (!StackEmpty(S)){Pop(S, p);p = p->lchild;}}}while (!StackEmpty(SS)){Pop(SS, p);if (!Visit(p->data)) return ERROR;}return OK;}利用数组存储一个班学生信息ElemType a[] = { 51, "陈继真", 88,82, "黄景元", 89,53, "贾成", 88,44, "呼颜", 90,25, "鲁修德", 88,56, "须成", 88,47, "孙祥", 87, 38, "柏有患", 89, 9, " 革高", 89, 10, "考鬲", 87, 31, "李燧", 86, 12, "夏祥", 89, 53, "余惠", 84, 4, "鲁芝", 90, 75, "黄丙庆", 88, 16, "李应", 89, 87, "杨志", 86, 18, "李逵", 89, 9, "阮小五", 85, 20, "史进", 88, 21, "秦明", 88, 82, "杨雄", 89, 23, "刘唐", 85, 64, "武松", 88, 25, "李俊", 88, 86, "卢俊义", 88, 27, "华荣", 87, 28, "杨胜", 88, 29, "林冲", 89, 70, "李跃", 85, 31, "蓝虎", 90, 32, "宋禄", 84, 73, "鲁智深", 89, 34, "关斌", 90, 55, "龚成", 87, 36, "黄乌", 87, 57, "孔道灵", 87, 38, "张焕", 84, 59, "李信", 88, 30, "徐山", 83, 41, "秦祥", 85, 42, "葛公", 85, 23, "武衍公", 87, 94, "范斌", 83, 45, "黄乌", 60, 67, "叶景昌", 99, 7, "焦龙", 89, 78, "星姚烨", 85, 49, "孙吉", 90, 60, "陈梦庚", 95,};数组查询函数void ArraySearch(ElemType a[], int key, int length){int i;for (i = 0; i <= length; i++){if (key == a[i].key){cout << "学号:" << a[i].key << " 姓名:" << a[i].name << " 成绩:" << a[i].grade << endl;break;}}}二叉树查询函数上文二叉树根本函数中的SearchBST()即为二叉树查询函数。
一种二叉树非递归遍历算法的C语言实现

T e l : + 8 6 — 5 5 1 - 6 5 6 9 0 9 6 3 6 5 6 9 0 9 6 4
一
种 二 叉树 非 递 归 遍历 算 法 的 C语 言实 现
龚 佳 , 袁 赘 , 刘 远 军
( 邵阳学院 信息工程系 , 湖南 邵阳 4 2 2 0 0 4 )
摘要 : 针对二叉树 的链 式存储 结构 , 分析 了二叉树 的各种遍 历算法 , 探 讨 了递 归算 法的递推 消除问题 , 提 出了一种改进的 非递归遍 历算法并用C语言 予以实现。
收 稿 日期 : 2 0 1 3 — 1 1 — 1 5
me nt e d i n C l a ng ua ge . Ke y wo r ds :bi na y r t r e e ; t r a ve r s a l a l g or i t h m; non— — r e c u r s i ve ;C l a ng ua ge
GONG J i a , Y UA N Y u n , L I U Y u n - j t i n
( I n f o r ma t ip a r t me n t , S h a o y a n g Un i v e r s i t y , S h a o y a n g 4 2 2 0 0 4 , C h i n a )
一
个结点 至少 由3 个 域组成 , 即数据域 、 左子结点域和右子结点域 ( 如图1 所示 ) 。
图1
为了更好 的对树结构进行计算和处理 , 我们 可以加上一个 双亲结点域( 如 图2 所示 ) 。
!f l ! !
图2
L
_
! I ! 二 ! J
I D a t e
树的先序、中序、后序遍历及其代码、层序遍历

树的先序、中序、后序遍历及其代码、层序遍历树是一种常见的数据结构,它由节点和边组成,可以用于存储和表示层次关系。
树的遍历是指按照特定的规则,依次访问树中的每个节点,以达到查找、打印或其他操作的目的。
树的先序遍历是指先访问根节点,然后递归地先序遍历左子树,最后递归地先序遍历右子树。
这种遍历方式常常用于复制一颗树,或者打印一颗树的结构。
以下是先序遍历的代码实现:```def preOrderTraversal(root):if root is None:returnprint(root.val) # 访问根节点preOrderTraversal(root.left) # 先序遍历左子树preOrderTraversal(root.right) # 先序遍历右子树```树的中序遍历是指先递归地中序遍历左子树,然后访问根节点,最后递归地中序遍历右子树。
这种遍历方式常常用于对树进行排序操作。
以下是中序遍历的代码实现:```def inOrderTraversal(root):if root is None:returninOrderTraversal(root.left) # 中序遍历左子树print(root.val) # 访问根节点inOrderTraversal(root.right) # 中序遍历右子树```树的后序遍历是指先递归地后序遍历左子树和右子树,最后访问根节点。
这种遍历方式常常用于先处理子节点,再处理根节点的情况。
以下是后序遍历的代码实现:```def postOrderTraversal(root):if root is None:returnpostOrderTraversal(root.left) # 后序遍历左子树postOrderTraversal(root.right) # 后序遍历右子树print(root.val) # 访问根节点```除了先序、中序和后序遍历,树的层序遍历是指按照树的层次依次访问每个节点,常用于打印树的结构,或者按层计算树的宽度等。
c语言哈夫曼树的构造及编码

c语言哈夫曼树的构造及编码一、哈夫曼树概述哈夫曼树是一种特殊的二叉树,它的构建基于贪心算法。
它的主要应用是在数据压缩和编码中,可以将频率高的字符用较短的编码表示,从而减小数据存储和传输时所需的空间和时间。
二、哈夫曼树的构造1. 哈夫曼树的定义哈夫曼树是一棵带权路径长度最短的二叉树。
带权路径长度是指所有叶子节点到根节点之间路径长度与其权值乘积之和。
2. 构造步骤(1) 将待编码字符按照出现频率从小到大排序。
(2) 取出两个权值最小的节点作为左右子节点,构建一棵新的二叉树。
(3) 将新构建的二叉树加入到原来排序后队列中。
(4) 重复上述步骤,直到队列只剩下一个节点,该节点即为哈夫曼树的根节点。
3. C语言代码实现以下代码实现了一个简单版哈夫曼树构造函数:```ctypedef struct TreeNode {int weight; // 权重值struct TreeNode *leftChild; // 左子节点指针struct TreeNode *rightChild; // 右子节点指针} TreeNode;// 构造哈夫曼树函数TreeNode* createHuffmanTree(int* weights, int n) {// 根据权值数组构建节点队列,每个节点都是一棵单独的二叉树TreeNode** nodes = (TreeNode**)malloc(sizeof(TreeNode*) * n);for (int i = 0; i < n; i++) {nodes[i] = (TreeNode*)malloc(sizeof(TreeNode));nodes[i]->weight = weights[i];nodes[i]->leftChild = NULL;nodes[i]->rightChild = NULL;}// 构建哈夫曼树while (n > 1) {int minIndex1 = -1, minIndex2 = -1;for (int i = 0; i < n; i++) {if (nodes[i] != NULL) {if (minIndex1 == -1 || nodes[i]->weight < nodes[minIndex1]->weight) {minIndex2 = minIndex1;minIndex1 = i;} else if (minIndex2 == -1 || nodes[i]->weight < nodes[minIndex2]->weight) {minIndex2 = i;}}}TreeNode* newNode =(TreeNode*)malloc(sizeof(TreeNode));newNode->weight = nodes[minIndex1]->weight + nodes[minIndex2]->weight;newNode->leftChild = nodes[minIndex1];newNode->rightChild = nodes[minIndex2];// 将新构建的二叉树加入到原来排序后队列中nodes[minIndex1] = newNode;nodes[minIndex2] = NULL;n--;}return nodes[minIndex1];}```三、哈夫曼编码1. 哈夫曼编码的定义哈夫曼编码是一种前缀编码方式,它将每个字符的编码表示为二进制串。
c语言红黑树遍历序算法

c语言红黑树遍历序算法红黑树是一种自平衡的二叉查找树,它具有良好的平衡性能,能够保持在较低的高度范围内。
在C语言中,我们可以使用递归或者非递归的方式来实现红黑树的遍历。
下面我将分别介绍中序遍历、前序遍历和后序遍历的算法。
1. 中序遍历算法:中序遍历的顺序是先遍历左子树,然后访问根节点,最后遍历右子树。
在C语言中,我们可以使用递归实现中序遍历:c.void inOrderTraversal(struct Node root) {。
if (root != NULL) {。
inOrderTraversal(root->left);printf("%d ", root->data);inOrderTraversal(root->right);}。
}。
2. 前序遍历算法:前序遍历的顺序是先访问根节点,然后遍历左子树,最后遍历右子树。
同样可以使用递归实现前序遍历:c.void preOrderTraversal(struct Node root) {。
if (root != NULL) {。
printf("%d ", root->data);preOrderTraversal(root->left);preOrderTraversal(root->right);}。
}。
3. 后序遍历算法:后序遍历的顺序是先遍历左子树,然后遍历右子树,最后访问根节点。
同样可以使用递归实现后序遍历:c.void postOrderTraversal(struct Node root) {。
if (root != NULL) {。
postOrderTraversal(root->left);postOrderTraversal(root->right);printf("%d ", root->data);}。
}。
另外,以上是使用递归实现的遍历算法,也可以使用非递归的方式来实现,利用栈来辅助实现遍历。
二叉排序树c语言代码实现

if ((*n) != NULL) {
free (*n);
*n = NULL;
}
}
/* 查找结点 */
PNODE find_node (PNODE n, int value) {
in_order_traversal ( n->right);
}
}
int main() {
char buf[50],a[1000];
int i,n,option,s[80],p;
PNODE tree = NULL;/*树的第一个结点*/
PNODE node = NULL;
{
r = (PNODE)malloc(sizeof(NODE));
if(!r)
{
printf("内存分配失败!");
exit(0);
zjm3:fgets (buf, sizeof(buf), stdin);
sscanf (buf, "%i", &option);
printf ("\n\n");
if(option<0) {
printf ("输入错误,请重新输入该元素\n",n);
goto zjm3;}
if(find_node (tree, option))
{
(*n)->value = value;
(*n)->left = NULL;
(*n)->right = NULL;
}
}
c 遍历数组

C 语言数组遍历本文介绍 C 语言中数组遍历的方法,包括 for 循环、while 循环和数组指针等多种方式,并结合实际案例进行说明。
下面是本店铺为大家精心编写的3篇《C 语言数组遍历》,供大家借鉴与参考,希望对大家有所帮助。
《C 语言数组遍历》篇1在 C 语言中,数组是一种常用的数据结构,可以用来存储多个同类型的数据。
数组遍历是指按照一定的顺序依次访问数组中的每个元素,以便进行某些操作。
在 C 语言中,有多种方式可以实现数组遍历,下面介绍几种常用的方法。
一、for 循环遍历数组for 循环是 C 语言中最常用的循环语句之一,可以用来遍历数组。
使用 for 循环遍历数组时,需要使用数组的首地址作为循环变量,并在循环体内访问数组元素。
下面是一个使用 for 循环遍历数组的示例代码:```c#include <stdio.h>int main() {int arr[] = {1, 2, 3, 4, 5};int i;for (i = 0; i < 5; i++) {printf("%d ", arr[i]);}return 0;}```在这个例子中,我们首先定义了一个整型数组 arr,然后使用for 循环遍历数组。
循环变量 i 从 0 开始,每次循环访问数组元素 arr[i],并将其打印到控制台上。
最后,循环执行完毕,程序返回 0。
二、while 循环遍历数组while 循环是 C 语言中另一种常用的循环语句,也可以用来遍历数组。
使用 while 循环遍历数组时,需要使用数组的首地址作为循环变量,并在循环体内访问数组元素。
下面是一个使用 while 循环遍历数组的示例代码:```c#include <stdio.h>int main() {int arr[] = {1, 2, 3, 4, 5};int i;i = 0;while (i < 5) {printf("%d ", arr[i]);i++;}return 0;}```在这个例子中,我们同样定义了一个整型数组 arr,然后使用while 循环遍历数组。
数据结构-C语言-树和二叉树

练习
一棵完全二叉树有5000个结点,可以计算出其
叶结点的个数是( 2500)。
二叉树的性质和存储结构
性质4: 具有n个结点的完全二叉树的深度必为[log2n]+1
k-1层 k层
2k−1−1<n≤2k−1 或 2k−1≤n<2k n k−1≤log2n<k,因为k是整数
所以k = log2n + 1
遍历二叉树和线索二叉树
遍历定义
指按某条搜索路线遍访每个结点且不重复(又称周游)。
遍历用途
它是树结构插入、删除、修改、查找和排序运算的前提, 是二叉树一切运算的基础和核心。
遍历规则 D
先左后右
L
R
DLR LDR LRD DRL RDL RLD
遍历规则
A BC DE
先序遍历:A B D E C 中序遍历:D B E A C 后序遍历:D E B C A
练习 具有3个结点的二叉树可能有几种不同形态?普通树呢?
5种/2种
目 录 导 航 Contents
5.1 树和二叉树的定义 5.2 案例引入 5.3 树和二叉树的抽象数据类型定义 5.4 二叉树的性质和存储结构 5.5 遍历二叉树和线索二叉树 5.6 树和森林 5.7 哈夫曼树及其应用 5.8 案例分析与实现
(a + b *(c-d)-e/f)的二叉树
目 录 导 航 Contents
5.1 树和二叉树的定义 5.2 案例引入 5.3 树和二叉树的抽象数据类型定义 5.4 二叉树的性质和存储结构 5.5 遍历二叉树和线索二叉树 5.6 树和森林 5.7 哈夫曼树及其应用 5.8 案例分析与实现
二叉树的抽象数据类型定义
特殊形态的二叉树
只有最后一层叶子不满,且全部集中在左边
c语言二叉树的先序,中序,后序遍历
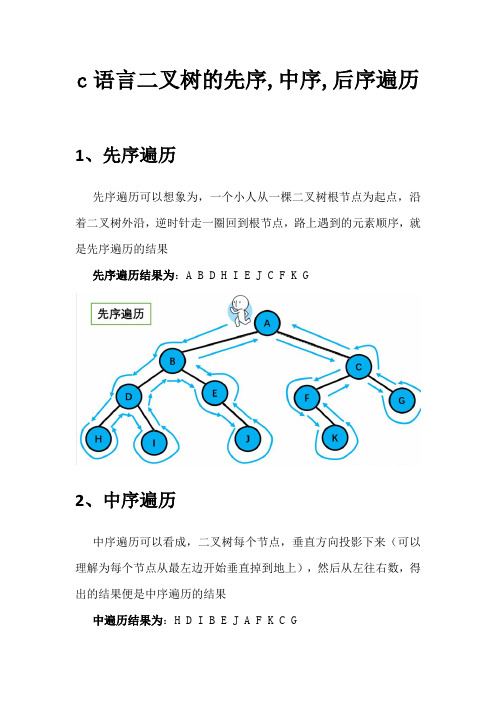
c语言二叉树的先序,中序,后序遍历1、先序遍历先序遍历可以想象为,一个小人从一棵二叉树根节点为起点,沿着二叉树外沿,逆时针走一圈回到根节点,路上遇到的元素顺序,就是先序遍历的结果先序遍历结果为:A B D H I E J C F K G2、中序遍历中序遍历可以看成,二叉树每个节点,垂直方向投影下来(可以理解为每个节点从最左边开始垂直掉到地上),然后从左往右数,得出的结果便是中序遍历的结果中遍历结果为:H D I B E J A F K C G3、后序遍历后序遍历就像是剪葡萄,我们要把一串葡萄剪成一颗一颗的。
还记得我上面提到先序遍历绕圈的路线么?(不记得翻上面理解)就是围着树的外围绕一圈,如果发现一剪刀就能剪下的葡萄(必须是一颗葡萄)(也就是葡萄要一个一个掉下来,不能一口气掉超过1个这样),就把它剪下来,组成的就是后序遍历了。
后序遍历中,根节点默认最后面后序遍历结果:H I D J E B K F G C A4、口诀先序遍历:先根再左再右中序遍历:先左再根再右后序遍历:先左再右再根这里的根,指的是每个分叉子树(左右子树的根节点)根节点,并不只是最开始头顶的根节点,需要灵活思考理解5、代码展示#include<stdio.h>#include<stdlib.h>typedef struct Tree{int data; // 存放数据域struct Tree *lchild; // 遍历左子树指针struct Tree *rchild; // 遍历右子树指针}Tree,*BitTree;BitTree CreateLink(){int data;int temp;BitTree T;scanf("%d",&data); // 输入数据temp=getchar(); // 吸收空格if(data == -1){ // 输入-1 代表此节点下子树不存数据,也就是不继续递归创建return NULL;}else{T = (BitTree)malloc(sizeof(Tree)); // 分配内存空间T->data = data; // 把当前输入的数据存入当前节点指针的数据域中printf("请输入%d的左子树: ",data);T->lchild = CreateLink(); // 开始递归创建左子树printf("请输入%d的右子树: ",data);T->rchild = CreateLink(); // 开始到上一级节点的右边递归创建左右子树return T; // 返回根节点}}// 先序遍历void ShowXianXu(BitTree T) // 先序遍历二叉树{if(T==NULL) //递归中遇到NULL,返回上一层节点{return;}printf("%d ",T->data);ShowXianXu(T->lchild); // 递归遍历左子树ShowXianXu(T->rchild); // 递归遍历右子树}// 中序遍历void ShowZhongXu(BitTree T) // 先序遍历二叉树{if(T==NULL) //递归中遇到NULL,返回上一层节点{return;}ShowZhongXu(T->lchild); // 递归遍历左子树printf("%d ",T->data);ShowZhongXu(T->rchild); // 递归遍历右子树}// 后序遍历void ShowHouXu(BitTree T) // 后序遍历二叉树{if(T==NULL) //递归中遇到NULL,返回上一层节点{return;}ShowHouXu(T->lchild); // 递归遍历左子树ShowHouXu(T->rchild); // 递归遍历右子树printf("%d ",T->data);}int main(){BitTree S;printf("请输入第一个节点的数据:\n");S = CreateLink(); // 接受创建二叉树完成的根节点printf("先序遍历结果: \n");ShowXianXu(S); // 先序遍历二叉树printf("\n中序遍历结果: \n");ShowZhongXu(S); // 中序遍历二叉树printf("\n后序遍历结果: \n");ShowHouXu(S); // 后序遍历二叉树return 0;}。
关于树的各种C语言代码

集合了树的各种算法,已经运行过,本人亲自所写,先序,后序,等全包括#include<stdio.h>#include<malloc.h>#define Max 100typedef int Status;typedef struct BiTNode{char data;struct BiTNode *lchild,*rchild;}BiTNode,*BiTree;int count;Status CreatBiTree(BiTree *bt) /*1.按先序遍历序列创造二叉树的二叉链表*/ {char ch;getchar();scanf("%c",&ch);if (ch == ' '){*bt = NULL;}else{*bt = (BiTree)malloc(sizeof(BiTNode));(*bt)->data = ch;printf("\n\t请输入%c结点的左孩子:",(*bt)->data);CreatBiTree(&((*bt)->lchild));printf("\n\t请输入%c结点的右孩子:",(*bt)->data);CreatBiTree(&((*bt)->rchild));}return 1;}void PreOrder(BiTree bt) /*2.先序遍历二叉树*/{if (bt != NULL){printf("%c\n",bt->data);PreOrder(bt->lchild);PreOrder(bt->rchild);}}void InOrder(BiTree bt) /*3.中序遍历二叉树*/{if (bt != NULL){InOrder(bt->lchild);printf("%c\n",bt->data);InOrder(bt->rchild);}}void PostOrder(BiTree bt) /*4.后序遍历二叉树*/{if (bt != NULL){PostOrder(bt->lchild);PostOrder(bt->rchild);printf("%c\n",bt->data);}}void PreOrderLeaf(BiTree bt) /*5.输出所有的叶子结点*/{if (bt != NULL){if ((bt->lchild == NULL) && (bt->rchild == NULL)){printf("%c\n",bt->data);}PreOrderLeaf(bt->lchild);PreOrderLeaf(bt->rchild);}}Status Leaf(BiTree bt) /*6.统计叶子结点数目,即度为零的结点数目*/ {if (bt == NULL){count = 0;}else if ((bt->lchild == NULL) && (bt->rchild == NULL)){count = 1;}else{count = Leaf(bt->lchild) + Leaf(bt->rchild);}return count;}void Degree1Node(BiTree bt) /*7.输出度为一的结点*/{if (bt != NULL){if (((bt->lchild != NULL) || (bt->rchild != NULL))&& (!((bt->lchild != NULL) && (bt->rchild != NULL)))) {printf("%c\n",bt->data);}Degree1Node(bt->lchild);Degree1Node(bt->rchild);}}void Degree2Node(BiTree bt) /*8.输出度为二的结点*/{if ( bt != NULL){if ((bt->lchild != NULL) && (bt->rchild != NULL)){printf("%c\n",bt->data);}Degree2Node(bt->lchild);Degree2Node(bt->rchild);}}Status CountNode(BiTree bt) /*9.统计二叉树中结点的总数*/{if (bt == NULL){return 0;}else{count++;CountNode(bt->lchild);CountNode(bt->rchild);return count;}}Status TreeDepth(BiTree bt) /*10.求二叉树的深度*/{int ldep, rdep;if (bt == NULL){return 0;}else{ldep = TreeDepth(bt->lchild);rdep = TreeDepth(bt->rchild);if (ldep > rdep){return (ldep +1);}else{return (rdep + 1);}}}void PrintTree(BiTree bt, int nlayer) /*11.按树状打印二叉树*/ {if (bt == NULL) /*如果是空则直接退出函数*/{return;}PrintTree(bt->rchild,nlayer + 1);for ( int i = 0; i < nlayer; i++){printf("----");}printf("%c\n",bt->data);PrintTree(bt->lchild,nlayer + 1);}void PreOrderTree(BiTree bt) /*12.非递归先序遍历*/BiTree Stack[Max];BiTree p = bt;int top = 0;while (p != NULL || top != 0){if (p != NULL){printf("%c",p->data);top++;Stack[top] = p;p = p->lchild;}else{p = Stack[top];top--;p = p->rchild;}}}void InOrderTree(BiTree bt) /*13.非递归中序遍历*/ {BiTree Stack[Max];BiTree p = bt;int top = 0;do{while (p != NULL){top++;Stack[top] = p;p = p->lchild;}if (top != 0){p = Stack[top];top--;printf("%c",p->data);p = p->rchild;}}while ((p != NULL) || (top != 0));void PostOrderTree(BiTree bt) /*14.非递归后序遍历*/ {BiTree p, q;int top = 0;BiTree Stack[Max];q = NULL;p = bt;while ((p != NULL) || (top != 0)){while (p != NULL){top++;Stack[top] = p;p = p->lchild;}if (top > 0){p = Stack[top];if ((p->rchild == NULL) || (p->rchild == q)){printf("%c",p->data);q = p;p = NULL;top--;}else{p = p->rchild;}}}}void LayerOrder(BiTree bt) /*15.层次遍历*/{int front,rear;BiTree Q[Max];front = 0;rear = front;BiTree r, s, p;r = s = p = bt;if (p == NULL) return;Q[rear] = p;rear++;while (front != rear){s = r = Q[front];printf("%c",Q[front]->data);front++;if (r->lchild){Q[rear] = r->lchild;rear++;}if (s->rchild){Q[rear] = s->rchild;rear++;}}}int main(){BiTree bt;int choice;int i,j,k;int nlayer = 1;printf("请用数字选择操作:\n");printf("1.按先序序列创建二叉树(二叉链表)\n");printf("2.递归先序遍历二叉树\n");printf("3.递归中序遍历二叉树\n");printf("4.递归后序遍历二叉树\n");printf("5.输出叶子结点(即度为零的结点)\n");printf("6.统计叶子结点数目\n");printf("7.输出度为一的结点\n");printf("8.输出度为二的结点\n");printf("9.统计二叉树中结点总数\n");printf("10.求二叉树的高度(即深度)\n");printf("11.按树状打印二叉树\n");printf("12.非递归先序遍历二叉树\n");printf("13.非递归中序遍历二叉树\n");printf("14.非递归后序遍历二叉树\n");printf("15.层次遍历二叉树\n");printf("0.则退出\n");while (1){printf("请输入你要执行的操作(0-15):");scanf("%d",&choice);if (choice == 0){break;}else switch (choice){case 1 : printf("\n请输入按先序建立二叉树的结点序列:");printf("\n说明:逐个输入,输入空格代表后继结点为空,按回车输入下一个结点。
《数据结构——C语言描述》第6章:树

先根遍历: -+a*b–cd/ef 中根遍历: a+b*c–d–e/f 后根遍历: abcd-*+ef/-
typedef struct Node { datatype data; struct Node *Lchild; struct Node *Rchild; } BTnode,*Btree;
满二叉树:一棵深度为k且有2k-1个结 点的二叉树称为满二叉树。 完全二叉树:深度为k,有n个结点的 二叉树当且仅当其每一个结点都与深度 为k的满二叉树中编号从1至n的结点一一 对应时,称为完全二叉树。
1 2 4 8 9 10 5 11 12 6 13 14 3 7 15 4 6 2
1 3 5 7
树的度:树中最大的结点的度数即为 树的度。图6.1中的树的度为3。 结点的层次(level):从根结点算起, 根为第一层,它的孩子为第二层……。 若某结点在第l层,则其孩子结点就在 第l+1层。图6.1中,结点A的层次为1, 结点M的层次为4。 树的高度(depth):树中结点的最大层 次数。图6.1中的树的高度为4。 森林(forest):m(m≥0)棵互不相交的 树的集合。
数据结构——用C语言描述(第3版)教学课件第6章 树与二叉树

6.2 二叉树 6.2.1 二叉树的定义与基本操作 6.2.2 二叉树的性质 6.2.3 二叉树的存储结构
6.2.1 二叉树的定义与基本操作 定义:我们把满足以下两个条件的树型结构叫做二 叉树(Binary Tree): (1)每个结点的度都不大于2; (2)每个结点的孩子结点次序不能任意颠倒。
有序树:在树T中,如果各子树Ti之间是有先后次序的,则称为有序树。 森林:m(m≥0)棵互不相交的树的集合。将一棵非空树的根结点删去,树就变成一 个森林;反之,给森林增加一个统一的根结点,森林就变成一棵树。
同构:对两棵树,通过对结点适当地重命名,就可以使两棵树完全相等(结点对应相 等,对应结点的相关关系也像等),则称这两棵树同构。
二叉树的基本结构由根结点、左子树和右子树组成
如图示
LChild Data RChild
Data
LChild RChild
用L、D、R分别表示遍历左子树、访问根结点、遍 历右子树,那么对二叉树的遍历顺序就可以有:
(1) 访问根,遍历左子树,遍历右子树(记做DLR)。 (2) 访问根,遍历右子树,遍历左子树(记做DRL)。 (3) 遍历左子树,访问根,遍历右子树(记做LDR)。 (4) 遍历左子树,遍历右子树,访问根 (记做LRD)。 (5) 遍历右子树,访问根,遍历左子树 (记做RDL)。 (6) 遍历右子树,遍历左子树,访问根 (记做RLD)。
(8) NextSibling(Tree,x): 树Tree存在,x是Tree中的某个结点。若x不 是其双亲的最后一个孩子结点,则返回x后面的下一个兄弟结点,否则 返回“空”。
基本操作:
(9) InsertChild(Tree,p,Child): 树Tree存在,p指向Tree 中某个结点,非空树Child与Tree不相交。将Child插入Tree中, 做p所指向结点的子树。
c语言经典算法题

c语言经典算法题
C语言经典算法题目涵盖了多个领域,包括排序、查找、递归、动态规划等。
以下是一些经典的C语言算法题目,它们对于提高编程能力和理解算法思想都是很有帮助的:
1. 冒泡排序:
实现冒泡排序算法,对一个数组进行升序或降序排序。
2. 快速排序:
实现快速排序算法,对一个数组进行升序或降序排序。
3. 选择排序:
实现选择排序算法,对一个数组进行升序或降序排序。
4. 二分查找:
实现二分查找算法,在有序数组中查找一个特定的元素。
5. 递归:
编写一个递归函数,计算斐波那契数列的第n 个数字。
6. 动态规划:
解决经典的动态规划问题,比如背包问题、最长公共子序列等。
7. 链表反转:
反转一个单链表或双链表。
8. 树的遍历:
实现二叉树的前序、中序和后序遍历。
9. 图的深度优先搜索(DFS)和广度优先搜索(BFS):
实现图的深度优先搜索和广度优先搜索算法。
10. 最短路径算法:
实现Dijkstra算法或Floyd-Warshall算法来求解图中的最短路径。
11. 素数判断:
编写一个函数判断一个给定的数是否是素数。
12. 最大公约数和最小公倍数:
实现求两个数的最大公约数和最小公倍数的算法。
这些题目旨在帮助你熟悉常见的算法思想和数据结构,提高编程和问题求解的能力。
解决这些题目时,不仅要注重正确性,还要考虑算法的效率和优化。
c++实现树(二叉树)的建立和遍历算法(一)(前序,中序,后序)

c++实现树(⼆叉树)的建⽴和遍历算法(⼀)(前序,中序,后序)最近学习树的概念,有关⼆叉树的实现算法记录下来。
不过学习之前要了解的预备知识:树的概念;⼆叉树的存储结构;⼆叉树的遍历⽅法。
⼆叉树的存储结构主要了解⼆叉链表结构,也就是⼀个数据域,两个指针域,(分别为指向左右孩⼦的指针),从下⾯程序1,⼆叉树的存储结构可以看出。
⼆叉树的遍历⽅法:主要有前序遍历,中序遍历,后序遍历,层序遍历。
(层序遍历下⼀篇再讲,本篇主要讲的递归法)下篇主要是,之后会有c++模板实现和。
如这样⼀个⼆叉树:它的前序遍历顺序为:ABDGHCEIF(规则是先是根结点,再前序遍历左⼦树,再前序遍历右⼦树)它的中序遍历顺序为:GDHBAEICF(规则是先中序遍历左⼦树,再是根结点,再是中序遍历右⼦树)它的后序遍历顺序为:GHDBIEFCA(规则是先后序遍历左⼦树,再是后序遍历右⼦树,再是根结点)如果不懂的话,可以参看有关数据结构的书籍。
1,⼆叉树的存储结构(⼆叉链表)//⼆叉树的⼆叉链表结构,也就是⼆叉树的存储结构,1个数据域,2个指针域(分别指向左右孩⼦)typedef struct BiTNode{ElemType data;struct BiTNode *lchild, *rchild;}BiTNode, *BiTree;2,⾸先要建⽴⼀个⼆叉树,建⽴⼆叉树必须要了解⼆叉树的遍历⽅法。
//⼆叉树的建⽴,按前序遍历的⽅式建⽴⼆叉树,当然也可以以中序或后序的⽅式建⽴⼆叉树void CreateBiTree(BiTree *T){ElemType ch;cin >> ch;if (ch == '#')*T = NULL; //保证是叶结点else{*T = (BiTree)malloc(sizeof(BiTNode));//if (!*T)//exit(OVERFLOW); //内存分配失败则退出。
中序遍历二叉树的递归算法c语言代码

中序遍历二叉树的递归算法c语言代码二叉树的中序遍历递归算法是左子树-> 根节点-> 右子树。
以下是C语言代码实现:```c#include <stdio.h>#include <stdlib.h>// 定义二叉树节点结构体struct TreeNode {int val;struct TreeNode *left;struct TreeNode *right;};// 定义二叉树中序遍历函数void inorderTraversal(struct TreeNode *root) {if (root == NULL) { // 如果根节点为空,直接返回return;}inorderTraversal(root->left); // 先遍历左子树printf("%d ", root->val); // 输出根节点值inorderTraversal(root->right); // 最后遍历右子树}int main() {// 创建一棵二叉树struct TreeNode *root = (struct TreeNode*)malloc(sizeof(struct TreeNode));struct TreeNode *node1 = (struct TreeNode*)malloc(sizeof(struct TreeNode));struct TreeNode *node2 = (struct TreeNode*)malloc(sizeof(struct TreeNode));struct TreeNode *node3 = (struct TreeNode*)malloc(sizeof(struct TreeNode));struct TreeNode *node4 = (struct TreeNode*)malloc(sizeof(struct TreeNode));struct TreeNode *node5 = (struct TreeNode*)malloc(sizeof(struct TreeNode));struct TreeNode *node6 = (struct TreeNode*)malloc(sizeof(struct TreeNode));struct TreeNode *node7 = (struct TreeNode*)malloc(sizeof(struct TreeNode));struct TreeNode *node8 = (struct TreeNode*)malloc(sizeof(struct TreeNode));struct TreeNode *node9 = (struct TreeNode*)malloc(sizeof(struct TreeNode));node1->val = 1;node1->left = node2;node1->right = node3;node2->val = 2;node2->left = NULL;node2->right = NULL;node3->val = 3;node3->left = node4;node3->right = node5;node4->val = 4;node4->left = NULL;node4->right = NULL;node5->val = 5;node5->left = NULL;node5->right = NULL;root->val = 0; // 设置根节点值为0,这样在遍历时会跳过根节点输出0,避免输出多个根节点值。
浅析一种二叉树非递归遍历算法的C语言实现论文.doc

浅析一种二叉树非递归遍历算法的C语言实现论文一种二叉树非递归遍历算法的C语言实现论文导读:本论文是一篇关于一种二叉树非递归遍历算法的C语言实现的优秀论文范文,对正在写有关于递归论文的写有一定的参考和指导作用,摘要:针对二叉树的链式存储结构,分析了二叉树的各种遍历算法,探讨了递归算法的递推消除理由,提出了一种改善的非递归遍历算法并用C语言予以实现。
关键词:二叉树;遍历算法;非递归;C语言实现1009-3044(2014)01-0223-031 概述树形结构是一种非常常见的数据结构,而二叉树又是其中最重要的一种树形结构。
二叉树的遍历是指按照一定的规则和次序将二叉树中的每一个结点都访问一次,既不能重复,也不能漏掉。
一般而言,对二叉树的遍历有前序遍历、中序遍历、后序遍历和按层遍历等几种方式。
在具体的算法设计上,以上遍历方式一般采取递归算法来实现,该文将探讨采用非递归算法来实现二叉树的遍历。
2 二叉树的数据结构描述二叉树作为一种非线性结构,每个结点最多有一个双亲结点和两个子结点。
二叉树可以采用顺序存储结构和链式存储结构。
对于完全二叉树而言,采用顺序存储是非常方便并且节省空间的,但是对于大部分的非完全二叉树而言,采用顺序存储将导致空间浪费严重且结构混乱、效率低下。
因此,更多的时候,大家都更愿意用链式存储结构来表示二叉树,这样结构更加清晰,尤其是对于一种二叉树非递归遍历算法的C语言实现由写论文的好帮手.zbjy.提供,.左右子树的描述和双亲节点的描述更加方便。
该文中拟采用链式结构来表示二叉树。
用链式存储结构来表示二叉树,一个结点至少由3个域组成,即数据域、左子结点域和右子结点域(如图1所示)。
3 二叉树的遍历及递归算法实现3.1 二叉树的遍历二叉树的遍历就是一个不漏的访问树中的每个结点,同时也不能重复。
所谓“访问”,就是指对结点的数据域进行某种操作,比如说读取、删除、更新、求该节点深度等等。
对于二叉树中的任意一个部分,都可以把它看作三部分,根节点、左子树、右子树,我们用D表示访问跟结点,用L表示遍历左子树,用R表示遍历右子树,则共有以下6种遍历方式[1]。
c语言中序非递归遍历求树的高度

C语言是一种广泛应用于系统程序设计和应用软件开发的高级编程语言。
在C语言中,常常需要对树进行遍历操作,以求取树的高度。
其中,序非递归遍历是一种常用的遍历方式。
本文将针对C语言中对树进行序非递归遍历求树的高度进行详细的讲解。
一、序非递归遍历1.序非递归遍历是一种在树的遍历过程中不使用递归的方式。
通过借助栈这一数据结构来完成遍历操作。
2.在序非递归遍历中,我们首先将树的根节点入栈,然后循环执行以下步骤:a.将栈顶节点弹出,并输出该节点的值;b.将该节点的右子节点入栈(如果存在的话);c.将该节点的左子节点入栈(如果存在的话)。
3.直到栈为空为止,遍历结束。
二、求树的高度1.树的高度是指树中从根节点到叶节点的最长路径的节点数。
求树的高度是树的常见操作之一。
2.在进行序非递归遍历的过程中,我们可以借助一个变量来记录树的高度。
具体做法如下:a.在栈中入栈的使用一个额外的变量记录当前节点的高度;b.每次遇到叶子节点时,将该节点的高度与之前记录的最大高度进行比较,并更新最大高度。
3.遍历结束后,最大高度即为树的高度。
三、C语言实现以下是C语言实现序非递归遍历求树高度的示例代码:```c#include <stdio.h>#include <stdlib.h>// 树的节点结构typedef struct Node {int data;struct Node* left;struct Node* right;} Node;// 栈的结构typedef struct Stack {Node* data[100]; // 假设栈的最大容量为100 int top;} Stack;// 初始化栈void init(Stack* s) {s->top = -1;}// 入栈void push(Stack* s, Node* node) {s->data[++(s->top)] = node;}// 出栈Node* pop(Stack* s) {return s->data[(s->top)--];}// 判断栈是否为空int isEmpty(Stack* s) {return s->top == -1;}// 求树高度int getHeight(Node* root) {Stack s;init(s);int maxHeight = 0;Node* curr = root;Node* prev = NULL;while (curr != NULL || !isEmpty(s)) { if (curr != NULL) {push(s, curr);if (s.top + 1 > maxHeight) { maxHeight = s.top + 1;}curr = curr->left;} else {curr = pop(s);curr = curr->right;}}return maxHeight;}// 主函数int m本人n() {// 构建一棵树(这里用简单的示例,实际情况中树的构建可能更加复杂)Node* root = (Node*)malloc(sizeof(Node));root->data = 1;root->left = (Node*)malloc(sizeof(Node));root->left->data = 2;root->left->left = NULL;root->left->right = NULL;root->right = (Node*)malloc(sizeof(Node));root->right->data = 3;root->right->left = NULL;root->right->right = NULL;printf("树的高度为:d\n", getHeight(root));return 0;}四、总结通过以上的讲解和示例代码,我们详细地介绍了C语言中如何利用序非递归遍历求树的高度。
基于C语言的遍历二叉树构造方法研究

的 问题 越 来 越 复杂 : 解 决 同 一 个 问 题 . 造 不 同 的 数 据 结 构 会 不 足 。 若 构 对 应 复 杂 程 度 不 同的 算 法 . 而设 计一 个 合 适 的 数 据 结 构 能 使 算 C + 言 仅 增 加 一 些 编 程 概 念 . 编 写 5 0 ~ 00 +语 在 0 0 1 0 0行 以下 法 的复 杂 程 度 大大 降 低 。 编程 人 员 在 实 践 中 体 会 到 : 好 一 种 高 的程 序 与 C语 言 相 比并 无 优 势 而 言 .反 而 不 如 C源 程 序 简 洁 。 学 级 语 言 仅 能 解 决三 成 所 遇 到 的 问题 .而 学 好 数 据 结 构 却 能 解 决 下 面 的 C源 程 序 Te 1 re . 按 现 行 通 用 指 针 函数 构 思 编 写 的建 c是 八 成 所 遇 到 的 问题 . 因此 . 软 件设 计 中 选 择 一 个 合 适 的数 据 结 立 与 中 序 遍 历 一 棵 二 叉 树 ; 输 人 为 一 串字 符 , 立 二 叉 树后 , 在 其 建 构 越 发 显 得 重要 经 过 中序 线 性 遍 历 搜 索 、 出为 按 字 典 大 小 顺 序 排 列 的 字 符 串 输 在 管 理 科 学 领 域 中 .很 多 问 题 都 可 以 转 化 为 树 Te re型 结 由 于这 不是 一 个 递 归 程 序 . 们在 静 态 阅读 和 比较 后 . 我 就会 感 觉 构 , 多叉 树又 都 可 以转 化 为 一 棵 等 价 的二 叉 树 B— re 而 iTe 。在 这 到不 如 本 文 第 3部 分 的递 归 函 数程 序 T e . 构 思清 晰 re c
上 面 提 到二 叉 树 是 递 归定 义 的 .如 同解 递 归 函数 的典 型 例 题 ” 诺 塔 ” 样 . 叉 树 的建 立 过 程 只有 使 用 递 归 算 法 才 能 达 汉 一 二 到 最 完 美 。 Psa语 言 中的 形 式 参 数 有 赋 值 和变 量 两 种 . 中 在 ac l 其 变 参传 递 的是 地 址 。 二叉 树 中根 指 针 的 内容 ( 根 地 址 1 空 二 而 即 从 叉 树 到 有一 个 根 结 点 的 二叉 树 是 变 化 的 .必 须 使 用 变量 参 数 传 递 地 址 功 能来 修 改 这个 根结 点 的 地 址 值 。在 P sa 语 言 中变 量 acl 参 数 可 以很 自然 地 编 写使 用 递 归 函数 建 立 二 叉 树 的 程 序 而 这 个 源 程 序 比较 简 洁 、 于 静 态 阅读 和 进 行 教 学 分 析 . 此 使 用 递 易 因 归 函数 建 立 与遍 历 二叉 树 是 数 据 结 构 中 的经 典 算 法 本 文 第 五 部 分 C语 言 源 程 序 Te. 通 过 经 典 的 P sa语 言 建 立 二 又 树 re c是 acl 源 程 序 清单 逐 句 翻 译 过来 .由 于可 以按 照 不 同 编 程 语 言 的 语 法 规 则 逐 句进 行 对 照 和参 考 .故 下 面 省 略 了 P s a 语 言 的 源 程 序 ac l
用C语言编写二叉树的建立与遍历

用C语言编写二叉树的建立与遍历1.对题目要有需求分析在需求分析中,将题目中要求的功能进行叙述分析,并且设计解决此问题的数据存储结构,设计或叙述解决此问题的算法。
给出实现功能的一组或多组测试数据,程序调试后,将按照此测试数据进行测试的结果列出来。
如果程序不能正常运行,写出实现此算法中遇到的问题和改进方法;2.对题目要有相应的源程序源程序要按照写程序的规则来编写。
要结构清晰,重点函数的重点变量,重点功能部分要加上清晰的程序注释。
(注释量占总代码的四分之一)程序能够运行,要有基本的容错功能。
尽量避免出现操作错误时出现死循环;3.最后提供的主程序可以象一个应用系统一样有主窗口,通过主菜单和分级菜单调用课程设计中要求完成的各个功能模块,调用后可以返回到主菜单,继续选择其他功能进行其他功能的选择。
二叉树的建立与遍历[问题描述]建立一棵二叉树,并对其进行遍历(先序、中序、后序),打印输出遍历结果。
[基本要求]从键盘接受输入,以二叉链表作为存储结构,建立二叉树,并对其进行遍历(先序、中序、后序),将遍历结果打印输出。
以下是我的数据结构实验的作业:肯定好用,里面还包括了统计树的深度和叶子数!记住每次做完一个遍历还要重新输入你的树哦!#include "stdio.h"#include "string.h"#define NULL 0typedef struct BiTNode{char data;struct BiTNode *lchild,*rchild;}BiTNode,*BiTree;BiTree Create(BiTree T){char ch;ch=getchar();if(ch=='#')T=NULL;else{if(!(T=(BiTNode *)malloc(sizeof(BiTNode))))printf("Error!");T->data=ch;T->lchild=Create(T->lchild);T->rchild=Create(T->rchild); }return T;}void Preorder(BiTree T){if(T){printf("%c",T->data); Preorder(T->lchild); Preorder(T->rchild);}}int Sumleaf(BiTree T){int sum=0,m,n;if(T){if((!T->lchild)&&(!T->rchild)) sum++;m=Sumleaf(T->lchild);sum+=m;n=Sumleaf(T->rchild);sum+=n;}return sum;}void zhongxu(BiTree T){if(T){zhongxu(T->lchild);printf("%c",T->data); zhongxu(T->rchild);}}void houxu(BiTree T){if(T){houxu(T->lchild);houxu(T->rchild);printf("%c",T->data);}}int Depth(BiTree T){int dep=0,depl,depr;if(!T) dep=0;else{depl=Depth(T->lchild);depr=Depth(T->rchild);dep=1+(depl>depr?depl:depr);}return dep;}main(){BiTree T;int sum,dep;T=Create(T);Preorder(T);printf("\n");zhongxu(T);printf("\n");houxu(T);printf("\n");sum=Sumleaf(T);printf("%d",sum);dep=Depth(T);printf("\n%d",dep);}在Turbo C的环境下,先按Ctrl+F9运行程序,此时就是建立二叉树的过程,例如输入序列ABC##DE#G##F###(其中的“#”表示空,并且输入过程中不要加回车,因为回车也有对应的ASCII码,是要算字符的,但是输入完之后可以按回车退出),然后再按ALT+F5显示用户界面,这时候就能够看到结果了。
二叉树二叉链表的层序遍历(C语言)

⼆叉树⼆叉链表的层序遍历(C语⾔)所谓⼆叉树层序遍历,即从⼆叉树根结点开始,按从上到下、从左到右的顺序访问每⼀个结点。
每个结点只访问⼀次。
#include <stdio.h>#include <stdlib.h>/*** ⼆叉树⼆叉链表之⾮递归遍历:层序遍历* 算法思想:借助⼀个队列;根树进队;队不为空时循环“从队列中出⼀个树p,访问该树根结点;* 若它有左⼦树,左⼦树进队;若它有右⼦树,右⼦树进队。
”* (保证了元素进队顺序是从树的上层到下层,且同层元素在队列中从左到右相邻)* (注:为了节约空间,这⾥的树进队,是指树的地址进队,⽽不是树结点进队,队列中存放的是对各树地址的引⽤)*/#define OK 1;#define TURE 1;#define FALSE 0;#define ERROR 0;const int OVERFLOW = -2;const int MAXSIZE = 100;typedef int Status;typedef char TElemType;//⼆叉链表结构定义typedef struct BiNode{TElemType data;struct BiNode *lchild, *rchild;} BiNode, *BiTree;//顺序循环队列定义typedef struct {BiTree *base; //存放树型指针int front; //头指针,若队列不为空,指向队列头元素int rear; //尾指针,若队列不为空,指向队列尾元素的下⼀个位置} SqQueue;//由字符序列创建⼆叉树Status CreateBiTree(BiTree *tree,TElemType data[],int *j,int len){if((*j)<=len-1){if(data[(*j)]=='#'){(*tree)=NULL;(*j)++;} else {(*tree)=(BiTree)malloc(sizeof(BiNode));if(!(*tree)) return OVERFLOW;(*tree)->data=data[(*j)]; //⽣成根结点(*j)++;CreateBiTree(&((*tree)->lchild),data,j,len); //构造左⼦树CreateBiTree(&((*tree)->rchild),data,j,len); //构造右⼦树}}return OK;}//访问⼆叉树结点Status Visit(BiTree tree){printf("%c",tree->data);return OK;}//借助队列实现⼆叉链表的层序遍历Status LevelOrder_ByQueue(BiTree tree) {BiTree p;SqQueue queue1;InitQueue(&queue1);EnQueue(&queue1,tree); //根结点⼊队while(queue1.front!=queue1.rear){ //队不为空DeQueue(&queue1,&p); //根节点出队Visit(p);if(p->lchild!=NULL) EnQueue(&queue1,p->lchild); //有左孩⼦就进队if(p->rchild!=NULL) EnQueue(&queue1,p->rchild); //有右孩⼦也进队}return OK;}/***⽤到队列的相关函数***///循环队列初始化Status InitQueue(SqQueue *queue) {queue->base=(BiTree*)malloc(sizeof(BiTree)*MAXSIZE); //分配队列数组空间if(!queue->base) return OVERFLOW; //分配失败queue->front=0;queue->rear=0;return OK;}//循环队列⼊队操作Status EnQueue(SqQueue *queue,BiTree elem){if((queue->rear+1)%MAXSIZE==queue->front){ //队满return ERROR;} else {queue->base[queue->rear]=elem;queue->rear=(queue->rear+1)%MAXSIZE;return OK;}}//循环队列出队操作Status DeQueue(SqQueue *queue,BiTree *elem){if(queue->front==queue->rear){ //队空return ERROR;} else {(*elem)=queue->base[queue->front];queue->front=(queue->front+1)%MAXSIZE;return OK;}}int main(void){//⽰例⼆叉树的结构/*A/B/ \C D/ \E F\G*///指向⼆叉树的指针BiTree bitree1;//创建⼆叉树待⽤数据TElemType data1[]={'A','B','C','#','#','D','E','#','G','#','#','F','#','#','#',}; //先序遍历序列int len1=sizeof(data1)/sizeof(data1[0]);int* j1=(int*)malloc(sizeof(int));*j1=0;//按先序遍历序列创建⼆叉树Status createBiTreeResult = CreateBiTree(&bitree1,data1,j1,len1);printf("⼆叉树创建结果:%d\n",createBiTreeResult);//层序遍历⼆叉树Status levelOrder_ByQueue = LevelOrder_ByQueue(bitree1); //注:这⾥参数是⼆叉树根结点,⽽不是指针 printf("\n层序遍历⼆叉树结果:%d\n",levelOrder_ByQueue);printf("\nEND");return0;}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
int i = 0; /* 用i扫描数组a中存储的二叉树广义表字符串,初值为0 */
*bt = NULL; /* 把树根指针置为空,即从空树开始建立二叉树 */
/* 每循环一次处理一个字符,直到扫描到字符串结束符为止 */
}
return;
}
/* 9.中序遍历 */
void inOrder(struct BTreeNode *bt)
{
if(bt != NULL){
inOrder(bt->left); /* 中序遍历左子树 */
printf("%c ", bt->data); /* 访问根结点 */
printf("n");
printf("前序:"); /* 前序遍历 */
preOrder(bt);
printf("n");
printf("中序:"); /* 中序遍历 */
inOrder(bt);
printf("n");
printf("后序:"); /* 后序遍历 */
elemType *findBTree(struct BTreeNode *bt, elemType x)
{
if(bt == NULL){
return NULL;
}else{
if(bt->data == x){
return &(bt->data);
}else{ /* 分别向左右子树递归查找 */
printf("(");
printBTree(bt->left);
if(bt->right != NULL){
printf(",");
}
printBTree(bt->right);
printf(")");
}
}
return;
}
/* 7.清除二叉树,使之变为一棵空树 */
i++; /* 为扫描下一个字符修改i值 */
}
return;
}
/* 3.检查二叉树是否为空,为空则返回1,否则返回0 */
int emptyBTree(struct BTreeNode *bt)
{
if(bt == NULL){
return 1;
}else{
return 0;
}
*/
struct BTreeNode *q[QUEUE_MAX_SIZE];
int front = 0, rear = 0;
/* 将树根指针进队 */
if(bt != NULL){
rear = (rear + 1) % QUEUE_MAX_SIZE;
q[rear] = bt;
}
void clearBTree(struct BTreeNode* *bt)
{
if(*bt != NULL){
clearBTree(&((*bt)->left));
clearBTree(&((*bt)->right));
free(*bt);
*bt = NULL;
}
return;
}
/* 8.前序遍历 */
void preOrder(struct BTreeNode *bt)
{
if(bt != NULL){
printf("%c ", bt->data); /* 访问根结点 */
preOrder(bt->left); /* 前序遍历左子树 */
preOrder(bt->right); /* 前序遍历右子树 */
while(front != rear){ /* 队列非空 */
front = (front + 1) % QUEUE_MAX_SIZE; /* 使队首指针指向队首元素 */
p = q[front];
printf("%c ", p->data);
/* 若结点存在左孩子,则左孩子结点指针进队 */
q[rear] = p->right;
}
}
return;
}
/************************************************************************/
/*
int main(int argc, char *argv[])
inOrder(bt->right); /* 中序遍历右子树 */
}
return;
}
/* 10.后序遍历 */
void postOrder(struct BTreeNode *bt)
{
if(bt != NULL){
postOrder(bt->left); /* 后序遍历左子树 */
postOrder(bt->right); /* 后序遍历右子树 */
printf("%c ", bt->data); /* 访问根结点 */
}
return;
}
/* 11.按层遍历 */
void levelOrder(struct BTreeNode *bt)
{
struct BTreeNode *p;
s[top] = p;
k = 1;
break;
case ')':
if(top == -1){
printf("二叉树广义表字符串错误!n");
exit(1);
}
top--;
break;
case ',':
k = 2;
break;
default:
p = malloc(sizeof(struct BTreeNode));
{
struct BTreeNode *b *b; /* 用于存入二叉树广义表的字符串 */
elemType x, *px;
initBTree(&bt);
printf("输入二叉树广义表的字符串:n");
/* scanf("%s", b); */
void createBTree(struct BTreeNode* *bt, char *a)
{
struct BTreeNode *p;
struct BTreeNode *s[STACK_MAX_SIZE];/* 定义s数组为存储根结点指针的栈使用 */
int top = -1; /* 定义top作为s栈的栈顶指针,初值为-1,表示空栈 */
#include <stdio.h>
#include <stdlib.h>
#define STACK_MAX_SIZE 30
#define QUEUE_MAX_SIZE 30
#ifndef elemType
typedef char elemType;
#endif
/************************************************************************/
void printBTree(struct BTreeNode *bt)
{
/* 树为空时结束递归,否则执行如下操作 */
if(bt != NULL){
printf("%c", bt->data); /* 输出根结点的值 */
if(bt->left != NULL || bt->right != NULL){
int dep2 = BTreeDepth(bt->right); /* 计算右子树的深度 */
if(dep1 > dep2){
return dep1 + 1;
}else{
return dep2 + 1;
}
}
}
/* 5.从二叉树中查找值为x的结点,若存在则返回元素存储位置,否则返回空值 */
elemType *p;
if(p = findBTree(bt->left, x)){
return p;
}
if(p = findBTree(bt->right, x)){
return p;
}
return NULL;
}
}
}
/* 6.输出二叉树(前序遍历) */
struct BTreeNode *right;
};
/* 1.初始化二叉树 */
void initBTree(struct BTreeNode* *bt)
{
*bt = NULL;
return;
}
/* 2.建立二叉树(根据a所指向的二叉树广义表字符串建立) */
b = "a(b(c), d(e(f, g), h(, i)))";
createBTree(&bt, b);
if(bt != NULL)
printf(" %c ", bt->data);
